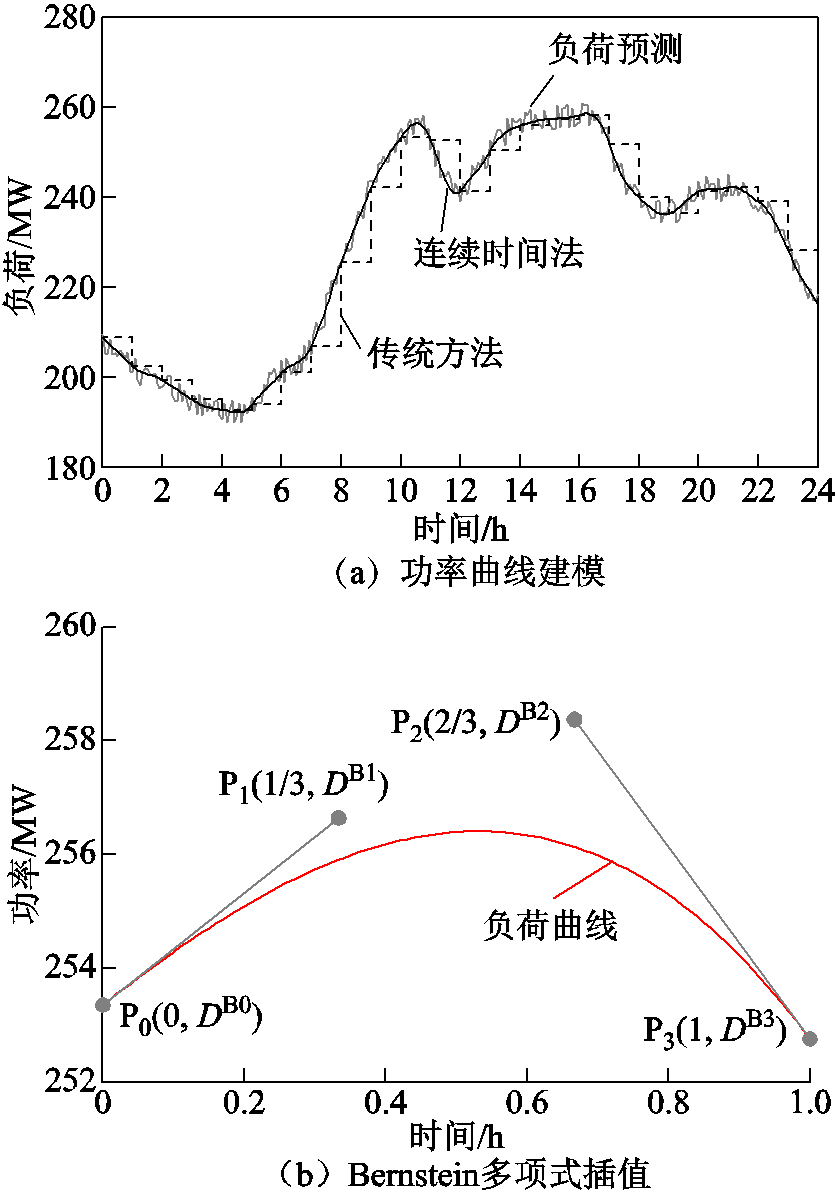
图1 连续时间建模方法
Fig.1 Continuous-time modeling
摘要 随着风电在电力系统中渗透率的提高,调度时段内的风电出力波动越发剧烈,可能导致时段内爬坡不足,威胁电力系统在时段内的运行安全。针对这一问题,提出计及超分辨率风电出力不确定性的连续时间鲁棒机组组合模型和求解算法,该方法充分考虑时段内风电出力变化,给出对超分辨率风电出力不确定性鲁棒的调度方案。首先,基于连续时间建模方法,建立连续时间鲁棒经济调度模型,并对其中的超分辨率不确定性模型进行分析;然后,通过解空间变换,将代数空间的优化问题转换为易求解的函数空间优化问题,并通过列和约束生成算法进行求解,计算结果还原到代数空间;最后,通过算例结果验证了所提方法能够充分计及超分辨率风电出力的不确定性,提高调度方案的鲁棒性。
关键词:风电出力不确定性 经济调度 鲁棒优化 连续时间建模 超分辨率
为实现低碳、高效、可持续的能源发展战略,风电等可再生能源发电在电力系统中的占比逐年上升[1]。国家能源局数据显示,截至2019年底,全国新增风电并网装机2 574万kW,累计风电装机2.1亿kW·h,约占全部发电装机的10.4%;2019年风电发电量4 057亿kW·h,约占全部发电量的5.5%[2]。但是,风电渗透率的提高也给电力系统运行带来了一系列挑战[3-4]。其中,如何应对风电出力的随机性和波动性,保证系统运行安全,引起了广泛研究。
风电出力不确定性的建模是上述研究的重点之一。文献[5]利用截断通用分布的混合形式对风电出力概率进行建模,提出基于多风电场总功率条件分布的经济调度模型,更加精确地考虑风电出力不确定性,进而降低系统运行成本。文献[6]采用鲁棒优化方法处理风电出力不确定性,提出风电、火电和电动汽车协调的鲁棒双层随机优化模型,兼顾鲁棒性和经济性。文献[7]采用极限场景法处理运行优化问题中的随机变量,提出基于极限场景的配网无功优化模型,避免抽样导致的海量场景,同时也能保证系统运行的安全性。文献[8]将极限场景法拓展应用到交直流混联系统的日前调度中,充分利用风电出力的时空相关性,在保证鲁棒性的同时提高经济性。文献[9]基于Kullback-Leibler散度建立风电出力的分布函数集合,提出基于分布鲁棒优化的综合能源系统经济调度问题,在鲁棒性和经济性上进行平衡。以上方法针对风电出力的不确定性,采用不同方式进行建模,能够较好地适应风电出力在时段间的随机变化。
然而,随着风电渗透率的持续上升,其时段内出力波动越发剧烈,可能导致时段内爬坡不足,威胁电力系统运行安全。文献[10]分析了风电波动对系统的影响,结果表明,考虑次小时级风电波动后,对系统的爬坡需求有显著提升。已有部分研究探讨了时段内出力变化对系统的影响。文献[11]分析了时段长度选取对电力系统随机机组组合的影响,对比了调度时段取60min、30min、20min、10min时的调度结果,发现次小时级的调度不仅可以降低期望运行费用,而且可以使结果更加精确。文献[12]提出一种基于滚动优化的多时间尺度随机调度方法,将最近2h内调度时段长度进一步细化,分别取15min与30min。文献[13]提出一种基于表达谱的时间粒度自适应调度方法,引入粒计算理论,将相似的负荷、风电时序信息粒合并,更好地适应净负荷变化。文献[14]提出一种调度时段自适应的机组组合模型,根据负荷曲线、风电出力曲线特点,采用聚类方法将整个调度周期划分为长度不均匀的若干调度时段,在不增加计算负担的同时,更加充分地利用系统灵活性,增加风电消纳。文献[15]提出一种考虑双时间尺度调度周期的储能容量配置方法,同时考虑了小时级调度约束与小时内功率调整约束,以满足小时级能量需求和小时内爬坡需求。尽管上述文献对调度时段的划分进行灵活调整,但在其调度分辨率下,时段内部的变化仍然无法体现。文献[16]对时段内风电爬坡事件进行研究,综合风电爬坡速度与爬坡时间建立爬坡事件约束,能够保证风电波动速率较大时系统的安全性,但该方法依赖风电爬坡事件的精确预测。文献[17]基于次小时级功率响应速率需求和响应时间建立次小时尺度灵活性约束,提出一种考虑次小时灵活性的调度方法,兼顾日前调度和实时运行,提升次小时尺度运行灵活性,但其考虑的次小时变化较为单一,对时段内出力变化的描述不够灵活。
为了准确描述时段内出力变化,文献[18]提出一种基于连续时间建模的机组组合模型,在连续时域上建立电力系统运行优化模型。文献[18]中,通过Bernstein多项式插值将负荷或风电功率变化拟合为在时间上连续的光滑曲线,相应的机组出力也建模为时变函数,从而整个机组组合问题建模为一个类最优控制问题,并基于Bernstein多项式插值的性质将其转换为传统优化问题以便求解。连续时间建模方法直接对时段内的功率变化进行建模,因此在应对时段内功率波动方面具有较大的应用潜力。文献[19]基于连续时间建模方法,提出了连续时间定价方法,更加精确地安排机组和储能爬坡,充分利用系统灵活性。文献[20]提出一种连续时间的气电联合系统协调运行方法,采用信息间隙决策理论对风电出力进行建模,综合利用需求响应和天然气网络调节能力来应对次小时级风电出力波动。文献[21]考虑风电出力的不确定性,采用二阶矩匹配法生成风电出力随机场景,提出基于多保真度连续时间建模的随机调度方法。但是上述方法无法全面考虑风电出力在时段内变化的不确定性,故无法保证调度方案的鲁棒性。
针对以上问题,本文提出了计及超分辨率风电出力不确定性的连续时间鲁棒机组组合模型和求解算法。所提方法可充分考虑时段内风电出力变化,给出对超分辨率风电出力不确定性鲁棒的调度方案。首先,基于连续时间建模方法,建立计及超分辨率不确定性的连续时间鲁棒机组组合模型,并对超分辨率不确定性模型进行分析;其次,为高效求解上述优化问题,提出一种基于解空间变换的求解方法,并采用列和约束生成(Column-and-Constraint Generation, C&CG)算法进行计算;最后,通过算例分析验证所提方法在应对超分辨率风电出力不确定性方面的有效性。
首先介绍基于Bernstein多项式插值的连续时间建模方法,并分析其重要数学性质。
根据文献[22],预测负荷曲线由一系列负荷预测点构成,如图1a中灰色实线所示为华东地区某日预测负荷曲线。在传统调度方法中,调度周期被划分为24或96个时段,并假定每个时段都对应于某个功率值,功率曲线建模为图1a中的阶梯曲线。可以看到,阶梯曲线对预测负荷曲线的拟合程度较低,未充分利用预测信息且不能体现时段内的功率变化。文献[18]采用连续时间光滑曲线来拟合预测负荷曲线,如图1a中黑色实线所示,可以计及超出传统调度方法分辨率的时段内功率变化。

图1 连续时间建模方法
Fig.1 Continuous-time modeling
考虑到模型后续求解问题,连续时间建模方法中采用三次Bernstein多项式插值来拟合各时段中的预测负荷曲线,图1b为图1a中第11时段的插值曲线。Bernstein多项式如式(1)所示,拟合的负荷曲线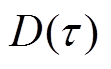 可表示为
可表示为
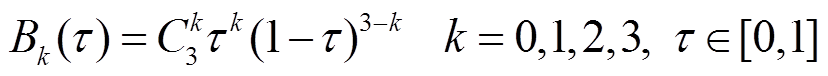 (1)
(1)
式中,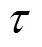 为时间,h;
为时间,h;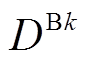 为插值系数,取决于预测负荷曲线,MW;
为插值系数,取决于预测负荷曲线,MW;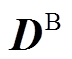 与
与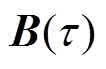 为相应的向量。结合式(1)和式(2),可得
为相应的向量。结合式(1)和式(2),可得
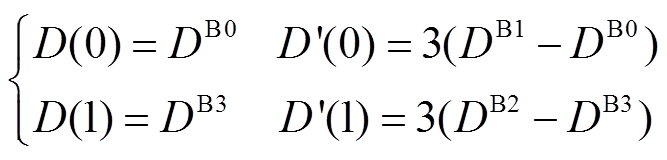 (3)
(3)式中, 为
为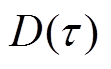 的导数,MW/h。D(0)与
的导数,MW/h。D(0)与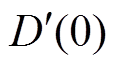 分别为负荷曲线在时段初的大小和斜率;D(1)与
分别为负荷曲线在时段初的大小和斜率;D(1)与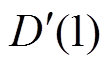 分别为负荷曲线在时段末的大小和斜率。根据式(3)可进一步解得
分别为负荷曲线在时段末的大小和斜率。根据式(3)可进一步解得
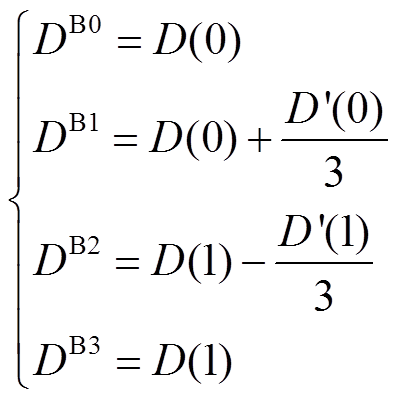 (4)
(4)根据式(4),可由预测负荷曲线在该时段首末两端的大小和斜率计算出插值系数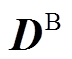 ,从而得到拟合曲线。
,从而得到拟合曲线。
基于Bernstein多项式插值的连续时间建模方法中,有以下几项重要的数学性质。
1)积分项变换,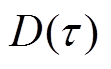 积分后与时间
积分后与时间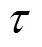 无关。
无关。
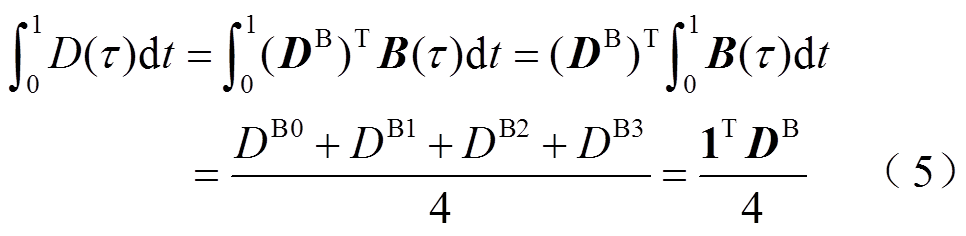
2)导数项变换,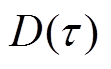 的导数为降一阶后的Bernstein多项式插值曲线。
的导数为降一阶后的Bernstein多项式插值曲线。
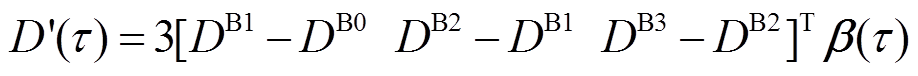 (6)
(6)式中, 为二次Bernstein多项式;
为二次Bernstein多项式;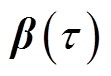 为向量。
为向量。
3)等式方程变换。根据待定系数法,可得
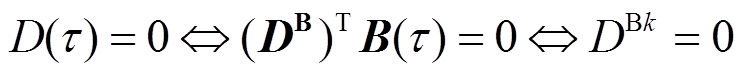 (7)
(7)即若插值曲线恒等于0,则其插值系数也都必为0。
4)不等式方程变换[18]。根据Bernstein插值曲线的凸包性质,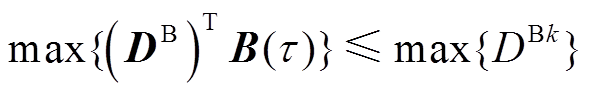 ,可得
,可得
 (8)
(8)即若要使插值曲线恒小于0,可使插值系数小于0。
基于连续时间建模方法,建立计及超分辨率不确定性的鲁棒机组组合模型,并对超分辨率不确定性模型进行分析。
结合文献[23]中所提出的传统机组组合模型,建立基于连续时间建模的机组组合模型。目标函数为
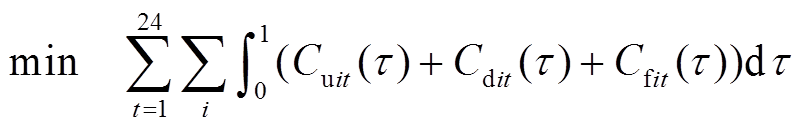 (9)
(9)式中,t为时段编号;i为节点编号;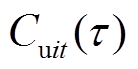 、
、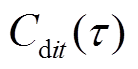 、
、 分别为节点i处机组在第t时段的
分别为节点i处机组在第t时段的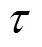 时刻的开机成本、停机成本与燃料成本,即
时刻的开机成本、停机成本与燃料成本,即
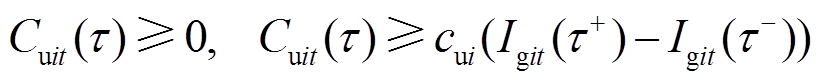 (10)
(10)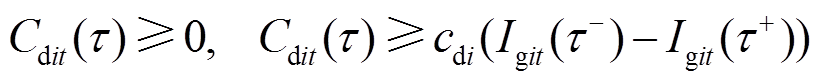 (11)
(11)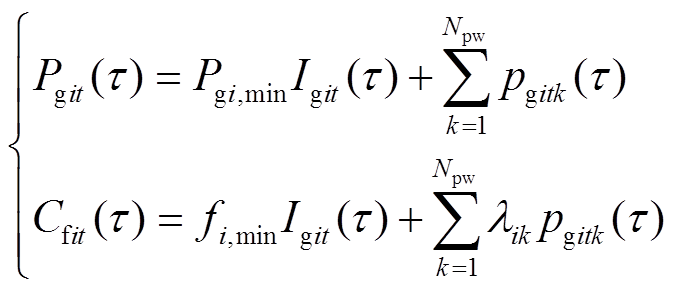 (12)
(12)式中, 、
、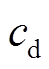 为每次开机或关机的成本,$;
为每次开机或关机的成本,$;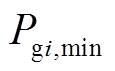 为机组最小出力,MW;
为机组最小出力,MW; 为机组最小出力时的燃料成本,$/h;
为机组最小出力时的燃料成本,$/h;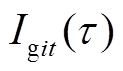 为机组开机状态;
为机组开机状态;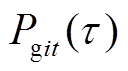 为火电机组出力;
为火电机组出力;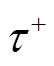 与
与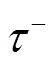 分别为
分别为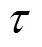 时刻的后一瞬间与前一瞬间;
时刻的后一瞬间与前一瞬间;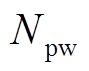 为分段数量。式(10)与式(11)分别为开机成本与关机成本计算方法;燃料成本通常为出力的二次函数,式(12)为其分段线性化计算方法[16],将二次函数分为
为分段数量。式(10)与式(11)分别为开机成本与关机成本计算方法;燃料成本通常为出力的二次函数,式(12)为其分段线性化计算方法[16],将二次函数分为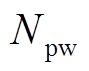 段,机组在第k段的出力为
段,机组在第k段的出力为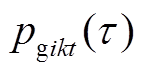 ,第
,第![]() 段的费率为
段的费率为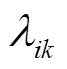 ,单位为$/(MW·h)。
,单位为$/(MW·h)。
约束条件包含
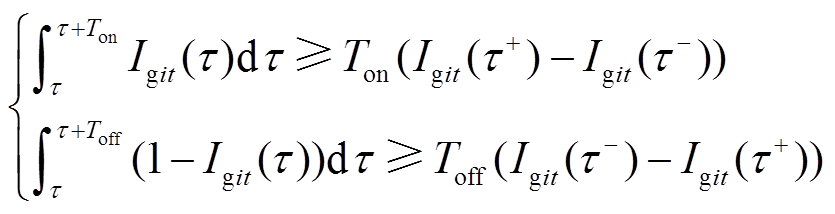 (13)
(13)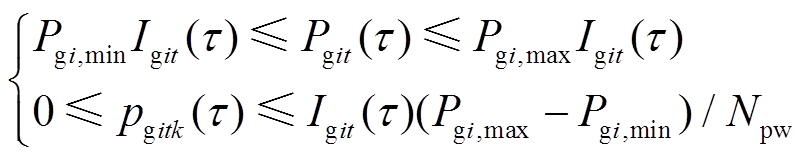 (14)
(14)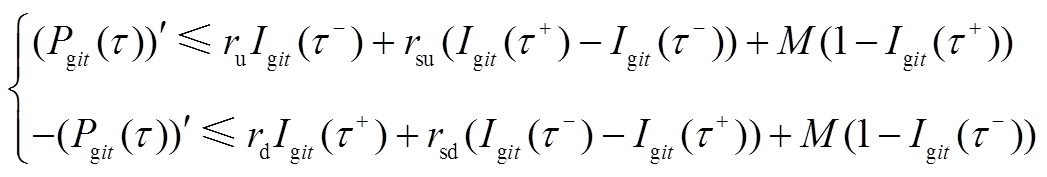 (15)
(15)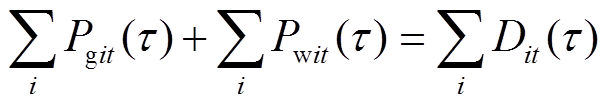 (16)
(16)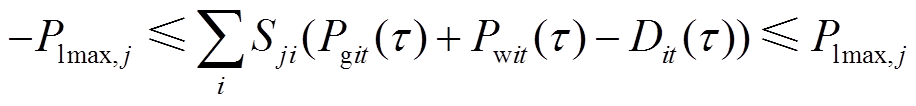 (17)
(17)式中,Ton、Toff为最小开机、停机时间,h;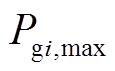 为机组最大出力,MW;ru、rd为最大上、下爬坡速度,MW/h;rsu、rsd为开机、关机时刻最大爬坡速度,MW/h;M为一很大正数;
为机组最大出力,MW;ru、rd为最大上、下爬坡速度,MW/h;rsu、rsd为开机、关机时刻最大爬坡速度,MW/h;M为一很大正数;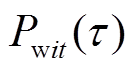 为风电出力;
为风电出力;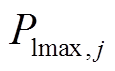 为第j条线路的最大输送容量,MW;S为潮流灵敏度矩阵。式(13)为最小起停时间约束,式(14)为出力范围约束,式(15)为爬坡约束,式(16)为功率平衡约束,式(17)为潮流约束。
为第j条线路的最大输送容量,MW;S为潮流灵敏度矩阵。式(13)为最小起停时间约束,式(14)为出力范围约束,式(15)为爬坡约束,式(16)为功率平衡约束,式(17)为潮流约束。
上述连续时间机组组合模型可简写为
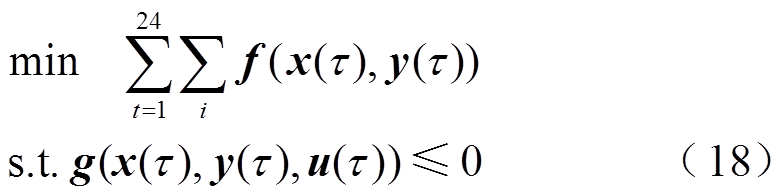
式中,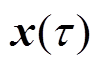 为一阶段变量,包含
为一阶段变量,包含 、
、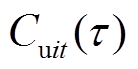 和
和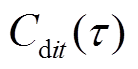 ;
;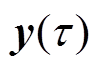 为二阶段变量,为
为二阶段变量,为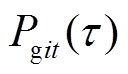 ;
;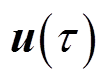 为随机量,即
为随机量,即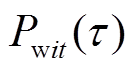 ;
; 和
和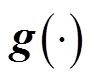 为式(9)~式(17)中的相应函数。
为式(9)~式(17)中的相应函数。
随着风电在电力系统中占比的增加,时段内出力变化对电力系统运行安全的影响逐渐显著。图2中黑色实线是某个时段的风电预测出力,考虑预测误差,阴影区域是实际风电出力曲线可能处于的范围。不明显是可能出现的某条实际风电出力曲线,其最大功率变化率如图中虚线所示,记为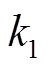 。然而传统调度方法中能够计及的最大风电出力变化为另外一条虚线所对应的斜率,记为k2。从图中可以看到,
。然而传统调度方法中能够计及的最大风电出力变化为另外一条虚线所对应的斜率,记为k2。从图中可以看到,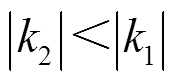 ,即传统调度方法中考虑到的最大出力变化小于实际出力变化,可能导致爬坡不足,从而影响实际运行安全。
,即传统调度方法中考虑到的最大出力变化小于实际出力变化,可能导致爬坡不足,从而影响实际运行安全。
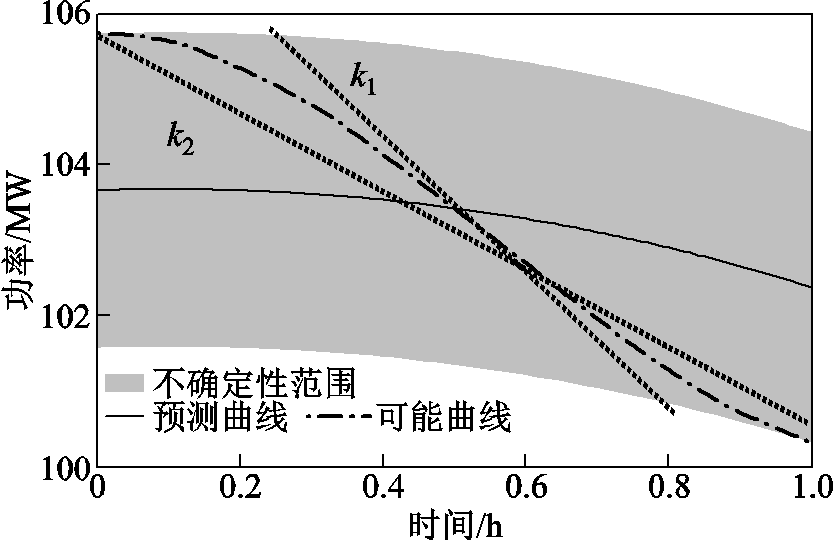
图2 时段内波动
Fig.2 Beyond-the-resolution variation
本文将超出传统调度方法分辨率的时段内风电出力变化的不确定性简称为超分辨率不确定性,并建立超分辨率不确定性模型为
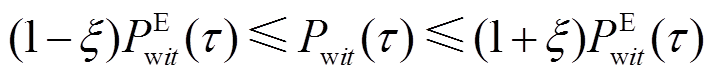 (19)
(19)式中, 为风电预测出力的拟合曲线,MW;
为风电预测出力的拟合曲线,MW;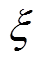 为预测误差;
为预测误差;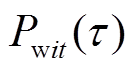 为风电实际出力曲线。式(19)所构成的不确定性范围记为
为风电实际出力曲线。式(19)所构成的不确定性范围记为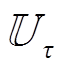 。若目标函数选为预测场景下的运行成本最低,则计及超分辨率不确定性的连续时间鲁棒机组组合模型可改写为
。若目标函数选为预测场景下的运行成本最低,则计及超分辨率不确定性的连续时间鲁棒机组组合模型可改写为
 (20)
(20)式中,![]() 代表期望场景下的相应变量。式(20)中第二行为期望场景下的系统运行约束,第三行对一阶段变量x(τ)进行约束,使得u(τ)在
代表期望场景下的相应变量。式(20)中第二行为期望场景下的系统运行约束,第三行对一阶段变量x(τ)进行约束,使得u(τ)在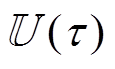 中任意取值时,都存在一组y(τ)能够满足系统运行约束。
中任意取值时,都存在一组y(τ)能够满足系统运行约束。
如图2和式(19)所示,超分辨率不确定性范围为功率-时间图中的一个带状区域,实际出力变化可能为带状区域中的任一条曲线。在连续时间建模方法中,出力变化由Bernstein插值系数唯一确定,则超分辨率不确定性可用插值系数的不确定性来体现。基于连续时间建模方法,风电出力预测曲线和实际曲线可建模为
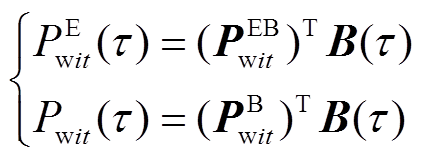 (21)
(21)式中,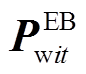 和
和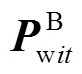 分别为
分别为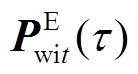 和
和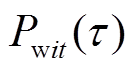 对应的插值系数的向量。将式(21)代入式(19)可得
对应的插值系数的向量。将式(21)代入式(19)可得
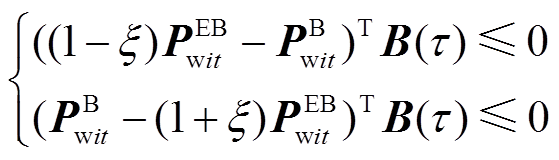 (22)
(22)由不等式方程变换的性质,即式(8),可推导得到
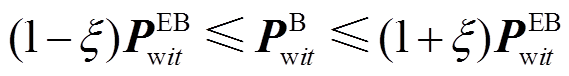 (23)
(23)根据上述推导可见,式(19)所示的超分辨率不确定性可用插值向量不确定性描述,不确定性范围由时域的带状区域转换为函数域上插值系数向量的盒式集合。由于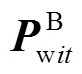 为四维向量,故盒式集合顶点共有16个,其第n个顶点
为四维向量,故盒式集合顶点共有16个,其第n个顶点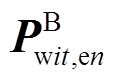 为
为
 (24)
(24)由于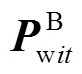 在盒式集合内部,故式(23)可重构为
在盒式集合内部,故式(23)可重构为
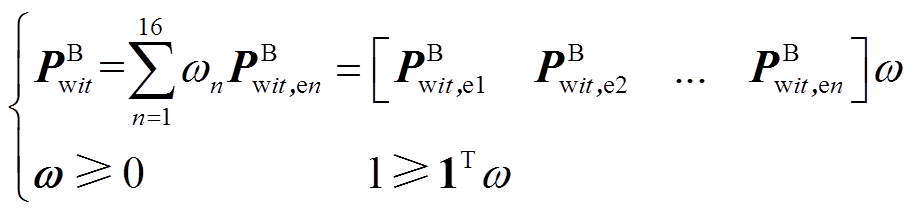 (25)
(25)式中, 为权重系数向量。
为权重系数向量。
可见,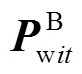 是
是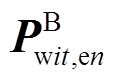 的线性组合,而每个
的线性组合,而每个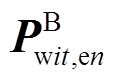 都对应带状区域内的一条曲线
都对应带状区域内的一条曲线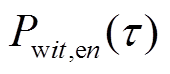 ,如图3所示。
,如图3所示。

图3 超分辨率基本变化曲线
Fig.3 Basic beyond-the-resolution variation
根据式(25)可推导得到
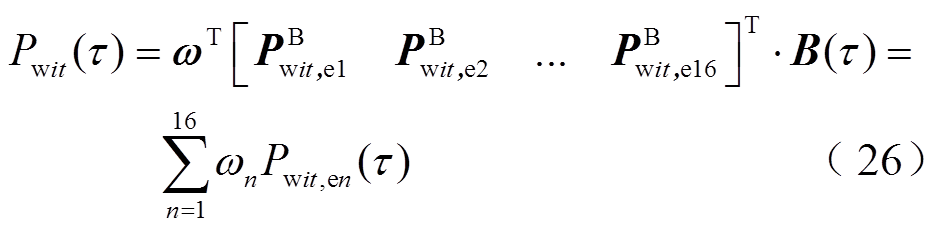
由式(26)可以看出,带状区域内任意超分辨率变化可由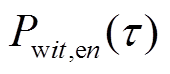 线性组合得到,因此称
线性组合得到,因此称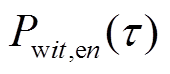 为超分辨率基本变化曲线。若能计及所有基本变化曲线,则可保证任意超分辨率变化下的系统安全。
为超分辨率基本变化曲线。若能计及所有基本变化曲线,则可保证任意超分辨率变化下的系统安全。
利用连续时间建模方法的数学性质,将连续时间鲁棒机组组合问题转换为易求解的函数空间优化问题,并采用C&CG算法进行求解。
根据连续时间建模方法的数学性质,将优化问题转换到函数空间。目标函数式(9)改写为
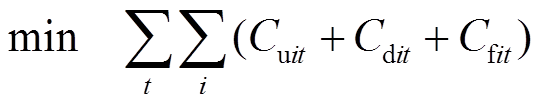 (27)
(27)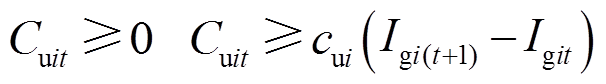 (28)
(28)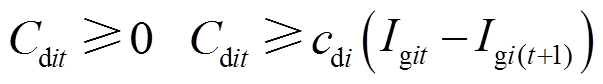 (29)
(29)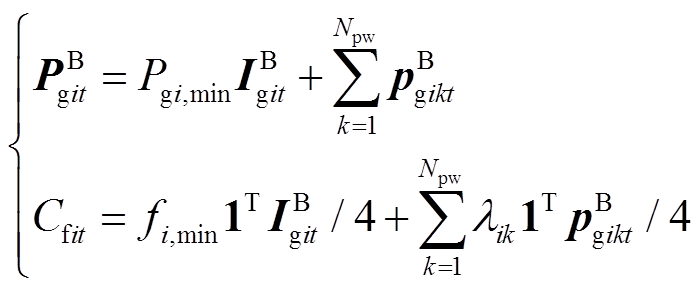 (30)
(30)式中,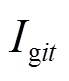 为第i台机组在t时段内的开机状态;
为第i台机组在t时段内的开机状态;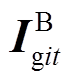 =
=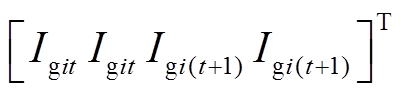 ;
;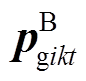 和
和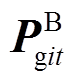 分别为
分别为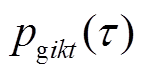 和
和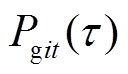 对应的插值系数的向量。
对应的插值系数的向量。
转换到函数空间后,约束条件改写为
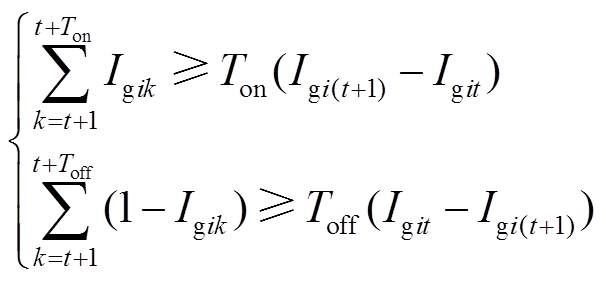 (31)
(31)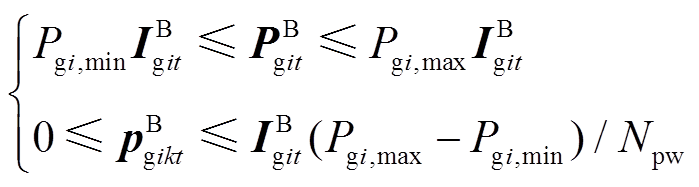 (32)
(32)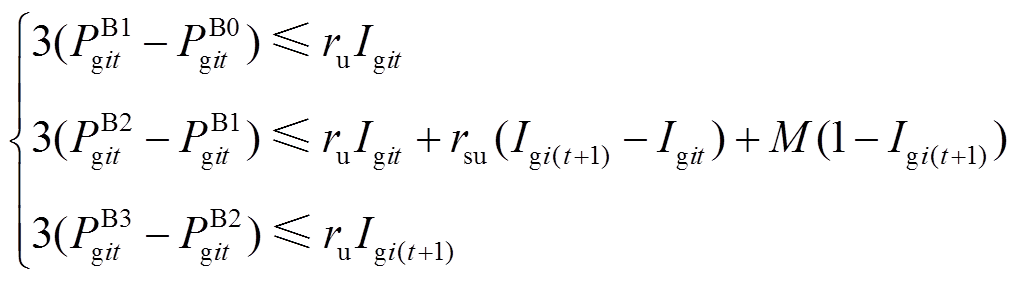 (33)
(33) (34)
(34)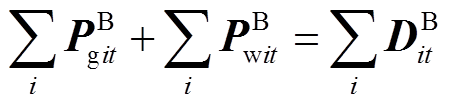 (35)
(35)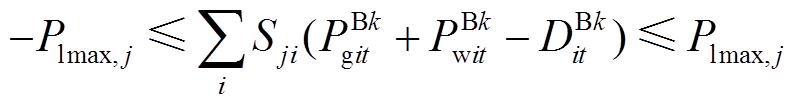 (36)
(36)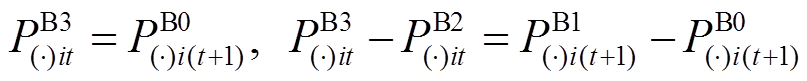 (37)
(37)式(31)为转换到函数空间的最小起停时间约束。式(32)为转换到函数空间的出力范围约束。式(33)和(34)为转换到函数空间的爬坡约束。式(35)为转换到函数空间的功率平衡约束。式(36)为转换到函数空间的约束。式(37)为补充的插值曲线一阶连续性约束,以确保前一时段末与后一时段初的功率曲线的大小与斜率相等。
上述变换到函数空间的优化问题可简写为
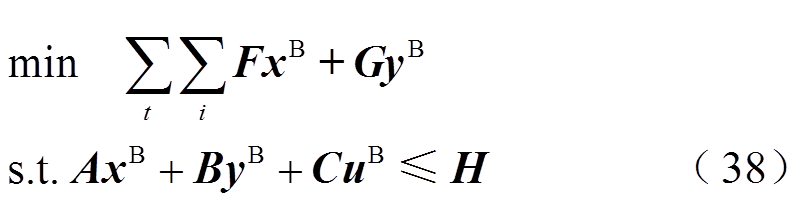
式中,xB、yB和uB分别为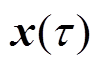 、
、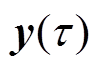 和
和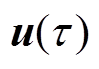 的插值系数向量;A、B、C、F、G和H分别为式(27)~式(37)中的相应系数矩阵。将式(23)描述函数空间的超分辨率不确定性集合记为
的插值系数向量;A、B、C、F、G和H分别为式(27)~式(37)中的相应系数矩阵。将式(23)描述函数空间的超分辨率不确定性集合记为 ,则计及超分辨率不确定性的鲁棒机组组合模型(20)可改写为式(39),式中
,则计及超分辨率不确定性的鲁棒机组组合模型(20)可改写为式(39),式中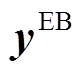 和
和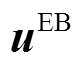 分别为
分别为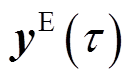 和
和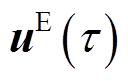 的插值系数向量。
的插值系数向量。
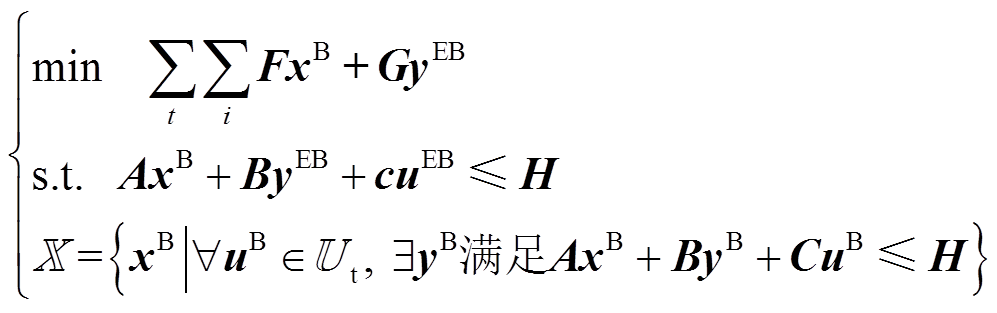 (39)
(39)通过解空间变换,将连续时间鲁棒机组组合问题从代数空间转换到函数空间,使得优化问题转换为混合整数线性规划问题,可以采用C&CG算法进行求解,计算结果可以通过类似式(2)的方式还原到代数空间。
采用C&CG算法将式(39)分解为如下主问题式(40)和子问题式(41)。
 (40)
(40)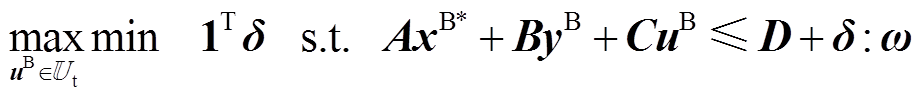 (41)
(41)式中,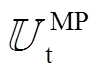 为主问题中考虑到的随机性场景的集合;
为主问题中考虑到的随机性场景的集合;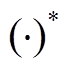 为主问题中相应变量的计算结果;
为主问题中相应变量的计算结果; 为子问题的松弛变量;
为子问题的松弛变量;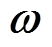 为对偶乘子。主问题中,
为对偶乘子。主问题中,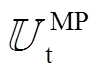 仅考虑了少量可能场景,降低计算量。子问题校验主问题解得的xB是否能够应对
仅考虑了少量可能场景,降低计算量。子问题校验主问题解得的xB是否能够应对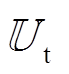 中的任意场景,若不能应对不确定性,即
中的任意场景,若不能应对不确定性,即 之和不为0,则将子问题解得的场景uB增添到
之和不为0,则将子问题解得的场景uB增添到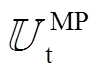 中,并进入下一次迭代。
中,并进入下一次迭代。
主问题式(40)是混合整数线性规划问题,可以用商业求解器直接求解。子问题式(41)是一个max-min问题,需对偶变换后再行求解,其对偶问题如下。
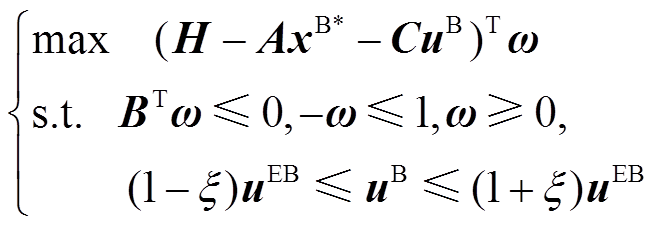 (42)
(42)考虑不确定性范围极值,将式(42)改写为
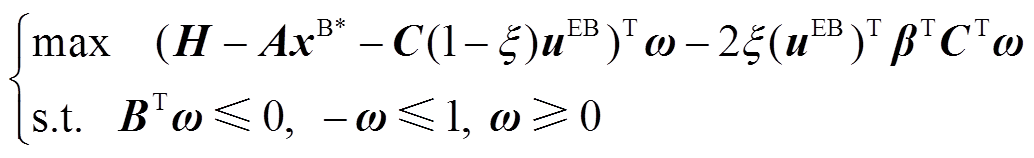 (43)
(43)式中,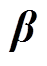 为引入的整数变量,指示风电出力位置。采用大M法将目标函数线性化得到
为引入的整数变量,指示风电出力位置。采用大M法将目标函数线性化得到
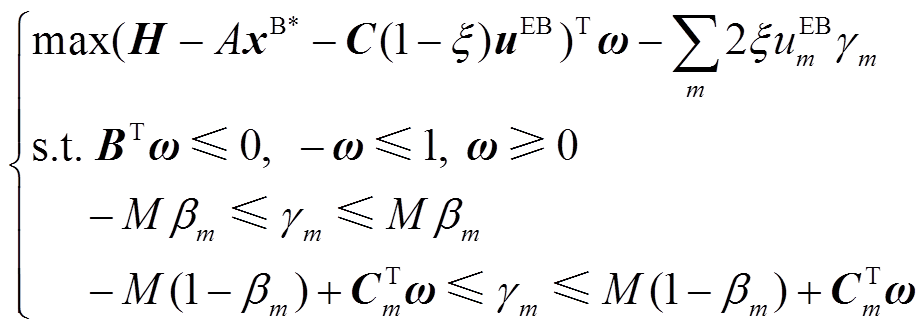 (44)
(44)式中,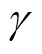 为辅助的连续变量;M为足够大正数;Cm为矩阵C的第m列。式(44)是混合整数线性规划问题,可以用商业求解器直接求解。
为辅助的连续变量;M为足够大正数;Cm为矩阵C的第m列。式(44)是混合整数线性规划问题,可以用商业求解器直接求解。
整体算法流程如图4所示。
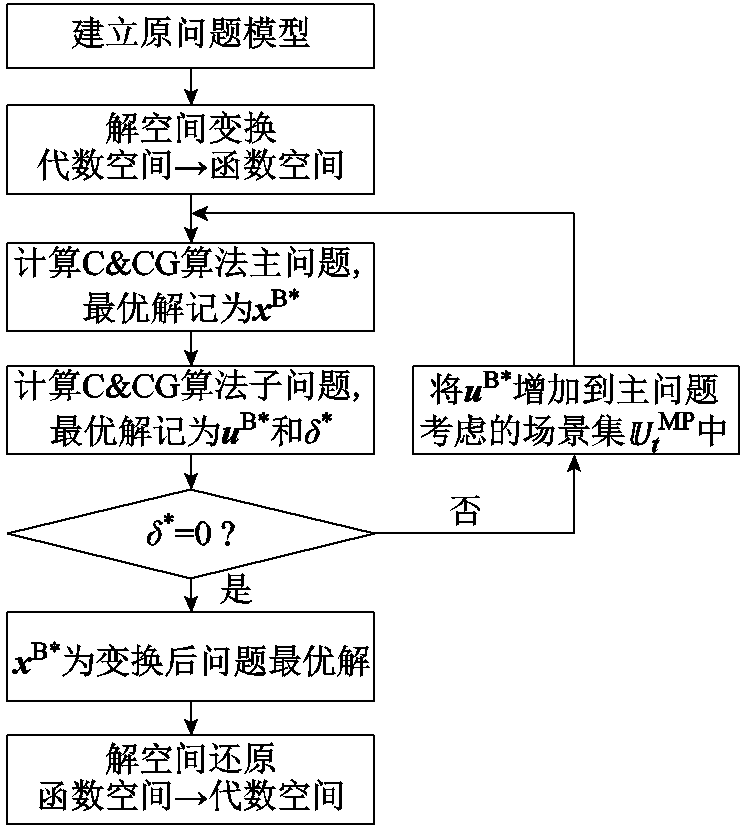
图4 算法流程
Fig.4 Algorithm flowchart
在Matlab 2016a平台上对所提方法有效性进行验证,测试环境为i7-7700 CPU@3.60GHz,16G内存。本文中所有优化问题均为混合整数线性规划,均采用商业求解器GUROBI进行求解。本节分别在14节点系统和IEEE RTS-79系统中对比传统鲁棒优化方法与所提计及超分辨率不确定性的连续时间鲁棒优化方法。传统鲁棒优化方法指的是采用传统的阶梯状功率曲线建模的鲁棒调度方法,其无法计及超分辨率不确定性。
修改后的14节点测试系统拓扑如图5所示,最大总负荷259MW,功率变化曲线如图1;系统中共有5台发电机,具体参数见表1;节点3与节点6处各增加一处风电场,容量均为60MW,其预测出力曲线如图6,预测误差取15%。
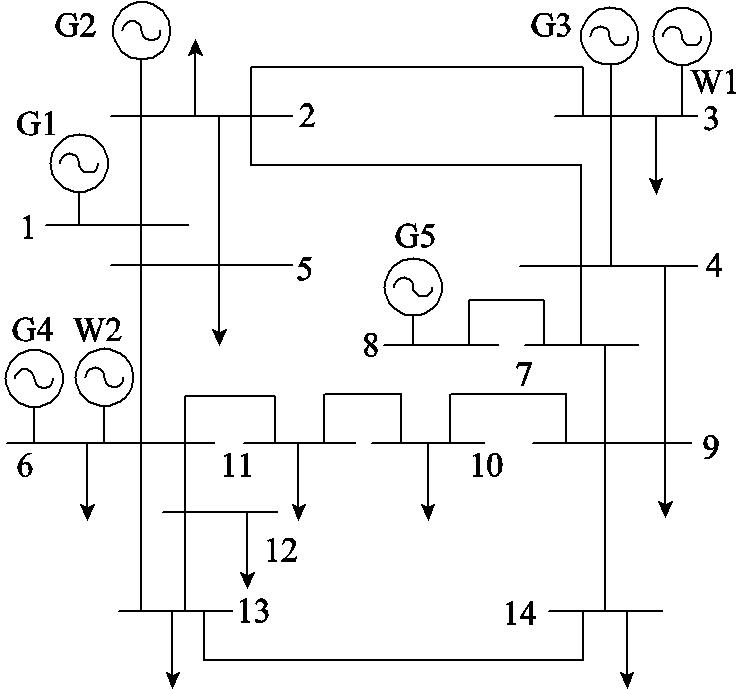
图5 IEEE 14节点系统
Fig.5 IEEE 14-bus test system
表1 14节点系统机组参数
Tab.1 Technical parameters of units in 14-bus system
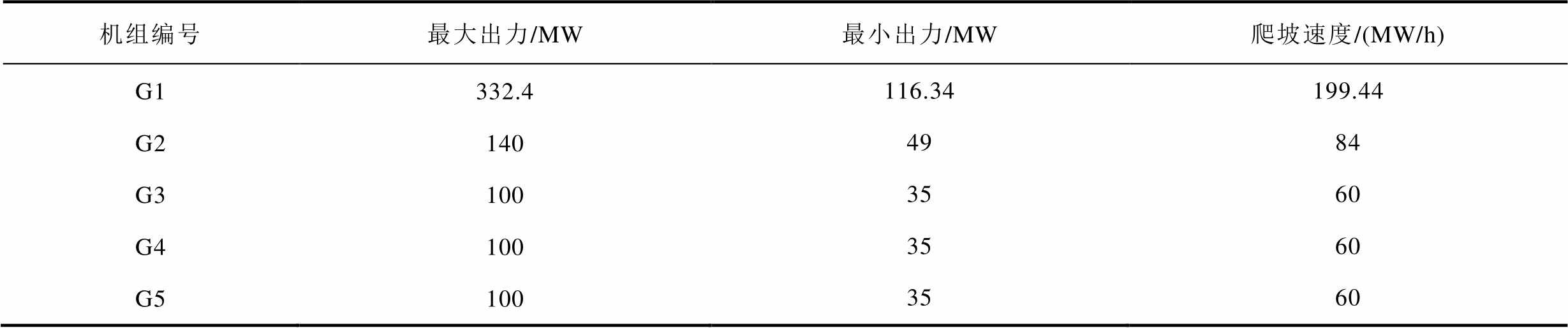
机组编号最大出力/MW最小出力/MW爬坡速度/(MW/h) G1332.4116.34199.44 G21404984 G31003560 G41003560 G51003560
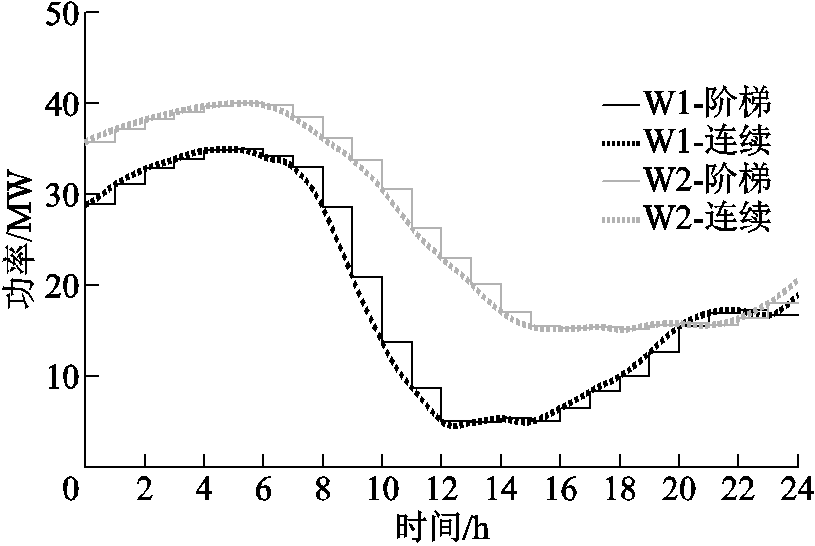
图6 风功率预测曲线
Fig.6 Wind power forecast curve
图7给出了两种方法计算得到的开机方式和预测场景下的出力计划,总体结果在表2中汇总。表2中,机组在线时长定义为各台机组开机时间之和;鲁棒性用于评估开机方式的安全性。在风电出力不确定性范围内随机生成10 000组时段长度为5min的场景,代入计算得到的开机方式,若不出现弃风或切负荷等情况的场景数为Nf,则开机方式的鲁棒性可估算为Nf/10 000。需要注意的是,此处的鲁棒性估算结果是指:具有较长时段长度(1h)的调度模型给出的开机方式在面对超过其调度分辨率的实际可能场景(如5min)时,所仍然具有的鲁棒性。
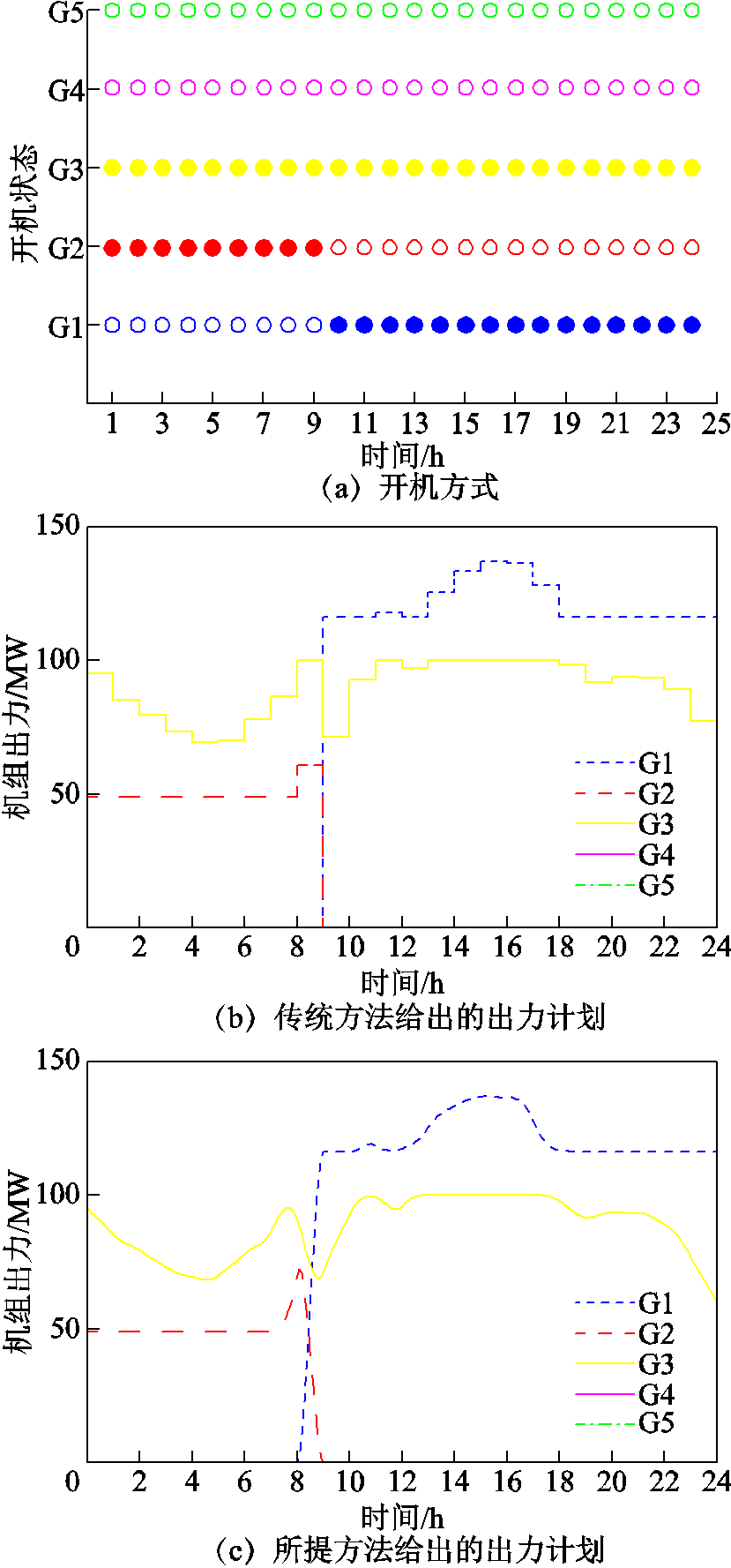
图7 开机方式和预测场景下的出力
Fig.7 Unit commitment and expected generation
表2 14节点系统中结果对比
Tab.2 Results comparison in the 14-bus system
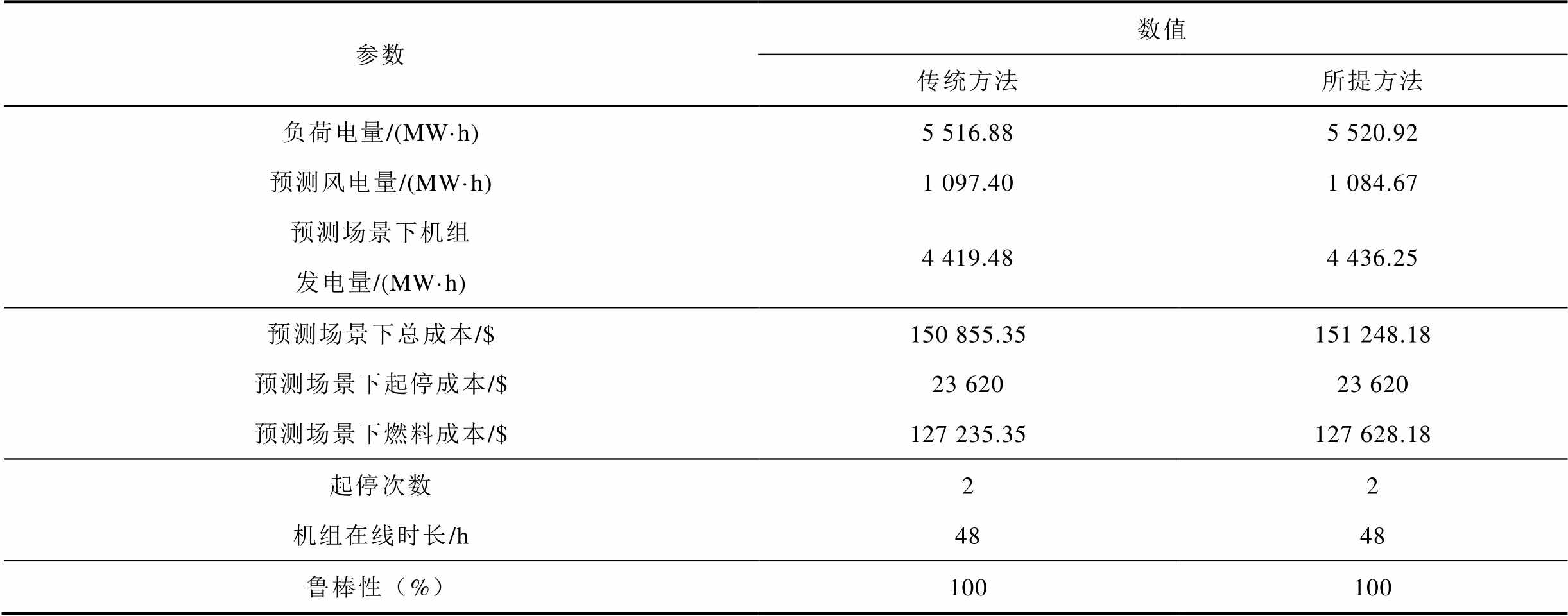
参数数值 传统方法所提方法 负荷电量/(MW·h)5 516.885 520.92 预测风电量/(MW·h)1 097.401 084.67 预测场景下机组发电量/(MW·h)4 419.484 436.25 预测场景下总成本/$150 855.35151 248.18 预测场景下起停成本/$23 62023 620 预测场景下燃料成本/$127 235.35127 628.18 起停次数22 机组在线时长/h4848 鲁棒性(%)100100
此算例中,两种方法计算得到的开机方式相同,均如图7a所示。在净负荷较大时,如第10时段后,较为经济的机组G1和G3出力;在净负荷较小时,如前9个时段,由于G1最小出力较高,故选用机组G2和G3共同出力。图7b和图7c分别展示了传统方法与所提方法计算出的预测场景下出力计划,两者趋势基本相同,可以证明所提方法的有效性。由于采用连续时间建模,所提方法计及的负荷与风电电量与传统方法略有不同,相应的运行成本有存在一定差别,见表2。由于两种方法开机方式相同,故起停次数和在线总时长也相同。两种方法得出开机方式的鲁棒性均为100%,说明两种方法均可以较好的应对此时的风电出力不确定性。
以下针对影响不确定性范围的两个因素,预测误差和风电容量,分别进行敏感性分析,预测场景下总成本和开机方式鲁棒性估算结果如图8所示。由图8a可以看出,当预测误差不超过25%时,总成本变化不大,鲁棒性均为100%;当预测误差增加到30%时,所提连续时间鲁棒优化方法为保证超分辨率鲁棒性改变开机方式,成本骤增,鲁棒性仍为100%,而传统鲁棒优化方法成本基本不变,鲁棒性略有下降;当预测误差超过35%时,超分辨率随机性影响显著,所提连续时间鲁棒优化方法找不到鲁棒的开机方式,传统鲁棒优化方法尽管可以给出调度结果,但其开机方式的鲁棒性显著下降,无法保证系统运行安全。由图8b可以看出,随着风电容量增加,火电出力减少,总成本总体上呈现下降趋势;但在风电容量放大倍数为0.5时,由于风电不确定性影响变得显著,导致需要更改开机方式,故两种方法总成本均变大;当风电容量放大倍数达到1.25后,超分辨率随机性影响变得显著,所提连续时间鲁棒优化方法为保证鲁棒性更换开机方式,导致总成本变大,并在倍数增加到1.5时找不到鲁棒的开机方式,而传统鲁棒优化方法无法计及超分辨率随机性,成本继续下降,但其鲁棒性随风电容量的增加而快速降低,无法保证系统运行安全。

图8 敏感性分析
Fig.8 Sensitivity analysis
在此选取两处风电场预测出力分别增了25%与50%的案例进行具体分析,此时由C&CG算法生成的场景如图9所示。传统方法中仅生成一个场景,即风电出力最大场景;而所提方法中共生成5个场景,包含风电最大出力场景和时段内波动的场景。可见,所提方法不仅能够计及传统方法中考虑到的不确定性,也能够计及超分辨率不确定性。
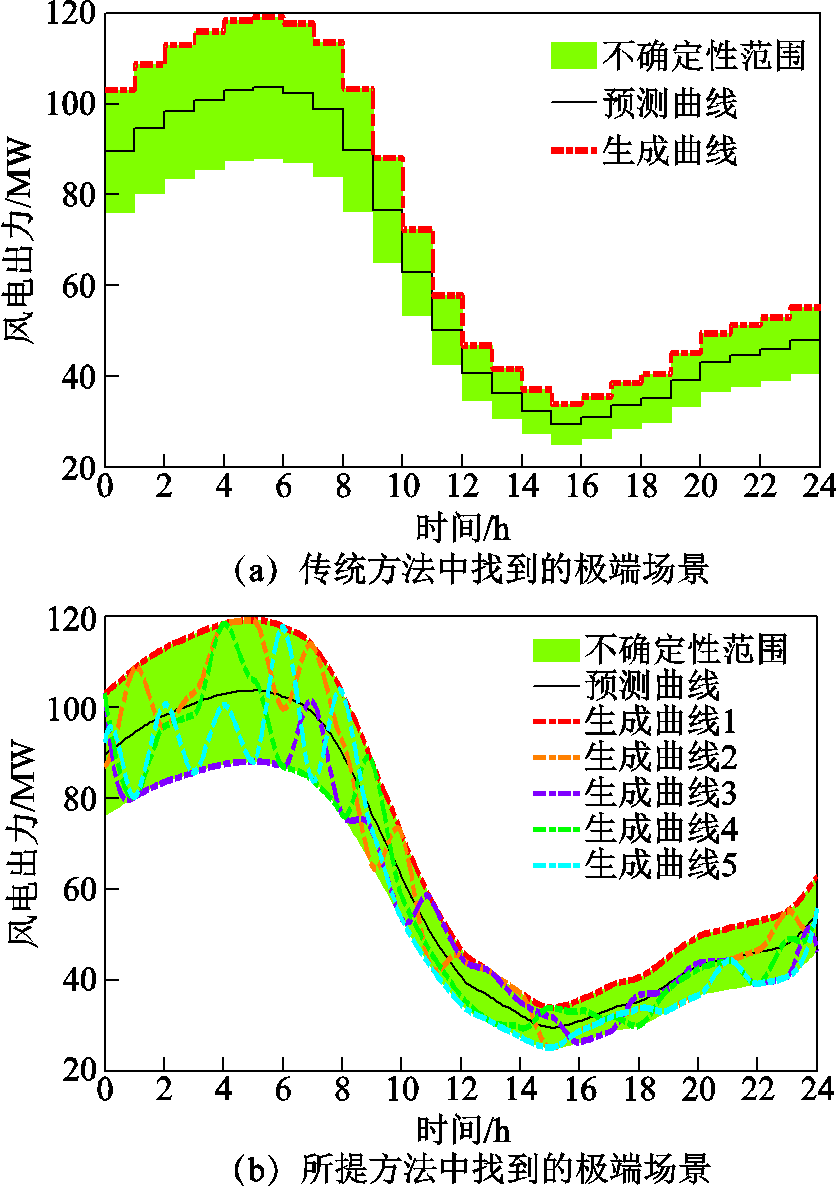
图9 14节点系统中生成的场景
Fig.9 Generated scenarios in the 14-bus system
表3对比了两种方法的整体结果,具体开机方式和出力计划如附图1所示。由附图1,两种方法中开机方式与出力计划不同,所提方法中起停次数更多,且机组在线总时长更长。由表3可见,尽管所提方法中起停成本较低,但由于采用费率较高的G2和G4代替传统方法中的较为经济的机组G1出力,故总成本高于传统方法。但是,所提方法的鲁棒性估算为99.40%,高于传统方法的鲁棒性估算71.35%,这是因为所提方法计及了超分辨率不确定性,在应对此时的风电不确定性时更加安全。所提方法鲁棒性并非100%的原因是,由于解空间变换中不等式(8)并非完全充要的,存在小部分超分辨率不确定性未被考虑。但从鲁棒性估算结果可以看到,这部分超分辨率不确定性影响相对较小,所提方法相对于传统方法仍具有较大优势。根据上述分析,随着风电出力占比增加,超分辨率不确定性影响逐渐显著,而所提方法可以较好地应对超分辨率不确定性,保证系统运行安全。
表3 风电较大时14节点系统中结果对比
Tab.3 Result comparison in large wind power generation

参数数值 传统方法所提方法 负荷电量/(MW·h)5 516.885 520.92 风电发电量/(MW·h)1 531.181 513.36 机组发电量/(MW·h)3 985.704 007.56 预测场景下总成本/$137 377.92155 077.92 预测场景下起停成本/$21 62017 000 预测场景下燃料成本/$115 757.92138 077.92 起停次数23 机组在线时长/h4859 鲁棒性(%)71.3599.40
采用修改后的IEEE RTS-79系统进一步验证所提方法的有效性,其最大总负荷2 850MW,负荷率变化同14节点系统。系统中共有33台机组,总容量3 405MW。在节点2和节点14处分别增加一处风电场,容量均为600MW,预测曲线变化趋势同14节点系统,预测误差取30%。由C&CG算法生成的极端场景如总体结果如图10所示,总体计算结果见表4。
由图10,所提方法生成的随机性场景能够计及时段内变化,考虑的随机性更为全面。表4中,虽然所提方法给出的开机方式中起停次数较少,但机组在线总时长更长,费率较高的机组出力导致总体成本变大。但所提方法开机方式鲁棒性估算为98.41%,远高于传统方法开机方式的鲁棒性估算43.42%,能够避免传统方法中的安全隐患。对比14节点系统结果可见,随着风电出力不确定性范围的变大,超分辨率不确定性对系统安全影响更加显著,而在本算例中所提方法可以保证98%以上情况下系统的运行安全。
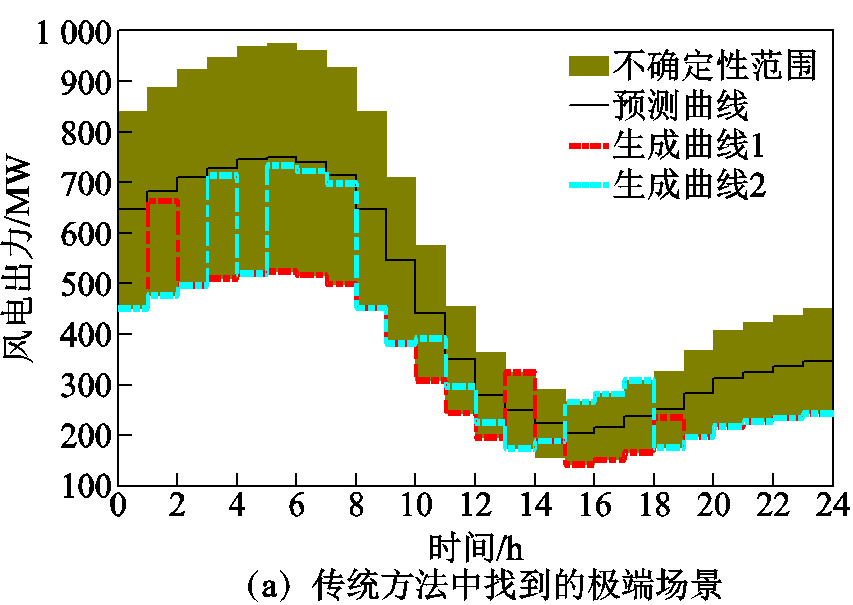
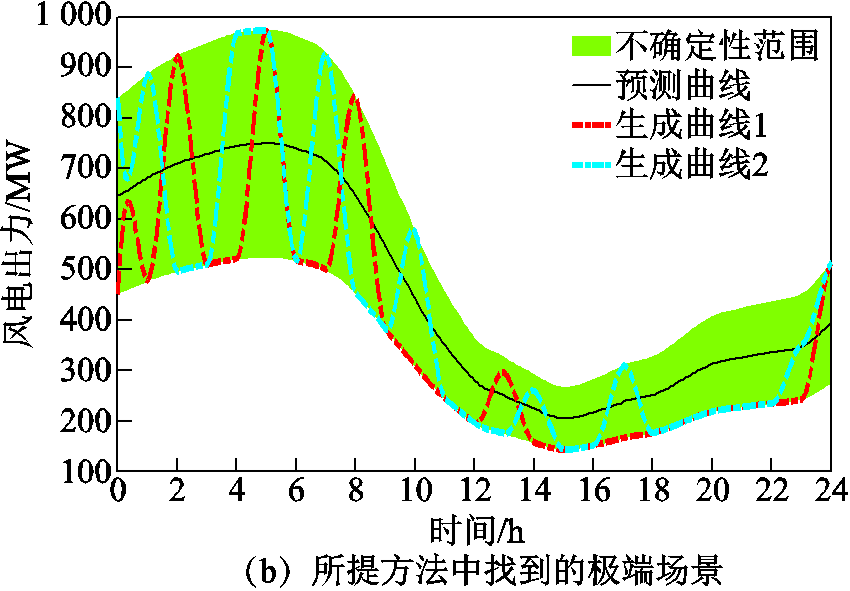
图10 RTS-79系统中生成的场景
Fig.10 Generated scenarios in the RTS-79 system
表4 RTS-79系统中结果对比
Tab.4 Result comparison in the RTS-79 system

参数数值 传统方法所提方法 负荷电量/(MW·h)60 706.9960 751.52 预测风电量/(MW·h)10 974.0310 846.76 预测场景下机组发电量/(MW·h)49 732.9649 904.75 预测场景下总成本/$579 145.44606 358.07 预测场景下起停成本/$16 50015 000 预测场景下燃料成本/$562 645.44591 358.07 起停次数1110 机组在线时长/h398434 鲁棒性(%)43.4298.41
本文提出了一种计及超分辨率风电出力不确定性的连续时间鲁棒机组组合模型和求解算法。针对超分辨率不确定性带来的安全隐患,建立连续时间
鲁棒机组组合模型,并提出一种基于解空间变换和C&CG算法的求解方法。分别在14节点系统与IEEE RTS-79系统上进行算例分析,验证了所提方法的有效性。根据算例结果可以看出:
1)当风电渗透率较低时,超分辨率风电出力不确定性影响不显著,所提方法能够得到与传统方法相似的结果。
2)随着风电渗透率的增加,超分辨率风电出力不确定性影响逐渐显著,传统方法给出的调度结果无法保障足够的鲁棒性,存在较大的安全隐患。
3)所提方法能够充分计及超分辨率风电出力不确定性,以牺牲部分经济性为代价,显著提高调度方案的鲁棒性。本文算例中,当传统方法调度方案的鲁棒性不及50%时,所提方法能够保证98%以上鲁棒性,显著提高系统运行安全性。

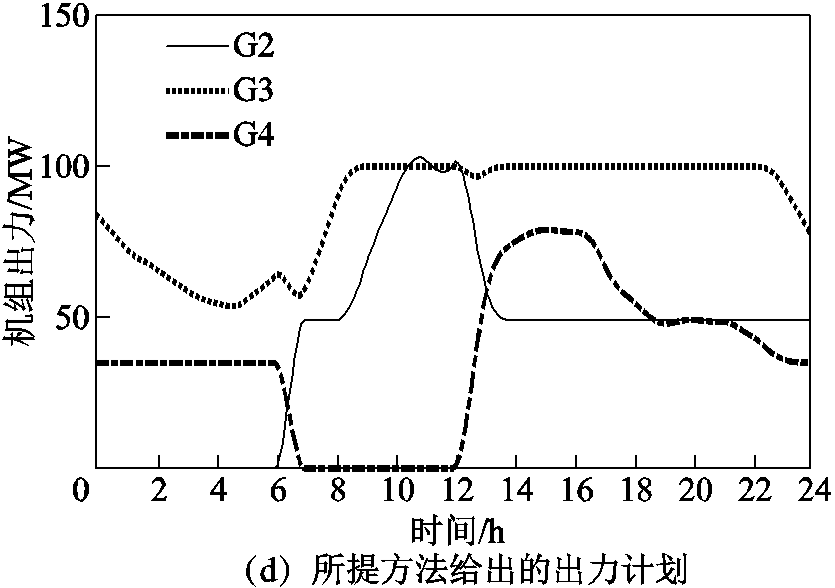
附图1 风电较大时开机方式和预测场景下出力
App.Fig.1 Unit commitment and expected generation in large wind power generation
参考文献
[1]International Renewable Energy Agency. Renewable energy statistics 2020[R]. Abu Dhabi: International Renewable Energy Agency, 2020.
[2]国家能源局. 2019 年风电并网运行情况[EB/OL]. 北京: 国家能源局, 2020[2020-02-28]. http:// www.nea.gov.cn/2020-02/28/c_138827910.htm.
[3]易文飞, 张艺伟, 曾博, 等. 多形态激励型需求侧响应协同平衡可再生能源波动的鲁棒优化配置[J]. 电工技术学报, 2018, 33(23): 5541-5554. Yi Wenfei, Zhang Yiwei, Zeng Bo, et al. Robust optimization allocation for multi-type incentive-based demand response collaboration to balance renewable energy fluctuations[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5541-5554.
[4]别朝红, 林超凡, 李更丰, 等. 能源转型下弹性电力系统的发展与展望[J]. 中国电机工程学报, 2020, 40(9): 2735-2745. Bie Zhaohong, Lin Chaofan, Li Gengfeng, et al. Development and prospect of resilient power system in the context of energy transition[J]. Proceedings of the CSEE, 2020, 40(9): 2735-2745.
[5]唐程辉, 张凡, 张宁, 等. 基于风电场总功率条件分布的电力系统经济调度二次规划方法[J]. 电工技术学报, 2019, 34(10): 2069-2078. Tang Chenghui, Zhang Fan, Zhang Ning, et al. Quadratic programming for power system economic dispatch based on the conditional probability distribution of wind farms sum power[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2069-2078.
[6]葛晓琳, 郝广东, 夏澍, 等. 考虑规模化电动汽车与风电接入的随机解耦协同调度[J]. 电力系统自动化, 2020, 44(4): 54-62. Ge Xiaolin, Hao Guangdong, Xia Shu, et al. Stochastic decoupling collaborative dispatch considering integration of large-scale electric vehicles and wind power[J]. Automation of Electric Power Systems, 2020, 44(4): 54-62.
[7]张艺镨, 艾小猛, 方家琨, 等. 基于极限场景的两阶段含分布式电源的配网无功优化[J]. 电工技术学报, 2018, 33(2): 380-389. Zhang Yipu, Ai Xiaomeng, Fang Jiakun, et al. Two-stage reactive power optimization for distribution network with distributed generation based on extreme scenarios[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 380-389.
[8]Zhou Bo, Ai Xiaomeng, Fang Jiakun, et al. Data-adaptive robust unit commitment in the hybrid AC/DC power system[J]. Applied Energy, 2019, 254: 113784.
[9]高晓松, 李更丰, 肖遥, 等. 基于分布鲁棒优化的电-气-热综合能源系统日前经济调度[J]. 电网技术, 2020, 44(6): 2245-2254. Gao Xiaosong, Li Gengfeng, Xiao Yao, et al. Day-ahead economical dispatch of electricity-gas-heat integrated energy system based on distributionally robust optimization[J]. Power System Technology, 2020, 44(6): 2245-2254.
[10]Milligan M, Kirby B. Analysis of sub-hourly ramping impacts of wind energy and balancing area size[R]. National Renewable Energy Lab (NREL), 2008.
[11]Gangammanavar H, Sen S, Zavala V. Stochastic optimization of sub-hourly economic dispatch with wind energy[J]. IEEE Transactions on Power Systems, 2016, 31(2): 949-959.
[12]Bakirtzis E, Biskas P. Multiple time resolution stochastic scheduling for systems with high renewable penetration[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1030-1040.
[13]栗然, 韩怡, 丁星, 等. 基于表达谱的时间粒度自适应调度模式[J/OL]. 电力系统自动化[2020-09-15]. http://kns.cnki.net/kcms/detail/32.1180.TP. 20200731. 1431.004.html.Li Ran, Han Yi, Ding Xing, at al. Time-granularity adaptive dispatch mode based on expression spectrum. [J/OL]. Automation of Electric Power Systems [2020-09-15]. http://kns.cnki.net/kcms/detail/32.1180.TP. 20200731.1431.004.html.
[14]Pineda S, Fernandez-Blanco R, Morales J. Time-adaptive unit commitment[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3869-3878.
[15]吴雅仪, 陈红坤, 徐坤领, 等. 考虑双时间尺度调度周期的储能最优容量配置[J]. 电力系统保护与控制, 2018, 46(5): 106-113. Wu Yayi, Chen Hongkun, Xu Kunling, et al. Optimal capacity allocation of energy storage system considering two time scale scheduling cycles[J]. Power System Protection and Control, 2018, 46(5): 106-113.
[16]艾小猛, 韩杏宁, 文劲宇, 等. 考虑风电爬坡事件的鲁棒机组组合[J]. 电工技术学报, 2015, 30(24): 188-195. Ai Xiaomeng, Han Xingning, Wen Jingyu, et al. Robust unit commitment considering wind power ramp events[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 188-195.
[17]张利, 杨建, 菅学辉, 等. 考虑次小时尺度运行灵活性的含储能机组组合[J]. 电力系统自动化, 2018, 42(16): 48-56. Zhang Li, Yang Jian, Jian Xuehui, et al. Review of coupled system between power and natural gas network[J]. Automation of Electric Power Systems, 2018, 42(16): 48-56.
[18]Parvania M, Scaglione A. Unit commitment with continuous-time generation and ramping trajectory models[J]. IEEE Transactions on Power Systems, 2016, 31(4): 3169-3178.
[19]Khatami R, Parvania M, Khargonekar P. Scheduling and pricing of energy generation and storage in power systems[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4308-4322.
[20]Nikoobakht A, Aghaei J, Shafie-Khah M, et al. Continuous-time co-operation of integrated electricity and natural gas systems with responsive demands under wind power generation uncertainty[J]. IEEE Transactions on Smart Grid, 2020, 11(4):3156-3170.
[21]Khatami R, Parvania M. Stochastic multi-fidelity scheduling of flexibility reserve for energy storage[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 1438-1450.
[22]李滨, 覃芳璐, 吴茵, 等. 基于模糊信息粒化与多策略灵敏度的短期日负荷曲线预测[J]. 电工技术学报, 2017, 32(9): 149-159. Li Bin, Tan Fanglu, Wu Yin, et al. Short-term daily load curve forecasting based on fuzzy information granulation and multi-strategy sensitivity[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 149-159.
[23]魏韡, 刘锋, 梅生伟. 电力系统鲁棒经济调度(二)应用实例[J]. 电力系统自动化, 2013, 37(18): 60-67. Wei Wei, Liu Feng, Mei Shengwei. Robust and economical scheduling methodology for power systems part two application examples[J]. Automation of Electric Power Systems, 2013, 37(18): 60-67.
Continuous-Time Modeling Based Robust Unit Commitment Considering Beyond-the-Resolution Wind Power Uncertainty
Abstract With the increasing penetration of wind power in the power system, the intra-period fluctuation of wind power gets more and more violent, which may induce the scarcity of intra-period ramping capacity and threaten the intra-period operational security of the power system. In this paper, the model and solution algorithm of continuous-time modeling based robust unit commitment is proposed considering beyond-the-resolution (BtR) wind power uncertainties, which can fully access the intra-period wind power variation and give the robust solution to the BtR uncertainties. First, the continuous-time robust unit commitment model considering BtR uncertainties is established, and the BtR uncertainty model is analyzed. Second, by the solution space transformation, the optimization problem is shifted from the algebraic space to the function space for tractable computation. The column-and-constraint generation (C&CG) algorithm is adopted to solve the optimization problem in the function space and the solution is then recovered to the algebraic space. Finally, the simulation results validate that BtR uncertainties can be fully considered in the proposed method so as to enhance the robustness of the scheduling solution.
keywords:Wind power uncertainty, economic dispatch, robust optimization, continuous-time modeling, beyond-the-resolution
中图分类号:TM71
DOI:10.19595/j.cnki.1000-6753.tces.L90460
国家自然科学基金资助项目(51707070)。
收稿日期 2020-07-11
改稿日期 2020-10-19
周 博 男,1995年生,博士研究生,研究方向为含可再生能源的电力系统灵活运行。E-mail:zhoubo563@foxmail.com
艾小猛 男,1986年生,博士,讲师,研究方向为储能优化配置、鲁棒优化理论在电力系统中的应用,可再生能源特性分析与并网优化运行等。E-mail:xiaomengai@hust.edu.cn(通信作者)
(编辑 赫蕾)