图1 VPP多级优化调度框架
Fig.1 Multi-level optimized scheduling framework
摘要 虚拟电厂（VPP）日前计划和日内运行方案是其在内、外部随机性上，实现经济或技术效益的有力保证。提出VPP日前计划-滚动计划-实时调度在内的全时域优化调度框架，建立不同尺度优化模型并通过“多级调度、逐级细化”的思想达到优化鲁棒性。在日前计划中，以虚拟电厂最大化市场效益为目标建立模型；在日内优化中，基于马尔科夫决策过程（MDP）融合30min尺度滚动和5min尺度超短期两层优化以减少建模层级。在MDP模型中，建立熵值回馈函数表征滚动优化过程，用以减少因日前预测误差带来的日内运行偏差值；建立模糊-概率策略表征超短期优化过程，用以调节储能荷电状态、均衡其充电与放电能力，最终实现跟踪日前计划的目标，最大化经济效益。最后通过算例计算对所提方案进行了验证。
关键词：虚拟电厂 优化调度 多时间尺度 马尔科夫决策过程 模糊-概率策略
当前电力系统正处于从集中式发展过渡到分散式发展的态势，大规模多元、分散、异构的分布式电源无序接入中低压配电系统给电网的管控带来了极大的困难[1-2]。在众多的解决方案中，虚拟电厂（Virtual Power Plant, VPP）技术相比微电网/微网群[3]、综合能源[4]、主动配电网[5]、分布式电源集群等技术[6]，对先进通信技术和电力市场适应度更高，更适合电力系统分散式发展的方向。
站在电力市场角度，VPP多层次优化技术是保证其收益最大化的重要前提[7-9]。当前针对VPP优化研究，按照VPP前期规划、计划、运行、结算四个先后时段，可归为四类：①基于灵活性资源聚合的VPP配置优化；②基于日前计划的VPP对外交易策略优化；③基于滚动与实时调度的VPP日内运行方案优化；④基于博弈的VPP内部多主体利益分配优化。其中②和③构成了VPP日前-滚动-实时的多时间优化调度框架，在该框架下，文献[10]基于分时电价建立了VPP日前计划模型，以各时段内获得收益最大为目标进行优化，同时分析了VPP中随机性单元对最终经济效益的影响。文献[11]在最大化收益的日前计划模型基础上，通过VPP运行典型工况的生成和缩减来描述内部不确定性，通过源、荷两端的功率调整来修正间歇性单元的预测误差。文献[12]从技术型虚拟电厂运营模式出发，结合配电网安全运行约束条件，建立了VPP日前优化调度策略。文献[13]指出随着大量资本涌入发电侧，多个VPP协同参与市场的格局成为趋势，构建了多虚拟电厂非合作动态博弈的日前市场优化交易模型。
上述研究从不同角度构建了VPP日前交易计划模型，日前计划有充足的时间进行动态优化，实现利益最大化，可称作最优控制。但是随着预测时间的增加，预测误差会逐渐增大，因此日前功率预测结果与实际往往存在较大偏差。为减小这种偏差、保证最优目标，在日前计划基础上，一些研究考虑了日内滚动以及超短期调度模型，通过更短时间尺度预测调整出力计划，消除不确定因素。文献[14]提出了一种计及需求差异的电动汽车并网滚动时域优化策略，用以将并网电动汽车充放电状态切换频次及功率波动最小化。文献[15]在日前计划基础上，设计了一种VPP滚动调度策略，以使下一时刻因间歇性电源出力场景变化导致的日前优化结果差异化最小。因此滚动优化相对于日前计划的最优控制，又可称作保优控制，起到了承接日前计划和实时调度的关键作用。在日前和滚动优化基础上，文献[16]为提高VPP对间歇性电源消纳能力，减少预测误差的影响，提出包含日前、日内的多时间尺度优化策略，通过多VPP的协调互动，实现收益最大化和区域内供需平衡。文献[17]针对燃料机组、风电机组以及可控负荷的虚拟电厂，建立了日前计划、滚动优化、超短期优化多级调度模型来逐级消除因日前预测误差导致的实际运行偏差。在上述多时间尺度优化中，针对日前、滚动、超短期时间尺度分别建立了三个层级优化模型，各层级优化相对独立，依次作为彼此的输入输出。
综上所述，为减小VPP中随机性单元因预测误差而使得实际运行大范围偏离日前优化的情况，将建立VPP包含日前、滚动、实时在内的三级优化体系。另一方面，为减小优化层级，在日内优化中，以弥科夫决策过程（Markov Decision Process, MDP）模型融合滚动优化和实时优化两个层级以简化建模层级，其中将滚动优化写入MDP的回馈函数，将超短期调度写入MDP策略集中进行实时反馈调节。最后通过算例计算对所提出的VPP多级优化体系进行验证。
VPP多时间尺度调度框架如图1所示，分别包含日前计划层、滚动优化层和超短期调度层。
由图1可知，VPP在日前计划中，将根据短期发电功率预测制定日前计划模型；在滚动优化中，根据扩展短期发电功率预测及优化模型对日前计划因预测偏差进行修正，并给超短期优化中VPP灵活可调节性单元留有足够容量来跟踪日前计划；在超短期优化中，根据超短期功率预测衔接滚动优化并对前一级优化进行实时反馈调节形成闭环，同时将优化指令下发到VPP各单元。每层级优化调度模型建模过程将在后文详细介绍。
本文所提VPP由风电、微型燃气轮机（Micro Turbine, MT）、储能系统（Energy Storage System, ESS）及可控负荷（Controllable Load, CL）构成。VPP作为竞价者参与电力市场日前交易，同时也可向配电网中的负荷售电。
VPP日前优化调度的目标为其整体利润最高。VPP的收益包括向日前电力市场和VPP内部负荷售电收益，VPP的成本包括从日前电力市场购电成本、MT成本、ESS成本及CL成本。其目标函数可表示为
图1 VPP多级优化调度框架
Fig.1 Multi-level optimized scheduling framework
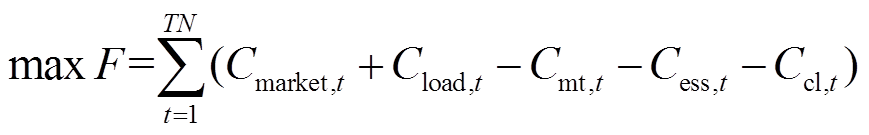（1）式中，TN为调度周期；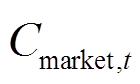
、
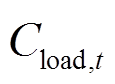分别为t时刻VPP的售电收益、向负荷售电收益；
、
、
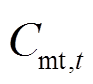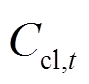分别为MT成本、ESS成本、CL成本。
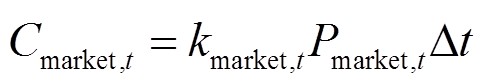（2）
式中，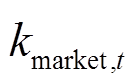
为t时刻日前电力市场的电价；
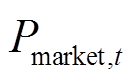为t时刻VPP与日前电力市场的交易量；
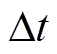为时间间隔；Nmt为微燃机数量；
为t时刻第m个微燃机组的有功功率；Nwind为风电单元数量；
为t时刻第p台风电单元的有功功率；Ncl为可控负荷用户数量；
为t时刻第c个可控负荷用户的负荷中断功率；Ness为ESS数量；，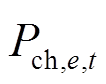
和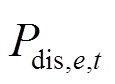
分别为t时刻第e个ESS的充放电功率；N为VPP内节点数；
为t时刻第i个用户的期望用电功率；
为所有以节点i为首节点的支路末节点的集合；rij为支路ij的电阻值；Iij为支路ij的电流。
为正表示VPP向日前电力市场售电，为负表示VPP从日前电力市场购电。
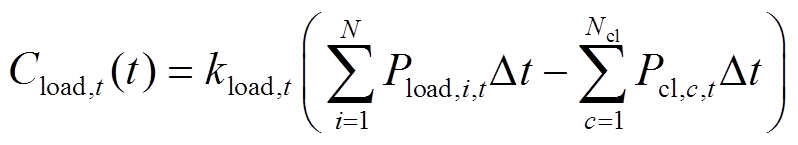（4）式中，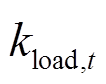
为t时刻VPP向内部负荷供电的售电电价。
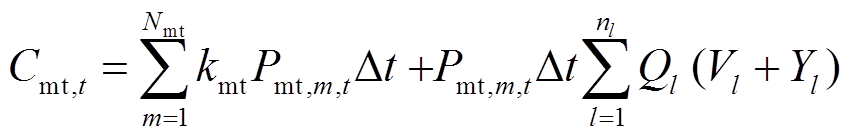（5）式中， kmt为单位功率发电成本；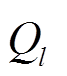
为MT机组单位功率第l项污染物的排放量；
和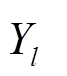
分别为第l项污染物的环境价值与罚款数量级[18]。MT成本分为运行成本及环境成本两部分。
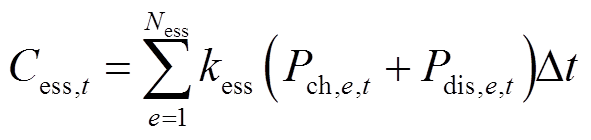（6）
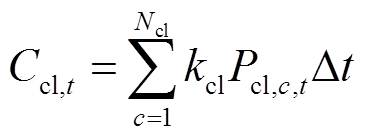（7）式中，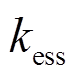
为ESS单位充放电成本；
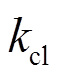为对CL用户的单位补偿费用。
约束条件包括常规的燃气轮机出力上下限约束、爬坡功率约束、启停时间约束，储能单元荷电状态、最大充放电约束和可控负荷最大调节量约束，以及整个配网系统的潮流约束，这里不再赘述。
VPP日内调度方案中总体目标是运用单元间的协调来消除日前预测的不准确性，确保日前计划的跟踪，因此更注重各时段之间的内在联系，属于随机动态规划问题。而随机动态规划是马尔科夫链的扩展，常将其建模为马尔科夫决策过程（MDP）[19]。MDP包含六个基本要素如式（8）所示。
MDP=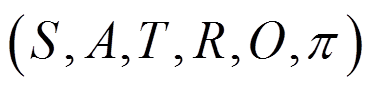
（8）
式中，S表征状态合集，文中为VPP中储能单元荷电状态（State of Charge, SOC）值；A表征行动合集，文中为VPP中微型燃气轮机、风电输出功率值和储能单元的充放电功率值；T表征状态转移函数，用T(s1,a,s2)表示状态s1经行动指令a∈A转移到状态s2的概率分布，文中为储能当前SOC1经指令a后到SOC2的概率分布；R表征回馈函数，文中为VPP滚动优化的目标函数，具体建模过程见3.2小节；O表征状态s1经行动指令a∈A转移到状态s2后所观测到状态o的概率分布，文中认为在通信正常且不丢包情况下，观测到的状态o=s2；π表征求解回馈函数R结果的算法，即策略，文中为超短期调度模型，是S集合到A集合的映射，对应R最优值的为最优策略，具体建模过程见3.3小节。
滚动优化又称作保优控制，即运用VPP中调节能力较强的单元来降低因日前计划不准而导致最终优化结果偏离日前计划太多。通过VPP内多元之间协同以对风电和负荷的预测误差ΔPwind和ΔPload进行滚动修正，使两者叠加功率偏差ΔP=(ΔPwind-ΔPload)最小。为减小功率偏差及功率波动性，建立熵值模型对其进行刻画。在熵值中，当熵值等于0时，表征波动最小；当熵值等于1时，表征波动最大。按照滚动优化30min时间尺度的设定，则在第t个30min整数倍时刻，系统熵值H(t)为
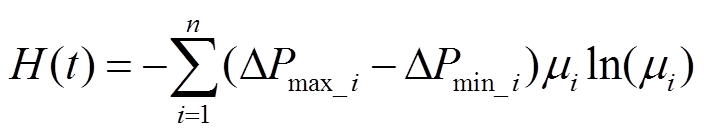（9）式中，n为到时刻t时，将出现过的功率偏差ΔP值分成的n个区间，这里可设定分成5个区间，即n=5；ΔPmax_i和ΔPmin_i分别为区间i内出现ΔP的最大值与最小值，以表征偏差的幅值；ui为ΔP值在区间i内出现的频次，以表征偏差的波动率。式（9）将所关心的误差功率偏差幅值及波动大小进行了整合，最终以熵值表征，当H值越接近0时，代表误差功率偏差幅值及波动越小，则在滚动优化中保优控制越佳；反之则越差。在t个整数倍时刻，系统在状态s，采取策略π(s)、经行动a{a∈A}后，系统获取的回馈值R为
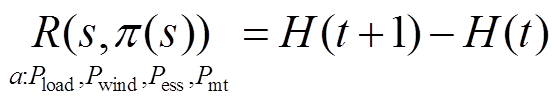（10）式中，H(t+1)、H(t)分别为第t+1和t个30min整数倍时刻的熵值，分别映射系统由t-1时刻状态转移到状态s和从s状态转移到t+1时刻状态的熵值。则在策略集π下，系统不断累积R值，定义值函数并写成递归形式为
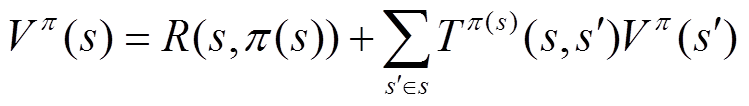（11）式中，R(s, π(s))为状态s、策略π(s)下的回馈值；Vπ(
)为状态s转移到的回馈值；Tπ(s)(s, )表示状态s经过策略π(s)转移到状态的概率分布函数，其获取过程详见3.3小节。普遍地对于任意策略，均有一个回馈函数值，因此可用执行策略得到的积累回馈值Vπ来评价选取策略的优劣。策略集π下的累积回馈值函数Vπ实际上是系统每个时间段内熵值H的叠加，这里理想的策略以及行动指令是使其值最小。
因此，基于熵值回馈函数的滚动优化目的在于结合扩展短期预测，对日前预测误差功率的波动进行度量，同时通过VPP内灵活调节单元来最大程度地减小这种误差波动，从而使实际运行曲线偏离日前计划的偏离量最小。
超短期优化又称作实时调度，对VPP中内部主要调节单元储能的充放电指令在滚动优化基础上进行实时矫正，以保证储能充放电指令始终维持在合理水平。采用模糊理论对储能充放电功率进行客观调节，考虑到模糊理论中隶属度并不能表征变量的随机过程，因此为求得MDP中状态转移概率T，在模糊理论基础上引入随机理论，形成变量-模糊-随机三位一体的模糊概率策略集π，其运行流程如图2所示。输入变量x，首先对其进行随机、模糊建模，分别输出概率密度函数和模糊规则来进行模糊推理，最后经过反模糊化和概率计算，输出转移概率T和策略集π。因此，基于概率模糊策略集的超短期调度目的在于对储能单元充放电功率在分辨率为0.5h的滚动优化基础上，进行分辨率为5min的实时调节，以保证储能SOC能够维持在合理状态。
图2 概率模糊建模流程
Fig.2 Probabilistic fuzzy modeling process
首先对输入变量x进行建模，这里x为表征储能是否充放电合理的变量，定义储能充放电能力x1和储能充放电合理度x2分别为
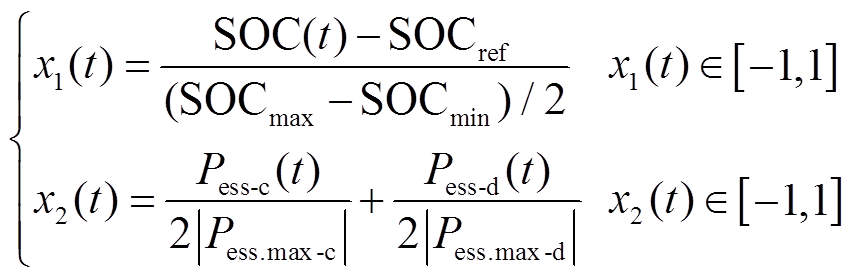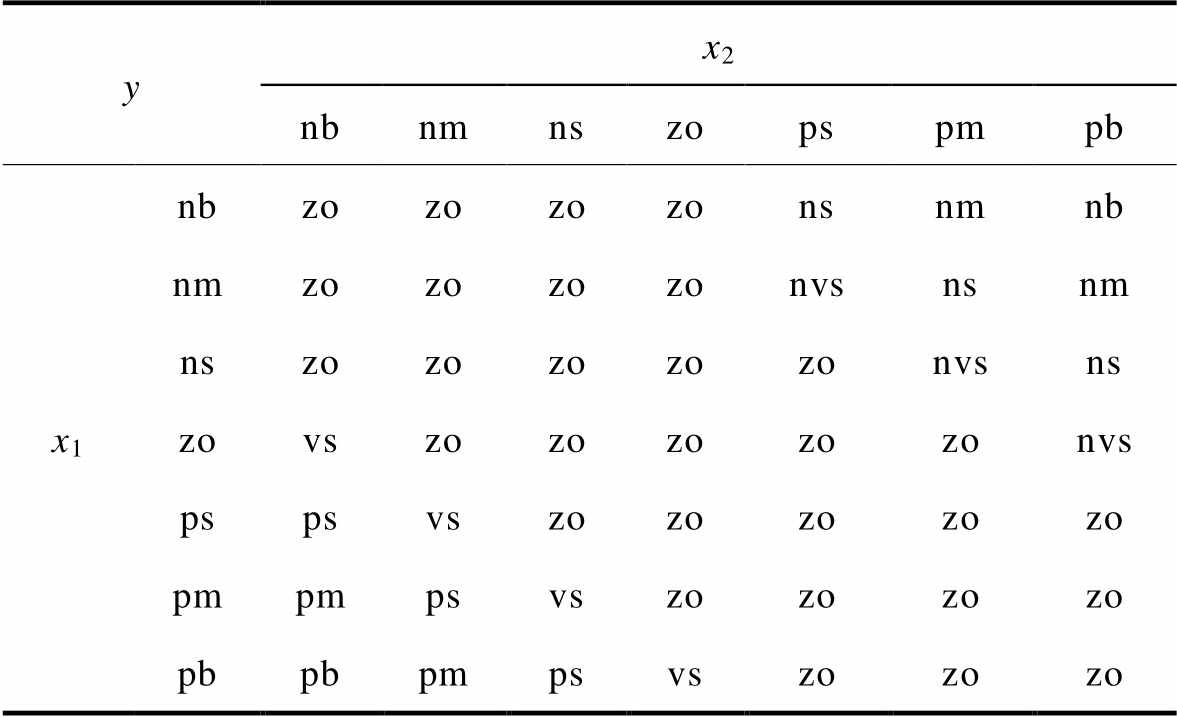
（12）式中，SOCref为储能SOC的参考值；SOC(t)为t时刻储能SOC值。为保持SOC值能够尽量处于平衡状态，令SOCref=(SOCmax+SOCmin)/2。当x1(t)=1时，则储能有很强的放电能力；当x1(t)=-1时，代表储能有很强的充电能力。Pess-c(t)为t时刻储能待充电功率值；Pess.max-c、Pess.max-d分别为其最大充电、放电功率。当x2(t)=1时，储能放电能力最大；当x2(t)=-1时，储能充电能力最大。x1(t)、x2(t)作为模糊控制的两个输入变量，经一定模糊规则得到模糊输出变量y，定义y为储能充放电修正功率。模糊规则制定原则如下：①当SOC适中时，模糊规则为空集，即y=0；②当SOC较高或较低时，且当前需要充电或放电时，基于提前设定的模糊规则对当前功率进行校正，模糊原则见表1。
表1 模糊原则
Tab.1 Fuzzy rules
yx2 nbnmnszopspmpb x1nbzozozozonsnmnb nmzozozozonvsnsnm nszozozozozonvsns zovszozozozozonvs pspsvszozozozozo pmpmpsvszozozozo pbpbpmpsvszozozo
表1中，x1、x2的模糊词集同选为{nb, nm, ns, zo, ps, pm, pb}，表征{负大，负中，负小，零，正小，正中，正大}；y的模糊词集选为{vs, s, ms, mb, b, vb}，代表{非常小，小，中小，中大，大，非常大}。编制x1、x2、y的隶属度函数如图3所示。
在模糊建模基础上加入随机轴，对于输入变量x1、x2，其对应的隶属度不再是单个值，而是一个随机变量[20]。设该随机变量服从正态分布的形式，L~N(μ,σ2)。包含随机轴在内的三维隶属度函数示意图如图4所示。由图4可知，当σ取值较小时，变量的隶属度取值将大概率落在隶属度曲线上，以突出逻辑中的模糊调节强度；反之，则随机性占主导地位，即状态s经策略π后转换到状态s′随机性更强。因此可以通过控制参数σ实现概率模糊策略中模糊强度和随机强度。本文将σ来设定为一个较小的数以保证其模糊性，同时较小的随机性用以产生状态转移概率T。
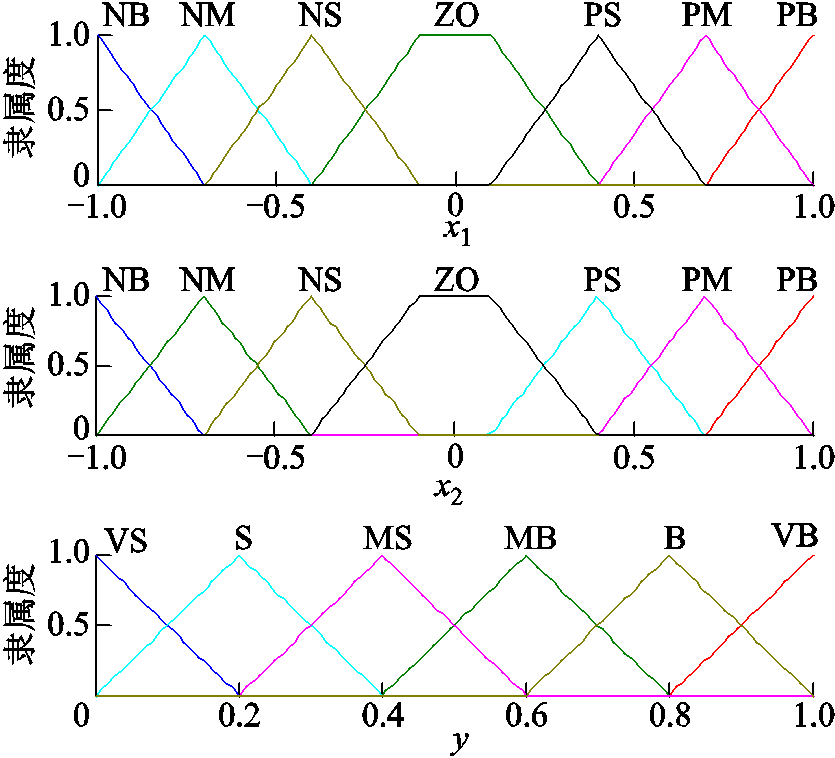
图3 输入输出隶属度函数
Fig.3 Input and output membership functions
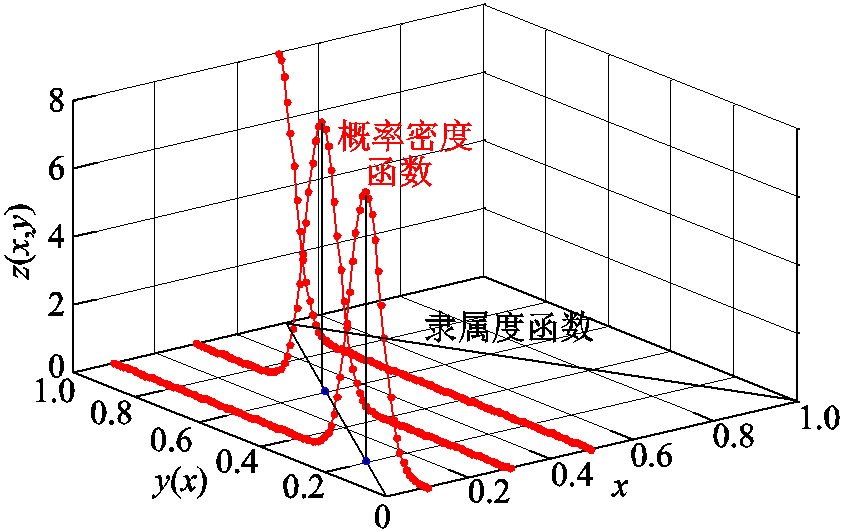
图4 概率模糊函数
Fig.4 Probability fuzzy set
综上所述，在超短期优化中：①首先根据储能当前状态s建立变量x1、x2，然后先后进行模糊化和随机化；②定义模糊规则，并根据变量x1、x2实际值制定模糊策略集π；③经概率模糊逻辑系统中模糊策略π，得到储能充放电修正功率来修正储能行动指令a；④经概率模糊逻辑系统中概率计算得到概率集，即转移概率T (s, π, a)，由于对于确定的行动指令，待转换状态s′与其一一对应，因此MDP中T ( s, a, s′)= T ( s, π, a)；⑤结合滚动优化中建立的回馈函数R。至此完成了MDP{S, A, T, R, O, π}建模过程，通过MDP实现了VPP两个层级的优化过程，即30min滚动优化和5min超短期优化。综上所述，本文包含日前计划和日内调度的多级优化计算流程如图5所示。日前计划输出的分辨率为1h的日前计划作为日内调度的输入，MDP首先根据日前计划以及扩展短期预测，初始化分辨率为0.5h的行动指令并代入熵值回馈值，然后通过特定策略进行迭代，在迭代过程中同步更新超短期预测值，最终输出日内分辨率为5min的行动指令。
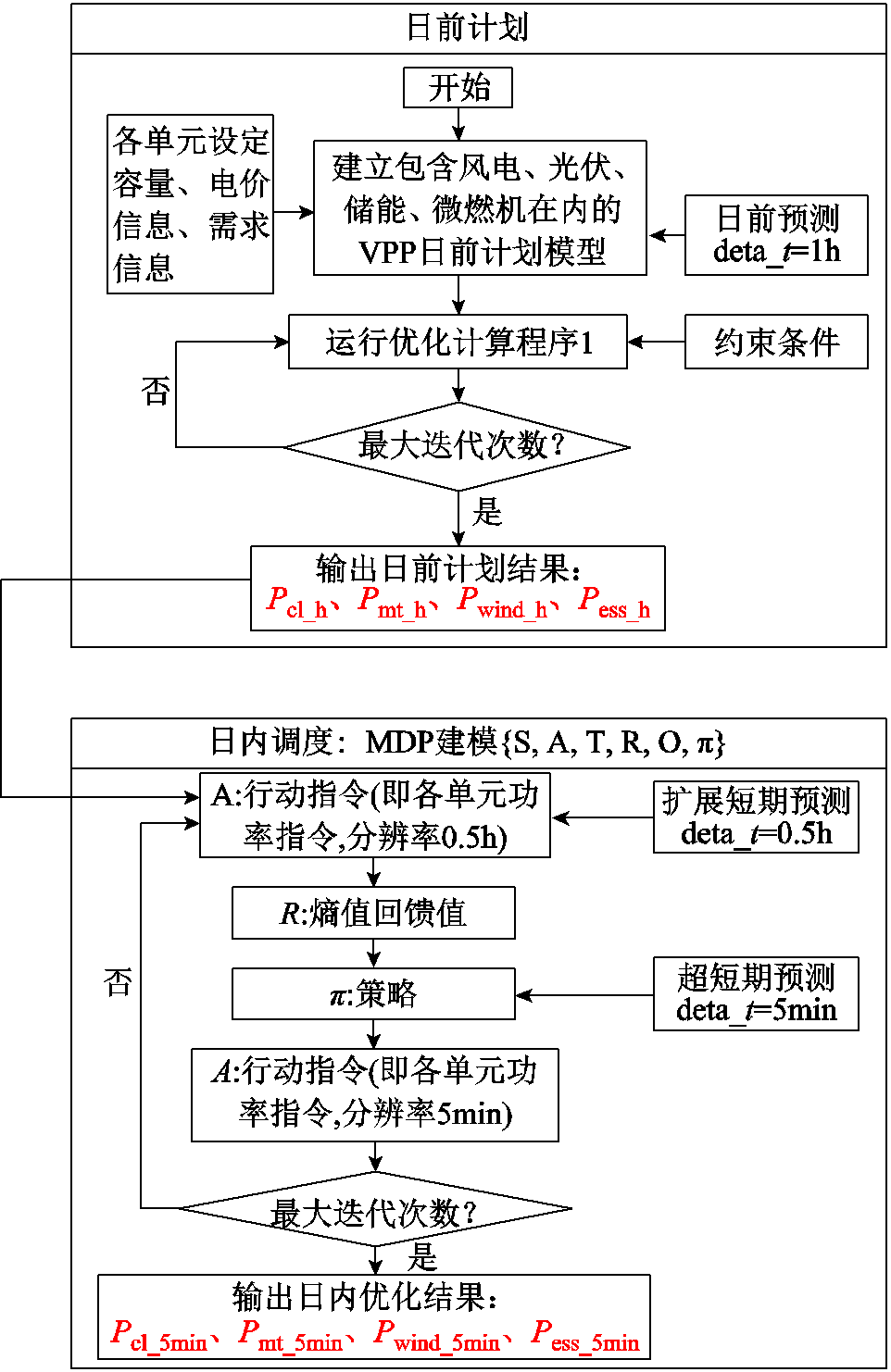
图5 多级优化调度计算流程
Fig.5 Multi-level optimal scheduling calculation flow chart
VPP算例配置如图6所示，VPP管控平台通过不同时间尺度的预测数据及与电网交互信息来进行优化决策，下发VPP参与市场交易电量，同时下发VPP中各聚合单元的优化指令。在优化决策中，设定风电与负荷日前、滚动、超短期预测的误差分别为25%、15%、5%；σ =0.05；微燃机MT单位功率调节成本0.65元/(kW·h)，储能调节成本0.3元/(kW·h)，可中断负荷中断成本0.2元/(kW·h)；Z1=0.145+j0.068，Z2=0.092+j0.021，Z3=0.051+j0.012，Z4=0.045+j0.008，Z5=0.02+j0.003。运行VPP多级调度优化程序，VPP参与市场交易的电价信息及多级优化曲线结果如图7所示，可控负荷调节量、微燃机优化调度曲线如图8所示。
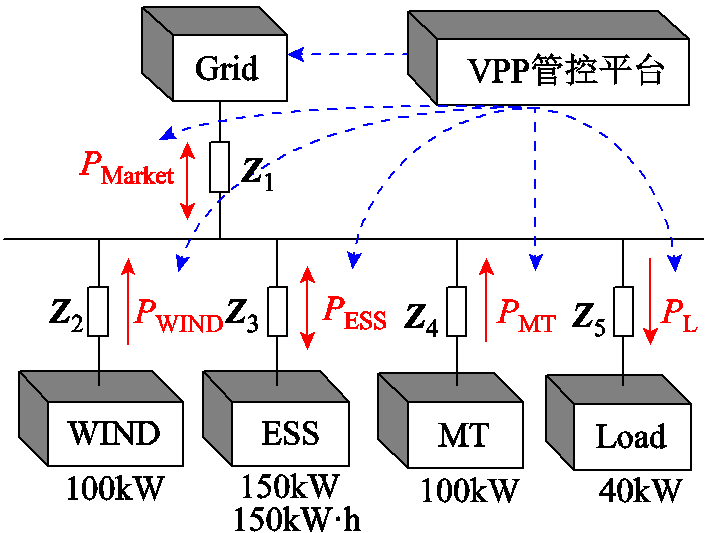
图6 VPP算例示意图
Fig.6 Schematic diagram of VPP calculation example
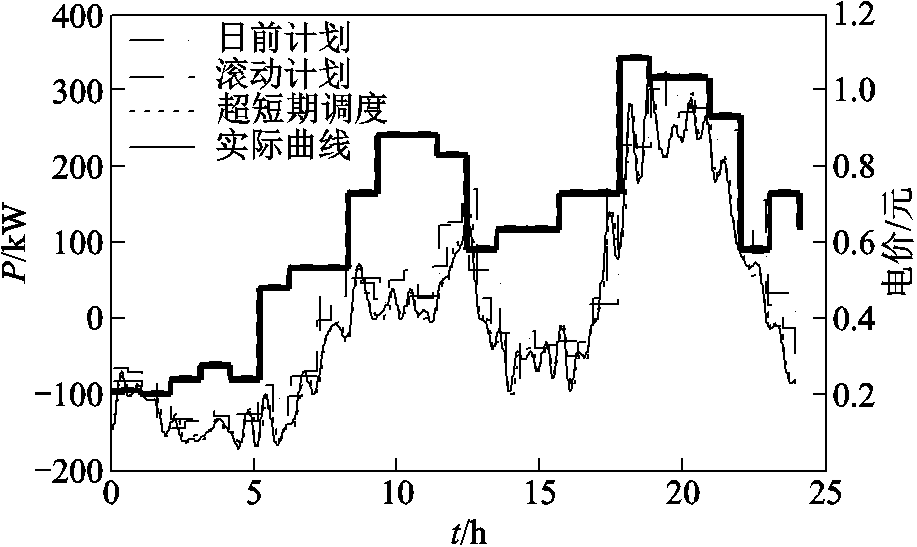
图7 VPP多级优化调度结果
Fig.7 VPP multi-level optimization scheduling results
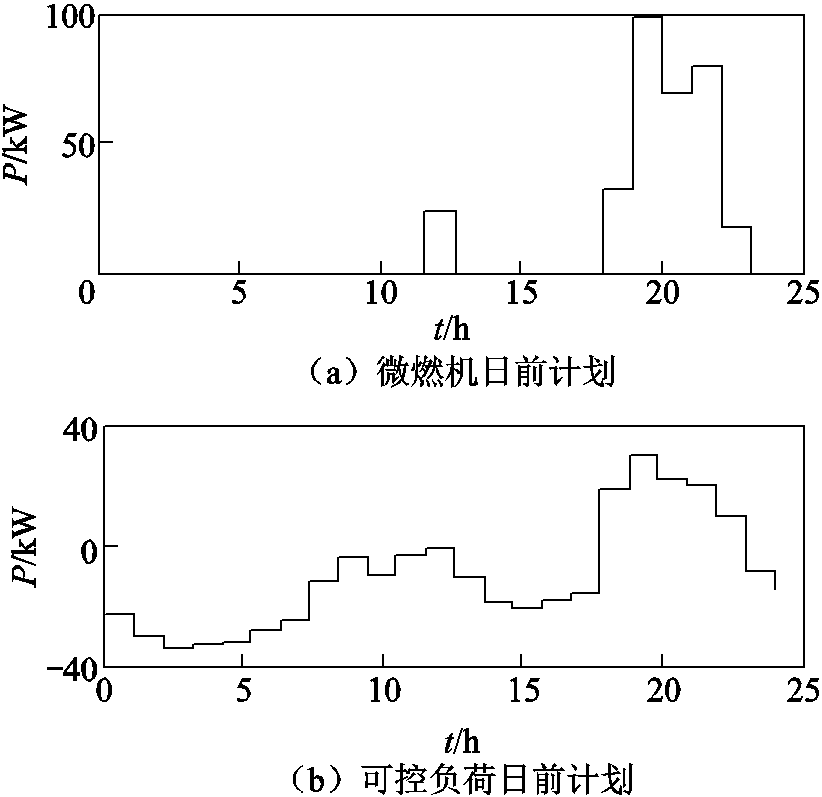
图8 微燃机及可控负荷优化调节曲线
Fig.8 MT and CL optimization curve
如图7所示，在多级优化中，日前计划根据电价信息、结合VPP中各单元运行及调节成本、环境成本等，在高电价时让VPP尽量多地参与市场，而在电价较低时，则让VPP以从市场购电储存为主。滚动优化根据日内预测对日前计划做小范围的修正，而超短期优化则在滚动基础上来实施反馈调节以保证VPP双向可调节的灵活性，最终实际曲线与日前计划接近，能够很好地按照既定的优化指令来执行，从而获得最优运行值。图8中，微燃机因环境成本，在储能调节能力不足时安排了计划出力，即在两个电价高峰时配合VPP向外售电；而可控负荷由于其双向调节特性，可灵活响应电价信息，对自身进行多用电、少用电或中断用电，图8中可调节负荷日前计划调节量为正时表示少用电的量，为负表示多用电的量。
储能单元在MDP中的概率模糊输出策略如图9所示。由图9可知，储能在超短期调度中对储能充放电功率进行了不同程度的模糊修正工作，以实现反馈调节，达到优化储能运行工况、平衡储能充放电能力，最终提高VPP可调节灵活性的目标。因为σ取了一个较小的值0.05，所以在概率模糊策略中，隶属度以大概率落在了隶属度函数曲线及邻域内，即保证了策略集的模糊力度。映射到图10的储能各级优化曲线中，超短期调度在滚动基础上进行了频繁的调整，最终使得实际运行曲线在整个时域内充电与放电相对平衡。
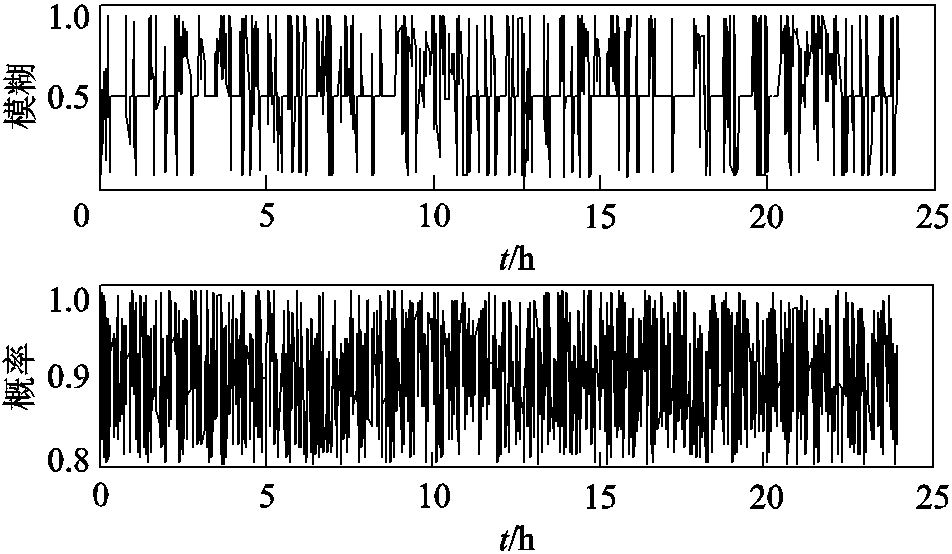
图9 储能概率模糊输出结果
Fig.9 Fuzzy probability output result of ESS
图10 储能多级优化调度结果
Fig.10 Multi-level optimized scheduling results of ESS
基于本文采用的多级优化调度方案的计算结果，对MDP模型中所采用的熵值回馈函数和概率-模糊策略进行对比讨论。
在分辨率为0.5h的滚动优化中，熵值函数的目的是通过VPP中灵活可调节单位来减小因日前预测误差带来的功率偏差，在一定范围内对日前计划进行修正。当回馈函数不以熵值进行建模，而以传统功率偏差的平均值为模型进行优化时，两者对比结果如图11所示。
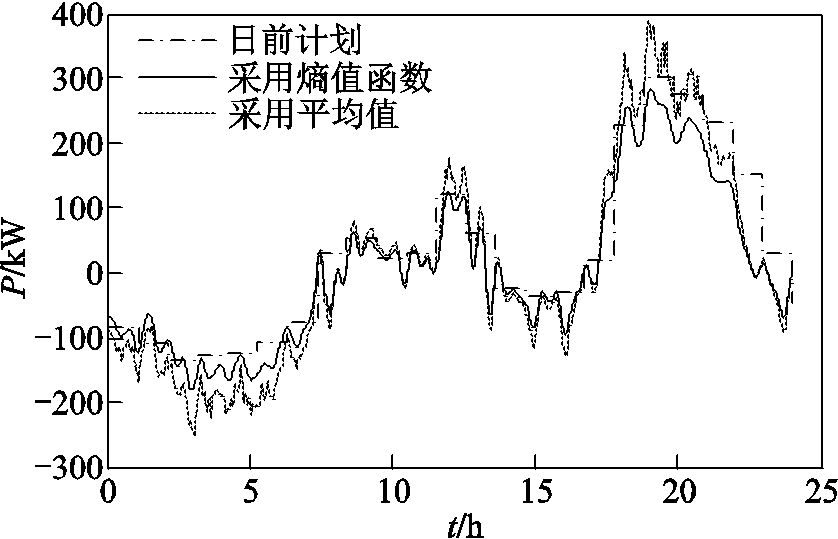
图11 方案对比结果
Fig.11 Comparison results
图11中，由于采用熵值函数模型中分别计入了峰谷差值和波动性，而传统平均值模型中并不能刻画波动性与峰谷差值，因此对比中采用熵值模型一方面在跟踪日前计划的跟踪能力更强，另一方面功率的波动性要小很多，两者波动性如图12所示。
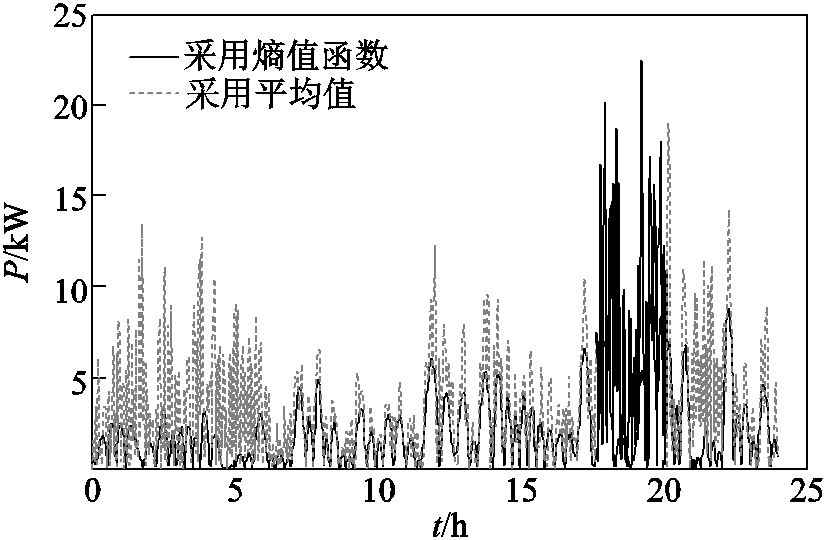
图12 波动性对比曲线
Fig.12 Volatility comparison curve
图12中，采用熵值模型的波动性明显要小，其方差为3.329，熵值为0.235；而采用传统平均值模型的方差为15.234，熵值为0.673，明显大于采用熵值模型来优化的结果。
在分辨率为5min的超短期优化中，概率模糊策略的目的是基于储能当前SOC及待充放电功率大小，通过指定模糊规则，并加入随机性，对储能单元在滚动优化中得到的指令进行调整，以使其SOC值在每一次充放电后尽量维持在合理的状态，从整个时域长度来均衡其充电和放电的能力。当超短期调度不以概率模糊策略来建模时，两者对比结果如图13所示。
由图13可知，未采用概率模糊策略对储能充放电功率进行实时调节，会导致其在跟踪日前计划曲线尖峰时，出现充放电能力不足的情况。两种方案下储能单元SOC曲线如图14所示。
图13 方案对比结果
Fig.13 Comparison results
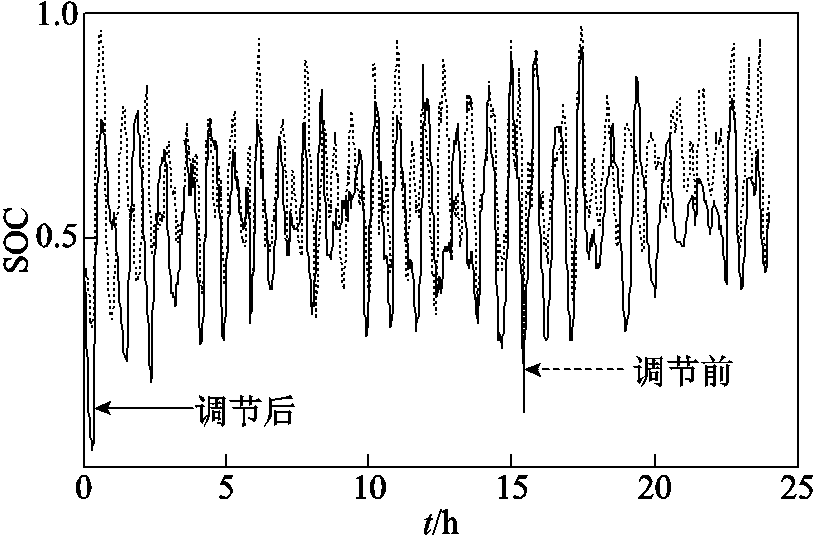
图14 储能SOC对比曲线
Fig.14 SOC comparison curve
如图14所示，在超短期优化中通过概率模糊策略集对储能充放电功率进行调节后的SOC曲线在整个时域内比未调节的SOC曲线，整体要居中，表征其充电与放电能力相对均衡。尤其是在SOC值较高、同时需要放电时，表现出一定优势，映射了图13中在跟踪日前计划尖峰功率值时刻，其跟踪能力更强。
综上所述，采用本文方案、未采用熵值回馈函数和未采用概率模糊策略三种方案下，VPP运行收益依次为4 819.5元、4 710.3元和4 546.8元。经对比，本文所提出的基于MDP的多级调度能够有效跟踪日前计划，从而使得VPP根据电价信息参与市场获利最多。
本文针对VPP提出了一种包括日前、滚动优化和超短期调度多时间尺度多层级的优化调度方法，具体结论如下：
1）在日内优化中，以MDP建模融合了滚动优化和超短期调度两极优化，减小建模层级，同时又能达到多级协调、逐级细化的目的。
2）在第二级滚动优化中，将滚动优化目标函数以熵值模型写入MDP的回馈函数中，可有效减少因预测误差导致的功率偏差峰谷值及波动性。
3）将超短期优化写入MDP的策略集中，利用概率模糊策略进行实时反馈调节，可有效均衡储能单元充电和放电能力，最终提升跟踪日前计划的能力，确保VPP整体获益最大化。
参考文献
[1]丛鹏伟, 唐巍, 娄铖伟, 等. 含高渗透率可再生能源的主动配电网两阶段柔性软开关与联络开关协调优化控制[J]. 电工技术学报, 2019, 34(6): 1263-1272. Cong Pengwei, Tang Wei, Lou Chengwei, et al. Two-stage coordination optimization control of soft open point and tie switch in active distribution network with high penetration renewable energy generation[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1263-1272.
[2]潘舒扬, 李勇, 贺悝, 等. 考虑微电网参与的主动配电网分区自动电压控制策略[J]. 电工技术学报, 2019, 34(21): 4580-4589. Pan Shuyang, Li Yong, He Li, et al. Automatic voltage control strategy based on zone-division for active distribution network with microgrids[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4580-4589.
[3]肖繁, 夏勇军, 张侃君, 等. 含新能源接入的配电网网络化保护原理研究[J]. 电工技术学报, 2019, 34(增刊2):709-719. Xiao Fan, Xia Yongjun, Zhang Kanjun, et al. Research on a principle of networked protection in distribution network with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2019, 34(S2):709-719.
[4]熊雄, 吴鸣, 季宇, 等. 微网群混合协调控制及功率管理策略研究[J]. 中国电机工程学报, 2018, 38(5): 1419-1427. Xiong Xiong, Wu Ming, Ji Yu, et al. Power management and coordinated control strategy research of multi-microgrids[J]. Proceedings of the CSEE, 2018, 38(5): 1419-1427.
[5]窦晓波, 常莉敏, 倪春花, 等. 面向分布式光伏虚拟集群的有源配电网多级调控[J]. 电力系统自动化，2018, 42(3): 21-31. Dou Xiaobo, Chang Limin, Ni Chunhua, et al. Multi-level dispatching and control of active distribution network for virtual cluster of distributed photovoltaic[J]. Automation of Electric Power Systems, 2018, 42(3): 21-31.
[6]丁明, 刘先放, 毕锐, 等. 采用综合性能指标的高渗透率分布式电源集群划分方法[J]. 电力系统自动化, 2018, 42(15): 47-52. Ding Ming, Liu Xianfang, Bi Rui, et al. Method for cluster partition of high-penetration distributed generators based on comprehensive performance index[J]. Automation of Electric Power Systems, 2018, 42(15): 47-52.
[7]麻秀范, 余思雨, 朱思嘉, 等. 基于多因素改进Shapley的虚拟电厂利润分配研究[J]. 电工技术学报, 2020, 10.19595/j.cnki.1000-6753.tces.191515. Ma Xiufan, Yu Siyu, Zhu Sijia, et al. Research of profit allocation to virtual power plant members based on improved multifactor shapley value method[J]. Transactions of China Electrotechnical Society, 2020, 10.19595/j.cnki.1000-6753.tces.191515.
[8]王宣元, 刘敦楠, 刘蓁, 等. 泛在电力物联网下虚拟电厂运营机制及关键技术[J]. 电网技术, 2019, 43(9): 3175-3183. Wang Xuanyuan, Liu Dunnan, Liu Zhen, et al. Operation mechanism and key technologies of virtual power plant under ubiquitous internet of things[J]. Power System Technology, 2019, 43(9): 3175-3183.
[9]黄昕颖, 黎建, 杨莉, 等. 基于投资组合的虚拟电厂多电源容量配置[J]. 电力系统自动化, 2015, 39(19): 75-81. Huang Xinying, Li Jian, Yang Li, et al. Investment portfolio based multi energy capacity allocation of virtual power plant[J]. Automation of Electric Power System, 2015, 39(19): 75-81.
[10]袁桂丽, 陈少梁, 刘颖, 等. 基于分时电价的虚拟电厂经济性优化调度[J]. 电网技术, 2016, 40(3): 826-832. Yuan Guili, Chen Shaoliang, Liu Ying, et al. Economic optimal dispatch of virtual power plant based on time-of-use power price[J]. Power System Technology, 2016, 40(3): 826-832.
[11]张高, 王旭, 蒋传文. 基于主从博弈的含电动汽车虚拟电厂协调调度[J]. 电力系统自动化, 2018, 42(11):48-55. Zhang Gao, Wang Xu, Jiang Chuanwen. Stackelberg game based coordinated dispatch of virtual power plant considering electric vehicle management[J]. Automation of Electric Power Systems, 2018, 42(11): 48-55.
[12]孙国强, 周亦洲, 卫志农, 等. 能量和旋转备用市场下虚拟电厂热电联合调度鲁棒优化模型[J]. 中国电机工程学报, 2017, 37(11): 3118-3128. Sun Guoqiang, Zhou Yizhou, Wei Zhinong, et al. Thermal and electrical scheduling of a virtual power plant for participating in energy and spinning reserve markets based on robust optimization[J]. Proceedings of the CSEE, 2017, 37(11): 3118-3128.
[13]陈妤, 卫志农, 胥峥, 等. 电力体制改革下的多虚拟电厂联合优化调度策略[J]. 电力系统自动化, 2019, 43(7): 42-49. Chen Yu, Wwei Zhinong, Yu Zheng, et al. Optimal scheduling strategy of multiple virtual power plants under electricity market reform[J]. Automation of Electric Power Systems, 2019, 43(7): 42-49.
[14]张丙旭, 许刚. 计及需求差异的电动汽车并网滚动时域优化[J]. 电力系统自动化, 2020, 44(13): 106-114. Zhang Bingxu, Xu Gang. Rolling horizon optimization for grid-connected electric vehicles considering demand difference[J]. Automation of Electric Power System, 2020, 44(13): 106-114.
[15]车泉辉, 娄素华, 吴耀武, 等. 计及条件风险价值的含储热光热电站与风电电力系统经济调度[J]. 电工技术学报, 2019, 34(10): 2047-2055. Che Quanhui, Lou Suhua, Wu Yaowu, et al. Economic dispatching for power system of concentrated solar power plant with thermal energy storage and wind power considering conditional value-risk[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2047-2055.
[16]刘思源, 艾芊, 郑建平, 等. 多时间尺度的多虚拟电厂双层协调机制与运行策略[J]. 中国电机工程学报, 2018, 38(3): 753-761. Liu Siyuan, Ai Qian, Zheng Jianping, et al. Bi-level coordination mechanism and operation strategy of multi-time scale multiple virtual power plants[J]. Proceedings of the CSEE, 2018, 38(3): 753-761.
[17]田立亭, 程林, 郭剑波, 等. 虚拟电厂对分布式电源的管理和互动机制研究综述[J]. 电网技术, 2020, 44(6): 2097-2108. Tian Liting, Cheng Lin, Gu Jianbo, et al. A review on the study of management and interaction mechanism for distributed energy in virtual power plants[J]. Power System Technology, 2020, 44(6): 2097-2108.
[18]钱科军, 袁越, 石晓丹, 等. 分布式发电的环境效益分析[J]. 中国电机工程学报, 2008, 28(29): 11-15. Qian Kejun, Yuan Yue, Shi Xiaodan, et al. Environmental benefits analysis of distributed generation[J]. Proceedings of the CSEE, 2008, 28(29): 11-15.
[19]熊雄. 微网群混合协调控制及其有功功率优化研究[D].北京: 中国农业大学, 2017.
[20]Meghdadi A H, Akbarzadeh-T M R. Probabilistic fuzzy logic and probabilistic fuzzy systems[C]//The 10th IEEE International Conference on Fuzzy Systems, Melbourne, Australia, 2001: 1127-1130.
Research on Multi-Time Scale Optimal Scheduling of Virtual Power Plant Based on Real-Time Feedback of Fuzzy-Probability Strategy
Abstract The day-ahead plan and operation scheme of virtual power plant (VPP) are the strong guarantee for realizing economic or technical benefits under its internal and external randomness. The multi-level optimization scheduling framework of VPP including day-ahead plan, rolling plan and real-time scheduling is proposed, and optimization models of different scales are established to achieve optimization robustness through the idea of ‘multi-level scheduling and step-by-step refinement’. In the day-ahead plan, a model is established with the goal of maximizing market benefits of virtual power plants. In intra-day optimization, based on the Markov decision process (MDP), the two-layer optimization of 30-min scale rolling plan and 5-min scale real-time scheduling are combined to reduce the modeling level. In the MDP model, the entropy feedback function is established to characterize the rolling optimization process, and the fuzzy-probability strategy is established to characterize the real-time optimization process to adjust the state of charge of energy storage (state of charge, SOC), which are finally effectively track the goals of day-ahead plan to maximize economic benefits. Finally, the proposed scheme was verified by calculation examples.
Keywords: Virtual power plan (VPP), optimal scheduling, multi-time scale, Markov decision process (MDP), fuzzy-probability strategy
中图分类号：TM62; TM73
DOI:10.19595/j.cnki.1000-6753.tces.200929
国家重点研发计划资助项目（2017YFB0902600）。
收稿日期 2020-07-31
改稿日期 2020-10-12
李翔宇 男，1988年生，博士研究生，研究方向为新能源并网运行及其控制。E-mail：410489024@qq.com（通信作者）
赵冬梅 女，1968年生，教授，博士生导师，研究方向为电力系统分析、稳定和控制、电力市场及新能源并网运行。E-mail：zhao-dm@ncepu. edu. cn
（编辑 赫蕾）