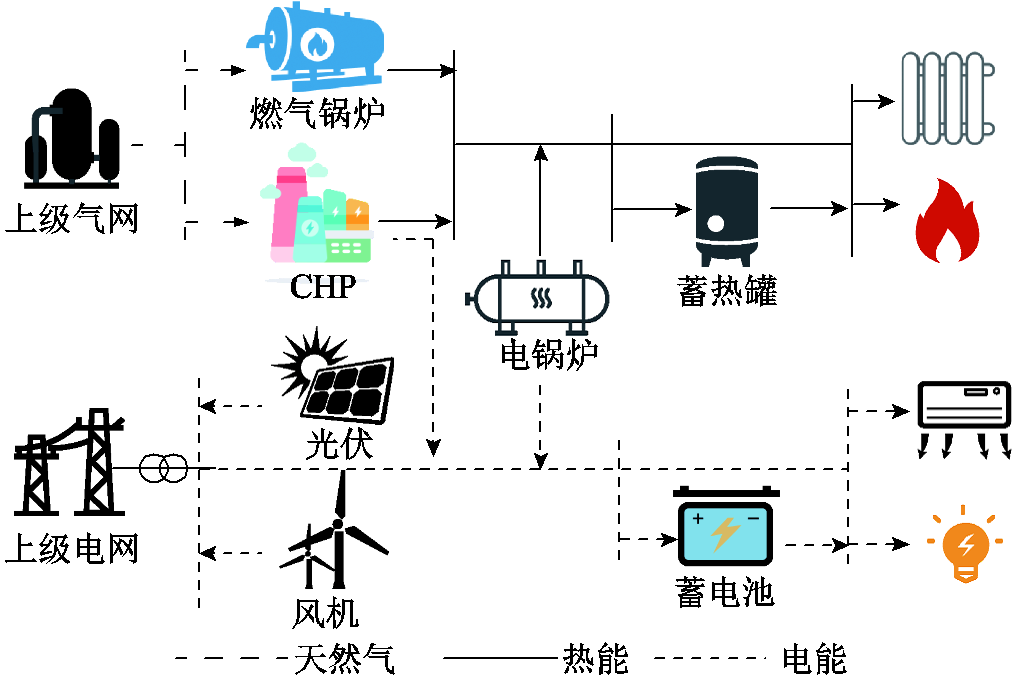
图1 多能耦合系统基本结构
Fig.1 Basic structure of MECS
摘要 提高能源系统运行经济性、减少污染排放、改善能源利用效率是我国未来能源系统发展的重要目标。但是,在实际能源系统规划中,由于上述不同目标之间具有复杂的关联性,因此当问题的目标函数数量多于3个且存在不确定性参数时,现有方法往往难以实现对该类问题的有效求解。为应对上述挑战,该文提出一种面向多能耦合系统规划的高维多目标优化分析框架。首先,在深入剖析多能源系统中源荷耦合特性及其对系统运行影响的基础上,提出了综合考虑经济-环境-社会因素的综合能源系统多目标规划范式;然后,鉴于不同规划目标之间存在的天然矛盾性并充分考虑系统中供需侧行为的不确定性,分别以投资运行成本最小、用能效率最高、碳排放最小以及供能不满意度最小作为目标,构建了针对多能系统规划的高维多目标优化模型,该模型综合考虑系统元件容量配置以及终端负荷管理,并利用区间方法计及各不确定性因素的影响,从而使最终规划方案可有效兼顾最优性与鲁棒性;接着,根据所建模型的特点,利用模糊偏好函数法分别对目标函数和约束条件进行处理,将其转换为确定性优化问题,采用基于降维分解的带精英策略非支配排序遗传算法(DNSGAⅡ)对此进行求解;最后,通过相关算例分析,验证所提方法的有效性。
关键词:多能耦合系统 高维多目标优化 规划 不确定性 社会因素
随着社会工业的迅猛发展,经济、能源、生态三者之间的矛盾愈益显现,如何开发利用可再生能源(Renewable Energy Source, RES)、提高能效、降低环境污染成为全球共同关注的热点问题[1]。作为未来能源系统的重要组织形态,多能耦合系统(Multi-Energy Coupled System, MECS)集电、热、气等能源于一体,通过灵活配置与统一管理,可有效提升能源系统整体运行的经济性与可靠性,降低污染排放,并促进可再生能源利用及终端能源利用效率的提高[2]。
在实际应用中,要确保MECS在满足用户负荷需求的条件下实现经济、绿色、高效运行,首先需要对系统的设备选择和容量配置进行科学规划[3]。为此,目前国内外学者已开展了广泛研究。例如,文献[4]针对系统设备选型以及容量配置构建多能源系统的混合整数线性规划模型,增强系统运行的灵活性和经济性。文献[5]提出考虑动态能源定价策略的环境经济双层博弈模型,对多能耦合系统进行容量规划,提高能源的利用效率和环境效益。文献[6]提出多能源系统的电热气耦合基础设施最优协调扩展规划模型,并验证其有效性和经济性。为充分挖掘电化工产业对RES消纳的贡献,文献[7]提出计及电转气的电/热/气耦合系统规划模型,大大提高了RES的利用效率,从而实现了系统用能成本的降低,提高系统经济性。文献[8]针对城市地区的分布式能源系统,提出一种基于增强ε约束技术的多目标优化规划方法,对系统的总年度成本和温室气体排放进行优化,实现了系统的最佳设计规划和运行。然而,在上述研究中,并没有考虑各类RES出力的不确定性对系统优化产生的影响。为此,文献[9]以区域综合能源系统为研究对象建立概率优化模型,采用两点估计法处理光伏出力的不确定变量。文献[10]采用基于数据驱动的两阶段鲁棒规划方法处理风电不确定性,并利用列和约束生成算法求解。文献[11]考虑短期和长期负荷的不确定性,构建了基于机会约束的优化模型,以最小化系统的投资成本为优化目标,确保满足未来的随机功率和天然气需求所需的置信容量。文献[12]提出了一种含有电转气(Power to Gas, P2G)的电气耦合系统实时调度模型,有效降低了RES出力不确定性对系统的影响。此外,文献[13]还提出了一种针对含风力、太阳能和燃料电池混合分布式发电系统的多目标规划模型,采用基于Hammersley序列采样的ε约束方法进行求解,并验证其可有效兼顾供电的可靠性与经济性。在上述研究中,均假设用户负荷需求恒定或符合特定的分布,未考虑MECS下需求侧管理措施的潜在作用。对此,文献[14]研究并提出一种综合考虑需求响应与MECS容量规划的多目标优化模型,深入分析了实施需求响应对于提升MECS运行经济性和灵活性的贡献。此外,文献[15]还提出一种考虑消费者行为耦合效应的多能源系统的综合需求响应模型,仿真结果表明该模型在提高系统经济性和用户满意度等方面有良好表现。此外,文献[16]还提出一种考虑复杂需求响应不确定性的区域级电-气耦合系统调度模型,深入分析源荷交互对MECS综合效益的影响。
虽然目前针对MECS规划问题已获得学术界的广泛关注,但要满足实际工程需要,现有研究仍存在以下不足,亟待进一步解决:①现有研究大多只从经济或环境等单一或两个维度建立规划模型,未能充分考虑市场环境下MECS优化目标的多样性与可拓展性,例如缺少对终端能效及用户用能舒适度的必要考量。②针对MECS规划中的不确定性问题,现有研究大多采用基于最劣场景的鲁棒优化或基于概率场景的随机优化方法进行处理。其中,鲁棒优化方法求解结果通常较为保守,对规划方案的经济性会产生不利影响;而随机优化所需要的大量历史数据在实际工程中往往无法获得。
鉴于此,本文提出一种面向多能耦合系统规划的高维多目标优化分析框架,构建能够有效适应RES出力及直接负荷控制(Direct Load Control, DLC)不确定性的多能耦合系统区间优化方法。与现有研究不同,本文模型综合考虑经济、环境、能效以及用户满意度需求,建立高维多目标优化模型,并采用区间方法描述RES出力和需求侧响应可用率两方面的不确定性因素对系统的影响,使规划方案兼具最优性与鲁棒性,并利用模糊偏好函数将其转换为确定性的多目标优化问题,采用基于降维分解的遗传算法实现求解,算例仿真结果证明了本文所提方法的合理性和有效性。
本文以含有电、热、气的园区级MECS为研究对象,其基本结构如图1所示。在实际运行过程中,系统内部的光伏(Photovoltaic, PV)、风机(Wind Generation, WG)及热电联产机组(Combined Heat and Power, CHP)产电供给终端用户。当系统内部产生的电能无法满足负荷需求时,系统运营商向上级配电网购电用以满足终端负荷需求;当产电量过剩时,将多余电量储存在蓄电池(Electricity Storage, ES)中作为备用;系统运营商向天然气网购气,通过CHP、燃气锅炉(Gas Boiler, GB)和电锅炉(Electric Boiler, EB)将其转换成热能,用于满足用户的热负荷需求或输送到蓄热罐(Thermal Storage, TS)中进行存储,实现能量的有效利用。系统运营商通过优化其投资策略以及在运行阶段协调调度供应侧和需求侧资源,以满足用户的能源需求。
本文提出了一种多能源耦合系统通用建模工具,例如:居民住房、智能楼宇、工业园区、整座城市等均可采用该模型进行建模。作为多能源系统的一种典型实现范式,园区级MECS通常规模较小,内部设备容量也较低,因此本文以其作为研究对象可有效降低建模及求解的复杂性。但需强调的是,除了能满足上述综合园区形式的规划需求之外,本文所提方法也能满足其他形式多能源系统规划的应用需要。相关能源形式也不仅局限于电能、热能、天然气,亦可包括冷等其他形式。

图1 多能耦合系统基本结构
Fig.1 Basic structure of MECS
在实际规划决策时,对于投资商而言,一方面希望尽量降低系统投资和运行总成本,另一方面还希望尽可能提高对RES的利用,增加RES在系统用能所占比例;但是对于用户而言,希望能够尽量拥有较高的供能质量和用能舒适度,降低因参与需求侧响应项目带来的效用损失。根据上述目标的相互作用与内在联系,几个目标相互具有明显的矛盾。因此,MECS规划属于典型的高维多目标优化问题。相比于传统双目标优化,本文问题的优化目标数量更多,且不同目标之间存在复杂的关联性。此外,系统中RES出力与需求侧参与的天然不确定性还导致决策的可行空间是动态变化的。这些因素的共同作用使得上述模型建立和求解均存在很大挑战。
为解决上述问题,本文提出一种针对MECS规划的高维多目标区间优化框架,其规划框架如图2所示。该模型综合考虑实际MECS规划中对于经济、环境、能效及用能舒适度等多方面因素的要求,并通过引入区间优化方法处理系统中的不确定性因素,以实现所得规划方案能够同时兼顾最优性与抗风险能力。
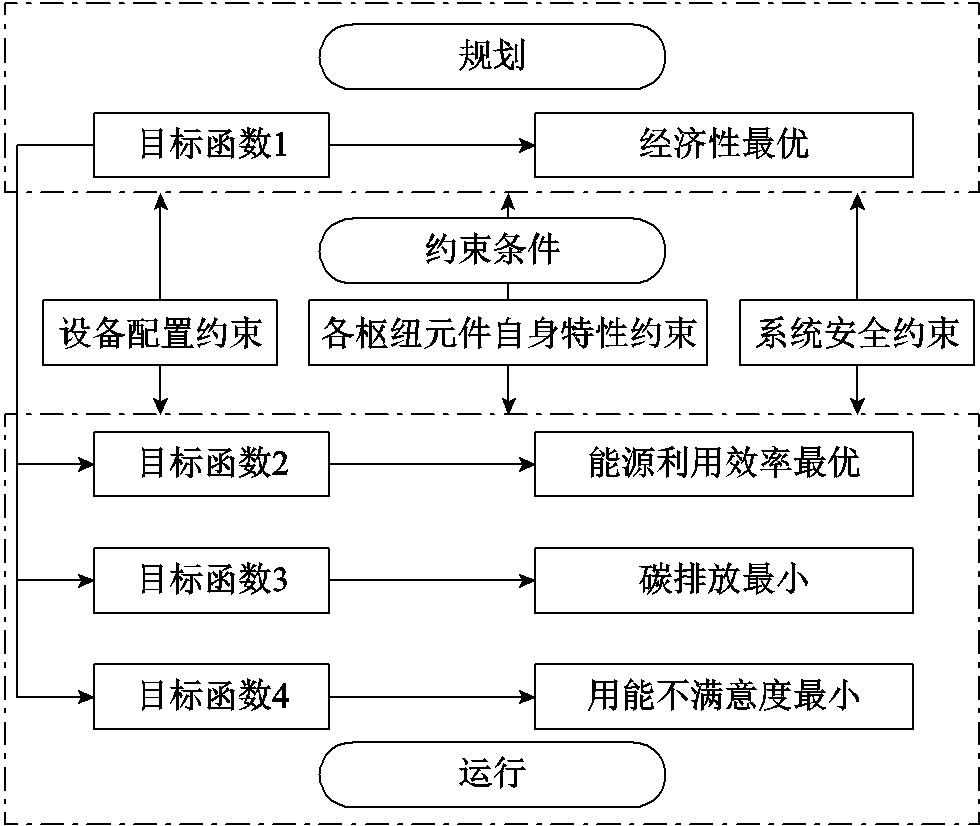
图2 MECS规划框架
Fig.2 Framework of MECS planning
CHP由燃气轮机和余热锅炉构成,能够生产电能和热能。其中,CHP的发电功率是其消耗的天然气量的一次函数,并小于其配置容量,如式(1)和式(2)所示。CHP产热功率与产电功率之间受到其热电比限制,如式(3)所示。
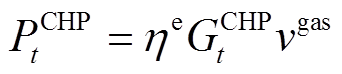 (1)
(1)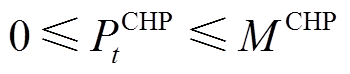 (2)
(2)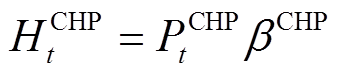 (3)
(3)式中,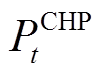 为t时刻CHP的发电功率;
为t时刻CHP的发电功率;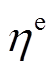 为CHP的产电效率;
为CHP的产电效率;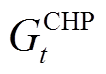 为t时刻CHP的耗气量;
为t时刻CHP的耗气量;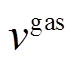 为天然气热值;
为天然气热值;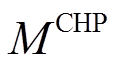 为CHP的容量配置;
为CHP的容量配置;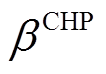 为CHP的热电比。
为CHP的热电比。
风电机组的输出功率主要受所在位置风速的影响。在大自然中,由于风速具有随机性和间歇性,因此风机出力是不确定变量。为此,本文定义载荷因数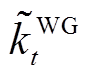 表示时段t风速下风机实际发电功率与其额定容量之比,进而风电出力可表示为
表示时段t风速下风机实际发电功率与其额定容量之比,进而风电出力可表示为
 (4)
(4)式中,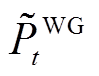 为风机的发电功率;
为风机的发电功率;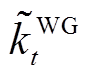 为描述随机风速下风机载荷率变化的区间变量,
为描述随机风速下风机载荷率变化的区间变量,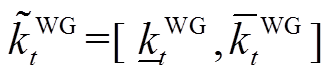 ,
,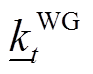 和
和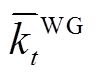 分别为波动区间的下界和上界;
分别为波动区间的下界和上界;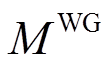 为风机的容量配置。
为风机的容量配置。
太阳光照强度和环境温度是影响光伏发电输出功率的关键因素。考虑到自然中温度和光照的不确定性,与风机模型类似,PV的运行特性可表示为
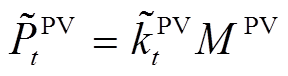 (5)
(5)式中,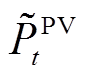 为光伏的发电功率;
为光伏的发电功率;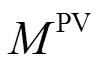 为光伏的容量配置;
为光伏的容量配置; 为表征PV载荷率随机变化的区间变量,
为表征PV载荷率随机变化的区间变量,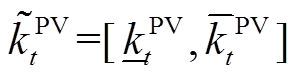 。
。
电/燃气锅炉分别以电力和天然气作为能源并可转换为热能。对于上述设备,产热功率与耗电/耗气之间的关系为
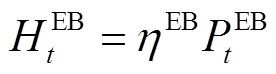 (6)
(6)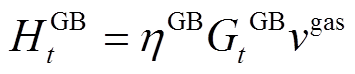 (7)
(7)此外,最大产热功率还受到配置容量的限制,即
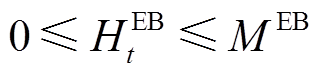 (8)
(8)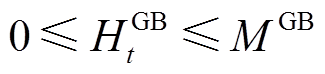 (9)
(9)式中,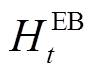 、
、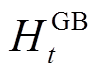 分别为t时刻电锅炉和燃气锅炉的产热功率;
分别为t时刻电锅炉和燃气锅炉的产热功率;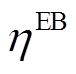 、
、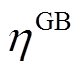 分别为t时刻电锅炉和燃气锅炉的产热效率;
分别为t时刻电锅炉和燃气锅炉的产热效率;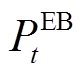 为t时刻电锅炉的用电功率;
为t时刻电锅炉的用电功率;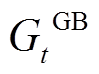 为t时刻燃气锅炉的耗气量;
为t时刻燃气锅炉的耗气量;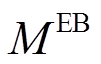 、
、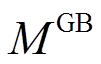 分别为电锅炉和燃气锅炉的配置容量。
分别为电锅炉和燃气锅炉的配置容量。
在EH运行中,电/热储能设备的储能状态(State of Charge, SOC)随充放电/热功率的变化关系为
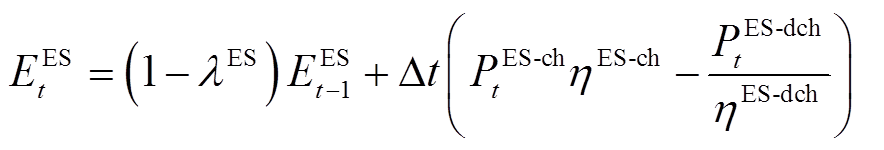 (10)
(10)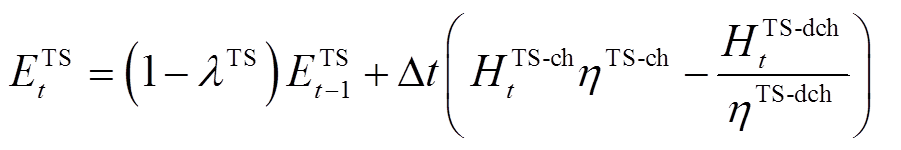 (11)
(11)式中,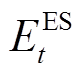 、
、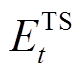 分别为t时刻电储能和热储能的储能状态;
分别为t时刻电储能和热储能的储能状态;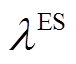 为电储能的自放电率;
为电储能的自放电率;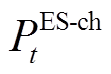 、
、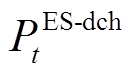 分别为电储能的充电和放电功率;
分别为电储能的充电和放电功率;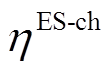 、
、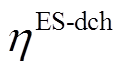 分别为电储能的充电和放电效率;
分别为电储能的充电和放电效率;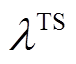 为热储能的自放热率;
为热储能的自放热率;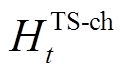 、
、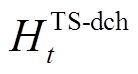 分别为热储能的充热和放热功率;
分别为热储能的充热和放热功率;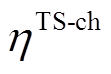 、
、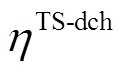 分别为热储能的充热和放热效率。
分别为热储能的充热和放热效率。
为防止储能设备过度充放,需对其SOC可变范围进行约束,即
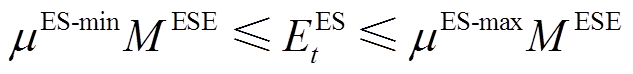 (12)
(12)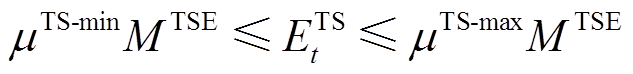 (13)
(13)式中,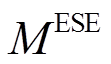 和
和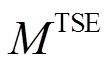 分别为电储能和热储能的配置容量;
分别为电储能和热储能的配置容量;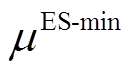 及
及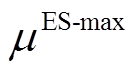 分别为电储能的最小和最大储能系数;
分别为电储能的最小和最大储能系数;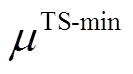 和
和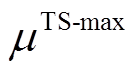 分别为热储能的最小和最大储能系数。
分别为热储能的最小和最大储能系数。
此外,同一时刻充放电/热不能同时进行,储能设备的充放功率约束为
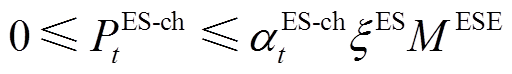 (14)
(14)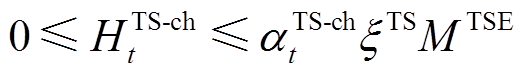 (15)
(15)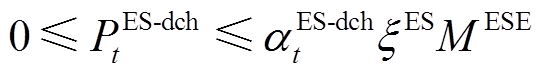 (16)
(16)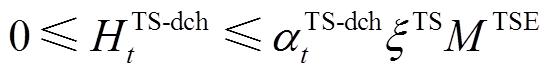 (17)
(17) (18)
(18)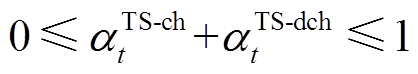 (19)
(19)式中,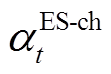 和
和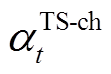 分别为电储能和热储能充电/热状态的0-1变量;
分别为电储能和热储能充电/热状态的0-1变量;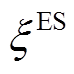 及
及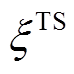 分别为电储能和热储能的功率-容量比值;
分别为电储能和热储能的功率-容量比值;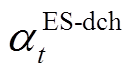 和
和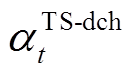 分别为电储能和热储能放电/热状态的0-1变量。
分别为电储能和热储能放电/热状态的0-1变量。
最后,为确保储能设备可持续运行,要求在一个调度周期内始末SOC应保持不变,即
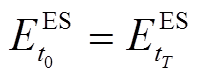 (20)
(20)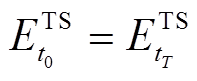 (21)
(21)式中,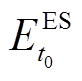 及
及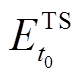 分别为t0时刻电储能/热储能的储能状态;
分别为t0时刻电储能/热储能的储能状态;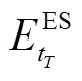 、
、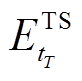 分别为tT时刻电储能/热储能的储能状态。
分别为tT时刻电储能/热储能的储能状态。
在MECS中,DLC项目的实施对象通常为热电联合调度的负荷,具体可包括电储热、电采暖及具有储能的中央空调负荷等。
根据系统调度需求,t时刻实际控制的负荷功率为
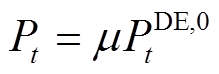 (22)
(22) (23)
(23)式中,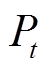 为t时刻可调控的负荷功率;
为t时刻可调控的负荷功率;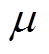 为系统中可调控负荷在总负荷中的占比;
为系统中可调控负荷在总负荷中的占比;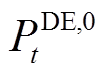 为t时刻的基准负荷功率;
为t时刻的基准负荷功率;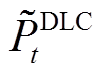 为t时刻的受控负荷功率值;
为t时刻的受控负荷功率值;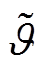 为负荷可调控率,反映了终端用户对于需求响应项目的参与度。由于不同用户在生活习惯与行为偏好上的不同以及负荷响应DLC时所处的状态不同,因此在实际系统运行时,
为负荷可调控率,反映了终端用户对于需求响应项目的参与度。由于不同用户在生活习惯与行为偏好上的不同以及负荷响应DLC时所处的状态不同,因此在实际系统运行时,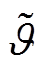 对于MECS运营者而言属于不确定性参数。
对于MECS运营者而言属于不确定性参数。
受控负荷在中断时段从系统中断开,在中断时段结束后,形成反弹负荷(Energy Payback, EP)[17]。本文采用三阶段自回归模型拟合EP特性,具体表达式为
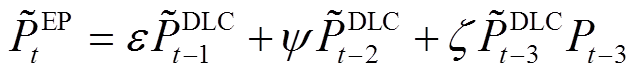 (24)
(24)式中,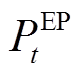 为t时刻的反弹负荷;
为t时刻的反弹负荷;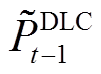 、
、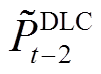 、
、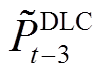 分别为t-1、t-2、t-3时刻的受控负荷;
分别为t-1、t-2、t-3时刻的受控负荷;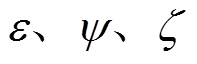 为反弹系数。
为反弹系数。
通过综合式(22)~式(24)可知,DLC模式下各时段系统的总负荷为
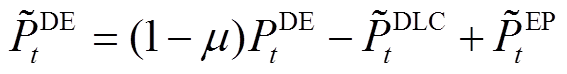 (25)
(25)如第1节所述,综合考虑经济-环境-社会因素的MECS规划旨在在满足系统基本特性约束的条件下,通过对设备配置及需求侧管理策略进行协同优化,以实现系统在上述目标属性上的协同趋优。针对上述问题,本文构建了与此相适应的数学模型,具体说明如下。
本文分别以系统投资运行经济性最优、综合能效最大、碳排放最低和用户不满意度最低为目标,构建MECS高维多目标区间优化规划模型。
1)投资经济性最优
以系统投资和运行成本年值最小化作为反映MECS规划经济性的目标函数,即
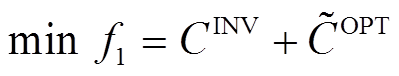 (26)
(26)式中,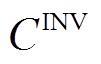 和
和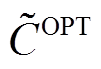 分别为系统投资成本年值、系统年运行成本,其具体计算式为
分别为系统投资成本年值、系统年运行成本,其具体计算式为
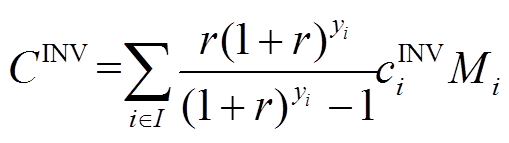 (27)
(27)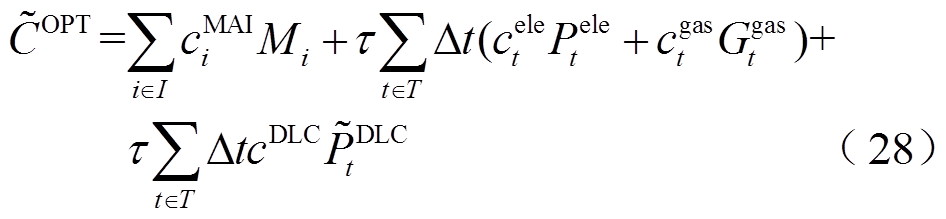
式中,I为系统设备元件类型集合(包括CHP、GB、EB、WG、PV、ES和TS);i为设备类别;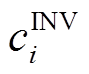 和
和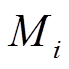 分别为设备i的单位容量投资成本及总配置容量;
分别为设备i的单位容量投资成本及总配置容量;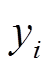 为设备寿命期;r为折现率,本文取8%;
为设备寿命期;r为折现率,本文取8%;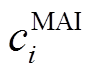 为设备i的单位容量年固定维护成本;T为系统运行时段;
为设备i的单位容量年固定维护成本;T为系统运行时段;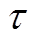 为一年中的天数;
为一年中的天数;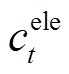 和
和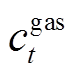 分别为系统从外部市场的购电和购气价格;
分别为系统从外部市场的购电和购气价格;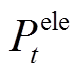 和
和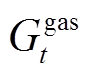 分别为系统购电和购气量;
分别为系统购电和购气量; 为系统向参与需求响应用户提供的补偿电价。
为系统向参与需求响应用户提供的补偿电价。
2)能源利用效率最优
MECS通过将多种类型能源深度融合以提升能源利用效率。本文以系统输出能量与上级电网和气网输入的能量之间的比值最大化作为反映MECS中能源利用效率的目标函数,其中可再生能源出力不作为系统的输入能量[18],即
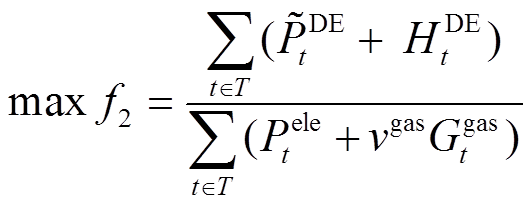 (29)
(29)式中,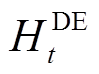 为系统的热负荷值。
为系统的热负荷值。
3)碳排放最低
MECS通过提高终端用能中可再生能源发电占比,降低传统化石能源消耗并减少污染物排放,以带来可观的环境效益。本文以系统总体碳排放量最小作为反映MECS环境效益的优化目标,具体表达式为
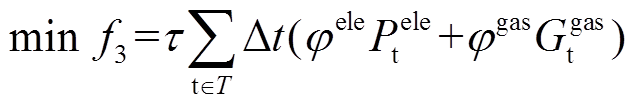 (30)
(30)式中,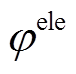 、
、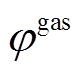 分别为外部系统中电能和天然气的碳排放系数。
分别为外部系统中电能和天然气的碳排放系数。
4)用户效用损失最小
MECS运营商通过实施需求响应项目可提高系统运行经济性并降低碳排放。但在这个过程中,对负荷进行直接控制往往会造成用户用能舒适度降低(即效用降低)。为避免上述不利影响,本文以用户不满意度[19]最小作为反映系统服务质量的优化目标,其具体表达式为
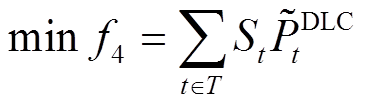 (31)
(31)式中,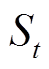 为时刻t因负荷转移引起的用户不满意量。该值越大,说明该时段实施DLC造成的用户舒适度损失也越大。
为时刻t因负荷转移引起的用户不满意量。该值越大,说明该时段实施DLC造成的用户舒适度损失也越大。
本文所建MECS规划模型的约束条件主要包括元件配置容量、系统安全及设备运行特性约束三个方面,具体说明如下。
系统配置约束要求MECS中各类设备的最大配置容量不能超过一定限度,以满足物理空间的限制,即
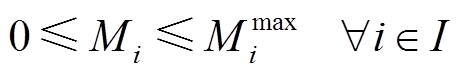 (32)
(32)系统安全约束主要包括内部电/热/气功率平衡约束式(33)~式(35)、系统与外部市场之间的能量交互约束式(36)和式(37)。
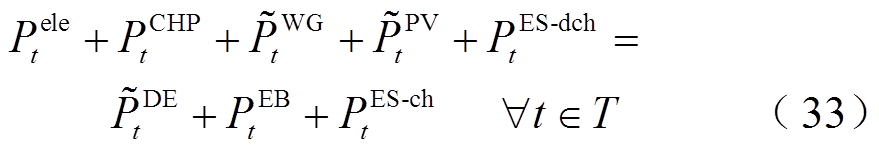
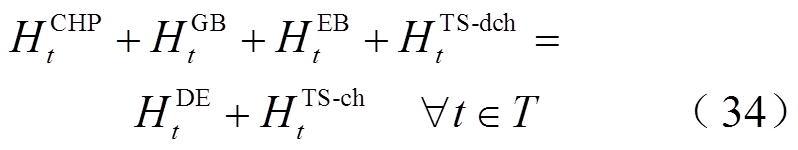
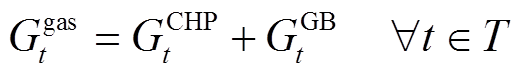 (35)
(35)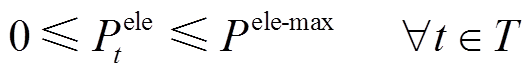 (36)
(36)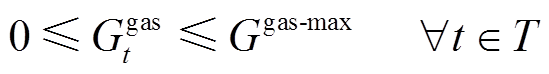 (37)
(37)此外,在MECS运行过程中,还需满足各设备元件自身特性约束。相关模型已在第2节中给出,在此不再赘述。
上述模型的优化变量包括:MECS中各类设备的配置容量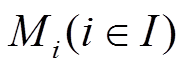 、系统从外部市场的购电/气量
、系统从外部市场的购电/气量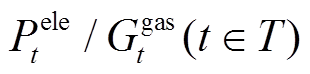 以及系统设备在各时段的运行状态
以及系统设备在各时段的运行状态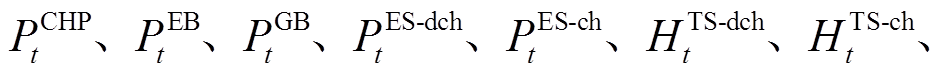
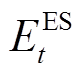 、
、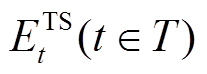 。
。
在求解上述模型之前,需要对问题中的区间变量进行处理,将其转变为确定性优化问题。
根据文献[20],区间数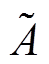 可用其中点值和半径值表示,即
可用其中点值和半径值表示,即
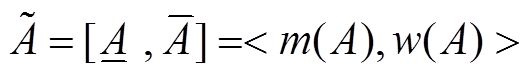 (38)
(38)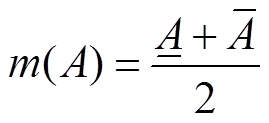 (39)
(39)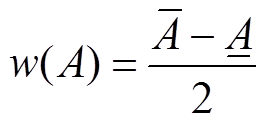 (40)
(40)进一步采用模糊偏好函数法[21]对区间数进行比较,即
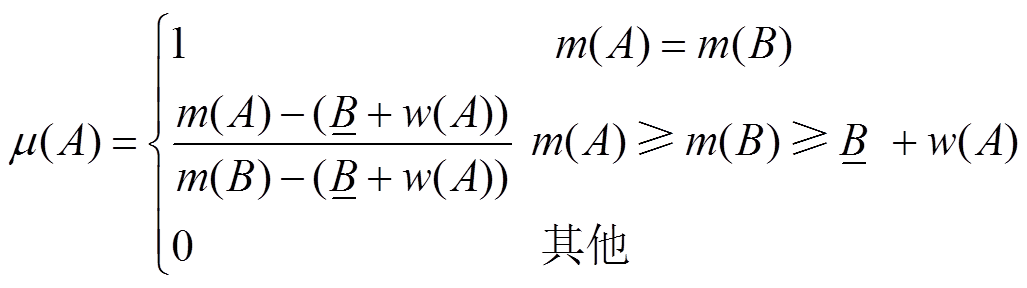 (41)
(41)式中,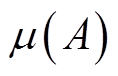 为区间数A大于B的等级,
为区间数A大于B的等级,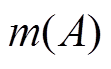 越大或
越大或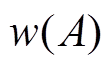 越小,则
越小,则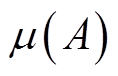 越大。
越大。
基于式(41)中的判断逻辑,对于给定阈值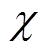 ,若
,若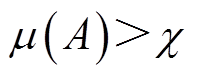 ,则选择区间数A,否则选择区间数B,如式(42)所示。
,则选择区间数A,否则选择区间数B,如式(42)所示。
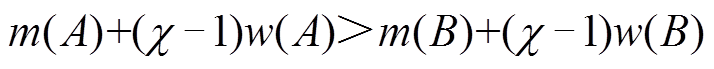 (42)
(42)式中,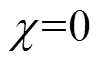 表示决策者倾向于区间半径小的区间数,而
表示决策者倾向于区间半径小的区间数,而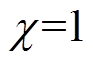 表示决策者只关心区间中点值。
表示决策者只关心区间中点值。
利用式(42)分别对含有区间变量的目标函数和约束条件进行转换,得到如式(43)~式(45)所示确定性模型。

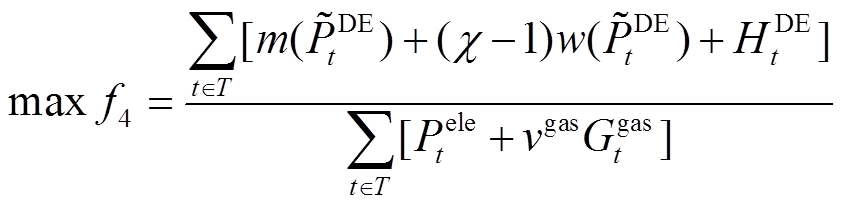 (44)
(44)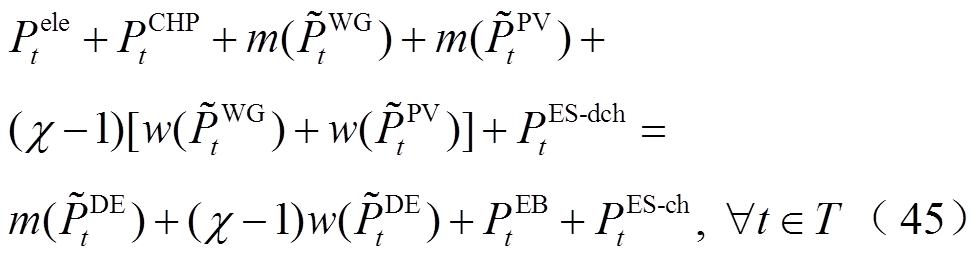
通过上述步骤将模型转换为一个常规确定性优化问题。
为高效求解所得确定性高维多目标优化问题,本文采用基于降维分解的带精英策略非支配排序遗传算法[22-23](Decomposition-based Non-dominated Sorting Genetic Algorithm-II, DNSGA-II)进行求解。通过对高维多目标优化问题分解,得到多个子问题,能够有效降低求解的难度。对多个子种群并行求解,将子问题帕累托解集存储到外部保存集,以进一步提高算法的求解效率。
具体求解流程如图3所示,具体如下:
1)利用模糊偏好函数处理含有不确定变量的目标函数和约束条件,使其转换为确定性优化问题。
2)计算目标函数之间的相关系数,基于相关系数对目标函数进行分组,实现高维多目标优化向多个子问题转换。
3)计算各个组内目标的相关系数平均值,以此来评价目标函数分组的合理性,并在子优化问题中引入聚合目标来反映其他目标函数的信息。
4)读取系统中设备参数,设置算法相关参数,初始化各个子种群。
5)对各个子问题并行求解,将所得子问题帕累托解集存储到外部的保存集中。
6)判断是否满足输出要求,若是,则输出帕累托最优解集;否则,返回步骤5,继续求解。
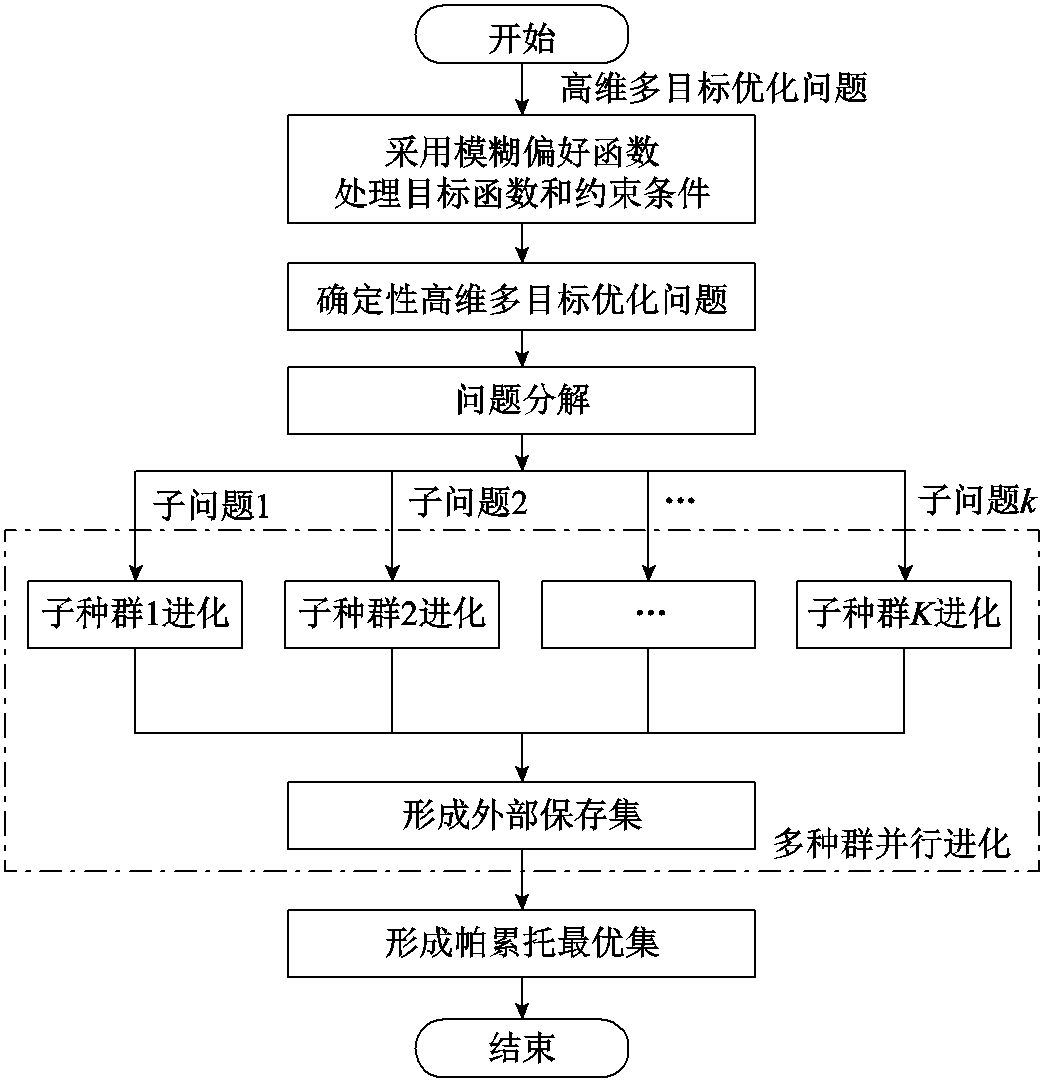
图3 求解流程
Fig.3 Solution procedure
本文以文献[24]中园区级电-热-气MECS为例进行仿真分析,验证本文所提方法的有效性。该系统的基本结构如图1所示,其设备关键参数见表1和表2。假设MECS从外部市场购买天然气的价格为3.45元/m3[19],购电价格见表3 [25]。系统的碳排放系数见表4。在正常运行条件下,系统的基准电/热负荷曲线如附图1所示。
表1 能量转换设备参数
Tab.1 Parameters of energy conversion equipment
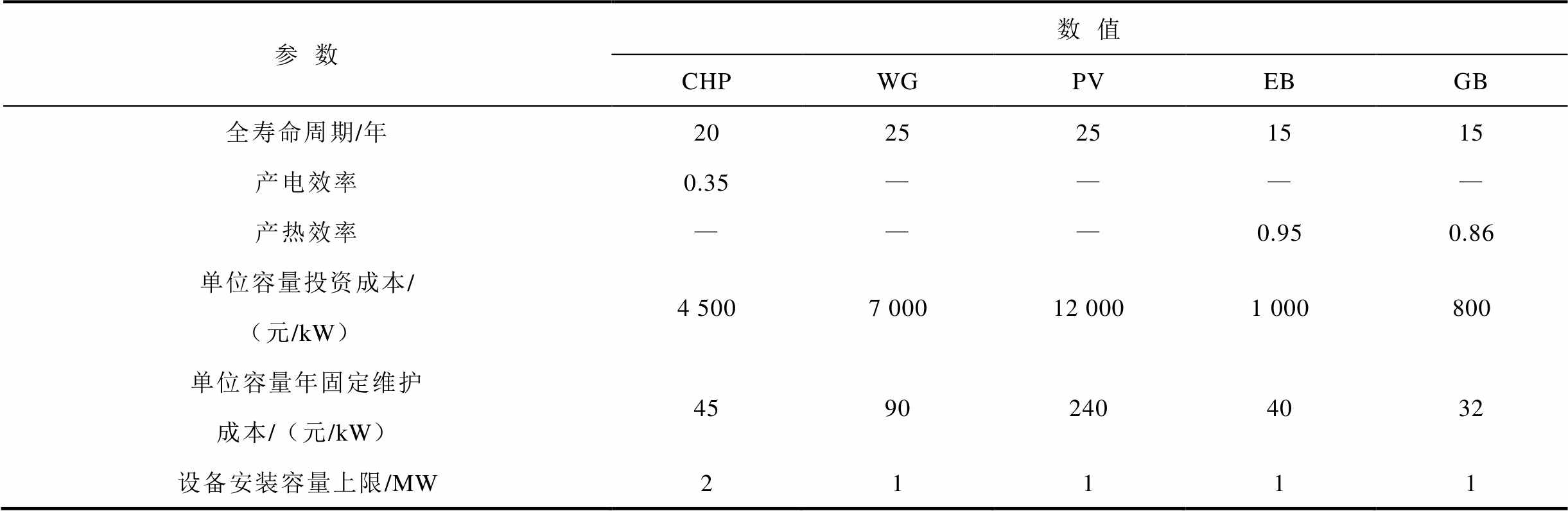
参数数值 CHPWGPVEBGB 全寿命周期/年2025251515 产电效率0.35———— 产热效率———0.950.86 单位容量投资成本/(元/kW)4 5007 00012 0001 000800 单位容量年固定维护成本/(元/kW)45902404032 设备安装容量上限/MW21111
表2 能量存储设备参数
Tab.2 Parameters of energy storage equipment

参数数值 ESTS 全寿命周期/年1020 充电/热效率0.950.88 放电/热效率0.950.88 最小储能系数0.20.1 最大储能系数0.90.9 自放电/热率0.0010.01 功率-容量比0.250.25 单位容量投资成本/[元/(kW·h)]1800200 单位容量年固定维护成本/ [元/(kW·h)]182 设备安装功率上限/kW500500 设备安装容量上限/(kW·h)2 0002 000
表3 购电电价
Tab.3 Electricity procurement price

时段电价/[元/ (kW·h)] 0∶00~7∶00, 22:00~24∶000.47 7∶00~9∶00, 12:00~17∶000.89 9∶00~12∶00, 17:00~22∶001.34
表4 碳排放系数
Tab.4 Carbon emission factor

能量来源碳排放系数/[kg/(kW·h)] 外部电网0.889 天然气0.2
针对典型日,风机和光伏的日前出力预测曲线分别如附图2和附图3所示。根据现有商业气象软件的预测精度,本文考虑风电和光伏出力的预测误差分别为各自预测值的±20%和±15%。此外,系统在不同时段可调控负荷的占比变化情况见表5,并假设需求侧负荷调控率的波动范围为±15%。
表5 不同时段可调控负荷的占比
Tab.5 Proportion of adjustable loads in different periods

时段22∶00~7∶007∶00~8:0011∶00~18:008∶00~11∶0018∶00~22∶00 比例0.20.30.5
在优化过程中,取系统运行仿真周期为1d(即24个时段),且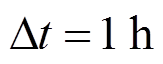 。受配变容量与燃气压力限制,MECS与外部系统之间传输的电功率和天然气流量上限分别取为1MW和300m3/h。
。受配变容量与燃气压力限制,MECS与外部系统之间传输的电功率和天然气流量上限分别取为1MW和300m3/h。
基于前期测试结果,对于算法的参数设置如下:种群规模为100,最大进化代数为300,变异因子为0.2,交叉因子为0.6。以处理器为Intel Core(TM)i7-8700@3.2GHz、内存为8G的计算机作为计算平台,基于Matlab R2014a平台编程,实现模型求解。相关程序的平均计算时间为31min。
5.2.1 高维多目标优化结果分析
基于第5.1节参数设置并考虑有关计算结果的工程意义,图4分别择选并展示了基于本文方法得到的三组帕累托前沿情况。相关结果分别描述了系统经济-环境、经济-供能质量及能效-供能质量等目标之间的关联关系。
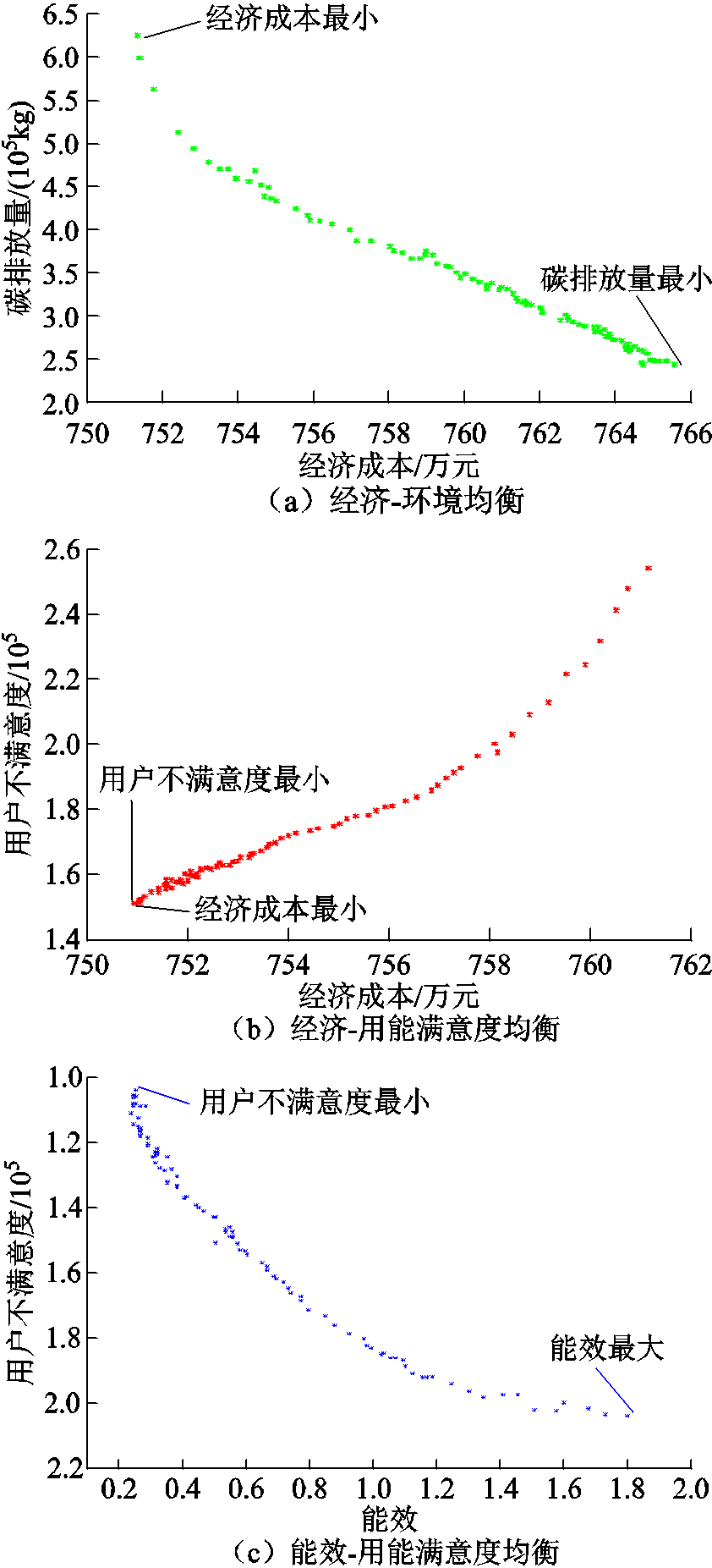
图4 帕累托前沿集
Fig. 4 Pareto frontier sets
由图4a可知,若系统以消纳可再生能源为目标,将导致系统的经济成本显著增加。此外,图4b表明系统的经济成本和用户不满意度呈正相关的关系,这是由于负荷削减和转移量的增加,同时造成了系统补偿成本和用户不满意度的增大。最后,图4c还表明在提高能源利用效率的同时,用户不满意度也随之增加。因而,在规划的过程中,需充分考虑目标之间的相互关系,对系统进行整体优化。
针对上述所得帕累托前沿,假设决策者对各优化目标具有相同的权重偏好,进一步采用改进逼近理想解排序法[26]确定唯一的折中方案。所得最终决策方案及其综合效益情况见表6。
表6 系统规划方案
Tab.6 Planning scheme of system

设备类型配置容量 热电联产/kW1 430 电锅炉/kW810 燃气锅炉/kW950 风机/kW746 光伏/kW306 蓄电池/(kW·h)1 332 储热罐/(kW·h)1 043 总成本/万元758.93 碳排放量/(105kg)3.78 能效1.25 用户不满意度/1051.93
由表6可见,本文方案风机和光伏的配置容量较大,虽然在投资成本方面略高,但是在经济性、环境、能效及用能舒适度四个方面均有较好的表现。出现上述结果的主要原因是,在本文研究中,系统运营商可通过采用DLC对高峰负荷进行削减,避免了高峰时段从外部市场购电,降低系统总运行成本的同时减少了系统的碳排放,使得MECS系统获得了较好的经济和环境效益。此外,在夜间电负荷低谷时,采用电锅炉进行供暖,实现了电热之间的能量转换,夜间电负荷的增加能够消耗更多的风电,从而减少了外部输入能源,提升了系统的用能效率。然而,由于需求响应的作用,负荷的削减和转移在提升能效的同时,也使得用户用能舒适度的降低。因此,作为系统运营商,在规划过程中需要充分计及各个指标,不能只以提升系统经济性或用能效率为目的,而完全不考虑用户用能舒适度。
5.2.2 不确定性建模方法的有效性分析
为验证本文所提方法的优势,对本文所提出的方案分别与确定性优化和鲁棒优化[27]方案在实际情况下的效益对比。基于5.1节参数设置,表7给出了10 000次随机模拟下的结果对比情况。
表7 不同规划模型下的最优方案
Tab.7 Optimal solution derived from different planning models

规划方法波动范围(%)预期成本/万元预期碳排放/(105kg)预期能效预期用户不满意度/105实际成本均值/万元实际碳排放均值/(105kg)实际能效均值实际用户不满意度均值/105 确定±10718.343.261.341.66782.424.141.122.01 ±20795.014.521.092.27 ±30811.334.891.052.38 鲁棒±10815.564.211.212.24742.243.771.161.94 ±20778.193.911.112.18 ±30791.354.171.072.29 区间±10758.933.781.251.93732.643.591.281.81 ±20750.483.631.221.87 ±30761.383.951.212.05
由表7结果可见,相比于确定性优化,区间优化考虑了供需侧不确定性因素,虽然其预期经济成本略高,但是所得的规划方案具有更强的抗风险能力,使得系统在实际运行过程中不会因为天气变化等原因导致运行结果出现很大的偏差,而确定性优化的实际运行偏差会跟随不确定性波动的提高而增加。此外,相对于鲁棒优化方案,区间优化能够有效兼顾决策方案的最优性与抗风险能力,不会过于保守而导致系统的经济成本大幅增加,因此具有更好的工程实用性。
5.2.3 算法性能分析
为揭示本文所用基于降维分解的非支配排序遗传算法的求解性能,本节通过引入世代距离指标和逆世代距离指标[23]并进一步使用无参统计假设检验方法[28]以分析相关指标值的统计学意义。相关计算结果见表8。
表8 评价指标计算结果
Tab.8 Calculation of evaluation indices

指标均值方差 世代距离指标2.434×10-47.57×10-5 逆世代距离指标3.967×10-21.02×10-1
由表8可见,两个指标的计算值均很小,这表明算法具有较好的收敛性和分布性。出现上述结果的主要原因是在DNSGA-II算法中,通过采用基于分解的快速非支配排序策略大大降低了计算的复杂度,并且采用拥挤距离比较算子代替传统多目标遗传算法中的适应度共享方法,可使当前帕累托前沿中的个体能够扩展到整个帕累托前沿面,并尽可能地实现均匀分布。此外,本文算法还通过采用精英保留策略将父代中的优良个体保存下来进入子代,再进行非支配排序,可提高种群的整体进化水平,因此该算法能有效地解决较低维度的多模、退化和不连续优化问题。最后,通过在进化过程中引入正态分布交叉算子,能够有效地解决搜索空间狭窄及容易陷入局部最优等问题,增强了算法的空间搜索能力,从而提高了算法总体优化性能。
为实现对经济、环境及社会效益等多目标的科学兼顾,本文提出了一种面向多能耦合系统规划的高维多目标优化模型及其求解框架。相比现有研究,本文重点考虑了能源系统规划中高维多目标之间复杂的关联性,并通过对系统设备配置与负荷控制策略进行协同优化,以实现上述目标同时趋优。以一个园区级MECS为例,对所提方法的有效性进行仿真验证,所得结论如下:
1)在MECS规划中,不同目标之间具有复杂的关联性,使用所提规划方法不仅能够提高系统运行经济性,减少污染排放,而且能够改善能源利用效率,同时尽可能降低终端用户因参与需求响应造成的效用损失。
2)科学的需求侧管理策略可有效提高系统运行效益,但由于RES出力及需求侧负荷的可调控率存在一定的不确定性,因此在规划决策时需对供需侧行为的不确定性进行充分考虑,以保证所得方案的有效性。
3)通过采用DNSGA-II对所建模型进行求解,能够有效地解决搜索空间狭窄及容易陷入等问题,增强算法的空间搜索能力,具有良好的工程实用性。
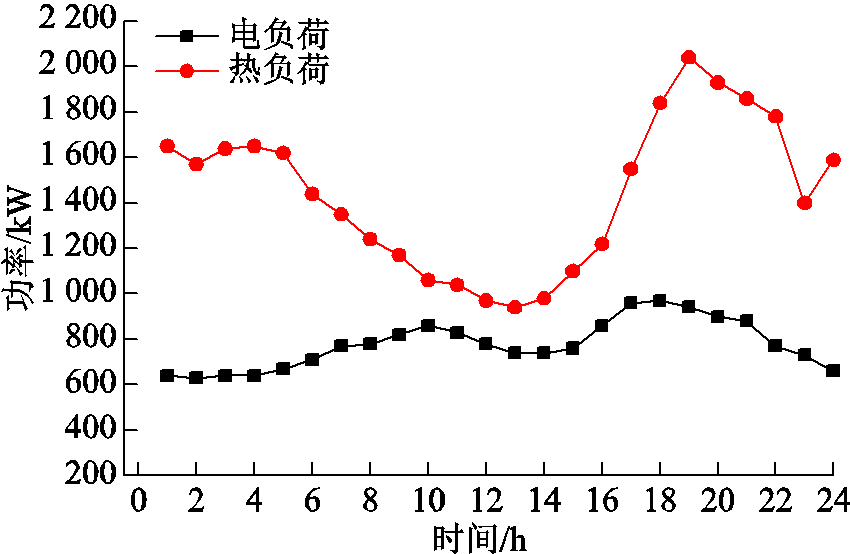
附图1 系统电/热负荷需求
App.Fig.1 Electricity/heat load of system
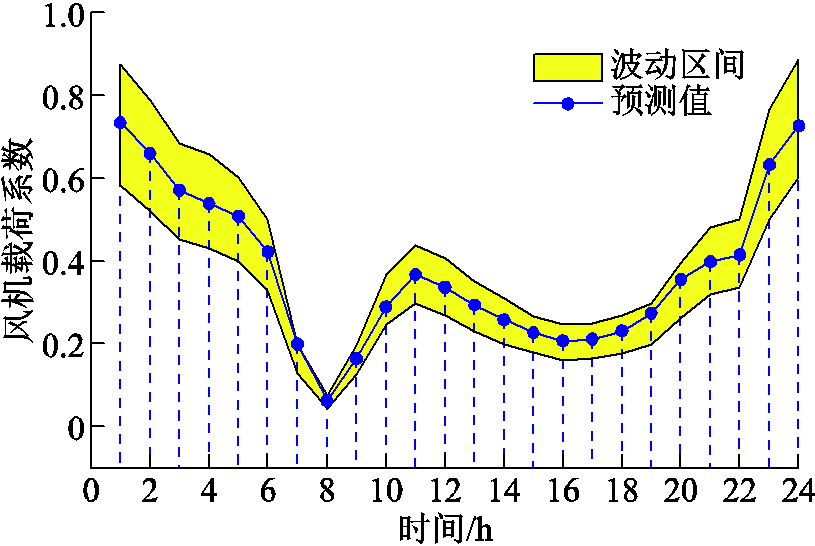
附图2 风机出力预测曲线
App.Fig.2 Forecast curve of wind power output
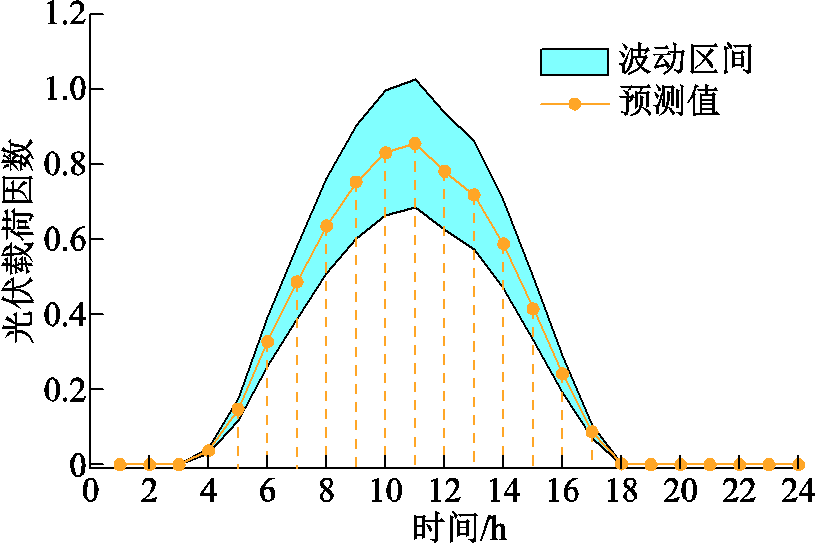
附图3 光伏出力预测曲线
App.Fig.3 Forecast curve of PV output
参考文献
[1]赵冬梅, 殷加玞. 考虑源荷双侧不确定性的模糊随机机会约束优先目标规划调度模型[J]. 电工技术学报, 2018, 33(5): 1076-1085. Zhao Dongmei, Yin Jiafu. Fuzzy random chance constrained preemptive goal programming scheduling model considering source-side and load-side uncertainty[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1076-1085.
[2]张雨曼, 刘学智, 严正, 等. 光伏-储能-热电联产综合能源系统分解协调优化运行研究[J]. 电工技术学报, 2020, 35(11): 2372-2386. Zhang Yuman, Liu Xuezhi, Yan Zheng, et al. Decomposition-coordination based optimization for PV-BESS-CHP integrated energy systems[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2372-2386.
[3]周长城, 马溪原, 郭祚刚, 等. 面向工程应用的用户级综合能源系统规划[J]. 电工技术学报, 2020, 35(13): 2843-2854. Zhou Changcheng, Ma Xiyuan, Guo Zuogang, et al. User-level integrated energy system planning for engineering applications[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2843-2854.
[4]Ma Tengfei, Wu Junyong, Hao Liangliang, et al. The optimal structure planning and energy management strategies of smart multi energy systems[J]. Energy, 2018, 160: 122-141.
[5]Lin Lin, Bao Jiaruiqi, Zheng Jian, et al. Capacity planning of micro energy grid using double-level game model of environment-economic considering dynamic energy pricing strategy[J]. IEEE Access, 2020, 8: 103924-103940.
[6]Fan Hong, Yuan Qianqian, Xia Shiwei, et al. Optimally coordinated expansion planning of coupled electricity, heat and natural gas infrastructure for multi-energy system[J]. IEEE Access, 2020, 8: 91139-91149.
[7]黄国日, 刘伟佳, 文福拴, 等. 具有电转气装置的电-气混联综合能源系统的协同规划[J]. 电力建设, 2016, 37(9): 1-13. Huang Guori, Liu Weijia, Wen Fushuan, et al. Collaborative planning of integrated electricity and natural gas energy systems with power-to-gas stations[J]. Electric Power Construction, 2016, 37(9): 1-13.
[8]Maroufmashat A, Sattari S, Roshandel R, et al. Multi-objective optimization for design and operation of distributed energy systems through the multi-energy hub network approach[J]. Industrial & Engineering Chemistry Research, 2016, 55(33): 8950-8966.
[9]郭尊, 李庚银, 周明, 等. 考虑网络约束和源荷不确定性的区域综合能源系统两阶段鲁棒优化调度[J]. 电网技术, 2019, 43(9): 3090-3100. Guo Zun, Li Gengyin, Zhou Ming, et al. Two-stage robust optimal scheduling of regional integrated energy system considering network constraints and uncertainties in source and load[J]. Power System Technology, 2019, 43(9): 3090-3100.
[10]Shui Yue, Gao Hongjun, Wang Lingfeng, et al. A data-driven distributionally robust coordinated dispatch model for integrated power and heating systems considering wind power uncertainties[J]. International Journal of Electrical Power & Energy Systems, 2019, 104: 255-258.
[11]Odetayo B, Kazemi M, MacCormack J, et al. A chance constrained programming approach to the integrated planning of electric power generation, natural gas network and storage[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6883-6893.
[12]Bao Zhejing, Ye Yangli, Wu Lei. Multi-timescale coordinated schedule of interdependent electricity-natural gas systems considering electricity grid steady-state and gas network dynamics[J]. International Journal of Electrical Power & Energy Systems, 2020, 118: 105763.
[13]Chen Hao, Yang Chen, Deng Kangjie, et al. Multi-objective optimization of the hybrid wind/solar/fuel cell distributed generation system using hammersley sequence sampling[J]. International Journal of Hydrogen Energy, 2017, 42(12): 7836-7846.
[14]Shao Changzheng, Ding Yi, Wang Jianhui, et al. Modeling and integration of flexible demand in heat and electricity integrated energy system[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 361-370.
[15]Zheng Shunlin, Sun Yi, Li Bin, et al. Incentive-based integrated demand response for multiple energy carriers considering behavioral coupling effect of consumers[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 3231-3245.
[16]曾博, 胡强, 刘裕, 等. 考虑综合需求响应复杂不确定性的电-气互联系统动态概率能流分析[J]. 中国电机工程学报, 2020, 40(4): 1161-1171. Zeng Bo, Hu Qiang, Liu Yu, et al. Dynamic probabilistic energy flow calculation for interconnected electricity-gas system considering complex uncertainties of demand response[J]. Proceedings of the CSEE, 2020, 40(4): 1161-1171.
[17]艾欣, 陈政琦, 孙英云, 等. 基于需求响应的电-热-气耦合系统综合直接负荷控制协调优化研究[J]. 电网技术, 2019, 43(4): 1160-1171. Ai Xin, Chen Zhengqi, Sun Yingyun, et al. Study on integrated DLC coordination optimization of electric-thermal-gas coupling system considering demand response[J]. Power System Technology, 2019, 43(4): 1160-1171.
[18]Wang Yongli, Ma Yuze, Song Fuhao, et al. Economic and efficient multi-objective operation optimization of integrated energy system considering electro-thermal demand response[J]. Energy, 2020, 205: 118022.
[19]Li Kangping, Zhang Peng, Li Gang, et al. Day-ahead optimal joint scheduling model of electric and natural gas appliances for home integrated energy management[J]. IEEE Access, 2019, 7: 133628-133640.
[20]姜潮, 韩旭, 谢慧超. 区间不确定性优化设计理论与方法[M]. 北京: 科学出版社, 2017.
[21]Liu Yangyang, Li Min, Lian Hongbo, et al. Optimal dispatch of virtual power plant using interval and deterministic combined optimization[J]. International Journal of Electrical Power & Energy Systems, 2018, 102: 235-244.
[22]柏卉. 高维多目标进化算法的收敛性与分布性研究[D]. 湘潭: 湘潭大学, 2017.
[23]刘益萍. 高维多目标进化优化理论与方法[D]. 徐州: 中国矿业大学, 2017.
[24]Pazouki S, Haghifam M. Optimal planning and scheduling of energy hub in presence of wind, storage and demand response under uncertainty[J]. International Journal of Electrical Power and Energy Systems, 2016, 80: 219-239.
[25]黄伟, 柳思岐, 叶波, 等. 基于电-热-气混合潮流的园区综合能源系统站网协同规划[J]. 电力建设, 2019, 40(11): 73-82. Huang Wei, Liu Siqi, Ye Bo, et al. Collaborative planning of the station's integrated energy system based on the mixed power-heat-gas flow[J]. Electric Power Construction, 2019, 40(11): 73-82.
[26]朱泽安, 周修宁, 王旭, 等. 基于稳暂态联合仿真模拟的区域多可再生能源系统评估决策[J]. 电工技术学报, 2020, 35(13): 2780-2791. Zhu Zean, Zhou Xiuning, Wang Xu, et al. Evaluation and decision-making of regional multi-renewable energy system based on steady-transient integrated simulation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2780-2791.
[27]易文飞, 张艺伟, 曾博, 等. 多形态激励型需求侧响应协同平衡可再生能源波动的鲁棒优化配置[J]. 电工技术学报, 2018, 33(23): 5541-5553. Yi Wenfei, Zhang Yiwei, Zeng Bo, et al. Robust optimization allocation for multi-type incentive-based demand response collaboration to balance renewable energy fluctuations[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5541-5553.
[28]李金昌. 统计学[M]. 北京: 高等教育出版社, 2018.
High-Dimensional Multiobjective Optimization for Multi-Energy Coupled System Planning with Consideration of Economic, Environmental and Social Factors
Abstract Improving economic performance, reducing pollution emission, and improving energy efficiency are important goals for future energy system development. However, due to the complex correlations between different goals, it tends to be difficult to achieve the above aim when the system planning goals is over three. In order to resolve this challenge, this paper proposes a high-dimensional multi-objective optimization analysis framework for multi-energy system planning. First, based on an in-depth analysis of the source-load coupling characteristics, a multi-objective planning model for an integrated energy system is proposed, which comprehensively considers the impacts of economy, environmental, and social factors. In view of the contradictions between different goals and the inherent uncertainties associated with supply and demand-side behaviors, the model is constructed under the objectives of economic cost, energy efficiency, carbon emissions and consumption comfort. This model comprehensively considers the system component capacity configuration and demand-side management schemes, and uses an interval-based method to allow for the impact of potential uncertainties in the system. The objective functions and constraints are processed by using the fuzzy preference function method and reformulated into a deterministic optimization problem first, and then the non-dominated sorting genetic algorithm-II with dimensionality reduction decomposition is employed as the solution approach for the problem. Finally, the effectiveness of the proposed method is verified and demonstrated through numerical studies.
keywords:Multi-energy coupled system, high-dimensional multi-objective optimization, planning, uncertainty, social factor
中图分类号:TM732
DOI:10.19595/j.cnki.1000-6753.tces.L90096
国家自然科学基金项目(61773384)和国家社会科学基金重大项目(19ZDA081)资助。
收稿日期 2020-06-27
改稿日期 2020-11-11
曾 博 男,1987年生,博士,副教授,研究方向为综合能源系统优化规划、电力信息物理社会系统建模与分析等。E-mail:alosecity@126.com(通信作者)
徐富强 女,1995年生,硕士研究生,研究方向为综合能源系统优化规划。E-mail:1401868217@qq.com
(编辑 赫蕾)