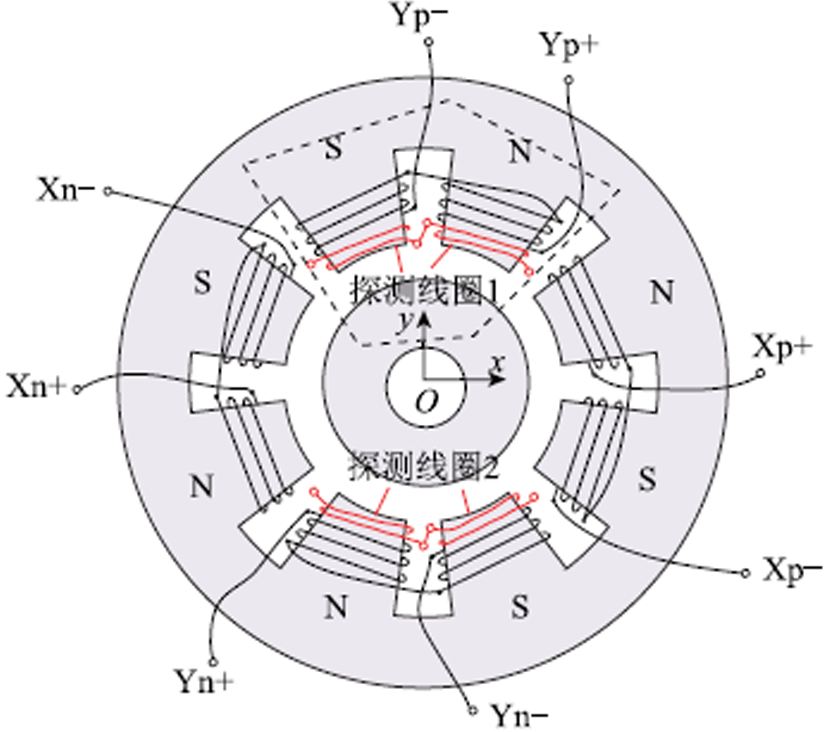
图1 复合传感耦合方案
Fig.1 Compound sensor coupling scheme
摘要 针对传统磁轴承位移传感器结构复杂、适装性差、存在检测位置与执行器错位,而位移自传感方法鲁棒性、实用性差等问题,该文提出一种基于探测线圈的磁轴承位移检测方法,通过在磁轴承磁极上布置探测线圈可实现定转子相对位移测量。首先,建立等效电路模型,并通过Simulink仿真,证明模型正确性;其次,提出差动检测方案,并通过半桥检测电路将相对位移变化转换为电桥输出电压变化,提高了位移检测灵敏度与线性度;最后,在搭建的试验平台上对该传感器进行静态性能测试,当定转子相对位移在±0.3mm范围内变化时,位移检测灵敏度为1.2mV/μm,位移检测分辨率约为7μm,验证了基于探测线圈磁轴承定转子相对位移检测的可行性。该方法结构简单、鲁棒性好,为实现紧凑可靠的磁轴承位移测量奠定了基础。
关键词:磁轴承 位移测量 传感器 探测线圈
磁悬浮轴承是一种典型的机电一体化产品。由于磁轴承具有无磨损、寿命长、无需润滑和支承特性可控等优点,使得磁轴承在航空航天、真空洁净、飞轮储能系统、人工心脏泵、交通运输等领域呈现了良好的应用前景[1-3]。由于具有位移负刚度特性,磁轴承必须通过闭环控制才能实现悬浮运行。作为闭环控制的关键环节,转子轴径向位移的检测具有十分重要的作用,位移检测的精度及稳定性在很大程度上会影响整个磁轴承系统性能。
传统的磁轴承系统通过位移传感器来实现转子位置检测。常用的位移传感器主要有电涡流式、电感式、电容式、光电式等类型[4]。然而,电容式和光电式虽然测量精度高,但无法适应磁轴承在大多数工业应用中的实际工作环境,除了实验室环境条件外很少应用[5]。电涡流传感器精度高,对工作环境要求低,其研究和应用较多。于亚婷等[6]通过有限元法研究和分析了圆柱线圈内径、外径、厚度等级对电涡流传感器线性范围和灵敏度的影响;北航庞喜浪等[7]设计了一种数字化的电涡流传感器,但是其工作频段在MHz级,处理电路复杂,成本较高,高频涡流效应对材料比较敏感。电感式位移传感器适装性较好,价格相对较低,但精度和带宽较电涡流传感器略低,这方面的研究主要是通过有限元设计传感器结构、优化工作频率及提升系统带宽等,如李巍等[8]设计了一种分装式差动变压器式电感传感器,该传感器一个自由度由分离装配的两部分组成,信号自动构成差动输出。与电涡流传感器类似,由于位移测点与力作用点错位,该传感器也无法测得磁轴承作用面处的位移。
总的来说,实际应用较多的电涡流和电感位移传感器仍存在以下缺点:①需要单独的安装空间,造成系统结构复杂,成本增加;②传统磁轴承位移传感器一般安装在轴承磁极的侧面,传感器与轴承本体错位,使得传感器到轴承本体的柔性转子模态可能相位相反,进而造成系统不稳定[9-10]。
为解决上述问题,近些年磁轴承系统的自传感技术(或称无位移传感器技术)得到了较为广泛的研究。相较于传统磁轴承,采用自传感的磁轴承存在诸多优势[11]。自传感技术简化了位移传感器检测中的辅助电路,从而大大降低系统构建的成本和复杂度。同时自传感磁轴承的位移检测与执行器在结构上一体化[12],轴承本体与位置检测同位,避免了磁轴承因为柔性转子模态变化带来的系统不稳定。
对于自传感技术,主要有两种研究方法:参数估计法和状态观测法。参数估计法基本原理是检测磁轴承中控制线圈自感的变化以得到转子位移,其中又主要包括高频小信号注入法和脉宽调制(Pulse Width Modulation, PWM)非线性参数估计方法。高频小信号注入法在电机的无传感控制领域研究较多[13-14],但对于磁轴承控制系统,国内外对此研究较少。任双艳等[13]分析了小信号注入法的检测原理,并对单自由度的磁轴承系统进行了仿真研究,且基于线性功率放大器实现,只能用于小功率场合,局限性较大。对于PWM非线性参数估计方法,由于磁轴承高频开关信号可以代替外部信号作为载波信号对位移信号进行调制,可通过检测控制电流中PWM纹波信号估计线圈电感值的大小[16]。浙江大学唐明[17]对传统的非线性参数估计模型进行优化,实现磁轴承在0~3 000r/min内自传感稳定运行。浙江大学于洁等[18]分析了涡流对电流纹波的影响,提出一种转子位移估计策略,可提高位移估算精度。由于此法非常依赖电流纹波幅值的大小,因此对于采用三电平PWM开关功率放大器[19-20]的磁轴承来说,实用性较差。
自传感中的状态观测法是根据电压控制型磁轴承系统建立状态空间模型,由两个差动电压及检测到的电流计算得出转子位移,但状态观测器对磁轴承的参数变化十分敏感,鲁棒性较差,不利于工业应用[21]。综上所述,目前磁轴承自传感的研究均与实际应用有较大距离。
针对以上问题,本文设计了一种基于探测线圈检测的新型复合位移传感方法,其基本思路是:将探测线圈绕制在磁轴承铁心上,并通以高频激励电压,通过提取探测线圈中与高频激励相关的信息,解算位移的大小。由于该检测结构与磁轴承控制执行器相集成,且不依赖PWM电流纹波的大小,鲁棒性较好,因此可有效解决传统传感器位移检测中轴向不重合力问题和自传感实用性差等问题。
磁轴承位移复合传感耦合模型如图1所示,以八极磁轴承结构为例,探测线圈绕制于磁极齿部,并通入高频激励,与控制绕组在磁路上相耦合。位移检测基本原理为:当转子移动时气隙发生变化,磁路磁阻亦发生变化,进而导致线圈电感值发生改变,则通入高频信号的线圈电信号也会发生变化。因此通过测量与高频激励相关的信号变化即可计算出位移大小。

图1 复合传感耦合方案
Fig.1 Compound sensor coupling scheme
为从探测线圈信号中获取位移信息,需要建立考虑磁轴承控制信号影响的总体模型,进而推导出位移与探测线圈和控制线圈信号之间的关系。
为简化分析,取磁轴承磁极结构中一个独立的磁路回路,即图1中的虚线部分,进行理论推导,模型简化如图2所示。模型输入为控制线圈电流ic与两端电压uc,探测线圈电流id及两端电压ud,其中uc为PWM开关功放产生的控制电压。
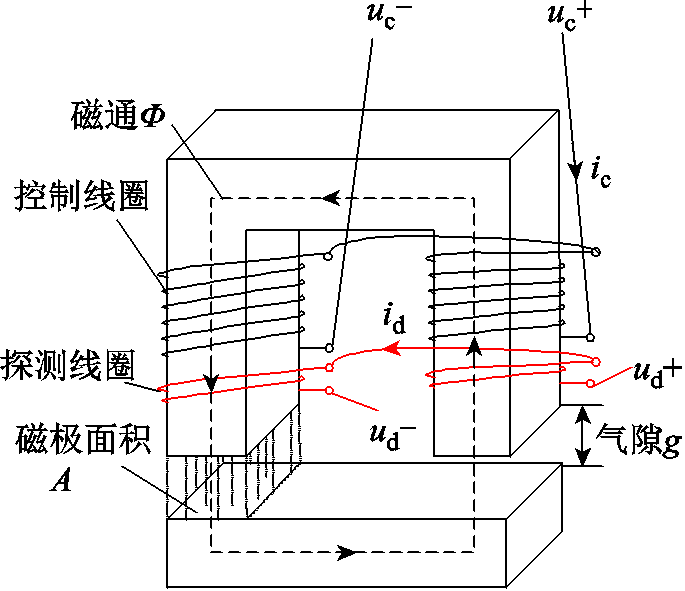
图2 加探测线圈的磁轴承电磁铁模型
Fig.2 Magnetic bearing electromagnet model with detection coil
由图2所示的磁路模型,根据磁路欧姆定律,线圈自感值为
 (1)
(1)式中,Φ为磁路磁通量;i为线圈电流;n线圈匝数;Rm为磁路总磁阻。
假定磁阻均匀分布,磁阻为
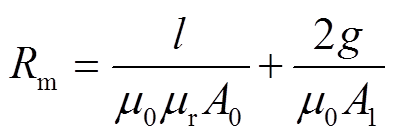 (2)
(2)式中,l为铁心磁路总长度,包括定转子铁心磁路长度;g为气隙大小;μ0、μr分别为真空磁导率及铁心相对磁导率;A0、A1分别为铁心截面积及气隙截面积。
忽略边缘效应情况下,有
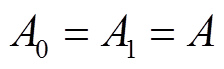 (3)
(3)则
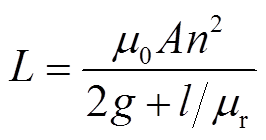 (4)
(4)同理,忽略铁心磁阻的影响,控制线圈自感Lc,探测线圈自感Ld及两线圈之间的互感M分别为
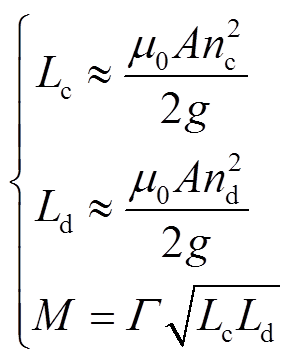 (5)
(5)式中,nc、nd分别为控制线圈与探测线圈匝数;Г为互感系数。
忽略控制电流反馈回路及功放开关器件开通阻抗的影响,控制线圈两端的功放输出信号近似为电压源信号,探测线圈两端由外部激励进行供电,等效电路如图3所示。图3中Lc、Rc分别为控制线圈自感与内阻,Ld、Rd分别为探测线圈等效自感与内阻,M为互感,ic、id为通过两线圈的电流,uc、ud为两线圈两端电压,R1为探测线圈回路限流电阻。
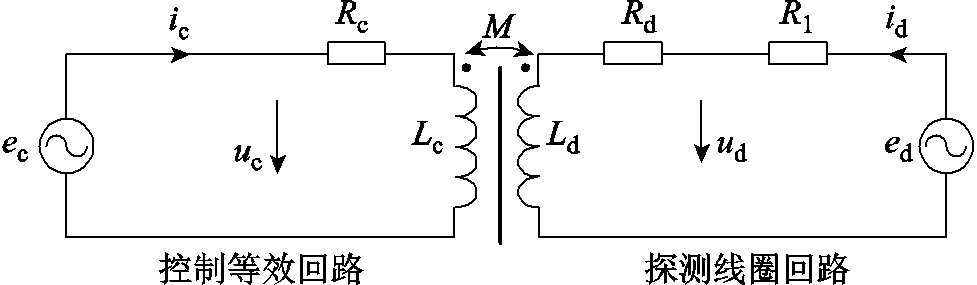
图3 等效电路
Fig.3 Equivalent circuit diagram
根据图3,有
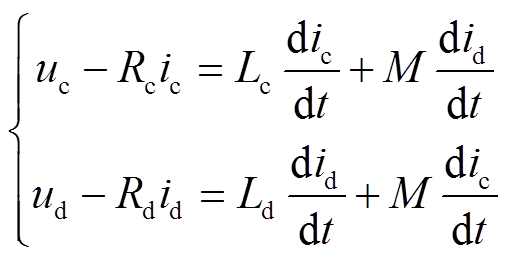 (6)
(6)可由式(6)得到如图4所示的T型等效电路。
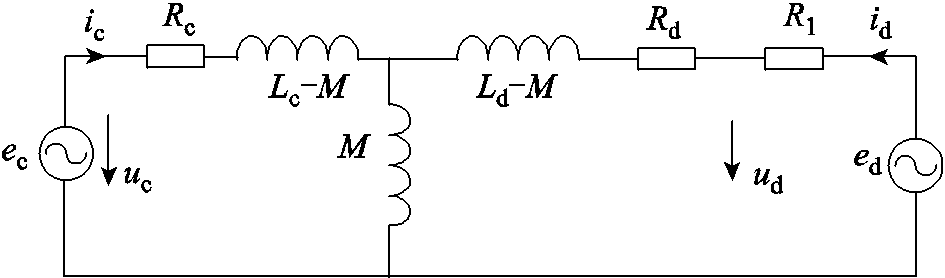
图4 T型等效电路
Fig.4 Equivalent T-type circuit diagram
由式(6)可知,探测线圈与控制线圈通过互感相耦合,可以在探测线圈施加与控制线圈功放输出频率不同的外部激励,根据信号频率不同进行信号解耦。
根据叠加定理,当仅考虑探测线圈激励ed=Kcos(ωt)单独作用时,功放近似的电压源ec等效短路,这时探测线圈两端阻抗电路如图5所示,分析得到探测线圈两端等效阻抗Zed为
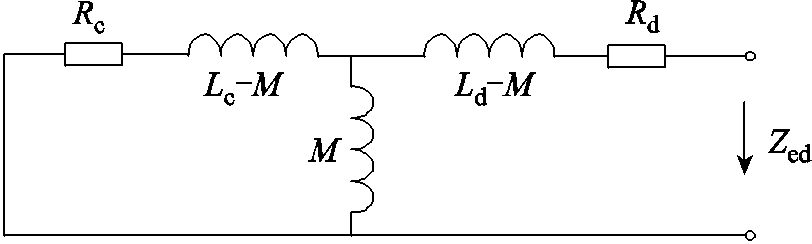
图5 探测线圈两端阻抗电路
Fig.5 Impedance circuit at both ends of the detection coil
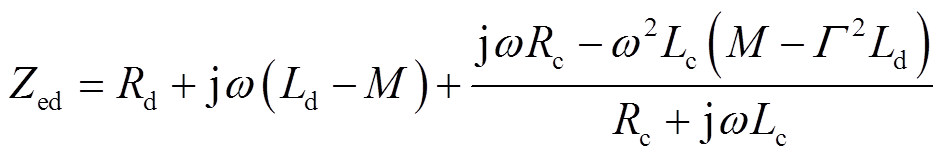 (7)
(7)化简可得
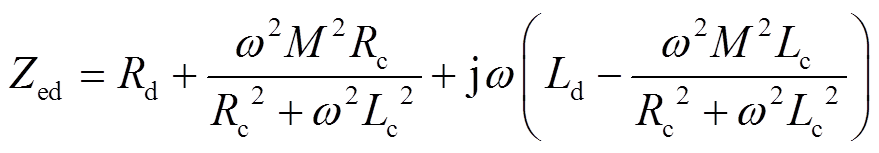 (8)
(8)通常来讲,有Rc <<ωLc,Rc2+ω2Lc2 ≈ ω2Lc2,则式(8)可化简为
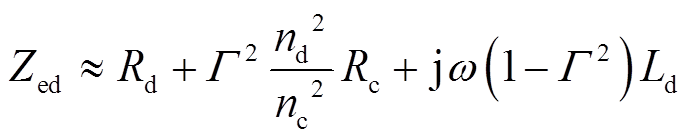 (9)
(9)设
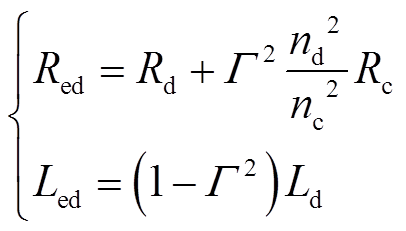 (10)
(10)则探测线圈两端等效阻抗为
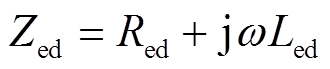 (11)
(11)由以上分析可知,探测线圈两端可等效为RL串联电路。由式(10)及式(5)可以看出,气隙与探测线圈两端等效电感Led成非线性关系,气隙变化会引起探测线圈两端等效电感的变化,本文主要是根据此原理进行转子位移复合传感设计。
由于气隙与电感成非线性关系,为了增加线性度并减小误差,同时提高灵敏度,采用如图6所示的差动复合传感等效电路。差动情况下,在定子同自由度对侧绕制相同的探测线圈,两探测线圈串联,由外部激励信号ed进行激励。
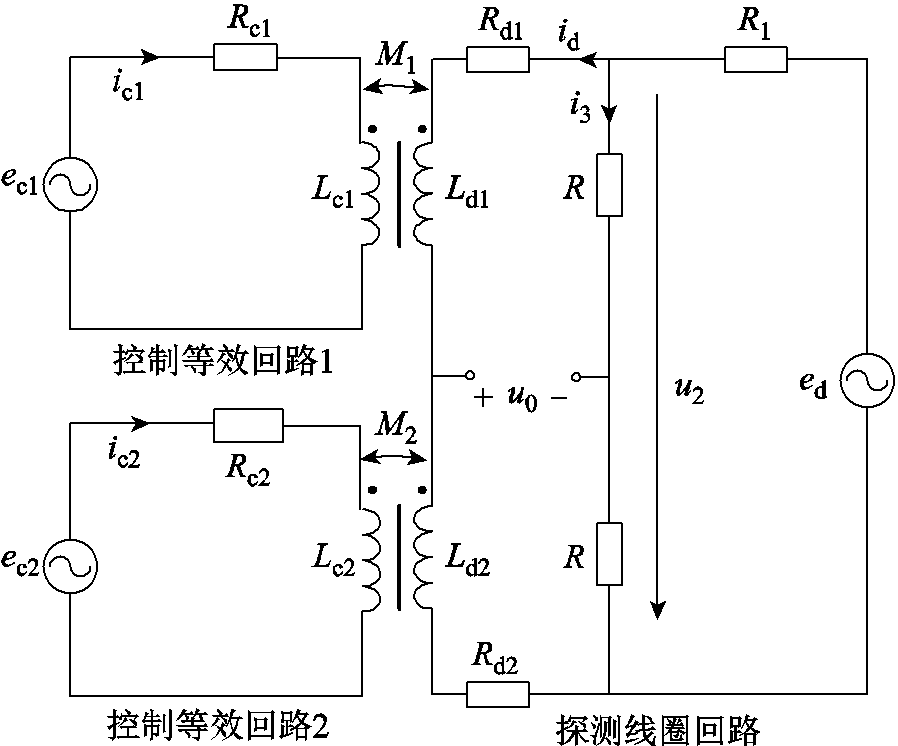
图6 差动复合传感等效电路
Fig.6 Differential composite sensing equivalent circuit
图6中Lc1、Rc1、Lc2、Rc2分别为单自由度对侧两控制线圈自感与内阻,Ld1、Rd1、Ld2、Rd2分别为相应的探测线圈等效自感与内阻,M1、M2为互感,ic1、ic2为两控制回路电流,id为通过探测线圈的电流,u2为探测线圈电桥电路两端输入电压,R1为探测线圈回路限流电阻,R为电桥电阻,ec1、ec2为控制线圈两端电压信号,ed为激励信号。
当转子在小范围内向下移动x=∆g时,上侧气隙增大,下侧气隙减小。取额定气隙g0,即位移为0时探测线圈等效自感为Led0,由式(5)及式(10)可以得出,两探测线圈两端等效电感分别为
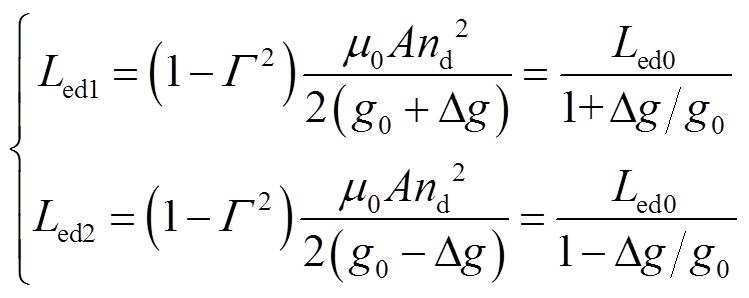 (12)
(12)忽略探测线圈等效电阻的影响,则电桥电路输出电压
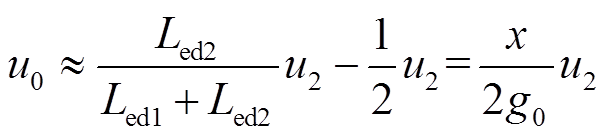 (13)
(13)由于电桥两端电压u2在一定转子位移范围内近似不变,则无论转子向上或向下移动,输出电压都与其位移成近似线性关系。因此,只要检测出输出电压中激励频率分量幅值的大小,便可以确定转子的位移。
复合传感中的探测线圈由正弦波激励电路驱动,其激励信号经传感器输出后为同频的调制信号。为了获得转子位移变化的信息,必须对传感器输出的调制信号进行解调、滤波等处理,最终才能得到能反映转子位移变化的直流信号,复合传感测量电路的整体方案如图7所示。
正弦波发生电路选用AD698SQ芯片,该器件通过简单的外围元件就可产生频率和幅值在一定范围的正弦波。可通过选择合适的电路元件产生所需的正弦信号。
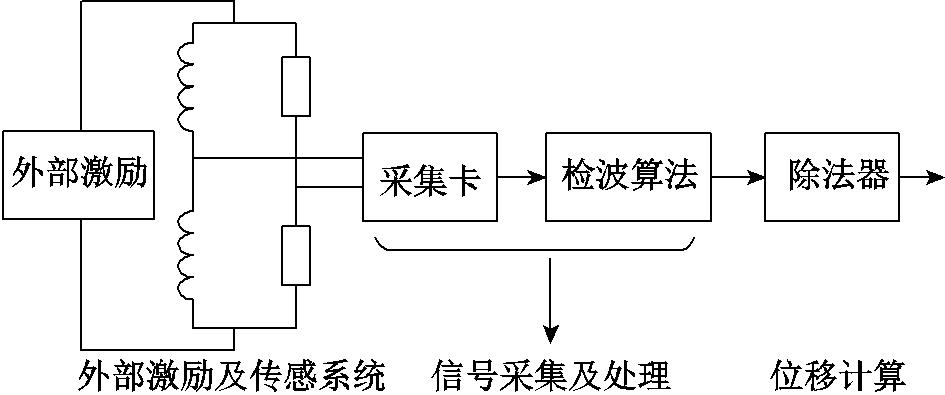
图7 测量方案
Fig.7 The plan of measurement
相较于传统的电感式位移传感器的输出信号,本文所设计的传感方法中,由于探测线圈与控制线圈共用磁路回路,根据变压器原理,控制信号任何变化都会体现在探测线圈两端电压中,导致输出信号中会产生与激励频率无关的噪声信号,因此需要采用高性能信号检测方法。由式(13)可得,转子位移与输出的正弦电压幅值有关。常用的傅里叶变换(Fast Fourier Trans formation, FFT)幅值计算方法存在栅栏效应,幅度求解精度低,因此本文采用正交锁相放大的方法对信号进行检波处理。
正交锁相放大相当于一个高Q值的带通滤波器,基本原理为:对于待测信号S=Asin(ωt+φ)+N,其中Asin(ωt+φ)为信号S中待测频率分量,N为信号中与待测频率ω无关的分量,建立一个与信号中待测频率相同的标准正弦信号Sref1= sin(ωt)为参考信号,将Sref1与S相乘,即
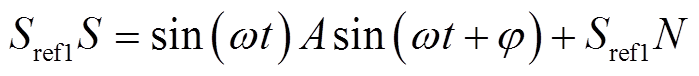 (14)
(14)化简可得
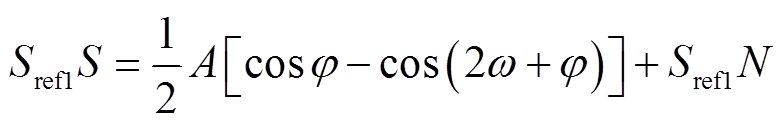 (15)
(15)式中,0.5Acosφ为直流信号,其他部分为高频交流信号,因此可通过低通滤波器对计算后的结果滤波得到0.5Acosφ。理论上知道参考信号与待测信号之间的相位差即可计算得出待测信号中与参考信号同频分量幅值。但实际复合传感位移检测中,由于探测线圈两端等效阻抗随转子位移变化,则输出信号相位也为变化量,难以实时确定两信号之间的相位差。因此可选取另一参考信号为Sref2= cos(ωt),按照相同方法可计算得出0.5Asinφ,再通过进一步计算得到待测信号中特定频率分量的幅值A。
正交锁相幅值检测方法原理如图8所示。
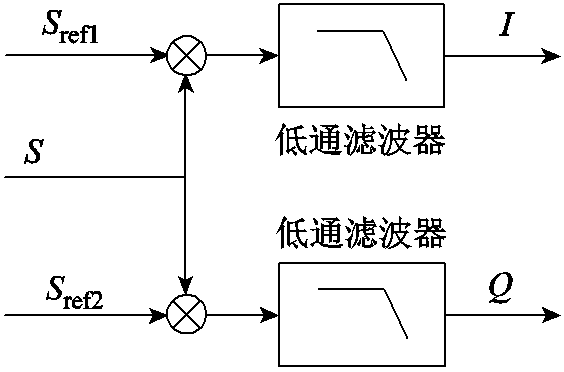
图8 锁相放大原理
Fig.8 Principle of lock-in amplifier
图8中
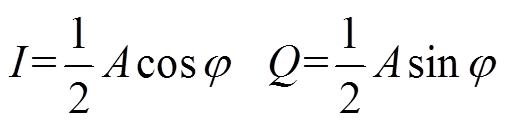 (16)
(16)则待测信号中特定频率幅值
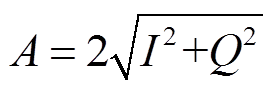 (17)
(17)由于在正交锁相检波方法中用到了较多的乘法器、滤波器及开方器,位移检测需要除法器,因此本文采用数字实现方法,具有更好的稳定性。
采用NI公司的DAQmx采集卡对待测信号进行采样,并在Labview中实现位移检测算法,如图9所示。由于正交锁相算法需要两个正交的与输出信号同频的标准正弦信号作为参考信号,而本次试验所设计的正弦激励电路的激励信号与待测信号同频,因此可将其采样作为一路参考信号,另一个正交的参考信号可由激励信号经希尔伯特变换得出,最终可将计算得出的位移信号实时地反馈到控制器中。
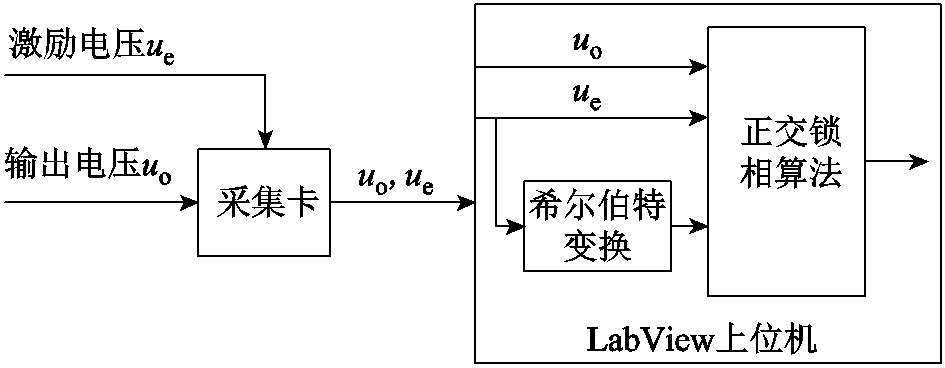
图9 算法设计示意图
Fig.9 Algorithm design diagram
为了验证本文所提复合位移传感原理及检测方法,在Simulink中建立包括磁轴承功放、控制线圈与探测线圈结构解析模型及信号处理模块的仿真模型,模型结构及其内部关系如图10所示。
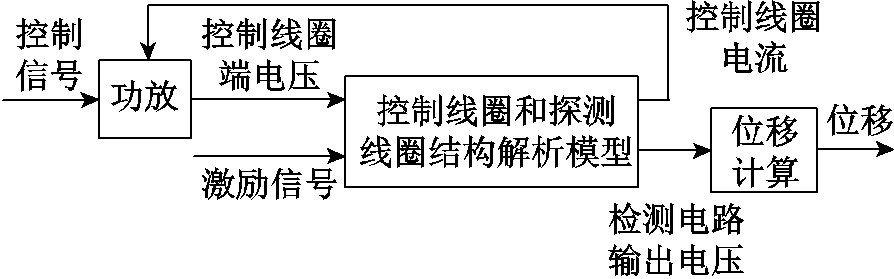
图10 仿真模型结构
Fig.10 Simulation model structure
控制绕组的供电采用三电平功放,其仿真参数如下:直流侧母线电压为220V,参考电流为1A,负载为RL电路,L=0.83mH,R=0.3Ω时,功放输出PWM波形特性如图11所示。
由式(5)可得,气隙的变换会影响电路中元件参数L和M的改变,Simulink中变压器模型不能直接反映气隙与电感之间的关系,因此结合控制线圈和探测线圈电气量之间的相互约束关系,根据图6所示电路搭建包括控制线圈与探测线圈的解析模型。
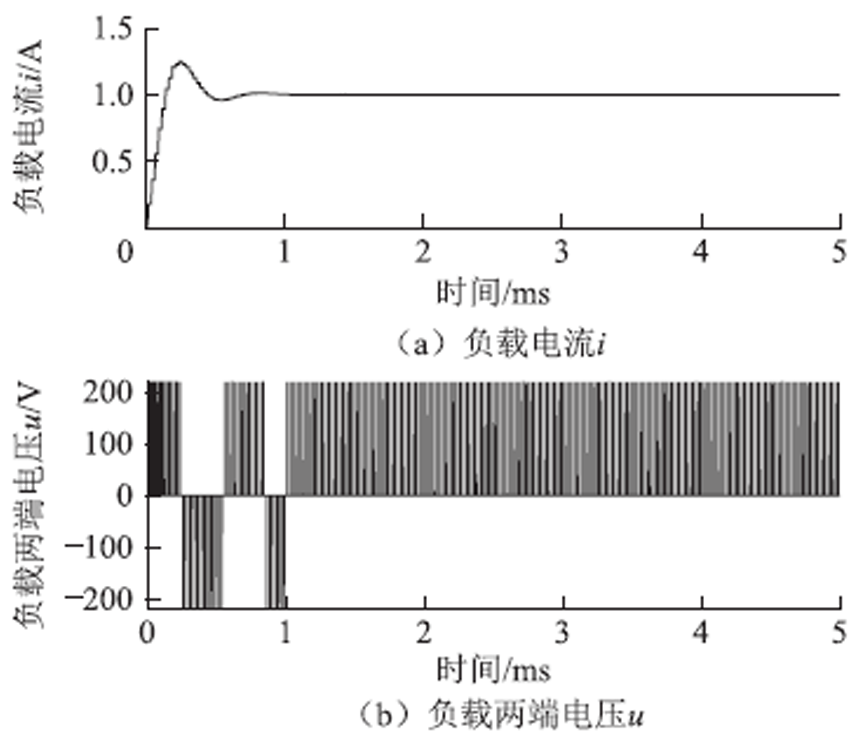
图11 功放运行特性
Fig.11 Power amplifier operating characteristics
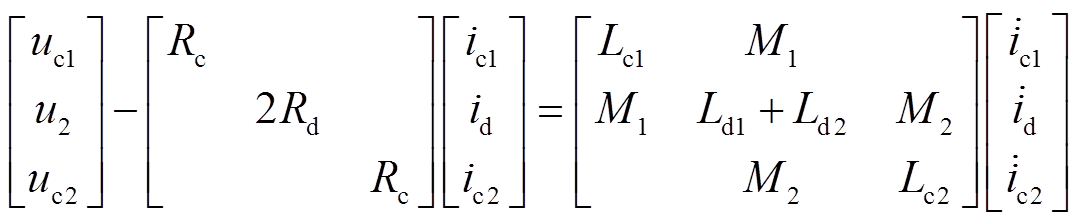 (18)
(18)仿真模型参数见表1。
表1 仿真模型参数
Tab.1 Simulation model parameters

参数数值 开关频率fs/kHz20 额定气隙g0/mm0.5 控制线圈内阻Rc/Ω12.24 控制线圈工作点自感Lc/mH1.63 探测线圈内阻Rd/Ω3.06 探测线圈工作点自感Ld/mH0.41 控制线圈与探测线圈匝数比n2 激励信号幅值/V12 激励频率f0/kHz6.5 探测回路限流电阻R1/Ω50 电桥电阻R/Ω12
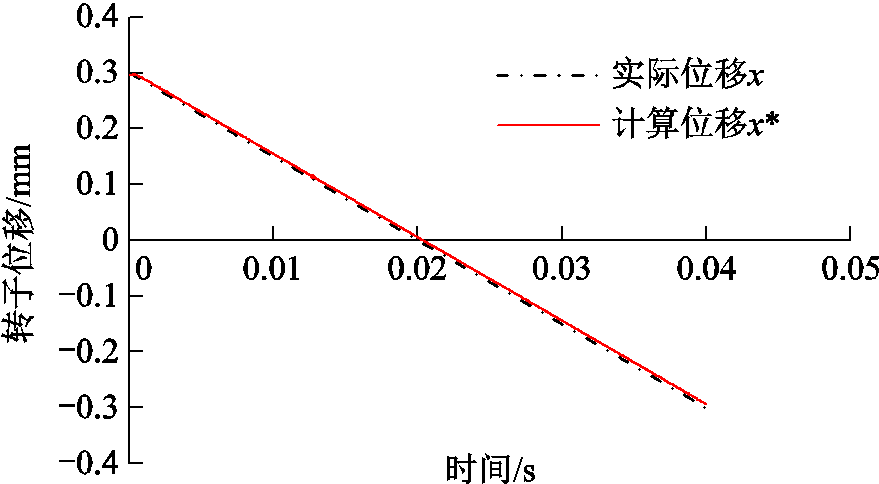
图12 仿真计算位移与实际位移关系
Fig.12 The relationship between simulated and actual displacement
图12为气隙成线性变化时通过测量输出电压幅值计算得出的转子位移。气隙变化为-0.3~0.3mm,变化率为15mm/s,控制电流大小为1.2A。从图12中可以看出,所建立的仿真模型计算出的位移可以有效反映出转子位移的大小。
针对本文中所设计的位移检测方案设计单自由度简化原理验证试验平台,平台结构如图13及图14所示。本实验设计一对U型铁心作为磁轴承定子部分,环形铁心作为转子部分,铁心采用硅钢片叠压。单自由度移动平台可通过摇杆调节中间移动部分的位置,将定子铁心固定于机座上,转子固定于平台移动部分,可由摇杆改变定转子间气隙大小并通过千分表实时读取当前转子位移值。定子铁心上绕制控制线圈绕组,由上位机控制PWM功放驱动板产生控制信号,在同一铁心磁极上按与控制线圈相同方式绕制探测线圈,探测线圈由外部电路产生的激励信号驱动,经过检测桥式电路的高频差分输出电压,可依据式(13)计算得出位移。

图13 试验平台机械部分
Fig.13 Experimental platform mechanical part

图14 试验平台电路部分
Fig.14 Experimental platform circuit part
表2为本次试验的试验参数,其中绕组参数为阻抗分析仪在6.5kHz激励频率下测出的测量值。
表2 试验参数
Tab.2 Test parameters
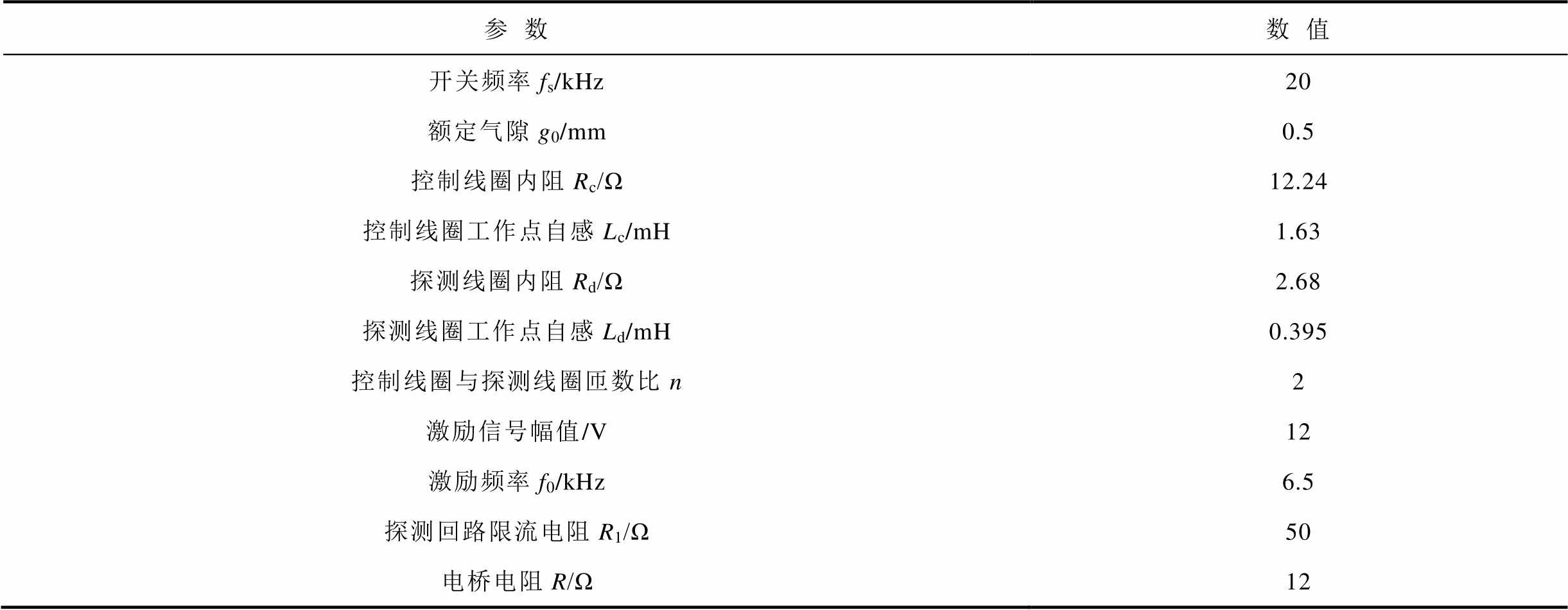
参数数值 开关频率fs/kHz20 额定气隙g0/mm0.5 控制线圈内阻Rc/Ω12.24 控制线圈工作点自感Lc/mH1.63 探测线圈内阻Rd/Ω2.68 探测线圈工作点自感Ld/mH0.395 控制线圈与探测线圈匝数比n2 激励信号幅值/V12 激励频率f0/kHz6.5 探测回路限流电阻R1/Ω50 电桥电阻R/Ω12
试验时通过调节气隙大小,记录在转子不同位置时输出电压幅值及噪声,试验结果如图15和图16所示。
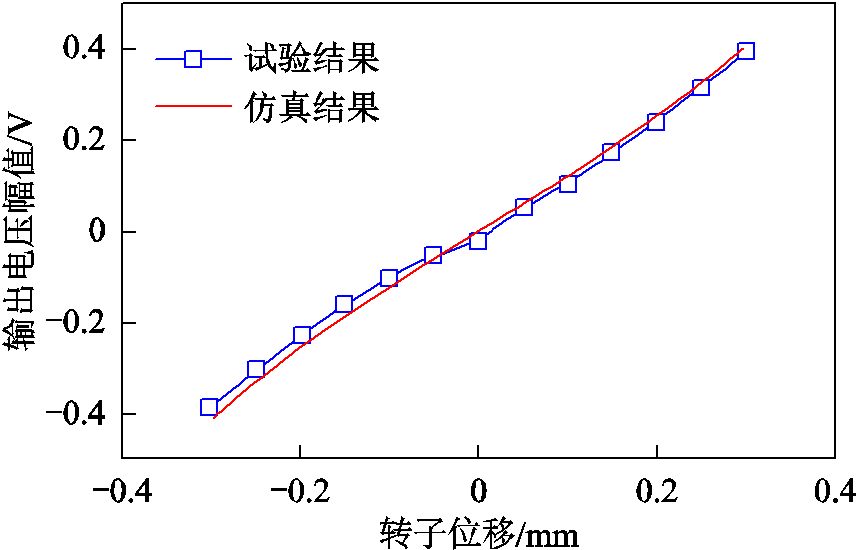
图15 检测电路输出信号幅值与位移关系对比
Fig.15 Comparison of relationship between output signal amplitude and displacement of detection circuit
由图15可以看出,试验结果与仿真结果吻合度较好,且输出信号幅值与位移之间线性度较好。根据所测量结果进行数据拟合,灵敏度约为1.2mV/μm。图示结果中误差主要来源是机械装置,由人工调节转子的相对位移,会产生一定的位移调节误差。图16为不同位移下的检测信号幅值噪声,噪声幅值(峰-峰值)约为8mV,因此位移检测分辨率约为7μm。
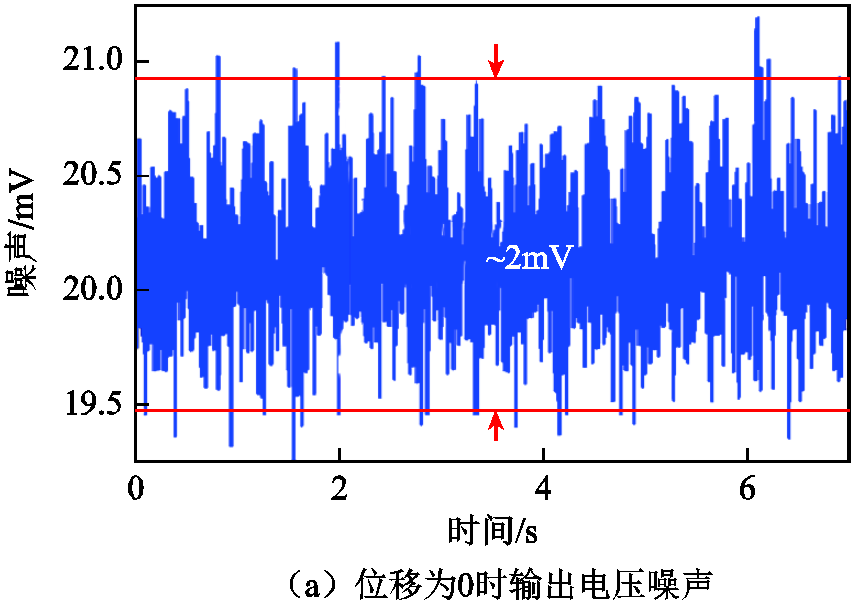
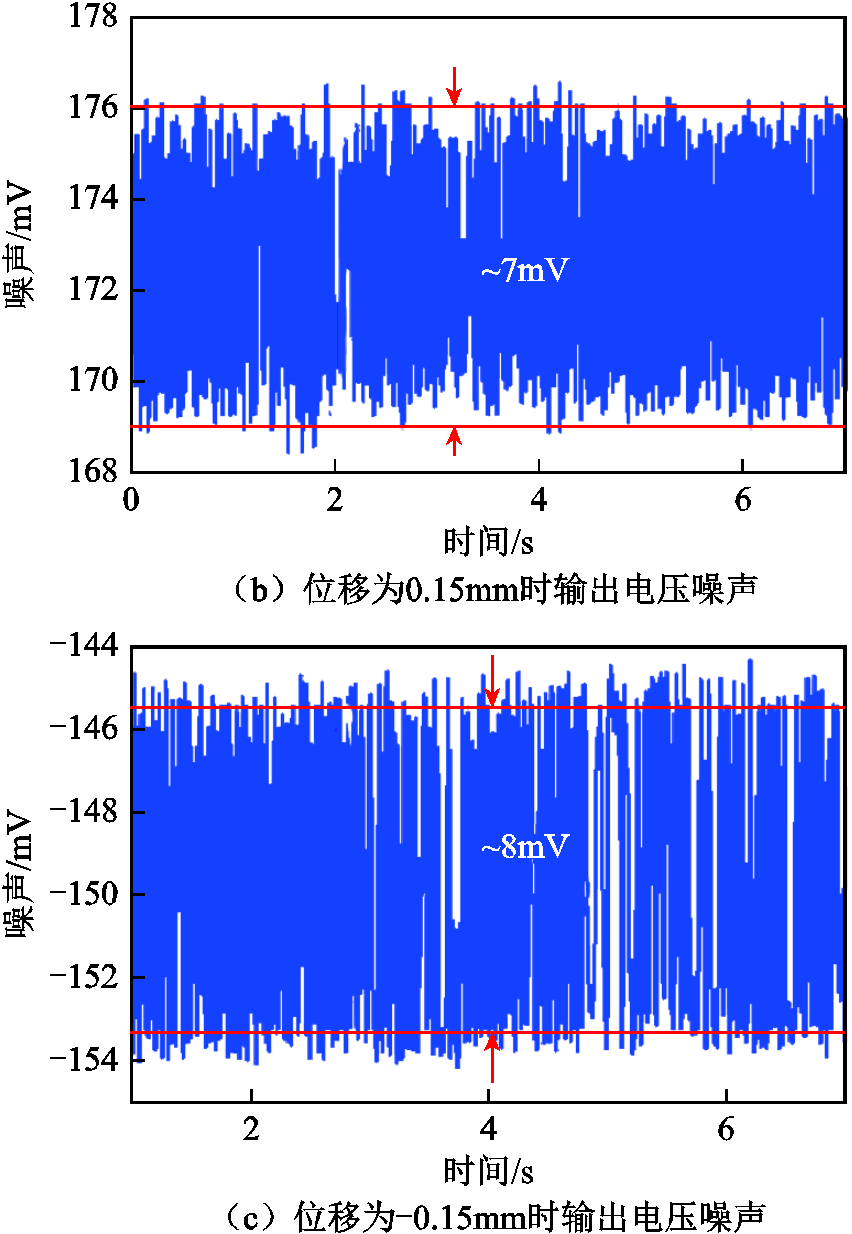
图16 不同位移下的输出电压噪声
Fig.16 Output voltage noise under different displacements
本文提出了一种基于探测线圈的新型磁轴承位移传感方案,建立了位移传感结构的基本理论模型,并设计了位移检测电路及算法。建立Simulink模型验证了所提方法的正确性,通过所搭建的验证平台测量所提位移传感器方法的静态灵敏度及分辨率,结果显示其灵敏度为1.2mV/μm,分辨率约为7μm,表明所提方法能有效实现位移测量,并且充分利用了磁轴承本体磁路,增加了磁轴承紧凑型,又克服了自传感位移检测方法鲁棒性差等问题。
参考文献
[1]Schweitzer G, Maslen E H. Magnetic bearing: theory, design, and application to rotating machinery[M]. Berlin Heidelberg: Springer-Verlag, 2009: 15-17.
[2]张维煜, 朱熀秋, 袁野. 磁悬浮轴承应用发展及关键技术综述[J]. 电工技术学报, 2015, 30(12): 12-20. Zhang Weiyuan, Zhu Huangqiu, Yuan Ye. Study on key technologies and applications of magnetic bearings[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 12-20.
[3]姜豪, 苏振中, 王东. 运动平台上磁轴承-转子系统的动力学建模[J]. 电工技术学报, 2019, 34(23): 4880-4889. Jiang Hao, Su Zhenzhong, Wang Dong. Dynamic modeling of magnetic bearing-rotor system on moving platform[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4880-4889.
[4]汪希平, 崔卫东. 电磁轴承用非接触式位移传感器的研究[J]. 上海大学学报(自然科学版), 1998(1): 3-5. Wang Xiping, Cui Weidong. Research on non-contact displacement sensors for magnetic bearings[J]. Journal of Shanghai University(Natural Science), 1998(1): 3-5.
[5]陆陈. 轴向磁悬浮轴承位移检测技术研究[D]. 南京: 南京理工大学, 2011.
[6]于亚婷, 杜平安, 廖雅琴. 线圈形状及几何参数对电涡流传感器性能的影响[J]. 仪器仪表学报, 2007, 28(6): 1045-1050. Yu Yating, Du Pingan, Liao Yaqin. Study on effect of coil shape and geometric parameters on performance of eddy current sensor[J]. Chinese Journal of Scientific Instrument, 2007, 28(6): 1045-1050.
[7]庞喜浪, 刘刚, 文通. 用于磁轴承位移检测的数字式电涡流位移传感器设计与实验研究[J]. 传感技术学报, 2011, 24(3): 360-364. Pang Xilang, Liu Gang, Wen Tong. Design and experiment study of digital eddy current displacement sensor used for displacement detection of magnetic bearing[J]. Chinese Journal of Sensors and Actuators, 2011, 24(3): 360-364.
[8]李巍, 李勇, 陆永平. 应用于电磁轴承的分装式位置传感器[J]. 电工技术学报, 2008, 23(9): 76-79, 85. Li Wei, Li Yong, Lu Yongping. A structure separable position sensor used in electromagnetic bearings[J]. Transactions of China Electrotechnical Society, 2008, 23(9): 76-79, 85.
[9]Siva Srinivasa R, Tiwaria R, Kannababub C. Application of activemgnetic bearings in flexible rotordynamic systems – a state-of the-art review[J]. Mechanical Systems and Signal Processing, 2018, 106: 537-572.
[10]刘程子, 湛江, 杨艳, 等. 主动磁悬浮轴承–柔性转子的研究和发展综述[J]. 中国电机工程学报, 2020, 40(14): 4602-4614, 4739. Liu Chengzi, Zhan Jiang, Yang Yan, et al. Review of research status and development of flexible rotor-magnetic bearing[J]. Proceedings of the CSEE, 2020, 40(14): 4602-4614, 4739.
[11]Ranfta E O, van Schoorb G, du Randa C P. Self-sensing for electromagnetic actuators[J]. Sensors and Actuators A, 2011, 172(2): 400-419.
[12]祝文公, 自传感轴向磁轴承的设计与研究[D]. 杭州: 浙江工业大学, 2016.
[13]郭磊, 杨中平, 林飞. 带误差补偿的高频信号注入永磁同步电机无传感器控制策略[J]. 电工技术学报, 2019, 34(21): 4458-4466. Guo Lei, Yang Zhongpin, Lin Fei. A sensorless control strategy for high frequency signal injection permanent magnet synchronous motor with error compensation[J]. Transactions of China Electrote-chnical Society, 2019, 34(21): 4458-4466.
[14]薛哗, 魏佳丹, 周波. 三级式同步电机低速阶段无位置传感器起动控制高频信号注入法的对比[J]. 电工技术学报, 2018, 33(12): 2703-2712. Xue Hua, Wei Jiadan, Zhou Bo. Comparative investigation on sensorless control of three-stage synchronous motor based on high-frequency injection method at low speed[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2703-2712.
[15]任双艳, 边春元, 刘杰. 自检测磁轴承系统转子位置检测方法的研究[J]. 机械科学与技术, 2008, 27(6): 815-818. Ren Shuangyan, Bian Xiyuan, Liu Jie. Study on estimation of rotor position of self sensing active magnetic bearings[J]. Mechanicl Science and Technology for Aerospace Engineering, 2008, 27(6): 815-818.
[16]Matsuda K, Okada Y. Self-sensing magnetic bearing using the principle of differential transformer[C]// Proceeding of 5th International Symposium on Magnetic Bearings, Japan, 1996, 63(609): 1441-1447
[17]唐明. 径向四自由度主动电磁轴承系统的自传感运行研究[D]. 杭州: 浙江大学, 2013.
[18]于洁, 祝长生, 余忠磊. 考虑涡流的自传感主动电磁轴承转子位置估计策略[J]. 电工技术学报, 2018, 33(9): 1946-1956. Yu Jie, Zhu Changsheng, Yu Zhonglei. Rotor position estimation strategy for self-sensing active magnetic bearing considering eddy currents[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1946-1956.
[19]余忠磊, 祝长生. 二电平电流型开关功率放大器稳定性分析[J]. 电工技术学报, 2019, 34(2): 306-315. Yu Zhonglei, Zhu Changshen. Analysis on the stability of two-level current mode switching power amplifiers[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 306-315.
[20]张亮, 房建成. 电磁轴承脉宽调制型开关功放的实现及电流纹波分析[J]. 电工技术学报, 2007, 22(3): 13-20. Zhang Liang, Fang Jiancheng. Analysis of current ripple and implementation of pulse width modulation switching power amplifiers for active magnetic bearing[J]. Transactions of China Electrotechnical Society, 2007, 22(3): 13-20.
[21]Kucera L. Robustness of self-sensing magnetic bearing[C]//Proceeding of MAG’97 Industrial Conference and Exhibition on Magnetic Bearings, Zurich, Switzerland, 1997: 261-270.
Design and Experimental Research of Magnetic Bearing Compound Displacement Sensor
Abstract In order to solve the problems of traditional magnetic bearing displacement sensor with complex structure, poor adaptability, misplacement between detection position and actuator, and poor robustness and practicability of self-sensing method, this paper presents a novel approach for radial displacement detection in magnetic bearing system based on the detection coil. By arranging detection coils around teeth of a magnetic bearing, relative displacement along radial direction between stator and rotor can be achieved. Theory model of the proposed method is built and verified through Simulink simulation. A differential detection scheme is present to improve sensitivity and linearity, and displacement is achieved by detecting the output voltage of the half-bridge detection circuit. Static performance of the proposed method is tested on a platform. And, when the displacement is in the range of -0.3mm to 0.3mm, sensitivity and resolution are 1.2mV/μm and 7μm, respectively, showing the feasibility of displacement detection of the proposed method. The method is simple and robust, and lays a foundation for the realization of compact and reliable magnetic bearing displacement detection.
keywords:Magnetic bearing, displacement measurement, sensor, detection coil
中图分类号:TM722.7
DOI:10.19595/j.cnki.1000-6753.tces.201050
国家自然科学基金资助项目(51707201, 51690181, 51825703)。
收稿日期 2020-08-19
改稿日期 2020-10-22
李 志 男,1998年生,硕士研究生,研究方向为磁轴承技术。E-mail:673551353@qq.com
苏振中 男,1989年生,副研究员,硕士生导师, 研究方向为磁悬浮技术、电力集成技术。E-mail:suayst@163.com(通信作者)
(编辑 郭丽军)