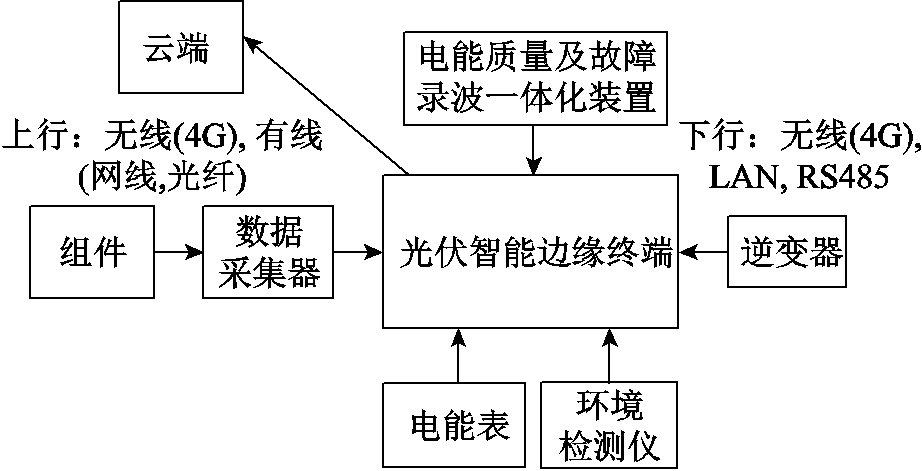
图1 PVIET的通信方式
Fig.1 Communication mode of PVIET
摘要 光伏智能边缘终端(PVIET)是实现分布式光伏规模化接入配电网高效率智慧运维的重要设备之一。该文构建光伏智能边缘终端优化配置的数学模型,为实现模型的准确求解,进一步提出一种改进的郊狼优化算法(ICOA)。为解决郊狼优化算法精度不足、收敛速度缓慢等问题,提出全新的社会互助郊狼成长策略和单维组内最优郊狼扰动策略,引入模拟退火、自适应精英保留策略,以让该算法更加适合所提出的工程问题,实现对PVIET的数量、位置及与光伏电站连接方式三个方面的求解。最后,改进的IEEE 69案例验证了模型的有效性,通过算法对比,验证了改进郊狼优化算法在精度、稳定性和收敛性等方面的优越性。
关键词:分布式光伏 光伏智能边缘终端 优化配置模型 改进郊狼优化算法
光伏智能边缘终端(Photovoltaic Intelligent Edge Terminal, PVIET)是一种新型的分布式光伏智慧运维设备,具有数据采集、处理、存储、上传等功能,可为有效解决分布式光伏运维难度大、成本高、效率低等问题提供基础,为分布式光伏功率预测[1-2]和故障诊断[3-5]等提供数据支撑。然而,单台PVIET价格相对昂贵,实际规模化应用中,一般采用多个分布式光伏站共用一台PVIET以降低成本;但是,如何保证PVIET配置的经济性,同时在复杂通信环境下保障运维数据采集的可靠性和准确性,其挑战大,但非常值得深入研究。
PVIET在2019年才刚面世,上市时间较短,当前在国际国内的应用案例有限,国内外专家学者关于PVIET优化配置的研究相对较少,但是国内外学者们在类似研究方面有一些涉及,如配电自动化终端[6-12]、同步相量测量单元[13-14]、分布式发电数据采集终端等配电装置的优化配置,学者们从模型构建、求解算法优化、配置准则等进行了一些研究,值得借鉴。尤其在求解算法方面,由J. Pierezen等率先提出的元启发式算法[15],即郊狼优化算法(Coyote Optimization Algorithm, COA)在电气领域有一些成果。文献[16]将郊狼优化算法应用于分布式发电优化规划中,以解决复杂的实数参数优化问题。文献[17]采用郊狼优化算法对单相和三相电力变压器进行参数估计。文献[18]针对风电综合经济调度问题,用郊狼优化算法求解文中风电经济调度一体化方法模型,并与遗传算法、粒子群算法等进行了比较,结果表明郊狼优化算法的性能更加优越。
为实现一台PVIET高效率、低成本采集管理区域配电网内多个分布式光伏站,本文提出了一种基于改进COA的PVIET优化配置方法。首先,阐述了PVIET的主要功能与支持的通信方式。其次,考虑PVIET的等年值投资成本、年通信成本及保障数据采集可靠性的成本,提出了一种PVIET优化配置模型,并应用改进郊狼优化算法对模型进行求解,获得PVIET在配电网中布点数量和位置。其中,改进的郊狼优化算法通过引入随机分组策略加强郊狼种群的信息交流,建立基于社会互助的新型郊狼成长方式,并应用混合模拟退火算法提高算法求解精度,引入自适应的精英保留策略提升算法收敛速度。通过单维组内最优郊狼扰动策略,提高组内最优狼质量的同时避免郊狼的全维度成长对部分维度的优良信息的掩盖。最后,通过改进的IEEE 69节点仿真算例,验证了本文提出PVIET优化配置模型的可行性,通过算法对比,说明了改进郊狼优化算法在精度、稳定性和收敛性等方面的优越性。
PVIET是分布式光伏站智慧运维的重要数据支撑装备,其功能主要有:①实现与电站现场逆变器通信,获取总直流功率、支路直流功率等逆变器数据;②实现与电站现场环境监测仪通信,获取包含风速、光照等环境监测数据;③实现与电站现场数据采集器通信,获取现场数据采集器采集到的电压、电流、温度等光伏组件数据;④实现与电站现场电能表进行通信;⑤实现与电能质量及故障录波一体化装置进行通信,获取电能质量及故障录波一体化装置实时数据,并对数据进行分析;⑥实现对所接收光伏数据的存储,存储结构带本地时间戳,并且能够将相关数据上传至云端;⑦目前市面上的数据采集器普遍不具备对采集的数据进行分析处理的功能,该设备能够实现对光伏数据的预处理,提高数据分析的实时性,减轻云平台数据处理压力。
此外,由于分布式光伏站的设备供应厂商众多,通信方式多样、通信规约不一致及智能与非智能化设备的差异大,导致集成多类型设备数据及状态难度大,为此,PVIET支持多种通信方式,如图1所示。

图1 PVIET的通信方式
Fig.1 Communication mode of PVIET
PVIET优化布局的目的是实现一台PVIET高效采集管理多个分布式光伏站。但是在实际应用过程中,因一台PVIET与多个分布式光伏站进行通信,不同距离、不同通信方式导致通信质量出现偏差,进而影响数据采集的可靠性。于是,PVIET的优化配置原则不仅要确保经济性即多分布式光伏站接入配电网条件下配置PVIET的数量尽量少,也要保证数据采集的高可靠性。
2.2.1 等年值投资成本
PVIET投资成本主要包括购买成本和运行维护成本,计算式分别为
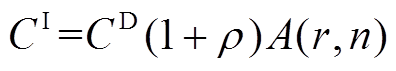 (1)
(1)其中
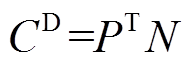 (2)
(2)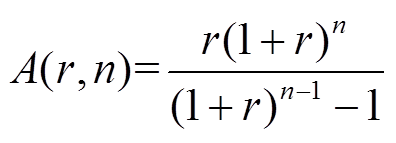 (3)
(3)式中,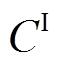 为等年值投资成本;
为等年值投资成本;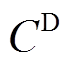 为PVIET的总购买成本;
为PVIET的总购买成本;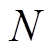 为PVIET配置的总数量;
为PVIET配置的总数量;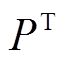 为PVIET的现值单价;
为PVIET的现值单价;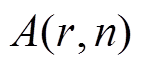 为衡量经济性的因子;
为衡量经济性的因子;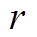 为贴现率;
为贴现率;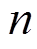 为PVIET的使用年限;
为PVIET的使用年限; 为PVIET运行维护成本占购买PVIET成本的比例。
为PVIET运行维护成本占购买PVIET成本的比例。
2.2.2 年通信成本
PVIET年通信成本计算公式为
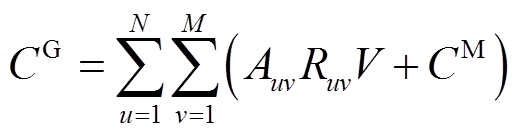 (4)
(4)式中,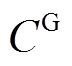 为年通信费用;
为年通信费用;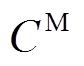 为PVIET与分布式光伏站通信的固有成本;V为单位距离的通信成本;
为PVIET与分布式光伏站通信的固有成本;V为单位距离的通信成本;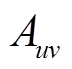 为0-1变量,若区域内第
为0-1变量,若区域内第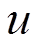 台PVIET与区域内第
台PVIET与区域内第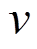 个分布式光伏站建立通信连接,则为1,反之,则为0;
个分布式光伏站建立通信连接,则为1,反之,则为0;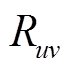 表示第
表示第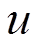 台PVIET与第
台PVIET与第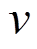 个分布式光伏站之间的通信距离。
个分布式光伏站之间的通信距离。
2.2.3 保障采集可靠性的成本
数据采集可靠性降低所引起的经济损失是PVIET采集可靠性和准确性的重要量化经济指标,分为PVIET故障与正常工作(未故障)两种状态进行讨论,其计算过程如下。
1)PVIET发生故障的损失成本
一台PVIET负责区域中多个分布式光伏站的数据采集工作。一旦单台PVIET发生故障时,将会造成多个分布式光伏站数据无法采集,降低了区域内光伏数据采集的可靠性,不计各个分布式光伏站的规模差异,PVIET发生故障造成的年期望损失成本为
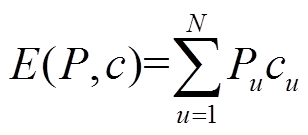 (5)
(5)其中
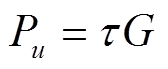 (6)
(6)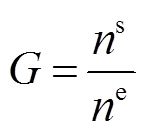 (7)
(7)则有
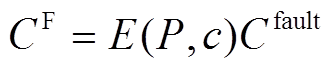 (8)
(8)式中,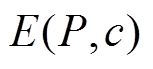 为每年PVIET发生故障时受影响分布式光伏站数目的期望;
为每年PVIET发生故障时受影响分布式光伏站数目的期望;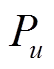 为第
为第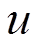 台PVIET每年发生故障的概率;
台PVIET每年发生故障的概率;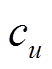 为第u台PVIET负责的分布式光伏站数量;
为第u台PVIET负责的分布式光伏站数量;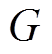 为PVIET资源的冗余度;
为PVIET资源的冗余度;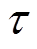 为故障系数;
为故障系数;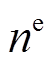 为单台PVIET负责的分布式光伏站的推荐数目;
为单台PVIET负责的分布式光伏站的推荐数目;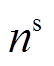 为单台PVIET当前负责的分布式光伏站数目;
为单台PVIET当前负责的分布式光伏站数目;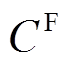 为考虑PVIET故障时的总年损失成本;
为考虑PVIET故障时的总年损失成本;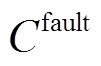 为单个分布式光伏站没有将光伏数据及时上传至PVIET造成的损失成本。
为单个分布式光伏站没有将光伏数据及时上传至PVIET造成的损失成本。
2)PVIET未故障的损失成本
通信距离的增大会导致通信质量降低,进而影响PVIET的采集效果。其中,通信距离与数据采集可靠性的关系为
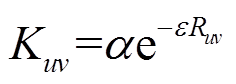 (9)
(9)式中,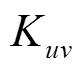 为第
为第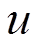 台PVIET与第
台PVIET与第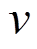 个分布式光伏站之间的通信可靠性程度,在区间[0,1]上;
个分布式光伏站之间的通信可靠性程度,在区间[0,1]上;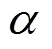 、
、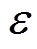 为与可靠性相关的系数。
为与可靠性相关的系数。
PVIET正常工作时的损失成本可以用式(10)和式(11)表示,由于各个分布式光伏站的数据规模不同,上传到PVIET数据量并不相同,所以通信质量差引起的可靠性降低对各个分布式光伏站的影响程度也不同。因此,本文以各个分布式光伏站上传至PVIET的年数据总量与数据采集可靠性共同来评价PVIET未发生故障时可靠性降低对PVIET优化配置经济性的影响。
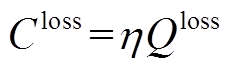 (10)
(10)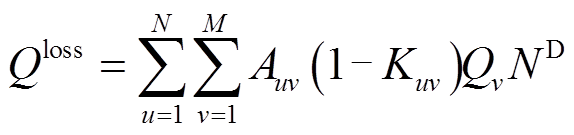 (11)
(11)式中,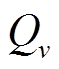 为第v个分布式光伏站每年上传至PVIET的数据总量;
为第v个分布式光伏站每年上传至PVIET的数据总量;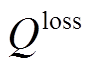 为通信质量变差对数据采集可靠性的影响程度;
为通信质量变差对数据采集可靠性的影响程度;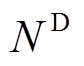 为一年的天数;
为一年的天数;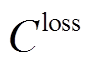 为数据采集可靠性降低带来的经济损失;
为数据采集可靠性降低带来的经济损失;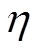 为数据采集可靠性降低与成本损失之间的转换系数。
为数据采集可靠性降低与成本损失之间的转换系数。
综上所述,PVIET优化配置模型的目标函数为
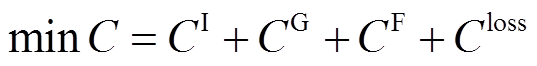 (12)
(12)2.3.1 通信连接约束
所有分布式光伏站必须与一台且只能与一台PVIET建立通信连接;同时,PVIET至少要与一个分布式光伏站建立通信连接。因此,配电网区域内任意一个分布式光伏站与一个PVIET通信连接约束表征为
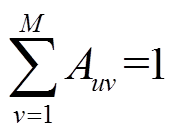 (13)
(13)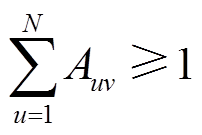 (14)
(14) (15)
(15)2.3.2 配电网条件约束
本文的PVIET均配置在配电网中,且一个节点最多只能配置一台PVIET。
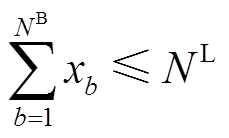 (16)
(16)式中,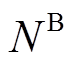 为安装PVIET的节点总数;
为安装PVIET的节点总数;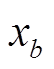 为节点
为节点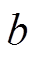 安装的PVIET的数量;
安装的PVIET的数量;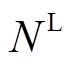 是配电网所有节点数。
是配电网所有节点数。
2.3.3 总资金约束
由于区域范围内配电网的投资资金有限,购买PVIET费用不能超过项目初期的总投资资金。
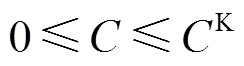 (17)
(17)式中,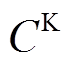 为该工程初期的总投资资金。
为该工程初期的总投资资金。
2.3.4 PVIET数据容量约束
分布式光伏站工作在白天,PVIET也工作在固定时间,且每天PVIET均会将采集到的数据上传至光伏云端,因此,每日一个PVIET的光伏数据总采集量不能超过PVIET能储存、处理的最大数据总量。
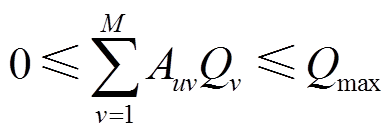 (18)
(18)式中,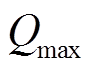 为PVIET每天能储存、处理的最大数据总量;
为PVIET每天能储存、处理的最大数据总量;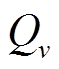 为区域内第
为区域内第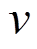 个分布式光伏站内各个光伏设备的数据量之和。
个分布式光伏站内各个光伏设备的数据量之和。
2.3.5 通信距离约束
为保证PVIET的正常数据采集工作,区域内PVIET与分布式光伏站之间的通信距离必须限制在一定范围内,否则会严重影响通信质量。
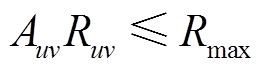 (19)
(19)式中,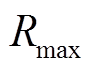 为PVIET与分布式光伏站能够正常通信的最大通信距离。
为PVIET与分布式光伏站能够正常通信的最大通信距离。
2.3.6 通信连接数量约束
PVIET支持的通信方式多样,但每种通信方式的连接数量有限,与站内各种光伏设备通信的连接数量不能超过PVIET某种通信方式下的最大允许连接数量。
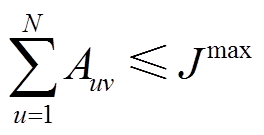 (20)
(20)式中,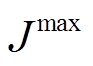 为PVIET在单一通信方式下的最大允许连接数量。
为PVIET在单一通信方式下的最大允许连接数量。
2.3.7 非故障条件下年通信可靠性降低程度约束
为了不使总的数据采集可靠性受到严重影响,设定PEIVT非故障时每年的可靠性降低程度不超过每年最大允许的可靠性降低程度。
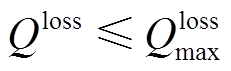 (21)
(21)式中,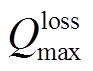 为PVIET非故障时最大能够允许的可靠性降低程度。
为PVIET非故障时最大能够允许的可靠性降低程度。
综上所述,PVIET优化配置模型的解主要包括PVIET总数量、PVIET安装在配电网中的位置(节点号)以及单台PVIET负责采集管理的分布式光伏站编号。所构建的PVIET优化配置模型是一个混合整数非线性规划模型,且整数之间存在强耦合关系,传统的整数优化规划算法对其求解难度大。为此,提出一种改进的郊狼优化算法,解决传统郊狼优化算法收敛速度慢、求解精度低、稳定性差的问题,实现模型的准确快速求解。
目前,郊狼优化算法(COA)广泛应用于交通、电力、能源等多个工程领域,其主要步骤如下[19]。
3.1.1 郊狼种群初始化与随机分组
郊狼最初被随机分成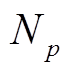 组,每组有
组,每组有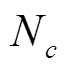 只郊狼,因此种群数量
只郊狼,因此种群数量 。第
。第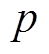 组的第
组的第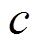 只郊狼个体中每一维变量可以按以下方式进行初始化。
只郊狼个体中每一维变量可以按以下方式进行初始化。
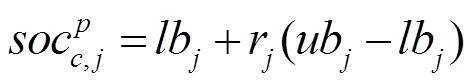 (22)
(22)式中,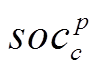 为组群
为组群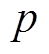 中第c只郊狼的第
中第c只郊狼的第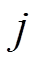 维变量;
维变量; 与
与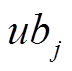 分别为第
分别为第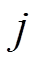 维变量的上限、下限;
维变量的上限、下限;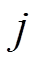 的取值范围为[1,D],D为解的维度;
的取值范围为[1,D],D为解的维度;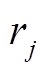 为[0,1]范围内的随机数。
为[0,1]范围内的随机数。
郊狼当前的社会状况可由适应度函数表示为
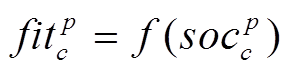 (23)
(23)式中,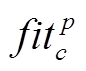 为组群p中第c只郊狼的社会适应能力。
为组群p中第c只郊狼的社会适应能力。
3.1.2 组内郊狼成长
郊狼成长受组内等级制度(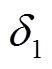 )和组内文化(
)和组内文化(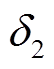 )的影响,计算方法如式(24)和式(25)所示。
)的影响,计算方法如式(24)和式(25)所示。
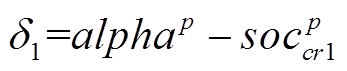 (24)
(24)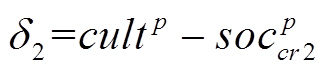 (25)
(25)式中,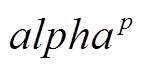 为组群p内最优郊狼;
为组群p内最优郊狼;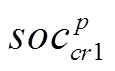 和
和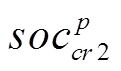 为组群p中随机选取的两个郊狼;
为组群p中随机选取的两个郊狼;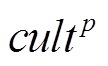 为组群p文化趋势,代表一组组群内郊狼的平均社会状况,计算式为
为组群p文化趋势,代表一组组群内郊狼的平均社会状况,计算式为
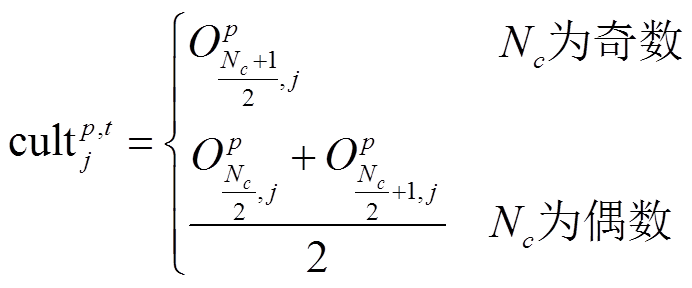 (26)
(26)式中,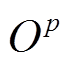 为组群
为组群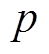 中由小到大排序后的郊狼序列;
中由小到大排序后的郊狼序列;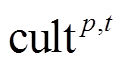 为组群
为组群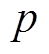 的组文化趋势。
的组文化趋势。
组群p中第c只郊狼成长后的新解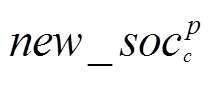 为
为
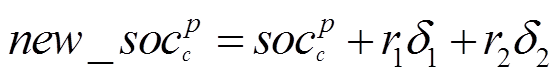 (27)
(27)式中,r1和r2为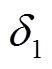 和
和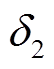 的随机权重值,其值在[0,1]之间。
的随机权重值,其值在[0,1]之间。
组内一只郊狼成长后,对其社会适应能力进行评估,并应用贪心策略,选择保留或淘汰掉成长后的郊狼。
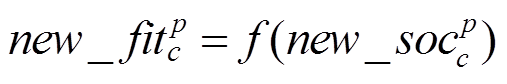 (28)
(28)式中,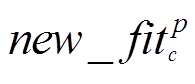 为组群p中第c只郊狼成长后,新解的适应度值。
为组群p中第c只郊狼成长后,新解的适应度值。
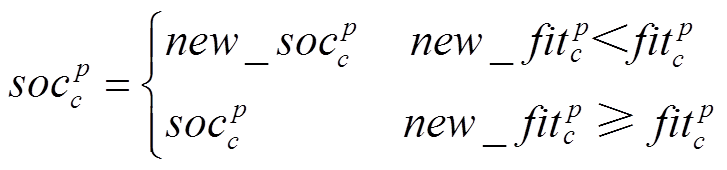 (29)
(29)3.1.3 郊狼的生死
新郊狼的出生如式(30)所示。
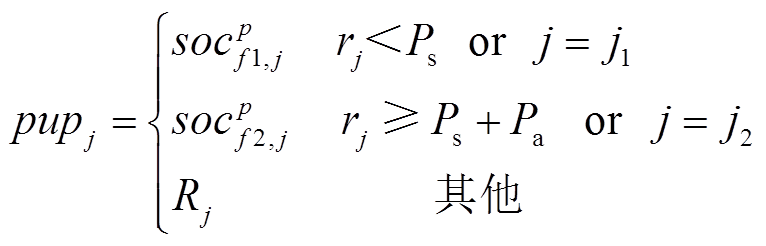 (30)
(30)式中,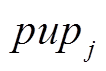 为新生郊狼的第j维变量;
为新生郊狼的第j维变量;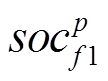 和
和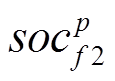 为组群p中随机选取的两个父母郊狼;
为组群p中随机选取的两个父母郊狼;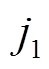 和
和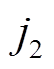 为两个随机维度号;
为两个随机维度号;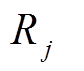 为在第
为在第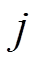 维变量范围内的随机值;
维变量范围内的随机值;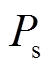 为
为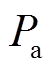 分别为分散概率和关联概率,计算方法分别为
分别为分散概率和关联概率,计算方法分别为
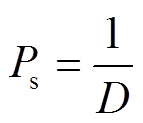 (31)
(31)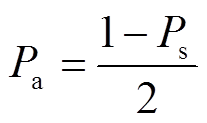 (32)
(32)新郊狼出生后,依照如下规则决定组内郊狼的生存与死亡:①组内所有郊狼都比新生郊狼强时,新生郊狼死亡。②组内存在郊狼比新生郊狼差时,这些郊狼中年龄最大的郊狼死亡;如果这些郊狼的年龄相同,最差的郊狼死亡,新生郊狼存活,并设新生郊狼的年龄为0。
3.1.4 郊狼被驱离和接纳
在COA中,郊狼有时会离开原来的组群,加入其他组群中,郊狼离开自己组群的概率用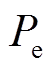 表示,即
表示,即
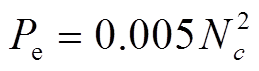 (33)
(33)郊狼被驱离和接纳操作完成后,所有郊狼年龄加1,一次迭代结束。
PVIET优化规划模型是一个混合整数非线性规划模型,且整数之间存在强耦合关系,直接使用郊狼优化算法对其求解时,常出现精度不足、稳定性差、收敛速度缓慢等问题,于是,本文提出了一种改进的郊狼优化算法(Improved Coyote Optimization Algorithm, ICOA),主要改进如下。
3.2.1 郊狼种群的随机分组
每只郊狼在自己的区域内并行搜索,且成长不受其他组群的影响,仅受组内最优郊狼与组文化趋势的影响。这种搜索方式具有防止整个郊狼种群陷入局部最优的特点,但也使组群之间的信息交流严重不足,导致PVIET优化配置模型求解过程中算法搜索能力弱、收敛速度慢。于是,本文在郊狼成长、生死后,不进行郊狼的驱逐操作,而是对整个郊狼种群重新随机分组;这种方式既保留了分成多个组群分别并行搜索的优势,也加强了整个种群之间的交流与信息共享,平衡了算法的开采能力与搜索能力。
3.2.2 社会互助成长策略
社会互助是指在自然界中,当某个郊狼组群遭遇天敌威胁、食物短缺等问题时,其他组群的郊狼会对这组郊狼进行援助,帮助组群内的郊狼成长。在传统郊狼优化算法中,郊狼的分组完全随机,常会出现一个组群郊狼个体差异很小的情况,即组群内的郊狼个体在成长中几乎不会发生变化,导致种群搜索范围小,求解本文所提出的模型时,精度较低。因此,受郊狼社会互助行为的启发,本文提出一种社会互助成长策略,在郊狼之间形成一种组与组、组与整个种群的“互助”机制。种群互助的主要步骤如下:
首先,根据组群的差异判断组内郊狼是否需要组群外郊狼的帮助。以最优狼与组文化趋势之间的距离代表组群的差异度,计算方法为
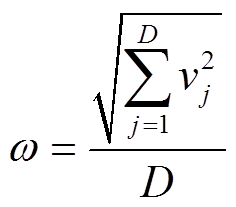 (34)
(34)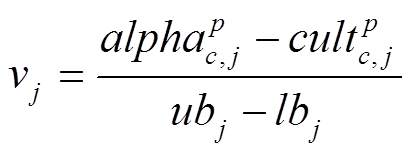 (35)
(35)式中,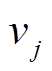 为组内最优郊狼和组文化趋势每一维变量的差值与每一维变量上界与下界之间差值之间的比值。
为组内最优郊狼和组文化趋势每一维变量的差值与每一维变量上界与下界之间差值之间的比值。
当判断组群内郊狼成长困难时,用全局最优郊狼与随机一个组群内的组内最优郊狼引导该组群中郊狼的成长,新的引导算子为
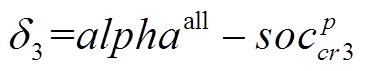 (36)
(36) (37)
(37)式中,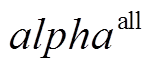 与
与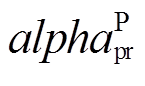 分别为全局最优郊狼与随机选择的一组组群的最优郊狼;pr为随机选取的一组郊狼组群;
分别为全局最优郊狼与随机选择的一组组群的最优郊狼;pr为随机选取的一组郊狼组群;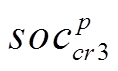 、
、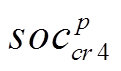 分别为随机选取的组内郊狼。于是,社会互助成长策略可表示为
分别为随机选取的组内郊狼。于是,社会互助成长策略可表示为
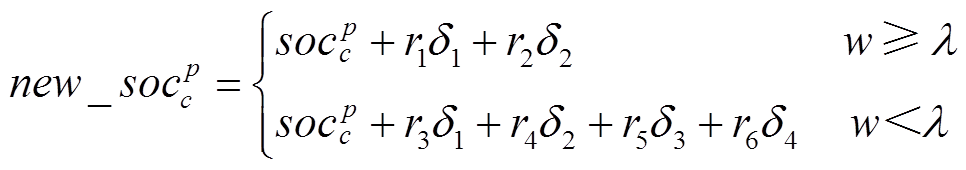 (38)
(38)式中,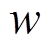 为郊狼组群的种群差异度;
为郊狼组群的种群差异度;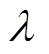 为阈值,应根据求解问题的实际情况选择合适的
为阈值,应根据求解问题的实际情况选择合适的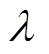 值,如果
值,如果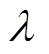 选择过大,算法将失去原有组内成长策略的优点,如果
选择过大,算法将失去原有组内成长策略的优点,如果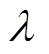 选择过小,当一组组群差异过小时,不利于组群的成长;
选择过小,当一组组群差异过小时,不利于组群的成长;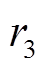 、
、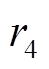 、
、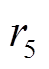 、
、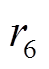 为[0,1]间的随机数。
为[0,1]间的随机数。
3.2.3 混合模拟退火提高求解精度
郊狼成长后的个体,一般以贪心策略决定是否保留新生成的解。此种策略对于只有一个最优解的优化问题,算法可很快寻找到最优解,但是本文所提出的PVIET优化配置模型常出现多个最优解,从而使算法存在很大的陷入局部最优的风险。为此,本文采用模拟退火策略代替原郊狼优化算法的贪心策略,让一些成长后社会适应能力差于成长前的郊狼有一定概率保留下来,避免算法早熟的发生[20]。成长后个体的保留策略如下
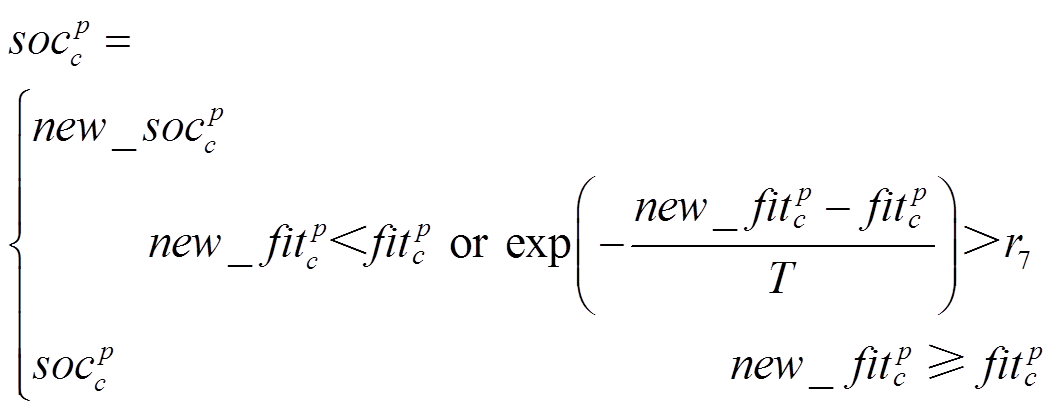 (39)
(39)式中,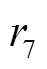 为[0,1]间的随机数;
为[0,1]间的随机数;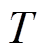 为退火温度,按如下方式降温
为退火温度,按如下方式降温
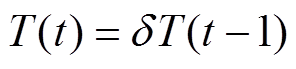 (40)
(40)式中,t为当前迭代次数;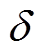 为降温速率。
为降温速率。
3.2.4 自适应精英保留策略提升收敛速度
精英保留策略是指把一个种群中社会适应能力最强的个体保留到下一代种群的方法,能够显著提高算法收敛速度,但该策略具有容易导致算法早熟的缺点。为此,本文为提高算法后期的收敛速度,采用一种自适应的精英保留策略,即在算法前期,因当前的最优解并不是全局最优解,为防止算法过早收敛,以较低的概率保留当前最优解;而在算法后期,以较高的概率保留当前最优解,减少算法后期解的波动,提高算法后期的收敛速度。决定是否保留当前最优解的概率为
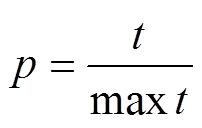 (41)
(41)式中,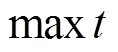 为最大迭代次数。
为最大迭代次数。
3.2.5 组内最优郊狼单维扰动策略
在郊狼优化算法中,郊狼的成长都是围绕组内最优郊狼展开的,组内最优郊狼的好坏直接决定组内其他郊狼的成长效果,进而影响算法整体的优化效果。因此,本文仅对组内最优郊狼进行扰动。
在传统郊狼优化算法郊狼成长中,候选解中的变量同时改变,然而,这种同时多个维度改变的成长方式会掩盖部分维度的优良信息,因此,在对组内最优郊狼个体的扰动中,仅对少量维度进行扰动,扰动后的解 为
为
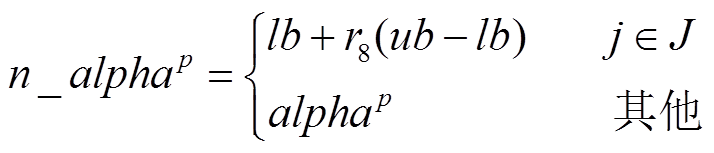 (42)
(42)式中,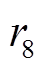 为[0,1]间的随机数;
为[0,1]间的随机数;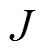 中所取的元素数量NJ由决策变量的数量决定,即
中所取的元素数量NJ由决策变量的数量决定,即
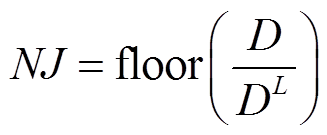 (43)
(43)式中,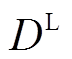 为扰动维度数量增加的临界阈值;
为扰动维度数量增加的临界阈值;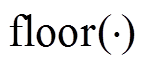 代表朝零方向取整。
代表朝零方向取整。
对 进行扰动之后,采用贪心策略决定是否保留新解,即
进行扰动之后,采用贪心策略决定是否保留新解,即
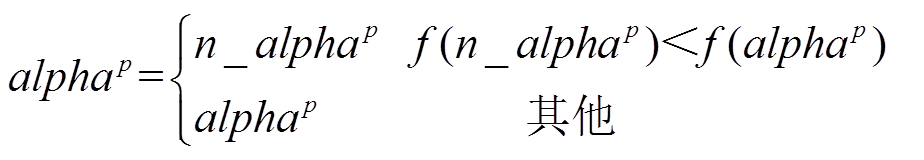 (44)
(44)设置郊狼组群初始参数;随机初始化郊狼种群,进行适应度计算,并记录全局最优郊狼与各个组群的最优郊狼,改进的郊狼优化算法的伪代码如下:

更新郊狼年龄,重新对郊狼进行随机分组
end for
输出最优郊狼
应用改进的郊狼优化算法对本文所提的PVIET优化配置模型的求解流程如下:
(1)根据约束条件,确定需要配置的最少PVIET的数量N。
(2)由于区域配电网接入的分布式光伏数量有限,所以采用穷举法列举所有可能的PVIET数量,获知最大的PVIET数量。
(3)在确定数量的基础上,通过本文的改进郊狼优化算法,得出在该数量条件下使数据采集可靠性最高的PVIET的位置与单台PVIET负责进行数据采集工作的分布式光伏。
(4)比较不同配置方案的经济性,最终确定最优的PVIET优化配置方案。
以IEEE69节点系统的拓扑结构为例,验证本文所述模型与算法的有效性。不考虑分布式光伏接入容量与其对配电网的影响,仅仅为验证本文方法的效果,假设1~20号分布式光伏接入节点分别为[6,8,12,20,21,22,26,28,29,31,35,38,39,42,46,47,55,60, 62,63],PVIET可以与分布式光伏接入节点重叠,也可以不与分布式光伏接入节点重叠。
PVIET对分布式光伏站内多种光伏设备数据进行采集,设1~20号分布式光伏站上述设备的日数据总量见表1。
表1 1~20号分布式光伏站的每日数据总量
Tab.1 Daily data volume of 1~20 distributed PV station

分布式光伏站编号数据量/Mbit 10.232 0 20.965 0 30.598 3 40.216 2 50.240 5 60.791 7 70.321 2 80.775 6 91.053 5 100.232 0 110.866 2 120.426 5 130.593 7 140.420 6 150.342 0 160.692 8 170.421 6 180.664 1 191.100 0 200.332 8
设PVIET单台价格为1.5万元/台,贴现率为10%,设备使用年限为15年,运行维护成本占比为20%,总投资成本不超过15万元。每台PVIET日最大数据采集量为4Mbit。每台PVIET均采用无线通信的方式对PVIET的数据进行采集,该通信方式下PVIET最多只连接六个分布式光伏站。PVIET与分布式光伏站建立通信连接的固有年通信成本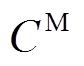 为40元/站,单位距离的通信成本
为40元/站,单位距离的通信成本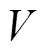 为20元/km;故障系数
为20元/km;故障系数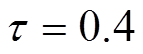 ;单台PVIET负责的分布式光伏站的推荐数目
;单台PVIET负责的分布式光伏站的推荐数目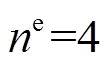 ;单个分布式光伏站没有将光伏数据及时上传至PVIET造成的损失成本
;单个分布式光伏站没有将光伏数据及时上传至PVIET造成的损失成本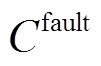 为400元/站。数据采集可靠性降低与成本损失之间的转换系数
为400元/站。数据采集可靠性降低与成本损失之间的转换系数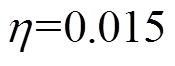 ;系数
;系数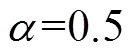 、
、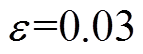 ,最大能够允许的可靠性降低程度
,最大能够允许的可靠性降低程度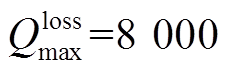 。PVIET所在节点与分布式光伏节点之间的距离近似为配电网节点之间的距离,节点间距离与IEEE 69节点的线路电抗标幺值的比例为15:1。
。PVIET所在节点与分布式光伏节点之间的距离近似为配电网节点之间的距离,节点间距离与IEEE 69节点的线路电抗标幺值的比例为15:1。
本文设定郊狼优化算法的参数如下:郊狼的组数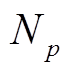 =10,组内郊狼个数
=10,组内郊狼个数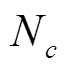 =10,种群数量
=10,种群数量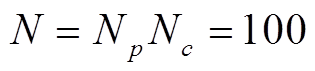 ,成长方式的转换阈值
,成长方式的转换阈值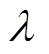 =0.5,退火温度
=0.5,退火温度 ,降温数率
,降温数率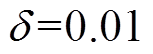 ,扰动维度数量增加的临界阈值
,扰动维度数量增加的临界阈值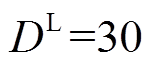 ,对比的算法为未经改进的传统郊狼优化算法,组数与组内郊狼数等参数设置与改进的郊狼优化算法相同。
,对比的算法为未经改进的传统郊狼优化算法,组数与组内郊狼数等参数设置与改进的郊狼优化算法相同。
4.2.1 PVIET优化配置模型求解结果
PVIET优化配置模型求解结果见表2,其中方案1为一个PVIET负责一个分布式光伏站的配置方案(但这种情况并不满足本文的约束条件,且经济性最差,这里仅仅作为对比参考);方案2为COA求解出的最佳配置方案;方案3为ICOA求解出的最佳配置方案。三种方案的PVIET的位置分别如图2~图4所示。
表2 不同优化配置方案的对比
Tab.2 Comparison of different optimal
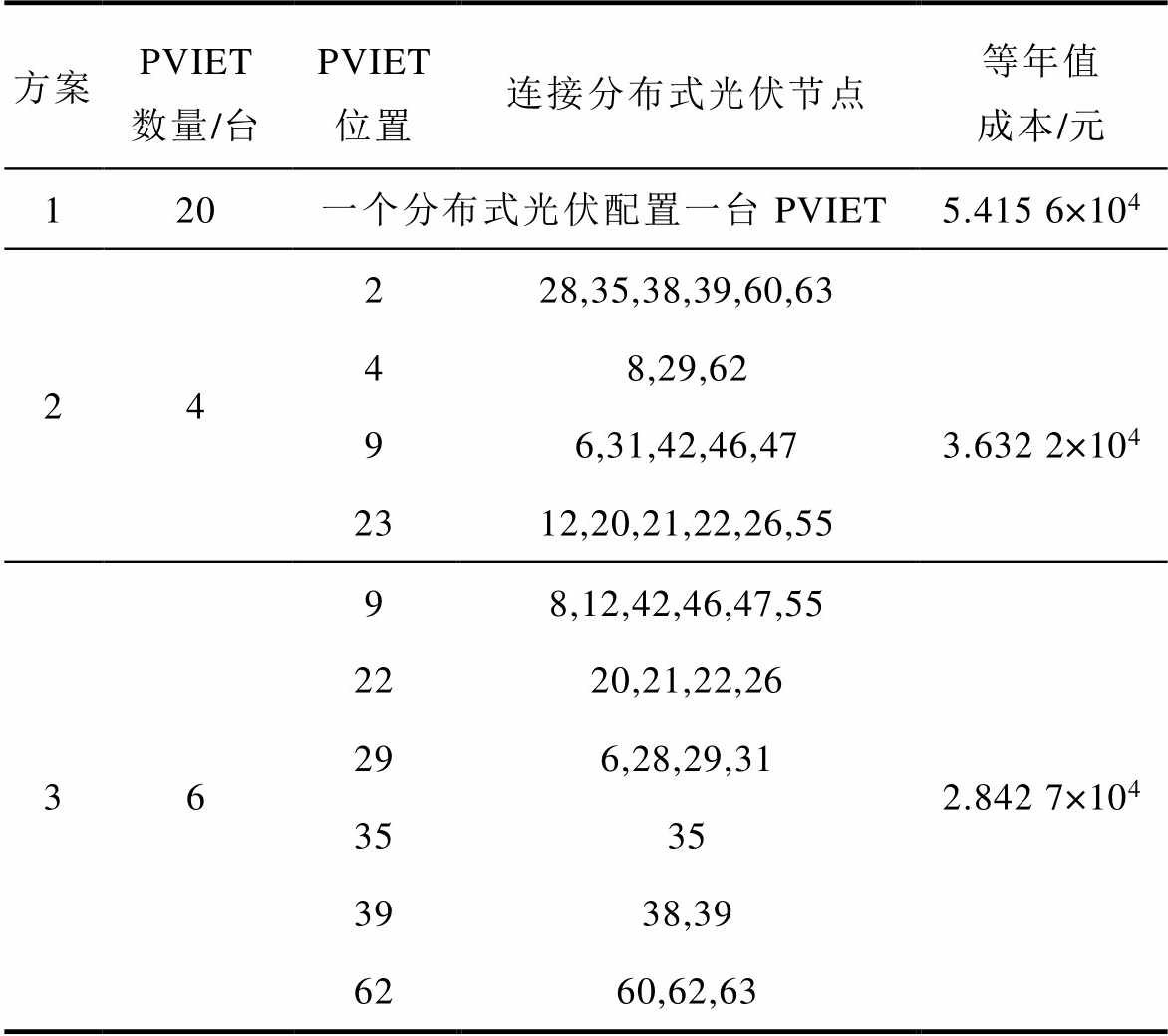
方案PVIET数量/台PVIET位置连接分布式光伏节点等年值成本/元 120一个分布式光伏配置一台PVIET5.415 6×104 24228,35,38,39,60,633.632 2×104 48,29,62 96,31,42,46,47 2312,20,21,22,26,55 3698,12,42,46,47,552.842 7×104 2220,21,22,26 296,28,29,31 3535 3938,39 6260,62,63
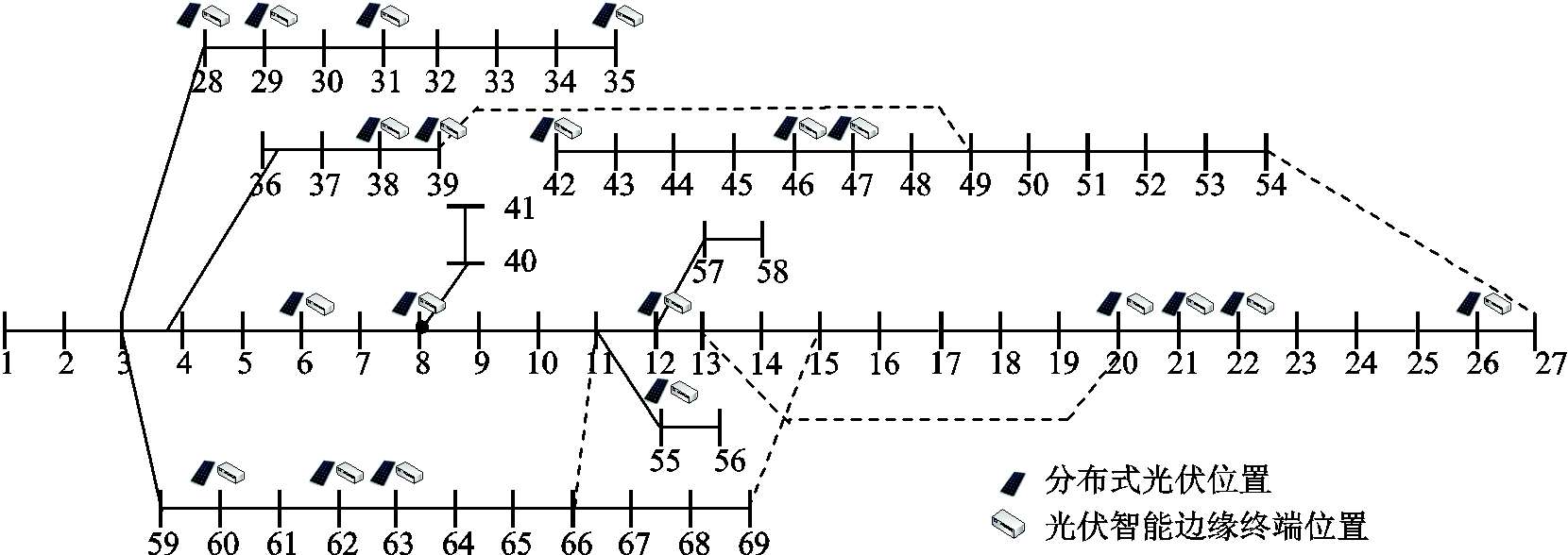
图2 方案1中PVIET在配电网中的位置
Fig. 2 Location of PV IETs in distribution network in scheme 1
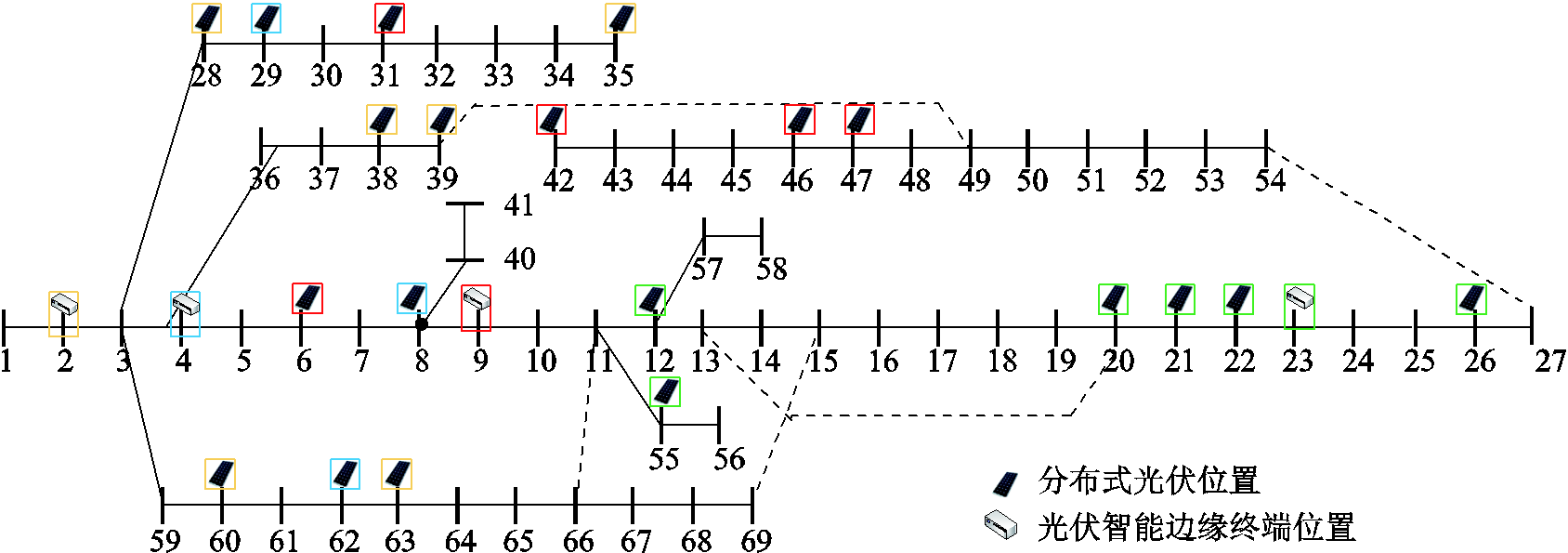
图3 方案2中PVIET在配电网中的位置
Fig.3 Location of PV IETs in distribution network in scheme 2
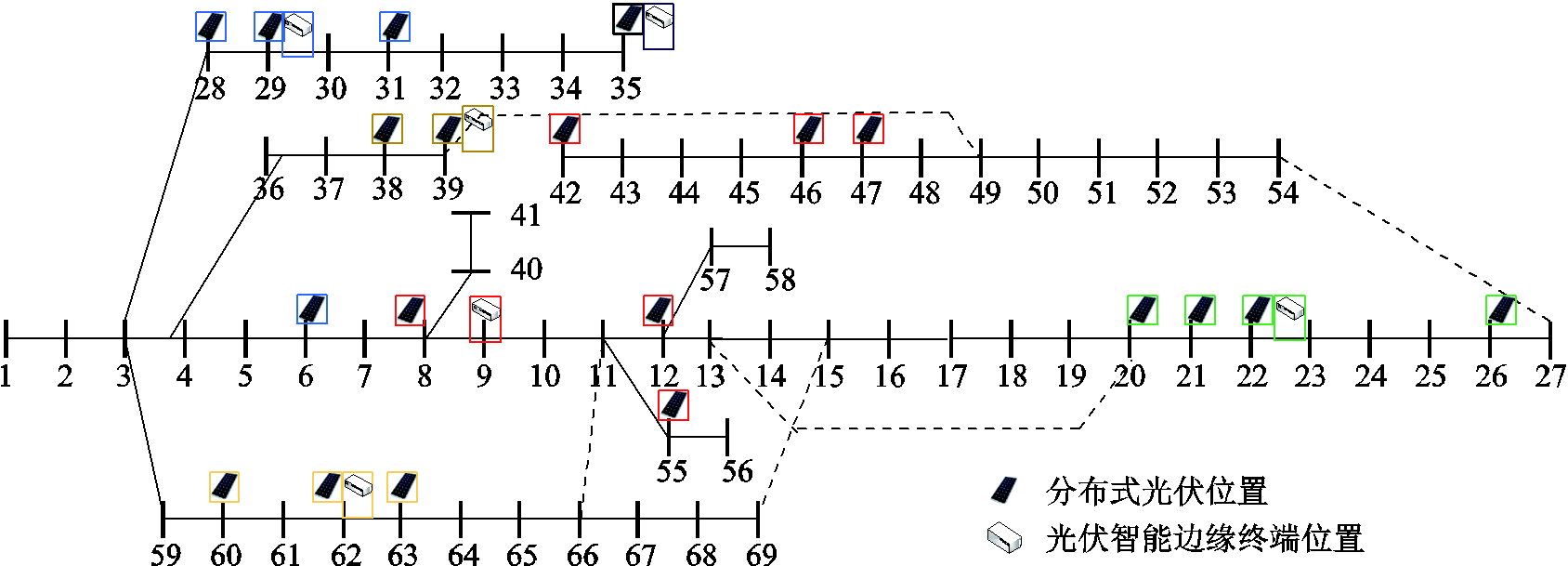
图4 方案3中PVIET在配电网中的位置
Fig.4 Location of PV IETs in distribution network in scheme 3
从表2中可以看出:
(1)三种方案需要的PVIET台数分别为20台、4台、6台,等年值成本分别为5.415 6万元、3.632 2万元、2.842 7万元,方案2与方案3求得的等年值成本相比于方案1分别降低了1.783 4万元、2.572 9万元。说明了本文的优化配置方法在计及可靠性降低引起的成本损失的情况下,相对于一站一台式的PVIET配置方法依旧能够显著降低成本,从而证实了PVIET优化配置模型的可行性。
(2)方案3的等年值年成本远低于方案2,二者之间相差了7 895元。说明方案3引起的数据采集可靠性降低程度较方案2更小,PVIET的配置数量、位置,以及每一个PVIET负责管理的分布式光伏站的划分更加合理,改进郊狼优化算法的求解精度比传统郊狼优化算法更高。
4.2.2 算法分析
在上述模型求解的基础上,进一步对算法的性能进行分析,将本文提出的算法与郊狼优化算法(COA)、粒子群优化(Particle Swarm Optimization, PSO)算法[21]、正余弦算法(Sine Cosine Algorithm, SCA)[22]进行对比;粒子群算法的参数设置为:惯性权重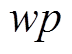 为0.5,学习因子
为0.5,学习因子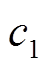 =2,
=2,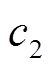 =3;正余弦算法的收敛常数
=3;正余弦算法的收敛常数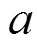 在[2,0]线性递减。首先采用均值(mean)和方均差(std)来评估算法的精度与稳定性,为了公平起见,确定PVIET的数量为4~10台的相同条件下,算法独立运行50次取最优解,各个算法对模型的求解结果见表3。
在[2,0]线性递减。首先采用均值(mean)和方均差(std)来评估算法的精度与稳定性,为了公平起见,确定PVIET的数量为4~10台的相同条件下,算法独立运行50次取最优解,各个算法对模型的求解结果见表3。
由表3可以看出,本文改进的郊狼优化算法无论是在平均值(mean)还是在方均差上(std)均小于未经改进的郊狼优化算法。在PVIET为4~10台时,改进后的郊狼优化算法相对于改进前精度分别提升了18.37%、27.72%、35.67%、38.91%、42.95%、45.65%、46.14%。18.37%、27.72%、35.67%、38.91%、42.95%、45.65%、46.14%;相对于粒子群算法精度分别提升了18.20%、23.52%、29.79%、33.95%、36.49%、39.33%、39.82%;相对于正余弦算法精度分别提升了20.39%、26.43%、31.95%、35.42%、38.19%、40.48%、41.05%。
表3 不同PVIET数量条件下的算法求解结果对比
Tab.3 Comparison of algorithm results under the condition of different number of PV IETs
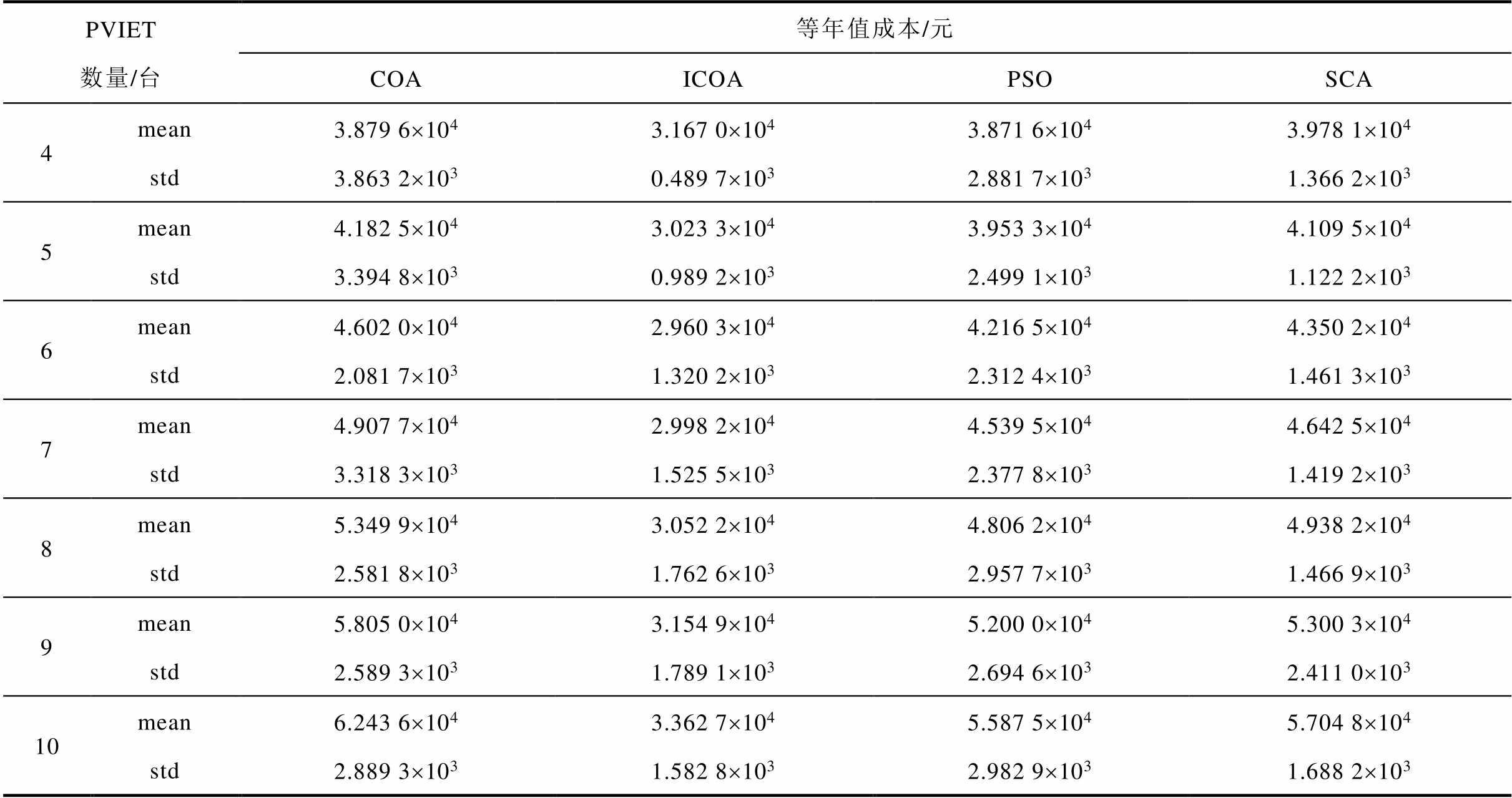
PVIET数量/台等年值成本/元 COAICOAPSOSCA 4mean3.879 6´1043.167 0´1043.871 6´1043.978 1´104 std3.863 2´1030.489 7´1032.881 7´1031.366 2´103 5mean4.182 5´1043.023 3´1043.953 3´1044.109 5´104 std3.394 8´1030.989 2´1032.499 1´1031.122 2´103 6mean4.602 0´1042.960 3´1044.216 5´1044.350 2´104 std2.081 7´1031.320 2´1032.312 4´1031.461 3´103 7mean4.907 7´1042.998 2´1044.539 5´1044.642 5´104 std3.318 3´1031.525 5´1032.377 8´1031.419 2´103 8mean5.349 9´1043.052 2´1044.806 2´1044.938 2´104 std2.581 8´1031.762 6´1032.957 7´1031.466 9´103 9mean5.805 0´1043.154 9´1045.200 0´1045.300 3´104 std2.589 3´1031.789 1´1032.694 6´1032.411 0´103 10mean6.243 6´1043.362 7´1045.587 5´1045.704 8´104 std2.889 3´1031.582 8´1032.982 9´1031.688 2´103
在PVIET数量为4与5时,以改进的郊狼优化算法与传统郊狼优化算法的最优值分布为例说明本文算法的稳定性。上述50次独立实验中两种算法每一次寻到的最优值如图5与图6所示。本文改进算法求得的结果在均值3.167 0´104元和3.023 3´104元(见表3)处波动,波动范围较小,曲线较为平稳。而传统郊狼优化算法求得的结果分别在均值3.879 6´104元和4.182 5´104元(见表3)处波动,波动范围较大,一些点偏离求得的平均值较远,曲线陡峭,峰谷差异明显。综上所述,改进郊狼优化算法无论是在求解精度还是算法的稳定性上均优于传统的郊狼优化算法。
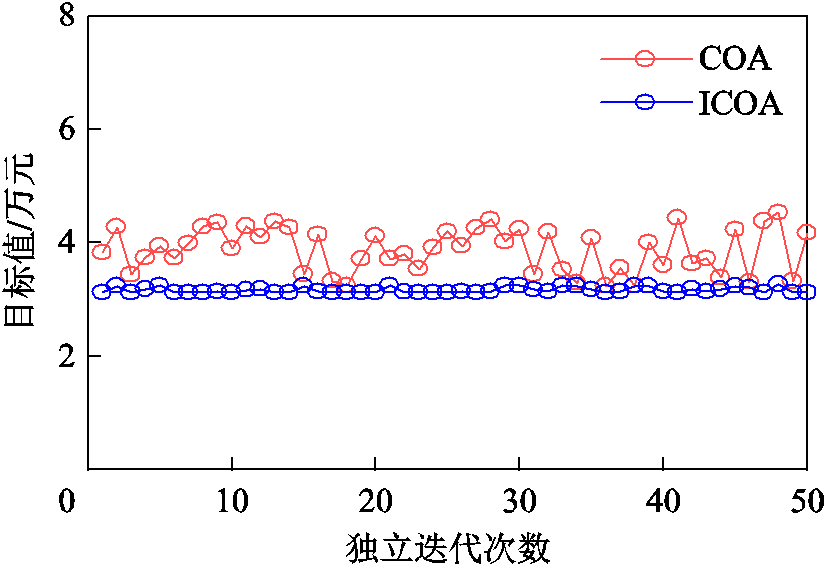
图5 PVIET的数量为4时算法的稳定性对比
Fig.5 Stability comparison of algorithm when the number of PV IETs is 4
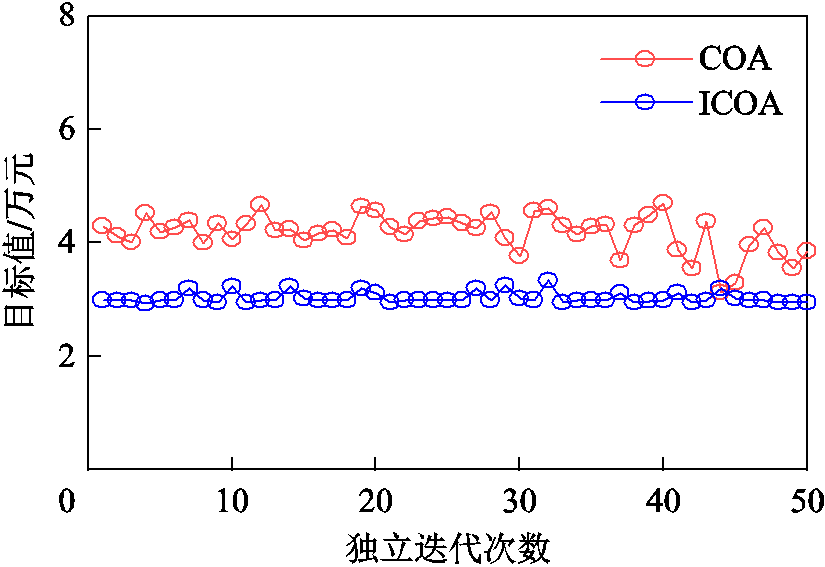
图6 PVIET的数量为5时算法的稳定性对比
Fig.6 Stability comparison of algorithm when the number of PV IETs is 5
下面对算法的收敛性能进行比较,当PVIET的配置数量为4~9时,选取代表性的收敛曲线如图7所示。
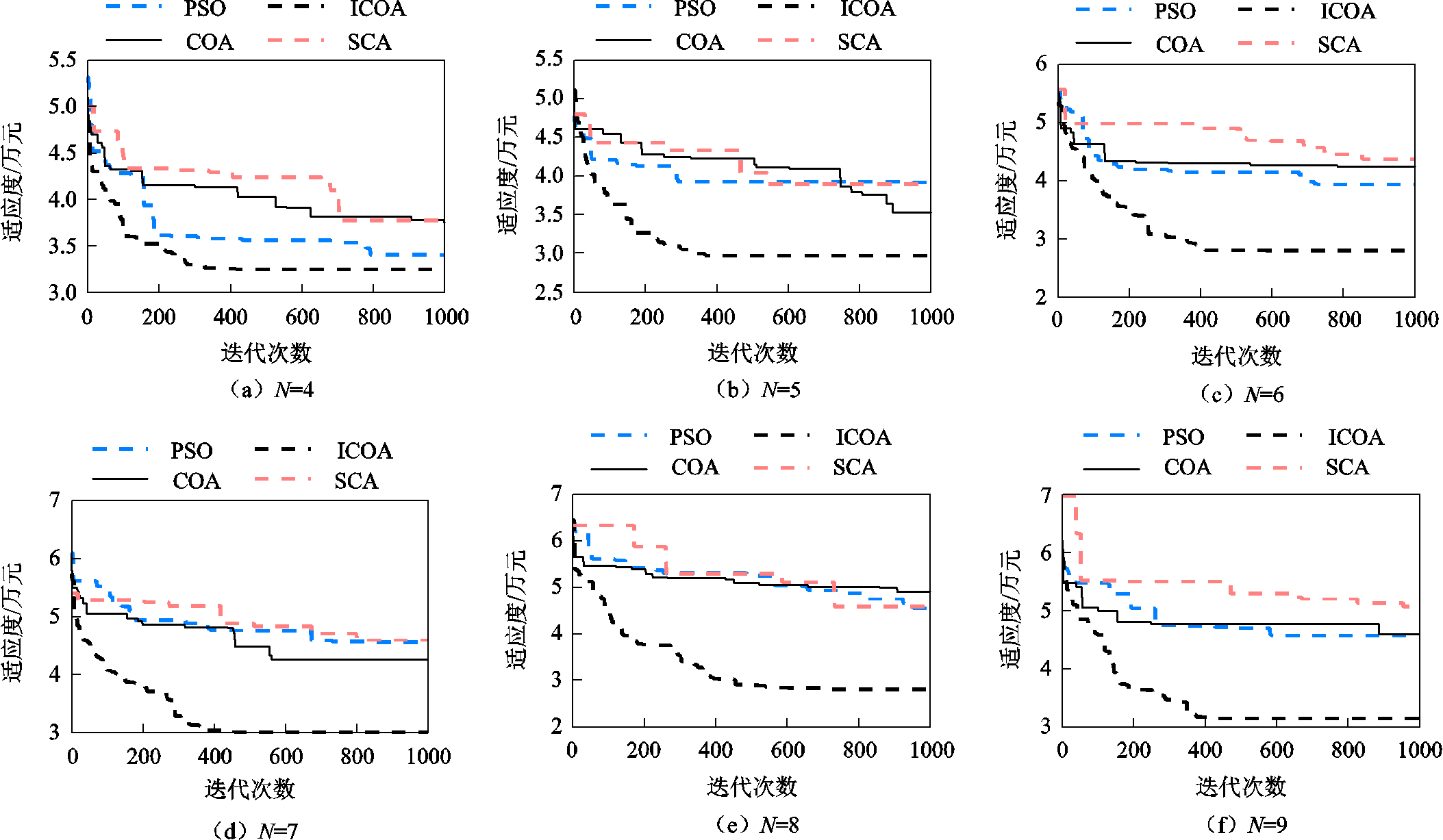
图7 不同PVIET数量条件下的算法收敛性能对比
Fig.7 Comparison of algorithm convergence performance under different number of PV IETs
从图7中可以看出,改进郊狼优化算法收敛速度快,具有较高的精度,而传统郊狼优化算法、粒子群算法、正余弦算法求解速度慢,容易陷入局部最优。以N=5时收敛曲线为例进行说明,改进郊狼优化算法在400多代就可以收敛得到一个精度较高的结果,而传统郊狼优化算法在接近迭代结束时才能收敛,且精度远远低于改进的郊狼优化算法,说明改进郊狼优化算法不仅在精度上有了很大提高,且收敛速度优于传统郊狼优化算法;正余弦算法在500多代收敛,其收敛性能差于本文算法,且算法精度较低;粒子群算法虽然收敛的代数与改进郊狼优化算法相差不大,但其求解精度较低。总的来说,改进郊狼优化算法在精度、稳定性与收敛性等方面均具有优越性。
1)本文为实现一台价格昂贵的PVIET采集管理区域配电网中多个分布式光伏站的优化设计,提出了基于改进郊狼优化算法的PVIET优化配置模型。仿真结果表明,在充分考虑保障数据采集可靠性成本的前提下,达成了PVIET的合理优化配置,大幅度降低成本,可为PVIET优化规划设计提供依据。
2)为解决郊狼优化算法处理复杂问题精度不足以及收敛速度缓慢的问题,本文提出一种全新的社会互助郊狼成长策略,以及利用随机分组策略、模拟退火与自适应精英保留策略的改进郊狼优化算法。仿真结果表明,改进算法在PVIET数量为4~9时进行50次独立实验时,改进郊狼优化算法的精度较原来分别提升了18.37%、27.72%、35.67%、38.91%、42.95%、45.65%、46.14%;相对于粒子群算法精度分别提升了18.20%、23.52%、29.79%、33.95%、36.49%、39.33%、39.82%;相对于正余弦算法精度分别提升了20.39%、26.43%、31.95%、35.42%、38.19%、40.48%、41.05%,且最优解与最劣解之间峰谷差小。同时,在收敛性比较中,改进郊狼优化算法相比于COA、PSO、SCA的收敛速度更快。本文在算法上的改进可为郊狼优化算法在电力系统中的推广应用提供参考。
参考文献
[1]吉锌格, 李慧, 刘思嘉, 等. 基于MIE-LSTM的短期光伏功率预测[J]. 电力系统保护与控制, 2020, 48(7): 50-57. Ji Zige, Li Hui, Liu Sijia, et al. Short-term photovoltaic power forecasting based on MIE-LSTM[J]. Power System Protection and Control, 2020, 48(7): 50-57.
[2]赖昌伟, 黎静华, 陈博, 等.光伏发电出力预测技术研究综述[J]. 电工技术学报, 2019, 34(6): 1201-1217. Lai Changwei, Li Jinghua, Chen Bo, et al. Review of photovoltaic power output prediction technology[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1201-1217.
[3]徐瑞东, 陈昊, 胡义华, 等. 基于高斯过程的光伏阵列故障定位[J].电工技术学报, 2013, 28(6): 249-256. Xu Ruidong, Chen Hao, Hu Yihua, et al. Fault location of photovoltaic array based on Gaussian process[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 249-256.
[4]李元良, 丁坤, 陈富东, 等. 基于快速过采样主成分分析法的光伏阵列故障诊断[J]. 电网技术, 2019, 43(1): 308-315. Li Yuanliang, Ding Kun, Chen Fudong, et al. Fault diagnosis method of PV array based on fast OS-PCA[J]. Power System Technology, 2019, 43(1): 308-315.
[5]陈凌, 韩伟, 张经炜. 基于数据融合的光伏组件故障诊断[J]. 电网技术, 2017, 41(6): 1864-1873. Chen Ling, Han Wei, Zhang Jingwei. PV module fault diagnosis based on data fusion[J]. Power System Technology, 2017, 41(6): 1864-1873.
[6]陈得宇, 沈继红, 张仁忠, 等. 配电网故障可观测的实现及馈线终端单元配置方法[J]. 电网技术, 2011, 35(2): 94-99. Chen Deyu, Shen Jihong, Zhang Renzhong, et al. Realization of fault observability of distribution system and corresponding optimal configuration method of feeder terminal units[J]. Power System Technology, 2011, 35(2): 94-99.
[7]郑玲玲, 王铮, 杨丽徙. 不同网络结构及可靠性要求环境下FTU的最优配置[J]. 电力系统保护与控制, 2015, 43(24): 69-74. Zheng Lingling, Wang Zheng, Yang Lixi. FTU optimal configuration under different distribution network structures and reliability requirement[J]. Power System Protection and Control, 2015, 43(24): 69-74.
[8]周勐, 么军, 姚远, 等. 基于故障可观性指标的配电网FTU最优配置模型研究[J]. 电力系统保护与控制, 2019, 47(17): 117-124. Zhou Meng, Mo Jun, Yao Yuan, et al. Research on FTU optimal configuration model of distribution network based on fault observability index[J]. Power System Protection and Control, 2019, 47(17): 117-124.
[9]王秋杰, 金涛, 申涛, 等. 利用多因素降维的配电网区段定位完全解析模型[J]. 电工技术学报, 2019, 34(14): 3012-3024. Wang Qiujie, Jin Tao, Shen Tao, et al. A complete analytic model of section location in distribution network based on multi-factor dimensionality deduction[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3012-3024.
[10]李子韵, 成乐祥, 王自桢, 等. 配电自动化终端布局规划方法[J]. 电网技术, 2016, 40(4): 1271-1276. Li Ziyun, Cheng Lexiang, Wang Zizhen, et al. A method of layout planning for distribution automation terminal[J]. Power System Technology, 2016, 40(4): 1271-1276.
[11]Xu Junjun, Wu Zaijun, Yu Xinghuo, et al. A new method for optimal FTU placement in distribution network under consideration of power service reliability[J]. Science China: Technological Sciences, 2017, 60(12): 1885-1896.
[12]罗深增, 李银红, 石东源. 广域测量系统可观性概率评估及其在PMU优化配置中的应用[J]. 电工技术学报, 2018, 33(8): 1844-1853. Luo Shenzeng, Li Yinhong, Shi Dongyuan. Wide area monitoring system observability probabilistic evaluation and it’s application in optimal PMU placement[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1844-1853.
[13]Aghaei J, Baharvandi A, Rabiee A, et al. Probabilistic PMU placement in electric power networks: an MILP-based multi-objective model[J]. IEEE Transactions on Industrial Informatics, 2015, 11(2): 332-341.
[14]于华楠, 李永鑫, 王鹤. 基于过完备字典设计的电力系统扰动定位方法[J]. 电工技术学报, 2020, 35(7): 1444-1453. Yu Huanan, Li Yongxin, Wang He. Disturbance location method of power system based on over-complete reconstruction dictionary design[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1444-1453.
[15]Pierezan J, Dos Santos Coelho L. Coyote optimization algorithm: a new metaheuristic for global optimization problems[C]//2018 IEEE Congress on Evolutionary Computation(CEC), Rio de Janeiro, Brazil, 2018, DOI: 10.1109/CEC.2018.8477769 .
[16]Abdelwanis M I, Abaza A, El-Sehiemy R A, et al. Parameter estimation of electric power transformers using coyote optimization algorithm with experimental verification[J]. IEEE Access, 2020, 8: 50036-50044.
[17]Chang G W, Chinh N Cong. Coyote optimization algorithm-based approach for strategic planning of photovoltaic distributed generation[J]. IEEE Access, 2020, 8: 36180-36190.
[18]Güvenç U, Kaymaz E. Economic dispatch integrated wind power using coyote optimization algorithm[C]// International Istanbul Smart Grids and Cities Congress and Fair(ICSG), Istanbul, Turkey, 2019.
[19]张新明, 王豆豆, 陈海燕, 等. 强化最优和最差狼的郊狼优化算法及其二次指派问题应用[J]. 计算机应用, 2019, 39(10): 2985-2991. Zhang Xinming, Wang Doudou, Chen Haiyan, et al. Best and worst coyotes strengthened coyote optimization algorithm and its application to quadratic assignment problem[J]. Journal of Computer Applications, 2019, 39(10): 2985-2991.
[20]刘任, 李琳, 王亚琦, 等. 基于随机性与确定性混合优化算法的Jiles-Atherton磁滞模型参数提取[J].电工技术学报, 2019, 34(11): 2260-2268. Liu Ren, Li Lin, Wang Yaqi, et al. Parameter extraction for jiles-atherton hysteresis model based on the hybrid technique of stochastic and deterministic optimization algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2260-2268.
[21]王玙, 杨中平, 李峰, 等. 有轨电车混合动力系统能量交互型管理策略与容量配置协同优化研究[J]. 电工技术学报, 2019, 34(8):1780-1788. Wang Yu, Yang Zhongping, Li Feng, et al. Energy management strategy with energy interaction and configuration optimization for the tram’s hybrid storage system[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1780-1788.
[22]Mirjalili Seyedali. SCA: a sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120-133.
Optimal Configuration Method of Photovoltaic Intelligent Edge Terminal Based on Improved Coyote Optimization Algorithm
Abstract Photovoltaic intelligent edge terminal (PV IET) is one of the important devices to achieve efficient and intelligent operation and maintenance of distributed PV large-scale access to distribution network. In this paper, a mathematical model for optimizing the configuration of PV IETs is presented, and an improved coyote optimization algorithm (ICOA) is proposed to achieve an accurate solution of the model. In order to solve the problems of insufficient precision of the coyote optimization algorithm and slow convergence speed, a new social mutual assistance coyote growth strategy and the optimal coyote single-dimensional disturbance strategy in group are proposed, and simulated annealing and adaptive elite retention strategies are introduced to make the algorithm more suitable the engineering issues raised in this article. Realize the three aspects of the number, location and connection mode of PVIET to the PV power station. Finally, the validity of the model is verified by the improved IEEE69 cases, and the superiority of the ICOA in accuracy, stability and convergence is verified by the comparison of algorithms.
keywords:Distributed photovoltaic, photovoltaic intelligent edge terminal, optimal configuration model, improved coyote optimization algorithm
中图分类号:TM711
DOI:10.19595/j.cnki.1000-6753.tces.200511
国家重点研发计划(2018YFB1500800)和国家自然科学基金(51807134)资助项目。
收稿日期 2020-05-14
改稿日期 2020-11-30
刘嘉恒 男,1997 年生,硕士研究生,研究方向为分布式光伏数据采集、传输和处理技术。E-mail:1277330496@qq.com
葛磊蛟 男,1984 年生,博士,讲师,研究方向为智能配用电、云计算和大数据。E-mail:legendglj99@tju.edu.cn(通信作者)
(编辑 郭丽军)