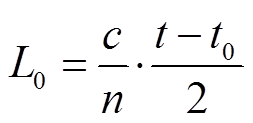（1）式中，n为光纤纤芯折射率；c为真空中光速。
图1 OTDR技术原理图
Fig.1 OTDR schematic diagram
摘要 为了实现变压器绕组辐向变形的定位与程度判断，将分布式光纤传感技术应用于绕组变形在线检测领域。在导线表面开一浅槽，将两根传感光纤布置于其中，制造了光纤复合电磁线。使用COMSOL Multiphysics对其进行了静电场仿真，结果显示光纤复合电磁线相较正常导线未发生明显电场畸变和绝缘强度降低。对该导线进行了固体力学仿真，结果显示在内凹和外凸两种变形条件下，光纤应变与导线变形程度（以挠度作为指标）之间关系可以用二次函数来描述，R2＞0.999。之后使用粘贴光纤的铜排模拟实际绕组，搭建试验平台，在仿真结论的基础上，获得了绕组挠度与光纤布里渊频移之间的关系。最后使用光纤复合电磁线绕制了一台35kV连续式绕组模型，使用该模型借助布里渊光时域反射技术，完成对变形的准确定位，定位精度在1饼之内，并完成了变形程度的检测，检测误差小于10%。
关键词：变压器 绕组变形 分布式光纤传感 布里渊光时域反射技术
电力发展对于经济发展至关重要，而变压器作为电能传输和转换中的重要组成部分，其安全稳定运行对电网意义重大。研究发现，大型变压器因遭受多次区外故障造成绕组变形直至最终发展成为内部匝间故障的事故较为多见，对电网安全影响极大[1-3]。传统的检测手段，如短路阻抗法、频率响应法[4-6]和扫频阻抗法[7-8]等，具有易受现场环境干扰、无法实现变形定位与程度准确判断等缺点。在对电网运行安全要求逐渐提高的今天，急需一种能够准确实现绕组变形定位和变形程度检测的新型传感手段。
分布式光纤传感技术[9-10]在近年逐渐兴起，其使用光纤作为信号传输媒质和传感媒质，能获得沿线各点处的温度、应变、振动等各种信息，相比于其他点式传感器具有测量点数多（上千乃至上万点）、传感距离远（数千米至数十千米）等优势，被广泛应用于建筑健康监测[11]、桥梁隧道[12]和飞机等航天器状态监测等各领域。这一技术还具有传感光纤体积小和材质均为绝缘、不受电磁干扰等优点，使得其在电力设备状态监测中也能有用武之地[13]。
文献[14]探讨了基于分布式光纤传感技术的绕组变形检测的可行性，并提出了基于极限学习机（Extreme Learning Machine, ELM）的变形模式识别算法。文献[15]研究了基于布里渊光时域反射技术（Brillouin Optical Time Domain Reflection, BOTDR）的变压器绕组变形检测技术，将光纤敷设在绕组每饼导线最外匝外表面上，实现了对绕组变形的定位与模式识别，但这种方式每饼上只附着了1圈光纤，有效传感长度较短，对于文中直径为700mm的绕组，每饼仅对应约2.2m传感光纤，由于BOTDR技术空间分辨率只能达到2~5m量级，所以其精确度稍低。文献[16]研制了一种嵌入裸纤的漆包铜导线的生产工艺，以实现对绕组的应变传感，使用布喇格光栅（Fiber Bragg Gratings, FBG）对光纤嵌入过程中的应变量进行了监测，结果显示FBG在嵌入过程中所承受的应变不会对传感精度造成影响。但这一工艺目前只实现了200m的连续生产，且裸纤没有护套层的防护，极易发生断裂，所以其距离实用化还有一定的距离。
上述文献[14-16]中都未涉及光纤检测到的应变量与绕组实际变形量之间的关系，使得通过测得的绕组应变曲线只能推断绕组不同区域是否发生变形，无法判断变形量大小。
对于分布式和准分布式光纤应变传感中的应变传递机理和传递模型，有很多研究者进行了卓有成效的研究。文献[17-18]研究了FBG粘贴方法与粘贴长度等对应变测量准确度的影响，指出为了实现准确的应变测量，FBG粘贴需要达到一定的长度，如果可能，采取埋入式敷设能达到更好的效果。但这一研究仅适用于FBG等点式传感器。对于分布式传感技术，文献[19]中基于光频域反射技术（Optical Frequency Domain Reflection, OFDR）研究了在等强度梁上的光纤应变传递特性，得出光纤粘贴区域中部应变传递率最高，两侧会有低应变区域。OFDR技术空间分辨率高，一般在mm量级或更高，但测量距离很短，常规商业仪器只能实现70m范围内的应变分布式测量，无法满足变压器内部的测量需求。同时OFDR空间分辨率远小于一般应变区域的空间尺度，而BOTDR空间分辨率在2~5m左右，与应变区域空间尺度接近，所以二者在应变传递规律上有较大不同。
文献[20]中通过试验和理论计算对变压器绕组模型变形程度与BOTDR所测得应变值之间关系进行了研究，但其试验组数较少，未能获得较为明确的结论。
为继续探究使用BOTDR技术检测绕组变形时具体变形程度判断这一问题，本文使用了一种表面开槽的电磁线作为研究对象，通过在导线表面开槽，槽中铺设直径0.5mm的护套紧包纤作为传感介质。根据此导线的参数建立了仿真模型，对绕组变形的挠度和应变之间的关系进行了研究，并通过建立模拟模型来验证这一结论，获得了导线和光纤应变量与变形程度之间的关系。最后使用该导线绕制了1台35kV连续式绕组模型，搭建了分布式绕组应变检测平台，对绕组变形的挠度与应变之间的关系呈现规律进行了验证，完成了基于BOTDR技术的绕组变形定位和变形程度检测。
光时域反射技术（Optical Time Domain Reflection, OTDR）是分布式光纤传感定位的基础。当一束激光射入光纤，在光束沿光纤向前传播的同时，光子会与光纤介质发生相互作用而产生后向散射，根据散射光产生机制的不同，可以分为瑞利散射、布里渊散射和拉曼散射。测量入射光入射时间t0和散射光返回的时间t，通过式（1）即可得到散射事件发生处距离光纤端部的距离L0，从而实现定位。
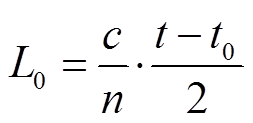（1）式中，n为光纤纤芯折射率；c为真空中光速。
图1 OTDR技术原理图
Fig.1 OTDR schematic diagram
布里渊散射是入射光场与光纤中声学声子发生的非弹性光散射现象，其特点是散射光的中心频率变化量以及峰值功率的相对变化量与光纤温度和所受应变线性相关，如式（2）所示。
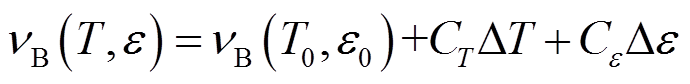（2）式中，T为温度；e为应变；下标“0”代表初始值；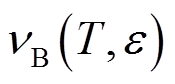
、
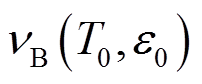分别为
、
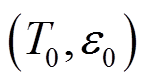条件下的布里渊中心频率；CT、Ce分别为光纤的布里渊频移温度系数和应变系数；DT、De 分别为相对初始值的温度、应变变化量。
由式（2）可知，通过测定布里渊散射谱，可以拟合出布里渊中心频率，计算布里渊频移，从而获得光纤沿线的温度和应变信息。但由于布里渊频移对温度和应变交叉敏感，需要对其进行温度补偿，常用的方法包括参考光纤法[21]、多参量传感法[22]、拉曼散射联合测量法和特种光纤法[22]等，本文采用拉曼联合测量法进行温度补偿，即使用拉曼光时域反射技术（Raman Optical Time Domain Reflection, ROTDR）测量光纤温度，从而补偿温度变化引起的布里渊频移。
光子与晶体内微观粒子振动、转动、各种元激发相互作用而引起的非弹性散射，称为拉曼散射。该散射谱线包含频率较低的斯托克斯光（Stokes Light）和频率较高的反斯托克斯光（Anti-Stokes Light），分布在瑞利散射谱线两侧。这两种散射光的光强之比只与温度有关，如式（3）所示，经过推导即可解得光纤的温度。再结合OTDR技术即可实现分布式测温。
（3）式中，Ias、Is分别为Anti-Stokes光强、Stokes光强；nas、ns分别为Anti-Stokes散射光子和Stokes散射光子的频率；Dn 为Raman上、下能级差；h为Planck常量；k为Boltzmann常数；T为绝对温度。
绕组常见的辐向变形主要包括内凹变形和外凸变形。为建立光纤应变量与绕组变形具体形式之间的对应关系，使用了COMSOL Multiphysics软件进行了固体力学仿真。
仿真模型按照设计的光纤复合电磁线模型搭建。导线尺寸为2mm´6mm，导线中部有宽1.0mm，深0.5mm的细槽，在凹槽边缘设置倒圆角过渡，经计算，由于开槽导致的载流面积变化量仅为6.19%，可以忽略。电场仿真和击穿电压测试均显示导线开槽对其电气性能未造成显著影响。将一根用于BOTDR的应变传感单模光纤（Single-Mode Fiber, SMF）和一根用于ROTDR的温度传感多模光纤（Multi-Mode Fiber, MMF）并排置入凹槽内，两根光纤外径均为0.5mm。外侧使用绝缘纸进行包裹，外表面尺寸不变。电磁线截面如图2所示。
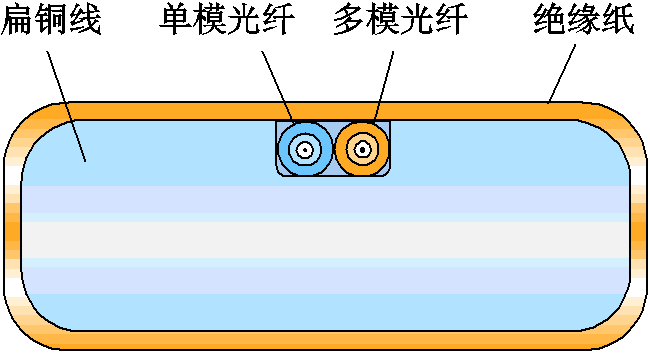
图2 光纤复合电磁线截面图
Fig.2 Cross-sectional of fiber composite electromagnetic wire
同一撑条间隔内的各匝绕组变形方式及应变分布情况十分类似，为了简化计算及提高仿真效率，只截取了变压器一个撑条间隔内的一匝绕组进行分析。建立了如图3所示的三维模型，各材料参数见表1。设置导线两端截面和两侧撑条为固定约束，在导线外表面均匀施加幅向应力，以指向圆心为正方向，范围从-2GPa到800kPa，步长为200kPa。
图3 固体力学仿真结果
Fig. 3 Simulation results of solid mechanics
表1 仿真材料参数
Tab.1 Simulation parameters
参数铜ETFE二氧化硅 密度/( kg·m-3)8 9402 2002 203 杨氏模量/GPa1260.473.1 泊松比0.340.40.17
仿真结果如图4所示，绕组变形区域应变分布较为均匀，未出现局部应力过大的情况。当绕组幅向外凸时，位于绕组内侧的光纤受到拉力，应变为正值；当幅向内凹时，内侧光纤受到压力，应变为负值。变形区域应变均值随弯曲程度的关系如图4所示，在仿真所选取的绕组变形程度（绕组最突出部分的位移，即图3中绕组表面z坐标的变化量，也称为挠度）范围内，绕组变形区域内光纤应变值与挠度呈分段二次函数关系，分段点位于原点处。左右两侧拟合R2分别为0.999 4和0.999 8。故在一定变形范围内，可以根据光纤的应变量大小来定量判断绕组变形量的大小。
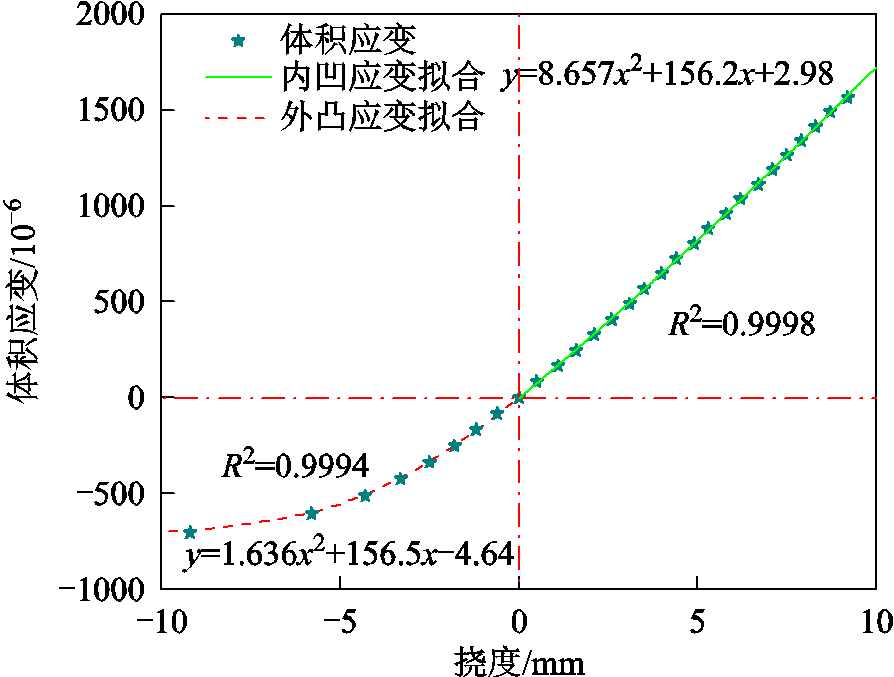
图4 固体力学仿真结果
Fig.4 Simulation results of solid mechanics
由于布里渊散射的特性涉及光纤中声学光子与入射光光子之间的非线性相互作用，使得光纤实际所受应变与通过BOTDR检测到的布里渊频移换算得到的微应变值在数值大小和空间分布上有一定的区别。为了初步探究在开槽导线上敷设的传感光纤的应变传感特性，设计了模拟模型进行试验验证。
在绕组发生辐向变形时一般绕组整饼都会发生内凹或外凸，甚至连续几饼都在相同位置发生相同的变形，这种变形所导致的应变反映到光纤轴线上为光纤每间隔一段距离就会有一段应变区域。为了研究这种应变分布下使用BOTDR测量应变的可行性，搭建如图5所示试验装置。使用一根长1m、宽30mm、厚3mm的铜排，上边并排粘贴五回光纤，每回光纤粘贴长度约0.8m，同时在不同回之间留出一定长度的松弛光纤，控制变形区域内光纤总长为8m，以模拟在光纤复合绕组发生变形后光纤的应变分布情况。应变的施加采用全自动拉/压力试验机，以铜排向粘贴光纤一侧弯曲为挠度的正方向，此时光纤发生拉伸为正应变。
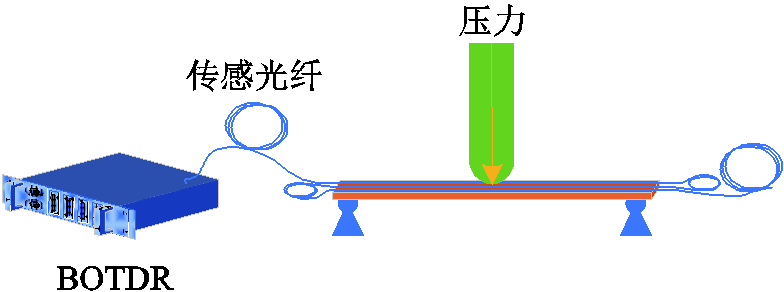
图5 应变试验装置
Fig.5 Strain test device
如图5所示控制压力使得挠度从-10mm以10mm为步长变化至-80mm，每组试验改变压力后静置2min使系统稳定，之后使用BOTDR设备采集布里渊频移信息。再将铜排翻转在另一面并施加压力完成挠度10~80mm的数据采集。
BOTDR系统测试参数及技术参数见表2。
表2 BOTDR参数
Tab.2 BOTDR parameter settings
参数数值 脉宽/ ns50 采样分辨率/m0.2 扫频范围/MHz300 扫频步长/MHz5 采集长度/km1 平均次数/次213 空间分辨率/m3
试验结果如图6所示。从图6中可以看出，当铜排挠度增大时，布里渊频移也随之增大。取初始状态作为布里渊频移的初值，也就是式（2）中的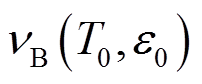，对应的微应变值显示在右轴。
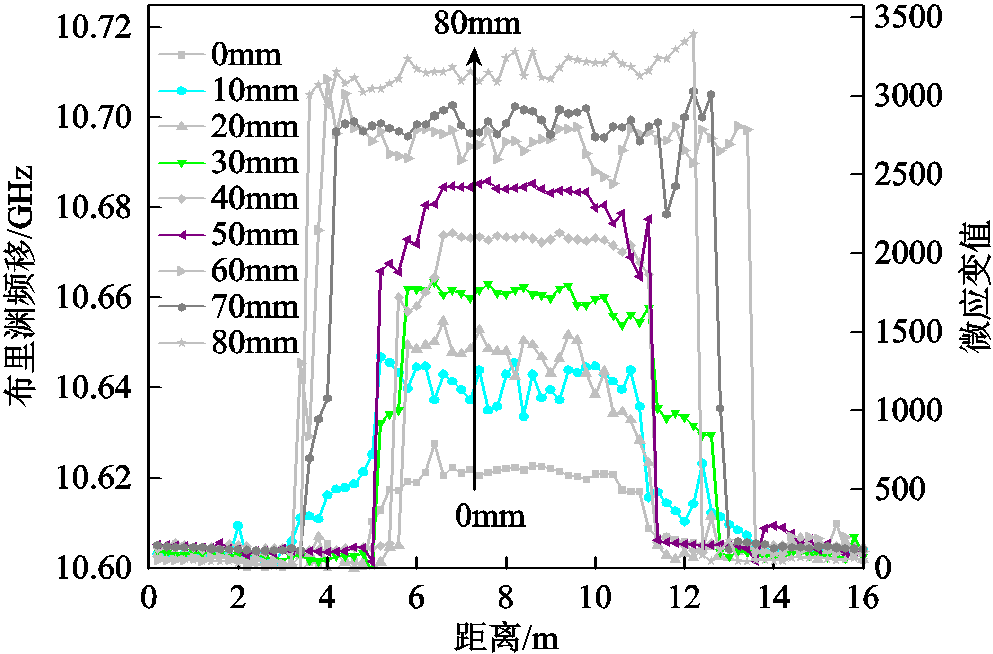
图6 应变试验结果
Fig.6 Strain test results
可以看出在3~13m范围内，光纤的布里渊频移出现明显变化，其变化幅度与挠度大小正相关，在布里渊频移上升下降沿附近有少许波动。布里渊频移稳定的区间长度（5~11m）与光纤所受应力的长度吻合，将每组试验中应变区域对应的布里渊频移平均值与挠度之间关系进行拟合，拟合结果如图7所示，拟合参数见表3。
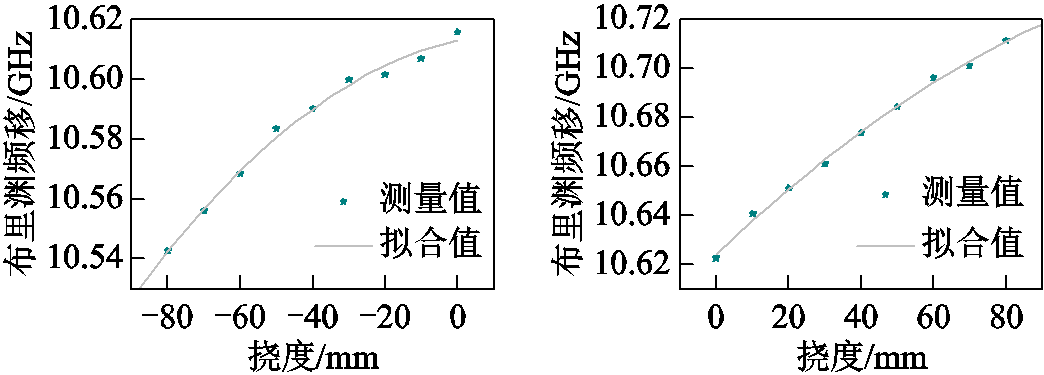
图7 应变试验拟合结果
Fig.7 Strain test fitting results
拟合结果显示，在一定变形范围内，BOTDR测得的应变量与挠度之间呈现分段二次函数关系，分界点位于所取的零应变点。光纤拉伸条件下，对应绕组外凸，BOTDR也检测到了正应变的发生，反之亦然。这也和2.1节所述仿真结果相吻合。
表3 拟合参数
Tab.3 Fitting parameters
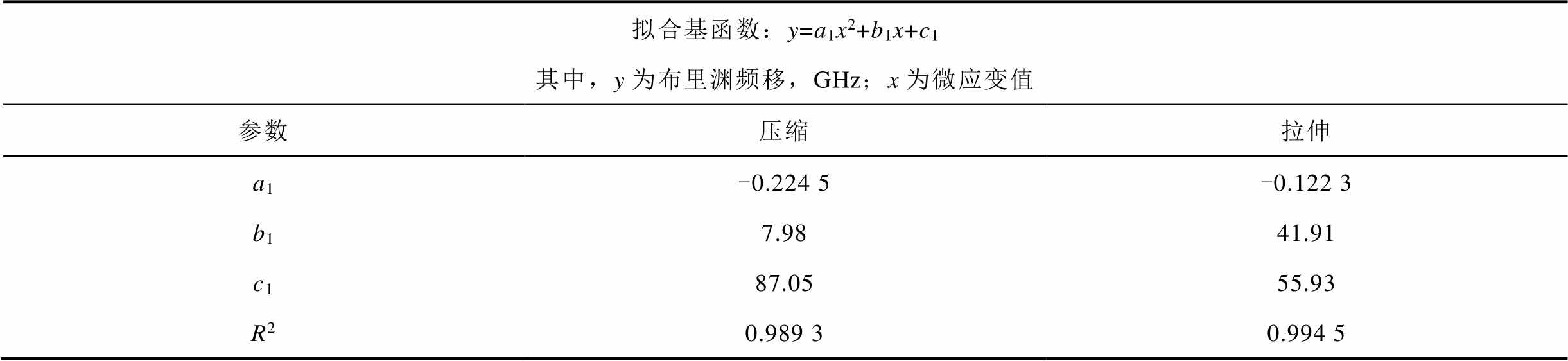
拟合基函数：y=a1x2+b1x+c1其中，y为布里渊频移，GHz；x为微应变值 参数压缩拉伸 a1-0.224 5-0.122 3 b17.9841.91 c187.0555.93 R20.989 30.994 5
使用光纤复合电磁线按照某35kV变压器高压绕组尺寸进行绕组绕制，绕组外径为440mm，共40饼，每饼5匝，使用单根导线连续绕制，绕组导线总长约270m，经计算每饼导线和光纤长度均为6.75m。在绕制过程中，保持光纤位于绕组内径侧，以防光纤受到过分拉伸。最后绕组实物图如图8所示。
图8 光纤复合式绕组
Fig.8 Optical fiber composite winding
为了消除绕组尾部传感盲区以及光纤末端端面菲涅尔反射对散射信号的影响，在绕组首尾两端的光纤引出后，分别连接5m长的松弛光纤，之后再连接跳线，以供接入仪器。
按图9所示搭建试验平台，ROTDR技术参数见表4。
表4 ROTDR参数
Tab.4 ROTDR parameter settings
参数数值 采集长度/km1 采样分辨率/m0.8 空间分辨率/m2 测量精度/℃±0.5
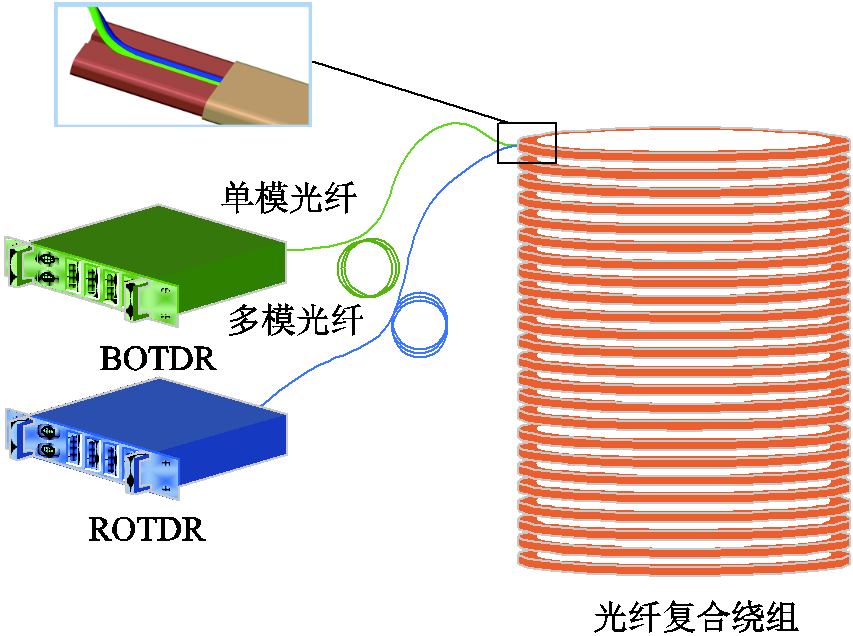
图9 试验平台示意图
Fig.9 Schematic diagram of the test platform
试验首先对绕组原始状态布里渊频移信息进行采集，作为式（2）中的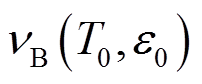，之后对其施加变形。试验中在绕组内部酚醛纸筒上开一定大小的窗口，使用千斤顶对特定一饼或多饼绕组施加应力将其顶出形成外凸变形，使用木槌对一饼或多饼绕组向内敲击形成内凹变形，如图10所示。
图10 绕组施加变形
Fig.10 Winding deformation
为了探究上文所述二次函数关系能否实现对绕组变形程度的判断，试验分为内凹变形和外凸变形两部分，每部分首先进行四组不同位置、不同程度的变形，之后使用四组数据进行曲线拟合，确定挠度-应变关系，再进行1~2组验证性实验，确定由函数关系得到的绕组变形程度与实测值是否相同。
各组试验变形信息见表5，表中5、6、11组试验为验证组。
在采集布里渊频移信息的同时，使用ROTDR设备对绕组整体温度分布进行监测，监测发现本试验过程中整个绕组部分温度变化小于1℃，可以认为其保持温度均匀且恒定的状态，从而忽略温度对布里渊频移的影响。对于如何联合BOTDR和ROTDR两种测量手段来消除绕组温度分布不均以及温度变化造成的影响，在之前的研究[23]中进行了描述，此处不再赘述。
表5 变形试验信息
Tab.5 Deformation test information
实验组数变形位置/饼变形方向变形程度/mm 内凹试验120内凹-20 233内凹-15 324内凹-12 44内凹-10 515内凹-15 627内凹-10 外凸试验725外凸9 836外凸15 92外凸20 107外凸25 116外凸15
由于绕组发生的是塑性变形，在前一组变形施加后无法恢复原状，本试验中每次变形都将前一组变形所测得的应变曲线作为标准曲线来计算下一组试验的应变变化。
11组试验的应变分布曲线如图11所示，可以发现当某一饼出现变形时，对应位置的应变量将发生明显变化，相较原始曲线，应变变化区域大致为1~3饼，除第3组24饼内凹和第8组36饼外凸两组试验实际测得变形区域为第26饼和第34饼，有2饼左右的误差外，其余各组应变曲线变化区域与施加变形区域重合，变化的方向也反映了变形的方向，说明BOTDR技术结合绕组上敷设的光纤能很好地实现对绕组变形的定位和识别。
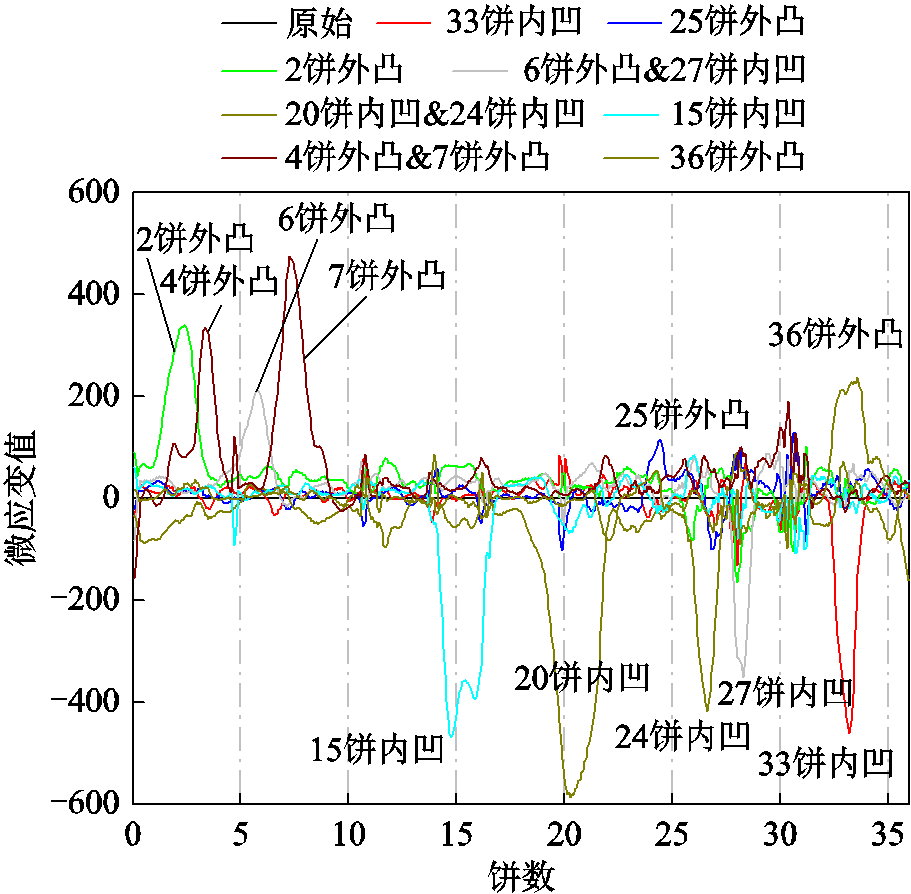
图11 应变量对比图
Fig.11 Comparison of the strains
将试验组中对应变形位置的变形最大值作为此处的应变量检测值，以挠度作为自变量，分内凹和外凸两组分别进行二次函数拟合，得到关系式见表6。
表6 试验数据拟合参数
Tab.6 Experimental data fitting parameters
拟合基函数：，其中，q为挠度(mm)，p为微应变量 参数内凹外凸 a20.155 20.347 4 b228.0010.74 c2-30.12-10.28 R20.964 40.999 5
根据得出的函数关系，将验证组所测得的应变量代入，求解得出对应的挠度，与试验中设置的挠度相对比，如图12所示，使用表6的函数关系得到的挠度预测值与实测值差距在10%以内，可以满足工程需要[24-25]。
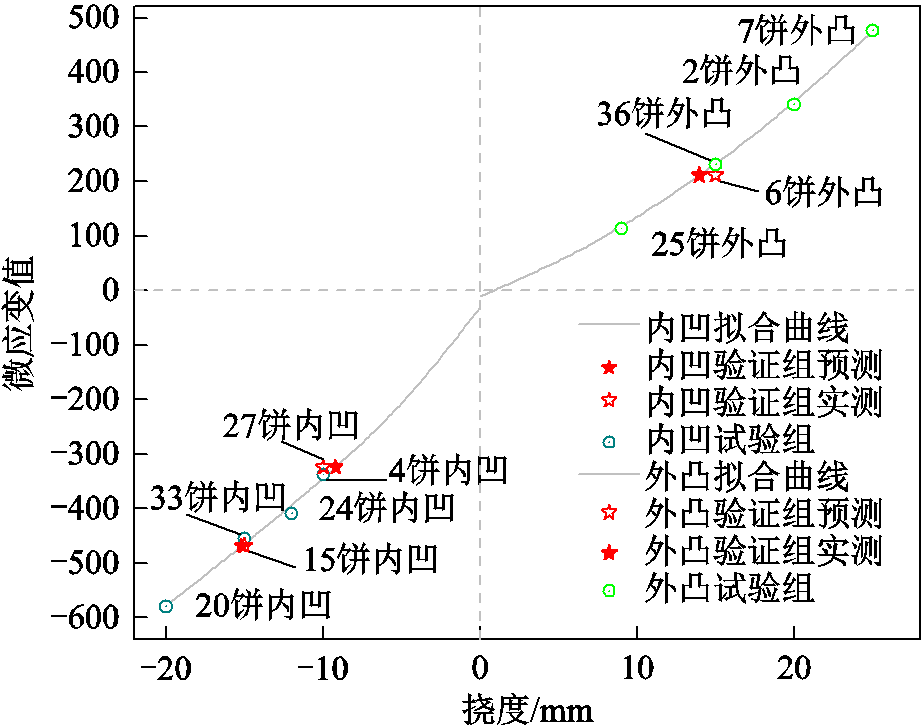
图12 绕组变形程度判断
Fig.12 Degree detection of winding deformation
为了解决变压器绕组变形在线监测困难、传统检测手段精确度较差等缺点，本文提出了一种基于分布式光纤传感技术（BOTDR）的变压器绕组变形检测手段，以实现对变压器绕组的变形定位、类型判别和程度检测。
1）使用COMSOL Multiphysics软件研究了绕组发生辐向变形时光纤应变量与绕组变形程度之间的关系，结果显示在一定范围内，光纤所受的平均应变与绕组挠度呈二次函数关系，R2=0.999 4，应变的正负反映绕组变形的方向。
2）通过设计模拟实验进一步验证了在绕组变形的条件下，使用BOTDR所检测到的应变量与绕组模型变形程度之间呈现二次函数关系，为真型绕组试验提供了依据。
3）使用光纤复合电磁线绕制了一个35kV变压器绕组模型，并搭建了基于分布式光纤传感的变压器绕组变形监测试验平台，基于此平台，对绕组施加11组辐向变形，使用BOTDR技术实现了精度在2饼以内的绕组变形定位。在内凹和外凸两种变形下，绕组变形程度与应变量之间均呈二次函数关系，R2分别为0.964 4和0.999 5，通过这一关系计算出的绕组变形程度与实际值误差在10%以内，能较好地满足工程需求。
4）这一技术不易受电磁干扰、振动等影响，可以实现对变压器内部绕组变形程度、变形位置的准确实时在线检测，为变压器的智能传感和智能运维提供一种新的解决方案。
参考文献
[1]刘旸, 周志强, 陈浩. 大型电力变压器短路事故分析与反事故措施[J]. 东北电力技术, 2015, 36(5): 30-32. Liu Yang, Zhou Zhiqiang, Chen Hao. Analysis and countermeasures of short-circuit accidents of large power transformers[J]. Northeast Electric Power Technology, 2015, 36 (5): 30-32.
[2]中国电力科学研究院. 国家电网公司变压器抗短路研究报告[R]. 北京: 中国电力科学研究院, 2006. China Electric Power Research Institute. State Grid Corporation transformer short circuit research report[R]. Beijing: China Electric Power Research Institute, 2006.
[3]赵义焜, 张国强, 韩冬, 等. 高频变压器用匝间绝缘材料沿面放电特性的实验研究[J]. 电工技术学报, 2019, 34(16): 3464-3471. Zhao Yikun, Zhang Guoqiang, Han Dong, et al. Study on surface discharge characteristics of inter-turn insulation materials in high-frequency transformers[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3464-3471.
[4]沈明, 尹毅, 吴建东, 等. 变压器绕组变形在线监测实验研究[J]. 电工技术学报, 2014, 29(11): 184-190. Shen Ming,Yin Yi, Wu Jiandong, et al. Experimental investigating on on-line monitoring of winding deformation of power transformers[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 184-190.
[5]赵仲勇, 唐超, 李成祥, 等. 基于频率响应二值化图像的变压器绕组变形故障诊断方法[J]. 高电压技术, 2019, 45(5): 1526-1534. Zhao Zhongyong, Tang Chao, Li Chengxiang, et al. Diagnosis method of transformer winding deformation faults based on frequency response binary image[J]. High Voltage Engineering, 2019, 45(5): 1526-1534.
[6]李成祥, 夏麒, 朱天宇, 等. 基于脉冲频率响应法的变压器绕组变形带电检测仪[J]. 电力自动化设备, 2018, 38(1): 110-115,120. Li Chengxiang, Xia Qi, Zhu Tianyu, et al. Live transformer winding deformation detector based on impulse frequency response method[J]. Electric Power Automation Equipment, 2018, 38(1): 110-115, 120.
[7]刘勇, 汲胜昌, 杨帆, 等. 检测变压器故障的扫频阻抗法特性研究及应用[J]. 高电压技术, 2016, 42(10): 3237-3245. Liu Yong, Ji Shengchang, Yang Fan, et al. Characteristics and application of sweep frequency impedance method for detecting transformer fault[J]. High Voltage Engineering, 2016, 42(10): 3237-3245.
[8]刘勇, 杨帆, 张凡, 等. 检测电力变压器绕组变形的扫频阻抗法研究[J]. 中国电机工程学报, 2015, 35(17): 4505-4516. Liu Yong, Yang Fan, Zhang Fan, et al. Research on sweep frequency impedance method for detecting winding deformation of power transformer[J]. Proceedings of the CSEE, 2015, 35 (17): 4505-4516.
[9]张旭苹. 全分布式光纤传感技术[M]. 1版. 北京: 科学出版社, 2013.
[10]周延辉, 赵振刚, 李英娜, 等. 埋入35kV干式空心电抗器的光纤布拉格光栅测温研究[J]. 电工技术学报, 2015, 30(5): 142-146. Zhou Yanhui, Zhao Zhengang, Li Yingna, et al. The study on the temperature measurement for the 35 kV dry-type air-core reactor with the embedded optical fiber Bragg grating[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 142-146.
[11]孟令健. 缠绕式光纤应变传感器开发及在道路工程中的应用[D]. 北京: 北京科技大学, 2019.
[12]董鹏, 夏开文, 于长一, 等. 浅埋隧道覆岩变形沉降的分布式光纤监测与分析[J]. 防灾减灾工程学报, 2019, 39(5): 724-732. Dong Peng, Xia Kaiwen, Yu Changyi, et al. Distributed optical fiber monitoring and analysis of deformation and settlement of cover rock in shallow tunnels[J]. Journal of Disaster Prevention and Mitigation Engineering, 2019, 39(5): 724-732.
[13]王鹤, 李兴宝, 路俊海, 等. 基于叠加原理的光纤复合低压电缆热路模型建模[J]. 电工技术学报, 2019, 34(7): 1381-1391. Wang He, Li Xingbao, Lu Junhai, et al. Modeling method of OPLC thermal circuit model based on superposition principle[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1381-1391.
[14]刘云鹏, 步雅楠, 田源, 等. 基于分布式光纤传感的变压器绕组变形检测与故障识别可行性研究[J]. 高电压技术, 2019, 45(5): 1483-1489. Liu Yunpeng, Bu Yanan, Tian Yuan, et al. Feasibility study on transformer winding deformation detection and fault identification based on distributed optical fiber sensing[J]. High Voltage Engineering, 2019, 45(5): 1483-1489.
[15]Liu Yunpeng, Tian Yuan, Fan Xiaozhou, et al. Detection and identification of transformer winding strain based on distributed optical fiber sensing[J]. Applied Optics, 2018, 57(22): 6430-6438.
[16]张书琦, 普天, 向李程, 等. 变压器绕组线光纤嵌入过程的应变监测[J]. 光通信技术, 2020, 44(7): 52-55. Zhang Shuqi, Pu Tian, Xiang Licheng, et al. Strain monitoring of transformer winding wire fiber embedding process[J]. Optical Communication Technology, 2020, 44(7): 52-55.
[17]权志桥, 方新秋, 薛广哲, 等. 表面粘贴布拉格光纤光栅传感器的应变传递耦合机理研究[J]. 中国激光, 2020, 47(1): 163-172. Quan Zhiqiao, Fang Xinqiu, Xue Guangzhe, et al. Strain transfer coupling mechanism of surface-bonded fiber Bragg grating sensor[J]. Chinese Journal of Lasers, 2020, 47(1): 163-172.
[18]周延辉, 赵振刚, 李英娜, 等. 光纤光栅在干式空心电抗器固化中的应变监测研究[J]. 电工技术学报, 2015, 30(13): 27-31. Zhou Yanhui, Zhao Zhengang, Li Yingna, et al. Strain monitoring with fiber grating for dry-type air-core reactor solidification[J]. Transactions of China Electrotechnical Society, 2015, 30(13): 27-31.
[19]章征林, 高磊, 孙阳阳, 等. 分布式光纤传感器应变传递规律研究[J]. 中国激光, 2019, 46(4): 285-293. Zhang Zhenglin, Gao Lei, Sun Yangyang, et al. Strain transfer law of distributed optical fiber sensor[J]. Chinese Journal of Lasers, 2019, 46(4): 285-293.
[20]田源. 基于分布式光纤传感的变压器绕组变形检测方法研究[D]. 北京: 华北电力大学(北京), 2019.
[21]董玉明, 张旭苹, 路元刚, 等. 布里渊散射光纤传感器的交叉敏感问题[J]. 光学学报, 2007(2): 197-201. Dong Yuming, Zhang Xuping, Lu Yuangang, et al. Cross sensitivity of Brillouin scattering distributed fiber sensor[J]. Acta Optica Sinica, 2007, 27(2): 197-201.
[22]Liu Xuan, Bao Xiaoyi. Brillouin spectrum in LEAF and simultaneous temperature and strain measurement[J]. Journal of Lightwave Technology, 2012, 30(8): 1053-1059.
[23]Gao Shuguo, Liu Yunpeng, Li Huan, et al. Transformer winding deformation detection based on BOTDR and ROTDR[J]. Sensors, 2020, 20(7): 2062. DOI:10.3390/ s20072062.
[24]杜江, 孙铭阳. 基于变权灰云模型的变压器状态层次评估方法[J]. 电工技术学报, 2020, 35(20): 4306-4316. Du Jiang, Sun Mingyang. Hierarchical assessment method of transformer condition based on weight-varying grey cloud model[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4306-4316.
[25]梁得亮, 柳轶彬, 寇鹏, 等. 智能配电变压器发展趋势分析[J]. 电力系统自动化, 2020, 44(7) : 1-14. Liang Deliang, Liu Yibin, Kou Peng, et al. Analysis of development trend for intelligent distribution transformer[J]. Automation of Electric Power Systems, 2020, 44(7):1-14.
Winding Deformation Detection Based on Distributed Optical Fiber Sensing
Abstract In order to locate and evaluate the radial deformation of transformer windings, distributed optical fiber sensing technology is applied to the field of online transformer winding deformation detection. A shallow groove is cut on the surface of the copper wire, where two sensing fibers are arranged to produce a fiber composite wire. The electrostatic field simulation was carried out using COMSOL Multiphysics, and the results showed that compared with normal wires, there was no obvious electric field distortion or insulation strength decrease. The simulation of solid mechanics was also carried out, the results of which showed that under both concave and convex deformation conditions, the relationship between fiber strain and wire deformation (taking deflection as an index) can be described by a quadratic function, R2＞0.999. Then, the actual windings were simulated using copper bars pasted with fibers, and a test platform was built on the basis of the simulation conclusions to obtain the relationship between the winding deflection and the Brillouin frequency shift. Finally, a 35kV continuous winding prototype was wound with fiber-composite wire s. Using this winding, with the help of brillouin optical time domain reflection (BOTDR) technology, accurate positioning of the deformation was completed, with an accuracy within 1 turn.The determination of deformation degree is also implemented, with an error less than 10%.
Keywords：Transformer, winding deformation, distributed fiber sensing, Brillouin optical time domain reflection
中图分类号：TM41
DOI:10.19595/j.cnki.1000-6753.tces.200542
河北省重点研发计划资助项目（19212110D）。
收稿日期 2020-05-25
改稿日期 2020-12-07
刘云鹏 男，1976年生，教授，博士生导师，研究方向为电气设备在线监测及故障诊断E-mail：liuyunpeng@ncepu.edu.cn
范晓舟 男，1990年生，工程师，研究方向为电气设备在线监测及故障诊断E-mail：fxz@ncepu.edu.cn（通信作者）
（编辑 郭丽军）