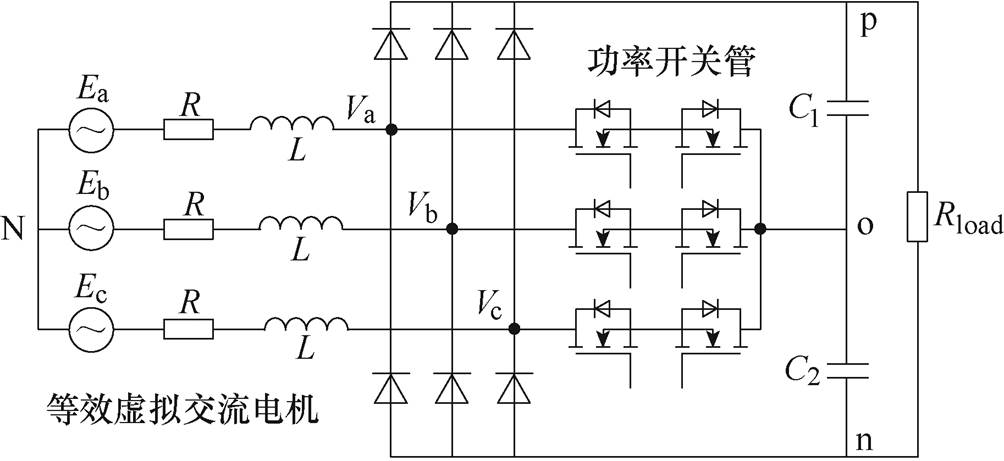
图1 三相Vienna整流器拓扑
Fig.1 Three-phase Vienna rectifier topology
摘要 设计三相Vienna整流器的闭环控制系统时需要采集电网电压信息,而使用传感器会增加系统硬件成本和复杂度,为此该文提出一种适用于三相Vienna整流器的无网压传感器控制策略。首先,在两相静止坐标系中建立三相Vienna整流器的虚拟磁链数学模型,利用二阶低通滤波器来改进电压观测器,对电网电压进行估算,在不增加算法复杂性的前提下避免了纯积分运算。其次,由于该方法估算的电网电压存在一定误差,因此运用预测电流控制策略构建控制系统,并针对实际系统中采集与处理环节所引起的信号滞后问题,提出二步预测电流法以补偿信号滞后。最后,对所提出控制策略进行仿真分析和实验验证。其结果表明,网侧输入电流谐波含量低,直流侧输出电压准确跟踪给定值,保持单位功率因数运行,系统具有良好的动态、稳态性能,从而验证了该文所提策略的正确性和可行性。
关键词:Vienna整流器 无网压传感器 虚拟磁链 预测电流控制
相对于两电平整流器,三相维也纳(Vienna)整流器具有谐波含量低、效率高等优点。相对于传统三电平整流器,Vienna整流器具有更少的开关器件、无需设置死区时间、开关管应力低等优点。因此,Vienna整流器具有重要的研究价值和广泛的应用前景[1-2]。
三相Vienna整流器控制策略主要分为电流控制和功率控制。电流控制又包括直接电流控制和间接电流控制。直接电流控制以网侧电流作为反馈和被控量形成电流闭环;间接电流控制则无电流环,但两者都需采集电网电压形成电压环。功率控制需提取电网电压基波幅值、相位等信息来控制网侧有功、无功功率,从而实现直流侧输出电压恒定、单位功率因数运行等控制目标。各种控制策略不尽相同,但都依赖于电网电压信息的正确提取[3]。在实际运用中可安装电网电压传感器以获得电网电压信息,但相应地会增加系统成本和硬件复杂度、降低系统可靠性,此外还存在噪声灵敏度高、分辨率受限等问题[4]。为此,无网压传感器控制策略成为国内外学者研究热点之一。
无网压传感器控制策略可解决上述诸多问题,但目前鲜有文献关注三相Vienna整流器无网压传感器控制策略的研究。无网压传感器控制策略基本思路是利用推算出的交流侧电压与交流侧滤波器压降相加来估算电网电压[5-6]。由于该方案需对电流进行微分运算而导致噪声灵敏度高,继而提出了基于虚拟磁链、自适应全阶观测器、自适应神经网络滤波器等算法[4],其中自适应观测器、神经网络滤波器等算法复杂,因此,基于虚拟磁链的无网压传感器控制策略由于其算法较为简单而更适合于较为复杂的三相Vienna整流器。
虚拟磁链法将网侧部分等效为虚拟交流电机,电网电压看作一个虚拟的磁链微分量,通过对微分量积分得到虚拟磁链。由于纯积分环节的引入,带来积分初值、直流偏置等问题。文献[7]提出带有初值估算的低通滤波器代替纯积分环节来估算磁链,从而达到降低冲击电流、提高系统动态性能的目的。文献[8]在电网电压不平衡情况下,利用二阶广义积分器构建三相并网逆变器电压观测器。文献[9]采用带有补偿项的一阶低通滤波器代替纯积分得到虚拟磁链信号,算法简单易于实现。文献[10]利用三阶广义积分器构造正交信号发生器对交流电压进行估算,从而避免纯积分运算。以上方法对初值、直流偏置等问题均有不同程度的解决,但都没有将虚拟磁链无网压传感器算法与三电平整流器相结合来 研究。
模型预测控制(Model Predictive Control, MPC)策略是一种对模型参数精度要求不高但对控制质量要求较高的控制方法,得到国内外学者的广泛研究。文献[11]在三相功率因数校正中引用预测电流控制以降低算法的复杂性。文献[12-15]对整流器MPC策略展开深入的研究。文献[16-17]分析了MPC策略的不足之处,并做出相应的改进。
三相Vienna整流器无网压传感器的实现方法有别于两电平、传统三电平整流器。为此,本文提出了一种三相Vienna整流器电网电压估算方法,该方法包含三相Vienna整流器交流侧电压计算算法、改进的电网电压观测器,并结合预测电流控制展开研究,根据瞬时功率理论计算出瞬时功率,并以功率跟踪误差最小为目标预测电流,从而形成本文的无网压传感器控制策略。针对实际系统中采集和处理过程会引起信号滞后问题,利用二步预测电流法和拉格朗日插值法加以补偿,从而更为精准地得到期望交流侧电压矢量。最后,在Matlab/Simulink仿真平台和实验样机上,对本文所提出的三相Vienna整流器无网压传感器预测电流控制策略进行仿真和实验,从而验证了该策略的正确性和可行性。
三相Vienna整流器拓扑如图1所示,图中,Ea、Eb、Ec分别为A、B、C三相电网电压,L为滤波电感,R为滤波电感和线路的等效电阻,Va、Vb、Vc分别为A、B、C三相交流侧电压,C1、C2分别为直流侧上、下滤波电容,Rload为阻性负载。

图1 三相Vienna整流器拓扑
Fig.1 Three-phase Vienna rectifier topology
三相Vienna整流器在三相静止坐标系中的数学模型为
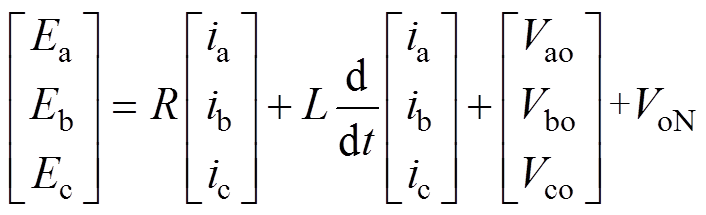 (1)
(1)式中,Vao、Vbo、Vco分别为a、b、c与o之间的电压;VoN为o与N之间的电压。
为了便于推导Va、Vb、Vc表达式,假定所有开关管和二极管均为理想器件,电网平衡时,开关频率远大于电网基波频率。
此时三相桥臂开关管可等效为一个三值逻辑开关函数为
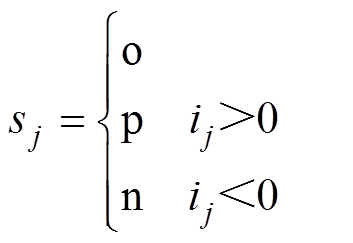
 (2)
(2)式中,sj为j相交流侧电压的电位状态,j =a、b、c;Sj为j相开关管;ij为j相电流。
将开关函数sj分解成sjo、sjp、sjn三个开关状态,当开关导通时其值为1,关断为0。由此得到各开关量之间的关系见表1。
表1 各开关量之间关系
Tab.1 The relation between the switch quantities

Sjijsj电位sjosjpsjn 导通—o100 关断>0p010 关断<0n001
交流侧电压与直流侧电容中性点电压关系式为
 (3)
(3)三相交流电压对称时,有
 (4)
(4)
整理式(1)、式(3)和式(4)得
 (5)
(5)将Va、Vb、Vc进行Clarke变换得
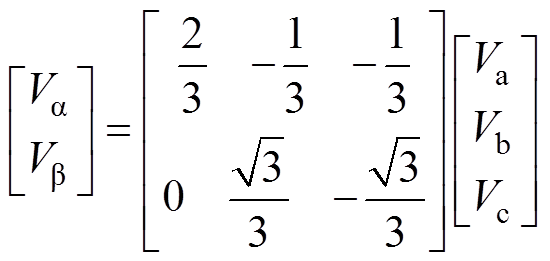 (6)
(6)
将式(3)、式(5)相加得
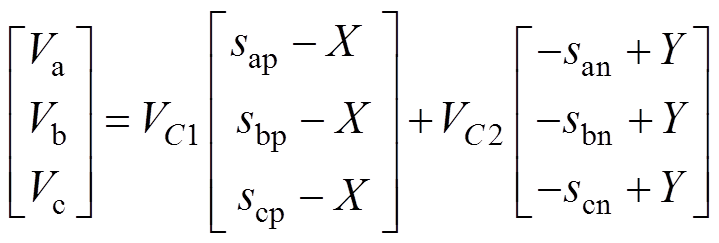 (7)
(7)其中

三相Vienna整流器在两相静止坐标系中的数学模型为
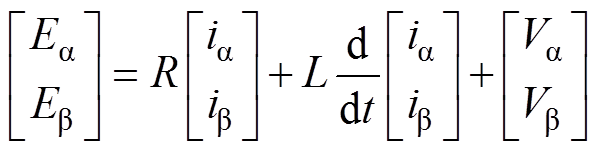 (8)
(8)式中,Va 和Vb 由式(6)、式(7)整理可得。
式(5)的sjp、sjn可根据表1中Sj、ij之间关系得到。以A相为例,当Sa导通时,sap=0、san=0;当Sa关断且ia>0时,sap=1、san=0;当Sa关断且ia<0时,sap=0、san=1。
根据式(8)可得到三相Vienna整流器的电网电压估算方法,但估算电网电压时需要微分计算,将导致较高的噪声灵敏度,不利于实际应用。故对式(8)两边同时积分得
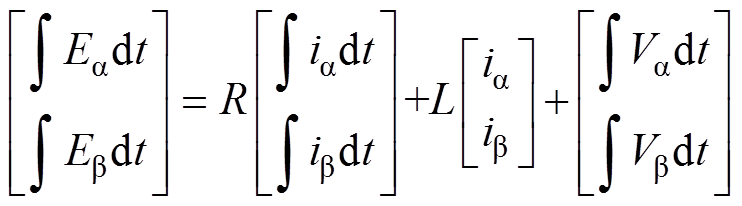 (9)
(9)根据磁链公式,有电网虚拟磁链矢量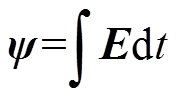 。电网电压矢量E、电网虚拟磁链矢量y 及交流侧电压矢量V在ab 坐标系中的关系如图2所示。
。电网电压矢量E、电网虚拟磁链矢量y 及交流侧电压矢量V在ab 坐标系中的关系如图2所示。
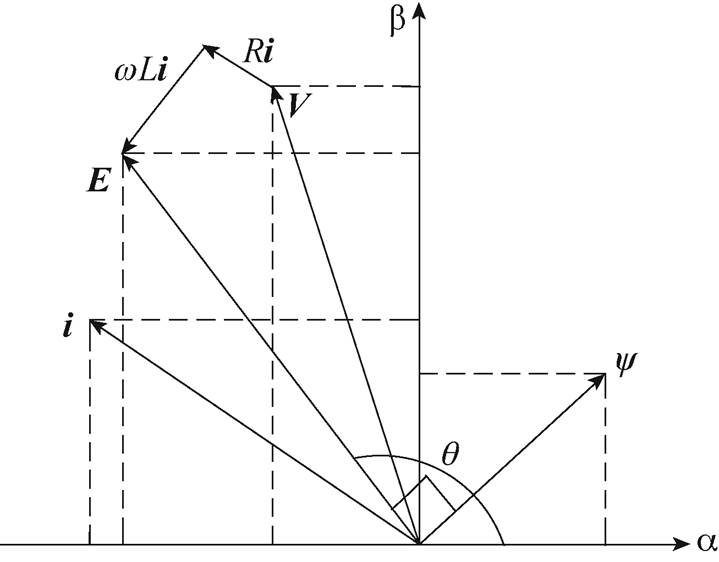
图2 ab 坐标系下整流器稳态矢量
Fig.2 Rectifier steady state vector diagram in ab coordinate system
图2中,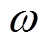 为电网电压基波角频率。根据电网电压矢量超前虚拟电网磁链矢量
为电网电压基波角频率。根据电网电压矢量超前虚拟电网磁链矢量 ,且幅值增长
,且幅值增长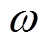 的特性,并结合图2中各变量矢量位置关系,可得
的特性,并结合图2中各变量矢量位置关系,可得
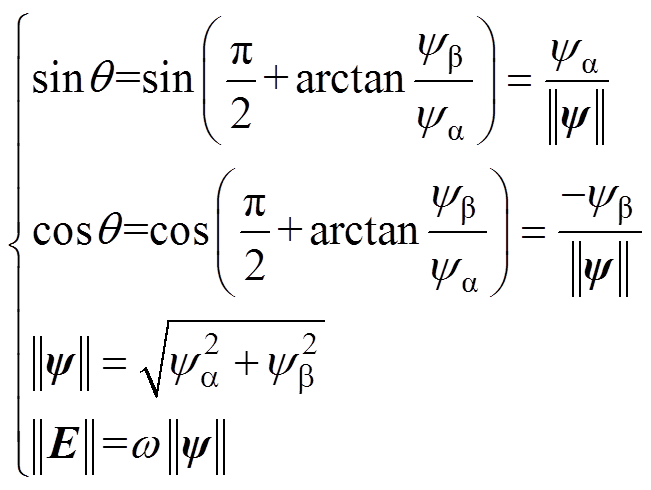 (10)
(10)式中,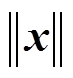 为对
为对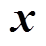 求模。由式(10)推导出电网虚拟磁链与交流侧电压关系式为
求模。由式(10)推导出电网虚拟磁链与交流侧电压关系式为
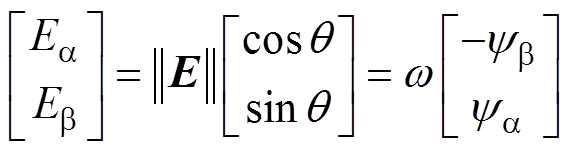 (11)
(11)
结合式(9)、式(11)可推算出电网电压估算式为
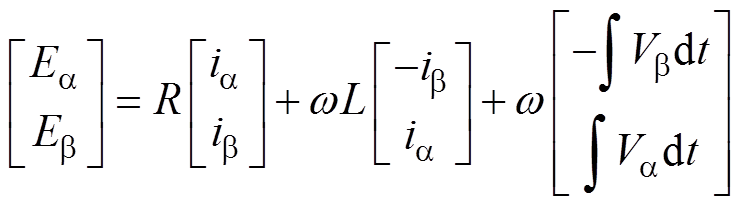 (12)
(12)式(12)存在积分项,而积分环节的初值和积分偏置问题会导致整流器冲击电流过大甚至无法起动。根据交流侧电压积分项可知,积分后幅值衰减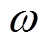 倍、相位滞后
倍、相位滞后 ,因此
,因此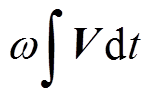 的输出幅值仍为
的输出幅值仍为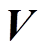 的幅值,相位滞后
的幅值,相位滞后 。
。
由一阶低通滤波器特性可知,输入信号频率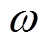 等于截止频率
等于截止频率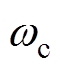 时,输出幅值为
时,输出幅值为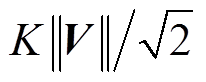 、相移为
、相移为 。故可设计两个增益K=
。故可设计两个增益K=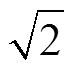 的一阶低通滤波器代替纯积分项,其传递函数为
的一阶低通滤波器代替纯积分项,其传递函数为
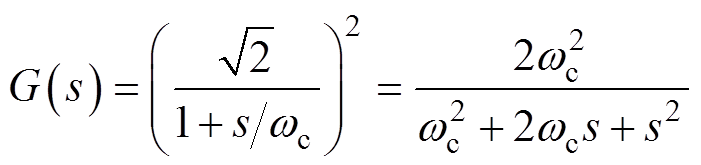 (13)
(13)式中,取wc=314.16rad/s。根据式(12)、式(13),设计出一种基于二阶低通滤波器的改进电网电压观测器,有效地避免了纯积分运算,电网电压观测器结构框图如图3所示。
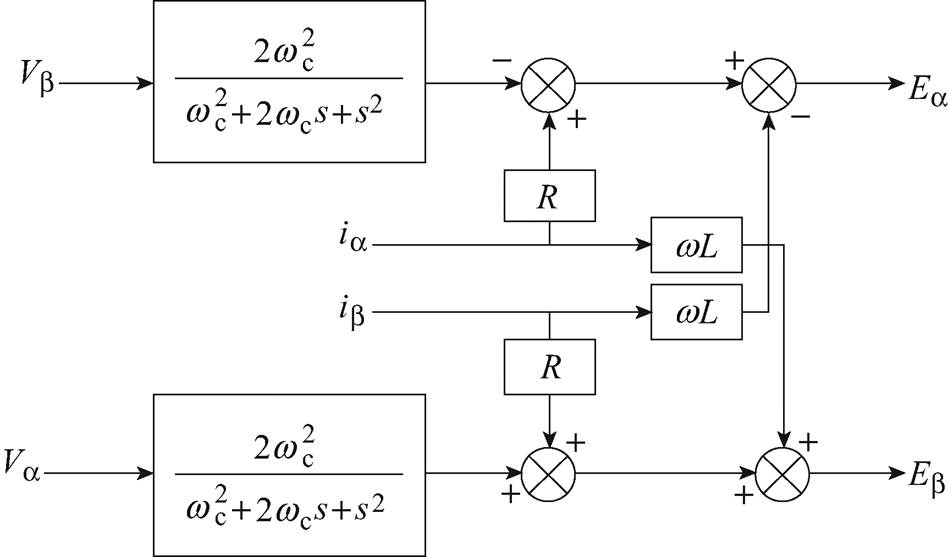
图3 电网电压观测器结构框图
Fig.3 Grid voltage observer structure diagram
三相Vienna整流器系统采样周期Ts远小于电网基波周期,因此在一个采样周期内对电流微分量进行离散化得
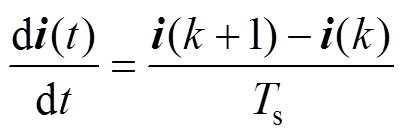 (14)
(14)将式(14)代入式(8)得
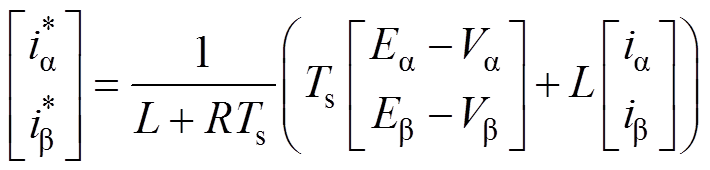 (15)
(15)
式中,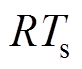 乘积项较小可忽略;
乘积项较小可忽略;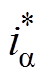 、
、 为网侧电流
为网侧电流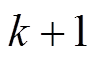 拍预测值。后文中标有*号的变量均表示
拍预测值。后文中标有*号的变量均表示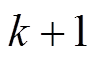 拍预测值,标有**号表示
拍预测值,标有**号表示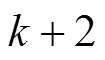 拍预测值。
拍预测值。
根据瞬时功率理论,有
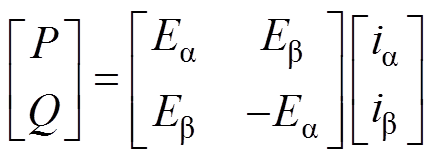 (16)
(16)式中,P为三相Vienna整流器瞬时有功功率;Q为其瞬时无功功率。
对式(16)求导并离散化,得到采样周期内整流器的瞬时功率预测值为
 (17)
(17)本文以满足功率跟踪误差最小为目标预测电流,定义目标函数为
 (18)
(18)
式中,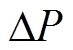 、
、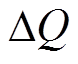 分别为瞬时功率给定值(
分别为瞬时功率给定值(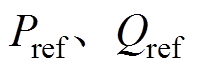 )与预测值(
)与预测值(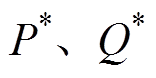 )之差[18]。
)之差[18]。
若要瞬时功率跟踪误差达到最小,只需满足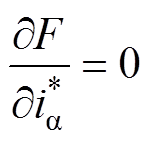 、
、 成立,则有
成立,则有
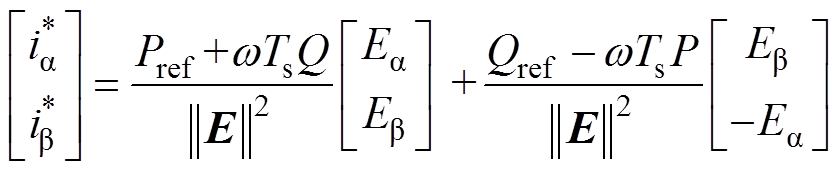 (19)
(19)由式(19)得到预测电流值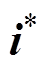 ,将其代入式(15)即可求得交流侧电压
,将其代入式(15)即可求得交流侧电压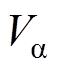 、
、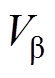 ,从而获得空间矢量调制信号。
,从而获得空间矢量调制信号。
在整流器实际运用中,系统的采集、处理无法瞬时完成,会导致信号滞后一个开关周期[19]。为此,本文利用二步预测法补偿信号延迟,通过解算 代替
代替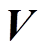 ,以抵消延迟作用的影响。
,以抵消延迟作用的影响。
二步预测优化后的目标函数为
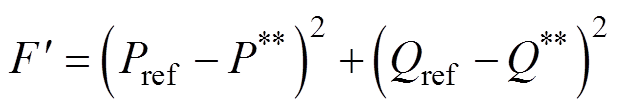 (20)
(20)对式(16)进行二阶求导,并经离散化得
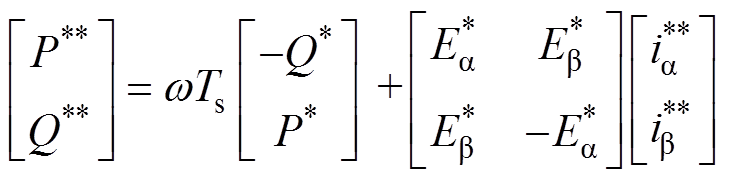 (21)
(21)
根据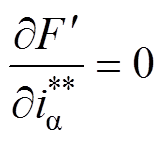 ,
, 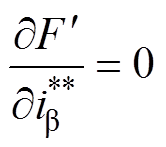 ,则有
,则有
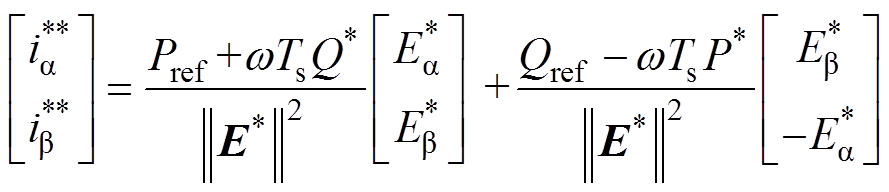 (22)
(22)得到在两相静止坐标系下的交流侧电压矢量期望值 为
为
 (23)
(23)
式(23)的电网电压预测值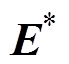 无法直接得到,传统预测控制常令
无法直接得到,传统预测控制常令 ,当开关频率与电压基波频率较小时,将会产生较大误差。为了提高精度,可采用
,当开关频率与电压基波频率较小时,将会产生较大误差。为了提高精度,可采用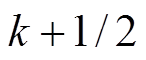 拍电网电压值代替预测值
拍电网电压值代替预测值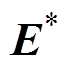 。故本文根据拉格朗日插值法推算出下一周期中点位置电压为
。故本文根据拉格朗日插值法推算出下一周期中点位置电压为
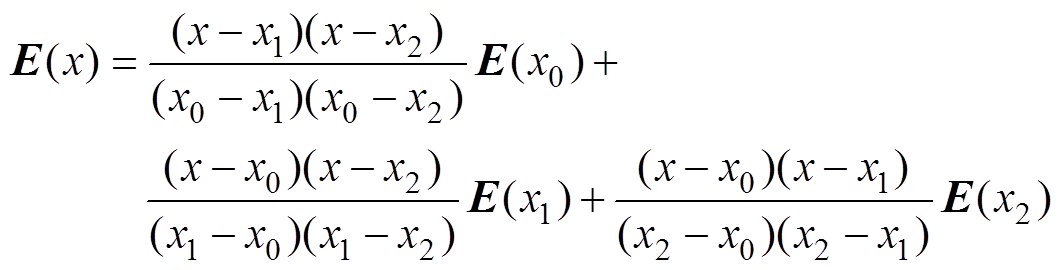 (24)
(24)式中,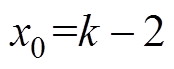 ,
, 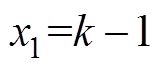 ,
, 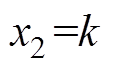 ,
, 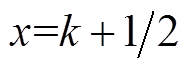 。经整理得到
。经整理得到
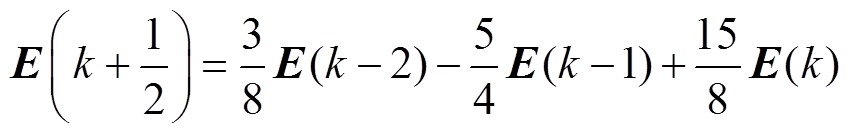 (25)
(25)
将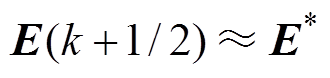 代入式(23)中,得到修正后的交流侧电压矢量期望值。
代入式(23)中,得到修正后的交流侧电压矢量期望值。
综上分析,三相Vienna整流器无网压传感器预测电流控制策略的系统结构框图如图4所示。
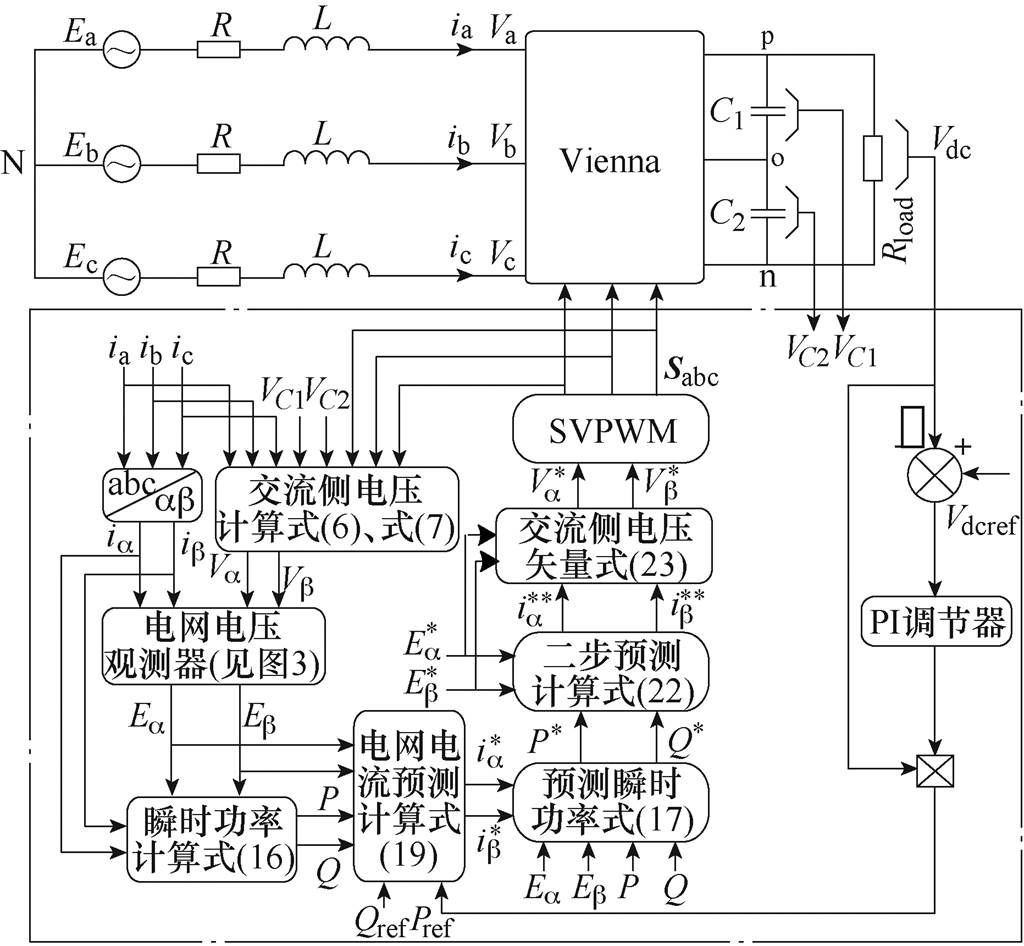
图4 系统结构框图
Fig.4 System structure diagram
为保证三相Vienna整流器保持单位功率因数运行,图4中无功分量给定值 =0。
=0。
为验证本文所提出的无网压传感器预测电流控制策略的正确性和可行性,利用Matlab/Simulink建立仿真模型,并搭建了实验样机。仿真和样机中参数一致,Vienna整流器参数指标见表2。
表2 Vienna整流器参数指标
Tab.2 Parameters of Vienna rectifier

参 数数 值 电网电压/V220 输出电压/V700 开关频率/kHz20 网侧电感/mH4.5 直流侧电容/mF4 400 额定功率/kW10
图5为三相Vienna整流器实验样机,该样机由功率主拓扑、电压电流传感器、信号调理电路、主控芯片、滤波单元、驱动电路及供电电源等构成。

图5 Vienna整流器实验样机
Fig.5 Experimental prototype of Vienna rectifier
在Matlab/Simulink中建立仿真模型,设定仿真总时长t =1.5s,系统运行至0.5s时刻,负载电阻Rload由49W(10kW)突变为98W(5kW),运行至1s时,由98W 突变为73.5W。直流侧输出电压波形如图6所示。
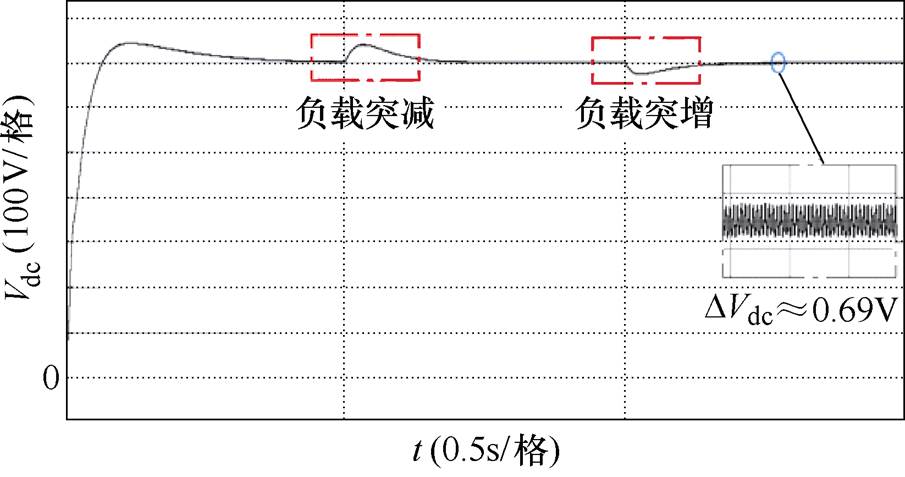
图6 直流侧输出电压波形
Fig.6 DC-side output voltage waveform
由图6可知,系统起动及负载突变过程中,直流侧输出电压均能较快调节至给定值700V,且无静差;当功率突减至额定功率50%(5kW)时,其超调量约为5.7%,调节时间为97.5ms;当功率突增变化时,电压跌落2.9%,调节时间为78.8ms,整个过程输出电压幅值波动较小且能较快跟踪电压给定值,系统具有良好的动态特性。直流侧电容电压波形如图7所示,综合图6、图7可知,直流侧输出电压纹波峰峰值约为0.69V,纹波系数约为0.1%,直流侧中点电位波动较小,具有良好的输出特性。
图8为系统起动、额定负载运行、负载突减及突增四个阶段中A相电网电压与输入电流波形。可以看出,整个过程中电网电压与输入电流始终保持同相位,实现单位功率因数。
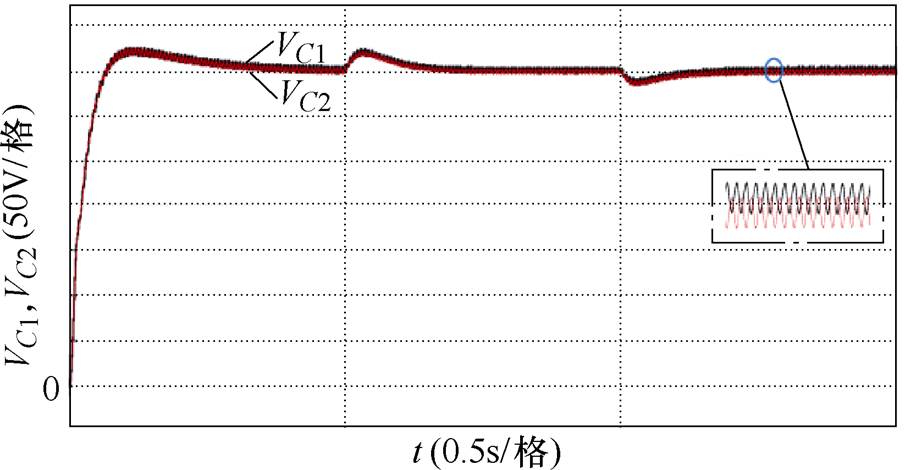
图7 直流侧电容电压波形
Fig.7 DC-side capacitor voltage waveforms
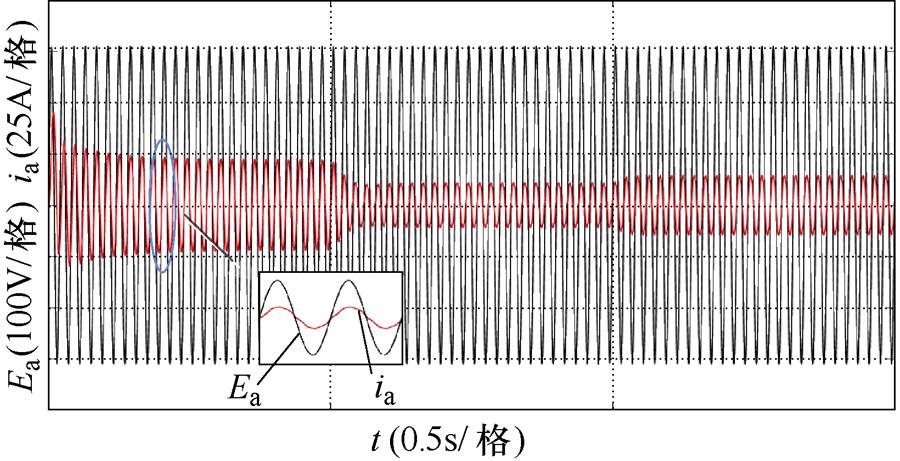
图8 A相电网电压及电流波形
Fig.8 A phase grid voltage and current waveforms
图9为额定负载下AB相线电压波形,可以看出,AB相线电压为典型的五电平阶梯波。
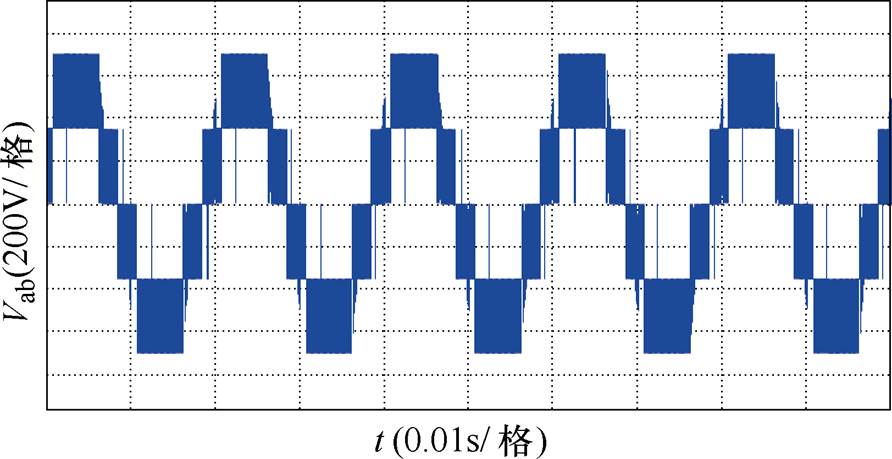
图9 额定负载下AB相线电压波形
Fig.9 AB phase line voltage waveform at rated load
在额定负载运行下,A相电流总谐波畸变率(Total Harmonic Distortion, THD)如图10所示,THD为4.68%,系统具有良好的输入特性。
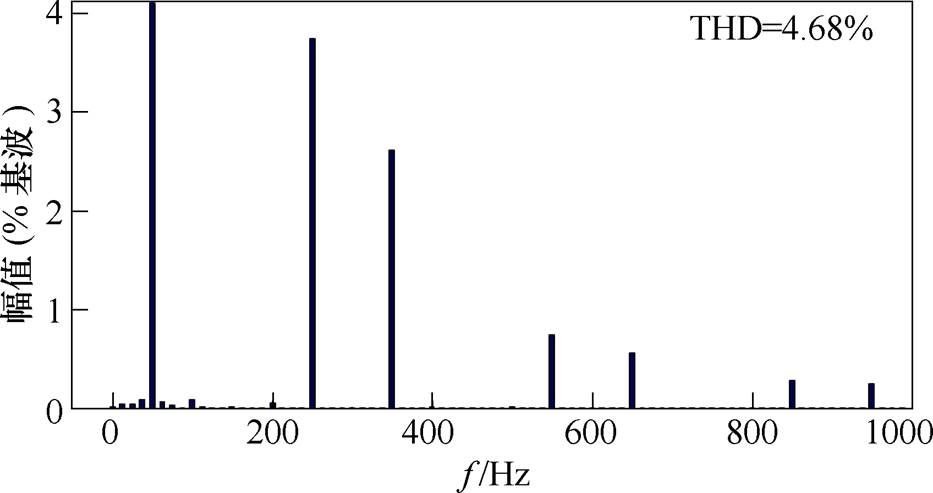
图10 额定负载运行时A相电流谐波畸变率
Fig.10 A phase current harmonic distortion rate at rated load
图11为系统稳态下两相静止坐标系中的电网电压实际值与估算值波形。可以看出,实际值与估算值波形几乎一致,验证了本文提出的电网电压估算方法的正确性。
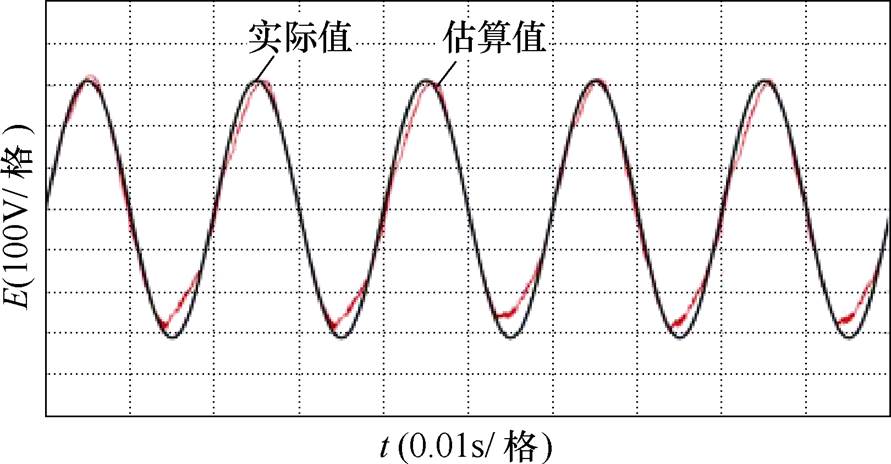
图11 稳态下电网电压实际值与估算值波形
Fig.11 Actual value and estimated value waveforms of grid voltage in steady state
图12为整个过程,整流器输入有功功率、无功功率及功率因数波形。由图12可知,整流器发生负载突减、突增时,瞬时有功功率能快速准确地跟踪给定值,而无功功率稳定在零值附近,整个运行过程中功率因数始终大于0.95,实现了系统功率因数校正。

图12 有功功率、无功功率和功率因数波形
Fig.12 Active power, reactive power and power factor waveforms
为进一步验证所提控制策略的性能,本文在10kW三相Vienna整流器实验样机中进行验证。
图13为负载突变时直流侧上、下电容电压、A相电网电压及电流波形。从直流侧上、下电容电压波形可知,中点电位波动较小,在切换负载时,直流侧输出电压仅需5个工频周期左右便能实现平稳过渡并稳定到电压给定值;在不同负载运行过程中,输入电流畸变均保持较小值,且在负载切换过程中能够平稳过渡至新的稳定状态,具有良好的输入特性,与仿真结果保持一致。
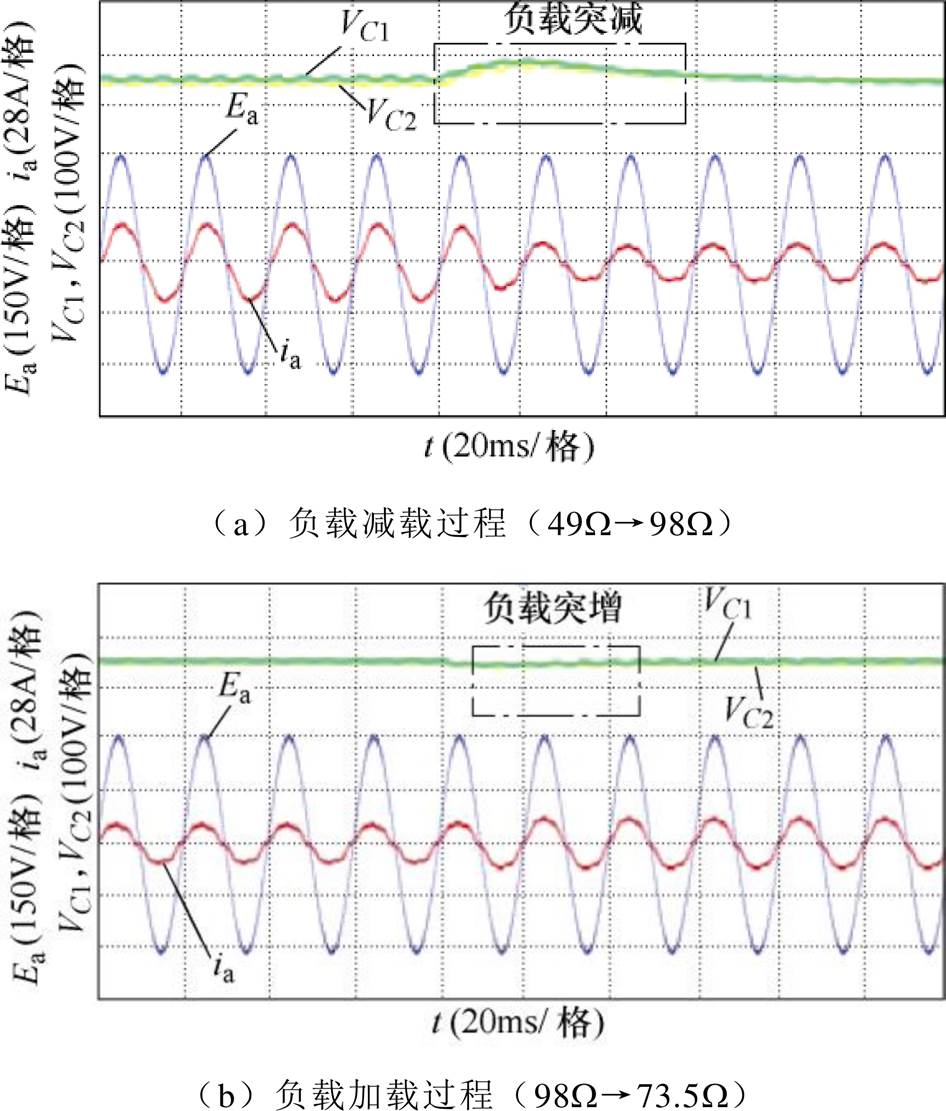
图13 动态响应实验波形
Fig.13 Dynamic response experimental waveform
图14为额定负载下AB相线电压实验波形,与仿真结果基本保持一致。

图14 额定负载下AB相线电压实验波形
Fig.14 Experimental waveform of AB phase line voltage at rated load
将A相电流实验波形导入Simulink中,进行快速傅里叶变换分析可得到,额定负载下A相电流THD如图15所示。从图15中可看出,A相电流的THD为4.89%,考虑到实际电路中的非理想因素,该结果与仿真结果基本一致。

图15 额定负载下A相电流实验波形THD
Fig.15 THD of A phase current experimental waveform at rated load
本文针对三相Vienna整流器提出了一种无网压传感器预测电流控制策略。本文设计了适用于三相Vienna整流器的电网电压估算方法,该方法提出了交流侧电压计算算法,改进了纯积分环节,得以准确估算电网电压;控制部分采用基于瞬时功率理论的预测电流控制,针对实际系统中采样与处理环节引起的信号滞后问题,提出二步预测电流法和拉格朗日插值法加以补偿,以得到更为准确的交流侧电压矢量。最后对该策略进行仿真分析和实验验证,仿真及实验结果表明,本文所提出的基于三相Vienna整流器无网压传感器预测电流控制策略具有以下优点:
1)无需电网电压传感器,亦可形成闭环控制系统,能实现输出电压准确快速地追踪给定值,保持电网电压电流同相位,输入电流谐波较低,具有良好的稳态、动态性能。
2)该算法易于实现,且能推广至其他衍生Vienna整流器拓扑。
参考文献
[1] 朱文杰, 陈昌松, 段善旭. 一种改善Vienna整流器输入电流品质的载波钳位调制方法[J]. 电工技术学报, 2019, 34(8): 1677-1688.
Zhu Wenjie, Chen Changsong, Duan Shanxu. A carrier-based modulation method with clamped area for input current performance of Vienna rectifier[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1677-1688.
[2] 王涛, 陈昌松, 段善旭, 等. 用于改善电流过零点畸变的Vienna整流器空间矢量调制策略[J]. 电工技术学报, 2019, 34(18): 3854-3864.
Wang Tao, Chen Changsong, Duan Shanxu, et al. An improved space-vector modulation for Vienna rectifier to eliminating current distortion around zero-crossing point[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3854-3864.
[3] 刘碧, 冯晓云, 邓睿, 等. 基于模型参考自适应的单相脉冲整流器无网压传感器控制方法[J]. 中国电机工程学报, 2019, 39(20): 6065-6074, 6187.
Liu Bi, Feng Xiaoyun, Deng Rui, et al. Grid voltage sensorless control strategy of single-phase PWM rectifiers with model reference adaptive system[J]. Proceedings of the CSEE, 2019, 39(20): 6065-6074, 6187.
[4] Rahoui A, Bechouche A, Seddiki H, et al. Grid voltages estimation for three-phase PWM rectifiers control without AC voltage sensors[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(1): 859-875.
[5] Malinowski M, Kazmierkowski M P, Hansen S, et al. Virtual-flux-based direct power control of three- phase PWM rectifiers[J]. IEEE Transactions on Industry Applications, 2001, 37(4): 1019-1027.
[6] Norniella J G, Cano J M, Orcajo G A, et al. Improving the dynamics of virtual-flux-based control of three- phase active rectifiers[J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 177-187.
[7] 赵仁德, 贺益康. 无电网电压传感器三相PWM整流器虚拟电网磁链定向矢量控制研究[J]. 中国电机工程学报, 2005, 25(20): 56-61.
Zhao Rende, He Yikang. Virtual line-flux-linkage oriented vector control of three-phase voltage source PWM rectifier without line voltage sensors[J]. Pro- ceedings of the CSEE, 2005, 25(20): 56-61.
[8] 胡书举, 孟岩峰, 李丰林, 等. 电网电压不平衡时逆变器无交流电压传感器控制策略[J]. 电工技术学报, 2017, 32(24): 146-152.
Hu Shuju, Meng Yanfeng, Li Fenglin, et al. AC voltage sensorless control strategy of grid-connected inverter under unbalanced grid voltage[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(24): 146-152.
[9] 张清鹏, 万健如. PWM整流器无电压传感器预测电流控制[J]. 电子测量与仪器学报, 2016, 30(5): 817-823.
Zhang Qingpeng, Wan Jianru. Predictive current control without voltage sensor for PWM rectifier[J]. Journal of Electronic Measurement and Instruments, 2016, 30(5): 817-823.
[10] 卢子广, 林远, 胡立坤, 等. 新型三相PWM整流器无交流电压传感器控制方法[J]. 电力自动化设备, 2017, 37(5): 28-33, 47.
Lu Ziguang, Lin Yuan, Hu Likun, et al. Three-phase PWM rectifier control without AC-voltage sensors[J]. Electric Power Automation Equipment, 2017, 37(5): 28-33, 47.
[11] 方宇, 裘迅, 邢岩, 等. 基于预测电流控制的三相高功率因数PWM整流器研究[J]. 中国电机工程学报, 2006, 26(20): 69-73.
Fang Yu, Qiu Xun, Xing Yan, et al. Research on three-phase high power factor correction based on predictive digital current controller[J]. Proceedings of the CSEE, 2006, 26(20): 69-73.
[12] 邓知先, 宋文胜, 曹梦华. 单相PWM整流器模型预测电流控制算法[J]. 中国电机工程学报, 2016, 36(11): 2996-3004.
Deng Zhixian, Song Wensheng, Cao Menghua. A model predictive current control scheme for single- phase PWM rectifiers[J]. Proceedings of the CSEE, 2016, 36(11): 2996-3004.
[13] Calle-Prado A, Alepuz S, Bordonau J, et al. Predi- ctive control of a back-to-back NPC converter-based wind power system[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4615-4627.
[14] Bouafia A, Gaubert J, Krim F. Predictive direct power control of three-phase pulse-width modulation (PWM) rectifier using space-vector modulation (SVM)[J]. IEEE Transactions on Power Electronics, 2010, 25(1): 228-236.
[15] Zhang Yongchang, Qu Changqi. Model predictive direct power control of PWM rectifiers under unbalanced network conditions[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4011-4022.
[16] 杨立永, 杨烁, 张卫平, 等. 单相PWM整流器改进无差拍电流预测控制方法[J]. 中国电机工程学报, 2015, 35(22): 5842-5850.
Yang Liyong, Yang Shuo, Zhang Weiping, et al. The improved deadbeat predictive current control method for single-phase PWM rectifiers[J]. Proceedings of the CSEE, 2015, 35(22): 5842-5850.
[17] 王伟华, 肖曦, 丁有爽. 永磁同步电机改进电流预测控制[J]. 电工技术学报, 2013, 28(3): 50-55.
Wang Weihua, Xiao Xi, Ding Youshuang. An improved predictive current control method for permanent magnet synchronous motors[J]. Transa- ctions of China Electrotechnical Society, 2013, 28(3): 50-55.
[18] 杨兴武, 姜建国. 电压型PWM整流器预测直接功率控制[J]. 中国电机工程学报, 2011, 31(3): 34-39.
Yang Xingwu, Jiang Jianguo. Predictive direct power control for three-phase voltage source PWM rectifiers[J]. Proceedings of the CSEE, 2011, 31(3): 34-39.
[19] 罗德荣, 姬小豪, 黄晟, 等. 电压型PWM整流器模型预测直接功率控制[J]. 电网技术, 2014, 38(11): 3109-3114.
Luo Derong, Ji Xiaohao, Huang Sheng, et al. Model predictive direct power control for three-phase voltage source PWM rectifiers[J]. Power System Technology, 2014, 38(11): 3109-3114.
Predictive Current Control of Three-Phase Vienna Rectifier Without Grid Voltage Sensors
Abstract Designing the closed loop control system of the Vienna rectifier requires the collection of grid voltage information. However, the use of sensors will increase the cost and complexity of the system hardware. Therefore, a grid voltage sensorless control strategy for Vienna rectifier is proposed. Firstly, the virtual flux mathematical model of the Vienna rectifier was established in the two-phase static coordinate system, and the second-order low-pass filter was used to improve the voltage observer and estimate the grid voltage, which avoids the pure integral operation without increasing the algorithm complexity. Secondly, because the grid voltage estimated by this algorithm has errors, the predictive current control strategy is used to construct the control system. Aiming at the signal lag problem in the acquisition and processing stage of the actual system, a two-step predictive current method is proposed. Finally, the control strategy is proposed for the simulation analysis and experimental verification. The results show that the grid side input current has low harmonic content, the DC output voltage can accurately track the given value and keep running unit power factor, and the system has good dynamic and steady state performance.
keywords:Vienna rectifier, grid voltage-sensorless, virtual flux, predictive current control
中图分类号:TM461
DOI: 10.19595/j.cnki.1000-6753.tces.191855
重庆市基础科学与前沿技术研究项目(cstc2016jcyjA1527)和重庆市教委科学技术研究项目(KJZD-K201901102)资助。
收稿日期 2020-01-01
改稿日期 2020-03-05
肖蕙蕙 女,1964年生,教授,硕士生导师,研究方向为电力电子与电力传动、新能源发电与控制等。E-mail: xhh@cqut.edu.cn
郭 强 男,1984年生,博士,讲师,研究方向为大功率整流器、新型逆变器、汽车电子等。E-mail: guoqiang@cqut.edu.cn(通信作者)
(编辑 陈 诚)