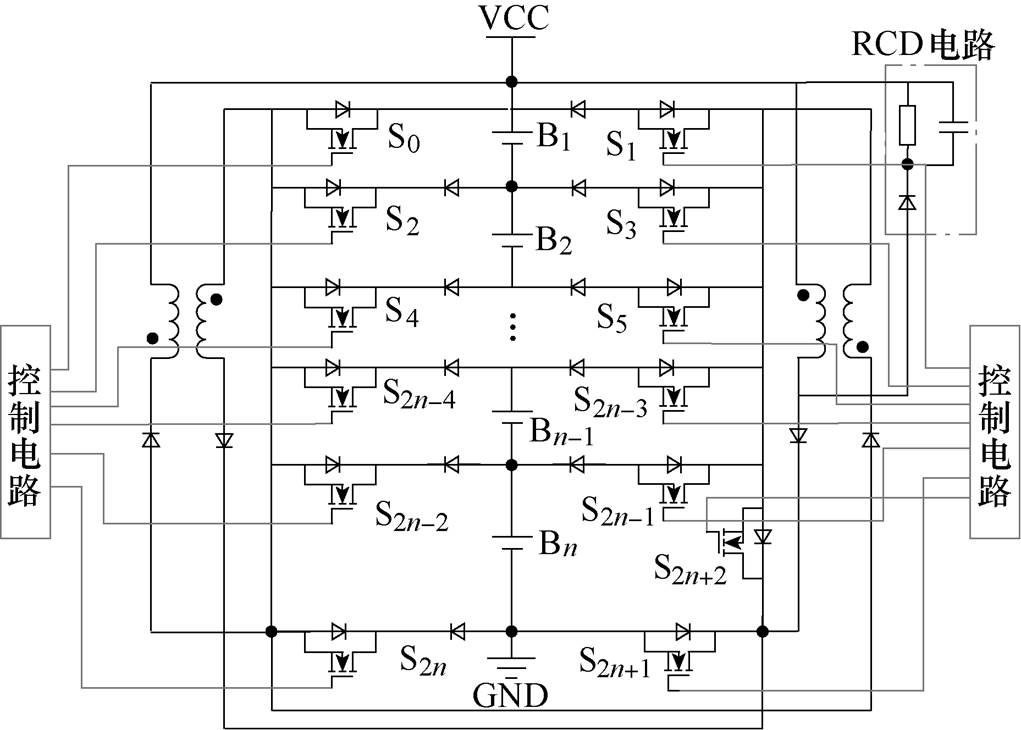
图1 均衡拓扑结构
Fig.1 Structure diagram of balancing topology
摘要 新能源汽车串联电池组各单体间不可避免的不一致性将会降低电池组的能量利用率及循环寿命，甚至危及新能源汽车使用安全。为改善串联电池组的不一致性，该文创新性地提出一种基于反激变换器的均衡拓扑，利用结构简单可靠的反激变换器实现均衡能量在整组电池和任意单体间转移，所提出的拓扑减少了储能元件的数量，降低了均衡系统的体积，而且能量传递的一次侧仅需一组控制信号，降低了控制难度；在此拓扑基础上，提出一种双目标直接均衡控制策略，将充电过程和放电过程的均衡合二为一，同时实现充/放电过程最高端电压的降低和最低端电压的升高。仿真及实验结果表明，该文所提新型均衡方法具有良好的动静态均衡效果，能够显著地改善串联电池组的一致性。
关键词：串联电池组 反激变换器 双目标 直接均衡
锂电池作为新能源汽车动力电池的第一选择[1]，其应用于新能源汽车时，通常需要将多个电池串并联构成电池组以达到应用要求。而各单体间不可避免的不一致性问题会导致电池组的能量利用率及循环寿命降低，甚至危及新能源汽车的使用安全。有效的均衡系统能够显著改善电池组一致性[2]，而串联电池组的可靠性相比于并联电池组更容易受到单体不一致性的影响[3-4]。本文针对串联电池组的均衡展开研究。
均衡技术的研究主要包含拓扑结构及其控制方式。根据均衡能量耗散情况的不同，均衡拓扑可分为能耗型和非能耗型[5-6]。能耗型拓扑的典型代表是电阻放电式拓扑，其利用电阻进行多余能量的消耗[7]，优点是体积小、成本低，缺点是容易造成能量浪费且影响电池组整体的热平衡。非能耗型主要利用电容器、电感器、变压器等储能元件来实现能量转移。基于开关电容器的均衡拓扑[8-10]体积小、控制简单，但其依据压差进行均衡，当单体压差不大时，均衡过程容易受到回路开关器件的影响。基于电感的均衡拓扑[11-14]均衡速度快，但其所需电感数量较多，不利于均衡系统体积的缩小和成本的降低。基于变压器的均衡拓扑[15-18]具有较高的均衡效率，且与主电路隔离。例如，一种基于多绕组变压器的拓扑结构[17]，其优点是能量可以在任何单体之间传递，但多绕组变压器具有体积大、复杂度高、漏磁严重等问题。基于多绕组变压器的模块化均衡方法[18]，相比于前者减少了体积、降低了成本，但模块结构相对复杂，变压器漏磁严重，且不利于扩展。均衡控制的研究主要涉及均衡指标的确定，由于单体电压作为不一致性指标比较容易搭建实验平台且不影响均衡效果的验证[16-18]，本文以单体电压作为均衡 指标。
基于以上分析，结合反激变换器结构简单、输入电压范围广、转换效率高的特点，本文创新地提出一种基于反激变换器的体积小、易于扩展、控制简单的均衡拓扑。在此基础上，将充放电过程的均衡合二为一，提出最高端电压、最低端电压同时均衡的双目标直接均衡控制策略，以实现新型拓扑的“物尽其用”。与单端电压相比，均衡速度显著提高。
均衡拓扑结构如图1所示。n个单体组成的电池组包含2n+4个二极管，2n+3个MOS管，以及一个RCD吸收电路和两个反激变换器。将电池组中每个单体依次标记为B1, B2, B3,…, Bn，将每个MOS管依次标记为S0, S1, S2,…, S2n+2；左边的变换器用于给最高端电压对应的单体放电均衡，其一次侧的上、下两端分别连接各单体电池左右两侧的MOS管，二次侧通过一个MOS管和整个电池组相连；右边的变换器用于给最低端电压对应的单体充电均衡，其一次侧经过一个MOS管和电池组整体连接，二次侧的上、下两端分别与各单体电池左右两边的MOS管相连。电池组右边的开关矩阵另需增加一个MOS管S2n+2，在左边变换器工作时导通此MOS管；而在右边变换器工作时断开此MOS管，以防止均衡过程发生短路。因为右侧变换器一次侧和整个电池组连接，为减小漏感尖峰电压对MOS管安全性的影响，需要在右侧的变换器增加一个吸收电路，本文采用成本低、结构简单且应用广泛的RCD吸收电路来减小漏感尖峰电压对MOS管的影响。
图1 均衡拓扑结构
Fig.1 Structure diagram of balancing topology
新型均衡拓扑的特点在于：①仅需两组变换器，均衡系统体积大大缩小、成本降低；②均衡能量可以在任意单体和电池组间直接转移，缩小均衡路径，提高均衡速度；③电池单体数量变化时，在满足器件极限值的前提下，仅需增减相应的MOS管和二极管即可，电路易于扩展。
本小节以如图2所示四节单体串联均衡拓扑进行均衡原理的研究。
图3所示为四节单体串联均衡工作原理。设B3电压最高，B2电压最低，且电池组不一致性满足均衡电路工作条件。左边变换器能量传递分为两个阶段，这两个阶段MOS管S10保持导通。第一阶段，如图3a所示，导通MOS管S4和S7，电池B3为一次侧电感充电，一次侧电感感生一个电动势，其极性为“上正下负”；第二阶段，如图3b所示，将MOS管S4和S7断开，并导通变换器二次侧MOS管S8，一次侧电感将感生一个“上负下正”的感应电动势，此感应电动势耦合到二次侧电感，极性为“上正下负”，二次侧电感为电池组充电，整个过程实现均衡能量从B3到整组电池的转移。右边变换器能量传递过程分为三个阶段，这三个阶段MOS管S10保持断开。第一阶段，如图3c所示，导通一次侧MOS管S9，整个电池组给一次侧电感充电，一次侧电感电流不断上升，将感生一个“上正下负”的感应电动势；第二阶段，如图3d所示，断开反激变换器一次侧MOS管S9，此时，吸收电路中的电阻将储存的漏感能量消耗掉，降低因漏感引起的尖峰电压，保证电路安全工作；第三阶段，如图3e所示，导通B2对应的MOS管S3和S4，此时，S9断开导致一次侧电感感生的“上负下正”的感应电动势耦合到二次侧电感，极性为“上正下负”，二次侧电感给单体B2充电，整个过程实现均衡能量从整组电池到B2的转移。
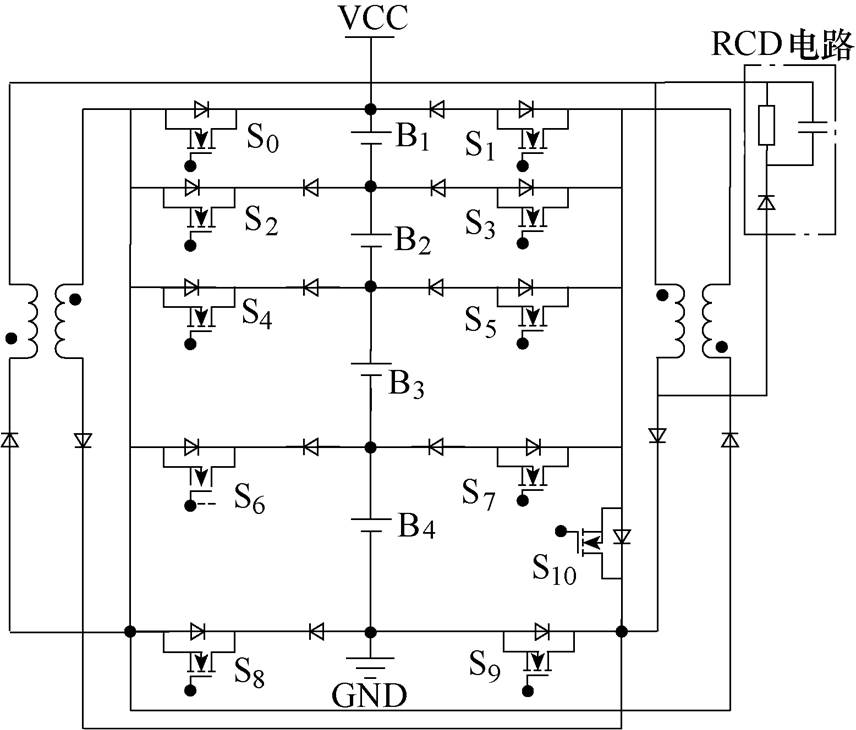
图2 四节单体串联均衡拓扑
Fig.2 Four-cell series balancing topology
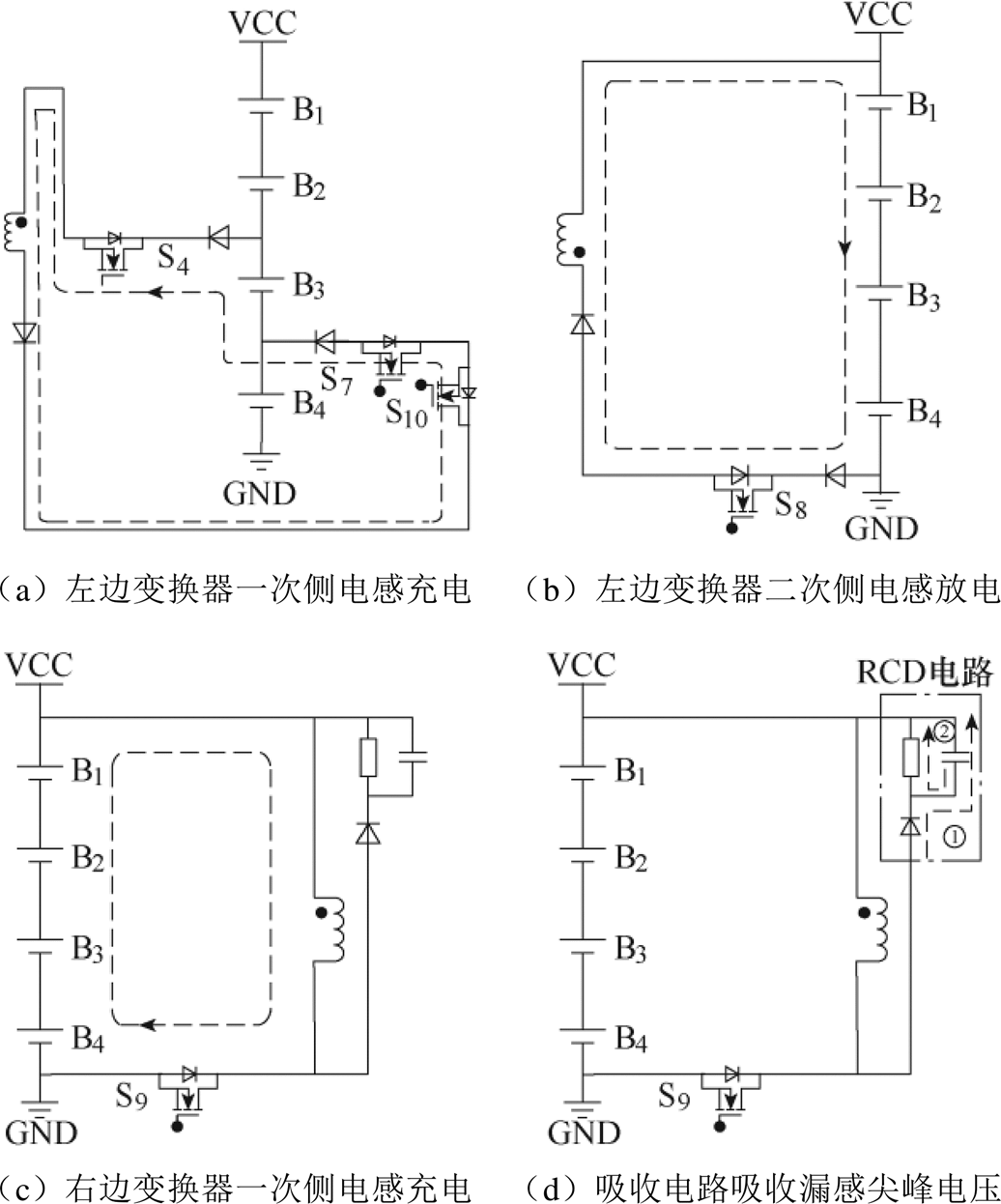
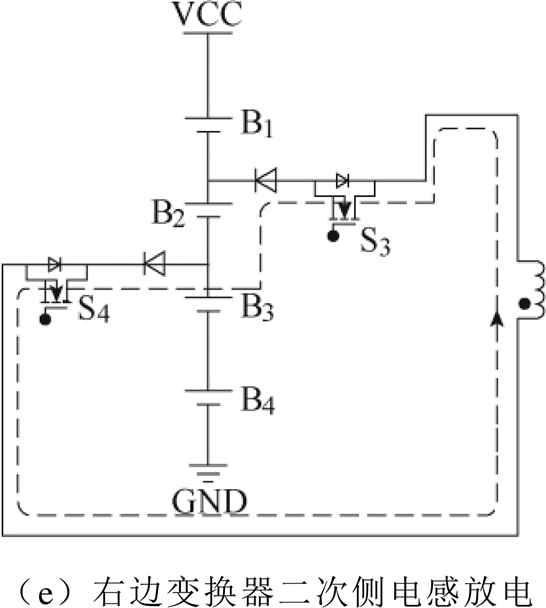
图3 四节单体串联均衡工作原理
Fig.3 Balancing principle of four-cells battery pack
均衡拓扑的参数主要涉及左右两个变换器的匝比，一次、二次侧电感量以及MOS管控制信号的占空比等。为防止磁滞饱和，变换器必须工作在电流断续模式。为保证均衡速度及可靠性，首先需要确定最大均衡电流。本文均衡实验MOS管为意法半导体IRF630，其开关损耗和截止损耗很小，忽略不计。具体参数计算的过程如下所述。
首先，对两边变压器制定同样规则：变换器的匝数记为N；一次侧电感记为LP，二次侧电感记为LS；一次侧均衡电流记为iP，最大值记为IP；二次电流记为iS；整组电池电压为Vn，均衡对象电压记为Vi；VD为二极管导通压降；f为开关频率，T为周期；一个均衡周期内，一次侧电感电流上升时间占空比记为D，二次电流下降时间占空比记为D¢；二次侧电压反射到一次电压记为Vf。本节以左边反激变换器为例进行参数计算的研究。
由1.2节可知，当断开变换器一次侧MOS管时，二次侧感生极性为“上正下负”的感应电动势，同时一次侧产生极性为“上负下正”的感应电压，称为反射电压Vf，有
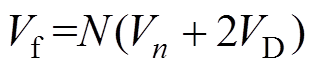（1）此时，一次侧MOS管上承受的压降为Vi+Vf。由此可知，MOS管上承受的压降由匝比决定。为减少一次侧MOS管的电压应力，匝比的设计不宜过大，但过小又影响均衡效果，所以匝比的选择非常重要。
确定匝比后，还需确定一次、二次侧电感量。最大均衡电流为
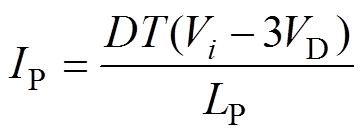（2）根据所需的最大均衡电流与选定的开关频率可得电感LP，有
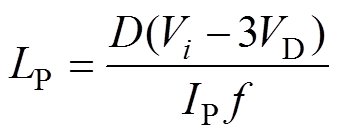（3）
则二次侧电感为
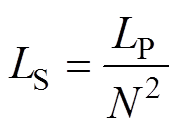（4）一个均衡周期内，一次侧电感电流为
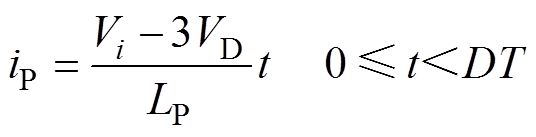（5）
二次侧电感电流的表达式为
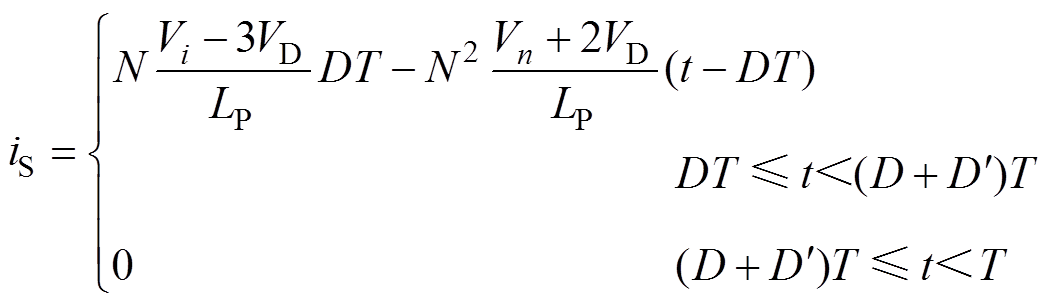（6）为保证电感复位，将t=T代入式（6）可得
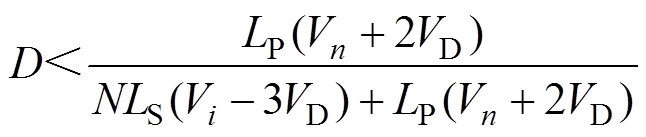（7）
根据伏秒平衡原理，即
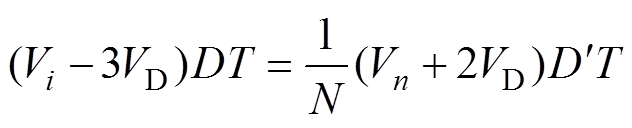（8）可得
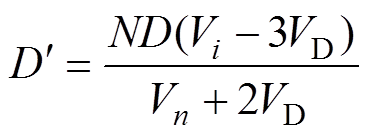（9）
左右两边变换器参数计算的不同在于，右边变换器需要设计RCD吸收电路。吸收电路由电阻并联电容再串接二极管构成，整体和右边变换器一次线圈并联。吸收电路中，如果RC过小，电容充电过快，电阻将很快消耗漏感能量，接着消耗部分一次侧励磁电感能量；如果RC过大，电容器充电过慢，导致能量传递给变压器二次侧电感延迟，则电阻将消耗部分一次侧励磁电感能量。若要避免这种情况发生，则需要计算出合适的RC值，使电阻只消耗漏感能量。RCD吸收电路的设计思路如下所述。
（1）确定吸收电容的电压VRCD，通常取反射电压的2～2.5倍，但是VRCD+Vn不能超过0.85VDSS[19]，其中，VDSS为MOS管的漏源极击穿电压。
（2）确定吸收电阻。VRCD确定了以后，RCD吸收电路的损耗为
（10）式中，LK为变换器漏感，三明治绕法的变换器漏感通常为2%～3%[19]。由式（10）可知，VRCD越小，其回路损耗越大。电阻R上的损耗为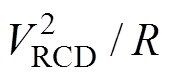
。根据能量守恒原则，可得
（11）（3）确定吸收电容。吸收电容上的最大纹波电压为
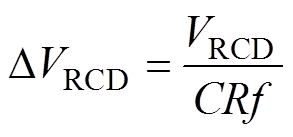（12）
可根据合适的纹波电压确定吸收电容的大小。
以上参数为均衡拓扑正常工作的功能性参数，新型均衡拓扑其中一个特点是易于扩展，扩展过程中，为保证MOS管及二极管安全稳定工作，必须使整组电池电压小于MOS管及二极管的击穿电压。综上，即可完成均衡拓扑的参数设计。
以往较多文献[20-21]所研究的均衡控制策略是充电过程仅对能量较高的单体放电均衡，放电过程仅对能量较低的单体充电均衡。本文基于新型均衡拓扑，将充放电过程的均衡控制合二为一，提出如图4所示的双目标直接均衡策略。
充放电过程中，双目标直接均衡同时实现最大电压的降低和最小电压的升高，此控制策略可使差异最大的单体首先得到均衡，从而提高均衡速度。具体控制方式如下：均衡过程，检测电路及控制电路，首先判别出最大单体电压ULmax，最小单体电压ULmin，以及平均电压ULave，设置均衡指标Uref。如果ULmax-ULave＞Uref，且ULave-ULmin≤Uref，左边反激变换器对最大电压对应的单体放电均衡；如果ULmax-ULave≤Uref，且ULave-ULmin＞Uref，右边的反激变换器对最小电压对应的单体充电均衡；如果ULmax-ULave＞Uref，且ULave-ULmin＞Uref，继续比较两个差值的大小，如果ULmax-ULave≥ULave-ULmin，则左边反激变换器对最大电压对应的单体放电均衡；如果ULmax-ULave＜ULave-ULmin，则右边反激变换器对最小电压对应的单体充电均衡，如此往复至ULmax-ULave≤Uref且ULave-ULmin≤Uref，均衡电路停止工作。
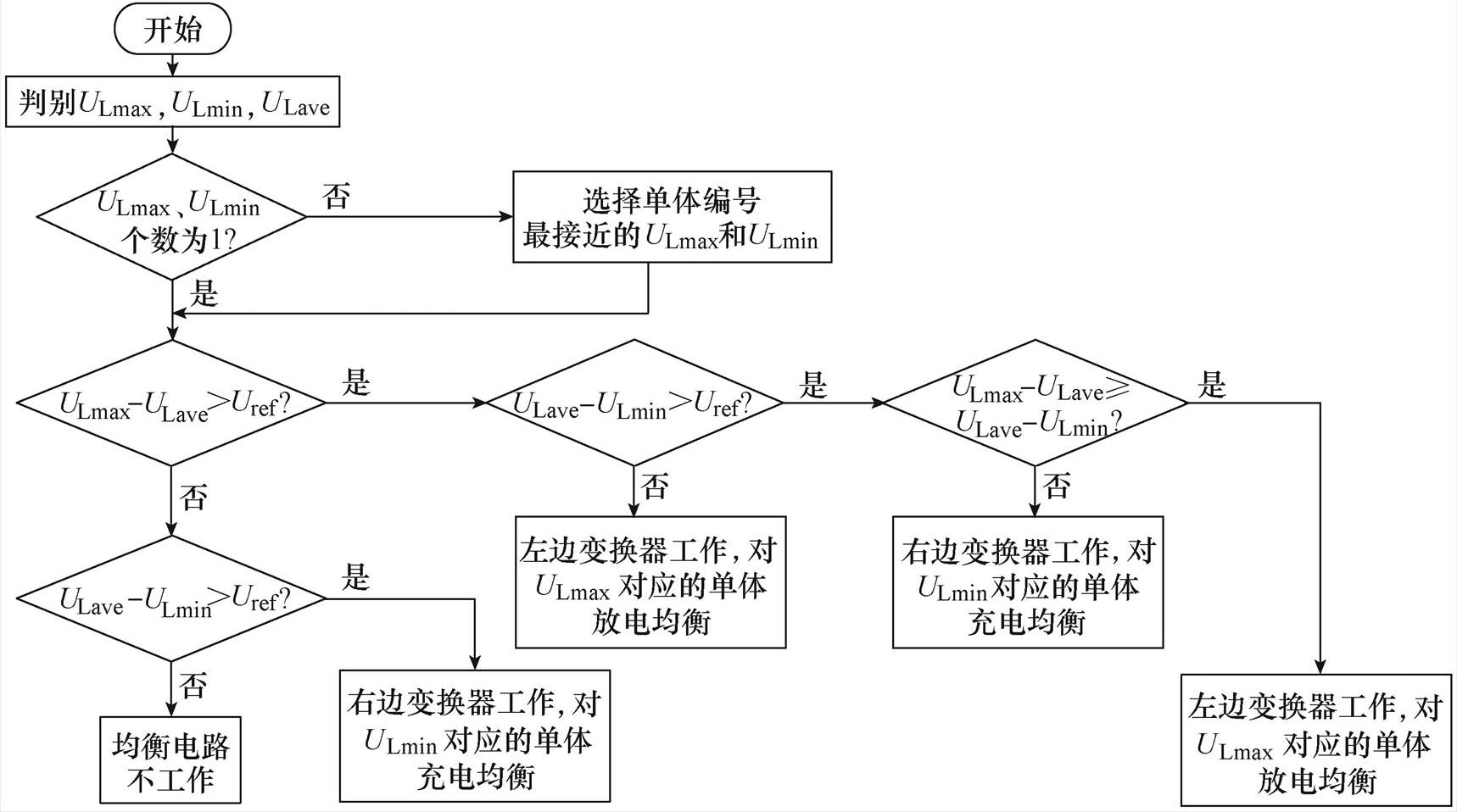
图4 双目标直接均衡流程
Fig.4 Flow chart of dual-objective direct balancing
本文所提出的基于反激变换器的双目标直接均衡方法相比于单目标均衡方法的一个显著优点是提升了均衡速度，通过在Matlab/Simulink中搭建仿真模型验证这一优点。在本文所提拓扑的基础上设置两组仿真环节：一组采用单目标均衡控制策略，放电过程中只针对电压最小的单体均衡，充电过程中只针对电压最大的单体均衡；另一组采用本文所提出的双目标直接均衡控制策略，同时对最大电压和最小电压对应的单体均衡。两组仿真均采用相同的拓扑，相同的开关周期（10kHz），相同的变换器匝比（1
1），相同的电池容量（3.2A·h），相同的充电/放电电流（1A），相同的均衡精度（5mV）。充电均衡仿真结果如图5所示，充电过程仿真数据见表1。
由图5和表1可知，充电过程，双目标均衡用时5.8s，而单目标均衡用时15.2s，双目标均衡速度显著提高。放电均衡仿真结果如图6所示，放电过程仿真数据见表2。
由图6和表2可知，放电过程，双目标均衡用时12s，单目标均衡用时41s，双目标均衡速度显著提高。综合分析，相比于单目标，双目标均衡速度显著提高。另外，单目标均衡有个核心问题，随着单体个数的增加，多个单体同时具备最高电压或者最低电压的可能性增加，可能出现均衡电路无法判断均衡对象的情况，而双目标均衡可以显著减少此种情况的出现。
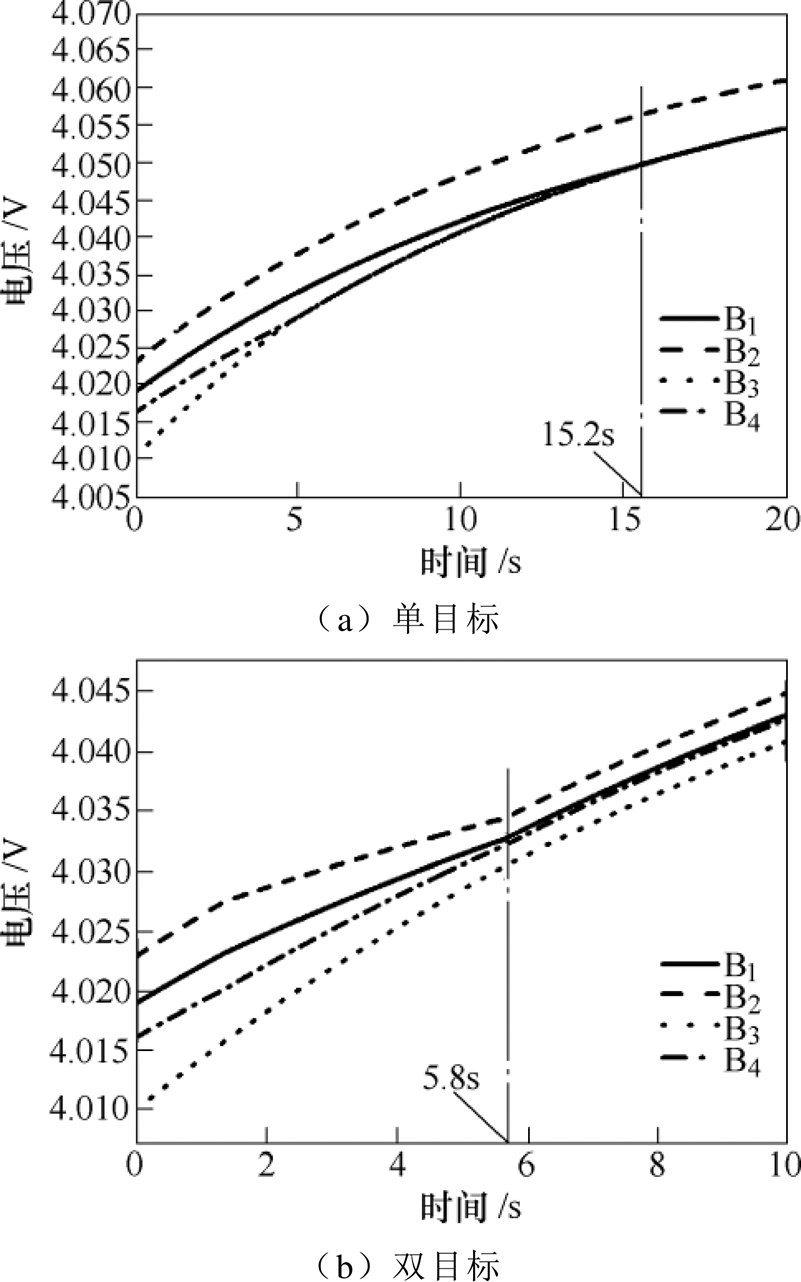
图5 充电均衡仿真结果
Fig.5 Charging balanced simulation results
表1 充电过程仿真数据
Tab.1 Simulation data of charging process
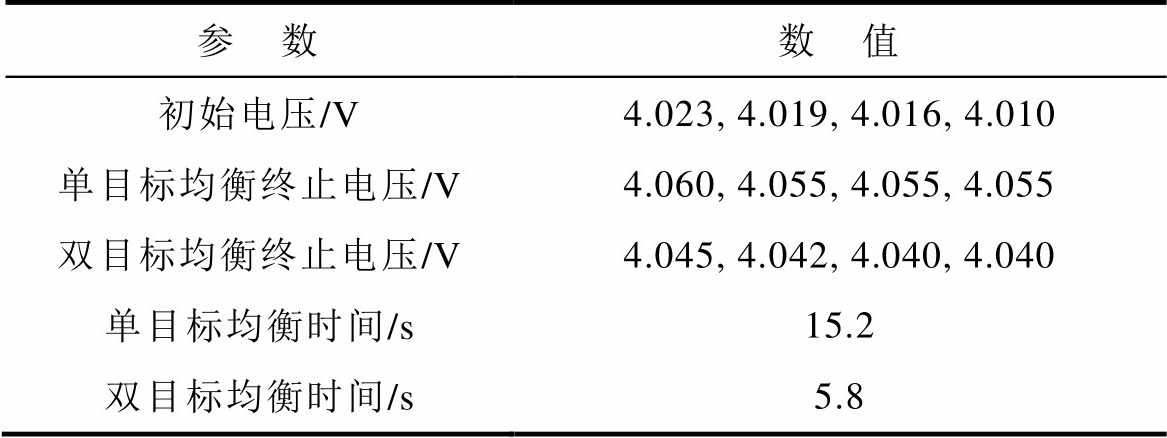
参 数数 值 初始电压/V4.023, 4.019, 4.016, 4.010 单目标均衡终止电压/V4.060, 4.055, 4.055, 4.055 双目标均衡终止电压/V4.045, 4.042, 4.040, 4.040 单目标均衡时间/s15.2 双目标均衡时间/s5.8
图6 放电均衡仿真结果
Fig.6 Discharging balanced simulation results
表2 放电过程仿真数据
Tab.2 Simulation data of discharging process
参 数数 值 初始电压/V3.995, 3.990, 3.987, 3.982 单目标均衡终止电压/V3.955, 3.950, 3.950, 3.950 双目标均衡终止电压/V3.965, 3.963, 3.960, 3.960 单目标均衡时间/s41 双目标均衡时间/s12
为验证新型均衡方法的有效性，搭建了如图7所示采用四节单体串联的均衡实验平台。单体电池为日本索尼公司生产的18650型三元锂电池，标称电压为3.7V，额定容量为3.2A·h。
实验中，首先，需要设定最大均衡电流。其次，在此基础上设置电感值和开关频率，开关频率太低，均衡速度慢，太高则开关损耗大；最后，电感值也不能太大或者太小，太大，电感的损耗增加，太小则易饱和。具体实验参数见表3，PWM1、PWM2、PWM3、PWM4分别为左、右变换器一次侧和二次MOS管对应的驱动信号。
图7 均衡实验平台
Fig.7 Balancing experiment platform
表3 均衡拓扑参数
Tab.3 The parameters of the balancing topology
参 数数 值 各单体初始电压/V3.80, 3.74, 3.70, 3.30 PWM1周期/kHz14 占空比(%)75 PWM2周期/kHz14 占空比(%)25 PWM3周期/kHz10 占空比(%)20 PWM4周期/kHz10 占空比(%)80 左边变换器均衡电流/A0.5 右边变换器均衡电流/A1.2 均衡精度DV/V＜0.05 左、右变换器匝比11 左边变换器一次、二次侧电感/mH70 右边变换器一次、二次侧电感/mH50 二极管导通压降/V0.4 电容/mF0.44 电阻/W100 充/放电电流/A0.7
图8所示为左边变换器均衡实验波形。图8a所示为左边变换器一次侧MOS管的控制信号及一次、二次侧均衡电流。一个控制信号周期内，一次电流直线上升，说明均衡目标在给变换器充电，二次电流直线下降，说明变换器在给整个电池组充电，一次、二次电流最大值分别为0.6A和0.5A；图8b所示为一个控制信号周期内四个单体电池电压的变化，第一阶段，最高电压电池给一次侧电感充电，最高电压先下降，当最高电压电池给变换器充电结束后，因为极化效应，又上升一部分；第二阶段，二次侧电感给整个电池组充电，四个单体电池电压先整体上升，当均衡电流为零后，因为极化效应，又下降一部分。
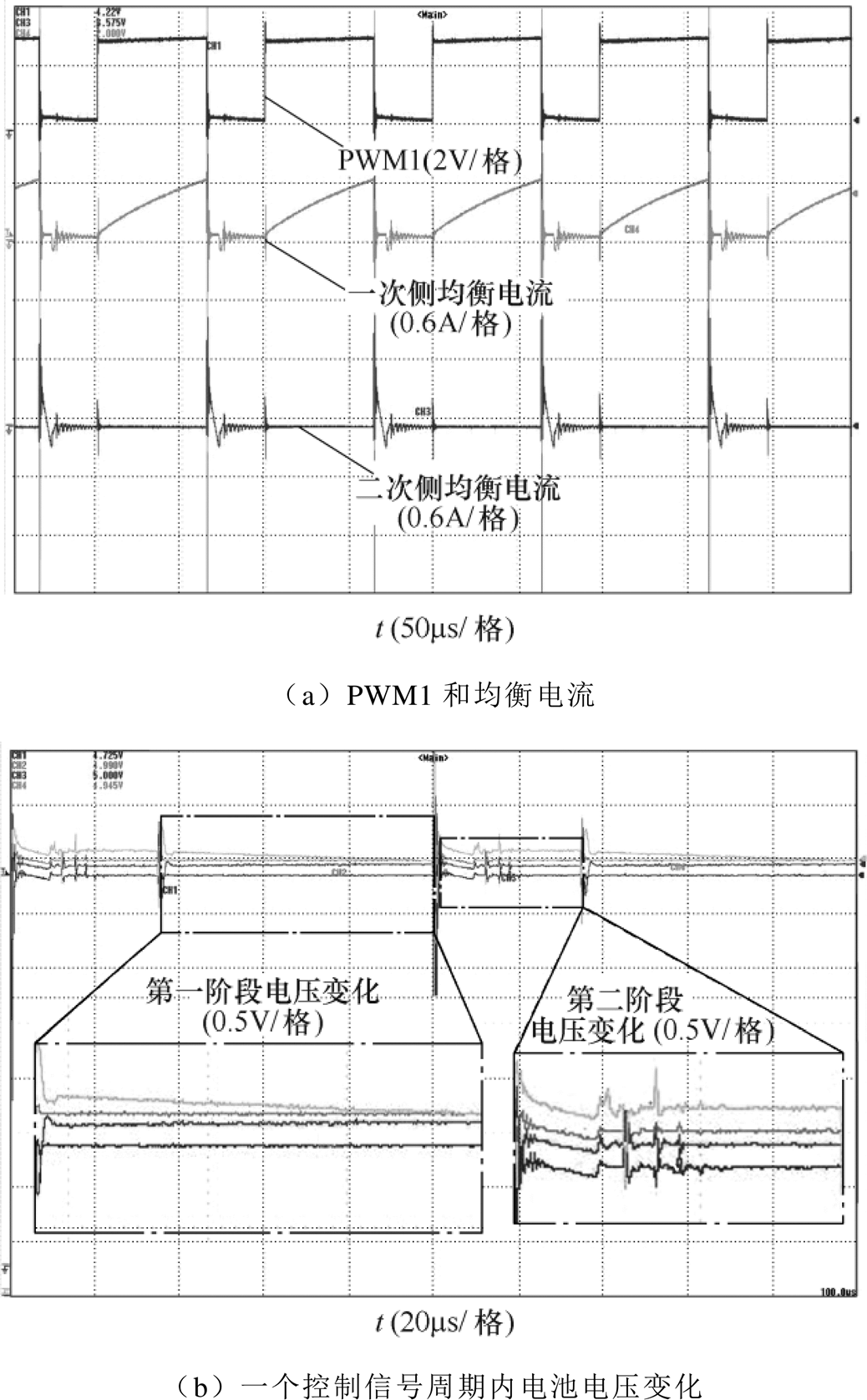
图8 左边变换器均衡实验波形
Fig.8 Left converter balancing experimental waveforms
图9所示为右边变换器均衡实验波形。图9a为右边变换器一次侧MOS管的控制信号及一次、二次侧均衡电流。一个控制信号周期内，一次电流直线上升，说明整组电池在给变换器充电，二次电流直线下降，说明变换器在给均衡目标充电。一次、二次电流最大值分别为1.5A和1.2A。图9b为一个控制信号周期内四个单体电池电压的变化，第一阶段，电池组给一次侧电感充电，四个单体电池电压先整体下降，当电池组给变换器充电完成后，因为极化效应，各单体电压又上升一部分；第二阶段，二次侧电感将能量转移给最低单体电池，最低电压先上升，当均衡电流为零后，因为极化效应，又下降一部分。图9c和图9d是当右边变换器一次侧MOS管断开瞬间，均衡拓扑有无RCD吸收电路所对应的一次侧电感电压波形，由图9d可知，RCD电路吸收显著降低了一次侧的尖峰电压，抑制了过高的dv/dt，保证了均衡电路安全有效的工作。
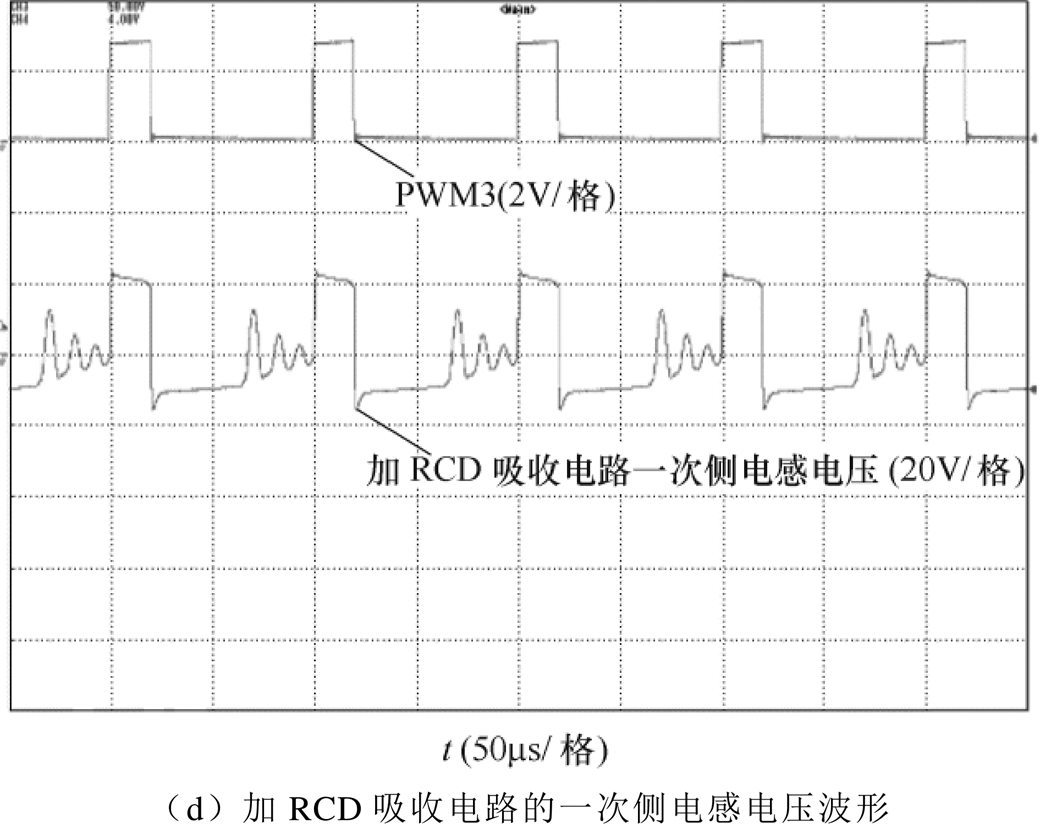
图9 右边变换器均衡实验波形
Fig.9 Right converter balancing experimental waveforms
为更好地验证均衡效果，设计了三组均衡实验，分别是放电、充电和动态均衡实验，实验结果如图10所示。放电均衡实验的初始电压分别为3.963V、4.005V、3.704V、3.952V，均衡结果如图10a所示。图中，UB1～UB4为每个电池的电压。
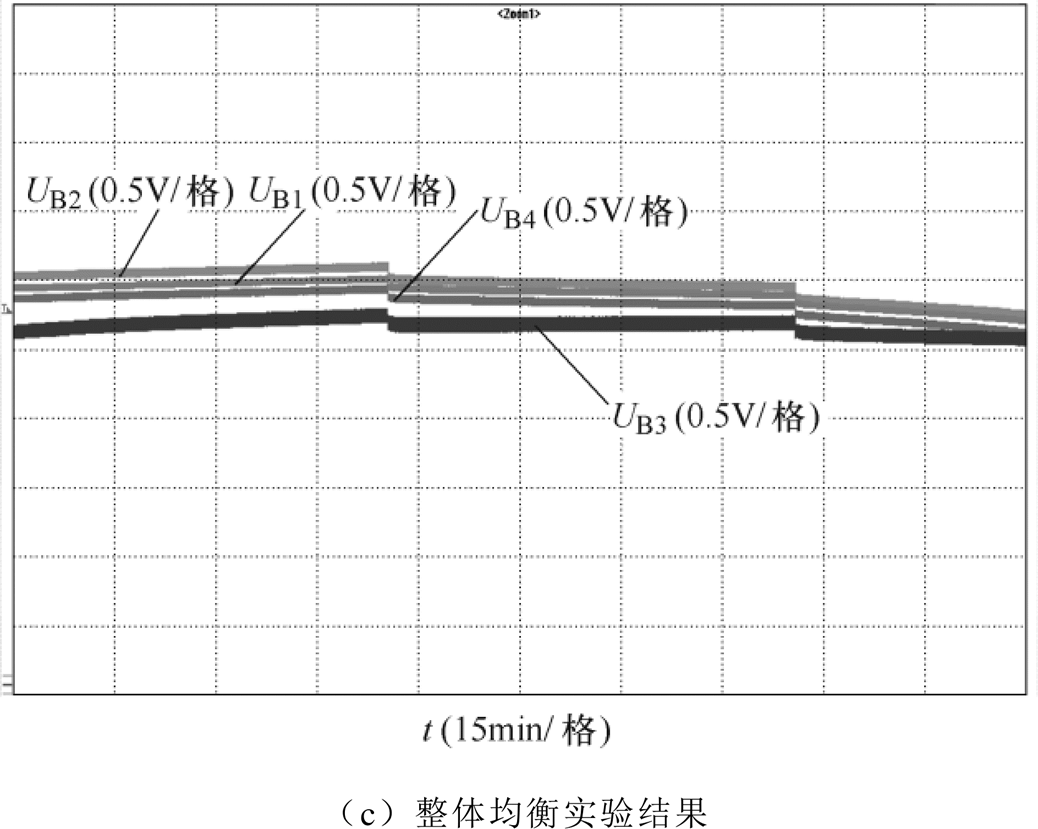
图10 均衡实验结果
Fig.10 Results of the balancing experiment
充电均衡实验的初始电压分别为3.551V、3.584V、3.303V、3.605V，均衡结果如图10b所示。动态均衡实验初始电压分别为3.762V、3.804V、3.303V、3.751V，其过程为：先以0.7A的电流充电60min，再搁置60min，最后以0.7A的电流放电30min，其结果如图10c所示。由图10可知，新型均衡方法在动态充放电过程中也有良好的均衡表现。
以n个单体构成的电池组为例，分析比对所提均衡拓扑与常见均衡拓扑，以进一步明确新型拓扑的特点，对比内容见表4。
文献[21]基于储能电感构建均衡拓扑，电路连线简单、开关管控制方便，但其需要较多的电感，难以缩小均衡系统体积。文献[22]属于开关电容型均衡拓扑，均衡速度随电压差缩小而降低，均衡过程容易受到回路开关器件的影响。文献[23]基于LC谐振建立均衡方法，虽然其储能单元仅需一个电感、一个电容和一个二极管，但其所需开关管数量较多且控制复杂。文献[24]基于单绕组变压器建立均衡拓扑，所用开关管和二极管较少，理论上具有更高的均衡效率，但其结构复杂，且为防止电感电容谐振，对开关速度提出了更高要求。文献[25]虽然使用开关器件较少，但其储能单元结构复杂，且变压器磁饱和问题突出。文献[26]利用软开关技术建立均衡方法，使得开关管的损耗得以降低，但仍未解决绕组过多带来的体积庞大、漏感严重等问题。综上所述，新型均衡拓扑具有储能单元体积小、均衡速度快、易扩展等特点。
表4 所提均衡拓扑与常见均衡拓扑的对比（以n个单体串联为例）
Tab.4 Comparison of the proposed topology with common topologies (taking n cell units as an example)
拓扑类型元件类型性能参数 开关管电感电容二极管变压器电阻成本均衡效率均衡速度复杂度尺寸扩展性 电感型[21]2n+2n+10000SGGMSE 开关电容型[22]2n0n000GMMSGG LC谐振型[23]4n11300SGGSMG 单绕组变压器型[24]22n2n+22n10SGGSGM 多绕组变压器型[25]n000n0SEESSS 变换器型[26]4nn/2(n/2)+10n/20PGGSSG 新型变换器型2n+3012n+421MGGGGG
注：E—优秀；G—良好；M—中等；S—偏差；P—较差。
针对新能源汽车串联电池组的不一致性问题，本文提出一种基于反激变换器的双目标直接均衡方法。所提均衡拓扑具有储能单元体积小、成本低、均衡速度快、易于扩展的特点。双目标直接均衡控制策略将充/放电过程的均衡合二为一，同时实现充/放电过程最高电压的降低和最低电压的升高，提高均衡速度。仿真及实验结果表明，本文所提新型均衡方法具有良好的动静态均衡效果，能够显著改善串联电池组的一致性。
参考文献
[1] 张振宇, 汪光森, 聂世雄, 等. 脉冲大倍率放电条件下磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2019, 34(8): 1769-1779.
Zhang Zhenyu, Wang Guangsen, Nie Shixiong, et al. State of charge estimation of LiFePO4 battery under the condition of high rate pulsed discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1769-1779.
[2] 谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2019, 34(2): 419-426.
Gu Miao, Xia Chaoying, Tian Congying. Li-ion battery state of charge estimation based on com- prehensive Kalman filter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 419-426.
[3] 孙国强, 任佳琦, 成乐祥, 等. 基于分数阶阻抗模型的磷酸铁锂电池荷电状态估计[J]. 电力系统自动化, 2018, 42(23): 57-63.
Sun Guoqiang, Ren Jiaqi, Cheng Lexiang, et al. State of charge estimation of LiFePO4 battery based on fractional-order impedance model[J]. Automation of Electric Power Systems, 2018, 42(23): 57-63.
[4] 魏业文, 李应智, 曹斌, 等. 含Buck电路的锂电池低功耗电量均衡技术研究[J]. 电工技术学报, 2018, 33(11): 2575-2583.
Wei Yewen, Li Yingzhi, Cao Bin, et al. Research on power equalization of lithium-ion batteries with less- loss Buck chopper[J]. Transactions of China Electro- technical Society, 2018, 33(11): 2575-2583.
[5] 何耀, 曹成荣, 刘新天, 等. 基于可变温度模型的锂电池SOC估计方法[J]. 电机与控制学报, 2018, 22(1): 43-52.
He Yao, Cao Chengrong, Liu Xintian, et al. SOC estimation method for lithium battery based on variable temperature model[J]. Electric Machines and Control, 2018, 22(1): 43-52.
[6] 崔强, 王庆军, 童亦斌, 等. 基于半桥级联的电池柔性成组储能系统及控制策略[J]. 电工技术学报, 2019, 34(5): 954-962.
Cui Qiang, Wang Qingjun, Tong Yibin, et al. Flexible battery energy storage system and control strategy based on half-bridge cascade technology[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 954-962.
[7] 刘畅, 蔡旭, 陈强. 链式电池储能系统的荷电状态复合均衡控制策略[J]. 电力系统自动化, 2019, 43(10): 68-77.
Liu Chang, Cai Xu, Chen Qiang. Compound balan- cing control strategy of SOC for battery energy storage system based on cascaded H-bridge con- verter[J]. Automation of Electric Power Systems, 2019, 43(10): 68-77.
[8] Ye Yuanmao, Cheng K W E. Modeling and analysis of series-parallel switched-capacitor voltage equalizer for battery/supercapacitor strings[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(4): 977-983.
[9] Shang Yunlong, Bing Xia, Fei Lu, et al. A switched- coupling-capacitor equalizer for series-connected battery strings[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7694-7706.
[10] Schaef C, Din E, Stauth J T. A hybrid switched- capacitor battery management IC with embedded diag- nostics for series-stacked Li-ion arrays[J]. IEEE Journal of Solid State Circuits, 2017, 52(12): 3142-3154.
[11] Chen Yang, Liu Xiaofang, Fathy H K, et al. A graph-theoretic framework for analyzing the speeds and efficiencies of battery pack equalization cir- cuits[J]. International Journal of Electrical Power and Energy Systems, 2018, 98(6): 85-99.
[12] 刘红锐, 杜春峰, 李博, 等. 一种基于混合斩波电路的蓄电池组高速能量均衡器的研究[J]. 电工技术学报, 2018, 33(增刊2): 472-478.
Liu Hongrui, Du Chunfeng, Li Bo, et al. Research on high speed energy equalizer for battery pack based on mixed chopper circuit[J]. Transactions of China Elec- trotechnical Society, 2018, 33(S2): 472-478.
[13] Tashakor N, Farjah E, Ghanbari T. A bidirectional battery charger with modular integrated charge equalization circuit[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2133-2145.
[14] 李小龙, 徐顺刚, 许建平, 等. 一种单电感双向电池均衡电路[J]. 电机与控制学报, 2019, 23(4): 90-97.
Li Xiaolong, Xu Shungang, Xu Jianping, et al. Single-inductor bidirectional battery equalizer[J]. Electric Machines and Control, 2019, 23(4): 90-97.
[15] Zhang Zhiliang, Gui Handong, Gu Dongjie, et al. A hierarchical active balancing architecture for lithium- ion batteries[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(4): 2757-2768.
[16] Maurice C, Torsten E, Soren H. Systematic com- parison of active balancing: a model-based quanti- tative analysis[J]. IEEE Transactions on Vehicular Technology, 2018, 67(2): 920-934.
[17] Lee K M, Lee S W, Choi Y G, et al. Active balancing of Li-ion battery cells using transformer as energy carrier[J]. IEEE Transactions on Industrial Electro- nics, 2017, 64(2): 1251-1257.
[18] Shang Yunlong, Xia Bing, Zhang Chenghui, et al. A modularization method for battery equalizers using multiwinding transformers[J]. IEEE Transactions on Vehicular Technology, 2017, 66(10): 8710-8722.
[19] 刘凤君. 开关电源设计与应用[M]. 北京: 电子工业出版社, 2014.
[20] 张劲. 串联电池组多路径均衡电路研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
[21] Guo Xiangwei, Kang Longyun, Huang Zhizhen, et al. Research on a novel power inductor-based bidire- ctional lossless equalization circuit for series-connected battery packs[J]. Energies, 2015, 8(6): 5555-5576.
[22] Ye Yuanmao, Cheng K W E, Fong Y C, et al. Topology, modeling, and design of switched- capacitor-based cell balancing systems and their balancing exploration[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4444-4454.
[23] Yu Yanqi, Saasaa R, Khan A A, et al. A series resonant energy storage cell voltage balancing circuit[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2020, 8(3): 3151-3161.
[24] Uno M, Kukita A. String-to-battery voltage equalizer based on a half-bridge converter with multistacked current doublers for series-connected batteries[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1286-1298.
[25] Shang Yunlong, Xia Bing, Zhang Chenghui, et al. An automatic equalizer based on forward-flyback converter for series-connected battery strings[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 5380-5391.
[26] Zeltser I, Evzelman M, Kuperman A, et al. Zero current switching resonant converter based parallel balancing of serially connected batteries string[J]. IEEE Transaction on Industry Applications, 2019, 55(6): 7452-7460.
The Dual-Objective Direct Balancing Method Based on Flyback Converter
Abstract The inevitable inconsistency among the cells of series battery pack of new energy vehicles will reduce the energy efficiency and cycle life of the battery pack, and even endanger the safety of the battery system. In order to improve the consistency of series battery pack, this paper innovatively proposes a balancing topology based on flyback converter, which uses a simple and reliable structure to realize the energy transfer between the whole battery and any single cell. The proposed balancing topology reduces the number of components and the volume of the balancing system, and only requires one set of signals on the primary side of the energy transfer, which reduces the control difficulty. Based on this topology, a dual-objective direct balancing control strategy is proposed, which combines the balancing of the charging process and the discharging process into one. Meanwhile, the reduction of the highest terminal voltage and the increase of the lowest terminal voltage in the charging/discharging process are realized. The simulation and experimental results show that the novel balancing method proposed in this paper has a good dynamic and static balancing effect, and can significantly improve the consistency of the series battery pack.
keywords：Series battery pack, flyback converter, dual-objective, direct balancing
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.200022
国家自然科学基金（61703145）、河南省高等学校重点科研（19A470001）和河南省科技攻关（202102210093）资助项目。
收稿日期 2020-01-06
改稿日期 2020-05-05
郭向伟 男，1987年生，博士，副教授，研究方向为电动汽车能量管理系统。E-mail: gxw@hpu.edu.cn（通信作者）
耿佳豪 男，1996年生，硕士研究生，研究方向为电动汽车电池管理系统。E-mail: gjh809441455@126.com
（编辑 崔文静）