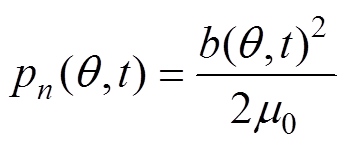 (1)
(1)摘要 针对交流牵引电机存在电磁噪声过大而影响其推广应用的问题,提出一种基于内切圆弧的交流牵引电机齿肩削角降噪方法。阐述交流牵引电机电磁噪声产生的根本原因及有关径向电磁力谐波空间阶次的计算方法,建立电机定子齿肩采用内切圆弧式削角处理前后定子齿槽与转子表面间气隙宽度随转子位置变化的函数关系式,分析定子齿肩削角处理对电机电磁噪声的影响,并对其效果进行仿真,同时与直线式齿肩削角法的效果进行对比分析。结果表明,交流牵引电机定子齿肩采用内切圆弧式削角处理后可显著降低其电磁噪声,并且具有比直线式削角法更好的降噪效果。最后对一台5.5kW交流牵引电机进行内切圆弧式定子齿肩削角,取得了8.4dB(A)的降噪效果,由此可见,该方法具有较好的应用价值。
关键词:交流牵引电机 齿肩削角降噪方法 内切圆弧 有限元法
交流牵引电机因具有结构简单坚固、运行可靠、功率大、转速高等系列优点而在众多领域得到了广泛应用。然而由于其运行时存在较大的噪声,不仅对工作环境与人类健康造成了不利影响,而且限制了其在某些特殊领域的推广应用,因此开展交流牵引电机的降噪研究具有重要意义。
引起交流牵引电机噪声的主要因素包括电磁噪声、机械噪声及空气动力噪声等[1],其中尤以电磁噪声的影响较为突出,因此有效降低电磁噪声是实现电机降噪的关键所在。目前国内外研究者在降低电机电磁噪声方面已开展了系列研究,提出了多种可行的降噪方法,以通过改进电机结构来降低电磁噪声的效果较为明显,因而得到了广泛重视。
在有关改进电机结构以降低电磁噪声的研究方面,最早可追溯到1931年G. Kron针对感应电机不同槽配合对其电磁噪声影响所开展的研究[2];随后在1974年,舒波夫研究指出,电机电磁噪声是由电磁力作用于定子齿上产生的[3],揭示了电磁噪声产生的根源;2001年,S. Huang等研究指出,永磁同步电机无定子槽结构及永磁体斜极结构均可减小其电磁噪声[4];2005年,D. Mori等分析了异步电机稳态运行时的电磁力特性,研究电机齿槽处径向电磁力状态及其与电磁噪声的关系[5];2009年,J. Le Besnerai等分别通过优化感应电机定转子槽数配合[6]、定转子槽开口大小[7]来降低电磁噪声,取得了较好的效果;2010年,I. Rakib等综合分析了电机极槽配合对电磁噪声的影响[8];2011年,Jin Hur等研究了转子开槽对内置式永磁无刷直流电机振动噪声的影响[9];2012年,Sun-Kown Lee等研究了极槽配合对永磁同步电机振动噪声的影响,结果表明,在槽数相同的情况下,极数少的电机振动噪声小[10];2014年,S. Mohammad等研究了几种细分槽永磁拓扑结构对电机电磁噪声的影响[11]。
国内有关通过改进电机结构以降低电磁噪声的研究始于20世纪70年代。在随后的数十年中,研究者在相关理论及分析手段方面开展了广泛研究,并取得了一定的成果。2010年,代颖等研究了感应电机电磁噪声与槽配合之间的关系[12];2015年,李岩等针对永磁同步电机提出一种定子齿肩削角降噪方法[13],取得了明显的降噪效果;2016年,鲍晓华等针对笼型感应电机提出一种双斜槽的转子结构,有效降低了电磁噪声[14];2017年,周桂煜则针对笼型感应电机提出一种定转子的开槽结构,取得较好的降噪效果[15];2018年,吴双龙等对车用发电机转子极爪进行倒角,亦有效降低了电磁噪声[16]。
然而纵观上述各种通过改进电机结构以降低电磁噪声的研究,尤以文献[13]所提出的一种定子齿肩削角降噪方法效果较为明显,因而具有更好的应用价值;但文献[13]所提出的直线式定子齿肩削角方式仍未能达到最佳的降噪效果。为此,文中针对定子齿肩削角降噪方法开展进一步研究,并针对交流牵引电机提出一种基于内切圆弧的定子齿肩削角降噪方式,显著提升了降噪效果。文中分析了交流牵引电机采用内切圆弧式齿肩削角降噪的基本原理与实现方法,并对其效果进行验证,同时与文献[13]所提出的直线式定子齿肩削角降噪方法进行了对比分析。
根据文献[1],电机电磁噪声主要是由径向电磁力作用于定子内壁上产生的,单位面积上径向电磁力的表达式为
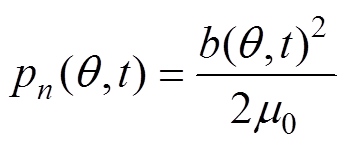 (1)
(1)式中,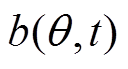 为气隙磁通密度;
为气隙磁通密度;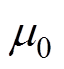 为真空磁导率,
为真空磁导率,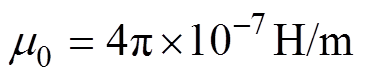 。
。
而在产生电磁噪声的径向电磁力中,起决定作用是由定转子齿谐波相互作用所产生的径向电磁力低次谐波[1]。对于中小型交流牵引电机而言,其电磁噪声主要由空间阶次小于4的径向电磁力谐波所产生[6],结合式(1),可得径向电磁力谐波空间阶次计算方法见表1[6, 15]。
表1 电机径向电磁力谐波空间阶次计算方法
Tab.1 Spatial order calculation method of radial electromagnetic force of motor

条 件空间阶次
表1中,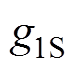 为计算定子谐波次数时所用系数,
为计算定子谐波次数时所用系数,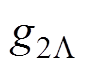 为计算转子谐波次数时所用系数,
为计算转子谐波次数时所用系数, = ±1, ±2, …;ZS为定子槽数,Zr为转子槽数,p为极对数。
= ±1, ±2, …;ZS为定子槽数,Zr为转子槽数,p为极对数。
交流牵引电机定子齿肩采用内切圆弧式齿肩削角示意图如图1所示。其削角方法是:从定子齿肩角顶点A开始,沿该齿肩角两侧边按一定长度等距离取两点,并以这两点作为内切圆弧的相切点D1和D2,再通过这两个相切点D1和D2作齿肩角的内切圆弧,并沿该内切圆弧削去该齿肩角。其中,内切圆弧的半径R由定子齿肩角顶点A到两侧边相切点D1或D2的距离L及齿肩角的夹角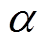 确定,具体为
确定,具体为
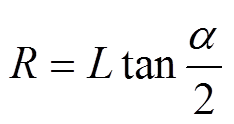 (2)
(2)式中,R为内切圆弧的半径;L为定子齿肩角顶点A到两侧内切圆弧相切点的距离;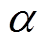 为齿肩角的 夹角。
为齿肩角的 夹角。
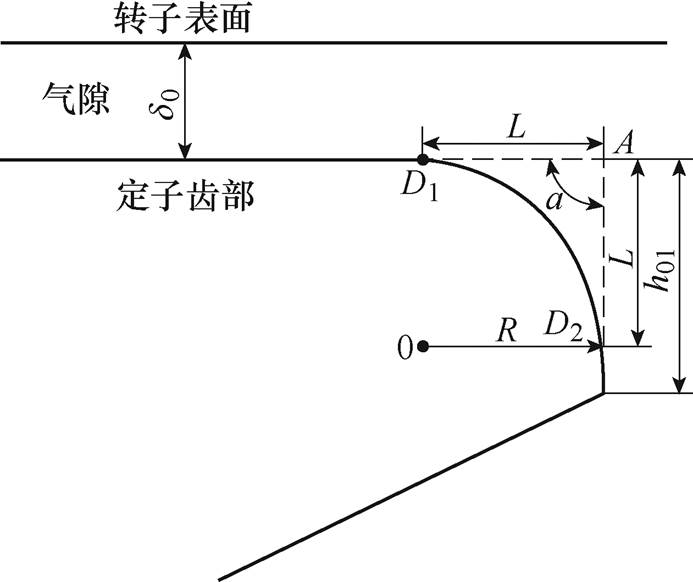
图1 内切圆弧式齿肩削角示意图
Fig.1 Schematic diagram of inscribed circular arc shoulder
交流牵引电机定子齿肩在按图1所示方法进行削角处理后,其定、转子间的气隙分布如图2所示。为简化分析,设定子齿槽形状为矩形;其中,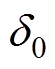 为定子齿冠与转子表面间的气隙宽度,l为两相邻定子齿中心距,b0为定子槽开口宽度,b1为定子齿宽, d1和d2为相应的相切点,h0为定子槽深度。
为定子齿冠与转子表面间的气隙宽度,l为两相邻定子齿中心距,b0为定子槽开口宽度,b1为定子齿宽, d1和d2为相应的相切点,h0为定子槽深度。
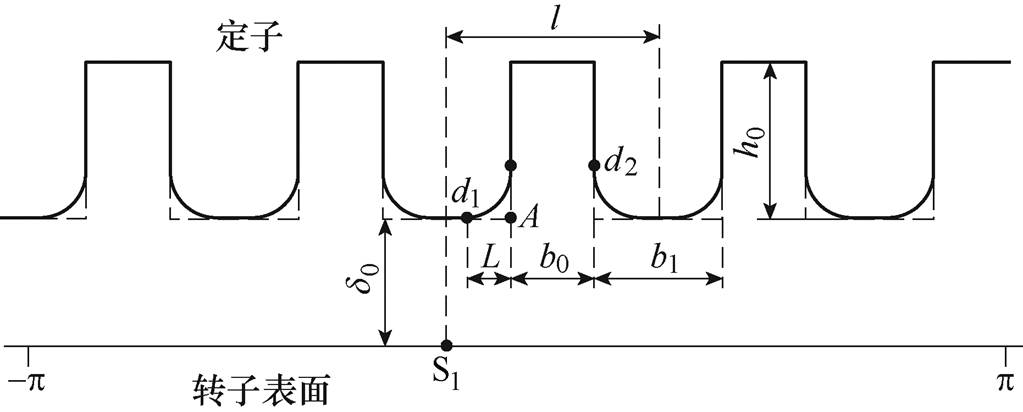
图2 定子齿肩削角后电机气隙宽度分布
Fig.2 Schematic diagram of motor air gap width distribution after stator shoulder chamfering
根据图2,若以图中S1点为参考点,可建立交流牵引电机定子齿肩削角前、后定子齿槽与转子表面间气隙宽度随转子位置变化的函数关系式,并分别以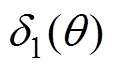 和
和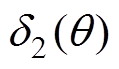 表示。
表示。
削角前,有
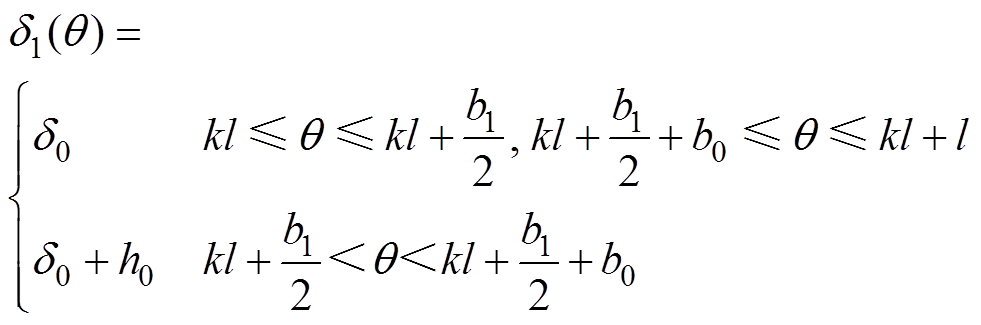 (3)
(3)削角后,有
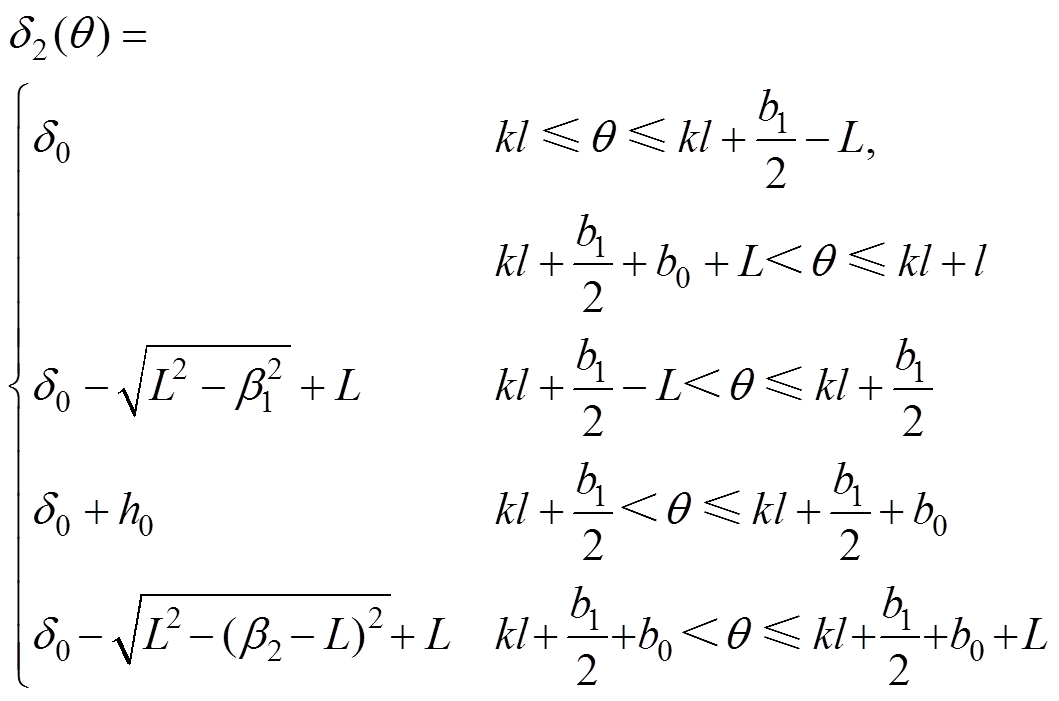 (4)
(4)
其中
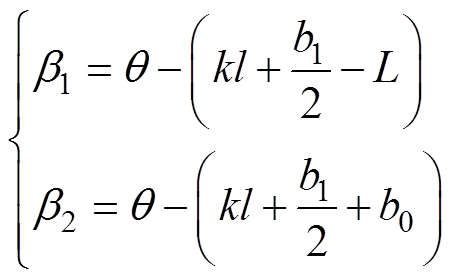 k=0, 1, 2, …
k=0, 1, 2, …式中, 为转子当前位置相对于参考点S1的距离;
为转子当前位置相对于参考点S1的距离;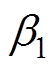 、
、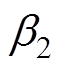 分别为转子当前位置相对于相切点d1、d2的距离。
分别为转子当前位置相对于相切点d1、d2的距离。
根据式(1),电机径向电磁力主要取决于其气隙磁通密度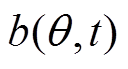 ,而
,而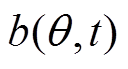 [1]可表示为
[1]可表示为
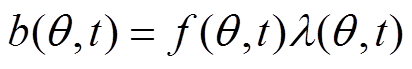 (5)
(5)式中,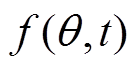 为气隙磁动势;
为气隙磁动势; 为气隙磁导率。
为气隙磁导率。
由式(5)可见,气隙磁通密度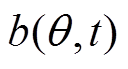 又分别与气隙磁动势和气隙磁导率有关。由于电机进行齿肩削角处理只是改变了其定、转子间的气隙宽度,这对于气隙磁动势的影响较小,可以忽略,但对气隙磁导率的影响较大[17],因此下面将对定子齿肩削角处理后的气隙磁导率展开分析。
又分别与气隙磁动势和气隙磁导率有关。由于电机进行齿肩削角处理只是改变了其定、转子间的气隙宽度,这对于气隙磁动势的影响较小,可以忽略,但对气隙磁导率的影响较大[17],因此下面将对定子齿肩削角处理后的气隙磁导率展开分析。
对定子齿肩进行削角处理改变了齿肩位置的气隙宽度,影响气隙磁导率的空间分布,但不会对时间分布造成影响;根据文献[18-19],交流牵引电机气隙磁导率可表示为
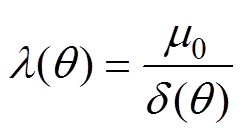 (6)
(6)式中,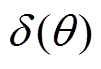 为气隙宽度。
为气隙宽度。
令定子齿肩削角前、后气隙宽度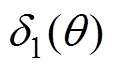 和
和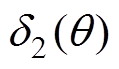 的倒数分别为
的倒数分别为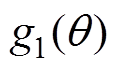 和
和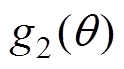 ,则相应的气隙磁导率分别为
,则相应的气隙磁导率分别为
削角前,有
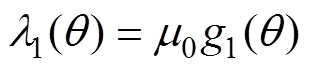 (7)
(7)削角后,有
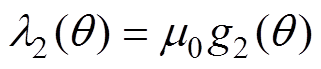 (8)
(8)
根据式(3),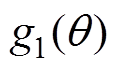 可表示为
可表示为
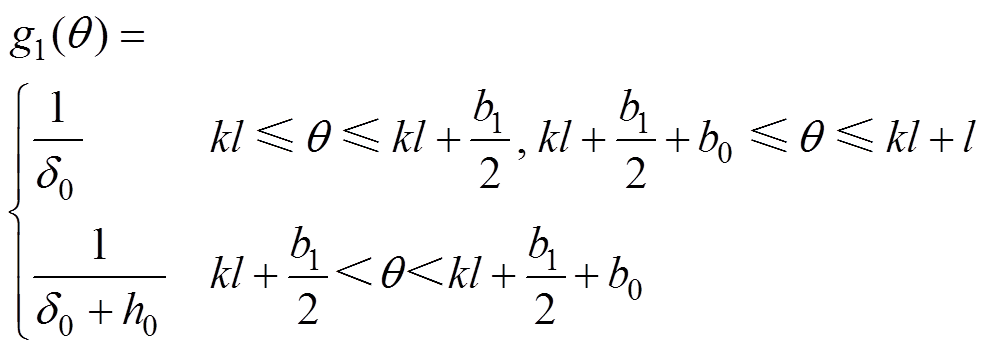 (9)
(9)将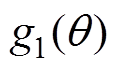 进行傅里叶级数分解[20-24],可得
进行傅里叶级数分解[20-24],可得
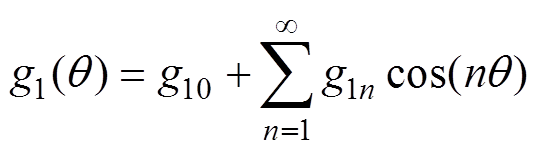 n=1, 2, 3, …(10)
n=1, 2, 3, …(10)
其中
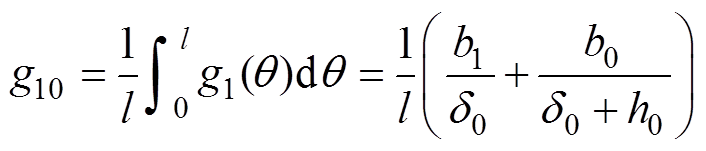 (11)
(11)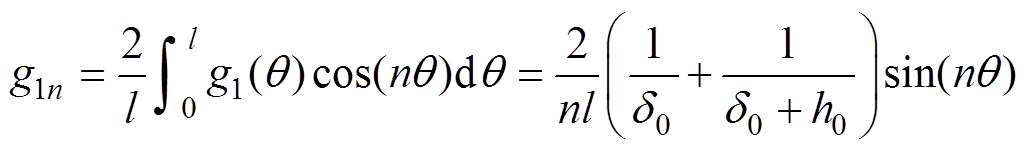 (12)
(12)
式中,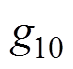 为函数
为函数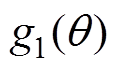 的直流分量;
的直流分量;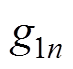 为函数
为函数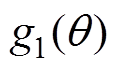 中基波与各次谐波的幅值;n为函数
中基波与各次谐波的幅值;n为函数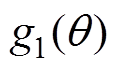 中基波与谐波的次数。
中基波与谐波的次数。
根据式(4),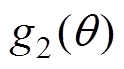 可表示为
可表示为
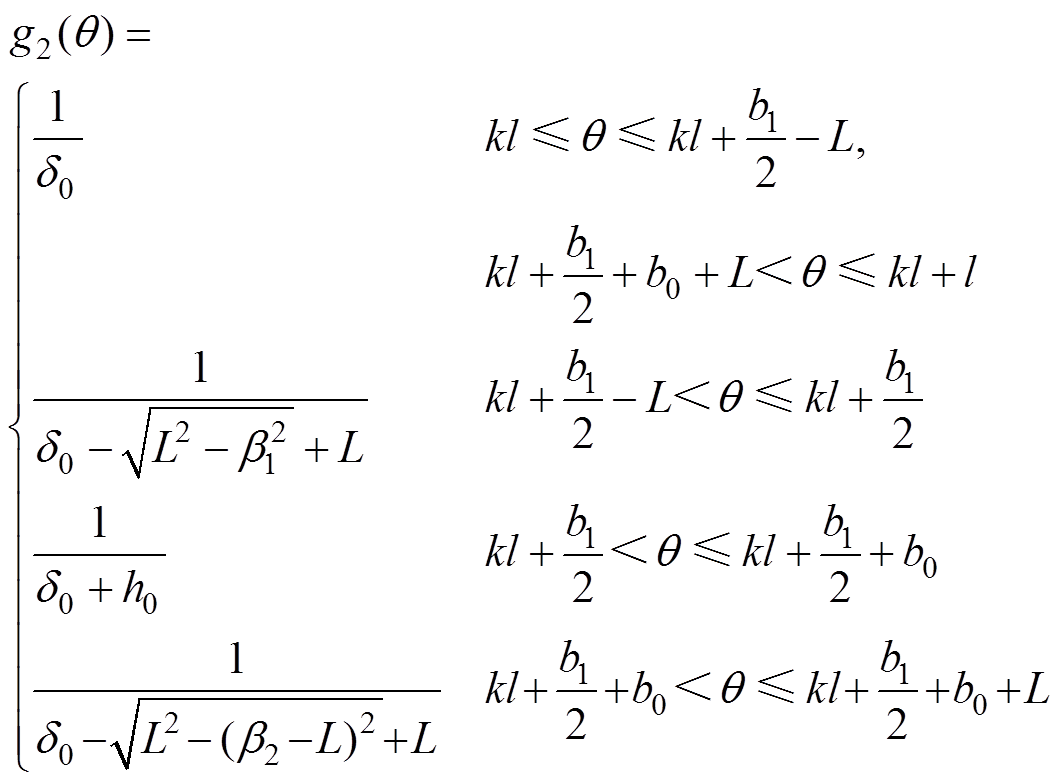 (13)
(13)同样,将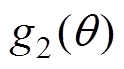 进行傅里叶级数分解[20-24],可得
进行傅里叶级数分解[20-24],可得
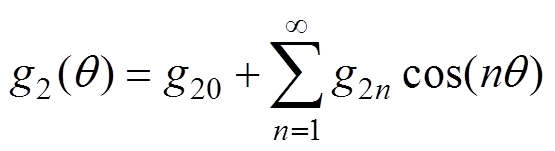 n=1, 2, 3, …(14)
n=1, 2, 3, …(14)
其中

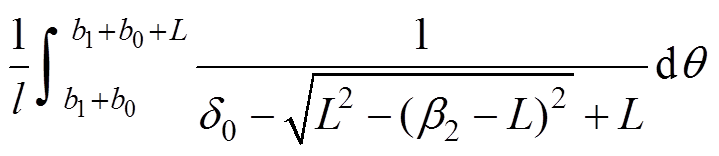 (15)
(15)
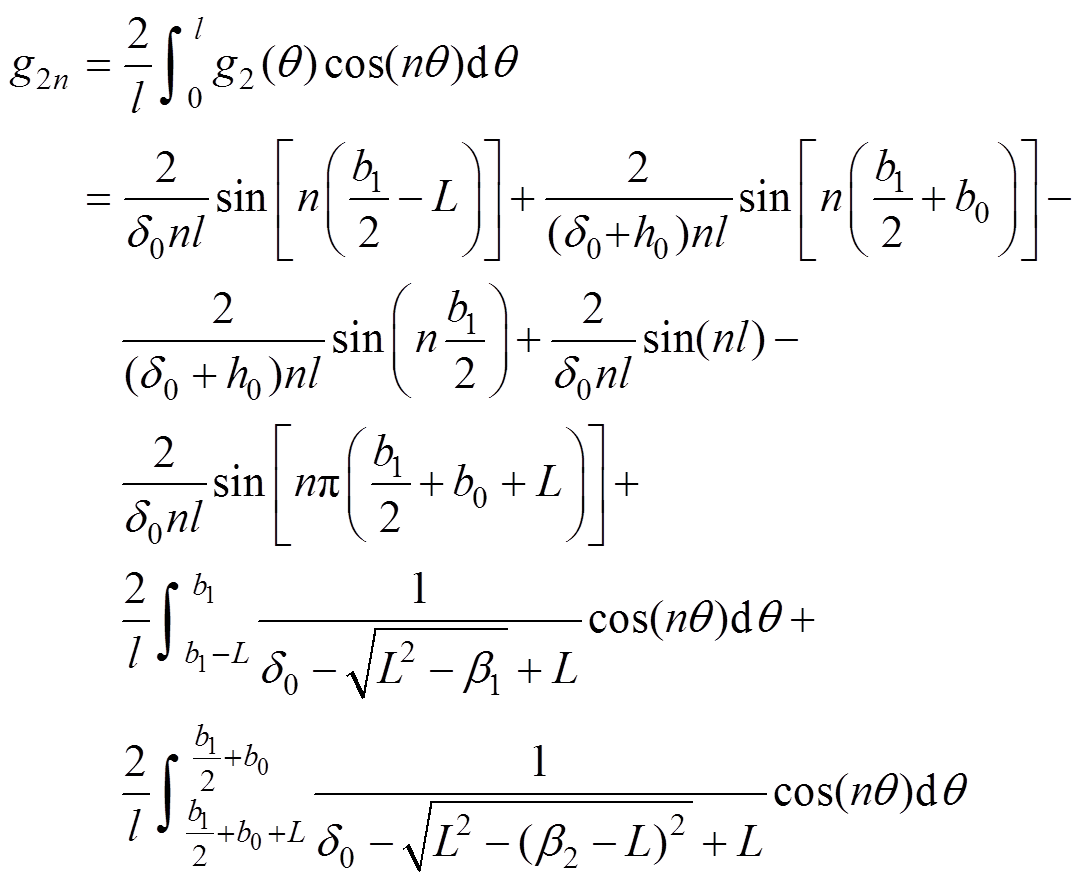 (16)
(16)
式中,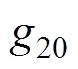 为函数
为函数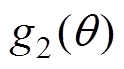 的直流分量;
的直流分量;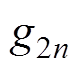 为函数
为函数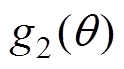 中基波与各次谐波的幅值;n为函数
中基波与各次谐波的幅值;n为函数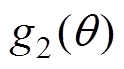 中基波与谐波的次数。
中基波与谐波的次数。
根据式(7)、式(8)、式(12)及式(16)并结合相应的数值计算可知,在针对电机定子齿肩采用内切圆弧式削角处理后,其气隙磁导率低次谐波幅值明显下降,由此可使相应的气隙磁通密度减小,并进而使径向电磁力的低次谐波幅值相应减小,从而达到降低电机电磁噪声的目的。
以某型号交流牵引电机为例,首先对其径向电磁力低阶谐波阶次进行计算,再建立其有限元分析模型,然后在此基础上进行相应的电磁场仿真与电磁噪声分析。
在分析交流牵引电机电磁噪声时,首先需确定引起其电磁噪声的径向电磁力主要低阶谐波阶次。下面以某型号交流牵引电机为例,对其径向电磁力主要低阶谐波阶次进行计算,电机主要参数见表2。
表2 电机主要参数
Tab.2 Main parameters of motor

参 数数 值 额定功率/kW5.5 额定转速/(r/min)2 900 额定电压/V380 频率/Hz50 相数3 极对数1 定子槽数30 转子槽数26 定子外径/mm210 定子内径/mm116 转子外径/mm114.9 铁心长度/mm105
根据文献[8],利用表2所示电机参数及表1所提供的径向电磁力谐波空间阶次计算公式,得到造成电机电磁噪声的径向电磁力主要低阶谐波阶次,见表3。可见,造成电机电磁噪声的主要谐波阶次为2和4,因此如能有效抑制上述两次谐波,则可实现电机降噪的目的。
表3 电机径向电磁力谐波空间阶次
Tab.3 Harmonic space order of radial electromagnetic force of motor

序号空间阶次 1-11-2 211-4
根据表2所示电机参数,建立交流牵引电机有限元模型,如图3所示。同时针对该电机定子齿肩采用内切圆弧式削角处理,并任取其齿肩角顶点与切削点间的距离L=0.6mm,得到交流牵引电机齿肩削角处理前后的定子齿部模型如图4所示。
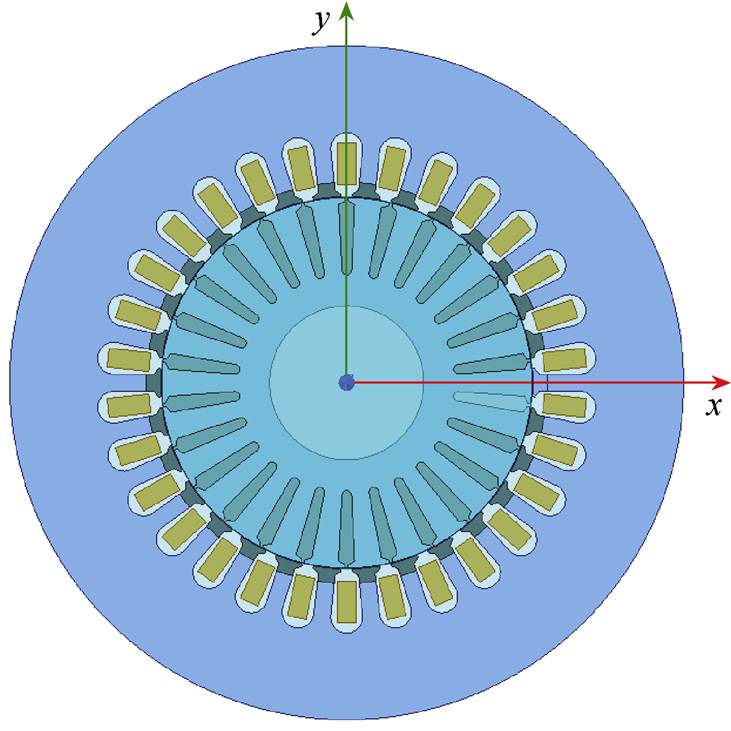
图3 交流牵引电机有限元模型
Fig.3 Finite element model of AC traction motor
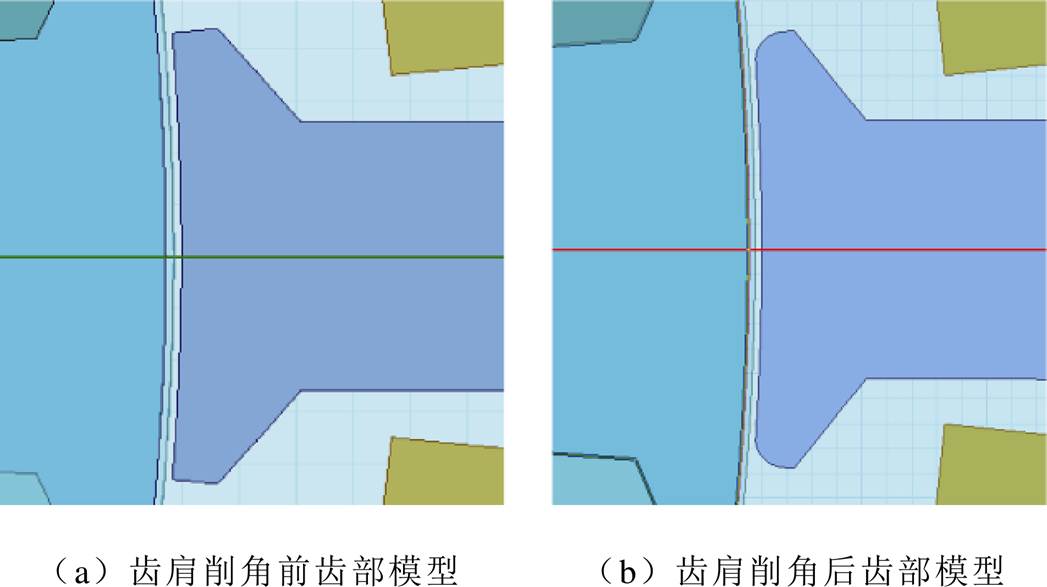
图4 交流牵引电机定子齿部模型
Fig.4 Tooth model of AC traction motor stator
根据上述所得交流牵引电机定子齿肩削角处理前后的有限元模型,采用Maxwell软件分别对其进行电磁场仿真分析[25],得到相应的气隙磁通密度随空间分布频谱图,如图5所示,其气隙磁通密度谐波幅值见表4。可见,在对电机定子齿肩进行削角处理后,其气隙磁通密度低阶谐波幅值均有明显的下降。
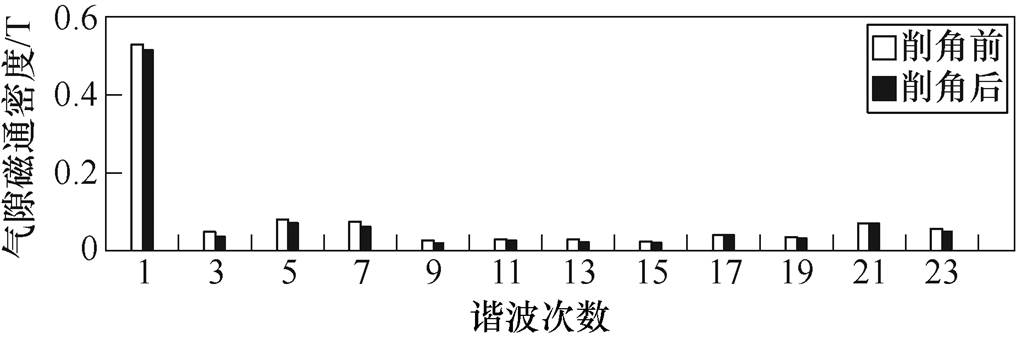
图5 削角处理前后气隙磁通密度频谱图
Fig.5 Spectrum diagram of air gap magnetic flux density before and after chamfering
表4 削角处理前后气隙磁通密度谐波幅值
Tab.4 Harmonic amplitude of air gap magnetic flux density before and after chamfering

阶次气隙磁通密度谐波幅值/T幅值下降率(%) 削角前削角后 30.049 60.038 123.18 50.082 30.073 310.93
再针对上述所得交流牵引电机电磁场仿真结果进行后处理,可得该电机在定子齿肩削角处理前后相应径向电磁力随空间分布的频谱图,如图6所示,其径向电磁力谐波幅值则见表5。可见,在定子齿肩削角处理后,其2次和4次径向电磁力谐波幅值均有显著下降。
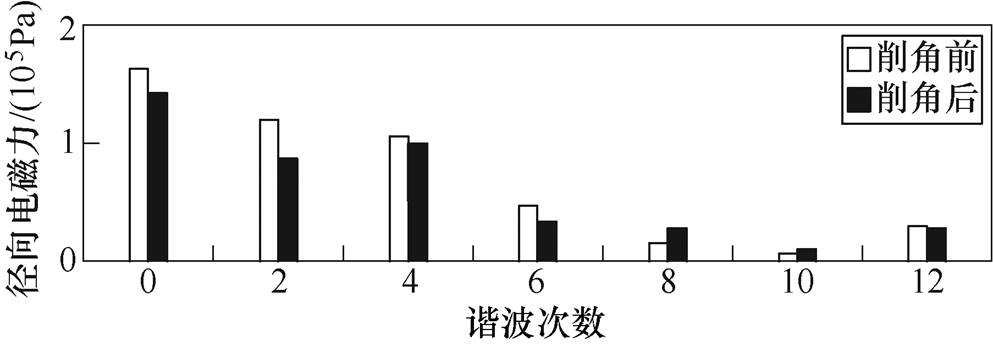
图6 削角处理前后径向电磁力频谱图
Fig.6 Spectrum diagram of radial electromagnetic force before and after chamfering
表5 削角处理前后径向电磁力谐波幅值
Tab.5 Harmonic amplitude of radial electromagnetic force before and after chamfering

阶次径向电磁力谐波幅值/Pa幅值下降率(%) 削角前削角后 2119 34087 20526.92 4105 69099 7385.63
在上述所得电磁场仿真结果的基础上,采用Ansys软件对其作进一步的分析处理,得到交流牵引电机在削角处理前后的平面声场分布云图以及相应的电磁噪声数据,分别如图7所示和见表6。其中,图7中所示两图的最大、最小标识为实际值的最大和最小值。可见,在针对电机定子齿肩采用内切圆弧式削角处理后,其声场强度和电磁噪声均有明显的下降,由此说明该削角处理方法具有良好的降噪效果。
如上所述,电机定子齿肩在采用内切圆弧式削角处理后可明显降低其电磁噪声,但是否会对电机其他性能产生影响?为此,在上述相同削角尺寸下对电机进行相应的有限元分析,得到削角前后主要性能指标对比,见表7。可见,削角处理对电机上述主要性能指标造成的影响很小。
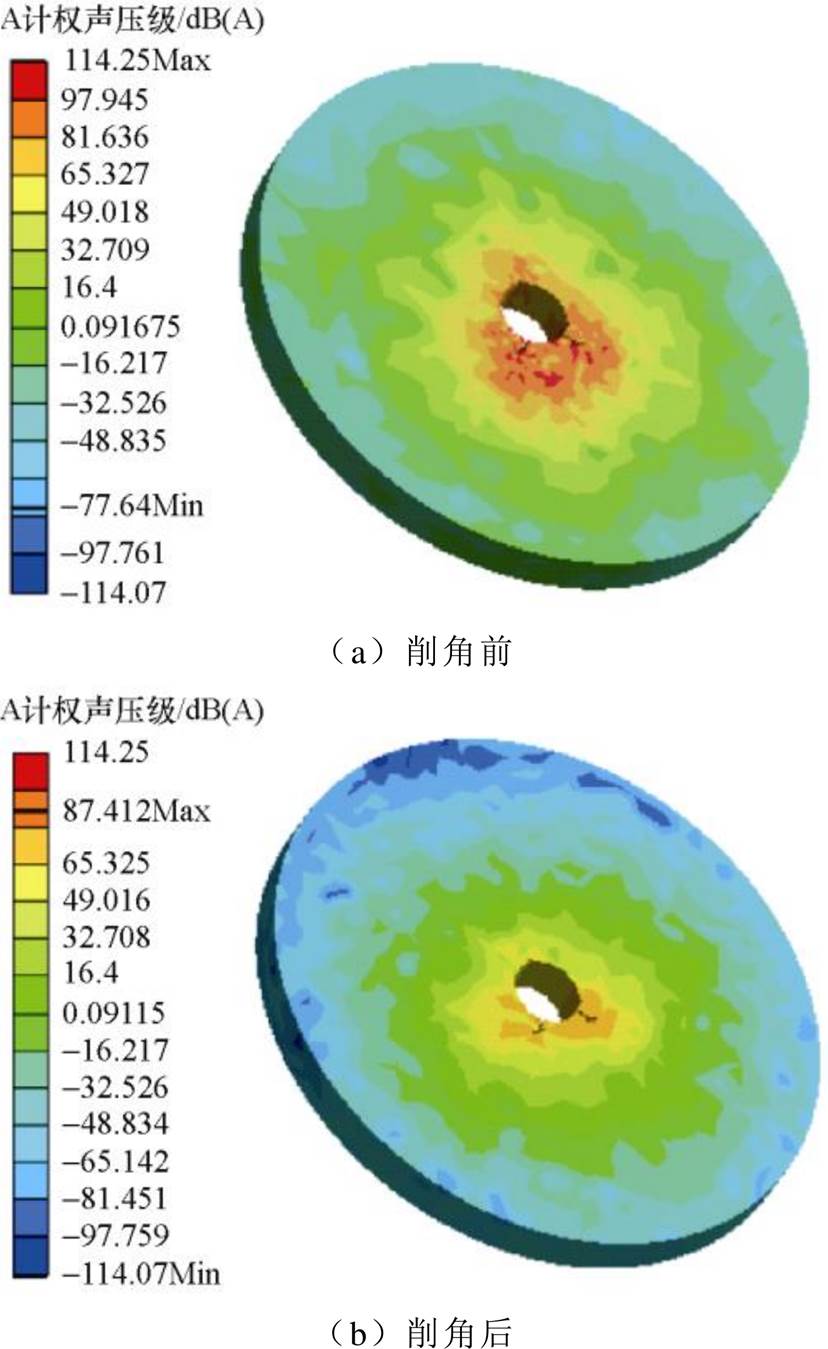
图7 削角处理前后电机平面声场分布云图
Fig.7 Contour map of motor plane sound field distribution before and after corner chamfering
表6 交流牵引电机削角前后的电磁噪声
Tab.6 Electromagnetic noise before and after corner chamfering of AC traction motor

电机状态电磁噪声/dB(A) 削角前67.9 削角后44.6
表7 电机削角处理前后性能指标对比
Tab.7 Comparison of performance indexes before and after motor angle cutting

性能指标削角前削角后 输入功率/W6 317.729 56 339.336 1 输出功率/W5 522.106 25 539.128 0 电磁转矩/(N·m)18.600418.657 8 功率因数0.949 30.945 4 效率(%)87.406 587.377 1
为验证本文提出的定子齿肩内切圆弧式削角降噪法相对于文献[19]中所提出的直线式削角降噪法的效果,将两种方法进行对比分析。
交流牵引电机定子齿肩采用直线式削角示意图如图8所示。与图1所示内切圆弧式削角方式类似,该削角方式也是从定子齿肩角顶点A开始,并沿该齿肩角两侧边按长度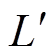 等距离取两点,分别以
等距离取两点,分别以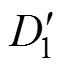 和
和 表示,再过这两点按直线方式削去该齿肩角。
表示,再过这两点按直线方式削去该齿肩角。
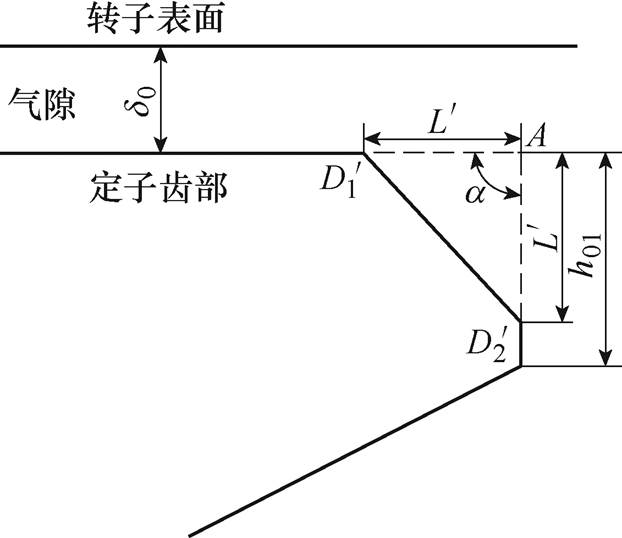
图8 直线式齿肩削角示意图
Fig.8 Schematic diagram of straight shoulder shaving
针对上述两种齿肩削角方式,采用表2所示电机参数并取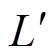 =L进行相应的电磁噪声分析;同时,为说明在不同削角尺寸下的降噪效果,分别取
=L进行相应的电磁噪声分析;同时,为说明在不同削角尺寸下的降噪效果,分别取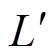 = L=0.2mm、0.4mm、0.6mm及0.8mm进行对比分析,得到相应的电磁噪声分析结果见表8,表9则为两种削角方式相对于未削角前电磁噪声的下降率。
= L=0.2mm、0.4mm、0.6mm及0.8mm进行对比分析,得到相应的电磁噪声分析结果见表8,表9则为两种削角方式相对于未削角前电磁噪声的下降率。
表8 两种削角方式对应的电磁噪声
Tab.8 Corresponding electromagnetic noise values of the two chamfering methods
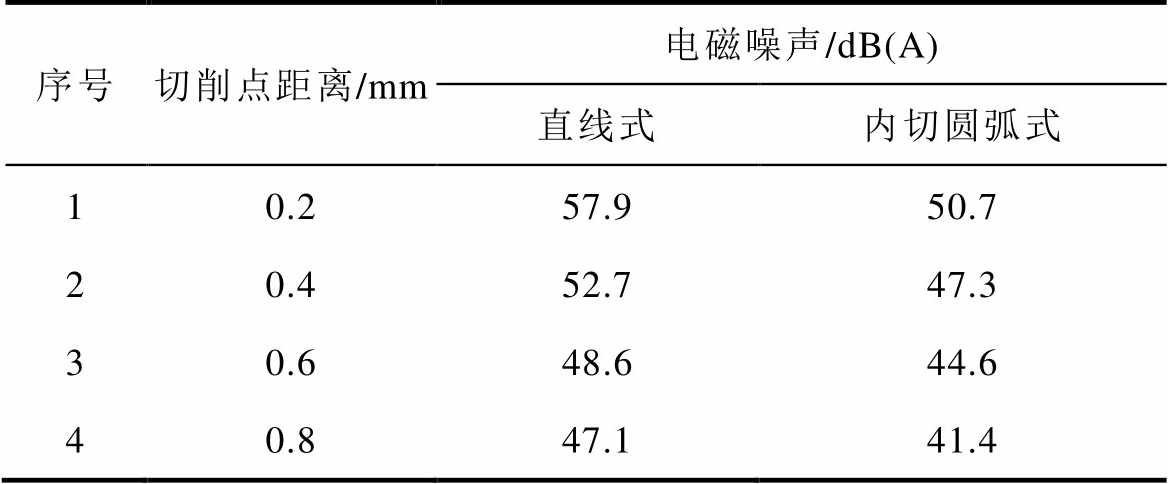
序号切削点距离/mm电磁噪声/dB(A) 直线式内切圆弧式 10.257.950.7 20.452.747.3 30.648.644.6 40.847.141.4
表9 两种削角方式下电磁噪声的下降率
Tab.9 Decrease rate of electromagnetic noise under two types of chamfering

序号切削点距离/mm下降率(%) 直线式内切圆弧式(%) 10.214.7225.33 20.422.3830.33 30.628.4234.31 40.830.6339.02
由表8、表9可见,交流牵引电机定子齿肩采用内切圆弧式削角处理后,其对应的电磁噪声值在不同削角尺寸下相对于直线式削角方式均有明显的下降,从而说明交流牵引电机定子齿肩采用内切圆弧式削角方式的降噪效果明显优于直线式削角方式的降噪效果。
为验证本文提出的交流牵引电机内切圆弧式定子齿肩削角降噪方法的效果,根据表2所示参数构建相应的电机噪声测试平台,如图9所示。该测试平台包括一台5.5kW交流牵引电机、噪声测试仪及计算机等,其中,电机参数与仿真时一致。电机噪声测试分削角处理前和处理后两种情况进行,针对定子齿肩的削角尺寸与仿真时一致,即仍取0.6mm,相应削角处理前后的实物照片如图10所示。

图9 电机噪声测试平台
Fig.9 Platform of noise experimental

图10 削角前后的定子齿部
Fig.10 View of stator teeth before and after chamfering
在噪声测试时,给电机通以380V/50Hz的三相交流电,并让电机空载运行;同时,为减小电机空气动力噪声对测试结果的影响,在测试时将电机的风扇予以拆除;由此得到电机在削角处理前后的实际噪声曲线如图11所示,具体结果见表10。可见,在电机起动至约1s时,电机噪声出现峰值,这是由于电机因采用全压直接起动,较大的起动电流在其定子绕组和转子导条上产生较大的冲击力,并引起较大的振动和噪声;在2s左右电机起动过程结束,之后进入稳定运行状态,此时电机噪声也趋于稳定,且削角后的噪声较削角前下降了8.4dB(A)。
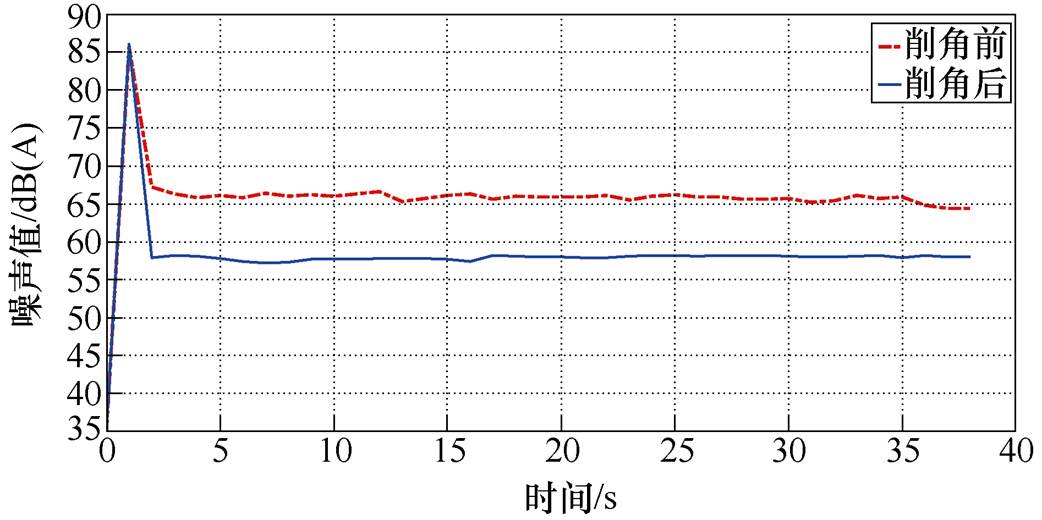
图11 交流牵引电机削角前后的实测噪声曲线
Fig.11 Measured noise curves of AC traction motor before and after corner chamfering
表10 交流牵引电机削角前后的实测噪声数据
Tab.10 Comparison between simulated and measured noise of AC traction motor before and after angle cutting

电机状态实测噪声/dB(A) 削角前66.6 削角后58.2
根据表6和表10,可得电机在削角处理前后的分析噪声相对于实测噪声的相对误差,见表11。可见,在针对电机进行削角处理前,其分析噪声相对于实测噪声的误差小,而在削角处理后误差大,其原因在于:实测噪声是多种噪声的综合噪声,即其不仅包含电磁噪声,而且还包含机械噪声与空气动力噪声等,其中,机械噪声与空气动力噪声基本不受定子齿肩削角的影响,而上述所得分析噪声仅是其电磁噪声这一种噪声,因而造成两者间存在较大的差别。但从实验结果看,内切圆弧式定子齿肩削角降噪的效果仍然相当明显。
表11 电机分析噪声相对于实测噪声的相对误差
Tab.11 The relative error of the motor analysis noise to the measured noise

电机状态分析噪声/dB(A)实测噪声/dB(A)相对误差(%) 削角前67.966.61.96 削角后44.658.223.36
本文针对交流牵引电机存在电磁噪声过大而影响其推广应用的问题,提出一种基于内切圆弧的定子齿肩削角降噪方法。阐述了交流牵引电机电磁噪声产生的根本原因及有关径向电磁力谐波空间阶次的计算方法,建立了电机定子齿肩采用内切圆弧式削角处理前后其定子齿槽与转子表面间气隙宽度随转子位置变化的函数关系式,分析了定子齿肩削角处理对电机电磁噪声与性能的影响,并与直线式齿肩削角法的效果进行了对比分析。最后通过搭建一个交流牵引电机噪声测试平台对其降噪效果进行验证,结果表明,交流牵引电机定子齿肩采用内切圆弧式削角处理后可显著降低电磁噪声,并且具有比直线式削角法更好的降噪效果,因而具有更好的应用价值。
参考文献
[1] 陈永校, 诸自强, 应善成. 电机噪声的分析和控制[M]. 杭州: 浙江大学出版社, 1987.
[2] Kron G. Induction motor slot combinations[J]. Electrical Engineering, 1931, 50(2): 404-412.
[3] 舒波夫. 电机的噪声和振动[M]. 北京: 机械工业出版社, 1980.
[4] Huang S, Aydin M, Lipo T A. Electromagnetic vibration and noise assessment for surface mounted PM machine[C]//IEEE Power Engineering Society Summer Meeting, Vancouver, BC, Canada, 2001: 1417-1426.
[5] Mori D, Takeo I. Force and vibration and analysis of induction motors[J]. IEEE Transactions on Magnetics, 2005, 41(5): 1948-1951.
[6] Le Besnerais J, Lanfranchi V, Hecquet M, et al. Optimal slot numbers of magnetic noise reduction in variable-speed induction motors[J]. IEEE Transa- ctions on Magnetics, 2009, 45(8): 3131-3136.
[7] Le Besnerais J, Lanfranchi V, Hecquet M, et al. Optimal slot opening width for magnetic noise reduction in induction motors[J]. IEEE Transactions on Energy Conversion, 2009, 24(4): 847-869.
[8] Rakib I, Iqbal H. Analtical model of predicting noise and vibration in permanent-magnet synchronous motors[J]. IEEE Transactions on Industry Appli- cations, 2010, 46(6): 2346-2353.
[9] Jin Hur, Jin-Wook Reu, Byeong-Woo Kim, et al. Vibration reduction of IPM-type BLDC motor using negative thrid harmonic elimination method of air- gap flux density[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1300-1309.
[10] Sun-Kwen Lee, Gyu-Hong Kang, Jin Hur. Finite element computation of magnetic vibration sources in 100kW two fractional-slot interior permanent magnet machines for ship[J]. IEEE Transactions on Magnetics, 2012, 48(2): 867-870.
[11] Mohammad S I, Rakib I, Tomy S. Noise and vibra- tion characteristics of permanent-magnet synchronousmotors using electromagnetic and structural anlyses[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3214-3222.
[12] 代颖, 张千帆, 宋立伟. 抑制车用异步电机电磁噪声的槽配合[J]. 中国电机工程学报, 2010, 30(27): 32-35.
Dai Ying, Zhang Qianfan, Song Liwei. Slot coor- dination for suppressing electromagnetic noise of induction motors for vehicles[J]. Proceedings of the CSEE, 2010, 30(27): 32-35.
[13] 李岩, 李双鹏, 周吉威, 等. 基于定子齿削角的近极槽永磁同步电机振动噪声削弱方法[J]. 电工技术学报, 2015, 30(6): 45-52.
Li Yan, Li Shuangpeng, Zhou Jiwei, et al. Vibration and noise reduction method of near-pole slot permanent magnet synchronous motor based on stator tooth chamfering[J]. Transactions of the China Electrotechnical Society, 2015, 30(6): 45-52.
[14] 鲍晓华, 狄冲, 汪朗. 笼型感应电机转子斜槽研究综述及展望[J]. 电工技术学报, 2016, 31(6): 1-12.
Bao Xiaohua, Di Chong, Wang Lang. Summary and prospect of research on rotor skew slot of cage induction motor[J]. Transactions of China Electro- technical Society, 2016, 31(6): 1-12.
[15] 周桂煜. 三相感应电机电磁噪声、电流谐波和附加损耗的分析与控制[D]. 杭州: 浙江大学, 2018.
[16] 吴双龙, 左曙光, 钟鸿敏, 等. 车用爪极发电机转子极爪倒角对电磁振动的影响研究[J]. 电工技术学报, 2018, 33(1): 48-54.
Wu Shuanglong, Zuo Shuguang, Zhong Hongmin, et al. Research on the influence of the chamfering of the rotor pole claw of a claw-pole generator for vehicle on electromagnetic vibration[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 48-54.
[17] 张欣, 李璞, 祝丽花, 等. 电机旋转磁场中磁致伸缩导致的振动频率特性[J]. 电机与控制学报, 2020, 24(2): 87-95.
Zhang Xin, Li Pu, Zhu Lihua, et al. Vibration frequency characteristics caused by magnetostriction in the rotating magnetic field of a motor[J]. Journal of Electric Machines and Control, 2020, 24(2): 87-95.
[18] 庞古才, 邓智泉, 张忠明. 基于改进广义磁路法的表贴式永磁电机空载气隙磁场解析计算[J]. 电工技术学报, 2019, 34(22): 4623-4632.
Pang Gucai, Deng Zhiquan, Zhang Zhongming. Analytical calculation of no-load air gap magnetic field of surface mount permanent magnet motor based on improved generalized magnetic circuit method[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4623-4632.
[19] 鲍晓华, 王春雨. 双斜槽感应电机气隙偏心时的径向电磁力分析[J]. 电机与控制学报, 2019, 23(4): 75-82.
Bao Xiaohua, Wang Chunyu. Radial electromagnetic force analysis of double-skewed induction motor when air gap is eccentric[J]. Journal of Electric Machines and Control, 2019, 23(4): 75-82.
[20] 王晋宁, 王磊, 韩肖清, 等. 基于谐波状态空间建模的变换器交直流谐波耦合特性分析[J]. 电力系统自动化, 2020, 44(4): 159-167.
Wang Jinning, Wang Lei, Han Xiaoqing, et al. Analysis of AC and DC harmonic coupling charac- teristics of converters based on harmonic state space modeling[J]. Automation of Electric Power Systems, 2020, 44(4): 159-167.
[21] 刘治鑫, 王东, 于忠军, 等. 基于磁性槽楔修正模型的感应电动机气隙磁场的分布磁路法[J]. 电工技术学报, 2019, 34(5): 3112-3123.
Liu Zhixin, Wang Dong, Yu Zhongjun, et al. Distributed magnetic circuit method of induction motor air gap magnetic field based on magnetic slot wedge correction model[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 3112-3123.
[22] 王巍. 多极少槽盘式永磁同步电动机电磁噪声的计算与抑制[D]. 沈阳: 沈阳工业大学, 2010.
[23] 杨定伟, 邓兆祥, 张河山, 等. 永磁轮毂电机磁场解析建模[J]. 电工技术学报, 2019, 34(7): 1423- 1433.
Yang Dingwei, Deng Zhaoxiang, Zhang Heshan, et al. Analytical modeling of permanent magnet hub motor magnetic field[J]. Transactions of China Electro- technical Society, 2019, 34(7): 1423-1433.
[24] 胡胜龙, 左曙光, 刘明田. 开关磁阻电机非线性径向电磁力解析建模[J]. 电工技术学报, 2020, 35(6): 1189-1197.
Hu Shenglong, Zuo Shuguang, Liu Mingtian. Analytical modeling of switched reluctance motor nonlinear radial electromagnetic force[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1189-1197.
[25] 夏晨阳, 马念, 陈锐, 等. 基波-谐波双通路并行感应耦合电能传输系统的电磁耦合机构[J]. 电力系统自动化, 2018, 42(17): 127-133.
Xia Chenyang, Ma Nian, Chen Rui, et al. Electro- magnetic coupling mechanism of fundamental wave- harmonic dual-path parallel inductive coupling power transmission system[J]. Automation of Electric Power Systems, 2018, 42(17): 127-133.
Method for Reducing Shoulder Noise of AC Traction Motor Based on Inscribed Arc
Abstract The electromagnetic noise of AC traction motor is too large, which affects its popularization and application. Therefore, this paper proposes a noise reduction method for the shoulder angle of AC traction motor based on inscribed arc. The fundamental reasons for the electromagnetic noise of AC traction motors and the calculation method of the spatial order of the radial electromagnetic force harmonics are described. The stator teeth of the motor stator are internally arc-cut, and the air gap between the stator teeth and the rotor surface is established. The functional relationship between the gap width and the rotor position is analyzed. The influence of the stator shoulder angle treatment on the electromagnetic noise of the motor is analyzed. The effect is simulated and verified. At the same time, the effect of the linear shoulder angle method is analyzed and compared. The results show that the stator tooth shoulder of the AC traction motor can significantly reduce its electromagnetic noise after inward arc cutting, and it has a better noise reduction effect than the linear angle cutting method. Finally, a 5.5kW AC traction motor was chamfered with an inscribed circular arc stator shoulder, and a noise reduction effect of 8.4dB(A) was obtained. It is shown that this method has good application value.
keywords:AC traction motor, tooth shoulder shaving method, inscribed arc, finite element method
中图分类号:TM34
DOI: 10.19595/j.cnki.1000-6753.tces.200269
长株潭国家自主创新示范区专项资助项目(2017XK2303)。
收稿日期2020-03-16
改稿日期 2020-07-19
刘东浩 男,1996年生,硕士研究生,研究方向为电力电子与电力传动。E-mail: cblcsc0731@163.com
张小平 男,1966年生,博士,教授,硕士生导师,研究方向为电力电子与电力传动、智能控制等。E-mail: zxp836@163.com(通信作者)
(编辑 崔文静)