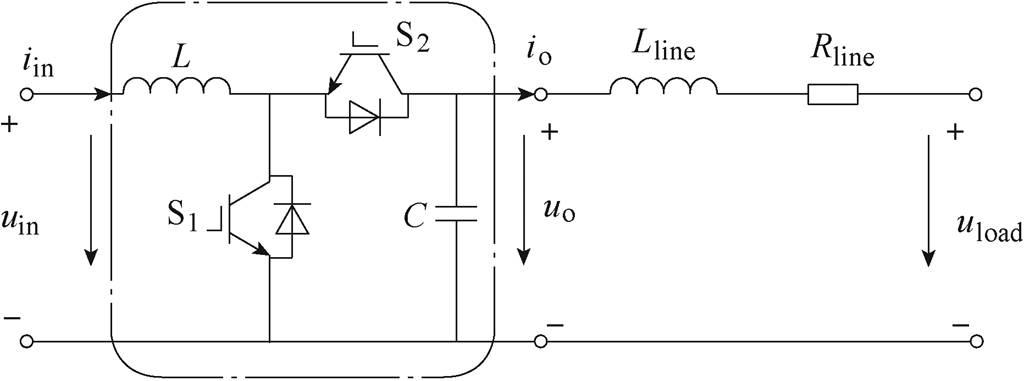
图1 直流电压源变换器示意图
Fig.1 DC-DC voltage source converterdiagram
摘要 直流微电网中传统P-U下垂控制由于只具备下垂特性、缺乏惯性，无法抑制直流母线电压波动，当网内功率突变时，直流母线电压瞬态特性较差，平稳性低。为抑制直流母线电压波动，提升直流母线电压动态稳定性，提出一种基于P-U下垂特性的虚拟直流电机（VDCM）控制策略。通过模拟直流电机机械惯性，将直流电机机电暂态响应过程与下垂控制特性进行等效，设计直流电压源变换器（VSC）P-U下垂控制环路，使直流变换器具备直流电机大惯性、高阻尼输出特性，有效地提升了母线电压动态稳定性，抑制直流母线电压波动。该文建立虚拟直流电机控制策略小信号模型，分析控制策略动作具体机理及系统稳定性，并与传统P-U下垂控制进行对比，通过仿真及实验验证了该策略的有效性。
关键词：直流微电网 P-U下垂特性 机械惯性 虚拟直流电机控制
随着越来越多的新能源通过电力电子装置接入电力系统，现代电力系统逐步从同步电机主导的大惯性、高阻尼强电网转向为以电力电子变换器主导的柔性弱电网[1-4]。光伏、风电等可再生能源的并网接口变换器相较于传统蒸汽轮机，“刚性”有余而惯性不足[5-6]。虽然电力电子变换器的引入使得供电系统能量流动可控，系统响应速度与效率得到提升，可以在多时间尺度下对供电系统能量流动进行管理，但其缺乏同步电机等旋转器件所具备的大惯性、高阻尼特性，进而造成大规模新能源接入电网后，电力系统整体的惯性降低，失稳风险上升[7-8]。
虚拟惯性控制策略的提出，确保了在电力电子装置大规模接入电网时，电网仍能具备足够惯性抑制网内频率及电压波动，传统虚拟惯性控制在控制环中引入微分调节环节，带来高频噪声干扰问题[9]。因此有学者提出通过对变换器控制环路进行适当调节，使得变换器输出特性表现出旋转器件大惯性、高阻尼的特点[10-12]。首先运用在以光伏、风电等可再生能源组成的交流电网并网接口上，通过模拟同步发电机运行特性使之具备同步发电机类似的旋转惯性、阻尼特性及下垂特性，称为虚拟同步发电机（Virtual Synchronous Generator, VSG）[13-18]控制策略。
交流系统引入虚拟同步发电机控制策略避免了电压源变换器（Voltage Source Converter, VSC）连接到电网带来的电网惯性减小、系统稳定性降低的问题。而在直流系统包括直流微电网内部及直流微电网群子网之间，为保持网内或网间功率波动的惯性响应，提升母线电压动态稳定性，提出模拟直流电机输出特性的虚拟直流电机（Virtual DC Motor, VDCM）控制策略，直流VSC通过模拟直流电机机械惯性响应过程，提升直流微电网对网内及网间功率波动的惯性响应能力[19]。
文献[20]提出一种基于双向直流VSC拓扑的VDCM控制策略，将VSC拓扑的输入侧蓄能电路与直流电机电枢电路进行完全等效，并在其控制中加入直流电机转子运动方程，求解直流VSC控制占空比，模拟直流电机大惯性、高阻尼输出特性，增强了直流母线电压对功率波动的惯性响应能力。但其仅针对特定的双向VSC电路拓扑进行了研究，控制策略通用性不强，且对拓扑内部参数变化鲁棒性较差。
文献[21-23]将传统下垂控制的下垂特性方程与直流电机电枢方程进行等效，而直流电机转子运动方程则作为虚拟机械转动环节嵌入到直流变换器PI双环控制中，模拟直流电机转速惯性响应过程，抑制母线电压波动，提升母线电压惯性。该控制策略有效地提升了直流母线电压惯性，增强直流微电网稳定性，但其策略在提升母线电压惯性的同时，抑制了电压环的调节，且控制需假设变换器工作在理想状态。
针对传统VDCM控制存在的上述缺陷，本文基于P-U下垂特性提出一种通用VDCM控制模型，降低VDCM控制对直流变换器拓扑参数的依赖，且在不影响电压环调节的基础上，模拟直流电机大惯性、高阻尼输出特性，实现直流变换器虚拟惯性控制。建立VDCM控制策略的小信号模型，分析控制策略具体机理，搭建光储微电网仿真及实验平台，与传统P-U下垂控制进行对比仿真实验，从而验证该策略的有效性。
直流VSC拓扑示意图如图1所示，图中将直流VSC看做一个二端口网络，端口输入侧电压为分布式微源电压uin，输入电流为iin，输出侧为变换器输出电压uo，输出电流为io，负载电压为uload；同时端口输出侧考虑到线路阻抗影响，存在线路电阻Rline与线路电感Lline。
图1 直流电压源变换器示意图
Fig.1 DC-DC voltage source converterdiagram
由图1可得，直流VSC输出电压uo与负载电压uload关系为
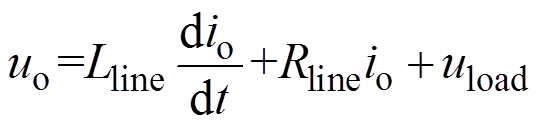（1）由式（1）可得，负载电压由线路阻抗与变换器输出电压uo决定。
图2所示为直流电机等效示意图，由图2可得，直流电机电枢电压方程为
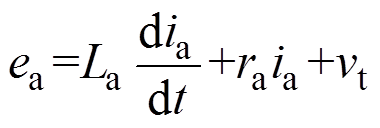（2）式中，ra、ia分别为电枢电阻与电枢电流；La为电枢绕组电感；vt为电枢电压；ea为直流电机感应电动势。图2中，vf、if分别为励磁电压与励磁电流；rf、Lf分别为励磁电阻与励磁电感；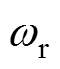
为电机转动角速度；J为电机转动惯量。
图2 直流电机工作原理示意图
Fig.2 DC motor working principle diagram
由式（2）电枢电压方程可得，电枢电压vt取决于直流电机感应电动势ea与电枢绕组阻抗。
对比式（1）与式（2）可知，直流VSC输出电路可完全等效为直流电机电枢，线路阻抗对应直流电机电枢绕组，直流VSC输出电压uo对应直流电机感应电动势ea，从而实现直流VSC输出电路与直流电机电磁环节的等效过程，且等效模型不受VSC内部拓扑结构变化的影响。
根据直流电机电磁感应原理，可得感应电动势ea与直流电机转动角速度w存在关系为
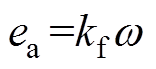（3）式中，kf为直流电机励磁常数。
由式（3）可得，直流电机感应电动势ea与直流电机转动角速度w 呈线性比例关系。
直流电机在功率波动时转子能够瞬时释能抑制转速变化，实现转速对功率波动的惯性响应，而直流VSC由于缺乏机械转动部件，因此其输出无法具备与直流电机相同的且对功率扰动的惯性响应能力。因此为模拟直流电机大惯性、高阻尼输出特性，在直流VSC控制中需嵌入直流电机机械转动方程，来提升直流母线电压对功率波动的惯性响应能力。
图3为传统直流VSC所采取的P-U下垂控制控制框图，变换器下垂特性方程为
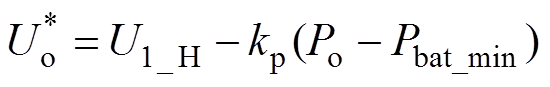（4）式中，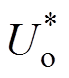
、U1_H分别为直流VSC给定电压与最大输出电压；Po、Pbat_min分别为直流VSC输出功率和最小吸收功率；kp为下垂控制中的下垂系数，其表达式为
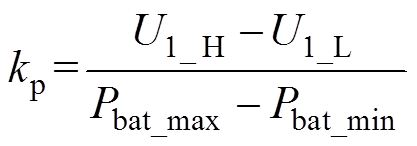（5）式中，U1_L为直流VSC最小输出电压；Pbat_max为直流VSC最大输出功率。
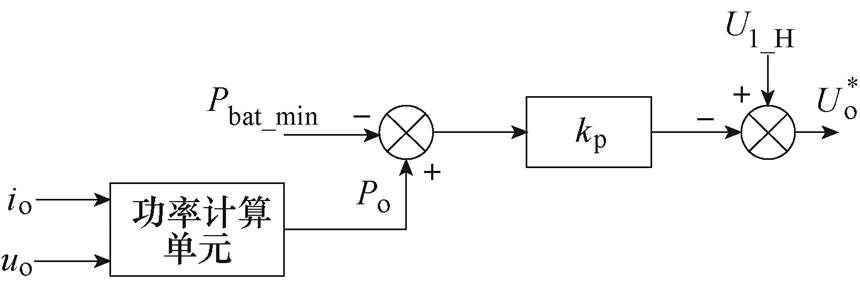
图3 直流电压源变换器P-U下垂控制框图
Fig.3 DC VSC P-U droop control block diagram
由式（4）与式（5）可得，传统直流VSC采用的P-U下垂特性示意图如图4所示。图4中，Unom为直流VSC空载电压。
图4 P-U下垂特性示意图
Fig.4 P-U drooping characteristics diagram
变换器输出功率根据图4中下垂曲线进行分配，实现对变换器输出功率的有效调节。
在图2直流电机工作原理示意图中，机械转动环节转速与功率波动存在直流电机转子运动方程为
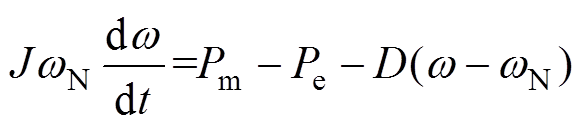（6）式中，Pm、Pe分别为直流电机输入机械功率与输出电磁功率；J为转子惯性常数；wN为直流电机的额定角速度；w 为转子运动角速度；D为阻尼系数。
直流电机产生功率波动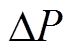
时，直流电机转子机械势能通过瞬时释能，保持转速平稳过渡，使直流电机转速对功率波动具备较强的惯性响应能力。为提升直流母线电压对功率波动的惯性响应能力，在直流VSC中加入虚拟机械转动环节，如图5所示。
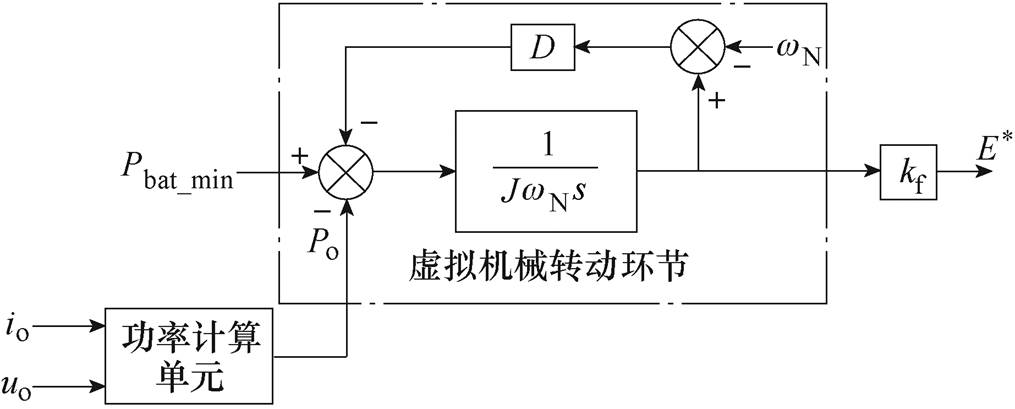
图5 VDCM控制框图
Fig.5 VDCM control block diagram
图5中，将直流VSC输出功率Po等效为虚拟机械转动环节输出电磁功率Pe，最小吸收功率Pbat_min等效为虚拟机械转动环节输入机械功率Pm。从而将直流电机转子运动方程代入到图3所示P-U下垂控制框图中，得到图5所示VDCM控制框图。虚拟转动环节输出为虚拟转子角速度，此时根据式（3）电磁感应方程得到感应电动势ea，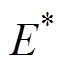
作为直流VSC给定电压，可等效为图3中给定电压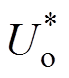。同时由式（3）可得额定转子角速度wN为
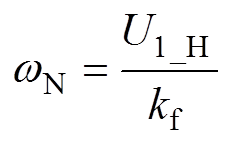（7）即虚拟机械转动环节额定转子角速度wN与下垂控制中直流VSC输出最大电压U1_H之间存在紧密联系，满足直流电机电磁感应特性。
由式（4）与式（6）可得，图5中阻尼系数D与下垂系数kp存在如下关系
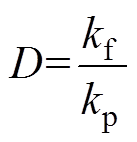（8）阻尼系数由下垂控制参数直接推导而得，整定简便。
通过在传统P-U下垂控制中引入直流电机转子运动方程，在其控制中虚拟出转子机械转动环节，并将下垂控制中直流VSC输出参量与直流电机机械参量进行等效，从而结合硬件拓扑等效，实现了直流VSC对直流电机的深层次模拟，使得直流VSC具备直流电机大惯性、高阻尼的输出特性。能够对直流系统网内功率波动进行惯性响应，从而达到提升直流母线电压惯性、增强直流子网内负载供电可靠性的目的。
以双向直流VSC电路拓扑作为控制对象，如图1中直流VSC电路所示，其数学模型为
（9）式中，RL为电感内阻；D1为开关管S1稳态占空比。
对式（9）进行小信号扰动，得其小信号模型为
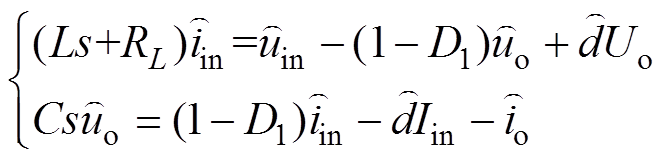（10）式中，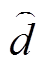
为直流VSC中S1占空比的扰动量；Iin、Uo分别为直流VSC稳态输入电流与输出电压。
依据式（10）推导出输入电流扰动量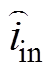
对输入侧电压扰动量
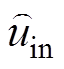的传递函数为
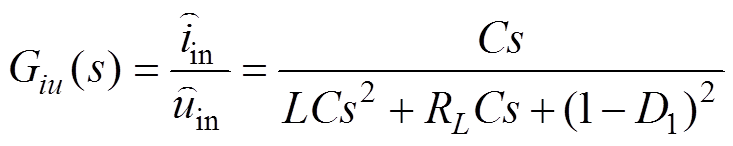（11）同理可得，输入侧电流扰动量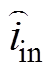对占空比扰动量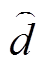与输出电流扰动量
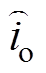的传递函数分别为
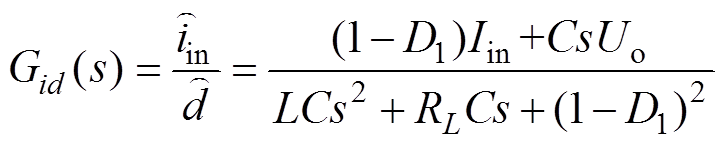（12）
（13）则输出电压扰动量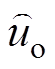
对输入电压扰动量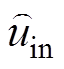与占空比波动量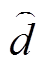的传递函数分别为
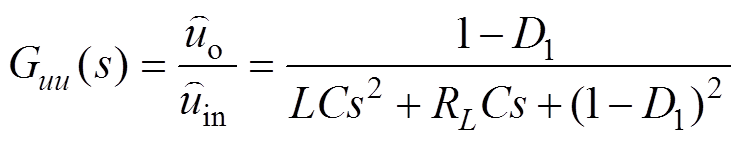（14）
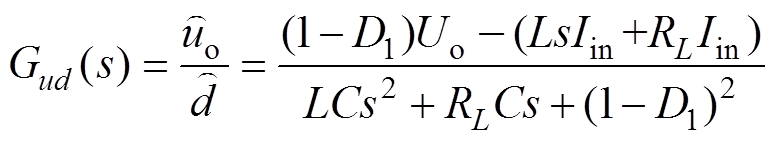（15）直流VSC输出阻抗为
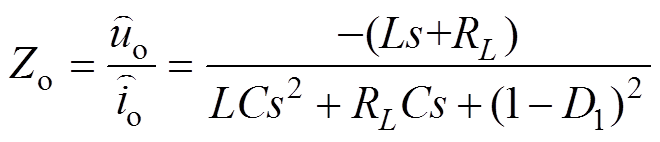（16）
由式（11）～式（16）可得直流VSC小信号模型，结合式（6）可得VDCM控制系统整体小信号模型如图6所示。
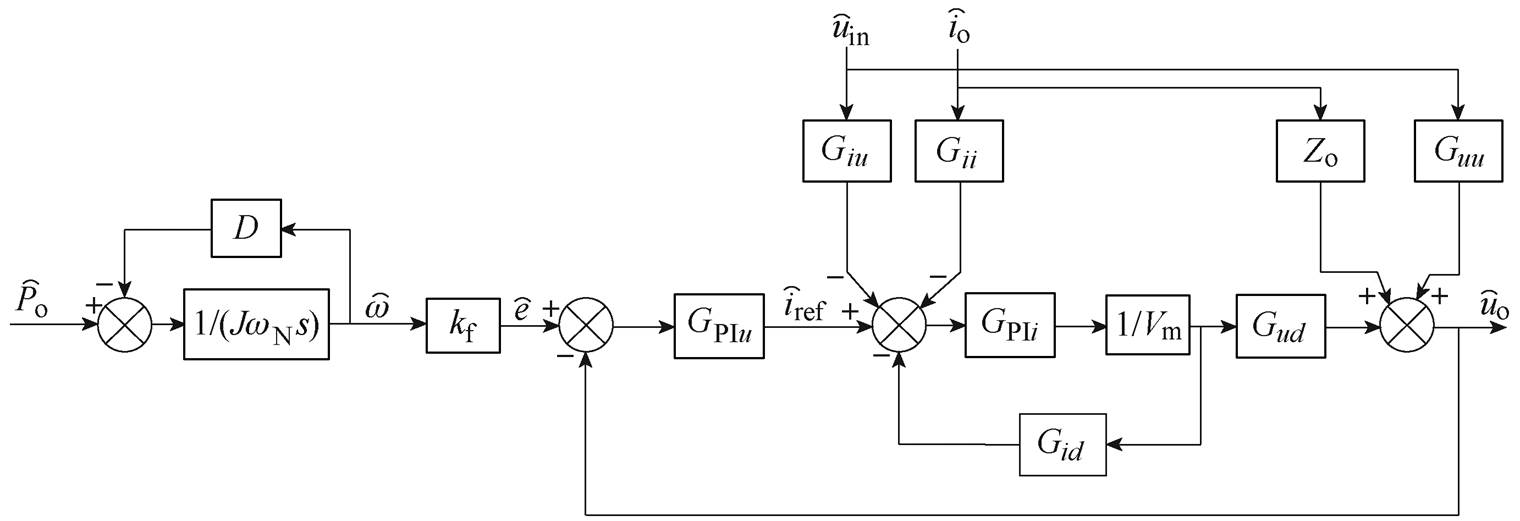
图6 VDCM控制系统小信号模型
Fig.6 Small signal model of VDCM control system
图6中，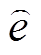
、
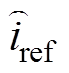分别为给定电压波动量与给定电流波动量，Vm为载波幅值。
直流VSC输出电压扰动量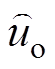对功率扰动量
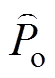的闭环传递函数为
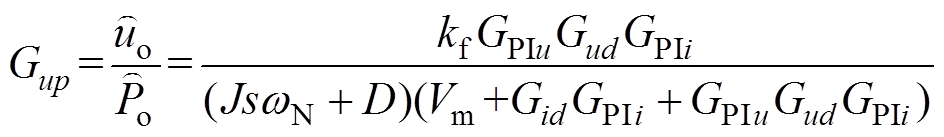（17）式中，GPIu、GPIi分别为电压、电流控制器函数。
式（17）反映了直流VSC输出电压对网内功率波动的响应特性。
图7为直流VSC采用VDCM控制下的闭环Nyquist曲线。图7中，当转动惯量J由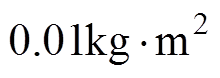
逐渐增大至
时，Nyquist曲线未包含点（-1, 0），VDCM控制系统处于稳定工作状态。且曲线包围点（0, 0）范围随转动惯量J的增加逐渐缩小，曲线远离点（-1, 0），表明直流VSC输出电压对功率波动的响应速度减缓，即当网内功率波动时，VSC输出电压变化更为平缓，增强了直流母线电压的惯性，提升了负载供电的可靠性。
图7 VDCM控制下转动惯量J变化Nyquist曲线
Fig.7 Nyquist curves of moment of inertia J change under VDCM control
同理，将式（4）下垂特性方程代入到直流VSC小信号模型中可得，传统P-U下垂控制下，直流VSC输出电压扰动量对功率扰动量的闭环传递函数为
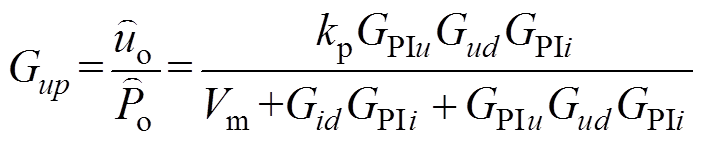（18）图8为下垂控制策略下闭环Nyquist曲线，可以看出，下垂控制Nyquist曲线未包含点（-1, 0），直流VSC处于稳定工作状态，但其曲线包含点（0, 0）范围比VDCM控制下曲线包含范围更宽，曲线更靠近点（-1, 0）。因此，母线电压对功率波动的响应更敏感，即当网内功率出现较小波动时，直流VSC输出电压产生较大的电压波动。
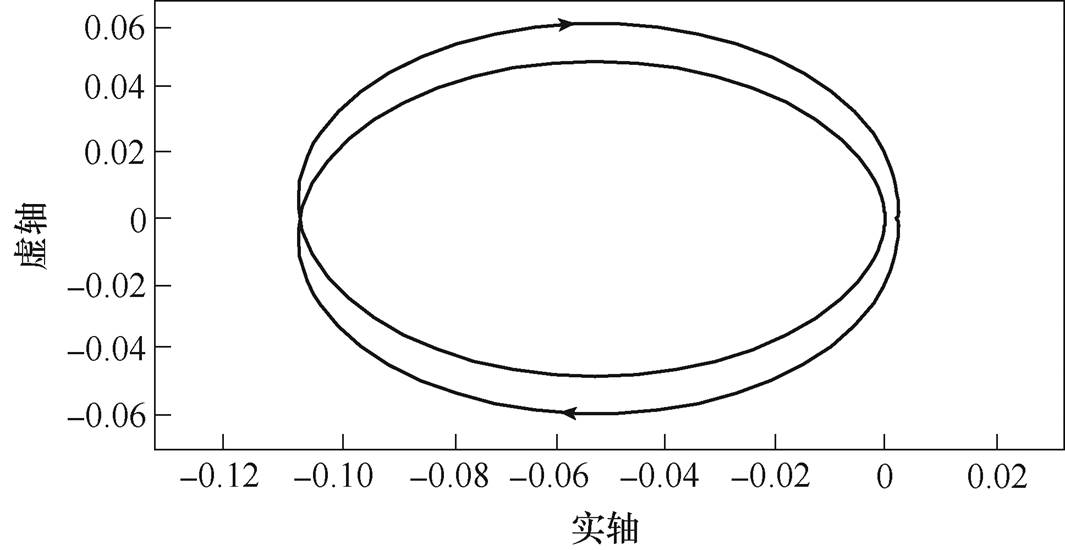
图8 下垂控制下Nyquist曲线
Fig.8 Nyquist curves of droop control
下垂控制功率阶跃变化时电压响应波形如图9所示。下垂控制策略下当输入功率出现阶跃变化时，直流VSC输出电压出现较大电压过冲，并经过4ms振荡后才能达到稳态值。
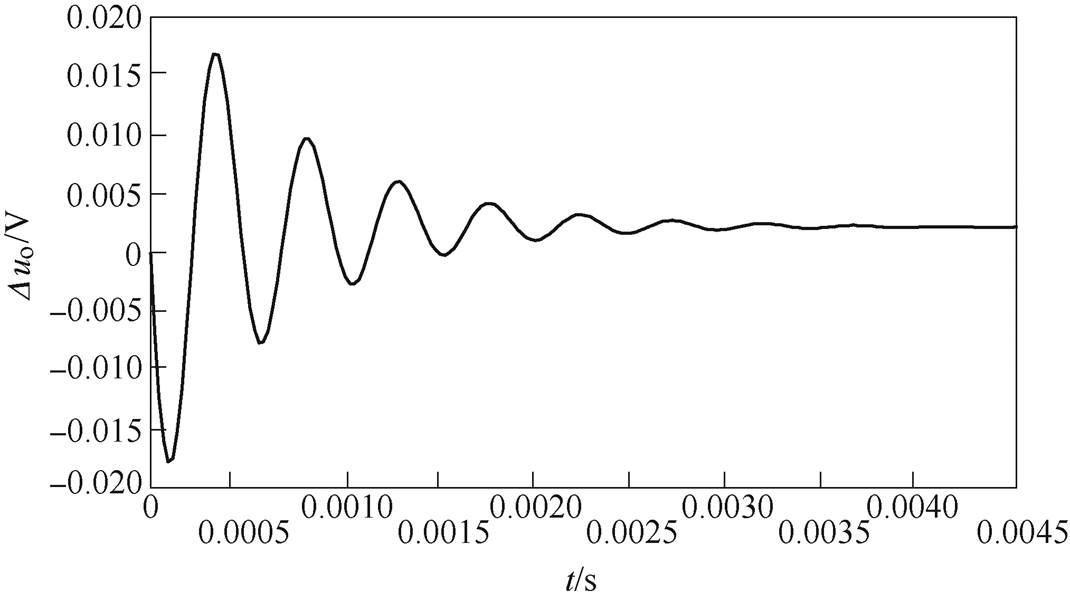
图9 下垂控制功率阶跃变化时电压响应波形
Fig.9 Voltage response waveforms under power step change in droop control
VDCM控制功率阶跃变化时电压响应波形如图10所示。相对应图10采用VDCM控制，输入功率出现阶跃变化时，直流VSC输出电压响应波形变化更为平缓，且无电压过冲，能够平滑达到稳态值。此外随转动惯量J的增加，电压变化更为平缓，直流VSC输出电压对功率波动的惯性响应能力增强，提升了母线电压的动态稳定性。
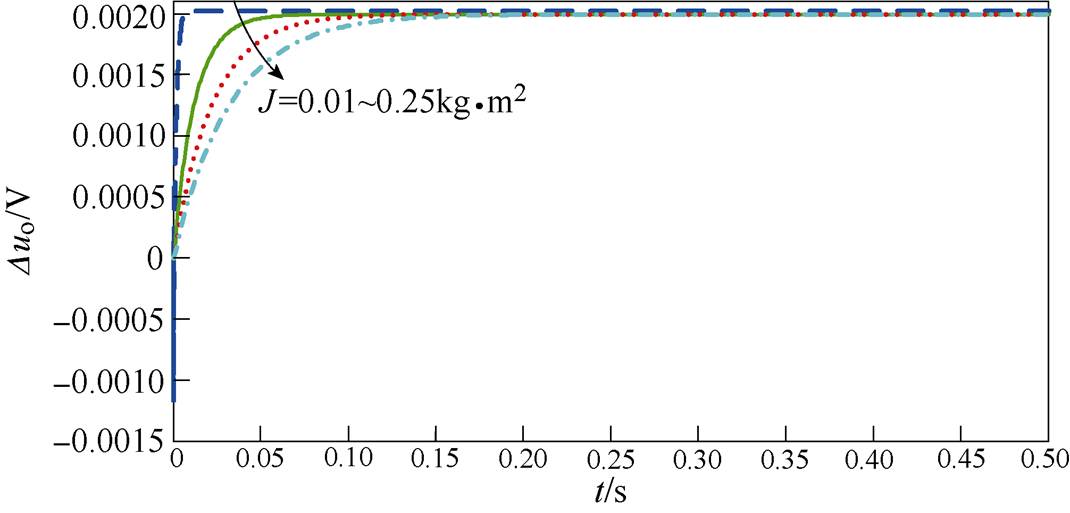
图10 VDCM控制功率阶跃变化时电压响应波形
Fig.10 Voltage response waveforms under power step change in VDCM control
图11为VDCM控制下阻尼系数D变化的Nyquist曲线。由图中可以看出，Nyquist曲线包围（0, 0）范围无明显变化，曲线与点（-1, 0）距离保持恒定，阻尼系数D对直流VSC动态响应过程无影响。因此，在如图12所示的功率阶跃变化下电压响应波形中，随着阻尼系数D变化，直流VSC动态响应过程无明显变化，仅对直流VSC输出电压稳态取值存在影响，符合式（8）所述阻尼系数D与下垂系数kp的比例关系。
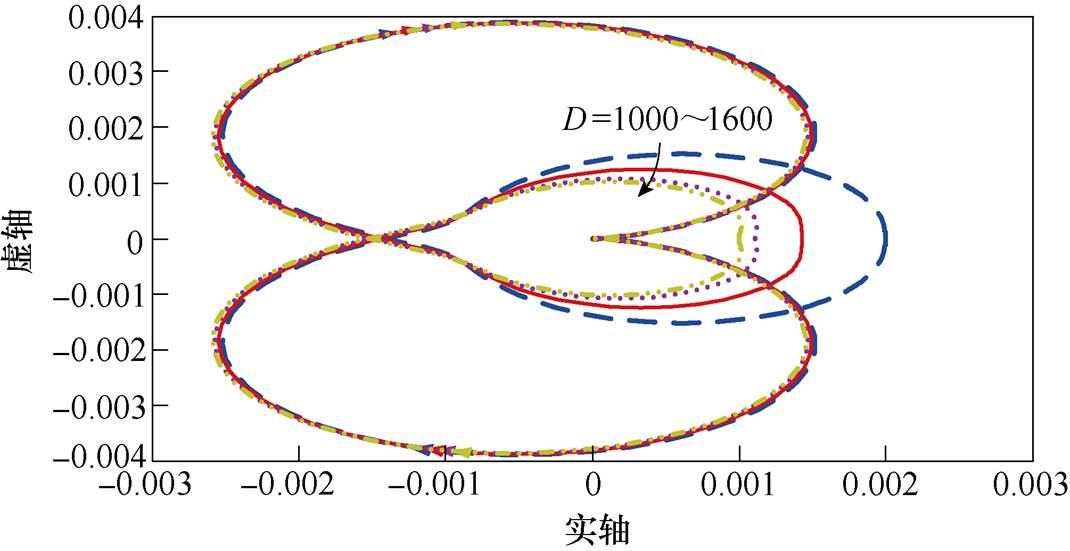
图11 VDCM控制下阻尼系数D变化Nyquist曲线
Fig.11 Nyquist curves of damping coefficient D change under VDCM control
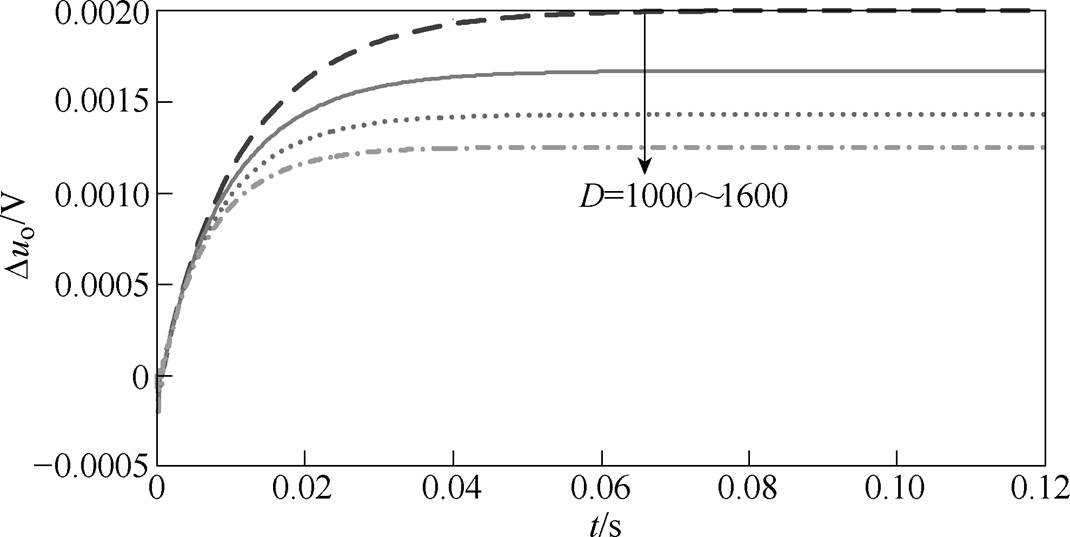
图12 VDCM控制功率阶跃变化时电压响应波形
Fig.12 Voltage response waveforms under power step change in VDCM control
为验证所提VDCM策略的有效性，搭建光储直流微电网仿真平台。光伏发电单元采用最大功率点跟踪（Maximum Power Point Tracking, MPPT）控制，储能装置变换器采用VDCM控制，其额定功率为5kW，仿真参数见表1。根据表1仿真参数在Matalab/ Simulink中进行仿真验证，得到如图13所示VDCM控制与传统P-U下垂控制对比仿真波形。
由图13可以看出，当网内功率突变时，采用传统P-U下垂控制仅具有下垂特性，对变换器输出功率进行调节，不具备电压惯性。如图13中0.5s所示，当负载投切使得直流VSC输出功率由初始吸收1.6kW功率突变至发出0.2kW功率时，下垂控制根据图4所示下垂曲线，调节给定电压取值，从而对直流VSC输出功率进行调整，实现对直流VSC输出功率的控制。但其仅具备下垂特性，缺乏对功率波动的惯性响应能力，因此下垂控制下直流VSC输出电压在0.5s功率突变时，出现电压过冲现象，直流VSC输出电压由403V骤降至398V后，再缓慢调节至稳态值400V。
表1 VDCM策略仿真参数
Tab.1 VDCM strategy simulation parameters
参 数数 值 空载电压Unom/V400 直流VSC额定功率Prate/kW5 光伏变换器输出侧电容Cpvout/mF1 200 光伏变换器输入侧电感Lpv/mH2 储能变换器输出侧电容Cbat/mF1 200 储能变换器输入侧电感Lbat/mH2 开关频率fs/kHz10 转动惯量J/(kg·m2)0.1 阻尼系数D1 000 下垂系数kp0.002 励磁系数kf2
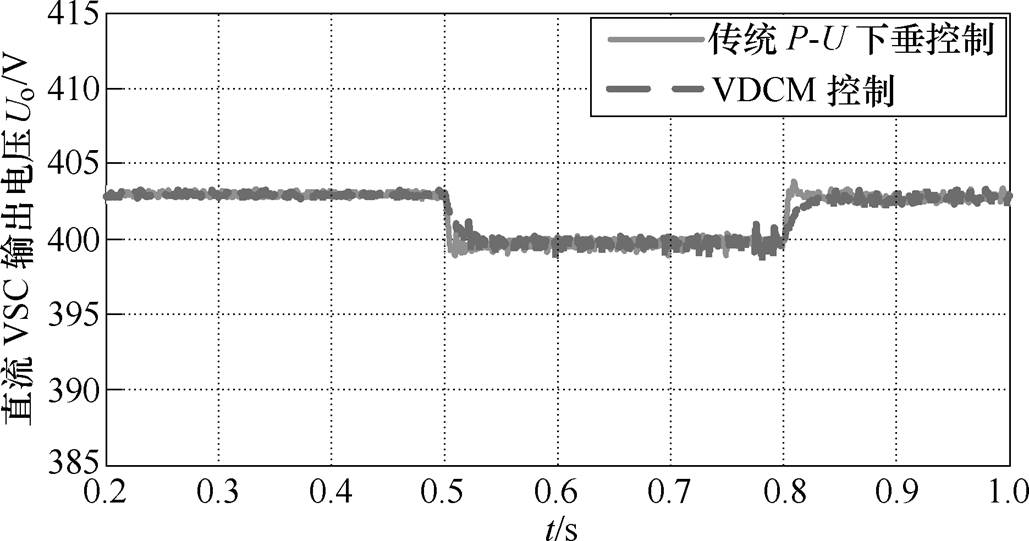
图13 直流VSC输出电压对比仿真波形
Fig.13 DC VSC output voltage comparison simulation waveforms
而采用VDCM控制策略时，VDCM策略通过图5所示虚拟机械转动环节，增强直流VSC输出电压惯性，提升直流VSC输出电压的动态稳定性。因此直流VSC输出电压平缓调节至稳态400V电压，未出现电压骤降及电压过冲现象。0.8s网内功率再次突变时，采用VDCM控制，直流VSC输出电压依旧能够平缓达到稳态值，从而验证VDCM策略的有效性。
图14为直流VSC输出功率对比仿真波形。图中，0.5s与0.8s网内负载功率突变时，直流VSC采用VDCM控制相较于传统P-U下垂控制，其瞬时功率响应速度更快，直流VSC能够快速响应负载功率波动，迅速对网内功率波动进行补偿，降低瞬时功率偏差，达到平抑网内功率波动、提升负载供电可靠性的目的。
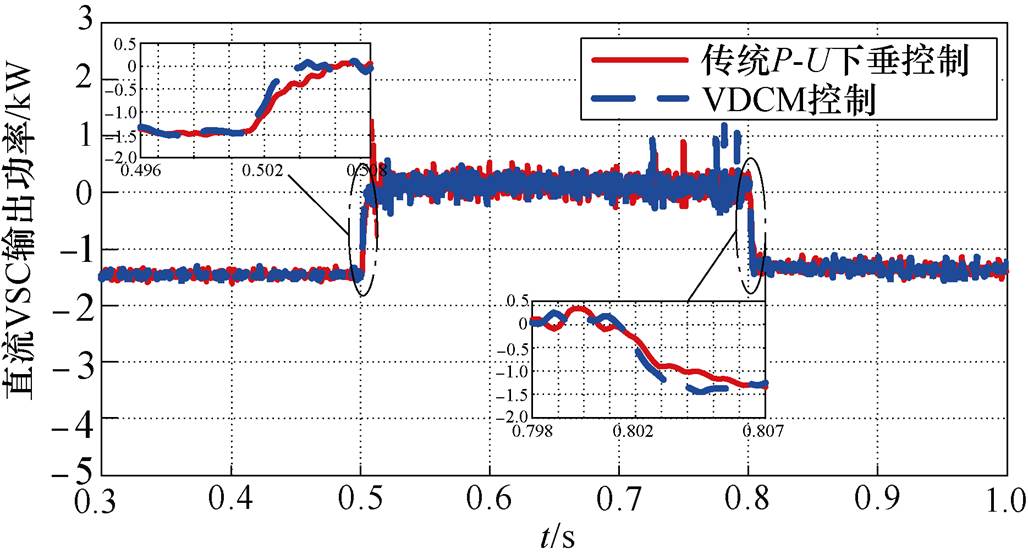
图14 直流VSC输出功率对比仿真波形
Fig.14 DC VSC output power comparison simulation waveforms
图15为直流VSC分别在传统P-U下垂控制与VDCM控制下给定电压波形。由图中可得，直流VSC采用VDCM控制，网内功率波动经图5所示虚拟机械转动环节产生具有惯性的给定电压值，相较传统P-U下垂控制环节产生的给定电压值，在0.5s与0.8s功率突变时，其给定电压变化更为平缓，具备对功率波动的惯性响应能力。
图15 直流VSC给定电压波形
Fig.15 DC VSC given voltage waveforms
图16为VDCM控制下转动惯量J增大至0.15kg·m2时，直流VSC输出电压波形。由图16可得，当转动惯量J增加时，直流VSC输出电压对功率波动的惯性响应能力增强，如图16中0.5s与0.8s所示，网内功率突变，直流VSC输出电压平缓达到稳态值。但对比图13中转动惯量J=0.05kg·m2时直流VSC输出电压波形可得，转动惯量取值越大，直流VSC输出电压变化越平缓，惯性越强。因此转动惯量J的取值决定直流VSC输出电压对功率的波动的惯性响应能力。
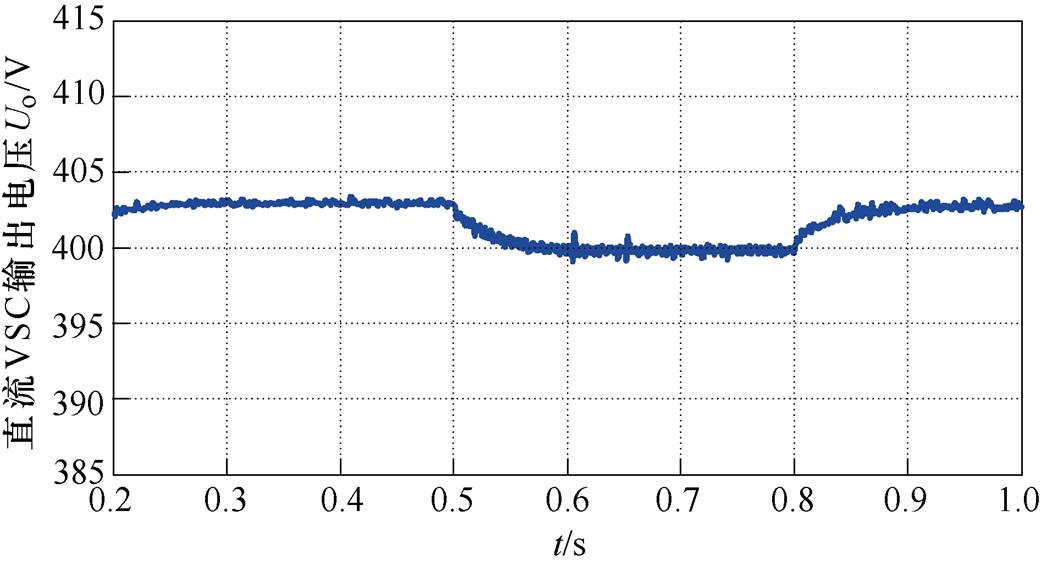
图16 转动惯量J=0.15kg·m2直流VSC输出电压波形
Fig.16 DC VSC output voltage waveforms when the moment of inertia J=0.15kg·m2
通过以上仿真可得，直流VSC采用VDCM控制策略有效地提升了VSC输出电压对功率波动的惯性响应能力，增强网内负载供电的可靠性。
为更进一步验证所提VDCM策略的有效性，搭建如图17所示光储微电网实验平台，直流VSC额定功率25kW，光伏发电单元工作在MPPT模式，储能装置采用VDCM控制策略，通过负载投切产生网内功率波动，实验参数见表2。
图17 光储微电网实验平台
Fig.17 Optical storage microgrid experimental platform
直流VSC最大输出电压U1_H=220V，分别在两种控制策略下进行对比实验。图18所示为采用传统P-U下垂控制实验波形，图中，光伏发电单元工作在MPPT模式，输出电流ipv恒定为2A，当负载功率突减时，储能VSC输出电流io由2.4A下降到1.2A，输出电压Uo经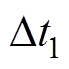
约0.12s时间调节，由214V上升至218V达到稳态点，但其动态过程不具备惯性，存在明显电压过冲。而相对应的采用VDCM控制策略实验波形如图19所示，其稳态值与传统P-U下垂控制策略相同，但在动态过程中，增强直流VSC对功率波动的惯性响应能力，其经
约0.22s时间调节，平缓达到稳态值，且未产生电压过冲现象。验证了所提VDCM策略，可有效地提升直流VSC输出电压对功率波动的惯性响应能力，增强负载供电的可靠性。
表2 VDCM策略实验参数
Tab.2 VDCM strategy experiment parameters
参 数数 值 空载电压Unom/V210 直流VSC额定功率Prate/kW25 光伏变换器输出侧电容Cpvout/mF705 光伏变换器输入侧电感Lpv/mH2.4 储能变换器输出侧电容Cbat/mF705 储能变换器输入侧电感Lbat/mH2.4 开关频率fs/kHz10 转动惯量J/(kg·m2)0.1 阻尼系数D5 000 下垂系数kp0.000 4 励磁系数kf2
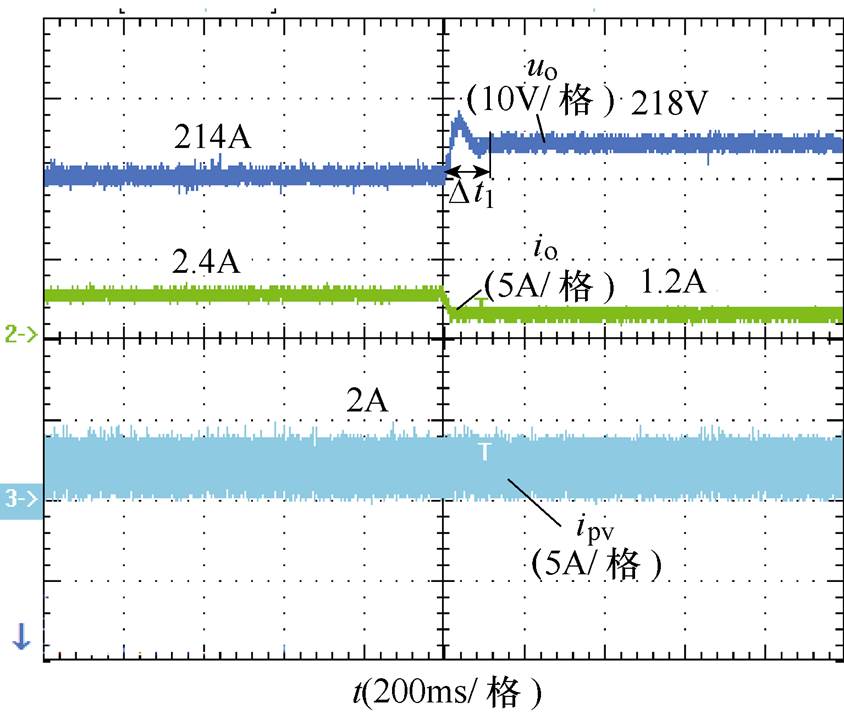
图18 传统下垂控制减载下实验波形
Fig.18 Experimental waveforms in traditional drop control when the load shedding
图19 VDCM控制减载下实验波形
Fig.19 Experimental waveforms in VDCM control when the load shedding
图20与图21分别为两种控制策略在负载功率突增时实验波形，传统P-U下垂控制在负载功率突增时，储能VSC输出电流io由初始1.2A突增至2.4A，输出电压由218V骤降至210V，动态过程经
约0.16s调节达到稳态值，产生明显电压过冲。而采用VDCM控制时，储能VSC稳态电压与传统下垂控制相同，在负载功率突增时，储能VSC输出电压平缓达到稳态点，未出现电压过冲现象。验证了所提VDCM策略在负载功率突增工况下，仍能保持直流VSC输出电压对功率突变的惯性响应能力。
图20 下垂控制加载下实验波形
Fig.20 Experimental waveforms in drop control when the load suddenly increase
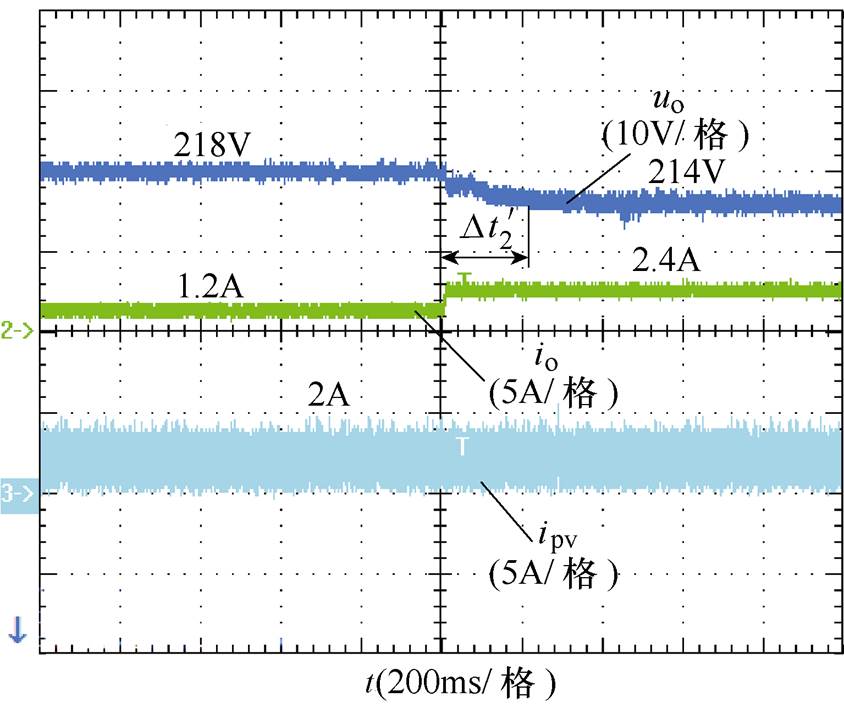
图21 VDCM控制加载下实验波形
Fig.21 Experimental waveforms in VDCM control when the load suddenly increase
图22与图23分别为VDCM控制，转动惯量增大至0.1kg·m2时，在不同工况下的实验波形。由图中可以看出，负载功率突变时，储能VSC输出电压由初始值平稳调节至稳态点，相较图19与图21，其动态调节过程更为平缓，因此转动惯量J增加，直流VSC输出电压对功率波动的惯性响应能力增强，改善了直流VSC动态响应性能。
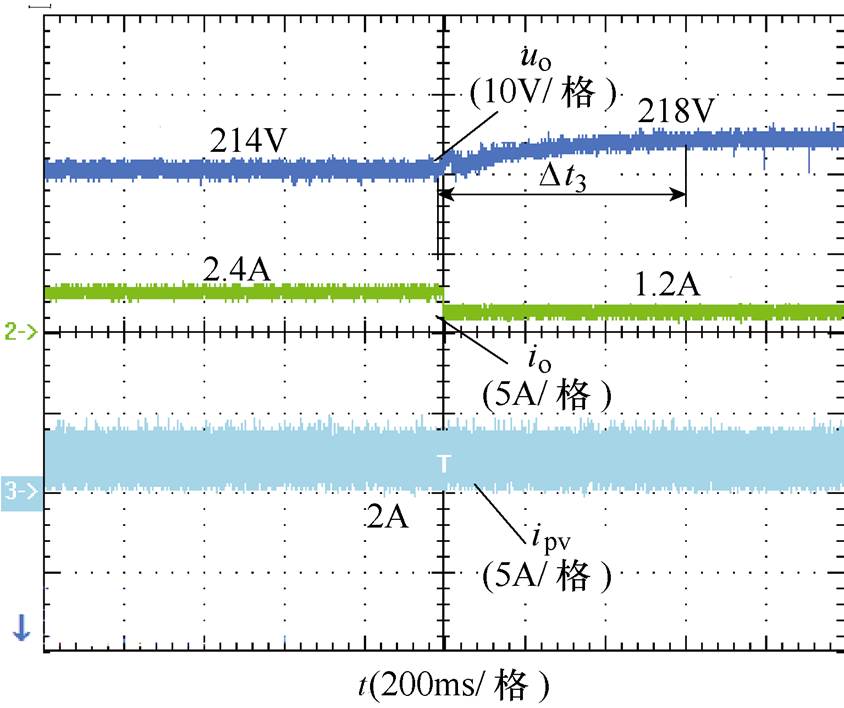
图22 VDCM控制转动惯量J=0.1kg·m2减载下实验波形
Fig.22 Experimental waveforms in VDCM control with moment of inertia J=0.1 kg·m2 when the load suddenly decrease
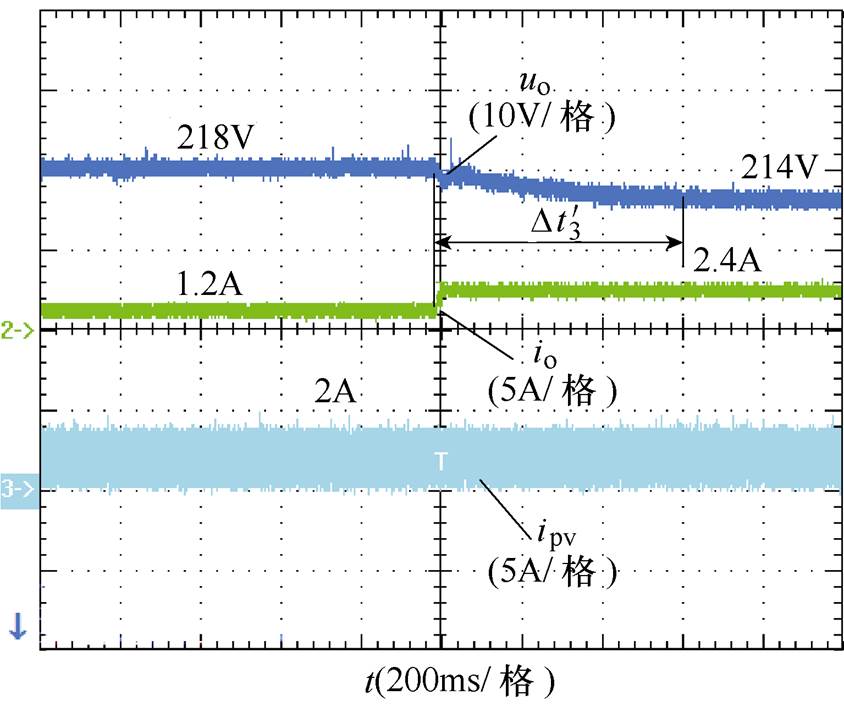
图23 VDCM控制转动惯量J=0.1kg·m2加载下直流VSC输出电压波形
Fig.23 DC VSC output voltage waveforms in VDCM control with moment of inertia J=0.1kg·m2 when the load suddenly increase
通过以上实验，验证了所提VDCM控制可有效地增强直流VSC输出电压对功率波动的惯性响应能力，平抑网内功率波动，提升网内负载供电的可靠性。
针对传统P-U下垂控制对网内功率波动缺乏惯性响应能力的缺陷，本文基于P-U下垂控制提出一种VDCM控制策略，通过将直流VSC与直流电机在电磁感应环节与机械转动环节进行等效，模拟直流电机转子对功率波动的惯性响应过程，建立VDCM控制通用控制模型，实现直流VSC输出电压对功率波动的惯性响应，提升直流母线电压惯性，增强网内负载供电的可靠性。通过小信号模型对其原理进行详细论证，并搭建仿真及实验平台，与传统下垂控制进行对比仿真实验，验证所提策略的有效性。
参考文献
[1] Ujjwol T, Dipesh S, Manisha M, et al. Virtual inertia: current trends and future directions[J]. Applied Sciences, 2017, 7(7): 654.
[2] Hasan A A, Radwan A A A, Ramadan E S. Modelling and analysis of a synchronous machine-emulated active intertying converter in hybrid AC/DC micro- grids[J]. IET Generation, Transmission & Distri- bution, 2018, 12(11): 2539-2548.
[3] 颜湘武, 王德胜, 贾焦心. 基于分散式微电网的虚拟同步发电机无通信预同步并网方案[J]. 电工技术学报, 2019, 34(19): 4143-4153.
Yan Xiangwu, Wang Desheng, Jia Jiaoxin. Non- communication pre-synchronization scheme of VSGs based on decentralized microgrids[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4143- 4153.
[4] Zhu Jiebei, Booth C D, Adam G P, et al. Inertia emulation control strategy for VSC-HVDC trans- mission systems[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1277-1287.
[5] Hosseinipour A, Hojabri H. Virtual inertia control of PV systems for dynamic performance and damping enhancement of DC microgrids with constant power loads[J]. IET Renewable Power Generation, 2018, 12(4): 430-438.
[6] Ravanji M H, Parniani M. Stability assessment of DFIG-based wind turbines equipped with modified virtual inertial controller under variable wind speed conditions[C]//43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 2017: 2695-2700.
[7] 伍文华, 陈燕东, 罗安, 等. 一种直流微网双向并网变换器虚拟惯性控制策略[J]. 中国电机工程学报, 2017, 37(2): 360-372.
Wu Wenhua, Chen Yandong, Luo An, et al. A virtual inertia control strategy for bidirectional grid- connected converters in DC micro-grids[J]. Pro- ceedings of the CSEE, 2017, 37(2): 360-372.
[8] 朱爱华, 赵涛, 徐宏健, 等. 基于虚拟同步发电机控制的T型三电平并网逆变器研究[J]. 电气技术, 2019, 20(11): 11-15.
Zhu Aihua, Zhao Tao, Xu Hongjian, et al. Research on T-type three-level energy storage inverter based on virtual synchronous generator control[J]. Elec- trical Engineering, 2019, 20(11): 11-15.
[9] 于明, 王毅, 李永刚. 基于预测方法的直流微网混合储能虚拟惯性控制[J]. 电网技术, 2017, 41(5): 1526-1532.
Yu Ming, Wang Yi, Li Yonggang. Virtual inertia control of hybrid energy storage in DC microgrid based on predictive method[J]. Power System Tech- nology, 2017, 41(5): 1526-1532.
[10] 陈文倩, 辛小南, 程志平. 基于虚拟同步发电机的光储并网发电控制技术[J]. 电工技术学报, 2018, 33(增刊2): 538-545.
Chen Wenqian, Xin Xiaonan, Cheng Zhiping. Control of grid-connected of photovoltaic system with storage based on virtual synchronous generator[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(S2): 538-545.
[11] 周晖, 王跃, 李明烜, 等. 孤岛并联虚拟同步发电机暂态功率分配机理分析与优化控制[J]. 电工技术学报, 2019, 34(增刊2): 654-663.
Zhou Hui, Wang Yue, Li Mingxuan, et al. Analysis and optimal control of transient active power sharing between islanded parallel virtual synchronous generators[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 654-663.
[12] Cao Yijia, Wang Weiyu, Li Yong, et al. A virtual synchronous generator control strategy for VSC- MTDC system[J]. IEEE Transactions on Energy Con- version, 2018, 33(2): 750-761.
[13] 孟建辉, 彭嘉琳, 王毅, 等. 多约束下光储系统的灵活虚拟惯性控制方法[J]. 电工技术学报, 2019, 34(14): 3046-3058.
Meng Jianhui, Peng Jialin, Wang Yi, et al. Multi- constrained flexible virtual inertial control method for photovoltaic energy storage system[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(14): 3046-3058.
[14] 朱晓荣, 孟凡奇, 谢志云. 基于虚拟同步发电机的直流微网DC-DC变换器控制策略[J]. 电力系统自动化, 2019, 43(21): 132-144.
Zhu Xiaorong, Meng Fanqi, Xie Zhiyun. Control strategy of DC-DC converter in DC microgrid based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2019, 43(21): 132-144.
[15] 兰征, 涂春鸣, 姜飞. 基于虚拟电机技术的直流微电网与主电网柔性互联策略[J]. 电工技术学报, 2019, 34(8): 1739-1749.
Lan Zheng, Tu Chunming, Jiang Fei. Flexible inter- connection strategy between DC microgrid and main power grid based on virtual motor technology[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1739-1749.
[16] 张波, 颜湘武, 黄毅斌, 等. 虚拟同步机多机并联稳定控制及其惯量匹配方法[J]. 电工技术学报, 2017, 32(10): 42-52.
Zhang Bo, Yan Xiangwu, Huang Yibin, et al. Stabi- lity control and inertia matching method of multi- parallel virtual synchronous generators[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(10): 42-52.
[17] Zhong Qingchang, Nguyen P L, Ma Z, et al. Self- synchronized synchronverters: inverters without a dedicated synchronization unit[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 617-630.
[18] Huang Linbin, Xin Huanhai, Wang Zhen, et al. A virtual synchronous control for voltage-source converters utilizing dynamics of DC-link capacitor to realize self-synchronization[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(4): 1565-1577.
[19] 盛万兴, 刘海涛, 曾正, 等. 一种基于虚拟电机控制的能量路由器[J]. 中国电机工程学报, 2015, 35(14): 3541-3550.
Sheng Wanxing, Liu Haitao, Zeng Zheng, et al. An energy router based on virtual motor control[J]. Proceedings of the CSEE, 2015, 35(14): 3541-3550.
[20] Soumya S, Prakash M J, Krishna R B. Virtual DC machine: an inertia emulation and control technique for a bidirectional DC-DC converter in a DC micro- grid[J]. IET Electric Power Applications, 2018, 12(6): 874-884.
[21] 崔健, 吕志鹏, 盛万兴, 等. 一种新型虚拟直流电机控制技术[J]. 中国电机工程学报, 2019, 39(10): 3029-3038.
Cui Jian, Lü Zhipeng, Sheng Wanxing, et al. A new control technology based on virtual DC motor[J]. Proceedings of the CSEE, 2019, 39(10): 3029-3038.
[22] 张辉, 谭树成, 肖曦, 等. 具有直流电机特性的储能接口变换器控制策略[J]. 高电压技术, 2018, 44(1): 119-125.
Zhang Hui, Tan Shucheng, Xiao Xi, et al. Control strategy of energy storage converter with DC machine characteristics[J]. High Voltage Engineering, 2018, 44(1): 119-125.
[23] 张辉, 张凯涛, 肖曦, 等. 模拟直流发电机特性的储能变换器控制策略[J]. 电力系统自动化, 2017, 41(20): 132-138
Zhang Hui, Zhang Kaitao, Xiao Xi, et al. Control strategy of energy storage converter for simulating DC generator characteristics[J]. Automation of Elec- tric Power Systems, 2017, 41(20): 132-138.
A Virtual DC Motor Control Strategy Based on P-U Drooping Characteristics
Abstract The traditional P-U droop control in DC microgrid only has drooping characteristic and a lack of inertia, which is unable to suppress voltage fluctuation. The sudden fluctuation of the power in the network can cause voltage overshoot. In order to suppress the voltage fluctuations and improve the transient behaviors of the bus voltage, a virtual DC motor control strategy based on the P-U droop characteristics is proposed. By simulating the mechanical inertia characteristics of the DC motor to adjust the P-U droop control loop, the large inertia and high damping output characteristic of the DC motor can be realized in the DC VSC. The specific mechanism of the VDCM control is analyzed, and the effectiveness of the proposed method is verified by the comparative simulation and experiments with the traditional P-U droop control base on the micro-grid experiment platform.
keywords：DC microgrid, P-U droop characteristics, mechanical inertia characteristics, virtual DC motor control
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.200102
国家自然科学基金面上项目（51877175）、陕西省重点项目（2017ZDXM-GY-003）和陕西省自然基金项目（2017JM5100）资助。
收稿日期 2020-02-04
改稿日期 2020-05-29
支 娜 女，1976年生，副教授，研究方向为新能源发电及微电网控制。E-mail: zhina@xaut.edu.cn（通信作者）
丁 可 男，1995年生，硕士研究生，研究方向为直流微电网及其协调控制。E-mail: 1597436271@qq.com
（编辑 陈 诚）