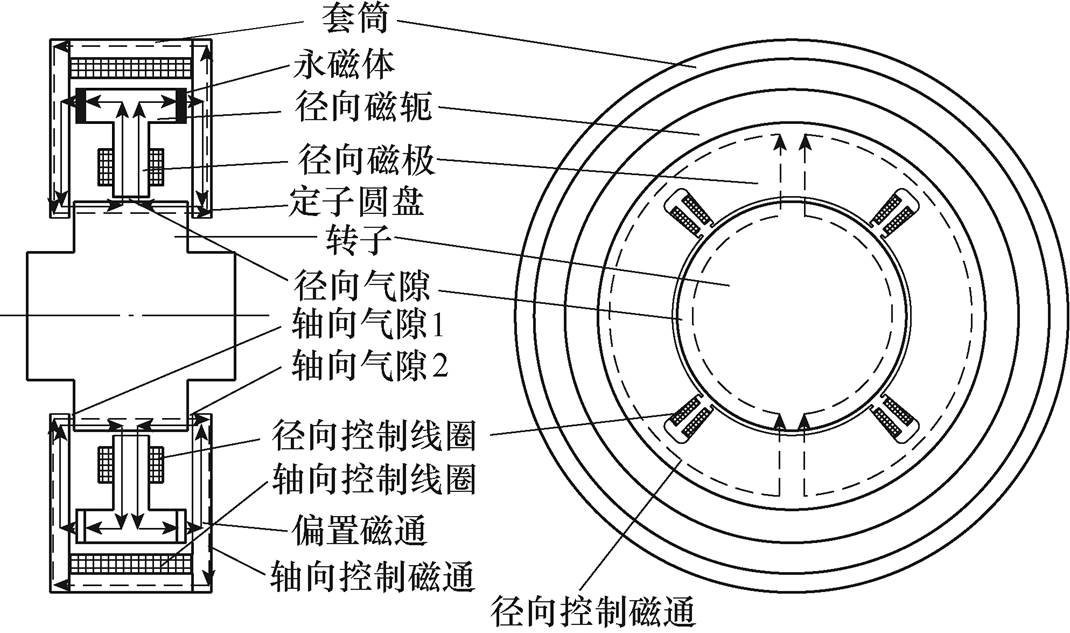
图1 轴向-径向永磁偏置磁轴承结构示意图
Fig.1 Structural schematic diagram of axial-radial permanent magnet biased magnetic bearings
摘要 该文基于一种实心同极性轴向-径向磁悬浮轴承结构,其具有磁场分布均匀、轴向空间较小的优点。针对该新型混合型轴向-径向磁悬浮轴承结构紧凑、磁场分布复杂等特点,结合有限元二维仿真结果,建立考虑漏磁的精确磁路模型。根据磁路模型,计算该结构的气隙磁通密度、刚度和承载力,并与有限元仿真进行对比,仿真与计算结果基本一致。实验结果表明转子能够在较高转速下实现稳定悬浮,验证了该结构的可行性。
关键词:混合型 轴向-径向磁悬浮轴承 等效磁路 漏磁 有限元
主动型磁悬浮轴承借助电磁铁、反馈回路、传感器、功率放大器等单元实现对转子位移的主动控制,被动型磁悬浮轴承利用永磁体与永磁体之间、永磁体与软磁材料之间的斥力或吸力来产生不可控的悬浮力[1]。混合型磁悬浮轴承结合了两者的特点,利用永磁体提供偏置磁场,电磁线圈产生控制磁场,显著减小了磁轴承的功耗,成为近年来磁悬浮轴承研究热点之一[2-7]。
混合型磁悬浮轴承又分为同极性结构和异极性结构[8-13],同极性结构具有较低的磁滞损耗,被广泛用于飞轮储能、高速涡轮机机械等场合[14-15]。用于支承高速旋转体时,传统的磁悬浮电机采用两个径向磁悬浮轴承和一个轴向磁悬浮轴承[16-17],会带来体积增大、临界转速降低及控制的复杂性提高等弊端。为了提高磁悬浮轴承的集成度,相关研究人员提出了轴向-径向磁悬浮轴承结构,永磁体同时提供轴向、径向偏置磁场,可以同时控制轴向单自由度和径向两自由度。文献[18]中并列式的轴向径向磁悬浮轴承,轴向气隙与永磁体不对称,存在偏置磁场不均匀、轴向空间大等问题。文献[19]提出一种径向充磁的永磁偏置轴向径向磁悬浮轴承,当需要提供较大的偏置磁通时,需要增加永磁体的轴向长度,从而导致磁轴承的轴向长度增加。
针对目前轴向-径向混合型磁悬浮轴承存在的问题,本文选用一种新型同极性轴向-径向混合磁悬浮轴承,永磁体采用轴向充磁,使磁悬浮轴承具有较小的轴向尺寸,轴向气隙与永磁体呈对称关系,不存在偏置磁场不均匀的问题。本文介绍了新型磁悬浮轴承的结构及工作原理。通过对磁场分布的分析,建立了考虑漏磁的精确等效磁路模型,基于磁路模型,分析了该模型的气隙磁通密度、刚度和承载力,并将有限元仿真结果与磁路法计算结果进行了对比分析。基于设计参数制作了实验样机,实现了24 000r/min的稳定悬浮。
混合型轴向-径向永磁偏置磁轴承的结构示意图如图1所示,定、转子铁心均由实心软磁材料制成,主要由两个定子圆盘、套筒、永磁体、转子、径向磁极、径向磁轭、轴向控制线圈、径向控制线圈组成。两个对称定子圆盘和套筒的内腔内设置轴向控制线圈,轴向定子圆盘在轴向上与转子留有轴向气隙;径向定子的内腔壁向轴心外延伸出圆周方向均匀分布的四个径向磁极,四个相同的径向磁极上分别绕有相同的径向控制线圈且在径向上与转子的外壁之间均留有径向气隙;径向磁轭设置在径向磁极的外壁;在径向磁轭的两侧分别设置轴向充磁的环形永磁体环,永磁体环的N极均朝向定子圆盘,S极均朝向径向磁轭。

图1 轴向-径向永磁偏置磁轴承结构示意图
Fig.1 Structural schematic diagram of axial-radial permanent magnet biased magnetic bearings
为了便于分析,本文使用的结构参数如图2所示。
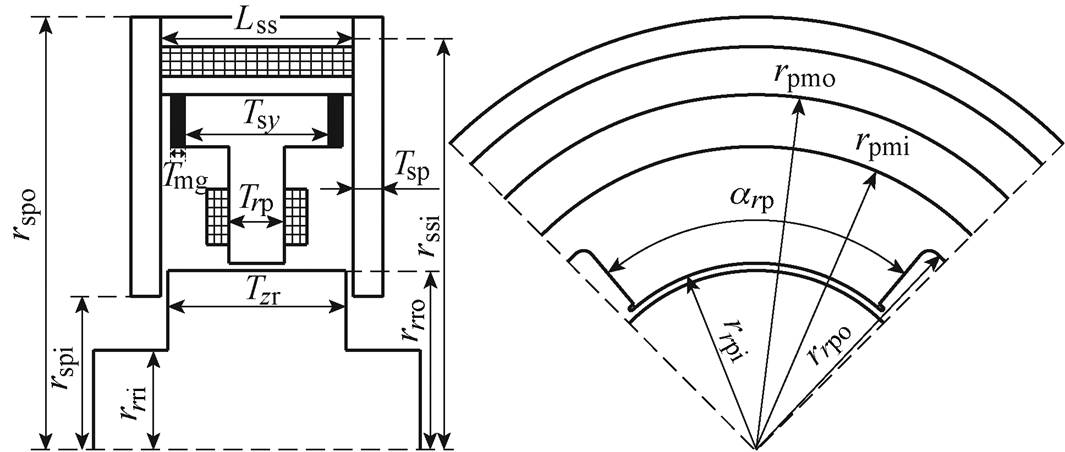
图2 轴向-径向永磁偏置磁轴承结构参数
Fig.2 Structure parameters of axial-radial permanent magnet biased magnetic bearings
偏置磁场由两个轴向充磁的环形永磁体建立,通过永磁体、定子圆盘、轴向气隙、转子、径向气隙、径向磁极、径向磁轭形成磁回路,如图1中的实线部分所示。
以垂直方向为例,当转子受到一个向下的冲击力使其偏离中心位置向下运动,导致上半部分的径向气隙增大,偏置磁场磁通密度减小;下半部分的径向气隙减小,偏置磁场磁通密度增大。此时转子受到的合力方向也向下,使得转子偏离径向中心位置。为了使转子回到中心位置,需要在径向线圈中通入一定的电流,产生的径向控制磁场如图1经过径向磁极的虚线部分所示,在上半部分的气隙中,偏置磁场与径向控制磁场的方向一致,合成磁通密度增加;在下半部分的气隙中,偏置磁场与径向控制磁场的方向相反,合成磁通密度减小,转子受到的合力向上,将其拉向中心位置。因此,通过调节径向控制线圈中电流的大小和方向,能够产生所需的磁场力,将转子稳定悬浮在径向中心位置。
轴向与径向水平方向类似,当转子受到一个向右的冲击力使其偏离中心位置向右运动,左半部分的轴向气隙增大,偏置磁场磁通密度减小;右半部分的轴向气隙减小,偏置磁场磁通密度增大。此时转子受到的合力方向也向右,使得转子偏离轴向中心位置。为了使转子回到平衡位置,需要在轴向线圈中通入一定的电流,产生的轴向控制磁场如图1经过定子圆盘的虚线部分,在左半部分的气隙中,偏置磁场与轴向控制磁场的方向一致,合成磁通密度增加;在右半部分的气隙中,偏置磁场与轴向控制磁场的方向相反,合成磁通密度减小,转子受到的合力向左,将其拉向中心位置。因此,通过调节轴向控制线圈中电流的大小和方向,能够产生所需的磁场力,将转子稳定悬浮在轴向中心位置。
综上所述,通过调节径向控制电流和轴向控制电流,使转子产生径向和轴向上的力,使转子稳定悬浮在中心位置。
等效磁路法可以清晰地考虑磁轴承的磁场分布,故在磁轴承本体设计中被广泛使用。根据磁路分布,混合型轴向-径向永磁偏置磁悬浮轴承可以从三个部分考虑磁通分布:①偏置磁通;②轴向控制磁通;③径向控制磁通。
根据仿真结果,偏置磁通经永磁体、定子圆盘、轴向气隙、转子、径向气隙、径向磁极、径向磁轭建立偏置磁场,如图3a所示。轴向控制磁通经套筒、定子圆盘、轴向气隙、转子、轴向气隙、定子圆盘建立轴向控制磁场,如图3b所示。径向控制磁通经径向磁轭、径向磁极、径向气隙、转子建立径向控制磁场,如图3c所示。图3a中,偏置磁场漏磁路径LFpm1~LFpm22对应的漏磁磁阻为Rpm1~Rpm22;图3b中,轴向控制磁场漏磁路径LFzc1~LFzc19对应的漏磁磁阻为Rlzc1~Rlzc19;图3c中,径向控制磁场漏磁路径LFrc对应的漏磁磁阻为Rlrc。
磁场路径几何分布如图4所示。根据图1偏置磁场磁路的分布,将模型铁心材料分成9个部分。如图4a所示,5代表径向磁极,3、7代表定子圆盘,4、6代表转子,1、9代表径向磁轭,2、8代表永磁体和定子圆盘之间的气隙。
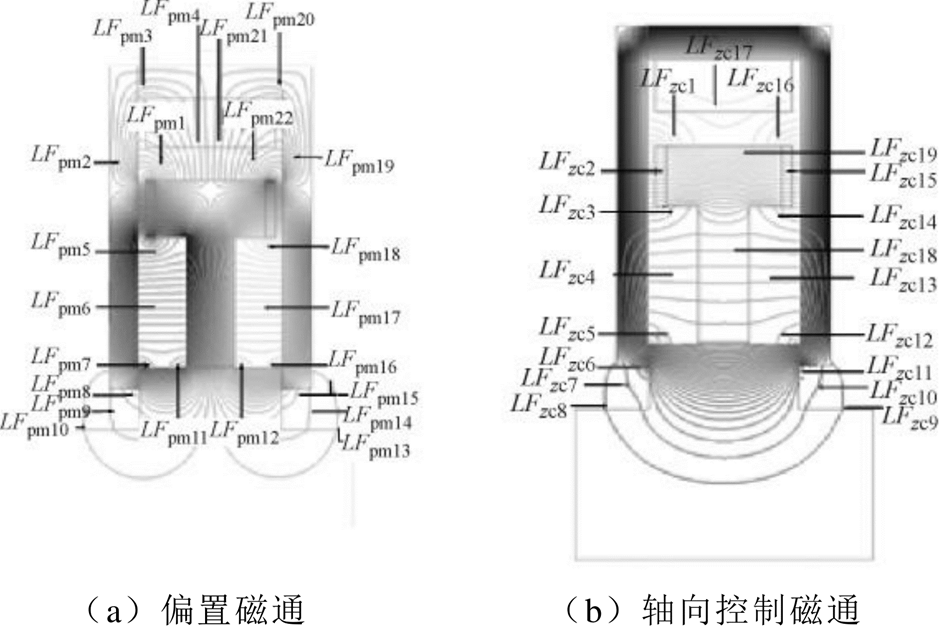
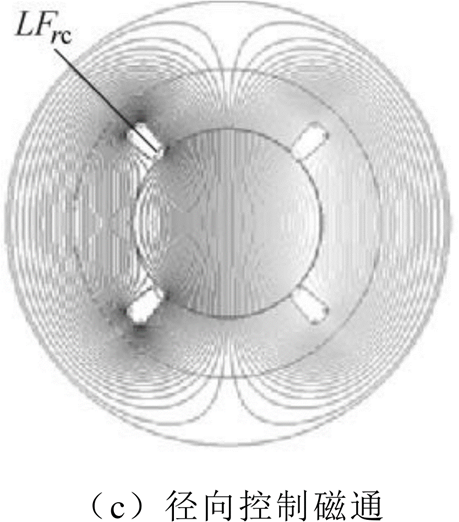
图3 考虑漏磁后的磁通分布
Fig.3 Flux distribution considering magnetic leakage
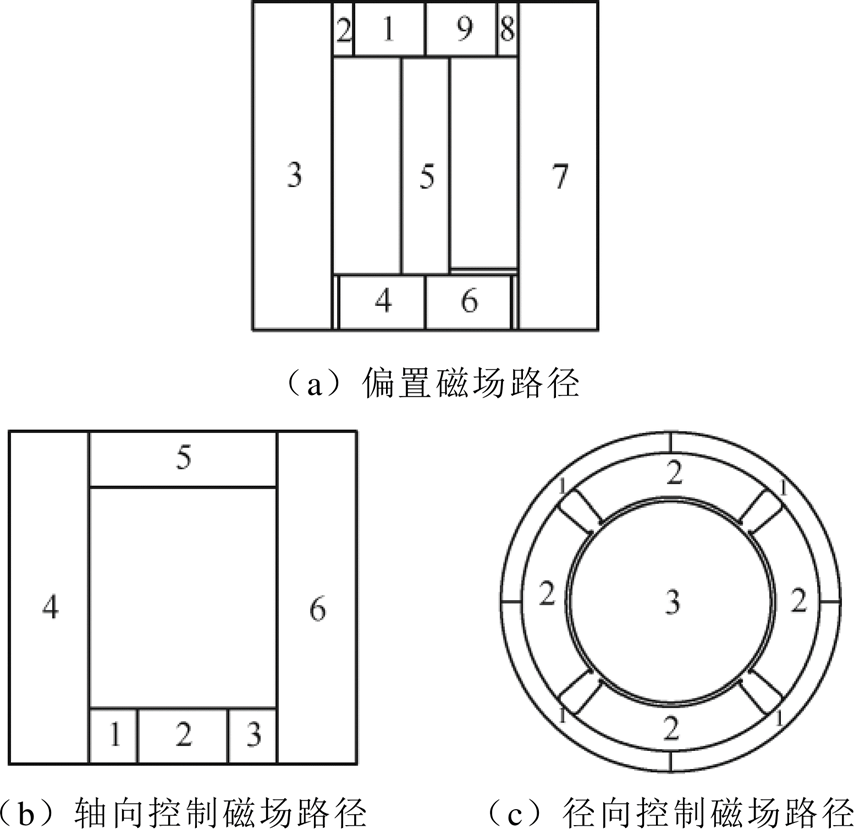
图4 磁场路径几何分布
Fig.4 Division of the geometry of magnetic field path
根据图1轴向控制磁场磁路的分布,将模型分成6个部分。如图4b所示,1、3代表轴向气隙,2代表转子,4、6代表定子圆盘,5代表套筒。
根据图1径向控制磁场磁路的分布,将模型分成3个部分。如图4c所示,1代表径向磁轭,2代表径向磁极,3代表转子。
根据以上分析及图4的磁路几何分布,建立考虑漏磁的精确磁路模型,如图5所示。
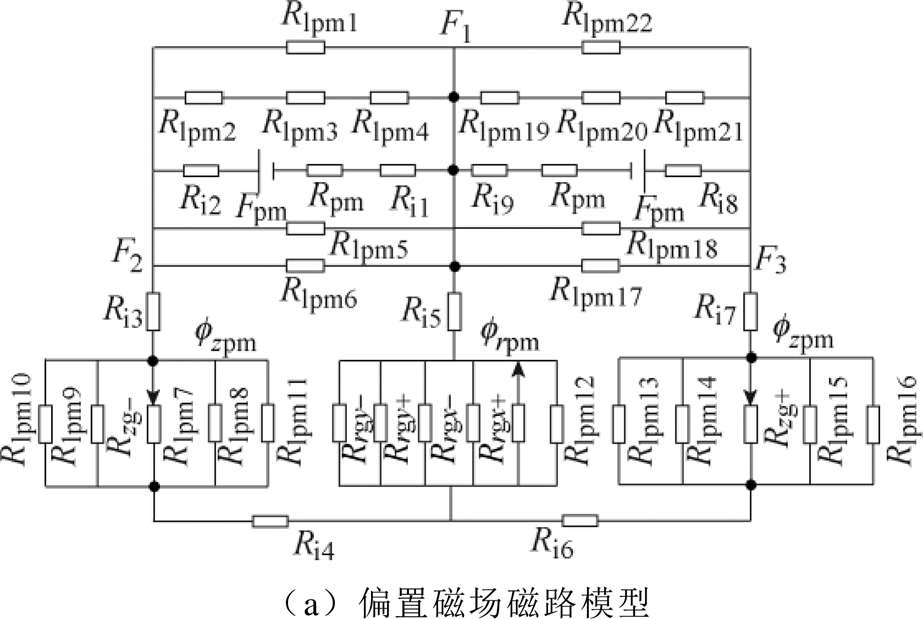
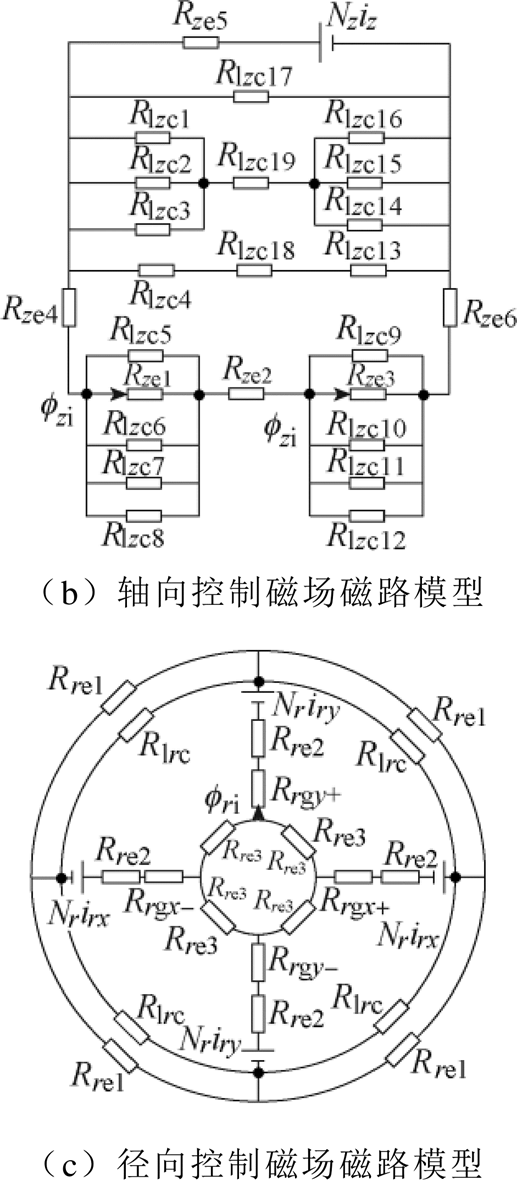
图5 考虑漏磁影响的磁路模型
Fig.5 Magnetic circuit model considering leakage effects
图5a中,Fpm为永磁体的矫顽磁动势,Rpm为永磁体的磁阻,有
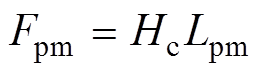 (1)
(1)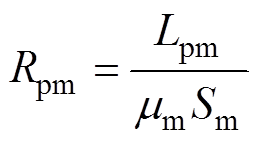 (2)
(2)
式中,Lpm为永磁体轴向厚度;Hc为永磁体的矫顽力;mm为永磁体磁导率;Sm为永磁体中性面面积。
Rrgx+、Rrgx-、Rrgy+、Rrgy-分别为径向四个气隙的磁阻,有
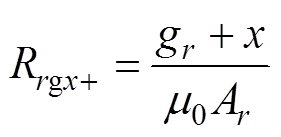 (3)
(3)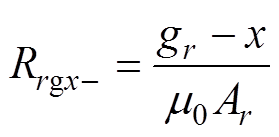 (4)
(4)
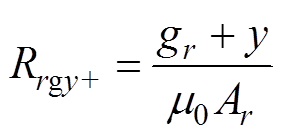 (5)
(5)
 (6)
(6)式中,gr为径向定转子间的气隙长度;x、y分别为转子径向x、y方向的偏移量;m0为直空磁导率;Ar为径向气隙的面积;Rrgx+、Rrgy+分别为x、y方向径向气隙增加的一侧气隙磁阻;Rrgx-、Rrgy-分别为x、y方向径向气隙减小的一侧气隙磁阻。
Rzg+、Rzg-分别为轴向两个气隙的磁阻,有
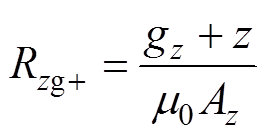 (7)
(7)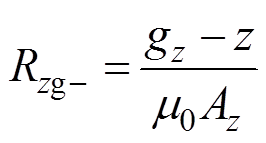 (8)
(8)
式中,gz为轴向定转子间的气隙长度;z为转子轴向的偏移量;Az为轴向气隙的面积。
为了计算偏置磁通,定义
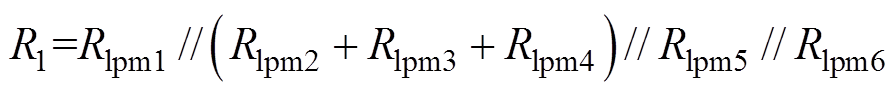 (9)
(9)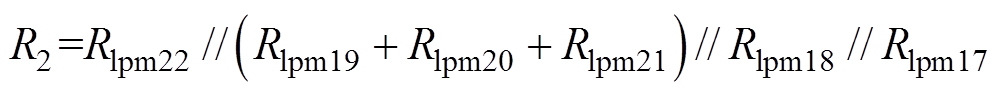 (10)
(10)
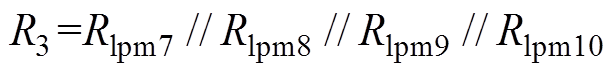 (11)
(11)
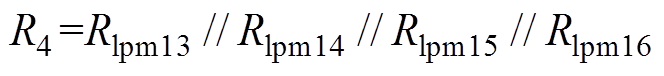 (12)
(12) (13)
(13)
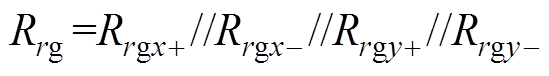 (14)
(14)
式中,Ri1、Ri3、Ri4、Ri5、Ri6、Ri7、Ri9为铁心材料的磁阻;Ri2、Ri8为永磁体与圆盘之间的气隙磁阻;F1、F2、F3为所在点的磁动势,根据节点电压法,计算出偏置磁场。
当转子悬浮在平衡位置时,轴向偏置磁通和径向偏置磁通分别为
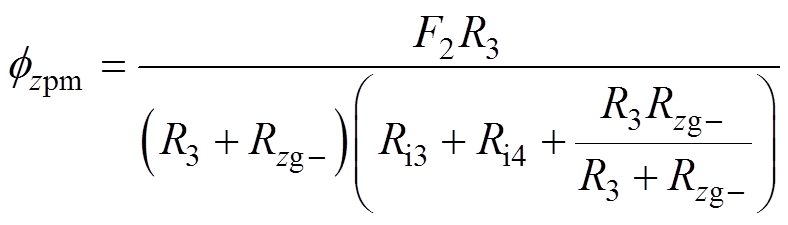 (15)
(15)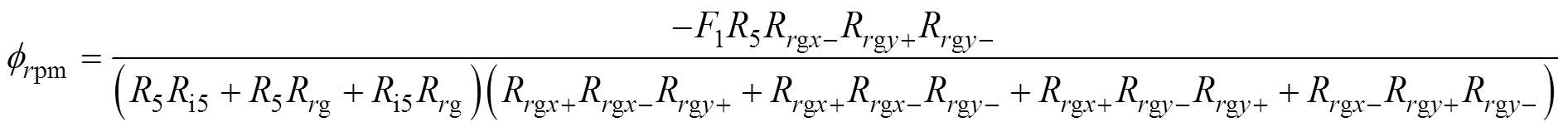 (16)
(16)
图5b中,Nz为轴向线圈匝数,iz为轴向控制电流。Rze2、Rze4、Rze5、Rze6为轴向控制磁路经过的铁心磁阻,Rze1、Rze3为轴向气隙磁阻,在平衡位置,Rzg+与Rzg-两者相等,有
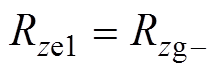 (17)
(17)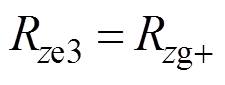 (18)
(18)
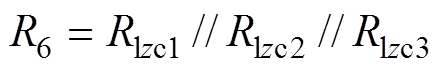 (19)
(19)
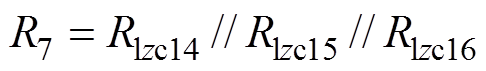 (20)
(20) (21)
(21)
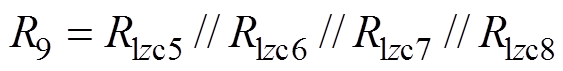 (22)
(22)
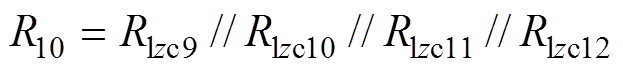 (23)
(23)为了计算整个回路的总磁阻,引入系数ozc1、ozc2、ozc3,有
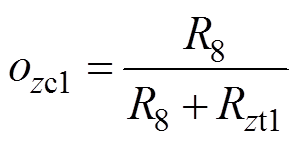 (24)
(24)
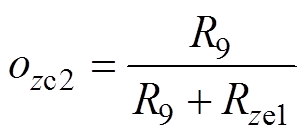 (25)
(25) (26)
(26)
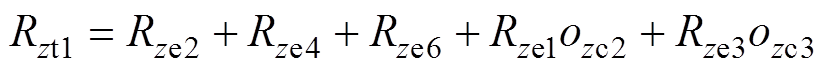 (27)
(27)
整个轴向控制磁场回路的磁阻为
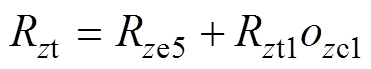 (28)
(28)轴向控制磁场磁通为
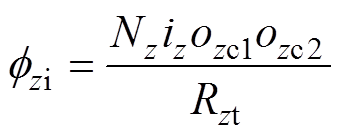 (29)
(29)
图5c中,Nr为径向线圈匝数,ix、iy分别为径向x、y方向上的控制电流。Rre1、Rre2、Rre3分别为径向磁轭、径向磁极、转子的磁阻,有
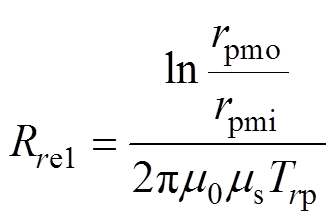 (30)
(30)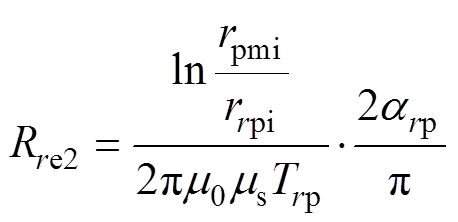 (31)
(31)
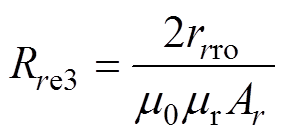 (32)
(32)
式中,rpmo、rpmi分别为永磁体的外径和内径,数值上也等于径向磁轭的外径和内径;rrpi为径向磁极的内径;Trp为径向磁极的厚度;rrro为转子的外径;ms为定子铁心的相对磁导率;mr为转子铁心的相对磁导率;arp为径向磁极的极弧度。
由于径向x和y是对称结构,以径向y方向为例,仅有y方向上的线圈通电时,该径向控制磁通回路的总磁阻为
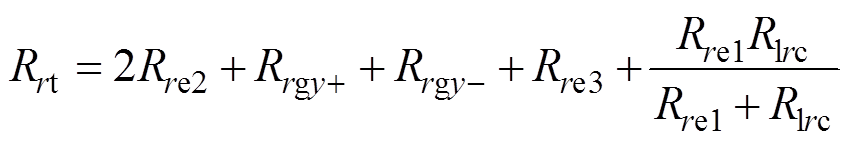 (33)
(33)径向控制磁场磁通为
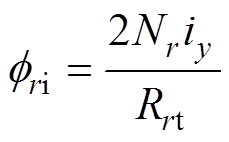 (34)
(34)
轴向承载力和径向承载力分别为
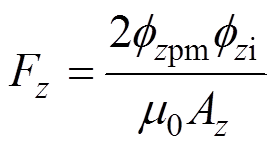 (35)
(35) (36)
(36)
径向电流刚度和径向位移刚度分别为
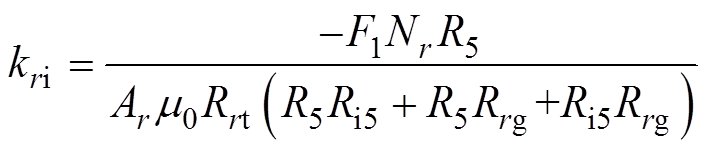 (37)
(37)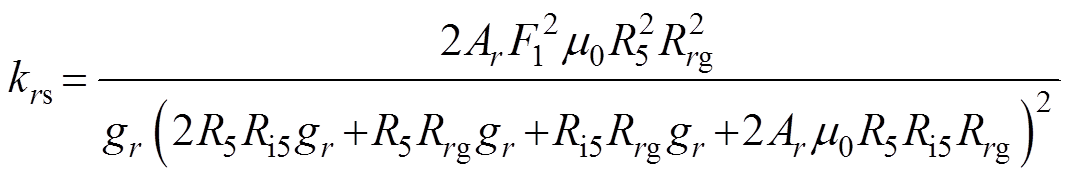 (38)
(38)
轴向电流刚度和轴向位移刚度分别为
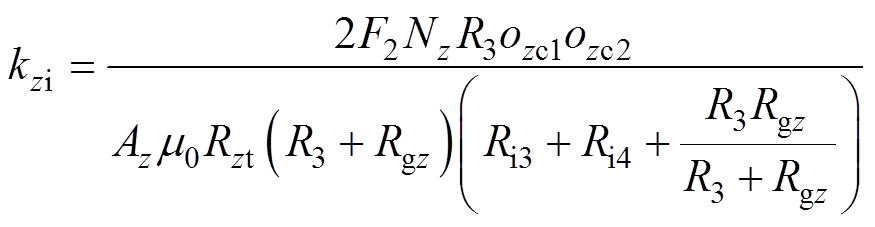 (39)
(39) (40)
(40)
其中
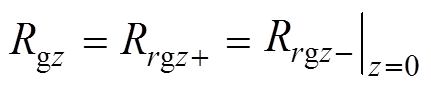 (41)
(41)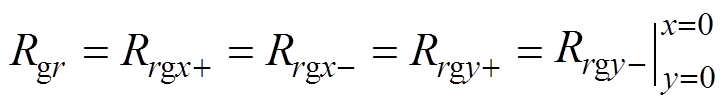 (42)
(42)
本文的轴向-径向磁悬浮轴承使用的材料属性见 表1,表中,转子、定子和永磁体分别使用40CrNiMoA、DT4E、SmCo材料。
表1 材料属性
Tab.1 Material property

材 料参 数数 值 40CrNiMoA相对磁导率mr376 电导率sr/(S/m)2762431 DT4E相对磁导率ms4494 电导率ss/(S/m)10 300 000 SmCo相对磁导率mm1.06 矫顽力Hc/(A/m)798 000
图2的结构主要参数见表2,表中,Izmax是轴向最大控制电流,Irmax是径向最大控制电流。
表2 主要参数
Tab.2 Main parameters

参数数 值参 数数 值 gr/mm0.5Tzr/mm35 gz/mm0.5Trp/mm13.6 rrri/mm35Tmg/mm2.5 rrro/mm50Tsp/mm7 rspi/mm45Tsy/mm27 rssi/mm116Lss/mm36 rspo/mm124Nz104 rrpi/mm50.5Nr113 rrpo/mm72Izmax/A6 rpmi/mm82Irmax/A3 rpmo/mm96arp4/9p
为了验证理论分析,使用有限元软件对本文的轴向-径向磁悬浮轴承进行仿真。
首先建立三维有限元模型如图6所示。由于轴向-径向磁悬浮轴承的偏置磁路与径向控制磁路不在一个平面,本文均采用了三维模型仿真。有限元中计算的轴向、径向气隙中偏置磁场的磁通密度沿圆周方向的变化如图7所示。轴向气隙中控制磁场的磁通密度沿圆周方向的变化如图8a所示;径向气隙中某一自由度控制磁场的磁通密度沿圆周方向的变化如图8b所示。
对比磁路法和有限元的磁通密度及刚度见表3。Bzpm1、Bzpm2分别为轴向气隙1、2的偏置磁通密度,Brpm为径向气隙偏置磁通密度,Bzi1、Bzi2分别为轴向气隙1、2控制磁通密度,Bri为径向气隙控制磁通密度。根据式(37)~式(40),分别计算出径向电流刚度kri、径向位移刚度krs、轴向电流刚度kzi、轴向位移刚度kzs。误差均在10%以内。其中,Bzpm1与Bzpm2及Bzi1与Bzi2完全一致,可以得出该模型的磁场分布较为均匀。
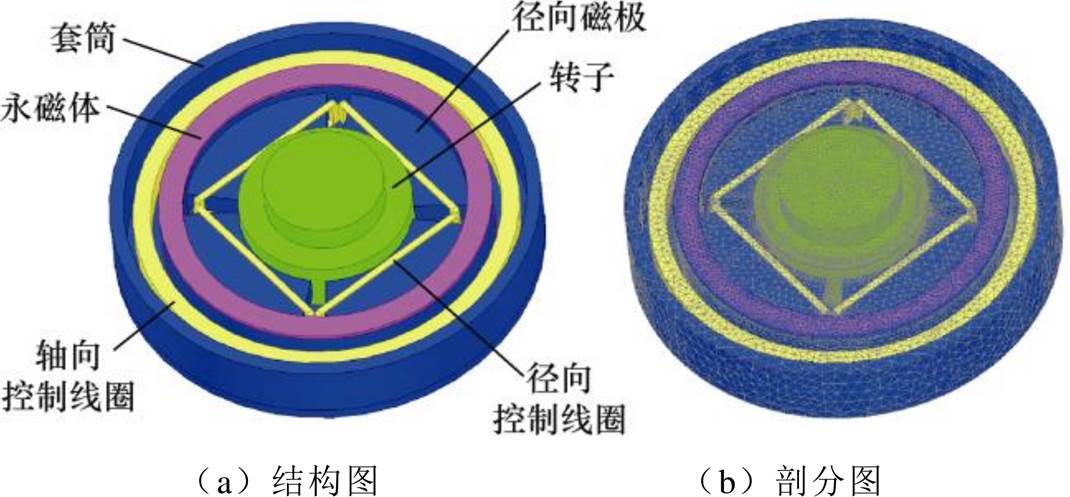
图6 三维有限元模型
图6 Three dimensional finite element model
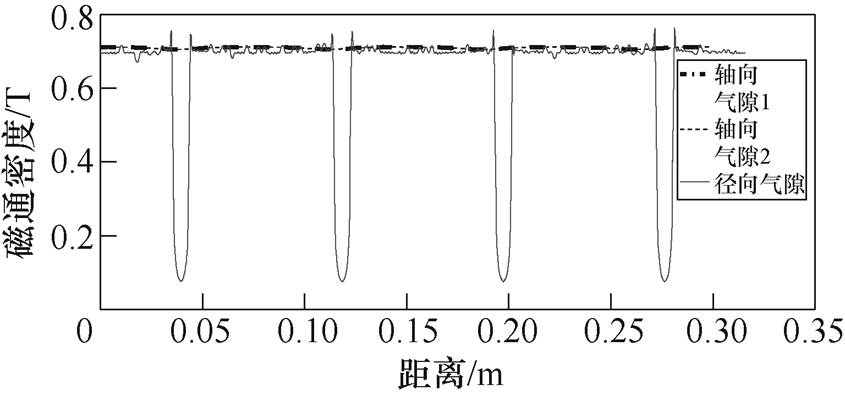
图7 气隙中的偏置磁场
Fig.7 Bias magnetic field in air gaps
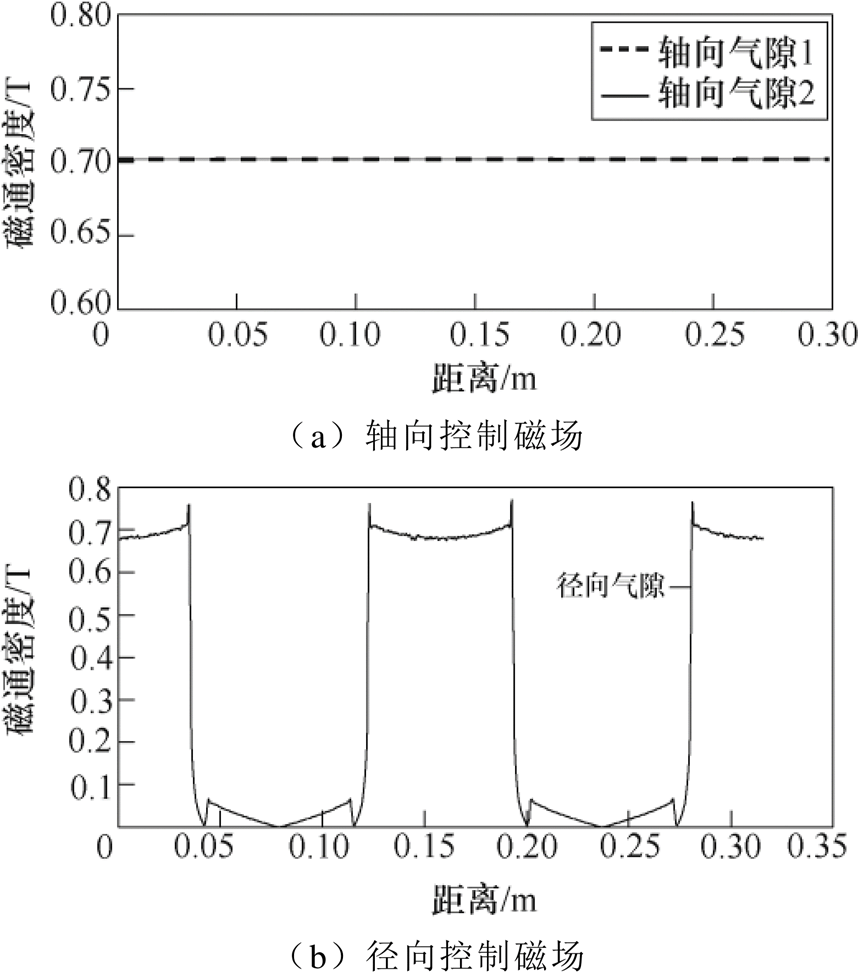
图8 气隙中的控制磁场
Fig.8 Control magnetic field in air gaps
径向、轴向电流刚度与位移刚度如图9所示,为径向、轴向电流刚度与位移刚度的拟合曲线。图中,实线为有限元的结果,虚线为磁路法的结果。由图9可以看出,磁路法与有限元计算的刚度较为接近,且在中心位置线性度较好。
表3 磁路法和有限元计算的磁通密度与刚度比较
Tab.3 Comparisons of magnetic density and stiffnesses calculated by magnetic circuit and finite element method

结果磁路法有限元误差(%) Bzpm1/T0.700.711.4 Bzpm2/T0.700.711.4 Brpm/T0.690.701.4 Bzi1/T0.700.700 Bzi2/T0.700.700 Bri/T0.670.681.5 Kzi/(N/A)194.8216.09.8 Kzs/(N/mm)2 326.42433.44.4 Kri/(N/A)233.6233.80.1 Krs/(N/mm)1448.01409.32.7
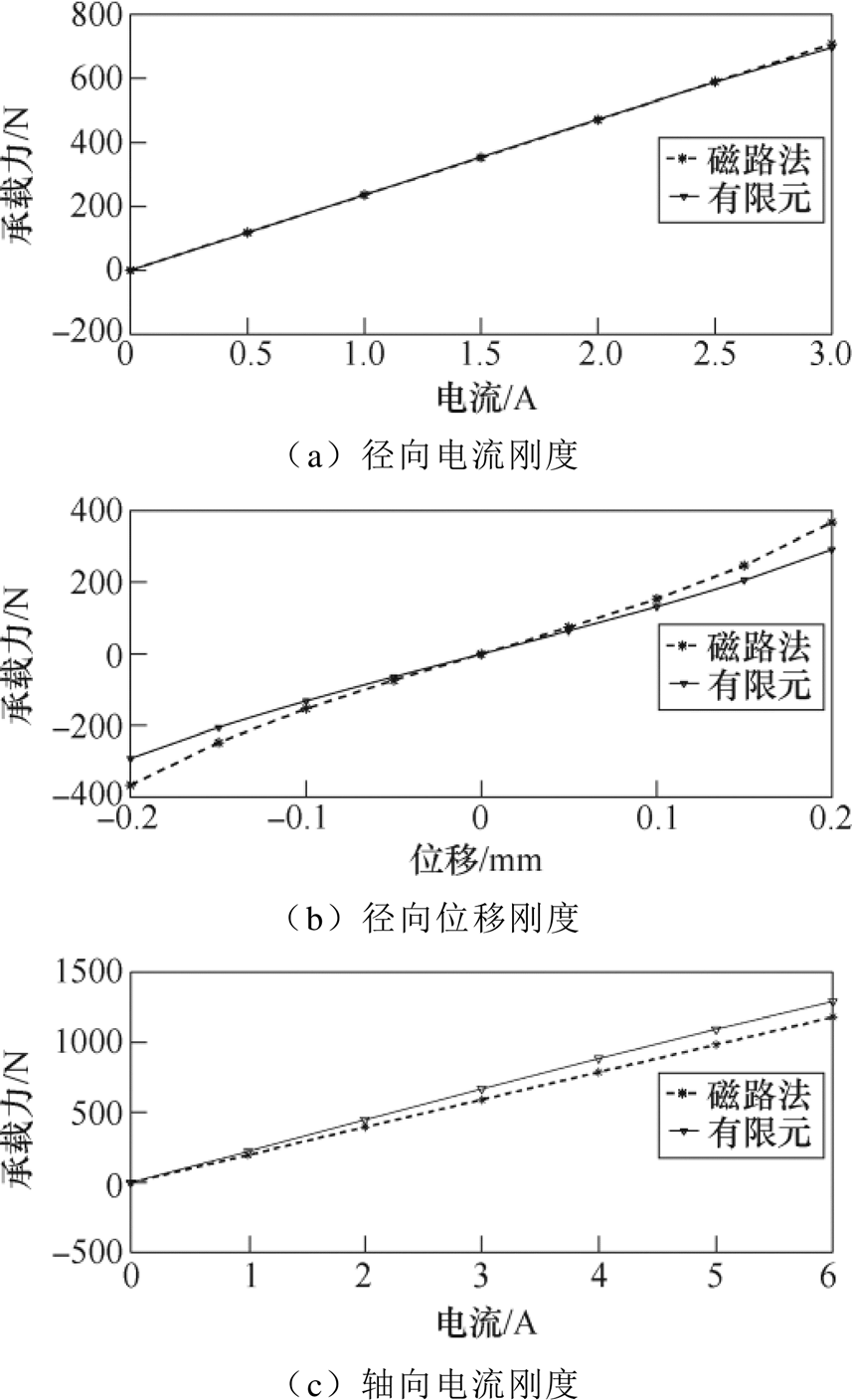
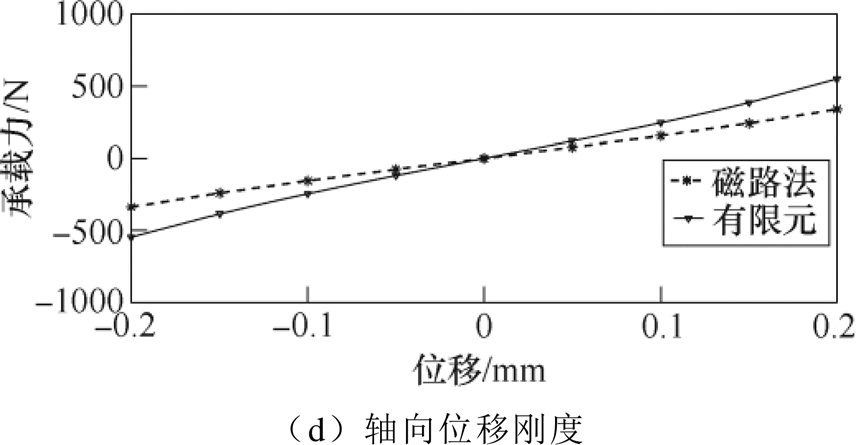
图9 径向、轴向电流刚度与位移刚度
Fig.9 Current stiffness and displacement stiffness in radial and axial
磁悬浮轴承的径向承载力取转子不平衡力和转子自重之和的2~3倍,本文取径向承载力600N,轴向承载力为1 200N,磁路法与有限元计算的最大承载力见表4,误差较小,基本满足设计要求。
表4 磁路法与有限元计算的承载力比较
Tab.4 Comparisons of capacity calculated by magnetic circuit and finite element method

承载力/N磁路法有限元误差(%) 轴向1179.71286.88.3 径向700.89696.40.6
根据第3节的参数设计与计算,设计了轴向-径向混合磁悬浮轴承样机如图10所示,用于支承200kW高速电机的转子,如图11所示。采用PID控制实现了轴向、径向的稳定悬浮。实验波形如图12所示,为24 000r/min时的位移和电流波形,图12a、图12b分别为径向位移信号和电流信号,图12c、图12d分别为轴向位移信号和电流信号。由于转子是水平放置的,图12c中径向y方向会承受转子重力,因此电流会存在直流偏置。

图10 轴向-径向永磁偏置磁悬浮轴承
Fig.10 Axial-radial permanent magnet biased magnetic bearings

图11 200kW高速电机
Fig.11 200kW high speed motor

图12 转子位移波形及控制电流波形
Fig.12 Waveforms of rotor’s displacement and control current
本文介绍了一种新型轴向-径向混合磁悬浮轴承,分析了其工作原理。该结构的永磁体采用轴向充磁,可以使得磁悬浮轴承具有较小的轴向尺寸,轴向气隙与永磁体呈对称关系,不存在偏置磁场不均匀的问题。根据磁场分布,建立了考虑漏磁的精确磁路模型,通过有限元仿真和磁路法分别计算气隙磁通密度、刚度和承载力,并进行了对比分析,误差均在10%以内,且磁场分布均匀。实验结果表明,该磁悬浮轴承能够实现转子在0~24 000r/min的稳定悬浮。
参考文献[20],漏磁磁阻RFpm2、RFpm4、RFpm9、RFpm14、RFpm19、RFpm21、RFzc7、RFzc10、Ri3、Ri5、Ri7可近似为附图1a所示两个同心圆柱之间的磁阻,其磁阻为
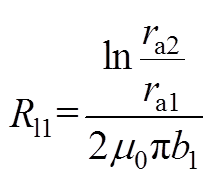 (A1)
(A1)式中,ra1、ra2分别为两个同心圆的半径;b1为两个圆柱的轴向长度。
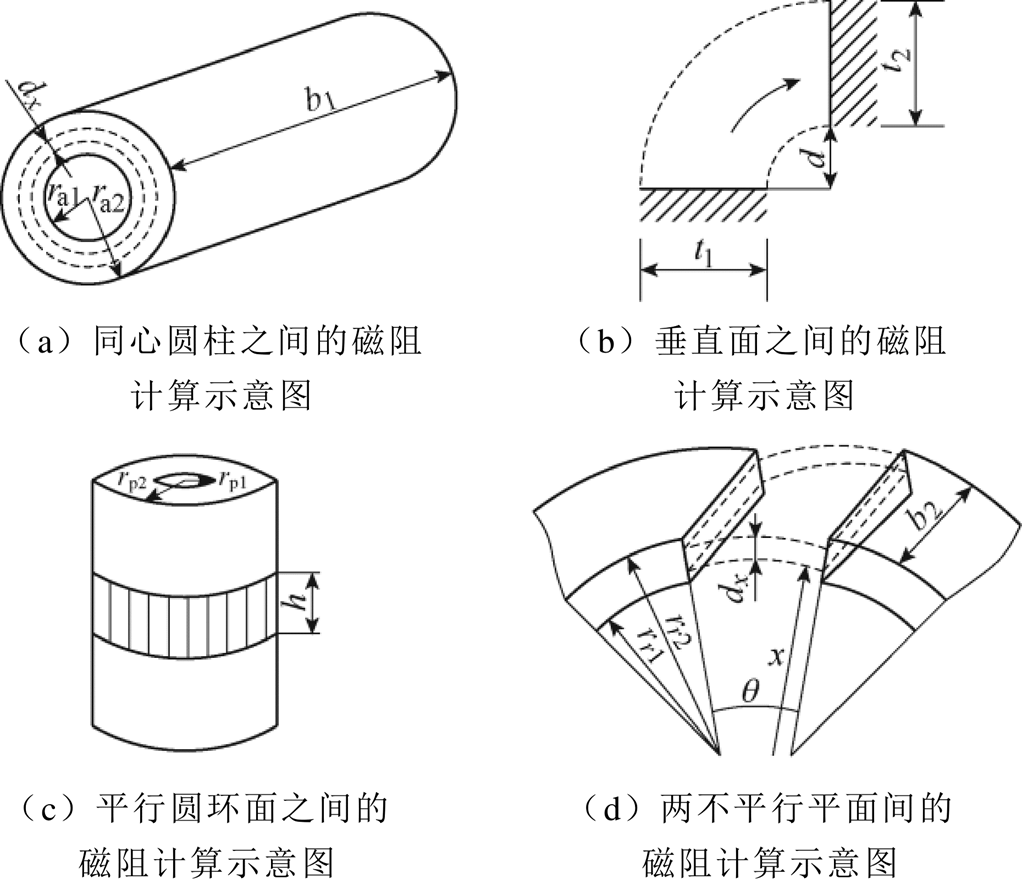
附图1 不同漏磁路径的模型
App.Fig.1 Models of different leakage flux paths
漏磁磁阻RFpm1、RFpm5、RFpm7、RFpm8、RFpm10、RFpm11、RFpm12、RFpm13、RFpm15、RFpm16、RFpm18、RFpm22、RFzc1、RFzc3、RFzc5、RFzc6、RFzc8、RFzc9、RFzc11、RFzc12、RFzc14、RFzc16可近似为附图1b所示垂直放置的两个面之间的磁阻,其磁阻为
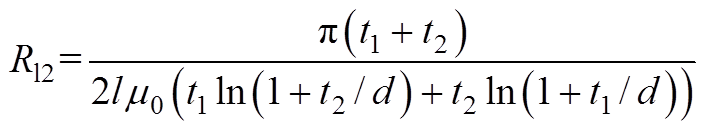 (A2)
(A2)式中,t1、t2分别为两个面的宽度;d为两个面之间的距离;l为磁路沿径向的圆弧长度。
漏磁磁阻RFpm3、RFpm6、RFpm17、RFpm20、RFzc2、RFzc4、RFzc13、RFzc15、RFzc17、RFzc18、RFzc19、Ri1、Ri4、Ri6、Ri9可近似为附图1c所示平行圆环面之间的磁阻,其磁阻为
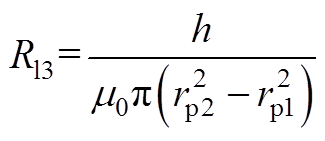 (A3)
(A3)式中,h为两个平面之间的距离;rp2、rp1分别为两个圆环面的外径和内径。
漏磁磁阻Rlrc可近似为附图1d所示两不平行平面的磁阻求解,其磁阻为
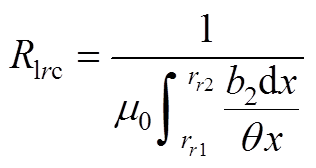 (A4)
(A4)式中,rr1、rr2分别为两个不平行平面的内径和外径;b2为平面的轴向长度;q 为不平行平面之间的角度。
铁心磁阻Ri3、Ri5、Ri7可近似为附图1a所示平行圆环面之间的磁阻,其磁阻为
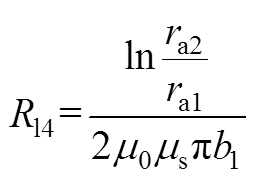 (A5)
(A5)铁心磁阻Ri2、Ri8,Ri1、Ri9和Ri4、Ri6可近似为附图1c所示平行圆环面之间的磁阻,其磁阻分别由式(A3)、式(A6)、式(A7)计算可得。
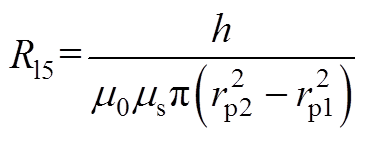 (A6)
(A6)
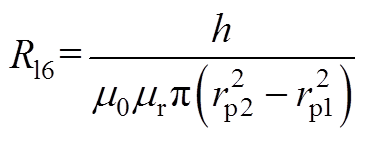 (A7)
(A7)参考文献
[1] Gerhard S, Eric H M, 等. 磁悬浮轴承: 理论、设计及旋转机械应用[M]. 徐旸, 张剀, 赵雷, 译. 北京: 机械工业出版社, 2012.
[2] 张云鹏, 薛博文, 刘淑琴, 等. 基于气隙磁通边缘效应的轴向混合磁轴承承载力解析计算[J]. 电机与控制学报, 2014, 18(9): 54-59, 67.
Zhang Yunpeng, Xue Bowen, Liu Shuqin, et al. Calculation of electromagnetic force of axial hybrid magnetic bearing based on fringe effect of magnetic flux[J]. Electric Machines and Control, 2014, 18(9): 54-59, 67.
[3] 邱文祥, 李大兴, 夏革非, 等. 一种新型低成本飞轮储能用永磁偏置磁轴承[J]. 电工技术学报, 2015, 30(增刊1): 58-62.
Qiu Wenxiang, Li Daxing, Xia Gefei, et al. A low cost permanent magnet biased bearing used in flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 58- 62.
[4] 刘程子, 邓智泉, 梅磊, 等. 基于漏磁与磁阻系数迭代的三自由度混合型磁悬浮轴承的设计[J]. 航空动力学报, 2013, 28(3): 603-612.
Liu Chengzi, Deng Zhiquan, Mei Lei, et al. Design of 3-DOF hybrid magnetic bearing based on leakage coefficient and magnetoresistance coefficient iterative method[J]. Journal of Aerospace Power, 2013, 28(3): 603-612.
[5] Fang Jiancheng, Wang Xi, Wei Tong, et al. Homo- polar 2-pole radial permanent-magnet biased magnetic bearing with low rotating loss[J]. IEEE Transactions on Magnetics, 2012, 48(8): 2293-2303.
[6] Han Bangcheng, Zheng Shiqiang, Wang Xi, et al. Integral design and analysis of passive magnetic bearing and active radial magnetic bearing for agile satellite application[J]. IEEE Transactions on Magnetics, 2012, 48(6): 1959-1966.
[7] 张维煜, 朱熀秋, 袁野. 磁悬浮轴承应用发展及关键技术综述[J]. 电工技术学报, 2015, 30(12): 12-20.
Zhang Weiyu, Zhu Huangqiu, Yuan Ye. Study on key technologies and applications of magnetic bearings[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 12-20.
[8] Eryong H, Kun L. A novel structure for low-loss radial hybrid magnetic bearing[J]. IEEE Transactions on Magnetics, 2011, 47(12): 4725-4733.
[9] Xu Yanliang, Dun Yueqin, Wang Xiuhe, et al. Analysis of hybrid magnetic bearing with a permanent magnet in the rotor by FEM[J]. IEEE Transactions on Magnetics, 2006, 42(4): 1363-1366.
[10] 赵旭升. 永磁偏置径向磁轴承拓扑研究及其进展[J].微特电机, 2016, 44(1): 81-86.
Zhao Xusheng. Research and development of permanent magnet biased radial magnetic bearing topology[J]. Small & Special Electrical Machines, 2016, 44(1): 81-86.
[11] 梅磊, 邓智泉, 赵旭升, 等. 新结构混合型径向磁悬浮轴承[J]. 电工技术学报, 2009, 24(5): 13-18.
Mei Lei, Deng Zhiquan, Zhao Xusheng, et al. New configuration hybrid radial magnetic bearing[J]. Transactions of China Electrotechnical Society, 2009, 24(5): 13-18.
[12] 赵旭升, 邓智泉, 汪波. 异极性永磁偏置径向磁轴承的参数设计与实现[J]. 电工技术学报, 2012, 27(7): 131-138, 159.
Zhao Xusheng, Deng Zhiquan, Wang Bo. Parameter design and realization of permanent magnet biased heterploar radial magnetic bearing[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 131-138, 159.
[13] 吴磊涛, 王东, 苏振中, 等. 异极式永磁偏置径向磁轴承的建模与实验[J]. 电工技术学报, 2018, 33(5): 1051-1057.
Wu Leitao, Wang Dong, Su Zhenzhong, et al. Modeling and experiment of permanent magnetic biased radial Heter-Polar magnetic bearing[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(5): 1051-1057.
[14] Munteanu G, Binder A, Schneider T. Loss measure- ment of a 40kW high-speed bearingless PM syn- chronous motor[C]//2011 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, USA, 2011: 722-729.
[15] Le Yun, Sun Jinji, Han Bangcheng. Modeling and design of 3-DOF magnetic bearing for high-speed motor including eddy-current effects and leakage effects[J]. IEEE Transactions on Industrial Electro- nics, 2016, 63(6): 3656-3665.
[16] Zhu Runze, Xu Wei, Ye Caiyong, et al. Novel heteropolar radial hybrid magnetic bearing with low rotor core loss[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1-5.
[17] 刘虎, 房建成. 新型永磁偏置轴向磁轴承的磁力特性[J]. 机械工程学报, 2010, 46(8): 167-174.
Liu Hu, Fang Jiancheng. Magnetic force characteri- stics of a novel permanent magnet biased axial magnetic bearing[J]. Journal of Mechanical Engin- eering, 2010, 46(8): 167-174.
[18] Zhong Yunlong, Wu Lijian, Huang Xiaoyan, et al. An improved magnetic circuit model of a 3-DOF magnetic bearing considering leakage and cross coupling effects[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1-6.
[19] 汪波, 邓智泉, 赵旭升, 等. 基于精确磁路的永磁偏置轴向径向磁轴承设计[J]. 中国机械工程, 2012, 23(17): 2036-2040, 2047.
Wang Bo, Deng Zhiquan, Zhao Xusheng, et al. Design of permanent magnet biased axial-radial magnetic bearing based on accurate magnetic cir- cuit[J]. China Mechanical Engineering, 2012, 23(17): 2036-2040, 2047.
[20] 王宝龄. 电磁电器设计基础[M]. 北京: 国防工业出版社, 1989.
Research of New Hybrid Axial-Radial Magnetic Bearing Based on Accurate Magnetic Circuit
Abstract This paper proposes a structure of solid homo-polar axial-radial magnetic bearing, which has the advantages of uniform magnetic field distribution and small axial space. Considering the characteristics of this new hybrid axial-radial magnetic bearing, such as compact structure and complex magnetic field distribution, an accurate magnetic circuit model considering magnetic flux leakage was established combined with the two-dimensional finite element simulation results. According to the magnetic circuit model, the magnetic density in air, stiffness and bearing capacity of the structure were calculated. The simulation results are basically consistent with the calculation results. It is shown that the rotor can achieve stable suspension at high speed, which verifies the feasibility of the structure.
keywords:Hybrid, axial-radial magnetic bearing, equivalent magnetic circuit, leakage magnetic field, finite element
中图分类号:TH133.3
DOI: 10.19595/j.cnki.1000-6753.tces.200029
国家自然科学基金资助项目(51577087)。
收稿日期2020-01-07
改稿日期 2020-02-13
禹春敏 男,1991年生,博士研究生,研究方向为混合型磁悬浮轴承。E-mail: ycm@nuaa.edu.cn
邓智泉 男,1969年生,教授,博士生导师,研究方向为高速电机技术、磁轴承技术、无轴承电机等。E-mail: dzq@nuaa.edu.cn(通信作者)
(编辑 崔文静)