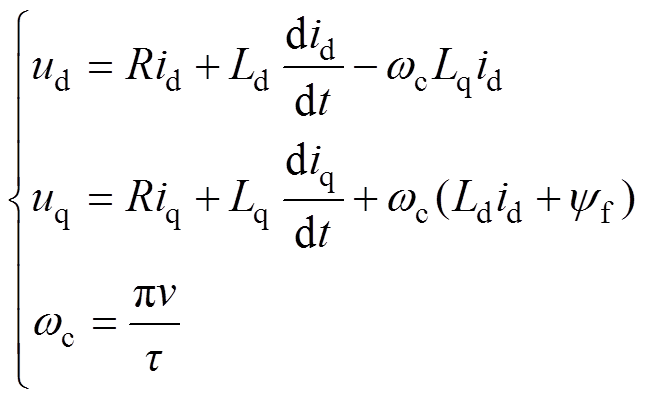（1）摘要 为了优化永磁同步直线电机的调速性能，解决永磁同步直线电机对速度传感器依赖程度高的问题，该文设计一种带模型参考自适应观测器的永磁同步直线电机预测电流控制系统（MPC-MRAS）。利用去除交叉耦合电动势的定子电压方程设计模型预测电流控制器，取代传统电流控制器；自适应观测器的参考模型利用电机的实际模型进行设计，可调模型利用估计的电流模型进行设计，电机估值速度通过参考模型和可调模型的电流差值设计的自适应律得出。该方案不仅降低电流控制器对电机参数的依赖程度，消除电流耦合对模型预测控制器的影响；同时，还使控制系统的复杂性和成本得到了简化，提高控制系统的控制性能和抗干扰能力。利用仿真软件搭建预测控制器和自适应观测器应用于电机控制系统验证所提控制策略的优越性。经过验证该控制策略可以实现对速度进行在线准确辨识，并且还可以有效地减少电流纹波和提高电流的跟踪性能。
关键词：永磁同步直线电机 无速度传感器 模型预测控制 模型参考自适应
近年来，随着稀有资源的开发和冶炼技术的发展，直流电机和交流异步电机正逐步落后于社会，并被永磁同步电机所替代。随着当今社会不断发展的高速加工技术、精密制造技术和数控技术等先进制造技术，永磁同步电机正在逐渐演变为当前数控设备的发展趋势。永磁同步直线电机直接驱动作为目前广泛应用于高精度工业领域的新型驱动方式，不仅可以很大程度上缩短给进系统的反应时间，而且也提高了控制系统的控制精度[1-2]。
高电流带宽和强鲁棒性正在逐渐成为高精密永磁同步直线电机电流闭环控制器的发展趋势[3]，目前主要的控制策略有滞环[4-5]控制、PI控制、重复控制[6]和预测控制[7-9]等控制方法。模型预测控制（Model Predictive Control, MPC）将控制系统中的信息，在不使用电机参数的情况下，预测将来几个周期时刻的控制量增量，再经过优化函数的计算得到最适合的控制值[10]。预测控制算法已经在电机控制系统领域广泛应用。文献[11-12]将基于电机数学模型设计的预测控制器分别应用到永磁同步电机控制系统和异步电机控制系中，使得控制系统的控制性能得到提高。
在电机控制系统中，为了更好地体现出控制器控制性能，控制系统反馈到控制器的信息必须是快速而准确的。为了简化电机控制系统的体积、降低安装费用以及适应各种严苛环境，将无速度传感器技术引入到电机控制系统中。无速度传感器同时克服了机械速度传感器存在的严重缺陷，并且为目前电机控制的发展开辟了新航路[13]。在无速度传感器技术中，前沿的控制器技术分为高频信号注入法和基波反电动势观测法[14-17]。自适应观测器是基于电机的电压方程在稳定性的基础上设计出来的一种可以辨识电机参数的控制策略。文献[18-19]设计的观测器通过调节估计数学模型的参数，使可调和参考模型的电流差值趋近于零，使参数估计值保持逐渐收敛，并使其在电机控制系统中保持优越的动态性能[17]。
本文设计了一种带自适应观测器的永磁同步直线电机预测电流控制的策略。利用去除交叉耦合电动势的定子电压方程设计预测电流控制器，取代传统的电流控制器，提高了电机控制系统的控制性能。本文提出的自适应观测器的参考模型利用电机的实际模型进行设计，可调模型利用估计的电流模型进行设计，可通过参考模型和可调模型的电流差值设计自适应律估计电机速度。最后，利用仿真软件验证所提出控制策略的优越性，并通过仿真和实验验证其有效性。
在永磁同步直线电机旋转坐标系下，利用定子电压方程对电流预测控制器进行设计，其定子电压方程可以表示为
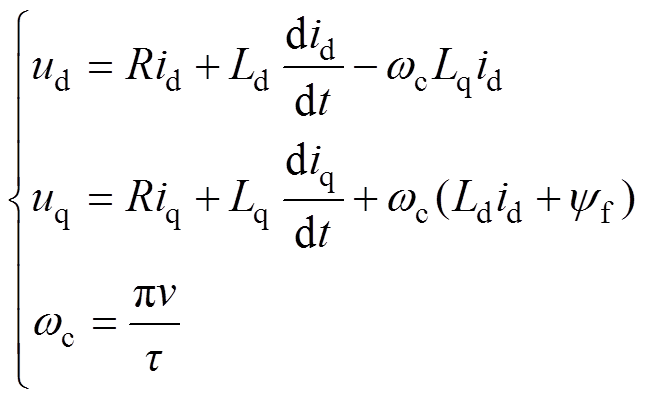（1）式中，R为定子电阻；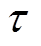
为直线电机极矩；v为电机运行的速度；
、
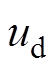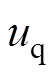分别为d轴和q轴的电压分量；
、
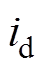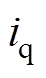分别为d轴和q轴的电流分量；
、
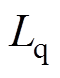为d轴和q轴的电感分量；
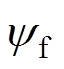为定子磁链；wc为电角速度。
可通过将旋转坐标系下的电压方程利用转化公式简化为两个单输入单输出系统[11]。将定子电流分别在d轴和q轴方向产生的交叉耦合电动势考虑为系统扰动，通过以上转化过程得到的电流控制的对象方程[20]表示为
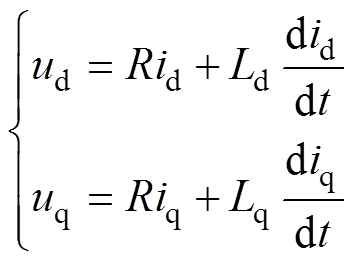（2）交叉耦合电动势为
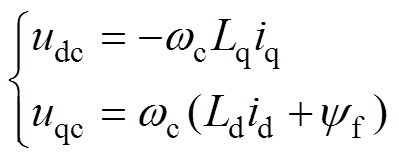（3）
将式（2）写成状态方程的形式为
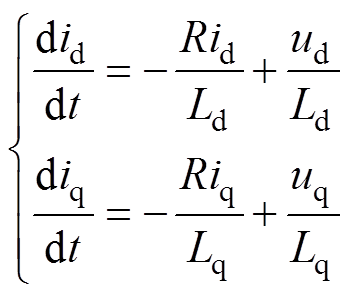（4）以d轴为例，对状态方程进行一阶欧拉公式离散化得到
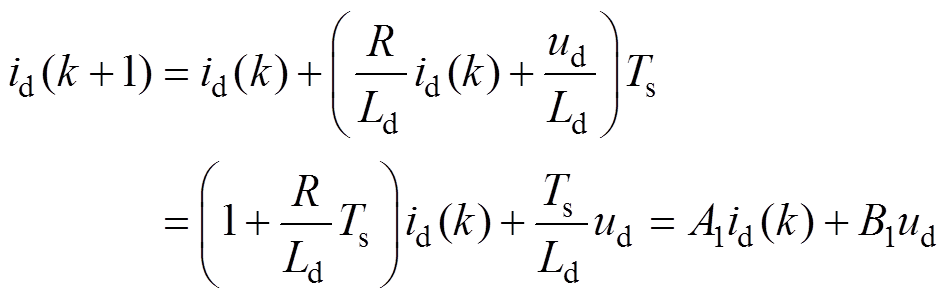（5）
其中
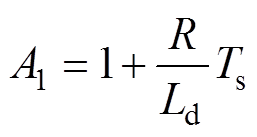
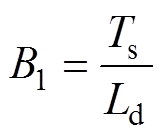
同样可以得到q轴电流的离散模型为
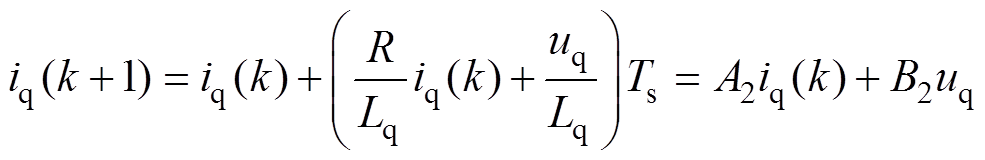（6）
其中
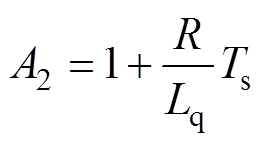
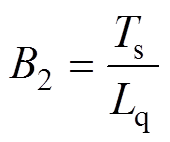
式中，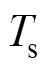
为采样时间。
模型预测的电流控制器算法采用三步预测法，算法的实现过程如下。
假设控制量保持不变，均为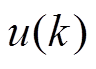
，用式（5）在第k个周期对未来3个周期的状态量进行预测，则可以得到控制对象的预测值为
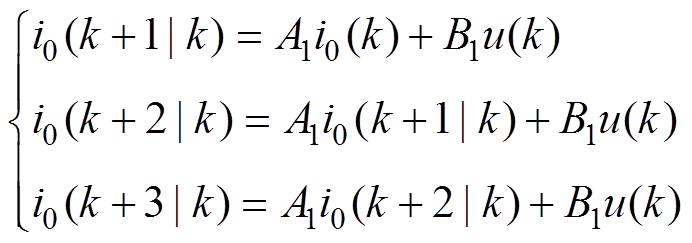（7）式中，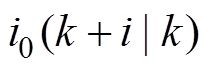
为在第k个周期开始得到的理想状态下的电流预测值，i=1, 2, 3。
在得到理想状态下的预测值，并充分考虑系统的控制量的变化过程后，假设每个周期的控制增量均为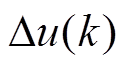
，利用式（7）和控制量的增量可以得到控制对象的实际预测值[11]为
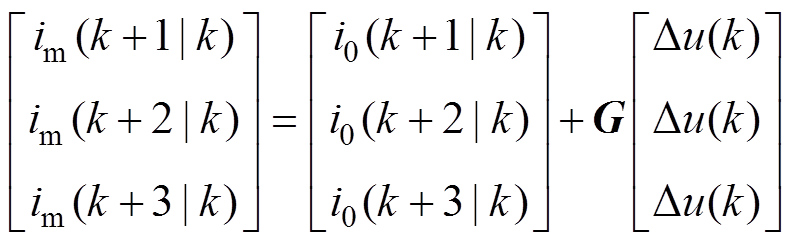（8）其中
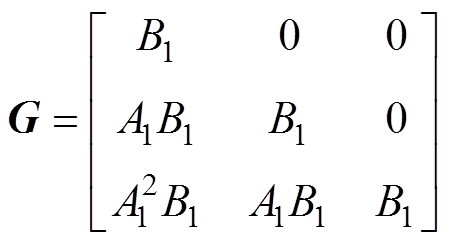
式中，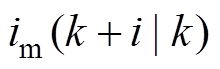
为考虑系统控制量变化时得到的电流预测值，i=1, 2, 3。
为了消除因各种误差因素给式（8）中的预测电流误差带来的影响，并确保控制系统中的预测值的准确性和系统本身的鲁棒性[21]，采用反馈校正的方式对预测的电流误差进行校正。
假设第k+1个周期d轴和q轴电流分量分别为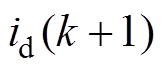
和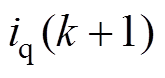
，则校正误差为
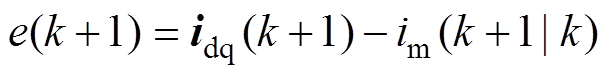（9）将式（9）得到的矫正误差e(k+1)对实际的电流进行补偿，可以得到校正后的电流预测值为
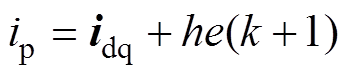（10）
式中，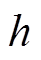
为反馈系数。
根据电流模型预测控制算法特点，由于在第k个周期几乎无法得到后面3个周期时的d轴和q轴电流，因此为了解决上述问题，在实际的控制中可以假设后面3个周期电流的给定值与当前值一致，表示为
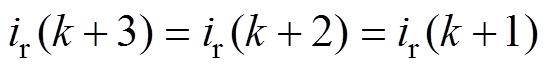（11）式中，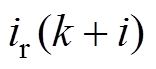
为每个周期电流的给定值，i=1, 2, 3。
控制器根据当前时刻的预测值和给定值可以得到最原始控制量的增量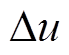
，但这种控制增量变化可能会很剧烈，这就使整个控制系统不易调节，所以应该对其进行一定的控制。采用评价函数得到最优的控制量，评价函数为
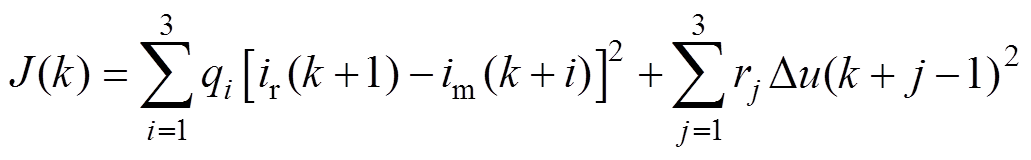（12）式中，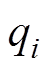
、
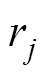为加权系数，分别表示对跟踪误差及控制量变化的抑制。对
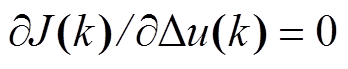求解，可得到第k个周期时的最优的控制增量
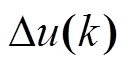为
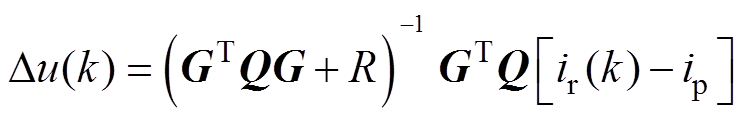（13）其中
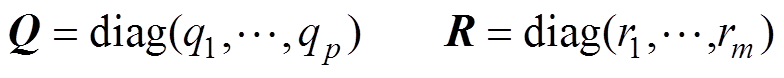
利用式（13），可通过计算得到在相应的计算周期中最优控制量的增量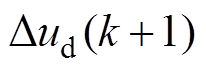
和
，则可计算出所需要的最优的控制量[11]为
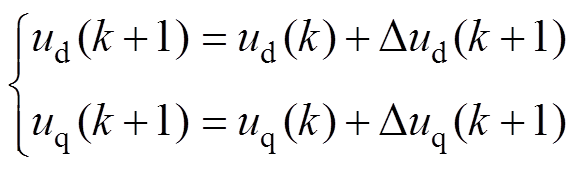（14）为了进一步加强对于系统的控制能力，将式（3）交叉耦合电动势作为前馈补偿项加到式（14）中，得最优控制量为
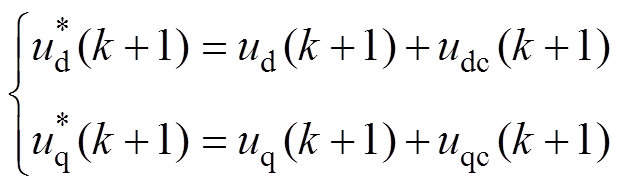（15）
在k+1时刻系统实际控制量为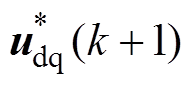
，到了下一个预测周期[21]，即新的计算最优控制量为
。
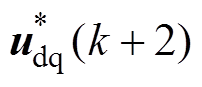以d轴为例，设计的电流预测控制器框图如图1所示。
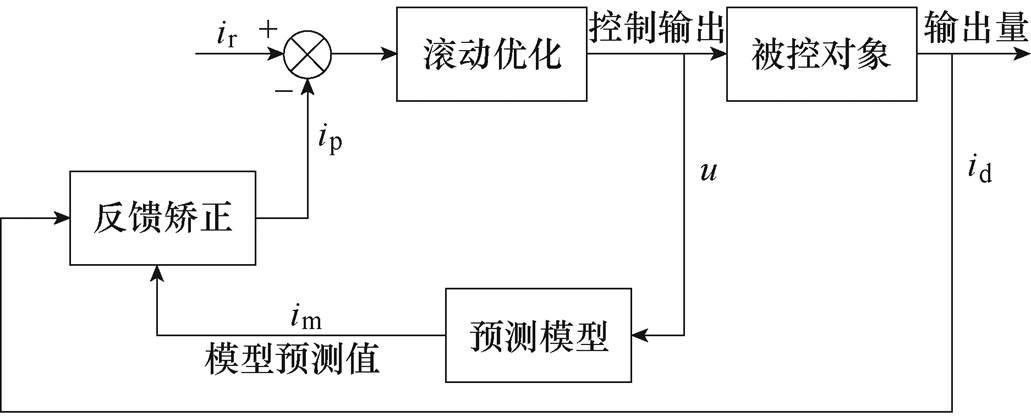
图1 电流预测控制器框图
Fig.1 Block diagram of current prediction controller
为了建立永磁同步直线电机的自适应辨识模型，并将其应用到电机控制系统中，参考模型将采用电机的实际模型。为了得到辨识系统的可调模型，可以将永磁同步直线电机的定子电流进行Clarke变换和Park变换，得到dq坐标系下的定子电流方程，根据所得的定子电流方程可得到辨识系统的可调模型。通过两个模型的并联作用，能够估算出速度，积分后得到估计的动子位置[22]。
在充分考虑永磁同步直线电机的电磁特点和运动特性下，其定子电流方程[23]可以表示为
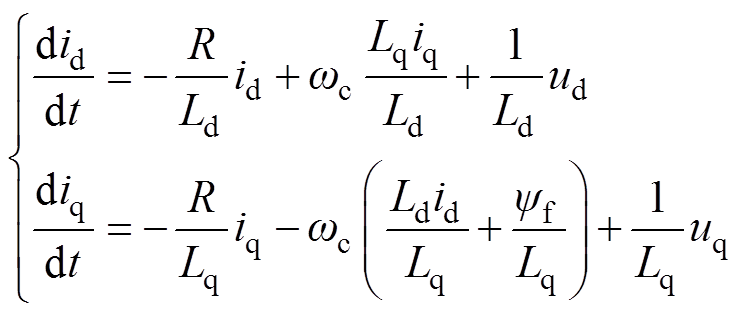（16）为了获得可调模型，对式（16）进行变换得
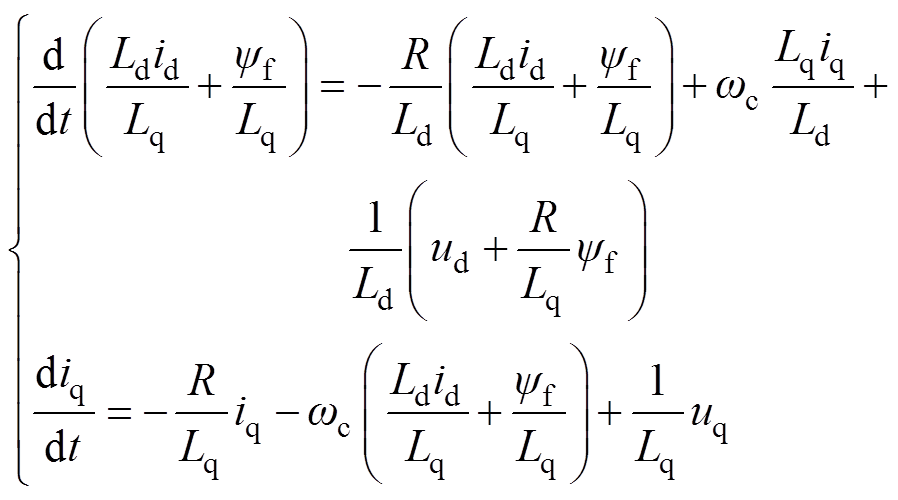（17）
为了便于分析，令式（17）中
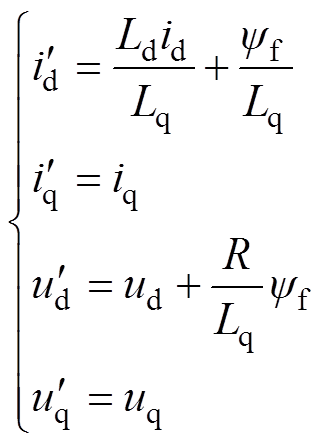
式（17）化简后为
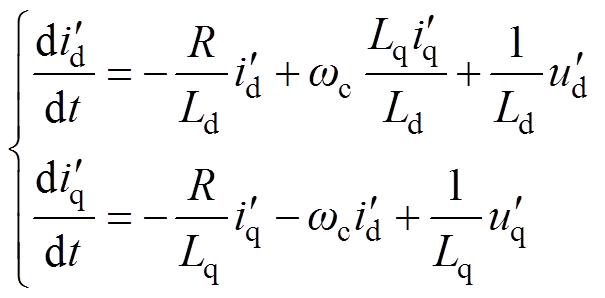（18）
将式（18）以估计值的形式表示为
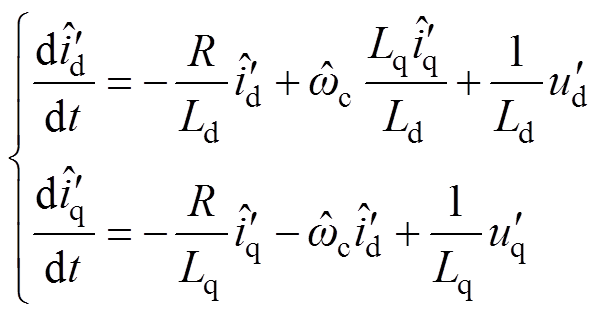（19）模型参考自适应系统（Model Reference Adaptation System, MRAS）框图如图2所示，将式（18）和式（19）分别设计为自适应观测器的参考模型和可调模型[24]。定义广义误差为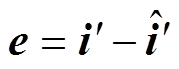
，式（18）减去式（19）为
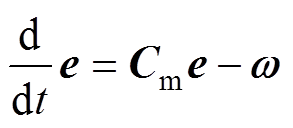（20）
其中
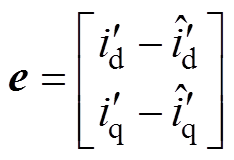
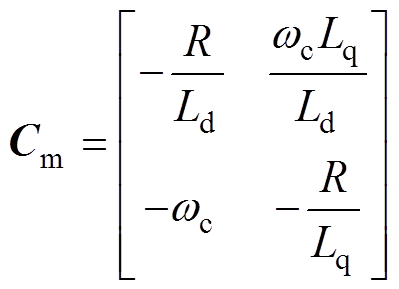
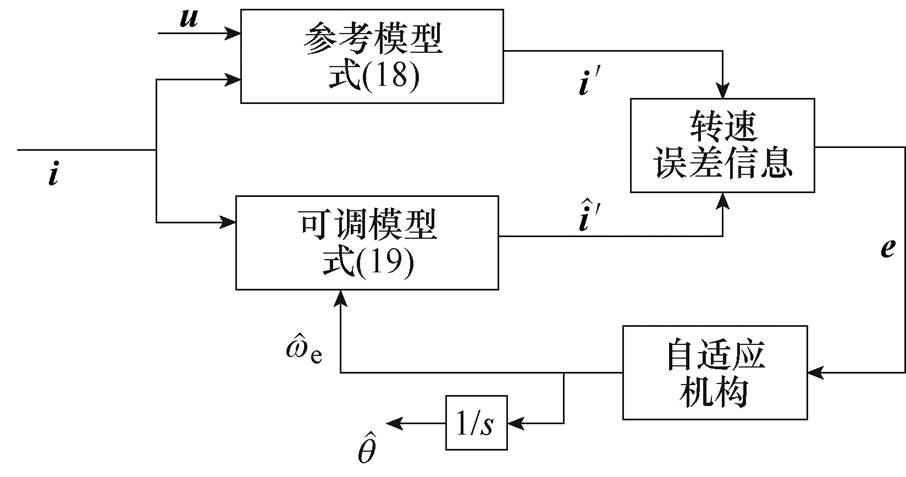
图2 模型参考自适应系统框图
Fig.2 Model reference adaptive system block diagram
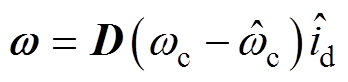
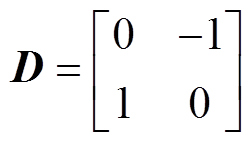
为了使该系统是稳定的[25]，需要使非线性时变的反馈环节满足波波夫超稳定理论的不等式，即
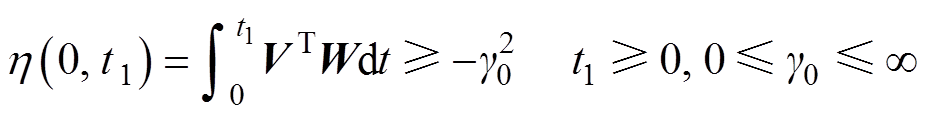（21）
式中，V为待证明稳定性的系统输入；W为待证明稳定性的系统输出。
对式（21）进行反向求值可以得到自适应系统的自适应律[26]，其结果为
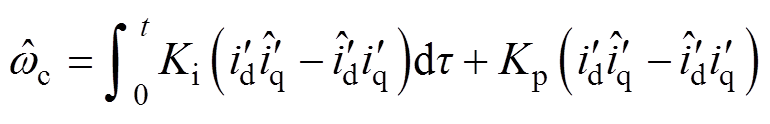（22）对式（22）中得到的电机估计速度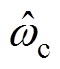
进行积分可以得到永磁同步直线电机的位置估计值
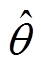为
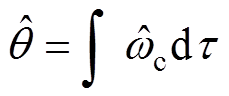（23）
模型参考自适应系统框图如图2所示[27]。
为了验证本文所提出的控制策略对速度进行辨识，可有效地抑制电流波纹和提高电流的跟踪性能，将设计的自适应观测器和模型预测控制器应用于电机控制系统中。利用仿真软件搭建PI控制、滑模控制（Sliding Mode Control, SMC）和本文提出的控制策略的仿真模型，并比较在调速和变负载情况下的电机速度和电路的波形。永磁同步直线电机的主要参数见表1。控制系统的采样时间为10ms。
图4和图5分别为电机在MPC-MRAS情况下的速度波形和与应用传统PI控制和SMC算法情况下的电机运行速度波形。负载为50N时，由图可以发现，本文所提的控制策略可以准确地辨识电机运行速度，速度误差绝对值的最大值仅为0.004m/s，与传统PI、SMC策略比较，MPC-MARS情况下设定速度改变后的电机运行速度波动范围非常小，电机运行速度稳定，说明了本文所提出的控制策略的控制性能比较优越。
图3 电机控制系统框图
Fig.3 Block diagram of motor control system
表1 电机主要参数
Tab.1 Main parameters of straight line
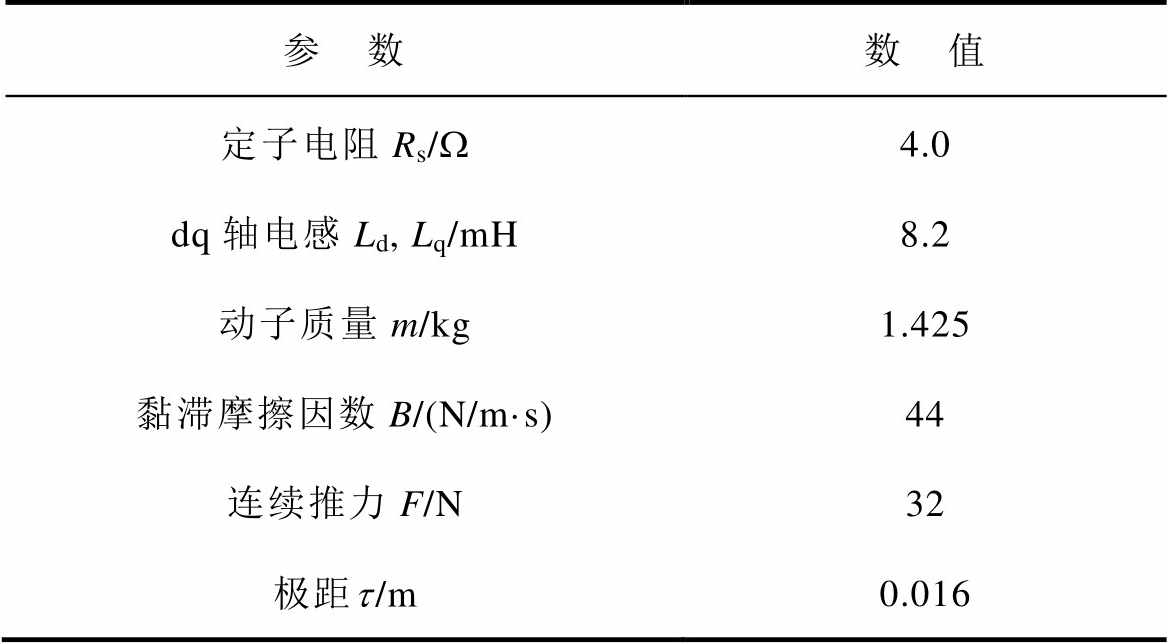
参 数数 值 定子电阻Rs/W4.0 dq轴电感Ld, Lq/mH8.2 动子质量m/kg1.425 黏滞摩擦因数B/(N/m·s)44 连续推力F/N32 极距t/m0.016
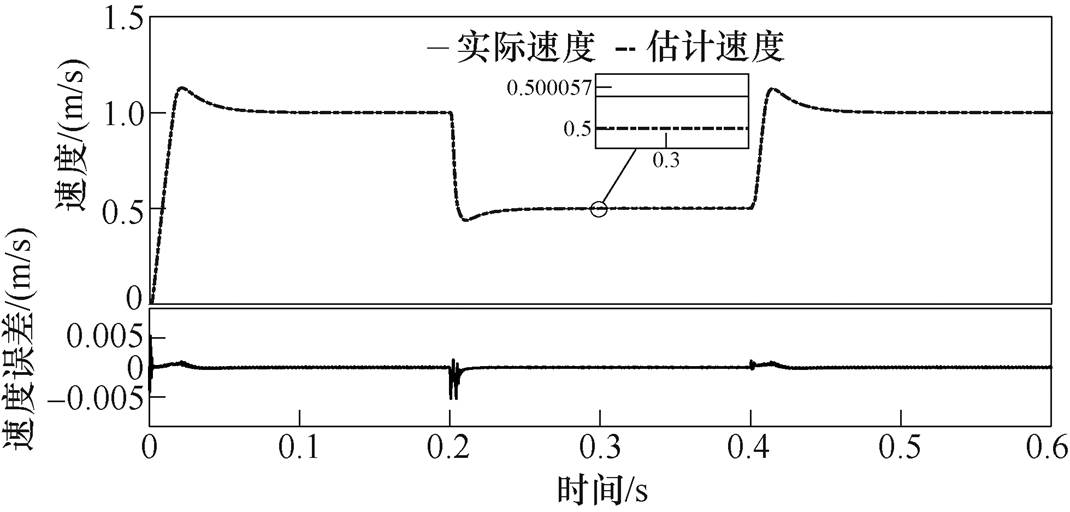
图4 在MPC-MRAS情况下，改变运行速度时波形
Fig.4 In the case of MPC-MRAS, the waveforms of changing the running speed
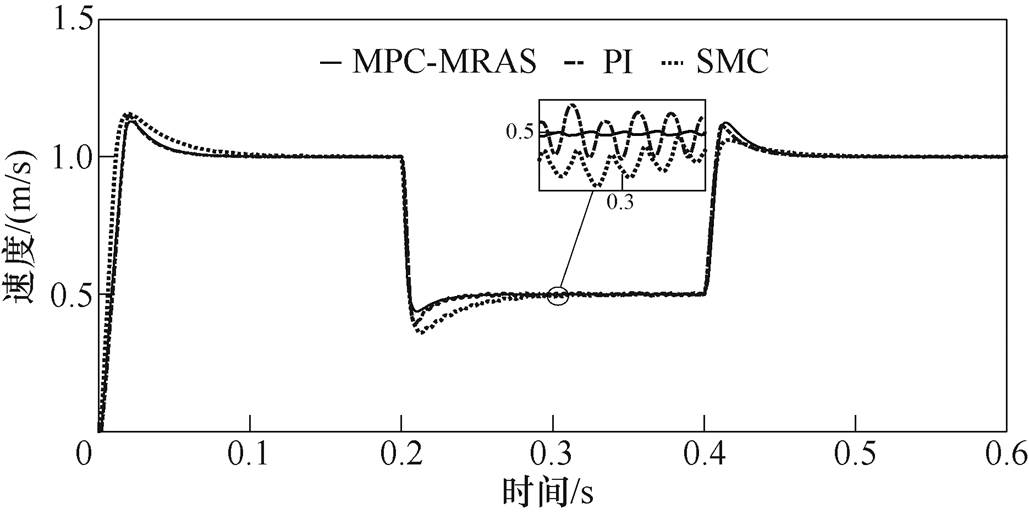
图5 MPC-MRAS与PI、SMC改变运行速度的对比波形
Fig.5 Contrast waveforms MPC-MRAS and PI, SMC speed changing operating speed
图6和图7分别为电机在MPC-MARS情况下与应用传统PI和SMC情况下电机q轴电流波形和与应用传统PI和SMC情况下的q轴电流跟踪的误差波形。负载转矩为50N时，在电机加减速运行过程中，本文所提的控制策略与传统PI、SMC策略相比，q轴电流不仅跟踪精度比较高，而且电流的波动变化非常小。
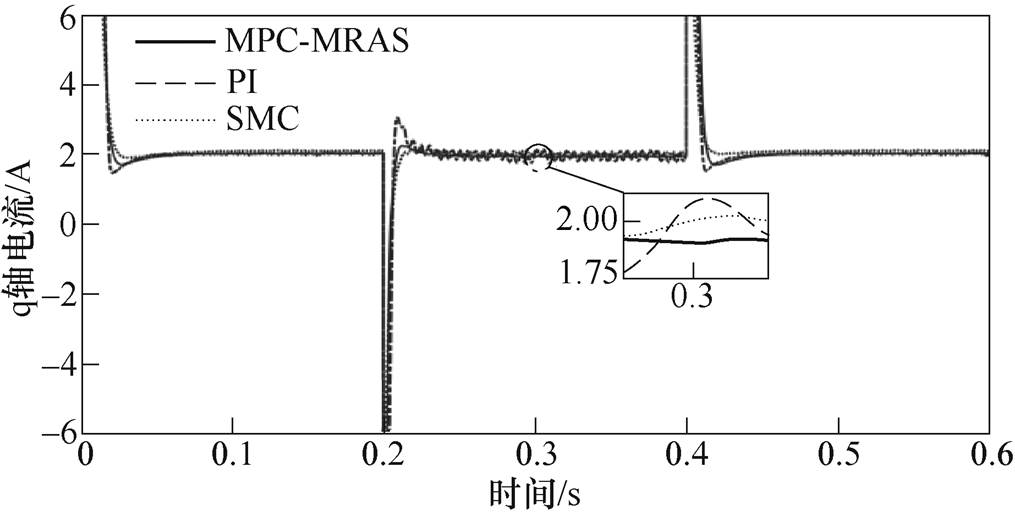
图6 速度改变时MPC-MRAS与PI、SMC电流波形
Fig.6 MPC-MRAS and PI, SMC current waveforms when the speed changes
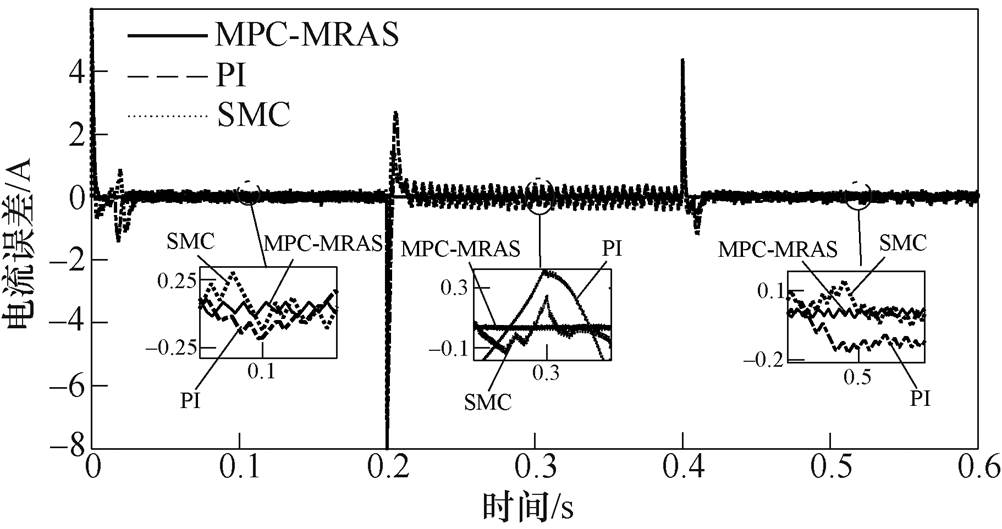
图7 速度改变时MPC-MRAS与PI、SMC电流误差波形
Fig.7 MPC-MRAS and PI, SMC current error waveforms when the speed is changed
图8为PMSLM运行过程中突然改变负载的情况下MPC-MRAS控制系统的电机速度跟踪波形，图9为所设计的控制策略与PI和SMC的速度对比波形。电机运行速度为1m/s时，在改变负载转矩的过程中，由图8可以发现，控制系统可以准确地辨识电机运行速度，仅在改变电机负载时速度跟踪误差出现微小波动。观察图9可以发现，与传统PI、SMC策略比较，MPC-MARS情况下负载改变后的电机运行速度可以迅速地保持以设定速度运行，电机运行速度稳定，说明了本文所提出策略的控制性能的优越性。
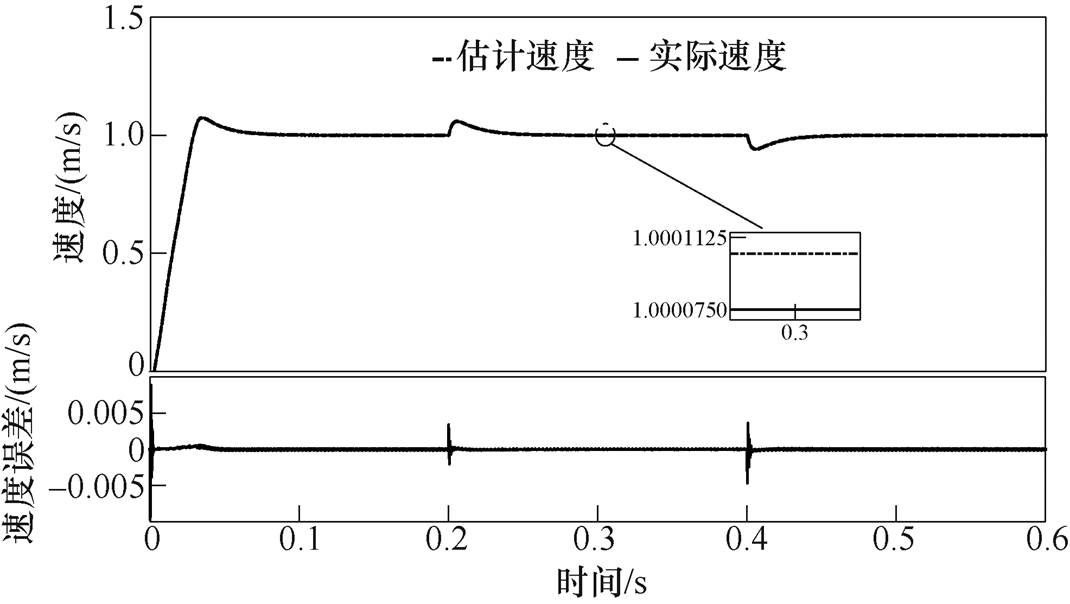
图8 MPC-MRAS情况下，改变负载时的速度波形
Fig.8 In the case of MPC-MRAS, the speed waveforms of changing the load
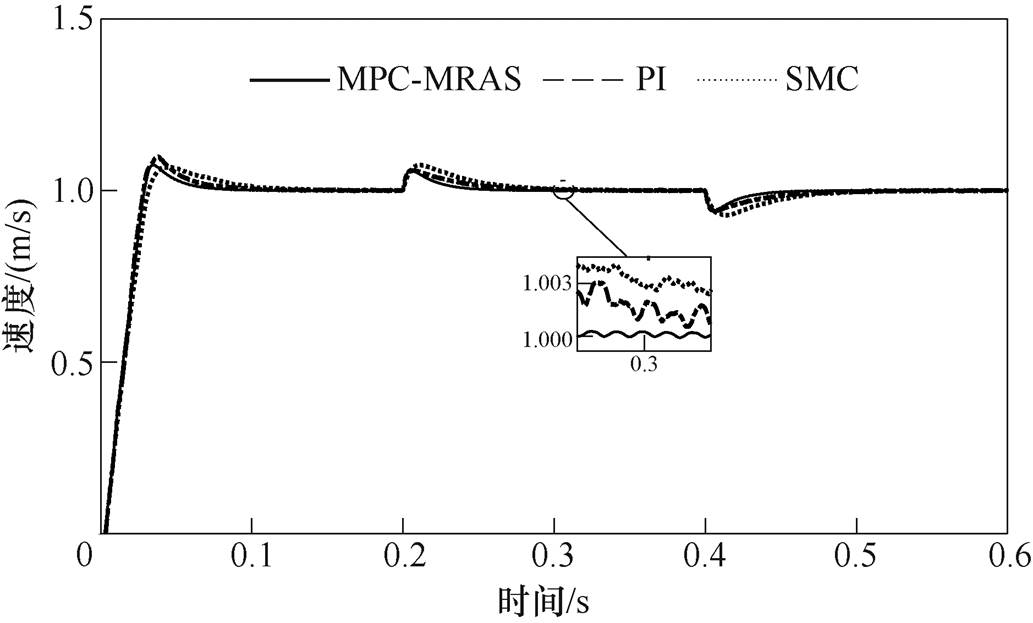
图9 MPC-MRAS与PI、SMC改变负载时速度对比波形
Fig.9 MPC-MRAS and PI, SMC speed comparison waveforms when changing the load
在改变电机负载的运行条件下，图10为MPC- MARS与PI、SMC策略的电流波形，图11为三种控制方案的电流误差波形。考虑到实际电机行程问题，将实验平台样机速度设定为1m/s，观察并分析整体实验过程，由图10可以发现，MPC- MARS的电流波形其波动范围较小。观察图11发现，与传统PI、SMC策略相比，MPC-MARS情况下q轴电流跟踪误差比较小，且无波动，说明MPC-MARS策略q轴电流跟踪精度较高。
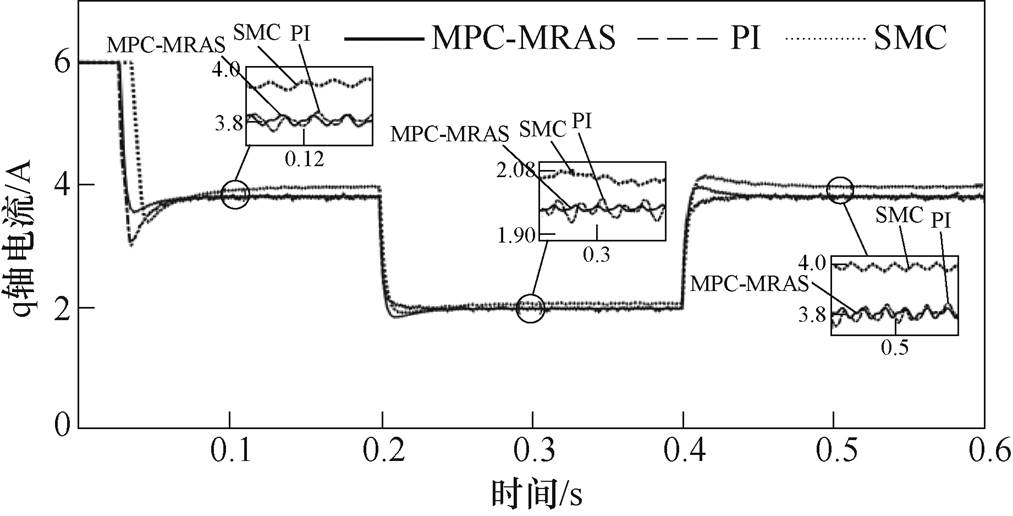
图10 改变负载时的MPC-MRAS与PI、SMC电流波形
Fig.10 MPC-MRAS and PI, SMC current waveforms when the load changes
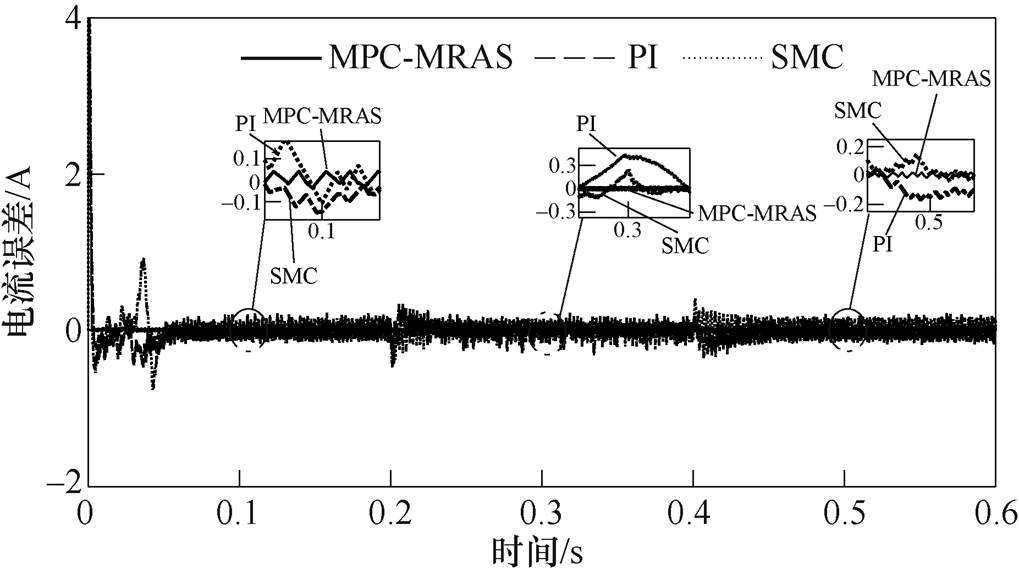
图11 改变负载时MPC-MRAS与PI、SMC电流误差波形
Fig.11 MPC-MRAS and PI, SMC current error waveforms when the load changes
本文的实验验证是基于STM32开发板和Matlab的自动代码生成工具为基础进行的。利用STM32CubeMX软件生成底层配置代码，提高了工作效率。算法实验平台如图12所示。永磁同步直线电机作为被控对象，采用代码生成工具生成了控制算法c代码，并在STM32开发板上进行了算法验证。实验中控制系统的采样频率为18kHz。
图12 实验平台
Fig.12 Experiment platform
轻载时，给定速度为1m/s，在0.2s将电机运行速度降至0.5m/s，电机运行0.2s后在0.4s时刻将电机运行速度升至1m/s。图13为MPC-MRAS、PI和SMC情况下电机运行速度波形，可以发现，电机运行过程中，MPC-MRAS与PI、SMC情况相比，在设定速度改变后，MPC-MRAS情况下电机速度较平稳，而PI、SMC情况下电机速度有波动。图14为电机运行过程中模型参考自适应系统估计的与电机运行速度的跟踪误差结果，可以发现，跟踪误差很小，即使在调速时刻跟踪误差的绝对值也小于0.006m/s。
电机运行过程中，MPC-MRAS、PI和SMC情况下d轴的电流与控制系统给定电流值的跟踪误差如图15所示。可以发现，MPC-MRAS与PI、SMC情况相比，在改变设定速度时q轴电流跟踪误差变波动很小。在电机加减速稳定运行过程中，PI、SMC情况下，q轴电流的跟踪误差峰值绝对值分别为3.8mA、2.9mA，而MPC-MRAS情况下q轴电流的跟踪误差峰值绝对值小于0.5mA，表明在MPC- MRAS情况下控制系统中q轴的电流可以较快速地跟踪上控制系统给定电流值。
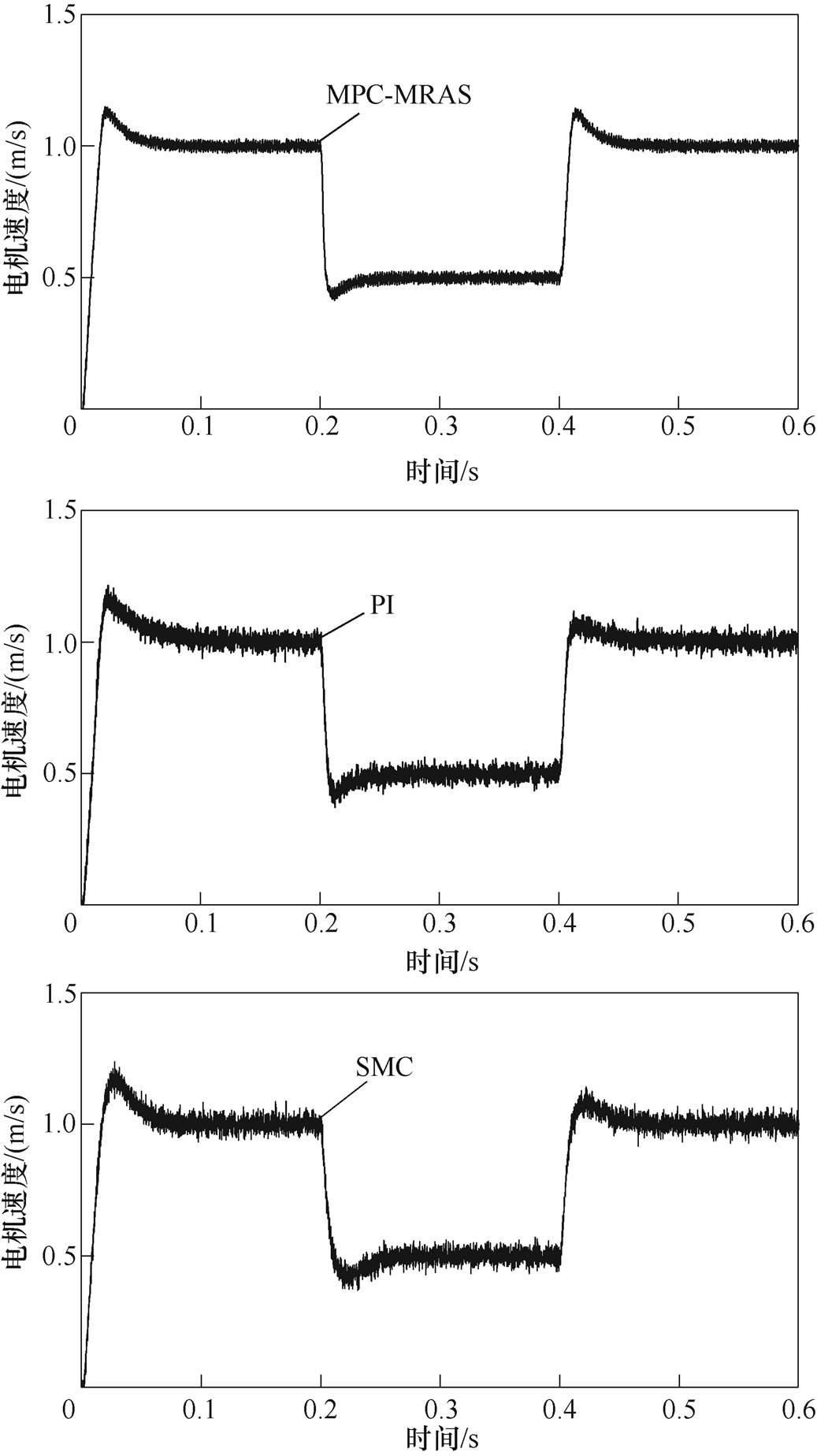
图13 速度改变时的电机速度对比波形
Fig.13 Comparison waveforms of motor speed when speed is changed
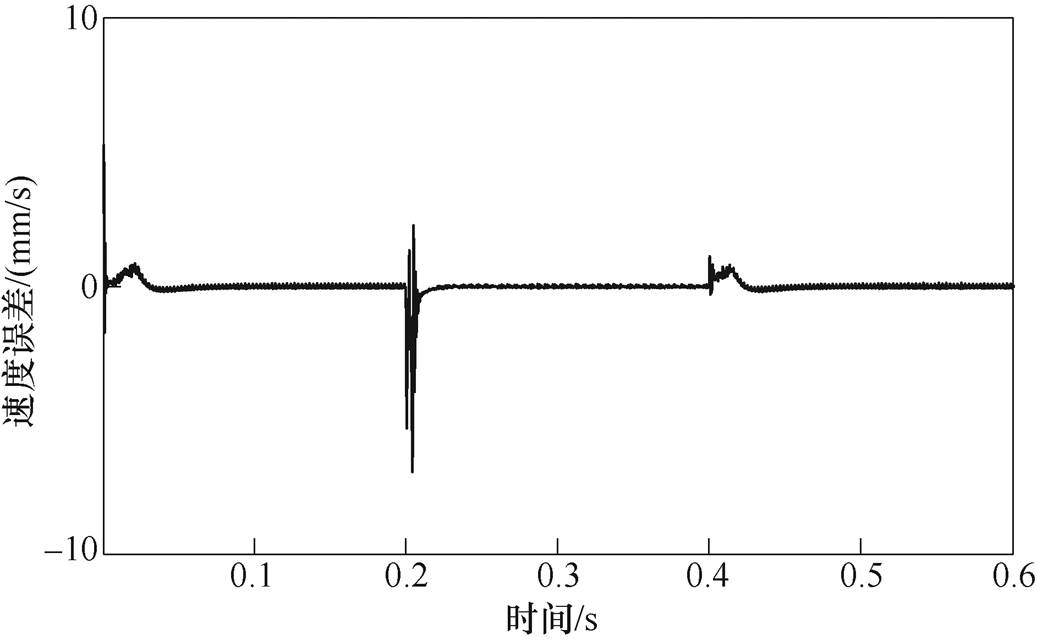
图14 速度改变时，MPC-MRAS的速度误差
Fig.14 The speed error of MPC-MRAS when the speed is changed
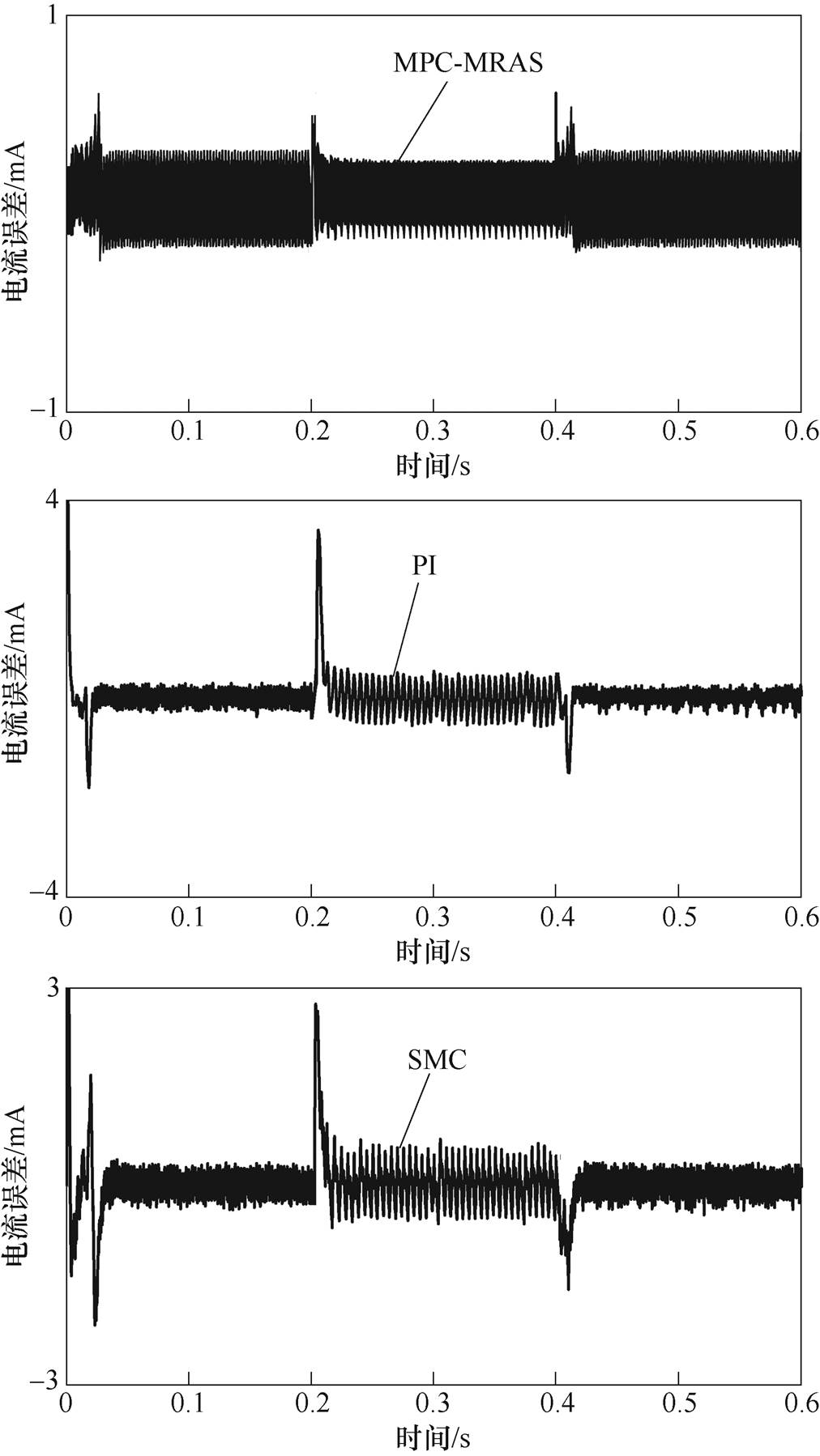
图15 负载变化时的电流误差
Fig.15 Current error when speed changes
给定速度为1m/s，电机重载起动，在稳定运行过程中改变所带负载。在0.2时刻突减负载，持续0.2s后在0.4s时刻突加回原负载。图16为MPC- MRAS、PI和SMC情况下电机运行速度波形，可以发现，电机运行过程中，MPC-MRAS与PI、SMC情况相比电机运行速度波动小，在改变负载后电机运行速度较快地恢复到设定速度。图17为MPC-MRAS情况下电机运行过程中模型参考自适应系统估计的速度与电机运行速度的跟踪误差结果，可以发现，跟踪误差很小，即使在负载改变后的瞬间跟踪误差的绝对值也小于0.005m/s。
电机运行过程中，MPC-MRAS、PI和SMC情况下d轴的电流与控制系统给定电流值的跟踪误差如图18所示。可以发现，MPC-MRAS情况与PI、SMC情况相比，在突然改变负载时q轴电流跟踪误差波形比较平稳波动较小。在电机带轻载和重载稳定运行过程中，PI、SMC情况下，q轴电流的跟踪误差峰值绝对值分别为2.1mA、1.5mA，而MPC-MRAS情况下q轴电流的跟踪误差峰值绝对值为0.5mA，表明在MPC-MRAS情况下控制系统中，q轴的电流可以较快速地跟踪上控制系统给定电流值。
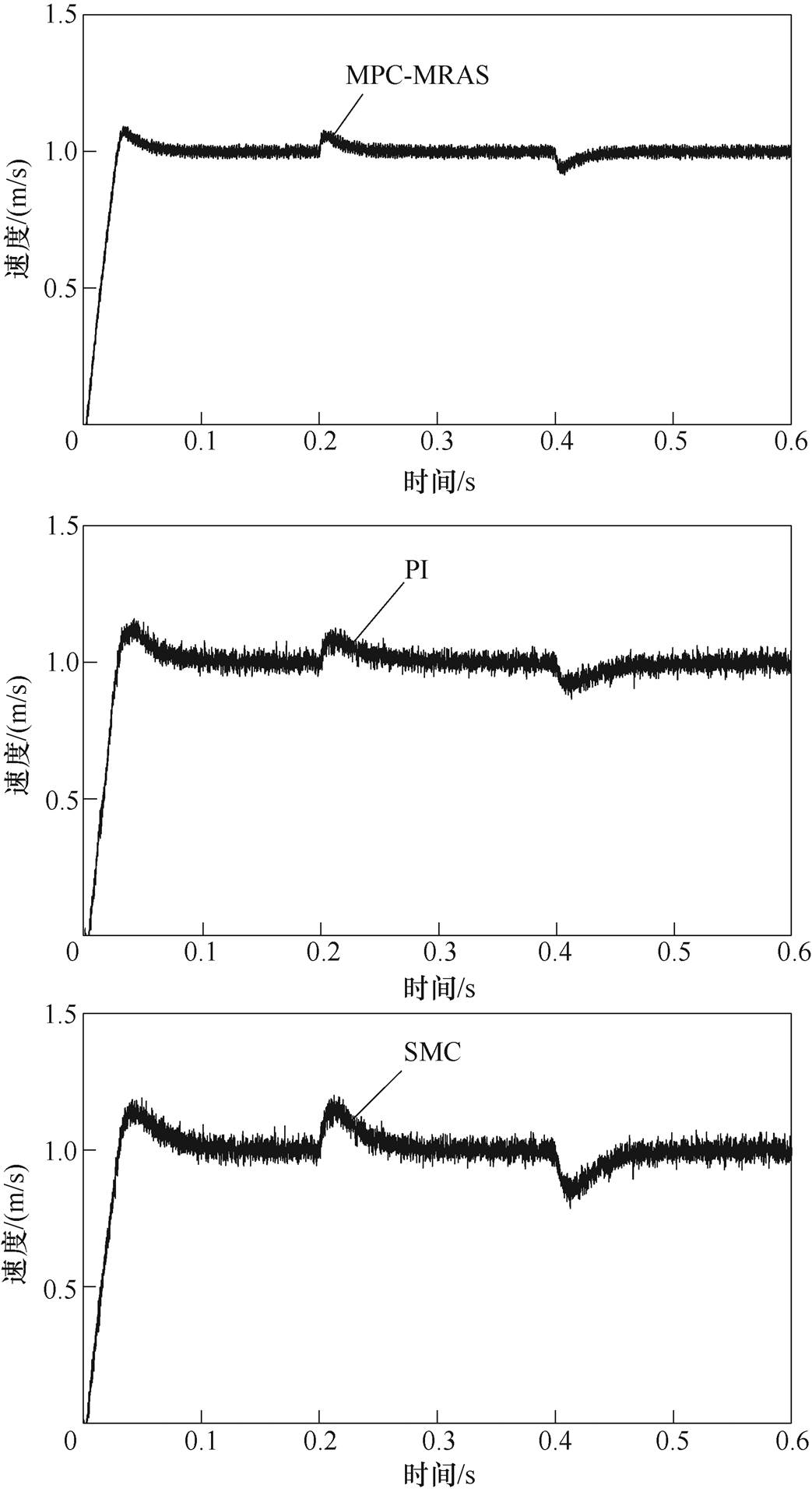
图16 负载变化时的对比波形
Fig.16 Comparison waveforms when load changes
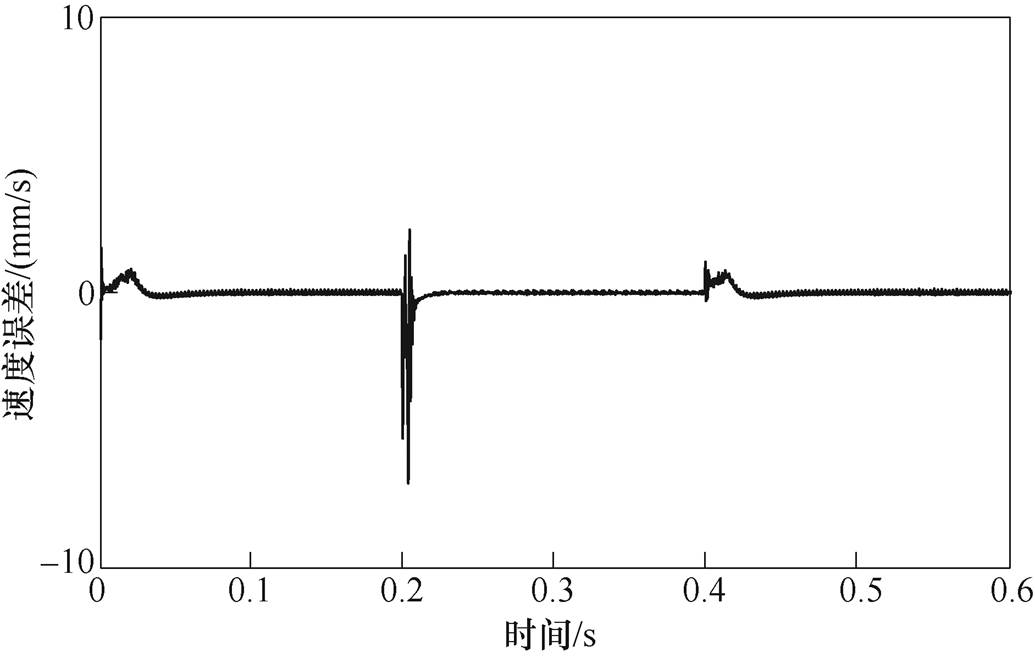
图17 负载变化时，MPC-MRAS速度误差
Fig.17 The speed error of MPC-MRAS when the load changes
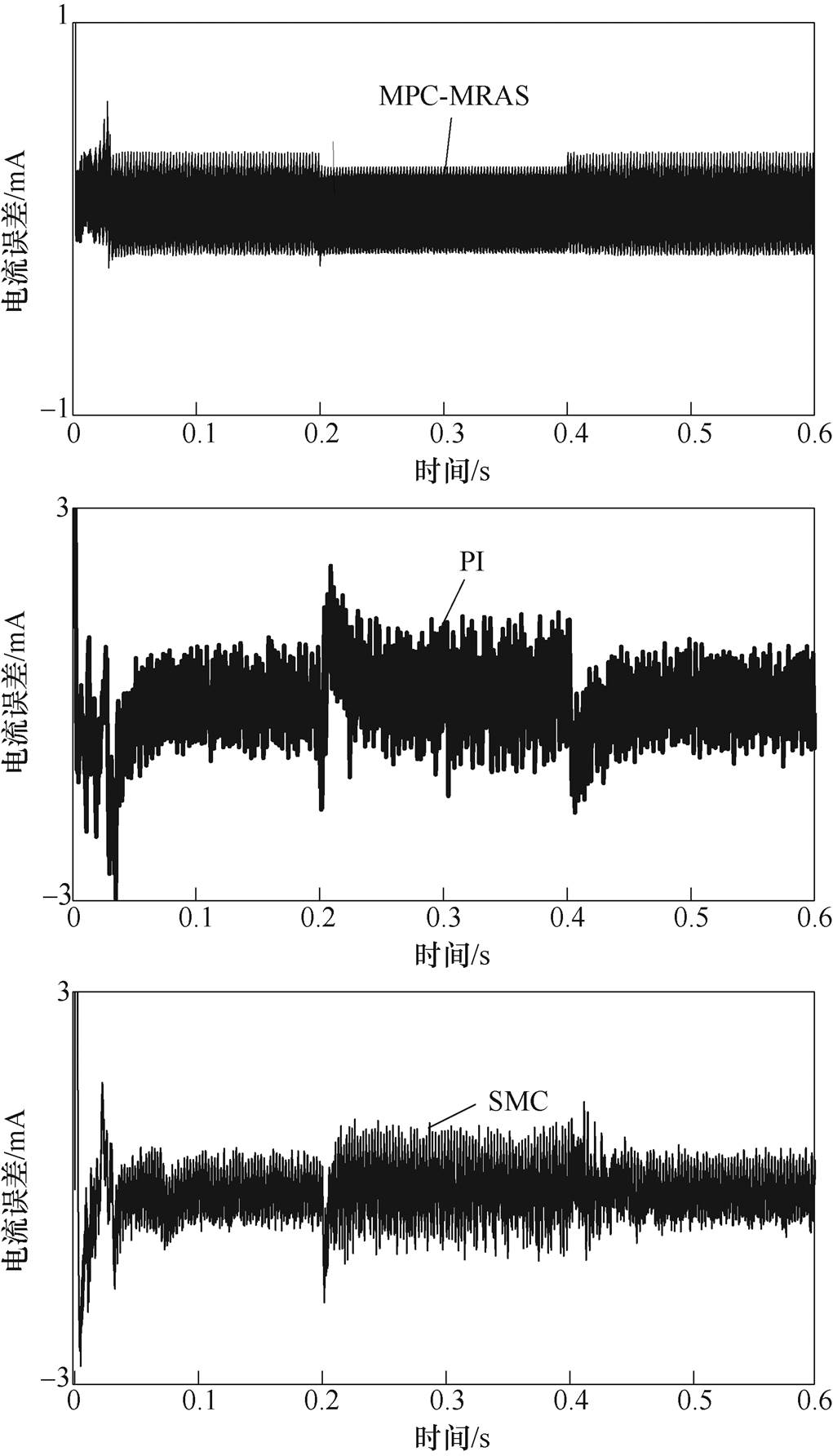
图18 负载变化时的电流误差
Fig.18 Current error when load changes
为了提高永磁同步直线电机的控制性能，本文采用模型预测控制器代替传统的PI控制器，并用模型参考自适应观测器替代机械传感器。在仿真与实验中，模型预测控制算法对永磁同步直线电机速度进行了有效地控制。模型参考自适应算法对于外界的干扰可以进行较为快速的反应，加快系统稳定。从实验结果进行分析，相较于传统控制方法，电流纹波得到了有效抑制，同时对电机速度进行了有效的跟踪。在速度实验与变载实验中，通过MPC- MARS算法控制，电机系统展现了对于外界干扰的强鲁棒特性，同时整体运行过程中电流波动小、系统恢复速度快、电机运行稳定。
参考文献
[1] 彭壮. 基于参数辨识的永磁同步电机无差拍电流预测控制[D]. 哈尔滨: 哈尔滨工业大学, 2017.
[2] 尹忠刚, 白聪, 杜超, 等. 基于内模干扰观测器的永磁同步直线电机无差拍电流预测控制方法[J]. 电工技术学报, 2018, 33(24): 5741-5750.
Yin Zhonggang, Bai Cong, Du Chao, et al. Non-beat current prediction control method of permanent magnet synchronous linear motor based on internal model interference observer[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5741- 5750.
[3] Wang Mingyi, Li Liyi, Pan Donghua, et al. High- bandwidth and strong robust current regulation for PMLSM drives considering thrust ripple[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6646-6657.
[4] Ho C N M, Cheung V S P, Chung H S H. Constant- frequency hysteresis current control of grid- connected VSI without band widthcontrol[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2484-2495.
[5] Berriri H, Naouar W, Bahri I, et al. Field pro- grammable gate array-based fault-tolerant hysteresis current control for AC machine drives[J]. IET Electric Power Applications, 2012, 6(3): 181-189.
[6] 武永燎, 李红, 宋欣达, 等. 基于改进型重复控制器的永磁同步电机电流谐波抑制方法研究[J]. 电工技术学报, 2019, 34(11): 2277-2286.
Wu Yongliao, Li Hong, Song Xinda, et al. Research on current harmonic suppression method of permanent magnet synchronous motor based on improved repetitive controller[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2277- 2286.
[7] Wang Xiaokun, Wei Xie, Wang Fengxiang. Finite- control-set model predictive torque control with a deadbeat solution for PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5402-5410.
[8] Martin D, Santi E. Autotuning of digital deadbeat current controllers for grid-tie inverters using wide bandwidth impedance identification[J]. IEEE Transa- ctions on Industry Applications, 2014, 50(1): 441- 451.
[9] Moon H T, Kim H S, Youn M J. A discrete-time predictive current control for PMSM[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 464-472.
[10] Yang Rui, Wang Mingyi, Li Liyi, et al. Robust predictive current control with variable-gain adaptive disturbance observer for PMLSM[J]. IEEE Access, 2018, 6(13): 13158-13169.
[11] 王东文, 李崇坚, 吴尧, 等. 永磁同步电机的模型预测电流控制器研究[J]. 电工技术学报, 2014, 29(增刊1): 73-79.
Wang Dongwen, Li Chongjian, Wu Yao, et al. Research on model predictive current controller of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2014, 29(S1): 73-79.
[12] 刘为杰. 异步电机模型预测控制系统设计[J]. 电气传动, 2018, 48(10): 11-15.
Liu Weijie. Design of asynchronous motor model predictive control system[J]. Electric Drive, 2018, 48(10): 11-15.
[13] 张立伟, 李行, 宋佩佩, 等. 基于新型滑模观测器的永磁同步电机无传感器矢量控制系统[J]. 电工技术学报, 2019, 34(增刊1): 70-78.
Zhang Liwei, Li Xing, Song Peipei, et al. Sensorless vector control system of permanent magnet synchronous motor based on a new sliding mode observer[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 70-78.
[14] Zhang Zhe, Zhao Yue, Qiao Wei, et al. A space- vector-modulated sensorless direct-torque control for direct-drive PMSG wind turbines[J]. IEEE Transa- ctions on Industry Applications, 2014, 50(4): 2331- 2341.
[15] Jain A K, Ranganathan V T. Modeling and field oriented control of salient pole wound field synchronous machine in stator flux coordinates[J]. IEEE Transactions on Industrial Electronics, 2011, 58(3): 960-970.
[16] Xu Z, Rahman M F. Comparison of a sliding observer and a Kalman filter for direct-torque-controlled IPM synchronous motor drives[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4179-4188.
[17] Fan Ying, Zhang Ling, Cheng Ming, et al. Sensorless SVPWM FADTC of a new flux-modulated permanent- magnet wheel motor based on a wide-speed sliding mode observer[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 3143-3151.
[18] 包广清, 祁武刚. 基于MRAS的异步电机无速度传感器应用研究[J]. 微特电机, 2020, 48(3): 43-47.
Bao Guangqing, Qi Wugang. Application research of speed sensorless asynchronous motor based on MRAS[J]. Small & Special Electrical Machines, 2020, 48(3): 43-47.
[19] 吴迪, 李岩, 李运. 六相永磁同步直线电机无传感器控制策略研究[J]. 仪表技术, 2016(11): 41-46.
Wu Di, Li Yan, Li Yun. Research on sensorless control strategy of six-phase permanent magnet synchronous linear motor[J]. Instrumentation Tech- nology, 2016(11): 41-46.
[20] 王小辉, 刘向辰, 寇水潮, 等. 基于两步模型预测控制的ACIM电流控制方法[J]. 电力电子技术, 2019, 53(8): 52-55.
Wang Xiaohui, Liu Xiangchen, Kou Shuichao, et al. ACIM current control method based on two-step model predictive control[J]. Power Electronics, 2019, 53(8): 52-55.
[21] 滕青芳, 左瑜君, 柏建勇, 等. 基于MRAS观测器的无速度传感器永磁同步电机模型预测控制[J]. 兰州交通大学学报, 2014, 33(4): 6-11.
Teng Qingfang, Zuo Yujun, Bai Jianyong, et al. Model predictive control of speed sensorless permanent magnet synchronous motor based on MRAS observer[J]. Journal of Lanzhou Jiaotong University, 2014, 33(4): 6-11.
[22] 潘峰, 秦国锋, 王淳标, 等. 电动汽车用永磁同步电机模型预测MRAS无速度传感器控制[J]. 电机与控制应用, 2019, 46(10): 104-110.
Pan Feng, Qin Guofeng, Wang Chunbiao, et al. Model prediction of MRAS speed sensorless control of permanent magnet synchronous motors for electric vehicles[J]. Electric Machines & Control Application, 2019, 46(10): 104-110.
[23] 齐放. 永磁同步电机无速度传感器技术的研究[D].南京: 南京航空航天大学, 2007.
[24] 白聪. 永磁同步直线电机电流预测控制方法研究[D]. 西安: 西安理工大学, 2019.
[25] 彭泓, 孔德伟, 靳明智. 永磁同步电机无速度传感器矢量控制系统[J]. 辽宁工程技术大学学报: 自然科学版, 2017, 36(6): 635-639.
Peng Hong, Kong Dewei, Jin Mingzhi. Sensorless vector control system of permanent magnet synchronous motor[J]. Journal of Liaoning Technical University: Natural Science, 2017, 36(6): 635-639.
[26] 杨俊华, 吕惠子, 吴捷, 等. 基于波波夫超稳定性的无刷双馈电机直接转矩控制[J]. 中国电机工程学报, 2009, 29(15): 107-113.
Yang Junhua, Lü Huizi, Wu Jie, et al. Direct torque control of brushless doubly-fed machines based on popov superstability[J]. Proceedings of the CSEE, 2009, 29(15): 107-113.
[27] 汪琦, 王爽, 付俊永, 等. 基于模型参考自适应参数辨识的永磁同步电机电流预测控制[J]. 电机与控制应用, 2017, 44(7): 48-53.
Wang Qi, Wang Shuang, Fu Junyong, et al. Current predictive control of permanent magnet synchronous motor based on model reference adaptive parameter identification[J]. Electric Machines & Control Application, 2017, 44(7): 48-53.
Design of Model Predictive Control System for Permanent Magnet Synchronous Linear Motor Based on Adaptive Observer
Abstract Permanent magnet synchronous linear motor has poor speed control performance and highly depends on speed sensor. Thus, this paper designs a permanent magnet synchronous linear motor predictive current control system (MPC-MRAS) based on model reference adaptive observer. The stator voltage equation model that removes the cross-coupled electromotive force is used to predict the current controller, replacing the traditional current controller. The mathematical model of the motor itself is used as the reference model of the model prediction adaptive system, and the mathematical model of the designed output estimated current is used as the adjustable model. The motor speed is obtained by the adaptive law of the current difference design of the reference model and the adjustable model. This solution not only reduces the dependence of the current controller on motor parameters, but eliminates the influence of current coupling on the model predictive model predictive controller. At the same time, it also simplifies the complexity and cost of the control system, and improves the control performance and anti-interference ability of the control system. Simulation software is used to build predictive controllers and adaptive observers to apply to motor control systems, which verifies the superiority of the proposed control strategy. It is shown that this control strategy can realize online and accurate speed identification, and can also effectively reduce current ripple and improve current tracking performance.
keywords：Permanent magnet synchronous linear motor, speed sensorless, model predictive control, model reference adaptation
中图分类号：TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.200682
国家自然科学基金项目（51877070，51577048）、河北省自然科学基金项目（E2018208155）、河北省高层次人才项目（A201905008）和高节能电机及控制技术国家地方联合工程实验室开放项目（KFKT201901）资助。
收稿日期 2020-06-28
改稿日期 2020-09-29
李 争 男, 1980年生, 博士, 教授, 博士生导师, 研究方向为特种电机及其控制技术。E-mail: Lzhfgd@163.com
孙鹤旭 男, 1956年生, 博士, 教授, 博士生导师, 研究方向为运动控制与新能源技术。E-mail: sunhxhb@outlook.com（通信作者）
（编辑 陈 诚）