
图1 US-PMSPLM结构
Fig.1 Structure of US-PMSPLM
摘要 在要求大推力、长行程的应用中,如垂直提升领域,永磁同步直线电机因受布置方式、安装空间等限制,在提高永磁利用率、实现更高推力密度方面就显得至关重要。该文提出一种U型永磁凸极直线电机,其次级永磁采用U型结构,能够充分利用永磁体,提高电机的空载反电动势和电磁推力。首先,通过电机结构和磁路分析,建立等效磁路模型,分析其气隙磁通密度变化规律;其次,采用有限元法与具有相同初级结构和次级永磁体用量的隐极永磁同步直线电机进行对比分析;最后,研制实验样机,完成空载反电动势和静推力的测试,样机实测与仿真结果基本一致,进而验证了所设计电机的合理性。
关键词:直线电机 U型永磁 有限元法 电磁特性 样机实验
直线电机具有直驱、高速、高加速度、高定位精度等优点[1-3],在现代工业、军事、垂直提升等领域具有广泛应用前景。随着城市不断密集化,人类日常活动对土地利用率提出更高的要求,牵引式提升系统已难以满足高层、超高层建筑的需求,因此,直驱垂直提升系统受到国内外学者的广泛关注。永磁同步直线电机(Permanent Magnet Synchronous Linear Motor, PMSLM)驱动的垂直提升系统,以其结构紧凑、力能指标高、安全性好、提升速度和高度不受限制、可实现多轿厢(罐笼)运行等显著优点,已成为垂直提升技术领域的研究热点。
根据永磁体的放置位置不同,永磁电机可以分为表贴式、磁阻式、内置式、凸极式等类型。表贴式永磁直线电机,永磁体安装在次级铁心表面,结构简单、安装方便,应用广泛;但其存在永磁体极间漏磁,降低了永磁体的利用率。文献[4]对双边永磁同步直线电机进行优化设计,并通过磁极错位抑制推力波动。文献[5]研究了分数槽永磁直线电机的极槽配合,得出单边型和双边型电机推力波动与推力比值最小的最佳方案。文献[6]提出一种双边横向磁通直线电机结构,电机的初级、次级铁心均采用硅钢片叠压而成,且简化了制作工艺;但该结构的永磁体用量稍多,铁心容易出现饱和现象。
磁阻式永磁直线电机,初级绕组和永磁体均位于初级侧,次级为导磁铁心,结构简单,适合长行程应用[7-10]。但其结构通常是永磁体夹在铁心模块之间,而初级绕组环绕永磁体布置,构成初级结构,运行过程中绕组发热永磁体易失磁,需对永磁体不可逆退磁进行研究。此外,初级绕组、铁心、永磁体的配置关系,导致电机初级结构整体性欠佳,结构强度受限,且从性能上而言推力波动相对较大。
内置式永磁直线电机,永磁体钳在次级铁心槽内,永磁体产生的磁通面积大于一个极距内的气隙面积,使得永磁产生的磁通在气隙交汇处汇聚,相对于表贴式永磁直线电机,内置式能够获得更大的气隙磁通密度和推力密度。文献[11-12]研究了一种内置式双边短次级横向磁通直线电机,其推力密度高,适用于低速直线电机直驱应用领域。
凸极式永磁同步直线电机采用高磁导率铁磁材料代替部分永磁磁极,铁磁极与永磁极极性相反。凸极式电机在提高反电动势(back Electromotive Force, back EMF)和电磁推力等方面优势明显,国内外学者对其进行了诸多研究。文献[13]建立了凸极PMSLM的解析模型。文献[14]对凸极PMSLM进行可行性研究,减少了永磁用量,且达到了常规PMSLM的输出性能。文献[15]提出一种带凸极和Halbach永磁阵列的游标直线电机,与传统永磁游标直线电机进行对比,空载反电动势和推力密度提高明显。文献[16]提出一种磁通反转凸极PMSLM,减少了永磁用量,降低了永磁成本。文献[17-19]提出一种新的绕组布置方式,利用多台电机组合以减少凸极PMSLM的推力波动,降低磁不平衡。文献[20]分析了凸极PMSLM的推力波动的影响因素,并通过优化端齿结构降低推力波动。文献[21]针对分段式垂直运动PMSLM,推导了其主要尺寸的电磁设计准则和计算公式,为垂直提升用分段式PMSLM设计提供了依据。文献[22]提出了一种用于垂直提升领域的Halbach交替极PMSLM结构,通过优化永磁体排列组合提高永磁体利用率,在一定程度上降低了电机成本。
在要求大推力、长行程的垂直提升应用领域,受布置方式、安装空间等的限制,对永磁同步直线电机提出了更高的要求,尤其是采用短初级、长次级、动初级式的驱动布置方式,提高永磁体利用率,实现更高推力密度,对于系统成本控制至关重要。
基于此,本文提出一种内置式U型永磁凸极直线电机(U-Shaped Permanent Magnet Salient Pole Linear Motor, US-PMSPLM),其次级永磁体采用U型结构,钳于次级铁心内;与隐极型永磁同步直线电机(Non-Salient Permanent Magnet Synchronous Linear Motor, NS-PMSLM)相比,在相同的电负荷、磁负荷以及等永磁体用量的条件下,为提高电机的空载反电动势,提供更高推力密度,满足PMSLM在垂直提升领域中的大推力性能要求和长行程下的永磁体成本控制。首先,对US-PMSPLM的结构和磁路进行分析,建立等效磁路模型(EquivalentMagnetic Circuit Model, EMCM),计算永磁体产生的气隙磁通;其次,通过有限元法(Finite Element Method, FEM)建立电机仿真模型,对电磁特性进行分析;最后,制作实验样机进行实验,对比分析仿真和实验结果,验证有限元结果的正确性。
本文提出的US-PMSPLM结构如图1所示,其由初级和次级两部分组成;初级绕组采用分数槽集中绕组结构,每个初级齿上套一个线圈,绕组端部短、铜耗低;次级由U型永磁阵列、凸铁极、次级铁心组成。U型永磁阵列,嵌在次级铁心槽内,由两块水平充磁的矩形永磁和一块径向向内充磁的半环形永磁组成;U型永磁阵列开口处为凸铁极,其通过两侧的非磁性夹板贴合,并用螺栓加固。

图1 US-PMSPLM结构
Fig.1 Structure of US-PMSPLM
US-PMSPLM与NS-PMSLM的不同之处主要在于次级永磁体的结构形态和布置方式。如图2所示为与本文提出的US-PMSPLM具有相同初级结构和次级永磁体用量的NS-PMSLM结构,其次级永磁体粘合于次级轭部表面。
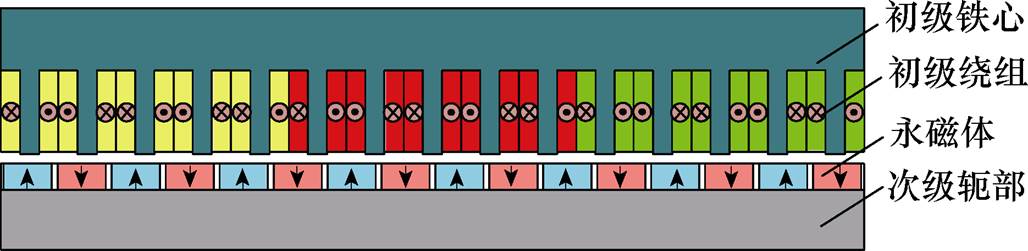
图2 NS-PMSLM结构
Fig.2 Structure of NS-PMSLM
针对NS-PMSLM,课题组在前期研究中,已完成了优化设计,制作了样机,并搭建了垂直提升系统,分别如图3和图4所示。
在NS-PMSLM样机系统的基础上,为了更进一步提高永磁利用率,实现更高的推力密度,本文提出一种US-PMSPLM,两者具有相同的初级和次级永磁体用量;主要结构参数见表1。

图3 NS-PMSLM样机
Fig.3 Prototype of NS-PMSLM

图4 NS-PMSLM驱动的垂直提升系统
Fig.4 Vertical hoist system driven by NS-PMSLM
表1 两类电机的主要结构参数
Tab.1 The main structural parameters of two motors

参 数数值(型号) US-PMSLMNS-PMSLM 初级齿数1515 初级齿宽/mm88 初级槽宽/mm1616 初级槽高/mm3535 每相绕组匝数323323 叠厚/mm7070 气隙长度/mm44 极距/mm22.522.5 水平永磁宽度/mm10.520 水平永磁高度/mm3.311 半环形永磁内半径/mm6— 凸铁极宽度/mm12— 永磁体用量/cm3246.5246.4 初级铁心材料50W47050W470 次级轭部材料A3钢A3钢 永磁体材料N48HN48H
US-PMSPLM的U型永磁阵列所产生的有效磁通有两条磁通路径:①经过U型永磁开口处的凸铁极,以及此时凸铁极对应的初级铁心齿,到达初级铁心轭部,再沿两侧相邻的初级铁心齿回到次级凸铁极,形成大循环磁通路径;②经过凸铁极,以及此时对应的初级铁心齿部,再回到次级凸铁极,而不经过初级铁心轭部,形成小循环磁通路径。US- PMSPLM磁通路径如图5所示。
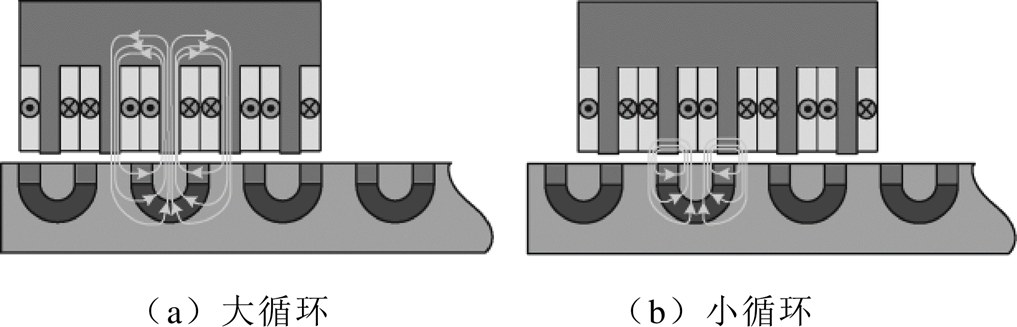
图5 US-PMSPLM磁通路径
Fig.5 Flux path of US-PMSPLM
根据电机的磁通路径,运用等效磁路法,建立US-PMSPLM单个U型磁极下的等效磁路模型如图6所示。
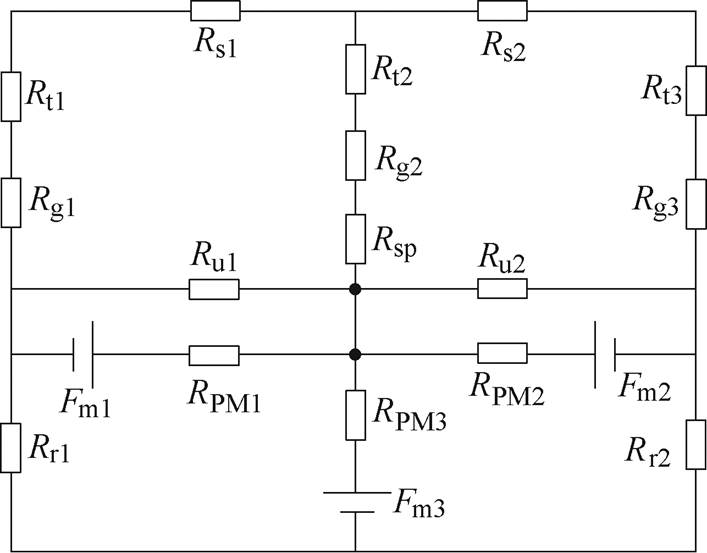
图6 等效磁路模型
Fig.6 Equivalent magnetic circuit model
图6中,Fm1、Fm2、Fm3分别为左、右两块水平充磁永磁和半环形永磁的磁动势;RPM1、RPM2、RPM3分别为左、右两块水平充磁永磁和半环形永磁的磁阻;Rt1、Rt2、Rt3为不同齿的齿部磁阻;Rg1、Rg2、Rg3为电机气隙磁阻;Ru1、Ru2为水平充磁永磁体的漏磁阻;Rs1、Rs2为初级铁心轭部磁阻;Rsp为U型永磁开口处的凸铁磁阻;Rr1、Rr2为U型永磁两侧相邻凸铁极磁阻。
由于初级铁心和次级轭部的磁导率远大于空气磁导率,为方便计算,忽略铁心磁阻,US-PMSPLM简化等效磁路模型如图7所示。
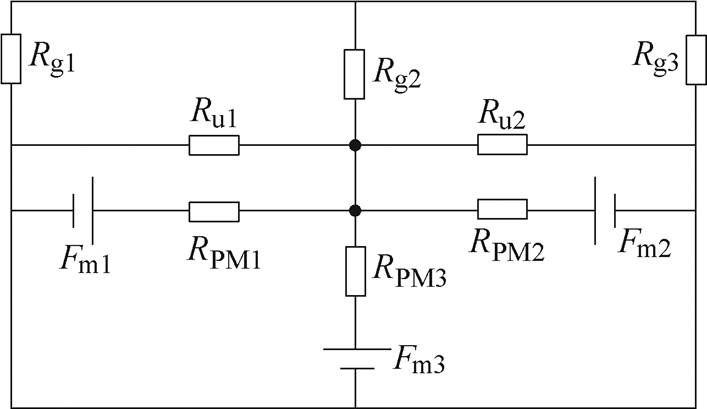
图7 简化等效磁路模型
Fig.7 Simplified equivalent magnetic circuit model
水平充磁永磁体磁阻为
 (1)
(1)半环形永磁体磁阻为
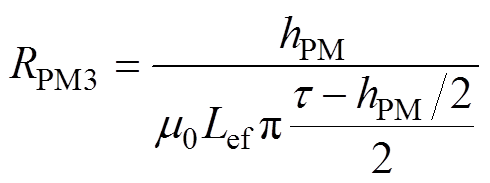 (2)
(2)
气隙磁阻为
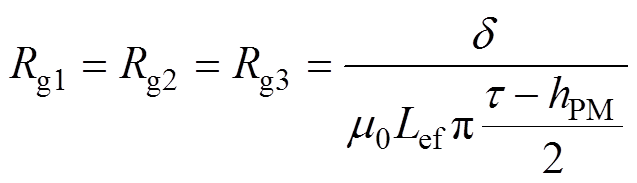 (3)
(3)漏磁磁阻为
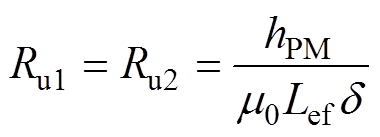 (4)
(4)
永磁体磁动势为
 (5)
(5)式中,hPM为水平充磁永磁体磁化方向长度;Lef为电机轴向有效长度;d为水平充磁永磁体高度;t 为极距;d 为气隙长度;Hc为永磁体的矫顽力;m0为真空磁导率,m0=4p×10-7。
气隙磁通密度为
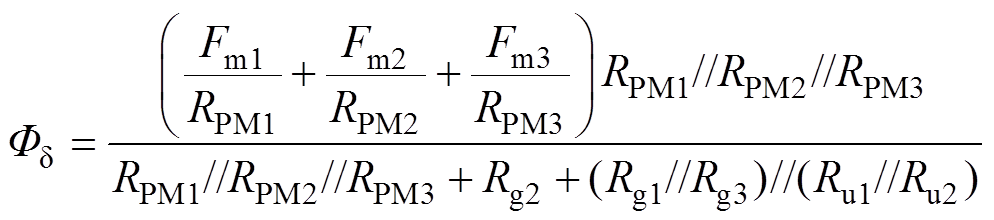 (6)
(6)利用式(6),计算电机空载状态下气隙磁通密度,并取气隙磁通密度的y轴分量By与有限元仿真结果对比,如图8所示。
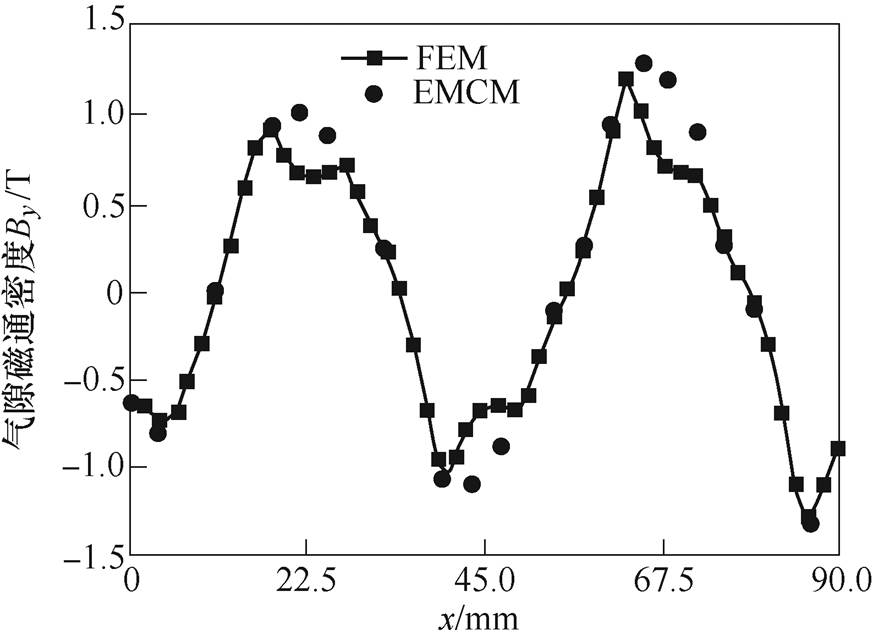
图8 空载气隙磁通密度
Fig.8 No-load air gap flux density
由图8可以看出,电机气隙磁通密度随着次级位置呈周期性变化,且有限元仿真结果与等效磁路计算结果基本一致;但由于等效磁路法无法充分考虑PMSLM的齿槽效应,进而导致计算出现误差,使得气隙磁通密度波形在波峰、波谷位置,与有限元结果存在一定的偏差。
为了分析所提出的US-PMSPLM的合理性,采用二维有限元建模仿真,在相同的电负荷、磁负荷以及等永磁体用量的条件下,与具有相同初级结构的NS-PMSLM进行性能对比分析。在建模分析时做如下假设:
(1)忽略机壳外的磁场。
(2)假设导体内的电流密度均匀分布。
(3)不计磁滞效应,通过磁化曲线和损耗曲线考虑铁心的非线性和涡流效应。
(4)根据实际运行情况,假定初级无限长,设偶对称边界条件。
图9为US-PMSPLM和NS-PMSLM两类电机的空载磁场分布。由于永磁体的相对磁导率为1,对于NS-PMSLM的隐极型次级结构而言,永磁体粘合于次级轭部表面,相当于增加了电机的等效电磁气隙长度,且相邻两块永磁体通过窄小的空气气隙隔开漏磁较多,如图9a所示;而US-PMSPLM的U型永磁凸极次级结构,利用U型永磁阵列和凸铁极,形成凸极效应,较US-PMSPLM等效电磁气隙长度减小,且U型永磁阵列产生的磁场由于凸极效应而汇集,起到了很好的聚磁效果,减少了漏磁,提高了永磁体的利用率,如图9b所示。
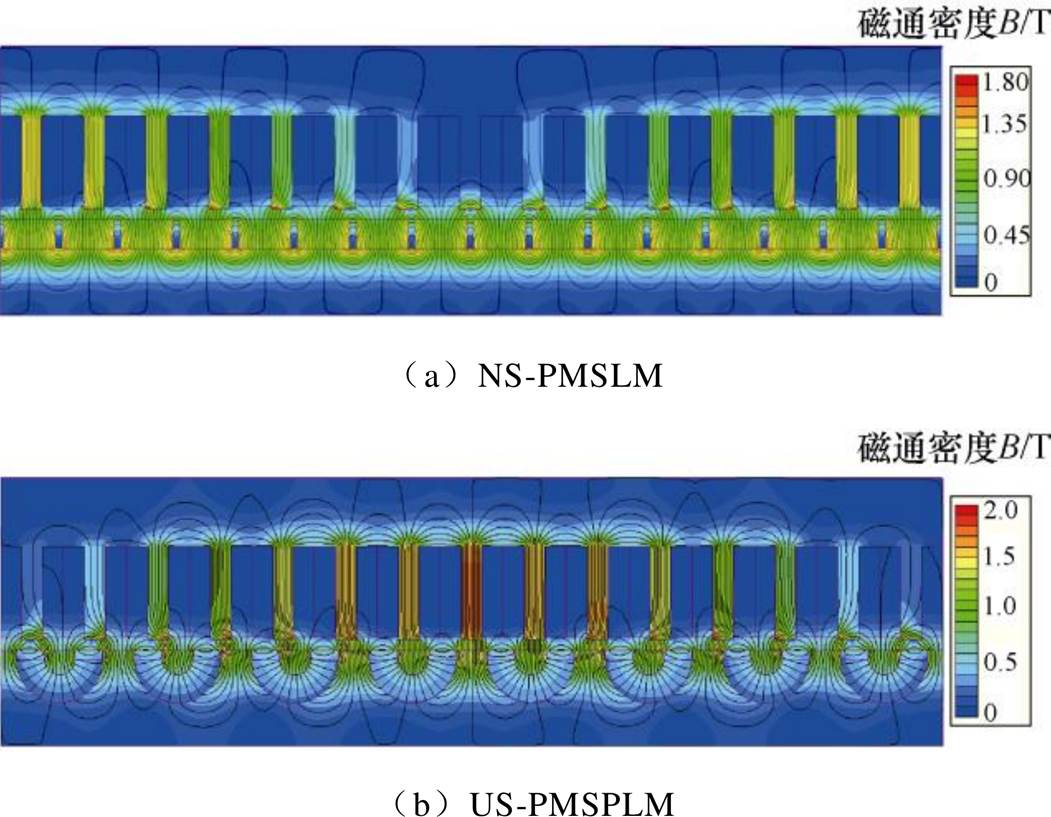
图9 空载磁场分布
Fig.9 No-load magnetic field distribution
由于US-PMSPLM较NS-PMSLM,等效电磁气隙长度减小,且U型永磁聚磁效果好,US-PMSPLM可获得更高的气隙磁通密度。图10为空载状态下,两类电机气隙中心磁通密度曲线。
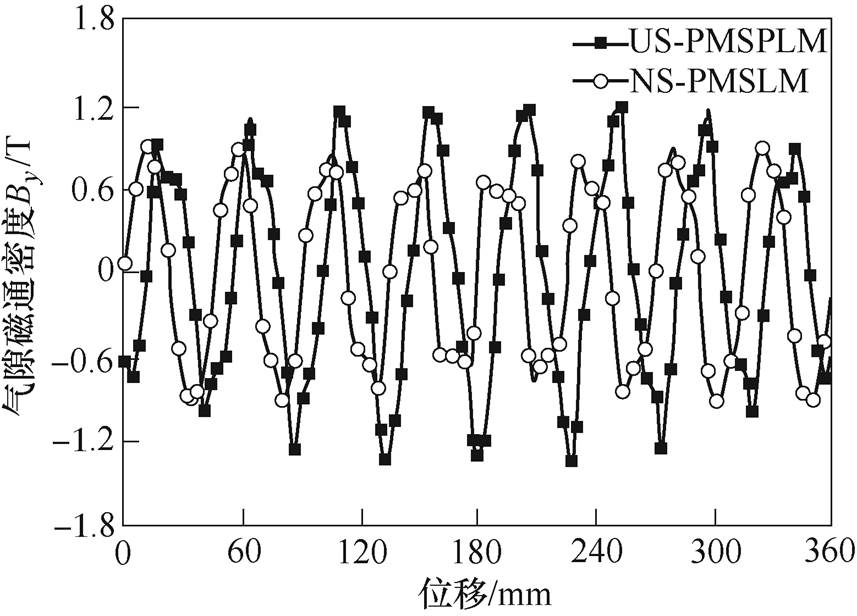
图10 气隙中心磁通密度曲线
Fig.10 Flux density curves of air gap center line
由图10可以看出,US-PMSPLM和NS-PMSLM的气隙磁通密度幅值分别为1.23T和0.89T,US- PMSPLM的气隙磁通密度幅值较NS-PMSLM增加了38.20%;结果表明,在相同永磁用量情况下,US- PMSPLM能够有效地提高气隙磁通密度。
磁链是电机初级绕组与励磁磁场交链产生的,并且和电机的次级位置有关,是分析电机性能的重要参数,图11为两类电机的磁链波形。

图11 磁链波形
Fig.11 Flux linkage waveforms
初级电枢绕组开路,电机以1.035m/s的恒定速度沿x轴正方向运动,得到两类电机空载反电动势波形如图12所示。
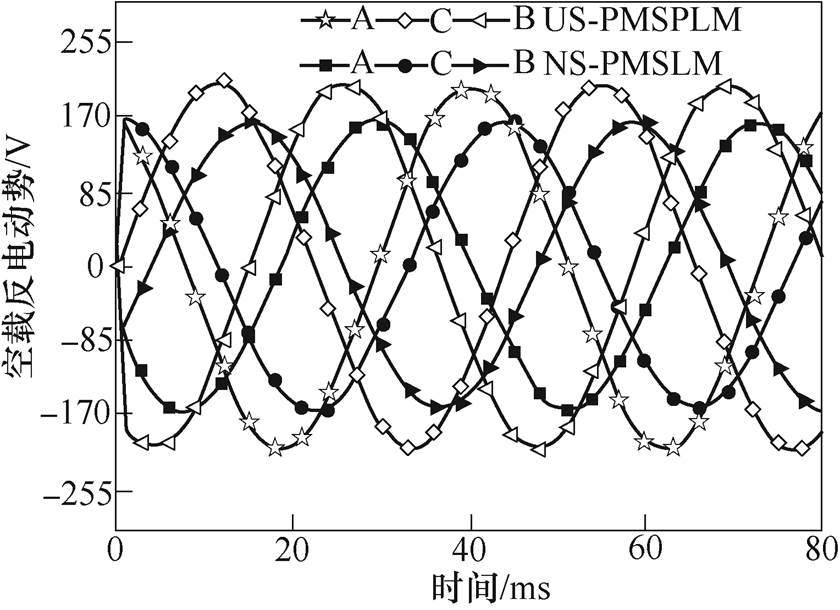
图12 空载反电动势波形
Fig.12 No-load back EMF waveforms
图11中,US-PMSPLM和NS-PMSLM两类电机的三相磁链均对称,波形正弦度较好,相位互差120°,且磁链随初级和次级的相对位置改变,以两个极距为周期且呈周期性变化;US-PMSPLM的磁链峰值为1.407Wb,而NS-PMSLM的磁链峰值为1.120Wb,US-PMSPLM的磁链较NS-PMSLM提高了25.63%,能够在更小的电流下获得更大的推力,提高推力密度。
由图12可以看出,两类电机的反电动势正弦度均较好,US-PMSPLM和NS-PMSLM的反电动势幅值分别为207.88V和165.34V;US-PMSPLM较NS- PMSLM的反电动势幅值提高了25.73%。US-PMSPLM可以得到更高的空载反电动势,而反电动势的高低直接反映电机输出推力的大小。
U型永磁凸极次级结构与NS-PMSLM的隐极型次级结构相比:①电机的等效电磁气隙长度减小;②U型永磁凸极聚磁效应,漏磁减少,永磁体利用率提高。因此,在等永磁体用量下,US-PMSPLM较NS-PMSLM可获取更高的气隙磁通密度和反电动势,从而得到更大的推力。
为了分析两类电机的空载反电动势谐波含量,对A相空载反电动势进行傅里叶分解,图13给出了各次谐波频谱,并计算其总谐波畸变率(Total Harmonic Distortion, THD)。THD计算公式为
 (7)
(7)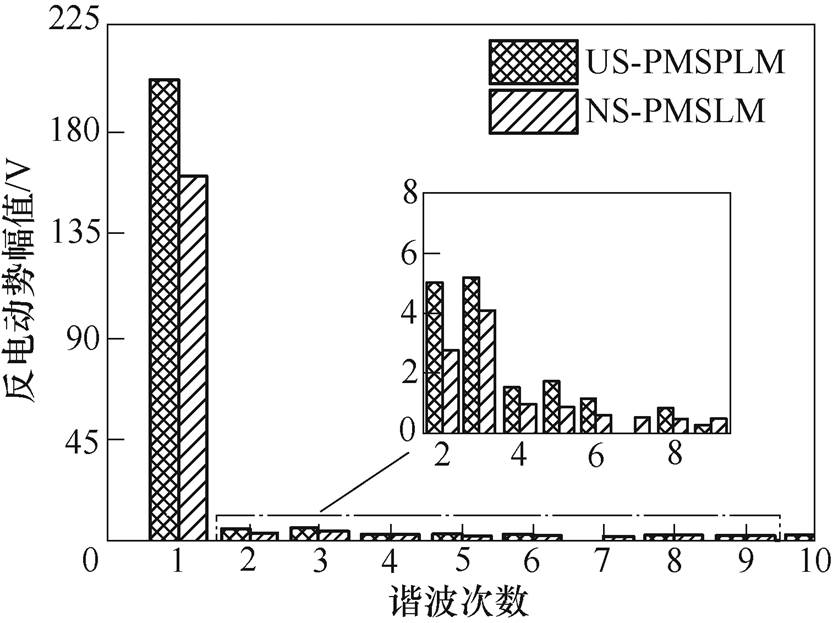
图13 空载反电动势谐波频谱
Fig.13 No-load back EMF harmonic spectrum
由图13可以看出,US-PMSPLM空载反电动势的基波幅值为203.74V,明显高于NS-PMSLM空载反电动势的基波幅值161.40V。由式(7)计算得US-PMSPLM和NS-PMSLM的THD分别为3.77%和3.20%。US-PMSPLM的空载反电动势THD略高于NS-PMSLM,其中,3次谐波含量较高,是导致THD高的主要因素。因此,电机绕组可以采用星形联结以消除反电动势中的3次谐波,提高电机的运行性能。
为了准确计算绕组电感,需要考虑永磁磁场和电枢磁场之间的耦合,利用有限元法进行电感计算时,在一相绕组中通入直流电流,得到该相绕组中匝链的总磁链为
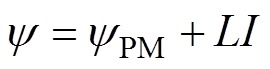 (8)
(8)式中,yPM为永磁体单独作用时产生的磁链;L为相绕组自感或互感;I为电枢绕组通入的电流。
由式(8)可得,电枢绕组的电感为
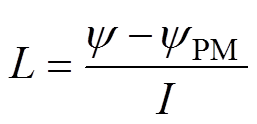 (9)
(9)由式(9)计算得到US-PMSPLM和NS-PMSLM的A相绕组自感,如图14所示。

图14 两类电机自感
Fig.14 Self-inductance of the two types motors
由图14可以看出,US-PMSPLM的自感随初级、次级相对位置的改变,以两倍极距为周期且呈周期性变化;NS-PMSLM的自感对初级、次级相对位置不敏感,近似为恒定值。US-PMSPLM的自感均值为0.234H,变化率为2.15%,NS-PMSLM的自感均值为0.203H;US-PMSPLM的自感较NS-PMSLM提高了15.27%,但其对初级、次级的相对位置较为敏感,将引起推力和速度波动,因而对US-PMSLM的控制提出更高的要求。
由于边端效应和齿槽效应的存在,永磁同步直线电机存在固有的边端力和齿槽力,合称为定位力。定位力是引起永磁同步直线电机推力波动的主要原因之一,其大小和方向与电机运行状况无关[23-25]。US-PMSPLM和NS-PMSLM两类电机的定位力对比曲线如图15所示。

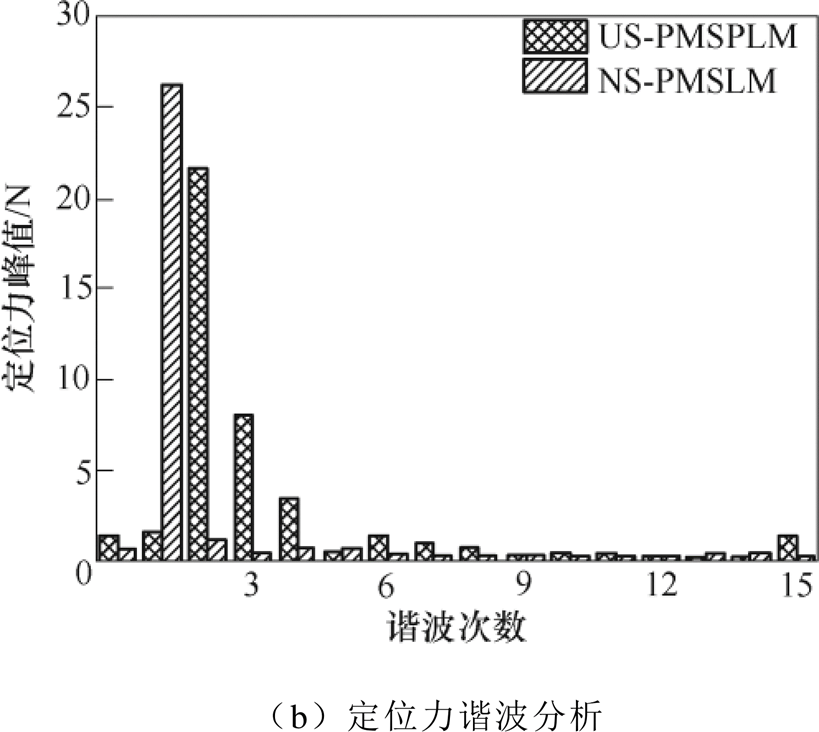
图15 定位力对比
Fig.15 Detent force comparison
由图15a可以看出,NS-PMSLM的定位力以一倍极距为周期,近似呈正弦变化;而US-PMSPLM的定位力是以两倍极距为周期,呈非正弦变化,原因是在US-PMSPLM中,一个U型永磁阵列和一侧相邻凸铁极的距离之和相当于NS-PMSLM极距的两倍。采用有限元法计算得到的定位力是边端力和齿槽力的合力[26-27]。为了进一步分析定位力,对两类电机的定位力进行傅里叶分解,得到如图15b所示的各次谐波频谱。图15b中,NS-PMSLM的定位力以1次谐波为基波,包含主要的边端力成分;而US-PMSPLM的定位力则以2次谐波为基波,且基波幅值小于NS-PMSLM,高次谐波幅值高于NS- PMSLM。
电机推力是永磁同步直线电机垂直提升系统的主要性能指标。永磁体的结构及性能是影响电机推力特性的关键因素,永磁宽度影响气隙磁通的分布特性,永磁厚度影响直轴电抗和气隙磁通的大小。因此,本文通过对U型永磁阵列的优化,提高电机推力。图16为次级U型永磁结构示意图,图中,h2为U型永磁的总高度,优化过程在电磁负荷、U型永磁用量基本不变的前提下进行,U型永磁结构参数应满足
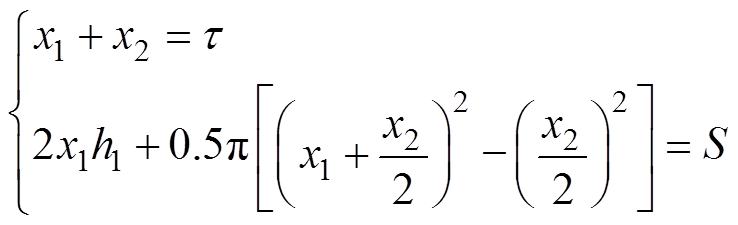 (10)
(10)式中,x1为水平磁化永磁的宽度,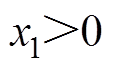 ;x2为凸铁极的宽度,
;x2为凸铁极的宽度,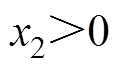 ;h1为水平磁化永磁的厚度,
;h1为水平磁化永磁的厚度,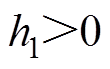 ;S为U型永磁截面面积。
;S为U型永磁截面面积。
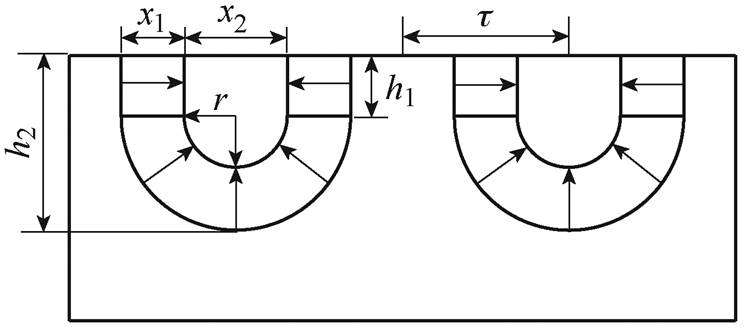
图16 次级U型永磁结构示意图
Fig.16 Secondary U-type PM structure diagram
图17为永磁充磁方式示意图,图中,半环形永磁充磁方向为径向向内,矩形充磁方向分为0°、30°、60°、90°等几种情况,综合分析永磁充磁方式对电机空载反电动势、平均推力及推力波动的影响。
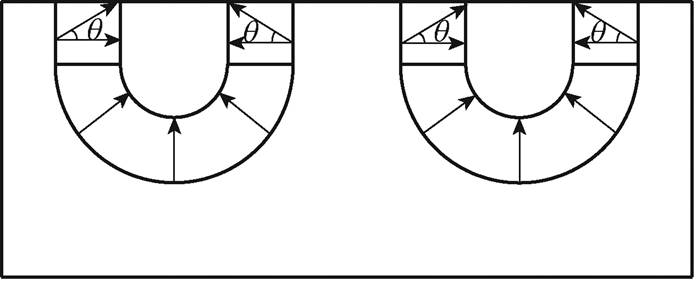
图17 永磁充磁方式示意图
Fig.17 Schematic diagram of PM magnetization
图18和图19分别给出了电机平均推力和推力波动随永磁宽度和充磁方向改变时的变化趋势。
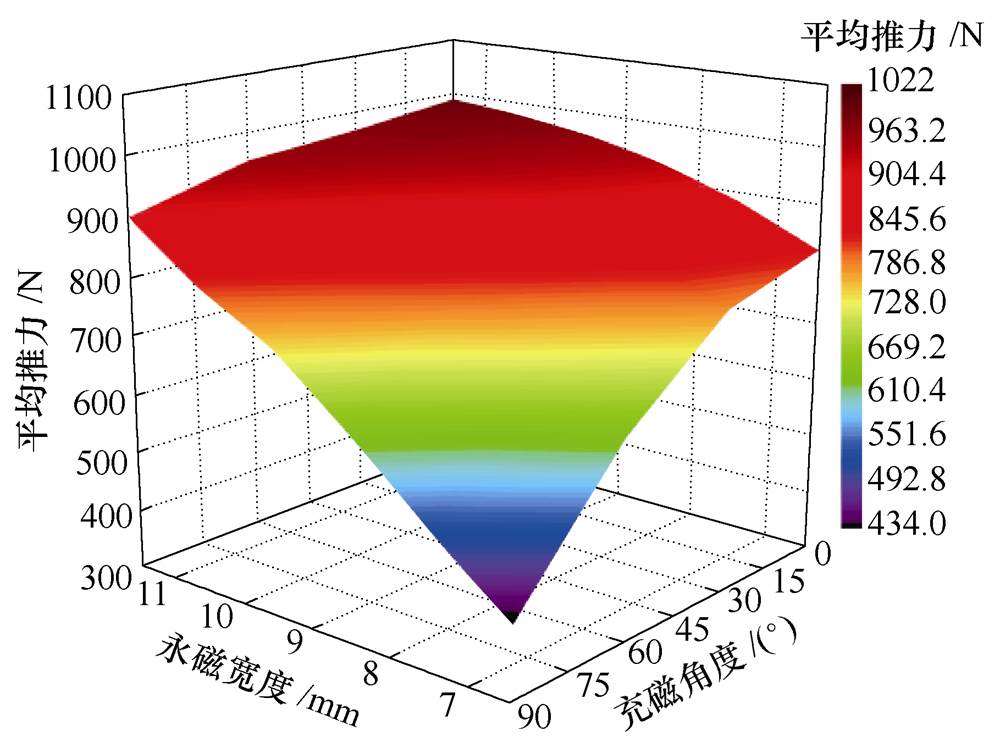
图18 平均推力随永磁宽度和充磁角度的变化
Fig.18 Variation of average thrust PM width and magnetization angle

图19 推力波动随永磁宽度和充磁角度的变化
Fig.19 Variation of thrust fluctuation with PM width and magnetization angle
由图18可知,当永磁宽度一定时,随着充磁角度的增大,电机的反电动势和平均推力逐渐减小,且永磁宽度越小,反电动势和平均推力随充磁角度增大而减小的趋势越明显;随着永磁宽度的增加,充磁角度的变化对反电动势和平均推力的影响也越小,增幅变缓;当充磁角度一定时,反电动势和平均推力随着永磁宽度的增加而呈现递增趋势,且充磁角度越小,随着永磁宽度增加,反电动势和平均推力增幅越缓慢;随着充磁角度的增大,反电动势和平均推力的增幅越大。图19中,电机的推力波动受永磁宽度和充磁角度的影响并不呈线性变化,但从整体来看,随着永磁宽度和充磁角度的增加,推力波动呈递增趋势。
从提高US-PMSPLM推力的角度考虑,永磁宽度在11.5mm、充磁角度为0°时,平均推力达到最大值;此时,电机的平均推力为987.54N,推力波动为2.74%。在相同的激励下,与NS-PMSLM的推力和推力波动进行对比,其对比曲线如图20所示,推力及推力波动数据见表2。
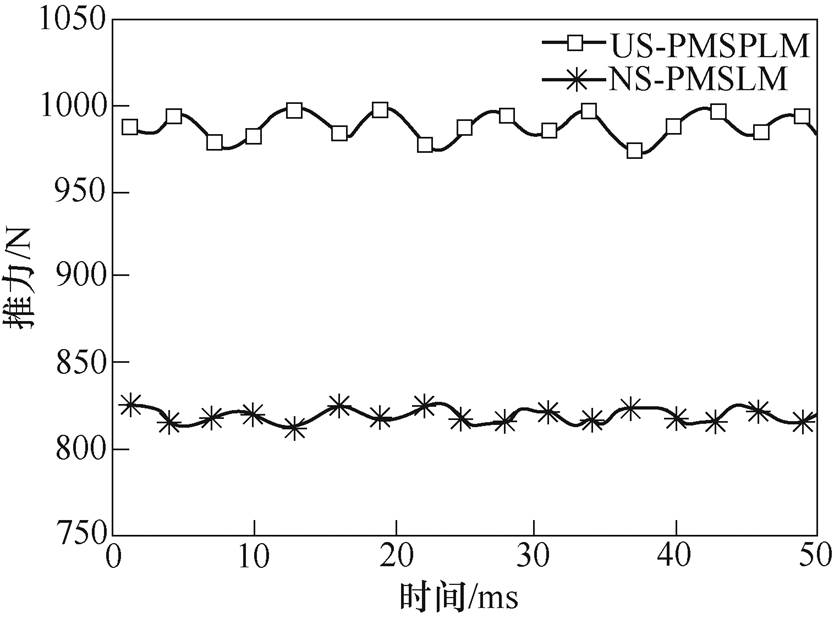
图20 推力对比曲线
Fig.20 Comparison curves of thrust
表2 推力及推力波动数据
Tab.2 Datas of thrust and thrust ripple
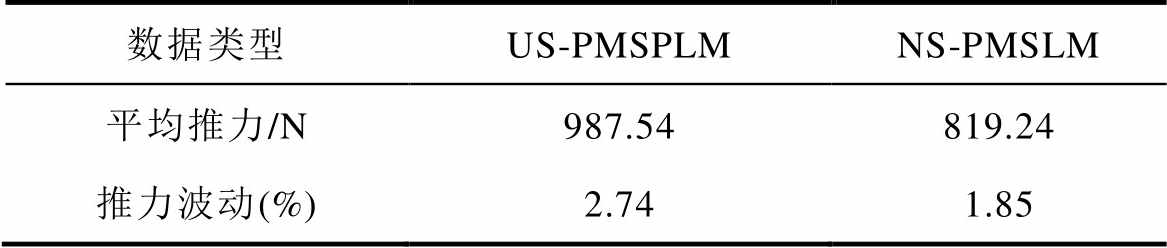
数据类型US-PMSPLMNS-PMSLM 平均推力/N987.54819.24 推力波动(%)2.741.85
由图20和表2可以看出,US-PMSPLM的平均推力为987.54N,推力波动为2.74%;NS-PMSLM的平均推力为819.24N,推力波动为1.85%。US- PMSPLM的平均推力较NS-PMSLM提高了20.54%,表明在相同电磁负荷和等永磁用量条件下,US- PMSPLM能够提供更大的电磁推力,但推力波动略高于NS-PMSLM。
基于上述分析,依据表3所示的电机优化后的主要设计参数,制作了一台US-PMSPLM样机,如图21所示。电机初级铁心由硅钢片叠压而成,嵌线后用环氧树脂进行封装;次级永磁体用高强度耐高温环氧胶粘贴在次级铁心槽内,带螺孔的凸铁通过两侧非磁性轭板用螺栓加固。
表3 样机参数
Tab.3 Prototype parameters

参 数数 值 初级齿数15 初级齿宽/mm8 初级槽宽/mm16 初级槽高/mm35 每相绕组匝数323 叠厚/mm70 气隙长度/mm4 极距/mm22.5 永磁磁化长度/mm11.5 水平永磁高度/mm2 半环形永磁内径/mm5.5 凸铁极宽度/mm11
由拖动电机带动US-PMSPLM初级,以1.035m/s的速度沿直线方向匀速运动,测得样机三相反电动势波形如图22所示。

图21 US-PMSPLM样机
Fig.21 US-PMSPLM prototype
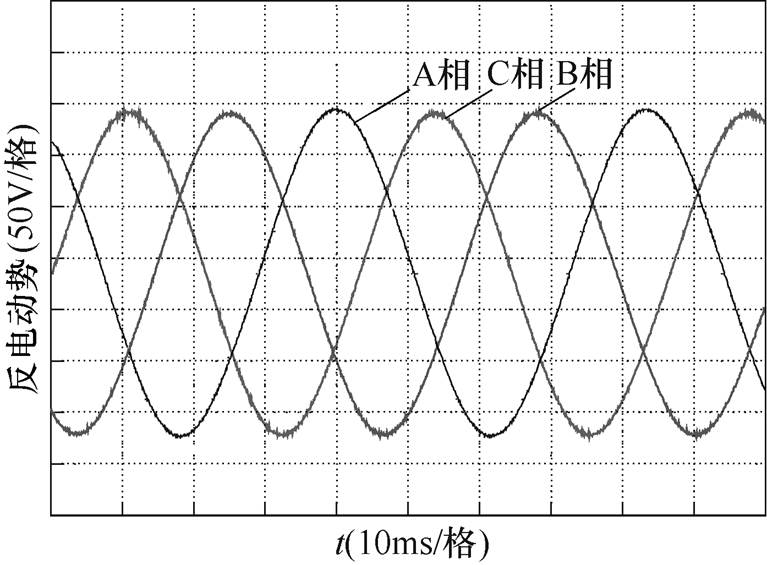
图22 样机三相反电动势
Fig.22 Three-phase back EMF of prototype
图22中,样机三相反电动势呈正弦分布,幅值基本相等,相位互差120°。取C相反电动势实测波形与有限元仿真波形的对比,如图23所示。图23中,C相实测反电动势幅值为198.12V,略小于有限元仿真值207.88V,误差为4.93%;考虑误差产生的原因,主要由装配工艺的不完善引起;样机加工制作过程中,次级表面的平整度影响平均气隙的分布,导致反电动势幅值产生误差。
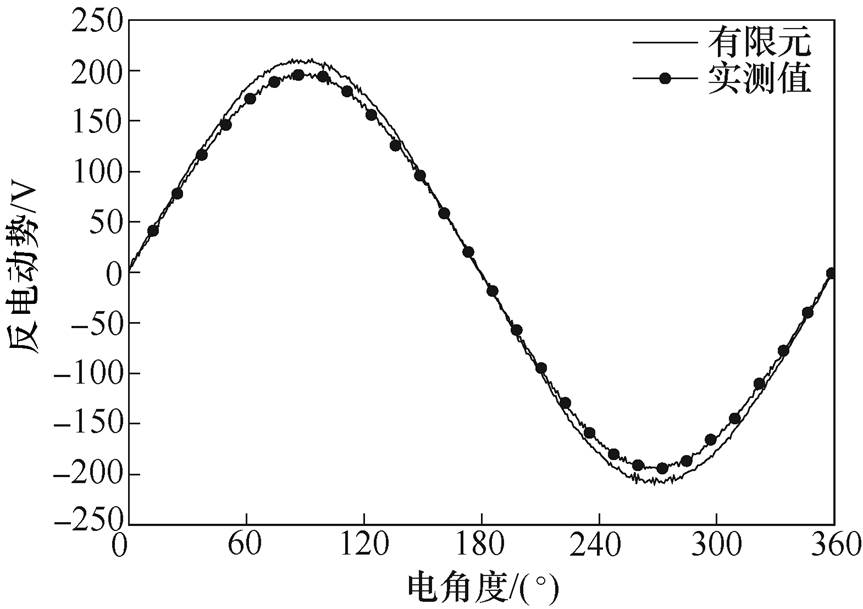
图23 反电动势实测值与有限元结果对比
Fig.23 Back EMF comparison between testing and FEM
通过静推力测试考察US-PMSPLM的力特性,初级绕组中任一相通入直流电,利用拖动电机带动丝杆推动样机初级沿直线方向做匀速运动,可以用拉力传感器检测该电机在不同位置时的推力变化情况。图24给出了A相绕组通入3.5A直流电时,电机静推力随位置的变化情况,实测波形与有限元仿真波形趋势基本一致,均以两倍极距为周期。考虑到样机装配误差和永磁体磁性能一致性问题,静推力实测值639.7N,小于有限元仿真值691.2N,误差约7.5%。
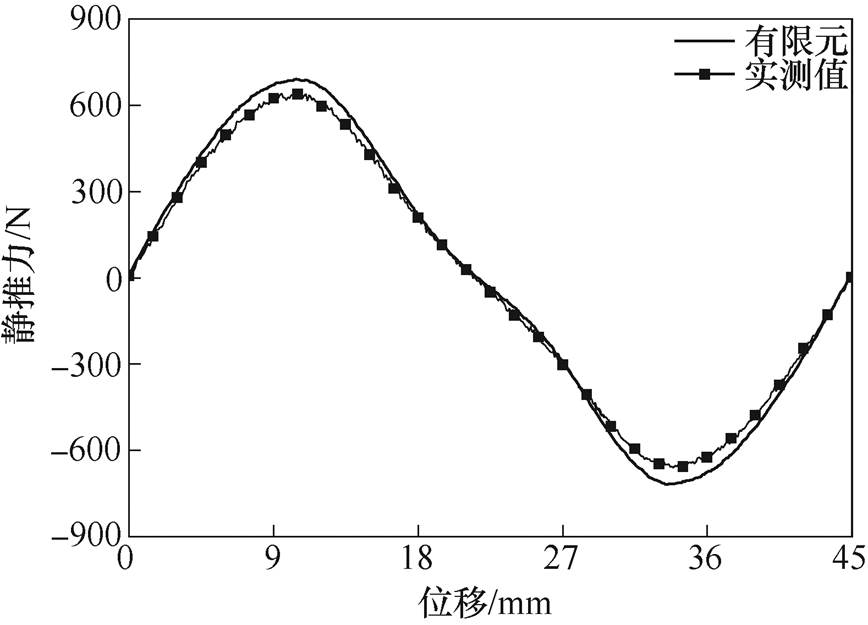
图24 静推力实测与有限元对比
Fig.24 Static force comparison betweentesting and FEM
图25所示为样机静推力随电流变化特性,电流从0A增加至10A,电机静推力实测值与有限元仿真结果基本保持一致,静推力随电流增大而呈递增趋势;电机初级铁心随电流增加磁路逐渐饱和,随着电流的持续增加,静推力增幅变缓。
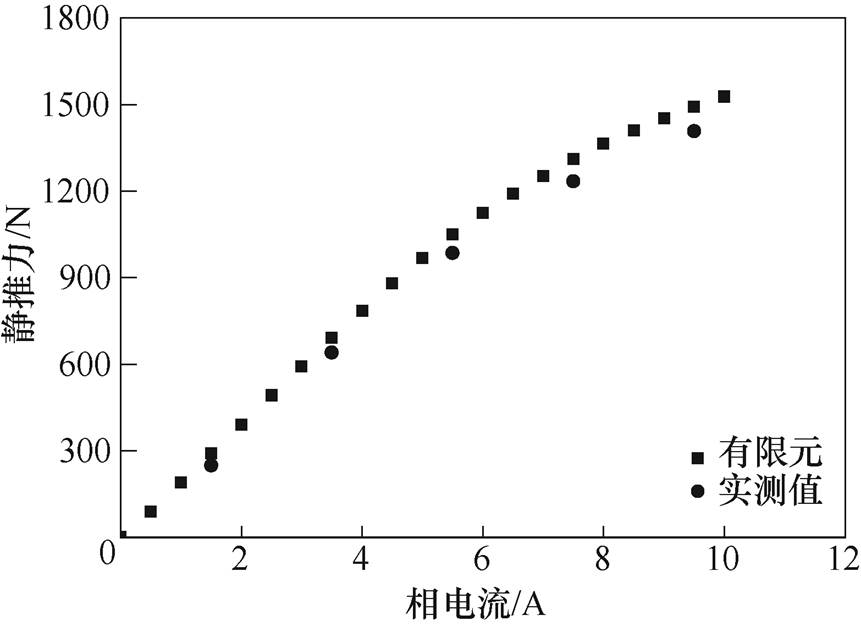
图25 静推力随电流变化特性
Fig.25 Static force characteristics vary with current
本文提出了一种次级U型永磁凸极直线电机,通过电机结构和磁路分析,搭建了等效磁路模型,进行了二维有限元建模、特性分析以及推力优化设计,并制作了样机,完成了实验验证,得出以下结论:
1)采用等效磁路法搭建单个U型磁极下电机的磁路模型,计算得到了永磁体产生的气隙磁通,与有限元分析值基本吻合。
2)与相同初级和等永磁体用量的NS-PMSLM相比,US-PMSPLM的气隙磁通密度幅值增大了38.20%,进而提高了电机空载反电动势和电磁推力,平均电磁推力从819.24N增加到987.54N,提高了20.54%,在一定程度上降低了永磁成本;但由于U型永磁的凸极效应,电机推力波动有所增加,由1.85%增加到2.74%。
3)样机空载反电动势和静推力测试结果与有限元分析基本一致,验证了有限元结果的正确性和电机设计的合理性,为其在垂直提升领域的应用提供了一定的参考价值。
参考文献
[1] 董顶峰, 黄文新, 卜飞飞, 等. 绕组周向分布圆筒型初级永磁直线电机结构及静态特性分析[J]. 中国电机工程学报, 2017, 37(21): 6181-6189.
Dong Dingfeng, Huang Wenxin, Bu Feifei, et al. Structure and static characteristic analysis of tubular primary permanent magnet linear machine with circumferential distribution of winding[J]. Pro- ceedings of the CSEE, 2017, 37(21): 6181-6189.
[2] Kim Sungan, Zhu Yuwu, Lee Sanggeon, et al. Electromagnetic normal force characteristics of a permanent magnet linear synchronous motor with double primary side[J]. IEEE Transactions on Magnetics, 2014, 50(1): 1204-1207.
[3] 王明杰, 徐伟, 杨存祥, 等. 基于精确子域模型的永磁直线同步电机空载磁场解析计算[J]. 电工技术学报, 2020, 35(5): 942-953.
Wang Mingjie, Xu Wei, Yang Cunxiang, et al. Analytical calculation of no-load magnetic field in permanent magnet linear synchronous motors based on an accurate subdomain model[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 942- 953.
[4] 卢琴芬, 张新敏, 黄立人, 等. 错位式双边型永磁直线同步电机优化设计[J]. 电工技术学报, 2013, 28(11): 35-41.
Lu Qinfen, Zhang Xinmin, Huang Liren, et al. Optimal design of shifted type double-sided permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 35-41.
[5] 卢琴芬, 程传莹, 叶云岳, 等. 每极分数槽永磁直线电机的槽极数配合研究[J]. 中国电机工程学报, 2012, 32(36): 68-74.
Lu Qinfen, Cheng Chuanying, Ye Yunyue, et al. Slot/pole number combination research of PM linear motors with fractional slots per pole[J]. Proceedings of the CSEE, 2012, 32(36): 68-74.
[6] Shin Jungseob, Takafumi Koseki, Kim Houngjoong. Proposal and design of short armature core double- sided transverse flux type linear synchronous motor[J]. IEEE Transactions on Magnetics, 2012, 48(11): 3871-3874.
[7] Wang Canfei, Shen Jianxin, Wang Lili, et al. A novel permanent magnet flux-switching linear motor[C]// 4th IET Conference on Power Electronics, Machines and Drives, York, UK, 2008: 116-119.
[8] 杜怿, 程明, 邹国棠. 初级永磁型游标直线电机设计与静态特性分析[J]. 电工技术学报, 2012, 27(11): 22-30.
Du Yi, Cheng Ming, Chau K T. Design and analysis of a new linear primary permanent magnet vernier machine[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 22-30.
[9] 张邦富, 程明, 王飒飒, 等. 基于改进型代理模型优化算法的磁通切换永磁直线电机优化设计[J]. 电工技术学报, 2020, 35(5): 1013-1021.
Zhang Bangfu, Cheng Ming, Wang Sasa, et al. Optimal design of flux-switching permanent magnet linear machine based on improved surrogate-based optimization algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1013-1021.
[10] 曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020, 35(5): 1001-1012.
Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001- 1012.
[11] Chang Junghwan, Kang Dohyun, Lee Jiyoung, et al. Development of transverse flux linear motor with permanent-magnet excitation for direct drive appli- cations[J]. IEEE Transactions on Magnetics, 2005, 41(5): 1936-1939.
[12] Lee Jiyoung, Hong Jungpyo, Chang Junghwan, et al. Computation of inductance and static thrust of a permanent-magnet-type transverse flux linear motor[J]. IEEE Transactions on Industry Appli- cations, 2006, 42(2): 487-494.
[13] Wang Xudong, Yuan Shiying, Jiao Liucheng, et al. Analysis of salient-pole permanent magnet linear synchronous motors using a unified integrity analytical method[C]//IEEE International Electric Machines and Drives Conference, Madison, WI, USA, 2003: 395-400.
[14] Chung Shiuk, Lee Hongjoo, Woo Byungchul, et al. A feasibility study on a new doubly salient permanent magnet linear synchronous machine[J]. IEEE Transactions on Magnetics, 2010, 46(6): 1572-1575.
[15] Shi Chaojie, Li Dawei, Qu Ronghai, et al. A novel linear permanent magnet vernier machine with consequent-pole permanent magnets and halbach permanent magnet arrays[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1-4.
[16] Chung Shiuk, Lee Hongjoo, Hwang Sangmoon. A novel design of linear synchronous motor using FRM topology[J]. IEEE Transactions on Magnetics, 2008, 44(6): 1514-1517.
[17] Chung Shiuk, Kim Jiwon, Woo Byungchul, et al. Force ripple and magnetic unbalance reduction design for doubly salient permanent magnet linear synchronous motor[J]. IEEE Transactions on Magnetics, 2011, 47(10): 4207-4210.
[18] Chung Shiuk, Kim Jiwon, Woo Byungchul, et al. Design and experimental validation of doubly salient permanent magnet linear synchronous motor for precision position control[J]. Mechatronics, 2013, 23(2): 172-181.
[19] Chung Shiuk, Kim Jiwon, Woo Byungchul, et al. Development of doubly salient permanent magnet linear synchronous motor for general-purpose automation applications[J]. International Journal of Precision Engineering & Manufacturing, 2013, 14(12): 2075-2080.
[20] Huang Xuzhen, Liang Jing, Zhou Bo, et al. Suppressing the thrust ripple of the consequent-pole permanent magnet linear synchronous motor by two- step design[J]. IEEE Access, 2018, 6: 32935-32944.
[21] 王淑红, 熊光煜. 分段式垂直运动永磁直线同步电动机的设计[J]. 煤炭学报, 2010, 35(3): 520-524.
Wang Shuhong, Xiong Guangyu. Design of sectional- primary permanent magnet linear synchronous motor for vertical transportation system[J]. Journal of China Coal Society, 2010, 35(3): 520-524.
[22] 许孝卓, 孙震, 汪旭东, 等. Halbach交替极永磁同步直线电机特性分析[J]. 电工技术学报, 2019, 34(9): 1825-1833.
Xu Xiaozhuo, Sun Zhen, Wang Xudong, et al. Characteristic of a novel permanent magnet linear synchronous motor with Halbach array consequent- pole[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1825-1833.
[23] Kim Yongjae, Dohmeki Hideo. Cogging force veri- fication by deforming the shape of the outlet edge at the armature of a stationary discontinuous armature PM-LSM[J]. IEEE Transactions on Magnetics, 2007, 43(6): 2540-2542.
[24] Youn Sungwhan, Lee Jongjin, Yoon Heesung, et al. A new cogging-free permanent-magnet linear motor[J]. IEEE Transactions on Magnetics, 2008, 44(7): 1785- 1790.
[25] Chen Yaowming, Fan Shuyuan, Lu Weishin. Per- formance analysis of linear permanent-magnet motors with finite-element analysis[J]. IEEE Transactions on Magnetics, 2008, 44(3): 377-385.
[26] 寇宝泉, 张赫, 郭守仑, 等. 辅助极一体式永磁同步直线电机端部定位力抑制技术[J]. 电工技术学报, 2015, 30(6): 106-113.
Kou Baoquan, Zhang He, Guo Shoulun, et al. End effect detent force reduction for permanent magnet linear synchronous motors with auxiliary poles one- piece structure[J]. Transactions of China Electro- technical Society, 2015, 30(6): 106-113.
[27] 李立毅, 祝贺, 刘家曦, 等. 初级绕组分段永磁直线电机段间推力优化控制[J]. 电机与控制学报, 2014, 18(4): 79-87.
Li Liyi, Zhu He, Liu Jiaxi, et al. Optimal inter- segment thrust control applied in primary winding segmented PMLSM[J]. Electric Machines and Control, 2014, 18(4): 79-87.
Structure and Electromagnetic Characteristics of U-Shaped Permanent Magnet Salient Pole Linear Motor
Abstract In some applications requiring high thrust and long stroke, such as vertical hoist system, permanent magnet synchronous linear motor (PMSLM) is limited by layout and installation space. Therefore, improving the utilization ratio of permanent magnet and achieving higher thrust density are very important. In this paper, a U-shaped permanent magnet salient pole linear motor (US-PMSPLM) is proposed. The secondary permanent magnets (PMs) with U-shaped structure can make full use of the PMs to increase the no-load back electromotive force (EMF) and thrust force obviously. Firstly, by analyzing the structure and magnetic circuit of the motor, the equivalent magnetic circuit model (EMCM) is established to analyze the variation of air gap flux density. Secondly, the finite element method (FEM) is used to compare the non-salient permanent magnet synchronous linear motor (NS-PMSLM) with the same primary structure and secondary PMs. Finally, an experimental prototype is developed, and the no-load back EMF and static thrust are tested. The experimental results are basically consistent with the simulation results, which verifies the rationality of the designed motor.
keywords:Linear motor, U-shaped permanent magnet, finite element method, electromagnetic characteristics, prototype experiment
中图分类号:TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.201128
国家自然科学基金项目(U1504506)、河南省科技攻关项目(202102210099,192102210073)和河南理工大学基本科研业务费项目(NSFRF200310)资助。
收稿日期 2020-09-02
改稿日期 2020-12-02
许孝卓 男,1981年生,博士,副教授,研究方向为特种电机理论与控制。E-mail: xxzhpu@163.com
封海潮 男,1983年生,硕士,副教授,研究方向为特种电机理论与控制。E-mail: fhc@hpu.edu.cn(通信作者)
(编辑 陈 诚)