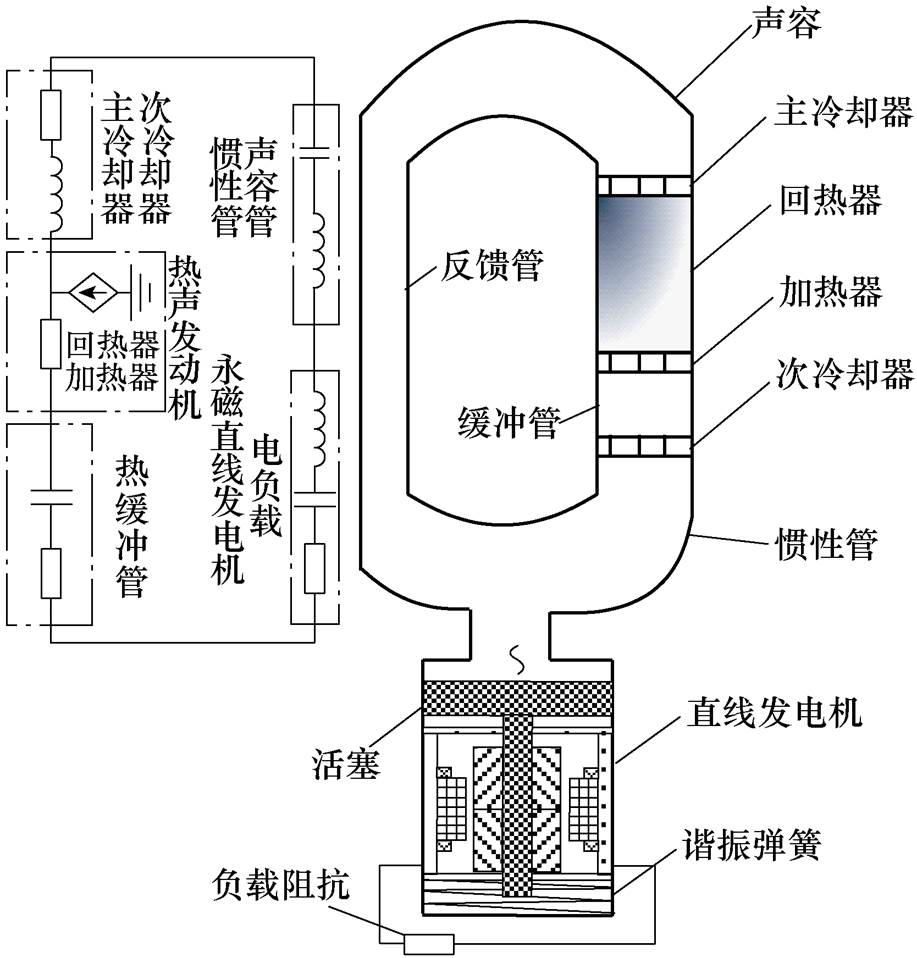
图1 TAEGS结构示意图
Fig.1 Schematic diagram of TAEGS
摘要 以热声发电系统(TAEGS)为应用背景,为了降低系统起振温度、缩短系统起振的时间,提出一种控制热声发电机电动运行将系统牵入谐振的自主协同起振综合控制策略,该控制策略以系统机械谐振时次级位移和初级电流相位差为90°作为频率跟踪控制的判定依据,通过采样次级位移和初级电流信号,经过改进二阶广义积分控制器输出相应的正交信号进行锁频,经过Park变换将交流信号变为直流信号,实现信号的无静差跟踪控制,进而使热声发电系统运行频率快速跟踪谐振频率。仿真分析和实验验证结果表明,所提出的起振控制策略既能使热声发电系统运行频率快速跟踪谐振频率,提高系统输出功率;又可改进二阶广义积分控制器,有效滤除检测信号的采样噪声和高频干扰,提高控制器的稳定性。
关键词:热声发电系统 永磁直线发电机 谐振频率 二阶广义积分
新兴的热声发电技术广泛应用于太阳能、燃烧余热、工业废热及汽车尾气等分布式能源系统发电领域,提高冷热电联产系统一次能源利用效率[1-3];为可再生能源的利用提供新方向,具有广泛的应用前景[4-7]。热声发电系统(Thermoacoustic Electric Generation System, TAEGS)由热声发动机和直线发电机构成,具有温度场、声场、磁场、电场等多场耦合的系统特性,TAEGS起振是实现由热能-机械能-电能转换的重要过程[8]。
TAEGS起振是热声发动机工作介质在外加温度梯度下由静止状态转变成周期性振荡流动状态的过程,因此在起振过程中经常出现跳频、声压饱和、声流等复杂的非线性因素,N. Rott提出热声系统运行在小振幅工况时的线性热声理论,可以近似为热声系统实际条件下的研究,但系统大振幅运行时却超出该理论的适用范围[8]。文献[9]采用非线性热声效应的二维模型和高效数值方法,分析了谐振管的形状对起振性能、振荡频率及非线性谐振频率跳变的影响。文献[10]建立热声系统的动力学模型求解出起振温度、谐振频率等重要参数,但对系统高频工况时集中参数处理却不适用。文献[11]建立了一套自激振荡热声发动机的理论模型,把输出声功为零设定为临界起振点,确定起振温度;由于引入经验频率公式,忽略了频率和起振温度的耦合,没有考虑充气压力对起振模态的影响。文献[12]利用CFD软件建立热声发动机在非平衡态自激振荡起振的模型,验证热力学稳定性分析的有效性。文献[13]利用温度梯度的板叠传输矩阵表达式,分析系统结构和参数对起振模态、起振温度的影响。由上述文献可以看出,为实现热声系统自激振荡起振,这些热声系统起振技术都是根据热动力学和声学原理,设计高效的行波型热声发动机,在热声发动机声波环路里加入谐振管的方式实现起振,但是谐振管消耗大量声功,很大程度上减小了热声发动机输入到直线发电机里的声功功率,也使得系统输出电功率的能力急剧下降。
近年来,国内外学者对关于TAEGS起振控制方法研究主要是基于TAEGS处于恒频稳态条件下取消谐振管,通过直流侧的蓄电池供电,驱动直线发电机电动运行,拖动热声发动机活塞振荡运动,使其行程逐渐增加直至达到所需振幅[14-16]。但是,这些TAEGS恒频稳态起振控制策略大都将热声发动机看成理想稳定的线性系统,简单把永磁直线电机看作电动机,没有从整个TAEGS的角度分析起振特性。由于低品质热源的不连续性和不稳定性,易导致TAEGS的运行频率不能一直工作在初始设计的谐振频率值。哪怕频率只漂移几赫兹,直线发电机从热声发动机里捕获声功的能力也将大大降低,从而导致系统输出电能急剧下降,限制了热声技术的应用。同时,永磁直线电机容易受到磁场耦合及齿槽力等因素的影响[17],尽管位移电压比值存在最大值,但其最大值所在频率点与谐振频率点并不重合,因此位移电压比不适合作为确定谐振频率点的判定依据。文献[18]在位移控制环稳态时,采样电流信号后进行模糊逻辑判定并搜索最小电流的运行频率点。此电流最小频率跟踪模糊控制算法中驱动频率与采样电流非单调函数关系,必须借助模糊控制进行搜索判定,因此频率跟踪搜索时间长,对位移影响较大,频率调节跳跃性大,准确性稍差,使系统的结构和控制变得复杂,很难使TAEGS快速运行在谐振状态,增加TAEGS由起振切换到稳态控制的时间。因此热声发动机谐振频率漂移、起振难、热声系统发电效率低成为制约热声发电技术发展的核心问题。
为了保证TAEGS高效运行,实现对热声发动机自激荡起振的有效补偿。本文提出了一种基于二阶广义积分控制永磁直线发电机电动运行将系统牵入谐振的自主协同起振控制策略。采用仿真分析和实验验证该控制策略,使TAEGS的起振频率迅速地跟踪谐振频率,可以有效降低系统起振温度,缩短系统起振的时间,从而获得较好的整机自主协同起振性能。
图1为TAEGS结构示意图,TAEGS利用热声发动机将具有温度梯度热能转化为机械能(声能),热声发动机输出近似正弦波形式的声功波动,驱动安装在热声发动机耦合输出端口的活塞,在系统运行过程中带动直线发电机次级进行高频短行程的往复直线运动,然后通过永磁直线发电机将机械能转化为电能[19]。
TAEGS由声学系统、机械振动系统和电学系统三部分组成[19],基于相似理论,建立TAEGS声-力-电类比模型将三个系统耦合起来进行分析,TAEGS的声-力-电类比模型如图2所示。

图1 TAEGS结构示意图
Fig.1 Schematic diagram of TAEGS
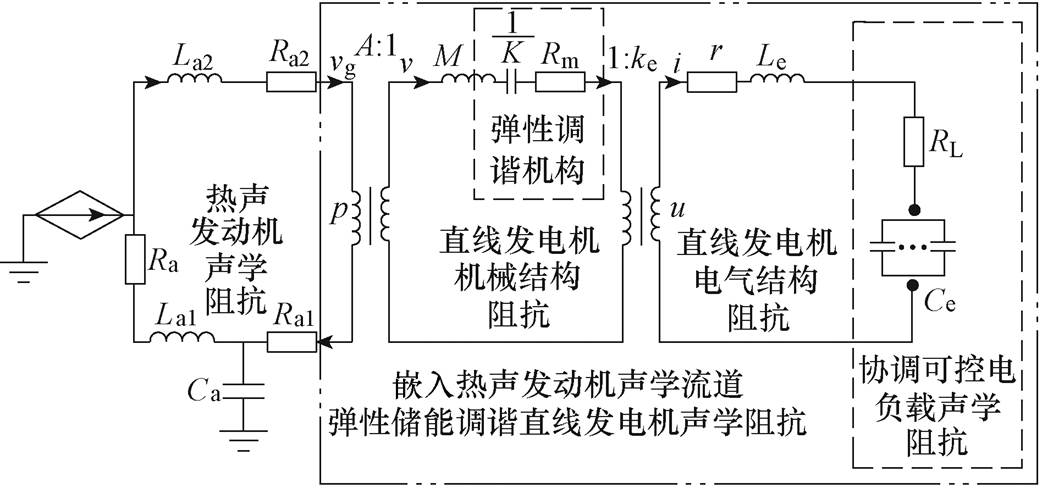
图2 TAEGS的声-力-电类比模型
Fig.2 Acoustical-mechano-electro analogic diagram of TAEGS
TAEGS控制方程为
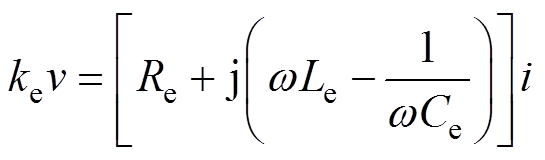 (1)
(1)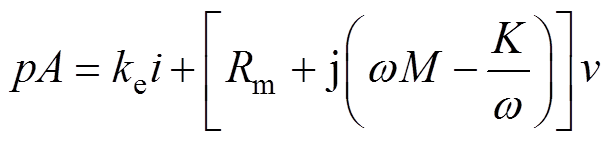 (2)
(2)
式中,p为热声发动机内气体工质的声波压力波动;A为活塞面积;Rm为等效机械机阻尼系数;ke为机电常数;K=km+kg,km为机械弹簧刚度系数,kg为背腔气体弹簧刚度系数,kg=A2cg p0/Vb,p0为热声发动机内气体工质平均压力,Vb为背腔容积,cg为定压比热容;v为次级速度,v=dx/dt,x为次级位移;M为活塞和动子质量,i为初级电流;Re=RL+r,r为初级绕组内阻,RL为负载电阻;Le为初级绕组等效电感;Ce为调谐电容;w 为TAEGS角频率。
通过式(1)、式(2)推导TAEGS两机耦合的声学阻抗为
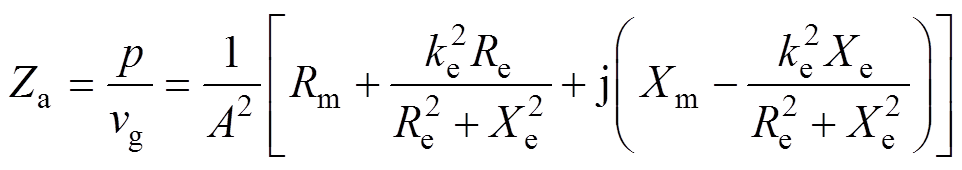 (3)
(3)进入发电机的声功率为
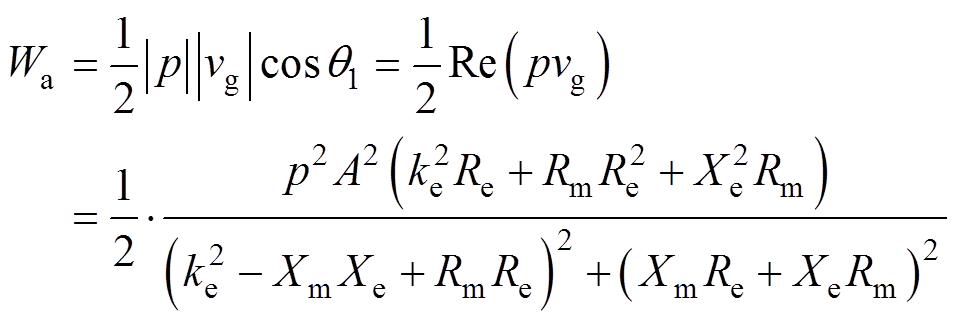 (4)
(4)
系统输出的电功率为
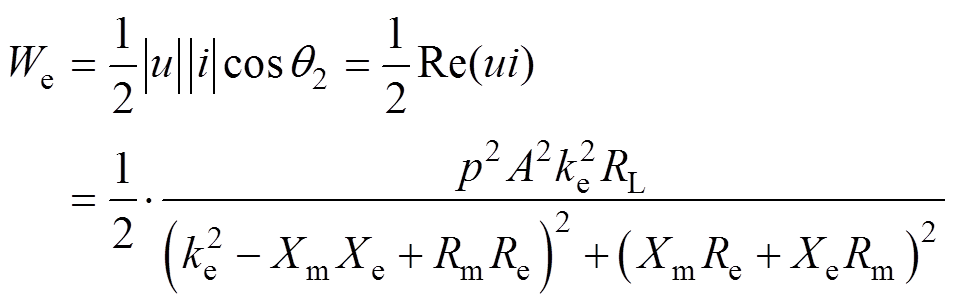 (5)
(5)式中,q1为声功波动和气体工质体积流速的相位差;q2为初级绕组端电压和电流的相位差;vg为气体工质体积流速;u为初级电压;Xm为机械阻抗虚部,Xm=wM-K/w ;Xe为电路阻抗虚部,Xe=wLe-1/(wCe)。
从TAEGS声电功率数学模型推导过程可知,合理匹配直线发电机与热声发动机声学阻抗可以提高TAEGS声电功率的输出[19]。由式(4)可知,TAEGS捕获的声功率不仅依赖声功率波动和气体工质体积流速的大小,还受两者相位q1的影响。当发电机电路谐振(Xe=0)时,即调谐电容参数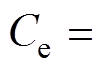
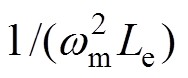 ;减小机械阻抗虚部Xm,当Xm=0时,即弹簧刚度系数
;减小机械阻抗虚部Xm,当Xm=0时,即弹簧刚度系数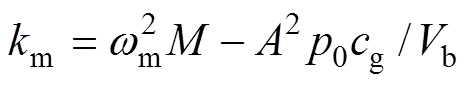 ,wm为机械谐振角频率,TAEGS谐振时声功率波动和体积流速如图3所示。此时发电机声阻抗角趋近零,声波压力和体积流速同相位运行,系统捕获最大声功率为
,wm为机械谐振角频率,TAEGS谐振时声功率波动和体积流速如图3所示。此时发电机声阻抗角趋近零,声波压力和体积流速同相位运行,系统捕获最大声功率为
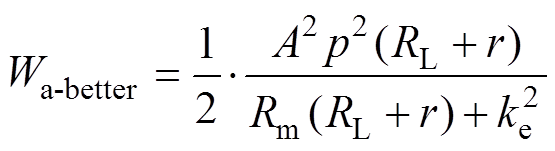 (6)
(6)同理,由式(5)可知,当初级绕组电流和端电压同相位运行时,系统可输出最大电功率。TAEGS谐振时发电机端电压和电流如图4所示,其捕获声功率和输出电功率如图5所示。可以看出,TAEGS在允许的额定电压、额定电流条件下,可输出最大电功率为
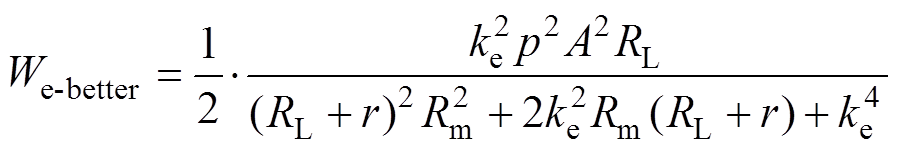 (7)
(7)
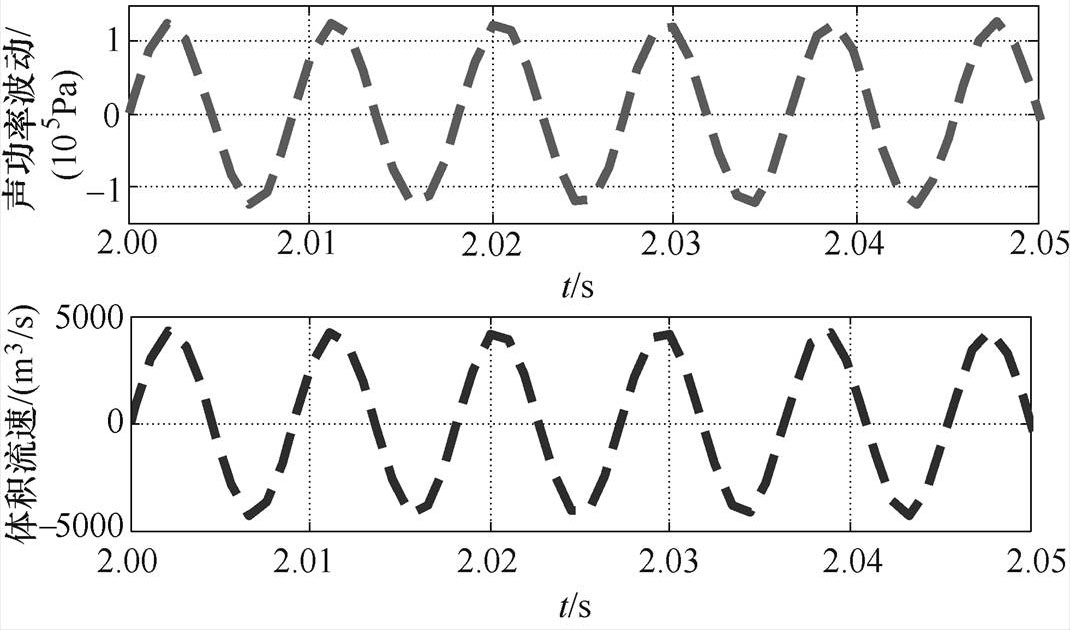
图3 TAEGS谐振时声功率波动和体积流速
Fig.3 Acoustic pressure and volume flow rate on the resonance of TAEGS
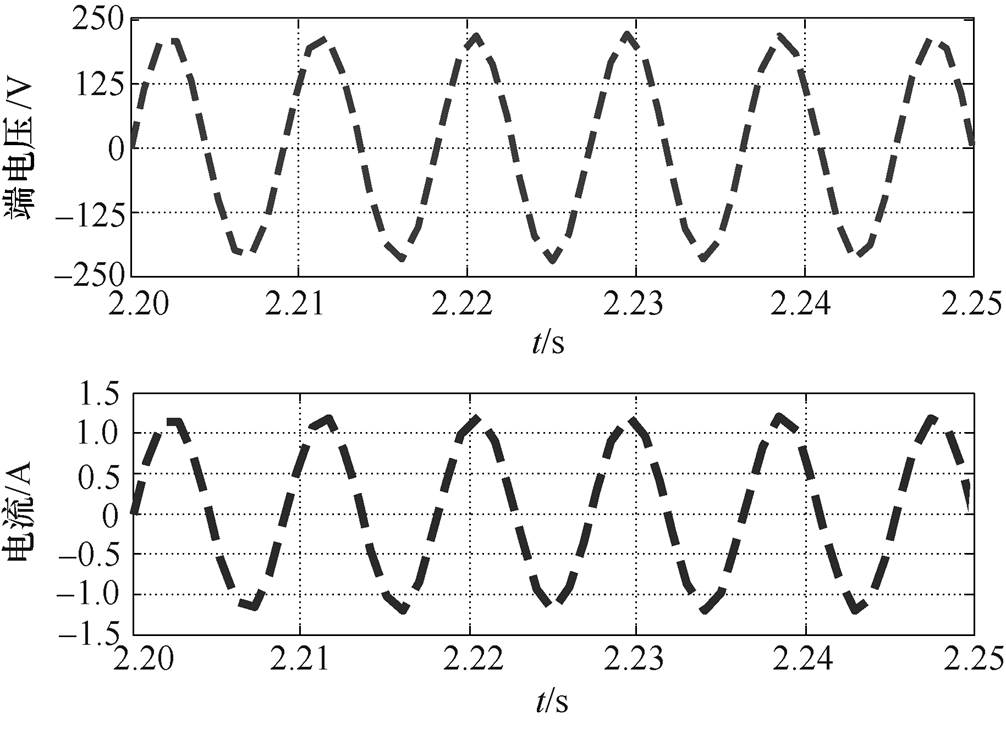
图4 TAEGS谐振时发电机端电压和电流
Fig.4 Voltage and current and on the resonance of TAEGS
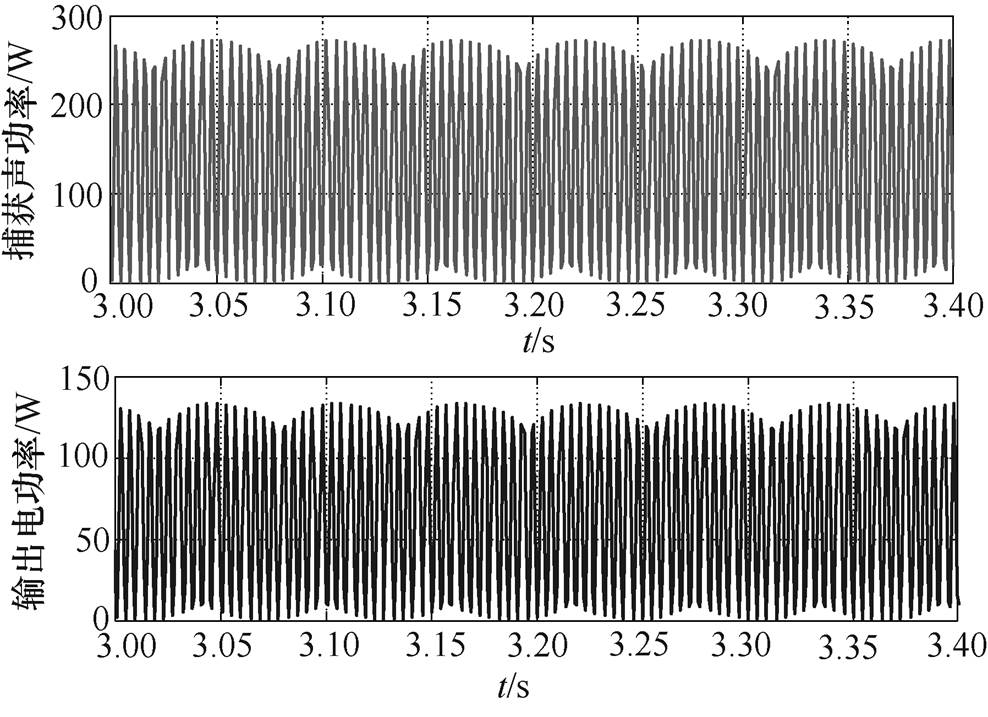
图5 TAEGS谐振时发电机捕获声功率和输出电功率
Fig.5 Capturing acoustic power and outputting electric power on the resonance of TAEGS
在TAEGS实现最大声功率捕获的基础上,选择合适的负载电阻提高系统输出最大电功率,由 得电阻参数设计方案。
得电阻参数设计方案。
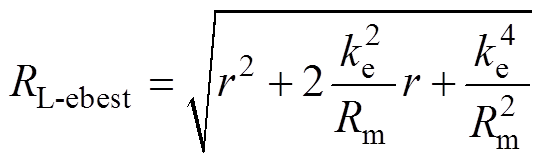 (8)
(8)则TAEGS输出最大电功率为
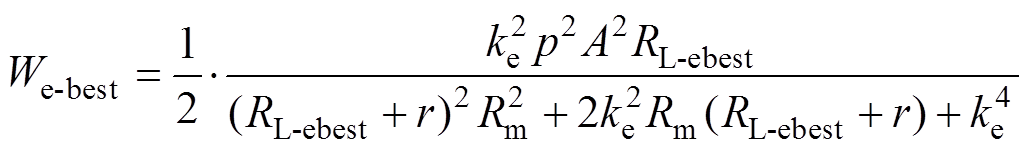 (9)
(9)
得到以提高捕获声功率为优化约束条件,以输出电功最大为优化设计目标的发电机机械阻抗和负载阻抗的参数设计方法。
从谐振特性分析可知,通过阻抗匹配优化设计,使TAEGS运行在系统机械谐振频率点上(w =wm),才能提高直线发电机声功率捕获的能力,进而使得系统输出的电功最大。此时,TAEGS谐振运行角频率wm满足
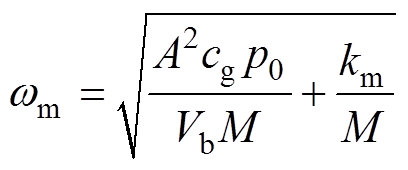 (10)
(10)式中, ,
,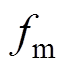 为TAEGS谐振运行频率。
为TAEGS谐振运行频率。
当TAEGS运行在谐振频率点时,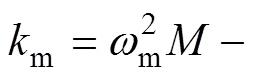
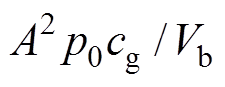 ,由式(1)、式(2)推导位移与电流的比为
,由式(1)、式(2)推导位移与电流的比为
 (11)
(11)由式(11)可知,当TAEGS谐振运行时,直线发电机次级位移和初级电流相位差为-90°,且二者的比值最大。当初级电流不变时,次级位移达到最大振幅;同理,当次级位移不变时,初级电流值最小。而且TAEGS运行频率与直线发电机次级位移和初级电流相位差之间为单调函数关系,因此无论TAEGS内部扰动如何变化,初级电流相位始终超前次级位移相位90°。因此,电流位移相位差的方法作为TAEGS谐振频率跟踪控制策略的判定依据较为适合。而且这种谐振频率跟踪方式响应迅速,对位移影响不大,能够准确地定位到谐振频率点,适宜应用在TAEGS起振控制时的高频短行程运行状态。
为了实现对热声发动机自激荡起振的有效补偿,使TAEGS的起振频率迅速地跟踪谐振频率,本文基于二阶广义积分锁频环的机械谐振频率跟踪的起振控制策略,通过检测次级位移和初级电流的相位,经过二阶广义积分正交信号发生器(Second- Order Generalized Integrator-Quadrature Signals Generator, SOGI-QSG)输出相应的正交信号进行锁频[20],进而使TAEGS运行频率快速跟踪谐振频率,为热声发电系统的自激荡起振控制提供新思路。
SOGI-QSG原理如图6所示。输出信号v′相位始终超前qv′相位90°,不受系统增益k、运行频率w、谐振频率wm的影响,因此SOGI-QSG既能有效地使输入次级位移和初级电流信号的相位发生90°的偏移,同时滤出输入信号的采样噪声和高频干扰,因此,SOGI-QSG也可看做是自适应滤波器[21]。
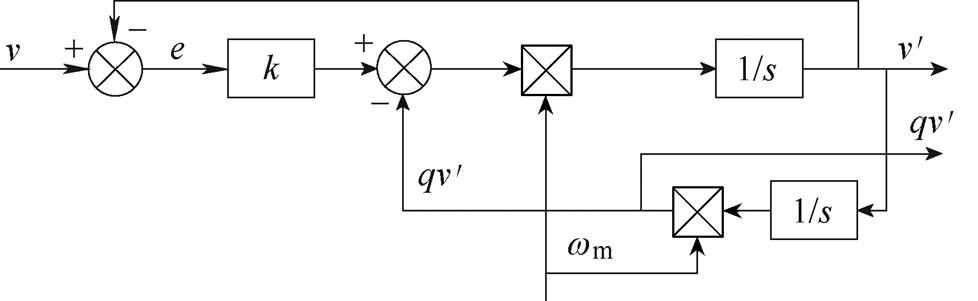
图6 SOGI-QSG原理
Fig.6 Schematic diagram of SOGI-QSG
定义SOGI-QSG的数学模型为
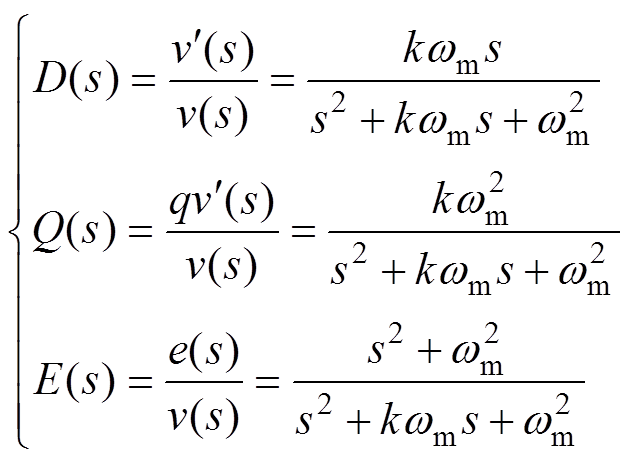 (12)
(12)由式(12)可得SOGI-QSG的幅相频域特性为
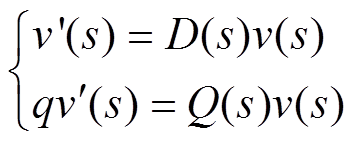 (13)
(13)
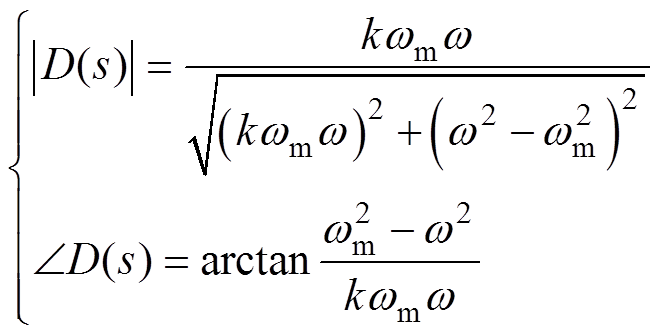 (14)
(14)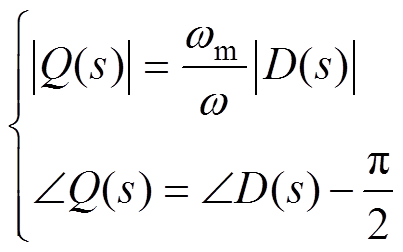 (15)
(15)
由式(15)可知,当TAEGS谐振运行(w=wm)时,输出次级位移和初级电流信号无静差跟踪给定信号,SOGI-QSG可以产生幅值相同而相位差90°的正交信号[22]。
热声发动机内气体工质不均衡和加热温度的不稳定会使TAEGS工作频率不断改变,通过改进上述二阶广义积分器对输入量加以锁频,实现输出量自动跟踪输入量的频率。
二阶广义积分锁频(Second-Order Genera- lized Integrator-FLL, SOGI-FLL)控制的基本原理如图7所示,当TAEGS运行在谐振频率时,输入量与输出量增益为零,且相位跳变180°[23]。因此令频率输出的偏差量为ef=eqv',当w<wm时,ef>0;w=wm时,ef=0;w>wm时,ef<0。利用带有负增益的积分环节对输出频率偏差量ef移相为输入信号的频率w,同时将TAEGS的稳定工作频率w0作为输出频率的前馈补偿量,减小SOGI-FLL的拉入时间,产生的频率信号通过积分环节转变成相位信号[23]。
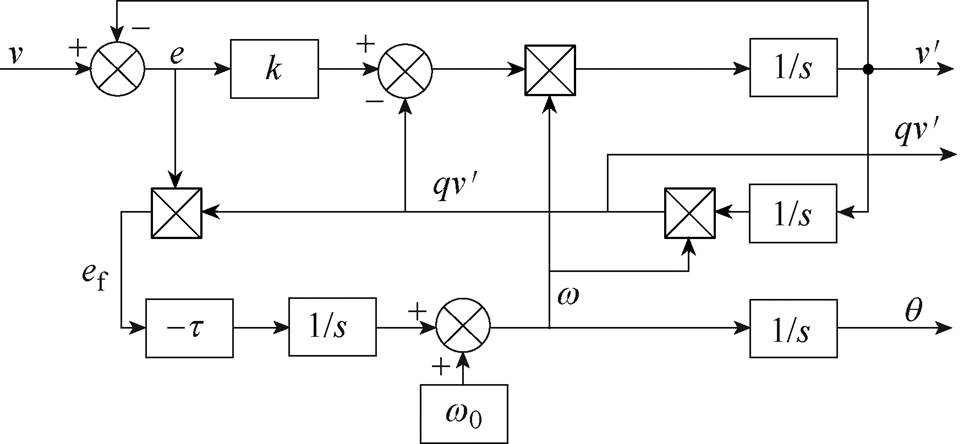
图7 SOGI-FLL原理
Fig.7 Diagram of SOGI-FLL
图8为采用基于二阶广义积分控制的TAEGS起振控制结构框图。直线发电机次级位移x和初级电流i分别通过改进二阶广义积分控制器产生相位信号及其正交信号,经Park坐标变换后,选取次级位移的直轴分量xd为相位参考信号;初级电流信号交轴分量iq相位为跟踪信号,当TAEGS运行频率等于机械谐振频率时,发电机初级电流和次级位移的相位差为90°,因此选用电流交轴分量iq为频率反馈调整量,产生的误差信号经过PI环节后作为频率调整量[23-24]。由于初级电流和次级位移幅值不同,将xd和iq做标幺化处理,允许误差信号区间0~1。
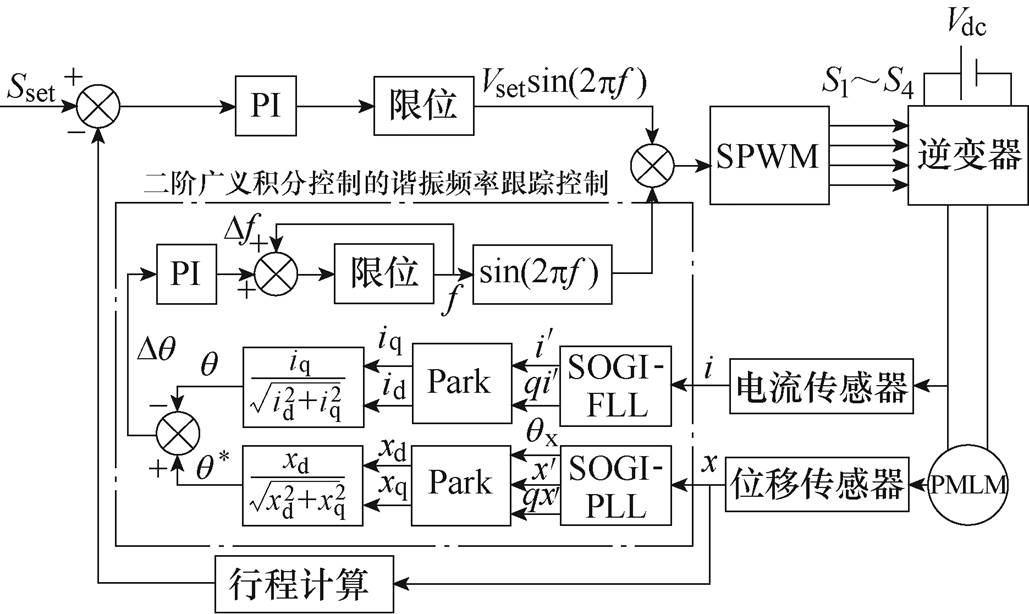
图8 TAEGS起振控制结构框图
Fig.8 Onset control block diagram of TAEGS
TAEGS起振运行时,电压变化波形如图9所示,行程变化波形如图10所示。起始时给定f=90Hz的控制电压,在0~1s的调节时间内,为了使热声发动机活塞位移迅速稳定在给定值,需要不断地增加控制电压的幅值,活塞的位移随着电压逐渐增大而不断增加,在t=1s时,活塞行程最终稳定在12mm处,此时控制电压的幅值约为167V。在t=1.5s启用SOGI谐振频率跟踪控制算法,控制电压的幅值迅速减小,活塞位移的幅值也随之急剧下降,在1.5~2.5s的调节时间内,控制电压幅值不断增加,t=1.7s控制电压幅值达到最大,此时位移控制开始跟随位移给定量不断增大,t=2.36s时行程稳定在最大行程12mm处。

图9 电压变化波形
Fig.9 Waveforms of voltage change
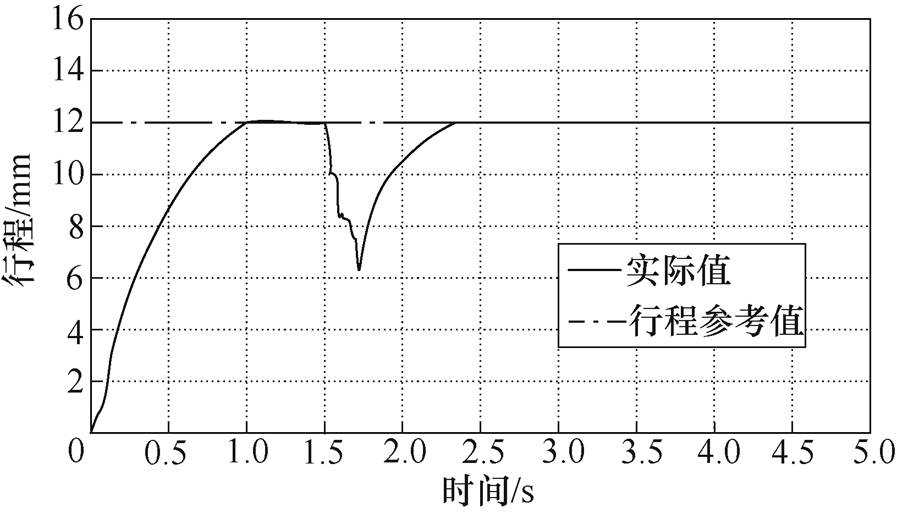
图10 行程变化波形
Fig.10 Waveforms of stroke change
TAEGS进入稳定运行状态,此时TAEGS运行频率等于驱动频率,即f=fm=110Hz,其输出电流与位移仿真波形如图11所示。由图11可以看出,电流与位移相位差约为90°,通过仿真结果对比发现,通过给定位移启用SOGI谐振频率跟踪控制算法,控制电压幅值下降很多,极大地降低了直线发电机输入功率,提高了整个TAEGS的运行效率。
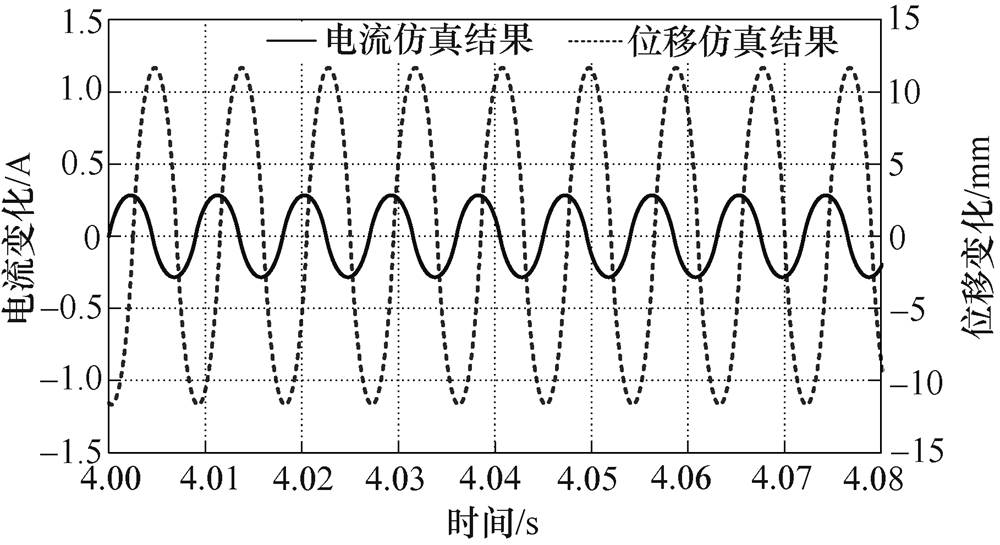
图11 f=fm=110Hz稳态时输出电流与位移仿真波形
Fig.11 Simulation waveforms of current and displacement steady-state response at 110Hz
电流位移相位差变化仿真波形如图12所示,当给定f=90Hz的驱动电压控制,即控制电压频率小于TAEGS的谐振频率;TAEGS稳定运行时次级位移和初级电流相位差为7°,而启用SOGI谐振频率跟踪控制算法后,驱动电压频率自动跟踪TAEGS谐振频率,TAEGS稳定运行时电流与位移相位差 为90°。
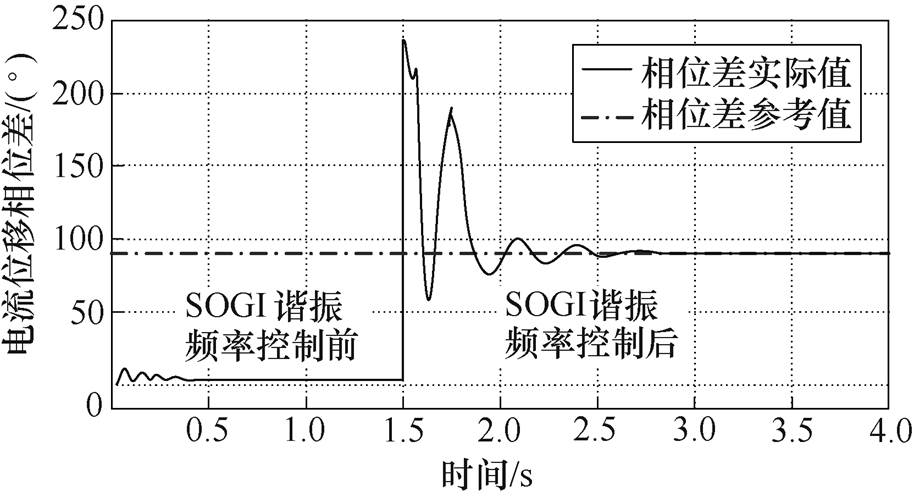
图12 电流位移相位差变化仿真波形
Fig.12 Simulation waveforms of phase betwen current and displacement
另外,谐振频率跟踪控制过程中存在检测电流和位移时的误差,通过仿真结果对比发现,启动频率跟踪算法频率仿真波形如图13所示,采用SOGI谐振频率跟踪控制算法,二阶广义积分环节通过滤波功能,消除高频噪声干扰,减小对频率控制影响。
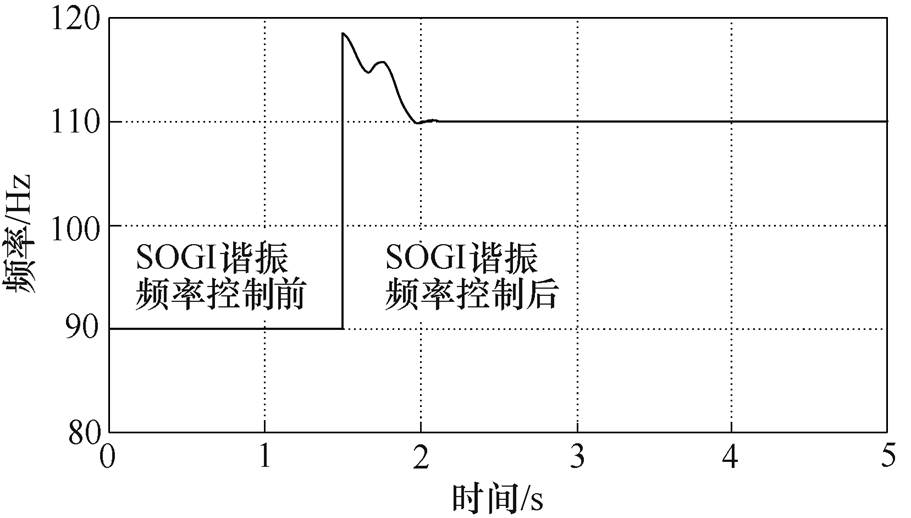
图13 启动频率跟踪算法频率仿真波形
Fig.13 Simulation waveform of frequency before and after SOGI resonant frequency tracking control
TAEGS实验平台主要由热声发动机、直线发电机、检测装置、低品质热源捕获器、系统起振控制
器和可控电负载组成,TAEGS实验平台如图14所示。TAEGS实验平台的热源捕获器捕获丁烷燃烧的热量,通过控制丁烷流量改变捕获的热能。当加热到2 159W时,TAEGS达到稳定工作状态。发电机在TAEGS起振运行时以电动方式工作,使用示波器实时测量直线发电机的电参数,次级位移通过位移传感器进行测量。实验平台相关参数见表1。

图14 TAEGS实验平台
Fig.14 Experimental platform of TAEGS
表1 TAEGS实验平台相关参数
Tab.1 Parameters of TAEGS
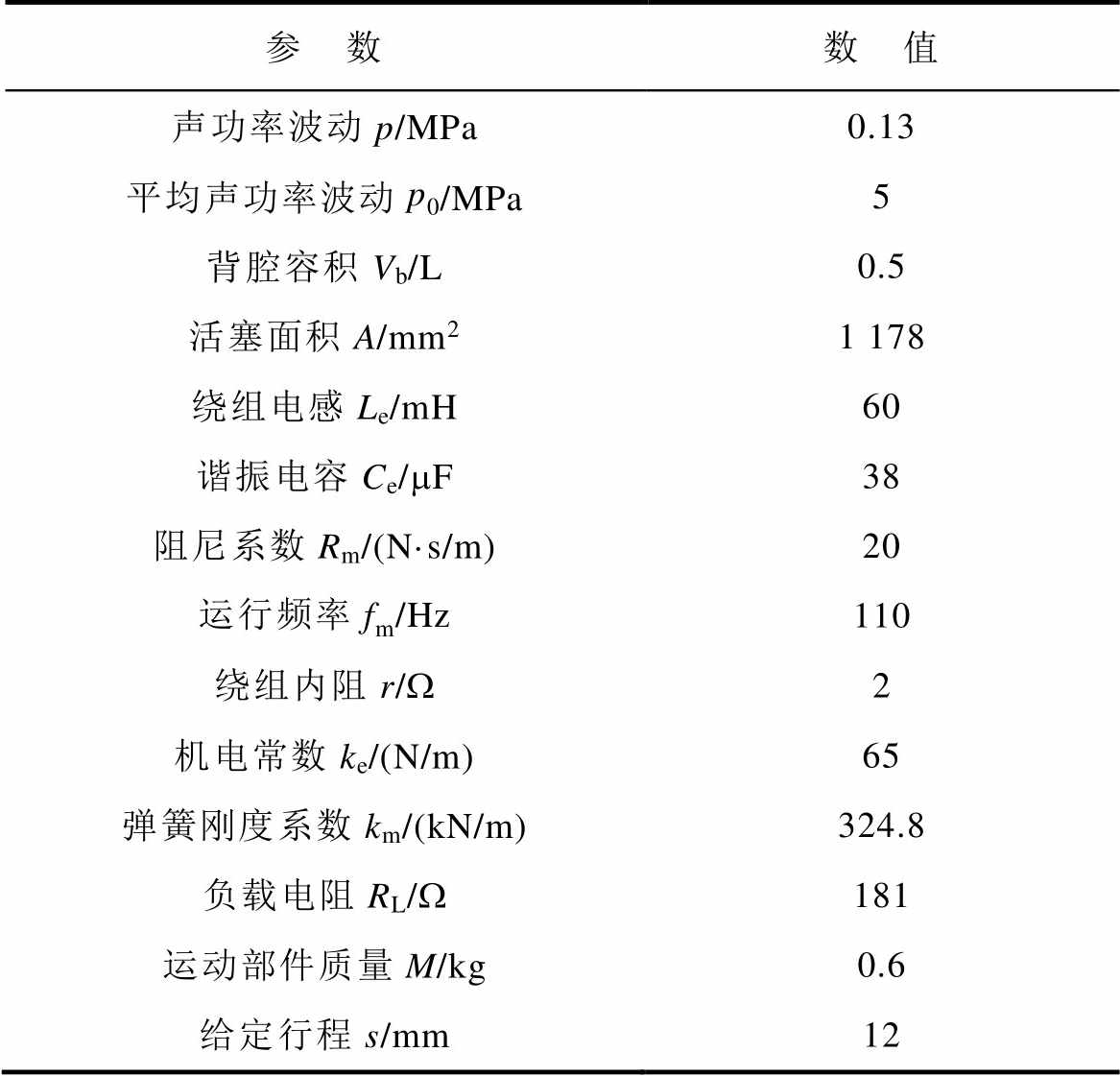
参 数数 值 声功率波动p/MPa0.13 平均声功率波动p0/MPa5 背腔容积Vb/L0.5 活塞面积A/mm21 178 绕组电感Le/mH60 谐振电容Ce/mF38 阻尼系数Rm/(N·s/m)20 运行频率fm/Hz110 绕组内阻r/W2 机电常数ke/(N/m)65 弹簧刚度系数km/(kN/m)324.8 负载电阻RL/W181 运动部件质量M/kg0.6 给定行程s/mm12
图15为加入SOGI谐振频率跟踪控制算法前后直线电机次级行程和频率变化的实验结果。TAEGS在驱动电压频率f=90Hz时起振,在t=1.5s时加入谐振频率跟踪控制算法,经过1s后TAEGS运行频率曲线最后稳定在110Hz,TAEGS平稳运行在谐振频率点上。TAEGS起振0.3s后行程变化进入稳定平衡状态,行程变化趋势跟随设定参考量,达到12mm。加入SOGI谐振频率跟踪控制算法0.5s后,行程变化趋势仍然跟随设定参考量。此时控制电压驱动频率由90Hz升至110Hz后保持稳定。
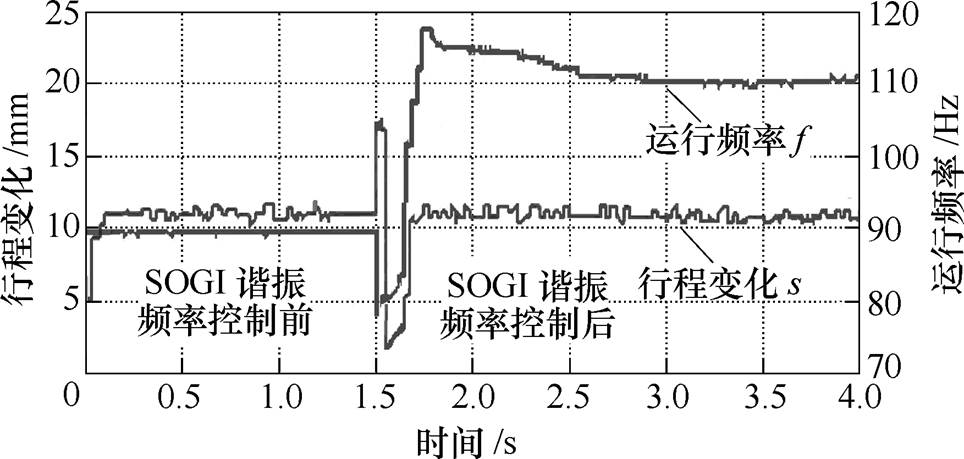
图15 SOGI频率控制前后行程和频率实验结果
Fig.15 Experimental results of stroke and frequency before and after SOGI resonant frequency tracking control
图16为SOGI谐振频率跟踪控制算法控制锁相环输出相位实验结果,从图中可以看出,相位稳定时间为0.8s,然后实现位移信息锁相。
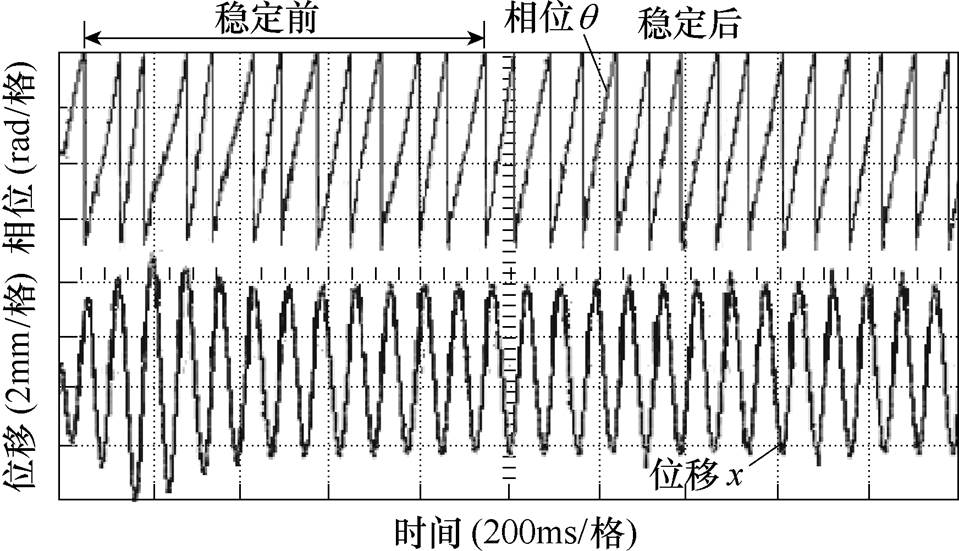
图16 SOGI频率控制算法锁相环输出相位实验结果
Fig.16 Experimental results of output phase based on SOGI resonant frequency tracking control
图17为SOGI谐振频率跟踪控制算法控制输出位移直轴分量信号和驱动频率实验结果,由图可知,经过SOGI谐振频率跟踪控制算法控制驱动频率由90Hz逐渐增加,最后稳定在110Hz。加入SOGI谐振频率跟踪控制算法前,位移直轴分量经过0.3s后趋于稳定;加入SOGI谐振频率跟踪控制算法控制0.5s后,位移直轴分量趋于稳定。
频率为90Hz时电流位移实验波形如图18所示,频率为110Hz时电流位移实验波形而如图19所示,TAEGS平稳运行时次级位移与初级电流的夹角为90°,实现位移锁相。当控制电压驱动频率为90Hz时,热声直线发电机初级电流约为1.3A;加入SOGI谐振频率跟踪控制算法后,热声直线发电机次级运行相同行程时,初级电流下降到0.3A。控制效率上升约为76.9%。
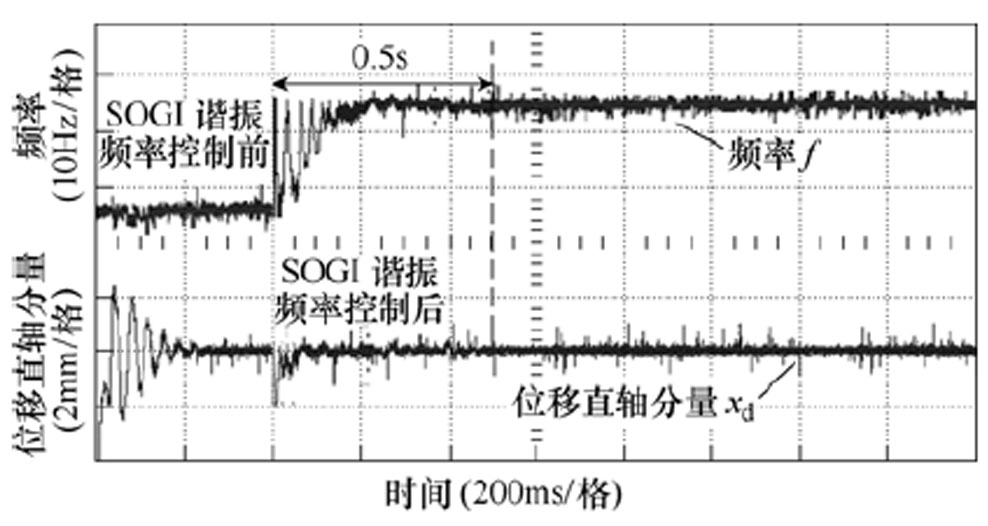
图17 SOGI频率控制前后位移直轴分量和频率实验结果
Fig.17 Experimental results of displacement direct axis and frequency before and after SOGI resonant frequency tracking control
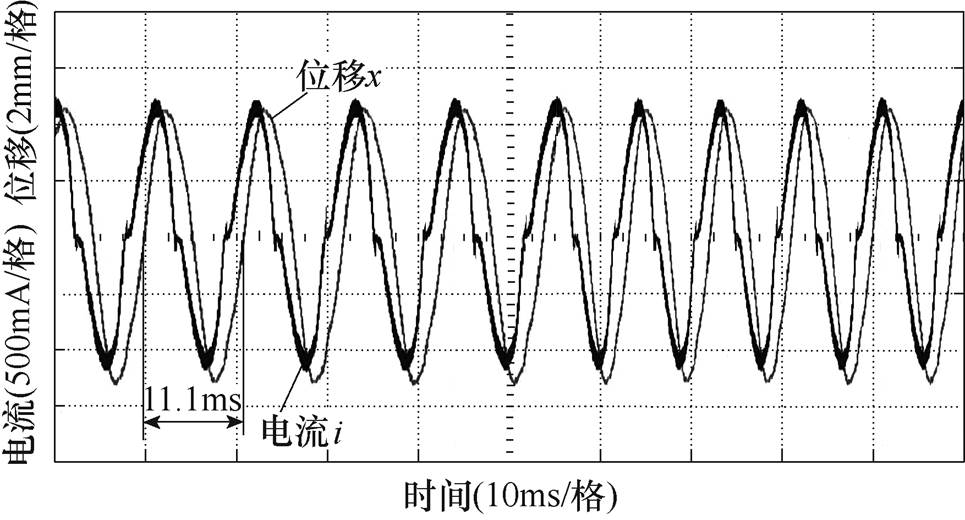
图18 频率为90Hz时电流、位移实验波形
Fig.18 Experimental waveforms of current and displacement at 90Hz
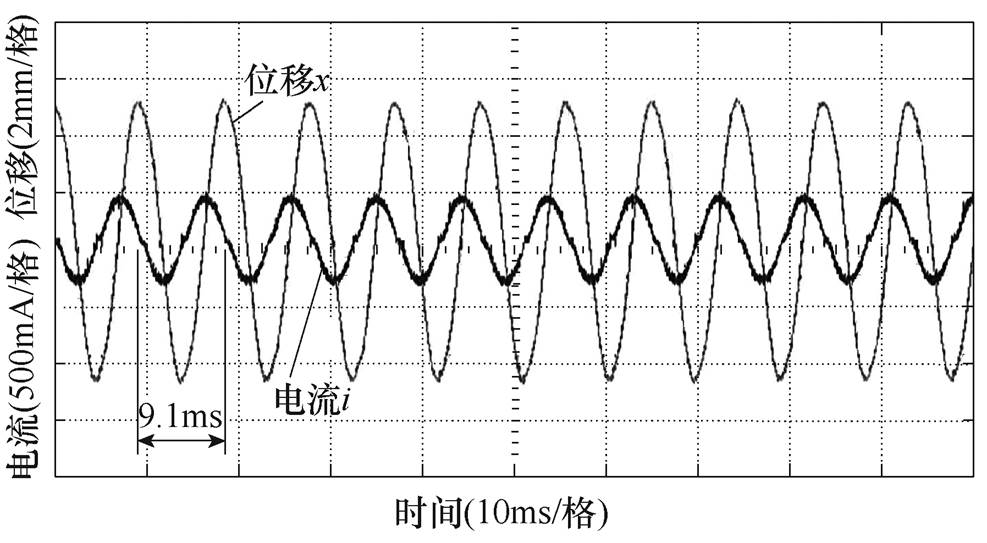
图19 频率为110Hz时电流、位移实验波形
Fig.19 Experimental waveforms of current and displacement at 110Hz
本文深入研究热声发电系统的自主协同起振控制策略。基于TAEGS的数学模型,对系统的谐振运性特性进行分析,得出TAEGS运行频率等于机械谐振频率时,直线发电机次级位移和初级电流相位差为90°,此时热声直线发电机捕获最大声功率,进而使得系统输出的电功率最大;并把TAEGS谐振特性作为谐振频率跟踪控制策略的判定依据,提出基于改进二阶广义积分的谐振频率跟踪的起振控制方法,通过采样次级位移和初级电流信号,经过改进二阶广义积分控制器输出相应的正交信号进行锁频,进而使TAEGS运行频率快速跟踪谐振频率。
通过仿真分析和实验证明,加入SOGI谐振频率跟踪控制算法后,控制电压驱动频率从90Hz快速上升到TAEGS谐振频率110Hz。TAEGS平稳运行在给定位移后,热声直线发电机初级电流由1.3A下降到0.3A,热声直线发电机次级运行相同行程时,控制效率上升约为76.9%。
参考文献
[1] 韩佶, 苗世洪, 李超, 等. 计及相关性的电-气-热综合能源系统概率最优能量流[J]. 电工技术学报, 2019, 34(5): 1055-1067.
Han Ji, Miao Shihong, Li Chao, et al. Probabilistic optimal energy flow of electricity-gas-heat integrated energy system considering correlation[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(5): 1055-1067.
[2] 王洋, 杜文娟, 王海风. 风电并网系统次同步振荡频率漂移问题[J]. 电工技术学报, 2020, 35(1): 146- 157.
Wang Yang, Du Wenjuan, Wang Haifeng. Frequency drift of sub-synchronous oscillation in wind turbine generator integrated power system[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 146-157.
[3] 陈柏翰, 冯伟, 孙凯, 等. 冷热电联供系统多元储能及孤岛运行优化调度方法[J]. 电工技术学报, 2019, 34(15): 3231-3243.
Chen Bohan, Feng Wei, Sun Kai, et al. Multi-energy storage system and islanded optimal dispatch method of CCHP[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3231-3243.
[4] 李建林, 郭斌琪, 牛萌, 等. 风光储系统储能容量优化配置策略[J]. 电工技术学报, 2018, 33(6): 1189-1196.
Li Jianlin, Guo Binqi, Niu Meng, et al. Optimal configuration strategy of energy storage capacity in wind/PV/storage hybrid system[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1189- 1196.
[5] 赵晶晶, 李敏, 何欣芹, 等. 基于限转矩控制的风储联合调频控制策略[J]. 电工技术学报, 2019, 34(23): 4982-4990.
Zhao Jingjing, Li Min, He Xinqin, et al. Coordinated control strategy of wind power and energy storage in frequency regulation based on torque limit control[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4982-4990.
[6] 吴青峰, 孙孝峰, 王雅楠, 等. 基于分布式下垂控制的微电网分布式储能系统SOC平衡策略[J]. 电工技术学报, 2018, 33(6): 1247-1256.
Wu Qingfeng, Sun Xiaofeng, Wang Yanan, et al. A distributed control strategy for SOC balancing of distributed energy storage systems in microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1247-1256.
[7] 李欣然, 崔曦文, 黄际元, 等. 电池储能电源参与电网一次调频的自适应控制策略[J]. 电工技术学报, 2019, 34(18): 3897-3908.
Li Xinran, Cui Xiwen, Huang Jiyuan, et al. The self- adaption control strategy of energy storage batteries participating in the primary frequency regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3897-3908.
[8] 李娟, 周刚, 李青. 热声起振机理的研究进展[J]. 低温与超导, 2015, 43(5): 7-12.
Li Juan, Zhou Gang, Li Qing. Advances in the research of onset mechanism of thermoacoustic systems[J]. Cryogenics & Superconductivity, 2015, 43(3): 7-12.
[9] Hamilton M F, Ilinskii Y A, Zabolotskaya E A. Nonlinear frequency shifts in acoustical resonators with varying cross sections[J]. Journal of the Acoustical Society of America, 2009, 125(3): 1310-1318.
[10] Huang Xin, Zhou Gang, Li Qing. Thermodynamic analysis of onset characteristics in a miniature thermoacoustic stirling engine[J]. Journal of Thermal Science, 2013, 22(3): 216-222.
[11] Benavides E M. An analytical model of self-starting thermoacoustic engines[J]. Journal of Applied Physics, 2006, 99(11): 1-7.
[12] Tang Ke, Lin Xiaogang, Tian Lei, et al. Study on self-excited oscillation in a thermoacoustic engine with Glansdorff-Prigogine stability criterion[J]. Journal of Non-Equilibrium Thermodynamics, 2011, 36(4): 393-404.
[13] Qiu Limin, Lai Bihui, Zhao Yitao, et al. Study on the onset temperature of a standing-wave thermoacoustic engine based on circuit network theory[J]. Science China Technological Sciences, 2012, 55(10): 2864- 2868.
[14] 夏加宽, 何新, 赵志强, 等. 热声发动机起振控制方法: 中国, 201010581563.6[P]. 2012-01-14.
[15] 夏加宽, 何新, 赵志强, 等. 热声系统专用电动发电双向谐振永磁直线发电装置: 中国, 201010568531.2[P]. 2010-12-01.
[16] 夏加宽, 贾海源, 何新. 热声系统混合磁路永磁直线发电机电磁分析[J]. 微电机, 2011, 44(5): 1-4.
Xia Jiakuan, Jia Haiyuan, He Xin. Electromagnetism analysis of hybrid magnetic circuit permanent magnet linear generator for thermoacoustic system[J]. Micromotors, 2011, 44(5): 1-4.
[17] 罗宏浩, 吴峻, 常文森. 动磁式永磁无刷直流直线电机的齿槽力最小化[J]. 中国电机工程学报, 2007, 27(6): 12-16.
Luo Honghao, Wu Jun, Chang Wensen. Minimization of cogging force in moving magnet type PMBLDCLM[J]. Proceedings of the CSEE, 2007, 27(6): 12-16.
[18] 于明湖, 张玉秋, 叶云岳, 等. 直线振荡电机谐振频率跟踪策略研究[C]//第29届中国控制会议, 北京, 2010: 3348-3352.
[19] 何新, 夏加宽, 苏浩, 等. 热声发电系统最大声电效率阻抗匹配分析[J]. 电工技术学报, 2017, 32(9): 92-100.
He Xin, Xia Jiakuan, Su Hao, et al. Analysis on impedance matching of thermoacoustic electric generation system for the maximum acoustic-to- electric efficiency[J]. Transactions of China Electro- technical Society, 2017, 32(9): 92-100.
[20] 辛振, 赵仁德, 郭宝玲. 基于二阶广义积分器-锁频环的异步电机同步角频率估计方法[J]. 电工技术学报, 2014, 29(1): 116-122.
Xin Zhen, Zhao Rende, Guo Baoling. New induction motor ynchronous angular frequency estimation method based on second order generalized integrator- frequency locked loop[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 116-122.
[21] 涂娟, 汤宁平. 基于改进型DSOGI-PLL的电网电压同步信号检测[J]. 中国电机工程学报, 2016, 36(9): 2350-2356.
Tu Juan, Tang Ningping. Synchronizing signal detection for grid voltage based on modified DSOGI- PLL[J]. Proceedings of the CSEE, 2016, 36(9): 2350- 2356.
[22] 王国玲, 何富桥, 刘旭, 等. 基于二阶广义积分器新能源船舶电网锁相技术[J]. 电机与控制学报, 2020, 24(7): 147-155.
Wang Guoling, He Fuqiao, Liu Xu, et al. Phase- locked loop technique in new energy shipboard grid based on second-order generalized integrators[J]. Electric Machines and Control, 2020, 24(7): 147- 155.
[23] 余海涛, 张涛. 直线振荡电机谐振频率跟踪控制技术研究[J]. 电机与控制学报, 2019, 23(6): 63-72.
Yu Haitao, Zhang Tao. Strategy of resonant frequ- ency tracking for linear oscillatory actuator[J]. Electric Machines and Control, 2019, 23(6): 63-72.
[24] Xu Wei, Wang Qizhe, Li Xiang, et al. A novel resonant frequency tracking control for linear compressor based on MRAS method[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 237- 242.
Autonomous Cooperative Onset Control Strategy of Thermoacoustic Electric Generation System
Abstract An autonomous cooperative onset control strategy of thermoacoustic electric generation system was presented in this paper to control the electric generator and bring TAEGS into resonance. The application background is TAEGS. In order to reduce the onset temperature and shorten the onset time of the system, according to the theory that phase angle between displacement and current is 90°, the quadrature signals of displacement and current were output by the improved second-order generalized integral controller to lock the frequency, and the AC signal was converted into DC signal by Park transformation. The zero steady-state error free tracking control of the signal was realized, and then the running frequency of TAEGS can quickly track the resonant frequency. The simulation and experimental results show that the proposed onset control strategy can make running frequency quickly track resonant frequency of TAEGS and improve the efficiency of the system. Besides, the second order general integral controller can filter out the sampling noise and high frequency interference of the signal, which improves the stability of the controller.
keywords:Thermoacoustic electric generation system (TAEGS), permanent magnet linear generator, resonant frequency, second order general integral
中图分类号:TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.200573
国家自然科学基金资助项目(51377108)。
收稿日期 2020-06-01
改稿日期 2020-10-21
张 健 男,1981年生,博士研究生,副教授,研究方向为热声发电系统设计及其控制。E-mail: 64755512@qq.com(通信作者)
夏加宽 男,1962年生,博士,教授,博士生导师,研究方向为直线电机及其控制。E-mail: xiajk_mail@163.com
(编辑 陈 诚)