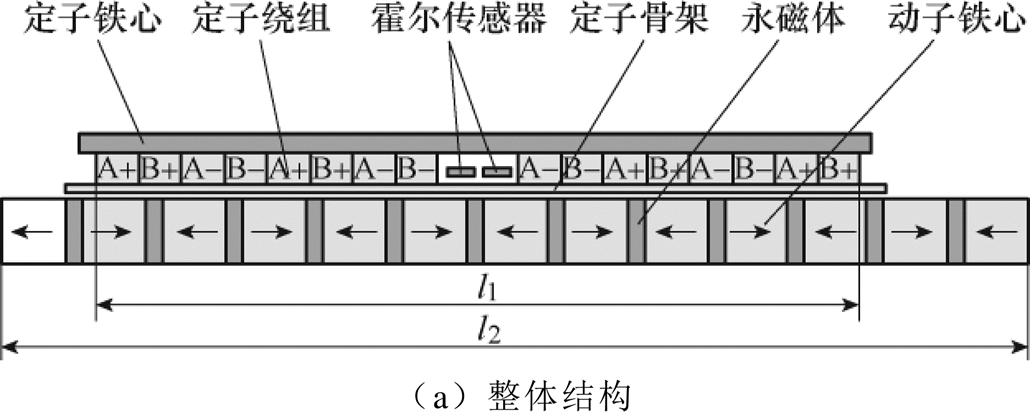
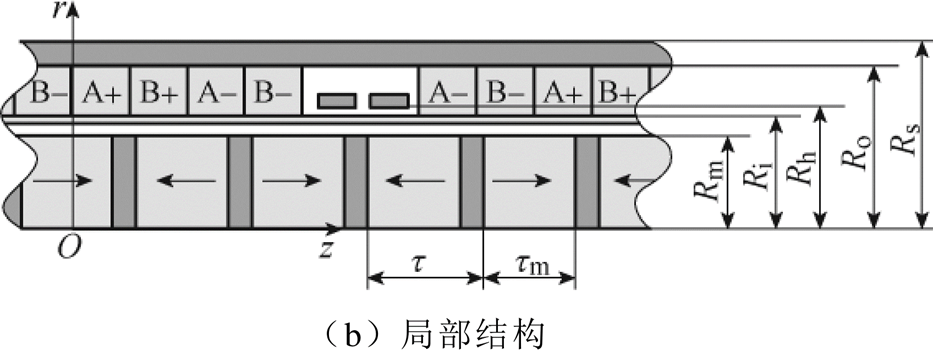
图1 两相无槽轴向充磁的TPMSLM电机结构示意图
Fig.1 Construction of the two-phase slotless TPMSLM with axial magnetized
摘要 在电机行程范围内,两相无槽圆筒型永磁同步直线电机的电感会受到电机绕组断开与耦合长度变化的影响,使其变化复杂,无传感控制算法难以实现。因此,需要对该电机电感进行精确的建模。该文基于轴向磁动势函数与轴向比磁导函数分别推导得到该电机在全耦合状态下和全行程范围内电感解析模型。在此基础上,利用有限元数值计算法对电感模型进行参数计算与验证分析,并总结电机全耦合状态下电感的特征,给出耦合长度变化对于电感直流分量与2次谐波幅值的影响规律。最后,对比了样机电感的实验测量值与模型计算值。结果表明,两者之间误差仅为0.04mH,证明了电感模型的正确性。
关键词:永磁同步直线电机 电感 磁动势 比磁导 有限元法
直线电机由于省去了中间传动机构直接提供直线运动,没有回程间隙,响应速度快,被大量应用于数控机床等工业自动化领域。圆筒型永磁同步直线电机(Tubular Permanent Magnet Synchronous Linear Motor, TPMSLM)因具有结构简单、推力密度高,且不存在横向端部效应的特点,具有广泛的应用前景[1-2]。
对于永磁同步电机的矢量控制,需要精确的位置反馈信号。直线电机常用的位置传感器包括线性光栅尺、电位计、线性霍尔传感器等[3]。但是安装这些机械传感器在提升电机制造成本的同时,也降低了电机控制系统的可靠性与鲁棒性。为了解决这一问题,无传感位置检测算法被提出与应用。常用的无传感算法包括反电动势辨识法[4]和高频信号注入法[5]。对于直线电机的高频信号注入法,由于存在端部效应,使电机三相自感和互感存在不对称性,dq轴电感变化复杂[6-7]。这使得直线电机高频注入方法实现困难,其无传感算法仍然为一个开放性的待解决问题[8]。因此,为了实现TPMSLM的无传感控制,需要对其运动范围内的电感变化规律进行研究并得到精确的电感解析模型。
电感的解析计算方法主要包括直接法[9-10]和间接法[11-16]。直接法首先求解磁场的泊松方程得到矢量磁位,再通过磁场储能计算得到电感的解析表达式。但对于轴向充磁的圆筒型直线电机,该方法存在边界条件确定困难、方程求解复杂的问题[17];间接法是通过对绕组函数(磁动势函数)与气隙比磁导函数的乘积积分计算电感的方法。相较于直接法,间接法在计算电机电感时更为简单直观,但其求解精度取决于气隙比磁导函数的准确性[18]。文献[11]通过间接法推导得到了磁阻同步电机的电感表达式,并分析了磁场高次谐波对于电机自感和互感的影响。文献[12]基于间接法计算了分数槽集中绕组的内埋式永磁同步电机的电感,并通过有限元与实验验证了解析模型的准确性。文献[13]针对间接法理论磁路与实际磁路存在偏差的问题,通过修正定子磁动势函数的解析表达式,提升了间接法电感计算的准确性。以上的研究主要针对旋转电机,对于两相无槽TPMSLM,还存在绕组断开与耦合长度变化的影响。本文在考虑这些影响因素的情况下,采用间接法计算该电机的电感。
本文分析计算了两相无槽TPMSLM的电感。首先,建立了完全耦合状态下电机动子轴向磁动势函数与轴向比磁导函数,在考虑直线电机绕组不连续的影响下,通过积分得到完全耦合状态下电机的电感解析模型。在扩展轴向比磁导函数的定义后,将电机耦合长度变化的影响引入到解析模型中,使解析模型适用于全行程范围内的电感计算。然后,基于解析模型与有限元分析结果,对TPMSLM完全耦合状态下与电机行程范围内的电感变化规律进行了定量分析。最后,将模型计算值与实验的测量结果相比较,进一步验证了解析模型的准确性。
本文的研究对象为两相无槽轴向充磁的TPMSLM。电机由定子和动子两部分构成,其中,定子包括铁心、线圈绕组、霍尔传感器与定子骨架。A、B两相线圈绕组以90°电角度等间隔缠绕在由聚酰亚胺材料制成的骨架上,因此该电机不存在齿槽效应。两线性霍尔传感器安装于定子绕组中部,相距90°电角度,用于测量电机动子位置。电机动子由永磁体和铁心组成。动子永磁体轴向充磁,其极性沿轴向交替变化并由动子铁心隔开。这种结构设计使得在动子移动过程中,定子绕组磁路磁阻会随着动子位置移动呈周期性变化,即电机呈现出凸极性。图1为两相无槽TPMSLM在圆柱坐标系下的结构示意图,图中,O为圆柱坐标系原点,r为圆柱坐标系半径,l1为定子线圈长度,l2为动子长度,Rs为电机半径,Ro为线圈绕组外径,Ri为线圈绕组内径,Rh为霍尔传感器安装位置,Rm为永磁体半径,t 为电机极距,tm为永磁体长度。


图1 两相无槽轴向充磁的TPMSLM电机结构示意图
Fig.1 Construction of the two-phase slotless TPMSLM with axial magnetized
TPMSLM的各结构参数的具体取值见表1。由于电机外形尺寸限制和实际行程的需求,使得动子长度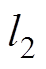 、绕组长度
、绕组长度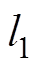 与电机行程
与电机行程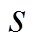 存在如下关系:
存在如下关系: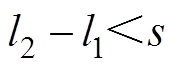 。这意味在80mm的电机行程范围内,会出现动子端部伸入定子绕组内部的情况。本文将这一状态定义为不完全耦合状态;反之,则为完全耦合状态。将动子与定子的重合长度定义为耦合长度,在运动过程中,随着TPMSLM耦合长度的不断减小,绕组磁路磁阻不断增加,永磁体A、B相绕组的自感和互感将随之减小。
。这意味在80mm的电机行程范围内,会出现动子端部伸入定子绕组内部的情况。本文将这一状态定义为不完全耦合状态;反之,则为完全耦合状态。将动子与定子的重合长度定义为耦合长度,在运动过程中,随着TPMSLM耦合长度的不断减小,绕组磁路磁阻不断增加,永磁体A、B相绕组的自感和互感将随之减小。
表1 TPMLSM的结构参数
Tab.1 The structural parameters of TPMLSM

参 数数 值 绕组长度l1/mm90 电机行程s/mm80 极距t/mm10 电机半径Rs/mm9 相绕组数n8 动子长度l2/mm128 永磁体长度tm/mm8 霍尔安装位置Rh/mm6.4 线圈半径Ro/mm7.8 剩余磁通密度Br/T1.42
为方便后续推导,定义定子坐标系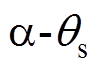 ,动子坐标系
,动子坐标系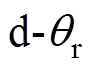 ,两坐标系之间距离为
,两坐标系之间距离为 ,TPMSLM坐标系示意图如图2所示。图中,
,TPMSLM坐标系示意图如图2所示。图中,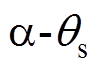 坐标系固定于定子上,并且
坐标系固定于定子上,并且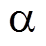 轴与A相绕组中心重合。
轴与A相绕组中心重合。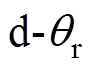 坐标系固结于动子上,d轴与铁心中心重合。其中所有角度定义为电机的电角度。可以得到两坐标系角度之间的换算关系为
坐标系固结于动子上,d轴与铁心中心重合。其中所有角度定义为电机的电角度。可以得到两坐标系角度之间的换算关系为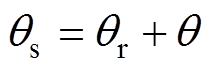 。
。
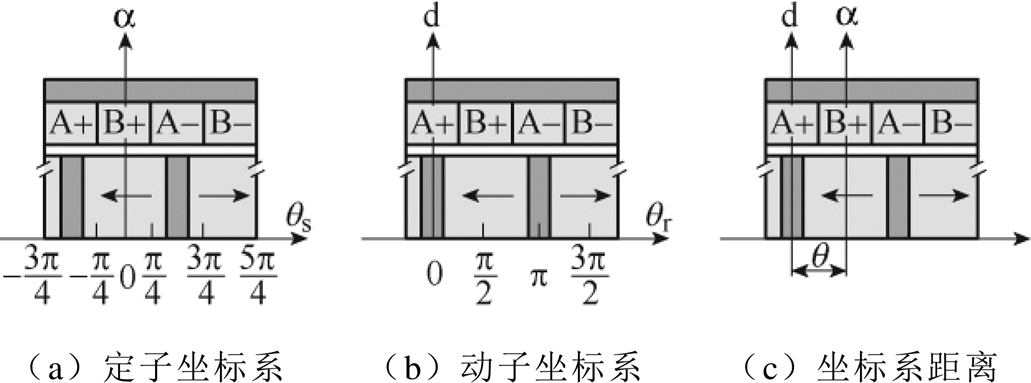
图2 TPMSLM坐标系示意图
Fig.2 The reference coordinate systems of TPMSLM
绕组产生的轴向磁通密度可以表示为轴向磁动势函数与轴向比磁导函数的乘积形式。为简化分析,假设电机的轴向磁动势函数和轴向比磁导函数与无限长直线电机一致。
轴向比磁导的函数建立在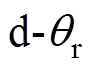 坐标系下,其关于0、
坐标系下,其关于0、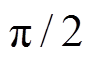 、
、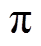 与
与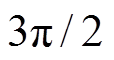 等电角度对称。因此,轴向比磁导函数
等电角度对称。因此,轴向比磁导函数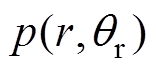 的傅里叶级数只包含余弦函数的偶次谐波,可以表示为
的傅里叶级数只包含余弦函数的偶次谐波,可以表示为
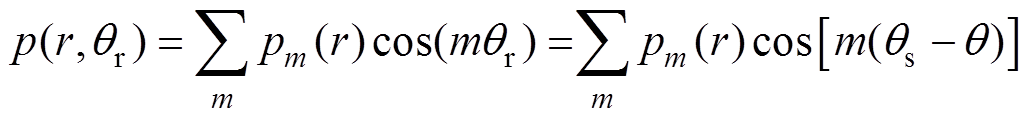 (1)
(1)式中,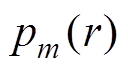 为比磁导的谐波幅值;
为比磁导的谐波幅值;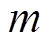 为对应的谐波次数,m=0, 2, 4,…。
为对应的谐波次数,m=0, 2, 4,…。
轴向磁动势函数建立在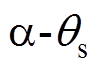 坐标系下。当单位电流注入到A相线圈时,产生的轴向磁动势关于
坐标系下。当单位电流注入到A相线圈时,产生的轴向磁动势关于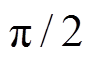 与
与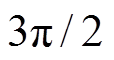 对称,所以轴向磁动势函数可以表示为
对称,所以轴向磁动势函数可以表示为
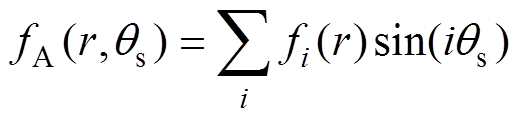 (2)
(2)式中,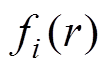 为轴向磁动势谐波幅值;i为对应的谐波次数,
为轴向磁动势谐波幅值;i为对应的谐波次数,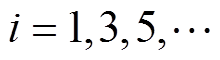 。
。
轴向磁通密度分布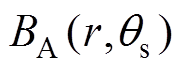 可以表示为式(1)和式(2)的乘积,即
可以表示为式(1)和式(2)的乘积,即
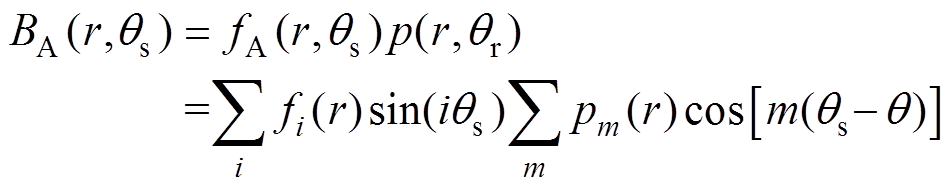 (3)
(3)则电机定子坐标系下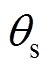 处的平均磁通量可以通过式(3)的积分得到,即
处的平均磁通量可以通过式(3)的积分得到,即
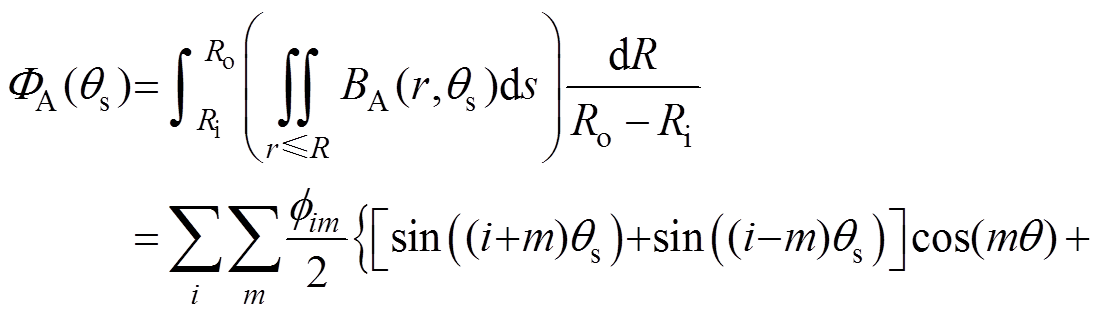
 (4)
(4)式中,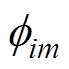 为对应由i次磁动势谐波和m次比磁导谐波产生的磁通量谐波幅值,表达式为
为对应由i次磁动势谐波和m次比磁导谐波产生的磁通量谐波幅值,表达式为
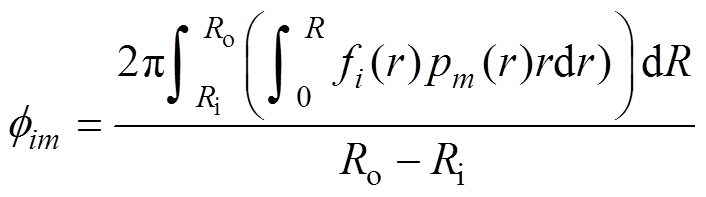 (5)
(5)
则A相绕组的磁链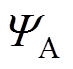 可以表示为
可以表示为
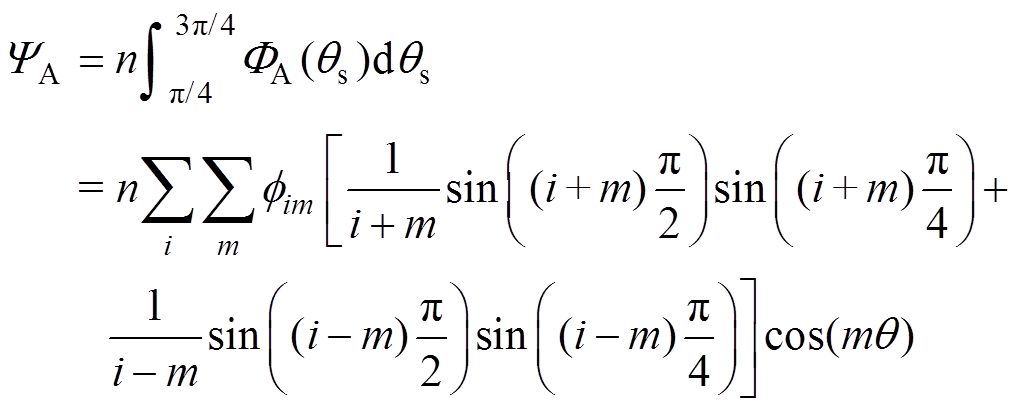 (6)
(6)式中,n为A相绕组个数。
在计算B相绕组的磁链时,需要考虑直线电机绕组不连续产生的影响。如图1所示,由于绕组不连续,在电机中部的B-线圈和在电机右侧端部的B+线圈只与单个A相线圈相邻。采用冻结磁链法得到TPMSLM在A相绕组通入单位电流时产生的磁感线如图3所示。
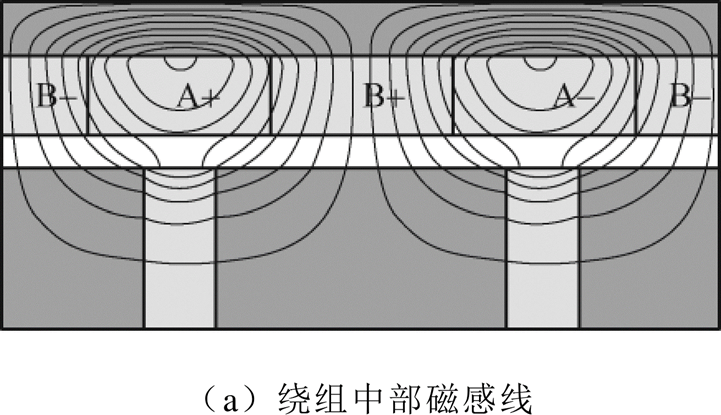
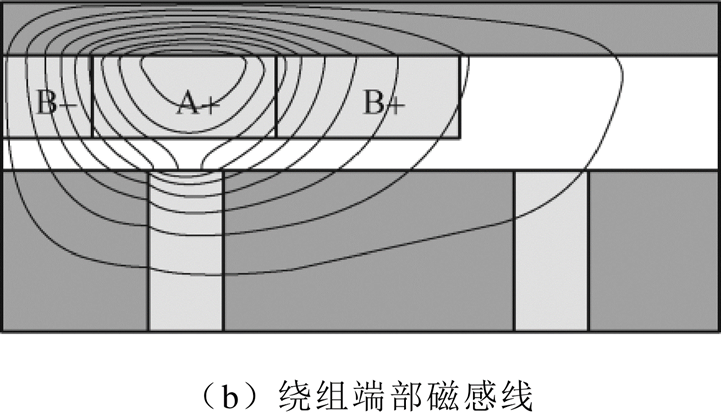
图3 TPMSLM的磁感线
Fig.3 The flux density line of TPMSLM
由图3中磁感线分布可知,位于绕组端部的B+线圈在失去A-线圈所提供的磁链的同时,其受到左侧A+线圈所产生的磁链增大。由于A+线圈与A-线圈在B+线圈处产生的轴向磁通密度方向相反,因此可以等效认为端部的B+线圈失去了k倍的A-线圈的磁链贡献值。k为磁场畸变系数,其取值大于1,表示由于绕组不连续对于B相线圈磁链的影响大小。则在A相绕组通入单位电流时,B相线圈磁链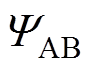 可以表示为
可以表示为
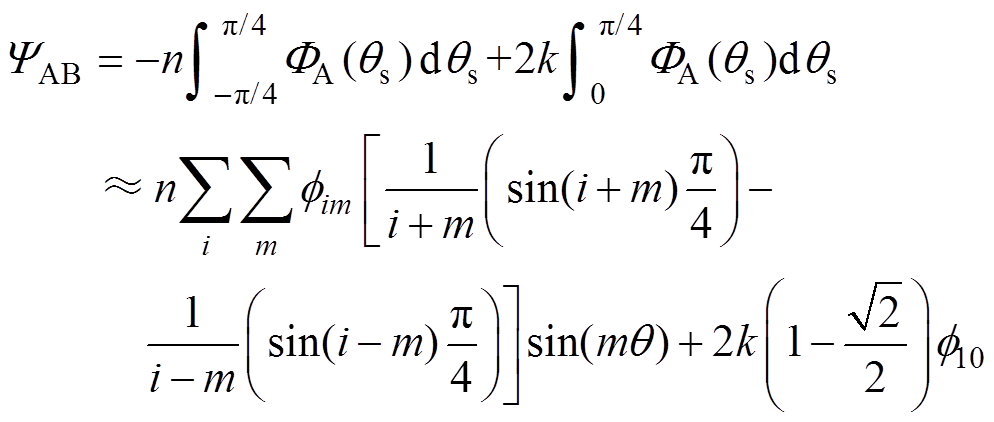 (7)
(7)式中,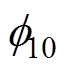 为
为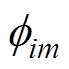 在i=1,m=0时的取值。
在i=1,m=0时的取值。
以上电感计算是在A相绕组通入单位电流的情况下进行分析的,因此所计算得到的磁链值与对应的电感值相等。由于TPMSLM绕组为分布式绕组,磁动势正弦性较高,在忽略磁动势高次谐波(i>1)和轴向比磁导(m>2)的高次谐波的情况下,A相线圈的自感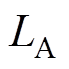 和A、B相线圈的互感
和A、B相线圈的互感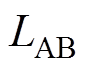 分别为
分别为
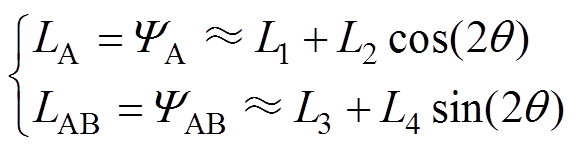 (8)
(8)式中,L1为自感直流分量;L2为自感2次谐波幅值;L3为互感直流分量;L4为互感2次谐波幅值。以上电感量可以通过将i=1和m=0、2代入式(6)和式(7)中求解得到。取值如下: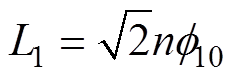 ,
,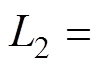
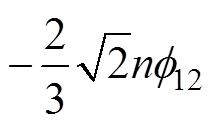 ,
,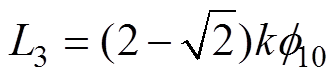 ,
,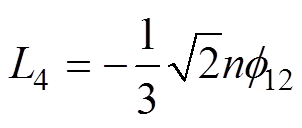 。其中,
。其中,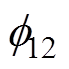 为
为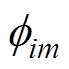 在i=1, m=2时的取值。
在i=1, m=2时的取值。
根据绕组相对位置关系,B相线圈的自感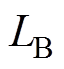 可以通过A相线圈自感超前90°电角度得到,即
可以通过A相线圈自感超前90°电角度得到,即
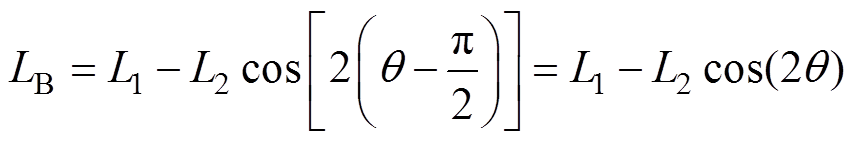 (9)
(9)由式(8)、式(9)可以得到,全耦合状态下TPMSLM的电感矩阵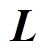 为
为
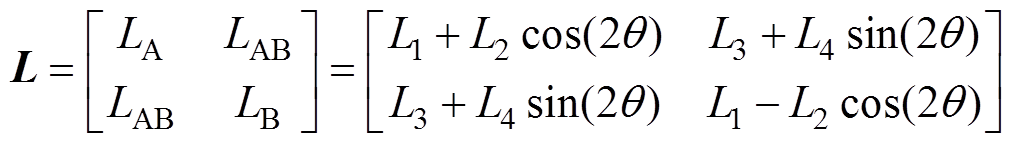 (10)
(10)
在整个电机行程范围内,电机包括完全耦合状态与不完全耦合状态。在不完全耦合状态下,通过将轴向比磁导函数分段表示引入耦合长度变化对电感的影响。令动子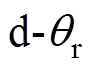 坐标系的d轴固定于图1a中最左侧铁心中心位置。动子
坐标系的d轴固定于图1a中最左侧铁心中心位置。动子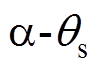 坐标系的
坐标系的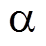 轴固定于图1a中最左侧B+绕组中心位置。考虑到永磁体磁导率与空气磁导率近似相同,认为动子两端以外的轴向比磁导不再发生变化。则电机行程范围内轴向比磁导函数
轴固定于图1a中最左侧B+绕组中心位置。考虑到永磁体磁导率与空气磁导率近似相同,认为动子两端以外的轴向比磁导不再发生变化。则电机行程范围内轴向比磁导函数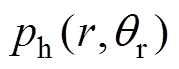 可以定义为
可以定义为
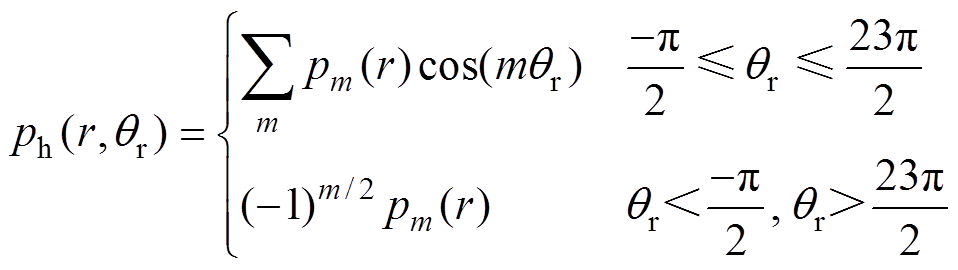 (11)
(11)式中,下标h为物理量定义域拓宽至电机动子的行程范围。
电机定子坐标系下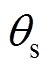 处的平均磁通量
处的平均磁通量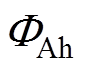 可以表示为
可以表示为
 (12)
(12)由此可以得到动子行程范围内A相自感为
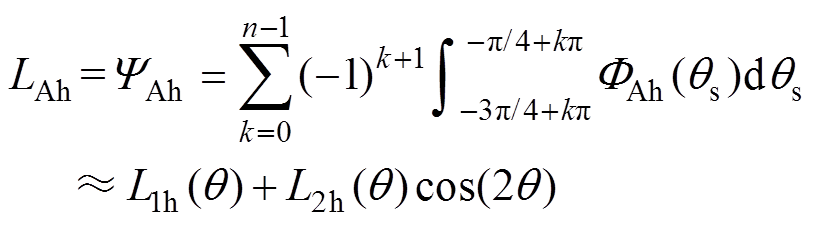 (13)
(13)
式中,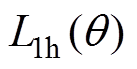 和
和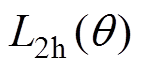 为忽略轴向磁动势函数和轴向比磁导函数高次谐波后的自感直流分量与2次谐波幅值,其表达式为分段函数形式且与位置相关,具体取值见表2。同样地,B相自感的表达式可以通过A相自感超前90°电角度得到。
为忽略轴向磁动势函数和轴向比磁导函数高次谐波后的自感直流分量与2次谐波幅值,其表达式为分段函数形式且与位置相关,具体取值见表2。同样地,B相自感的表达式可以通过A相自感超前90°电角度得到。
表2 A相绕组自感系数表达式
Tab.2 Self-inductance coefficient expression of winding A

动子位置
对于全行程范围内的AB相绕组的互感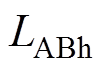 ,需要考虑A相绕组与B相绕组的综合影响。因此,AB相绕组互感的计算公式为
,需要考虑A相绕组与B相绕组的综合影响。因此,AB相绕组互感的计算公式为
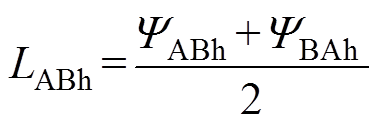 (14)
(14)式中,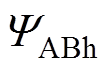 为A相绕组通入单位电流情况下B相绕组的磁链;
为A相绕组通入单位电流情况下B相绕组的磁链;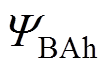 为B相绕组通入单位电流情况下A相绕组的磁链。与1.1节的式(7)相同,需要考虑绕组断开的影响,对应磁链计算表达式为
为B相绕组通入单位电流情况下A相绕组的磁链。与1.1节的式(7)相同,需要考虑绕组断开的影响,对应磁链计算表达式为
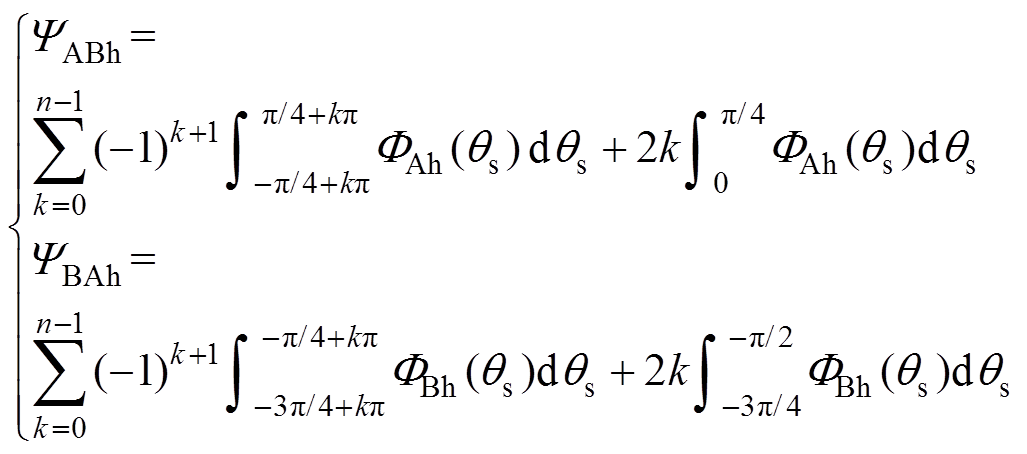 (15)
(15)
式中,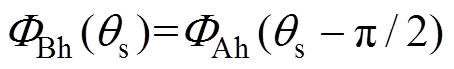 。
。
忽略轴向磁动势函数和轴向比磁导函数高次谐波后,式(14)的计算结果可以整理为
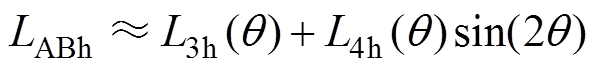 (16)
(16)式中,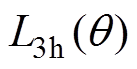 和
和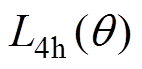 为与动子位置相关的互感直流分量与2次谐波幅值。其表达式同样为分段函数形式,具体取值见表3。
为与动子位置相关的互感直流分量与2次谐波幅值。其表达式同样为分段函数形式,具体取值见表3。
本节采用有限元法分析两相无槽TPMSLM的电感特性并验证解析模型准确性。有限元分析所用的电机电磁参数与电机结构参数见表1。
通过有限元分析得到电机在完全耦合状态下的自感和互感波形如图4所示。从图中可以看到,两相TPMSLM的电感波形有以下三个特征。
(1)电机的电感波形包含2次谐波,这是由于比磁导函数中存在2次谐波分量导致的,即电机的凸极性的影响。
表3 互感系数表达式
Tab.3 Mutual-inductance coefficient expression

动子位置
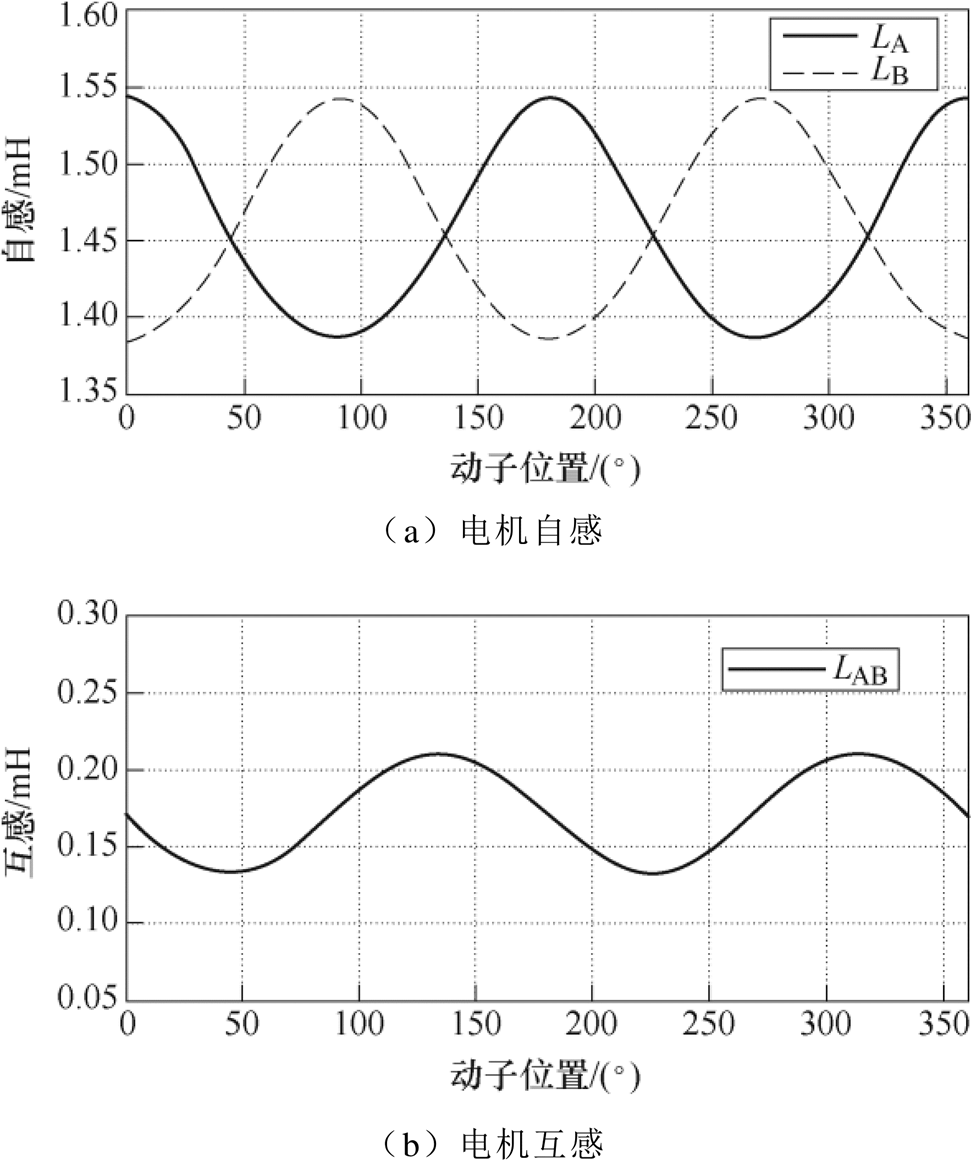
图4 完全耦合下的TPMSLM的电感波形
Fig.4 Inductance waveforms of fully coupled TPMSLM
(2)互感的直流分量不为0。由式(7)可知,这是电机绕组不连续、磁链断开所产生的影响。
(3)自感的2次谐波幅值是互感2次谐波幅值的两倍。即式(8)所推导得到的结果。这是由TPMSLM电机本身的结构特性所导致的。
通过快速傅里叶变换,可以得到电感系数中L1~L4取值分别为1.459mH、0.079mH、0.171mH和0.038mH,从而由式(8)可以求解得到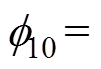

全耦合状态下,dq轴坐标系的电感系数矩阵可以由Park变换得到
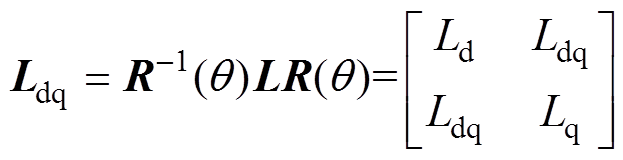 (17)
(17)式中,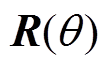 为Park变换矩阵,
为Park变换矩阵,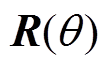 的表达式为
的表达式为
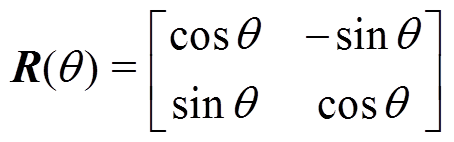 (18)
(18)
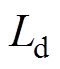 、
、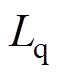 和
和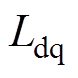 表达式分别为
表达式分别为
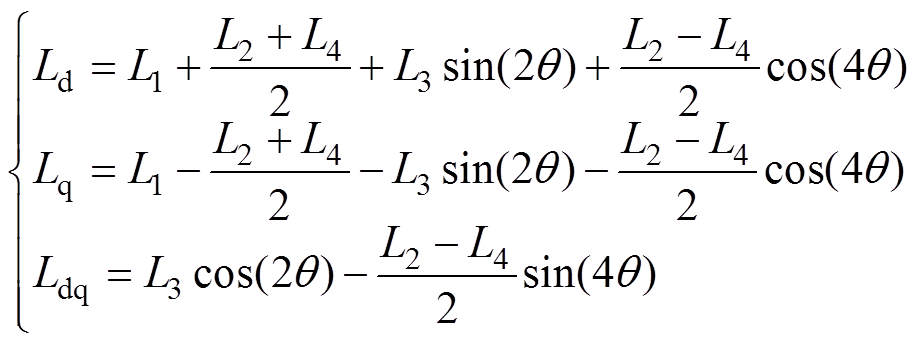 (19)
(19)
由式(19)可以发现,对于两相无槽TPMSLM,其dq轴自感和互感存在2次与4次谐波分量。其中,2次谐波分量是由于AB相绕组互感直流分量不为零产生的,4次谐波则是由于AB相绕组自感与互感的2次谐波幅值不同导致的。所得dq轴下的电感波形如图5所示。
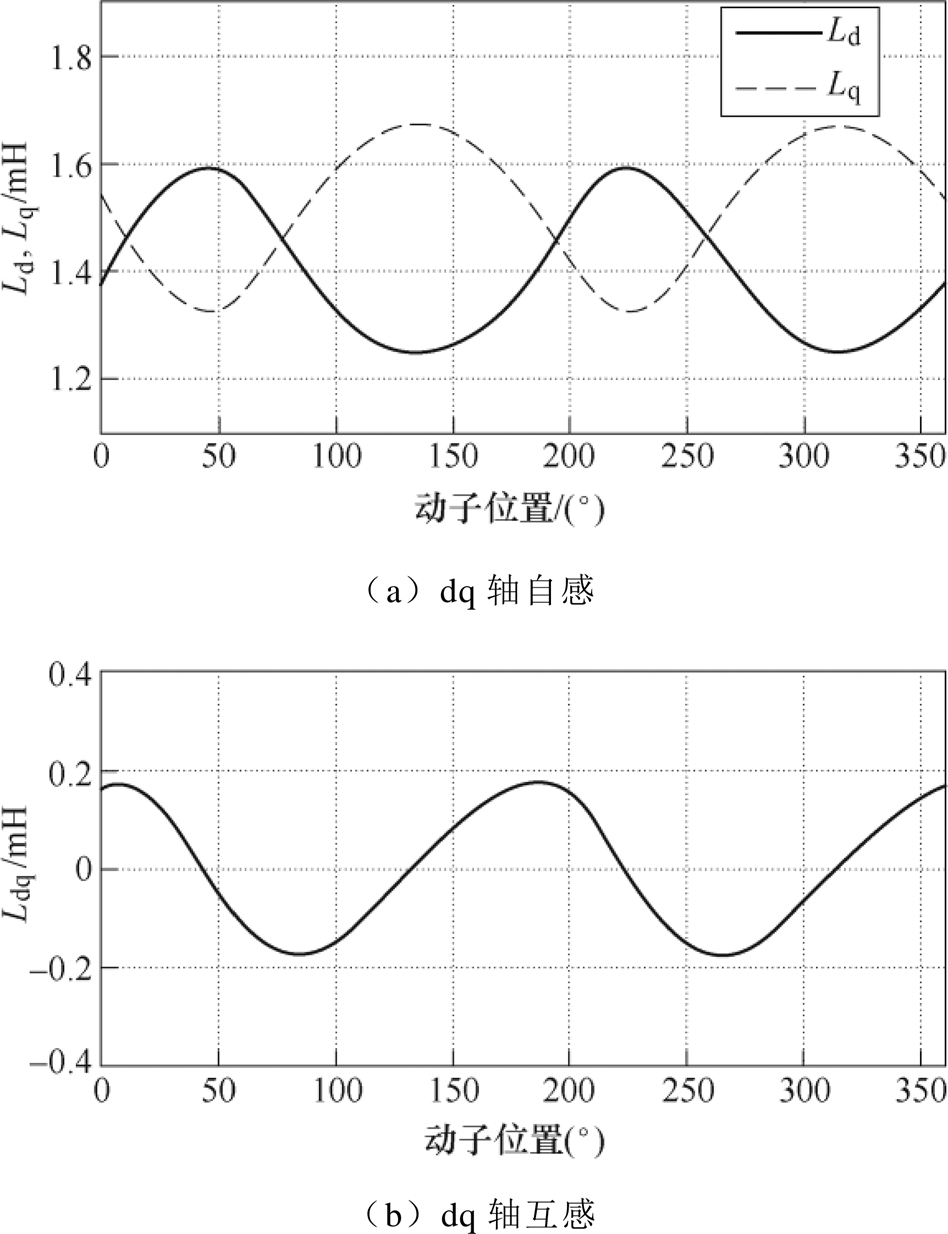
图5 TPMSLM完全耦合状态dq轴下电感波形
Fig.5 Inductance waveforms of fully coupled TPMSLM at dq reference frame
从图5中可以看到,由于2次和4次谐波的存在,dq轴自感同时呈现出表贴式永磁同步电机(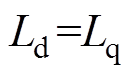 )和内置式永磁同步电机(
)和内置式永磁同步电机(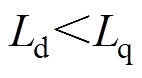 )的特征,并且会存在(
)的特征,并且会存在(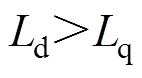 )的情况。同时dq轴互感也随着电角度变化不断波动。这些复杂的dq轴电感特征都使得TPMSLM的高频注入无传感算法实现困难。
)的情况。同时dq轴互感也随着电角度变化不断波动。这些复杂的dq轴电感特征都使得TPMSLM的高频注入无传感算法实现困难。
由表2和表3可以求得电机行程范围内的电感,与有限元分析所得结果对比如图6所示。图中,横坐标动子位置定义为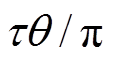 。当动子位置位于-32.5~-2.5mm之间时,电机处于完全耦合状态,其余位置为不完全耦合状态。
。当动子位置位于-32.5~-2.5mm之间时,电机处于完全耦合状态,其余位置为不完全耦合状态。

图6 全行程范围内TPMSLM电感波形
Fig.6 Inductance waveforms of TPMSLM in the whole moving range
图6中解析法得到的结果与有限元法相比最大误差为0.002mH,相对于自感与互感的直流分量和2次谐波的幅值,估计误差可以忽略不计。因此,解析法可以很好地描述电机行程范围内电感变化规律。同时可以观察到,在不完全耦合状态下,随着耦合长度不断减小,TPMSLM自感与互感的直流分量和2次谐波幅值也随之减小。为了更加清楚地描述电感变化规律,绘制直流分量和2次谐波幅值如图7所示。
从图7a和图7b中可以看到,自感直流分量和2次谐波幅值在电机耦合长度减少时,存在着衰减段和恒定段。以A相绕组自感为例:当电机动子端部穿过A相线圈时,A相绕组自感处于衰减状态。其直流分量在电机动子端部穿过单个A相绕组过程中下降0.35mH,2次谐波幅值则会下降0.1mH,即1/n的全耦合状态下的2次谐波幅值。当电机动子端部穿过B相线圈时,A相线圈自感位于恒定段,其直流分量与2次谐波幅值均不发生变化。图7c中,互感的直流分量只在电机动子端部穿过电机绕组左端的A+线圈或者右端部的B+线圈时发生变化,下降曲线为线性,由0.171mH下降至0.158mH。由图7d可知,互感2次谐波幅值随着耦合长度减少持续降低,每当电机动子端部穿过一个A相或B相线圈时,电机的2次谐波幅值下降全耦合状态下2次谐波幅值的6.25%,即1/(2n)全耦合状态下的互感2次谐波幅值。
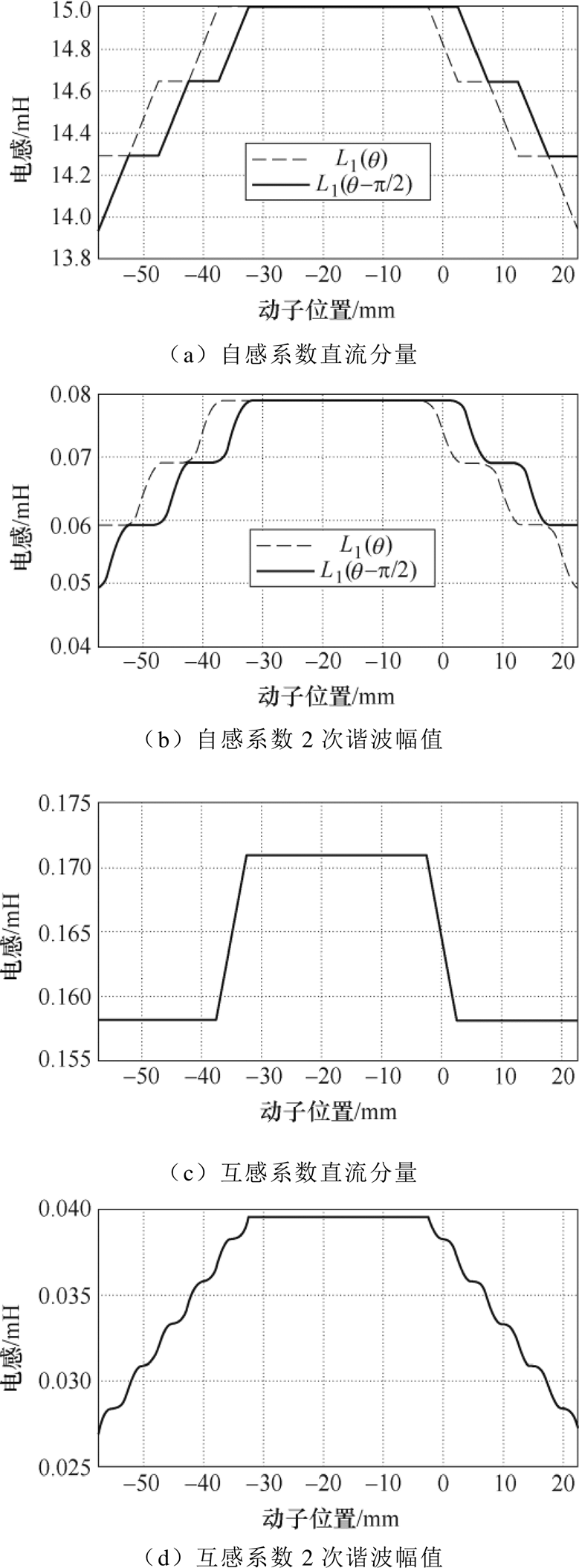
图7 全行程范围内电感系数曲线
Fig.7 Curves of inductance coefficients in the whole moving range
样机电感系数采用文献[19]所述方法进行测量。其中,A、B相绕组的自感通过LCR数字电桥进行直接测量。A、B相绕组的互感通过测量两相绕组同向连接和反向连接后的等效电感,再经过计算得到。测量互感时,A、B相绕组连接如图8所示。
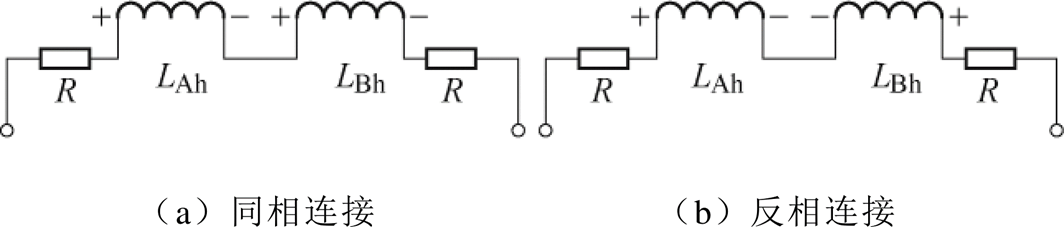
图8 绕组连接
Fig.8 Connection diagram
当两绕组同向连接时,等效电感表达式为
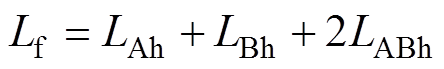 (20)
(20)当两绕组反向连接时,等效电感表达式为
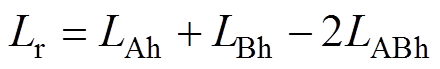 (21)
(21)
由式(20)、式(21)联立可以求得互感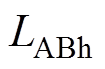 的表达式为
的表达式为
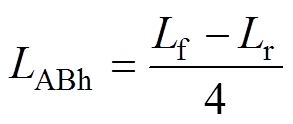 (22)
(22)基于该方法,在80mm的电机运动范围内,每隔1mm测量一组TPMSLM的电感。实验所用设备如图9所示。

图9 实验设备
Fig.9 Experimental equipment
采用LCR电表测量得到的电感解析法与实验法得到的结果对比如图10所示。图中,解析法中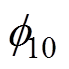 、
、 和
和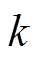 是通过完全耦合状态下实验电感值的傅里叶变换求得的,取值分别为0.112mH、0.011mH与1.7。可以看到,解析法得到的曲线与实验结果曲线一致性较高。与电感实验值相比,在不完全耦合状态下,解析法的最大估计误差为0.004mH。这表明使用轴向磁动势函数与轴向比磁导函数推导得到的全行程范围内电感解析表达式对于TPMSLM不完全耦合状态下电感有着较高的计算精度。
是通过完全耦合状态下实验电感值的傅里叶变换求得的,取值分别为0.112mH、0.011mH与1.7。可以看到,解析法得到的曲线与实验结果曲线一致性较高。与电感实验值相比,在不完全耦合状态下,解析法的最大估计误差为0.004mH。这表明使用轴向磁动势函数与轴向比磁导函数推导得到的全行程范围内电感解析表达式对于TPMSLM不完全耦合状态下电感有着较高的计算精度。
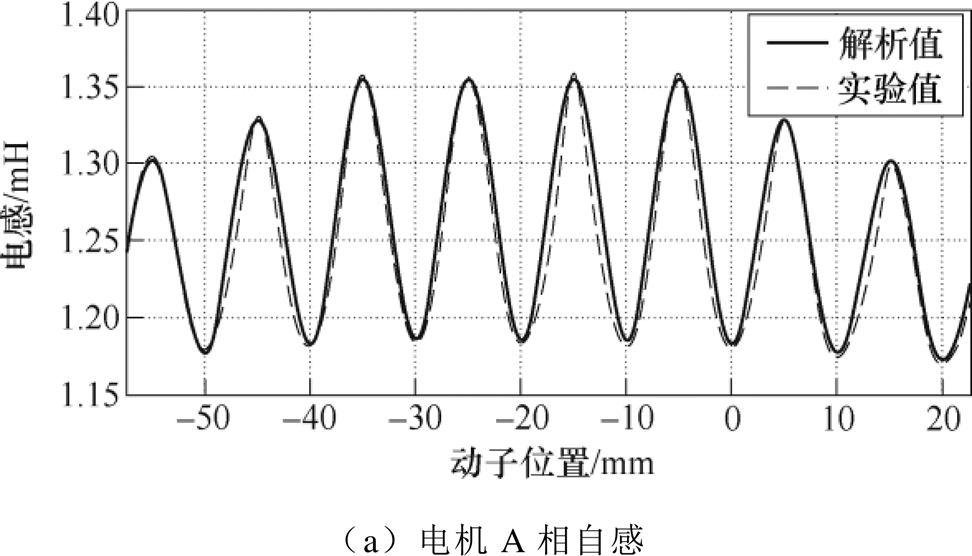

图10 解析法与实验法的电感波形
Fig.10 Inductance waveforms of analytical model and experiment
本文基于轴向磁动势函数与轴向比磁导函数推导得到了全行程范围内两相无槽TPMSLM的电感解析模型。并与有限元计算值和实验测量值进行了对比分析,证明该解析方法对于电机不完全耦合状态下电感计算的准确性。通过分析,该电机电感有如下特点:全耦合状态下,A、B相绕组互感直流分量不为零,自感2次谐波幅值为互感2次谐波幅值的两倍,且dq轴下的自感与互感存在明显的2次与4次谐波分量。在全行程范围内,A、B相绕组自感与互感的直流分量与2次谐波幅值会随着电机耦合长度减少而下降。本文所得到的两相无槽TPMSLM的电感解析式,为该电机后续无传感算法研究提供了一准确的数值模型。
参考文献
[1] Wang J B, Howe D. Tubular modular permanent- magnet machines equipped with quasi-halbach magnetized magnets-part I: magnetic field distri- bution, EMF, and thrust force[J]. IEEE Transactions on Magnetics, 2005, 41(9): 2470-2478.
[2] Abdalla I I, Ibrahim T, Nor N M. Analysis of tubular linear motors for different shapes of magnets[J]. IEEE Access, 2018, 6: 10297-10310.
[3] Paul S, Chang J, Rajan A, et al. Design of linear magnetic position sensor used in permanent magnet linear machine with consideration of manufacturing tolerances[J]. IEEE Sensors Journal, 2019, 19(13): 5239-5248.
[4] Morimoto S, Kawamoto K, Sanada M, et al. Sensorless control strategy for salient-pole PMSM based on extended EMF in rotating reference frame[J]. IEEE Transactions on Industry Applications, 2002, 38(4): 1054-1061.
[5] Yoon Y D, Sul S K, Morimoto S, et al. High- bandwidth sensorless algorithm for AC machines based on square-wave-type voltage injection[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1361-1370.
[6] Cupertino F, Pellegrino G, Giangrande P, et al. Sensorless position control of permanent-magnet motors with pulsating current injection and com- pensation of motor end effects[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1371-1379.
[7] 张春雷, 张辉, 叶佩青, 等. 两相圆筒型永磁同步直线电机无传感算法[J]. 电工技术学报, 2019, 34(23): 4901-4908.
Zhang Chunlei, Zhang Hui, Ye Peiqing, et al. Research on sensorless algorithm of two-phase tubular permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4901-4908.
[8] Sul S, Kwon Y, Lee Y. Sensorless control of IPMSM for last 10 years and next 5 years[J]. CES Transa- ctions on Electrical Machines and Systems, 2017, 1(2): 91-99.
[9] Zhu Z, Howe D, Mitchell J. Magnetic field analysis and inductances of brushless DC machines with surface-mounted magnets and non-overlapping stator windings[J]. IEEE Transactions on Magnetics, 1995, 31(3): 2115-2118.
[10] Wang J B, Jewell G W, Howe D. A general framework for the analysis and design of tubular linear permanent magnet machines[J]. IEEE Transa- ctions on Magnetics, 1999, 35(3): 1986-2000.
[11] Chiba A, Nakamura F, Fukao T, et al. Inductances of cageless reluctance-synchronous machines having nonsinusoidal space distributions[J]. IEEE Transa- ctions on Industry Applications, 1991, 27(1): 44-51.
[12] Dutta R, Rahman M, Chong L. Winding inductances of an interior permanent magnet (IPM) machine with fractional slot concentrated winding[J]. IEEE Transa- ctions on Magnetics, 2012, 48(12): 4842-4849.
[13] Chen Hong, Li Dawei, Qu Rongjun, et al. An improved analytical model for inductance calculation of interior permanent magnet machines[J]. IEEE Transactions on Magnetics, 2014, 50(6): 1-8.
[14] Chong L, Rahman M. Saliency ratio derivation and optimisation for an interior permanent magnet machine with concentrated windings using finite- element analysis[J]. IET Electric Power Applications, 2010, 4(4): 249-258.
[15] El-Refaie A M, Zhu Z Q, Jahns T M, et al. Winding inductances of fractional slot surface-mounted per- manent magnet brushless machines[C]//IEEE Industry Applications Society Meeting, Alberta, Canada, 2008: 1-8.
[16] 刘治鑫, 王东, 余中军, 等. 基于磁性槽楔修正模型的感应电动机气隙磁场的分布磁路法[J]. 电工技术学报, 2019, 34(15): 3112-3123.
Liu Zhixin, Wang Dong, Yu Zhongjun, et al. Distributed magnetic circuit method for calculating air-gap magnetic field of induction motor based on modified model considering the effect of magnetic slot wedges[J]. Transactions of China Electro- technical Society, 2019, 34(15): 3112-3123.
[17] 赵镜红, 张晓锋, 张俊洪, 等. 圆筒永磁直线同步电机磁场和推力分析[J]. 电机与控制学报, 2010, 14(1): 12-17.
Zhao Jinghong, Zhang Xiaofeng, Zhang Junhong, et al. Field and thrust analysis of tubular permanent magnet linear synchronous motor[J]. Electric Machines and Control, 2010, 14(1): 12-17.
[18] 于吉坤, 李立毅, 张江鹏, 等. 定子开槽永磁同步电机气隙比磁导解析计算[J]. 电工技术学报, 2016, 31(增刊1): 45-52.
Yu Jikun, Li Liyi, Zhang Jiangpeng, et al. Analytical calculation of air-gap relative permeance in slotted permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(S1): 45-52.
[19] Zhang Hailin, Kou Baoquan, Wang Liqiang, et al. A new inductance measurement method for permanent magnet synchronous linear motor[C]//17th Inter- national Conference on Electrical Machines and Systems, Hangzhou, China, 2015: 1-5.
Inductance Analysis of Two-Phase Slotless Tubular Permanent Magnet Synchronous Linear Motor
Abstract The inductances of two-phase slotless tubular permanent magnet synchronous linear motor (TPMSLM) are affected by the disconnection of windings and the change of coupling length. This makes the inductance change complicated and difficult to implement sensorless control. Therefore, the inductance of TPMSLM needs to be accurately modeled. Firstly, the axial magnetomotive force function and the axial specific permeance function were utilized to derive the analytical model in the fully coupled state. Then the domain of the axial specific permeance function was extended and the inductance expression in the whole moving range was calculated. The expression was verified by finite element method. And the characteristics of the inductance and the influence of the coupling length were analyzed. Finally, the inductance of a prototype was measured and compared with the analytical result. The maximum error between the two results is 0.04mH, which proves the correctness of the analytical model.
keywords:Permanent magnet synchronous linear motor, inductance, magnetomotive force, specific permeability, finite element method
中图分类号:TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.200461
国家自然科学基金资助项目(51875312)。
收稿日期 2020-05-07
改稿日期 2020-11-23
张春雷 男,1994年生,博士研究生,研究方向为电机设计及其控制。E-mail: clzhang13@163.com
张 辉 女,1969年生,博士,副教授,研究方向为先进制造装备及其自动化。E-mail: wwjj@mail.tsinghua.edu.cn(通信作者)
(编辑 陈 诚)