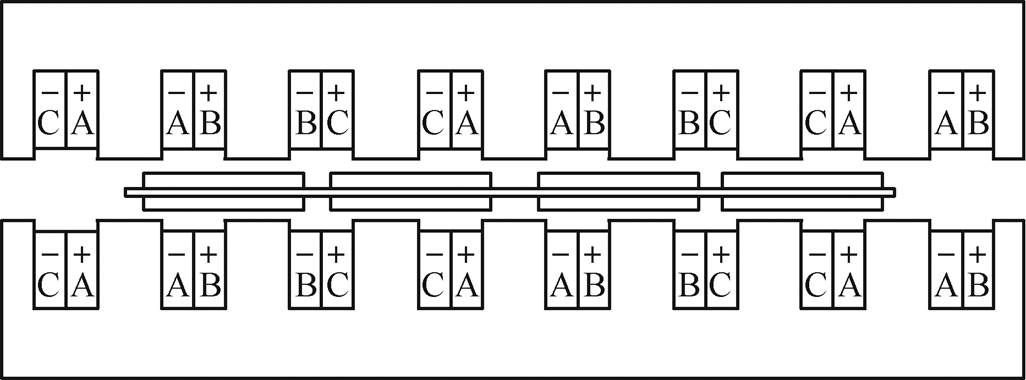
图1 DSSLP-PMLSM基本结构
Fig.1 Basic structure of DSSLP-PMLSM
摘要 针对传统的4极6槽双边对称长初级永磁直线同步电机,在保证电磁推力大小的情况下,提出采用双边错位来降低永磁体涡流损耗的有效方法。介绍电机的基本结构,阐明双边错位结构可以完全消除偶数次电枢谐波磁动势,进而能大幅度降低次级永磁体涡流损耗。利用有限元分析(FEA)软件对比分析对称结构和错位结构的定位力、电磁推力和次级涡流损耗,验证错位方法的正确性,并进行结构优化设计。最后,研制一台样机并搭建实验平台,测得样机的空载反电动势、定位力以及静推力。
关键词:双边错位 永磁直线同步电机 分数槽集中绕组 永磁体涡流损耗
20世纪90年代以来,电力电子技术的发展日趋成熟,用于电磁推进系统的直线电机逐渐成为研究的热点[1-3]。双边长初级永磁直线同步电机效率高、推力密度大、法向力小、次级结构简单质量轻、运行过程中不拖动电缆、安全可靠,非常适用于高速、高加速度场合。实际应用中,为了提高电机效率,减小对电源容量的要求,需要对长初级直线电机进行分段。采用分数槽集中绕组便于分段,初级可以模块化加工,同时具有槽利用率高、齿槽定位力小、线圈端部短、铜耗少和空载反电动势(back- Electromotive Force, back-EMF)波形正弦性好等一系列优点[4-7]。但是分数槽集中绕组的电枢磁动势谐波含量比较大,特别是高速场合,这些谐波磁动势相对于次级高速运动,进而在永磁体内感应出涡流,产生附加的涡流损耗,使得永磁体温度升高,甚至引起退磁[8-9]。
为了降低永磁体涡流损耗,国内外学者提出了多种方法[10-16],如增大气隙长度、减小槽口宽度、永磁体分块以及在永磁体外增加保护套和高电导率的屏蔽环。文献[17]提出采用多层绕组来消除低次空间谐波磁动势。文献[18-19]通过在定子齿部或者定子轭部放置不导磁材料来减小低次谐波磁动势幅值。上述方法可以降低永磁体涡流损耗,但都对电机的推力性能产生较大的不利影响。
本文针对4极6槽双边对称长初级永磁直线同步电机(Double-Sided Symmetrical Long Primary- Permanent Magnet Linear Synchronous Motor, DSSLP- PMLSM)提出一种新的结构方案,其双边初级铁心一侧的齿对应另一侧的槽,且沿运动方向,双边初级绕组错位布置。这样在保证电机推力大小的情况下,可以消除幅值比较大的电枢磁动势谐波,使得次级永磁体涡流损耗得到大幅度下降。
图1为传统4极6槽DSSLP-PMLSM基本结构。图2为提出的双边错位长初级永磁直线同步电机(Double-Sided Dislocation Long Primary-Permanent Magnet Linear Synchronous Motor, DSDLP-PMLSM)基本结构。电机主要由初级和次级两部分组成,初级包括初级铁心和两套初级绕组,次级包括基板和永磁体。

图1 DSSLP-PMLSM基本结构
Fig.1 Basic structure of DSSLP-PMLSM
双边初级形成串联磁路,两套绕组对应相串联连接。相比于传统对称结构,DSDLP-PMLSM的主要特点:①初级宽等于槽宽,双边铁心一侧的齿与另一侧的槽相对;②两套绕组不是对称布置,对应相之间错了一个极距,并且反向连接。
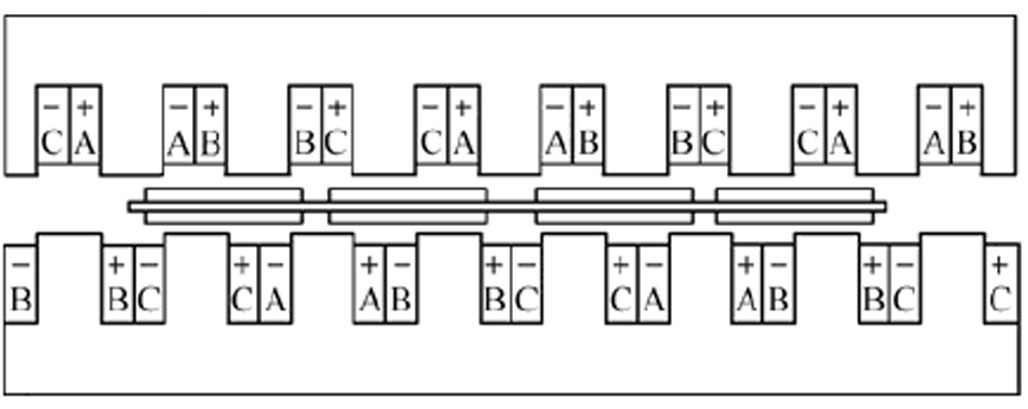
图2 DSDLP-PMLSM基本结构
Fig.2 Basic structure of DSDLP-PMLSM
4极6槽电机由两个2极3槽单元电机组成。对于2极3槽单元电机,根据单元电机三相合成磁动势相关公式[5],以基波幅值作为基值,把其他各次磁动势的幅值与此基值相比进行标幺化,单元电机前30对极的谐波分析结果如图3所示。由图可见,电机内部主要的电枢谐波磁动势为2次,其幅值为基波的一半。

图3 2极3槽单元电机磁动势谐波分析
Fig.3 Harmonic analysis of magnetomotive force of 2-pole 3-slot unit motor
DSSLP-PMLSM两套绕组各线圈空间位置相同,其产生的电枢磁动势也相同,电机内部会同时存在偶数次和奇数次谐波磁动势,磁动势谐波含量大。
基波磁动势波长为2t(t 为电机极距),谐波磁动势波长l 为
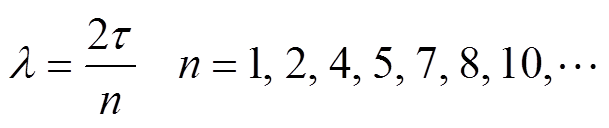 (1)
(1)首先,当上下同相绕组之间相错一个极距t 时,不难发现,错位距离是偶数次谐波波长的整数倍,是奇数次谐波半个波长的奇数倍。然后,当上下同相绕组反向连接时,偶数次谐波正好正负叠加,完全消除,奇数次谐波空间分布完全相同,正好正正叠加。
为了验证上述方法的有效性,选取同相相互错位的两个单线圈为对象,分析DSDLP-PMLSM的电枢磁动势。根据磁通连续性原理,可得到两个单线圈的磁动势分布,然后选取空间位置x为横坐标,对其进行傅里叶分解,进而可得到各次谐波磁动势分量,如图4所示(图中仅绘出前7次的谐波分量)。从图可见,相互错位的两个同相线圈产生的各次谐波磁动势有所差异,1、5、7次谐波磁动势分量空间分布相同,2、4次谐波磁动势分量空间分布正好反向。同理不难发现,包含基波在内的所有奇数次谐波磁动势空间分布都相同,所有偶数次谐波磁动势空间分布都相反,所以此两个线圈最终的合成磁动势中仅含有奇数次谐波磁动势,偶数次谐波磁动势被完全消除,并且对基波磁动势没有产生影响。
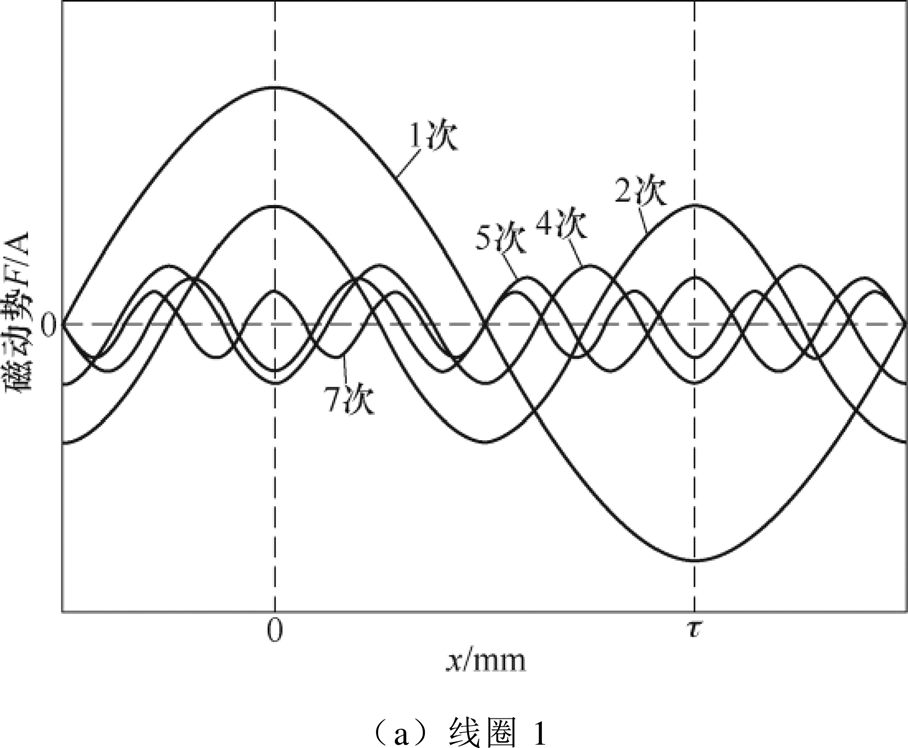
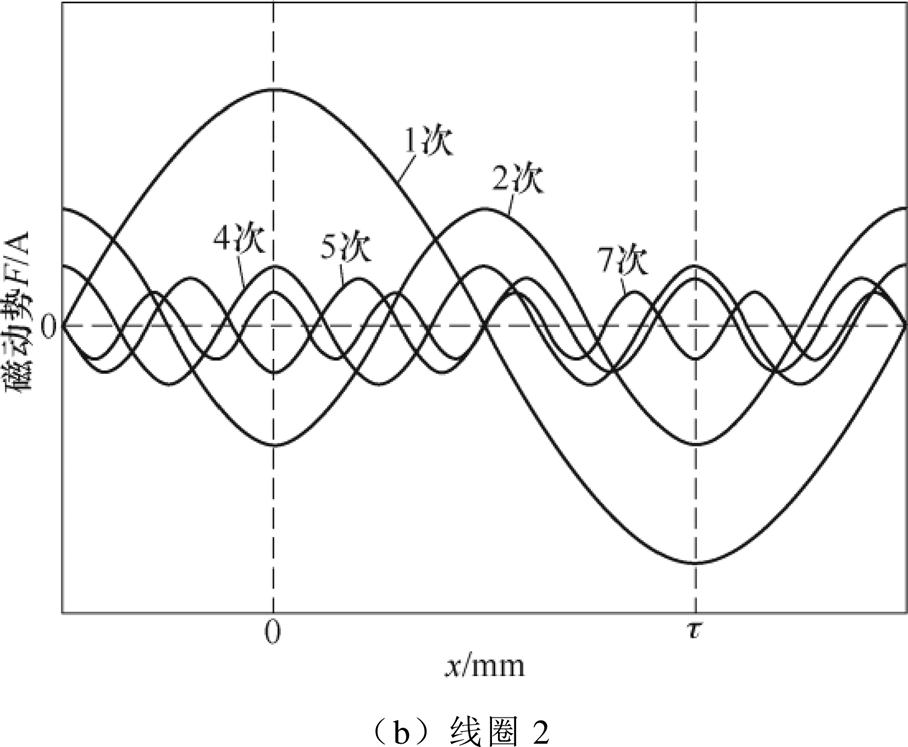
图4 磁动势谐波分析
Fig.4 Harmonic analysis of magnetomotive force
实际上对于传统的4极6槽永磁直线同步电机,它的初级绕组在N极和S极下的分布不同,使得N极和S极下的磁动势幅值不相等,所以其磁动势波形中除了含有奇数次谐波外,还含有偶数次谐波。而本文使上下两套绕组错位的目的就是在初级的一侧去构造另一侧每相绕组的负相带,这样就会使N极和S极下的电枢磁动势相等、相反,所以电机电枢磁动势除基波外,仅含有奇数次谐波。
当不考虑电流时间谐波时,对于永磁直线同步电机来说,永磁体涡流损耗产生的主要原因是初级铁心开槽和存在电枢磁动势空间谐波。在求解永磁体上的涡流损耗时作如下假设:①忽略初级铁心饱和的影响;②不考虑永磁体涡流的反作用;③永磁体相对磁导率为1;④分析区域在二维平面内,不考虑电机的端部效应;⑤假设双边初级之间的磁力线都是垂直直线。
以双边对称永磁直线同步电机为例分析电机的气隙磁导,DSSLP-PMLSM的初级铁心如图5所示。
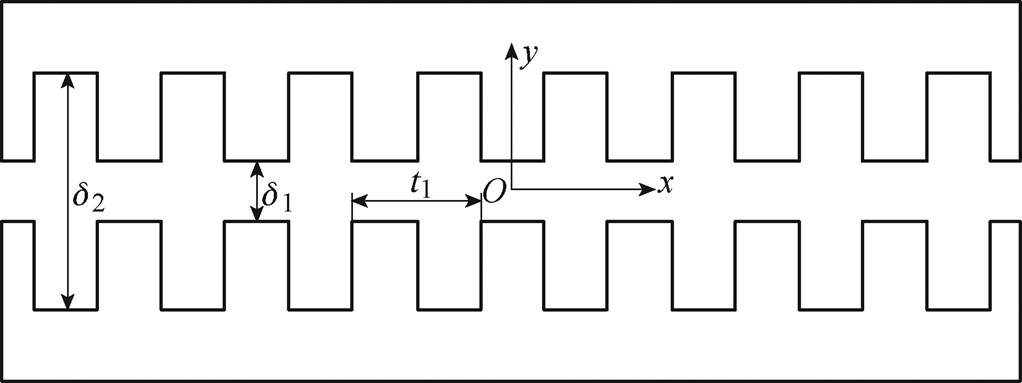
图5 DSSLP-PMLSM的初级铁心
Fig.5 Primary core of DSSLP-PMLSM
比磁导表达式为
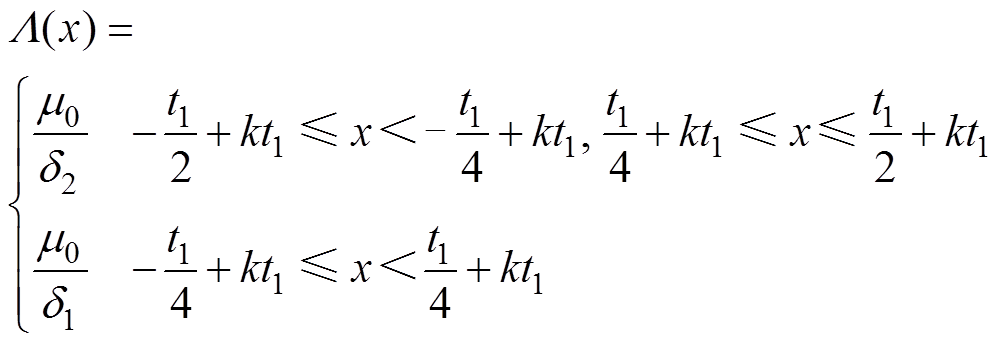 (2)
(2)式中,m0为真空磁导率;d1、d2分别为双边齿之间和槽之间的距离;t1为齿距;k为整数。
由式(2)可得比磁导的傅里叶表达式为
 (3)
(3)其中
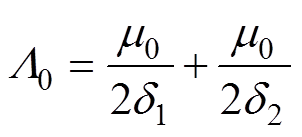 (4)
(4)
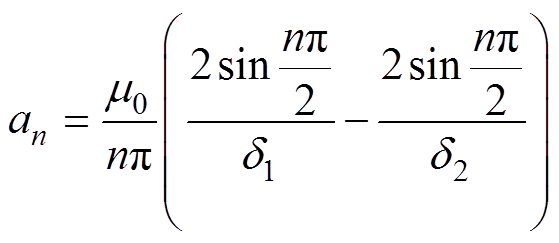 (5)
(5)式中,n为比磁导谐波阶数。
由文献[20]可知,永磁体磁动势傅里叶级数可表示为
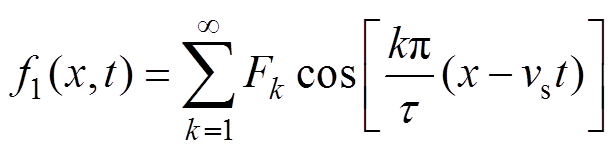 (6)
(6)其中
 (7)
(7)
式中,H为永磁体的矫顽力;vs为同步速度;hm为永磁体厚度;a 为计算极弧系数。
根据磁路的欧姆定律,空载气隙磁场可表示为
 (8)
(8)式中,cn、fn分别为第n次比磁导谐波的幅值和初始相位。
由文献[6]关于分数槽集中绕组磁动势的分析,可进一步推导出传统双边永磁直线同步电机以及本文提出的双边错位永磁直线同步电机的电枢磁动势表达形式。
双边对称永磁直线同步电机的电枢磁动势可表示为
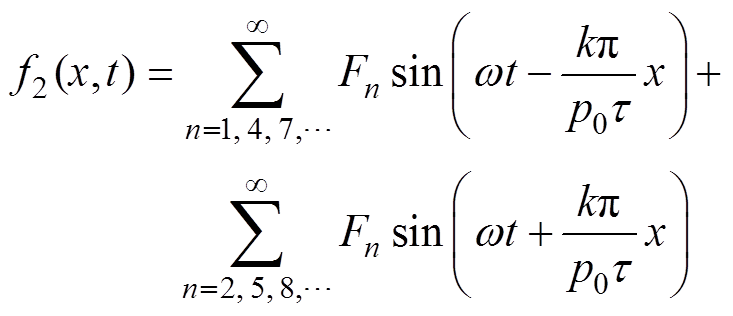 (9)
(9)其中
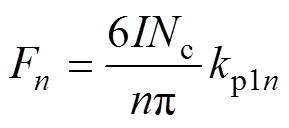
 (10)
(10)
式中,p0为单元电机的极对数;I为电枢电流幅值;Nc为单个线圈的匝数;kp1n为极对数为n的谐波绕组短距系数。
同理,双边错位永磁直线同步电机的电枢磁动势的表达式为
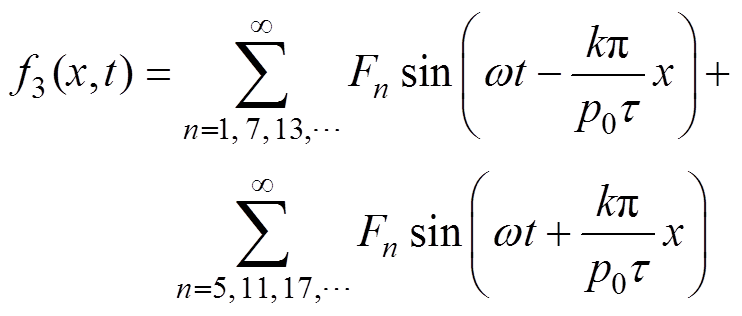 (11)
(11)其中
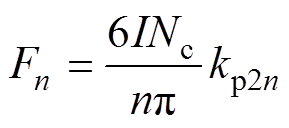
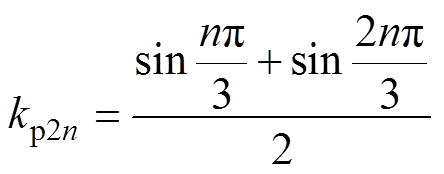 (12)
(12)
式中,kp2n为DSDLP-PMLSM的绕组系数。
同理,再根据磁路的欧姆定律就可以计算出电枢气隙磁场。
上文已经分别求解出空载气隙磁场和电枢气隙磁场,首先根据磁矢位A与B的关系
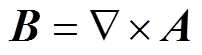 (13)
(13)计算出磁矢位A。然后计算出永磁体中的涡流密度J为
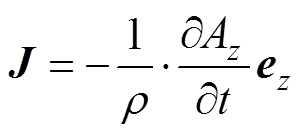 (14)
(14)
式中,r 为永磁体的电阻率。
在上述的推导过程中做了很多假设,为了更加准确地计算出涡流损耗,需要引入补偿电流密度J0对J进行修正,使其满足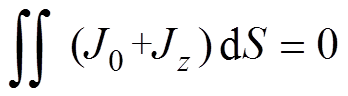 ,其中,S为永磁体横截面积,即永磁体厚度与宽度的乘积。
,其中,S为永磁体横截面积,即永磁体厚度与宽度的乘积。
最后根据焦耳定律,可得永磁体内的涡流损耗为
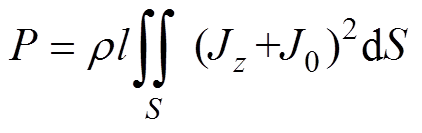 (15)
(15)式中,l为永磁体的横向长度。
为了验证双边错位结构和解析模型的有效性,利用有限元软件对双边错位永磁直线同步电机的定位力、电磁推力和次级永磁体涡流损耗进行分析,并对其结构进行优化。
长初级永磁直线同步电机的定位力主要成分是齿槽定位力。在一个机械周期内,分数槽永磁直线同步电机的齿槽定位力的周期数等于槽数与极数的最小公倍数[5]。图6为两种结构的定位力对比曲线。从图中可知,在一个电周期(20ms)内定位力都是波动6次,对称结构的定位力幅值为102N,错位结构的定位力为110N,增加了约8%,错位结构对定位力的影响很小,并且不会改变齿槽定位力的周期。

图6 定位力对比曲线
Fig.6 Comparison curves of detent force
图7为相同工况下两种结构的电磁推力对比曲线。从图中可知,两种结构电磁推力随时间的变化曲线相差不大,错位结构的平均电磁推力略小于对称结构。对称结构的平均电磁推力为596N,错位结构的平均电磁推力为566N,约降低了5%,错位结构对电机电磁推力的影响也很小。这是由于错位结构对电枢基波磁动势没有影响,只是磁路的等效气隙长度稍有增加,使得错位结构的电磁推力稍有降低。

图7 电磁推力对比曲线
Fig.7 Comparison curves of electromagnetic thrust
图8为错位结构的电枢反应气隙磁通密度以及对应的谐波分析结果。从图中可知,电枢磁场呈对称分布,不含有偶数次谐波,主要的谐波磁场为5次和7次,这与第2节关于电枢磁动势的分析相一致。

图8 电枢反应气隙磁通密度及其谐波分析
Fig.8 Armature reaction air gap flux density and harmonic analysis
电机电枢谐波磁动势将产生对应的谐波磁场。谐波磁场相对于永磁体高速运动,会在永磁体内感应出涡流,进而产生涡流损耗。图9为两种结构的永磁体涡流损耗对比曲线。从图中可知,对称结构的永磁体涡流损耗平均值为36.1W,错位结构为5.6W,降低了近84.5%;此外,对称结构的解析结果为37.8W,与仿真结果相比误差为4.7%;错位结构的解析结果为5.1W,与仿真结果相比误差为8.9%。可见,对称结构的解析精度要高于错位结构,这是因为对于错位结构,利用式(3)计算的比磁导是一个恒定的常数,也就无法计算出由于初级铁心开槽引起的涡流损耗,从而使得解析结果偏小。
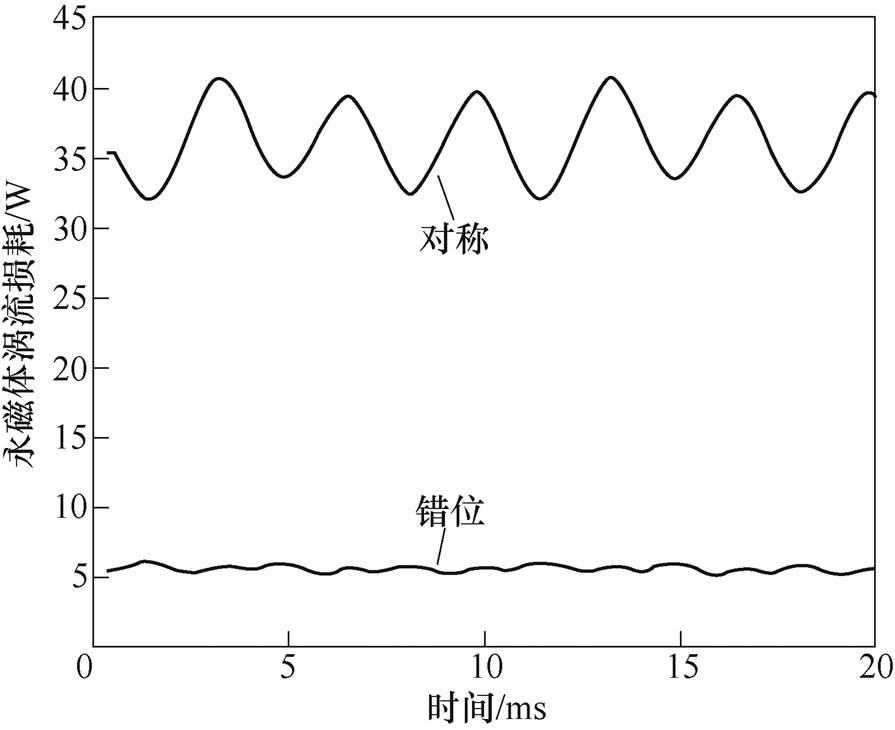
图9 永磁体涡流损耗对比曲线
Fig.9 Comparison curves of permanent magnet eddy current loss
另一方面,在一个电周期内对称结构的永磁体涡流损耗波动了6次,错位结构波动了12次,其主要的谐波次数提高了1倍。这正是由于错位结构中的电枢磁动势谐波次数也提高了一倍。
图10为永磁体涡流损耗分布。从图中可知,对于对称结构,基板两侧的永磁体涡流呈对称分布,错位结构基板两侧的永磁体涡流损耗分布不同,错位结构可以有效地降低永磁体涡流损耗。
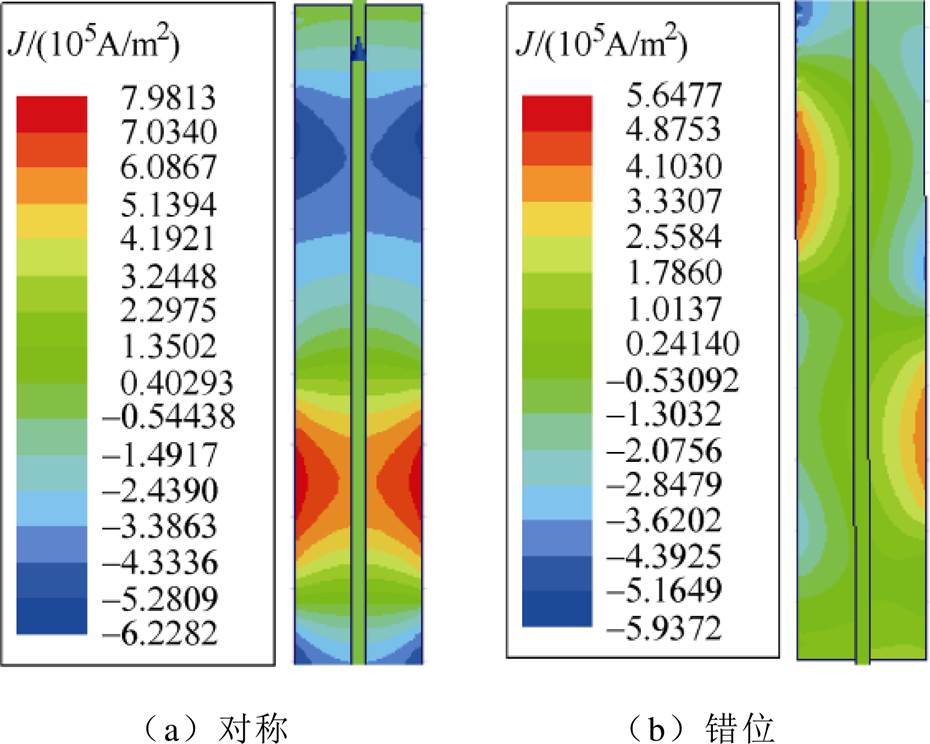
图10 永磁体涡流损耗分布
Fig.10 Distribution curves of permanent magnet eddy current loss
次级基板位于两侧永磁体的中间,是励磁磁场磁路的一部分,为了提高电机的推力密度,一般基板都选用铁磁材料。铁磁材料密度大、质量重。但是应用于电磁推进系统的直线电机要求能获得较大的加速度,需要尽可能地减小次级的质量,可选择密度小、质量轻的铝合金材料。图11为次级基板选用这两种材料下的电磁推力对比曲线。从图中可知,使用10号钢材料的电磁推力要略大于铝合金材料,使用铝合金的电磁推力相比于使用10号钢降低了约10%。
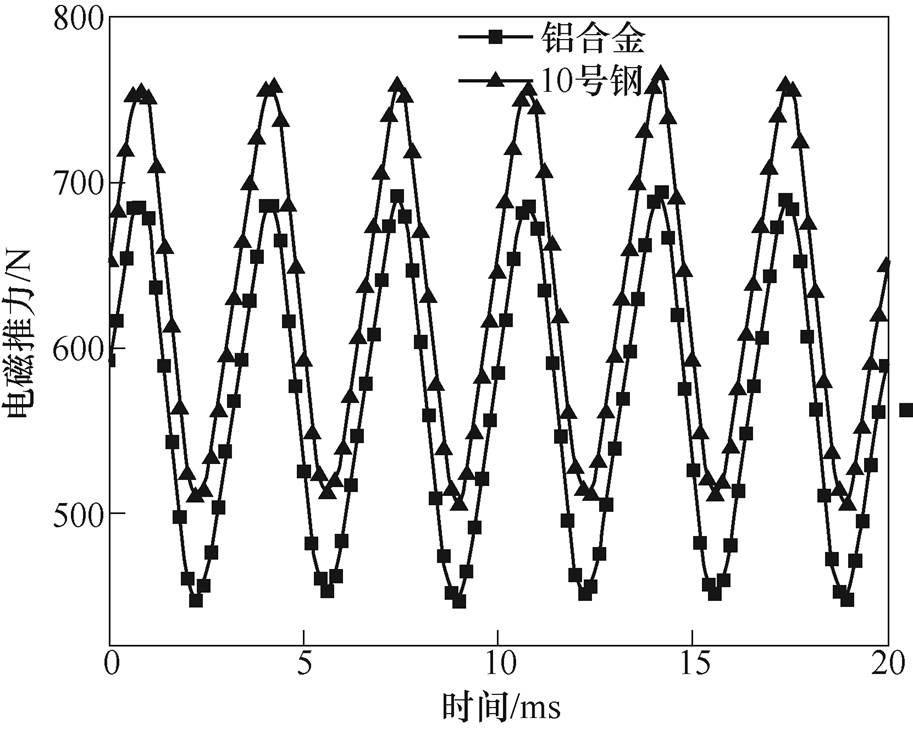
图11 不同材料下的电磁推力
Fig.11 Electromagnetic thrust in different materials
图12为次级基板选用不同材料下的永磁体涡流损耗对比曲线。从图中可知,使用10号钢材料的永磁体涡流损耗远大于铝合金材料,使用铝合金的涡流损耗相比于10号钢降低了约86.5%。这是由于10号钢相比于铝合金材料磁路磁阻要小,使电机气隙磁场变大,同时也会使磁导谐波幅值变大,从而会增加永磁体上的涡流损耗。可见,次级基板选用铝合金材料,能够有效降低永磁体涡流损耗。综合考虑,次级基板选用铝合金材料。
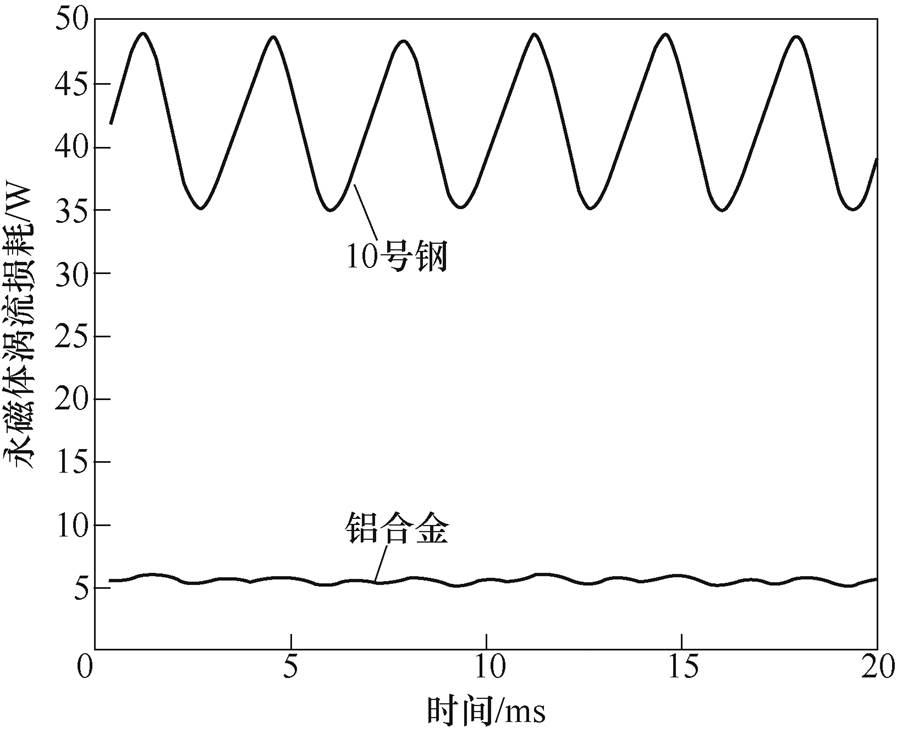
图12 不同材料下的永磁体涡流损耗
Fig.12 Permanent magnet eddy current Loss in different materials
在上述分析的基础上,以提高永磁体利用率、电磁推力和降低推力波动为目的,利用有限元软件对电机极弧系数、永磁体斜极角度进行优化,并根据优化结果设计了一台样机,样机具体参数见表1。表中的永磁体极对数指的是初级和次级耦合长度内的永磁体对数。
表1 DSDLP-PMLSM样机参数
Tab.1 The parameters of prototype DSDLP-PMLSM
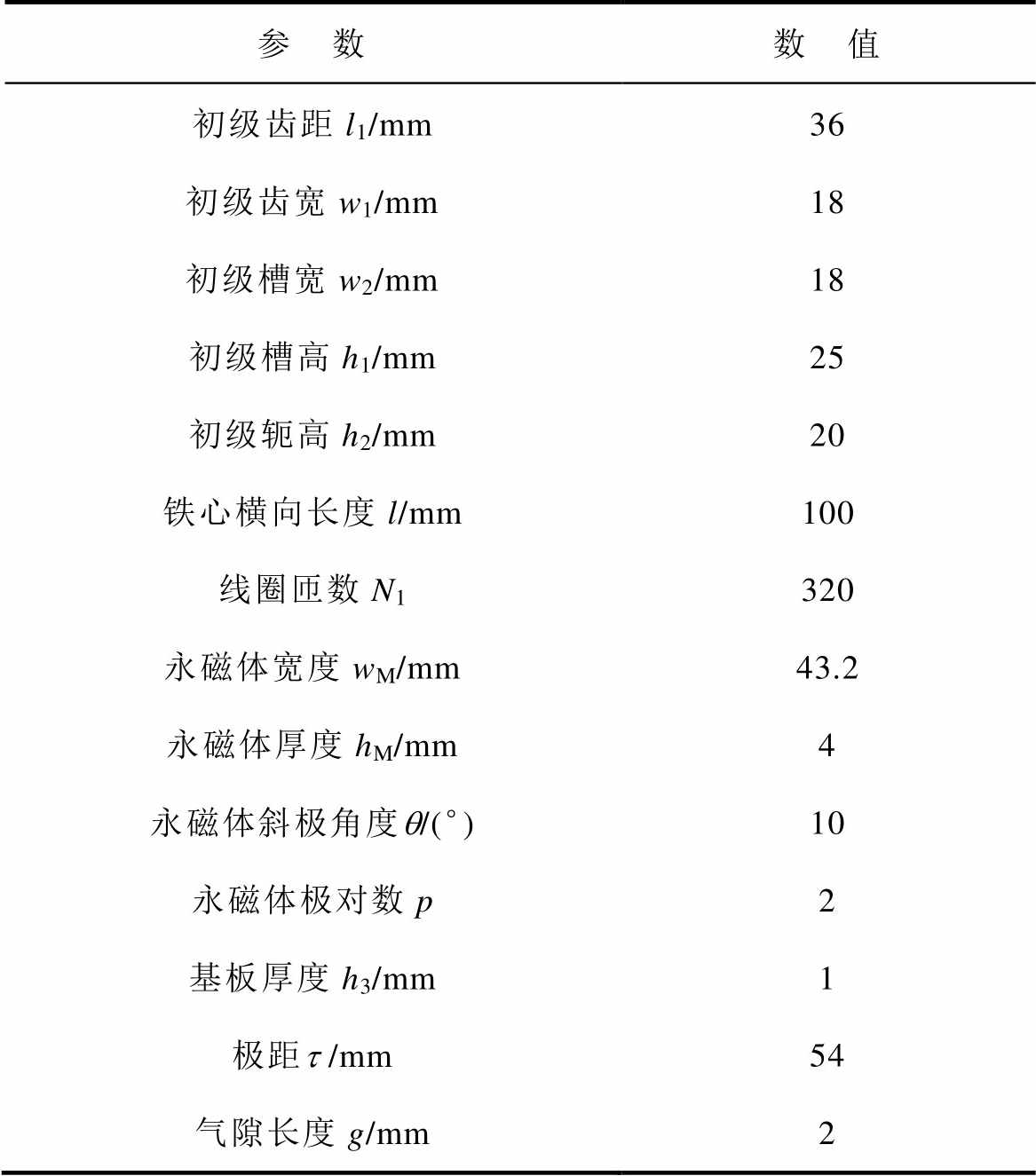
参 数数 值 初级齿距l1/mm36 初级齿宽w1/mm18 初级槽宽w2/mm18 初级槽高h1/mm25 初级轭高h2/mm20 铁心横向长度l/mm100 线圈匝数N1320 永磁体宽度wM/mm43.2 永磁体厚度hM/mm4 永磁体斜极角度q/(°)10 永磁体极对数p2 基板厚度h3/mm1 极距t /mm54 气隙长度g/mm2
样机结构如图13所示。电机铁心采用硅钢片叠压而成,通过螺丝与钢板底座紧密相连,如图13a所示。次级永磁体嵌在铝合金基板的平行四边形凹槽内,如图13b所示。整个次级部分通过滑块与安装在两侧钢板上的导轨连接,如图13c所示。

图13 样机结构
Fig.13 Prototype structure
为了测得电机的定位力、空载反电动势和静推力,搭建了如图14所示的实验平台。

图14 实验平台
Fig.14 Prototype experiment platform
伺服电动机和滚珠丝杠产生的恒定推力带动次级沿导轨做匀速运动,用示波器测量三相绕组产生的空载反电动势。由于电机初级长度有限,为了防止次级运动过快发生脱落,在实验过程中只对低速下的空载反电动势进行测量。图15所示为在0.34m/s速度下的空载反电动势测试结果。图16为样机实测数据与有限元计算结果的对比,实验得到的空载反电动势幅值为49.6V,有限元计算得到的结果为48.4V,两者结果很接近,误差为2.4%,实验结果证明了有限元计算的正确性。
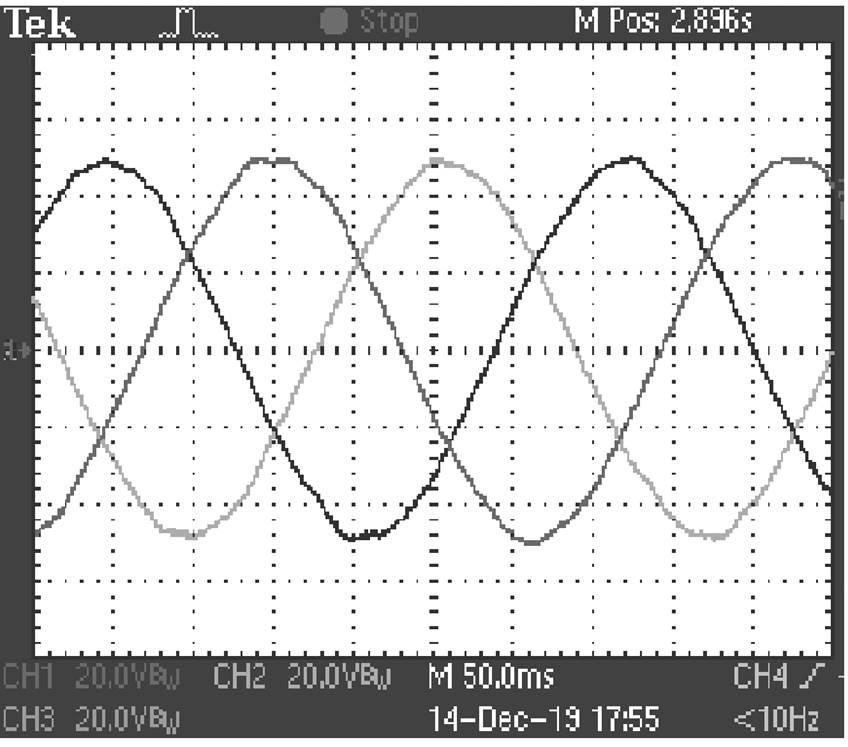
图15 样机空载反电动势
Fig.15 Experimental results of back-EMF
在电机空载情况下,用伺服电动机带动滚珠丝杠推动电机匀速运动。通过拉压力传感器检测定位力变化,结果如图17所示。从图中可知,定位力在一个电周期内波动6次,与有限元仿真结果相同。实验测得样机定位力幅值为12N(见图中1V对应5N),有限元计算结果为11N。
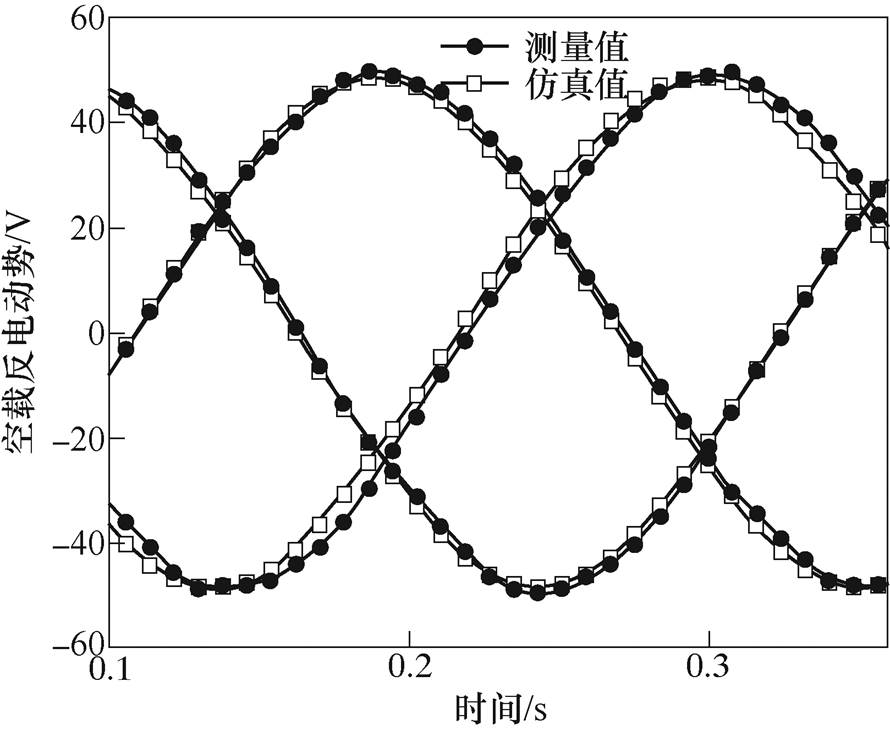
图16 空载反电动势结果对比
Fig.16 Back-EMF results comparison
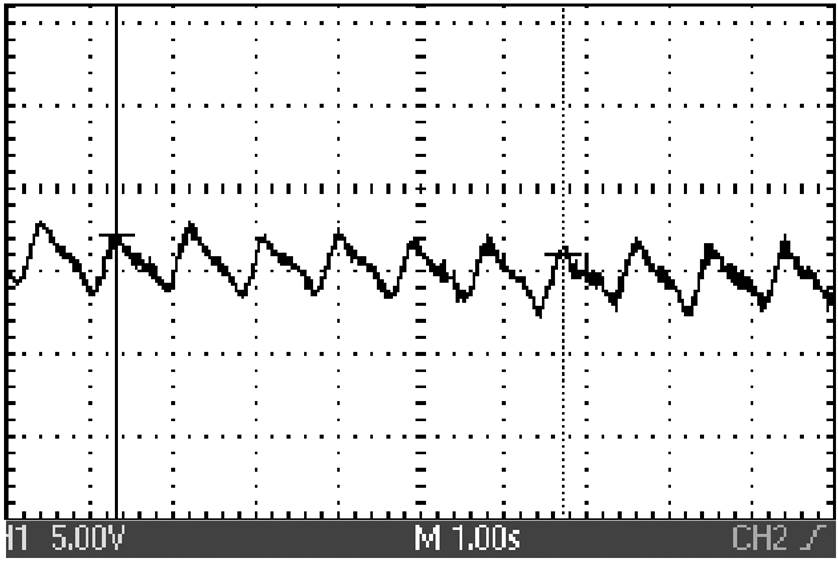
图17 样机定位力实验结果
Fig.17 Experimental results of detent force
给电枢绕组其中一相通入直流电流,用伺服电动机和滚珠丝杠带动样机次级做匀速直线运动,此时直线电机力的变化就是电机的静推力特性。
实验测试过程中,给A相绕组通入直流电流,然后改变电流的大小,得到电机静推力与通电电流的关系曲线。图18为A相绕组通入4A直流电流时电机静推力随空间位置的变化曲线(见图中1V对应50N)。图19为电机静推力与通电电流的关系曲线,两条曲线基本重合,最大误差为2.6%。对于图19,需要说明的是,由于直流电源功率的限制,没有能测量电机饱和状态下的静推力。
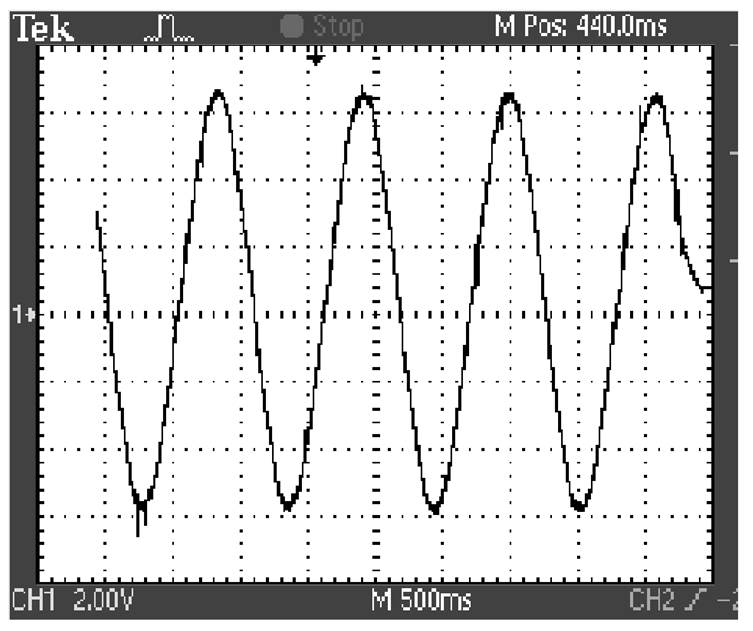
图18 样机静推力实验结果
Fig.18 Experimental results of static thrust
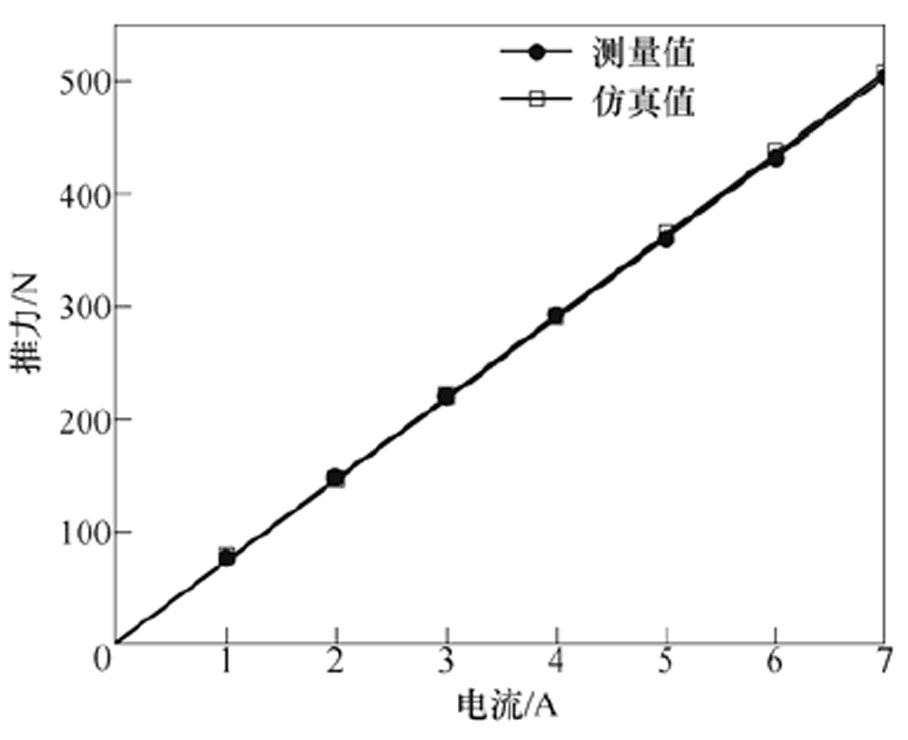
图19 样机静推力与通电电流的关系
Fig.19 Relationship between prototype static thrust and current
本文针对4极6槽双边对称长初级永磁直线同步电机,提出一种双边错位结构,采用双边错位的方法对电机电枢磁动势谐波进行削弱。首先,分析了双边错位结构的电枢磁动势,推导永磁体涡流损耗的计算公式,并利用有限元软件与双边对称结构分别从定位力、电磁推力和永磁体涡流损耗进行对比分析。结果表明,双边错位结构相比于双边对称结构,电枢谐波磁动势仅存在奇数次,偶数次被完全消除;双边错位结构对电机的定位力和电磁推力影响都很小,使电机定位力增加了约8%,电磁推力下降了5%左右,永磁体涡流损耗下降了近84.5%,该结构可以在保证电磁推力的情况下有效降低永磁体涡流损耗;双边对称结构的解析误差为4.7%,错位结构的解析误差为8.9%。其次,对次级基板材料的选取进行了分析,采用铝合金材料可以有效降低永磁体上的涡流损耗。最后,研制了一台双边错位永磁直线同步电机样机并进行初步的实验研究,实验结果与有限元计算结果很相近,空载反电动势误差为2.4%,静推力最大误差为2.6%。
参考文献
[1] Laithwaite E R. Adapting a linear induction motor for the acceleration of large masses to high velocities[J]. IEE Proceedings-Electric Power Applications, 1995, 142(4): 262-268.
[2] Fair H D. The science and technology of electric launch[J]. IEEE Transactions on Magnetics, 2001, 37(1): 25-32.
[3] 杜超, 孟大伟. 基于场路结合法的电磁弹射用新型永磁直线同步电机的研究[J]. 电机与控制学报, 2019, 23(9): 65-74.
Du Chao, Meng Dawei. Investigation of permanent magnet linear synchronous motor for electromagnetic launch based on field-circuit combined method[J]. Electric Machines and Control, 2019, 23(9): 65-74.
[4] 莫会成. 分数槽绕组与永磁无刷电动机[J]. 微电机, 2007, 40(11): 39-42.
Mo Huicheng. Fractional-slot winding and PM brush- less motor[J]. Micromotors, 2007, 40(11): 39-42.
[5] 谭建成. 三相无刷直流电动机分数槽集中绕组槽极数组合规律研究[J]. 微电机, 2007, 40(12): 72-77.
Tan Jiancheng. Investigation on slot/pole number combinations for 3-phase BLDCM with concentrated windings[J]. Micromotors, 2007, 40(12): 72-77.
[6] 陈益广, 潘玉玲, 贺鑫. 永磁同步电机分数槽集中绕组磁动势[J]. 电工技术学报, 2010, 25(10): 30-36.
Chen Yiguang, Pan Yuling, He Xin. Magnetomotive force in permanent magnet synchronous machine with concentrated fractional-slot winding[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 30-36.
[7] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160.
Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.
[8] Ishak D, Zhu Zhiqiang, Howe D. Eddy-current loss in the rotor magnets of permanent-magnet brushless machines having a fractional number of slots per pole[J]. IEEE Transactions on Magnetics, 2005, 41(9): 2462-2469.
[9] 陈萍, 唐任远, 佟文明, 等. 高功率密度永磁同步电机永磁体涡流损耗分布规律及其影响[J]. 电工技术学报, 2015, 30(6): 1-9.
Chen Ping, Tang Renyuan, Tong Wenming, et al. Permanent magnet eddy current loss and its influence of high power density permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 1-9.
[10] Takahashi I, Koganezawa T, Su Guijia, et al. A super high speed PM motor drive system by a quasi-current source inverter[J]. IEEE Transactions on Industry Applications, 1994, 30(3): 683-690.
[11] Cho H W, Jang S M, Choi S K. A design approach to reduce rotor losses in high-speed permanent magnet machine for turbo-compressor[J]. IEEE Transactions on Magnetics, 2006, 42(10): 3521-3523.
[12] Zhou Fengzheng, Shen Jianxin, Fei Weizhong, et al. Study of retaining sleeve and conductive shield and their influence on rotor loss in high-speed PM BLDC motors[J]. IEEE Transactions on Magnetics, 2006, 42(10): 3398-3400.
[13] Yamazaki K, Fukushima Y. Effect of eddy-current loss reduction by magnet segmentation in synchronous motors with concentrated windings[J]. IEEE Transa- ctions on Industry Applications, 2011, 47(2): 779- 788.
[14] 孙权贵, 邓智泉, 张忠明. 基于齿槽效应的高速永磁电机转子涡流损耗解析计算[J]. 电工技术学报, 2018, 33(9): 1994-2004.
Sun Quangui, Deng Zhiquan, Zhang Zhongming. Analytical calculation of rotor eddy current losses in high speed permanent magnet machines accounting for influence of slot opening[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1994- 2004.
[15] 张超, 陈丽香, 于慎波, 等. 不同保护型式下的高速表贴式永磁转子应力与温升分析[J]. 电工技术学报, 2019, 34(9): 1815-1824.
Zhang Chao, Chen Lixiang, Yu Shenbo, et al. Stress and temperature rise of high speed surface-mounted permanent magnet rotor with different protection types[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1815-1824.
[16] 朱龙飞, 祝天利, 于慎波, 等. 一种气隙磁导谐波引起的永磁体涡流损耗的解析计算方法[J]. 电工技术学报, 2020, 24(5): 10-16.
Zhu Longfei, Zhu Tianli, Yu Shenbo, et al. Analytical approach for calculation of eddy current losses in magnets caused by permeance harmonics in air gap[J]. Transactions of China Electrotechnical Society, 2020, 24(5): 10-16.
[17] Sun Afang, Li Jian, Qu Ronghai, et al. Effect of multilayer windings on rotor losses of interior permanent magnet generator with fractional-slot concentrated windings[J]. IEEE Transactions on Magnetics, 2014, 50(11): 1-4.
[18] Dajaku G, Gerling D. Low costs and high-efficiency electric machines[C]//2nd International Electric Drives Production Conference, Nuremberg, Germany, 2013: 1-7.
[19] Dajaku G, Xie Wei, Gerling D. Reduction of low space harmonics for the fractional slot concentrated windings using a novel stator design[J]. IEEE Transa- ctions on Magnetics, 2014, 50(5): 1-12.
[20] 徐广人, 唐任远, 安忠良. 永磁同步电动机气隙磁场分析[J]. 沈阳电力高等专科学校学报, 2001, 3(2): 1-4.
Xu Guangren, Tang Renyuan, An Zhongliang. The analysis of airgap magnetic field of permanent magnet synchronous motor[J]. Journal of Shenyang Electric Power Institute, 2001, 3(2): 1-4.
Design and Analysis of Double-Sided Dislocated High Speed Permanent Magnet Linear Synchronous Motors
Abstract As for the traditional 4-pole 6-slot double-sided symmetrical long primary permanent magnet linear synchronous motor, under the condition of ensuring the electromagnetic thrust, an effective method to reduce the permanent magnet eddy current loss was proposed by adopting bilateral dislocation. The basic structure of the motor was introduced. The double-sided dislocation structure could completely eliminate the even number of armature harmonic magnetomotive force, thereby greatly reducing the permanent magnet eddy current loss. The finite element analysis (FEA) software was adopted to analyze the detent forces of symmetric and dislocation structures, the electromagnetic thrust and the secondary eddy current losses. The accuracy of the dislocation method was proved and the structure was optimized. At last, a prototype was developed, and its back-electromotive force (back-EMF), detent force and static thrust were measured through an experimental platform.
keywords:Double-sided dislocation, permanent magnet linear synchronous motor, fractional-slot concentrated-windings, permanent magnet eddy current loss
中图分类号:TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.200802
国家自然科学基金(51520105010)国际(地区)合作与交流资助项目。
收稿日期 2020-07-07
改稿日期 2020-11-30
寇宝泉 男,1968年生,教授,博士生导师,研究方向为特种电机及其驱动控制技术。E-mail: koubq@hit.edu.cn(通信作者)
葛庆稳 男,1990年生,博士研究生,研究方向为新型永磁直线电机及其优化设计。E-mail: 17B906010@stu.hit.edu.cn
(编辑 崔文静)