图1 分段供电直线电机
Fig.1 The sectionally powered PMLSM
摘要 电枢分段供电永磁直线同步电机（PMLSM）中，相邻分段铁心的存在会导致气隙磁场脉振，动子穿过电枢定子段也会引发复杂的暂态过程。为准确描述电机的动态过程，该文考虑以上两种特有的电磁特性，建立双三相分段供电PMLSM的相空间模型。首先，采用解析法分析脉振气隙磁场的成因，研究电感不平衡以及饱和效应问题，将六相电流转化到ab 坐标系下建立二维电感查询表，有效地降低了模型的运算量。其次，引入易于求导的Sigmoid函数构造随动子位置变化的耦合系数，准确描述动子通过分段过程产生的空载磁链及反电动势。依据上述方法构建电机相空间模型，与有限元模型进行对比，两者电压与推力计算结果一致。最后，在RT-Lab中搭建基于相空间模型的半实物实验平台，结果表明，该模型能够准确地体现电机的各种效应，可以替代计算成本较大的有限元模型。
关键词：永磁直线同步电机 分段供电 磁场饱和效应 相空间模型
双三相永磁直线同步电机（Permanent Magnet Linear Synchronous Machine, PMLSM）由于具有响应速度高、定位精度高、控制品质好、系统可靠性高的优点[1-4]，同时兼具多相电机单相容量低、可靠性高的特点[5-7]，适用于高速磁悬浮交通直线驱动、高加速的电磁驱动系统。对于长行程应用场合，为了减小电源容量，降低制造和运营成本，通常采用长电枢短励磁的方案，并将长电枢侧分段，当动子运动到某一个分段下，则为该电枢供电[8-10]。
在研究电机动态过程或各种控制方法时，往往需要准确、全面、高效的动态数学模型[11]。动态数学模型主要分为分布参数模型和集总参数模型。有限元模型作为一种分布参数模型，因可以给出十分精确的计算结果而被广泛使用[12-14]；然而有限元模型计算成本大，因而对于行程较长的直线电机来说，进行一次仿真需要的时间过长。而传统的集总参数模型因具有计算成本小、计算效率高的特点也得到了广泛应用[15]。电机的集总参数模型主要包括dq轴模型和相空间模型[11]，其中dq轴模型是将相空间模型的电感矩阵通过Park正交变换成对角矩阵，从而达到dq轴解耦与简化计算的目的。对于电感矩阵循环对称且为常数或者仅为转子或动子位置正弦函数的情况，dq轴模型易于实施且容易计算[16-18]，但是当考虑饱和效应等非线性因素以及谐波磁场时，dq轴模型中的电感矩阵便不再是常量，此时相空间模型凭借其灵活性更加适合建立动态数学模型[15, 19-20]。文献[15]采用相磁链直接查表法建立了三相旋转永磁电机的非线性相空间模型，减小了查表的维度，降低了模型计算量。文献[19]采用三相电感直接查表法针对星形联结的旋转永磁电机建立了相空间模型，并通过有限元计算验证了该模型的正确性。文献[20]对三相盘式电机建立了非线性相空间模型，并同时在模型中考虑了铁心损耗。然而以上文献集中于旋转电机的动态模型，针对铁心开断且分段供电的长电枢永磁直线电机动态数学模型的文献较少。
与旋转电机不同的是，长电枢永磁直线电机存在磁极动子穿过定子电枢分段的过程，同时还存在由相邻分段电铁心引起脉振气隙磁场而导致的电感不平衡的现象[21-28]。文献[28-29]对分段供电三相永磁直线电机建立了相空间模型，在模型中同时考虑了动子的通过过程，并分析了电机运行的动态过程。但是由于该电机主要工作在持续运行工况，因而饱和程度不明显，因此该模型假设动子完全被定子覆盖时电感为恒定值。
然而由于高加速电磁驱动应用中的直线电机同时需要满足轻量化和大推力，往往工作在短时高过载的工况，因而面临深度饱和效应引发的电感波动问题。在短电枢直线电机和旋转电机中，饱和效应主要由行波磁场引发，电感波动循环对称；而长电枢分段供电PMLSM中的饱和效应主要由脉振气隙磁场引起，其结果是各相电感谐波几乎为同相位。采用精确且计算快速的数学模型描述电机的动态过程对分段供电PMLSM电磁瞬态过程研究、电机实施精确控制都具有重要意义。
本文建立准确且计算快速的双三相分段供电PMLSM的相空间模型，针对定子电枢分段造成的脉振磁场，采用解析法对其进行深入分析。提出将电机六相电流转化到ab 坐标系下建立二维电感查询表，在保证查表精度的同时，有效提升电感查表速度，降低生成电感查表所需的有限元仿真或实验次数。针对动子过分段的过程，提出采用易于求导的Sigmoid函数构造耦合因数，简单并准确地描述了电机的空载磁链和反电动势特性。最后基于RT-Lab搭建了半实物实验平台，验证了本文建立的相空间模型能够准确反映双三相分段供电PMLSM的电磁特性。
双三相长电枢直线电机定子由多个分段组成，设从左向右的分段编号为1～Nsec，分段供电直线电机如图1所示，一个分段下电机的结构如图2所示。图中，PMLSM参数见表1。为节约横向端部空间，方便绕线，定子采用背绕式分布绕组（即克莱姆绕组）。为了减少动子永磁体端部漏磁，动子采用端部半磁极结构。由于电机工作在短时状态，因此电流密度选取较高。
图1 分段供电直线电机
Fig.1 The sectionally powered PMLSM
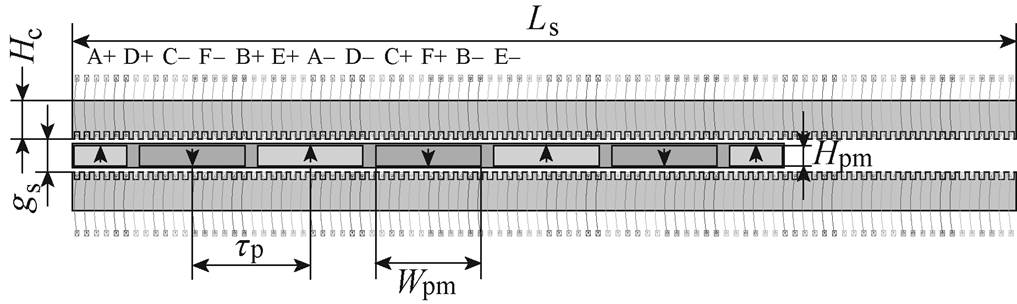
图2 一个分段电机的结构
Fig.2 The structure of one power section of the PMLSM
表1 PMLSM参数
Tab.1 The parameters of the PMLSM
参 数数值(型号) 相数m双三相 极对数p3 每极每相槽数q2 极距tp/mm170.4 电机横向宽度Lsw/mm100 单分段定子长度Ls/mm1 363.2 分段间轨缝宽度dgap/mm1.2 双边铁心间距gs/mm39 每槽导体数Ns4 动子长度Lmover/mm1 022.4 永磁体厚度Hpm/mm24 永磁体宽度Wpm/mm152 铁心高度Nc/mm48.2
永磁体的磁导率与空气相近，且动子中不存在铁磁材料，可单独研究电流在气隙中产生的磁场。绕组在气隙中产生的磁场可视为各个导体单独产生的磁场叠加的结果，因此先计算单个导体在气隙中产生的磁场，单个导体位于双边铁心中的模型如图3所示。
为简化计算过程，进行如下假设：①忽略齿槽，设导体内的电流为I，将单根载流导体视作一个紧挨铁心的点电流；②x＜-l1或x＞l2处的磁场为0；③气隙中只含y方向磁场；m0为真空磁导率；mFe为铁心磁导率；⑤忽略分段间轨缝。
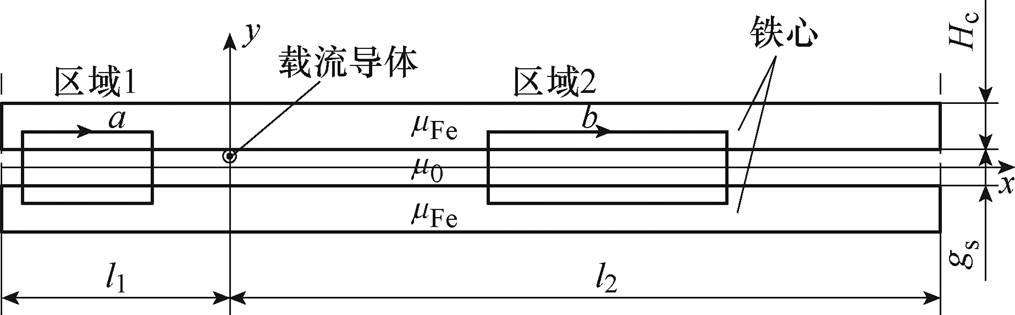
图3 单个载流导体位于双边铁心中
Fig.3 Single conductor between the iron cores
分别对区域2与区域3列写关于法向磁通密度的微分方程为
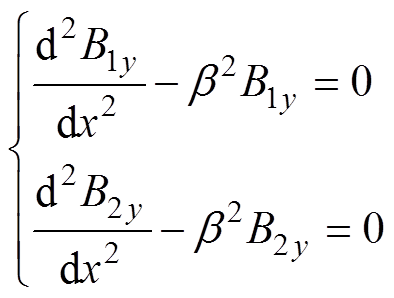（1）其中
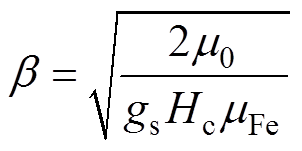
式中，B1y、B2y分别为区域a和区域b的气隙法向磁通密度。区域a与区域b满足的边界条件为
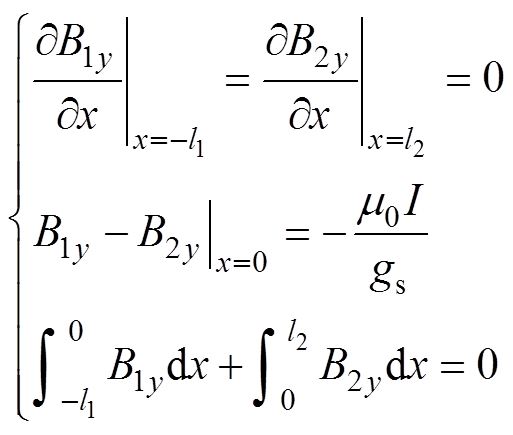（2）求解式（1）、式（2）得到单个导体在双边铁心下产生的气隙y方向磁通密度分布Bcony为
（3）
一相绕组通电后在气隙中产生的磁场为绕组中各导体产生磁场的叠加，各相绕组产生的气隙磁通密度表达式为
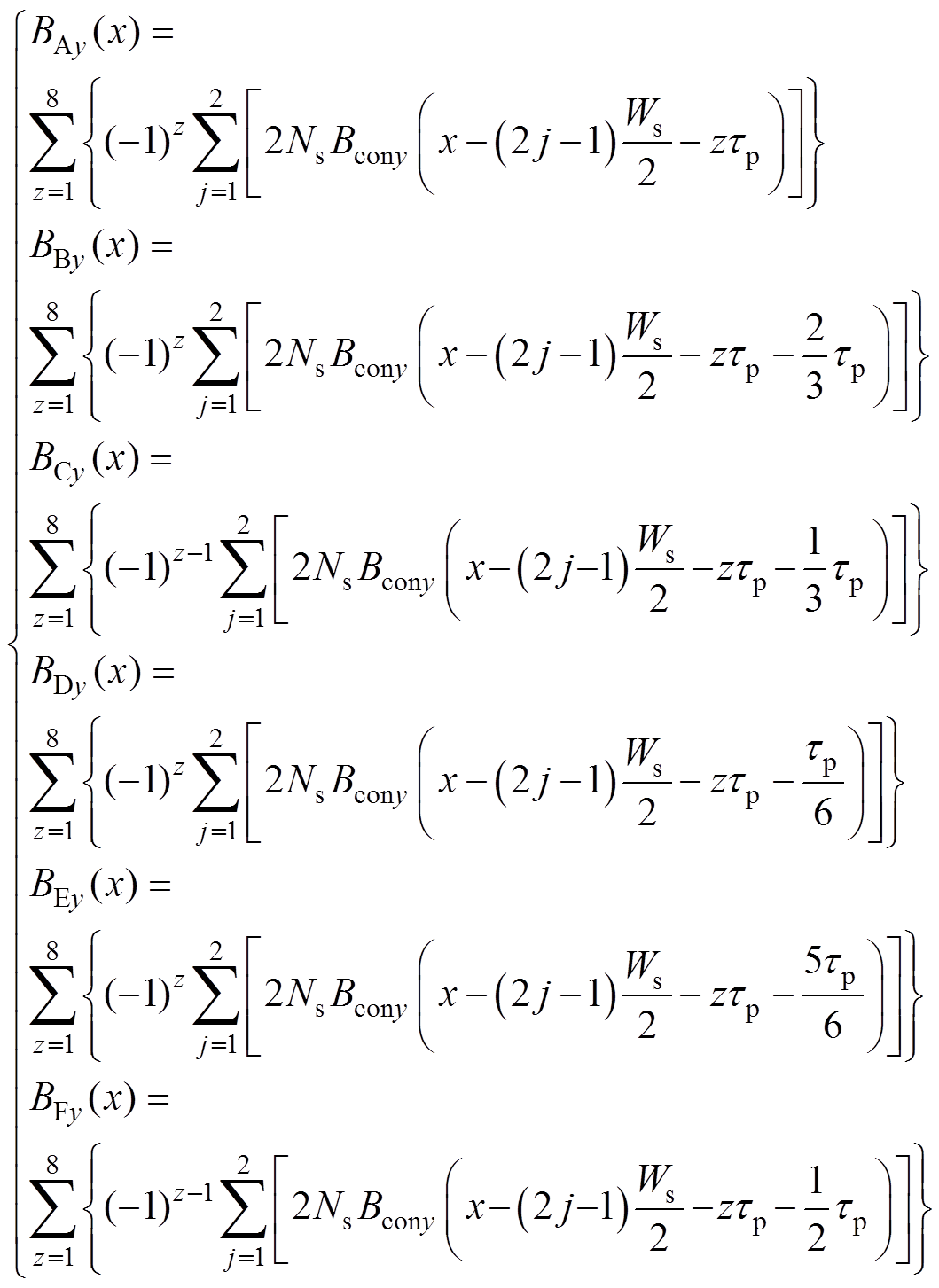（4）式中，x为以分段左端为原点，以右为正方向的位置坐标；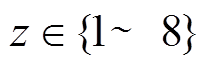
；
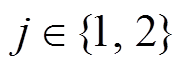；Ws为电机槽距；BAy、BBy、BCy、BDy、BEy、BFy分别为一个分段下A、B、C、D、E、F相绕组产生的气隙磁通密度。将某一时刻六相电流各自产生的气隙磁通密度相加即可得到六相电流产生的整体气隙磁通密度。
对应不同时刻（对应不同电角度）下的整体气隙磁通密度波形如图4所示。气隙磁场在向前运动的同时，还存在直流脉振分量。当电角度为p/2和3p/2时，气隙磁场的直流分量分别达到正、负最大值。由于供电分段的两侧存在未通电分段的铁心，根据磁通连续性定理，各相绕组产生的磁场在通电分段区间内存在直流分量，因此导致合成磁场中存在直流脉振分量[21]，从而形成脉振气隙磁场。
图4 不同电角度下的六相电流产生的气隙磁通密度
Fig.4 The flux distribution generated by six-phases current with different electrical degrees
双三相电机的绕组相量如图5所示，ABC和DEF分别为两套互差120°电角度的三相绕组，两套三相绕组间相差30°电角度。
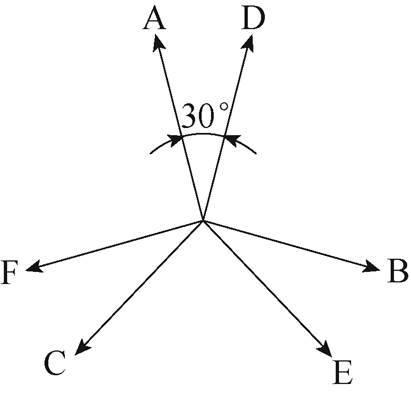
图5 双三相电机的绕组相量
Fig.5 The phase diagram of the dual-three phase PMLSM
双三相电机的电感可依据相间电角度分为五类。在旋转电机中，当忽略凸极效应及饱和因素时，各个类别中的电感是相等的。
（1）第一类电感：各相自感，包括Laa、Lbb、Lcc、Ldd、Lee、Lff。
（2）第二类电感：互差120°相间互感，包括Lab、Lbc、Lac、Lde、Lef、Ldf。
（3）第三类电感：互差30°相间互感，包括Lad、Lbe、Lcf。
（4）第四类电感：互差90°相间互感，包括Lbd、Lce、Laf。
（5）第五类电感：互差150°相间互感，包括Lae、Lcd、Lbf。
对于分段供电的双三相直线电机，当一相绕组通入电流时，绕组产生的气隙磁通密度存在直流分量。这部分直流分量交链到其他相绕组中会导致电感不平衡。直线电机的自感与互感表达式均为
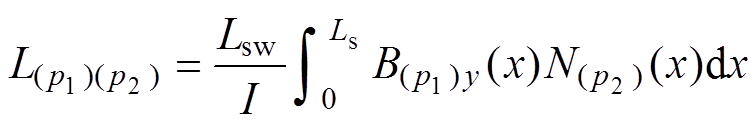（5）式中，p1、p2为相标号，即a～f；
为p2相的绕组函数[30]；Lsw为有效电机横向宽度。当p1=p2时，式（5）计算得到p1相自感；当p1≠p2时，式（5）计算得到p1与p2相间互感。
采用式（5）计算得到电机的五类电感见表2。第一类和第三类电感是内部相等的，但第二、四、五类电感内部均不相等。在旋转电机中应为0的第四类电感，在长初级直线电机中不为0。
电机工作于短时高过载状态，绕组的电流密度较大（最大达到44A/mm2），容易导致铁心饱和。六相电流产生的气隙磁场存在脉振分量，使得铁心轭部的饱和程度加深。忽略永磁体，单独向供电分段的绕组中通入一个电周期的六相电流，获得电角度为0、p/2、p、3p/2下的铁心磁通密度分布如图6所示。由于脉振磁场的影响，电角度为p/2和3p/2时，铁心局部磁通密度大幅增加，达到2T以上；而当电角度为0和p 时，铁心磁通密度仅为1.6T。
表2 一个分段的各类电感
Tab.2 The inductances of a power section
电感类别电感/mH 一Laa=Lbb=Lcc=Ldd=Lee=Lff=475.7 二Lab=Lde=-7.0, Lbc=Lac=Lef=Ldf=-207.5 三Lad=Lbe=Lcf=321.2 四Lbd=100.5, Lce=Laf =-100.1 五Lae=-119.4, Lcd=Lbf =-322.1
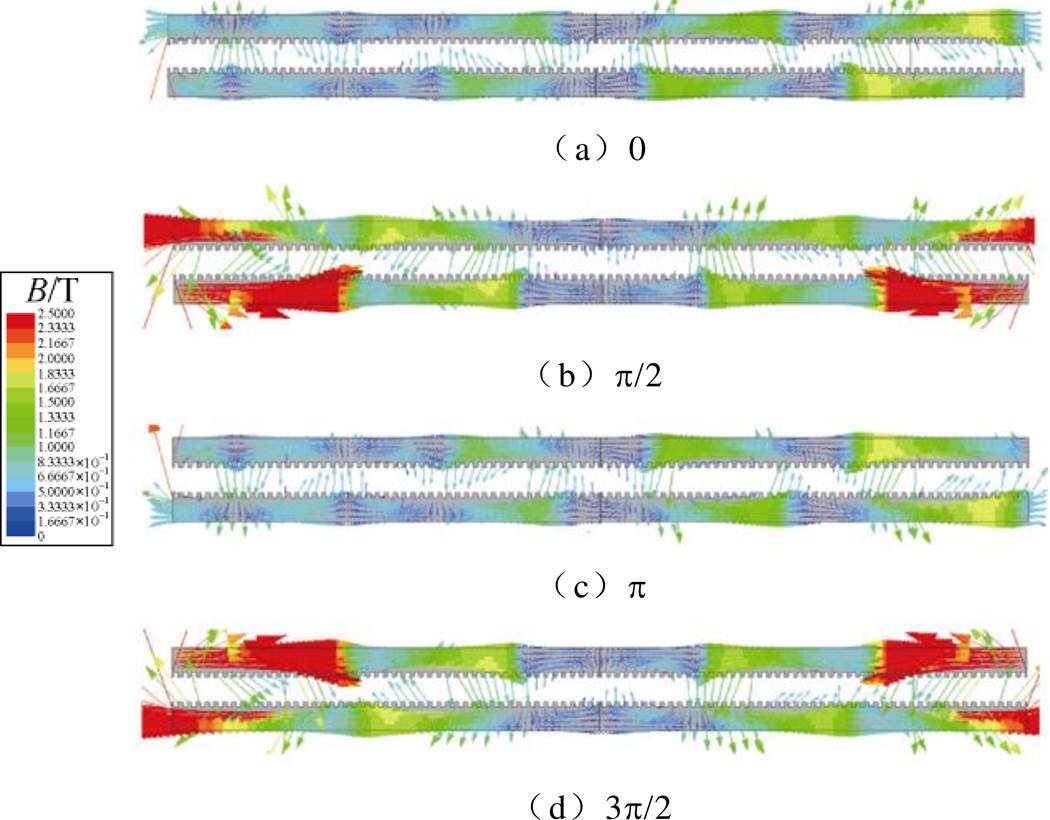
图6 一个电周期内不同电角度下的磁通密度分布
Fig.6 The flux distribution with different electrical degrees in an electrical period
一个电周期内，脉振磁场两次达到峰值，此时由于偏置引发的轭部磁通密度饱和程度加深则会导致各类电感下降，引发电感波形中产生2次谐波。且对于各相电感，2次谐波相位基本一致。通入额定六相电流，一个电周期内的五类动态电感波形如图7所示。
双三相电机的动态电感矩阵阶数r=6，共有r2个元素，考虑到电感矩阵的对称性，以及由相邻未通电铁心引起的电感矩阵不平衡及饱和效应，动态电感矩阵L中含有(r2-r)/2+r=21个独立变量。该21个变量均为六相电流（ia～if）的函数，即L(ia～if)，因此动态电感矩阵的查询表为一个6输入、21输出系统。
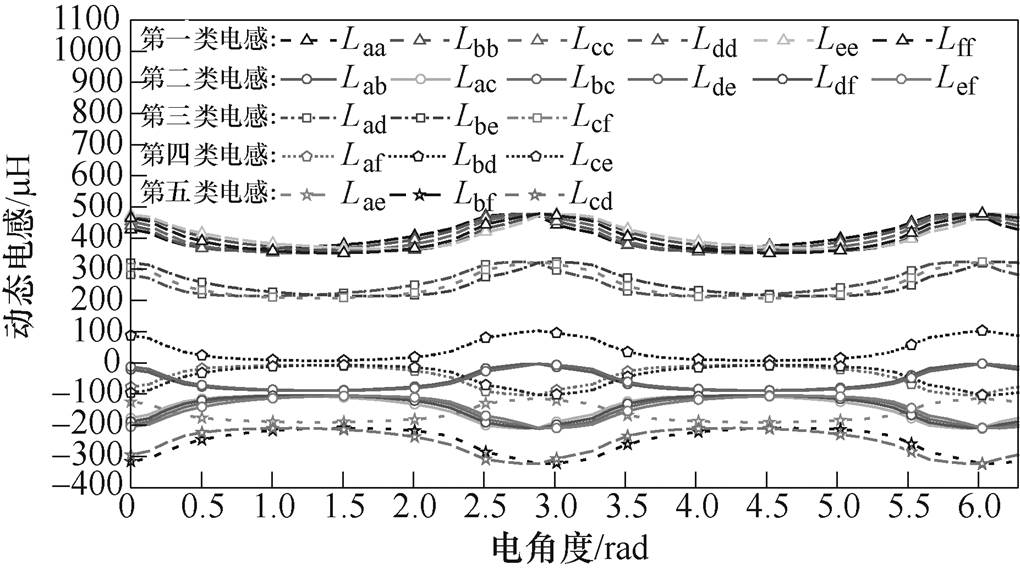
图7 额定电流下一个电周期内的动态电感
Fig.7 The dynamic inductances in an electrical period with rated current
在ABCDEF坐标系下，电感矩阵的输入有6个自由度，若对每个自由度均采样ns次，确定电感矩阵查询表需进行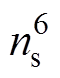
次实验（或有限元仿真）。为了降低输入量的自由度，本文将ABCDEF坐标系下的电流通过式（6）映射到静止的ab 坐标系下，由此仅需进行
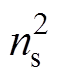次实验即可获取电感查询表。
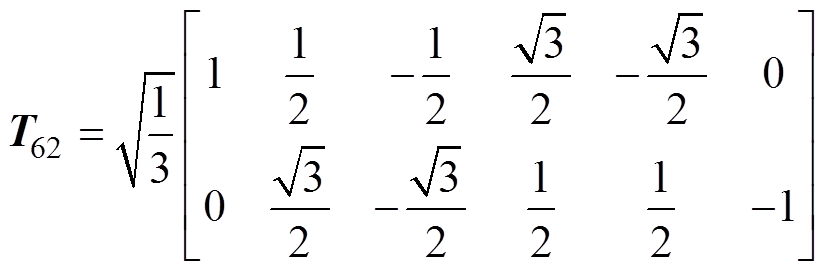（6）采用拉丁超立方采样（Latin Hypercube Sampling, LHS）在ab 平面中进行电流采样，获得各个电感随ia 与ib 变化的插值曲面，如图8所示。
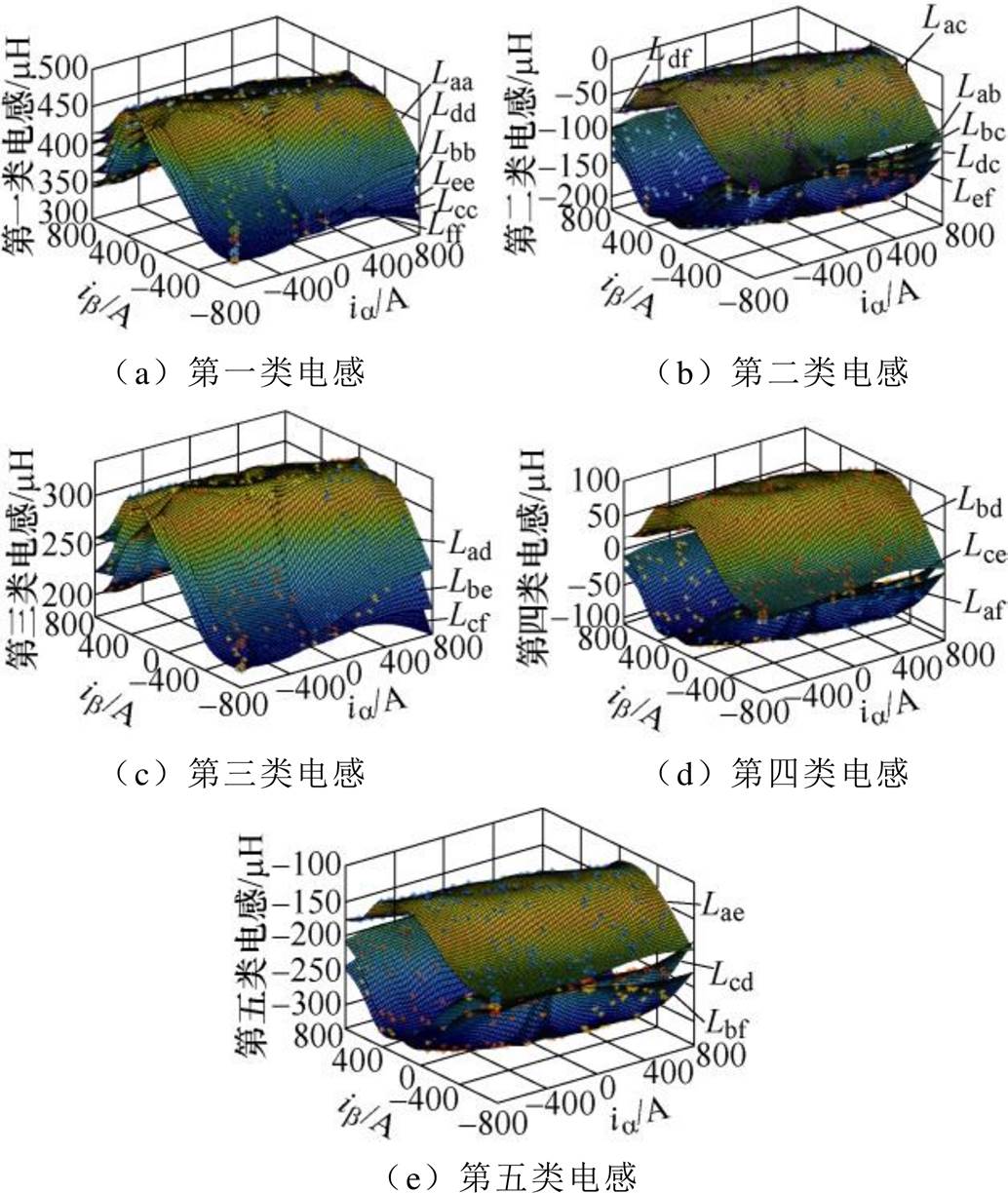
图8 动态电感与ia 和ib 的插值曲面
Fig.8 The dynamic inductances with different ia, ib
动子采用的是端部半磁极形式，以半个N极与半个S极为一个单元磁路。取分段中的A相绕组为例，动子通过供电分段的过程如图9所示。将运动坐标轴原点定于供电分段的左侧端部，x表示动子头部位置。随着动子进入分段，与A相绕组耦合的单元磁路个数逐渐增多，直到A相绕组耦合的单元磁路达到最大极数6，动子穿出过程与穿入过程相反。永磁体在A相中产生的磁链ypmA可分解为图9中的A相绕组耦合系数aA与A相单元磁路磁链ypmuA的乘积，即ypmA=aAypmuA。
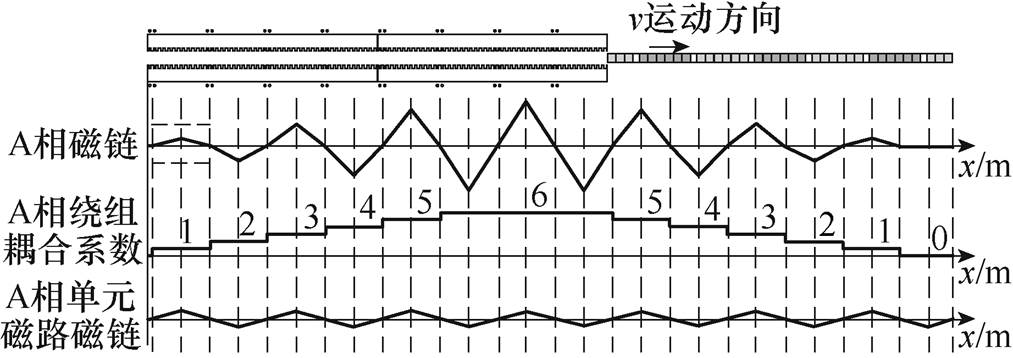
图9 动子通过一个分段时在A相绕组中产生的磁链
Fig.9 The flux generated by PMs in phase A when the mover moving through a section
A相的耦合因数aA为动子头部位置的函数。由于在求取空载反电动势时，需要对永磁体磁链求导，若aA采用阶跃函数则表示会在求导过程中产生冲激。为避免该现象，引入Sigmoid函数（即sig(x)）柔化aA的阶跃边缘，其导数可用函数本身的值求出，即sig'(x)=sig(x)(1-sig(x))。A相耦合因数为
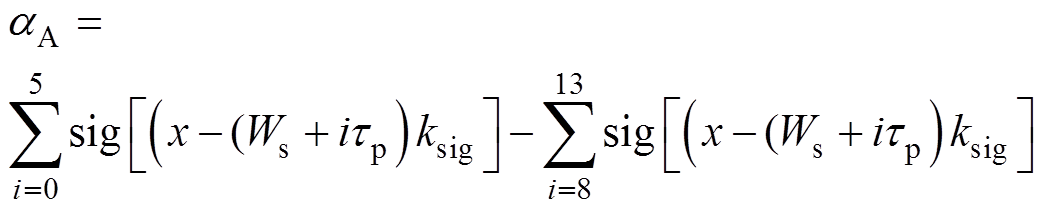（7）式中，ksig为Sigmoid函数的伸缩因子，ksig值越大，则阶跃边缘越锐化。其余相的耦合因数可以通过平移aA获得，即
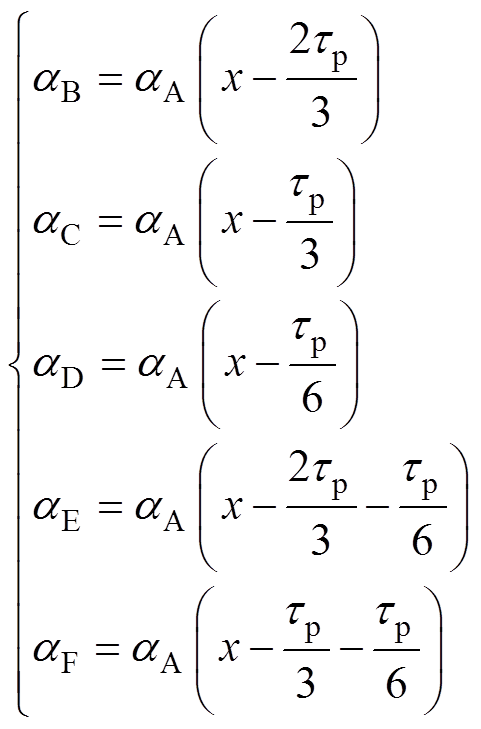（8）
动子运动过程中，耦合因数随动子位置的变化如图10所示。
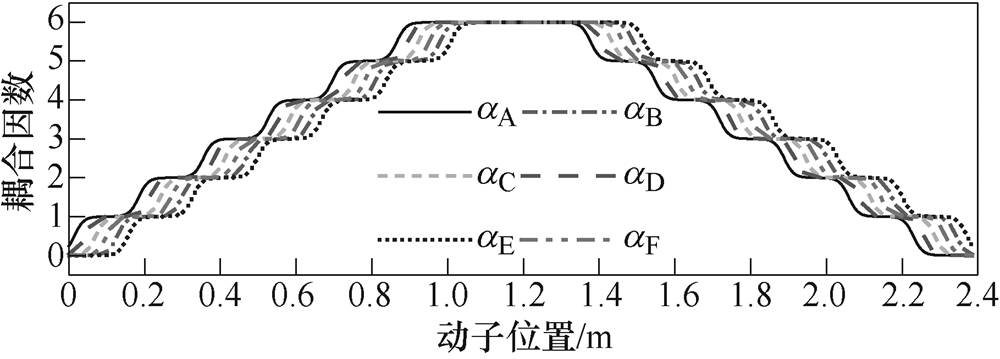
图10 耦合因数随动子位置的变化
Fig.10 The coupling coefficient with different mover positions
由图9可知，动子在分段绕组中产生的永磁体磁链可由单元磁路磁链与相应的耦合系数相乘得到。以A相为例，一个单元磁路在一个周期内产生的磁链及频谱如图11所示。
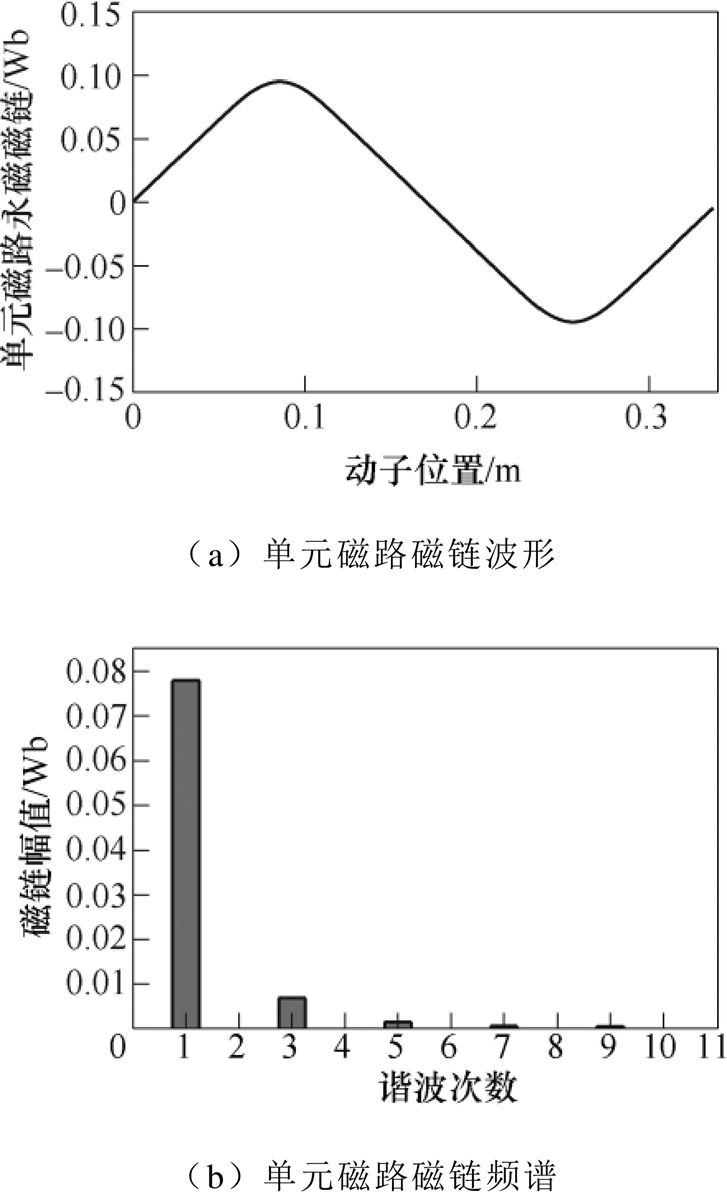
图11 单元磁路在A相中产生的永磁体磁链
Fig.11 PM flux in phase A of unit magnetic circuit
A相单元磁路永磁体磁链的傅里叶级数形式为
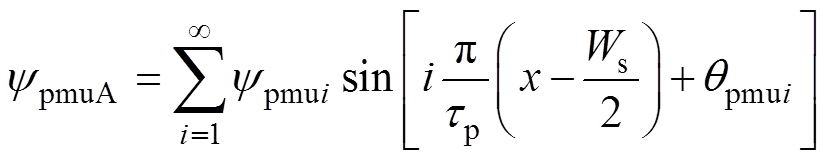（9）式中，ypmui与qpmui分别为第i次谐波的幅值和相位。其余各相的单元磁路永磁体磁链可通过平移ypmuA得到。六相永磁体磁链可表示为
（10）
动子穿过分段时产生的各相空载反电动势为永磁体磁链对时间的导数，即
（11）式中，p为各相符号，p=A～F；v为动子速度。将采用式（10）与式（11）计算得到的空载永磁体磁链与空载反电动势分别与有限元计算结果对比如图12所示，有限元和空载模型的计算结果一致。
图12 模型和有限元计算的空载下永磁体磁链及反电动势
Fig.12 The PM flux and no load back-EMF calculated by phase-domain model and finite element method
为描述电机整体运动过程，基于电机的动态电感查表方法、空载磁链及反电动势描述方法建立了电机的状态方程。一个分段下，电机的电压方程为
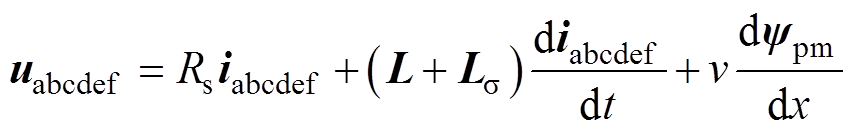（12）式中，uabcdef、iabcdef和ypm分别为六相相电压、相电流和空载磁链矢量；Rs为相电阻；L、Ls 分别为六相动态电感矩阵和漏感矩阵。采用虚功原理计算电机的电磁推力为
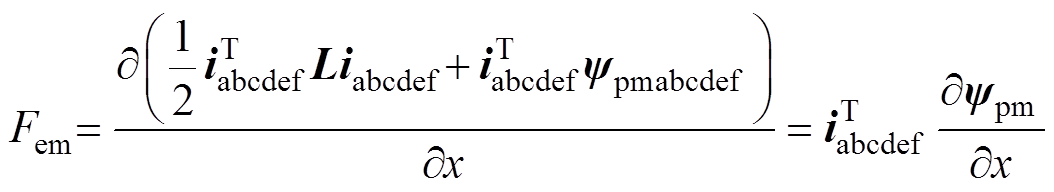（13）
选取动子速度v、六相电压uabcdef为控制量，iabcdef为状态量建立一个分段下的相空间模型为
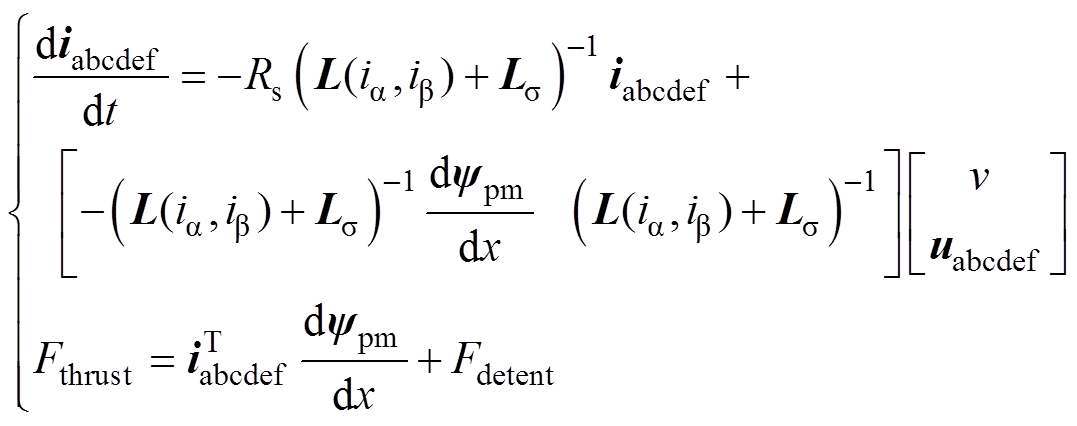（14）式中，Fthrust为电机产生的电磁推力；Fdetent为动子行进过程中由端部效应、齿槽效应引起的定位力。
一个分段下的电机相空间模型可更直观地以框图形式表示，电机状态方程的框图如图13所示。
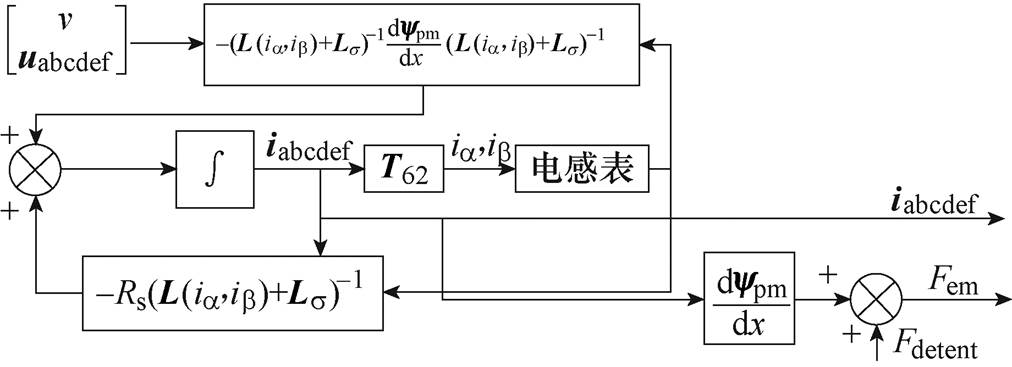
图13 电机状态方程的框图
Fig.13 The framework of the state function of PMSLM
通入六相平衡额定电流，采用式（14）对动子穿过一个分段时的负载性能进行计算，并将端口电压和推力波形与有限元结果对比如图14所示。为检验结果的一致性，计算相空间模型的各相电压波形与有限元之间的皮尔森相关系数（Pearson Correlation Coefficient, PCC）见表3，六相电压相关系数均在99%以上，说明由六相电感矩阵不平衡和饱和效应所导致的电压不平衡均准确地体现在相空间模型中。采用相空间计算得到的动子穿过分段时的推力波形与有限元计算结果的相关系数为99.6%，表明相空间模型可以精确地描述动子的过分段推力特性。
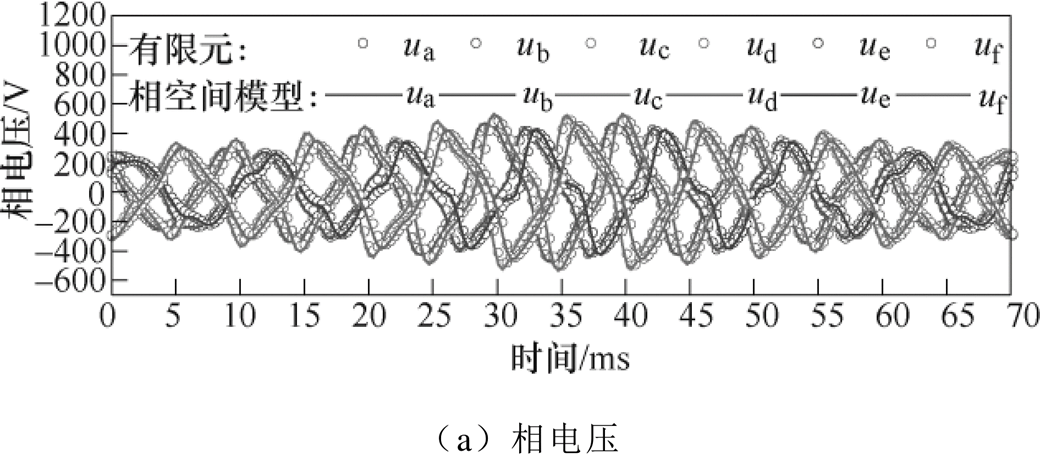
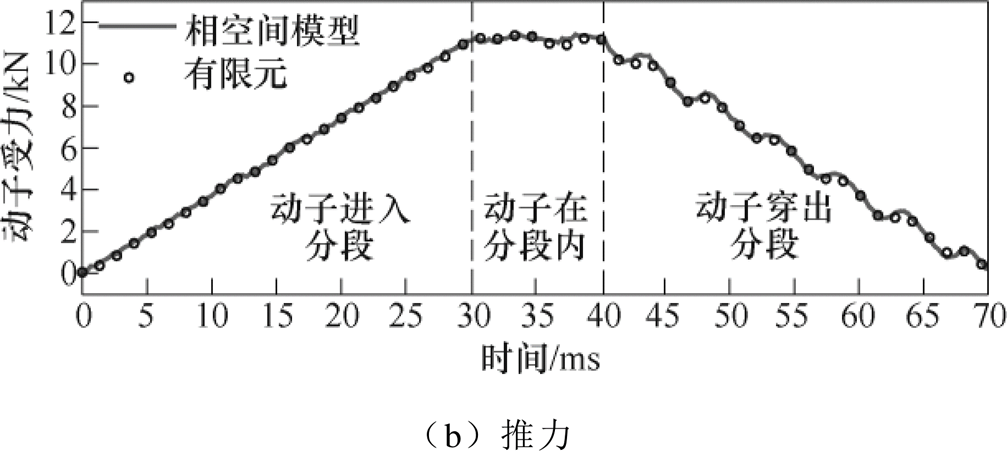
图14 动子穿过分段时的相电压与推力
Fig.14 The phase voltage and thrust force when the mover is moving through the power section
表3 相空间模型电压波形与有限元计算的相关系数
Tab.3 The correlation coefficient between phase voltage calculated by phase-domain model and FEM-model
相电压相关系数(%) A99.7 B99.4 C99.2 D99.5 E99.2 F99.3
为验证电机数学模型的有效性，在RT-LabOP5700半实物平台中搭建了电机相空间模型，并基于该模型实现电机全过程实时驱动系统。实验平台及驱动系统整体架构如图15所示。实验机箱由CPU板卡和Xilinx公司的Virtex7 FPGA板卡两部分组成。电机的驱动控制器采用CPU板卡实现，控制频率为10kHz。电机的相空间模型则编写在FPGA中，其离散化精度为500ns。
由于分段供电的电机最多有2个分段同时供电，为节省计算资源，在模型中仅需两台双三相变流器对两个电机相空间模型交替供电，长电枢电机的分段供电方式如图16所示。两个电机相空间模型分别代表实际系统中的奇数号分段和偶数号分段。如图15b所示，在FPGA中，包含奇数号分段和偶数号分段的电机模型以及动子运动方程。电机模型计算得到电磁推力后作为输入送入运动方程中进行动子位置和速度的计算。动子运动方程将动子位置和速度反馈到电机模型完成空载反电动势与Park变换矩阵的计算。
图15 基于RT-Lab OP5700的半实物实验平台及驱动系统整体架构
Fig.15 The experiment platform based on the RT-Lab OP5700 and the structure of the drive system
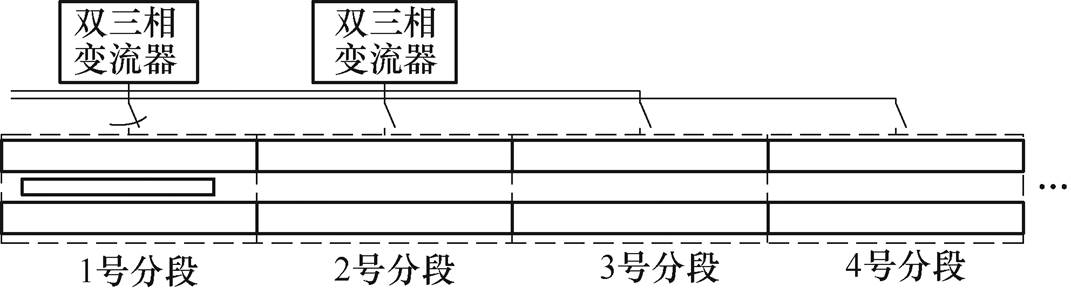
图16 长电枢电机的分段供电方式
Fig.16 The power strategy of the PMLSM
为节省计算资源，在建立基于FPGA的电机模型时，所有数据均采用定点数进行运算。同时，复杂的函数（如Sigmoid函数及其导数、三角函数等）均采用查表的方式进行计算。两个电机方程以及一个动子运动方程总共占用FPGA的主要资源见表4。FPGA中的电机模型离散化精度为500ns，而FPGA的晶振频率为200MHz。本文建立的电机模型可以在100个晶振周期之内完成计算。
表4 电机模型以及动子运动方程所占用的FPGA资源
Tab.4 The resources in FPGA occupied by PMLSM model and motion equation
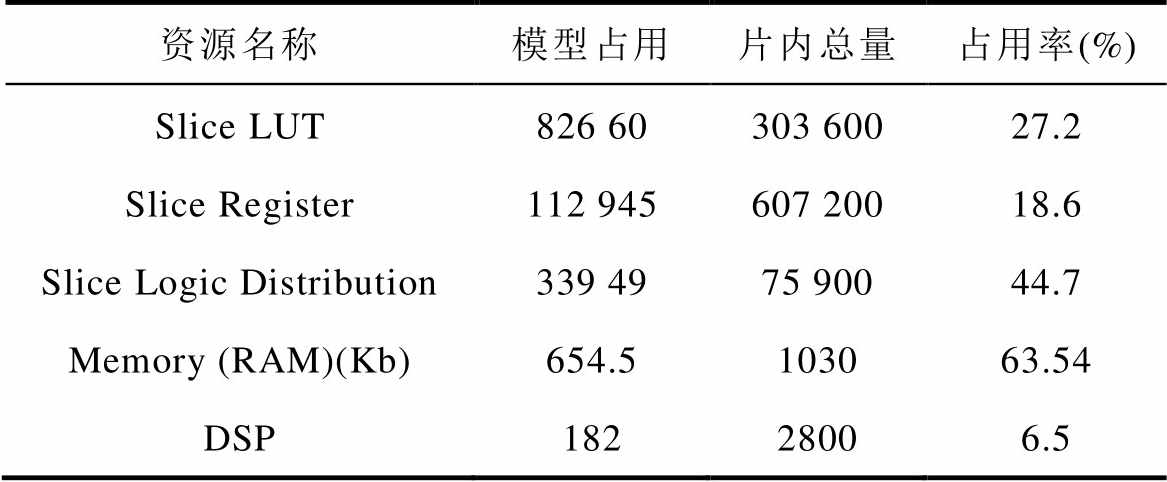
资源名称模型占用片内总量占用率(%) Slice LUT826 60303 60027.2 Slice Register112 945607 20018.6 Slice Logic Distribution339 4975 90044.7 Memory (RAM)(Kb)654.5103063.54 DSP18228006.5
采用id=0的控制策略，将280kg的动子以90m/s2的加速度跟踪最大为30m/s的三角波速度给定。采用数学模型计算得到的电机加速性能如图17所示。图17a表明，整个过程中动子成功地跟踪了参考速度。在加速过程中，不同的供电分段交替为动子提供推力，如图17b所示，可以看出，当动子过分段时，电机的相空间模型可以准确体现动子耦合因数下降引起的推力下降，以及由定位力引发的波动。电机dq轴电流给定及各分段的dq轴电流波形如图17c所示。图17d为各个分段六相电流波形。电机运动过程中的空载反电动势如图17e所示，随着速度提高，空载反电动势幅值随之升高，同时在动子过分段时，动子所离开的分段空载反电动势逐渐减小为0，因此所建立的模型可以准确描述动子过分段时的反电动势特性。
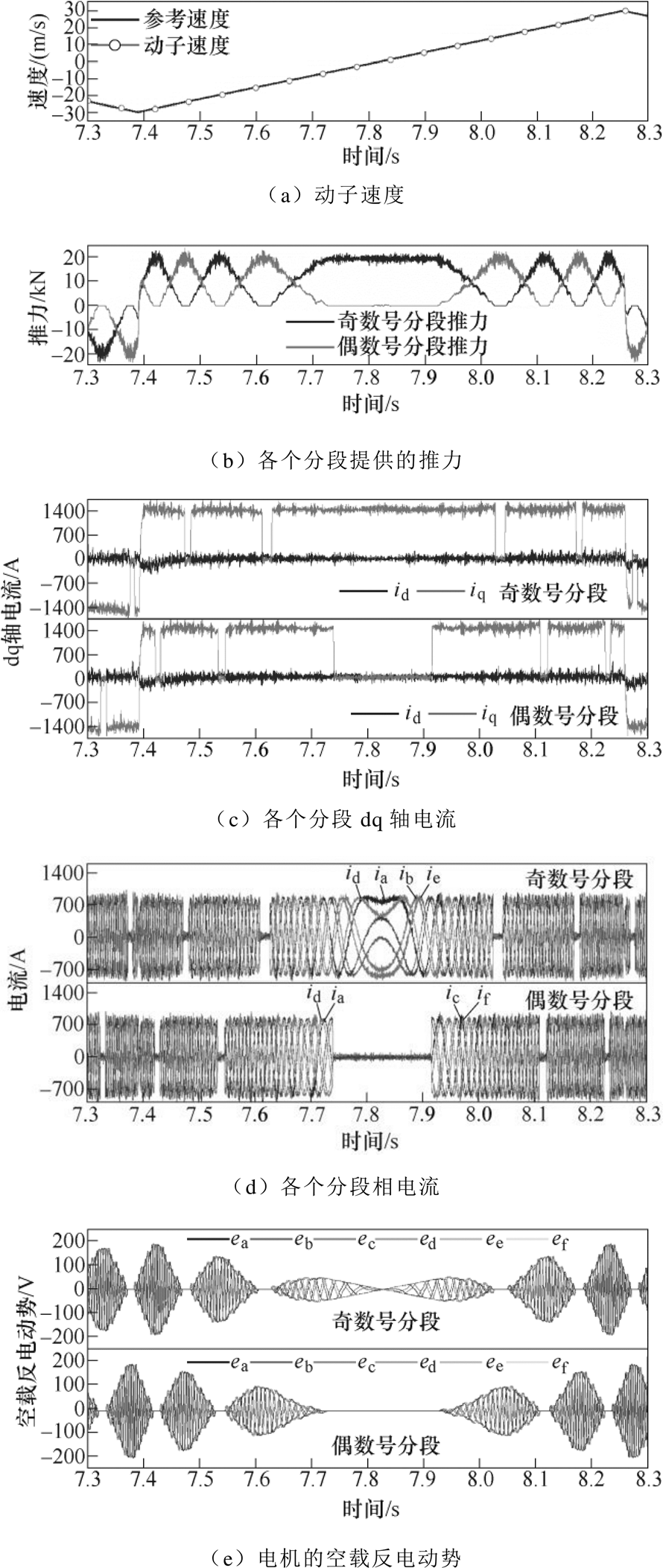
图17 采用数学模型计算得到的电机加速性能
Fig.17 The accelerating proceeding of PMLSM calculated by the math model
以上结果表明，本文建立的相空间模型不仅保证了与有限元模型接近的精度，同时作为集中参数模型，相空间模型的计算成本小于有限元模型，可以方便地搭建在半实物实验平台中，提高控制系统调试和分析的准确性。
本文建立了电机的非线性相空间模型，可以准确地描述多相分段供电PMLSM中由绕组分段引起的电感不平衡、饱和效应和动子通过分段时的暂态过程。主要结论如下：
1）由于通电电枢段两侧存在未通电电枢段的铁心，从而导致气隙磁通密度中含有脉振分量，脉振分量导致相电感存在不平衡现象。
2）在高过载工况下，电机的饱和效应主要由脉振磁场引起，从而使得各相自感和互感同步波动。六相电机的电感矩阵阶数较高，将多相电流从多相坐标系映射到ab 坐标系，通过ia 和ib 查询的二维动态电感查询表，可有效地削减电感查询表构建所需的仿真或实验数量，降低了模型的计算成本。
3）采用Sigmoid函数构造耦合因数，并基于耦合因数和单元磁路永磁体磁链建立的动子，通过分段时的空载磁链及空载反电动势模型，准确地描述电机特性。
4）建立了一个分段下的电机状态方程，对比负载状态下相空间模型和有限元模型的电压与推力，结果表明二者计算结果的一致性为99%以上。
通过实验验证的相空间模型可有效地应用于相应控制系统调试和分析中，相空间模型不仅保证了近于有限元模型的精度，同时作为集中参数模型，其计算成本远小于有限元模型。
参考文献
[1] 张邦富, 程明, 王飒飒, 等. 基于改进型代理模型优化算法的磁通切换永磁直线电机优化设计[J]. 电工技术学报, 2020, 35(5): 1013-1021.
Zhang Bangfu, Cheng Ming, Wang Sasa, et al. Optimal design of flux-switching permanent magnet linear machine based on improved surrogate-based optimization algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1013-1021.
[2] 曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020, 35(5): 1001-1012.
Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001- 1012.
[3] 王明杰, 徐伟, 杨存祥, 等. 基于精确子域模型的永磁直线同步电机空载磁场解析计算[J]. 电工技术学报, 2020, 35(5): 942-953.
Wang Mingjie, Xu Wei, Yang Cunxiang, et al. Analytical calculation of no-load magnetic field in permanent magnet linear synchronous motors based on an accurate subdomain model[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 942- 953.
[4] 许孝卓, 孙震, 汪旭东, 等. Halbach交替极永磁同步直线电机特性分析[J]. 电工技术学报, 2019, 34(9): 1825-1833.
Xu Xiaozhuo, Sun Zhen, Wang Xudong, et al. Characteristic of a novel Halbach array consequent- pole[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1825-1833.
[5] 麦志勤, 肖飞, 刘计龙, 等. 基于准比例谐振级联PI的双三相永磁同步电机谐波电流抑制策略[J]. 电工技术学报, 2018, 33(24): 5751-5759.
Mai Zhiqin, Xiao Fei, Liu Jilong, et al. Harmonic current suppression strategy of dual three-phase permanent magnet synchronous motor based on quasi proportional resonant cascading PI[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5751-5759.
[6] 高闯, 赵文祥, 吉敬华, 等. 低谐波双三相永磁同步电机及其容错控制[J]. 电工技术学报, 2017, 32(增刊1): 124-130.
Gao Chuang, Zhao Wenxiang, Ji Jinghua, et al. Low harmonic dual three-phase permanent magnet synchronous motor and fault-tolerant control[J]. Transactions of China Electrotechnical Society, 2017, 32(S1): 124-130.
[7] 李小庆, 朱景伟, 孙军浩, 等. 双绕组永磁容错电机矢量控制系统研究[J]. 电工技术学报, 2016, 31(5): 26-34.
Li Xiaoqing, Zhu Jingwei, Sun Junhao, et al. Study on the vector control system for dual winding fault- tolerant permanent magnet motors[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 26-34.
[8] 张明元, 马伟明, 何娜. 长初级直线电动机分段供电技术综述[J]. 中国电机工程学报, 2013, 33(27): 96-104, 14.
Zhang Mingyuan, Ma Weiming, He Na. Application of block feeding methods in long primary linear motors[J]. Proceedings of the CSEE, 2013, 33(27): 96-104, 14.
[9] 马名中, 马伟明, 范慧丽, 等. 长初级直线感应电机分段供电切换暂态过程[J]. 电机与控制学报, 2015, 19(9): 1-7.
Ma Mingzhong, Ma Weiming, Fan Huili, et al. Switch transient process of section powered long- primary linear induction motor[J]. Electric Machines and Control, 2015, 19(9): 1-7.
[10] 张明元, 马伟明, 徐兴华, 等. 一种考虑电流过零的直线电机分段供电策略[J]. 海军工程大学学报, 2019, 31(4): 11-16.
Zhang Mingyuan, Ma Weiming, Xu Xinghua, et al. A block feeding strategy for linear motor considering switching at current-crossing point[J]. Journal of Naval University of Engineering, 2019, 31(4): 11-16.
[11] Quéval L, Ohsaki H. Nonlinear abc-model for electrical machines using N-D lookup tables[J]. IEEE Transactions on Energy Conversion, 2015, 30(1): 316-322.
[12] Leonardo L D, Parasiliti F, Tursini M, et al. Transient analysis of PM synchronous motor drives by finite element model co-simulation[C]//IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, 2013: 6834-6840.
[13] Parasiliti F, Villani M, Tassi A. Dynamic analysis of synchronous reluctance motor drives based on simulink® and finite element model[C]//IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, 2006: 1516-1520.
[14] Jabbar M A, Liu Zhejie, Dong Jing. Time-stepping finite-element analysis for the dynamic performance of a permanent magnet synchronous motor[J]. IEEE Transactions on Magnetics, 2003, 39(5): 2621-2623.
[15] Tursini M, Villani M, Tullio A D, et al. Nonlinear model suitable for the offline cosimulation of fault- tolerant PM motors drives[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3719-3729.
[16] Wang L, Jatskevich J, Dommel H W. Re-examination of synchronous machine modeling techniques for electromagnetic transient simulations[J]. IEEE Transa- ctions on Power Systems, 2007, 22(3): 1221-1230.
[17] Fernandez-Bernal F, Garcia-Cerrada A, Faure R. Determination of parameters in interior permanent- magnet synchronous motors with iron losses without torque measurement[J]. IEEE Transactions on Industry Applications, 2001, 37(5): 1265-1272.
[18] Rafaq M S, Mwasilu F, Kim J, et al. Online parameter identification for model-based sensorless control of interior permanent magnet synchronous machine[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4631-4643.
[19] Mohammed O A, Liu S, Liu Z. Physical modeling of PM synchronous motors for integrated coupling with machine drives[J]. IEEE Transactions on Magnetics, 2005, 41(5): 1628-1631.
[20] Fasil M, Mijatovic N, Jensen B B, et al. Nonlinear dynamic model of PMBLDC motor considering core losses[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9282-9290.
[21] 鲁军勇, 马伟明, 孙兆龙, 等. 多段初级直线感应电机静态纵向边端效应研究[J]. 中国电机工程学报, 2009, 29(33): 95-101.
Lu Junyong, Ma Weiming, Sun Zhaolong, et al. Research on static longitudinal end effect of linear induction motor with multi-segment primary[J]. Proceedings of the CSEE, 2009, 29(33): 95-101.
[22] 聂世雄, 付立军, 许金, 等. 分段供电直线感应电机动子不对称模型及参数计算[J]. 电机与控制学报, 2017, 21(2): 10-17.
Nie Shixiong, Fu Lijun, Xu Jin, et al. Asymmetrical model and parameter calculation of segment-powered linear inductive motor mover[J]. Electric Machines and Control, 2017, 21(2): 10-17.
[23] 许金, 马伟明, 鲁军勇, 等. 分段供电直线感应电机气隙磁场分布和互感不对称分析[J]. 中国电机工程学报, 2011, 31(15): 61-68.
Xu Jin, Ma Weiming, Lu Junyong, et al. Analysis of air-gap magnetic field distribution and mutual inductance asymmetry of sectionally powered linear induction motor[J]. Proceedings of the CSEE, 2011, 31(15): 61-68.
[24] 牟树君, 柴建云, 孙旭东, 等. 分段供电交流直线电机三相互感不对称分析及抑制[J]. 电工技术学报, 2015, 30(1): 81-88.
Mu Shujun, Chai Jianyun, Sun Xudong, et al. Analysis and restrain of mutual inductance asymmetry in the sectionally powered AC linear motor[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 81-88.
[25] 牟树君, 柴建云, 孙旭东, 等. 分段供电交流直线电机中偏置磁通密度的分析及其消除方法[J]. 电工技术学报, 2014, 29(3): 12-20.
Mu Shujun, Chai Jianyun, Sun Xudong, et al. Analysis and elimination of the off-set flux density in the sectionally powered AC linear motors[J]. Transa- ctions of China Electrotechnical Society, 2014, 29(3): 12-20.
[26] 牟树君, 柴建云, 孙旭东, 等. 长初级分段供电变极距直线感应电机的气隙磁场分布及电感参数特性[J]. 清华大学学报: 自然科学版, 2014, 54(9): 1161-1165, 1172.
Mu Shujun, Chai Jianyun, Sun Xudong, et al. Air-gap magnetic field distribution and inductance chara- cteristic in long primary sectional powered variable pole pitch linear induction motor[J]. Journal of Tsinghua University: Science and Technology, 2014, 54(9): 1161-1165, 1172.
[27] 孙兆龙, 马伟明, 鲁军勇, 等. 长初级双边直线感应电动机静态纵向边端效应及阻抗矩阵研究[J]. 中国电机工程学报, 2010, 30(18): 72-77.
Sun Zhaolong, Ma Weiming, Lu Junyong, et al. Research of static longitudinal end effect and impedance matrix for long primary double-sided linear induction motors[J]. Proceedings of the CSEE，2010, 30(18): 72-77.
[28] 上官璇峰, 励庆孚, 袁世鹰. 多段初级永磁直线同步电动机驱动系统整体建模和仿真[J]. 电工技术学报, 2006, 21(3): 52-57.
Shangguan Xuanfeng, Li Qingfu, Yuan Shiying. Integrated modeling and simulation of the systems driven by multi-segment primary permanent linear synchronous motors[J]. Transactions of China Elec- trotechnical Society, 2006, 21(3): 52-57.
[29] 上官璇峰, 励庆孚, 袁世鹰. 多段初级永磁直线同步电机驱动的垂直提升系统[J]. 中国电机工程学报, 2007, 27(18): 7-12.
Shangguan Xuanfeng, Li Qingfu, Yuan Shiying. The vertical hoist system driven by OMLSM with multi- segment primary[J]. Proceedings of the CSEE, 2007, 27(18): 7-12.
[30] 刘凯, 张炳义, 冯桂宏. 基于非对称绕组函数法永磁同步电机偏心电感参数的研究[J]. 电工技术学报, 2020, 35(增刊2): 387-394.
Liu Kai, Zhang Bingyi, Feng Guihong. Research on eccentric inductance of permanent magnet machine based on asymmetrical winding function approach[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 387-394.
Non-Linear Mathematic Model of a Segmented Powered Permanent Magnet Linear Synchronous Machine
Abstract Due to the segmented arrangement of windings in long primary dual-three phase permanent magnet linear synchronous machine (PMLSM), the adjacent segments will cause the off-set pulsating magnetic field, and the mover passing through the powered segment will also cause complex transient processes. In this paper, in order to describe the dynamic characteristics of the PMLSM precisely, a phase-domain mathematic model is established and the two fore-mentioned special effects are considered. The causes of off-set pulsation in the air-gap flux distribution are analyzed by the analytical method, and the unbalanced inductance and saturation effects caused by the off-set flux distribution are studied. A 2-D inductance look-up table in ab coordinate system is established to reduce the computation consumption of the model. Then, the easy-to-derivative Sigmoid function is introduced to describe the no load flux linkage and back electromagnetic force. Finally, the mathematic model is established, the voltage and thrust are calculated by the model and verified by the finite element method. Finally, an experiment platform based on the RT-Lab is built. The results show that the model can reflect the various effects of the motor and can replace the finite element model with a large computational cost.
keywords：Permanent magnet linear synchronous machine, segmented powered, saturation effect of magnetic field, phase-domain model
中图分类号：TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.201078
国家重点研发计划高速磁浮交通系统关键技术研究课题资助项目（2016YFB1200602-20）。
收稿日期 2020-08-30
改稿日期 2020-12-01
郭科宇 男，1993年生，博士研究生，研究方向为永磁直线同步电机设计及控制。E-mail: guoky93@mail.iee.ac.cn
史黎明 男，1964年生，研究员，研究方向为直线电机设计及其控制、无线电能传输技术。E-mail: limings@mail.iee.ac.cn（通信作者）
（编辑 陈 诚）