0 引言
随着直线电机的广泛应用，传统旋转电机与丝杠结合的传动结构在很多工业领域都逐渐被直线电机所取代，尤其在半导体制造、高精元件加工以及电路板贴片等领域都采用多轴直线电机协同工作系统，该系统提高了响应速度，保证了加工精度[1-3]。
双轴直线电机系统主要应用于平面轮廓加工领域，可完成二维的平面运动。然而在电机运行过程中，由于负载扰动、双轴机械结构的振动及双电机响应速度不匹配等因素都会影响最终的运行结果。
为更好地执行平面轮廓跟踪任务，基于轮廓误差的交叉耦合控制方法得到了广泛研究。当给定的参考轨迹存在尖角轮廓等曲率变化较大的点时，会严重影响轨迹的跟踪精度，并带来较大的机械结构振动，影响工作性能[4-5]。为进一步提高跟踪精度，文献[6]提出利用轮廓误差作为传递函数的鲁棒补偿器变增益控制方法，利用曲线的正切估计近似为参考轮廓进行插补运算，从而提高精度，但并没有对曲线不可导点等特殊位置进行考虑，难以适应广泛类型的参考轨迹。文献[7-8]提出滑模互补控制结构，并利用模糊控制方法，来提高系统响应速度，增强系统鲁棒性；同时设计双直线电机交叉耦合控制器，并利用神经网络等智能算法优化控制输出，从而减小各轴间的位置误差，保证双直线电机运行的精度，但该控制策略整体计算量较大，不利于协同控制时的速度响应匹配。文献[9-10]则提出了前瞻速度规划算法，针对运动路径进行数学解析，从而进行速度规划，避免了速度突变带来的机械冲击，减小了系统的振荡。
为提高双轴直线电机对于参考轨迹的跟踪能力，主要解决三个问题：①建立交叉耦合控制模型，该模型可以适应广泛曲线类型，并尽量减小在线计算量；②在实现单轴直线电机的跟随性能最优的同时，应匹配双轴响应速度，尽量同步双电机协同完成控制器指令的时间；③优化运行速度，在尖角折线点，高曲率点等特殊位置进行速度平滑处理，并增加插补点。基于以上考虑，本文以垂直布局的十字形双轴结构直线电机为研究对象，提出了一种基于速度前瞻型双轴直线电机交叉耦合控制策略，十字形双轴结构直线电机示意图如图1所示。首先设计能够适应多种路径类型的改进自适应插补算法交叉耦合控制器，并采用具有双环滑模控制（Sliding Mode Control, SMC）结构的单轴控制器来执行交叉耦合控制器传送的目标指令。通过速度前瞻算法，提前对参考轨迹进行五段式S型速度规划，在折线点和曲率变化较大点进行速度平滑处理，柔滑了系统运行过程，减小频繁速度突变冲击带来的系统振动。实验结果表明，所提出的控制方案有效可行，提高了系统的跟踪性能和鲁棒性能，明显减小了系统的轮廓误差。
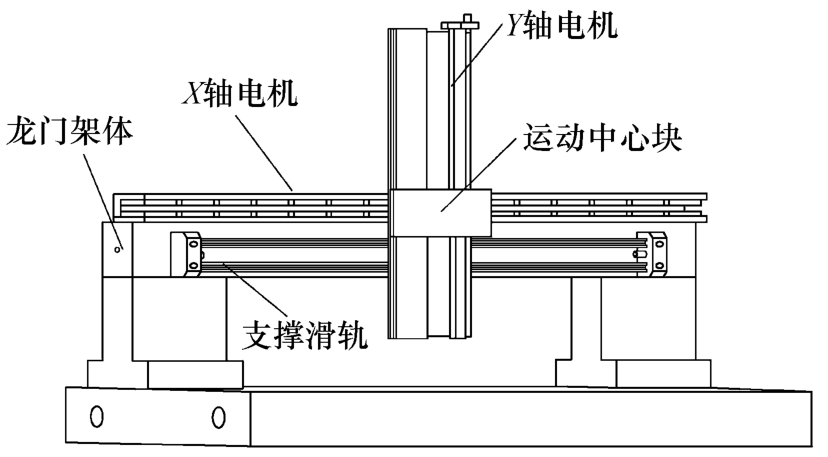
图1 十字形双轴结构直线电机示意图
Fig.1 Cross-shaped dual-axis structure line motor
1 直线电机工作平台数学模型
本文所使用的实验验证平台采用的是双边磁极无铁心永磁同步直线电机，双边直线电机基本结构如图2所示。
图2 双边直线电机基本结构
Fig.2 Basic structure of bilateral linear motor
根据永磁同步电机运行特点，需要理想化其电磁特性[11-15]：①忽略其非线性状态，设其状态是线性的；②电机的动子与定子之间的二次侧与一次侧的气隙磁场呈现均匀分布；③一次线圈均匀分布，无热效应。
得到永磁同步直线电机推力方程为
式中，Fem为电机推力；pn为电机极对数；Ld、Lq分别为直轴和交轴电感量；ψmf为永磁体磁链；τ为电机极距；id、iq分别为电机d轴和q轴电流。
直线电机的运动方程为
从式（1）、式（2）可以得到
式中，m为动子质量；v为直线电机运行速度；B为黏滞摩擦因数；f为系统扰动；
根据式（3）可以将电机的运动方程改写为
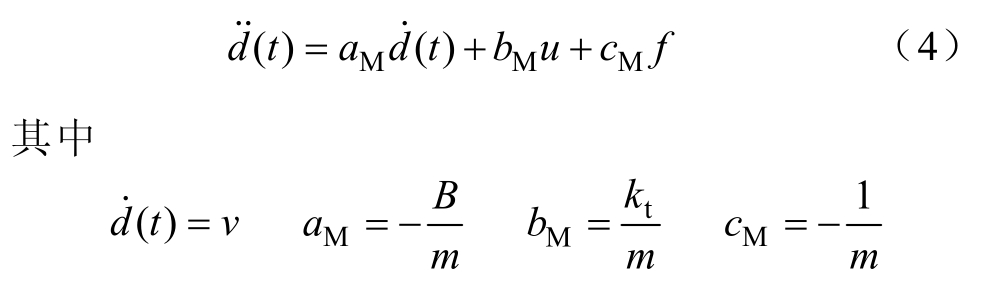
在电机运行系统中，考虑到由于机械冲击、电流谐波、不确定外部扰动等因素，会给整体系统带来参数扰动，所以电机运行方程[16-21]表示为
2 基于自适应插补的交叉耦合控制器
在双轴系统工作过程中，由于非线性摩擦、参数摄动、传感器精度等原因，必然会造成单轴跟踪误差，从而导致出现轮廓误差。轮廓误差示意图如图3所示，将理想轨迹与实际跟踪轨迹放大，可以较为明显地看到系统运动过程中的绝对位置误差与轮廓误差。将当前实际位置设为点P，理想位置点为P′，绝对位置的跟踪误差为e，此时对应的轮廓误差为ε。为完成轮廓跟踪任务，单纯的追求跟踪误差的e精度并不能完全提高运行精度，需要结合轮廓误差ε共同调节系统运动位置。
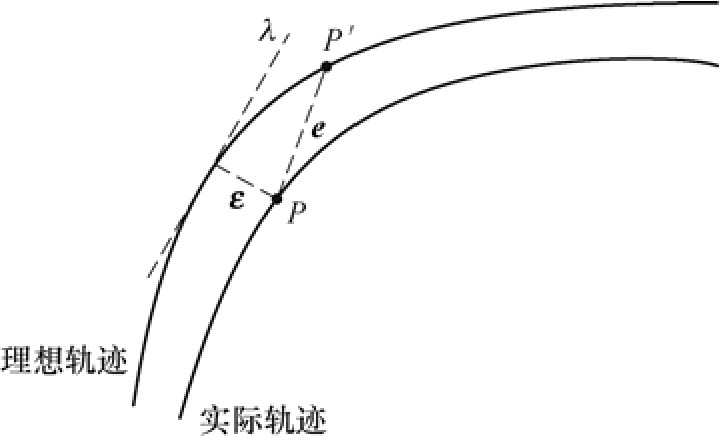
图3 轮廓误差示意图
Fig.3 Contour error diagram
然而在实际运行过程中，面临各种曲线情况，针对特殊拐点、尖峰点，现在已经存在多种插补计算的方法。在尽可能减少在线计算量的前提下，并同时能够满足对于更多种曲线计算的需求，本文提出一种自适应插补交叉解耦控制器。首先建立近似轮廓误差模型如图4所示，图4中，取轮廓轨迹上一段路径（见图4中矩形框部分），为减小处理负荷，将相邻极近的几个位置点可近似为圆弧上的点，以该段路径为例，假设在控制运动过程中，实际位置到达点为 P k ( x k , y k )，对应时刻期望点为
向前回溯的两个时刻的期望点分别是
因此当前位置与时刻期望点之间的跟踪误差向量表示为
首先判断该三点不共线，即
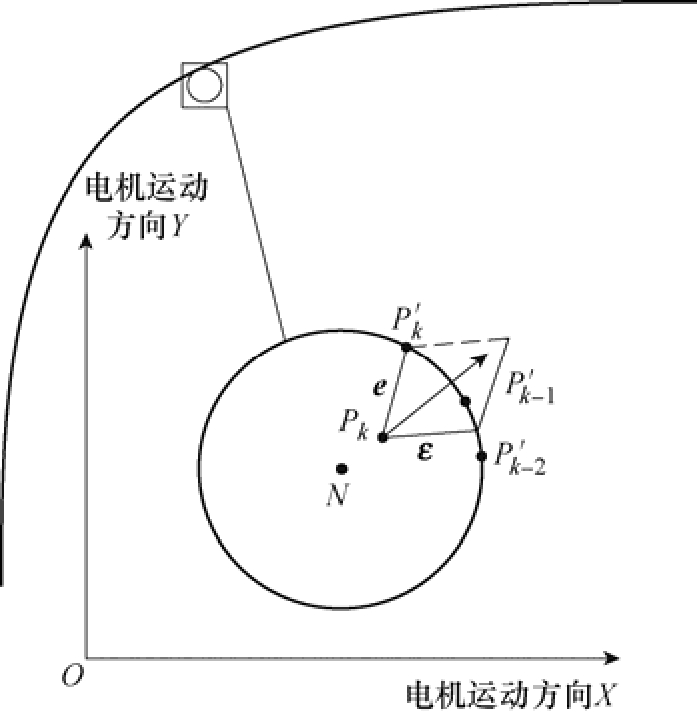
图4 近似轮廓误差模型
Fig.4 Approximate contour error model
如果三点共线，则无需进行自适应插补，不需要进行交叉耦合计算。通过式（7）判断符合三点不共线条件，则进入交叉耦合计算环节。轮廓误差的标准定义为当前位置点到达对应弧线的最短距离，然而对于给定曲线，如果在线对整体曲线进行曲率计算、切线求取、最短距离判断等操作，会对工控系统造成较为巨大的计算量，不利于系统实时性和工作效率的提高。因而本文中只利用实时更新的三个点，在保证一定精度的前提下，尽可能减少计算量。分别是对应当前时刻期望点
向前回溯两时刻期望点
与
并由这相邻极近的三点构成三点圆弧，由图4所示可以近似认为部分圆弧与理想给定轨迹重合。
设由这三点构成的圆为
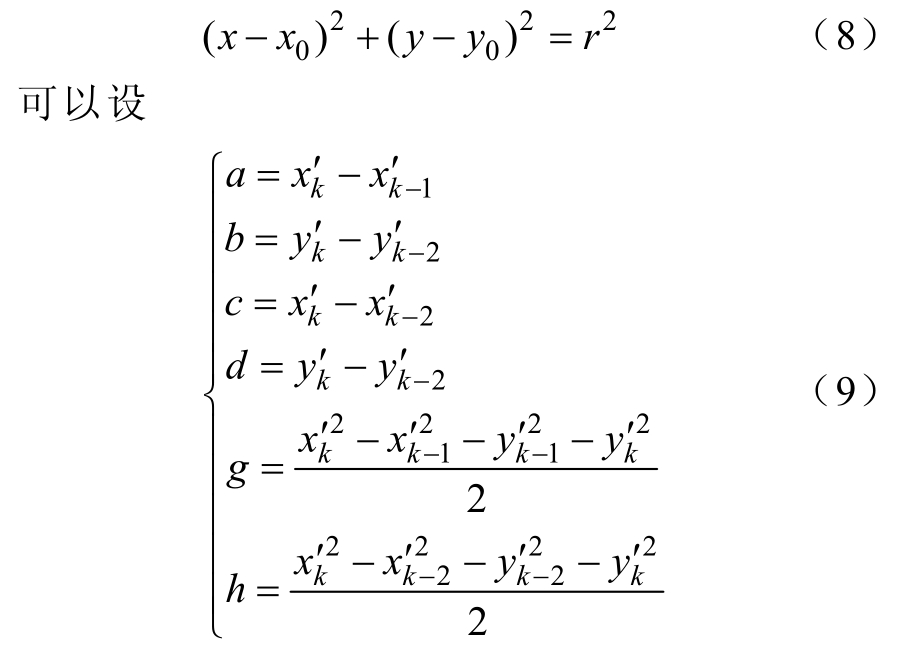
则由这三点可以构成的圆弧圆心为
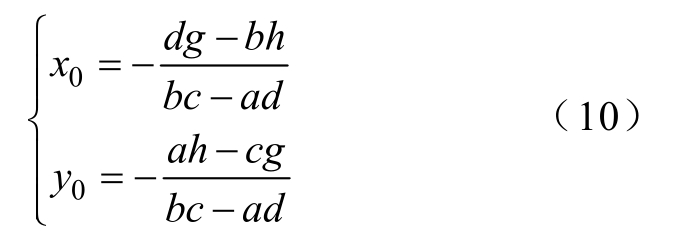
可以将实际位置点 P k ( x k , y k )到达该三点圆弧的最短距离近似为轮廓误差ε。
圆弧上的点以及实际位置点分别到达圆上的点的距离满足
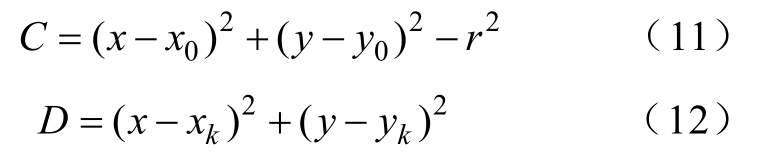
为求得 P k ( x k , y k )到达圆弧最短距离，可以设定函数为
式中，u为可调权重因子。
并分别求偏导得
求出偏导解析解，最短距离可以表示为
如图4所示，在综合考虑跟踪误差向量与轮廓误差向量后，实际的耦合误差插补向量可以设定为
式中，λ1、λ2为经过算法计算出的步长参数。
自适应插补示意图如图5所示。首先过
与
做割线l，根据λ的值不同，所给出的增补插补点可能出现位于l上部或者l下部两种情况，分别近似于增补插补点位于理想轨迹外部（见图5点δP′）与理想轨迹内部（见图5点δP′）两种情况。为了更好地满足加工需求，要求轮廓误差尽可能的小。因而需要对参数1λ、2λ进行有效地设计，尽量使得增补插补点位于理想轨迹之上（见图5点δP′）。
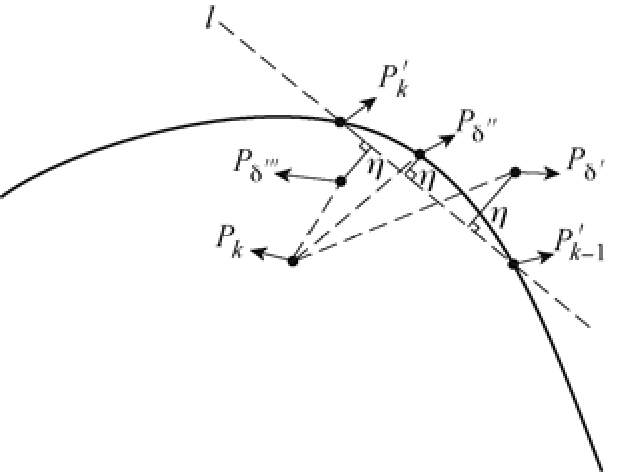
图5 自适应插补示意图
Fig.5 Schematic diagram of adaptive interpolation
基于上述目的，本文提出一种自适应可调节插补结构，在系统运行过程中，动态改变1λ、2λ的大小，起到调节插补向量δ的目的。其自适应结构为
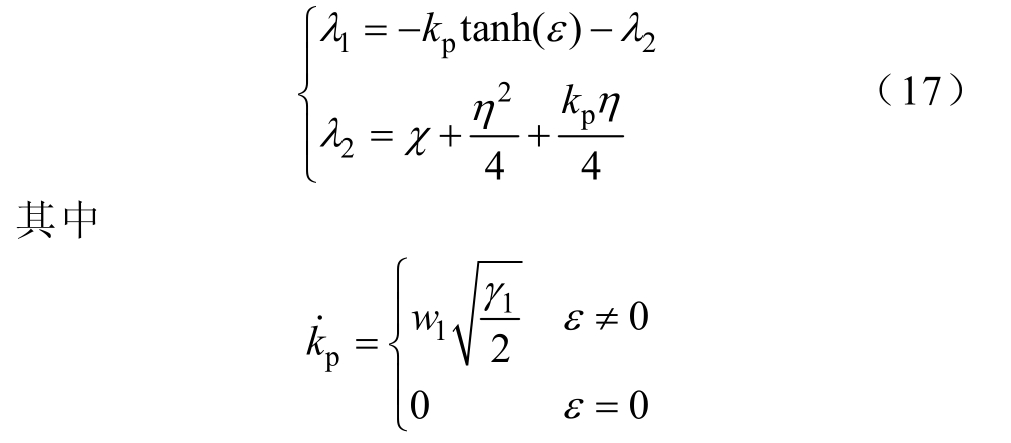
式中，χ、w1和1γ均为常值参数；
η为插补位置点 P (x δ,yδ )到割线l的垂直距离。结合式（17），自适应参数综合考虑轮廓误差ε和插补位置点 P (x δ,yδ )到割线l的垂直距离η，在系统运行过程中动态调节控制器输出，通过对其自适应结构分析，可以发现，参数λ1、λ2互为制衡变量，通过两个误差值ε和η构成了负反馈系统，在有效提高控制精度的同时避免了参数不收敛，造成控制超调的出现。同时参照式（16）最终的插补结果δ也是建立在单轴位置误差与轮廓误差二者综合的基础上，避免由于单方面误差跳跃过大带来的“过校”操作，增强了系统稳定性。
3 单轴直线电机双环控制
为了更好地实现单轴直线电机平台的轨迹运动控制，高效地执行来自交叉耦合控制器的指令信号，本文设计了基于双环滑模控制的单轴直线电机控制系统如图6所示。
图6 基于双环滑模控制的单轴直线电机控制系统
Fig.6 Single-axis linear motor control system based on double-loop sliding mode control
3.1 电流控制器
为了更好地适应控制过程中电流信号的快速变化，本文设计了基于Super-twisting二阶滑模控制算法的电流控制器，将滑模控制中不连续的控制作用施加在二阶控制量上，并进行积分输出，从而较大程度地削弱抖振作用[22]。依据式（1）和式（2）可以得到
一般地，非线性受控系统的二阶导可表示为
式中，
根据式（18）可以得到，
B、M、τ、Fl、ψf均为有界量，根据有限时间收敛的充分必要条件，存在 |A |≤AM ，B m ≤ B ≤ B M 。其中，AM为有界量 A的最大有界值，Bm、BM分别为有界量B的最小和最大有界值。
选取电流滑模面的函数为
因而基于 Super-twisting算法的二阶滑模电流控制器可以设计为
式中，r为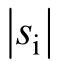
的指数次幂；ki、kq为待速写的控制正增益； t anh(si)为双曲正切函数。
根据式（21）可得，Super-twisting二阶滑模电流控制器如图7所示。
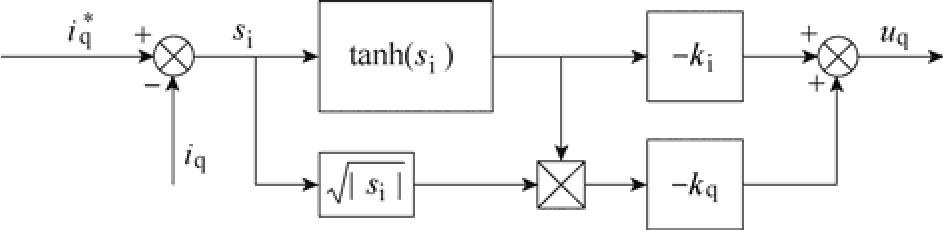
图7 Super-twisting二阶滑模电流控制器
Fig.7 Super-twisting second-order sliding mode current controller
3.2 位置控制器
为实现控制单轴直线电机平台能够准确跟踪交叉耦合控制器输出的轮廓误差指令，本文设计了基于指数趋近律的一阶滑模位置控制器，准确地跟踪轮廓误差的同时还可以通过调节所设计的趋近律参数减弱高频抖振，提高运行控制过程的动态品质。因此由式（2）可得
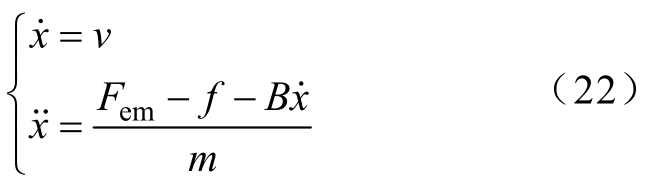
设计选取位置滑模面函数为
式中，cx为常数量；ex为单轴直线电机的位置误差，
为给定的跟踪位置信号，x为位置反馈；
基于指数趋近律，可以得到
式中，sgn(⋅)为符号函数。
结合上述式（22）～式（24），可以得到
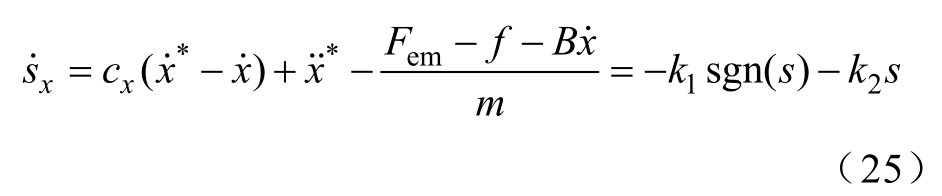
因此，结合式（1）、式（25），采用指数趋近律的一阶滑模位置控制器可以设计为
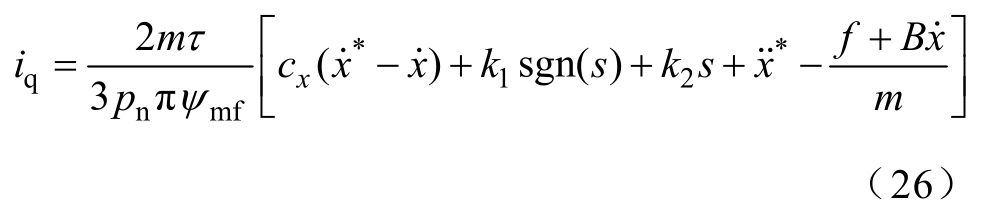
根据式（26）设计的一阶滑模位置控制器如图8所示。
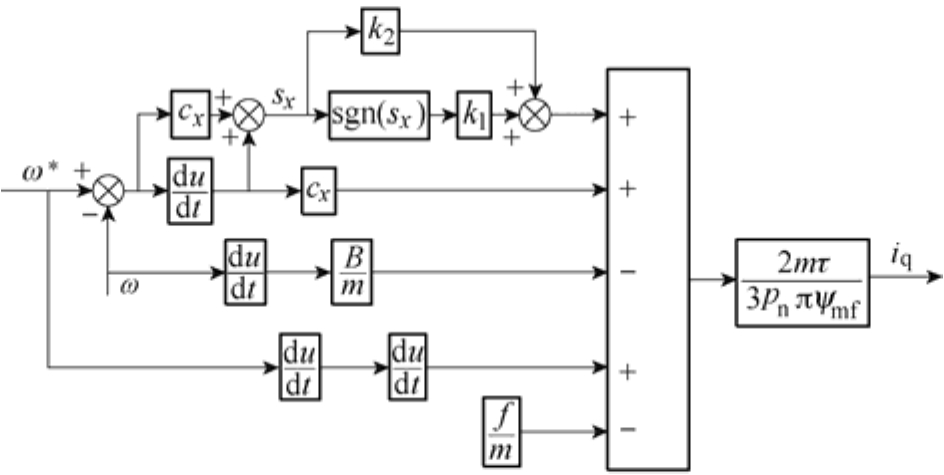
图8 一阶滑模位置控制器
Fig.8 First-order sliding mode position controller
4 基于速度前瞻的S型速度规划
考虑到系统运行过程中，电机的起动与加速，包括每次速度的变化，都会引起机械结构的振动，这样的振动必然影响到整体的运行精度，传统缺乏灵活性的速度设计无法对抗这种由于速度突变带来的系统扰动。为了更好地实现较为平稳的运行，需要对整体运行过程的速度进行规划。
在系统起动运行前，对于给定的参考轨迹，首先进行离散处理，并采用非均匀有理B样条进行插补，从而避免了不可导点的出现，获得较为柔性的运动路径。
一条k次NURBS曲线的有理分式可以表示为
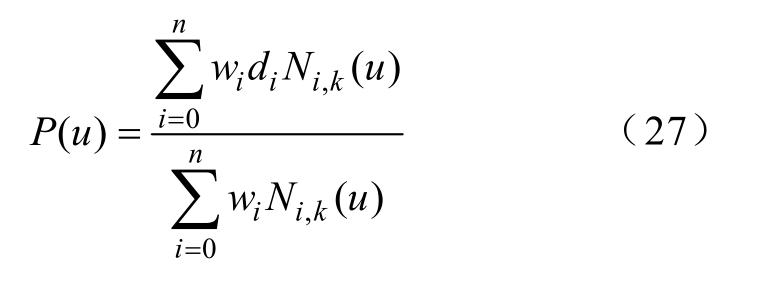
式中，P(u)为以参数u为自变量的曲线上的点；di (i = 0 ,1,… ,n )为控制点序列； w i(i = 0 ,1,… ,n )为权因子序列，权因子序列与控制点序列相互对应；N i, k(u)为k次规范B样条基函数。
利用德布尔算法（De Boor algorithm）进行曲率检测，可以将式（27）表示为
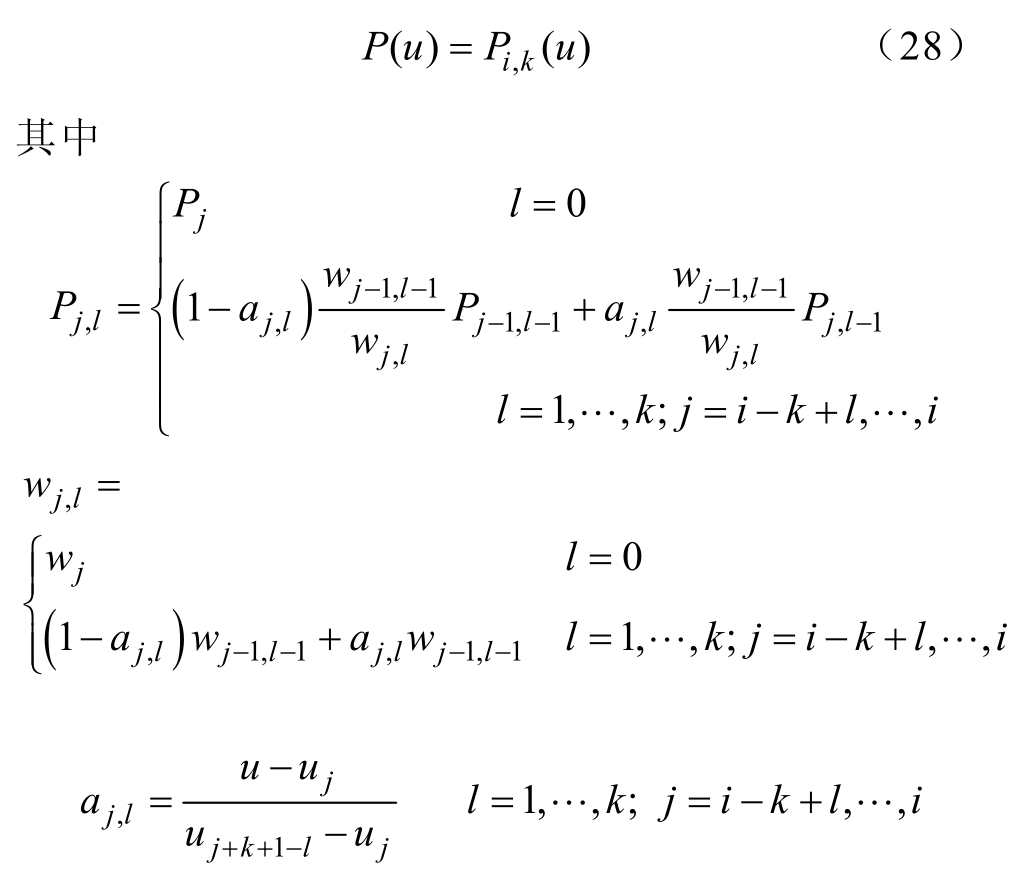
通过对NURBS曲线利用De Boor algorithm算法求导得
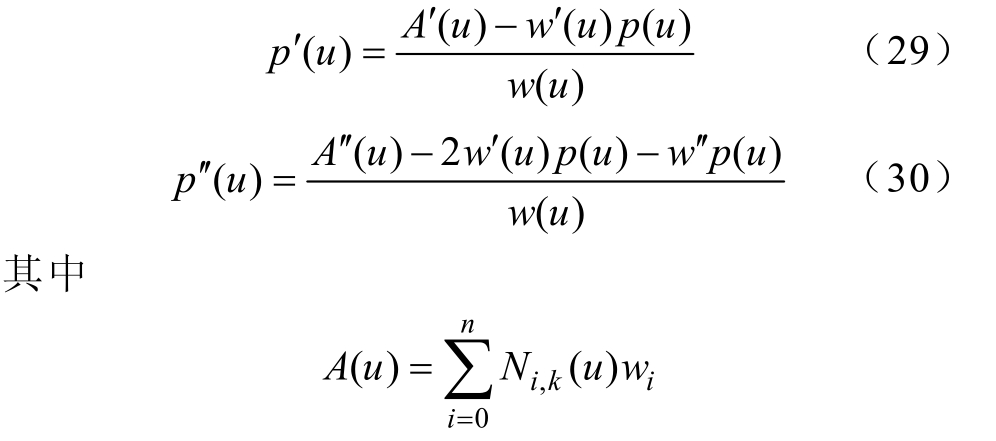
曲率检测示意图如图9所示，对于给定参考轨迹，可以求出其曲线斜率变化以及曲率变化率的关系。这样便可以提前定位曲率变化较大的位置，作为特别前瞻点，进行速度规划。
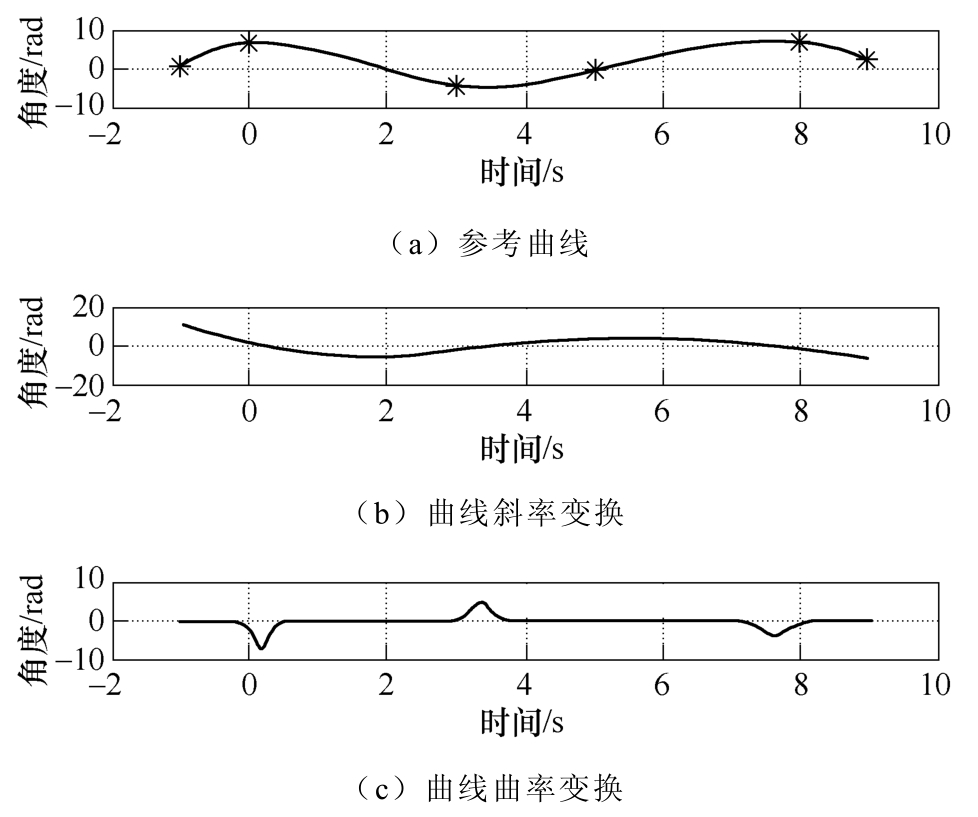
图9 曲率检测示意图
Fig.9 Curvature detection diagram
5段式S型速度规划示意图如图10所示，计算过程如式（31）和式（32）所示。该算法可以在尽量减小速度剧烈波动的情况下，柔和速度变化过程。
式中，J为加速度的导数。
图10 5段式S型速度规划示意图
Fig.10 5-stage S-type speed planning
5 系统实验分析
为进一步验证算法的可靠性，并通过实际的实验来完善控制系统，提高双轴直线电机运行性能，采用实验样机进行算法验证，十字形直线电机实验装置如图 11所示。该实验装置由精密直线电机平台、ACJ-005-09型Copley伺服驱动器、Galil DMC控制卡、VILT-0400光栅传感器和上位机组成。永磁同步直线电机主要参数见表 1，其中两台电机类型均为双边磁极无铁心永磁同步直线电机。
图11 十字形直线电机实验装置
Fig.11 Cross-shaped linear motor experimental device diagram
表1 永磁同步直线电机主要参数
Tab.1 Main parameters of permanent magnet synchronous linear motor
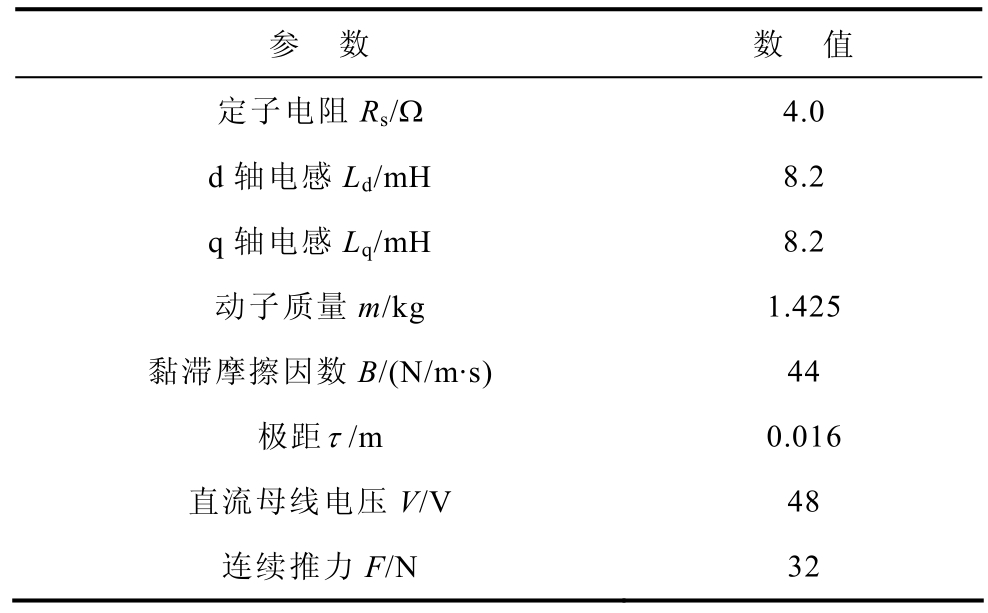
参 数 数 值定子电阻 Rs/Ω 4.0 d轴电感Ld/mH 8.2 q轴电感Lq/mH 8.2动子质量m/kg 1.425黏滞摩擦因数B/(N/m·s) 44极距τ /m 0.016直流母线电压V/V 48连续推力F/N 32
图12 系统工作流程
Fig.12 System work flow chart
系统工作流程如图12所示。系统正式运行前，需要进行初始化操作，主要包括永磁式电机磁极对准和双轴电机机械原点归零以及清空内部计算缓存。状态监测模块主要负责过电压、过电流和温度监测，当出现监测量异常时，系统将进行紧急制动，并掉电保护。初始工作完成后，进入任务执行模块，首先进行曲线预处理，包括生成 NURBS曲线，并进行速度规划，将规划好的速度存入缓存，配合速度时基模块，在运行过程中时刻调整速度。预处理完成后，双轴系统在交叉耦合控制器的控制下，执行运动任务。前瞻型速度规划与交叉耦合控制构成了主控制算法体系，位置反馈信号由光栅传感器获取。
本文以伯努利双钮线为跟踪对象，进行轮廓跟踪任务，通过对轮廓进行预处理，然后由交叉耦合控制实现高精度跟踪任务，伯努利双钮线如图 13所示。
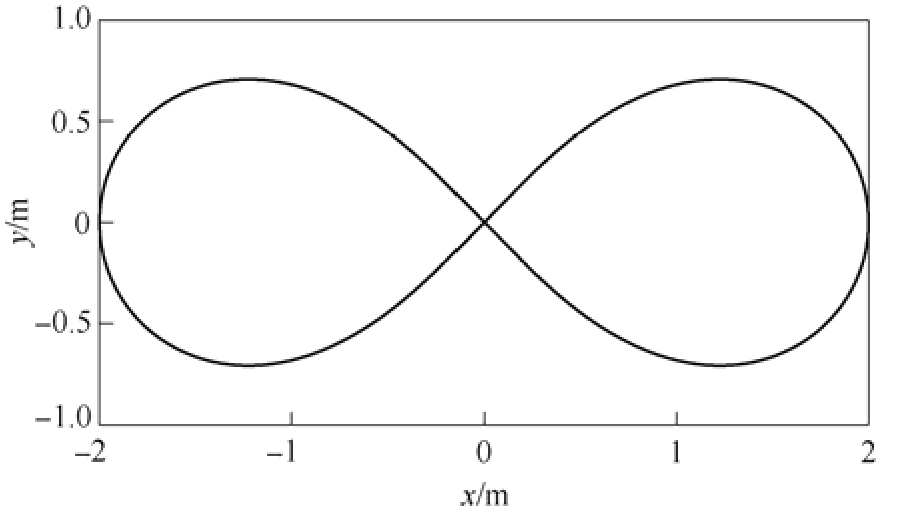
图13 伯努利双钮线
Fig.13 Bernoulli double button curve
首先对于给定的路径进行前瞻处理，并检测其曲率变化，从而在曲率变化较大的地方进行S型速度规划，柔滑整体的运行过程。
由于伯努利双钮线关于x轴对称，因而只需处理x轴上半部分，然后做对称处理，便能完成对于整体轮廓的预处理任务。半伯努利双纽线如图 14所示，曲率变化如图 15所示，可以得知，在 200点左右，曲率开始发生波动，于200点处曲率变化最大。按照曲率变化越大，对应速度越小的原则，利用5段式S型速度规划算法，其速度规划过程如图16所示。在100点前，速度柔滑上升，在100点后，为保证加工精度，并减小机械冲击，在100点后提前减速，保证在200点（曲率变化较大处）左右具有较小速度，避免在大曲率处出现较大误差。对应图 15、图16上的点依上述分析，都满足在曲率较大处，能够低速运行，整体速度平滑变化的要求。
图14 半伯努利双钮线
Fig.14 Half Bernoulli double button curve
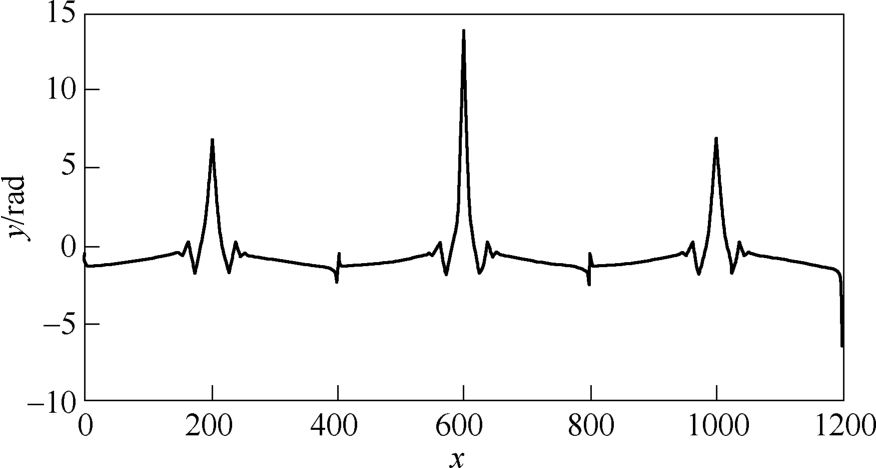
图15 曲率变化过程
Fig.15 Curvature change
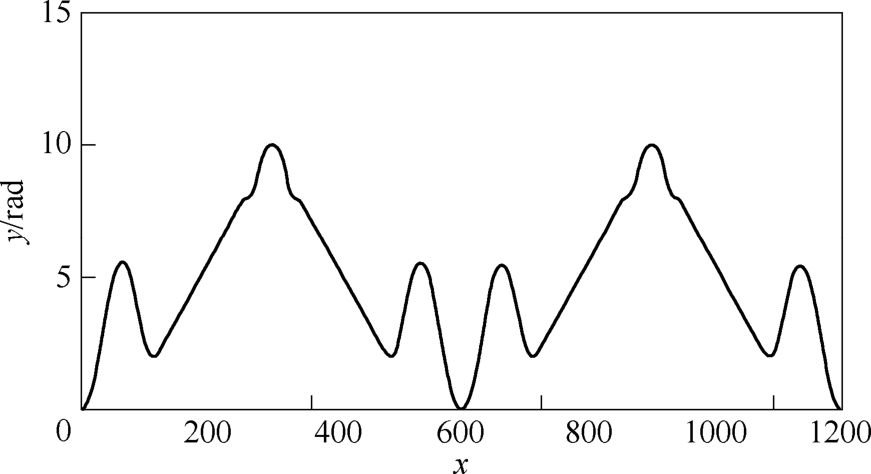
图16 速度规划过程
Fig.16 Speed planning diagram
图17 PID单轴控制器误差
Fig.17 PID single axis controller
仅从执行给定命令的角度看，通过比较不同单轴位置控制器，PID单轴控制器误差如图17所示，滑模控制器单轴控制器误差如图18所示。在起动瞬间，受起动电流和机械惯性影响，位置控制器均出现了较大的误差，在调节过程中，具有双环滑模控制结构的SMC控制器具有较快的响应速度，系统迅速调节，最后将单轴误差稳定在 15μm左右。相比来看，PID控制需要较长的调节时间，在2s左右，位置误差才趋于稳定，最终稳定在20～40μm。
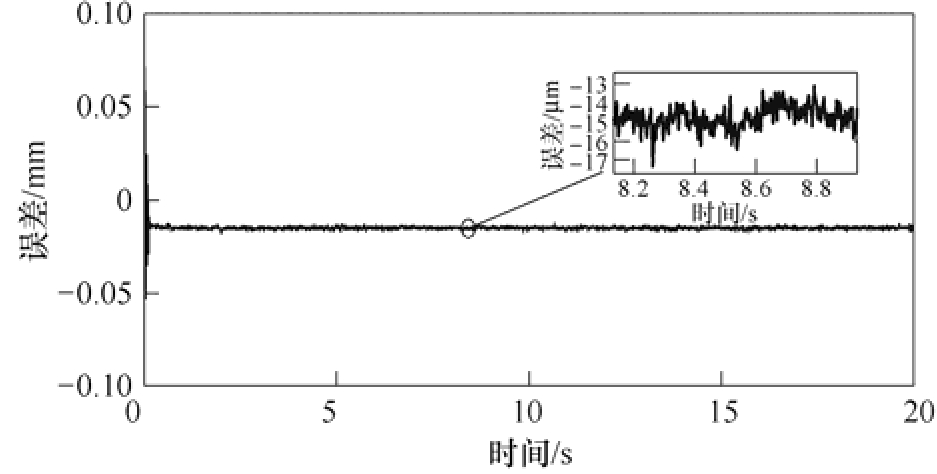
图18 SMC单轴控制器误差
Fig.18 SMC single axis controller
无耦合控制PID结构下轮廓误差如图19所示，在没有耦合控制下，通过对比图17和图19，可以发现，其单轴误差曲线与轮廓误差曲线具有一致性趋势，侧面说明了在无耦合控制下，双轴系统的轮廓误差大小完全取决于单轴控制器精度，仅提高单轴精度会带来硬件成本增加和提高系统复杂度，无法彻底解决轮廓误差问题，在无耦合控制器PID单轴控制结构下，轮廓误差稳定在60μm左右；在加入耦合控制器后，耦合控制PID结构下轮廓误差如图20所示。在没有进一步提高单轴控制器精度的条件下，依靠耦合控制结构使总体轮廓误差稳定时间提前，并且利用生成的自适应插补点，使其轮廓误差明显减小，最终稳定在20～25μm。
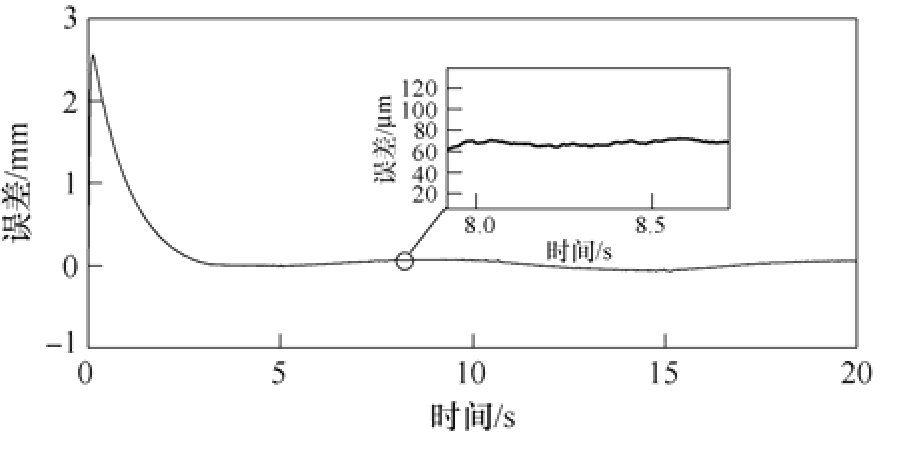
图19 无耦合控制PID结构下轮廓误差
Fig.19 Contour error under PID control without coupling
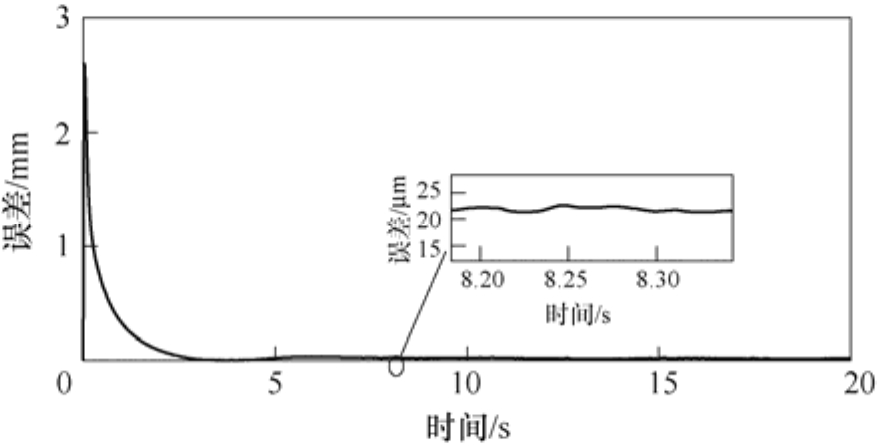
图20 耦合控制PID结构下轮廓误差
Fig.20 Contour error under coupled control PID structure
通过以上分析，说明设计的耦合控制器在减小轮廓误差方面具有较大潜力。为进一步改善控制结构，提高运行性能，本文提出了一种具有双滑模控制机制的双轴直线电机交叉耦合控制策略。双环滑模结构控制效果更优于 PID结构。图 18中，在没有耦合控制器的调控下，单轴控制精度已达到15μm，并且从误差收敛曲线来看，收敛平稳，无较大波动，体现了其较好的控制稳定性。无耦合控制SMC结构下轮廓误差如图21所示。在无耦合控制下，其轮廓误差稳定在 50μm以下，远高于单轴控制精度，因而再次体现了交叉耦合控制器存在的必要性。耦合控制SMC结构下轮廓误差如图22所示，在耦合控制的共同配合下，系统在经历起动时刻的波动后，迅速稳定，并将轮廓误差抑制在20μm以下。对比图20与图22可以明显发现，5s前双滑模耦合的控制结构收敛性优于传统PID耦合结构，体现出滑模快开关特性的优势。以上实验通过较高的轮廓误差控制精度和较快的响应速度，验证了基于速度前瞻型双轴直线电机交叉耦合控制策略的实用性。
图21 无耦合控制SMC结构下轮廓误差
Fig.21 Uncoupled control of contour error under SMC structure
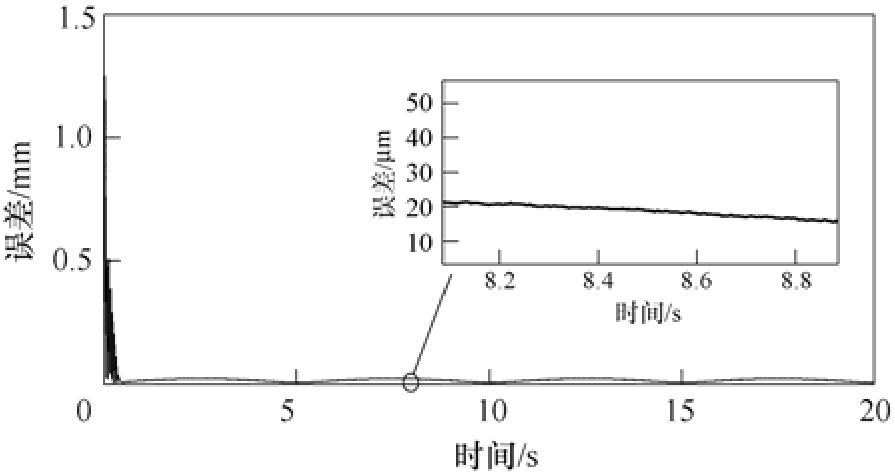
图22 耦合控制SMC结构下轮廓误差
Fig.22 Coupling control SMC structure contour error
6 结论
本文提出一种基于速度前瞻型双轴直线电机交叉耦合控制策略，并证明了该算法的有效性。通过理论推导与实验验证，体现了自适应插补交叉耦合控制器在减小轮廓误差方面的重要意义，同时利用双环滑模结构自有的收敛快、鲁棒性好的特点，为直线电机提供了高效控制策略，并为滑模变结构算法在直线电机上的应用提供了新的思路。
[1]凌志健, 赵文祥, 吉敬华. 高推力永磁直线作动器及其关键技术综述[J]. 电工技术学报, 2020, 35(5):1022-1035.Ling Zhijian, Zhao Wenxiang, Ji Jinghua. Summary of high thrust permanent magnet linear actuator and its key technologies[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1022-1035.
[2]原浩, 赵希梅. 基于动态轮廓误差估计的双轴直驱平台精密轮廓控制[J]. 电工技术学报, 2019, 34(21):4475-4480.Yuan Hao, Zhao Ximei. Precision contouring control based on dynamic contouring error estimation for dual axis direct drive platform[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4475-4480.
[3]Wan Ze, Hu Chuxiong, Yu Zhu, et al. Newwton-ILC contouring error estimation and coordinated motion control for precision multi-axis systems with comparative experiments[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1470-1480.
[4]王丽梅, 张宗雪. H型精密运动平台交叉耦合模糊PID同步控制[J]. 沈阳工业大学学报, 2018, 40(1):1-5.Wang Limei, Zhang Zongxue. Cross-coupled fuzzy PID synchronous control for H-type precision motion platform[J]. Journal of Shenyang University of Technology, 2018, 40(1): 1-5.
[5]钟前进, 王科, 丁信忠. 一种新型 S加减速算法研究[J]. 电气传动, 2019, 49(6): 8-12.Zhong Qianjin, Wang Ke, Ding Xinzhong. Research on a new S acceleration and deceleration algorithm[J].Electric Drive, 2019, 49(6): 8-12.
[6]Yeh S S, Hsu P L. Theory and applications of the robust cross-coupled control design[J]. ASME Journal of Dynamic Systems, Measurement and Control, 1999,121(3): 524-530.
[7]金鸿雁, 赵希梅. 基于Sugeno型模糊神经网络和互补滑模控制器的双直线电机伺服系统同步控制[J].电工技术学报, 2019, 34(13): 2726-2733.Jin Hongyan, Zhao Ximei. Synchronous control of double linear motor servo system based on Sugeno fuzzy neural network and complementary sliding mode controller[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2726-2733.
[8]武志涛, 杨永辉. 一种永磁直线电机驱动 X-Y平台精密轮廓跟踪控制策略[J]. 电工技术学报, 2018,33(17): 4037-4043.Wu Zhitao, Yang Yonghui. A precision contour tracking control strategy for X-Y platform driven by permanent magnet linear motor[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4037-4043.
[9]刘筱, 吴文江, 郑飂默. 柔性 S型加减速控制算法研究[J]. 组合机床与自动化加工技术, 2014(3):66-68.Liu Xiao, Wu Wenjiang, Zheng Limo. Flexible S deceleration control algorithm research[J]. Combined Machine Tool and Automatic Machining Technology,2014(3): 66-68.
[10]史步海, 孙会会. 基于新S型速度规划的B样条曲线算法研究[J]. 机床与液压, 2016, 44(15): 72-79.Shi Buhai, Sun Huihui. Research on B-spline curve algorithm based on new S-type velocity planning[J].Machine Tool & Hydraulics, 2016, 44 (15): 72-79.
[11]Lou Yunjiang, Hao Meng, Yang Jiangzhao, et al. Task polar coordinate frame-based contouring control of biaxial systems[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3490-3501.
[12]Tang L, Landers R G. Multiaxis contour control-the state of the art[J]. IEEE Transactions on Control Systems Technology, 2013, 21(6): 1732-1741.
[13]孙宜标, 王欢, 宋杨. 基于 PDFF的直线电机驱动XY 平台 H∞ 交叉耦合控制[J]. 组合机床与自动化加工技术, 2009(2): 60-63.Sun Yibiao, Wang Huan, Song Yang. H∞ crosscoupled control of linear motor driven XY table based on PDFF[J]. Combined Machine Tool and Automatic Machining Technology, 2009(2): 60-63.
[14]赵希梅, 赵久威, 李洪谊. 基于GPC和DOB的直驱XY平台鲁棒跟踪控制[J]. 电工技术学报, 2015,30(6): 150-154.Zhao Ximei, Zhao Jiuwei, Li Hongyi. Robust tracking control for direct drive XY table based on GPC and DOB[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 150-154.
[15]刘珅, 高琳. 永磁同步电机的改进模型预测直接转矩控制[J]. 电机与控制学报, 2020, 24(1): 10-17.Liu Shen, Gao Lin. Improved model predictive direct torque control for permanent magnet synchronous motors[J]. Electric Machines and Control, 2020, 24(1):10-17.
[16]Ghaffari A, Ulsoy A G. Dynamic contour error estimation and feedback modification for highprecision contouring[J]. IEEE/ASME Transactionson Mechatronics, 2016, 21(3): 1732-1741.
[17]Cheng Mingyang. Motion controller design for contour-following tasks based on real-time contour error estimation[J]. IEEE Transactions on Industrial Electronics, 2007, 54(3): 1686-1695.
[18]Chalanga A, kamal S, Fridmzn L, et al. Implementation of super-twistig control: super-twisting and higher order sliding mode observer based approaches[J]. IEEE Transactions on Industrial Electronics,2016, 63(6): 3677-3685.
[19]Yeh S, Hsu P. Estimation of the contouring error vector for the cross-coupled control design[J].Transactions on Mechatronics IEEE/ASME, 2002,7(1): 44-51.
[20]潘子昊, 卜飞飞, 轩富强, 等. 基于Smith预估器的永磁电机高动态响应电流环控制策略[J]. 电工技术学报, 2020, 35(9): 1921-1930.Pan Zihao, Bu Feifei, Xuan Fuqiang, et al. High dynamic response current loop control strategy for permanent magnet motors based on Smith predictor[J].Transactions of China Electrotechnical Society, 2020,35(9): 1921-1930.
[21]邱建琪, 留若宸. 永磁同步电机位置伺服系统改进自抗扰控制[J]. 电机与控制学报, 2019, 23(11): 42-50.Qiu Jianqi, Liu Ruochen. Improved active disturbance rejection control for permanent magnet synchronous motor position servo system[J]. Electric Machines and Control, 2019, 23(11): 42-50.
[22]Levant A. Higher order sliding modes, differentiation and output-feedback control[J]. International Journal of Control, 2003, 76(9/10): 924-941.