0 引言
永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)结合了永磁同步电机和直线电机的结构特点,具有推力密度大、定位精度高、可靠性好等优点,在电磁弹射系统、无绳电梯直驱系统、数控机床系统、轨道交通直线牵引系统等直线运动领域应用优势明显[1-4]。因此,近年来PMLSM 已成为国内外学者和科研机构的研究热点,其理论及实践研究越来越系统化,但是仍有一些基础研究需要进一步完善。
计及齿槽效应的影响,为了获得准确的电机参数,方便后期对电机进行优化设计,PMLSM中常采用解析法和有限元法分析电机的反电动势和推力。相对于有限元法,解析法物理概念直观、计算速度快。有限元法能够精确求解复杂电机结构的磁场,通用性好,但是前处理建模、后处理求解耗时长,未能直观地反映设计参数对电机性能的影响规律,在电机结构参数化计算中效率不高,常用来验证以上模型的正确性。解析法主要包括:二维气隙相对磁导函数模型[5-7]、保角变换模型[8-11]、精确子域模型[12-16]、等效磁网络模型[17-20]。文献[6]采用二维气隙相对磁导函数模型结合磁路法给出了PMLSM的反电动势和推力解析式,直观地反映了结构参数对推力的影响,由于二维气隙相对磁导函数模型的局限性,未能考虑切向上齿槽效应对电磁参数的影响。计及切向上齿槽效应对气隙磁场,文献[9]采用保角变换法分析PMLSM磁场,准确度较高,但需经过多次平面变换,计算较复杂。为了得到更加精确的电机磁场,文献[13]采用精确子域模型得到了电机的空载磁场和推力,计算结果基本上与有限元结果一致,但边界条件处理繁琐,需确定的各次谐波系数较多,公式繁多不直观,计算量较大。文献[19]提出新的网格生成方法建立PMLSM等效磁网络模型,很好地解决了磁路饱和、漏磁对PMLSM电磁参数的影响,但该方法类似于有限元网格剖分,建模工作量随着节点的增多而增加,导致计算效率不高。
上述解析模型中,二维气隙相对磁导函数模型与其他模型相比的显著优点是能以精简的解析式反映气隙相对磁导分布,从而能简便地确定气隙磁场。目前多数文献采用二维气隙相对磁导函数结合磁路法对PMLSM磁场进行计算,仅考虑了二维气隙相对磁导法向分量,尚未考虑其切向分量。
在保证准确度的前提下,考虑齿槽效应对电机电磁参数的影响,本文提出一种基于改进的二维气隙相对磁导函数求解电机参数,同时结合分离变量法,用于准确计算定子开槽时电机的气隙磁场、空载反电动势和推力。首先建立无槽PMLSM解析模型,给出改进的二维气隙相对磁导函数解决切向气隙相对磁导分布,以此建立其与气隙磁通密度的关系;其次结合改进的二维气隙相对磁导函数得到电机开槽时的气隙磁通密度法向和切向分布;最后计算出不同极槽配合下电机的磁链、空载反电动势和推力,并用有限元法验证解析法的准确性。
1 无槽PMLSM磁场解析模型
为简化分析,忽略端部效应,永磁体在各方向上磁导率相同且等于空气磁导率;定、动子铁心的磁导率为无穷大,磁路不饱和;忽略临近齿槽效应,定子槽为无限深。基于以上假设,以磁极轴线为原点,建立无槽PMLSM磁场分层模型,如图1所示,分为1、2、3、4四个求解区域,分别对应定子轭、永磁体、气隙、动子轭区域。

图1 无槽PMLSM磁场解析模型
Fig.1 Layered model of slotless LPMVM
永磁体磁化方向沿y方向,其磁化强度矢量为M=Myy,对其展开傅里叶级数形式,则

式中,M0为永磁体磁化强度;Br为永磁体剩磁;µ0为空气磁导率;αp永磁体极弧系数;Lm为永磁体长度,τ为极距。
以矢量磁位 Az(x,y)为求解变量,永磁体区域为泊松方程,气隙区域为拉普拉斯方程,即
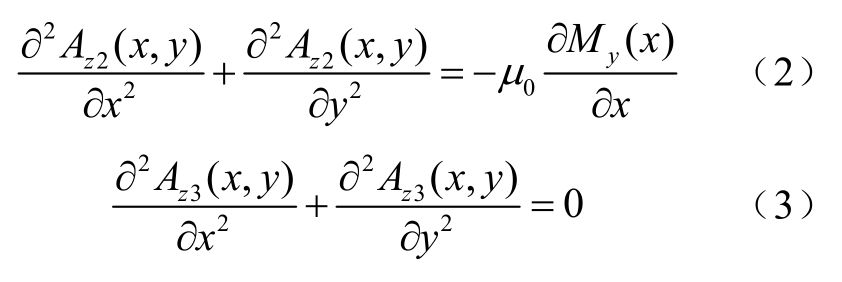
式中,Az2(x,y)、Az3(x,y)分别为永磁体区域、气隙区域的矢量磁位。
通过分离变量法知永磁体区域和气隙区域的矢量磁位通解为
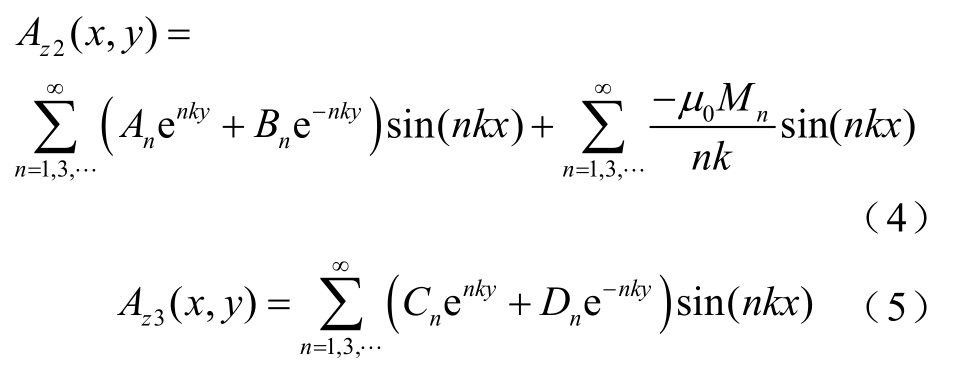
在各区域磁场边界条件满足
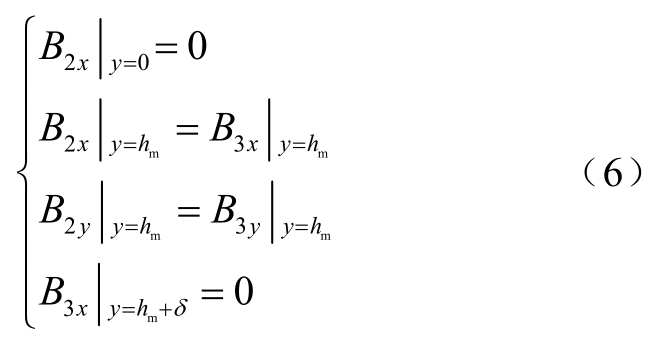
式中,hm为永磁体高度;δ为气隙长度。
根据式(4)~式(6),推出永磁体区域无槽磁通密度解析式为

气隙区域无槽磁通密度解析式为
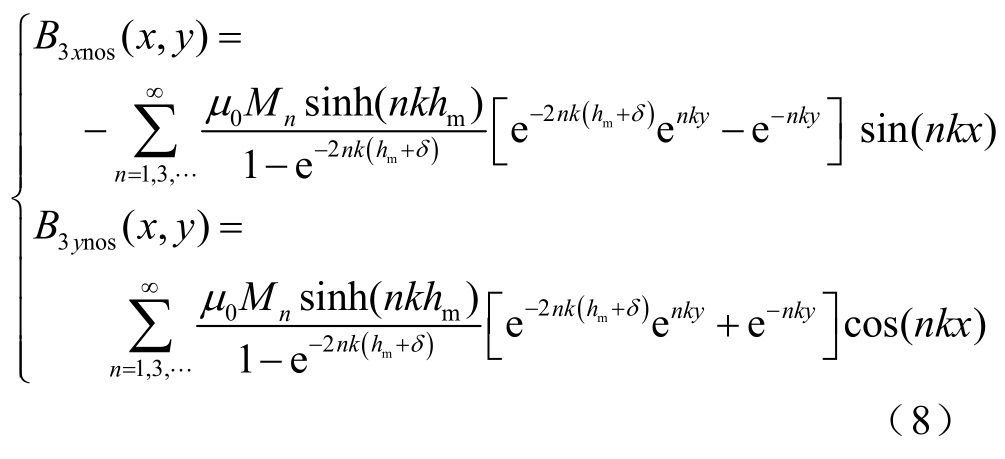
2 改进的二维气隙相对磁导函数及有槽气隙磁场解析
以一槽为分析模型,选取槽中心为原点,采用许-克变换法,PMLSM的二维气隙相对磁导函数表达式为[5]
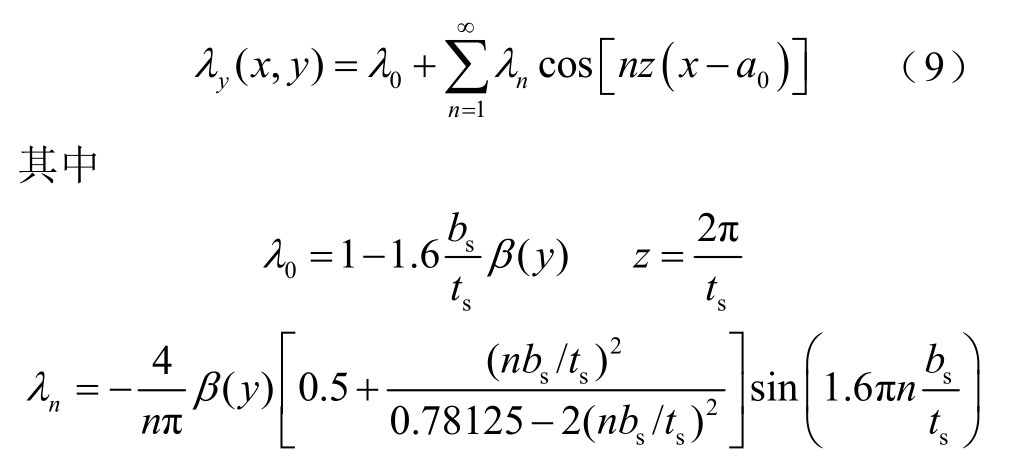
式中,a0为槽中心线与A相绕组轴线的距离;ts为齿距;bs为槽宽;β(y)为非线性函数[5],与槽宽、定动子间距离、气隙处位置有关,用来确定气隙相对磁导各次谐波大小。
式(9)中含有常数项和余弦级数项,可知法向气隙相对磁导分布为偶函数,关于槽中心线对称。式(9)仅能考虑齿槽效应在法向上对气隙相对磁导分布的影响,而对于切向上的影响目前未见文献给出详细的解析式。根据文献[8]分析可知,切向气隙相对磁导分布为奇函数,因此切向上的气隙相对磁导无常数项,且与法向上的谐波幅值具有相似性,可得切向气隙相对磁导表达式近似为
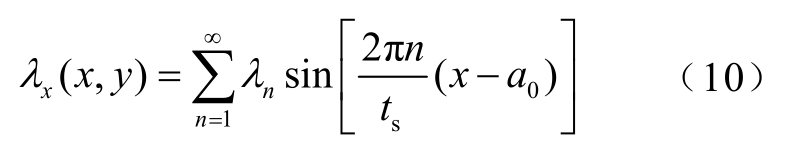
式(9)和式(10)构成了改进的二维气隙相对磁导函数。为了得到考虑齿槽效应时的气隙磁通密度,将改进的二维气隙相对磁导函数 λr(x,y)写成复数形式,即
式中,λy(x,y)、λx(x,y)分别为改进的二维气隙相对磁导函数的实部和虚部。若仅考虑实部,则为改进前的模型。根据式(11)可以得到气隙不同位置处的二维气隙相对磁导分布。
有槽气隙磁通密度等于无槽气隙磁通密度与改进的二维气隙相对磁导函数的共轭复数![]() 之积[8],即
之积[8],即
式中,Bs(x,y)为有槽磁通密度;Bnos(x,y)为无槽磁通密度。
有槽磁通密度和无槽磁通密度写成复数形式为
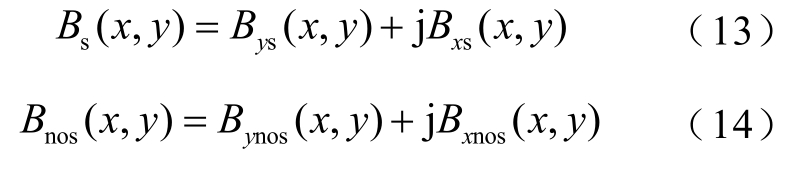
式中,实部表示法向磁通密度;虚部表示切向磁通密度。
由式(11)~式(14)得有槽气隙磁通密度的法向和切向分量分别为
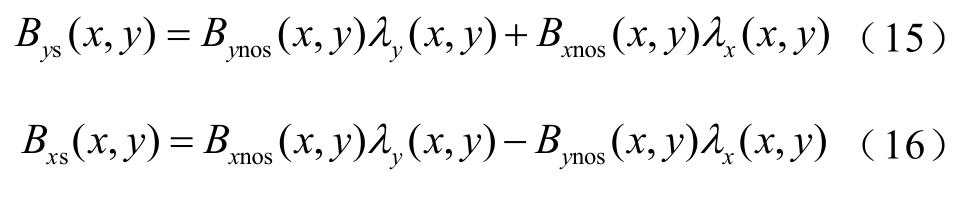
采用有限元验证改进的二维气隙相对磁导分布时 , 一 般 情 况 下 Bxnos(x,y)、 Bxnos(x,y)·λx(x,y)、Bxnos(x,y)·λy(x,y)比较小,因此有限元法计算二维气隙相对磁导公式可化简为
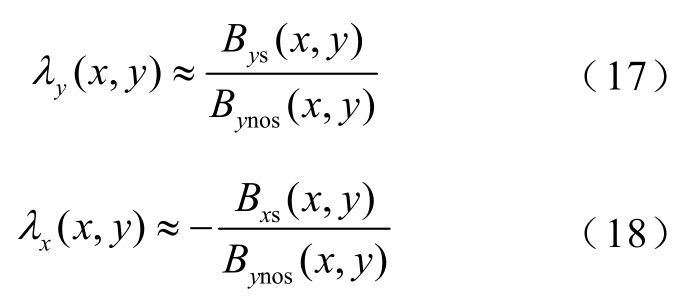
根据式(8)、式(15)、式(16),得到有槽时气隙区域的空载磁通密度为

3 空载反电动势和推力计算
为了得到线圈产生的磁链,将式(8)写成
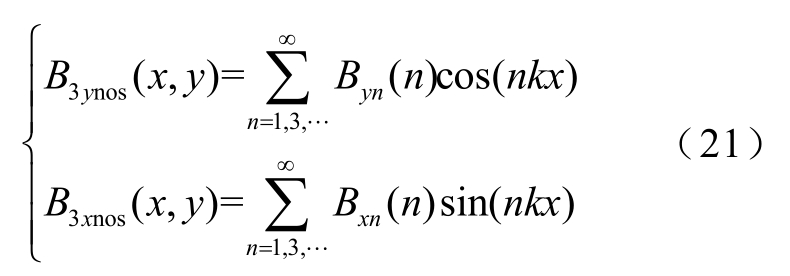
单匝线圈产生的磁链cψ为
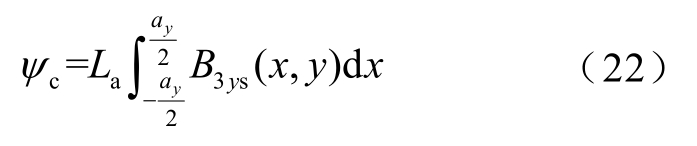
式中,La为铁心长度;ay为线圈节距,ay=y1ts,y1为线圈跨过的槽数。
单匝线圈感应的空载反电动势为
将式(21)代入式(19)得到气隙磁通密度B3ys(x,y)为
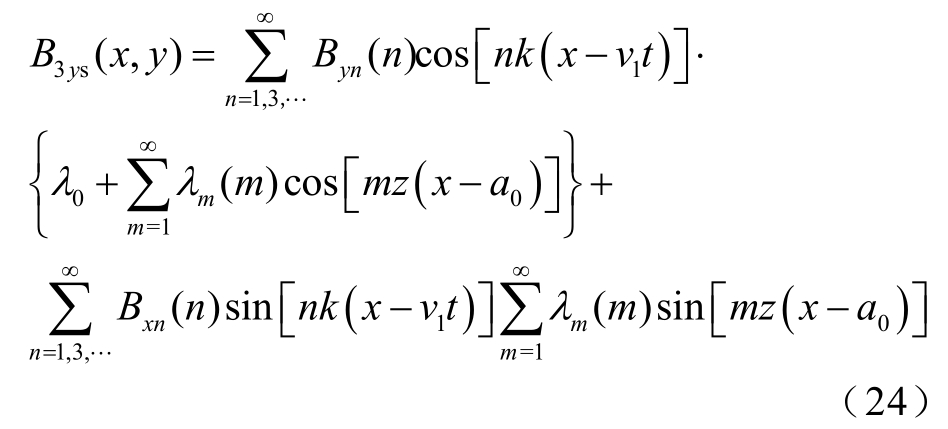
式中,v1为电机动子速度。
将式(24)代入式(22)得单匝线圈产生的磁链cψ为
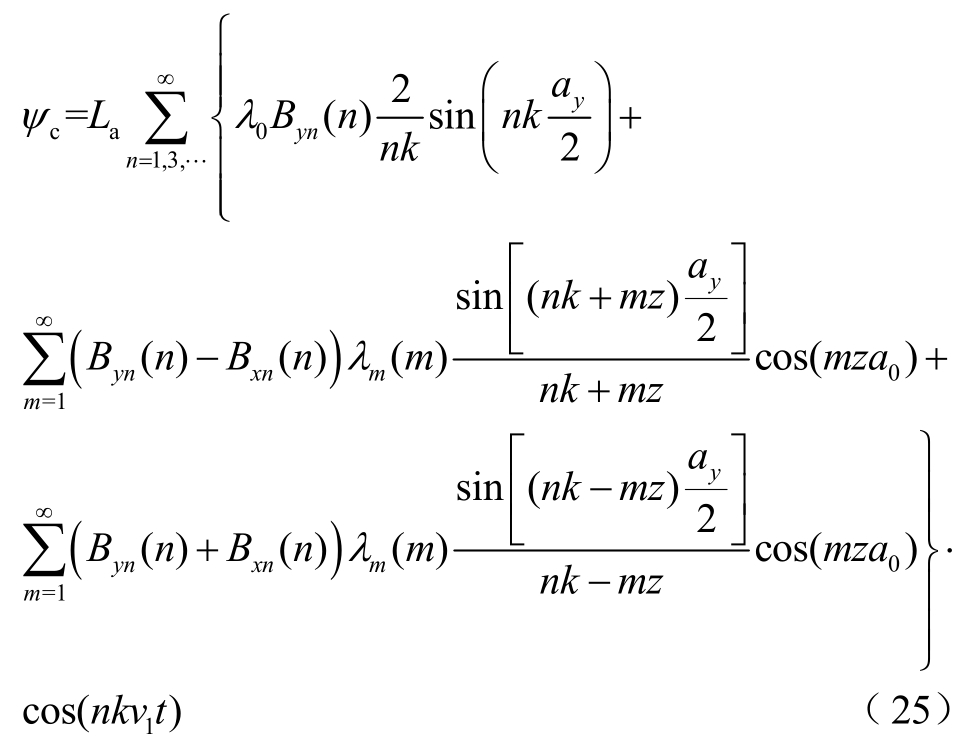
则一相绕组产生的空载反电动势为

式中,N1为每相绕组串联匝数;对于A相θ0=0°,B相 θ0=2π/3,C 相 θ0=4π/3;kdn 为 分 布 系 数 ;![]() 为槽开口系数;λ(x,y)、λ(x,y)yx的坐标原点为槽中心线,当y1为奇数槽,则a0=ts/2,cos(mza0)=cos(mπ);当 y1为偶数槽,则 a0=0,cos(mza0)=1。
为槽开口系数;λ(x,y)、λ(x,y)yx的坐标原点为槽中心线,当y1为奇数槽,则a0=ts/2,cos(mza0)=cos(mπ);当 y1为偶数槽,则 a0=0,cos(mza0)=1。
由空载反电动势的公式知,其大小与无槽气隙磁通密度的谐波幅值和二维气隙相对磁导的谐波幅值有关。一般情况下对于整数槽,切向磁通密度较小,可忽略Bxn(n)λm(m),进一步简化为只考虑法向磁通密度谐波幅值Byn(n),方便计算。对于分数槽,尤其是极数多于齿数的极槽配合,切向磁通密度较大,Bxn(n)λm(m)不可忽略。
电机推力为
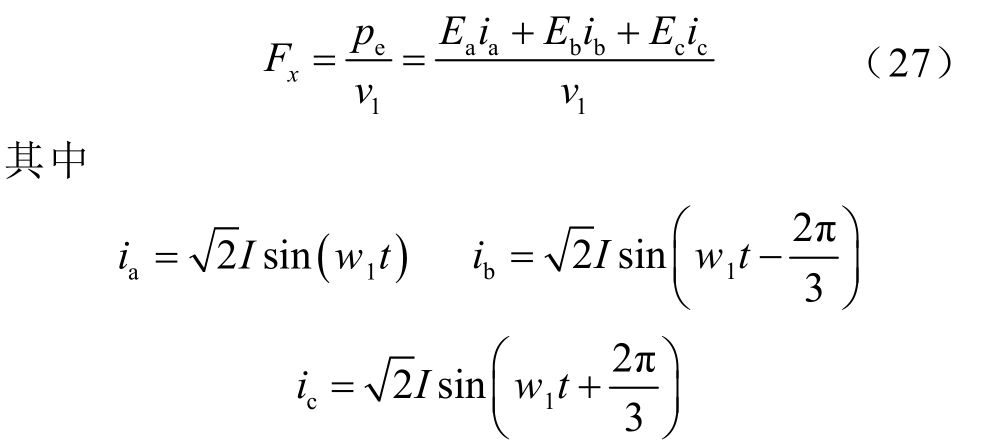
式中, pe为电磁功率;ia、ib、ic为定子三相电流;I为电流有效值;w1为电源角频率。
从以上分析可以看出,与其他解析法相比,空载反电动势和推力的最终解析式均为级数求和计算,避免了积分和微分计算,计算工作量小,提高了求解效率。
4 有限元验证
为了验证解析模型的正确性,分别对整数槽和分数槽两种结构进行分析,PMLSM结构参数见表1,其中每种电机采用两种槽型结构,分别是槽口宽较小的半闭口槽结构(bs≤ts/2)和槽口宽较大(bs≥ts/2)的矩形槽结构来说明槽口宽对电机参数的影响。图 2给出了12s14p PMLSM半闭口槽和矩形槽两种槽型的结构模型。
表1 PMLSM结构参数
Tab.1 The structure parameters of PMLSM
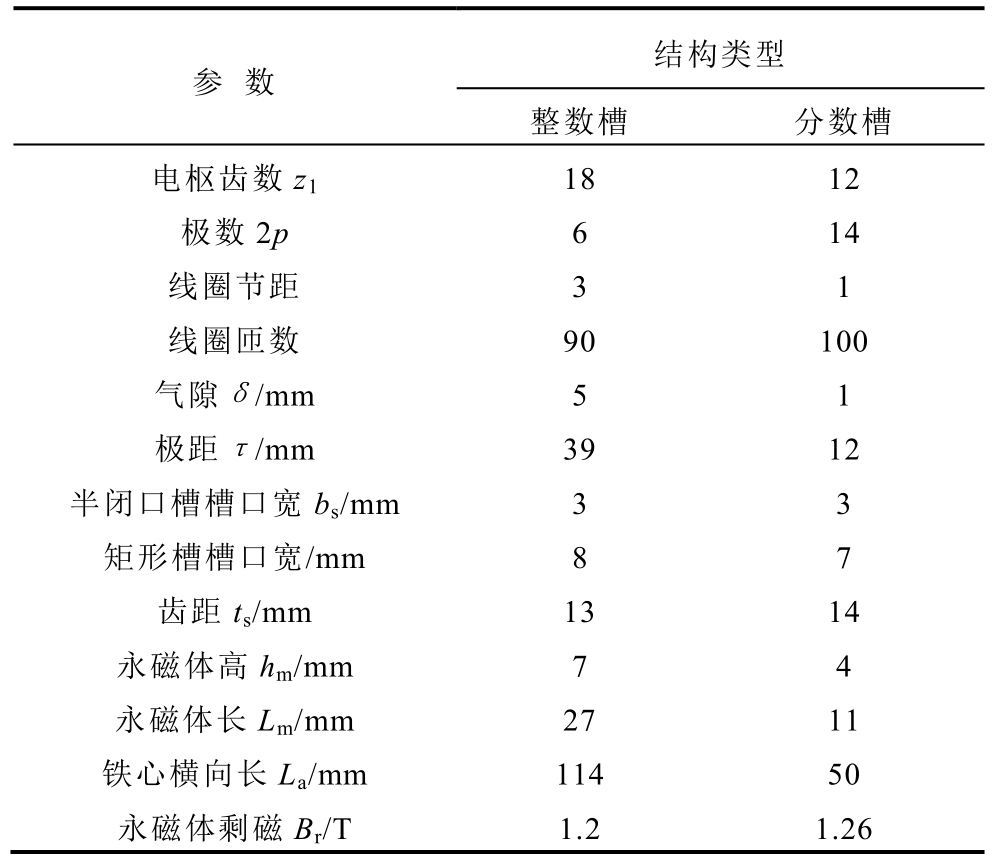
参 数 结构类型整数槽 分数槽电枢齿数z1 18 12极数2p 6 14线圈节距 3 1线圈匝数 90 100气隙δ/mm 5 1极距τ/mm 39 12半闭口槽槽口宽bs/mm 3 3矩形槽槽口宽/mm 8 7齿距ts/mm 13 14永磁体高hm/mm 7 4永磁体长Lm/mm 27 11铁心横向长La/mm 114 50永磁体剩磁Br/T 1.2 1.26
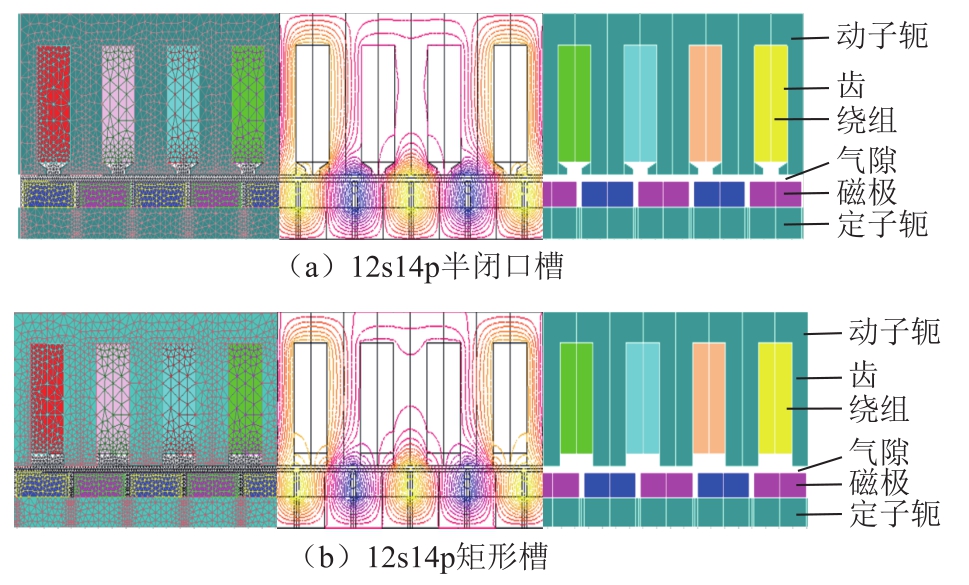
图2 PMLSM结构模型
Fig.2 Structural model of PMLSM
4.1 改进的二维气隙相对磁导和有槽气隙磁通密度计算
根据式(9)和式(10)得到18s6p、12s14p采用半闭口槽结构和矩形槽结构,在气隙中心y0=hm+δ/2时改进的二维气隙相对磁导分布如图 3、图4所示。有限元计算改进的二维气隙相对磁导方法为:以槽为中心在绕组中通入对称的直流电,使其产生的磁场关于槽中心对称,得到有槽磁通密度,然后将电机等效为无槽电机,计算同样的大小直流电流分布在槽口表面的无槽电机气隙磁通密度,根据式(17)和式(18)得到改进的二维气隙相对磁导分布。可以看到,解析法和有限元法结果拟合较好,改进的二维气隙相对磁导法向分量关于槽中心呈偶对称,切向分量关于槽中心呈奇对称。同时可以看到,随着槽宽的增加,切向磁导的误差稍微增大,这是因为气隙磁导模型为单槽模型,没有考虑临近齿槽效应的影响。
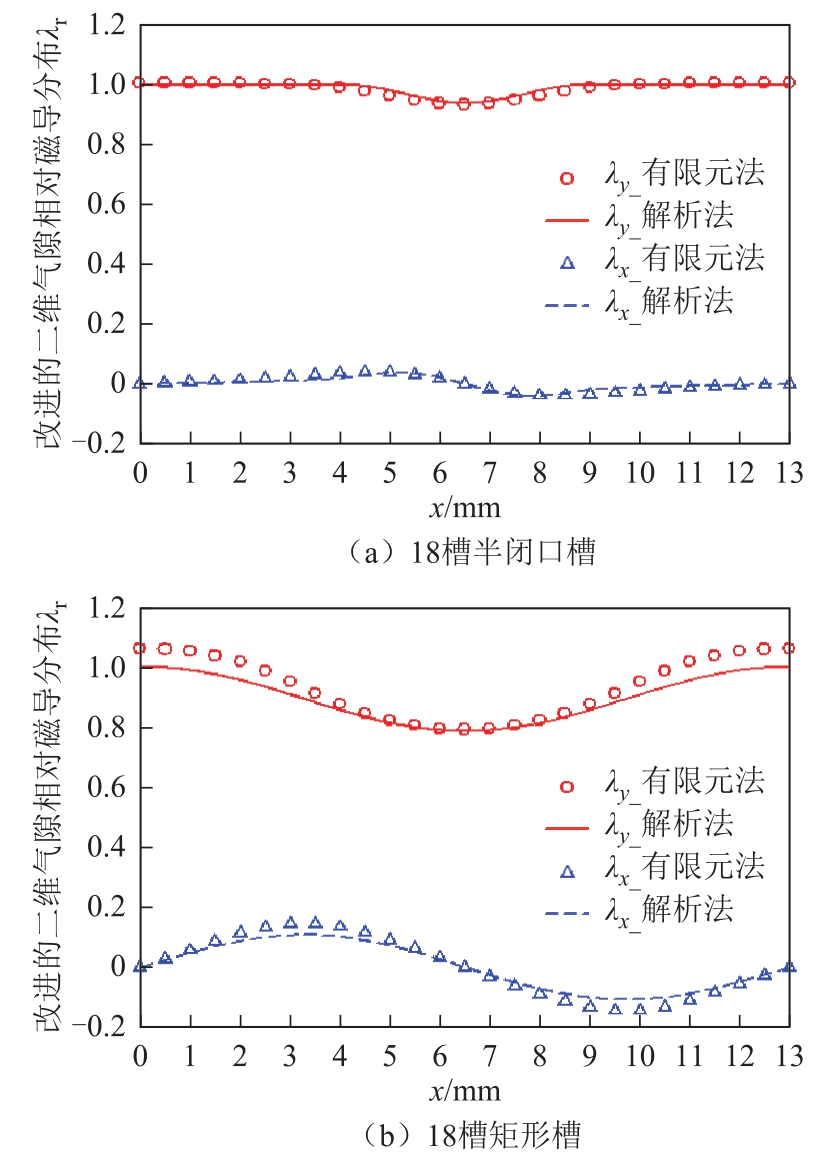
图3 改进的二维气隙相对磁导分布(18s6p)
Fig.3 The distribution of improved 2D relative permeance about 18s6p PMLSM

图4 改进的二维气隙相对磁导分布(12s14p)
Fig.4 The distribution of improved 2D relative permeance about 12s14p PMLSM
以18s6p为例,保持气隙δ=5mm不变,改变槽宽,用解析法得到气隙中心y0=hm+δ/2处改进的二维气隙相对磁导变化曲线如图5a所示。同理保持槽宽bs=3mm和永磁体高hm=7mm不变,气隙δ取不同长度时,定、动子之间的距离随气隙的增大而增大,得到如图5b所示曲线。由图5可知,当槽宽与齿距之比增大时,二维气隙相对磁导法向和切向幅值变化越大,在齿边角处变化最大。当气隙长度增大时,二维气隙相对磁导幅值的变化减小,曲线趋势逐渐越缓。


图5 改进的二维气隙相对磁导与槽宽和气隙的关系
Fig.5 The improved 2D relative permeance versus slot width and airgap
18s6p、12s14p不同槽宽下的气隙磁通密度分布如图6和图7所示,可知改进的二维气隙相对磁导较好地反映了齿槽效应对磁场法向和切向分布的影响,解决了目前切向磁场上求解困难的问题。
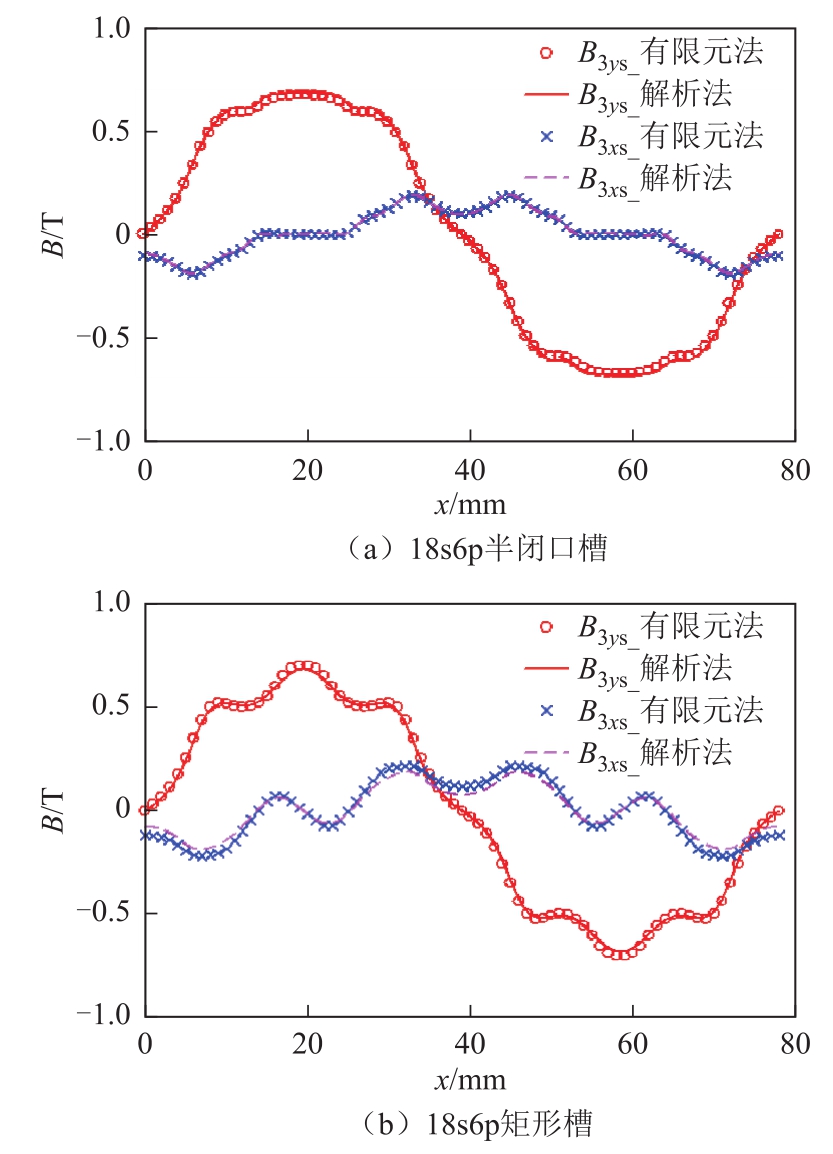
图6 18s6p气隙磁通密度分布
Fig.6 Flux density distribution of 18s6p PMLSM


图7 12s14p气隙磁通密度分布
Fig.7 Flux density distribution of 12s14p PMLSM
4.2 空载反电动势和推力计算:
18s6p、12s14p运行频率分别为f=4Hz、f=10Hz,由式(26)得到的空载反电动势结果如图 8和图9所示。两种电机电流有效值均为5A,由式(27)得到的推力计算曲线如图10和图11所示。其中图11给出了12s14p每相绕组串联匝数相同,分别采用单双层绕组时的推力对比曲线。表2和表3分别给出了 18s6p 和 12s14p在不同结构参数下的空载反电动势有效值、推力平均值的数值对比,表中的相对误差以各电机有限元结果为基准值。
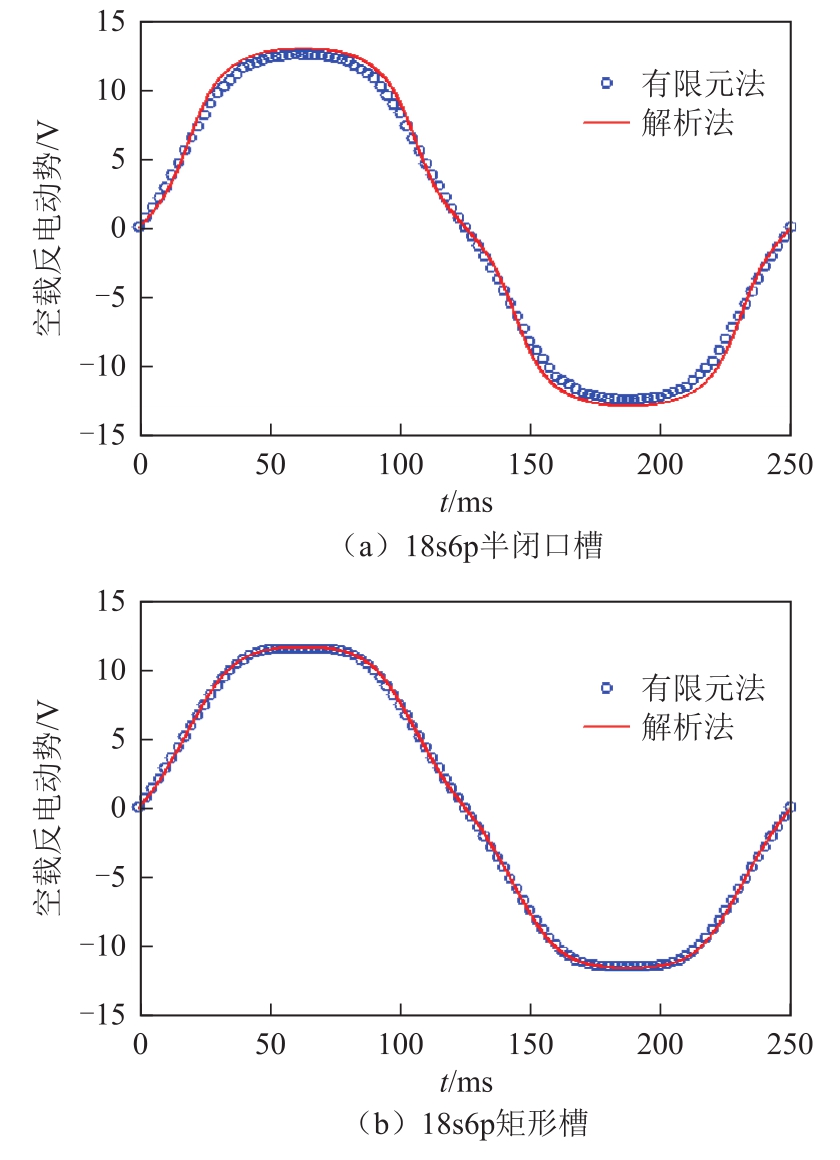
图8 18s6p空载反电动势波形
Fig.8 No-load EMF of 18s6p PMLSM

图9 12s14p空载反电动势波形
Fig.9 No-load EMF of 12s14p PMLSM

图10 18s6p推力波形
Fig.10 Thrust of 18s6p PMLSM
由图 8~图 11可知,利用解析法、有限元法得到的反电动势和推力结果基本一致,解析法较好地反映了空载反电动势、推力随时间的变化曲线。由表2和表3可以看到,整数槽、分数槽绕组半闭口槽结构结果误差较小,分数槽绕组矩形槽结构结果误差稍大。对于矩形槽结构,存在误差的原因为随着槽口宽与齿距之比的增大,临近齿槽效应的影响越来越大,由于气隙磁导为单槽模型,忽略了临近齿槽效应的影响,切向磁场误差变大,在反电动势和推力上会存在误差。
表2 18s6p PMLSM空载反电动势和推力数值对比
Tab.2 Comparison of no-load EMF and thrust of 18s6p PMLSM

空载反电动势推力平均值解析法/V 有限元法/V 相对误差(%) 解析法/N 有限元法/N 相对误差(%)半闭口槽 9.74 9.34 4.28 469.8 449.75 4.46矩形槽 8.67 8.65 2.31 418.82 416.16 0.64

图11 12s14p推力波形
Fig.11 Thrust of 12s14p PMLSM
表3 12s14p PMLSM空载反电动势和推力数值对比
Tab.3 Comparison of no-load EMF and thrust of 12s14p PMLSM

参数 解析法 有限元法 相对误差(%)空载反电动势/V半闭口槽单层绕组 3.698 3.632 8 1.79双层绕组 3.568 5 3.531 5 1.05单层绕组 3.028 4 3.255 1 6.96矩形槽双层绕组 2.934 3 3.020 5 2.85单层绕组 230.77 228.2 1.13推力平均值/N半闭口槽 双层绕组 223.25 219.87 1.54单层绕组 190.8 204.48 6.69矩形槽双层绕组 184.29 186.63 1.25
与其他解析法相比,在保证准确度的情况下简化了复杂的计算,方便了电机的参数计算分析。由图 8、图9可知电机为分数槽时的反电动势正弦性比整数槽时好。由图10、图11及表2和表3可以看出随着槽宽增大,根据卡氏系数知等效气隙增大,平均推力略有减小,电机为整数槽时矩形槽结构比半闭口槽推力波动大。由图11可知,由于分数槽单层绕组的基波绕组系数大于分数槽双层绕组,且分数槽单层绕组含有较大的电枢反应磁动势谐波,因此其平均推力、推力波动均大于分数槽双层绕组。
在求解时间对比上,以分数槽结构 PMLSM 12s14p为例,求解时长为一个电周期,采样点100个。解析法可一次性求解出二维气隙相对磁导、气隙磁通密度、空载反电动势、推力参数,当谐波最大次数取 M =N= 5 0时,计算结果已基本不变。有限元法后处理功能强大,但求空载反电动势、推力参数需单独建模,增加了建模时间,改变电机结构如不采用参数化模型同样增加前处理时间。有限元建模气隙处单元格剖分长度为0.5mm,模型总剖分节点 29 253个。计算机配置 CPU为 i7-7700HQ,2.8GHz,内存32G,解析法和有限元法仿真耗时分别为2.5s和100s。解析法中所有计算均为求和计算,能快速求出以上电磁参数,求解效率远高于有限元法,而有限元法求解精度高,计算时间随剖分网格的增加而增加。
5 结论
本文采用一种改进的二维气隙相对磁导函数结合分离变量法求解PMLSM电机参数,准确计算了不同电机结构下的改进的二维气隙相对磁导、气隙磁通密度、空载反电动势和推力,并用有限元法验证了解析结果的正确性。与其他方法相比,提出的方法准确度较高,降低了磁场求解过程的复杂性,是目前解析法中分析简便、工作量小、计算效率高、通用性好的一种,且适用于整数槽和分数槽结构PMLSM性能的分析,有益于 PMLSM的电磁分析和优化设计。
[1]凌志健, 赵文祥, 吉敬华. 高推力永磁直线作动器及其关键技术综述[J]. 电工技术学报, 2020, 35(5):1022-1035.Ling Zhijian, Zhao Wenxiang, Ji Jinghua. Overview of high force density permanent magnet linear actuator and its key technology[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1022-1035.
[2]曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020,35(5): 1001-1012.Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001-1012.
[3]杜超, 孟大伟. 基于场路结合法的电磁弹射用新型永磁直线同步电机的研究[J]. 电机与控制学报,2019, 23(9): 65-74.Du Chao, Meng Dawei. Investigation of permanent magnet linear synchronous motor for electromagnetic launch based on field-circuit combined method[J].Electric Machines and Control, 2019, 23(9): 65-74.
[4]许孝卓, 汪旭东, 封海潮, 等. 分数槽集中绕组永磁同步直线电机磁场解析计算[J]. 电工技术学报,2015, 30(14): 122-129.Xu Xiaozhuo, Wang Xudong, Feng Haichao, et al.Magnetic field calculation of the permanent magnet synchronous linear motor with fractional-slot concentrated windings[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 122-129.
[5]Zhu Z Q, Howe D, Bolte E, et al. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. III. Effect of stator slotting[J].IEEE Transactions on Magnetics, 1993, 29(1): 143-151.
[6]Zhou You, Qu Ronghai, Shi Chaojie, et al. Analysis of thrust performance of a dual-mover linear vernier machine with horizontal-magnetized PM arrays[J].IEEE Transactions on Energy Conversion, 2018,33(4): 2143-2152.
[7]Souissi A, Abdennadher I, Masmoudi A. Analytical prediction of the no-load operation features of tubularlinear permanent magnet synchronous machines[J].IEEE Transactions on Magnetics, 2016, 52(1): 1-7.
[8]Žarko D, Ban D, Lipo T A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeances[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1828-1837.
[9]Zeng Lizhan, Chen Xuedong, Li Xiaoqing, et al. A thrust force analysis method for permanent magnet linear motor using Schwarz-Christoffel mapping and considering slotting effect, end effect, and magnet shape[J]. IEEE Transactions on Magnetics, 2015,51(9): 101-108.
[10]于吉坤, 李立毅, 张江鹏, 等. 定子开槽永磁同步电机气隙比磁导解析计算[J]. 电工技术学报, 2016,31(增刊 1): 45-52.Yu Jikun, Li Liyi, Zhang Jiangpeng, et al. Analytical calculation of air-gap relative permeance in slotted permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2016, 31(S1): 45-52.
[11]Lu Qinfen, Wu Bocheng, Yao Yihua, et al. Analytical model of permanent magnet linear synchronous machines considering end effect and slotting effect[J].IEEE Transactionson Energy Conversion, 2020, 35(1):139-148.
[12]Amara Y, Barakat G. Analytical modeling of magnetic field in surface mounted permanent-magnet tubular linear machines[J]. IEEE Transactions on Magnetics,2010, 46(11): 3870-3884.
[13]Hu Hengzai, Zhao Jing, Liu Xiangdong, et al.Magnetic field and force calculation in linear permanent-magnet synchronous machines accounting for longitudinal end effect[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7632-7643.
[14]Hu Hengzai, Zhao Jing, Liu Xiangdong, et al. No-load magnetic field and cogging force calculation in linear permanent-magnet synchronous machines with semiclosed slots[J]. IEEE Transactions on Industrial Electronics, 2016, 64(7): 5564-5575.
[15]Shin K H, Cho H W, Lee S H, et al. Armature reaction field and inductance calculations for a permanent magnet linear synchronous machine based on subdomain model[J]. IEEE Transactions on Magnetics,2017, 53(6): 1-4.
[16]王明杰, 徐伟, 杨存祥, 等. 基于精确子域模型的永磁直线同步电机空载磁场解析计算[J]. 电工技术学报, 2020, 35(5): 942-953.Mingjie, Xu Wei, Yang Cunxiang, et al. Analytical calculation of no-load magnetic field in permanent magnet linear synchronous motors based on an accurate subdomain model[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 942-953.
[17]Sheikh-Ghalavand B, Vaez-Zadeh S, Hassanpour Isfahani A. An improved magnetic equivalent circuit model for iron-core linear permanent-magnet synchronous motors[J]. IEEE Transactions on Magnetics, 2010, 46(1): 112-120.
[18]Souissi A, Zouaghi M W, Abdennadher I, et al. MEC-based modeling and sizing of a tubular linear PM synchronous machine[J]. IEEE Transactions on Industry Application, 2015, 51(3): 2181-2194.
[19]Liu Guohai, Jiang Shan, Zhao Wenxiang, et al.Modular reluctance network simulation of a linear permanent-magnet vernier machine using new mesh generation methods[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 5323-5332.
[20]Liu Guohai, Ding Ling, Zhao Wenxiang, et al.Nonlinear equivalent magnetic network of a linear permanent magnet vernier machine with end effect consideration[J]. IEEE Transactions on Magnetics,2018, 54(1): 1-9.