0 引言
直线电机的特点是无需中间传动装置即可实现直线运动,具有结构简单、推力密度高[1]、定位精度高、可靠性高[2]和扩展性强等诸多优点。因此具有十分广泛的应用,如高精密数控机床[3]、地铁[4]、激光切割[5]、电磁弹射系统[6]及海洋波浪能的发电装置[7]等。
然而,在结构上直线电机初级铁心开断,其存在边端效应,且在平板型永磁同步直线电机(Permanent Magnet Linear Synchronous Motor,PMLSM)中更加显著。另外,对于有铁心的平板型永磁同步直线电机,其初级铁心还需开槽嵌入线圈,存在齿槽效应。由边端效应引起的边端力和齿槽效应引起的齿槽力导致电机具有较大推力波动,严重影响电机的稳定运行。因此,如何采取有效措施减少推力波动,提高输出的平均推力,以获得良好的推力特性是至关重要的。
针对此问题,在电机本体结构上,国内外学者做了大量的研究[8-18]。削弱边端力方面,文献[8]分别建立关于边端力的分析模型,提出最佳初级铁心长度。文献[10]提出双边初级和双边次级结构,形成闭合磁回路以有效地抑制边端力。文献[11]提出初级辅助极结构,通过优化辅助极几何形状和位置来削弱边端力。文献[13]提出双边初级错位半个极距。文献[14]提出初级端部弧形结构以达到削弱边端力的目的。削弱齿槽力方面,文献[15]提出格栅型次级的新型拓扑结构;文献[16]提出采用不等槽口宽度配合减小齿槽转矩;文献[17]研究初级铁心齿开虚拟槽个数与齿槽力的规律;文献[18]研究磁极偏移来消除齿槽谐波,推导出具体的磁极偏移距离公式。尽管这些方法有效地减小了推力波动,但可能会降低可控性或降低平均推力,且优化的设计参数和目标单一。因此,多设计参数多目标的优化设计是很有必要的。
本文基于有限元分析,从电机本体结构入手,实现平板型永磁直线同步电机多设计参数多目标的优化设计。本文首先介绍平板型永磁直线同步电机的拓扑结构和设计参数的有限元分析;然后介绍Taguchi法的敏感性分析,从12个设计参数中选出6个敏感参数;介绍Kriging模型与多目标粒子群优化算法相结合的优化设计方法;最后进行了实验验证。
1 电机结构及参数
图 1a为 12槽 10极平板型永磁直线同步电机的拓扑结构。图1b给出了13个设计参数,包括初级铁心长度ls,弧形辅助极位置d、高度h、弧形半径R和弧度θ,磁极宽度wpm和高度hpm,半闭口槽宽度 bs0、bs1、bs2 和高度 hs0、hs1、hs2。

图1 12槽10极永磁直线同步电机拓扑结构和设计参数
Fig.1 Topology and design parameters of 12-slot 10-pole permanent magnet linear synchronous motor(PMLSM)
表1给出了12槽10极平板型永磁直线同步电机的基本结构参数。对于13个设计参数,初始设计值分别是初级铁心长度ls为256mm,辅助极位置d和高度h皆为0mm,弧形半径R为4mm,弧度θ为0°,磁极宽度wpm为20mm,磁极高度hpm为4.5mm,半闭口槽宽度bs0为6mm、bs1为12mm、bs2为12mm,半闭口槽高度hs0为2mm、hs1为1mm、hs2为37mm。
表1 12槽10极平板型永磁直线同步电机基本结构参数
Tab.1 Basic structure parameters of 12s10p PMLSM
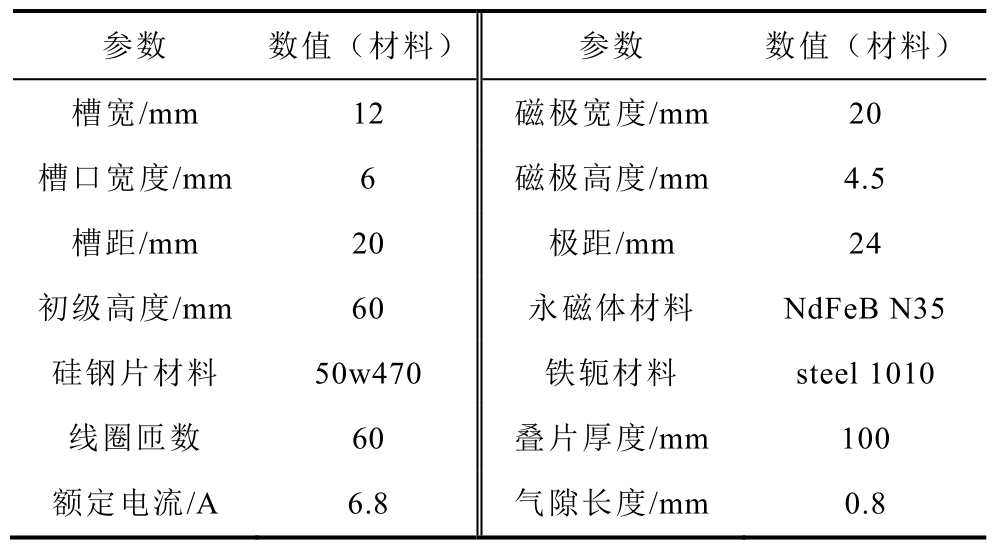
参数 数值(材料) 参数 数值(材料)槽宽/mm 12 磁极宽度/mm 20槽口宽度/mm 6 磁极高度/mm 4.5槽距/mm 20 极距/mm 24初级高度/mm 60 永磁体材料 NdFeB N35硅钢片材料 50w470 铁轭材料 steel 1010线圈匝数 60 叠片厚度/mm 100额定电流/A 6.8 气隙长度/mm 0.8
由于篇幅有限,本文仅对初级铁心长度 ls、辅助极位置d、高度h、弧形半径R和弧度θ、磁极宽度wpm和高度hpm、半闭口槽宽度bs0这八个设计参数进行有限元分析,研究各个参数对平板型永磁直线同步电机推力特性的影响,其余保持原始值不变。
1)初级铁心长度ls
初级铁心长度主要影响永磁直线同步电机边端力的大小。根据理论可知,使得永磁直线同步电机边端力最小的初级铁心长度落在kτ+τ/2(k为正整数,τ为极距)处。为了定量分析初级铁心长度对永磁直线同步电机边端力的影响,初级铁心长度范围设为240~264mm,递增量为1mm,边端力有限元结果及其前3次分量如图2所示。可以看出,使得边端力最小的最佳初级铁心长度为254.5mm,幅值为29.2N,边端力最大和最小可相差72.7N。
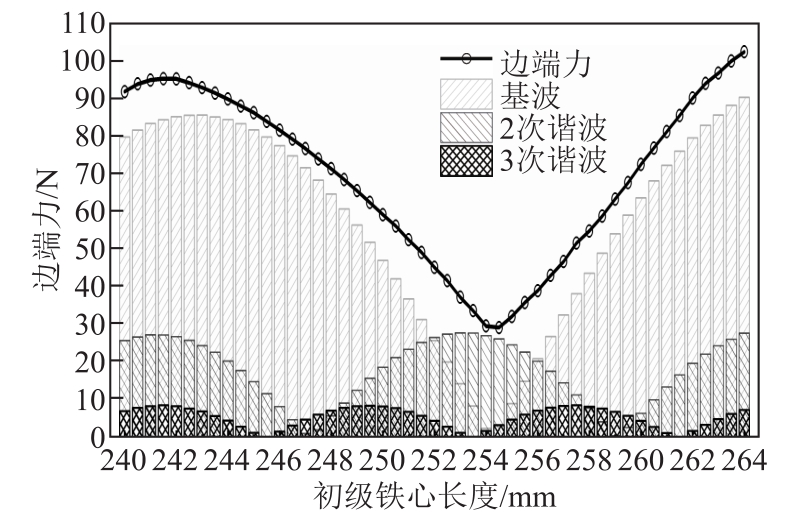
图2 初级铁心长度ls对永磁直线同步电机边端力的影响
Fig.2 The impact of primary core length on Side force of PMLSM
2)弧形辅助极
弧形辅助极有四个设计参数,分别为辅助极位置d、高度h、弧形半径R和弧度θ。采用控制变量分析法,单独对每个设计参数进行有限元分析,其他保持原始值不变,结果如图3所示。可以看出,四个设计参数主要影响永磁直线同步电机的推力波动,对平均推力影响不显著。可初步判定,当辅助极位置d为1mm、高度h为2mm、弧形半径R为16mm、弧度θ为50°时,可获得较好的推力特性。

图3 弧形辅助极对永磁直线同步电机推力波动的影响
Fig.3 The impact of arc-shaped auxiliary pole on thrust ripple of PMLSM
3)槽口宽度bs0
对于永磁直线同步电机初级铁心的半闭口槽,其包含六个设计参数,其中槽口宽度bs0对气隙磁场的影响最大。与旋转电机不同,永磁直线同步电机的端部为半填槽,槽口宽度为bs0的一半。将半填槽口宽度和中间槽口宽度看作两个独立设计参数,有限元参数化分析结果如图4所示。图4a显示半填槽口宽度为4.5mm、中间槽口宽度为10.5mm时推力波动达到最小值,图4b显示半填槽口宽度为3mm、中间槽口宽度为6mm时平均推力达到最大值,两者没落在同一点处,优化时应合理设计。
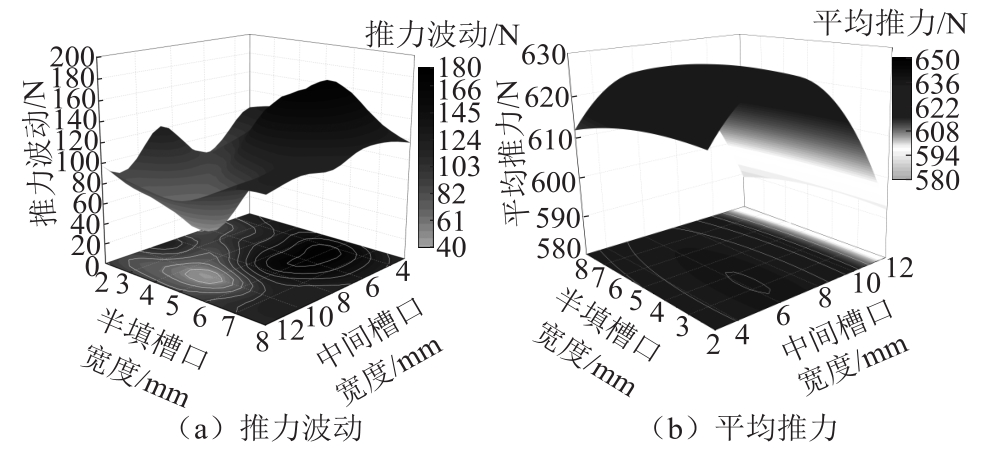
图4 槽口宽度对推动波动和平均推力的影响
Fig.4 The impact of notch width on thrust ripple and average thrust of PMLSM
4)磁极宽度wpm和高度hpm
图5a显示随着磁极宽度wpm的增大,永磁直线同步电机的平均推力呈缓慢递增趋势,推力波动先减小后增大。图5b显示永磁直线同步电机的平均推力和推力波动与磁极高度 hpm近似成正比关系。综合分析可得,磁极尺寸的增大有助于提高永磁直线同步电机的平均推力,同时会使推力波动增大,永磁材料的成本增加,设计时应统筹考虑。
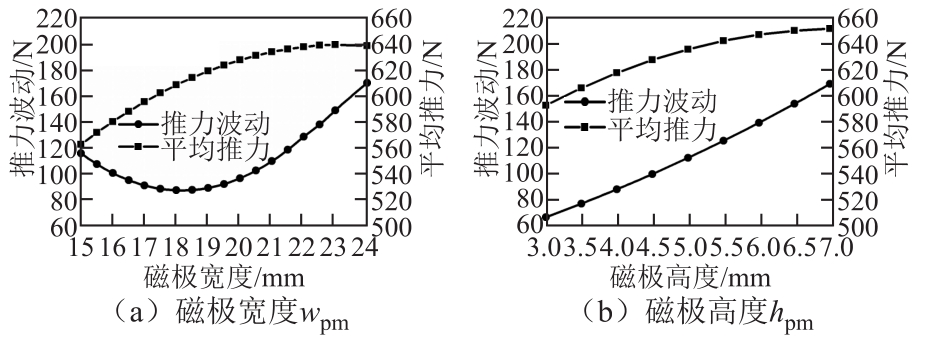
图5 磁极宽度和高度与永磁直线同步电机平均堆力与推力波动的关系
Fig.5 The impact of magnet width and height on thrust ripple and average thrust of PMLSM
2 参数敏感性分析
影响永磁同步直线电机平均推力和推力波动的设计参数有很多,为降低优化问题维度,提高优化效率,本文采用Taguchi法对12个设计参数(辅助极位置 d和高度 h、弧形半径 R和弧度 θ,磁极宽度wpm和高度hpm,半闭口槽宽度bs0、bs1、bs2和高度hs0、hs1、hs2)进行敏感性分析,初级铁心长度ls因间接体现在辅助极设计参数中被略去。通过Taguchi法的信噪比分析和方差分析,选出敏感参数,为后文多目标优化奠定基础。具体过程是将12个设计参数分为两组:第一组是关于弧形辅助极和磁极的六个设计参数d、h、R、θ、wpm、hpm;第二组是关于半闭口槽的六个设计参数 bs0、bs1、bs2、hs0、hs1、hs2,分别进行参数敏感性分析。
2.1 第一组设计参数敏感性分析
首先,建立一张关于六个设计参数的L25(56)正交表,即进行变量数为6、变量水平数为5、试验次数为25。接着,利用有限元分析计算出每次试验的目标值,包括推力波动和平均推力,填入表中;然后,对正交表进行信噪比分析和方差分析,推力波动的信噪比目标选择“望小”,平均推力的信噪比目标选择“望大”,信噪比分析和方差分析结果分别如图6和表2所示。

图6 第一组参数信噪比分析
Fig.6 Signal noise ratio analysis of the first set of parameters
表2 第一组设计参数方差分析
Tab.2 Analysis of variance of the first set of design parameters
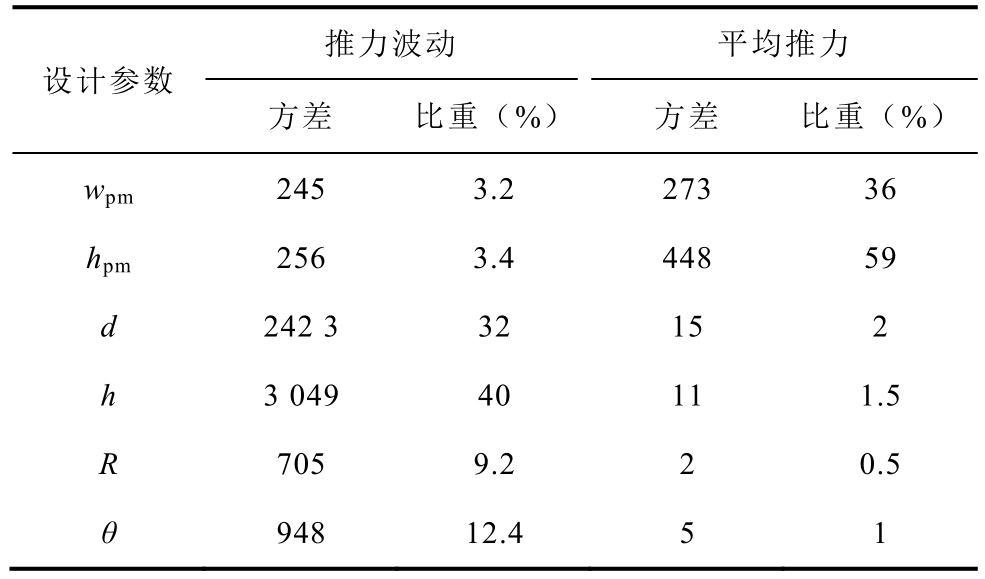
推力波动 平均推力设计参数方差 比重(%) 方差 比重(%)wpm 245 3.2 273 36 hpm 256 3.4 448 59 d 242 3 32 15 2 h 3 049 40 11 1.5 R 705 9.2 2 0.5 θ 948 12.4 5 1
由图6和表2可看出,对推力波动敏感的设计参数是d和h,而对平均推力敏感的设计参数是wpm和hpm。将d、h、wpm、hpm这四个变量选出确定为优化变量。至于对推力波动和平均推力影响比重都小的弧形半径R和弧度θ,根据图6的信噪比分析结果将两者值固定为R=16mm,θ=50°。
2.2 第二组设计参数敏感性分析
同样的步骤对第二组关于半闭口槽的六个设计参数再操作一次,信噪分析比和方差分析结果分别如图7和表3所示。
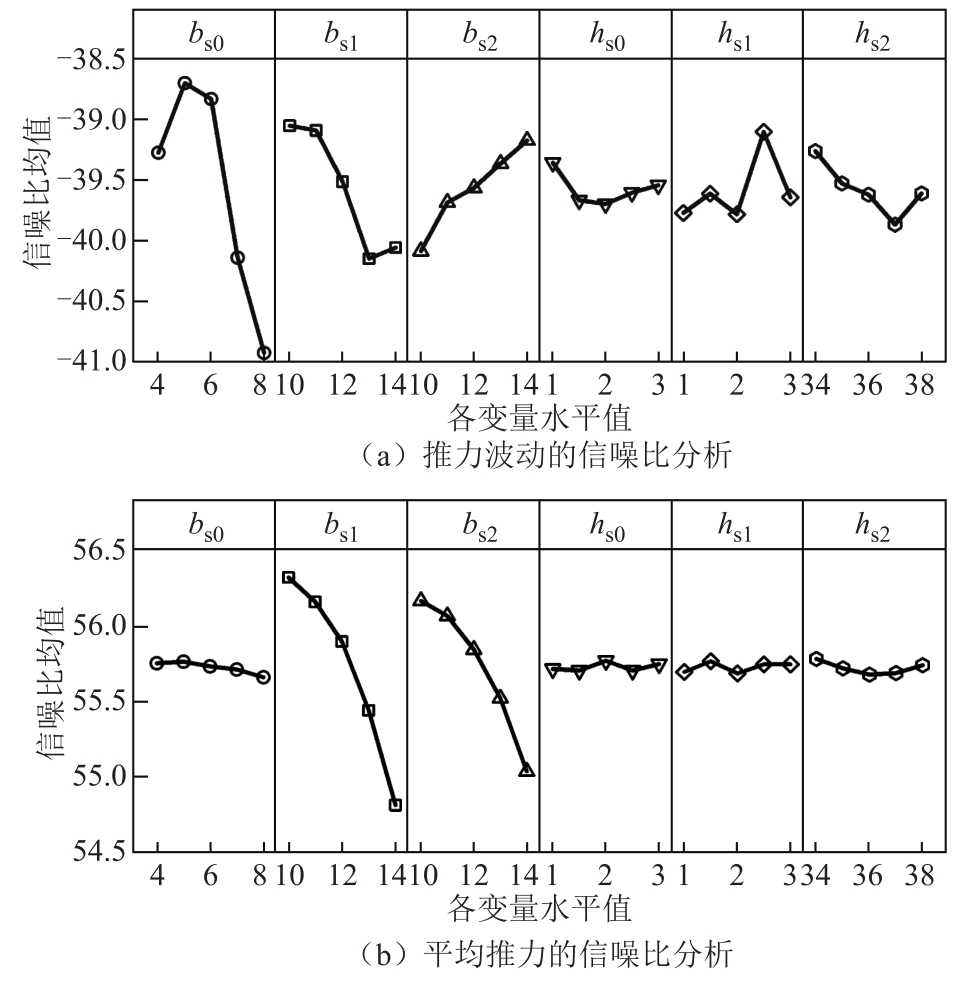
图7 第二组参数信噪比分析
Fig.7 Signal noise ratio analysis of the second set of parameters
表3 第二组设计参数方差分析
Tab.3 Analysis of variance of the second set of design parameters

推力波动 平均推力设计参数方差 比重(%) 方差 比重(%)bs0 439 65 47.8 0.4 bs1 129 19 696 0 62 bs2 41 6 403 5 36 hs0 9.5 1 22 0.2 hs1 35.4 5 47 0.4 hs2 18.7 3 50.3 0.5
图7信噪比分析结果和表3方差分析结果显示,半闭口槽的六个设计参数中对推力波动最敏感的参数是bs0,对平均推力敏感的参数是bs1和bs2。
本文最终采用原始bs1=bs2的平行槽结构,确定bs0和bs1为优化变量。其他参数影响比重小,分别固定为:hs0=1mm、hs1=2.5mm、hs2=34mm。
综上,确定弧形辅助极的位置 d和高度 h、磁极的宽度wpm和高度hpm、半闭口槽的槽口宽度bs0和槽宽 bs1共六个设计参数为优化变量,为下文的多目标优化奠定基础。
3 多目标优化
本文以上述六个敏感设计参数为优化变量,其约束条件为

优化目标是获得小的推力波动和大的平均推力,目标函数采用标幺值
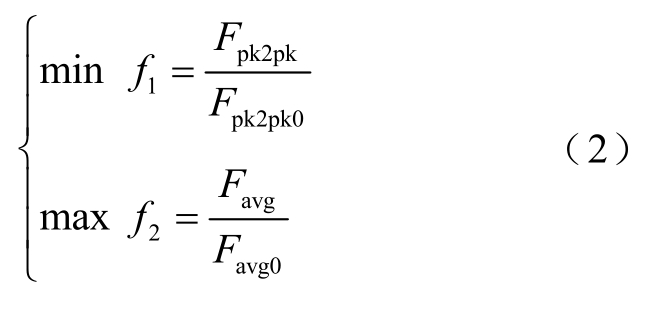
式中,Fpk2pk为推力波动;Fpk2pk0为推力波动原始值;Favg为平均推力;Favg0为平均推力原始值。
本文研究一种 Kriging代理模型与多目标粒子群优化算法相结合的优化设计方法,优化过程为:
(1)试验设计,对六个优化变量采用拉丁超立方试验设计,获取分布均匀的样本空间,有限元分析获取对应的目标函数值。
(2)代理模型,选取代理模型构建样本点中变量与目标函数值之间的函数关系。对于 Kriging模型,采用期望提高的加点准则,优化第一阶段多目标粒子群优化的目标函数为推力波动和平均推力的期望提高E[f1]和E[f2],目的是采用尽量少的样本点获取高精度预测的模型。
(3)多目标粒子群优化,也称优化第二阶段,以推力波动和平均推力为优化目标,算法中引入变异操作,获得两目标函数解的Pareto前沿。
3.1 试验设计
利用 Matlab的 lhsdesign函数来获得基于maxmin准则的拉丁超立方试验设计,样本空间维度和样本点数同样设为6和80,迭代次数设为200。对采样后的样本分别建立有限元模型,通过有限元分析得到每个样本点的推力波动和平均推力值。
3.2 代理模型
试验设计获得80个样本点后,分别利用多项式响应面模型和 Kriging模型来建立优化变量与目标函数之间代理模型。多项式响应面模型为

Kriging模型无具体的表达式,其回归部分为二次型,随机部分的相关函数采用高斯函数。代理模型建立后,利用第2节中的25组样本点进行检验,结果见表4。
表4 代理模型检验
Tab.4 Check of surrogate model

平均推力 推力波动代理模型多项式 Kriging 多项式 Kriging 期望提高的Kriging与有限元的方均误差 4.0 2.1 35.8 27.1 2.2
可以看出,平均推力与优化变量的函数关系简单,多项式模型和 Kriging模型皆能获得比较好的拟合效果。而对于推力波动,其与优化变量的函数关系复杂,非线性程度高,两模型都未能取得很好的拟合效果。但 Kriging模型通过期望提高的加点准则,样本点由初始的80个加到116个,最后获得较为理想的拟合效果。
3.3 基于Kriging模型的多目标粒子群优化
本文中,采用 Kriging模型辅助的多目标粒子群优化(Multi-Objective Particle Swarm Optimization,MOPSO)来实现永磁直线同步电机的多目标优化。其中,粒子的适应度计算由Kriging模型来完成,算法中引入变异操作,避免MOPSO算法过早陷入局部最优的可能性。
粒子群算法的结构形式十分简单,其主体部分是粒子速度和位置的更新公式,即
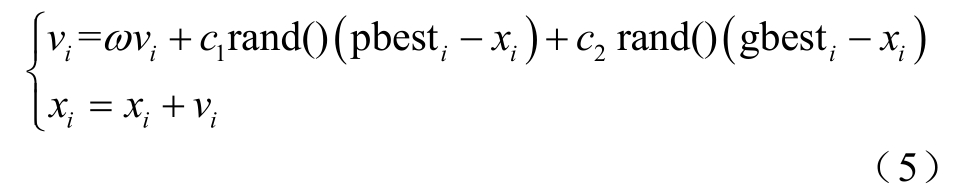
式中,vi为粒子速度;xi为粒子位置;ω为惯性权重;rand()为介于(0,1)之间的随机数;c1和c2是学习因子。
整个优化过程在Matlab中进行迭代运算,两目标函数值随着迭代次数变化的分布如图8所示。
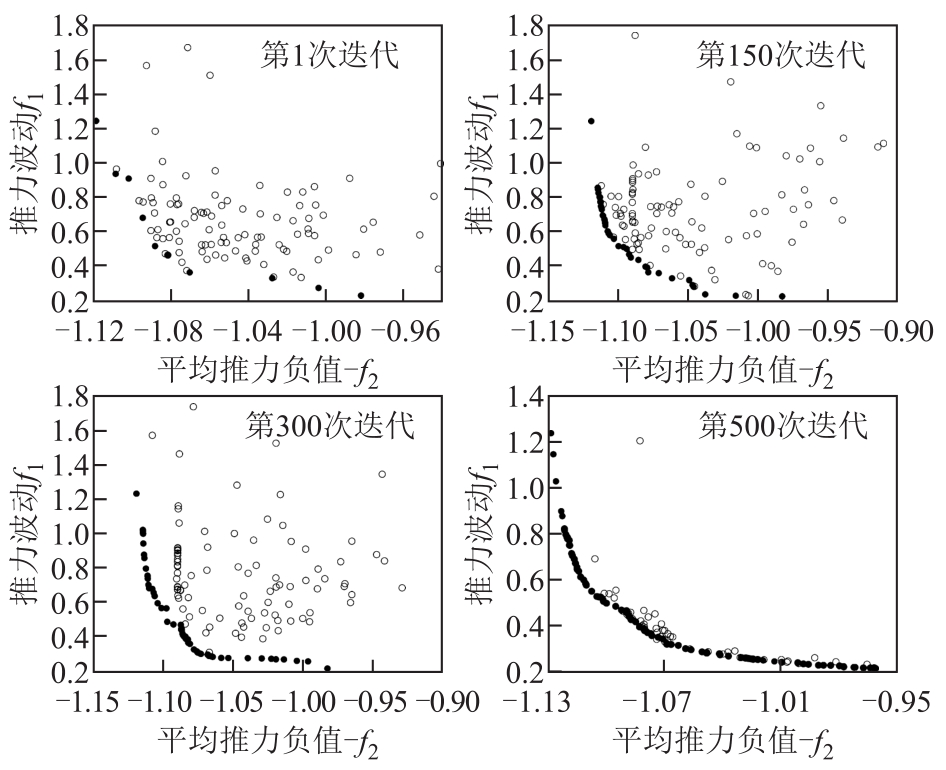
图8 不同迭代次数时的目标函数值分布
Fig.8 Distribution of objective function values at different iterations
可以看出,当迭代次数达到500时,MOPSO算法变化趋势不大,基本可以认为寻优结束。优化后的电机参数见表5,优化结果见表6和表7。
表5 平板型永磁直线同步电机设计参数优化结果
Tab.5 Optimization results of design parameters for flat-type PMLSM
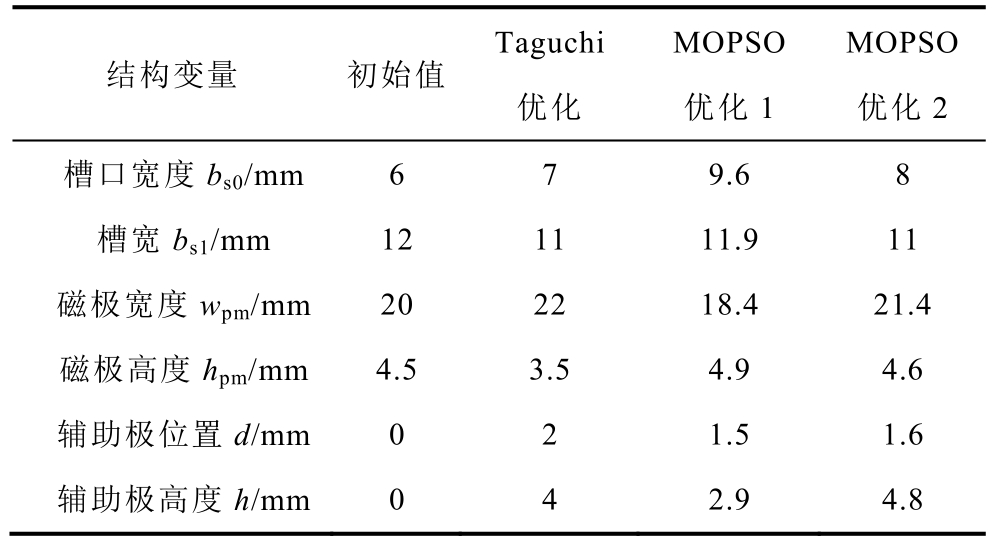
结构变量 初始值Taguchi优化MOPSO优化1 MOPSO优化2槽口宽度bs0/mm 6 7 9.6 8槽宽bs1/mm 12 11 11.9 11磁极宽度wpm/mm 20 22 18.4 21.4磁极高度hpm/mm 4.5 3.5 4.9 4.6辅助极位置d/mm 0 2 1.5 1.6辅助极高度h/mm 0 4 2.9 4.8
表6 平板型永磁直线同步电机优化结果
Tab.6 Optimization results of flat-type PMLSM
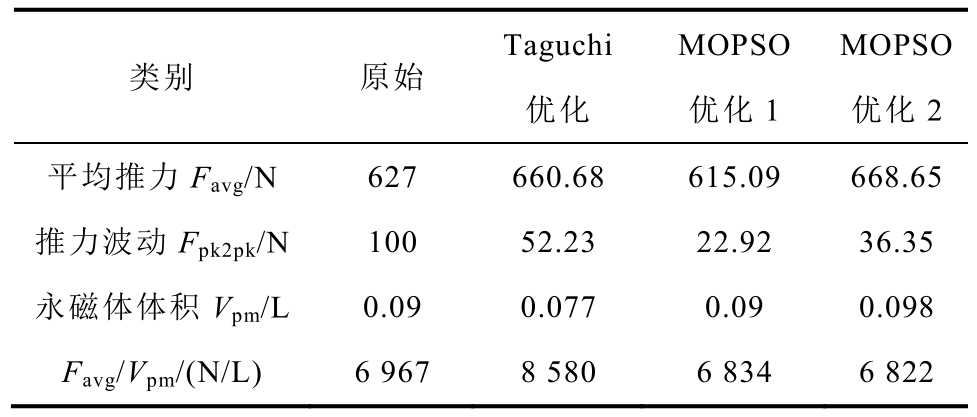
类别 原始Taguchi优化MOPSO优化1 MOPSO优化2平均推力Favg/N 627 660.68 615.09 668.65推力波动Fpk2pk/N 100 52.23 22.92 36.35永磁体体积Vpm/L 0.09 0.077 0.09 0.098 Favg/Vpm/(N/L) 6 967 8 580 6 834 6 822
表7 平板型永磁直线同步电机斜极优化结果
Tab.7 The skew optimization results of PMLSM

斜极8mm类别原始 Taguchi优化MOPSO优化1 MOPSO优化2平均推力Favg/N 595.3 630 584.8 640推力波动Fpk2pk/N 28.5 10 6 8永磁体体积Vpm/L 0.09 0.077 0.09 0.098 Favg/Vpm/(N/L) 6 614 8 182 6 498 6 531
由表6可以看出,若以减小推力波动为主要目标,MOPSO优化1的电机能获得最小的推力波动,其与原始推力波动相比减小了77%,对应的平均推力与原始平均推力相比下降了2%;若兼顾减小推力波动和提高平均推力,MOPSO优化 2的电机相比于原始电机,推力波动减小64%的同时其平均推力提高了6.6%。基于Taguchi法优化的电机,其推力波动和平均推力也分别获得 48%的减小和 5%的提高,虽然优化效果没有MOPSO优化2那么显著,但在单位体积永磁体的平均推力方面最大,该优化有效地提高了永磁体利用率。
优化后的电机主要残留6次以上谐波,可采用磁极斜极技术进一步地削弱推力波动。表7显示斜极8mm的原始电机,推力波动由100N减小到28.5N,减小了71.5%,平均推力由627N降到595.3N,下降了 5.06%。而斜极 8mm的 MOPSO优化 2的电机,推力波动进一步从36.35N减小到8N,减小了78%,平均推力由668.65N降到640N,下降了4.3%。可以看出,斜极是减小推力波动的有效措施,但过大的斜极距离将会使电机平均推力大幅度降低。因此小距离的斜极对平均推力影响很小,且抑制推力波动效果显著。
4 实验验证
依据本文优化的设计参数,就平板型永磁直线同步电机的实验测试平台所需装置及器件进行了选型。在完成测试平台的设计后,加工出样机和测试平台部件,搭建出了实验测试平台如图9所示。

图9 平板型永磁直线同步电机实验测试平台
Fig.9 Flat-type PMLSM experimental test platform
测得电机在126mm/s速度下的实验和有限元反电动势波形如图10所示。
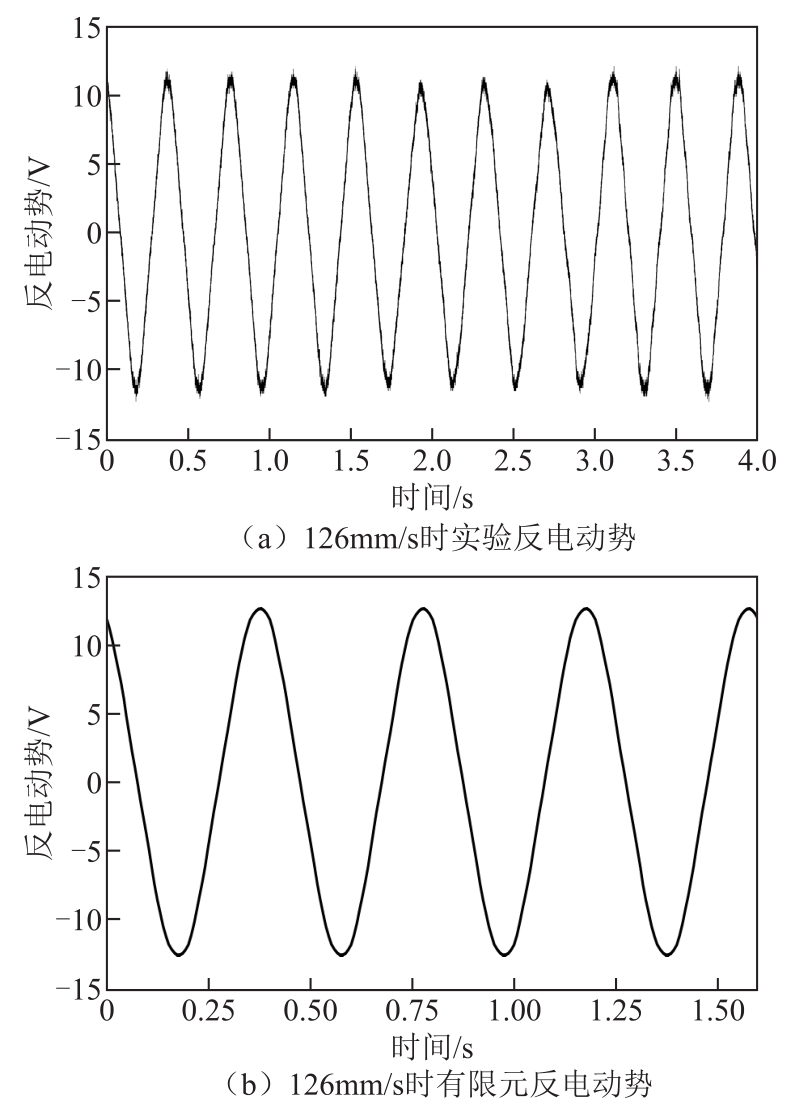
图10 实验与有限元反电动势
Fig.10 Back EMF of experiment and finite element
图 10a显示,1.5~3s由于斜极其反电动势幅值略微减小。实验反电动势峰值为 12V,计算得到反电动势常数为 95.2V/(m/s),而有限元分析的反电动势峰值为12.5V,计算得反电动势常数为99.2V/(m/s),二者相差4.2%,波形基本吻合。基于反电动势常数与推力常数成正比,故反电动势实验可以验证推力的优化,由此可见电机的实际优化效果与仿真一致,斜极也起到了优化的效果,在几乎没有减小平均推力的情况下推力波动得到了抑制。
5 结论
本文对12槽10极平板型永磁直线同步电机进行优化设计。电机设计参数的有限元分析结果显示,初级铁心最佳长度与理论分析的kτ+τ/2略有偏差,但理论结果为快速锁定最佳长度有参考价值;初级弧形辅助极主要对推力波动有影响,影响显著的设计参数为辅助极位置和高度;中间槽和端部半填槽两者的槽口宽度优化时推力波动最小和平均推力最大未落在同一点处,磁极用量与推力波动和平均推力基本呈正比关系,这些在优化设计时应统筹考虑。
在优化过程中,基于 Taguchi法的敏感性分析有助提炼敏感的设计参数,结果显示弧形辅助极的位置d和高度h、磁极的宽度wpm和高度hpm、半闭口槽的槽口宽度bs0和槽宽bs1是影响推力特性的敏感参数。通过对这六个敏感参数进行拉丁超立方试验设计和 Kriging辅助的多目标粒子群优化,优化后的平板型永磁直线同步电机的推力波动较原始减小了64%,平均推力提高了6.6%。优化后的平板型永磁直线同步电机推力中主要残留6次谐波,配合斜极,其推力波动可进一步达到92%的减小量且平均推力仍保有2%的提高。最后,实验与有限元分析的反电动势进行对比,波形吻合,且两者反电动势常数相差 4.2%,实验验证了有限元分析的正确性。
[1]许孝卓, 孙震, 汪旭东, 等. Halbach交替极永磁同步直线电机特性分析[J]. 电工技术学报, 2019,34(9): 1825-1833.Xu Xiaozhuo, Sun Zhen, Wang Xudong, et al.Characteristic of a novel permanent magnet linear synchronous motor with Halbach array consequentpole[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1825-1833.
[2]凌志健, 赵文祥, 吉敬华. 高推力永磁直线作动器及其关键技术综述[J]. 电工技术学报, 2020, 35(5):1022-1035.Ling Zhijian, Zhao Wenxiang, Ji Jinghua. Overview of high force density permanent magnet linear actuator and its key technology[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1022-1035.
[3]金鸿雁, 赵希梅. 基于Sugeno型模糊神经网络和互补滑模控制器的双直线电机伺服系统同步控制[J]. 电工技术学报, 2019, 34(13): 2726-2733.Jin Hongyan, Zhao Ximei. Dual linear motors servo system synchronization control based on Sugeno type fuzzy neural network and complementary sliding mode controller[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2726-2733.
[4]曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020,35(5): 1001-1012.Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001-1012.
[5]韩一, 聂子玲, 朱俊杰, 等. 考虑动态边端效应的六相直线感应电机数学模型及矢量控制[J]. 电机与控制学报, 2019, 23(3): 9-17.Han Yi, Nie Ziling, Zhu Junjie, et al. Mathematical model and vector control of six-phase linear induction motor considering dynamic end effect[J]. Electric Machines and Control, 2019, 23(3): 9-17.
[6]Rui Wanzhi, Xu Mingjin, Guo Penghui, et al.Improved study on position measurement system for linear motor applied in electromagnetic launch system[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2): 216-220.
[7]张静, 余海涛, 施振川. 一种波浪发电装置用低速双动子永磁直线电机运行机理研究[J]. 电工技术学报, 2020, 33(19): 4553-4562.Zhang Jing, Yu Haitao, Shi Zhenchuan. Research on a tubular linear permanent magnet machines with dual translators for low speed wave energy conversion[J].Transactions of China Electrotechnical Society, 2020,33(19): 4553-4562.
[8]韩雪岩, 祁坤, 张哲, 等. 永磁同步直线电机磁阻力分析及抑制措施[J]. 电工技术学报, 2015, 30(6): 70-76.Han Xueyan, Qi Kun, Zhang Zhe, et al. Magnetic drag analysis and suppression measures of permanent magnet synchronous linear motors[J]. Transactions of the China Electrotechnical Society, 2015, 30(6): 70-76.
[9]Hu Hengzai, Liu Xiangdong, Zhao Jing, et al. Analysis and minimization of detent end force in linear permanent magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2018, 65(3):2475-2486.
[10]Cui Fengrui, Sun Zhaolong, Xu Wei, et al.Comparative analysis of bilateral permanent magnet linear synchronous motors with different structures [J].CES Transactions on Electrical Machines and Systems,2020, 4(2): 142-150.
[11]Zhu Yuwu, Koo D, Cho Y. Detent force minimization of permanent magnet linear synchronous motor by means of two different methods[J]. IEEE Transactions on Magnetics, 2008, 44(11): 4345-4348.
[12]Wang Canfei, Shen Jianxin, Wang Yu, et al. A new method for reduction of detent force in permanent magnet flux-switching linear motors[J]. IEEE Transactions on Magnetics, 2009, 45(6): 2843-2846.
[13]Huang Xuzhen, Yu Hanchuan, Zhou Bo, et al. Detentforce minimization of double-sided permanent magnet linear synchronous motor by shifting one of the primary components[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 180-191.
[14]Kim S, Park E, Jung S, et al. Optimal design of reformed auxiliary teeth for reducing end detent force of stationary discontinuous armature PMLSM[J].IEEE Transactions on Applied Super-conductivity,2016, 26(4): 1-5.
[15]吕刚, 张贤. 不同槽配合格栅型直线感应电机电磁特性研究[J]. 电机与控制学报, 2019, 23(5): 18-24.Lü Gang, Zhang Xian. Investigation of electromagnetic characteristics of linear induction motor with ladder-type secondary under different slot combination[J]. Electric Machines and Control, 2019,23(5): 18-24.
[16]杨玉波, 王秀和, 陈谢杰, 等. 基于不等槽口宽配合的永磁电动机齿槽转矩削弱方法[J]. 电工技术学报, 2005, 20(3): 40-44.Yang Yubo, Wang Xiuhe, Chen Xiejie, et al. Cogging torque reduction method of permanent magnet motors based on unequal slot width coordination[J].Transactions of China Electrotechnical Society, 2005,20(3): 40-44.
[17]黄克峰, 李槐树, 周羽. 利用辅助槽削弱齿槽力的方法研究[J]. 电机与控制学报, 2014, 18(3): 54-59.Huang Kefeng, Li Huaishu, Zhou Yu. Research on the method of using auxiliary slots to weaken the cogging force[J]. Journal of Electrical Machines and Control,2014, 18(3): 54-59.
[18]崔皆凡, 秦超. 基于磁极偏移圆筒永磁直线电机齿槽力的削弱[J]. 沈阳工业大学学报, 2014, 36(2): 133-137.Cui Jiefan, Qin Chao. Cogging force reduction of cylindrical permanent magnet linear motor based on magnetic pole shift[J]. Journal of Shenyang University of Technology, 2014, 36(2): 133-137.