0 引言
电机设计通常仅考虑名义尺寸,因此加工过程的形位公差会使得实际电机的性能偏离设计值。为此,研究人员分析了永磁体尺寸误差对齿槽转矩[1-6]、反电动势[7]等的影响,进而提出了一些弥补电机性能的措施。但是,所有相关研究都隐含了一个假定条件,即硅钢片叠装成铁心时是完全整齐的,而这与实际情况不符。
在内置式永磁同步电机或无刷直流电机中,永磁体与转子硅钢片采用间隙配合,其间隙大小取决于加工工艺。若硅钢片采用高速冲床冲制和叠装,则配合间隙较小,且冲片叠装整齐,可以忽略叠装错位。但是,采用普通冲床冲制及手工叠装时,叠装错位比较严重,因此配合间隙必须设计得比较大。
根据已有文献的分析可知,较大的配合间隙显然会削弱气隙磁通密度。但是,冲片的叠装错位对气隙磁通密度又会带来什么影响?这在国内外文献中尚未见报道。本文针对内置式永磁电机搭建简化模型,分别就永磁体与硅钢片的间隙配合、硅钢片叠装错位对气隙磁场的影响进行理论分析和数值仿真。
1 名义尺寸下的理想电机
为了专注于研究间隙配合及叠装错位的影响而避免其他因素的干扰,并考虑三维有限元作精细网格剖分对计算资源的巨大需求,对永磁电机的物理模型进行简化:仅考虑一对极的情况,定、转子铁心用 “回”字形铁心替代,并在“转子铁心”中放置两个永磁体。简化模型如图1所示。假定电机无加工误差,均为名义尺寸,永磁体与转子冲片的配合没有间隙,冲片叠装完全整齐。

图1 理想电机的简化模型
Fig.1 Simplified model of ideal motor
以磁极中心位置(即图1中的仿真点位置)的气隙磁通密度为例进行研究。沿着图1中的主磁路(如虚线所示)做剖视图,则得图2。其中的叠厚方向就是图1的Z轴方向,可以看到定子、转子铁心均由若干硅钢片整齐叠装而成。图2的最左端应与最右端连接在一起,构成完整的定子磁路。主磁路中各部分的磁阻包括:Rs是定子铁心磁阻(注:图2中为了表示清晰,标注了两个Rs,但是实际上整个定子铁心用一个 Rs等效);两个 Rg表示两个极下的气隙磁阻;两个Rr2表示转子上气隙与永磁体之间铁心部位(即极靴)的磁阻;两个Rpm为两个永磁体的磁阻;而Rr1是转子上两个永磁体之间的铁心部位(即转子轭部)的磁阻。图2只标示了磁路各部分的磁阻,而没有标示永磁体的磁动势。为图示清晰,图1的二维图和图2均未按实际尺寸比例描绘。

图2 理想电机的主磁路
Fig.2 Main magnetic circuit in ideal motor
得到主磁路各部分的磁阻为

式中,Lpm、Lr1、Lr2、Lg、Ls分别为永磁体、磁阻Rr1、Rr2、Rg、Rs对应磁路的长度。为磁路各部分的长度;A为磁通经过的面积。永磁体磁导率μpm约等于空气磁导率μ0,铁心磁导率是μcore。令永磁体具有线性去磁曲线,剩余磁通密度为Br,则气隙磁通密度为
式中,系数KB表示极靴与永磁体不等宽、转子磁桥等各个部位的漏磁、三维效应等因素的影响,定、转子铁心磁阻对气隙磁通密度的影响也计入KB中。
考虑到磁路法的精度有限,式(1)和式(2)并不用以计算气隙磁通密度,而用于说明影响气隙磁通密度大小的因素。后续推导的磁通密度表达式同样如此。气隙磁通密度的精确计算则采用三维有限元法,如图1中的三维模型所示。并且模型中每片硅钢片单独作为一个零件进行刻画,而不是把整个铁心作为一个均质的整体。网格剖分时,每片硅钢片在厚度方向分两层,每个气隙(包括下文考虑的二次气隙)在长度方向分成2~3层,因此网格剖分足够精细。铁心由40片0.5mm厚的硅钢片叠装而成,即叠厚20mm;钕铁硼永磁体高度(Z轴方向)与铁心叠厚一致,宽度(Y轴方向)7mm,沿X轴方向充磁且厚度Lpm为3mm,剩磁通Br为1.37T,相对磁导率为1.014;硅钢片中永磁体槽的宽度(Y轴方向)为9mm,磁桥宽度0.5mm;气隙长度(X轴方向)Lg为0.8mm。图1仿真点处的气隙磁通密度波形如图3所示。忽略端部效应,即不考虑模型顶部和底部各3片硅钢片面对的气隙磁通密度,可见由于硅钢片叠装整齐,因此气隙磁通密度均匀,其值为427mT(称为理想磁通密度值)。

图3 理想电机的气隙磁通密度
Fig.3 Air gap field of ideal motor
2 考虑尺寸公差但假定硅钢片叠装整齐
为简化模型,假定两块永磁体实际厚度均为Lpm+Lσ1,硅钢片上永磁体槽的实际厚度均为Lpm+Lσ2,由于是间隙配合,Lσ2>Lσ1。假定永磁体与转子铁心之间的二次气隙均匀分布在每块永磁体的两侧,即每个二次气隙长度为(Lσ 2 −Lσ 1)/2,其磁阻为Rσ,则主磁路的磁阻模型如图 4所示。二 次 气 隙( L σ 2 −Lσ 1 )/2远 小 于 主 气 隙 Lg, 所 以Rσ ≪Rg。

图4 转子铁心叠装整齐的实际电机主磁路
Fig.4 Main magnetic circuit in real motor with evenly stacked rotor core
主磁路各部分的磁阻为

则气隙磁通密度为

虽然并不用式(4)直接计算气隙磁通密度,但是对比式(4)和式(2)可以看出间隙配合的二次气隙所造成的影响。由于永磁体的公差Lσ1相对其厚度Lpm较小,而 L σ 2 −Lσ1相对气隙长度Lg较大,因此间隙配合往往会减小气隙磁通密度,特别是当永磁体厚度为负公差(即Lσ1为负值)时,气隙磁通密度必定减小。
在不同加工条件下,公差配合有不同要求。一般来说,永磁体的公差带为-0.05~+0.05mm;采用高速冲床冲制硅钢片时,永磁体槽的公差带一般为+0.05~+0.1mm,而采用普通冲床时为+0.15~+0.2mm。假定两种冲制工艺下都能把硅钢片叠装得完全整齐。分别对公差配合的极端情况进行三维有限元仿真,所得气隙磁通密度波形与图3类似,忽略端部效应后气隙磁通密度依然均匀,其值为σ:①Lσ1=-0.05mm,Lσ2=+0.1mm,磁通密度为403mT,是理想磁通密度的 94.4%;②Lσ1=+0.05mm,Lσ2=+0.05mm,磁通密度为 430mT,是理想磁通密度的 100.7%;③ Lσ1=-0.05mm,Lσ2=+0.2mm,磁通密度为 389mT,是理想磁通密度的 91.1%;④Lσ1=+0.05mm,Lσ2=+0.15mm,磁通密度 413mT,是理想磁通密度的 96.7%。其中,①和②对应高速冲床工艺。③和④对应普通冲床工艺,假定叠装整齐,只要加工工艺引入二次气隙,必定会减小气隙磁通密度,这与对比式(4)和式(2)的定性分析结果一致,也是以往文献所报道过的[1-7]。
3 考虑间隙配合且转子硅钢片叠装错位
采用普通冲床加工硅钢片并手工叠装铁心时,配合间隙设计得较大,而且冲片叠装欠整齐。为专注于分析永磁体与转子硅钢片间隙配合的影响,这里假定定子铁心叠装整齐,仅转子硅钢片沿永磁体充磁方向(即图1中X轴方向)叠装错位,则主磁路各部分的磁阻如图5所示。与图4相比,图5中增加了六个错位区域,如相邻虚线之间的狭小空间所示。假设硅钢片随机错位范围为±ΔL,则每个错位区域的磁路长度(即相邻虚线之间的距离)为2ΔL。另一方面,每个气隙和二次气隙的长度均减小了ΔL;转子铁心的轭部(磁阻的下标为r1)和每个极靴(磁阻下标r2)的长度均减小了2ΔL。
错位区域的等效磁导率用μmix表示,显然,其值在0μ和μcore之间,则主磁路各部分的磁阻为

图5 转子铁心沿永磁体充磁方向叠装错位的实际电机主磁路
Fig.5 Main magnetic circuit in real motor with rotor core misalignment in magnetization direction of magnets

则得气隙磁通密度为

对比式(6)和式(4)可知,在 μ mix>2μ0前提下, μmix越大、冲片叠装错位范围ΔL越大,都越有利于弥补间隙配合造成的气隙磁通密度削弱部分。
建立三维有限元仿真模型,用随机函数对转子每片硅钢片在±ΔL范围内进行随机错位。所得仿真点处的气隙磁通密度波形如图6所示。对比图6和图 3,可以清楚地看到硅钢片的细微错位在三维有限元模型中得到了充分的反映,使得气隙磁通密度不再均匀,而是出现了随机波动。
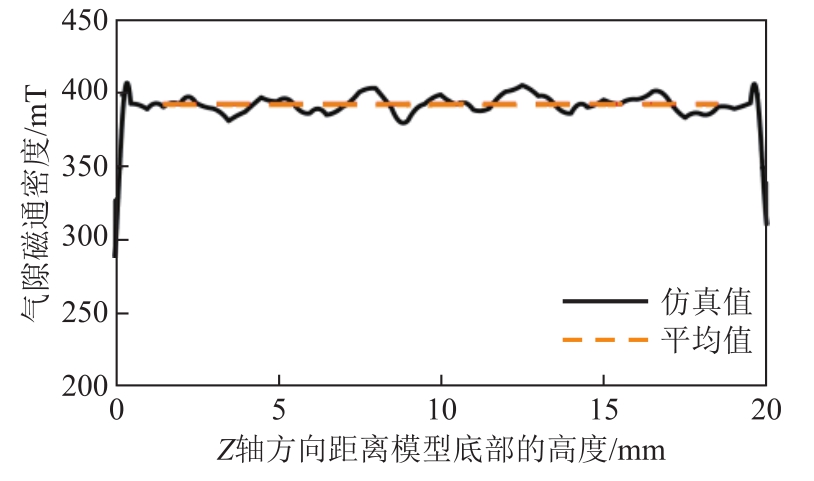
图6 转子铁心沿永磁体充磁方向叠装错位的实际电机的气隙磁通密度
Fig.6 Airgap field of real motor with rotor core misalignment in magnetization direction of magnets
针对普通冲床冲制的硅钢片,分别检验不同的错位范围±ΔL。对每种错位范围都进行多次随机错位和有限元仿真,并忽略端部效应后求取气隙磁通密度平均值,则得:⑤针对前述条件③,硅钢片错位范围±ΔL为±0.06mm,磁通密度为394mT,是理想磁通密度的 92.3%;⑥针对前述条件③,硅钢片错位范围±ΔL为±0.125mm,磁通密度为405mT,是理想磁通密度的 94.8%;⑦针对前述条件④,硅钢片错位范围±ΔL为±0.05mm,磁通密度为418mT,是理想磁通密度的97.9%。
对比⑤、⑥和③以及⑦和④,可以证明硅钢片叠装错位确实可以提升气隙磁通密度的大小,且错位范围越大则越有效。这与式(6)和式(4)的对比分析结果一致。
进一步,通过试凑法,利用三维有限元模型,推导了错位区域的等效相对磁导率 μ m ix /μ0,分别为2.21、2.45、2.22,均满足 μ m ix> 2μ0的条件,因此,定性地讲,有限元仿真与理论分析是一致的。
4 结论
众多文献已经报道,内置式永磁电机中永磁体与转子硅钢片之间的间隙配合会导致气隙磁通密度下降。本文通过磁路分析与三维有限元计算,证明了转子硅钢片沿永磁体充磁方向的叠装错位可以弥补间隙配合造成的气隙磁通密度下降。因此,采用高端装备提高加工精度固然是改善电机性能的基本要求;但是,在设备精度受限的情况下,在确定永磁体与转子硅钢片的间隙配合公差带之后,硅钢片叠装的不齐整性反而是有利的。本文的分析结果可以为内置式永磁电机以及具有类似转子结构的同步磁阻电机的形位公差设计及工艺要求提供参考。
[1]Ou Jing, Liu Yingzhen, Qu Ronghai. Experimental and theoretical research on cogging torque of PM synchronous motors considering manufacturing tolerances[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 3772-3783.
[2]Kim J, Yoon M, Hong J, et al. Analysis of cogging torque caused by manufacturing tolerances of surfacemounted permanent magnet synchronous motor for electric power steering[J]. IET Electric Power Applications, 2016, 10(8): 691-696.
[3]Gasparin L, Cernigoj A, Markic S, et al. Additional cogging torque components in permanent-magnet motors due to manufacturing imperfections[J]. IEEE Transactions on Magnetics, 2009, 45(3): 1210-1213.
[4]Coenen I, van der Giet M, Hameyer K. Manufacturing tolerances: estimation and prediction of cogging torque influenced by magnetization faults[J]. IEEE Transactions on Magnetics, 2012, 48(5): 1932-1936.
[5]夏彦. 表贴式永磁同步电机的齿槽转矩特性研究[D].武汉: 华中科技大学, 2017.
[6]孙建翎, 陈红. 计及加工误差的永磁电机齿槽转矩抑制研究[J]. 微电机, 2019, 52(8):42-47.Sun Jianling, Chen Hong. Study on cogging torque suppression of permanent magnet machine considering machining error[J]. Micro Motors, 2019, 52(8): 42-47.
[7]Lee S, Kim K, Cho S, et al. Optimal design of interior permanent magnet synchronous motor considering the manufacturing tolerances using Taguchi robust design[J]. IET Electric Power Applications, 2014, 8(1):23-28.