0 引言
目前，高速列车普遍采用电力牵引方式。受电弓是安装在高速列车上的一种从接触网上集取电流的专用设备，因此受电弓和接触网之间平稳的接触状态是保证列车受流质量优良的关键[1]，高速铁路受电弓-接触网系统示意图如图1所示。在高速列车受流质量的评价体系中，接触力是其非常重要的指标。随着高速列车速度的提升，受电弓与接触网之间复杂的耦合振动会更加剧烈，体现在接触力的波动变大，受流质量急剧变差，脆弱的弓网系统已经成为高速列车舒适性和可靠性提升的严重障碍[2]。当接触力波动幅度过大时，弓网系统容易出现离线、燃弧等现象，使得受流质量变差，受电弓也容易出现故障损坏。接触力过大时，既加重了受电弓滑板的磨损，同时也增加了运维成本。根据中国铁路总公司统计资料，牵引供电系统故障造成的铁路事故在2008年、2009和2010年分别占到了当年事故总数的28.8%、40.4%、29.6%，因此研究高速运行中受电弓-接触网系统的动态性能和改进措施对高速铁路安全运行有重要的意义[3]。
图1 高速铁路受电弓-接触网系统示意图
Fig.1 Schematic diagram of pantograph-catenary system of high speed railway
针对弓网接触力波动的问题，国内外学者对高速弓网关系进行了大量的分析与研究，比如优化受电弓结构[4]、优化接触网结构[5-6]和优化受电弓静态抬升力[7]等。由于受电弓结构优化难以及时调整，所以适应不同类型的接触网的灵活性较差。如果针对既有线路进行接触网结构优化，将涉及接触网的大规模改造，需要花费巨大的人力物力，成本极高。优化受电弓静态抬升力的作用效果又十分有限。
为解决上述问题，学者们提出受电弓主动控制方法以减小弓网接触力的波动。受电弓主动控制是根据弓网系统的部分状态量，运用现代控制理论，对受电弓施加控制力，通过调节受电弓弓头抬升量来减小弓网接触力的波动。与上面提到的方法相比，受电弓主动控制的适用性较高，该控制方法不需要针对具体类型的受电弓和接触网，控制算法确定的情况下只需调节控制参数便能应用于所有类型的弓网系统，并且受电弓主动控制只需适当改造受电弓，无需优化接触网的结构，无论是新建线路还是既有线路皆可应用，成本较低。
受电弓主动控制系统包括控制算法、量测系统和控制结构等。其中，控制算法是受电弓主动控制研究的核心和重点。文献[8]基于弓网接触力的伺服控制模型，设计了弓网接触力的线性二次型调节器（Linear Quadratic Regulator, LQR）。仿真结果表明，调节器能有效减小弓网接触力波动，改善弓网受流质量。文献[9]在弓网耦合振动系统全局输入-输出线性化模型的基础上，提出一种基于状态反馈线性化的弓网系统全局线性化主动控制策略。相较于LQR最优控制策略，对期望弓网接触压力均值都有更好的跟踪效果。文献[10]将鲁棒控制问题转换为最优控制问题，利用Lyapunov稳定性理论描述了一个合适的线性状态反馈控制律，以保证闭环系统的二次稳定性和性能鲁棒性，并通过仿真研究证明了有效性。文献[11]根据建立的弓网模型和接触力历史数据，利用预测控制技术，预测下一时刻接触力，使实际值接近于理论值。结果表明控制策略能有效抑制离线电弧的发生，改善了受流质量。文献[12]运用模糊自适应终端滑模控制解决弓网优载荷伺服控制问题，结果表明控制算法降低了对弓网模型精确性的要求，具有较好的伺服跟踪性能。文献[13]利用非线性系统的微分几何理论，构造微分同胚变换和状态反馈表达式，得到了受电弓线性化模型，设计反馈控制律解决弓网接触力的跟踪问题。研究结果表明，所提出的反馈线性化控制策略能有效解决弓网接触力的跟踪问题，为一定工况下弓网最优接触力的跟踪控制提供可行方案。
综上可知，大多数受电弓主动控制策略属于状态反馈控制方法，控制目标大都为减小接触力的波动，并没有考虑作动器的输出限制等实际问题；部分文献只对弓网接触力进行了估计，没有提及受电弓其他状态量的获取方法，在基于状态反馈的控制中，状态量的获取与精确性极为重要。控制算法的验证和分析大都在简单弓网模型上进行。在简单弓网模型中，接触网通常被看作为一根可变刚度的弹簧，与实际的接触网结构差别很大，不能完全反映接触网上波动传播和弓网系统振动状态。
本文以高速铁路受电弓-接触网系统为研究对象，以减小弓网接触力的波动，即降低接触力的标准差为主要目标，提出一种基于状态估计的受电弓鲁棒预测控制策略。首先，考虑到受电弓工作环境的强烈电磁干扰，提出一种考虑量测数据丢失的鲁棒卡尔曼滤波方法以获取受电弓的状态量，为控制器提供精确的受电弓状态估计值；然后，根据增广后的受电弓-接触网系统状态空间方程，设计基于状态估计的鲁棒预测控制方法；最后，在引用的非线性弓网系统模型上，验证了所提出的控制策略的有效性和鲁棒性。
1 问题描述
1.1 弓网系统模型
本文引用文献[14]中的弓网系统模型，该弓网系统模型通过受电弓归算质量模型和接触网有限元模型结合得到。
受电弓归算质量模型的动力学方程为
式中，m1、m2、m3分别为受电弓弓头、上框架、下框架的质量；k1、k2、k3分别为受电弓弓头、上框架、下框架的刚度；c1、c2、c3分别为受电弓弓头、上框架、下框架的阻尼；x1、x2、x3分别为受电弓弓头、上框架、下框架的位移；
分别为受电弓弓头、上框架、下框架的速度；
分别为各个质量块的加速度；Fpc为弓网之间的动态接触力；Fl为静态抬升力；u为主动控制力。
令状态量
动力学方程等效为
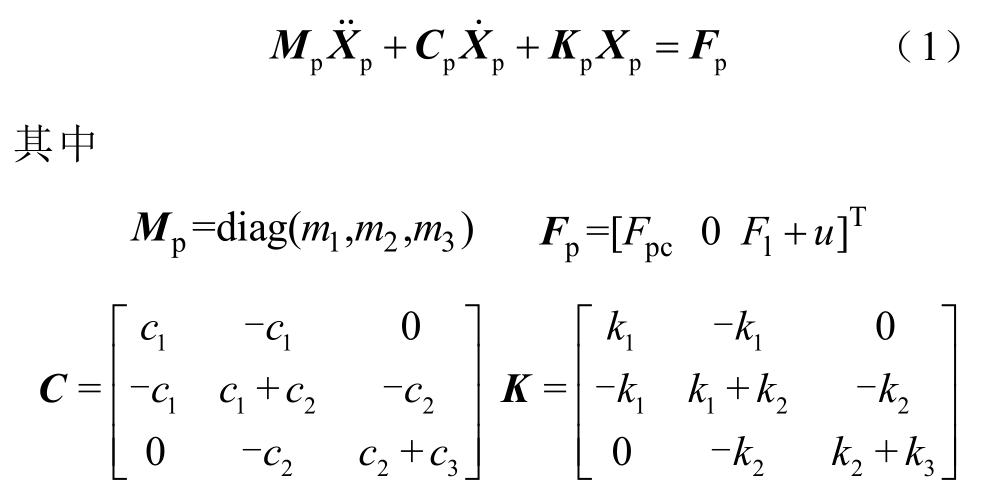
控制器可安装在有弓头、上下框架之间和下框架等位置，本文统一安装于下框架。
接触网有限元模型的动力学方程表示为
式中，Mc为接触网的集中质量矩阵；Kc为整体刚度矩阵；Cc为阻尼矩阵；
和Xc分别为接触网各个节点的加速度、速度及位移；Fc为外力。
根据式（1）和式（2），弓网系统模型表示为
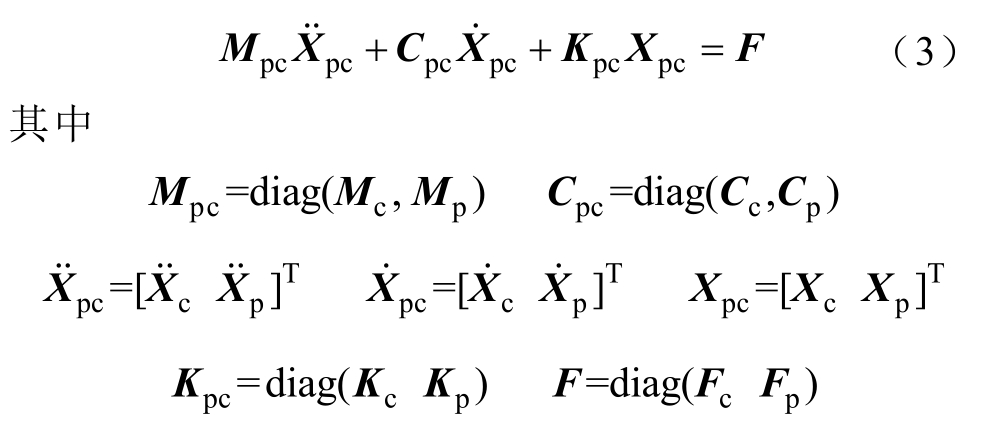
1.2 控制目标
在设计减小弓网接触力波动的控制器之前，应考虑以下几个方面。
1）减小弓网接触力波动：控制器的主要目标是在不影响弓网接触力平均值或影响较小的情况下降低接触力的标准差，即减小实时接触力Fpc(t)与接触力参考值Fr之间的差值
式中，e(t)为实时接触力与参考值的误差。
2）作动器输出限制：作为工程应用研究，实际中任何一种作动器都不可能输出无限能量。为了保证执行机构的稳定性能，必须在合理范围内限制控制力的大小。假定输出最大值为umax，则控制力的范围为
3）弓头抬升量限制：列车获取电能过程中，弓头抬升量是保证接触网正常工作的关键，必须保证主动控制不会让弓头抬升量超过安全范围。设抬升量最大值为x1max，则
在鲁棒预测控制器的设计阶段，需要一个面向控制的模型。接触线上刚度的不均匀分布是导致受电弓-接触网系统波动的主要原因，因此可以通过简化接触网对受电弓的影响来建立面向控制的受电弓-接触网系统模型。文献[15]利用有限元接触网模型计算得到接触网静态刚度系数，再用最小二乘法拟合获得平均刚度系数和刚度变化系数，即可得接触网刚度的表达式为
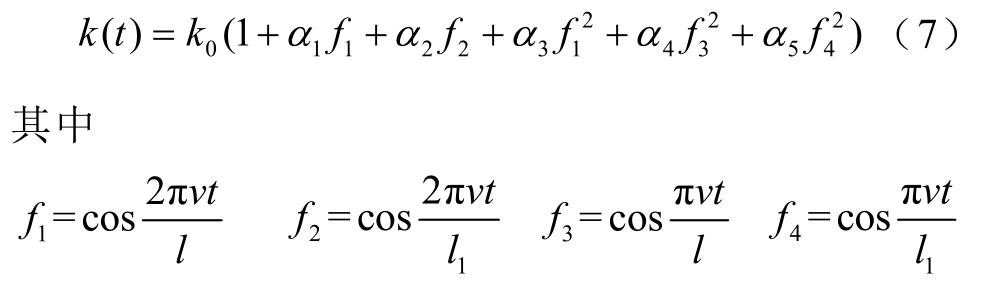
式中，v为车速；k0为接触网平均刚度系数；l为接触网跨距；l1为接触网相邻吊弦的间距； α 1、 α2、α3、 α4、 α5为接触网刚度变化系数。
结合式（1）和式（7），实时弓网接触力的表达式为 F p c ( t)=k(t)x1。令系统状态量
则弓网系统的状态空间方程为
式中，A、B、C为弓网系统状态空间方程的系数矩阵；u为系统输入；y为弓网接触力。系数矩阵具体表达式为
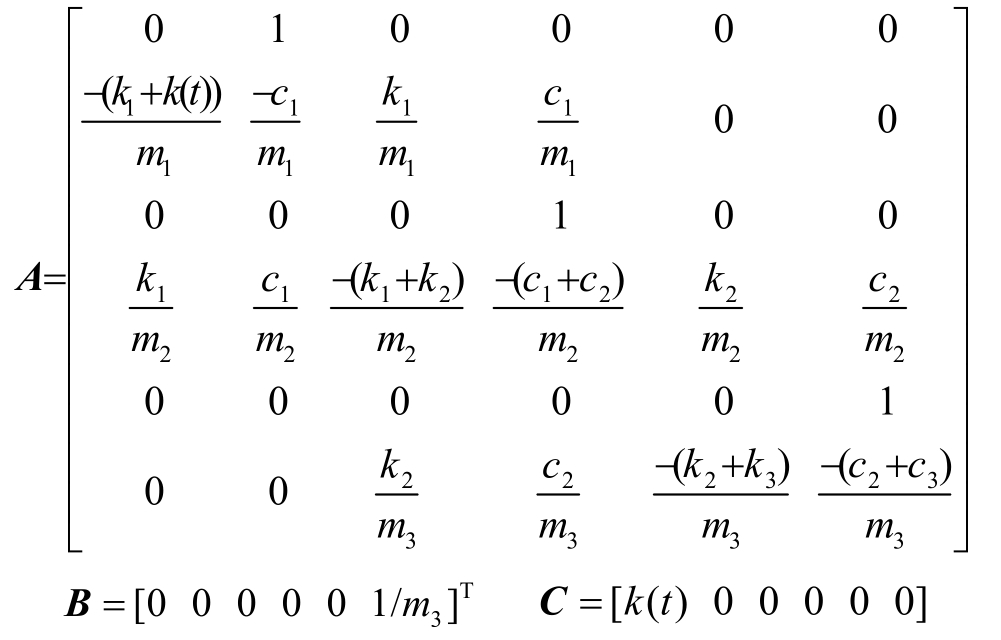
鲁棒预测控制器是通过最小化目标函数 J ∞(k)得到控制力 u ( k+i|k)，目标函数表达式为
式中，Q1和R1为对称正定加权矩阵；x ( k+i|k)为受电弓状态量，即位移和速度。因此min J ∞ (k)是对系统状态量的优化。而控制器的主要目标是减少接触力参考值与实际接触力的差值，弓网接触力是弓网系统的输出量而非状态量，因此需要将接触力跟踪误差的积分增广至弓网系统状态空间方程中。
结合式（4）～式（6），则式（8）增广形式为
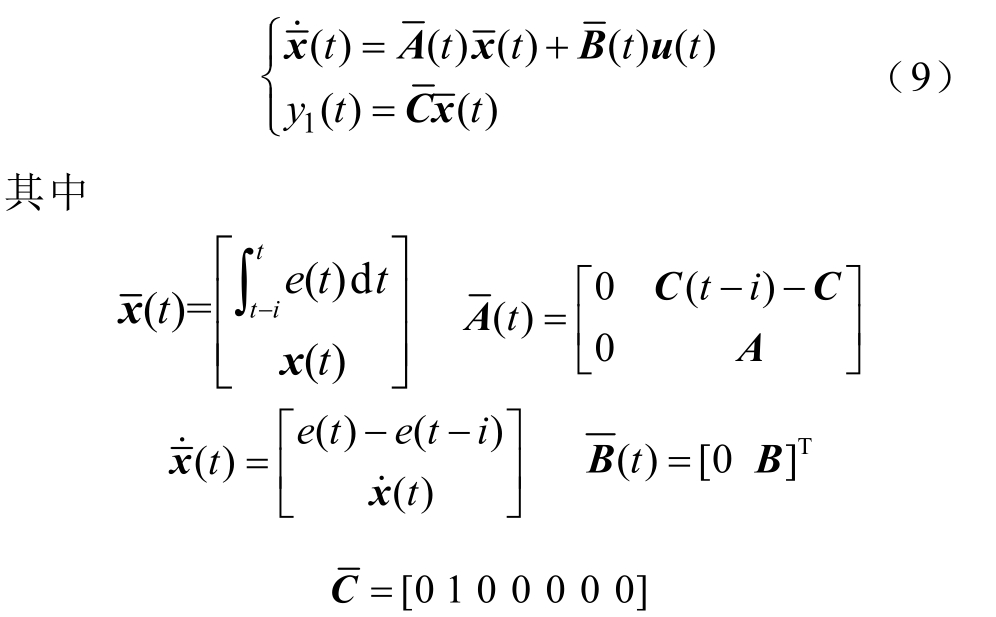
式中，y1(t)为受电弓弓头抬升量；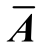
中的 C(t-i)表达式为C(t-i)=[k(t-i) 0 0 0 0 0]。
因此，整个问题可以转换为设计一个状态反馈控制律，即
式中，G(t)为控制增益矩阵，其由鲁棒预测控制器计算得到。
2 受电弓状态估计
由式（9）和式（10）可知，控制力的计算需要受电弓的状态量。然而，受电弓工作环境有强烈的电磁干扰，检测到的数据会包含大量的噪声成分，并有量测数据随机丢失的情况，同时在受电弓上安装多个传感器也会降低控制系统的可靠性。因此，本文通过状态估计方法估计受电弓的状态，不仅减少了传感器数量，而且还能获得较高精确度的受电弓状态量。可观测的状态量为受电弓质量块的垂直位移，采用改进后的卡尔曼滤波方程实时估计每个质量块的垂直位移和速度。
弓网系统的离散状态空间方程可以表示为
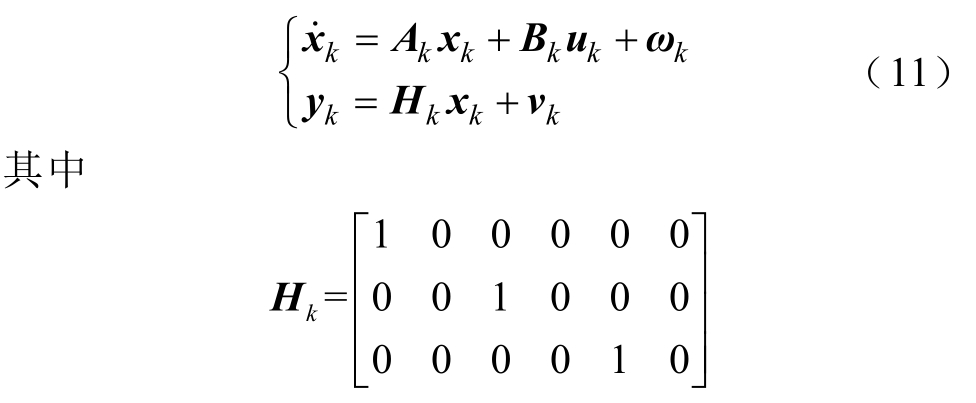
式中，Ak和Bk分别为与式（8）中A和B有关的系数矩阵；yk为量测输出；ωk为过程噪声；νk为量测噪声；ωk和νk为不相关的零均值高斯白噪声，其协方差矩阵为Qk和Rk；xk为k时刻的系统状态量；uk为系统输入。
γk是值为1或0的伯努利分布序列。γk=1表示弓网系统获得量测值，γ k =0表示量测失败即数据丢失，且不同时刻的γk是相互独立的，其统计特性为
当 γ k=1时，yk = Hkx k +νk ；当 γ k=0时，量测失败，系统不能得到量测值，此时定义当前时刻的虚观测值为[16]
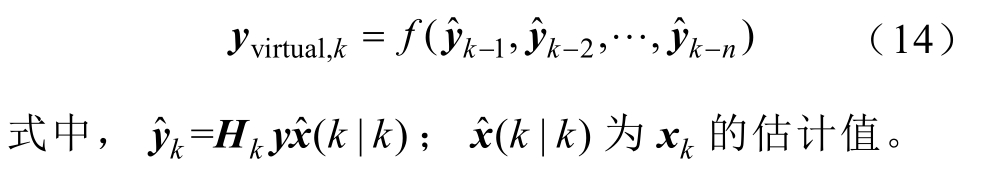
令数据获得时的观测值为 y r e al = Hkx k +νk ，虚观测值代替数据丢失时的观测信息，则等效的观测方程为
结合式（11）和式（15）给出标准卡尔曼滤波算法。
式中，
为k−1时刻对k时刻系统状态的预测值； P ( k|k−1)为预测值的协方差阵；Kk为卡尔曼增益；
为k时刻的状态估计值；P(k|k)为更新后的协方差阵。
由于虚观测值是在传感器观测值丢失时通过历史状态预测得到的，因此虚观测值相比于传感器真实观测值会有很大的误差，若直接将虚观测值代入卡尔曼滤波方程，则会增大状态估计的误差，同时由于环境的复杂性等原因，量测数据丢失的现象是不可避免的，经典的卡尔曼滤波方法不适合解决观测不确定的状态估计问题[16-22]。为此应用基于Huber的鲁棒卡尔曼滤波算法对受电弓状态进行估计[16]。将卡尔曼滤波方程的式（19）和式（20）修改为
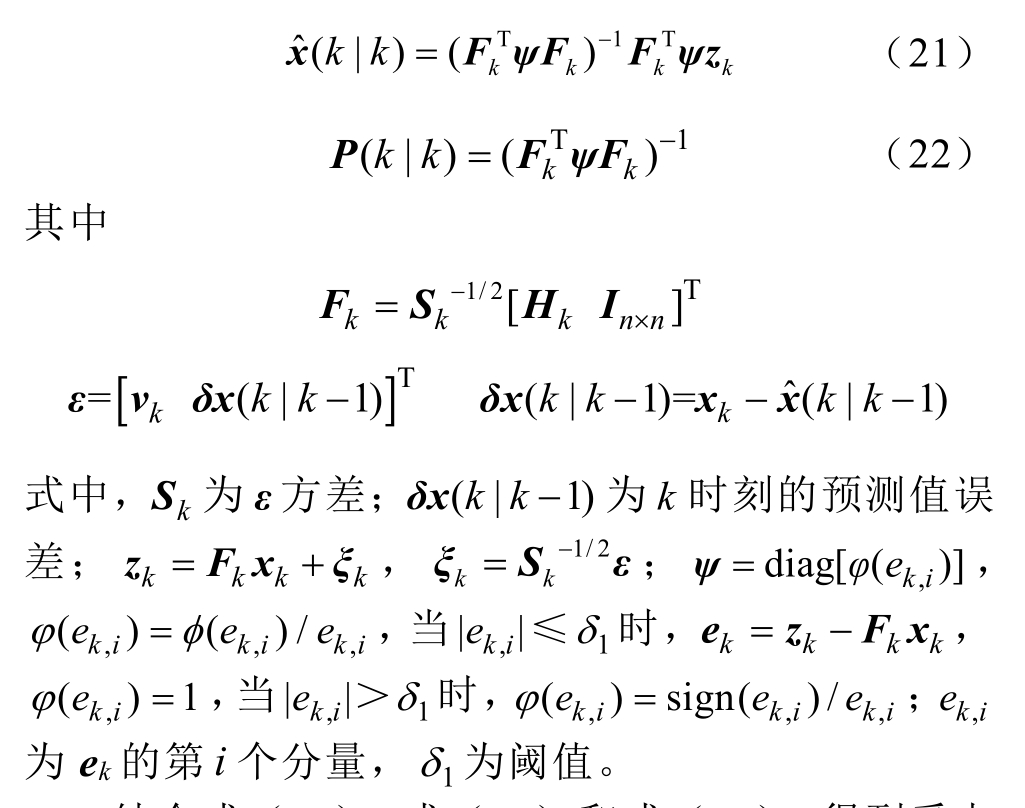
结合式（16）～式（19）和式（22），得到受电弓状态量量测数据丢失情况下的虚观测鲁棒卡尔曼滤波算法，为控制增益矩阵和控制力的计算提供实时受电弓状态估计值。
3 鲁棒预测控制器
受电弓复杂的工作环境会导致受电弓参数摄动，而传统模型预测控制在参数摄动的情况下，其控制效果会下降，为此设计受电弓鲁棒预测控制器[23]。将式（9）离散化，得到增广后的弓网系统离散状态空间方程为
式中，Q1和R1为对称正定加权矩阵，它表示在k时刻进行滚动优化时，应使模型参数在Ω内任意变化时对应于“最坏”情况的无穷时域性能指标最优。解决“极小-极大”优化问题的方法是给出极大问题的上界，将“极小-极大”优化问题转换为极小化问题。
为了解决控制变量数目无穷的问题，采用单一状态反馈控制律 u ( k + i |k ) = G x ( k + i |k),i ≥ 0，把系统状态保持在一个不变集内。
通过以上的转换，解决了“极小-极大”优化问题和控制变量数目无穷的问题，k时刻，G的表达式为
式中，Y从以下线性目标最小化问题的解中获得
4 仿真验证
为了验证上述提出的状态估计算法和鲁棒预测控制算法的有效性，取DSA380型受电弓和京津线接触网参数，见表1和表2。
表1 DSA380型受电弓归算质量模型参数
Tab.1 Parameters of calculation quality model of DSA380 pantograph
参 数 数 值弓头等效质量m1/kg 7.12弓头等效阻尼c1/(N·s/m) 0弓头等效刚度k1/(N/m) 9 430上框架等效质量m2/(kg) 6上框架等效阻尼c2/(N·s/m) 0上框架等效刚度k2/(N/m) 14 100下框架等效质量m3/(kg) 5.8下框架等效阻尼c3/(N·s/m) 70下框架等效刚度k3/(N/m) 0.1
表2 接触网结构参数
Tab.2 Structural parameters of catenary
参 数 数 值跨距/m 48结构高度/m 1.6承力索张力/kN 21
（续）
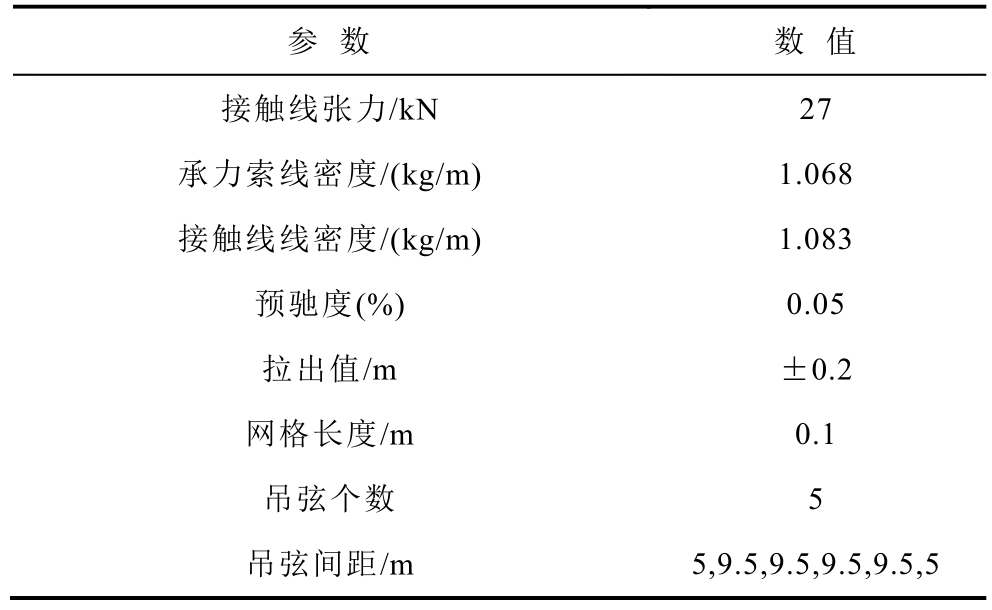
参 数 数 值接触线张力/kN 27承力索线密度/(kg/m) 1.068接触线线密度/(kg/m) 1.083预驰度(%) 0.05拉出值/m ±0.2网格长度/m 0.1吊弦个数 5吊弦间距/m 5,9.5,9.5,9.5,9.5,5
首先验证量测数据丢失情况下的估计算法在非线性弓网模型中的精确性，取初始值为
图2为受电弓位移状态的量测值、估计值和仿真值，图2a～图2c分别表示受电弓质量块一、二和三的垂向位移的量测值、估计值和实际值，虚线为量测值，实线为估计值，点画线为仿真值。图3为受电弓速度状态的估计值和仿真值，图3a～图3c分别为质量块一、二和三的垂向速度的估计值和仿真值。量测值是在量测数据部分丢失和工作环境有强烈噪声干扰的情况下，传感器检测获得的系统位移；仿真值是在不考虑任何外界干扰的情况下，仿真计算出的理论计算值。
仿真计算结果表明：图2的方均根误差分别为0.001 4，0.001 4和0.001 4，图3的方均根误差分别为0.007 1，0.009 3和0.007 1，验证了状态估计算法的精确性。
图2 受电弓位移状态的量测值、估计值和仿真值
Fig.2 Measured values, estimated values and simulation value of pantograph displacement state
图3 受电弓速度状态的估计值和仿真值
Fig.3 Estimated values and simulation values of pantograph speed state
用非线性弓网模型验证所提出的控制器的有效性，设弓头抬升量最大值x1max为0.1m，控制力最大值umax为200N，控制参数
系数矩阵
的参数摄动范围在10%以内。本文根据上述参数，在360km/h、300km/h和250km/h速度下分别进行弓网接触力仿真计算，图4为在非线性弓网模型中控制前后的接触力。
图4 不同速度下接触力控制前后比较
Fig.4 Comparison of contact force before and after control at different speeds
仿真结果表明：即使在受电弓参数摄动的情况下，控制器仍能表现出优良特性，大多数位置的接触力的极大值减小，极小值增大，不同速度下的接触力标准差都有所降低，在 360km/h、300km/h和250km/h速度下分别降低了 19.18%、21.16%和16.21%，接触力平均值降低了1.2%、4.7%和7.3%。在不同工况下，控制器在影响接触力平均值较小的情况下，能有效降低接触力的标准差，验证了控制器的有效性和鲁棒性。
5 结论
本文提出一种基于状态估计的受电弓鲁棒预测控制器，以减轻弓网之间的接触力波动，提高高速列车弓网受流质量。考虑受电弓工作环境中电磁干扰的影响和量测数据随机丢失的情况，采用带虚观测的鲁棒卡尔曼滤波算法实时估计受电弓状态。为了降低接触力的波动，提高列车受流质量，同时考虑作动器输出限制和受电弓弓头垂向位移的约束，提出一种基于状态估计的受电弓鲁棒预测控制策略。本文通过仿真验证了估计算法的精确性和控制器的有效性及鲁棒性。仿真结果表明，即便在受电弓-接触网系统参数摄动的情况下，提出的控制策略仍能有效降低接触力的波动，改善高速列车弓网受流质量。
[1]Wang Hongrui, Liu Zhigang, Song Yang, et al.Detection of contact wire irregularities using a quadratic time-frequency representation of the pantograph-catenary contact force[J]. IEEE Transactions on Instrumentation and Measurement,2016, 65(6): 1385-1397.
[2]Lee H, Park W, Oh K, et al. Analysis of dynamic interaction between catenary and pantograph with experimental verification and performance evaluation in new high-speed line[J]. Vehicle System Dynamics,2015, 53(8): 1117-1134.
[3]韩志伟, 刘志刚, 张桂南, 等. 非接触式弓网图像检测技术研究综述[J]. 铁道学报, 2013, 35(6): 40-47.Han Zhiwei, Liu Zhigang, Zhang Guinan, et al.Overview of non-contact image detection technology for pantograph-catenary monitoring[J]. Journal of the China Railway Society, 2013, 35(6): 40-47.
[4]Liu Zhendong, Jönsson P A, Stichel S, et al.Implications of the operation of multiple pantographs on the soft catenary systems in Sweden[J].Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit,2016, 230(3): 971-983.
[5]时光, 陈忠华, 郭凤仪, 等. 波动载荷下弓网接触电阻特性及建模研究[J]. 电工技术学报, 2019,34(11): 2287-2295.Shi Guang, Chen Zhonghua, Guo Fengyi, et al.Research on characteristic of the contact resistance of pantograph-catenary under load fluctuation[J].Transactions of China Electrotechnical Society, 2019,34(11): 2287-2295.
[6]Zhang Jing, Liu Zhigang, Song Yang, et al. Study on multidisciplinary integrated design of high-speed pantograph based on parameters design, dynamics analysis and optimal control[C]//35th Chinese Control Conference(CCC), Chengdu, China, 2016: 10253-10257.
[7]鲁小兵, 刘志刚. 高速铁路受电弓主动控制算法适用性研究[J]. 西南交通大学学报, 2015, 50(2): 233-240.Lu Xiaobing, Liu Zhigang. Applicability of active control algorithms for pantographs of high-speed railway[J]. Journal of Southwest Jiaotong University,2015, 50(2): 233-240.
[8]时光, 陈忠华, 刘健辰, 等. 基于伺服模型的受电弓LQR控制[J]. 电子测量与仪器学报, 2016, 30(7):1120-1126.Shi Guang, Chen Zhonghua, Liu Jiancheng, et al.Research of LQR control of pantograph based on servo model[J]. Journal of Electronic Measurement and Instrumentation, 2016, 30(7): 1120-1126.
[9]庄哲, 施莹, 彭飞, 等. 受电弓状态反馈线性化主动控制方法研究[J]. 机械科学与技术, 2017, 36(10):1604-1610.Zhuang Zhe, Shi Ying, Peng Fei, et al. Research on active control method of state feedback linearization for pantograph[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(10):1604-1610.
[10]Lin Y, Shieh N, Liu V. Optimal control for rail vehicle pantograph systems with actuator delays[J]. IET Control Theory and Applications, 2015, 9(13): 1917-1926.
[11]任志玲, 林冬, 王月, 等. 基于预测控制的弓网系统半主动控制策略研究[J]. 系统仿真学报, 2017,29(5): 1086-1092.Ren Zhiling, Lin Dong, Wang Yue, et al. Research on semi-active control strategy of high speed railway pantograph-catenary system based on model predictive control[J]. Journal of System Simulation,2017, 29(5): 1086-1092.
[12]时光, 陈忠华, 郭凤仪, 等. 基于最优载荷的受电弓自适应终端滑模控制[J]. 电工技术学报, 2017,32(4): 140-146, 153.Shi Guang, Chen Zhonghua, Guo Fengyi, et al.Adaptive terminal sliding mode control of pantograph based on optimal load[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 140-146, 153.
[13]时光, 陈忠华, 郭凤仪, 等. 弓网接触力反馈线性化控制[J]. 控制理论与应用, 2016, 33(1): 85-91.Shi Guang, Chen Zhonghua, Guo Fengyi, et al.Feedback linearization control of load between pantograph and catenary[J]. Control Theory &Applications, 2016, 33(1): 85-91.
[14]Song Yang, Liu Zhigang, Wang Hongrui, et al.Nonlinear modelling of high-speed catenary based on analytical expressions of cable and truss elements[J].Vehicle System Dynamics, 2015, 53(10): 1455-1479.
[15]崔营波. 高速列车受电弓半主动控制方法研究及应用[D]. 北京: 北京交通大学, 2018.
[16]黄珏, 颜冰, 徐朋豪. 带有量测数据丢失的虚观测鲁棒卡尔曼滤波算法[J]. 华中科技大学学报(自然科学版), 2016, 44(9): 55-58.Huang Yu, Yan Bing, Xu Penghao. Virtual observation robust Kalman filter algorithm with missing measurement[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2016, 44(9): 55-58.
[17]刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regress extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[18]李扬, 李京, 陈亮, 等. 复杂噪声条件下基于抗差容积卡尔曼滤波的发电机动态状态估计[J]. 电工技术学报, 2019, 34(17): 3651-3660.Li Yang, Li Jing, Chen Liang, et al. Dynamic state estimation of synchronous machines based on robust cubature Kalman filter under complex measurement noise conditions[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3651-3660.
[19]谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2019,34(2): 419-426.Gu Miao, Xia Chaoying, Tian Congying. Li-ion battery state of charge estimation based on comprehensive Kalman filter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 419-426.
[20]王大方, 李琪, 张鹏, 等. 带有相电压补偿基于EKF的无传感器感应电机转速估计[J]. 电机与控制学报, 2019, 23(1): 35-44.Wang Dafang, Li Qi, Zhang Peng, et al. Speed estimation method based on extended Kalman filter with phase voltage compensation for sensorless ACIM drives[J]. Electric Machines and Control, 2019, 23(1):35-44.
[21]Yin Zhonggang, Gao Fengtao, Zhang Yanqing, et al.A review of nonlinear kalman filter appling to sensorless control for AC motor drives[J]. CES Transactions on Electrical Machines and Systems,2019, 3(4): 351-362.
[22]沈锋, 徐广辉, 桑靖. 一种自适应变分贝叶斯容积卡尔曼滤波方法[J]. 电机与控制学报, 2015, 19(4):94-99.Shen Feng, Xu Guanghui, Sang Jing. Adaptive variational Bayesian cubature Kalman filtering[J].Electric Machines and Control, 2015, 19(4): 94-99.
[23]李伟, 张勇军, 肖雄. 实时电感辨识的模型预测并网逆变器控制方法[J]. 电工技术学报, 2018, 33(15):3450-3460.Li Wei, Zhang Yongjun, Xiao Xiong. The model predictive grid-connected inverter control method based on real-time inductance identification[J].Transactions of China Electrotechnical Society, 2018,33(15): 3450-3460.
[24]Minouchehr N, Hosseini-Sani S K, Vaezi N, et al.LMI-based robust constrained model predictive control of two-wheeled inverted pendulum[C]//Second International Congress on Technology,Communication and Knowledge, Mashhad, Iran, 2015,DOI: 10.1109/ICTCK.2015.7582658.