0 引言
为实现可再生能源逐步替代传统能源的目标,近年来,我国大力发展风能、太阳能等可再生能源,然而,风能、太阳能等时空分布特性和不确定性将导致电力系统运行方式发生巨大改变,无功功率、电压控制难度增大[1]。磁控式并联电抗器(Magnetically Controlled Shunt Reactor, MCSR)是解决上述问题的有效手段,可以根据系统需要,平滑地调整无功功率,且注入电网的谐波含量较小,具有良好的应用前景[2-3]。2013年,我国在新疆与西北主网联网的第二通道中的青海鱼卡站,投运了国内也是世界首台电压等级为750kV、额定容量为330Mvar的磁控式并联电抗器,有效解决了西北地区风电消纳能力不足的问题,在一定程度上缓解了“西电东送”过程中长距离输电的无功、电压控制难题[4]。
MCSR通过调节控制绕组中直流电流的大小改变铁心的饱和程度,进而实现电抗值和容量的平滑调节。目前针对MCSR容量调节的研究,主要围绕提升 MCSR励磁控制系统性能而展开。文献[5-6]分析了 MCSR响应速度受限的原因,提出了提高直流控制电压、利用放电电容等措施来改善MCSR调容过程中的快速性。文献[7]基于传统PI控制理论设计了控制系统传递函数,分析了 MCSR在负荷突变后的稳态电压保持能力和动态调节性能。文献[8-9]分析了MCSR励磁调节控制对系统工频过电压、操作过电压、潜供电流及恢复电压的影响。由此可见,已有的对于MCSR容量调节的研究,重点在于励磁控制策略,并未对容量调节过程中MCSR的暂态特性进行深入分析。
MCSR本体绕组联结方式复杂,匝间故障发生概率较高且难以识别,一旦发生故障,不仅会威胁到本体的安全稳定运行,更有可能影响所连接电网的无功平衡和电压稳定,因此,对MCSR匝间保护的性能要求较高[10-16]。针对匝间故障,一般采用零、负序功率方向保护方案,电流分量均取自网侧绕组近中性点电流互感器[17],当控制绕组发生匝间故障时,三相三角形联结的补偿绕组分流了大部分零序电流,导致零序功率方向灵敏度不足。为解决零、负序功率方向保护灵敏度不足这一问题,文献[18]提出了一种基于控制绕组总电流(下文简称为“总控电流”)基波分量的匝间保护(下文简称为“总控电流基波分量匝间保护”),能灵敏地动作于控制绕组匝间故障。然而,已有相关研究注意到,MCSR预励磁合闸过程中,每相分裂的左、右心柱磁场会产生较大的不平衡,从而导致总控电流基波分量产生,引起总控电流基波分量匝间保护误动。文献[19]提出通过提高定值来躲过合闸等暂态过程影响,但将降低总控电流基波分量匝间保护的灵敏度。文献[20]通过引入分相控制绕组电流基波分量与总控电流基波分量构成比值,构建总控电流基波分量匝间保护辅助判据,防止合闸引起的匝间保护误动;文献[21]通过计算控制绕组电流波形的自相关系数识别MCSR的合闸过程,上述两种方案既能保证匝间保护的灵敏度,又可躲过合闸暂态过程的影响。
MCSR容量大范围调节与预励磁合闸有相似之处,也可能引起每相MCSR两心柱间磁场的不平衡,从而导致总控电流基波分量匝间保护误动。然而,如上所述,容量大范围调节暂态特性尚不明确,目前已有的总控电流基波分量匝间保护方案并未考虑容量调节暂态过程的影响。本文以750kV磁控式并联电抗器为研究对象,首先介绍了其结构及基本工作原理,对其稳态特性及容量大范围调节的暂态特性展开研究;然后,重点分析容量调节暂态过程对总控电流基波分量匝间保护的影响,并提出了基于三相控制绕组电流基波分量差异度的容量调节过程识别判据;最后,通过仿真及动模实验验证了容量调节暂态特性及所提保护方案的正确性。
1 磁控式并联电抗器稳态与暂态特性
磁控式并联电抗器由磁放大器发展而来,通过调节控制回路的直流励磁改变铁心的工作点,从而达到平滑调节无功输出的目的[22]。
1.1 MCSR的结构及工作原理

图1 单相MCSR的铁心结构及绕组联结方式
Fig.1 Structure and winding connection of single-phase MCSR
图1为单相MCSR的铁心结构及绕组联结方式图,主铁心分裂为p、q两个心柱。匝数为Nw的两个网侧分支绕组同极性串联,端口接入电网;匝数为 Nk的两个控制侧分支绕组反极性串联,端口并联直流控制电源Uk;匝数为 Nb的两个补偿侧分支绕组同极性串联。通过调节控制绕组电流ik的大小,可以控制 p、q心柱的直流励磁及其饱和程度,进而控制电抗器的等效电抗值大小和工作容量,直流励磁越大,铁心越饱和,磁导越小,MCSR的等效电抗越小,在相同电网电压下输出的无功功率越大。iw、ib分别为网侧绕组、补偿绕组电流,Φp、Φq分别为左、右心柱主磁通,um为网侧绕组两端并联的交流励磁电压[23]。
超/特高压 MCSR是由三个独立的单相 MCSR构成三相电抗器组,三相MCSR电气主接线图如图2所示。网侧绕组三相为星形联结,中性点直接接地;每相两分支控制绕组反极性串联构成控制支路,三相控制支路并联于直流母线间,由外接励磁电源通过整流变压器给整流桥供电,ikA、ikB、ikC分别为三相控制绕组电流,izk为控制绕组总电流,uk为控制电压;补偿绕组三相为三角形联结,角外连接滤波器支路[24]。
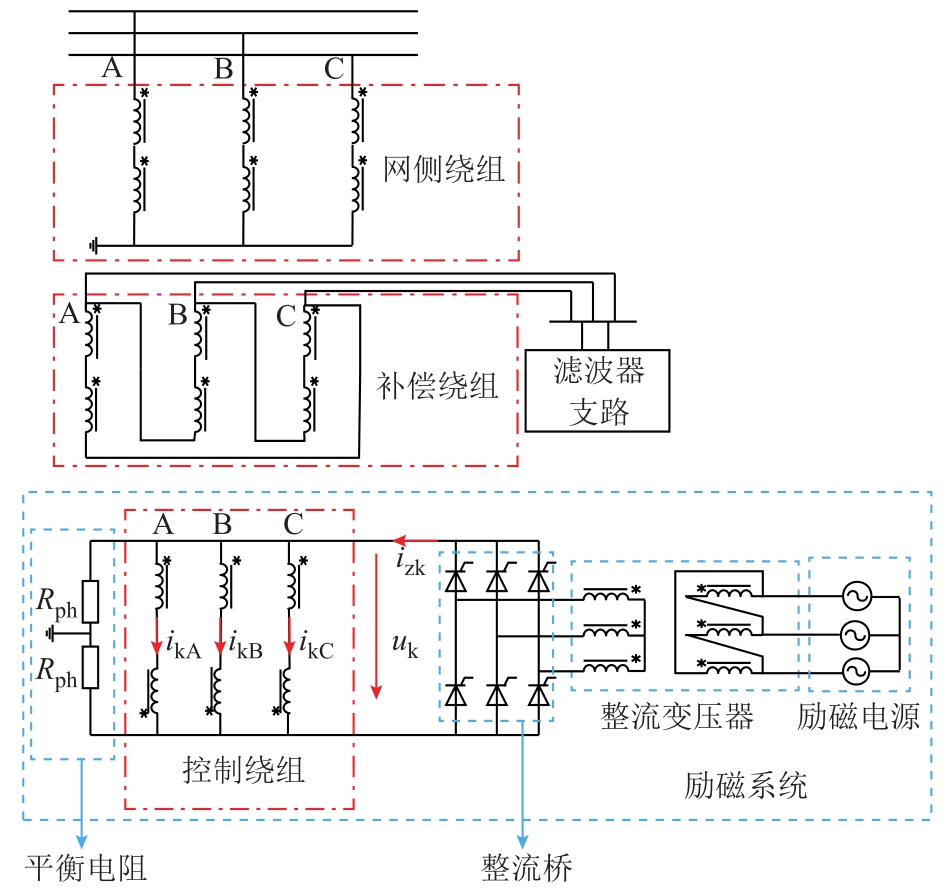
图2 三相超/特高压MCSR电气主接线图
Fig.2 Structure diagram of three-phase EHV/UHV MCSR
1.2 MCSR稳态特性
为便于分析,将MCSR的铁心磁化曲线简化为双折线模型,如图3所示。图3中,B、H分别为铁心磁感应强度及磁场强度,p、q心柱磁感应强度分别为Bp、Bq,μ0为真空磁导率,铁心在饱和区的磁导率近似于真空磁导率。正常运行时,p、q心柱的直流磁感应强度大小相等、方向相反,即图中 Bd、-Bd;叠加交流磁场后,p、q心柱分别在交流磁场的正、负半周进入饱和区(图中阴影部分),且两心柱进入饱和区的电角度相等。将一周期内铁心进入饱和区的电角度定义为磁饱和度 β( β ∈ [ 0 , 2π]),根据文献[25]及图3所示的计算示意图,可得到p、q心柱磁饱和度βp、βq的表达式为
式中,Bm为交流磁感应强度幅值;Bd为直流磁感应强度大小;Bs为铁心饱和点处的磁感应强度。
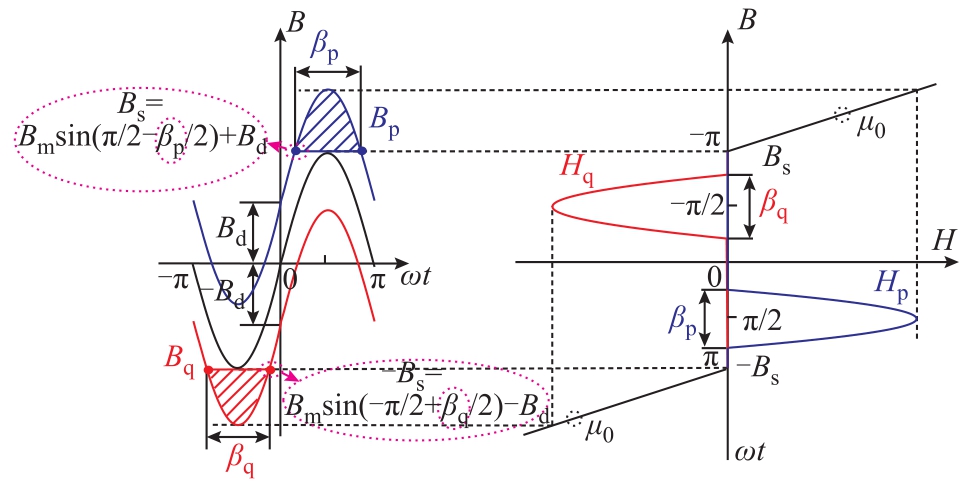
图3 铁心B-H 曲线及磁饱和度计算示意图
Fig.3 B-H curve and magnetic saturation calculation
在[-π,π]内,p、q 心柱的磁场强度 Hp、Hq分别为[26]

在正常运行时,补偿绕组只起到滤波的作用,为简化分析,可忽略补偿绕组电流。根据安培环路定理,p、q心柱磁场强度与网侧绕组电流iw、控制绕组电流ik的关系为
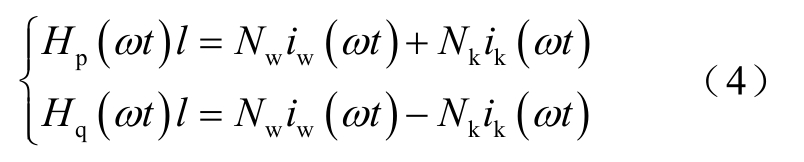
式中,l为铁心柱p、q的磁路长度。
根据式(2)~式(4),可得到控制绕组电流在[-π,π]区间内的表达式为
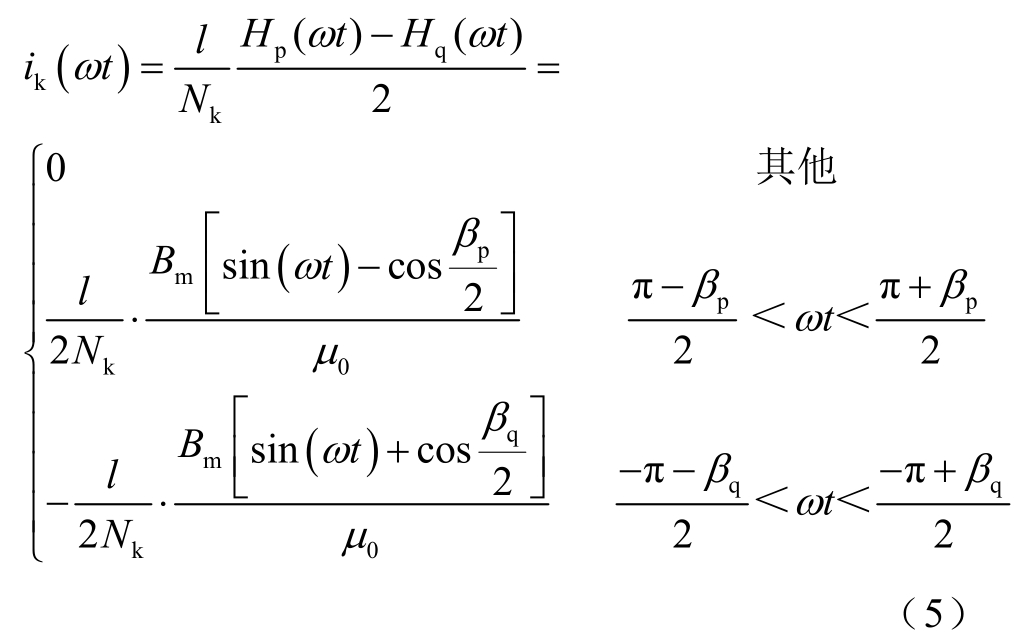
将式(5)利用傅里叶级数展开,可以得到控制绕组电流基波分量幅值如式(6)所示。根据式(6),正常稳态运行条件下,p、q心柱磁饱和度相等,因此控制绕组电流基波分量幅值为0。
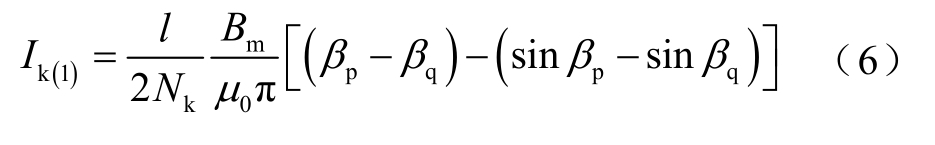
对于三相MCSR,其每一相的稳态特性均与单相MCSR相同,三相控制绕组电流基波分量幅值为
式中,φ代表A、B、C三相。
1.3 MCSR容量调节暂态特性
MCSR的容量调节通过改变控制绕组励磁系统整流桥的晶闸管触发延迟角实现,触发延迟角变化引起控制电压 uk改变,导致心柱中直流磁场发生变化,进而心柱磁饱和度改变,最终达到MCSR容量调节的目标[27]。假设调容前MCSR的控制电压为uk1,调容命令发出后,控制电压变为uk2,变化量为Δuk=uk2-uk1。控制侧回路调容过程中的动态方程可写成
式中,Rk、Lk分别为每相控制绕组等效电阻及等效漏感,三相的控制绕组等效电阻及漏感近似相等;Lmφ为每相铁心的等效励磁电感;ikφ为每相控制绕组电流。
t0为容量调节开始时刻,调容瞬间,控制绕组电流为ikφ(t0)=uk1/Rk,因此可得到调容过程中控制绕组电流变化为

式中,Leqφ为回路等效电感,Leqφ=Lk+Lmφ。
由于MCSR控制侧两分支绕组联结方式为反极性串联,由直流励磁产生的每相p、q心柱直流磁感应强度Bpdφ、Bqdφ大小相等、极性相反,如式(10)所示。由此可见,p、q心柱工作点在调容过程中将以相同的变化规律缓慢向目标工作点偏移,但始终关于原点对称。
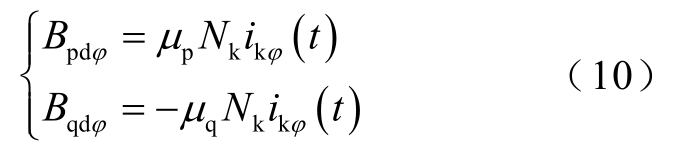
对于同一相 MCSR的 p、q心柱来说,虽然直流励磁下工作点始终对称,但是叠加交流励磁后,同一周期内进入饱和区的时间相差 T/2,那么 p、q心柱磁饱和度势必会产生一定的差异。根据式(7),同相两心柱间磁饱和度的差异将导致控制绕组电流基波分量升高,并且工作点偏移的速度越快,两心柱磁饱和度差异越大,控制绕组电流基波分量越高。
根据式(1)可得磁饱和度β变化率与控制绕组电流的变化率之间的关系为

式中,由于每相两心柱磁饱和度变化率相同,忽略下标p、q及φ。
根据式(11)可以得出,容量调节暂态过程中,铁心磁饱和度的变化率与控制电压变化量 Δuk成正比。对于不同的容量调节过程,初始容量相同条件下,目标容量与初始容量差距越大,在调容初始时刻铁心磁饱和度变化率越大,导致两心柱磁饱和度差异越大,控制绕组电流基波分量越高。随着容量调节过程的进行,当前容量与目标容量越来越接近,磁饱和度变化率逐渐减小,控制绕组电流基波分量逐渐减小。总控电流为三相控制绕组电流之和,因此容量调节过程中总控电流也有基波分量产生,其变化规律与每相控制绕组电流基波分量相同。
2 MCSR容量调节过程仿真分析
利用五段磁路分解方法[28-29],基于西北电网750kV MCSR实际参数,在Matlab/Simulink平台搭建了如附图1所示的三相MCSR仿真模型,模型主要参数见附表1。
目前,已投运的750kV MCSR的容量调节响应速度为:总控电流由1 000A(25%额定容量对应的总控电流)升至4 000A(100%额定容量对应的总控电流)时,响应时间约为1.79~1.89s[3]。以25%额定容量至100%额定容量的容量调节过程为例,分析容量大范围调节的暂态过程。图4为仿真模型在该调节过程中输出无功功率的变化,调容在60s开始,容量调节响应时间约1.7~1.8s,和实际工程接近。
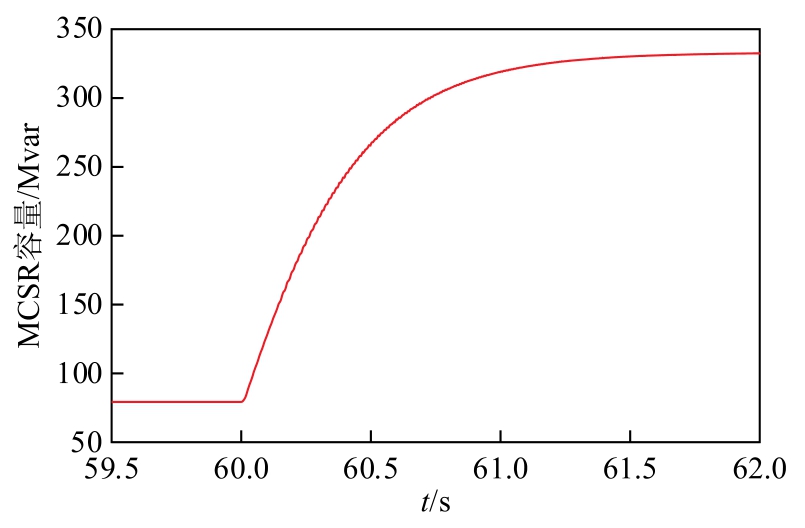
图4 MCSR 25% ~ 100%容量调节过程无功功率变化
Fig.4 Reactive power of MCSR during power regulation from 25% to 100% of rated capacity
p、q心柱的等效励磁电流为在两心柱中建立磁场所需的电流,其幅值可反映心柱饱和程度及差异。根据文献[30]磁控式并联电抗器p、q心柱的等效励磁电流计算式,可利用网侧、控制、补偿绕组电流计算每相两心柱等效励磁电流。图5为25% ~ 100%容量调节过程中p、q心柱的等效励磁电流及其放大图。容量调节暂态过程中,同一周期内(60.22~60.24s),p、q心柱和三相铁心的励磁电流幅值不同,磁饱和度有所差异,而到达稳态后(63.00~ 63.02s),p、q心柱间及三相之间的差异均消失。
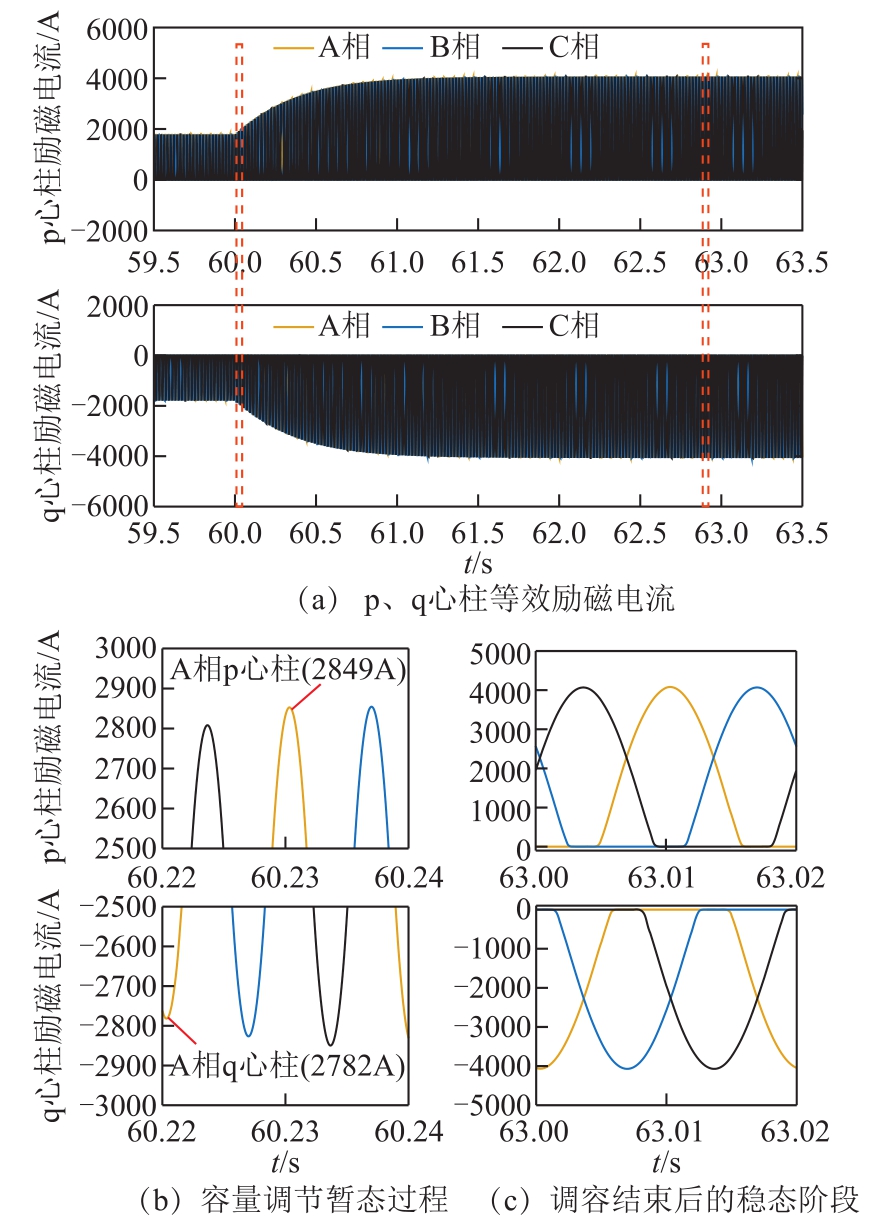
图5 25%~100%容量调节过程中的等效励磁电流及其放大图
Fig.5 Equivalent excitation currents and their enlarged view in the process of power regulation from 25% of rated capacity to 100% of rated capacity
图6和图7分别为调容过程中总控电流和控制绕组电流波形及基波分量幅值, 其中基波分量幅值由全波傅里叶算法得到。由图6可以看出,在容量升高过程中,总控电流逐渐增大。调容初始阶段,总控电流基波分量幅值升高,最大可达到 25.54A,且随着调容的进行逐渐减小。由图7可以看出,升高容量时,控制绕组电流增大且脉动幅度增大,分相控制绕组电流基波分量幅值受幅值变化的交流分量影响,将会产生波动,通过求解其滑动窗口平均值,即可消除波动的影响,如图7中实线所示。控制绕组电流基波分量平均值在调容开始后立即增大,随后逐渐减小,且三相控制绕组电流基波分量幅值的滑动窗口平均值近似相等。

图6 25%~100%容量调节过程初始阶段总控电流及其基波分量幅值
Fig.6 Waveforms of total control current and its fundamental component in the process of 25%~100%power regulation
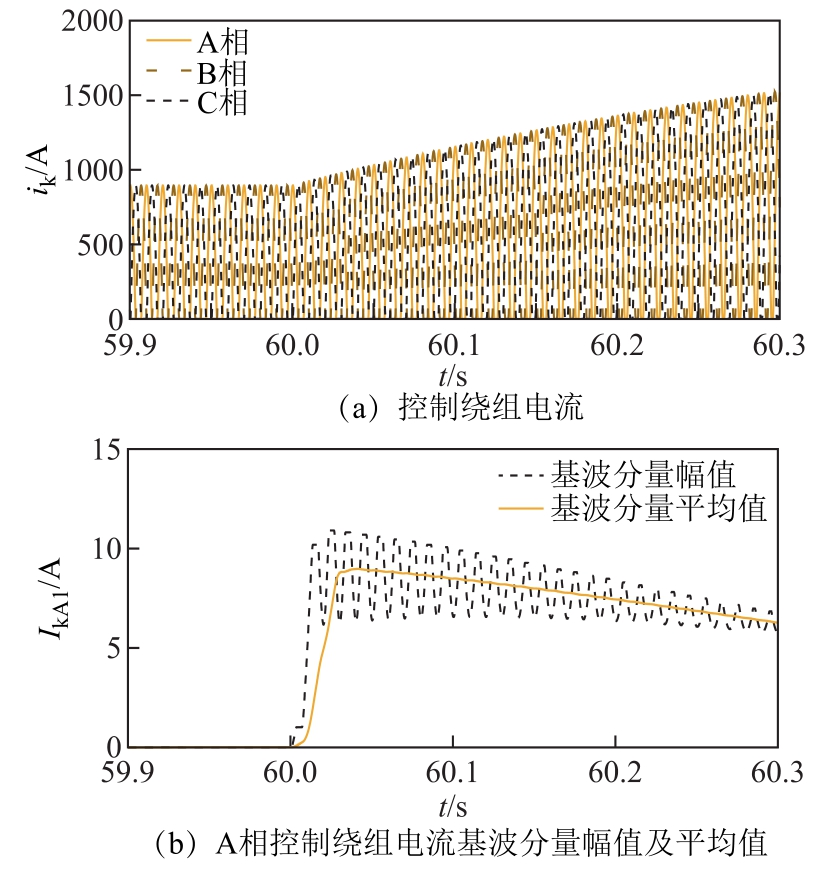

图7 25%~100%容量调节过程初始阶段控制绕组电流瞬时值及其基波分量幅值
Fig.7 Three-phase control winding currents and their fundamental components in the process of power regulation from 25% of rated capacity to 100% of rated capacity
3 MCSR容量调节对匝间保护的影响及解决措施
由第1.3节及第2节分析可知,调容暂态过程中,心柱间磁饱和度的差异将导致总控电流基波分量幅值增大。本节重点分析MCSR容量调节对总控电流基波分量匝间保护方案的影响,并提出解决措施。
3.1 容量调节对匝间保护的影响
由于磁控式并联电抗器的特殊性,其配置的电流差动主保护一般为绕组差动保护,利用网侧绕组首端、末端 CT所测量得到的电流,不反映绕组匝间故障。MCSR在正常运行条件下,每相p、q心柱的磁饱和度相同,因此控制绕组电流及总控电流基波分量幅值为 0;若有匝间故障发生于某一心柱上控制绕组,由于p、q心柱绕组匝数不平衡,将会产生大小不等的感应电动势,进而导致该相控制绕组电流及总控电流的基波分量幅值均不为 0。依据上述特征,文献[18]提出了基于总控电流基波分量的控制绕组匝间保护方案,在判断总控电流基波分量大于整定值并满足辅助判据后,立即发出跳闸指令,将MCSR退出运行。为保证匝间保护的灵敏度,总控电流基波分量匝间保护定值只须躲过正常运行时由于系统不平衡或者设备制作误差等原因引起的最大不平衡电流。根据文献[18],总控电流基波分量幅值整定值一般设置为15 ~ 20A,本文选取15A的定值,验证容量调节过程对总控电流基波分量匝间保护的影响。
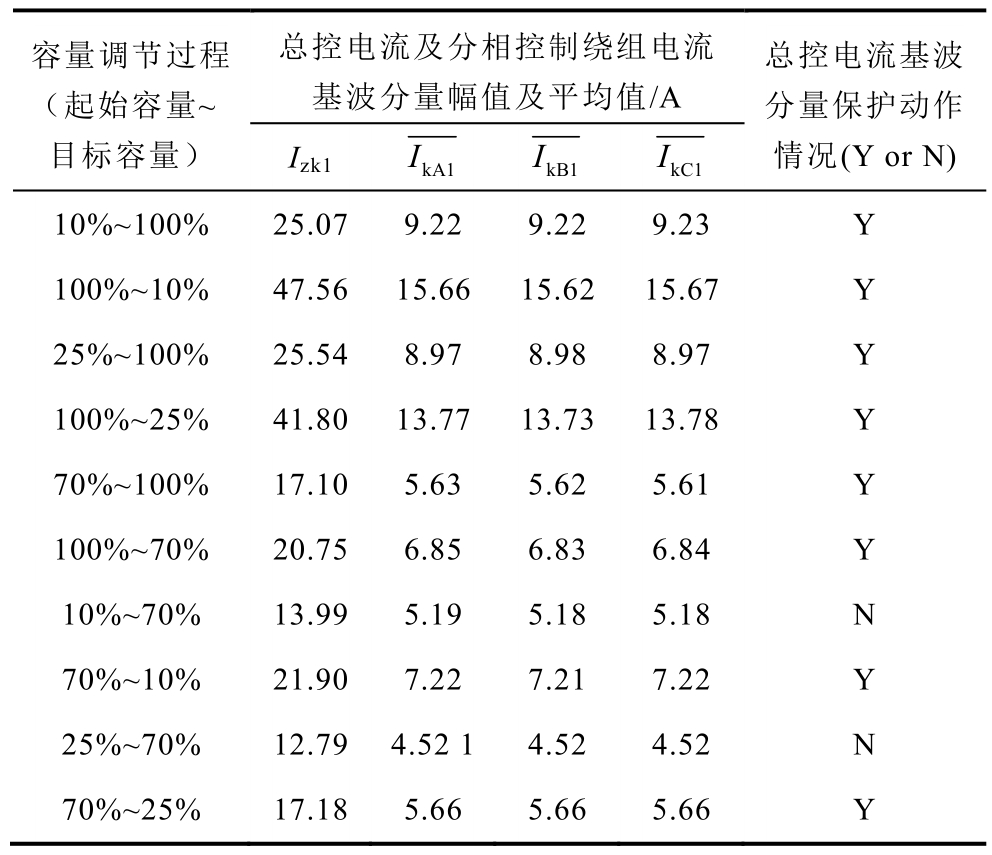
容量调节过程中,心柱间磁饱和度的差异将导致三相控制绕组电流及总控电流基波分量幅值增大,若超过15A则有可能导致总控电流基波分量匝间保护误动。根据 1.3节的理论分析,当初始容量和目标容量不同时,总控电流基波分量以及每相控制绕组电流基波分量平均值将不同。为验证上述分析的正确性,并衡量不同容量调节过程对总控电流基波分量匝间保护的影响,进行了多组MCSR容量调节过程的仿真测试,仿真结果见表1。表1中Izk1为总控电流基波分量幅值,![]() 为分相控制绕组电流基波分量幅值的滑动窗口平均值,表1中均为上述分量在调容后产生的最大值。
为分相控制绕组电流基波分量幅值的滑动窗口平均值,表1中均为上述分量在调容后产生的最大值。
表1 不同容量调节过程的仿真结果
Tab.1 Simulation results during different power regulation prcesses
容量调节过程(起始容量~目标容量)总控电流及分相控制绕组电流基波分量幅值及平均值/A Izk1I kA1IkB1IkC1总控电流基波分量保护动作情况(Y or N)10%~100% 25.07 9.22 9.22 9.23 Y 100%~10% 47.56 15.66 15.62 15.67 Y 25%~100% 25.54 8.97 8.98 8.97 Y 100%~25% 41.80 13.77 13.73 13.78 Y 70%~100% 17.10 5.63 5.62 5.61 Y 100%~70% 20.75 6.85 6.83 6.84 Y 10%~70% 13.99 5.19 5.18 5.18 N 70%~10% 21.90 7.22 7.21 7.22 Y 25%~70% 12.79 4.52 1 4.52 4.52 N 70%~25% 17.18 5.66 5.66 5.66 Y
由表1可知,相同起始容量下,起始容量与目标容量的差异越大,直流分量在容量调节起始阶段变化率越大,心柱之间不平衡度越大,总控电流及分相控制绕组的基波分量越大,基于总控电流基波分量的匝间保护发生误动的概率越高。若采取提高整定值的方式躲过容量调节的影响,势必造成总控电流基波分量匝间保护在弱故障下灵敏度降低,甚至有可能发生拒动。此外,根据第2节分析,总控电流基波分量将随着容量调节过程的持续逐渐衰减,但是由于衰减速度较慢,若利用设置延时的手段躲过容量调节对匝间保护的影响,势必对保护速动性不利。此外,匝间故障发展速度较快,较长的延时将会影响设备安全,因此需从其他角度出发使匝间保护躲过容量调节的影响,例如增加辅助判据,改进总控电流基波分量匝间保护,使其具有识别容量调节过程的功能。根据理论分析及表1所示的仿真结果,三相控制绕组电流基波分量平均值近似相等,与MCSR预励磁合闸以及匝间故障场景下的情况不同,针对总控电流基波分量匝间保护方案的改进可根据该特点制定。
3.2 MCSR容量调节识别判据
根据3.1节的分析,容量调节过程中控制绕组电流及总控电流的基波分量幅值增大,可能引起总控电流基波分量匝间保护误动。而调容过程中,三相控制绕组电流基波分量平均值近似相等,为准确识别容量调节状态,可通过衡量控制绕组电流基波分量三相差异度Fdiv,构建式(12)所示的容量调节识别判据,区分 MCSR的容量调节过程和其他工况。

式中,![]() 为利用全波傅里叶算法计算得到三相控制绕组电流基波分量的幅值后,为避免计算结果波动的影响,进一步求取得到的滑动窗口平均值;
为利用全波傅里叶算法计算得到三相控制绕组电流基波分量的幅值后,为避免计算结果波动的影响,进一步求取得到的滑动窗口平均值;![]() 表示
表示![]() 中的最大值。式(12)中,分子表征三相之间的差异,分母的作用为将差异度标准化,使得差异度门槛值的整定不受模型额定参数影响。各个工况下 Fdiv的取值范围分析如下:
中的最大值。式(12)中,分子表征三相之间的差异,分母的作用为将差异度标准化,使得差异度门槛值的整定不受模型额定参数影响。各个工况下 Fdiv的取值范围分析如下:
(1)匝间故障发生时,故障相控制绕组有基波分量产生,而非故障相分流得到的基波分量几乎可以忽略,因此Fdiv≈2。
(2)容量调节过程中,三相p、q心柱饱和度差距不大,因此三相控制绕组基波分量极为接近,Fdiv≈0。
(3)预励磁合闸时,至少两相控制绕组电流中产生基波分量,差异度取值分散性较大,但都远大于 0。
由此可见,为区分容量调节工况及其他工况,考虑三相系统不平衡或设备制造误差,将门槛值Fdiv_set设置为0.1。考虑容量调节影响后的改进匝间保护方案流程如图8所示。

图8 保护方案流程
Fig. 8 Flow chart of protection scheme
考虑容量调节暂态过程识别的改进保护方案具体流程如下:根据采样值实时计算总控电流的基波分量幅值及分相控制绕组电流基波分量滑动窗口平均值,若总控电流基波分量幅值大于整定值,进一步计算三相控制绕组电流基波分量差异度;若差异度小于整定值,则认为是容量调节过程,保护返回;若不满足式(12)的调容识别判据,则根据文献[20]提出的匝间故障识别方案,进一步区分匝间故障与预励磁合闸工况,若满足匝间故障判据,则保护跳闸,MCSR退出运行,否则返回采样步骤。
4 仿真与实验验证
为验证本文所提方案的正确性,本节将分别从仿真和动模实验方面进行分析。本文进行了不同容量调节过程、不同程度匝间故障以及以不同合闸角预励磁合闸等场景下的仿真,通过计算得到的三相控制绕组基波分量差异度可以验证本文方案;利用1.5kV磁控式并联电抗器进行了匝间故障、预励磁合闸以及容量调节过程实验,由于实验条件受限,无法像仿真一样进行同一工况下大量不同场景的实验,本节只选取每一工况下的代表性场景进行分析。
4.1 仿真验证
附表2为不同容量阶跃调节,70%、100%额定容量运行下,A相网侧、控制绕组发生5%、10%匝间故障,以及不同合闸角度下10%预励磁合闸的三相控制绕组电流基波分量差异度。由附表2可以得到:容量调节场景下差异度接近于 0;匝间故障场景下,差异度在2附近;预励磁合闸场景下,三相差异度明显大于 0。可见,利用容量调节识别判据可以准确识别出MCSR的容量调节过程。
4.2 动模实验验证
电压等级为 1.5kV的磁控式并联电抗器的参数见附表3。下面主要分析MCSR 10%容量运行下B相控制绕组发生 20%匝间故障、MCSR 10%~100%容量调节过程、100%预励磁合闸三种场景下的动模实验结果。由于本文所提方案主要关注各个工况下的三相控制绕组电流及总控电流,因此这里只具体分析三相控制绕组电流及总控电流波形。
由于参数不同,1.5kV MCSR控制绕组额定电流仅为3.28A,总控电流额定值为9.84A,而750kV控制绕组及总控电流额定值分别为1 314A、3 942A。因此总控电流基波分量匝间保护整定值不同,按照等比例缩减,1.5kV MCSR总控电流基波分量保护方案门槛值应设定为0.037 4A。由于Fdiv计算过程中进行了标准化,因此 1.5kV MCSR三相控制绕组电流基波分量差异度门槛值依然设定为 0.1。
上述三种场景下的总控电流及控制绕组电流录波如附图2所示,将录波结果利用快速傅里叶变换(Fast Fourier Transform, FFT)进行谐波分析得到各个场景下的谐波分析结果如附图3所示,图中基波分量用阴影标出。可以得出:①匝间故障场景下,故障后总控电流基波分量为0.570 1A,B相(故障相)控制绕组电流基波分量为 0.559 6A,A、C相(非故障相)控制绕组电流基波分量分别为0.010 7A、0.011 0A,三相控制绕组电流基波分量差异度为Fdiv≈1.962>0.1,接近2;②容量调节过程中,总控电流基波分量最大值为0.453 4A,A、B、C相控制绕组电流基波分量分别为 0.152 1A、0.152 5A、0.154A,可以得到该场景下三相控制绕组电流基波分量差异度为Fdiv≈0.025<0.1,接近0;③预励磁合闸时,总控电流基波分量最大值为 1.466A,A、B、C相控制绕组电流基波分量分别为 0.255 8A、0.488 8A、0.263 8A,可以得到该场景下三相控制绕组电流基波分量差异度为Fdiv≈0.953>0.1。
由动模试验结果可以得到,容量调节过程中,总控电流中基波分量增大,将会使得总控电流基波分量匝间保护误动,然而三相控制绕组电流基波分量近似相等,差异度小于门槛值0.1,因此可以通过图8所示的保护方案流程识别出容量调节过程,避免保护误动,提高了总控电流基波分量匝间保护的可靠性。
5 结论
本文围绕超/特高压磁控式并联电抗器的容量调节暂态特性及对本体保护的影响展开研究。首先对 MCSR正常运行稳态特性进行分析,引入磁饱和度概念,并得出控制绕组电流表达式。在此基础上,对MCSR调容暂态过程进行分析,得出了以下结论:
1)容量调节过程中,同相两心柱进入饱和区的时间具有一定分散性,导致暂态过程中心柱间磁饱和度产生差异。调容暂态过程结束后,MCSR过渡到另一个稳态,心柱间磁饱和度差异消失,恢复平衡。
2)调容暂态过程中,同相p、q心柱间的磁饱和度差异使得控制绕组电流及总控电流产生基波分量,从而可能导致总控电流基波分量匝间保护误动。根据调容过程中,三相控制绕组电流基波分量有效值近似相等,而在匝间故障、预励磁合闸场景下,三相控制绕组电流基波分量有明显差异的特征,构建了基于三相控制绕组电流基波分量差异度的MCSR容量大范围调节识别判据,有效解决了上述问题。
附 录

附图1 三相MCSR仿真模型
App.Fig. 1 Simulation model of three-phase MCSR
附表1 三相MCSR仿真模型的额定参数
App.Tab.1 Rated parameters of the three-phase MCSR simulation model
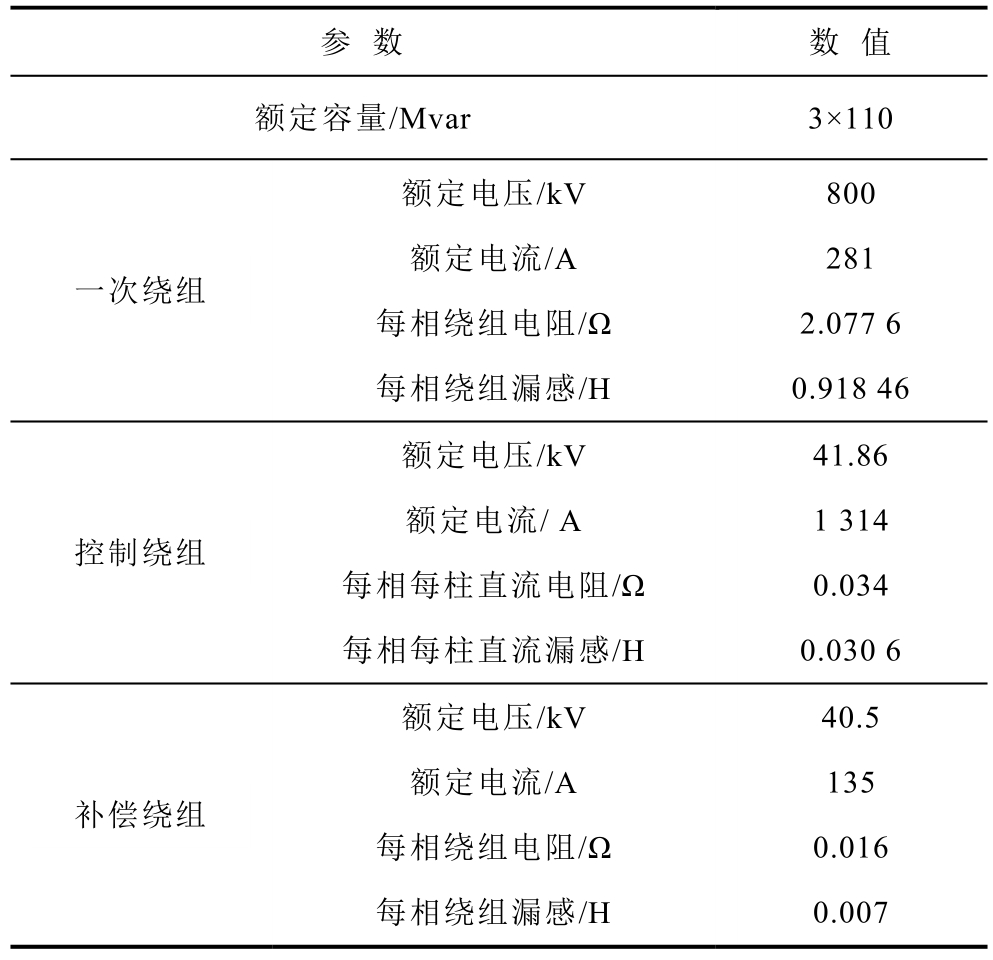
参 数 数 值额定容量/Mvar 3×110额定电压/kV 800一次绕组额定电流/A 281每相绕组电阻/Ω 2.077 6每相绕组漏感/H 0.918 46额定电压/kV 41.86控制绕组额定电流/ A 1 314每相每柱直流电阻/Ω 0.034每相每柱直流漏感/H 0.030 6额定电压/kV 40.5补偿绕组额定电流/A 135每相绕组电阻/Ω 0.016每相绕组漏感/H 0.007
附表2 容量调节及匝间故障下三相控制绕组电流基波分量差异度
App.Tab.2 Three-phase control winding frequency component difference during power regulation and turn-toturn fault conditions
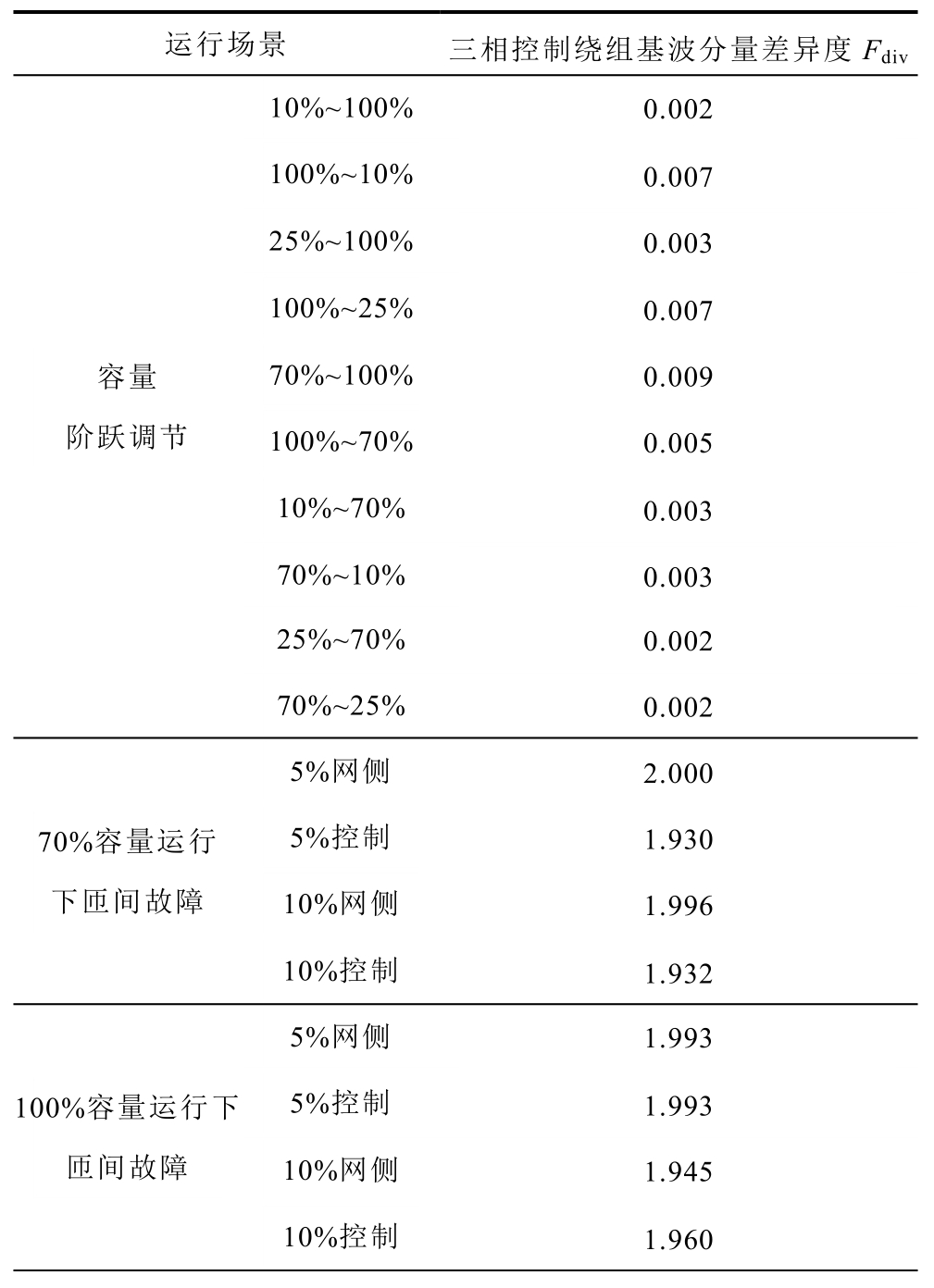
运行场景 三相控制绕组基波分量差异度Fdiv 10%~100% 0.002容量阶跃调节100%~10% 0.007 25%~100% 0.003 100%~25% 0.007 70%~100% 0.009 100%~70% 0.005 10%~70% 0.003 70%~10% 0.003 25%~70% 0.002 70%~25% 0.002 5%网侧 2.000 70%容量运行下匝间故障5%控制 1.930 10%网侧 1.996 10%控制 1.932 5%网侧 1.993 100%容量运行下匝间故障5%控制 1.993 10%网侧 1.945 10%控制 1.960
(续)

运行场景 三相控制绕组基波分量差异度Fdiv 0°合闸 0.812 10%预励磁合闸30°合闸 2.015 60°合闸 1.319 90°合闸 1.961网侧系统额定电压/kV 750网侧系统等值电感/H 0.183 78
表3 1.5kV MCSR物理模型的额定参数
Tab.3 Rated parameters of the1.5kV MCSR

参 数 数 值额定容量/kvar 1.52一次绕组额定电压/kV 1.5一次绕组额定电流/A 0.585控制绕组额定电压/kV 134/3控制绕组额定电流/A 3.28每相每柱直流电阻/Ω 0.94补偿绕组额定电压/ V 76补偿绕组额定电流/A 20网-控短路阻抗百分比(%) 77.5控-补短路阻抗百分比(%) 34.5网-补短路阻抗百分比(%) 23

附图2 总控电流及控制绕组电流录波图
App.Fig.2 Recordings of total control current and control winding currents

附图3 总控电流及控制绕组电流谐波分析结果
App.Fig.3 Harmonic analysis results of total control current and control winding currents
[1]程浩忠, 李隽, 吴耀武, 等. 考虑高比例可再生能源的交直流输电网规划挑战与展望[J]. 电力系统自动化, 2017, 41(9): 19-27.Cheng Haozhong, Li Jun, Wu Yaowu, et al.Challenges and prospects for AC/DC transmission expansion planning considering high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9): 19-27.
[2]张鹏宁, 李琳, 聂京凯, 等. 考虑铁心磁致伸缩与绕组受力的高压并联电抗器振动研究[J]. 电工技术学报, 2018, 33(13): 3130-3139.Zhang Pengning, Li Lin, Nie Jingkai, et al. Study on the vibration of high voltage shunt reactor considering of magnetostriction and winding force[J].Transactions of China Electrotechnical Society, 2018,33(13): 3130-3139.
[3]郑彬, 印永华, 班连庚, 等. 新疆与西北主网联网第二通道工程系统调试[J]. 电网技术, 2014, 38(4):980-986.Zheng Bin, Yin Yonghua, Ban Liangeng, et al. System commissioning for the second transmission channel project interconnecting xinjiang grid with northwest China main grid[J]. Power System Technology, 2014,38(4): 980-986.
[4]左玉玺, 王雅婷, 邢琳, 等. 西北 750kV 电网大容量新型 FACTS设备应用研究[J]. 电网技术, 2013,37(8): 2349-2354.Zuo Yuxi, Wang Yating, Xing Lin, et al. Applied research on new types of high capacity FACTS devices in northwest 750kV power grid[J]. Power System Technology, 2013, 37(8): 2349-2354.
[5]尹忠东. 磁阀式可控电抗器的理论研究及应用[D].武汉: 武汉水利电力大学, 1997.
[6]周丽霞. 大容量输电长线可控并联补偿与潜供电弧抑制的研究[D]. 北京: 华北电力大学(北京), 2009.
[7]田铭兴, 安潇, 顾生杰. 磁饱和式和变压器式可控高抗的电压控制方法及其仿真分析[J]. 高电压技术, 2013, 39(4): 791-796.Tian Mingxing, An Xiao, Gu Shengjie. Voltagecontrolling methods and simulation analysis of magnetically saturated and transformer-type controllable reactors[J]. High Voltage Engineering,2013, 39(4): 791-796.
[8]周勤勇, 郭强, 卜广全, 等. 可控电抗器在我国超/特高压电网中的应用[J]. 中国电机工程学报, 2007,27(7): 1-6.Zhou Qinqyong, Guo Qiang, Bu Guangquan, et al.Application of controllable reactors in China’s power grid at extra and ultra-voltage level[J]. Proceedings of the CSEE, 2007, 27(7): 1-6.
[9]郑彬, 班连庚, 宋瑞华, 等. 750kV 可控高抗应用中需注意的问题及对策[J]. 电网技术, 2010, 34(5):88-92.Zheng Bin, Ban Liangeng, Song Ruihua, et al. Notable issues in application of 750kV controllable shunt reactors and countermeasures[J]. Power System Technology, 2010, 34(5): 88-92.
[10]宋晗, 邹亮, 张秀群, 等. 基于空间磁场分布的干式空心电抗器匝间短路检测方法[J]. 电工技术学报, 2019, 34(增刊1): 105-117.Song Han, Zou Liang, Zhang Xiuqun, et al. Inter-turn short-circuit detection of dry-type air-core reactor based on spatial magnetic field distribution[J].Transactions of China Electrotechnical Society, 2019,34(S1): 105-117.
[11]郑涛, 赵彦杰. 超/特高压可控并联电抗器关键技术综述[J]. 电力系统自动化, 2014, 38(7): 127-135.Zheng Tao, Zhao Yanjie. Overview of key techniques of EHV/UHV controlled shunt reactor[J]. Automation of Electric Power Systems, 2014, 38(7): 127-135.
[12]Zheng Tao, Zhao Yanjie. Microprocessor-based protection scheme for high-voltage magnetically controlled shunt reactors[C]/12th IET International Conference Development Power System Protection,Copenhagen, Denmark, 2014, DOI: 10.1049/cp.2014.0147
[13]陈锋, 王嘉玮, 吴梦晗, 等. 基于 RBF 神经网络的干式空心电抗器涡流损耗计算[J]. 电工技术学报, 2018, 33(11): 2545-2553.Chen Feng, Wang Jiawei, Wu Menghan, et al.Calculation of eddy current loss of dry-type air-core reactor based on RBF neural network[J]. Transactions of China Electrotechnical Society, 2018, 33(11):2545-2553.
[14]Zheng Tao, Liu Xiaoxiao, Huang Ting. Novel protection scheme against turn-to-turn fault of magnetically controlled shunt reactor based on equivalent leakage inductance[J]. International Journal of Electrical Power & Energy Systems, 2019,112: 442-451.
[15]Zheng Tao, Liu Xiaoxiao, Wei Junqi, et al. Protection scheme for turn-to-turn faults of magnetically controlled shunt reactor based on waveform similarity comparison[J]. Electric Power System Research, 2019,177: 105980.
[16]刘校销, 郑涛, 黄婷. 基于等效漏电感参数辨识的磁控式并联电抗器匝间故障保护方案[J]. 电工技术学报, 2020, 35(1): 134-145.Liu Xiaoxiao, Zheng Tao, Huang Ting. Protection scheme based on the identification of equivalent leakage inductance against turn-to-turn fault of magnetically controlled shunt reactor[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 134-145.
[17]郑涛, 赵彦杰, 金颖. 特高压磁控式并联电抗器保护配置方案及其性能分析[J]. 电网技术, 2014,38(5): 1396-1401.Zheng Tao, Zhao Yanjie, Jin Ying. Research on protective configuration for a UHV magnetically controlled shunt reactor[J]. Power System Technology,2014, 38(5): 1396-1401.
[18]郑涛, 赵彦杰, 金颖, 等. 磁控式并联电抗器控制绕组匝间故障分析及保护方案[J]. 电力系统自动化, 2014, 38(10): 95-99.Zheng Tao, Zhao Yanjie, Jin Ying, et al. Analysis on and protective schemes against control winding turnto-turn fault of magnetic controllable shunt reactors[J].Automation of Electric Power Systems, 2014, 38(10):95-99.
[19]Zheng Tao, Zhao Yanjie, Jin Ying, et al. Design and analysis on the turn-to-turn fault protection scheme for the control winding of a magnetically controlled shunt reactor[J]. IEEE Transactions on Power Delivery,2015, 30(2): 967-975.
[20]郑涛, 刘校销. 基于控制绕组电流基波分量的磁控式并联电抗器匝间保护新原理[J]. 电网技术, 2019,43(8): 3016-3024.Zheng Tao, Liu Xiaoxiao. New principle of protection scheme based on fundamental component of control winding currents against turn-to-turn fault of MCSR[J]. Power System Technology, 2019, 43(8):3016-3024.
[21]郑涛, 刘校销. 基于波形自相关的磁控式并联电抗器合闸防误动方案[J]. 电力系统自动化, 2019,43(24): 156-164.Zheng Tao, Liu Xiaoxiao. Waveform auto-correlation based anti-maloperation scheme during energization of magnetically controlled shunt reactor[J].Automation of Electric Power Systems, 2019, 43(24):156-164.
[22]陈柏超. 新型可控饱和电抗器理论及应用[M]. 武汉: 武汉水利电力大学出版社, 1999.
[23]Zheng Tao, Huang Ting, Zhang Fenfen, et al.Modeling and impacts analysis of energization transient of EHV/UHV magnetically controlled shunt reactor[J]. International Transactions on Electrical Energy Systems, 2017, 27(7): e2330.
[24]陶力维, 郑涛, 赵彦杰. 基于网侧绕组串联的磁控式可控高抗控制绕组结构改进[J]. 电力系统自动化, 2015, 39(19): 101-106.Tao Liwei, Zheng Tao, Zhao Yanjie. Physical design of control windings for a three-phase magnetically controlled shunt reactor based on series-connected working windings[J]. Automation of Electric Power Systems, 2015, 39(19): 101-106.
[25]王青朋, 白保东, 陈德志, 等. 800kV超高压磁饱和可控电抗器的动态特性分析及谐波抑制[J]. 电工技术学报, 2020, 35(增刊1): 235-242.Wang Qingpeng, Bai Baodong, Chen Dezhi, et al.Dynamic characteristics and harmonic suppression of 800kV extra-high voltage magnetically saturation controlled reactor[J]. Transactions of China Electrotechnical Society, 202, 35(S1): 235-242.
[26]王轩, 邓占锋, 于坤山, 等. 超高压磁控式并联电抗器稳态特性[J]. 中国电机工程学报, 2008, 28(33):104-109.Wang Xuan, Deng Zhanfeng, Yu Kunshan, et al.Steady-state characteristics of extra-high voltage magnetically controlled shunt reactor[J]. Proceeding of the CSEE, 2008, 28(33): 104-109.
[27]蔡宣三, 高越农. 可控电抗器原理、设计与应用[M].北京: 中国水利水电出版社, 2008.
[28]邓占锋, 王轩, 周飞, 等. 超高压磁控式并联电抗器仿真建模方法[J]. 中国电机工程学报, 2008,28(36): 108-113.Deng Zhanfeng, Wang Xuan, Zhou Fei, et al.Modeling of extra-high voltage magnetically controlled shunt reactor[J]. Proceeding of the CSEE,2008, 28(36): 108-113.
[29]娄宝磊, 李晓明. 基于双饱和变压器模型的磁控电抗器仿真新方法[J]. 高压电器, 2017, 53(4): 191-196.Lou Baolei, Li Xiaoming. New method for simulation of magnetically controlled reactor based on double saturated transformers model[J]. High Voltage Apparatus, 2017, 53(4): 191-196.
[30]Zheng Tao, Liu Xiaoxiao, Wei Junqi. A novel protection scheme against turn-to-turn fault of MCSR based on equivalent magnetizing inductance[J].International Journal of Electrical Power & Energy Systems, 2020, 117: 105629.