0 引言
特高压及可再生能源发电系统容量的不断增大,导致电力系统转动惯量持续下降,系统调频困难且故障情况下所遭受的功率缺额也越来越大,频率稳定问题日益突出[1-2]。当前,系统调频仍主要由传统机组完成,随着储能技术的发展,储能也逐渐参与系统调频,改善系统的频率稳定性[3-4]。频率稳定控制措施主要为第二道防线的自动切负荷及第三道防线的低频减载,两者各有优缺点,均有广泛的应用。
作为最后一道防线的低频减载在防止频率崩溃方面有着不可替代的作用。低频减载整定方法主要有传统法、半适应法和自适应法[5]。传统法以系统可能出现的最大功率缺额事件确定切负荷总量,采用“逐次逼近”确定低频减载的动作轮次及各轮次切负荷量[6]。半适应法和自适应法采用初始频率下降率计算系统的功率缺额并进行低频减载整定。两者区别在于半适应法只有首轮切负荷量根据功率缺额计算结果整定,自适应法则是将所计算的功率缺额在所有轮次之间进行分配[7]。
低频减载整定的核心内容为切负荷总量的确定,即系统功率缺额的计算。功率缺额计算主要有单机等值模型法、时域仿真法以及基于广域量测数据的多机模型法。基于单机等值模型,文献[8]考虑旋转备用、负荷频率效应及水轮机调速系统进行低频减载方案整定和优化,减小了切负荷总量。基于多机系统的时域仿真结果,文献[9]建立系统动态频率与发电机出力增量、负荷增量之间的关系,获得系统的频率调节系数,计算功率缺额,进行低频减载整定。文献[10]使用惯性中心频率计算系统的功率缺额,提出一种计及电压稳定的自适应协调低频减载策略。文献[11]定义了频率暂态稳定指标,建立了单机系统频率响应的解析模型。基于广域量测数据,文献[12-13]使用线性化的方法建立多机系统动态频率与功率缺额之间的关系。文献[14]对复杂电网频率动态特性进行分析,建立了基于广域量测局部信息的系统功率缺额估计模型。文献[15]以总切负荷量最小为目标,提出受端电网分层优化切负荷策略。基于人工智能算法,文献[16]使用v-SVR支持向量机和机器学习方法快速计算扰动后系统频率动态特性。文献[17]在进行低频减载整定时,直接控制用户侧智能家居电器等用户侧的可控负荷,有效降低了切负荷量。
电力系统频率具有时空分布特性[18]。因此,扰动后系统各母线频率并不完全相同,仅使用扰动后瞬间各母线频率斜率并不能准确计算系统的功率缺额。发生功率缺额后,各母线频率由正常值下降到低频减载首轮动作值的时间约为零点几秒至几秒。因此,本文对低频减载首轮动作前各母线频率曲线所蕴含的系统信息进行挖掘,使用各母线频率偏移面积计算系统功率缺额;然后,根据功率缺额的大小,设计不同的低频减载方案,使低频减载方案更具有针对性和有效性。
1 基本假设及功率缺额计算思路
惯性中心(Center of Inertia, COI)频率反映了电力系统作为整体在遭受扰动后所呈现的动态行为,广泛应用于电力系统频率动态分析与低频减载整定等方面。图1和图2分别为IEEE 9母线系统及IEEE 145母线系统发生功率缺额事件后母线频率及系统惯性中心频率。
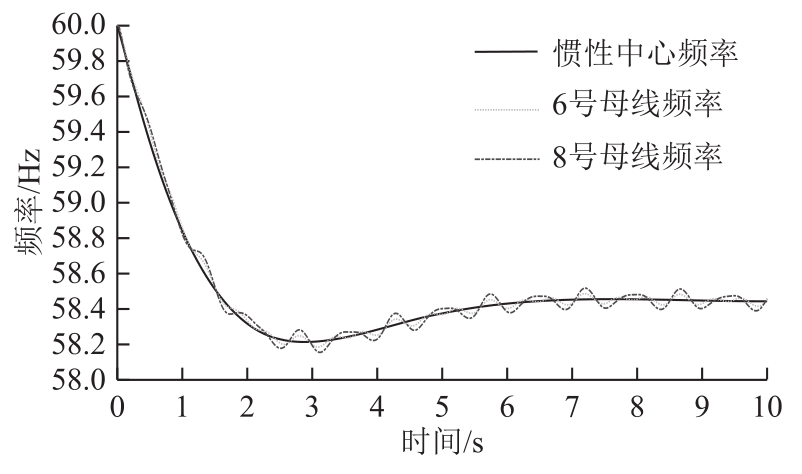
图1 IEEE 9系统负荷母线及系统惯性中心频率
Fig.1 Different frequencies of IEEE 9 system

图2 IEEE 145系统负荷母线及系统惯性中心频率
Fig.2 Different frequencies of IEEE 145 system
由图1和图2可以看出:发生功率缺额事件后,两个系统没都有发生暂态失稳,且各发电机保持同步,系统中各母线频率围绕惯性中心频率上下波动。进一步地,图3a分别画出图1中0~1s内母线频率与惯性中心频率,由于各母线频率围绕惯性中心频率上下波动,因此各频率曲线与额定频率在一相同时刻ts所围成的面积近似相等。A、B、C分别为系统惯性中心频率及各负荷母线频率与时间轴 ts的交点,O、P为额定频率与时间轴0、ts的交点。

图3 惯性中心及母线频率曲线偏移面积
Fig.3 Deviation area of COI and bus frequencies
进一步地,忽略负荷、网损的变化及调速器的作用,当系统发生功率缺额事件时,系统惯性中心频率将以恒定速度下降,当系统功率缺额分别为Pd1、Pd2时,系统惯性中心频率如图4所示。

图4 不同功率缺额情况下系统惯性中心频率
Fig.4 COI frequencies with different power deficits
图4中,fO、fs分别为系统的额定频率和低频减载首轮工作频率;t1、t2为功率缺额分别为 Pd1、Pd2时惯性中心频率达到低频减载首轮动作频率的时刻。
Pd1、Pd2所对应的惯性中心频率偏移面积分别为三角形OA1B1、OA2B2的面积,其表达式为

式中,Sd1、Sd2分别为Pd1、Pd2所对应的惯性中心频率偏移面积;Kd1、Kd2分别为 Pd1、Pd2所对应的惯性中心频率下降速度。
由式(1)可以看出,低频减载首轮动作频率确定后,惯性中心频率偏移面积与其下降速度成反比,而惯性中心频率下降速度与系统功率缺额成正比。因此,惯性中心频率偏移面积与功率缺额成反比。所以,系统惯性中心频率偏移面积能够在一定程度上反映系统功率缺额的情况。
基本假设:功率缺额后,如果系统没有发生暂态失稳,且各发电机保持同步,则各母线频率围绕着系统惯性中心频率上下波动,各母线频率与惯性中心频率曲线在同一时刻与额定频率所围面积近似相等,即图3b中8号母线频率偏移面积(OCPO所围阴影部分)与图 3c中惯性中心频率偏移面积(OAPO所围阴影部分)近似相等。
系统功率缺额计算思路:发生功率缺额后,系统各母线频率与系统惯性中心频率同一时刻的频率偏移面积近似相等。因此,安装在各母线的低频减载通过测量本地频率到达某一时刻的偏移面积,便可确定系统惯性中心频率在该相同时刻的偏移面积。如果假设低频减载首轮动作频率为59Hz,则以8号母线达到低频减载首轮动作频率59Hz的时刻ts为例,通过测量图3b中8号母线频率偏移面积,便可确定图3c中系统惯性中心频率在时刻ts的偏移面积。于是,如果能够确定系统惯性中心频率ts时刻偏移面积与系统功率缺额之间的关系,各低频减载装置便可通过测量其母线频率偏移面积来计算系统的功率缺额,进而进行低频减载的整定。
2 基于频率偏移面积的功率缺额计算
2.1 基本假设的理论证明
系统中各发电机转子运动方程[19]为

式中,δi为发电机i的功角;ωi为发电机i的角速度标幺值;TJi为发电机i的惯量;Tmi、Tei分别为发电机转子的机械转矩和电磁转矩;D为发电机转子的机械阻尼系数。
忽略D,时间基准取1s,式(2)可表示为

式中,Mi、Pmi、PeGi分别为发电机 i的惯性时间常数、转子的机械功率和电磁功率。
进一步得到发电机功角及角速度偏移值为

系统中发电机数量为 m,忽略网耗及发电机内阻抗,对网络方程进行线性化,则发电机电磁功率偏移值可表示[12]为
式中,ΔPe=[ΔPe1 … ΔPem]T;Δδ=[Δδ1 … Δδm]T;H与潮流计算中雅克比矩阵具有相同的表达形式。
假设发电机机械功率不变,将式(5)代入式(4),得到m台发电机转子运动的状态方程为

式中,M=diag(M1,…,Mm);Bω=diag(ωB,…,ωB)。
在t=0时刻,发电机母线i负荷突然增加Pdi,则式(6)可表示为
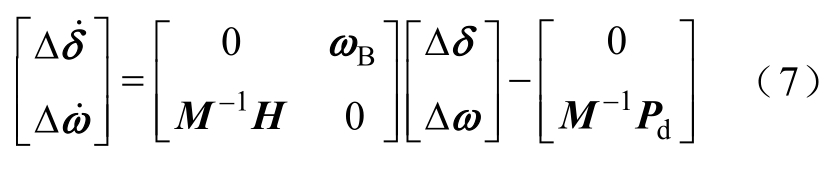
式中,Pd=[Pd1 … Pdi … Pdm]T。
Δδ与 Δω初始值为 0,对式(7)进行拉氏变换,得到角速度偏移值为
以两机系统为例,t=0时刻在发电机母线 2处突然增加负荷Pd2,发电机角速度偏移值为
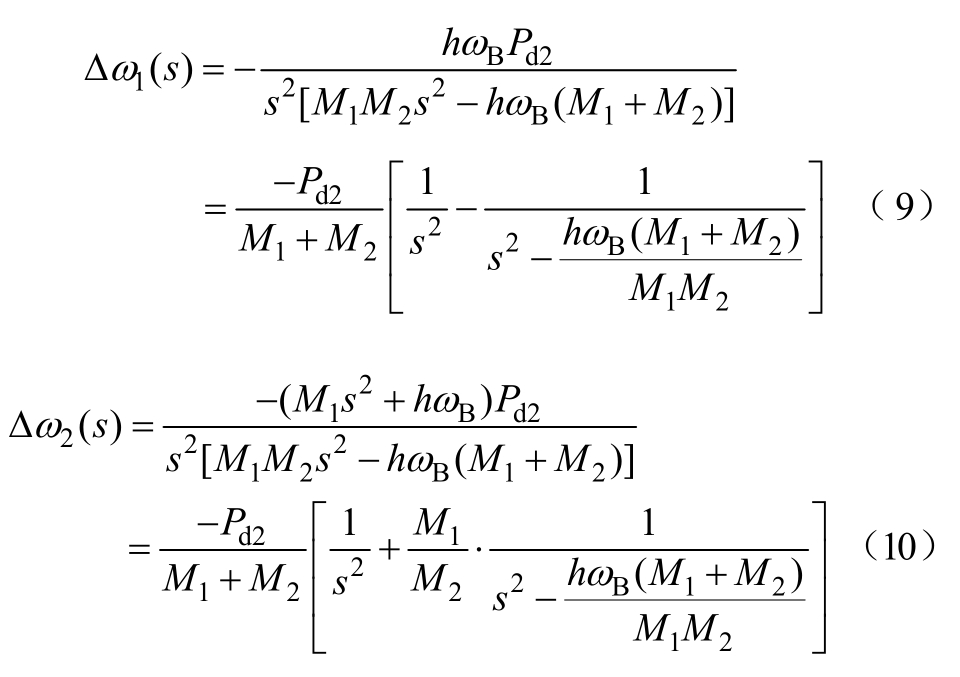
其中,h为矩阵H中的元素,其表达式为

式中,U1、U2分别为发电机 1、2机端电压,由于忽略了发电机内部阻抗,也为发电机电动势;B12为发电机1、2之间互导纳的虚部;δ120为t=0时刻发电机1、2之间的功角差。
系统惯性中心角速度偏移值为

式中,M1、M2分别为发电机1、2惯性常量。
由于发电机1、2没有发生暂态失稳,仍保持同步,则δ120的绝对值小于90°。在式(11)中,由于 B12>0,cosδ120>0,则 h<0,因此式(9)、式(10)、式(12)所对应的发电机1、2及惯性中心角速度偏移值的时域表达式分别为
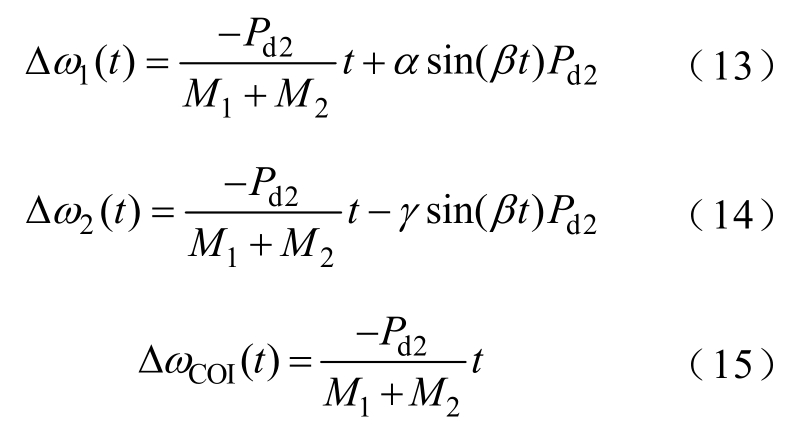
式中,α、β、γ分别为

由式(13)~式(15)可以看出:发电机2机端负荷突然增加后,各角速度围绕着惯性中心角速度上下波动,相当于在惯性中心角速度上叠加了一个正弦周期分量,其周期为
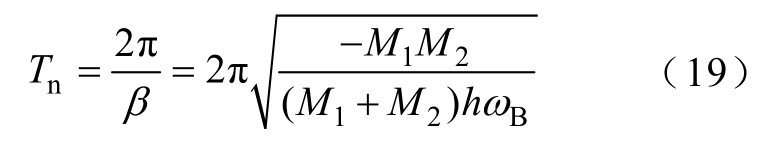
式中,Tn为正弦分量的周期。
标幺制下,发电机角速度与频率相等。因此,本文将角速度亦称为频率。假设功率缺额后频率达到低频减载首轮动作频率的时刻为ts,对式(13)~式(15)进行积分,得ts时刻各发电机频率及系统惯性中心频率偏移面积为

式中,S1、S2、SCOI分别为发电机1、发电机 2、惯性中心频率偏移面积。
由式(20)、式(21)可以看出:当 ts=nTn时,n为整数,各发电机与惯性中心频率偏移面积相等;当ts=(n+0.5)Tn时,各发电机与惯性中心频率曲线偏移面积误差达到最大值,最大误差与惯性中心频率偏移面积比值为

式中,E1、E2为发电机1、2最大偏移面积误差。
低频减载动作前,各发电机之间往往会发生多次摇摆,并且M1、M2一般处于同一数量级。所以,即使是最严重的情况,E1、E2仍较小,可认为ts时刻各发电机与惯性中心频率偏移面积近似相等。因此,本文假设系统各母线频率与惯性中心频率偏移面积近似相等,具有一定的理论依据。
2.2 系统功率缺额的计算
忽略网损,扰动后系统惯性中心频率偏移值为
式中,MT为系统总惯性时间常数;ΔωCOI为惯性中心频率偏移值;ΔPmT为全部发电机总机械功率增量;Pd为功率缺额,Pd>0表示发电机出力不足,Pd<0表示发电机出力过剩,Pd为阶跃函数。对式(24)进行拉氏变换,得
ΔωCOI0=0,式(25)可简化为
对系统进行单机等值,建立系统总机械功率增量与系统惯性中心频率偏移值之间的传递函数。本文使用 TGOV1模型对系统进行单机等值[13],系统总机械功率增量与系统惯性中心频率偏移值之间的传递函数为
式中,R 为系统总频率调差系数;T1、T2、T3为 TGOV1模型的时间常数。
联立式(26)、式(27),计算扰动后系统惯性中心角频率偏移值为
式中,K1=-1;K2=MTR-T2;K3=MTR(T1+T3);K4=MTRT1T3;k0=R;k1=R(T1+T3);k2=RT1T3。
由式(28)可以看出:系统惯性中心频率偏移值表达式的特征根由一个零根和三个非零根组成,系统惯性中心频率偏移值的时域表达式为
式中,r1、r2、r3为式(28)三个非零特征根;c1、c2、c3、c4为三个非零特征根及零根所对应时域表达式的系数,并且c1+c2+c3+c4=0。
假设某母线频率到达低频减载首轮动作频率的时刻为 ts,对式(29)在 0~ts积分,得惯性中心频率曲线偏移面积为

式中,C为常数,且C=-(c1/r1+c2/r2+c3/r3)。
式(30)的物理意义为系统惯性中心频率偏移曲线在时间ts处与额定频率所围区域面积,其建立了系统功率缺额与惯性中心频率偏移面积之间的关系。由式(30)得到系统功率缺额计算的表达式为

式(27)所描述的系统功率-频率特性可以通过定期对系统进行单机等值、时域仿真等方式获取,故式(31)中分母部分除ts外的全部参数可提前通过系统分析获取。低频减载只需要对其所安装母线的频率及频率曲线在低频减载首轮动作频率时刻的频率偏移面积进行测量,并记录该母线频率到达低频减载首轮动作频率的时刻 ts,便可利用式(31)快速计算系统的功率缺额。
3 基于频率偏移面积的低频减载整定
当前的低频减载方案整定后是固定的。对于大功率缺额事件,低频减载首轮或前几轮切负荷量有可能不足,导致系统频率恢复较慢;对于小功率缺额事件,低频减载首轮或者前几轮切负荷量又有可能过多,导致低频减载过切。
3.1 系统功率缺额算法的启动
本文所提出的基于频率偏移面积的系统功率缺额计算程序事先存储在低频减载装置内。各低频减载装置实时测量其所在母线的频率,功率缺额计算算法程序启动条件为

式中,am为系统最大允许频率下降率,是指无控制措施时系统所能承受的最小功率缺额所引起的初始频率下降率。
最大允许频率下降系数am的计算公式为
式中,PdM为无控制措施时系统所能承受的最大功率缺额;t=0+表示功率扰动发生后的瞬间。
系统最大允许功率缺额PdM可通过对系统进行单机等值或者仿真来获得,并应同时满足条件

式中,ΔMω、Δω∞分别为功率缺额事件后,系统频率偏移的最小值和稳态值;bM、b∞分别为无频率稳定控制措施时,系统所能承受的频率偏移和稳态频率偏移的极限值。
3.2 低频减载整定方案的设计
与当前电力系统低频减载整定方案各轮次切负荷量一经整定便不再变化不同,本文提出根据功率的缺额大小采取不同的低频减载整定方案,其基本思想为:当功率缺额较大时,低频减载应首先保证系统频率稳定性,尽快恢复系统功率平衡,此时低频减载首轮切负荷量或者前几轮切负荷量应大一些,更有利于系统频率的快速恢复;当功率缺额较小时,在保证频率稳定的基础上可以考虑适当降低切负荷量,此时低频减载首轮切负荷量可适当降低一些。
在实际应用中,工程技术人员可以根据电网的实际情况,按照基本思想设计各自的低频减载整定方案。低频减载轮次由基本轮和特殊轮组成,基本轮一般为3~8轮,本文基本轮采用5轮次,各轮次动作频率差值为 0.2Hz。本文简单地以功率缺额占系统总容量的大小为依据来刻画系统功率缺额的严重程度并进行低频减载的整定,低频减载整定方案见表1。表中,PT为系统总容量;a%、b%为比例参数,可根据系统实际情况选取不同的值。
表1 不同功率缺额的低频减载方案
Tab.1 UFLS schemes for different power deficits

轮次a b P P a P>%d T% %≥ ≥Pd T P b P<%d T 1 60%Pd 50%Pd 30%Pd 2 10%Pd 12.5%Pd 17.5%Pd 3 10%Pd 12.5%Pd 17.5%Pd 4 10%Pd 12.5%Pd 17.5%Pd 5 10%Pd 12.5%Pd 17.5%Pd
4 算例分析
4.1 基于频率偏移面积的系统功率缺额计算
4.1.1 IEEE 39母线系统功率缺额计算
IEEE 39母线系统总装机容量为7961.2MW,总有功负荷为6150.1MW,总惯性常量为 1565.4。为了构造功率缺额事件,在母线4处增加一台无穷大容量发电机,模拟外部向系统注入的不同功率。通过设置母线4处发电机退出于运行来构造不同功率缺额事件。31、35、36、37、38、39母线发电机为调频发电机,各发电机调速器模型均为TGOV1模型,调速器调差系数按各发电机容量取5%,调速器时间常数 T1、T2、T3分别取 0.5s、1.5s、5.0s。
对系统进行单机等值,式(31)中各系数的值见表2。
表2 式(31)中各参数的计算值
Tab.2 The values of parameters in Eqn.(31)

参 数 数 值r1 -1.83 r2 -0.19+j0.36 r3 -0.19-j0.36 r4 0 c1 3.48×10-4 c2 (-4.51-j7.51)×10-4 c3 (-4.51+j7.51)×10-4 c4 8.67×10-4
以各母线频率到达 59Hz为例,测量各母线频率偏移面积并记录各母线频率到达59Hz的时间ts,当系统功率缺额为1500MW时,使用式(31)计算系统功率缺额,计算结果见表3。
表3 59Hz频率偏移面积功率缺额计算
Tab.3 Pd calculation using 59Hz deviation area

母线 Pd/MW 母线 Pd/MW 母线 Pd/MW 1 1460.23 14 1476.19 27 1474.64 2 1478.49 15 1469.36 28 1476.17 3 1477.02 16 1464.94 29 1474.27 4 1477.81 17 1469.00 30 1470.18 5 1476.64 18 1472.52 31 1475.62 6 1476.02 19 1456.08 32 1474.55 7 1475.65 20 1451.77 33 1450.40 8 1475.52 21 1456.67 34 1442.29 9 1457.61 22 1448.27 35 1441.77 10 1475.80 23 1445.81 36 1423.34 11 1476.19 24 1462.57 37 1486.64 12 1475.92 25 1487.64 38 1470.04 13 1476.41 26 1479.01 39 1443.72
计算结果分析:通过测量各母线频率偏移面积,本文算法均能较好地计算系统的功率缺额,各母线计算结果相近。其中最大误差为36号母线计算结果,误差为-76.66MW,占功率缺额的5.1%。全部母线计算结果误差平均值为-35.7MW,占功率缺额的3.57%。
为进一步验证本文算法的有效性,使用文献[7]单机等值模型、各母线及系统惯性中心初始频率下降率计算系统功率缺额。初始频率下降率与功率缺额计算公式为
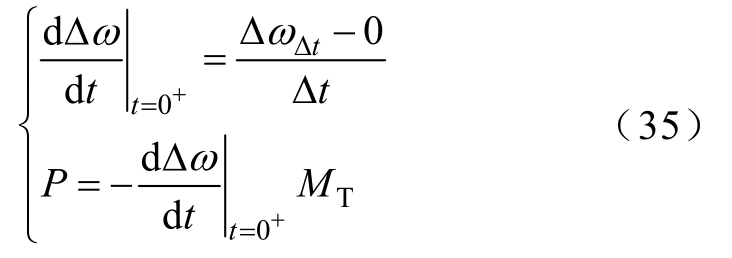
式中,ΔωΔt为功率扰动后 Δt时刻各母线或惯性中心频率偏移值;Δt为计算初始频率下降率的时间间隔,频率偏移初始值为0;P为使用各母线或惯性中心始频率下降率所计算的功率缺额。
本文中Δt取0.1s,即选取扰动后0s和 0.1s两个时刻各母线频率及惯性中心频率计算各母线及系统惯性中心的初始频率下降率,使用式(35)计算系统功率缺额,惯性中心初始频率下降率的计算结果为1 507.40MW,各母线初始频率下降率的计算结果见表4。
表4 基于初始频率下降率功率缺额计算结果
Tab.4 P calculation using initial df/dt

母线 P/MW 母线 P/MW 母线 P/MW 1 1346.94 14 1975.50 27 2005.65 2 2485.18 15 1898.72 28 1862.75 3 2209.50 16 1855.99 29 1808.82 4 2019.38 17 1975.58 30 3625.11 5 1940.44 18 2067.20 31 2300.73 6 1953.35 19 1662.74 32 2025.05 7 1860.93 20 1585.91 33 1588.69 8 1815.02 21 1779.81 34 1427.55 9 1105.69 22 1685.92 35 1649.04 10 1977.76 23 1648.12 36 1375.00 11 1970.04 24 1832.44 37 2044.73 12 1973.47 25 2284.11 38 1689.52 13 1976.51 26 2022.78 39 660.05
计算结果分析:各母线计算结果差异较大,计算结果分散。原因在于频率具有时空分布特性,同一时刻各母线频率下降率不同,使用单一母线某一时刻的频率下降率,并不能较好地反映系统的功率平衡情况。惯性中心频率与本文算法均能较好地计算系统的功率缺额,惯性中心频率计算结果略好于本文算法,但是使用惯性中心频率计算系统功率缺额需要广域通信系统。
下文将进一步验证不同频率时刻本文算法的有效性。系统功率缺额同样为1500MW时,分别使用59.2Hz和 58.8Hz时的部分母线频率偏移面积计算系统功率缺额,计算结果见表5。
表5 59.2Hz与58.8Hz频率偏移面积功率缺额计算
Tab.5 Pd calculation using 59.2Hz and 58.8Hz deviation areas

Pd/MW Pd/MW母线 母线59.2Hz 58.8Hz 59.2Hz 58.8Hz 3 1443.99 1485.16 23 1398.47 1474.10 4 1448.18 1485.47 24 1422.23 1480.10 7 1433.18 1486.41 25 1441.92 1485.17 8 1451.13 1486.50 26 1437.99 1481.62 15 1450.84 1482.19 27 1436.54 1482.21 16 1433.18 1480.78 28 1436.76 1477.87 18 1425.30 1483.47 29 1435.25 1476.31 20 1437.77 1481.11 39 1442.67 1469.45 21 1404.76 1477.71
由表 5可以看出:59.2Hz和 58.8Hz频率偏移面积都能较准确地计算功率缺额;计算结果为58.8Hz略好于59Hz,59Hz略好于59.2Hz。
验证不同功率缺额时算法的有效性。系统功率缺额分别为900MW和2000MW时,使用59.2Hz时频率偏移面积及惯性中心初始频率下降率计算系统功率缺额,惯性中心初始频率下降率的计算结果分别为904.68MW、2 001.01MW,部分母线频率偏移面积的计算结果见表6。
表6 900MW和2000MW功率缺额时计算结果
Tab.6 Pd calculation of 900MW and 2000MW deficit

Pd/MW Pd/MW母线 母线900MW 2 000MW 900MW 2 000MW 3 893.67 1925.31 23 884.99 1866.48 4 892.93 1932.30 24 889.00 1894.08 7 893.19 1937.67 25 892.38 1920.37 8 893.56 1937.08 26 890.39 1912.51 15 890.49 1908.65 27 890.92 1911.73 16 889.44 1897.14 28 887.92 1905.92 18 892.11 1915.50 29 886.90 1902.87 20 888.69 1865.55 39 897.04 1912.41 21 887.49 1884.27
计算结果分析:功率缺额为900MW和2000MW时,本文算法及使用惯性中心初始频率下降率算法依旧能准确计算系统的功率缺额。
验证不同负荷比例时本文算法的有效性。功率缺额同样为1500MW时,选取恒阻抗、恒电流及恒功率负荷比例为 30%、30%、40%,使用 59.2Hz、59Hz频率偏移面积及惯性中心初始频率下降率计算系统功率缺额,惯性中心初始频率下降率的计算结果为1 301.68MW,部分母线频率偏移面积的计算结果见表7。
表7 ZIP负荷功率缺额时计算结果
Tab.7 Pd calculation with ZIP load model

Pd/MW Pd/MW母线 母线59.2Hz 59Hz 59.2Hz 59Hz 3 1264.88 1267.46 23 1241.17 1257.06 4 1266.83 1267.13 24 1252.26 1261.85 7 1267.70 1268.07 25 1265.32 1266.89 8 1267.47 1268.29 26 1261.26 1262.64 15 1258.63 1264.00 27 1260.08 1263.44 16 1253.50 1262.56 28 1259.50 1258.10 18 1260.65 1265.59 29 1258.47 1256.40 20 1242.48 1260.25 39 1252.05 1258.01 21 1248.08 1259.89 COI 1301.68
计算结果分析:由于恒阻抗及恒电流负荷的压变效应,当系统发生功率缺额事件后,实际负荷往往变小。所以增加恒阻抗、恒电流负荷比例后,本文算法及使用惯性中心频率算法功率缺额计算结果都偏小,但仍能较好地计算系统的功率缺额。
4.1.2 IEEE 145母线系统功率缺额计算
IEEE 145母线系统来源于文献[20],为模拟不同的功率缺额,在117号母线增加一台无穷大容量电源。系统中,93号、139号、145号母线发电机为调频发电机,系统总容量为 32141MW,负荷为27096MW,恒功率与恒阻抗负荷比例分别为95%与5%。t=0时117号母线电源退出运行。使用各母线59.2Hz时频率偏移面积计算系统功率缺额。当功率缺额分别为 1000MW、1700MW及2500MW时,输出误差最大的 30个母线计算结果见表 8~表 10。
表8 1000MW功率缺额时计算结果
Tab.8 Pd calculation with 1000MW deficit

母线 Pd/MW 母线 Pd/MW 母线 Pd/MW 93 958.08 35 960.00 89 960.76 110 959.46 33 960.00 98 960.81 99 959.61 3 960.05 105 961.18 103 959.72 4 960.05 47 961.25 1 959.80 5 960.05 50 961.25 113 959.84 38 960.05 48 961.25 2 959.84 88 960.20 49 961.26 114 959.84 37 960.45 77 961.30 36 959.97 100 960.62 76 961.31 34 959.99 87 960.72 106 961.35
表9 1700MW功率缺额时计算结果
Tab.9 Pd calculation with 1700MW deficit

母线 Pd/MW 母线 Pd/MW 母线 Pd/MW 93 1589.17 33 1599.48 103 1606.63 110 1594.53 3 1599.68 47 1606.96 99 1594.88 4 1599.68 50 1606.97 1 1598.69 5 1599.68 48 1606.98 114 1598.90 38 1599.73 49 1606.98 2 1598.90 88 1600.42 100 1607.63 113 1598.90 37 1601.24 96 1607.82 36 1599.26 87 1603.62 102 1613.86 34 1599.42 105 1605.26 126 1614.40 35 1599.48 106 1606.14 119 1614.45
表10 2500MW功率缺额时计算结果
Tab.10 Pd calculation with 2500MW deficit

母线 Pd/MW 母线 Pd/MW 母线 Pd/MW 94 2281.65 36 2307.70 38 2309.80 90 2283.37 34 2308.09 1 2310.80 60 2292.17 5 2308.16 88 2311.04 80 2296.88 3 2308.16 2 2311.13 93 2297.10 4 2308.16 114 2311.13 79 2298.28 33 2308.24 113 2311.13 110 2298.43 35 2308.24 77 2313.12 103 2298.52 100 2308.63 76 2313.29 99 2299.88 89 2308.65 37 2313.40 92 2303.47 107 2309.39 98 2314.27
由表8计算结果可知:功率缺额为1000MW时,计算结果最大误差为93号母线,误差为-41.92MW,占功率缺额的 4.19%。全部母线计算结果误差平均值为-35.7MW,占功率缺额的3.57%。
由表9计算结果可知:功率缺额为1700MW时,计算结果最大误差为93号母线,误差为-110.83MW,占功率缺额的 6.52%。全部母线计算结果误差平均值为-77MW,占功率缺额的4.5%。
由表10计算结果可知:功率缺额为2500MW时,计算结果最大误差母线为 94号母线,误差为-218.35MW,占功率缺额的8.73%。全部母线计算结果误差平均值为-159.65MW,占功率缺额的 6.4%。
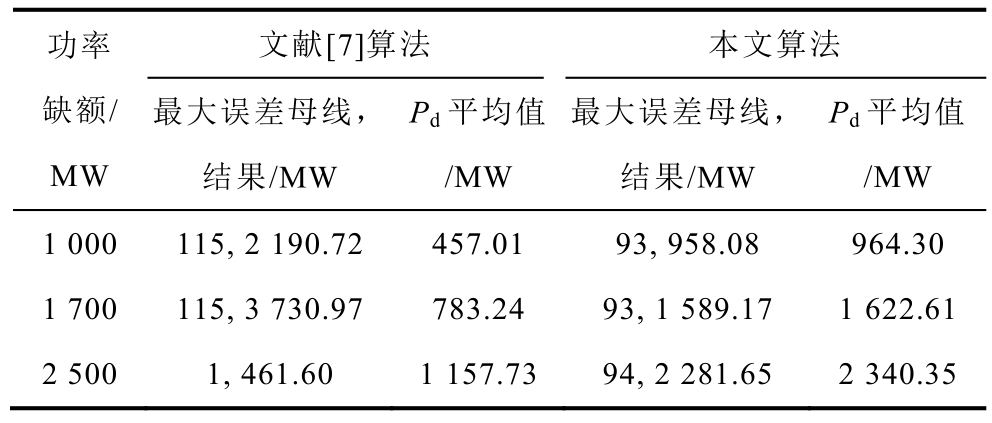
当系统实际功率缺额为1000MW、1700MW及2500MW 时,使用文献[7]算法计算系统功率缺额,并与本文算法进行对比,结果见表11。
由表11计算结果可知:本文算法均能准确计算系统功率缺额,计算准确性均好于文献[7]。
表11 文献[7]算法与本文算法计算结果对比
Tab.11 Algorithm comparisons in Ref.[7]and this paper
功率缺额/MW文献[7]算法 本文算法最大误差母线,结果/MW Pd平均值/MW最大误差母线,结果/MW Pd平均值/MW 1000 115, 2190.72 457.01 93, 958.08 964.30 1700 115, 3730.97 783.24 93, 1589.17 1622.61 2500 1, 461.60 1157.73 94, 2281.65 2340.35
4.2 基于频率偏移面积的低频减载整定
4.2.1 IEEE 39母线系统低频减载方案验证
对比本文方法、传统法及自适应法三种低频减载方案。选取功率缺额占系统总容量比例分别为15%≥Pd/PT、25%≥Pd/PT≥15%、Pd/PT≥25%,对应功率缺额为 900MW、1500MW、2000MW三种情况。在除12号母线外所有负荷母线安装低频减载装置,切负荷总量在低频减载间的分配比例见表 12。
表12 切负荷总量在各低频减载间的分配比例
Tab.12 The ratio of total load shed of every bus

母线 切负荷比例(%) 母线 切负荷比例(%)3 6 21 5 4 10 23 5 7 5 24 6 8 10 25 4 15 6 26 3 16 7 27 6 18 3 28 4 20 14 29 6
各低频减载方案首轮动作频率均为59.2Hz,动作轮次均为 5轮,各轮次级差均为 0.2Hz,动作延迟均为 0.1s。传统法采取系统可能出现的最大功率缺额,即39号母线发电机退出,导致系统最大功率缺额为1500MW,各低频减载方案见表13。
表13 低频减载整定方案
Tab.13 Different strategies of UFLS

轮次 频率/Hz 本文方法(%) 传统法(%) 自适应法(%)1 59.2 60/50/30 20 50 2 59.0 10/12.5/17.5 20 12.5 3 58.8 10/12.5/17.5 20 12.5 4 58.6 10/12.5/17.5 20 12.5 5 58.4 10/12.5/17.5 20 12.5
仿真测试不同功率缺额情况下三种低频减载方案的动作轮次、切负荷量见表14,低频减载动作后的系统惯性中心频率曲线,如图5~图7所示。
表14 低频减载动作轮次及切负荷量
Tab.14 Load shedding steps and amounts of UFLS(单位:MW)

动作轮次/总切负荷量功率缺额本文算法 传统法 自适应法900 1/267 1/300 1/560 1500 1/716 2/600 1/937 2000 2/1342 3/900 2/1552

图5 900MW功率缺额时频率曲线
Fig.5 Frequency curves of 900MW deficit

图6 1500MW功率缺额时频率曲线
Fig.6 Frequency curves of 1500MW deficit
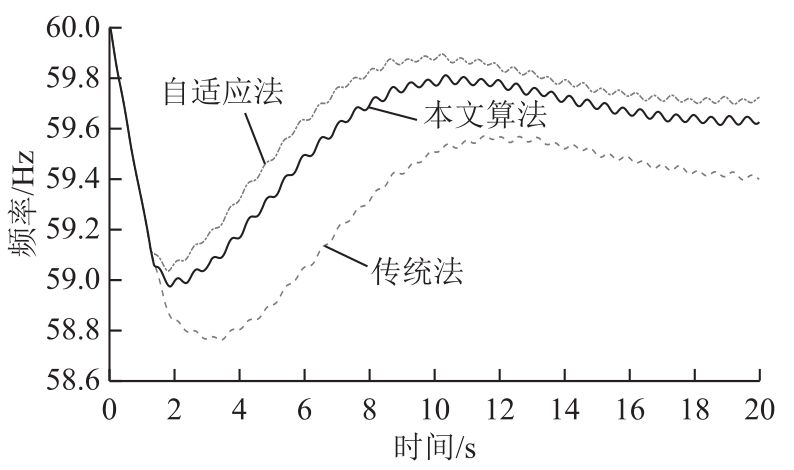
图7 2000MW功率缺额时频率曲线
Fig.7 Frequency curves of 2000MW deficit
在三种功率缺额下,自适应法切负荷量均大于本文方法。功率缺额为900MW时,三种方案均动作1轮,系统频率最低值均为59.18Hz,本文算法切负荷量最少;功率缺额为1 500MW时,本文方法最低频率为59.02Hz,自适应法最低频率为 59.18Hz,传统法最低频率为58.9Hz,本文方法切负荷量小于自适应法,频率恢复速度优于传统法;功率缺额为2 000MW时,本文方法及自适应法均动作2轮,传统法动作3轮,本文方法切负荷量小于自适应法,频率恢复速度优于传统法。
4.2.2 IEEE 145母线系统低频减载方案验证
IEEE 145母线系统负荷母线数量为80,选取负荷大于100MW的44个母线安装低频减载装置,切负荷量按照各母线负荷比例分配。传统法采用系统最大功率缺额为2500MW,选取表 13中低频减载方案,功率缺额为1000MW、1700MW、2500MW,低频减载动作轮次、切负荷量见表15,各方案的系统惯性中心频率曲线如图8~图10所示。
表15 低频减载动作轮次及切负荷量
Tab.15 Load shedding steps and amounts of UFLS(单位:MW)
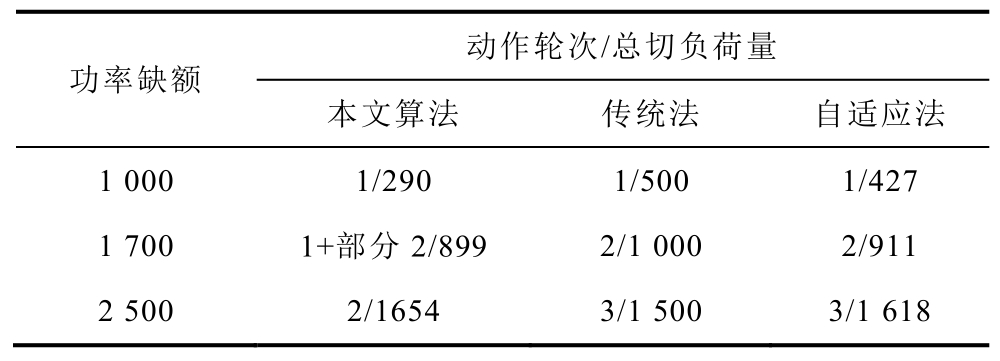
动作轮次/总切负荷量功率缺额本文算法 传统法 自适应法1000 1/290 1/500 1/427 1700 1+部分 2/899 2/1000 2/911 2500 2/1654 3/1500 3/1618

图8 1000MW功率缺额时频率曲线
Fig.8 Frequency curves of 1000MW deficit

图9 1700MW功率缺额时频率曲线
Fig.9 Frequency curves of 1700MW deficit

图10 2500MW功率缺额时频率曲线
Fig.10 Frequency curves of 2500MW deficit
功率缺额为1000MW时,三种方案均动作1轮,最低频率近似相等,在保证频率稳定的基础上,本文方法切负荷量相对较少;功率缺额为1700MW时,本文方法低频减载首轮全部动作,部分低频减载动作2轮,传统法和自适应法均动作2轮,本文方法最低频率高于自适应法和传统法,并且切负荷量最小;功率缺额为2500MW时,本文方法动作2轮,传统法和自适应法均动作3轮,本文方法最低频率均高于传统法和自适应法,频率恢复速度最快。
5 结论
本文建立频率偏移面积与系统功率缺额之间的关系,准确计算系统的功率缺额,提出了基于功率缺额大小的低频减载整定基本思想及方案。应用时,工程技术人员可根据实际情况,调整功率缺额的计算时刻、低频减载各轮次动作频率及切负荷量。本文得到以下结论:
1)以简化的两机系统推导了各发电机频率偏移面积与系统惯性中心频率偏移面积之间的关系,得到在低频减载首轮频率时刻母线频率偏移面积与惯性中心频率偏移面积近似相等的结论,并提出基于频率偏移面积的系统功率缺额计算算法。算例分析表明,该算法能够准确地计算系统的功率缺额。
2)基于各母线功率缺额的准确计算,提出基于功率缺额大小的低频减载整定基本思想及方案。算例分析表明,所提出的思路与方案在防止系统最低频率过低、加快频率恢复速度及降低切负荷量方面具有一定的优势。
[1]赵晶晶, 李敏, 何欣芹, 等. 基于限转矩控制的风储联合调频控制策略[J]. 电工技术学报, 2019,34(23): 4982-4990.Zhao Jingjing, Li Min, He Xinqin, et al. Coordinated control strategy of wind power and energy storage in frequency regulation based on torque limit control[J].Transactions of China Electrotechnical Society, 2019,34(23): 4982-4990.
[2]钟诚, 周顺康, 严干贵, 等. 基于变减载率的光伏发电参与电网调频控制策略[J]. 电工技术学报,2019, 34(5): 1013-1024.Zhong Cheng, Zhou Shunkang, Yan Gangui, et al. A new frequency regulation control strategy for photovoltaic power plant based on variable power reserve level control[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1013-1024.
[3]马智慧, 李欣然, 谭庄熙, 等. 考虑储能调频死区的一次调频控制方法[J]. 电工技术学报, 2019,34(10): 2102-2115.Ma Zhihui, Li Xinran, Tan Zhuangxi, et al. Integrated control of primary frequency regulation considering dead band of energy storage[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2102-2115.
[4]李欣然, 崔曦文, 黄际元, 等. 电池储能电源参与电网一次调频的自适应控制策略[J]. 电工技术学报, 2019, 34(18): 3897-3908.Li Xinran, Cui Xiwen, Huang Jiyuan, et al. The selfadaption control strategy of energy storage batteries participation in the primary frequency regulation[J].Transactions of China Electrotechnical Society, 2019,34(18): 3897-3908.
[5]Li Changgang, Wu Yue, Sun Yanli, et al. Continuous under-frequency load shedding scheme for power system adaptive frequency control[J]. IEEE Transactions on Power Systems, 2020, 35(2): 950-961.
[6]陈璟, 熊小伏, 胡剑, 等. 有功不平衡下计及低频减载影响的输电线路过载热保护[J]. 电力系统保护与控制, 2019, 47(23): 19-29.Chen Jing, Xiong Xiaofu, Hu Jian, et al. Thermal overload protection of transmission lines considering the influence of UFLS under active power imbalance[J]. Power System Protection and Control,2019, 47(23): 19-29.
[7]Anderson P M, Mircheydar M. An adaptive method for setting underfrequency load shedding relays[J]. IEEE Transactions on Power Systems, 1992, 7(2): 647-655.
[8]蔡国伟, 孙正龙, 王雨薇, 等. 基于改进频率响应模型的低频减载方案优化[J]. 电网技术, 2013,37(11): 3131-3136.Cai Guowei, Sun Zhenglong, Wang Yuwei, et al.Optimization of under frequency load shedding scheme based on improved system frequency response model[J]. Power System Technology, 2013, 37(11):3131-3136.
[9]李爱民, 蔡泽祥. 基于曲线分析的互联电网频率动态特性及低频减载的优化[J]. 电工技术学报, 2009,24(9): 171-177.Li Aimin, Cai Zexiang. Frequency dynamics analysis and load shedding assessment based on the dynamic simulation trajectory of interconnected power system[J]. Transaction of China Electrotechnical Society, 2009, 24(9): 171-177.
[10]李顺, 廖清芬, 唐飞, 等. 高风电渗透率下的自适应低频减载策略研究[J]. 电网技术, 2017, 41(4):1084-1090.Li Shun, Liao Qingfen, Tang Fei, et al. Adaptive underfrequency load shedding strategy considering high wind power penetration[J]. Power System Technology, 2017, 41(4): 1084-1090.
[11]李常刚, 张恒旭, 刘玉田, 等. 考虑机组低频保护的电力系统暂态频率稳定评估[J]. 电工技术学报,2013, 28(2): 271-278.Li Changgang, Zhang Hengxu, Liu Yutian, et al.Power system transient frequency stability assessment considering unit underfrequency relay protection[J].Transactions of China Electrotechnical Society, 2013,28(2): 271-278.
[12]刘克天, 王晓茹. 基于广域量测数据的电力系统动态频率分析方法[J]. 电网技术, 2013, 37(8): 2201-2206.Liu Ketian, Wang Xiaoru. A wide-area measurement data based method for power system dynamic frequency analysis[J]. Power System Technology,2013, 37(8): 2201-2206.
[13]刘克天, 王晓茹, 薄其滨. 基于广域量测的电力系统扰动后最低频率预测[J]. 中国电机工程学报,2014, 34(13): 2188-2195.Liu Ketian, Wang Xiaoru, Bo Qibin. Minimum frequency prediction of power system after disturbance based on the WAMS data[J]. Proceedings of the CSEE, 2014, 34(13): 2188-2195.
[14]杨德友, 蔡国伟. 基于广域局部量测信息的复杂电力系统自适应低频保护策略研究[J]. 电工技术学报, 2014, 29(10): 266-275.Yang Deyou, Cai Guowei. Adaptive under frequency load shedding schemes for complex power systems using local measurements[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 266-275.
[15]王增平, 朱劭璇, 王彤, 等. 受端电网分层优化切负荷策略[J]. 电工技术学报, 2020, 35(5): 1128-1139.Wang Zengping, Zhu Shaoxuan, Wang Tong, et al.Research on stratified optimal load shedding strategy for receiving end power grid[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1128-1139.
[16]薄其滨, 王晓茹, 刘克天. 基于 v-SVR的电力系统扰动后最低频率预测[J]. 电力自动化设备, 2015,35(7): 83-88.Bo Qibin, Wang Xiaoru, Liu Ketian. Minimum frequency prediction based on v-SVR for postdisturbance power system[J]. Electric Power Automation Equipment, 2015, 35(7): 83-88.
[17]孙毅, 李泽坤, 黄绍模, 等. 基于分布式需求侧资源备调池的低频减载优化策略研究[J]. 电网技术,2020, 44(3): 1016-1025.Sun Yi, Li Zekun, Huang Shaomo, et al. An improved UFLS strategy based on distributed demand side resource pools[J]. Power System Technology, 2020,44(3): 1016-1025.
[18]李铭, 安军, 穆钢, 等. 基于实测曲线的频率动态时空分布特性研究[J]. 电网技术, 2014, 38(10):2747-2751.Li Ming, An Jun, Mu Gang, et al. Measured trajectory based space-time distribution characteristics of frequency dynamics[J]. Power System Technology,2014, 38(10): 2747-2751.
[19]倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[20]Thorp J S, Wang X R, Hopkinson K M, et al. Agent technology applied to the protection of power systems.Autonomous systems and intelligent agents in power system control and operation, chapter 7 of the book:autonomous systems and intelligent agents in power system control and operation[M]. Berlin: Springer Press, 2003: 115-154.