0 引言
双馈感应发电机(Double-Fed Induction Generator,DFIG)装机容量约占90%的市场份额,是当今的主流机型[1-2]。由于传统DFIG采用最大功率跟踪运行方式,机组的转速与电网频率无关,即机组的出力不响应电网频率的波动。
为了提高风力发电系统的惯量支撑和频率响应能力,文献[3]在最大功率点跟踪的基础上附加虚拟惯性控制和下垂控制,有效增加了系统等效惯量和阻尼,但下垂控制依然无法实现风电机组捕获机械功率的作用,可能引起频率二次跌落现象。文献[4]提出了基于选择函数的风电机组新型虚拟惯量综合控制方法,避免了传统控制所造成的功率二次跌落。文献[5-7]提出超速减载运行控制的方法,使得风电机组预先留有功率裕度来参与电网调频。文献[8-10]提出通过桨距角控制来预留备用容量,通过调节桨距角改变机组出力,参与系统调频,但桨距角调整速度较慢,其机械部件的频繁动作增加了维修风险和维护成本。文献[11]在上述两种常规方法的基础上提出超速与变桨结合的协调控制方案,虽然在一定程度上改善风电机组整体性能和一次调频特性,但以上方法均未考虑DFIG自身发电效益,降低了风能利用率,故如何配置风电机组的调节机制来缓解发电效益和系统稳定性之间的关系是目前亟待解决的问题。
储能装置已广泛应用于风电场,在基于储能参与电网一次调频控制方面,文献[12]分析了具有快速响应的储能技术对高渗透率情况下的风电场频率响应的应用场景;文献[13]提出一种在储能技术的依托下对风电场的虚拟惯量进行补偿的策略;文献[14]分析风电出力特点,提出一种储能电源参与含风电电网的优化下垂控制策略,可有效平抑风电功率波动。倘若仅采用虚拟下垂控制,即使减小了稳态频率偏差,也无法减缓频率下降速度和降低最大频率偏差变化量。然而仅采用单一虚拟惯性控制,则只能在频率变化过程中起作用,无法降低稳态频率偏差。因此文献[15]给出了合理协调两者之间关系的方法,但储能电源循环周期寿命短,且不考虑储能SOC变化,大大增加了维护成本。
在基于储能的风电场参与电网一次调频配置方面,文献[16]论述了风电场集中储能承担一次调频的方案。但是,风电机组本身不具备自主运行参与系统调频的能力,终究是不完善的,应用的范围也将受到外部条件限制。文献[17]分别探索了在双馈感应发电机背靠背功率变流器的直流母线并联配置电池储能和超级电容器组储能单元,平抑风速变化,平滑功率输出;文献[18]探索了在直流母线上并联配置超导储能单元,改善双馈感应发电机组应对低压事件的动态性能。所以,针对储能装置参与风电场一次调频策略研究中,大多采用风电场集中式储能方案,其安全可靠性风险往往大于分布式模式[19-20],而目前风力发电集中并网点高压侧普遍出现频率、电压波动幅度增大现象,其中风电场内部或并网点变压器中低压侧的频率波动幅度更大,超过一次调频动作阈值(0.033Hz)的情形频繁出现[21];故提高单台风电机组的致稳性和抗扰性,使其具备一次调频能力显得尤为重要[22]。超级电容器目前仅应用于配合低电压穿越和平滑功率波动方面,由于具有功率密度大的优点,可瞬时大功率输出,故可为系统提供惯量支撑和一次频率调节[23]。
针对上述问题,本文兼顾 DFIG运行的经济性和系统一次频率调节需求,结合实际运行场景和DFIG网侧变流器的控制特性,提出了计及超级电容储能SOC控制DFIG的惯量与一次调频自适应控制策略。结合惯性与下垂控制模式各自优势,采用一种确定两种调频模式参与调频的比例系数模型,实现两种调频模式平滑切换。在此基础上综合考虑自身储能SOC实时修正虚拟惯性与下垂系数,其惯量支撑和一次频率调节都由超级电容储能模块扩展功能实现,无需修改或增加原风电机组的结构和控制方案,从而使风电机组的升级改造变得简单容易,提高了单台风电机组的致稳性和抗扰性。在系统稳定或发电需求增加(减小)期间风电机组始终运行在最大功率跟踪模式以达到最大发电效益。当发电需求减小或增大时,通过控制超级电容器充电与放电来参与系统频率调节,实现 DFIG在全工况运行下具有一次调频能力。最后基于Matlab/Simulink搭建含 DFIG的四机两区域仿真模型,验证所提方案有效性。
1 基于超级电容器储能装置的惯量支撑与一次调频自适应控制策略
1.1 总体控制思想及储能类型
为提高单台风电机组的致稳性和抗扰性,本文对单台风电机组配置储能装置,其优势在于控制灵活,功能模块化,在风机需要拓展惯量与一次调频功能时,不需要改变原风电机组控制系统的任何结构或逻辑,直接通过控制储能装置参与系统惯量与一次频率调节作用,使得单台风电机组具有良好的鲁棒性和兼容性,尤其适合现场已投运机组的升级改造。在储能装置选取方面,杨裕生院士从储能装置的性能指标和运行经济指标出发,推导出“规模储能装置的经济效益指数”YCC为

式中,Rout和Rin分别为储能装置的电能进价和出价,元/(kW·h);η为能量转换效率;C为1kW·h电能输出的初始投资,元/(kW·h);C0为输出1kW·h电能的运行成本,元/(kW·h);DOD为储能装置的充放电深度;L为相应DOD下的循环寿命(次)。由式(1)得到“储能装置的直接经济效益”即利润率Pm为
当计算得到YCC>1时,则 Pm>0,表示储能可盈利。根据相关数据,得到不同化学电源的经济效益评估[24-27]见表1。
表1 不同化学储能技术的性能及经济效益
Tab.1 Performance and economic benefits of different chemical energy storage technologies

注:Rin为 0.15 元/(W·h),Rout为 0.8 元/(W·h)。
储能类型能量效率(%)DOD×循环寿命初始投资/[(元/(W·h)]维护成本/[元/(kW·h)]利润率(%)铅酸电池 70~75 1×800 0.7×4 500 1 0.05-54 63锂离子电池 90~95 1×1 000 4.5 0.05 -86全巩液流电池 70~80 1×13 000 5~10 0.1 26~-30超级电容器 80~95 1×200 000 27 0.05 247
由表 1可知,超级电容器一方面可循环次数较多,满足频繁充放电的需求,在经济性评估方面占有绝对优势,利润率Pm高达247%;另一方面功率密度大,可瞬时大功率输出,符合电网一次调频需求。综上,本文选取超级电容储能系统辅助DFIG风电机组参与调频。基于超级电容储能装置控制的DFIG惯量与一次调频配置如图1所示。

图1 DFIG的储能配置
Fig.1 DFIG energy storage configuration
超级电容器经过双向DC-DC变换器与DFIG的直流侧母线电容相连接。本文结合 DFIG网侧变流器的控制特性,即网侧变流器的作用为维持直流母线电容电压的稳定,故超级电容储能装置的充放电功率通过网侧变流器直接流向负荷侧。结合实际,考虑网侧变流器输出功率的限制,分析超级电容储能装置最大放电时不会超过目前现有网侧变流器额定输出功率,为本文提出的方案提供了可行性。
1.2 基于超级电容器储能装置的自适应调频控制策略的设计与实现
1.2.1 控制系统模型
已知基于超级电容器储能装置控制的 DFIG机组参与电网一次调频控制方式主要分为虚拟惯性控制和虚拟下垂控制。基于对两种控制策略的研究,本文采用一种基于频率偏差和频率偏差变化率的自适应控制策略。在系统处于惯性响应阶段时,采用虚拟惯性为主,虚拟下垂为辅的控制方式来实现对超级电容器的控制;在系统处于一次调频阶段时,则采用虚拟下垂为主,虚拟惯性为辅的控制方式。故可得到上述自适应控制方式下超级电容器的出力为
式中,c1、c2分别为虚拟惯性模式和虚拟下垂模式的比例系数;KH、Kscss分别为超级电容器的虚拟惯性系数和下垂系数。
1.2.2 超级电容器参与一次调频控制的比例系数
1)惯性响应阶段的比例系数
结合惯性响应阶段的频率偏差变化率和频率偏差量的变化特点,得到此阶段下系数比例公式为

式中,0≥Δf ≥ln0.5/n。
图2和图3分别为式(4)所对应的系数分配随频率偏差和频率偏差变化率的曲线图。由图可得,在初始惯性响应阶段,|dΔf/dt|较大,|Δf |较小,虚拟惯性控制优势可得到充分发挥,可以在一定程度上减小频率偏差变化率的最大值,降低频率偏差的变化速度。在后期惯性响应阶段,|Δf |较大,|dΔf/dt|较小,可充分发挥虚拟下垂控制的优势,频率偏差最大值得到明显减小。

图2 频率偏差曲线(惯性响应阶段)
Fig.2 Frequency deviation curve(inertial response phase)

图3 频率偏差变化率曲线(惯性响应阶段)
Fig.3 Frequency deviation change rate curve(inertial response phase)
由图2和图3可知,比例系数c1和c2的渐变曲线与在整个惯性响应阶段中频率的变化特性相匹配,其具体取值和速度变化与式(4)中的n有关。不同n的值下系统频率偏差曲线和超级电容器出力曲线如附图1和附图2所示。若n过小,则即使|Δf |明显增大且|dΔf/dt|明显减小,c1和 c2的变化也较小,则惯性响应能力和下垂响应能力均不能得到充分发挥,最大频率偏差(Δfmax)过大,导致超级电容器的最大输出功率增大。同理,若n过大,则只要|Δf |略有增大或|dΔf/dt|略有减小,都将使c1急剧减小而c2急剧增大,此时难以充分发挥其下垂响应能力,且无法充分利用惯性响应的优势,对有效抑制频率偏差变化率产生不利影响。
2)一次调频阶段的系数比例
本节控制方式应以虚拟下垂为主,虚拟惯性为辅。故可得到此阶段的系数比例公式为

式中,![]() 为超级电容器参与电网一次调频的阈值;Δfmax为一次调频中最大频率偏差值。图4和图5,分别为式(5)所对应的系数分配随频率偏差和频率偏差变化率的变化曲线。已知在一次调频阶段,c1值以较快的速度减小到0,c2值以较快的速度增大到1,此时虚拟下垂控制优势得到显著体现,能够有效减小系统稳态频率偏差值。
为超级电容器参与电网一次调频的阈值;Δfmax为一次调频中最大频率偏差值。图4和图5,分别为式(5)所对应的系数分配随频率偏差和频率偏差变化率的变化曲线。已知在一次调频阶段,c1值以较快的速度减小到0,c2值以较快的速度增大到1,此时虚拟下垂控制优势得到显著体现,能够有效减小系统稳态频率偏差值。

图4 频率偏差曲线(一次调频阶段)
Fig.4 Frequency deviation curve(primary frequency modulation stage)

图5 频率偏差变化率曲线(一次调频阶段)
Fig.5 Frequency deviation change rate curve(primary frequency modulation stage)
一次调频阶段全过程中,存在c1<c2,c1+ c2=1,其中比例系数 c1和 c2的渐变曲线与在整个惯性响应阶段中频率的变化特性相匹配,其中一次调频阶段的系数比例数值及变化速度同样与式(5)中的参数n有关。当n取值太小时,存在c1= c2=0.5,此时的比例系数会导致惯性响应功率降低,且严重阻碍了下垂响应能力的发挥。当n取值太大时,| Δf |的细微变动会致使c1、c2剧烈变化,影响下垂响应能力发挥,导致超级电容器出力增大,未能优化利用超级电容器的容量。
综上所述,参数n过大或过小都会影响调频效果和储能装置的优化。故综合考虑上述因素,选择n为10。
1.2.3 计及SOC反馈的自适应控制
由于 DFIG所配置的超级电容器的容量有限,若一直采用最大下垂系数充放电,则超级电容器的荷电状态SOC易越线。为避免此问题,本文考虑在超级电容器SOC过高(充电)或过低(放电)时动态调整虚拟惯性和虚拟下垂系数,以此来减小该储能装置的出力。不仅可有效避免储能装置的过充放问题,提高使用寿命,而且还可减少SOC越限时对电网系统所造成的不利影响。
本文将超级电容器SOC划分为五个区间,如图6所示,Km为双馈风力发电机组的下垂系数,设定最小值 QSOC_min=0.1,较低值 QSOC_low=0.45,较高值QSOC_high=0.55和最大值QSOC_max=0.9。值得注意的是,以上取值并不是唯一的,取决于不同型号超级电容器的自身SOC特性。为了定量分析超级电容器SOC越限下的极限工况,本文将 SOC的最小值设置为 0.1。

图6 超级电容器单位调节功率与SOC 的关系
Fig.6 Relationship between unit regulation power of super capacitor energy storage and SOC
计及 SOC反馈的超级电容器虚拟惯性系数KH(QSOC)和虚拟下垂控制系数Kscss(QSOC)分别为

式中,Kc、Kd分别为超级电容器下垂控制过程中的充、放电系数;α为虚拟惯性系数与虚拟下垂系数之间的比例系数,本文取为0.3。为防止SOC越限所带来的问题,采用线性分段函数来设置充放电曲线,既可以实现平滑出力,还能避免复杂函数所带来的控制难题,更利于工程的实际应用。Kc和Kd分别为

1.2.4 自适应控制策略的流程
本文所提出基于综合考虑 SOC反馈的超级电容储能装置 DFIG一次调频自适应控制策略流程如图7所示。调频控制分为两大控制模式:①虚拟惯性为主、虚拟下垂为辅;②虚拟下垂为主、虚拟惯性为辅。

图7 一次调频自适应控制策略流程
Fig.7 The flow chart of self-adaptation control strategy in primary frequency regulation
1)将调频死区设定为|Δf |≤0.03Hz,此时可近似判定为系统无扰动,风电机组不参与惯性调节和一次频率调节。当电网频率f偏离电网额定频率时,Δf>0.03Hz时,系统负荷减小,超级电容器充电;Δf<-0.03Hz时,系统负荷增加,超级电容器充电。当存在负荷扰动时,为防止过充或过放,需要判定超级电容储能系统当前 SOC状态是否分别满足放电约束和充电约束条件。满足SOC约束后,可根据以下步骤进行充放电控制。
2)超级电容器首先在虚拟惯性为主,虚拟下垂为辅的控制模式下工作。首次设定虚拟惯性调频模式的分配系数c1=1,虚拟下垂调频模式的分配系数c2=0,并根据式(3)计算超级电容器的出力情况。
3)在惯性响应阶段内,根据式(4),对惯量支撑与下垂响应模式中的系数进行分配,在具体分配过程中满足虚拟惯性调频模式的分配系数c1≥0.5,虚拟下垂的调频模式的分配系数 c2≤0.5的前提条件。
4)在电网频率处于最大频率偏差Δfmax时,超级电容器的控制模式自动切换为虚拟下垂为主,虚拟惯性为辅,此时的分配系数c1=0.5,c2=0.5。
5)在下垂响应阶段内,根据式(5)对系数进行分配,取虚拟惯性调频模式的分配系数 c1≤0.5,虚拟下垂的调频模式的分配系数c2≥0.5。
6)当电网频率达到稳态频率偏差值时,基于超级电容器储能的DFIG机组参与一次调频结束。
综上分析可知,虚拟下垂和虚拟惯性控制决定了超级电容器的出力模式,而根据式(6)~式(9)的 SOC反馈自适应控制规律决定了下垂系数和惯性系数的大小,上述两种相辅相成共同决定了超级电容器的实际出力大小及方向。
2 超级电容器储能装置的容量及配置
中国电力科学研究院于 2016年牵头制定的风机虚拟同步发电机(Virtual Synchronous Generator,VSG)技术标准——《风电机组虚拟同步机技术要求和试验方法》[28]中提出“虚拟同步发电机若能调节有功输出参与电网一次调频,当系统频率下降时,其有功出力可增加量的最大值至少为10%Pn且一次调频调节时间应不大于30s”,故本文所采用的超级电容器储能装置的能量设置为150kW×30s,图8为超级电容器充放电的原理图。其中,超级电容器内阻为R,充电功率为Pc,放电功率为Pd,电容两端电压为UC,超级电容器储能装置两端电压为U,充放电深度为d=1-γ,γ=Umin/Umax为电压比率,超级电容最低工作电压为 Umin,最高工作电压为 Umax。

图8 超级电容器充放电的原理
Fig.8 Supercapacitor charging and discharge schematic
已知该超级电容储能装置充放电效率[28]为

若储能装置由m组超级电容模组串联,n组超级电容模组并联,且确保超级电容器达到最小电压时所输出的功率状态为满功率输出,由此需要满足
该超级电容器储能容量W满足

本文结合目前实际超级电容器规格,采用144V×55F 的超级电容模组,综合式(10)~式(12),可以得到表2所示超级电容器不同组合方式下的工作电压和效率及图9所示的储能装置效率曲线。
表2 超级电容器不同组合方式下的工作电压和效率
Tab.2 Operating voltage and efficiency in different combinations of supercapacitors

串联组数 并联组数 最小工作电压/V最大工作电压/V充放电效率(%)6 3 24 864 97.54 5 4 23 720 96.60 4 5 26 576 95.22
当超级电容器的充放电效率为97.54%时,其最高工作电压为864V,故为使超级电容器充放电效率大于97%,该工作电压必须高于864V,因此选为超级电容储能装置最高工作电压。经计算可得,需采用144V×55F(型号:MCP0055C0-0144R0SHB)超级电容模组6串3并共 18组组成该双馈风电机组的储能装置。已知该型号的超级电容器能量密度为1.9W·h/kg,计算可得单台风电机组配置的超级电容器模组总重量为 658kg,质量体积大小可接受,可将该储能柜放置于风机塔筒的变流器支架下,且接线方案可行。

图9 超级电容储能装置的效率曲线
Fig.9 Efficiency curve of super capacitor energy storage device
其次在超级电容储能模组的连接方式有如图10所示的两种方式。图10a所示m个超级电容器先进行串联,再对其进行n对并联组成储能阵列;图10b所示先将n个超级电容器并联,然后再将这m个并联模块串联起来组成储能阵列。以上不同的连接方式可对超级电容阵列的可靠性和容量分散度产生不同的影响。

图10 超级电容器不同阵列模式
Fig.10 Different array modes of supercapacitors
假定每个单体超级电容器的可靠性为a(0<a<1),且相互独立无影响,经计算可得,采用图10a中所示的超级电容器储能阵列的可靠性为 P1=1-(1-am)n,采用图 10b所示的超级电容器储能阵列的可靠性为P2=[1-(1-a)n]m。由此可知,m与n的数值越大,后者的连接方式越可靠。
在同一串联支路中同时出现容量最大和容量最小的超级电容时,此支路上超级电容的电压差达到最大,故对电压均衡电路提出了新的挑战。假设超级电容的额定电容为C,电容存在的分散度为d,d的范围为-10%~20%。单体超级电容器的容量分散度用d1, d2, …, dmn表示,且 d1<d2<…<dmn,则所有超级电容中容量最小值为 Cmin=C(1+d1),容量最大值为Cmax=C(1+dmn)。
在图 10a所示的先串联后并联方式中,Cmin和Cmax出现在同一个串联支路的概率为
在图10b所示的先并联后串联方式中,超级电容阵列可认为由m个模块串联构成,每个模块的容量可表示为
这m个模块中最小的容量为
最大的容量为
由式(15)和式(16)可知,超级电容的电容分散度范围为![]()
与连接之前的分散度(d1,dn)相比范围明显减小,并且分散度范围随着并联支数增大而不断减小,在该种连接方式下,C1min和C1max连接在同一串联支路中概率为
由式(17)得,随着并联支数n的增加,先并联后串联方式下的最大电容量和最小电容量在同一条串联支路上的概率远远小于先串联后并联方式。综上所述,采用如图10b所示的连接方式可靠性高,容量分散度较小,故此阵列对均压电路平衡能力要求较低。
3 仿真验证
3.1 仿真模型
本文在 Matlab/Simulink平台中搭建了四机两区域模型,并基于超级电容器储能调频控制策略对该模型进行控制仿真分析,其仿真模型如图 11所示。其中,G1~G3为容量900MW的火电厂,均配备了励磁调节器和调速器;G4为双馈风电场,含300台1.5MW的双馈风机,每台超级电容器组为27.5F,容量为 150kW×30s,风机额定风速为 10m/s。负荷Load1和Load2分别为880MW和950MW的恒定有功负荷,Load3为随机波动负荷,C1和C2为无功补偿装置。

图11 含双馈风电场的4机2区域系统
Fig.11 4-machine 2-area system with doubly-fed wind farm
3.2 系统负荷随机波动时DFIG机组仿真分析
为了充分验证所提策略的有效性,在风速恒定为10m/s且负荷随机波动场景下进行仿真。首先,系统负荷在20s时突增145MW,图12所示为基于超级电容器储能的虚拟下垂与虚拟惯性直接切换控制、惯性与下垂自适应分配系数控制以及计及SOC的虚拟惯性与下垂自适应控制的超级电容器储能装置的输出功率曲线对比图。其中前两种控制方法的惯性系数 KH和下垂系数 Kscss恒定不变,故也称为定K法。在上述工况下,由图12可得定K-惯性与下垂自适应控制和定K-直接切换法相比,在配置超级电容器储能装置额定功率方面减少20%,并且超级电容器的出力曲线较为平滑。但由于超级电容器本身容量限制问题,在时间为60s时,能量释放结束且不再发挥作用,此时采用上述两种控制方法则会再次产生一个频率较大跌落的过程。针对上述问题,本文则在虚拟惯性与下垂系数自适应分配的基础上考虑了超级电容器SOC状态值,根据式(6)~式(9)实时改变其惯量与下垂系数,由图12可知本文所提方法相对上述两种方法短时间内输出功率较小,但可防止频率出现突变情况,避免超级电容器过充过放的现象发生,提高其使用寿命。

图12 负荷突增145MW下超级电容器输出功率的曲线
Fig.12 The curves of super capacitor output power at 145MW load surge
为方便分析,本工况下超级电容器初始SOC设置为60%,初始工作电压Usc为670V,由图13可知,在持续放电工况下,不考虑SOC状态的惯性与下垂自适应控制在时间为60s时,SOC达到下限值10%,其工作电压Usc达到最低放电电压270V。而本文所提方法的超级电容器SOC的维持效果较佳,相比上述控制的SOC提高13.5%。

图13 负荷突增145MW下超级电容器参数
Fig.13 The value of super capacitor parameter under a sudden load increase of 145MW
图 14为上述工况下采用三种不同控制策略所对应的频率偏差曲线,其中定K-自适应控制在t0~tm时间段内的控制方式以虚拟惯性为主,虚拟下垂为辅,可抑制最大频率偏差变化率的同时降低最大频率偏差量。tm时刻过后,控制模式以虚拟下垂为主,虚拟惯性为辅。与定K-直接切换法相比,其频率最大偏差量减小10%。实现了平滑切换,避免直接切换对电网造成的冲击。当超级电容器能量一旦完全释放,系统频率会再次跌落0.015Hz。而本文所提方法在减小频率最大偏差量的基础上,系统频率整体相对稳定,不会出现频率突变的现象。

图14 固定参数与自适应参数下系统频率偏差对比(负荷突增145MW)
Fig.14 Comparison chart of system frequency deviation under fixed parameters and adaptive parameters(the load increased by 145MW)
为验证本文所提出的计及SOC自适应控制的超级电容储能控制双馈风力发电机组惯量与一次调频自适应控制策略相较于常规调频控制的优势,图 15所示为上述同样工况下不同调频方式所对应的频率偏差曲线。双馈风力发电机在超速减载 10%的一次调频控制下,稳态频率偏差约为 0.09Hz,但在本文所提出的调频控制策略下稳态频率偏差为 0.075Hz,相比于常规的 DFIG超速减载一次调频控制策略,其一次频率调节能力提高22.2%,提升效果显著。
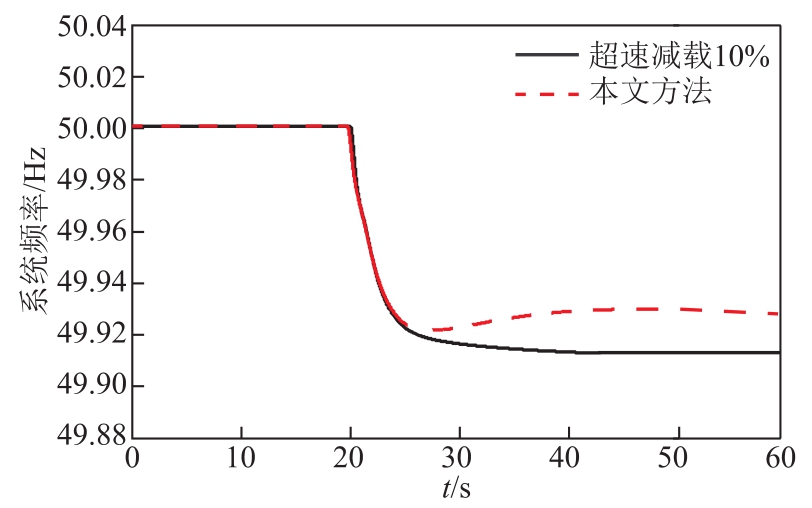
图15 传统控制与本文控制下系统频率偏差对比(负荷突增145MW)
Fig.15 Comparison chart of system frequency deviation under traditional control and text control(the load increased by 145MW)
在本文所提控制策略下风机保持最大功率输出,风能利用系数和转速保持最优值,其动态响应对比如图16和表3所示。由表3可知,当出现系统负荷增大 145MW 的扰动时,计及超级电容器储能SOC参与DFIG惯量支撑和一次调频自适应控制与超速减载10%调频控制相比,风能利用率提高3.2%,输出功率增大 31.4%。故本文所提出的计及超级电容储能 SOC为系统提供惯量支撑与一次调频自适应控制在负荷增大扰动下提高了一次频率调节能力,并且在一定程度上提高了发电效益。

图16 负荷突增145MW下风电机组响应对比
Fig.16 Comparison of response of wind turbines under load increase of 145MW
同样,针对上述仿真模型,负荷在20s时突减180MW,如图17所示为定K-直接切换控制、定K-自适应分配系数控制以及计及 SOC的虚拟惯性与下垂自适应控制的超级电容器储能装置的吸收功率曲线对比图。由图 17可知,在定 K-直接切换控制下系统进行一次调频时,在系统频率偏差达到最大值时才进行调频模式切换会导致超级电容器产生较大的功率超调量;在定K-自适应分配系数控制下的系统则不会出现这样的较大超调量,根据储能装置在各时间点的动作深度来配置储能电池的额定功率PE。针对此工况下定K-自适应分配系数控制法与定K-直接切换法相比,其储能装置的额定功率相较于直接切换控制下所配置的储能装置额定功率减小12.5%,可在有效减小超级电容器的额定功率配置裕量的同时实现超级电容储能装置的出力曲线平滑稳定。但同样存在上述问题,在55s时,超级电容器吸收能量达到极限值且不再发挥作用,此时采用上述两种控制方法则会再次产生一个频率较大抬升过程,影响系统稳定性。
表3 负荷突增145MW时响应性能指标
Tab.3 Response indices When load is increased by 145MW

控制策略风能利用系数风机输出功率(pu)最大转速(pu)桨距角/(°)本文方法 0.48 0.46 1 0超速减载10% 0.465 0.35 1.16 0

图17 超级电容器吸收功率的曲线
Fig.17 Curve of super capacitor output power
已知本文所提方法相对定 K-直接切换法与定K-自适应控制在短时间内吸收功率较小,但由图18可知,在此工况下超级电容器初始SOC设置为40%,初始工作电压Usc为545V,在持续充电工况下,不考虑SOC状态的惯性与下垂自适应控制,在时间为 55s时,SOC达到上限值 90%,其工作电压 Usc达到最低放电电压 870V。而本文所提方法的超级电容器SOC的维持效果较佳。相比上述控制SOC可降低15%,可具备更多的容量参与系统一次调频。

图18 负荷突减180MW下超级电容器参数
Fig.18 The value of super capacitor parameter under sudden load reduction of 180MW
图 19为负荷减小 180MW 下,采用上述三种控制策略所对应的频率偏差曲线。可以明显得到在直接切换控制方式下,频率最大偏差达到50.1Hz,而采用定K-自适应控制策略的频率最大偏差仅为50.08Hz,其频率最大偏差量相较于直接切换控制方式减小 20%。当超级电容器不断吸收能量,其SOC达到极限值,系统频率会出现再次抬高 0.025Hz;而本文所提方法在减小频率最大偏差量的基础上,维持了整个系统频率的相对稳定。
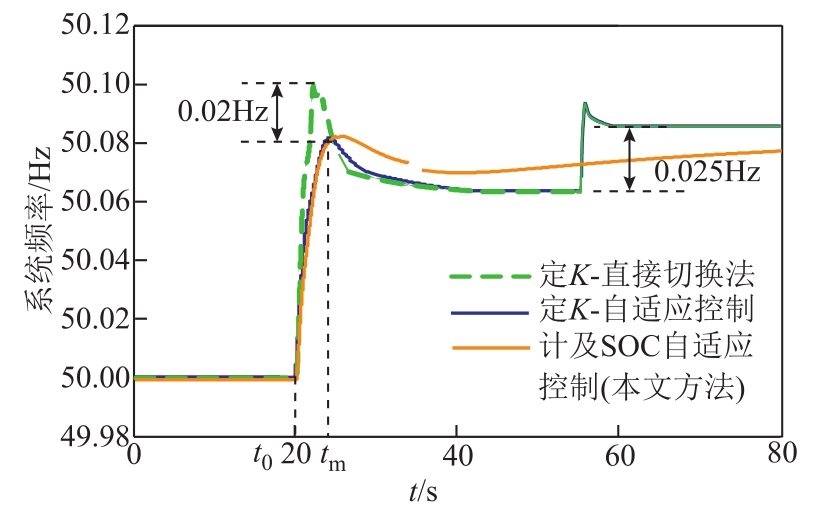
图19 固定参数与自适应参数下系统频率偏差对比(负荷突减180MW)
Fig.19 Comparison chart of system frequency deviation under fixed parameters and adaptive parameters(the load dropped by 180MW)
为了进一步验证本文所提出的计及 SOC自适应控制的超级电容储能控制双馈风力发电机组惯量与一次调频自适应控制策略相较于常规调频控制的优势,得到负荷减小 180MW时不同调频控制方式对应的频率偏差曲线,如图20所示。由图20可以看出双馈风力发电机在超速减10%的调频控制下其稳态频率偏差约为 0.085Hz,动态响应最大频率偏差量为0.084Hz,而在基于超级电容储能参与DFIG惯量支撑和一次调频控制策略下稳态频率偏差为0.07Hz,动态响应最大偏差量为0.08Hz,其动静态响应效果都优于常规的 DFIG超速减载一次调频控制策略,且频率调节能力相比于常规超速减载一次调频策略提高约17.7%,提升效果显著。

图20 传统控制与本文控制下系统频率偏差对比(负荷突减180MW)
Fig.20 Comparison chart of system frequency deviation under traditional control and text control(the load dropped by 180MW)
在计及 SOC自适应控制的超级电容储能控制双馈风力发电机组惯量与一次调频自适应控制策略时,转速和风能利用系数依然保持最优值,其风能利用系数、输出功率、转速和桨距角动态响应对比如图21所示。
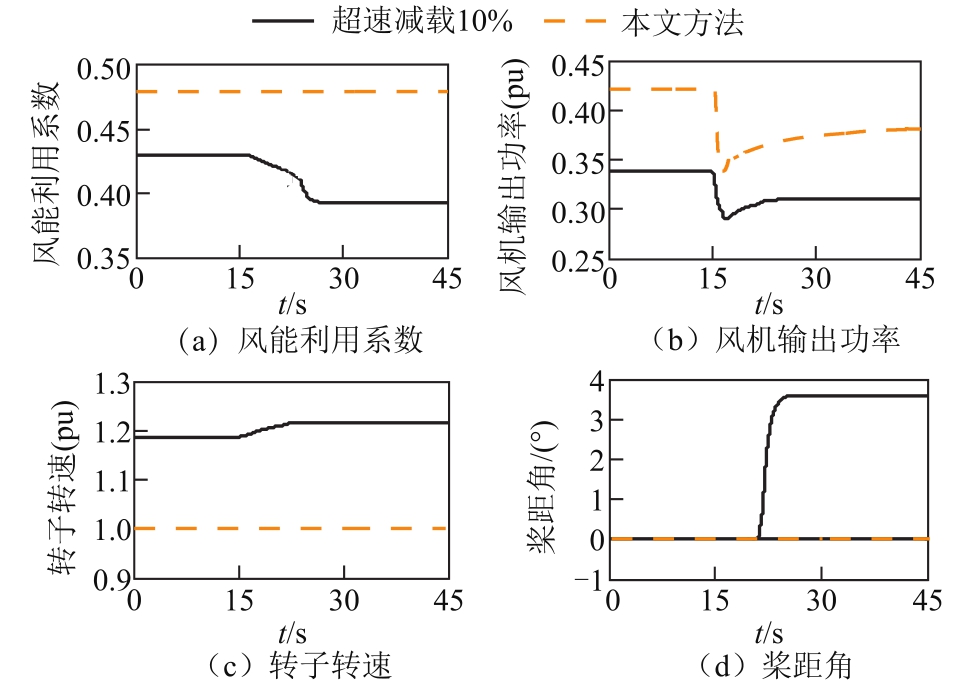
图21 负荷减小180MW下风电机组响应对比
Fig.21 Comparison of the response of wind turbines under 180MW load reduction
由表4可知,当出现系统负荷减小180MW的较大扰动时,本文所提控制策略和超速减载10%调频控制相比,风能利用率提高23.07%,风机输出功率增大22.6%。因此本文所提控制策略能够在提高发电效益的基础上提升一次频率调节能力。
表4 负荷突减180MW时响应性能指标
Tab.4 Response indices when load is reduced by 180MW

控制策略风能利用系数风机输出功率(pu)最大转速(pu)桨距角/(°)超级电容器 0.48 0.38 1 0超速减载10% 0.39 0.31 1.217 3.6
4 结论
本文提出的计及超级电容器储能 SOC状态参与DFIG惯量支撑与一次调频自适应控制策略结合虚拟惯性与虚拟下垂两种控制策略的优势,在不损失风电机组发电效益的前提下,参与系统惯量支撑和一次频率调节,通过理论与仿真分析,得到以下结论:
1)相较于传统的集中式储能参与系统调频,本文所提出的超级电容器控制策略使得单台风电机组具备一次频率调节能力,其惯量支撑和一次频率调节都由超级电容储能模块扩展功能实现,无需修改或增加原风电机组的结构和控制方案,使得单台风电机组具有良好的鲁棒性和兼容性,提高其单台风机的致稳性和抗扰性。尤其适合现场已投运机组的升级改造,为单台风机的改造和控制提出了新思路和新方向。
2)综合考虑超级电容SOC即时状态控制选择合适惯性和下垂系数进行出力来避免其储能装置的过充过放问题,且有效发挥了虚拟惯性和虚拟下垂对于频率偏差及其变化率的感知反应能力,实现平滑超级电容器更加高效的出力,减小其充放电深度,提高使用寿命。在频率下降阶段后期,虚拟下垂填补了虚拟惯性出力不足的问题,使得超级电容器的功率配置有了更大的考虑空间,其容量利用率得到了显著提升。
3)本文所提方法是在风机最大功率跟踪控制的基础上实现的,相比于常规的超速减载调频控制,既兼顾了发电效益,同时又大大提高了风机的惯量支撑和一次频率调节能力,继而超速减载调频控制的减载率越大,其转速和功率的实际可调节深度越小,风能利用率和输出功率越低,体现本文所提出的一次调频控制优越性。
4)本文接下来将对双馈风力发电机组参与系统一次调频的整个阶段进行更深入的分析,对分配系数曲线进行优化,以达到更好的调频效果与储能装置的优化问题。
附 录
为了分析不同n取值下对系统频率和超级电容器产生的影响,以本文四机两区域模型为基础模型,工况为负荷突增 145MW 为例,分别绘制了不同取值 n下的频率偏差曲线和超级电容器出力曲线如附图1、附图2所示。

附图1 系统频率偏差
App.Fig.1 System frequency deviation diagram

附图2 超级电容器输出功率曲线
App.Fig.2 Supercapacitor output power curves
[1]王涛, 诸自强, 年珩. 非理想电网下双馈风力发电系统运行技术综述[J]. 电工技术学报, 2020, 35(3):455-471.Wang Tao, Zhu Ziqiang, Nian Heng. Review of operation technology of doubly-fed induction generator-based wind power system under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 455-471.
[2]李世春, 吕翔生, 钟浩, 等. 大规模双馈风电机组参与调频的电网自适应低频减载策略[J]. 电力系统自动化, 2019, 43(15): 109-120.Li Shichun, Lü Xiangsheng, Zhong Hao, et al. Grid adaptive low-frequency load shedding strategy for large-scale doubly-fed wind turbines participating in frequency modulation[J]. Automation of Electric Power Systems, 2019, 43(15): 109-120.
[3]张祥宇, 付媛, 王毅, 等. 含虚拟惯性与阻尼控制的变速风电机组综合PSS控制器[J]. 电工技术学报,2015, 30(1): 159-169.Zhang Xiangyu, Fu Yuan, Wang Yi, et al. Integrated PSS controller for variable speed wind turbines with virtual inertia and damping control[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 159-169.
[4]李少林, 王伟胜, 张兴, 等. 风力发电对系统频率影响及虚拟惯量综合控制[J]. 电力系统自动化,2019, 43(15): 64-73.Li Shaolin, Wang Weisheng, Zhang Xing, et al. Effect of wind power generation on system frequency and virtual inertia comprehensive control[J]. Automation of Electric Power Systems, 2019, 43(15): 64-73.
[5]穆钢, 蔡婷婷, 严干贵, 等. 双馈风电机组参与持续调频的双向功率约束及其影响[J]. 电工技术学报, 2019, 34(8): 1750-1759.Mu Gang, Cai Tingting, Yan Gangui, et al.Bidirectional power constraints and influence of doubly fed induction generator participating in continuous frequency regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1750-1759.
[6]赵晶晶, 吕雪, 符杨, 等. 基于可变系数的双馈风机虚拟惯量与超速控制协调的风光柴微电网频率调节技术[J]. 电工技术学报, 2015, 30(5): 59-68.Zhao Jingjing, Lü Xue, Fu Yang, et al. Frequency adjustment technology of wind and light diesel microgrid based on variable coefficient-based double inertia fan virtual inertia and overspeed control[J].Transactions of China Electrotechnical Society, 2015,30(5): 59-68.
[7]胥国毅, 胡家欣, 郭树锋, 等. 超速风电机组的改进频率控制方法[J]. 电力系统自动化, 2018, 42(8):39-44.Xu Guoyi, Hu Jiaxin, Guo Shufeng, et al. Improved frequency control strategy for over-speed wind turines[J]. Automation of Electric Power Systems,2018, 42(8): 39-44.
[8]Vidyanandan K V, Senroy N. Primary frequency regulation by deloaded wind turbines using variable droop[J]. IEEE Transactions on Power System, 2013,28(2): 837-846.
[9]付媛, 王毅, 张祥宇, 等. 变速风电机组的惯性与一次调频特性分析及综合控制[J]. 中国电机工程学报, 2014, 34(27): 4706-4716.Fu Yuan, Wang Yi, Zhang Xiangyu, et al. Analysis and integrated control of inertia and primary frequency regulation for variable speed wind turbines[J]. Proceedings of the CSEE, 2014, 34(27):4706-4716.
[10]Fu Yuan, Wang Yi, Zhang Xiangyu. Integrated wind turbine controller with virtual inertia and primary frequency responses for grid dynamic frequency support[J]. IET Renewable Power Generation, 2017,8(11): 1129-1137.
[11]张昭遂, 孙元章, 李国杰, 等. 超速与变桨协调的双馈风电机组频率控制[J]. 电力系统自动化, 2011,35(17): 20-25.Zhang Zhaosui, Sun Yuanzhang, Li Guojie, et al.Frequency regulation by doubly fed induction generator wind turbines based on coordinated overspeed control and pitch control[J]. Automation of Electric Power Systems, 2011, 35(17): 20-25.
[12]姚伟, 文劲宇, 黄莹, 等. 大规模风电参与系统频率调整的技术展望[J]. 电网技术, 2014, 38(3): 638-646.Yao Wei, Wen Jinyu, Huang Ying, et al. Prospect of technology for large-scale wind farm participating into power grid frequency regulation[J]. Power System Technology, 2014, 38(3): 638-646.
[13]刘巨, 姚伟, 文劲宇, 等. 一种基于储能技术的风电场虚拟惯量补偿策略[J]. 中国电机工程学报,2015, 35(7): 1596-1605.Liu Ju, Yao Wei, Wen Jinyu, et al. A wind farm virtual inertia compensation strategy based on energy storage system[J]. Proceedings of CSEE, 2015, 35(7): 1596-1605.
[14]Daniel-Ioan, Vaclav Knap, Maciej Swierczynski, et al.Operational of a grid-connected lithium-ion battery energy storage system for primary frequency regulation: a battery lifetime perspective[J]. IEEE Transactions on Industry Application, 2017, 53(1):430-438.
[15]李欣然, 崔曦文, 黄际元, 等. 电池储能电源参与电网一次调频的自适应控制策略[J]. 电工技术学报, 2019, 34(18): 3897-3908.Li Xinran, Cui Xiwen, Huang Jiyuan, et al. Adaptive control strategy for battery energy storage power supply participating in primary frequency modulation of power grid[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3897-3908.
[16]赵晶晶, 李敏, 何欣芹. 基于限转矩控制的风储联合调频控制策略[J]电工技术学报, 2019, 34(33):4982-4990.Zhao Jingjing, Li Min, He Xinqin. Coordinated control strategy of wind power and energy storage in frequency regulation based on torque limit control[J].Transactions of China Electrotechnical Society, 2019,34(33): 4982-4990.
[17]蒋平, 熊华川. 混合储能系统平抑风力发电输出功率波动控制方法设计[J]. 电力系统自动化, 2013,37(1): 122-127.Jiang Ping, Xiong Huachuan. A control scheme design for smoothing wind power fluctuation with hybrid energy system[J]. Automation of Electric Power Systems, , 2013, 37(1): 122-127.
[18]Shiddiqyunus A M, Mohammad A S, et al. Application of SMES to enhance the dynamic performance of DFIG during voltage sag and swell[J]. IEEE Transactions on Applied Superconductivity, 2012,22(4): 5702009.
[19]Australian energy market operator. Black system south Australia 28 September 2016: final report [R].Australian energy market operator, 28 Mar. 2017: 130,45, 55, 37. http://apo. org. au/node/74886
[20]The British Electricity System Operator. Appendices to the technical report on the events of 9 August 2019[R]. The British Electricity System Operator, 2019: 7-10, 90, 39-43.
[21]刘辉, 葛俊, 巩宇, 等. 风电场参与电网一次调频最优方案选择与风储协调控制策略研究[J]. 全球能源互联网, 2019, 2(1): 44-52.Liu Hui, Ge Jun, Gong Yu, et al. Optimization scheme selection of wind farm participation in grid primary frequency modulation and study of wind-storage coordination control strategy[J]. Journal of Global Energy Interconnection, 2019, 2(1): 44-52.
[22]苗璐. 含风电及多端口直流—直流换流器的直流系统建模与控制[D]. 武汉: 华中科技大学, 2016.
[23]颜湘武, 崔森, 宋子君, 等. 基于超级电容储能控制的双馈风电机组惯量与一次调频策略[J]. 电力系统自动化, 2020, 44(14): 111-129.Yan Xiangwu, Cui Sen, Song Zijun, et al. Inertia and primary frequency modulation strategy of doubly-fed wind turbine based on supercapacitor energy storage control[J]. Automation of Electric Power Systems,2020, 44(14): 111-129.
[24]Execcutivesummary[EB/OL]. http: //www. ceic. unsw.edu. au/centers/ vrb >.
[25]Ponce de León C, Frías-Ferrer A, Gonzá lez-Garcí a J,et al. Redox flow cells f or energy conversion[J].Journal of Power Sources, 2006, 160(1): 716-732.
[26]Electrochemical capacitor module for hybrid transport application[EB/OL]. http: //www. esma-cap. com.
[27]Electrochemical energy storage-a mission to the USA,report of a DTI global watch mission [EB/OL]. [2004-11]. http : //www. Global watch online. com.
[28]北极星电力网. 清洁发展的技术方案: 虚拟同步机与储能技术[EB/OL]. [2016-11-30]. http: //www.sohu. com/a/ 120289888_131990.Polaris Power Network. Clean development technical solutions: virtual synchronization machine and energy storage technology[EB/OL]. [2016-11-30]. http://www. sohu. com/a/ 120289888_131990.