0 引言
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）具有结构简单、转动惯量高以及高功率因数的特点，在众多领域得到广泛应用[1-2]，如汽车、机器人、机床、矿井提升等驱动中，经常存在单双机切换工艺需求或单机功率难以满足大负载、高转矩、低转动惯量要求的情况，需要采用多电机进行同步驱动。因此多电机传动系统的协调控制研究更具现实意义。其中共轴双电机驱动是应用最广泛的一种，而主从结构下双永磁同步电机的高性能控制也是多电机协同运行的研究热点之一。
由于模型预测控制（Model Predictive Control,MPC）具有设计简单、易于工程实现，尤其在处理复杂非线性系统的优化问题上具有明显优势[3]，在电力电子与电气传动领域，特别是电机驱动系统中被广泛应用。为了解决矢量控制中动态响应慢、脉振较大的问题，J. Rodriguez等学者首次将MPC应用在直接转矩控制中，形成模型预测直接转矩控制（Model-Predictive Direct Torque Control, MPDTC）[4-5]，后被众多学者改进研究。为改善MPDTC电流内环性能，文献[6]提出一拍延时补偿的电流预测控制方法，消除反电动势项中参数误差的影响，增强了系统鲁棒性；文献[7]提出一种基于转矩和反作用力矩的新价值函数的MPDTC方法，消除了传统MPDTC系统中所需的加权因子，简化了计算过程；文献[8]将无差拍控制理论应用到MPDTC中，能有效地抑制转矩脉动和磁链纹波，减小定子电流畸变率。上述都是单电机的改进，而在多电机控制方面也有一定的应用研究，文献[9]将 MPC方法应用于永磁同步双电机五桥臂驱动系统，设计了三种 MPC策略以实现双电机的电流同步控制，并能够获得较好的动态性能；文献[10]介绍了一种双电机驱动系统的模型预测控制策略，该策略在减少计算和采样时间的同时消除逆变器固有的且无法实现的开关状态，能够快速地实现对转矩控制。根据上述应用及改进现状，可见MPDTC双电机控制方面也已成功应用，但双电机均为独立驱动，共轴驱动下的应用较少，尤其是双电机转矩均衡控制问题。因此本文拟采用MPDTC算法与主从结构控制相结合进行共轴双PMSM控制研究。
在PMSM双电机的MPDTC高性能控制调速系统中，除了需要满足系统响应性能要求，还必须具备较强的容错控制性能。驱动系统中速度反馈至关重要，MPDTC调速系统精确控制需要准确获取电机转速信息，而速度传感器的精度易受环境条件的影响，极易发生故障，使得系统不稳定[11]。因此本文进一步研究共轴双PMSM在MPDTC下的无速度传感器控制，以提高系统对速度反馈的容错能力。
目前大多数无速度传感器都是针对单电机的研究，比较成熟的速度估计算法包括：高频注入法（High Frequency Injection, HFI）[12-13]、模型参考自适应系统（Model Reference Adaptive System,MRAS）[14-15]、扩展卡尔曼滤波器（Extended Kalman Filter, EKF）[16-18]等，有学者将上述速度估计算法与MPDTC进行结合。文献[19]提出一种无速度传感器永磁同步电机MPDTC策略，利用波波夫稳定理论推导了控制系统模型参考自适应转速估算模型；文献[20]将 HFI方法与 MPDTC结合从电流纹波中提取速度和位置信息，无需外部中断。但上述估计算法都受相关因素的限制，HFI注入的高频噪声影响系统动态性能，且局限于具有凸极结构的转子速度估计；EKF对参数变化具有较强的鲁棒性，但算法复杂、执行难度较大；MRAS实质上是线性校正，不适用于参数变化或存在干扰的场合。为了提高转速估计性能，考虑到滑模观测器（Sliding Mode Observer, SMO）是非线性校正且具有有限时间收敛的快速无振荡特性，文献[21]提出一种滑模变结构转速观测器，但是传统SMO采用Sign函数作为切换函数会产生高频抖振；文献[22]提出用可变边界层厚度的Sigmoid函数取代Sign函数进行转速估计及转子位置预测，大大降低了抖振并提高了估算精度。以上研究均是对单电机的速度辨识，共轴双电机的无速度控制少有，本文考虑SMO的优势，拟采用SMO与MPDTC进行结合，并根据共轴双PMSM的特点，进行无速度传感器控制研究。
综合上述分析，本文基于双滑模估计的共轴双电机主从结构MPDTC无速度传感器控制策略，对双 PMSM 驱动系统的动态性能和容错性能提升进行研究。首先搭建了共轴双永磁同步电机的数学模型；然后，提出了二步反馈补偿的MPDTC动态性能优化控制，以及MPDTC下的无速度传感器容错性能优化控制及综合策略；最后，在基于Matlab/Simulink和共轴双电机实验平台上进行了仿真和实验验证。
1 双电机的模型转矩控制
1.1 共轴双电机数学模型
本文的研究对象为三相绕组的永磁同步电机，研究目标为双电机主从结构工作模式下的控制方法。本文采用三相六开关结构逆变器。为便于计算，首先做如下假设：①不存在电机铁心的饱和；②涡流和磁滞损耗为 0；③电机给定电流为对称的三相正弦波。经过变换后，两相静止αβ坐标系下数学模型可以表示为
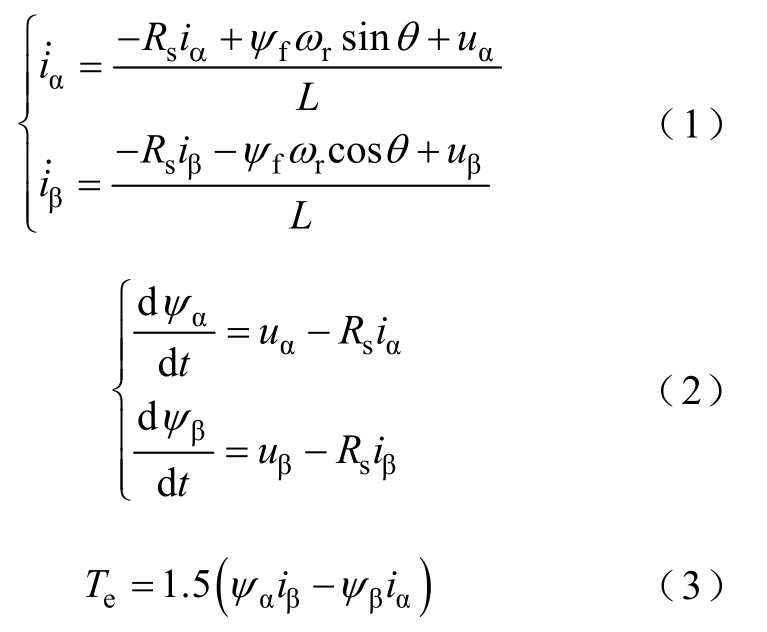
式中，iα、iβ，uα、uβ和αψ、βψ分别为αβ坐标系下定子电流、定子电压和定子磁链，fψ为永磁体磁链；Rs为定子电阻；L为定子绕组电感；rω为电机转子角速度；θ为转子角位置；Te为电磁转矩。
在双电机主从结构控制中，从电机与主电机共轴驱动负载，并将主电机的输出转矩作为从电机的参考值，得出双电机运动方程为
式中，Te1和Te2分别为主、从电机电磁转矩；TL为负载转矩；ωcom为共轴转速；J为转动惯量。
1.2 模型预测转矩控制
MPDTC控制是通过预测计算将来时刻的定子电流、定子磁链和转矩，并选择使代价函数最小的电压矢量的一种控制方法。
1.2.1 定子电流预测
以主电机为例，将式（1）离散化，可得到定子电流在k+1时刻的初步预测值为
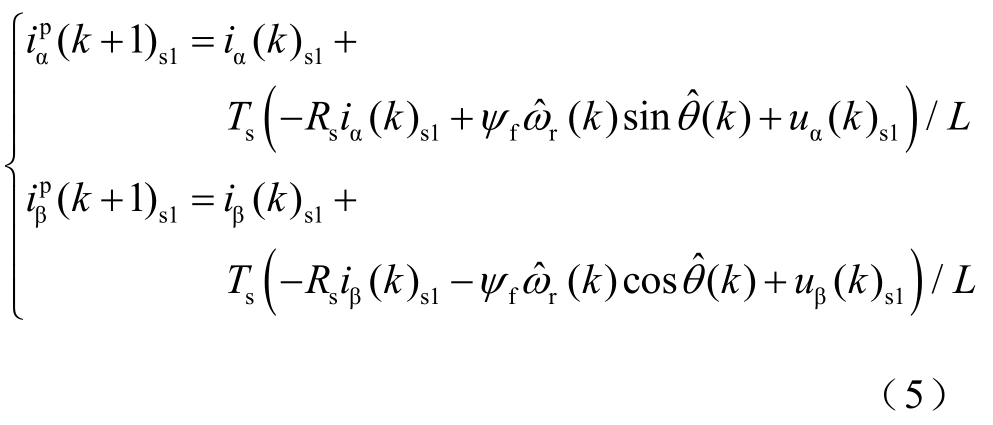
式中，Ts为采样周期；
为k+1时刻主电机在αβ坐标系下的定子电流预测值；
为 k时刻主电机在αβ坐标系下的定子电流测量值；
分别为k时刻主电机的定子转速和角位置。
同理可得从电机定子电流。
1.2.2 定子磁链、转矩预测
以主电机为例，对式（2）离散化，得到定子磁链在k+1时刻的预测值为
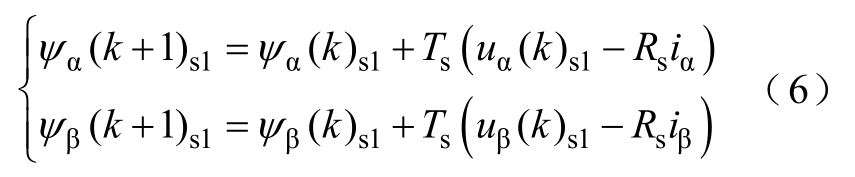
根据式（3）和式（6）可得定子磁链和转矩在k+1时刻的观测值为
同理可得从电机定子磁链与转矩。
2 MPDTC动态性能优化控制
在永磁同步电机的MPDTC控制中，由于系统运行状态和微处理器计算延时，会使得控制效果出现偏差。文献[23]中提出用电流补偿和二步反馈的方法来提高控制精度，本文将其结合应用在共轴双永磁同步电机驱动系统中来实现MPDTC动态性能优化。
2.1 电流补偿
定子电流的预测值与实际值之间存在一定的误差，现将定子电流预测值与实际值的误差作为观测误差，对观测值进行修正。
根据式（8），可得到k+1时刻修正后的电流预测
为
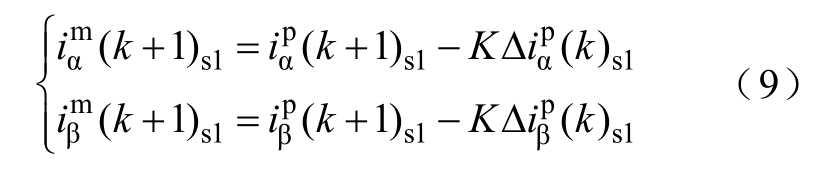
式中，K为大于0的误差反馈系数，取值范围为0～1，在绝对理想情况下为0.5，考虑实际干扰，通过多次调试本实验平台获得的最优值为0.4。
以α轴为例，定子电流补偿结构图如图1所示。
图1 电流反馈补偿结构
Fig.1 Current feedback compensation block digram
2.2 二步预测
实际的数字控制系统会存在一拍延迟，当变量x在k时刻被采集时，处理器需要经过一个时钟周期的计算得到最优电压矢量 v k。而此时的变量已经变为 x (k + 1 )，用k时刻的变量计算出的电压矢量来控制k+1时刻的逆变器，显然会影响到PMSM系统的控制精度，甚至会影响系统稳定。因此，可以在单步预测的基础上，预测k+2时刻的电流、磁链与转矩，以提高电机的运行效果。
根据式（5）～式（9）可得到主电机在二步预测下的定子电流、定子磁链与电磁转矩为
在双电机的控制中，从电机采用主电机的实际转矩作为转矩参考值。同时因为两个采样间隔极小，可以认为参考转矩 T *和磁链幅值参考值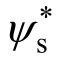
不发生变化。逆变器在每个采样周期可产生 V1 , … ,V6共计六个不同的电压矢量。根据这六个电压矢量可得到六个不同的转矩和磁链的预测值。主从电机可通过式（14）所示的最小代价函数来选择相应的电压矢量。
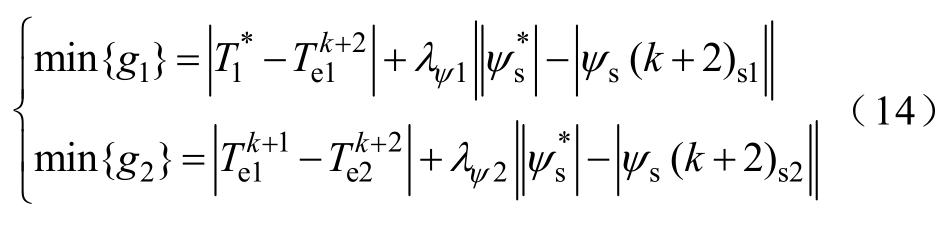
式中，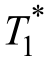
为主电机参考转矩；λψ为权重系数，用来调节磁链控制与转矩控制之间的相关性。
权重系数的初始值为
式中，Tn1、Tn2分别是主从额定转矩；ψn1、ψn2分别为主从电机额定磁通。综上，二步MPDTC控制结构如图2所示。
图2 双电机主从结构控制及MPDTC策略
Fig.2 Dual motor master-slave structure and MPDTC
3 基于双滑模估计的MPDTC无速度传感器容错性能优化控制
为了提高双 PMSM 驱动的容错性能，实现MPDTC下的无速度传感器控制，考虑到滑模观测器对系统模型的依赖性较低、响应速度快、结构简单、易于实现的特点，本文拟在单电机滑模转速估计的基础上研究共轴双电机转速估计，实现传感器故障下对动静态的实时跟踪。
3.1 基于Sigmoid函数的单电机转速估计
式（1）中的 ψ fω r si nθ 和 ψ fωr c osθ 为反电动势，包含了转速和角位置信息，若通过观测器得到反电动势大小，便可反推出转子转速。为避免传统滑模观测器中Sign切换函数容易引起系统抖动的问题，本文选用Sigmoid函数，通过改变其边界层厚度来抑制抖动。设 k 时刻的反电动势为εα(k)和εβ ( k)，即
构造滑模观测器状态方程为
式中，F(x)为Sigmoid函数，幅值在-1～1之间。则
为
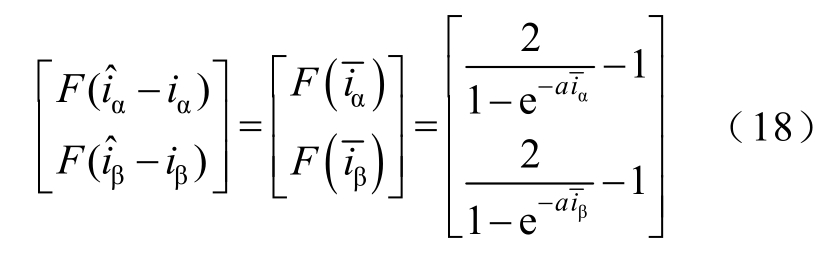
式中， a 为 Sigmoid函数的斜率系数，且a＞0，这里取a=1。
根据式（16）～式（18）可得到，在数字观测系统中的k+2时刻反电动势为
通过反电动势的估计值，可以得到单电机的转速与转子位置为
3.2 带随速因子的双电机无速度控制策略
为了实现传感器故障下的容错控制，在单电机转速估计的基础上，结合双电机共轴特性进行改进。
当单电机转速提高时，电压矢量的作用时间会随之变长。为保证开关具有足够的响应时间，需要降低控制系统响应速度。因此，可令滑模观测器的边界层随电机转速改变来解决上述问题。图3显示了随电机转速变化而改变Sigmoid函数边界层厚度的方法。
图3 边界层厚度可变Sigmoid函数曲线
Fig.3 Sigmoid function with variable boundary
设观测器增益为λ0，且λ0 = k0ωr。将式（17）改写为
由于系数k0的取值会影响到观测器的稳定性，下面构造一个Lyapunov函数为
式中，n为1时代表主电机，n为2时代表从电机。
代入观测器方程后，其导数为
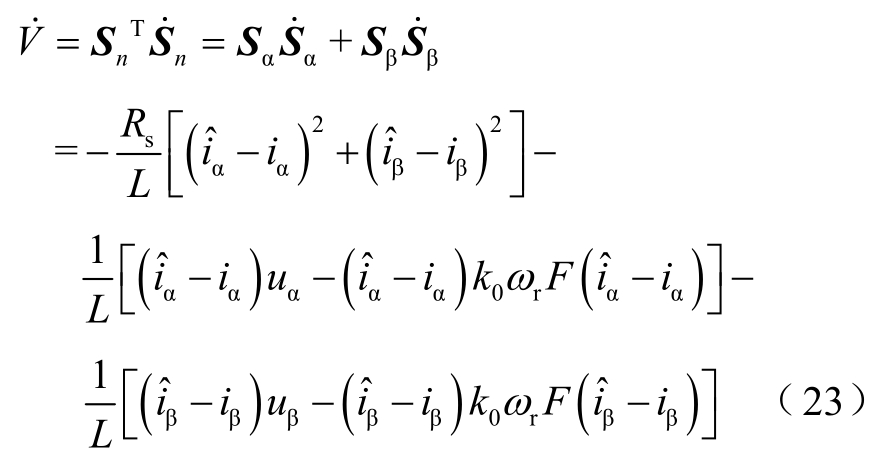
Lyapunov稳定的判定条件是
可解出k0的取值范围为
式中，
为电流估算误差的最大值，
通过分枝定界法得到最优解为1 250。
主从电机在 αβ坐标系下的共轴等效反电动势分量为
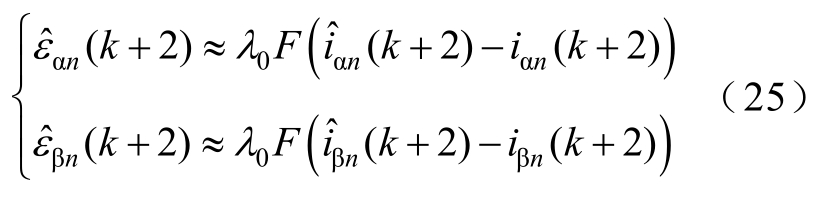
在实际生产中，电机会存在差异，因此主、从电机的共轴等效反电动势也存在不同。但若将共轴双电机抽象为一个电机整体，其共轴等效反电动势
必然等效于矢量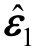
与矢量
经过一定的放缩之后的矢量和，那么新的共轴等效反电动势在αβ坐标系下的分量则为
式中，1λ为统一化设定的随速因子，理论值应该取0.5，由于其他因素的影响，最优值在0.5上下范围内，通过参数调试，取为0.45。
通过以上分析，可得双电机共轴角度与转速为
带随速因子的双电机观测器结构如图4所示。
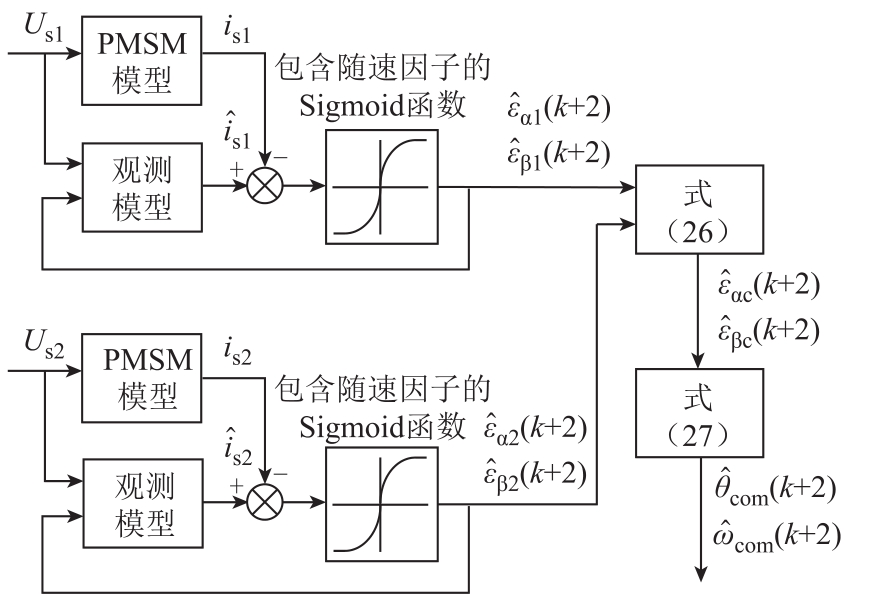
图4 共轴转速观测器
Fig.4 Coaxial motor speed observer
3.3 综合控制
本文以双电机主从结构系统为基础，将主电机输出的转矩作为从电机的设定转矩，来实现主从电机共轴连接。综合控制结构如图5所示。
图5 综合控制结构图
Fig.5 Integrated control structure
文中的控制方法在传统MPDTC的基础上引入了二步反馈补偿预测，并采用双滑模观测器，实现了无速度传感器下模型预测转矩优化控制。图5为基于双滑模估计的MPDTC无速度传感器容错性能优化控制结构。
4 仿真与实验
4.1 系统仿真
为了验证所提出策略的有效性，在 Matlab/Simulink中建立仿真模型，对基于双滑模估计的共轴双电机主从结构MPDTC无速度传感器控制策略（SMO-MPDTC）进行动静态仿真验证，为模型的电机参数与控制参数见表 1、表 2。为模拟双电机实际运行中，由于温度造成的定子电阻变化从而产生转矩差的情况，在仿真中设定从电机定子电阻为2.0Ω。
表1 电机参数
Tab.1 The parameters of induction motor
数 值参 数主电机 从电机母线电压udc/ V 300 300定子电阻 Rs/Ω 1.6 2.0转动惯量J/( kg/m2) 0.002 0.002转子磁通ψf/ Wb 0.185 2 0.185 2额定转矩 Trtd/( N⋅m) 3.86 3.86额定功率Prtd/ kW 1.21 1.21额定转速Nrtd/(r/min) 3 000 3 000
系统初始状态为空载，起始设定速度为350r/min，起始转矩为0N⋅m，得到有速度传感器单步MPDTC起动及稳态时的转矩与转矩差曲线如图6所示，图 7、图 8则为无速度传感器单步 SMOMPDTC起动及稳态时的转矩与转矩差、无速度传感器二步 SMO-MPDTC下起动及稳态时的转矩与转矩差曲线对比。其中图6a为主电机转矩T1，图6b为从电机转矩 T2，图 6c为主从电机转矩之差ΔT。
表2 控制参数
Tab.2 The parameters of control
参 数 数 值比例增益Kp 40积分增益Ki 4斜率系数a 1观测器系数k0 1 250误差反馈系数K 0.4统一化设定系数λ1 0.45
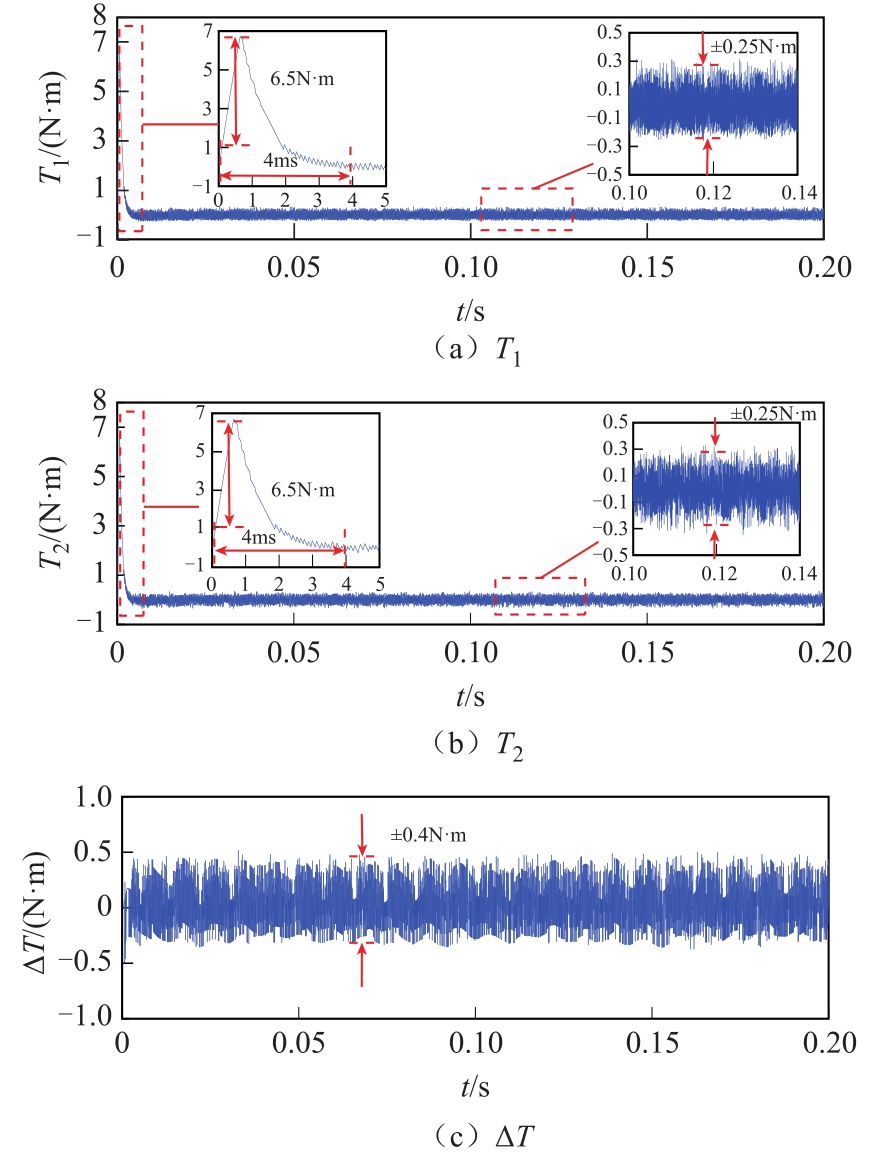
图6 有速度传感器单步MPDTC起动及稳态下的转矩与转矩差
Fig.6 Torque and torque difference of single-step MPDTC speed sensorless at startup and steady state
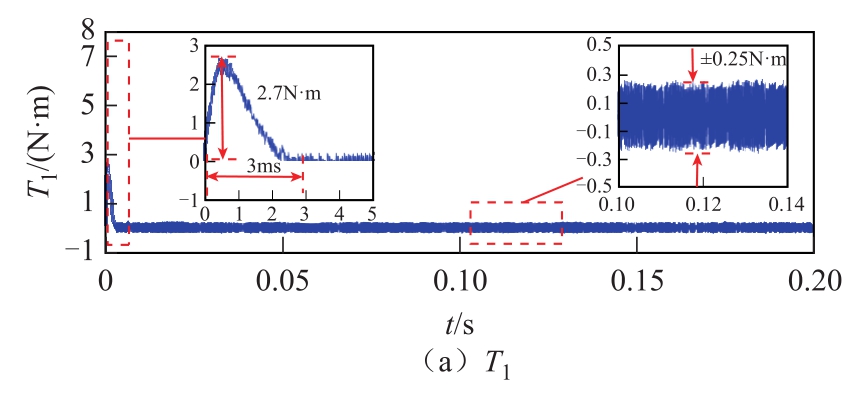
图7 无速度传感器单步SMO-MPDTC起动及稳态下的转矩与转矩差
Fig.7 Torque and torque difference of single-step SMOMPDTC speed sensorless at startup and steady state
图8 无速度传感器二步SMO-MPDTC起动及稳态下的转矩与转矩差
Fig.8 Torque and torque difference of two-step SMOMPDTC speed sensorless at startup and steady state
从图 6～图 8可以看出，有速度传感器的单步SMO-MPDTC与无速度传感器的单步SMO-MPDTC相比，采用双滑模观测器的MPDTC在一定程度上抑制了起动时的波动，加快了起动时间。从图7和图8可以看出，相比于单步预测，引入二步预测后，转矩差从±0.5N·m变为±0.3N·m，二阶滑模观测器能够减小主从转矩差。
图 9为无速度传感器二步 SMO-MPDTC策略下的电机起动及稳态时的速度仿真曲线。由于双电机采用了刚性连接，所以主从转速一致。从图9可以看出起动时转速无超调，收敛时间为 7ms，达到稳态时转速波动约在1r/min之间，具有良好的起动及稳态性能。
图9 无速度传感器二步SMO-MPDTC起动及稳态下的速度仿真结果
Fig.9 Speed simulation results of two-step SMO-MPDTC speed sensorless at startup and steady state
图 10为 MPDTC控制下速度传感器测得的实际转速、双滑模观测器估计的转速与转速估计误差在稳态时的仿真结果，其中图10a为实际速度，图10b为估计速度，图10c为速度估计误差。从图10中可以看出，滑模观测器可实现对速度的准确估计，估计速度与实际速度基本重合，估计误差约为上下1r/min，可以实现速度的精确估计。
图10 MPDTC稳态时实际转速、估计转速与转速估计误差仿真结果
Fig.10 Simulation results of actual speed, estimated speed and speed estimation error of MPDTC at steady state
为验证SMO-MPDTC策略的动态性能，在0.2s时速度由350r/min阶跃至1 500r/min，0.3s转矩由0N·m阶跃至2N·m，图11和图12分别为动态阶跃下 SMO-MPDTC的转矩与转矩差仿真对比图和实际速度、估计速度与速度估计误差仿真图，图11和图12中的各分图与图8和图10相对应。
图11 无速度传感器二步SMO-MPDTC动态阶跃下的转矩与转矩差
Fig.11 Torque and torque difference of two-step SMOMPDTC speed sensorless under dynamic step
图12 SMO-MPDTC动态阶跃下实际转速、估计转速与转速估计误差仿真结果
Fig.12 Simulation results of actual speed, estimated speed and speed estimation error of SMO-MPDTC under dynamic step
由图11可知，在速度阶跃下主从转矩最大波动为8N⋅m，收敛时间为8ms，在转矩阶跃下主从转矩不存在波动，而且能够快速收敛到稳定状态，收敛时间仅为0.5ms，从图11c可以看出主从转矩在转速阶跃和转矩阶跃时均不存在转矩差。从图12可以看出转速在变化时不存在超调，转速的收敛时间为6.5ms，从图10c和图12c可以看出在，实际与估计转速之差在转速阶跃时产生瞬间波动，约为5r/min。相比于采用传感器测得的实际转速，采用双滑模估计的转速在转矩阶跃下波动有所减少，最大波动为12 r/min，收敛时间为0.5ms，实际与估计转速之差在转矩阶跃时产生瞬间波动，仅为3r/min。以上说明双电机在转矩和转速变化时具有较好的动态性能。
图13为速度传感器发生故障时，设定式切换到滑模转速观测器下与自动切换到滑模转速观测器下转速仿真结果。其中图13a为设定式切换的转速仿真图，在 0.2s速度传感器发生故障，转速变为0r/min，在0.25s设定切换到滑模观测器下，由双滑模观测器估计出转速并恢复至 350r/min，恢复时间为 15ms，最大波动为 14r/min。图 13b为自动切换的转速仿真图，在0.2s速度传感器发生故障，转速波动大于5 r/min时自动切换到滑模观测的转速下，恢复时间为5ms，最大波动为1.2r/min。从图13中可以看出，速度传感器发生故障时，滑模观测器能够快速地跟踪电机转速，瞬时恢复到稳定状态，证明本文所设计的观测器具有较高的准确率。
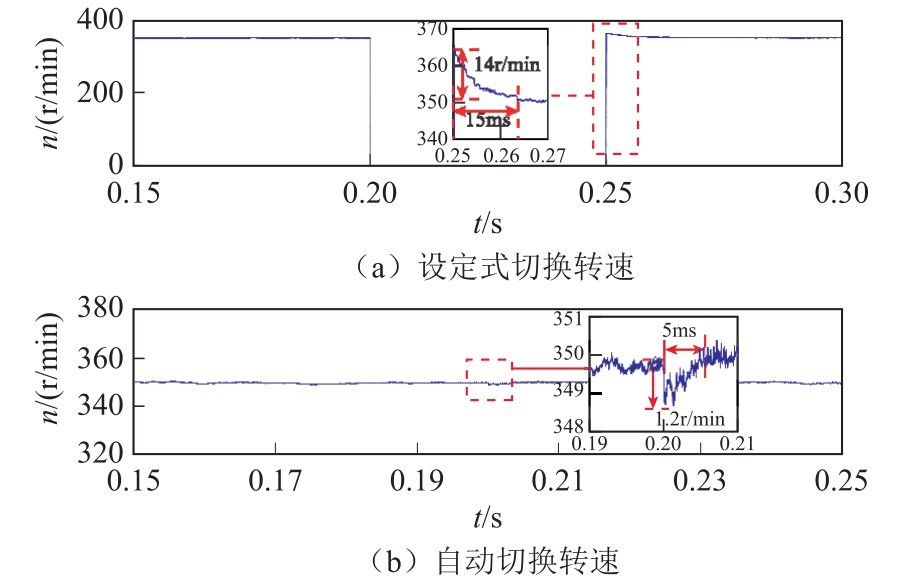
图13 速度传感器发生故障时设定式切换与自动切换到滑模观测器下的转速仿真结果
Fig.13 Speed simulation results of setting switching and automatic switching to sliding mode observer when the speed sensor fails
图14为无速度传感器二步SMO-MPDTC策略在转速阶跃时有无随速因子的转速仿真图，在 0.2s时速度由350 r/min阶跃至1 500 r/min。
图14 无速度传感器二步SMO-MPDTC在转速阶跃下有无随速因子的转速仿真结果
Fig.14 Speed simulation results with or without speed factor of two-step SMO-MPDTC sensorless under speed step
图 14a为无随速因子的转速仿真结果，图 14b为有随速因子的转速仿真结果。随着转速的增大，无随速因子的转速抖振更加剧烈，而采用随速因子转速可以根据转速的大小来调节，这样既保证系统稳定又削弱了抖振，在电机低速和高速运行时估算的转速波形都可以跟踪实际转速。
4.2 实验验证
为了对上述优化控制策略进行验证，基于双滑模估计的共轴双电机主从结构MPDTC无速度传感器控制策略在自主研发的实验平台进行了实验。该实验系统采用DSP（TMS320F28335）处理器控制逆变侧变换器系统。
图15 实验装置
Fig.15 Experimental device
图 16与图 17为无速度传感器单步 SMOMPDTC和二步SMO-MPDTC在起动及稳态下的实验结果。
图16 无速度传感器单步SMO-MPDTC起动及稳态下的实验结果
Fig.16 Experimental results of single-step SMO-MPDTC speed sensorless at startup and steady state
图17 无速度传感器二步SMO-MPDTC起动及稳态下的实验结果
Fig.17 Experimental resuts of two-step SMO-MPDTC speed sensorless at startup and steady state
在实验中，主从电机转矩由式（3）计算得到，用以不同方法之间的定性对比。其中图 16和图 17中上、中、下三条曲线分别为主电机转矩、从电机转矩和主从电机转矩差。从图16、图17可以看出二步预测的加入减小了主从转矩差，改善了主从转矩的性能。图18和图19为无速度传感器二步SMOMPDTC在转速阶跃下主从转矩、转矩差及转速实验曲线图。图 18为主电机转矩、从电机转矩、主从电机转矩差；图 19中上、中、下曲线分别为速度传感器测量的实际转速、观测器估计转速、观测误差。
图18 无速度传感器二步SMO-MPDTC转速阶跃下与转矩差实验结果
Fig.18 Experimental results of torque and torque difference of two-step SMO-MPDTC speed sensorless under speed step
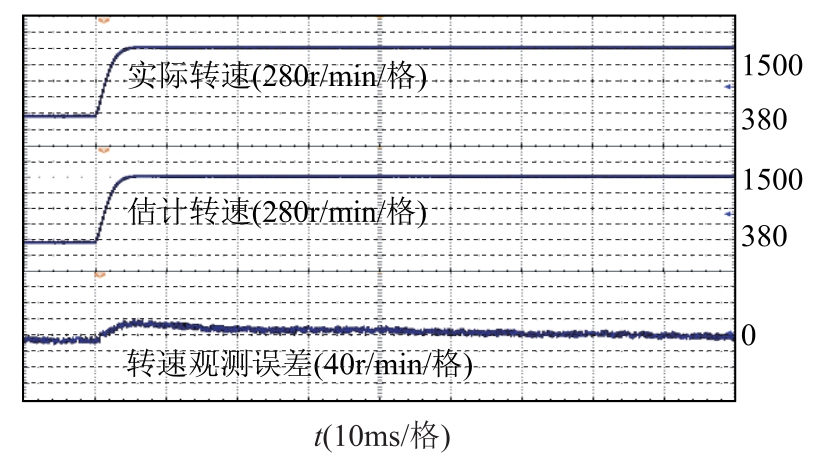
图19 无速度传感器二步SMO-MPDTC转速阶跃下转速实验结果
Fig.19 Speed experimental results of two-step SMOMPDTC speed sensorless under speed step
可以看出，发生速度阶跃时主从电机稳态转矩差未发生明显改变，产生的转矩脉振可及时收敛，主从电机在动态过程时存在小范围转速估计误差，但稳态基本一致，说明速度观测器具有较好的动态性能和较强的鲁棒性。
图 20和图 21为无速度传感器二步 SMOMPDTC在转矩阶跃下主从转矩、转矩差及转速实验曲线。同样可以看出，发生转矩阶跃时主从转矩差保持不变，在丢速情况下速度观测器能很好地跟踪动态转速，动态估计误差在4r/min内。
图20 无速度传感器二步SMO-MPDTC转矩阶跃下转矩与转矩差实验结果
Fig.20 Experimental results of torque and torque difference of two-step SMO-MPDTC speed sensorless under torque step
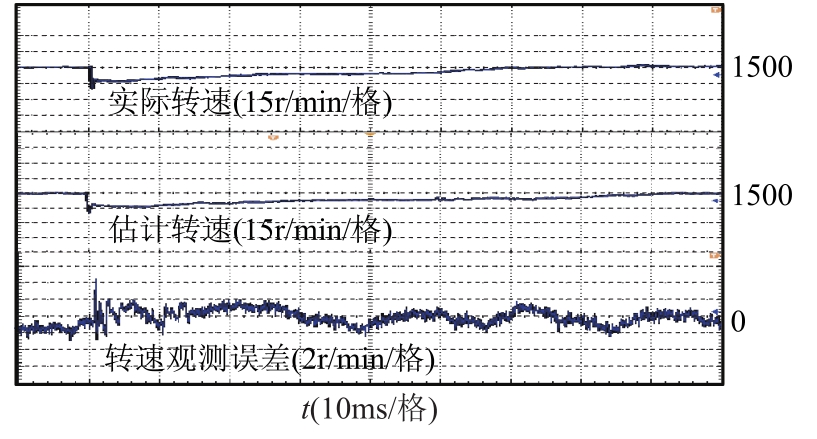
图21 无速度传感器二步SMO-MPDTC转矩阶跃转速实验结果
Fig.21 Speed experimental results of two-step SMOMPDTC speed sensorless under torque step
图 22为速度传感器发生故障时不同方式切换下的转速曲线对比图。在0.2s人为设置速度传感器发生故障，其中图22上图为发生故障时传感器输出的转速实验图；图22中间曲线为设定式切换下转速曲线，在0.2s固定时间点设定切换为双滑膜转速观测模式；图22下方曲线为自动切换式转速曲线，设置当转速波动大于5r/min时自动切换到双滑模观测模式。从图22可以看出速度传感器发生故障时，传感器实际输出为 0r/min，而对比固定时间点切换，当处于自动切换时，系统会短暂处于开环状态，转速升高，当波动超出设定差值时切换为双滑模观测模式进入闭环控制，可以看出转速观测器能够快速跟踪电机转速。
图22 速度传感器发生故障时不同切换方式的转速对比
Fig.22 Speed contrast diagram between different switching modes in the case of failure of speed sensor
图23为无速度传感器二步SMO-MPDTC转速阶跃下有无随速因子实验的转速，在0.2s做速度阶跃由350r/min至1 500r/min。图23上方曲线为无随速因子的转速波形，图23下方曲线为有随速因子的转速波形。从图23中看出，随速因子的加入，使得滑模观测器随着转速的变化而改变，改善了转速在阶跃后的波形。
图23 无速度传感器二步SMO-MPDTC转速阶跃下有无随速因子的转速
Fig.23 Speed with or without speed factor of two-step SMO-MPDTC speed sensorless under speed step
综上所述，实验验证了在双滑模观测器下的MPDTC双电机控制策略能够准确地估计出电机转速，实时地跟踪实际转速，而且转速与转矩的突变得到了很好的抑制，改善了系统的稳态性能与动态性能，具有良好的鲁棒性。
5 结论
本文结合双PMSM直接转矩控制，引入了二步反馈补偿的模型预测控制，并在此基础上构建基于双滑模估计的转速观测器，实现了共轴双电机SMO-MPDTC无速度传感器控制方法。根据所提出的方法进行系统仿真和实验验证表明：
1）主从结构下引入二步反馈补偿模型预测转矩控制，能有效抑制稳态下的转矩脉振，在提高系统动态性能的同时能进一步减小主从电机转矩差，实现双电机转矩均衡控制。
2）在对转矩、电流进行预测控制的基础上，结合双滑模估计进行转速观测，能很好地实现动静下的转速实时跟踪，尤其是速度传感器发生故障时，能快速自动切换估计出实时转速，恢复到稳定的工作状态，提高了电机调速系统容错性能。
综上所述，本文提出的控制策略具有较强的鲁棒性和稳定性，适用于对转速与转矩高性能需求的应用场合下，具有较好的工程应用价值。
[1]张永昌, 杨海涛, 魏香龙. 基于快速矢量选择的永磁同步电机模型预测控制[J]. 电工技术学报, 2016,31(6): 66-73.Zhang Yongchang, Yang Haitao, Wei Xianglong.Predictive control of permanent magnet synchronous motor model based on fast vector selection[J].Transactions of China Electrotechnical Society, 2016,31(6): 66-73.
[2]Davari S A, Rodriguez J. Predictive direct voltage control of induction motor with mechanical model consideration for sensorless applications[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2018, 6(4): 1990-2000.
[3]Xiao Xiong, Zhang Yongjun, Wang Jing, et al. An improved model predictive control scheme for the PWM rectifier-inverter system based on powerbalancing mechanism[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 5197-5208.
[4]Rodriguez J, Pontt J, Vargas R, et al. Predictive direct torque control of an induction motor fed by a matrix converter[C]// IEEE European Conference on Power Electronics & Applications, Aalborg, Denmark, 2007,DOI: 10.1109/EPE.2007.4417295.
[5]吕帅帅, 林辉, 李兵强, 等. 一种改进的 PMSM 模型预测直接转矩控制方法[J]. 电机与控制学报,2020, 24(7): 102-111.Lü Shuaishuai, Lin Hui, Li Bingqiang, et al. Improved model predictive direct torque control for permanent magnet synchronous motor[J]. Electric Machines and Control, 2020, 24(7): 102-111.
[6]张永昌, 高素雨. 考虑延时补偿的永磁同步电机电流预测控制[J]. 电气工程学报, 2016, 11(3): 13-20.Zhang Yongchang, Gao Suyu. Predictive current control for permanent magnet synchronous motor with delay compensation[J]. Journal of Electrical Engineering, 2016, 11(3): 13-20.
[7]Wang Tianshi, Liu Chengcheng, Lei Gang, et al.Model predictive direct torque control of permanent magnet synchronous motors with extended set of voltage space vectors[J]. IET Electric Power Applications, 2017, 11(8): 1376-1382.
[8]刘珅, 高琳. 永磁同步电机的改进模型预测直接转矩控制[J]. 电机与控制学报, 2020, 24(1): 10-17.Liu Kun, Gao Lin. Improved model of predictive direct torque control for permanent magnet synchronous motor[J]. Electric Machines and Control,2020, 24(1): 10-17.
[9]Lim C S, Levi E, Jones M, et al. A comparative study of synchronous current control schemes based on FCS-MPC and PI-PWM for a two-motor three-phase drive[J]. IEEE Transactions on Industrial Electronics,2014, 61(8): 3867-3878.
[10]Gu Xin, Jiang Bo, Geng Qiang, et al. Model predictive control for two permanent magnet synchronous motors with five-leg voltage source inverter[J]. Advanced Technology of Electrical Engineering and Energy,2015, 34(12): 25-30.
[11]孙兴法, 聂子玲, 朱俊杰. 基于低阶串行双扩展卡尔曼滤波的永磁直线同步电机无速度传感器控制策略[J]. 电工技术学报, 2018, 33(12): 2685-2694.Sun Xingfa, Nie Ziling, Zhu Junjie. A speed sensorless control strategy for a permanent magnet linear synchronous motor based on low-order serial dual extended Kalman filters[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2685-2694.
[12]郭磊, 杨中平, 林飞. 带误差补偿的高频信号注入永磁同步电机无传感器控制策略[J]. 电工技术学报, 2019, 34(21): 4458-4466.Guo Lei, Yang Zhongping, Lin Fei. A sensorless control strategy for high frequency signal injection permanent magnet synchronous motor witherror compensation[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4458-4466.
[13]金光哲, 徐殿国, 高强, 等. 高频注入电压预估同步电机转子位置检测方法[J]. 中国电机工程学报,2014, 34(9): 1376-1383.Jin Guangzhe, Xu Dianguo, Gao Qiang, et al. A synchronous motor rotor position detection method based on high-frequency injection voltage prediction[J]. Proceedings of the CSEE, 2014, 34(9):1376-1383.
[14]许中阳, 郭希铮, 邹方朔, 等. 永磁同步电机无速度传感器控制离散化方法研究[J]. 电工技术学报,2019, 34(增刊 1): 52-61.Xu Zhongyang, Guo Xizheng, Zou Fangshuo, et al.Research on digital discretization method of speed sensorless control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 52-61.
[15]Zbede Y B, Gadoue S M, Atkinson D J. Model predictive MRAS estimator for sensorless induction motor drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3511-3521.
[16]尹忠刚, 李国银, 张延庆, 等. STEKF 协同残差归一化的感应电机转速辨识方法[J]. 电工技术学报,2017, 32(5): 86-96.Yin Zhonggang, Li Guoyin, Zhang Yanqing, et al. A speed estimation method based on strong tracking extended Kalman filter with normalized residuals for induction motors[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 86-96.
[17]Alonge F, Cangemi T, D'Ippolito F, et al. Convergence analysis of extended Kalman filter for sensorless control of induction motor[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 2341-2352.
[18]张春雷, 张辉, 叶佩青, 等. 两相圆筒型永磁同步直线电机无传感算法[J]. 电工技术学报, 2019,34(23): 4901-4908.Zhang Chunlei, Zhang Hui, Ye Peiqing, et al.Research on sensorless algorithm of two-phase tubular permanent magnet synchronous linear motor[J].Transactions of China Electrotechnical Society, 2019,34(23): 4901-4908.
[19]高素雨. 永磁同步电机模型预测控制与无速度传感器控制研究[D]. 北京: 北方工业大学, 2016.
[20]Rovere L , Formentini A, Gaeta A , et al. Sensorless finite-control set model predictive control for IPMSM drives[J]. IEEE Transactions on Industrial Electronics,2016, 63(9): 5921-5931.
[21]Teng Qingfang, Bai Jianyong, Zhu Jianguo, et al.Sensorless model predictive torque control using sliding-mode model reference adaptive system observer for permanent magnet synchronous motor drive systems[J]. Control Theory & Applications,2015, 32(2): 150-161.
[22]张勇军, 汪伟, 张小庆, 等. 带电阻在线辨识的改进型永磁同步电机滑模观测方法[J]. 电机与控制学报, 2017, 21(6): 10-17.Zhang Yongjun, Wang Wei, Zhang Xiaoqing, et al.Study on improved sliding-mode control with resistance estimation of PMSM[J]. Electric Machines and Control, 2017, 21(6): 10-17, 25.
[23]肖雄, 王健翔, 张勇军, 等. 一种优化的双电机主-从模型转矩预测控制策略[J]. 电工技术学报, 2018,33(24): 5720-5730.Xiao Xiong, Wang Jianxiang, Zhang Yongjun, et al.An optimized master-slave model predictive direct torque control scheme for the dual motor[J].Transactions of China Electrotechnical Society, 2018,33(24): 5720-5730.