0 引言
地磁暴、直流输电工程的单极不对称运行、电网中的非线性电力电子元件都会导致直流电流流过电网中的变压器,引起变压器的直流偏磁问题。而电压等级越高的电网,由于输电距离长、导线电阻小等原因,其变压器更易受直流偏磁的影响[1-3]。
直流偏磁后铁心发生半波饱和、漏磁增多、结构件损耗增大[4-5],并可能导致结构件上出现局部热点。在受漏磁影响较严重的区域,往往采用非导磁材料或加装电磁屏蔽来降低局部损耗;并在温度设计中留有较大的裕度,以降低直流偏磁等非正常情况对变压器可能造成的损害。
文献[6]在空载情况下,对于某一个固定的直流偏磁电流值,施加不同的交流电压,提取变压器损耗与交流电压有效值的关系,进而得到某一直流偏磁电流下的铁损曲线。对于小容量试验变压器,直流偏磁后的绕组损耗和拉板等结构件的损耗在变压器总损耗中的占比较大,且很难从测试损耗中分离出各结构的损耗。用此方法得到的铁损曲线会带来较大的计算误差。
文献[7]的试验结果指出,心式变压器铁心拉板为直流偏磁的关键过热部位,并给出了其温升与磁场强度的关系;当将拉板等结构件由导磁钢板替换为非导磁钢板后,热点温度降为原来的 1/10以下。
文献[8]基于设计的两台110kV单相单柱旁轭变压器,开展空负载工况下的直流偏磁关键性能测试和分析,直流电流导致变压器绕组和结构件温升均显著增大,注入36A直流电流时的绕组和拉板热点温升均超过90K,同时油中出现碳氢气体。
对变压器正常运行下的结构件热点温度的计算通常采用磁热流耦合方法[9-12],或在计算温度场时采用常数导热系数[13-14]。变压器的磁热流耦合计算需要建立较精细的流场模型,在液-固交界面的液体侧的边界层内划分多层网格,模型设置复杂,计算量大。采用常数导热系数计算温度场的方法不能反映温度等对导热系数的影响,计算误差较大。
现有的文献对变压器绕组热点和顶层油温[15-16]的试验和计算研究较多,对直流偏磁下的热点温升的试验研究也较多,对直流偏磁下的结构件热点温度的计算研究较少。变压器直流偏磁下的温升计算的关键与难点在于损耗计算模型与温度计算模型的准确建模。本文基于定制的单相四柱式变压器试验模型,开展了直流偏磁下的温升试验;建立了试验变压器的损耗和温升的计算模型,并与试验结果进行对比以验证计算模型的正确性。
1 试验变压器参数
本文研究的试验变压器为单相四柱自耦变压器,其额定参数见表1。后文的研究均针对此试验变压器进行。绕组联结方式如图1a所示,其中的符号“*”表示同名端;“左”“右”表示绕向。4个HV线圈并联,2个MV线圈并联。试验变压器实物如图 1b所示。在后文的试验及计算分析中,高压侧(A-X)施加额定电压,中压侧(Am-X)加额定负载,低压侧(a-x)空载;其对应的电路如图 1c所示。变压器部分结构的尺寸参数如图1d所示。
表1 试验变压器参数
Tab.1 Parameters of test transformer

参 数 数 值额定容量(HV/MV/LV)/(kV·A) 5/5/1.8额定频率/Hz 50额定电压(HV/MV/LV)/V 360/180/60额定电流(HV/MV/LV)/A 13.9/27.8/30线圈匝数(HV/MV/LV) 63/63/21串联绕组直流电阻/Ω 0.083公共绕组直流电阻/Ω 0.032
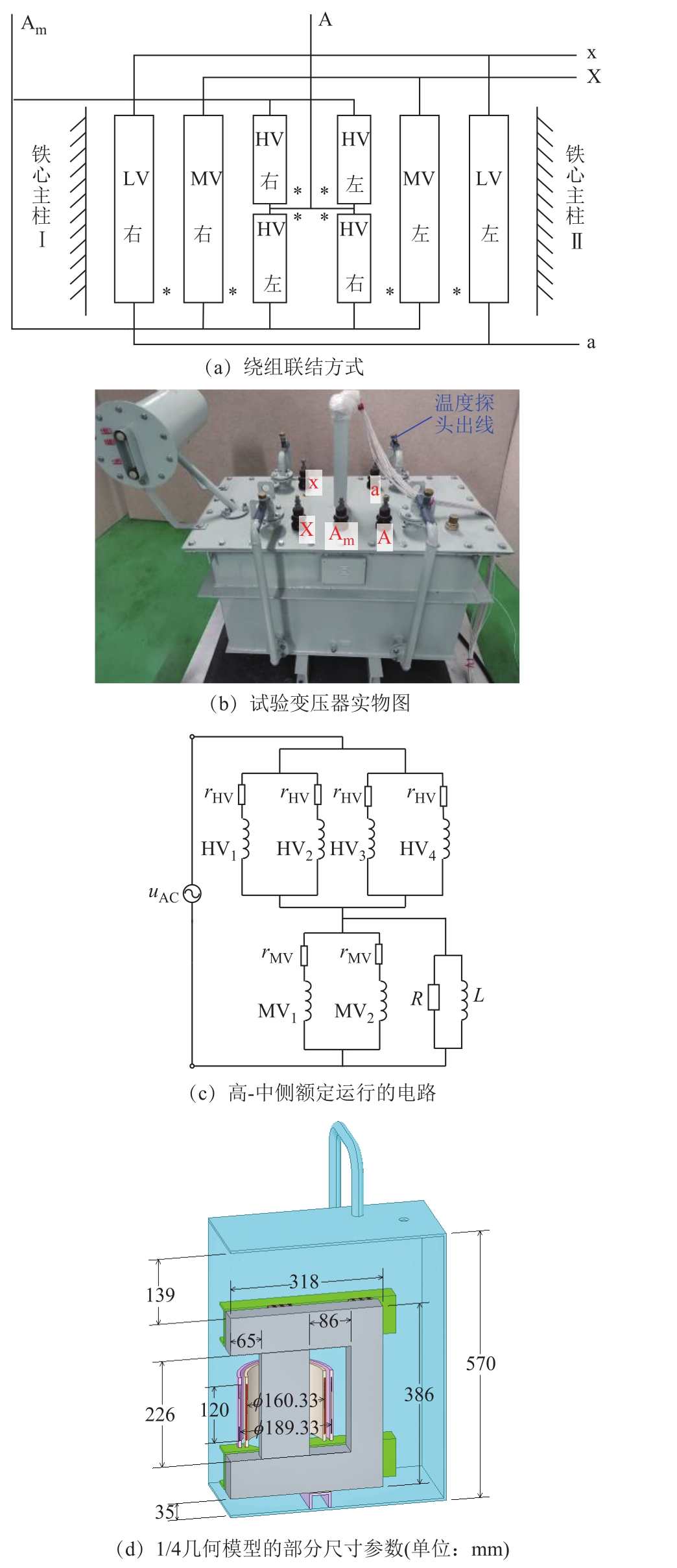
图1 试验变压器的绕组接线及结构
Fig.1 Winding connection and structure of test transformer
2 直流偏磁下的温升试验及结果分析
直流偏磁下的温升试验的接线如图 2所示,220V市电经调压器和隔离变压器连接试验变压器的高压侧(A-X)。图 2a中的隔离变压器的作用为变压;图 2a中的电容 C的作用为防止直流电流进入隔离变压器,否则会引起隔离变压器的直流偏磁;电阻R与电感L的并联作为额定负载,使变压器满容量运行。

图2 直流偏磁下的温升试验的接线图
Fig.2 Schematic diagram of temperature test under DC bias
温升试验流程共分四个试验阶段,持续 24h,各阶段在直流回路施加的直流电流Idc分别为0A、8A、16A、0A,具体见表2。温度测点布置如图3和表3所示,其中仅显示了典型位置的测点。在每个测点布置1个PT100温度传感器,并通过采集设备每隔1min将温度数据采集到计算机。其中,环境温度用插入四个1 000mL的悬空的金属油瓶的PT100温度传感器测量,取其平均值作为环境温度。
表2 试验流程
Tab.2 Test process

阶段 时间/h 电压(pu) 直流电流Idc/A 1 0~7 1 0 2 7~15 1 8 3 15~22 1 16 4 22~24 0 0
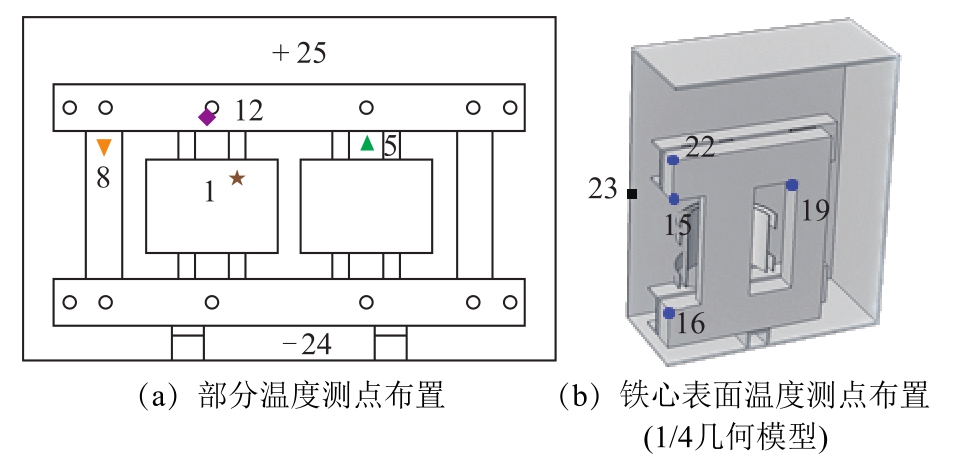
图3 温度测点位置
Fig.3 Location of temperature measuring point
表3 温度传感器位置编号及说明
Tab.3 Temperature sensor number and location description

位置编号 位置说明 符号1 HV线圈表面 ★5 主柱拉板顶部表面 ▲8 旁柱拉板顶部表面 ▼12 夹件表面 ◆15, 16, 19, 22 铁心表面 ●23 油箱内表面 ■24 底层油 -25 顶层油 +
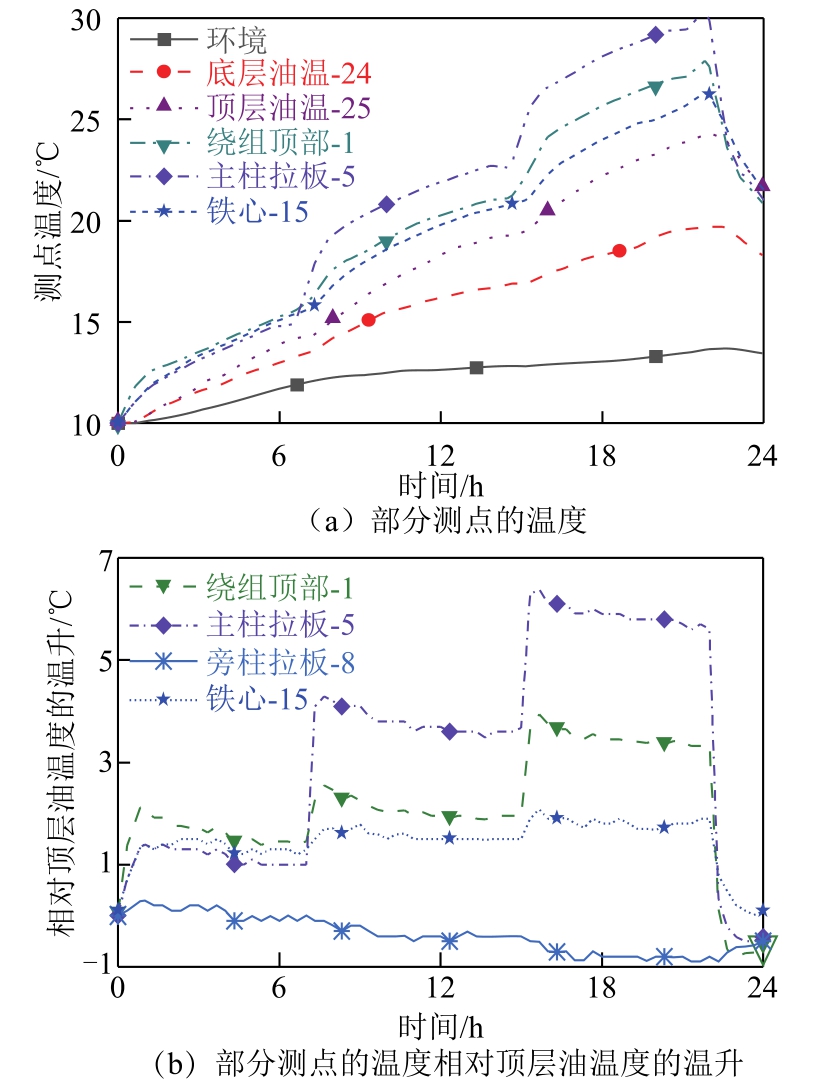
图4 测点温度或温升的变化曲线
Fig.4 Change curve of temperature or temperature rise at measuring point
测量得到各测点的温度、温升的变化曲线如图4所示。由图4a可见,直流偏磁后各测点温度先快速增加,随后增速变缓;由图4b可见,各测点对顶层油的温差很快达到稳定,即结构件对油温差达到稳定后,结构件温度随着油温的升高而增大。主柱拉板顶部表面(测点5)在16A直流偏磁下对顶层油的稳态温差最高,达到了 5.6℃。绕组表面(测点1)在8A、16A直流偏磁下对顶层油的稳态温差分别为2.2℃、3.3℃。旁柱拉板顶部表面(测点8)的温度低于顶层油温,其原因是旁柱拉板的损耗较小。
绕组表面(测点1)和主柱拉板顶部(测点5)对油的温差,在各阶段的起始段先达到一个较大值,随后缓缓地稳定到一个较小的值。其原因为:油的时间常数比结构件的时间常数大;在各阶段的起始段,油的流速还未达到稳定;随着油温的持续升高,油对测点的散热能力增强,测点对油的温差逐渐达到一个稳定值。
3 直流偏磁下的损耗的仿真计算
本节分别计算了不同直流偏磁下各结构的损耗,并通过与试验测试的总损耗的对比验证了损耗计算模型的正确性。
3.1 绕组损耗
试验测得的直流偏磁下的绕组电流如图 5所示。绕组电流中含有较多的谐波分量,且400Hz以上的谐波分量幅值较低。试验变压器线圈导线均为铜导体,其中高压线圈(圆截面导线)单匝导线的半径为 0.99mm,中压线圈(矩形截面导线)单匝导线的尺寸为 1.8mm×4.71mm。铜导体在 50Hz、400Hz下的趋肤深度分别为9.42mm、3.33mm;趋肤深度大于或接近导线尺寸,即可直接由电流有效值乘以绕组直流电阻近似计算直流偏磁下的绕组损耗。
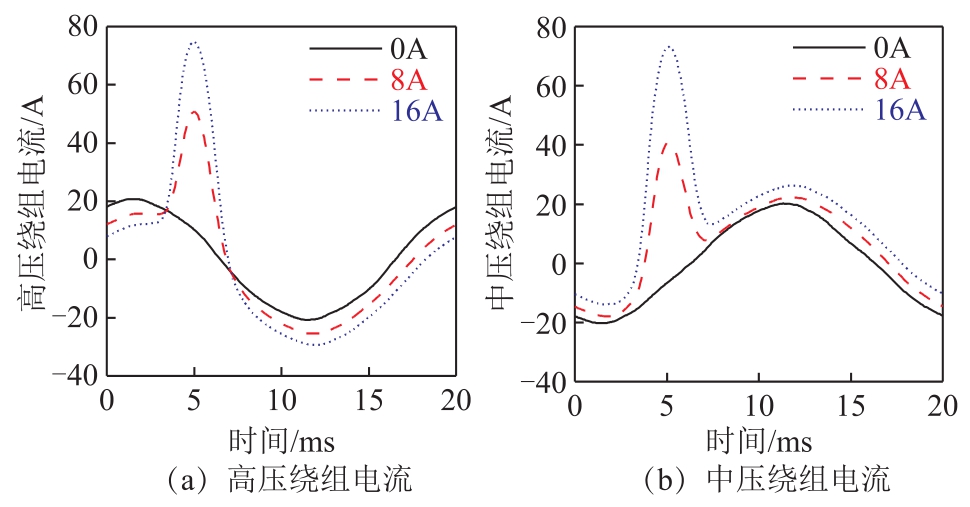
图5 试验测得的直流偏磁下的绕组电流
Fig.5 Measured winding currents under DC bias
3.2 场路耦合模型
有限元法较多地应用在变压器直流偏磁问题的计算分析中。按照温升试验的实际电路连接方式建立场路耦合模型,其中的有限元模型为基于对称性建立的1/4有限元模型,如图6a所示(隐藏了填充在结构件间的变压器油的网格)。在建模过程中做了以下假设:①将线圈构建为块状导体;②铁心硅钢片型号为B23R85,构建铁心块模型,用硅钢片的直流磁化曲线表征铁心的磁特性;③拉板、夹件、油箱的材料型号为 A3钢,考虑趋肤效应的影响,对这些结构件进行多层网格剖分;④有限元模型的边界条件为:在图6a所示模型的x轴负方向的外侧面施加磁力线垂直边界条件,其他五个外侧面施加磁力线平行边界条件。通过外加电压源的方法进行时域场路耦合仿真。

图6 损耗仿真的场路耦合模型
Fig.6 Field-circuit coupling model for loss simulation
3.3 铁心损耗
直流偏磁下,铁心磁感应强度波形整体上移或下移。本节采用文献[17-18]中的半波平均法计算直流偏磁下的铁心损耗。其方法简要介绍如下:在图6a所示的有限元模型中,提取tp时刻(铁心n0点的磁感应强度波形最大值对应的时刻)的铁心有限元网格的各个单元的磁感应强度,并基于无直流偏磁下的硅钢片的铁损曲线(如图6c所示)插值得到每个单元的损耗 ep(W/kg);再由式(1)得到 tp时刻的铁心的体损耗Ptp。
式中,ksym为对称系数,ksym=4;ρ为硅钢片密度(kg/m3);Ve为单元体积(m3)。同理可以得到tb时刻(铁心n0点的磁感应强度波形最小值对应的时刻)铁心的体损耗Ptb。对二者求平均值可得到铁心的周期平均体损耗Pcore为
3.4 结构件损耗
基于场路耦合模型,计算得到结构件的涡流损耗。汇总各结构的周期平均体损耗,见表4。
表4 各结构的周期平均体损耗
Tab.4 Periodic average body losses of each parts
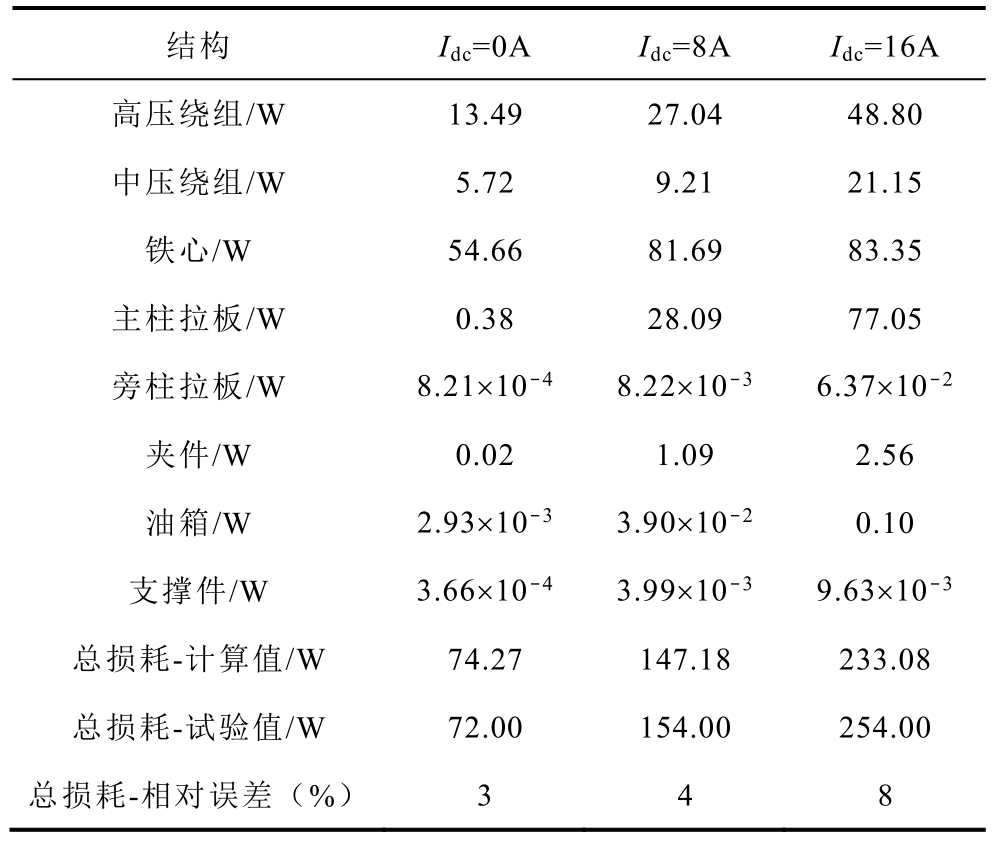
结构 Idc=0A Idc=8A Idc=16A高压绕组/W 13.49 27.04 48.80中压绕组/W 5.72 9.21 21.15铁心/W 54.66 81.69 83.35主柱拉板/W 0.38 28.09 77.05旁柱拉板/W 8.21×10-4 8.22×10-3 6.37×10-2夹件/W 0.02 1.09 2.56油箱/W 2.93×10-3 3.90×10-2 0.10支撑件/W 3.66×10-4 3.99×10-3 9.63×10-3总损耗-计算值/W 74.27 147.18 233.08总损耗-试验值/W 72.00 154.00 254.00总损耗-相对误差(%) 3 4 8
由表4可见,0A、8A、16A情况下的总损耗计算值与试验值的相对误差分别为3%、4%、8%。无直流偏磁时,总损耗的计算误差较小,损耗中主要为绕组损耗和铁心损耗。直流偏磁下,铁心损耗、主柱拉板损耗、绕组损耗增加较多;总损耗的计算误差增大,原因主要为铁心损耗采用半波正弦法近似计算带来的误差和忽略结构件的磁滞损耗带来的计算误差。
4 结构件温度分布的计算分析
自然对流散热情况下的导热系数和流体的温度、流速、被冷却物体的形状、位置等因素有关,使得在很多情况下,不得不从经验或试验得出导热系数的试验关联式[19]。本节结合结构件表面的散热系数的试验关联式,利用有限元方法计算各结构的瞬态温度变化。
4.1 温度场计算模型
为避免损耗插值引起的误差,温度场计算的有限元网格剖分与前文损耗计算的有限元网格剖分相同。在进行温度场仿真时,做出以下假设:①对于铁心等结构件,提取其每个单元的损耗密度,并将此损耗密度值导入温度场计算模型,作为温升仿真的热源。不同位置处的损耗密度值不同,从而能更真实地反映结构件的热点位置分布。②已知顶层油温(试验结果)、底层油温(试验结果),假设变压器油的温度沿高度方向呈线性变化。③给出结构件表面的导热系数的计算关系式(随温度的变化而变化,并与结构件的形状、位置有关);有限元软件将导热系数作为未知变量之一进行温度场计算。④由前文的计算结果可以看出,试验变压器的油箱损耗可以忽略,因此未对油箱的温度分布进行计算分析,仅分析油箱内部各结构件的瞬态温度。
试验变压器的冷却方式为自然对流冷却,即ONAN。自然对流情况下竖直壁的表面平均导热系数[20]为

式中,特征长度L1为竖直壁的高度;k为变压器油的热导率;v为变压器油的黏度;cp为变压器油的定压比热容;Ra为瑞利数(无量纲数),即
式中,ρ为变压器油的密度;β为变压器油的热膨胀系数;ΔT为结构件表面温度Tw与变压器油温度To的温差。变压器油的热属性参数在 (Tw+To)/2温度下计算。
自然对流情况下热平壁的顶表面或冷平壁的底表面的表面平均散热系数的表达式为[20]
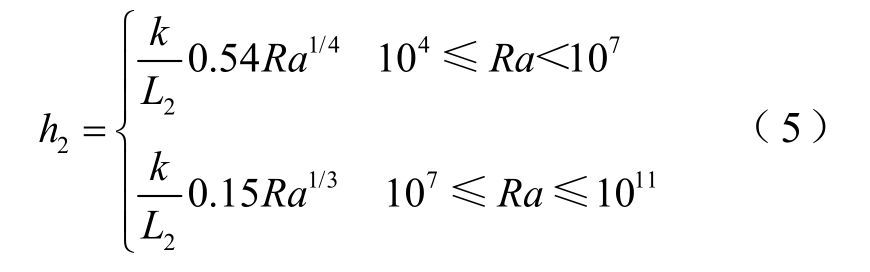
式中,特征长度L2为表面的面积与周长之比。
自然对流情况下热平壁的底表面或冷平壁的顶表面的表面平均散热系数的表达式[20]为

式中,特征长度L3为表面的面积与周长之比。
变压器各结构件的热属性参数见表5。
表5 各结构件的热属性参数
Tab.5 Thermal property parameters of each structure
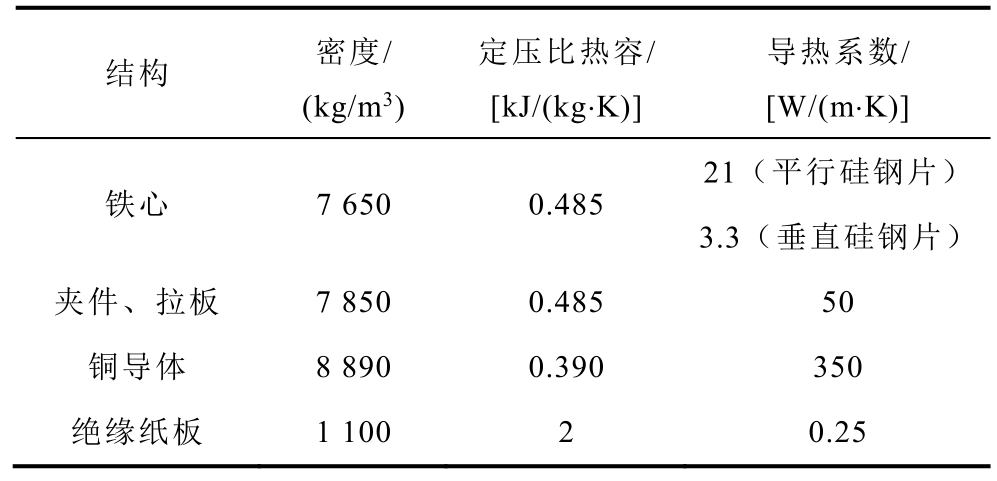
结构 密度/(kg/m3)定压比热容/[kJ/(kg⋅K)]导热系数/[W/(m⋅K)]21(平行硅钢片)铁心 7 650 0.485 3.3(垂直硅钢片)夹件、拉板 7 850 0.485 50铜导体 8 890 0.390 350绝缘纸板 1 100 2 0.25
变压器油的热属性参数(导热系数 k、黏度 v、定压比热容cp、密度ρ)随温度的变化而变化,如图7所示。

图7 变压器油的热属性参数
Fig.7 Thermal characteristics of transformer oil
当变压器油的温度取为20℃,垂直壁的特征长度L1取为0.386(铁心高度),水平壁的特征长度L2取为0.039 4时(铁心上轭上表面或下表面),得到瑞利数和表面平均散热系数随温度增大的变化曲线分别如图8a和图8b所示。由图8a可见,竖直壁表面流体为湍流流态(Ra>1×10-9),水平壁表面流体为层流状态(Ra<1×10-9)。对于朝上的冷表面或朝下的热表面,流体的下降和上升趋势被平壁阻挡,流动必须在水平方向进行,因而对流散热效果较差;而对于朝下的冷表面或朝上的热表面,流动分别受到下降和上升的流体团的驱动,同时被周围上升或下降的流体所取代,因此散热效果较好[20],与图8b中的结果一致。

图8 瑞利数和散热系数随温差增大的变化曲线
Fig.8 Curves of Rayleigh number and heat transfer coefficient with temperature difference increasing
4.2 温度仿真结果及对比分析
基于温度场仿真模型,仿真得到各个位置的瞬态温度。图 9给出了各测点的瞬态温度的试验值与仿真值的对比。由图9可见,仿真结果与试验结果的变化趋势一致。各阶段终止时刻(7h、15h、22h)各测点的温度计算结果的相对误差见表6。由表6可见,仿真结果与试验结果的最大相对误差不超过10%,验证了损耗和温度场计算模型和方法的正确性。
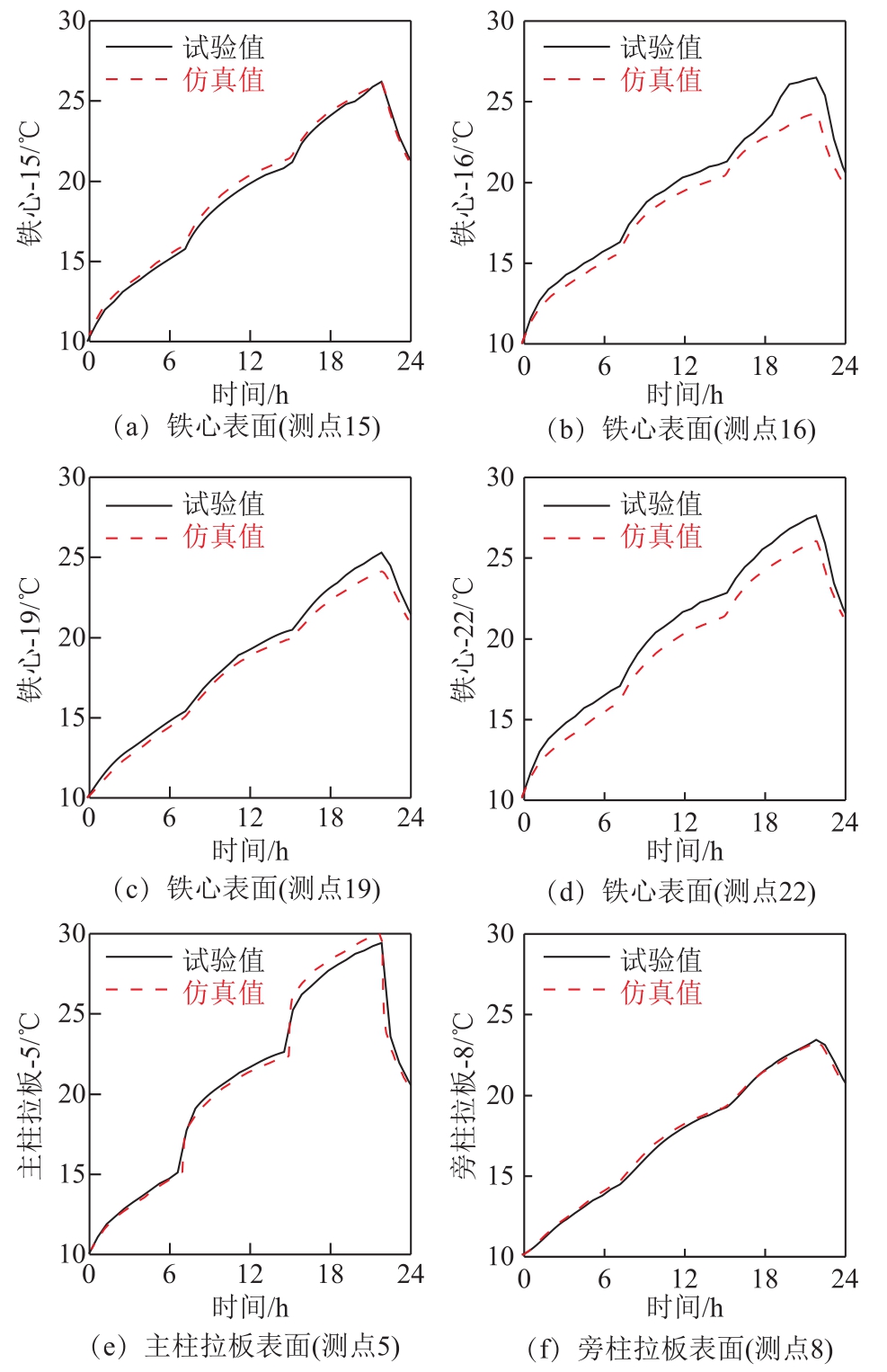
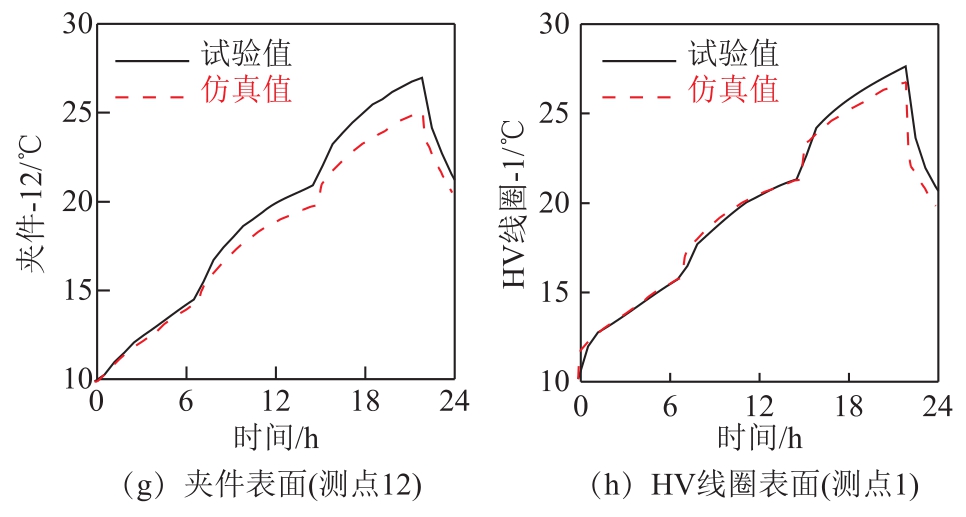
图9 瞬态温度对比
Fig.9 Transient temperature comparison
表6 各阶段终止时刻的各测点的温度的相对误差
Tab.6 Relative error of temperature at each measuring point at the end of each stage

时刻/h 测点15 16 19 22 5 8 12 1 7 0.012 -0.049 -0.028 -0.064 -0.012 0.002 -0.024 -0.007 15 0.018 -0.044 -0.025 -0.063 -0.023 0.003 -0.061 -0.008 22 -0.002 -0.087 -0.046 -0.057 0.021 -0.012 -0.073 -0.033
仿真得到22h的温度分布云图,如图10所示。由图10可见,此时的主柱拉板和铁心上轭上表面中间位置的温度较高,结构件表面最大温度为30.2℃,最小温度为20.2℃。

图10 22h时刻的温度分布云图
Fig.10 Temperature cloud diagram at time 22h
5 结论
基于定制的单相四柱式变压器试验模型,进行了直流偏磁下的温升试验;测量得到直流偏磁下的变压器损耗和结构件表面不同位置的瞬态温度变化。铁心、绕组、主柱拉板温度受直流偏磁的影响较大。绕组表面(测点1)和主柱拉板顶部(测点5)对油的温差,在各阶段的起始段先达到一个较大值,随后缓缓地稳定到一个较小的值。
建立了损耗计算模型,计算得到直流偏磁下的各结构件的损耗。铁心损耗、主柱拉板损耗和绕组损耗受直流偏磁影响较大。无直流偏磁时,总损耗的计算误差较小。直流偏磁情况下的总损耗的计算误差增大,其原因为铁心损耗采用半波正弦法近似计算带来的误差和忽略结构件的磁滞损耗的带来的计算误差。
建立了温度场计算模型,假设变压器油沿高度方向线性增加,结合导热系数表达式和各结构的损耗,仿真得到各测点的瞬态温度,温度计算结果与试验结果的相对误差不超过10%。
[1]黄天超, 王泽忠. 地磁暴对直流输电逆变侧换相角及谐波的影响机理分析[J]. 电工技术学报, 2020,35(16): 3377-3384.Huang Tianchao, Wang Zezhong. Mechanism analysis of geomagnetic storm on commutation angle and harmonic of invert side of HVDC transmission[J].Transactions of China Electrotechnical Society, 2020,35(16): 3377-3384.
[2]李冰, 王泽忠, 刘恪, 等. 特高压变压器直流偏磁对绕组电流的影响[J]. 电工技术学报, 2020, 35(7):1422-1431.Li Bing, Wang Zezhong, Liu Ke, et al. Research on winding current of UHV transformer under DC-bias[J].Transactions of China Electrotechnical Society, 2020,35(7): 1422-1431.
[3]刘连光, 刘春明, 张冰. 磁暴对我国特高压电网的影响研究[J]. 电网技术, 2009, 33(11): 1-5.Liu Lianguang, Liu Chunming, Zhang Bing. Effects of geomagnetic storm on UHV power grids in China[J].Power System Technology, 2009, 33(11): 1-5.
[4]赵志刚, 刘佳, 郭莹, 等. 非正弦励磁环境磁性材料改进损耗模型的研究[J]. 电工技术学报, 2019,34(13): 2693-2699.Zhao Zhigang, Liu Jia, Guo Ying, et al. Investigation on the improved loss model of magnetic materials under non-sinusoidal excitation environment[J].Transactions of China Electrotechnical Society, 2019,34(13): 2693-2699.
[5]康丽, 张艳丽, 唐伟, 等. 基于变系数 Steinmetz公式的直流偏磁下铁心损耗计算[J]. 电工技术学报,2019, 34(增刊 1): 1-6.Kang Li, Zhang Yanli, Tang Wei, et al. Calculation of core loss under DC bias based on the variable coefficient Steinmetz formula[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 1-6.
[6]郭满生, 梅桂华, 张喜乐, 等. 直流偏磁条件下单相三柱电力变压器的损耗计算[J]. 电工技术学报,2010, 25(7): 67-71.Guo Mansheng, Mei Guihua, Zhang Xile, et al.Calculation of losses in single phase three limb transformer under DC-biasing[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 67-71.
[7]Takasu N, Oshi T, Miyawaki F, et al. An experimental analysis of DC excitation of transformers by geomagnetically induced currents[J]. IEEE Transactions on Power Delivery, 1994, 9(2): 1173-1182.
[8]张书琦, 汪可, 李金忠, 等. 单相单柱旁轭变压器空负载工况下的直流偏磁关键性能测试[J]. 中国电机工程学报, 2019, 39(14): 4334-4345.Zhang Shuqi, Wang Ke, Li Jinzhong, et al. Tests of DC bias key performances of power transformer with single-phase three-limb core under no-load and ratedload conditions[J]. Proceedings of the CSEE, 2019,39(14): 4334-4345.
[9]刘国坚, 王丰华. 油浸式电力变压器温度场分布的计算分析[J]. 科学技术与工程, 2015, 32(15): 36-41.Liu Guojian, Wang Fenghua. Temperature field calculation and analysis of oil-immersed transformers[J]. Science Technology and Engineering,2015, 32(15): 36-41.
[10]井永腾, 王宁, 李岩, 等. 电磁-热-流弱耦合的变压器绕组温升研究[J]. 电机与控制学报, 2019,23(10): 41-48.Jing Yongteng, Wang Ning, Li Yan, et al. Research on temperature rise of transformer windings with electromagnetic-thermal-flow weak coupling[J].Electric Machines and Control, 2019, 23(10): 41-48.
[11]王小飞, 代颖, 罗建. 基于流固耦合的车用永磁同步电机水道设计与温度场分析[J]. 电工技术学报,2019, 34(增刊 1): 22-29.Wang Xiaofei, Dai Ying, Luo Jian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29.
[12]谢颖, 郭金鹏, 单雪婷, 等. 油田抽油机用感应电动机三维瞬态温度场计算分析[J]. 电机与控制学报, 2019, 23(10): 59-67.Xie Ying, Guo Jinpeng, Shan Xueting, et al. Threedimensional transient temperature field calculation and analysis of induction motor for oilfield pumping unit[J]. Electric Machines and Control, 2019, 23(10):59-67.
[13]陈起超. 大型油浸式变压器涡流损耗和温度场分析[D]. 哈尔滨: 哈尔滨理工大学, 2015.
[14]谢道伟. 油浸式三相电力变压器电磁场及温度场的瞬态仿真分析[D]. 吉林:吉林大学, 2015.
[15]王丰华, 周翔, 高沛, 等. 基于绕组热分布的改进油浸式变压器绕组热点温度计算模型[J]. 高电压技术, 2015, 41(3): 895-901.Wang Fenghua, Zhou Xiang, Gao Pei, et al. Improved thermal circuit model of hot spot temperature in oilimmersed transformers based on heat distribution of winding[J]. High Voltage Engineering, 2015, 41(3):895-901.
[16]滕黎. 油浸式变压器热路计算及热点温度遗传支持向量机预测研究[D]. 重庆: 重庆大学, 2012.
[17]马健, 刘文里,李航, 等. 直流偏磁对换流变压器空载损耗的影响[J]. 变压器, 2016, 53(1): 35-40.Ma Jian, Liu Wenli, Li Hang, et al. Influence of DC bias on no-load loss of converter transformer[J].Transformer, 2016, 53(1): 35-40.
[18]党艳阳, 张欣宜, 马嫱, 等. 直流偏磁条件下变压器励磁电流及铁心损耗计算[J]. 变压器, 2019,56(10): 1-6.Dang Yanyang, Zhang Xinyi, Ma Qiang, et al.Calculation of excitation current and core loss of transformer under DC bias[J]. Transformer, 2019,56(10): 1-6.
[19]谢毓城. 电力变压器手册[M]. 北京: 机械工业出版社, 2014.
[20]Ted Bergman, Adrienne Lavine. Fundamentals of heat and mass transfer[M]. New Jersey: Wiley, 2007.