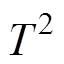 和平方预测误差(SPE)及其各自的控制限,通过电弧故障发生前后的
和平方预测误差(SPE)及其各自的控制限,通过电弧故障发生前后的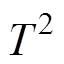 和SPE值与各自的控制限的比较,实现航空交流电弧故障的检测。分析结果表明,该方法结合了各特征量的优势,不需要人工设置阈值,能够较为准确地判别电弧故障的发生。最后利用三维熵空间,给出几种典型的电弧故障类型的分类方法。在实现电弧故障检测的同时,给出电弧故障的类型,能够更加有效地对不同电弧故障的发生做出有针对性的应对。
和SPE值与各自的控制限的比较,实现航空交流电弧故障的检测。分析结果表明,该方法结合了各特征量的优势,不需要人工设置阈值,能够较为准确地判别电弧故障的发生。最后利用三维熵空间,给出几种典型的电弧故障类型的分类方法。在实现电弧故障检测的同时,给出电弧故障的类型,能够更加有效地对不同电弧故障的发生做出有针对性的应对。摘要 鉴于常用的时频域分析方法在航空电弧故障检测中的局限性,同时为避免单特征量的偶然性,该文提出利用三维熵距的方法实现三种信息熵的特征融合,为减少特征融合带来的噪声与冗余,利用主元分析(PCA)故障检测技术以实现特征矩阵的降维处理。分别分析小波能量熵、功率谱熵、样本熵以及三种信息熵的三维熵距在电弧故障发生前后的特征差异。利用PCA故障检测技术将特征矩阵降维处理,同时给出各试验负载下的PCA的监测统计量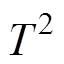 和平方预测误差(SPE)及其各自的控制限,通过电弧故障发生前后的
和平方预测误差(SPE)及其各自的控制限,通过电弧故障发生前后的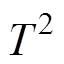 和SPE值与各自的控制限的比较,实现航空交流电弧故障的检测。分析结果表明,该方法结合了各特征量的优势,不需要人工设置阈值,能够较为准确地判别电弧故障的发生。最后利用三维熵空间,给出几种典型的电弧故障类型的分类方法。在实现电弧故障检测的同时,给出电弧故障的类型,能够更加有效地对不同电弧故障的发生做出有针对性的应对。
和SPE值与各自的控制限的比较,实现航空交流电弧故障的检测。分析结果表明,该方法结合了各特征量的优势,不需要人工设置阈值,能够较为准确地判别电弧故障的发生。最后利用三维熵空间,给出几种典型的电弧故障类型的分类方法。在实现电弧故障检测的同时,给出电弧故障的类型,能够更加有效地对不同电弧故障的发生做出有针对性的应对。
关键词:航空电弧故障 三维熵距 特征融合 PCA检测技术 熵空间 故障分类
对于飞机而言,恶劣的飞行条件如振动、高温、水雾、紫外线等极易导致电缆老化、连接松动从而可能引起电弧故障。电弧故障发生时会伴随着高温,影响飞机的飞行安全。飞机电弧故障属于间歇性故障,故障电弧持续时间短、电流强度小、检测难度大、危害性强。因此,研究航空交流电弧故障的检测方法具有重要意义。
电弧故障检测的方法主要是根据电流、电压的变化来检测,由于电弧故障的位置无法提前确定,通常提取电流信号来检测电弧故障[1]。国内外学者在较为直观的时域方面提取故障特征,利用电流的峰值变化来检测电弧故障[2]。基于串联交流电弧的时域特性的研究还包括使用电流信号的均值、电弧电流的变化率[3]等来检测电弧故障。虽然时域信号采集简单、检测直观有效,但抗干扰性差,在航空复杂的飞行条件下易受其他信号的干扰,且大多需要人工设置阈值,检测的随机性相对较大。为了避免时域特征的不足,部分学者开始在频域方面进行电弧特征量的提取。但简单地利用傅里叶变化在处理非平稳信号时缺少局部的时频特性,小波变换理论以其良好的局部化性质弥补了傅里叶变换分析局部时域信号的不足[4-5];同样,希尔布特黄变换相比傅里叶变换在三维时频谱能够更好地反映信号的局部特征[6]。另外,随着计算机算法的发展,时频域特征量结合深度卷积神经网络以及改进的径向基神经网络来识别电弧故障[7-8];利用信息维数[9]和支持向量机[10]进行电弧故障的识别;利用小波包分解结合灰度-梯度共生矩阵进行特征量的提取[11];利用机器学习进行监督特征选择的电弧故障检测[12];利用相空间重构和遗传算法进行电弧故障检测[13]等基于大数据分析和人工智能算法的电弧故障检测。这类算法需要处理和训练大量的样本数据。
为了更好地处理大量的检测样本,本文以航空交流系统为研究背景,引入信息熵的理论。同时为了兼具小波包变换和傅里叶变换的优点,利用三维熵距将小波能量熵、功率谱熵、样本熵三种熵特征量进行融合,为了减少噪声和冗余,采用主元分析(Principal Component Analysis, PCA)故障检测技术对得到的信息矩阵的维度进行降维处理,同时得到监测指标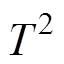 和SPE与其各自控制限的大小,在反映电弧电流时频域特征的同时,能全面结合各信息熵的优势,减少检测过程中的噪声与冗余,准确可靠地对航空交流电弧故障做出判断。本文在研究电弧故障检测的同时,还利用三维熵空间对电弧故障做了分类研究,在对电弧故障进行检测的同时也实现电弧故障的分类。
和SPE与其各自控制限的大小,在反映电弧电流时频域特征的同时,能全面结合各信息熵的优势,减少检测过程中的噪声与冗余,准确可靠地对航空交流电弧故障做出判断。本文在研究电弧故障检测的同时,还利用三维熵空间对电弧故障做了分类研究,在对电弧故障进行检测的同时也实现电弧故障的分类。
本文按照美标UL 1699[14]进行航空电弧故障试验。试验中,航空电源参数为115V/400Hz,电源柜如图1所示。点接触试验的电弧故障是由电弧故障发生器和步进电机产生的。电弧故障发生器由步进电机驱动的动触点铜棒、静触点碳棒组成。试验过程中,两电极由接触状态,通过步进电机控制使两电极逐渐拉开,产生交流电弧故障。点接触电弧试验平台如图2所示。所涉及的负载类型有线性负载和非线性负载。线性负载包括纯阻(57.5W)、阻感(57.5W+ 5mH)、阻容(57.5W+47mF);非线性负载采用自耦变压整流器(Auto Transformer Rectifier Units, ATRU)。
本试验采用的采样频率为400kHz,采样周期从正常到故障共20个。为了对比正常波形与电弧故障波形的差异,将所有数据做归一化处理,将电流绝对值的最大值设为1,并将所有采样点的电流除以最大值。不同负载从正常到故障的归一化的电流波形如图3所示。

图1 115V/400Hz电源柜
Fig.1 115V/400Hz power cabinet

图2 点接触电弧试验平台
Fig.2 Schematic diagram of contact test circuit
分析图3各负载下的电流波形可得出如下结论:
(1)对于线性负载,在电弧故障发生前电流波形呈平稳的正弦波,当发生电弧故障时,电流过零点时都会存在电流接近零的区域,这是因为电弧在电流过零前后会有一个熄灭再重燃的过程。
(2)当发生电弧故障时,电流的高频分量明显增多,且电流幅值会明显减小。


图3 几种负载电流波形
Fig.3 The current waveforms of several load
(3)对于非线性负载ATRU,在电弧故障发生前后,都存在着高频噪声,这是由于ATRU自身在正常工作时,其电流也会存在“零休现象”。但电弧故障发生时,其高频噪声会明显增多。此外,电流的幅值也会有所下降。
在实际中,电流中的高频分量不仅仅是由电弧故障产生的,也会受到其他负载或者电源质量的影响而产生类似电弧电流特征的谐波干扰。所以,只是单纯以时域的电流电压作为判别电弧故障的特征量往往会产生误判。单独对电流信号进行傅里叶变换也会由于谐波的影响不足以准确判断电弧故障的发生。
工程中处理一些非平稳信号,一般选用小波分析和小波包分析的方法。相对小波分析,小波包分析对信号分析更加精细,可以将时频平面划分得更为细致,对信号的高频部分的分辨率要好于小波分析,它可以根据信号的特征,自适应地选择最佳小波基函数,以便更好地对信号进行分析。但小波包变换会使需要处理的信息大幅增多,增加了系统的复杂度。为此引入小波能量熵的理论,同时本文还将结合功率谱熵和样本熵理论,发挥功率谱熵对信号在频率谱上能量的描述优势,更好地描述电流信号从正常周期到电弧故障周期频谱上能量的变化;以及利用样本熵在处理复杂序列样本时的统计特征的优势。为了更好地结合三种信息熵的优点,本文将利用信息融合技术,引入三维信息熵距实现三种信息熵的特征融合,更加准确地反映电弧故障前后特征的差异。
结合信息熵对系统复杂度和不确定性的描述,对电流信号进行小波能量熵特征提取。
设E(i, m)为信号电流x(t)在分解层数为i,分解尺度为m下的小波能量,m=1,2,…, j。
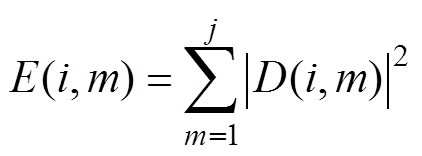 (1)
(1)设 ,其中,
,其中,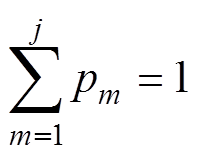 ,有
,有
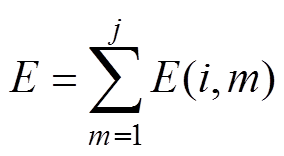 (2)
(2)
根据信息熵的理论可以得到小波能量熵(wavelet energy entropy)的定义为
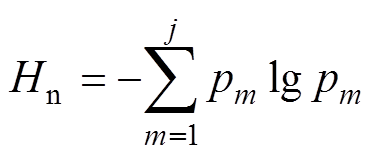 (3)
(3)基于小波包分解理论,可以将频带部分进行多层次划分,根据待分析信号的不同特征,自适应地选择相应频带,使之与信号频谱相匹配,从而提高时频分辨率。为了更好地区分电弧故障和正常周期,本文采用db4小波对数据进行分解重构,现以点接触试验(纯阻57.5W)为例,得到各层细节信号如图4所示。
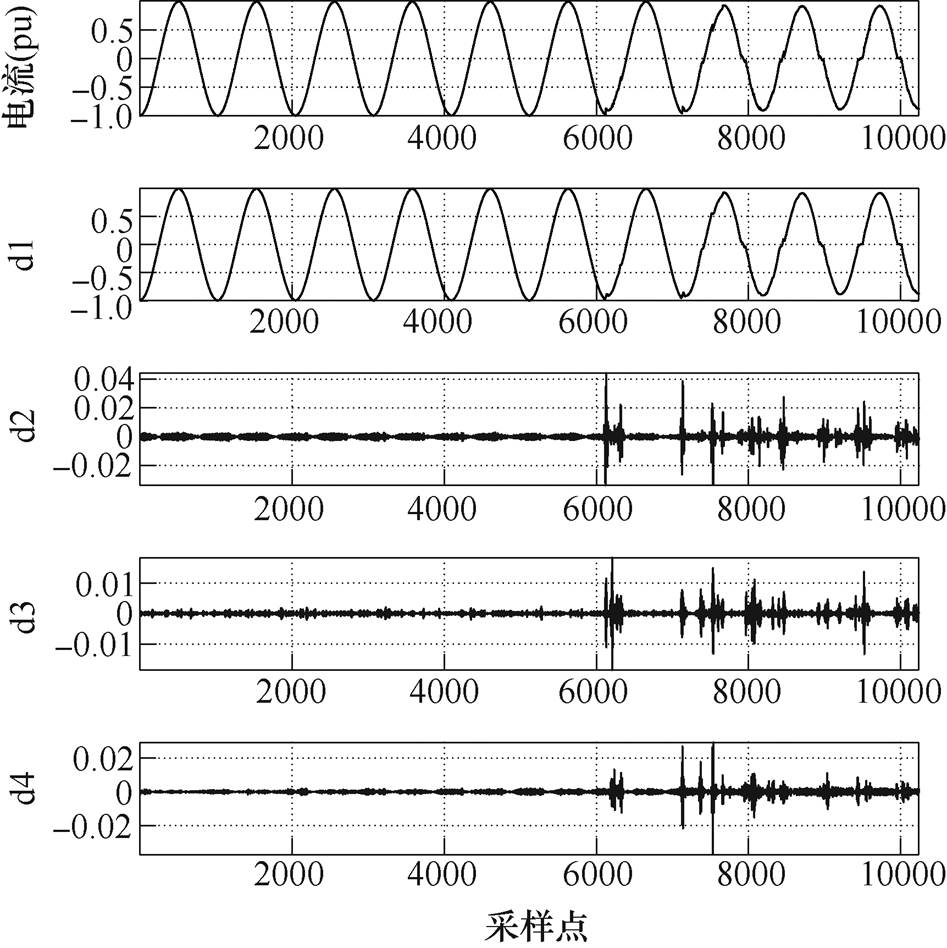
图4 小波分解重构细节信号
Fig.4 Detail signal by wavelet decomposition and reconstruction
通过比较电弧故障发生前后的细节分量可以发现,电流中频率成分都发生明显变化,如图4中d2~d4频段在电弧故障发生前后均发生明显变化。结合信息熵的理论,可以知道,当电弧故障发生时,小波包分解的各频带的频率成分显著变化,其能量分布呈现随机性,小波能量熵会越大。由于小波能量熵在信号发生改变的时刻均会发生改变,且随着谐波含量和频率成分的变化而变化,小波能量熵很好地表征了电弧故障发生前后电流信号的变化。
对小波能量熵特征量的提取步骤具体如下:
(1)以每周期电流信号作为待分解信号,正常和故障周期共20个。
(2)对每个周期的电流信号采用db4小波,分解层数为4层的分解重构。
(3)依据式(1)求每个周期的重构信号的能量谱。
(4)依据式(2)将每一层小波尺度下的重构信号的能量值相加,并求得每一层尺度下的能量在总能量E中的概率pm。
(5)依据式(3)求得每个周期分解重构后的小波能量熵。
本文将每周期的电流信号作为分析信号,绘制出从正常到故障的20个周期信号的小波能量熵的熵值曲线如图5~图8所示。
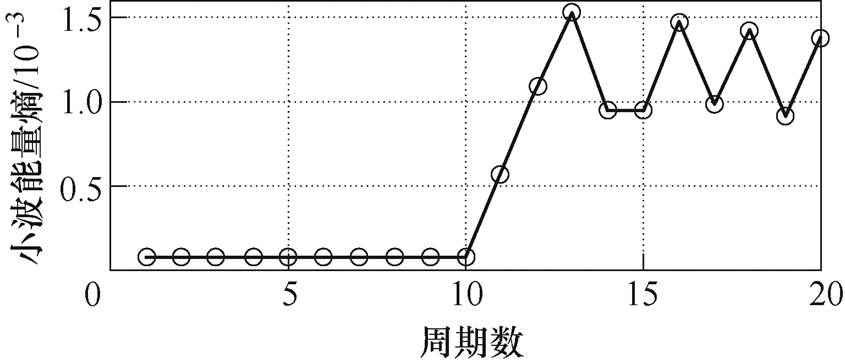
图5 纯阻(57.5W)的小波能量熵值曲线
Fig.5 Wavelet energy entropy curve of pure resistance (57.5W)
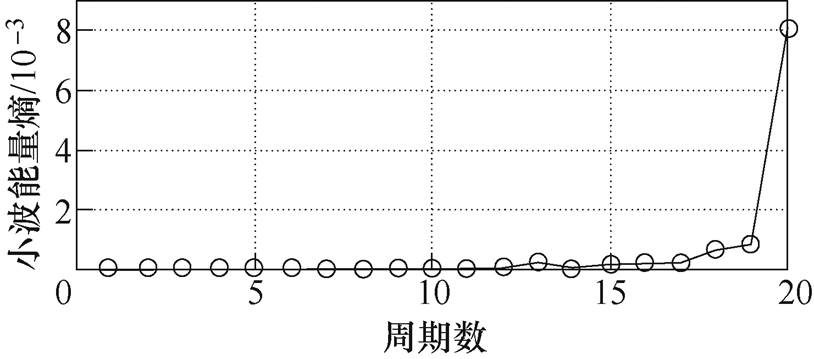
图6 阻感(57.5W+5mH)的小波能量熵值曲线
Fig.6 Wavelet energy entropy curve of RL (57.5W+5mH)
通过对图5~图8的分析可知,当负载为纯阻、阻容和非线性负载时,故障周期的小波能量熵值会明显区别于正常周期,正常周期的熵值基本呈一条水平线,波动较小。故障周期的熵值波动较大且呈增大的趋势。但对于感性的负载,电弧故障发生后,会存在熵值变化不明显的现象。当发生剧烈电弧故障时,小波能量熵才会有明显变化。
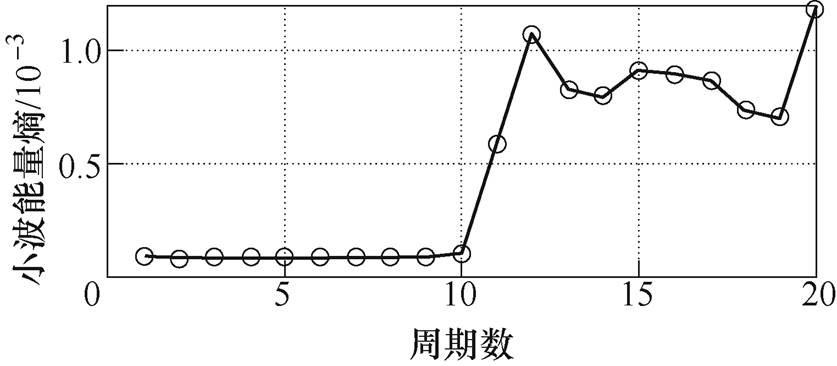
图7 阻容(57.5W+47mF)的小波能量熵值曲线
Fig.7 Wavelet energy entropy curve of RC (57.5W+47mF)
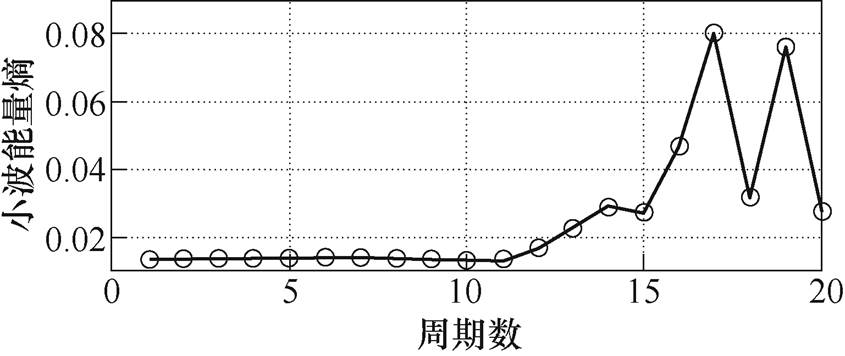
图8 ATRU的小波能量熵值曲线
Fig.8 Wavelet energy entropy curve of ATRU
功率谱是依据时域信号通过傅里叶变换,在时域变换到频域的过程中遵循能量守恒原则的一种能量描述[15]。现以点接触试验(纯阻57.5W)为例,选取0~6kHz的频段对电流正常波形和电弧故障波形进行傅里叶变换并求其功率谱。绘制出对数功率谱对比如图9所示。
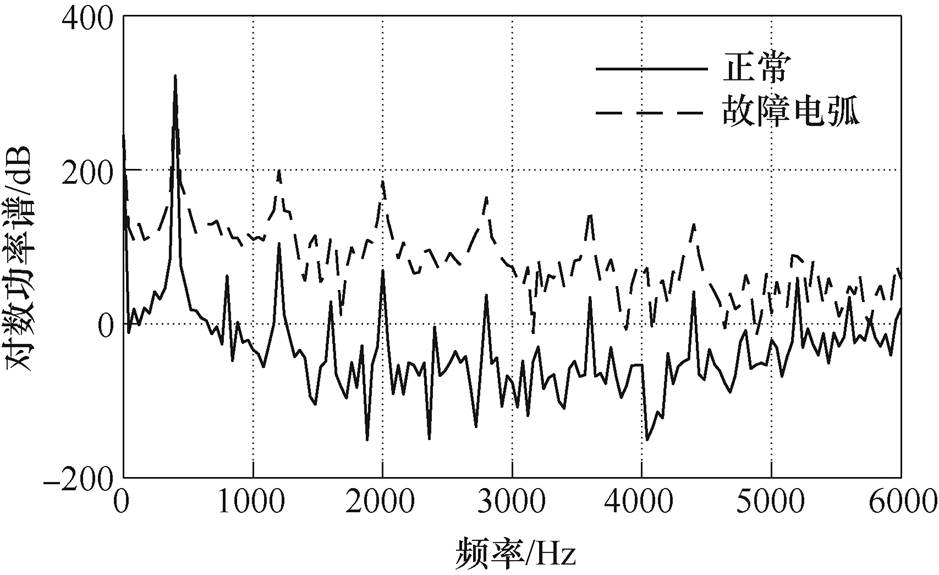
图9 对数功率谱
Fig.9 Logarithmic power spectrum
由图9可知,故障电弧的功率谱在0~6kHz范围内的幅值要明显高于正常周期的功率谱幅值。其谐波含量和功率谱能量都将高于正常周期。功率谱熵可以描述信号在频率谱上能量的大小,当发生电弧故障后可反映电流信号在频率谱中能量的变化。
本文将提取功率谱熵作为检测电弧故障的特征量。功率谱熵为
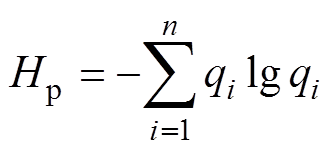 (4)
(4)式中,qi为第i个功率谱在整个功率谱中所占的百分比,有
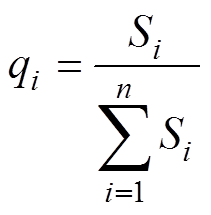 (5)
(5)
式中,Si为频率谱序列yi在对应频率处的功率谱 值,其中,yi为时域信号的傅里叶变换,有
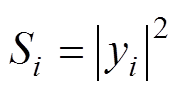 (6)
(6)绘制功率谱熵的熵值曲线如图10~图13所示。
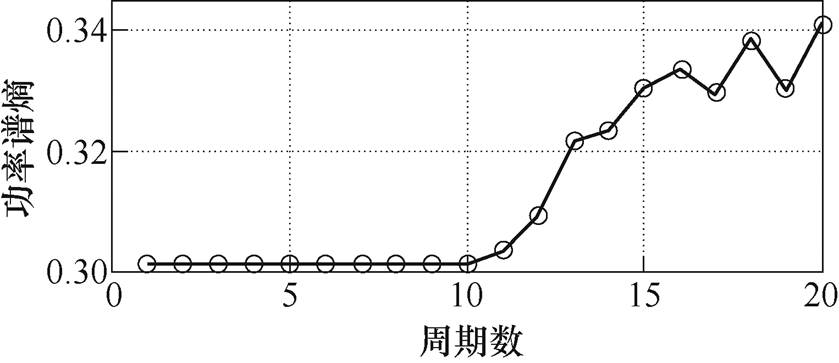
图10 纯阻(57.5W)的功率谱熵值曲线
Fig.10 Power spectrum entropy curve of pure resistance (57.5W)
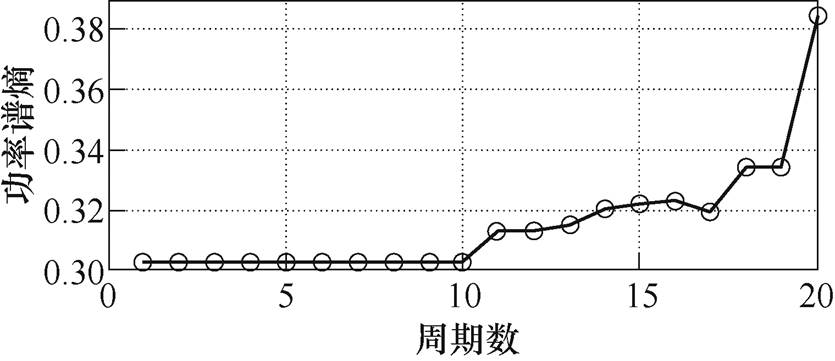
图11 阻感(57.5W+5mH)的功率谱熵值曲线
Fig.11 Power spectrum entropy curve of RL (57.5W+5mH)
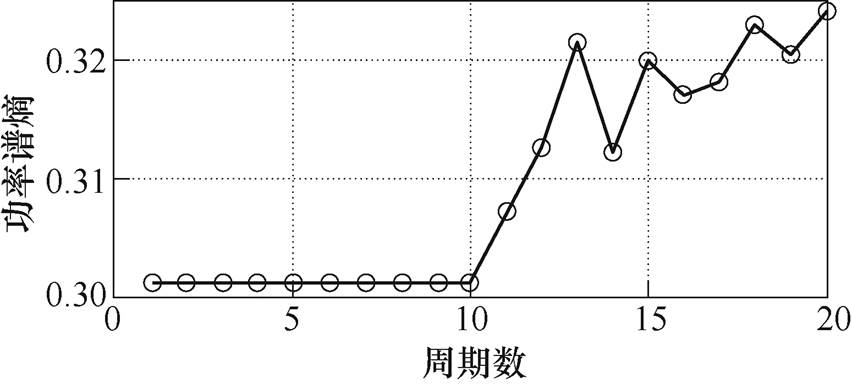
图12 阻容(57.5W+47mF)的功率谱熵值曲线
Fig.12 Power spectrum entropy curve of RC (57.5W+47mF)
分析图10~图13的熵值曲线可知,功率谱熵在电弧故障发生前后有明显变化。在对线性负载和非线性负载的特征分析上,功率谱熵较小波能量熵有更好的表现。
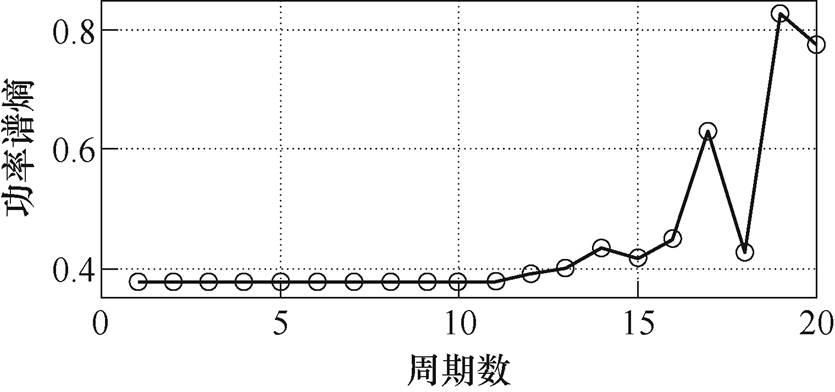
图13 ATRU的功率谱熵值曲线
Fig.13 Power spectrum entropy curve of ATRU
样本熵(SampEn)是基于近似熵(ApEn)的一种用于度量时间序列复杂性的改进方法[16],与近似熵相比,样本熵具有其计算不依赖数据长度和更好的一致性两个优势,即参数的变化对样本熵的影响程度是相同的。样本熵的值越低,序列自我相似性就越高;样本熵的值越大,样本序列就越复杂。根据这一特点,样本熵可在时域方面更直接地反映电弧故障发生前后电流信号样本的序列复杂度的变化。
样本熵的计算步骤如下:
(1)将一个周期内N个采样点分成一组维数为m的向量序列Im(1), Im(2),…, Im(N-m+1)。
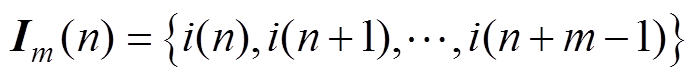 1≤n≤N-m+1(7)
1≤n≤N-m+1(7)(2)定义向量序列Im(n), Im(t)之间的距离为d,有
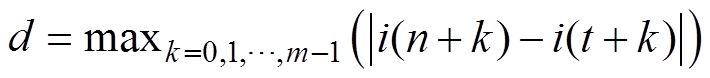 (8)
(8)
(3)对于给定的Im(n),统计Im(n)与Im(t)之间距离小于等于r的t的个数,记为An。
定义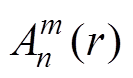 为
为
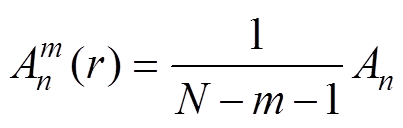 (9)
(9)(4)定义Am(r)为
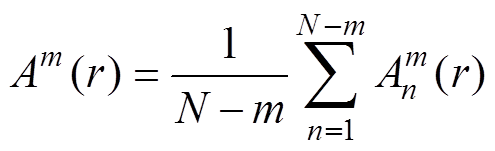 (10)
(10)
(5)令k=m+1,重复步骤(3)和步骤(4)得
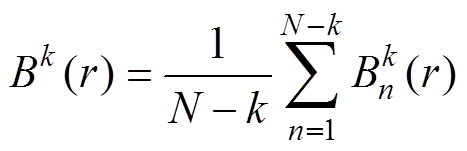 (11)
(11)(6)样本熵定义为
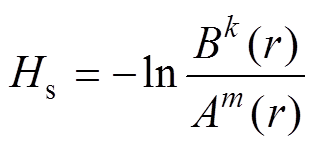 (12)
(12)
同样以每周期的电流信号作为分析信号,绘制出各个试验负载下从正常周期到故障周期共20个周期的电流信号的样本熵的熵值曲线如图14~图17所示。
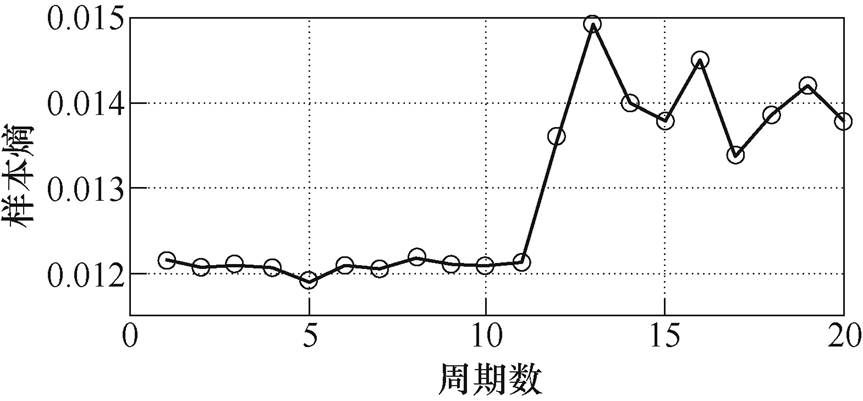
图14 纯阻(57.5W)的样本熵值曲线
Fig.14 Sample entropy curve of pure resistance (57.5W)

图15 阻感(57.5W+5mH)的样本熵值曲线
Fig.15 Sample entropy curve of RL (57.5W+5mH)
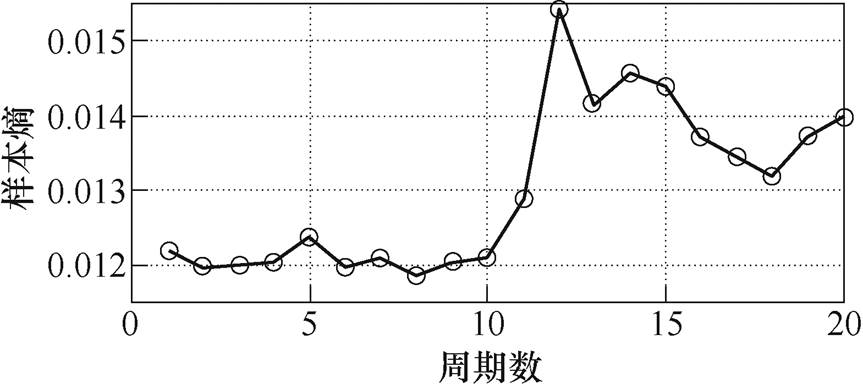
图16 阻容(57.5W+47mF)的样本熵值曲线
Fig.16 Sample entropy curve of RC (57.5W+47mF)

图17 ATRU的样本熵值曲线
Fig.17 Sample entropy curve of ATRU
分析图14~图17可知,在纯阻和阻容负载下的样本熵可较好地反映电弧故障发生前后电流的变化,但对于阻感和非线性负载,存在电弧故障发生后熵值变化较正常周期不明显或变化无规律的问题。
基于以上三种信息熵各自的特点,为结合三种信息熵在电弧故障检测中各自的优势,避免单一熵特征量的不确定性,本文应用三维熵距理论实现三种熵特征量的融合。
2.1~2.3节分别以小波能量熵、功率谱熵、样本熵作为单一特征量对电弧故障发生前后做了差异性分析。结果发现,使用单一特征量时存在电弧故障发生后个别熵值较正常熵值变化不明显或故障发生后延迟几个周期熵值才有明显变化的问题,为了更好地表征从正常周期到电弧故障周期电流的变化,将上述每一种信息熵分别看做一个维度,则这三种信息熵就被看做三个维度,由此组成了一个三维空间,则由原来的单一熵特征量的一维变化变为三种熵特征量共同作用从而产生的三维空间的空间距离变化,避免单一熵特征量在电弧故障发生后变化不明显或延时变化的问题。分别以小波能量熵、功率谱熵、样本熵作为三维空间的x、y、z轴。纯阻负载下的正常周期与电弧故障周期的三维熵点(Hnx, Hpx, Hsx)分布如图18所示。
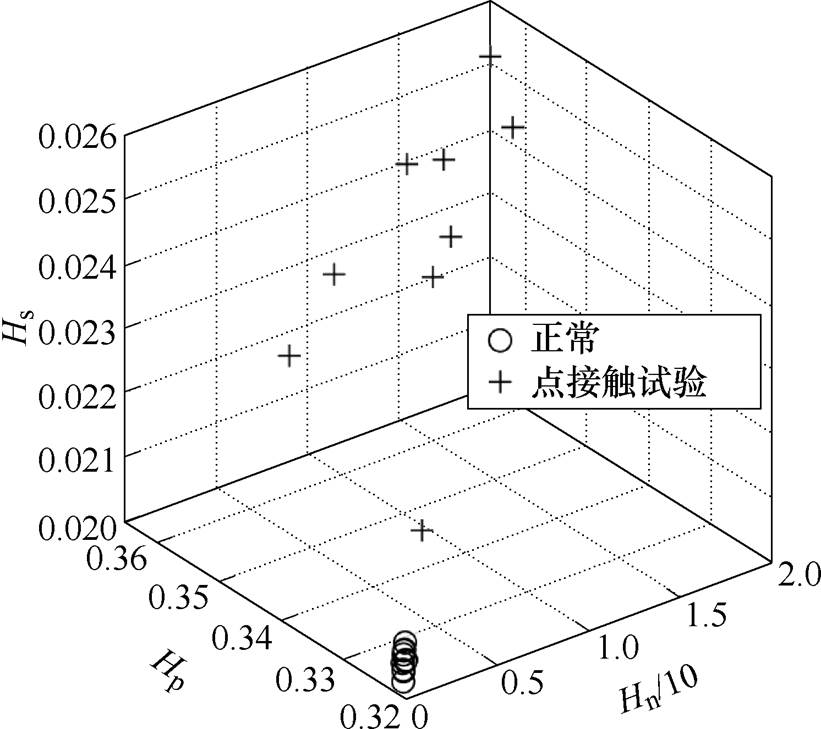
图18 点接触试验正常与故障周期熵点的三维分布
Fig.18 Three-dimensional distribution of entropy points of the normal and fault period of point contact test
当发生点接触电弧故障后,由图18可知,三种信息熵在各自的维度上有不同程度的偏离从而使得正常与点接触电弧故障的三维熵点有了明显不同的空间分布。正常周期与点接触故障周期的熵点之间存在明显的空间距离。
为了消除三种信息熵不同量级的影响,对三种信息熵进行Z-score标准化处理,即预先求出信号样本的三种信息熵的均值和标准差,再取前十个正常周期为一组样本,经Z-score标准化处理,可以得到这组样本的三种熵值(Hn, Hp, Hs),从而唯一确定三维空间中的一点。将该点定义为正常周期的熵值中心。表1中列举了不同试验负载下的熵值中心。
表1 试验负载在三维空间的熵值中心
Tab.1 The entropy center of the test load in three-dimensional space

熵值中心纯阻阻感阻容ATRU 小波能量熵Hn-0.848 9-0.271 5-0.912 30.011 4 功率谱熵Hp-0.910 7-0.434 7-0.897 00.374 8 样本熵Hs-0.809 6-0.641 3-0.880 30.019 5
再将每个周期视为一个样本,同样经Z-score标准化处理,则可以求出对应于每个周期的熵点(Hnx, Hpx, Hsx)。
定义三维空间距离SH为“信息熵距”,简称“熵距”,有
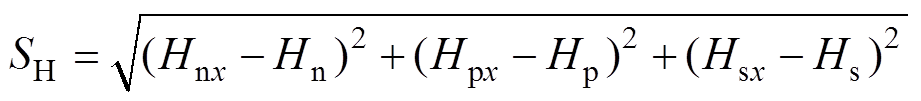 (13)
(13)将每个周期的熵点与对应试验负载的熵值中心求三维空间距离及熵距SH。绘制试验负载从正常到电弧故障的20个周期信号的熵距曲线如图19~图22所示。
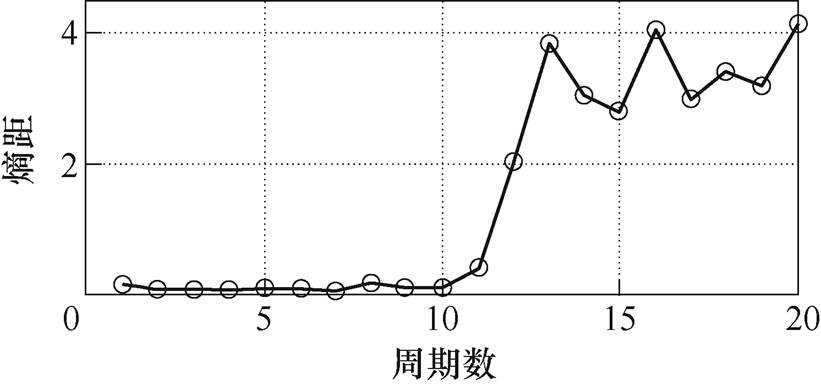
图19 纯阻(57.5W)的熵距曲线
Fig.19 Entropy distance curve of pure resistance (57.5W)
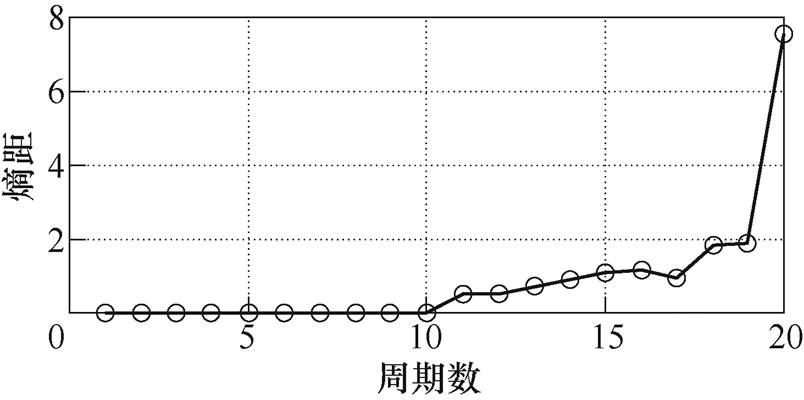
图20 阻感(57.5W+5mH)的熵距曲线
Fig.20 Entropy distance curve of RL (57.5W+5mH)
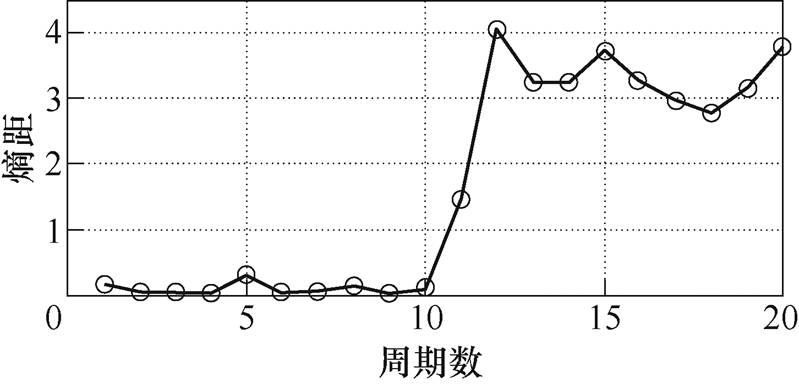
图21 阻容(57.5W+47mF)的熵距曲线
Fig.21 Entropy distance curve of RC (57.5W+47mF)

图22 ATRU的熵距曲线
Fig.22 Entropy distance curve of ATRU
分析图19~图22的熵距曲线可知,在正常周期的三维熵距基本保持不变,当发生电弧故障时,熵距曲线呈上升趋势,且有较大的波动。也就是说,在三维空间中正常周期的熵点与熵值中心的距离很小,可以判断此时的周期为正常周期,当发生电弧故障时,三维空间中故障周期熵点与熵值中心的距离超出一定范围,即电弧故障周期的熵距要比正常周期的熵距大,且距离的波动性较大,可以判断此时的周期与正常周期有较大差异,从而对是否发生电弧故障做出判断。
由以上电流信号的熵特征分析可知,提取小波能量熵、功率谱熵、样本熵作为特征量来描述电弧故障发生前后各特征的变化在不同负载下各有利弊,为此结合信息融合技术引入三维熵距的概念,结果表明,三维熵距很好地结合了三种信息熵在面对不同负载时所表现出的各自的优势,避免了单一熵特征量延时变化或变化不明显等问题,增加了检测的准确性。虽然三维熵距很好地解决了单一熵特征在某些负载上会出现误判的问题,但信息的融合将不可避免地带来信息量增多的问题,虽然熵在解决大数据时有其统计上的优势,但多特征仍然会增加特征的数量。虽然结合了各特征的优势,但另一方面也增加了无用信息量,产生了冗余和多余的噪声,给检测的准确性带来了麻烦。为了结合各特征熵的优势,同时减少对无用信息的处理,本文将利用PCA技术对四种熵特征进行降维处理,保留与原始数据最为接近的部分,除去冗余与噪声,同时利用PCA的两种故障监测指标,给出正常与电弧故障的控制限,更加准确可靠地对电弧故障做出判别。
作为多元统计分析的经典方法,通过主元分析进行故障检测的主要思想是:把正常工作过程所获得的数据,采用空间投影技术,在最大限度地保持原有信息不受损失的情况下,把这些采集的大量相关的过程变量投影到一个低维子空间中,获得能够表征体系内部关系的几个主要成分,也就是PCA主元模型。主元模型不仅包含了系统的主要相关信息,还能降低系统过程数据的维数,从而简化分析过程,提高检测效率[17]。
当建立主元模型后,用该模型计算出系统数据的估算值,然后对比监测系统给出的检测指标,就可以判断此时系统是否处于正常工作状态。
PCA主元模型的故障监测指标有两种: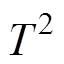 和平方预测误差(Squared Prediction Error, SPE)。
和平方预测误差(Squared Prediction Error, SPE)。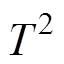 统计量反映了每个主成分在变化趋势和幅值上偏离模型的程度;SPE统计量刻画了输入变量的测量值在残差空间中对主元模型的偏离程度。PCA故障检测技术的一个很大的优点是完全无参数限制。在PCA的计算过程中完全不需要人为地设参数或是根据任何经验模型对计算进行干预,最后的结果只与数据有关。检测的具体流程如图23所示。
统计量反映了每个主成分在变化趋势和幅值上偏离模型的程度;SPE统计量刻画了输入变量的测量值在残差空间中对主元模型的偏离程度。PCA故障检测技术的一个很大的优点是完全无参数限制。在PCA的计算过程中完全不需要人为地设参数或是根据任何经验模型对计算进行干预,最后的结果只与数据有关。检测的具体流程如图23所示。
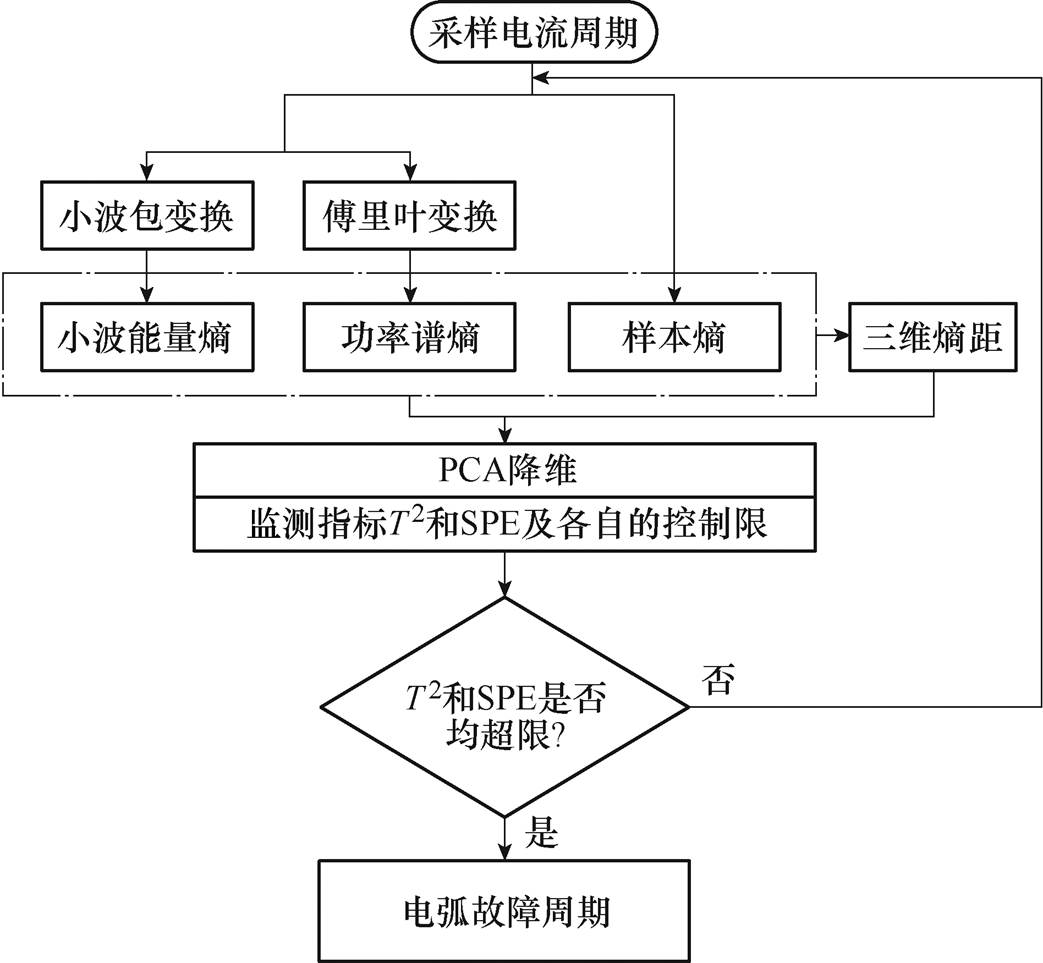
图23 检测流程
Fig.23 Detection flowchart
(1)选择正常状态下的各变量的样本,组成训练样本矩阵,记为Xtrain,有
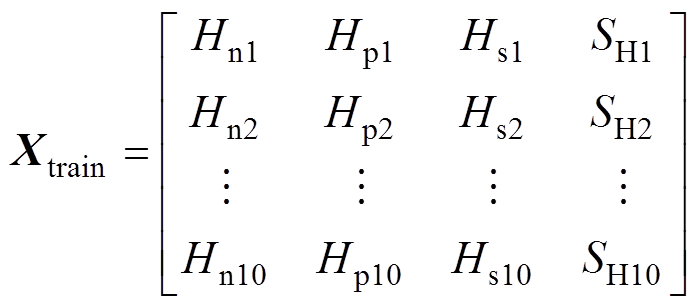 (14)
(14)式中,Xtrain为10×4矩阵,即10个正常周期样本;Hn、Hp、Hs、SH为4个观察变量。
(2)增加故障周期组成检测样本矩阵,记为Xtest。
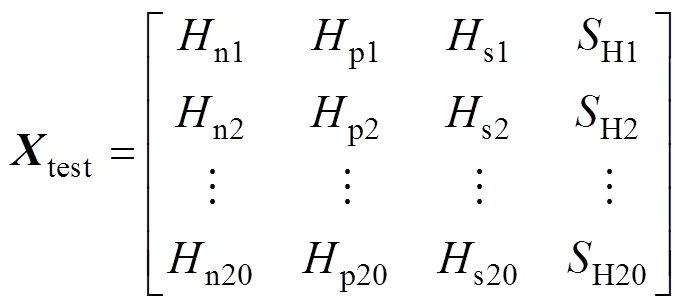 (15)
(15)(3)对Xtrain和Xtest进行中心化和标准化处理得Xstrain和Xstest。
(4)求Xstrain的协方差矩阵并确定主元个数u,得u个特征值和u个特征向量p1,p2,…, pu。
(5)建立PCA主元模型为
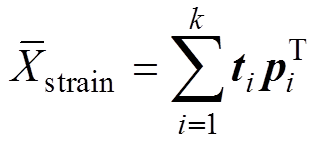 (16)
(16)其中
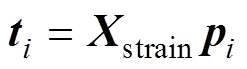 (17)
(17)
式中,ti为第i个主元。
(6)利用Xstest矩阵求得的特征值和特征向量计算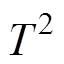 和SPE统计量的控制上限TUCL和QUCL。
和SPE统计量的控制上限TUCL和QUCL。
(7)采集每周期的观察变量矩阵,重复步骤(3)~步骤(6),求出各试验负载的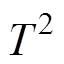 和SPE统计量以及分别控制上限TUCL和QUCL。
和SPE统计量以及分别控制上限TUCL和QUCL。
各试验负载的SPE和其控制上限QUCL的值以及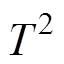 和其控制上限TUCL的值分别见表2和表3。
和其控制上限TUCL的值分别见表2和表3。
表2 试验负载的SPE和QUCL的数值
Tab.2 Test load values of SPE and QUCL
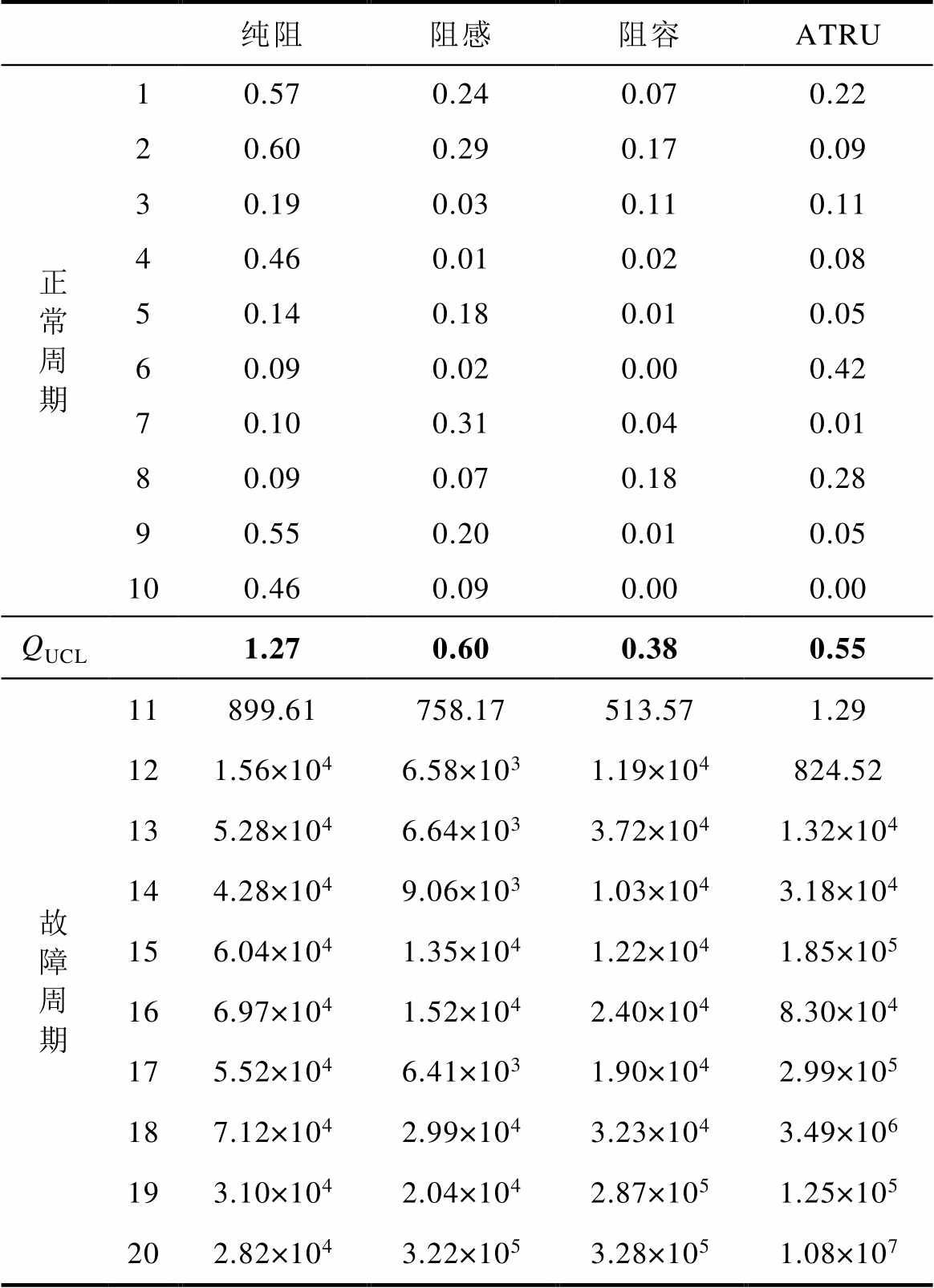
纯阻阻感阻容ATRU 正常周期10.570.240.070.22 20.600.290.170.09 30.190.030.110.11 40.460.010.020.08 50.140.180.010.05 60.090.020.000.42 70.100.310.040.01 80.090.070.180.28 90.550.200.010.05 100.460.090.000.00 QUCL1.270.600.380.55 故障周期11899.61758.17513.571.29 121.56×1046.58×1031.19×104824.52 135.28×1046.64×1033.72×1041.32×104 144.28×1049.06×1031.03×1043.18×104 156.04×1041.35×1041.22×1041.85×105 166.97×1041.52×1042.40×1048.30×104 175.52×1046.41×1031.90×1042.99×105 187.12×1042.99×1043.23×1043.49×106 193.10×1042.04×1042.87×1051.25×105 202.82×1043.22×1053.28×1051.08×107
表3 试验负载的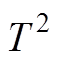 和TUCL的数值
和TUCL的数值
Tab.3 Test load values of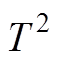 and TUCL
and TUCL
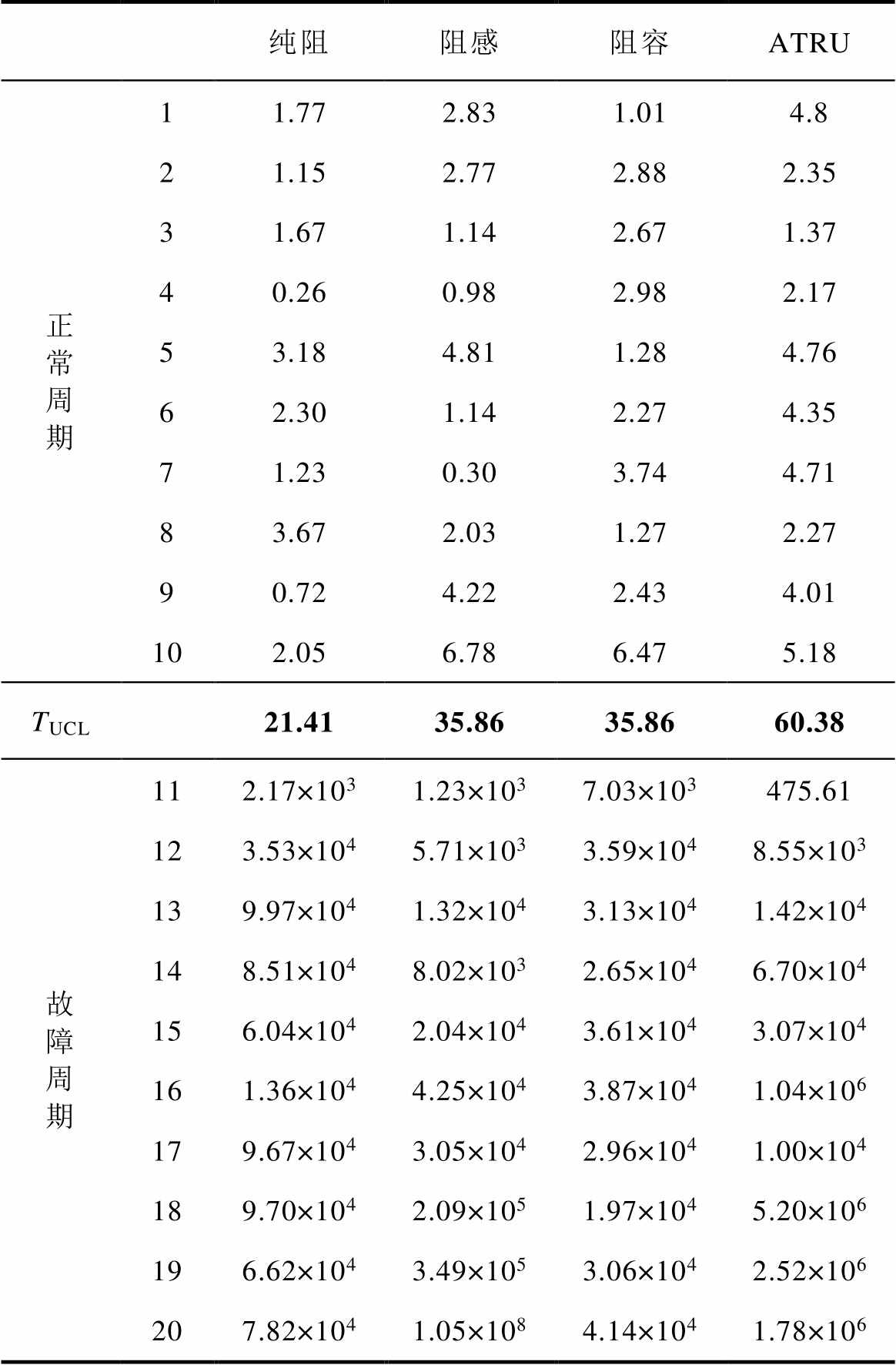
纯阻阻感阻容ATRU 正常周期11.772.831.014.8 21.152.772.882.35 31.671.142.671.37 40.260.982.982.17 53.184.811.284.76 62.301.142.274.35 71.230.303.744.71 83.672.031.272.27 90.724.222.434.01 102.056.786.475.18 TUCL21.4135.8635.8660.38 故障周期112.17×1031.23×1037.03×103475.61 123.53×1045.71×1033.59×1048.55×103 139.97×1041.32×1043.13×1041.42×104 148.51×1048.02×1032.65×1046.70×104 156.04×1042.04×1043.61×1043.07×104 161.36×1044.25×1043.87×1041.04×106 179.67×1043.05×1042.96×1041.00×104 189.70×1042.09×1051.97×1045.20×106 196.62×1043.49×1053.06×1042.52×106 207.82×1041.05×1084.14×1041.78×106
分析表2和表3的计算结果可知,正常周期的SPE值小于控制上限QUCL,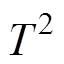 值小于控制上限TUCL,当发生电弧故障后,SPE值和
值小于控制上限TUCL,当发生电弧故障后,SPE值和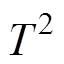 值将分别超过控制上限QUCL和TUCL,且超过的数量级远远大于正常周期的值。由此可知,当发生电弧故障后,故障样本数据在分解的维度方向上方差变化较大,远远偏离正常周期的样本值。SPE值和
值将分别超过控制上限QUCL和TUCL,且超过的数量级远远大于正常周期的值。由此可知,当发生电弧故障后,故障样本数据在分解的维度方向上方差变化较大,远远偏离正常周期的样本值。SPE值和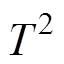 值均超过各自的控制限时可认为此时发生了电弧故障。
值均超过各自的控制限时可认为此时发生了电弧故障。
第2节利用小波能量熵、功率谱熵、样本熵作为分析点接触电弧故障的特征量,很好地表征了正常周期与故障周期的差异,并结合三维熵距和PCA的检测技术对点接触电弧故障做出了较为准确的检测。本节将利用三种信息熵组成的三维熵空间对不同类型的电弧故障进行分类研究。
依据美标UL 1699和SAE AS5692[18]在纯阻、阻感、阻容负载下分别进行点接触电弧试验、截断试验、三相串话干扰试验。试验电源、采样频率均与之前一致。分别以小波能量熵、功率谱熵、样本熵作为三维空间的x、y、z轴。绘制不同试验下的故障周期的三维熵点(Hnx, Hpx, Hsx)。此处由于不需要考虑三种信息熵的结合,为了更加准确直观地体现三种信息熵的信息,不做标准化处理。绘制正常周期以及三种电弧试验故障周期的三维空间熵点,如图24~图26所示。
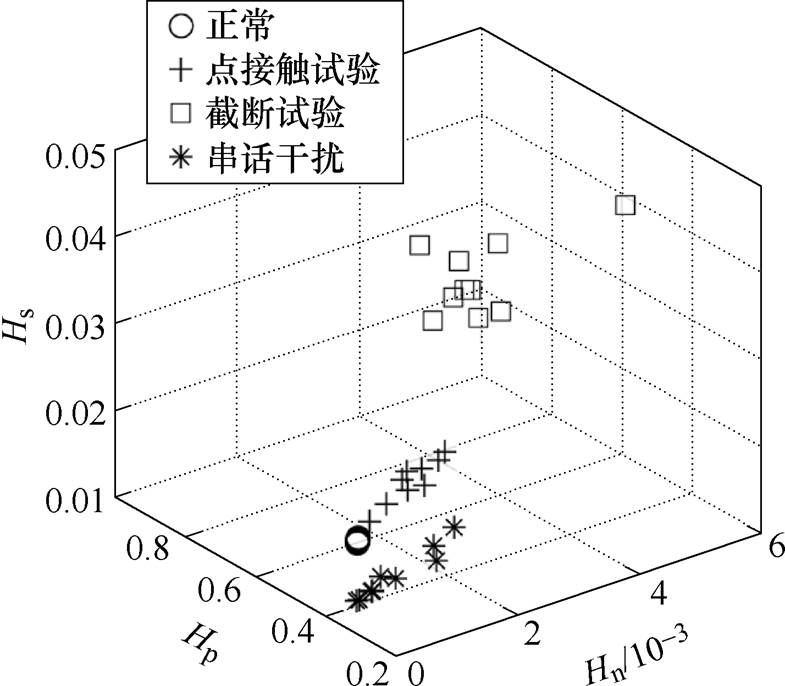
图24 三种电弧试验的故障周期的三维分布(纯阻57.5W)
Fig.24 Three-dimensional distribution of entropy points of fault period of three kinds of tests (57.5W)
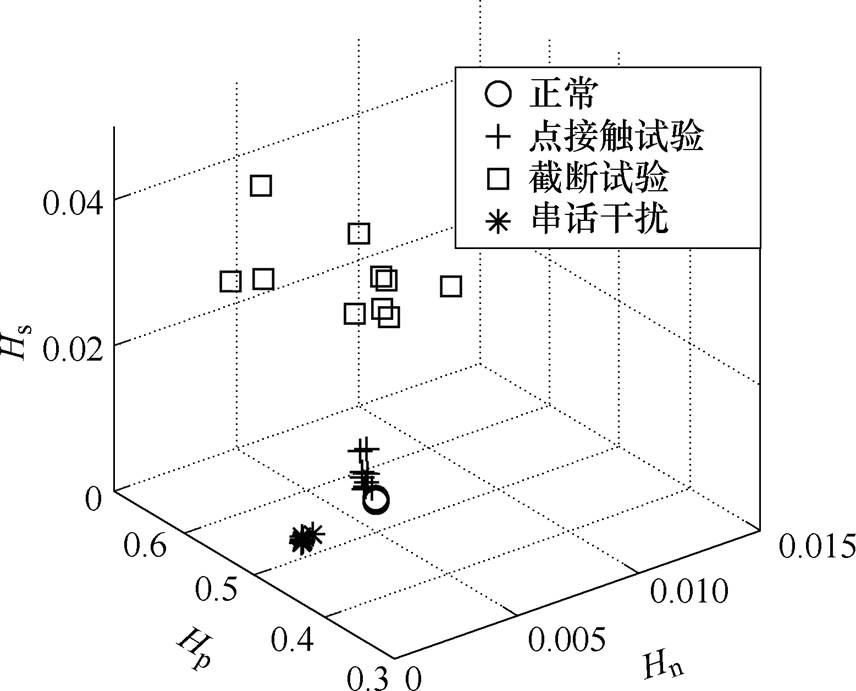
图25 三种电弧试验的故障周期的三维分布(阻感57.5W+5mH)
Fig.25 Three-dimensional distribution of entropy points of fault period of three kinds of tests (57.5W+5mH)
分析图24~图26可以看出,由于截断试验在电弧故障发生时会短路负载,导致电弧电流增加,电弧故障电流的高频噪声更加明显,所以其三维熵点较其他试验更加远离正常周期的三维熵点。而串话干扰试验是在模拟当航空交流三相电路中有一相发生电弧故障时对其他相的影响,意在区别于其他类型的电弧故障,防止误判。串话干扰试验的故障周期的三维熵点接近于正常周期且与其他电弧故障类型有明显不同的空间分布。

图26 三种电弧试验的故障周期的三维分布(阻容57.5W+47mF)
Fig.26 Three-dimensional distribution of entropy points of fault period of three kinds of arc test (57.5W+47mF)
通过三维熵空间对各个电弧故障试验的表述,在负载不发生变化的情况下可以依据各个电弧故障试验的三维熵空间分布与正常周期的三维熵空间分布的相对位置对不同的电弧故障类型进行空间的划分,进而对几种典型的电弧故障进行分类。在检测电弧故障的同时,也能识别电弧故障的类型,从而有效地检测和应对航空电弧故障。
1)小波能量熵、功率谱熵、样本熵从各自的角度描绘了电弧故障发生前后电流信号的变化,可以作为电弧故障检测中的特征量。
2)利用三维熵距可以实现三种信息熵的结合,避免了单一特征量的偶然性。
3)PCA的电弧故障检测技术解决了信息融合带来的噪声和冗余的问题,并给出用以判断是否发生电弧故障的统计量SPE和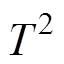 及其各自的控制限,有效地实现了电弧故障的检测。
及其各自的控制限,有效地实现了电弧故障的检测。
4)三维熵空间对不同的电弧故障类型有很好的空间划分,在负载不发生变化的情况下可以较为直观地对电弧故障类型进行故障分类。
5)本文提到的电弧故障检测技术结合了电弧电流时频域的特点,弥补了单一特征的不确定性,不需人工设置阈值,监测指标随监测周期自动更新,可以较为准确地实现航空电弧故障的检测。
参考文献
[1] Zeng Ke, Xing Lidong, Zhang Yaojia, et al. Characteri- stics analysis of AC arc fault in time and frequency domain[C]//Prognostics and System Health Management Conference, Harbin, China, 2017: 1-5.
[2] Jiang Jun, Wen Zhe, Zhao Mingxin, et al. Series arc detection and complex load recognition based on principal component analysis and support vector machine[J]. IEEE Access, 2019, 7: 47221-47229.
[3] 王尧, 韦强强, 葛磊蛟, 等. 基于电弧电流高频分量的串联交流电弧故障检测方法[J]. 电力自动化设备, 2017, 37(7): 191-197.
Wang Yao, Wei Qiangqiang, Ge Leijiao, et al. Series AC arc fault detection based on high-frequency com- ponents of arc current[J]. Electric Power Automation Equipment, 2017, 37(7): 191-197.
[4] 刘晓明, 赵洋, 曹云东, 等. 基于小波变换的交流系统串联电弧故障诊断[J]. 电工技术学报, 2014, 29(1): 10-17.
Liu Xiaoming, Zhao Yang, Cao Yundong, et al. Series arc fault diagnosis based on wavelet transform in AC system[J]. Transactions of China Electro- technical Society, 2014, 29(1): 10-17.
[5] 卢其威, 王涛, 李宗睿, 等. 基于小波变换和奇异值分解的串联电弧故障检测方法[J]. 电工技术学报, 2017, 32(17): 208-217.
Lu Qiwei, Wang Tao, Li Zongrui, et al. Detection method of series arcing fault based on wavelet transform and singular value decomposition[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(17): 208-217.
[6] 张瑶佳, 王莉, 尹振东, 等. 基于HHT的航空直流串行电弧特征提取方法[J]. 航空学报, 2019, 40(1): 254-266.
Zhang Yaojia, Wang Li, Yin Zhendong, et al. Research on characteristics extraction method of aviation DC serial arc fault based on HHT[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(1): 254- 266.
[7] Yu Qiongfang, Huang Gaolu, Yang Yi. Low voltage AC series arc fault detection method based on parallel deep convolutional neural network[C]// Proceedings of the 2nd International Symposium on Application of Materials Science and Energy Materials, Shanghai, China, 2018: 1391-1399.
[8] Liu Yuwei, Wu C J, Wang Y C. Detection of serial arc fault on low-voltage indoor power lines by using radial basis function neural network[J]. International Journal of Electrical Power & Energy Systems, 2016, 83: 149-157.
[9] 马少华, 鲍洁秋, 蔡志远, 等. 基于信息维数和零休时间的电弧故障识别方法[J]. 中国电机工程学报, 2016, 36(9): 2572-2579.
Ma Shaohua, Bao Jieqiu, Cai Zhiyuan, et al. A novel arc fault identification method based on information dimension and current zero[J]. Proceedings of the CSEE, 2016, 36(9): 2572-2579.
[10] 杨凯, 张认成, 杨建红, 等. 基于分形维数和支持向量机的串联电弧故障诊断方法[J]. 电工技术学报, 2016, 31(2): 70-77.
Yang Kai, Zhang Rencheng, Yang Jianhong, et al. Series arc fault diagnostic method based on fractal dimension and support vector machine[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(2): 70-77.
[11] 郭凤仪, 邓勇, 王智勇, 等. 基于灰度-梯度共生矩阵的串联故障电弧特征[J]. 电工技术学报, 2018, 33(1): 71-81.
Guo Fengyi, Deng Yong, Wang Zhiyong, et al. Arc fault characteristics based on gray level-gradient co- occurrence matrix[J]. Transactions of China Electro- technical Society, 2018, 33(1): 71-81.
[12] Hien D V, Calderon E, Schweitzer P, et al. Multi criteria series arc fault detection based on supervised feature selection[J]. International Journal of Electrical Power and Energy Systems, 2019, 113: 23-34.
[13] 崔芮华, 曹欢. 基于相空间重构的航空电弧故障识别方法[J]. 电工技术学报, 2020, 35(增刊1): 243- 250.
Cui Ruihua, Cao Huan. An arc fault identification method in aircraft based on phase space recon- struction[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 243-250.
[14] UL 1699-2006. Standard for arc-fault circuit- interrupters[S]. USA: Underwriters Laboratories, 2006.
[15] 谢平, 陈矛, 祝刚. 基于功率谱熵距的航空发动机转子振动故障诊断方法研究[J]. 电子测量技术, 2018, 41(21): 99-102.
Xie Ping, Chen Mao, Zhu Gang. Research on diagnosis of vibration faults for aero-engine based on distance of power spectrum entropy[J]. Electronic Measure- ment Technology, 2018, 41(21): 99-102.
[16] 徐赛, 金炜东. 一种基于样本熵的雷达辐射源信号分选[J]. 电子世界, 2018, 555(21): 10-12.
Xu Sai, Jin Weidong. A kind of radar radiation source signal sorting based on sample entropy[J]. Electro- nics World, 2018, 555(21): 10-12.
[17] 张芷瑜. 基于多元统计分析的故障检测在化工过程中的应用[D]. 辽宁: 辽宁石油化工大学, 2019.
[18] SAE AS 5692-2009. Arc fault circuit breaker (AFCB), aircraft, trip-free single phase and three phase 115V AC, 400Hz-constant frequency[S]. USA: Society of Automotive Engineer, 2009.
Arc Fault Detection and Classification Based on Three-Dimensional Entropy Distance and Entropy Space in Aviation Power System
Abstract In view of the limitations of common time-frequency domain analysis methods in aviation arc fault detection and to avoid the contingency of single feature, this paper put forward the method of using three dimensional entropy to achieve the feature fusion of three kinds of information entropy. PCA fault detection technology was used to realize dimensionality reduction of the feature matrix for reducing the noise and redundancy of feature fusion. The characteristics of wavelet energy entropy, power spectrum entropy, sample entropy and the three dimensional entropy distance of three kinds of information entropy were analyzed respectively before and after arc faults. The monitoring statistics 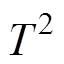 , SPE and their respective control limits under each test load were acquired by the PCA fault detection technology. The detection of aviation AC arc faults was realized by comparing the values of
, SPE and their respective control limits under each test load were acquired by the PCA fault detection technology. The detection of aviation AC arc faults was realized by comparing the values of 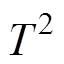 and SPE before and after arc faults with their respective control limits. The analysis results show that this method combines the advantages of each characteristic quantity and does not need to set the threshold manually, which can identify the occurrence of arc faults reliably and accurately. Finally, by the three-dimensional entropy space, the classification methods of several typical arc fault types are given. The proposed method provides a reference for realizing the arc fault detection and identifying the type of arc fault.
and SPE before and after arc faults with their respective control limits. The analysis results show that this method combines the advantages of each characteristic quantity and does not need to set the threshold manually, which can identify the occurrence of arc faults reliably and accurately. Finally, by the three-dimensional entropy space, the classification methods of several typical arc fault types are given. The proposed method provides a reference for realizing the arc fault detection and identifying the type of arc fault.
keywords:Aviation arc fault, three-dimensional entropy distance, feature fusion, PCA detection technology, entropy space, fault classification
中图分类号:TM501
DOI: 10.19595/j.cnki.1000-6753.tces.191717
河北省自然科学基金资助项目(E2016202106)。
收稿日期2019-12-06
改稿日期 2020-02-10
崔芮华 女,1962年生,博士后,教授,研究方向为电弧电接触。E-mail: 710667045@qq.com
李 泽 男,1996年生,硕士研究生,研究方向为电工装备可靠性理论及应用。E-mail: 1226147543@qq.com(通信作者)
(编辑 崔文静)