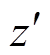为回击瞬时发展高度，
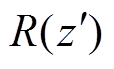为回击前沿高度处的电流微元
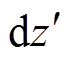与观测点之间的距离，Hup(t)为观测到的上行回击前沿高度，Hdown(t)为观测到的下行回击前沿高度。摘要 传统回击模型认为回击从地面始发往云层发展，最新针对闪电连接过程的观测事实表明，闪电的先导连接过程发生在地面以上高度，先导连接后闪电连接高度处会产生上行回击电流和下行回击电流，并沿通道分别向云层和地面发展。该文提出考虑闪电连接高度的回击发展模型，计及在连接高度处的回击电流双向传输模式，利用该模型计算分析距闪电通道不同距离（50km、5km、50m）的地面电场。结果发现，地面电场波形受回击电流波前陡度的影响，下行回击的存在可能导致电场强度波形在上升阶段出现尖锐的初始尖峰。用电场初始尖峰过冲百分比来描述电场尖峰过冲程度，进一步分析连接高度、回击电流波前陡度和下行回击速度对电场初始尖峰过冲程度的影响，发现随着闪电连接高度的增加，电场初始尖峰过冲增大，持续时间增加；回击电流波前陡度增大，电场初始尖峰过冲增大；下行回击速度增大，电场初始尖峰过冲增大，但持续时间缩短。10m内较低闪电连接高度下，波前陡度为20～60kA/ms的电流在下行回击速度大范围变化下，电场强度波形中无明显初始尖峰。相比传统回击发展模型，考虑闪电连接高度回击发展模型的地面电场计算结果与观测事实更吻合，揭示了闪电连接高度对地面电场初始尖峰形成的影响机制。
关键词：雷电流 闪电连接高度 电场初始尖峰 传输线模型 电流波前陡度 回击速度
雷电回击模型在研究闪电电磁场与电气系统或通信线路的耦合情况、决定雷电激发的感应电压以及雷电定位等方面发挥了重要作用。传统的传输线回击发展模型，如M. A. Uman等提出的回击电流发展过程中不衰减的传输线（Transmission-Line, TL）模型[1]、C. A. Nucci等提出的回击电流在空间呈指数衰减的传输线（Modified Transmission-Line with Exponential current decay, MTLE）模型[2]和V. A. Rakov等提出的回击电流在空间呈线性衰减的传输线（Modified Transmission-Line with Linear current decay, MTLL）模型[3]，均假定回击从地面始发沿通道向上发展，未考虑闪电连接高度及连接高度处的回击双向传输问题。
闪电的下行先导发展到离地面一定高度时，在地面诱发上行先导，下行先导和上行先导在空中存在连接过程，闪电连接点距离地面的高度称为连接高度。最新关于地闪回击雷电起始过程的观测结果表明，当下行先导与上行先导在连接高度处相遇时，发生强烈的回击放电过程，通道中先导连接高度处会产生上行回击电流和下行回击电流，沿着已经电离的先导通道分别向云层和地面发展[4-6]。根据Wang Daohong等、N. Tsukamoto等、V. A. Rakov等和J. D. Hill等对人工触发闪电和自然雷电中连接过程的研究，可知典型继后回击的连接高度范围在10～30m之间，电流峰值大的回击连接高度更高[4-9]。此外，闪电连接高度与闪电击距密切相关，上行连接先导从地面始发时，将下行先导距离地面的高度定义为雷击地面的击距。因此，回击电流峰值越大，闪电击距越大[10-12]。
使用闪电回击模型计算地表电磁场，与实测电磁场结果对比可反演雷电放电参数，并进一步估算回击通道电流的时空衰变现象[13-14]，对研究闪电电磁场与电气系统的耦合效应[15-19]、雷电激发的感应电压[20-24]等具有重要意义。值得注意的是，闪电回击电场实测资料中，常在波形初始上升阶段呈现数微秒的缓前沿和快变化[8-9, 25]，随后出现尖锐的初始尖峰。Lin Yuntao等在距离回击通道50km处[26]、 J. C. Willett等在20km处[27]以及M. A. Haddad等在数十千米至数百千米的电场波形中[28]均观察到了初始尖峰。J. C. Willett等和C. Weidman等在距 离通道5.15km、J. Howard等在百余米处以及C. Leteinturier等在50m处的电场波形中也发现了该初始尖峰[27-31]。已有的同步测量闪电通道底部电流均未发现存在相似的初始尖峰。针对这一差异，J. C. Willett等和C. Weidman等都推测过闪电回击可能发生在地面上方一定高度的连接点处[27, 29]，但对于电场初始尖峰的具体物理形成机制，目前尚不清楚。
雷电定位系统依据测量的电场峰值可将雷电的回击进行分类并确定各种回击极性和峰值电流[32]。回击通道数千米之外的电场波形中，初始尖峰峰值往往是电场波形最大峰值。因此，对电场初始尖峰特征及成因的研究，对闪电探测和定位系统有十分重要的参考价值。
本文提出了考虑闪电连接高度的回击发展模型，计及在连接高度处的回击电流双向传输模式，利用两种不同的通道底部电流分别模拟首次回击和继后回击电流，分析了不同观测距离时上行回击和下行回击的地面电场。开展不同闪电连接高度对地面电场波形影响的研究，研究了不同连接高度时回击电流波前陡度和下行回击速度对电场初始尖峰的影响规律，揭示了闪电连接高度对地面电场初始尖峰形成的影响机制。
本文提出的考虑闪电连接高度处的回击电流双向传输模式及其引发电场的计算模型如图1所示。图1中，总长度为Htot的回击通道垂直于水平地面，r为水平观测距离，P为地面电场观测点，hri为闪电连接高度，vu为上行回击电流速度，vd为下行回击电流速度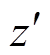，为回击瞬时发展高度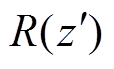，为回击前沿高度处的电流微元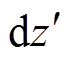与观测点之间的距离，Hup(t)为观测到的上行回击前沿高度，Hdown(t)为观测到的下行回击前沿高度。
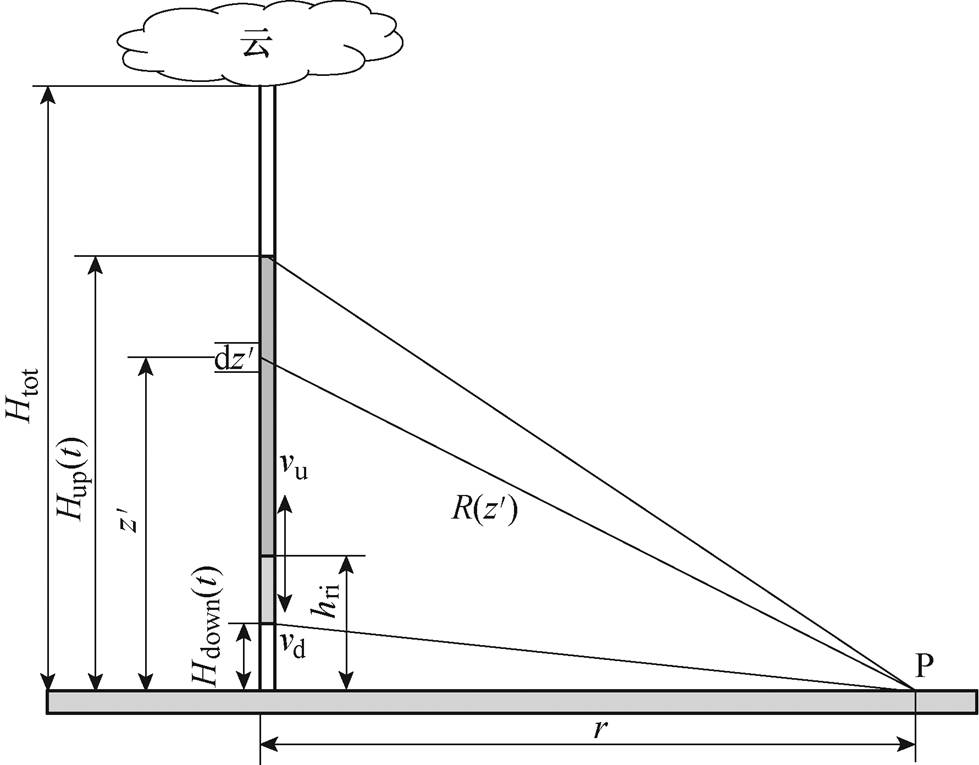
图1 考虑闪电连接高度处的回击电流双向传输模型
Fig.1 Geometry incorporating bidirectional propagation of the return stroke at the junction height
在柱面坐标系下，具有时空衰变特性的回击通道电流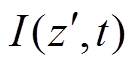
，在距离回击通道水平观测距离为r处的地面P点产生的垂直电场强度Ez为
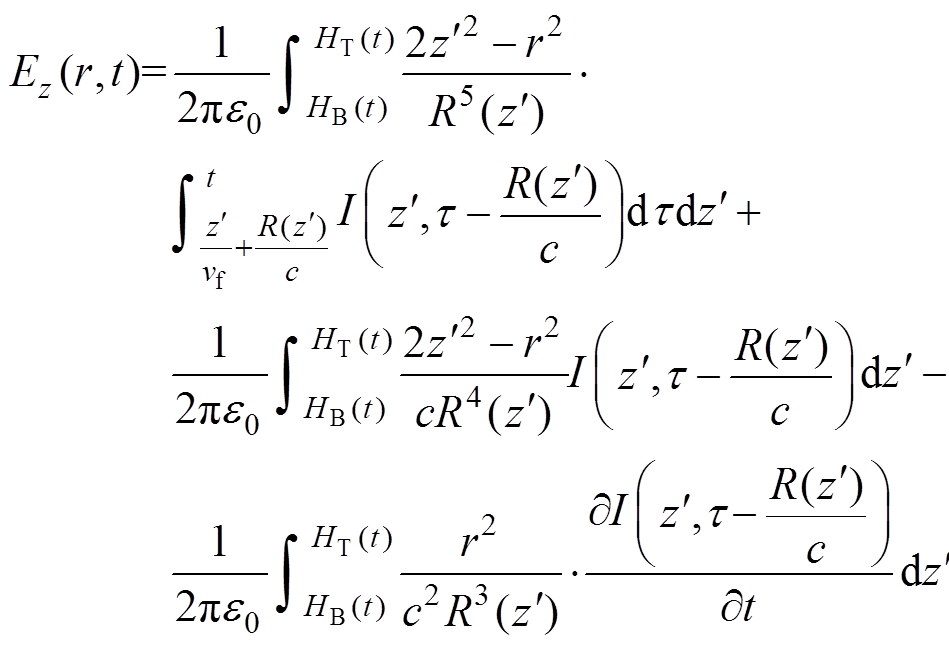（1）式中，e0为真空介电常数；vf为回击发展速度；c为光速；HB(t)、HT(t)分别为t时刻通道底部和顶部的高度。式（1）右侧的时域回击垂直电场依次为静电场分量、感应场分量和辐射场分量。
从P点观测到的上行回击前沿的高度为Hup(t)，根据
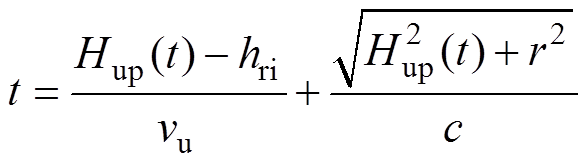（2）求解得Hup(t)为
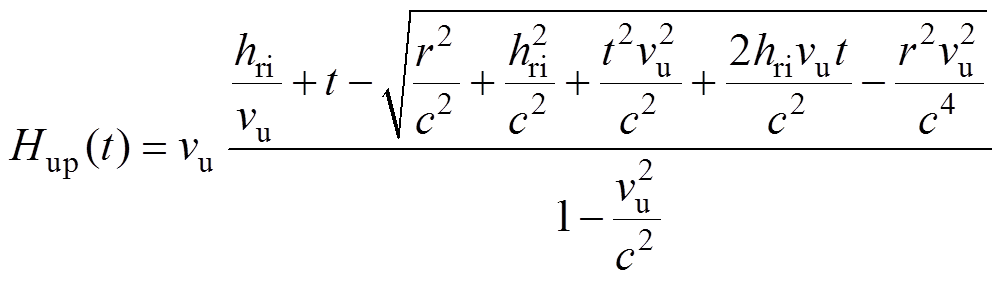（3）
上行回击通道的底部高度HB(t)=hri，顶部高度HT(t)=Hup(t)。上行回击电流沿通道hri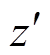＜＜Htot的电流分布为
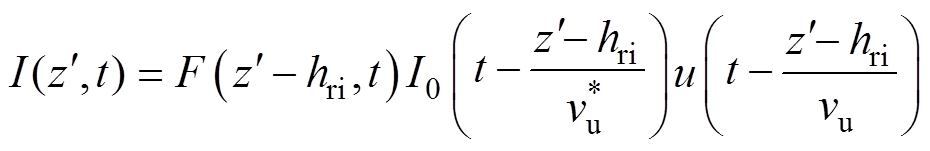（4）式中，F为电流衰减因子；I0为连接点的通道电流；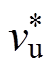
为上行回击电流波速度；
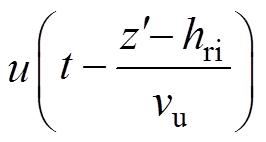为Heaviside函数，也称单位阶跃函数，t≥(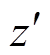-hri)/vu时为1，否则为0。
从P点观测到的下行回击前沿高度为Hdown(t)，根据
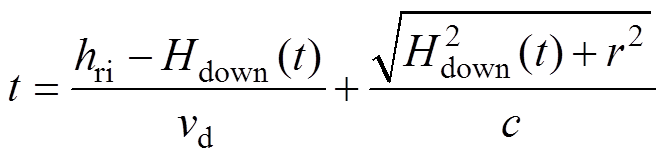（5）求解得Hdown(t)为
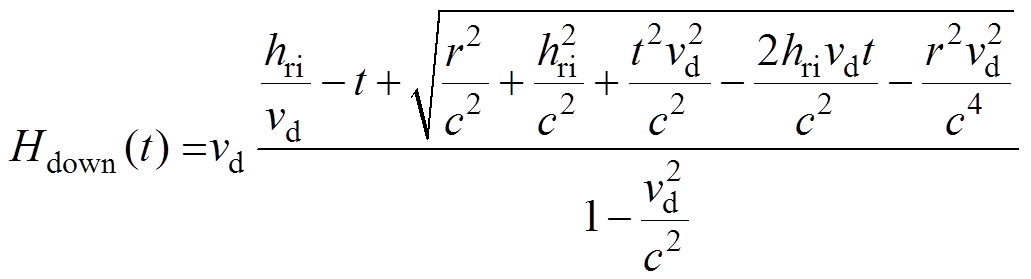（6）
下行回击通道的顶部高度HT(t)=hri，底部高度HB(t)=Hdown(t)u(hri-Hdown(t))。下行回击电流沿通道0＜＜hri的电流分布为
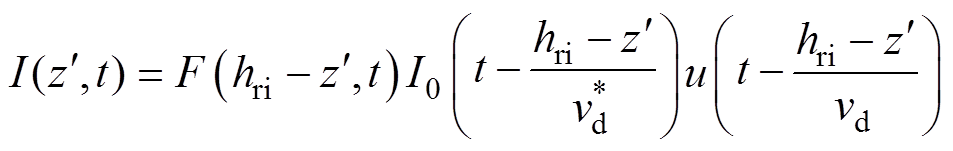（7）式中，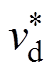
为下行回击电流波发展速度；u在t≥(hri-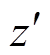)/vd时为1，否则为0。
常用的传输线（TL、MTLL、MTLE）模型的电流衰减因子F、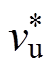、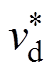表达式见表1。传输线模型中回击电流波发展速度与回击前沿速度相等，即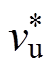=vu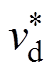，=vd。表1中，Htot为回击通道总长度，l 为MTLE模型的衰减因子。
表1 不同传输线模型F、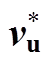
和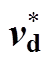
Tab.1 F,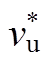 
, and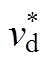 
for different transmission line models
模型上行回击下行回击 F(-hri)F(hri-) TL1vu1vd MTLL1-(-hri)/Htotvu1-(hri-)/Htotvd MTLEexp[-(-hri)/l]vuexp[-(hri-)/l]vd
值得注意的是，电流波沿通道无衰减发展的TL模型是最简单的传输线模型，不论观测距离远近，该模型都能够相对较好地模拟闪电回击前几微秒的电场强度波形特征[27, 33]。本文闪电连接高度处的上行、下行回击均采用TL模型进行计算，后文计算结果仅呈现初始数微秒的地面电场波形。
采用单Heidler函数模拟雷电流，其具备t =0时刻电流及其变化率为0，以及电流峰值、电流变化率和转移电荷量基本相互独立地由函数中各项参数控制等优点，但不能展现电流波形起始部分的缓前沿（尤其是首次回击）。为克服以上缺陷，本文采用多重Heidler函数模拟连接点通道回击电流。
考虑了两种多重Heidler函数表示的连接点通道电流，分别对首次回击和继后回击进行模拟，可体现电流波形起始的缓前沿部分和之后的快变化特征，所采用的多重Heidler函数表达式为
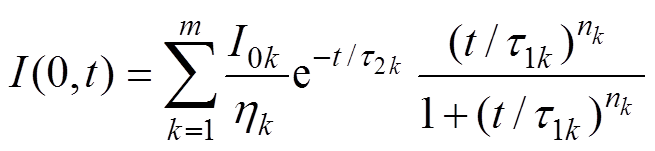（8）
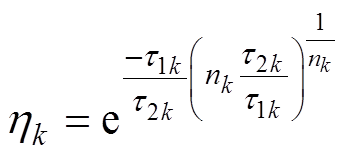（9）
式中，I0k为控制电流幅值；nk为控制波形起始部分陡度；t1k为波前时间常数；t2k为衰减时间常数；hk为幅值修正系数。
多重Heidler函数的参数见表2，是A. De Conti等和W. R. Gamerota等在大量实测闪电电流特性上总结得到的典型回击电流[34-35]，对应生成的电流波形如图2所示。首次回击电流峰值为31kA，最大波前陡度为25kA/ms，10%～90%上升时间为5.2ms。继后回击电流峰值为11kA，最大波前陡度为100kA/ms，10%～90%上升时间为0.6ms。由图2a可知，所取首次回击电流波形具有十分明显的缓前沿，继后回击的缓前沿在幅值上比首次回击小，持续时间比首次回击短。
表2 多重Heidler函数计算连接点通道电流的参数
Tab.2 Parameters of the multiple Heidler functions used to represent the channel current at the junction height
kI0k/kAnkt1k/mst2k/ms 首次回击12.821.2100 24.833100 32.954.825 44.17660 516.7366.644 6112100600 继后回击17.5571.115 2521.2500
图2 首次回击及继后回击连接点通道电流及电流陡度波形
Fig.2 Channel current and current derivative for first and subsequent return strokesat the junction height
回击的发展速度很快，一般为光速的1/3～2/3[14, 36]，下行回击发展速度通常比上行回击速度 小[4-5]。使用图2电流研究不同观测距离r（r =50km, 5km, 50m）时地面电场及各分量波形特征，上行回击速度为2×108m/s，下行回击速度为1×108m/s，连接点高度为20m。
2.1.1 观测距离r =50km
观测距离r =50km时，首次回击和继后回击引发的地面垂直电场及各分量的波形如图3所示。图3中，下行回击引发的电场主要是辐射场分量，波形表现为一尖峰，峰值时刻记为tdmax；上行回击电流引发电场也主要是辐射场分量，OA段为上行回击辐射场波形的缓前沿部分，AB段为快变化部分，BC段为快变化结束后部分。
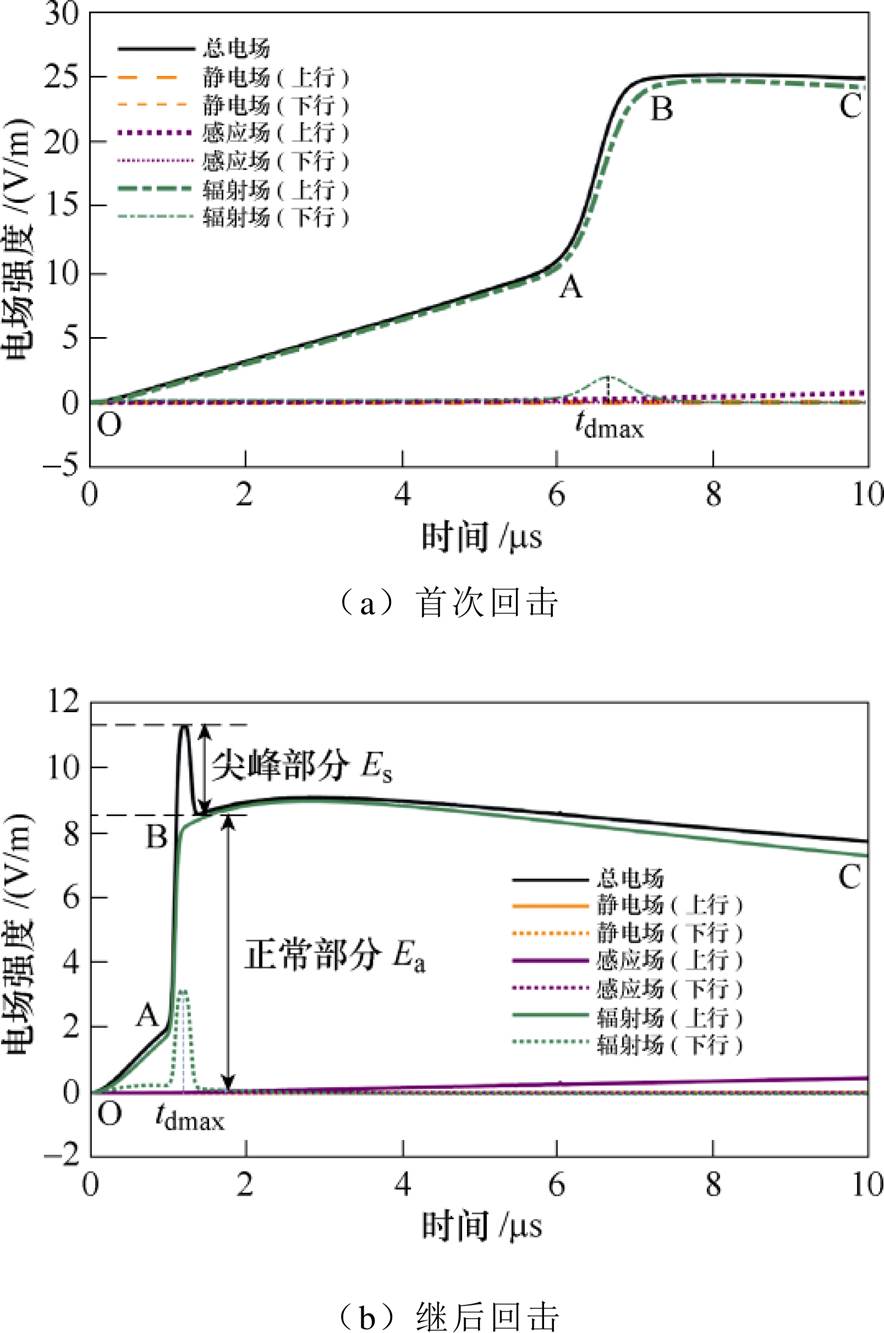
图3 r =50km垂直电场（前10ms）
Fig.3 Calculated vertical electric fields at a distance r =50km within 10ms
图3b继后回击引发电场的下行辐射场分量具有较大峰值和陡度，叠加在上行回击辐射场分量快变化结束后的部分，即图3b中tdmax对应BC段，因此，继后回击引发电场波形的上升沿部分存在尖锐的初始尖峰。图3a首次回击下行辐射场分量的尖峰幅度和陡度很小，叠加在上行回击辐射场分量的快变化部分，即图3a中tdmax对应AB段，因此引发电场的波形中无明显尖峰。
用电场初始尖峰过冲百分比来描述电场波形中尖峰部分的过冲程度，电场初始尖峰过冲百分比为Es/Ea×100%（见图3b），Es为电场波形中尖峰部分的幅度，Ea为尖峰跌落后电场正常部分波形幅值。图3b中，继后回击引发电场的初始尖峰过冲百分比为32.1%。
图3首次回击和继后回击引发的电场波形主要为辐射场分量，静电场分量和感应场分量相对微弱，对电场波形无影响。电场波形缓前沿部分具有和相应电流波形一样的特征，电场缓前沿的持续时间和峰值时间与对应电流大致相同。50km时电场波形缓前沿主要来自上行回击的辐射场分量，几乎不含下行回击的电场分量。
已有距离闪电通道数十千米远的地面电场波形中出现上述类似初始尖峰的研究，如Lin Yuntao等测量了50km处负极性地闪回击的电场波形，发现首次回击和继后回击对应的电场波形均存在初始尖峰[26]。J. C. Willett等在距离闪电通道20km处测量不同闪电继后回击引发的电场波形，也发现了此类尖峰，如图4所示[27]。M. A. Haddad等在距离负极性自然雷电回击通道10～330km范围内，测量了265次首次回击和349次继后回击引发的电场，在电场波形中大多数能观察到此类初始尖峰[28]。
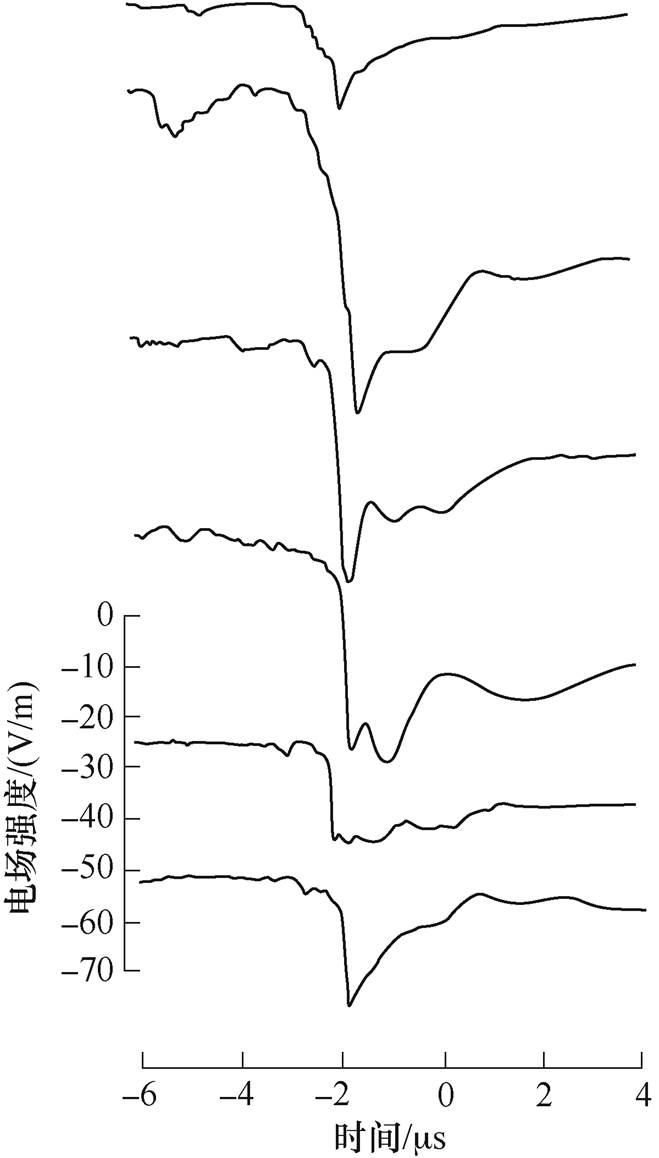
图4 J. C. Willett等测量的20km处电场波形
Fig.4 Electric fields measured by J. C. Willett et al at a distance r =20km
2.1.2 观测距离r =5km
观测距离r =5km时由首次回击和继后回击引发的地面垂直电场及各分量的波形如图5所示。相比图3，图5地面电场波形在快变化后存在缓慢上升，该变化来自上行回击的静电场、感应场分量的增加。电流的缓前沿部分也可在电场波形中再现，该缓前沿主要由上行回击的辐射场分量组成，包含少量感应场分量。与上行回击引发电场的波形相比，下行回击对缓前沿的影响基本可以忽略。观测距离为5km时，地面电场依然主要为辐射场分量，但此时感应场分量作用开始增加。与图3a一样，图5a首次回击引发的电场中无明显初始尖峰。根据图5b，继后回击引发的电场波形因下行回击辐射场分量导致波形出现明显初始尖峰，持续时间约200ns，过冲百分比为30.9%，而由图2可知，相应的继后回击电流波形不存在此类尖峰。
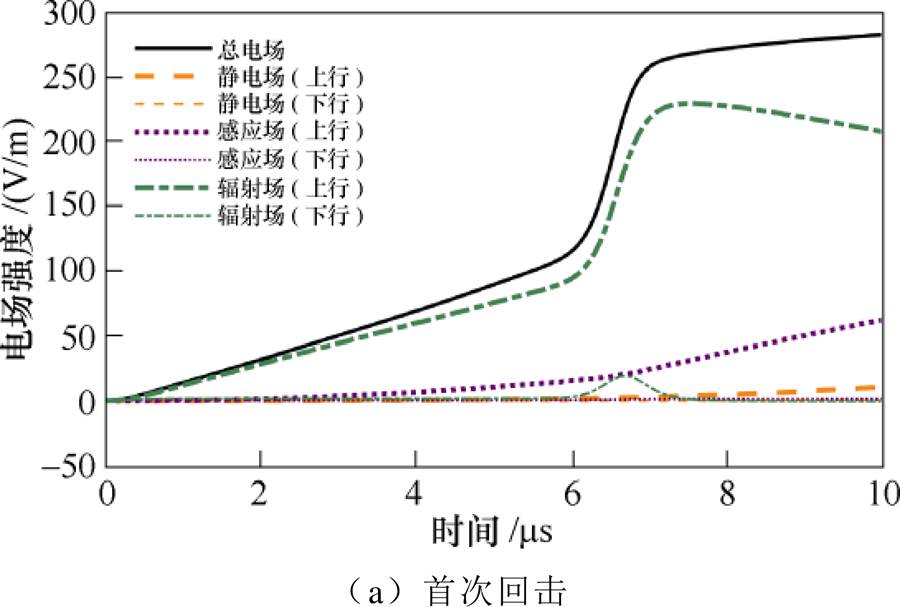
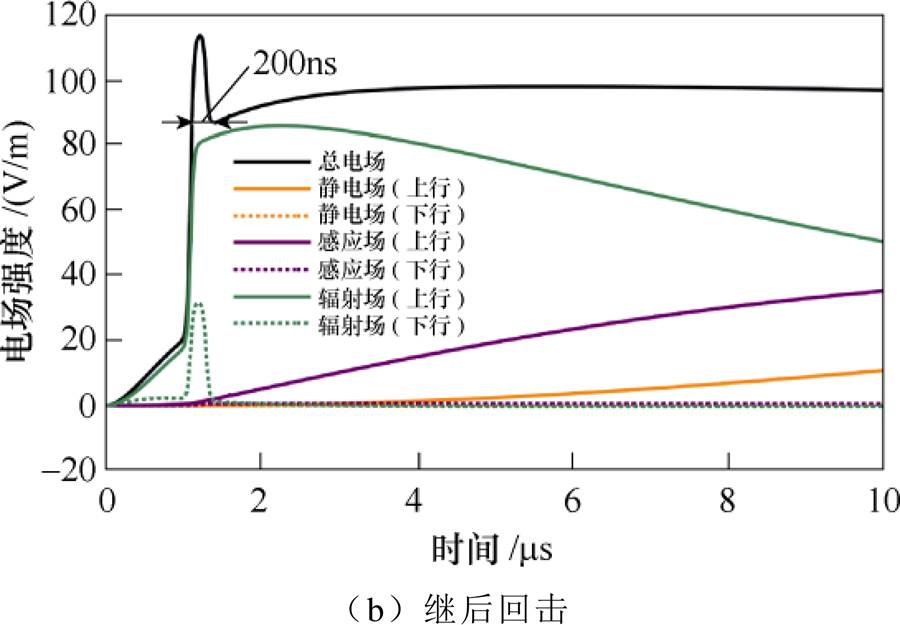
图5 r =5km处垂直电场（前10ms）
Fig.5 Calculated vertical electric fields at a distance r =5km within 10ms
J. C. Willett等和C. Weidman等测量了人工触发闪电距离通道5.15km的电场和对应的通道底部电流，发现在电场波形中可观察到初始尖峰，对应的同步通道底部电流波形中却无法观测到相似的初始尖峰[27, 29]。图6为C. Weidman等测量的5.15km电场波形及对应通道底部电流[29]。J. C. Willett等测量的电场初始尖峰持续时间约200～500ns[27]，图5b继后回击引发的电场波形初始尖峰持续时间约200ns，与J. C. Willett等测量结果接近。J. C. Willett等和C. Weidman等都推测过雷电回击可能发生在地面上方一定高度的连接点处，下行与上行先导在连接点相遇，两条回击电流波以特定的幅值分别向两个方向发展，导致了初始尖峰的存在[27, 29]，这一推测在本文考虑闪电连接高度计算的地面电场波形中得到了验证。
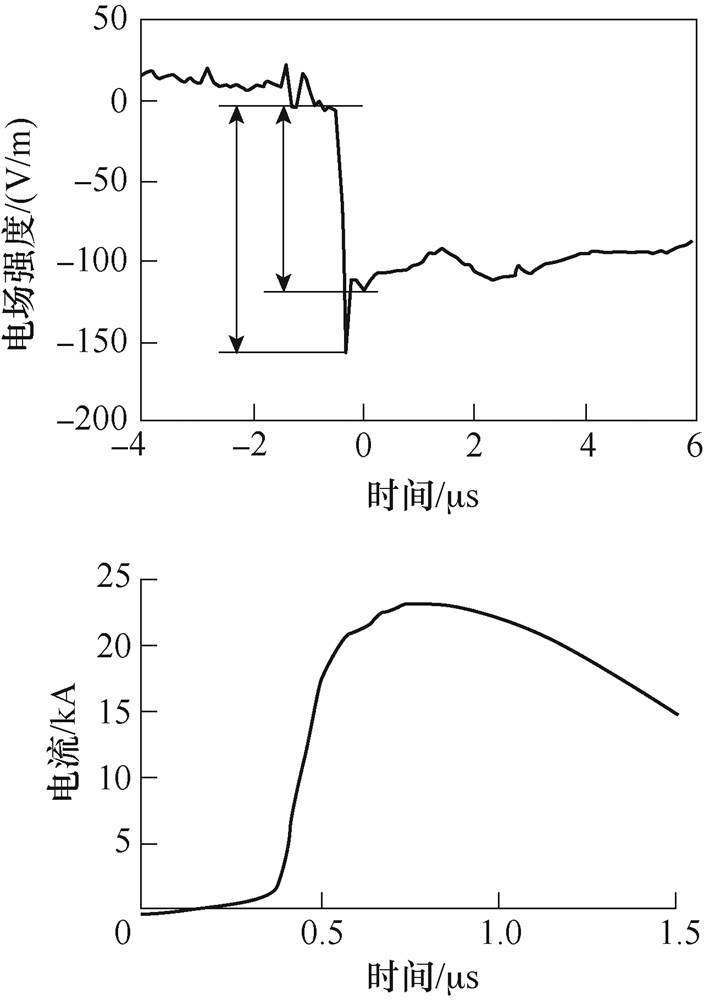
图6 C. Weidman等测量的5.15km处电场和通道电流
Fig.6 Electric fields at 5.15km and channel current measured by C. Weidman et al
2.1.3 观测距离r =50m
首次回击和继后回击电流在观测距离r =50m时引发的地面垂直电场及各分量波形如图7所示，图中上行回击和下行回击引发的静电场分量极性相反，数微秒后，静电场分量远大于感应场和辐射场分量，电场主要由上、下行回击的静电场分量组成。继后回击引发电场的初始尖峰主要来自上、下行回击的辐射场分量，也包含静电场和感应场分量（见图7b）。继后回击的电场波形存在明显倾角，电场初始尖峰呈现肩状结构波形。
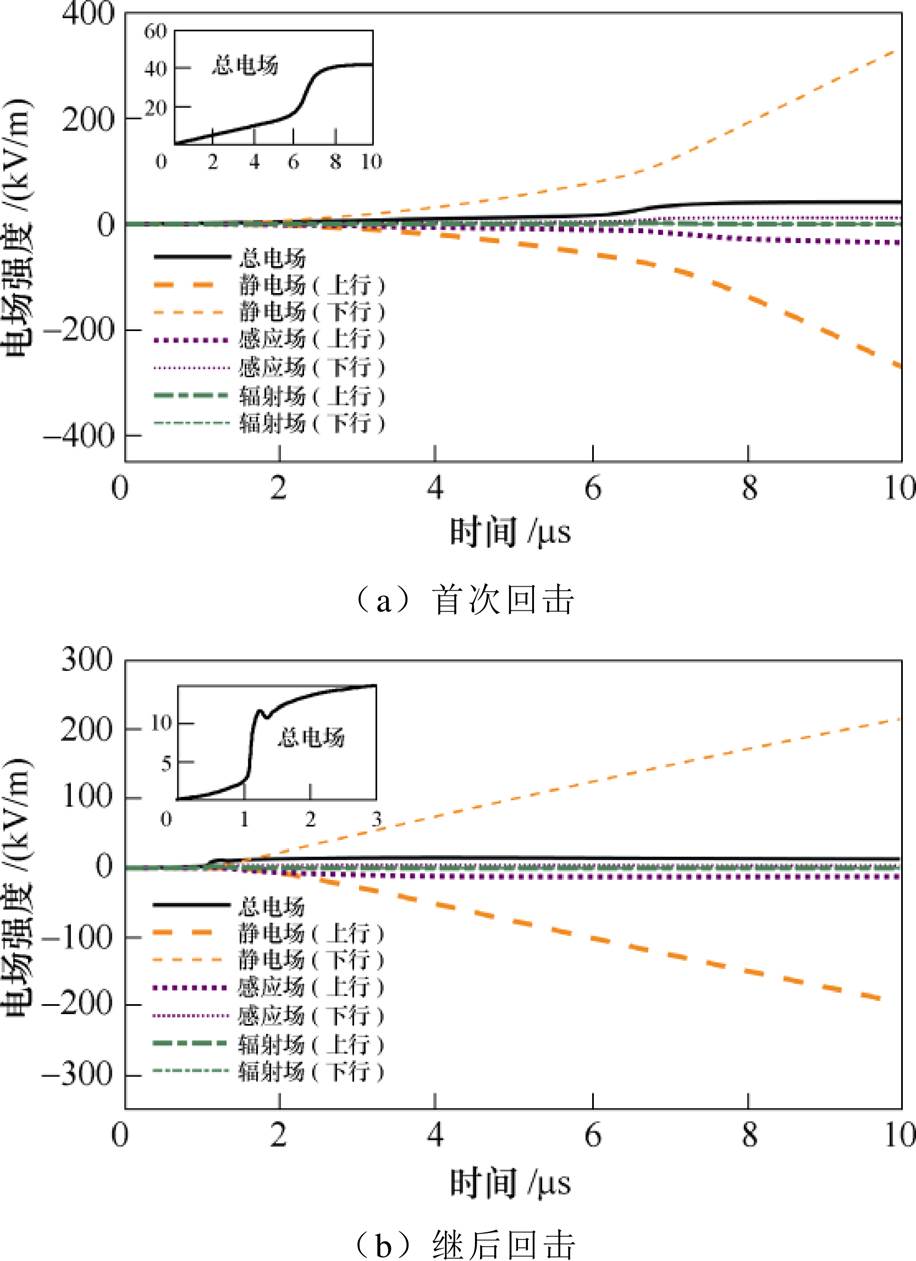
图7 r =50m处垂直电场（前10ms）
Fig.7 Calculated vertical electric fields at a distance r =50m within 10ms
电场极性与下行回击的静电场及感应场极性相同，表明观测距离为50m时下行回击（波速为1×108m/s）比上行回击（波速为2×108m/s）对总场影响更大。若下行回击和上行回击的速度均取2×108m/s，下行回击贡献的电场所占总场的比重会更大。因此，当观测距离为50m时，更接近地面的下行回击电流的影响占据主导地位。
C. Leteinturier等测量人工触发闪电50m处电场时，发现了初始尖峰的存在，但对应电流无初始尖峰，如图8所示[31]，与本文计算结果一致。此外，J. Howard等报道的一次负极性自然地闪回击，在距离闪电通道195m处的电场波形中，上升阶段也存在肩状结构尖峰[30]。
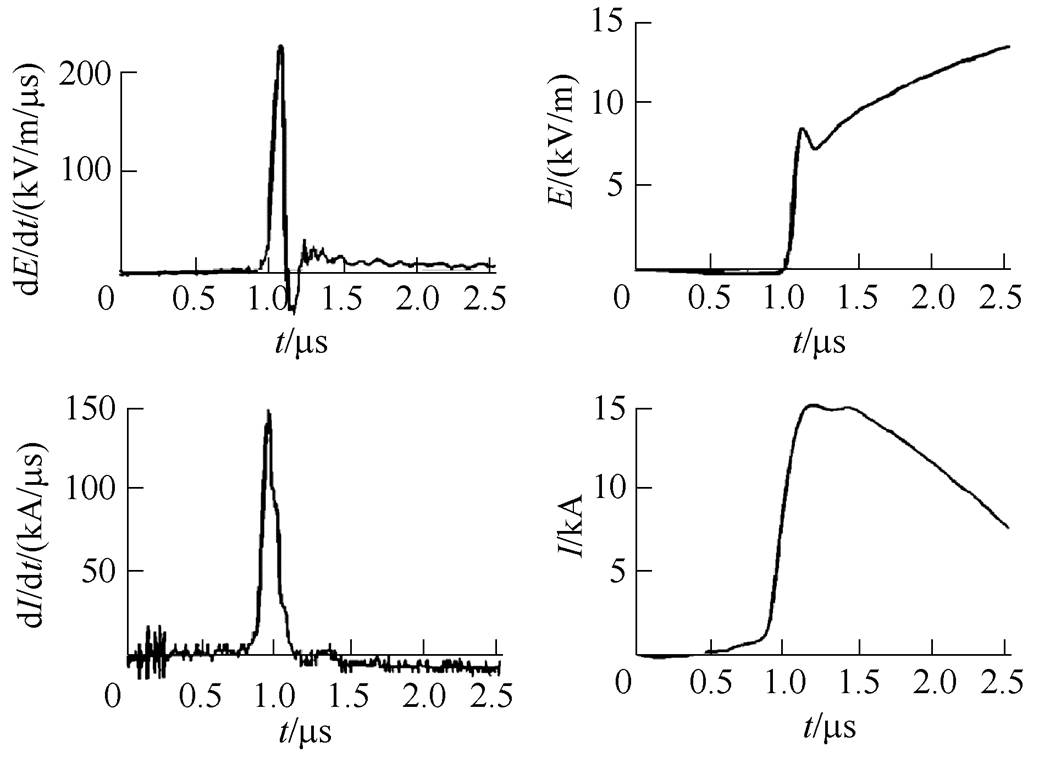
图8 C. Leteinturier等测量的50m处电场及通道电流
Fig.8 Electric field at 50m and channel current measured by C. Leteinturier et al
在上述三种不同观测距离下，连接高度为20m时，下行回击的存在均导致继后回击引发的电场波形出现尖锐的初始尖峰。根据Wang Daohong等对闪电连接过程的观测，闪电连接高度约为数十米[4-6]。图9为上行、下行回击速度分别为2×108m/s和1×108m/s时，使用图2电流在观测距离r=50km时计算的地面电场，连接高度hri考虑了10m、20m和50m。作为对比，回击从地面沿着垂直通道向上发展，波速为2×108m/s的传统TL模型计算结果也一并包含在图9中。
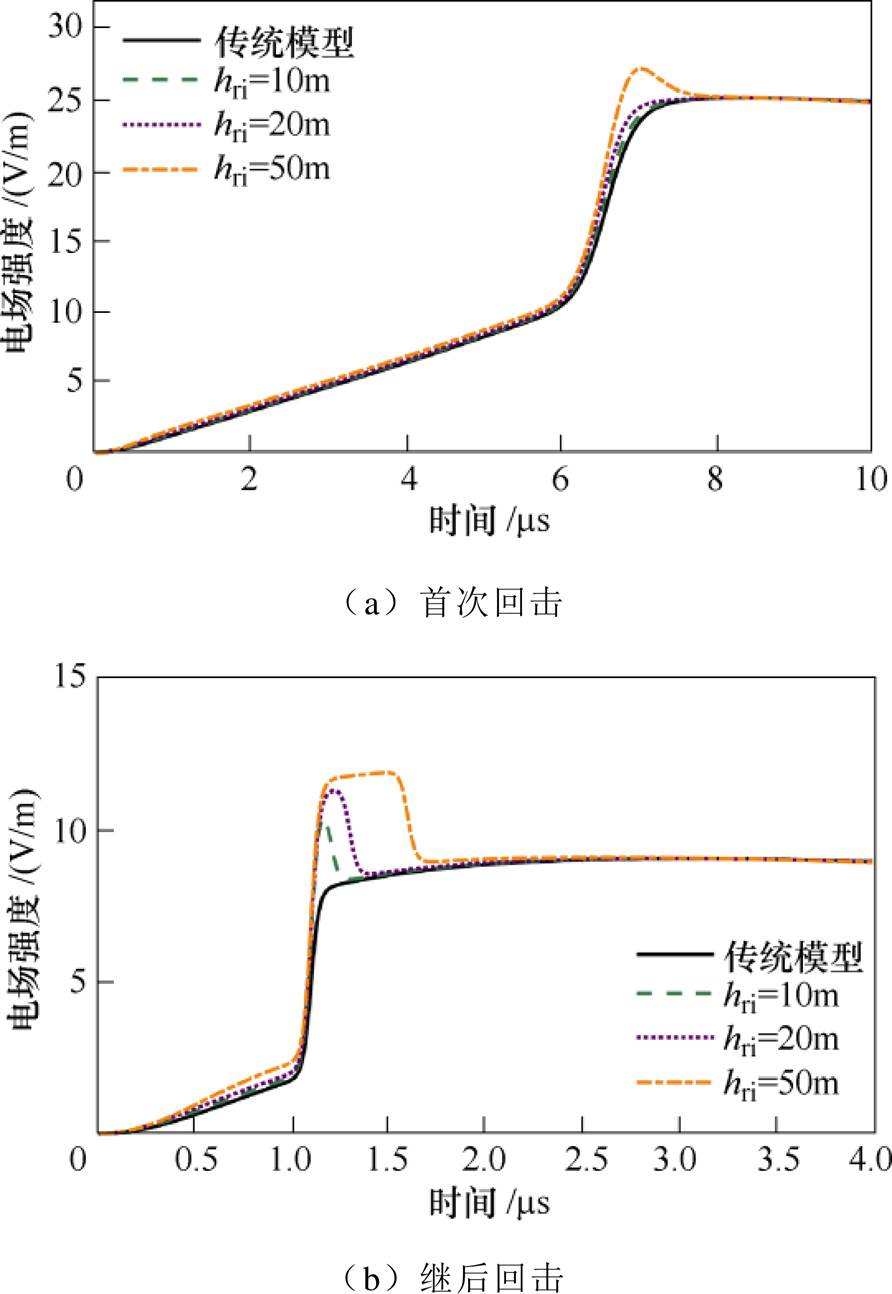
图9 不同连接高度下r=50km处垂直电场
Fig.9 Calculated vertical electric fields for various junction heights at a distance r=50km
根据图9a，首次回击引发的电场波形在连接高度为10m和20m处无初始尖峰，连接高度增加至50m时，下行回击引发电场的尖峰对应时刻tdmax增大，峰值也增大，叠加在上行回击引发电场波形的BC部分（见图3a），因此，电场波形出现过冲百分比为7.5%的初始尖峰。图9b中闪电连接高度越高，初始尖峰的幅值越大，持续时间也越长。
值得注意的是，图9中，基于回击从地面始发的传统TL模型计算的电场波形无法观察到初始尖峰。引言和2.1节中已经提及，该尖峰存在于闪电回击电场的测量波形。考虑闪电连接高度后，利用模型计算的电场结果可以展现实际测量的电场初始尖峰。因此，相比传统TL模型，考虑闪电连接高度的回击发展模型计算地面电场的结果与观测事实更吻合，针对回击电场的计算，有必要考虑闪电连接高度的存在。
电流陡度是闪电回击电流的重要参数，常通过测量通道底部电流时间变化率di/dt，利用di/dt对时间积分来获取通道底部电流波形[9, 29, 31]。C. Leteinturier等测量了人工触发闪电的通道底部电流，得到电流最大波前陡度绝大多数在22～186kA/ms之间[31]。M.A. Uman统计了负极性继后回击最大波前陡度典型值，发现90%的继后回击电流最大波前陡度在12～120kA/ms之间[32]。
在式（8）中，改变陡度控制因子n生成不同波前陡度的继后回击电流，分别取n1=10, 22, 34, 45, 57，相应回击电流最大波前陡度分别为20kA/ms、40kA/ms、60kA/ms、80kA/ms和100kA/ms。图10为这些不同最大波前陡度电流下，观测距离为50km的地面电场波形，上行、下行回击速度分别为2×108m/s和1×108m/s，考虑了10m、20m和50m三种连接高度的影响。表3统计了图10中不同电流波前陡度下电场初始尖峰过冲百分比。
根据图10a，若连接高度为10m，电流最大波前陡度为20kA/ms时，电场波形中无初始尖峰；最大波前陡度40kA/ms时，电场初始尖峰不明显，其尖峰过冲为1.7%；电流最大波前陡度为60～100kA/ms时，电场波形出现明显初始尖峰，对应的电场初始尖峰过冲均超过10%，不同电流波前陡度下电场初始尖峰过冲统计见表3。根据图10b，连接高度为20m，电流最大波前陡度为40kA/ms或更大时，电场波形出现明显的初始尖峰，电流波前陡度越大，相应电场初始尖峰幅度越大，尖峰过冲越大。
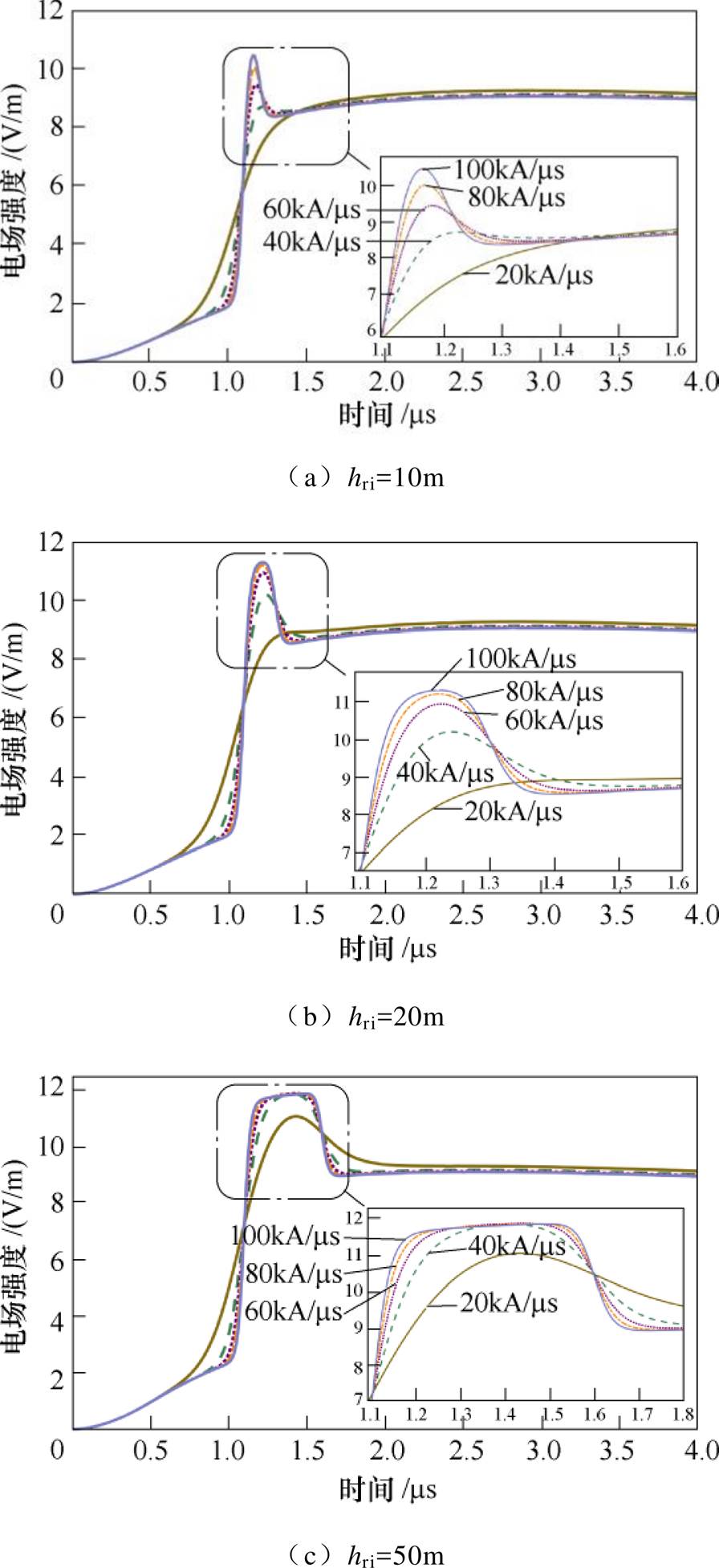
图10 不同电流波前陡度下r =50km处垂直电场（前4ms）
Fig.10 Calculated vertical electric fields for current with various wavefront steepnesses at 50km within 4ms
表3 不同电流波前陡度下电场初始尖峰过冲百分比统计
Tab.3 Sharp initial peak overshoot of electric field generated by current with various wavefront steepnesses
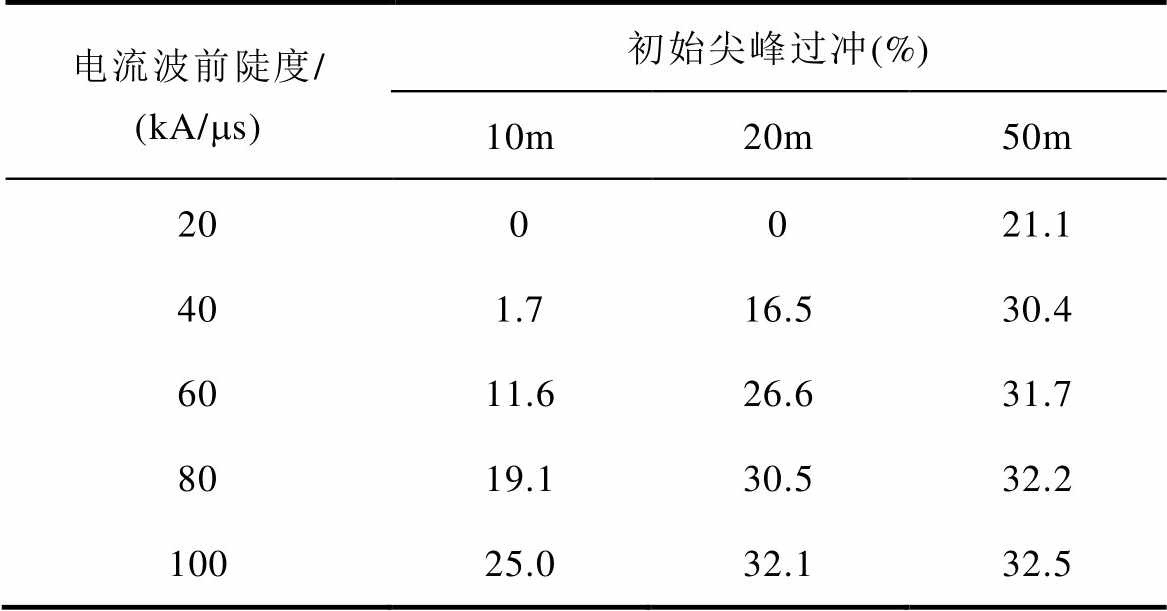
电流波前陡度/ (kA/ms)初始尖峰过冲(%) 10m20m50m 200021.1 401.716.530.4 6011.626.631.7 8019.130.532.2 10025.032.132.5
图10c连接高度为50m时，最大波前陡度为20kA/ms的回击电流在50km处电场也能观察到明显的初始尖峰，尖峰过冲可达21.1%。对比图10a和图10c可知，电场的初始尖峰随电流陡度增大而增大的现象受连接高度的影响十分明显。根据表3统计结果，连接高度为50m时，电流波前陡度大于40kA/ms的回击电流引发的电场，电场初始尖峰过冲随电流陡度增大并没有显著增大。出现上述现象的原因是在下行回击电流引发的电场波形中，tdmax对应的电场峰值是由闪电连接高度处的下行回击初始几微秒发展的一定长度的通道内电流决定的，随着连接高度的增加，并且大于该段通道长度后，下行回击电流引发的tdmax对应的电场峰值不再变化。因此，电场初始尖峰过冲随电流波前陡度增大而增大的趋势在闪电连接高度为50m时不明显。
除通道电流外，回击发展速度是回击模型的另一项基本输入参数。根据Wang Daohong等研究的闪电发展过程，4次测量得到下行回击发展速度的回击中，第1次回击的下行发展速度为2.2×107m/s，比另外3次下行回击发展速度低5～10倍[5]。J. D. Hill等研究了3次火箭触发闪电的下行回击发展速度，在4.3×107～1.6×108m/s之间[9]。以上结果均表明下行回击电流速度在较大范围内变化。
图11为观测距离r =50km，上行回击速度为2×108m/s，连接高度分别为10m、20m和50m时，由图2继后回击电流引发的地面电场波形，下行回击速度分别取0.2×108m/s、1×108m/s、2×108m/s和2.99×108m/s，同样对比了传统TL模型计算的回击电场波形。表4统计了图11中不同下行回击速度时电场初始尖峰过冲百分比。根据图11b和图11c，连接高度为20m和50m时，下行回击速度增大，电场初始尖峰的幅值增大，持续时间缩短，产生的初始尖峰更为尖锐，表4电场初始尖峰过冲百分比也增大。
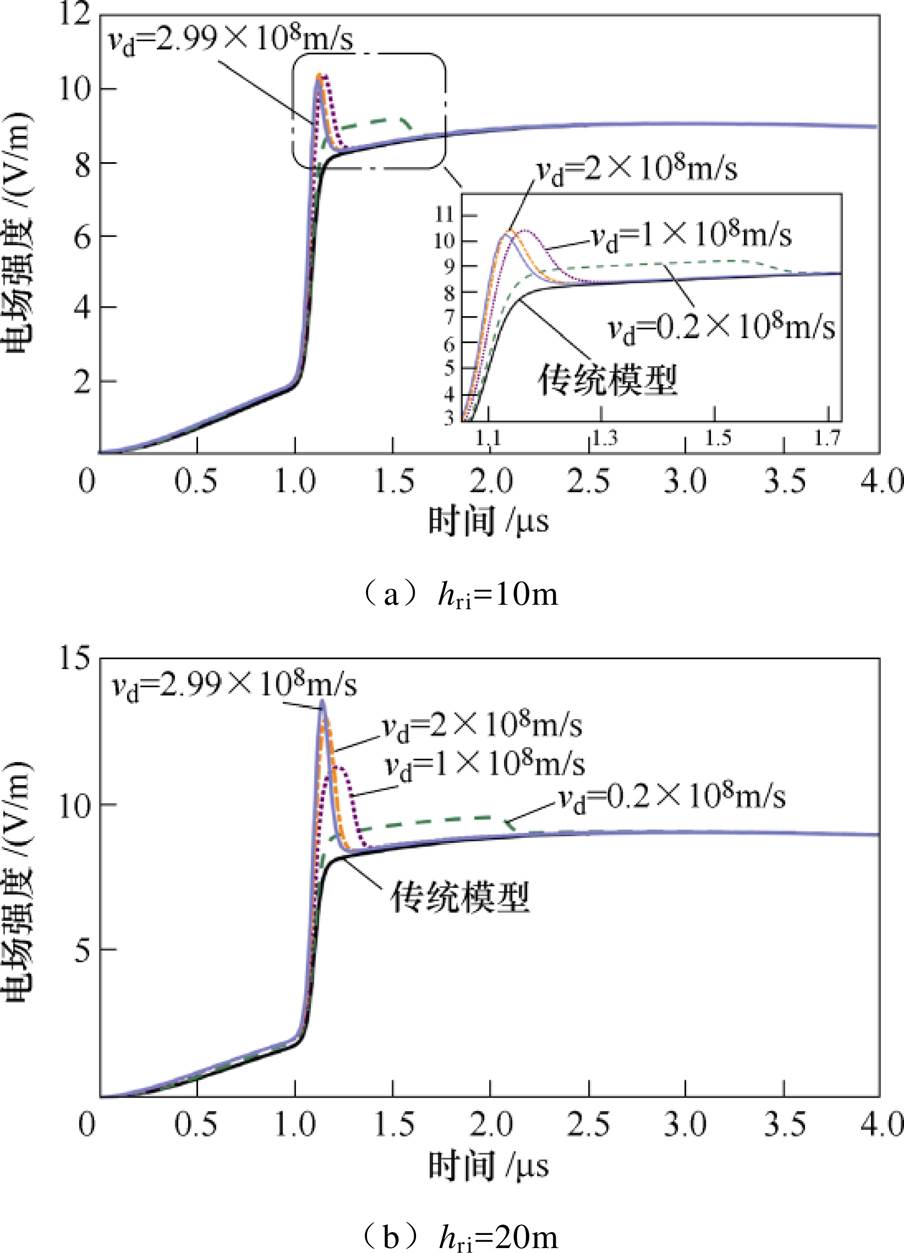
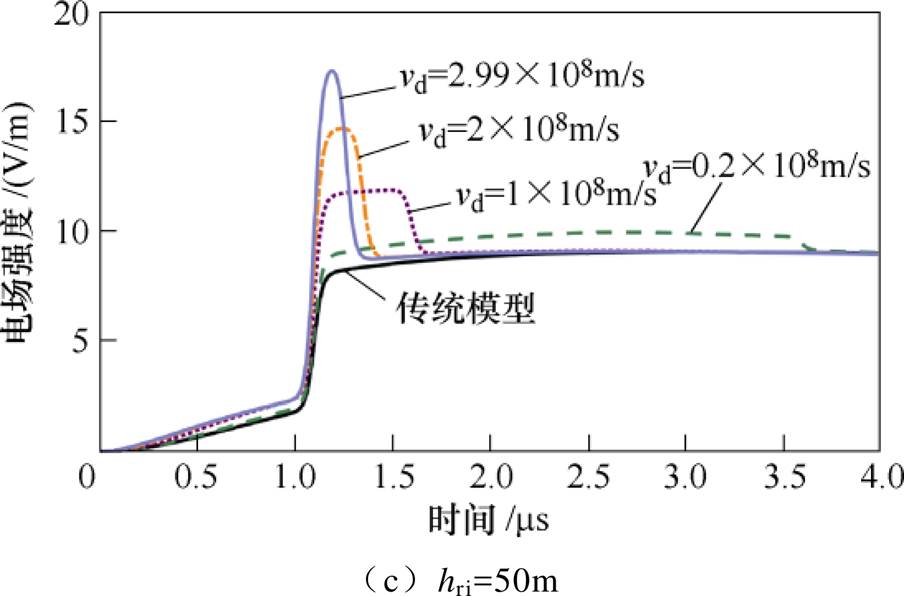
图11 不同下行回击速度下r =50km处垂直电场（前4ms）
Fig.11 Calculated vertical electric fields for various downward return-stroke speeds at 50km within 4ms
表4 不同下行回击速度时初始尖峰过冲百分比统计
Tab.4 Sharp initial peak overshoot of electric field for various downward return stroke speeds
下行回击速度/ (m/s)初始尖峰过冲(%) 102050 0.2×1085.36.09.0 1×10824.232.132.5 2×10825.253.666.5 2.99×10823.361.097.7
根据表4，连接高度为10m时，初始尖峰过冲随下行回击速度增大而增大的趋势受到抑制。如表4中下行回击速度由1×108m/s增大至2×108m/s时，对应的尖峰过冲仅增大1%，下行回击速度为2.99×108m/s时尖峰过冲略微减小到23.3%。因此，连接高度较小（如10m）时，回击速度的增加导致尖峰过冲的增加受到抑制，原因是随着回击速度增大，下行回击辐射场尖峰的峰值虽增大，但峰值时刻tdmax减小，尖峰叠加在上行回击电场快变化部分（见图3b中AB段），电场尖峰部分Es增加不明显，以致电场初始尖峰过冲百分比变化受到抑制。
连接高度为20m和50m时，下行回击辐射场尖峰的峰值时刻tdmax较大，尖峰部分Es叠加在上行回击电场快变化结束后的部分（见图3b中BC段），因此，连接高度较大时，电场初始尖峰过冲随速度增大而增大的趋势更明显。
由2.3节和2.4节可知，电场初始尖峰随电流波前陡度和下行回击速度增大而增大的现象受连接高度的影响。取上行回击速度为2×108m/s，连接高度分别为10m、20m和50m，研究连接高度、电流波前陡度和下行回击速度对电场初始尖峰的共同作用，计算50km处电场初始尖峰过冲百分比，结果如图12所示，初始尖峰过冲百分比临界线也包含在图12中。
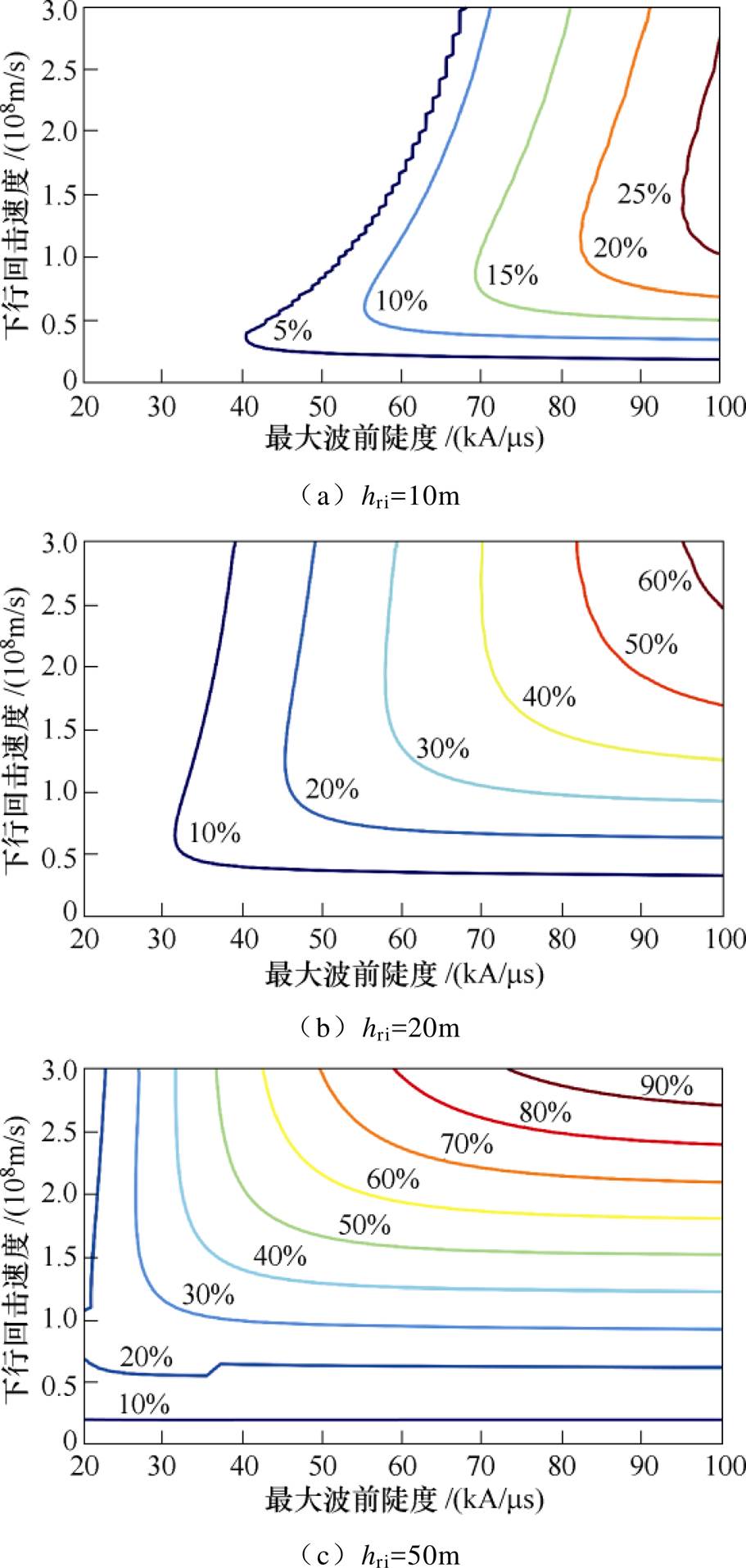
图12 三种连接高度下尖峰过冲变化
Fig.12 Variation of sharp initial peak overshoot at three junction heights
图12中，电场初始尖峰过冲百分比临界线右上方区域的尖峰过冲大于该临界值。对比图12a～图12c，连接高度增大，电场初始尖峰过冲百分比增大，电场初始尖峰过冲百分比为10%和20%临界线，沿电流波前陡度和下行回击速度减小的方向移动。根据图12a，连接高度为10m，电流波前陡度大于70kA/ms，且下行回击速度大于0.4×108m/s时，电场初始尖峰过冲大于10%；电流波前陡度为20～60kA/ms时，在下行回击速度大范围变化下，电场初始尖峰过冲百分比很小，电场波形无法观察到明显初始尖峰。图12b对应连接高度为20m的电场初始尖峰过冲百分比，初始尖峰过冲为10%时，电流波前陡度和下行回击速度的临界值分别约为40kA/ms和0.3×108m/s。若连接高度为50m（见图12c），对于波前陡度为20～100kA/ms的电流，回击速度大于0.2×108m/s时，电场初始尖峰过冲超过10%。
2.4节中已经提及，连接高度为10m时，尖峰过冲随下行回击速度增大而增大的趋势受到抑制。结合图12a，连接高度为10m时，在某一电流最大波前陡度（如100kA/ms）下，尖峰过冲随下行回击速度增大的变化趋势为先增大后减小，且在下行回击速度达到光速前，尖峰过冲已经开始减小。
本文提出了考虑闪电连接高度的回击发展模型，计及在连接高度处的回击电流双向传输模式，分析了不同观测距离地面电场及各分量波形特征，研究了闪电连接高度、电流波前陡度和下行回击速度对电场波形初始尖峰的影响，得出主要结论如下：
1）计算结果显示，下行回击的存在可能导致数十米、数千米和数十千米处等不同距离的地面电场波形的上升段中出现明显的初始尖峰，与地表电场观测事实吻合。观测距离超过数千米时，电场初始尖峰主要是下行回击的辐射场分量；观测距离为数十米时，电场初始尖峰由辐射场、静电场和感应场分量共同作用，解释了电场波形初始尖峰的形成机制。
2）假定电流从地面始发的传统TL模型不能模拟出电场初始尖峰，考虑闪电连接高度的地面电场波形存在初始尖峰，更符合实际测量结果。闪电连接高度增加，地面电场波形的初始尖峰幅度增大，电场初始尖峰过冲百分比增大，持续时间更长。
3）电流波前陡度增大时，地面电场初始尖峰过冲幅度增大，电场初始尖峰过冲增大的趋势在闪电连接高度较高（如50m）时不明显。
4）下行回击速度增大，地面电场初始尖峰过冲幅度增大，持续时间缩短，电场初始尖峰过冲增大的趋势在闪电连接高度较低（如10m）时被抑制。
5）闪电连接高度较低（如10m）时，波前陡度较小（如20～60kA/ms）的回击电流在下行回击速度大范围的变化下，下行回击的存在也不能使电场波形中出现明显的初始尖峰。
参考文献
[1] Uman M A, Mclain D K. Magnetic field of lightning return stroke[J]. Journal of Geophysical Research, 1969, 74(28): 6899-6910.
[2] Nucci C A, Mazzetti C, Rachidi F, et al. On lightning return stroke models for LEMP calculations[C]//19th International Conference on Lightning Protection. Graz, Austria, 1988: 463-470.
[3] Rakov V A, Dulzon A A. Calculated electromagnetic fields of lightning return strokes[J]. Tekhnicheskaya Elektrodinamika, 1987(1): 87-89.
[4] Wang Daohong, Takagi N, Gamerota W R, et al. Initiation processes of return strokes in rocket- triggered lightning[J]. Journal of Geophysical Research: Atmospheres, 2013, 118(17): 9880-9888.
[5] Wang Daohong, Gamerota W R, Uman M A, et al. Lightning attachment processes of an “anomalous” triggered lightning discharge[J]. Journal of Geophy- sical Research: Atmospheres, 2014, 119(3): 1524- 1533.
[6] Wang Daohong, Takagi N, Gamerota W R, et al. Lightning attachment processes of three natural lightning discharges[J]. Journal of Geophysical Research: Atmospheres, 2015, 120(20): 10637- 10644.
[7] Tsukamoto N, Wu Ting, Wang Daohong, et al. Light intensity profiles of return strokes at the bottom of rocket-triggered and natural lightning channels[J]. Journal of Atmospheric Electricity, 2017, 37(1): 1-9.
[8] Rakov V A, Tran M D. The breakthrough phase of lightning attachment process: from collision of opposite- polarity streamers to hot-channel connection[J]. Electric Power Systems Research, 2019, 173: 122- 134.
[9] Hill J D, Uman M A, Jordan D M, et al. The attachment process of rocket-triggered lightning dart- stepped leaders[J]. Journal of Geophysical Research: Atmospheres, 2016, 121(2): 853-871.
[10] 任瀚文, 郭子炘, 马宇飞, 等. 雷击风机叶片的跃变击距特性与定量表征[J]. 电工技术学报, 2017, 32(15): 216-224.
Ren Hanwen, Guo Zixin, Ma Yufei, et al. Quanti- tative characterization of the striking saltus distance of wind turbine blade[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 216-224.
[11] 王宇, 王建国, 周蜜, 等. 双接闪器叶片风电机组缩比模型雷击附着特性[J]. 中国电机工程学报, 2018, 38(18): 5307-5315.
Wang Yu, Wang Jianguo, Zhou Mi, et al. Lightning attachment characteristic of wind turbine blade with two-receptors[J]. Proceedings of the CSEE, 2018, 38(18): 5307-5315.
[12] 雷宇航, 蔡国伟, 潘超. 大气条件下雷击风机叶片初始流注区电场强度与临界长度研究[J]. 电工技术学报, 2019, 34(20): 4392-4399.
Lei Yuhang, Cai Guowei, Pan Chao. Research of electric field of lightning initial streamer from wind turbine blade and critical length based on atmo- spheric conditions[J]. Transactions of China Electro- technical Society, 2019, 34(20): 4392-4399.
[13] Zhou Mi, Wang Daohong, Wang Jianguo, et al. Cor- relation between the channel-bottom light intensity and channel-base current of a rocket-triggered lightning flash[J]. Journal of Geophysical Research: Atmospheres, 2014, 119(23): 457-473.
[14] Zhou Mi, Su Xiaowei, Wang Jianguo, et al. On the variation of optical return stroke speed along the bottom of lightning channel[J]. IEEE Transactions on Electromagnetic Compatibility, 2019, 61(3): 766-777.
[15] 张岩, 刘福贵, 汪友华, 等. 改进的双指数函数雷电流波形及其辐射电磁场的计算[J]. 电工技术学报, 2013, 28(增刊2): 133-139.
Zhang Yan, Liu Fugui, Wang Youhua, et al. A modify double exponential base-current and its application in evaluating the lightning EM fields[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 133-139.
[16] 陈剑, 刘春明, 王茂海, 等. 广义有限差分法在静态电磁场计算中的应用[J]. 电工技术学报, 2018, 33(7): 1579-1587.
Chen Jian, Liu Chunming, Wang Maohai, et al. Application of the generalized finite difference method to static electromagnetic problems[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(7): 1579-1587.
[17] Li Quanxin, Wang Jianguo, Rachidi F, et al. Impor- tance of taking into account the soil stratification in reproducing the late-time features of distant fields radiated by lightning[J]. IEEE Transactions on Elec- tromagnetic Compatibility, 2018, 61(3): 935-944.
[18] 王泽忠, 石雨鑫, 刘丽平. 应用快速多极子曲面边界元法的换流阀塔电场计算[J]. 电工技术学报, 2019, 34(2): 203-211.
Wang Zezhong, Shi Yuxin, Liu Liping. Calculating of electric field of converter valve tower by using fast multipole curved boundary element method[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 203-211.
[19] 张刚, 于洪海, 王立欣. 一种时域电磁仿真终止判断的新方法[J]. 电机与控制学报, 2017, 21(9): 15-21.
Zhang Gang, Yu Honghai, Wang Lixin. Stopping criterion of time domain electromagnetic simu- lation[J]. Electric Machines and Control, 2017, 21(9): 15-21.
[20] Chen Shaodong, Zhang Yijun, Zhou Mi, et al. Influence on low-voltage surge protective devices of overhead distribution lines due to nearby return strokes[J]. IEEE Transactions on Power Delivery, 2017, 33(3): 1099-1106.
[21] 樊亚东, 于建立, 詹清华, 等. 基于多阶FDTD雷电感应过电压计算新方法[J]. 电工技术学报, 2015, 30(12): 336-343.
Fan Yadong, Yu Jianli, Zhan Qinghua, et al. New method of lightning induced over-voltage based on multiple order FDTD[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 336-343.
[22] 王孝波, 陈绍东, 张义军, 等. 一次多回击自然闪电引发的输电线路感应过电压特征分析[J]. 电网技术, 2011, 35(2): 163-168.
Wang Xiaobo, Chen Shaodong, Zhang Yijun, et al. Analysis on characteristics of induced over-voltage in transmission line caused by natural lightning with multi return strokes[J]. Power System Technology, 2011, 35(2): 163-168.
[23] 肖翔, 张小青, 李聪. 风电机组雷电过电压的仿真分析[J]. 电工技术学报, 2015, 30(24): 237-244.
Xiao Xiang, Zhang Xiaoqing, Li Cong. Simulation analysis on overvoltage in wind turbines by lightning stroke[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 237-244.
[24] 蔡国伟, 雷宇航, 葛维春, 等. 高寒地区风电机组雷电防护研究综述[J]. 电工技术学报, 2019, 34(22): 4804-4815.
Cai Guowei, Lei Yuhang, Ge Weichun, et al. Review of research on lightning protection for wind turbines in alpine areas[J]. Transactions of China Electro- technical Society, 2019, 34(22): 4804-4815.
[25] Wang Jianguo, Li Quanxin, Cai Li, et al. Multiple- station measurements of a return-stroke electric field from rocket-triggered lightning at distances of 68- 126km[J]. IEEE Transactions on Electromagnetic Compatibility, 2018, 61(2): 440-448.
[26] Lin Yuntao, Uman M A, Tiller J A, et al. Characteri- zation of lightning return stroke electric and magnetic fields from simultaneous two-station measurements[J]. Journal of Geophysical Research: Oceans, 1979, 84(C10): 6307-6314.
[27] Willett J C, Idone V P, Orville R E, et al. An experimental test of the “transmission-line model” of electromagnetic radiation from triggered lightning return strokes[J]. Journal of Geophysical Research: Atmospheres, 1988, 93(D4): 3867-3878.
[28] Haddad M A, Rakov V A, Cummer S A. New measurements of lightning electric fields in Florida: waveform characteristics, interaction with the ionosphere, and peak current estimates[J]. Journal of Geophysical Research: Atmospheres, 2012, 117: D10101.
[29] Weidman C, Hamelin J, Leteinturier C, et al. Cor- related current derivative (dI/dt) and electric field derivative (dE/dt) emitted by triggered lightning[C]// International Aerospace and Ground Conference on Lightning and Static Electricity, Dayton, Ohio, 1986: 1-6.
[30] Howard J, Uman M A, Biagi C, et al. RF and X-ray source locations during the lightning attachment process[J]. Journal of Geophysical Research, 2010, 115: D06204.
[31] Leteinturier C, Weidman C, Hamelin J. Current and electric field derivatives in triggered lightning return strokes[J]. Journal of Geophysical Research, 1990, 95(D1): 811-828.
[32] Uman M A. The art and science of lightning pro- tection[M]. USA: Cambridge University Press, 2008.
[33] Schoene J, Uman M A, Rakov V A, et al. Test of the transmission line model and the traveling current source model with triggered lightning return strokes at very close range[J]. Journal of Geophysical Research: Atmospheres, 2003, 108(D23): 4737.
[34] De Conti A, Visacro S. Analytical representation of single-and double-peaked lightning current wave- forms[J]. IEEE Transactions on Electromagnetic Compatibility, 2007, 49(2): 448-451.
[35] Gamerota W R, Elismé J O, Uman M A, et al. Current waveforms for lightning simulation[J]. IEEE Transa- ctions on Electromagnetic Compatibility, 2012, 54(4): 880-888.
[36] Rakov V A, Uman M A. Lightning: physics and effects[M]. USA: Cambridge University Press, 2003.
Effect of Lightning Junction Height on Ground Electric Field Waveform
Abstract It was assumed by traditional return stroke models that the return stroke originates from the ground and develops towards the cloud. However, recent observation results show that, at the junction height, the lightning return stroke will generate bidirectional currents to the cloud and to the ground, respectively. Combined with the recent observation results about the lightning initiation process, an extended return stroke model incorporating bidirectional propagation of the return stroke at the junction height is proposed. Then, the ground electric field at different distances (50km, 5km, 50m) is calculated. The results show that, depending on the wavefront steepness of the current, the existence of the downward return stroke may generate a sharp initial peak in the rising portion of the electric fields. The sharp initial peak overshoot is defined to represent the extent of sharpness. The influence of junction height, current wavefront steepness and downward return stroke speed on overshoot is further analyzed. It can be seen that, as the junction height increases, the amplitude and duration of the sharp initial peak increase. Besides, a larger wavefront steepness and a larger downward return stroke speed tend to produce a larger initial field peak overshoot. The increase of downward return stroke speed results in a shorter duration of initial field peak. The electric field waveforms calculated by the proposed return stroke model are more consistent with the measured ones than the conventional models, revealing the physical mechanism of sharp initial electric field peak.
keywords：Lightning current, lightning junction height, initial sharp electric field peak, trans- mission line model, wavefront steepness of current, return stroke speed
中图分类号：TM865
DOI: 10.19595/j.cnki.1000-6753.tces.191805
国家自然科学基金（51877155，51807144，41775007）和某重大基础科研计划（2019207029）资助项目。
收稿日期 2019-12-24
改稿日期 2020-05-07
周 蜜 男，1986年生，博士，副教授，研究方向为雷电防护和接地技术。E-mail: zhoumi927@whu.edu.cn
王建国 男，1968年生，教授，博士生导师，研究方向为雷电防护与接地技术、高电压绝缘与测量技术等。E-mail: wjg@whu.edu.cn（通信作者）
（编辑 陈 诚）