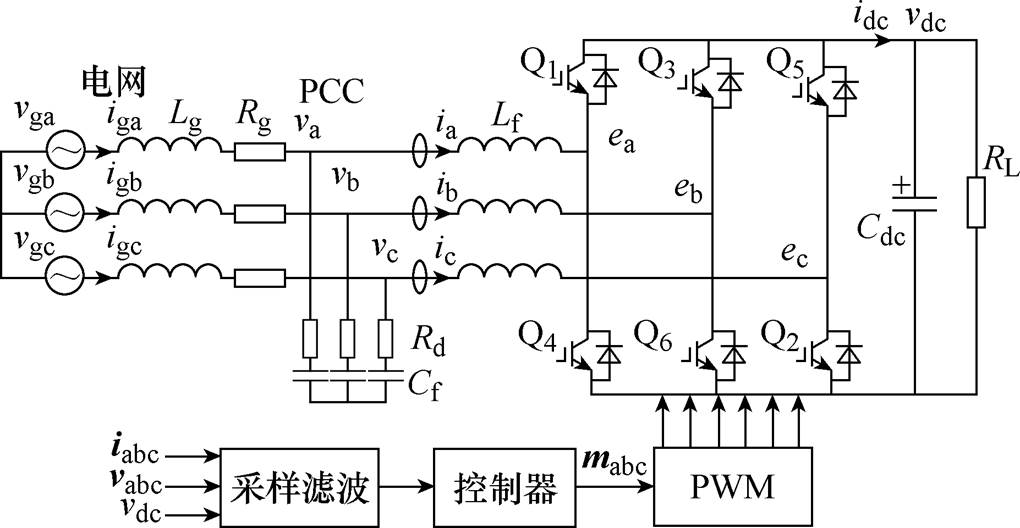
图1 三相负荷变换器拓扑结构
Fig.1 Topology of load converter
摘要 负荷虚拟同步机(LVSM)与基于直流侧电容虚拟惯性控制的负荷变换器(DLCVIC-LC)都能增强系统惯性,但也可能在弱电网下发生谐波振荡等交互稳定性问题。该文考虑直流电压控制以及频率耦合的影响,推导三相负荷变换器的序阻抗计算通式,并据此建立LVSM以及DLCVIC-LC的精确序阻抗模型,进而对比分析两者的序阻抗特性。分析发现LVSM的正序阻抗基本呈感性,与电网的阻抗特性基本一致,不易发生谐波振荡问题;而DLCVIC-LC的正序阻抗在中频段呈负阻容性(相位在-90°~-180°),容易在弱电网中引发谐波振荡问题。此外,该文基于所建序阻抗模型和Nyquist稳定判据分析电网阻抗及控制参数对两种负荷变换器并网系统稳定性的影响。最后,通过实验验证了该文分析的正确性。
关键词:负荷变换器 虚拟惯性 序阻抗建模 稳定性分析 弱电网
近年来,以电力电子变换器为接口的可再生能源与负荷大规模地接入电网,由于其缺乏传统同步电机的阻尼与惯性,给电力系统的安全稳定运行带来了不可忽视的影响[1]。为此,虚拟同步机(Virtual Synchronous Machine, VSM)技术被提出,其模拟了同步电机的惯性及阻尼特性,能有效抑制电网频率的波动,提高系统的稳定性[2-3]。
由于VSM技术优良的控制性能,其最早被推广应用于光储发电[4]、风力发电[5]以及柔性直流输电[6]等领域。同时,随着越来越多的负荷通过电力电子变换器接入电网,同样要求负荷变换器能为电网提供惯性支撑,使新能源与负荷都能像常规电源一样自主参与电网调节,从而实现电网的自主运行[7]。因此,有学者提出了负荷虚拟同步机(Load Virtual Synchronous Machine, LVSM)控制策略[8-10]。文献[11]将LVSM技术应用到电动汽车充电接口,提高并网接口的惯性与阻尼。文献[12]将LVSM技术应用到柔性直流输电整流侧,使整流侧变换器在动态情况下为电网提供相应的惯性支撑。此外,文献[13-14]提出了基于直流侧电容虚拟惯性控制的负荷变换器(Load Converter based on DC-Link Capacitor Virtual Inertia Control, DLCVIC-LC)概念,其将变换器直流侧电容电压与电网频率联系起来,利用直流侧电容储存能量的特性来为电网提供惯性支撑。
由于大多数负荷变换器连接在配电网的末端,此处电网往往呈现出弱电网的特征[15-16]。而在弱电网条件下,变换器容易与电网交互作用引发系统振荡,危害系统的稳定运行[17-18]。因此,有必要研究负荷变换器在弱电网下的运行稳定性问题。文献 [12]推导了LVSM的闭环小信号传递函数模型,给出了控制参数设计方法,并指出虚拟转动惯量和直流电压PI控制参数对系统的相位裕度有直接的影响。文献[14]推导了DLCVIC-LC的闭环小信号传递函数模型,并据此分析了在弱电网下虚拟惯性控制可能会引起系统不稳定。此外,文献[19-20]建立了负荷变换器在dq坐标系下的阻抗模型,并指出其恒功率负荷特性和锁相环会影响系统稳定性,但其忽略了直流电压控制对dq阻抗耦合的影响。文献[21]则考虑直流侧电压的影响,建立了负荷变换器的dq阻抗模型,指出直流侧电压控制可能导致负荷变换器低频振荡。此外,文献[22]考虑锁相环、交流电压环、直流电压环和输出电流环,推导了静止同步补偿器的dq阻抗模型,并据此分析了控制参数的变化对系统运行稳定性的影响。
但是上述研究主要通过闭环传递函数或者dq阻抗模型来分析负荷变换器的运行稳定性,这些分析方法的物理意义不够明确[23]。为此,文献[24]提出采用谐波线性化的方法建立变换器在三相静止坐标系下的序阻抗模型。随后,序阻抗建模被应用到高压直流输电[25]、并网风电场[26]、孤岛微电网[27]、虚拟同步发电机[28-29]等领域来分析变换器与电网的交互稳定性。其中,文献[28-29]基于序阻抗模型与Nyquist稳定判据比较分析了电压控制型虚拟同步发动机、电流控制型虚拟同步发电机以及传统并网逆变器接入弱电网的运行稳定性,并为变换器与电网的交互稳定性提供了清晰的物理意义解释。然而,上述序阻抗建模和稳定性分析主要集中于逆变器。尚未有文献从序阻抗的角度分析带虚拟惯性的负荷变换器与电网的交互稳定性问题。此外,负荷变换器通常需要控制直流侧电压,使得正、负序扰动频率耦合更为严重[30-32],若忽略它们的影响,所建阻抗模型会不精确,不能正确反映变换器与电网的交互作用。
为此,本文充分考虑频率耦合与直流电压扰动的影响,首先推导三相负荷变换器通用的序阻抗计算式,并据此计算DLCVIC-LC和LVSM这两种带虚拟惯性的负荷变换器的序阻抗模型,进而对比分析两者的序阻抗特性。然后分析两种负荷变换器的判稳阻抗比形式,进而利用Nyquist稳定判据分析不同电网阻抗、虚拟惯性控制系数以及锁相环带宽对系统稳定性的影响。分析结果表明,在弱电网条件下,LVSM比DLCVIC-LC具有更好的运行稳定性,不易与电网交互产生振荡。最后通过实验验证了理论分析的正确性。
三相负荷变换器拓扑结构如图1所示。图1中,vdc、idc分别为变换器的直流侧电压和电流;eabc为变换器的桥臂输出电压;vabc、iabc分别为变换器的交流输入电压和电流;vgabc、igabc分别为电网电压和电流;RL为直流侧负载等效电阻;Cdc为直流侧电容;Lf、Cf和Rd分别为变换器的交流滤波电感、滤波电容和阻尼电阻;Lg和Rg分别为电网的等效线路电感和电阻。

图1 三相负荷变换器拓扑结构
Fig.1 Topology of load converter
由图1可得三相负荷变换器主电路模型的时域表达式为
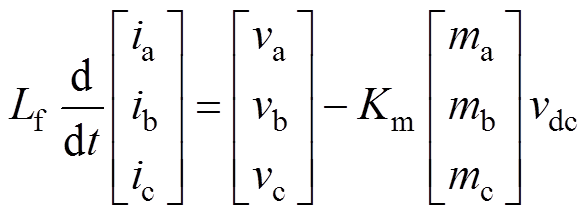 (1)
(1)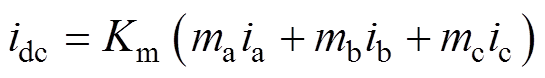 (2)
(2)
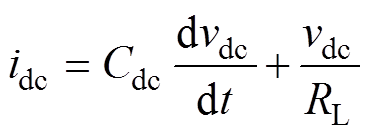 (3)
(3)
式中,mabc为PWM波;Km为调制度。
首先不考虑电网阻抗的影响,在负荷变换器交流端口施加正、负序小信号电压扰动后,a相输入电压和输入电流在频域中可以表示为
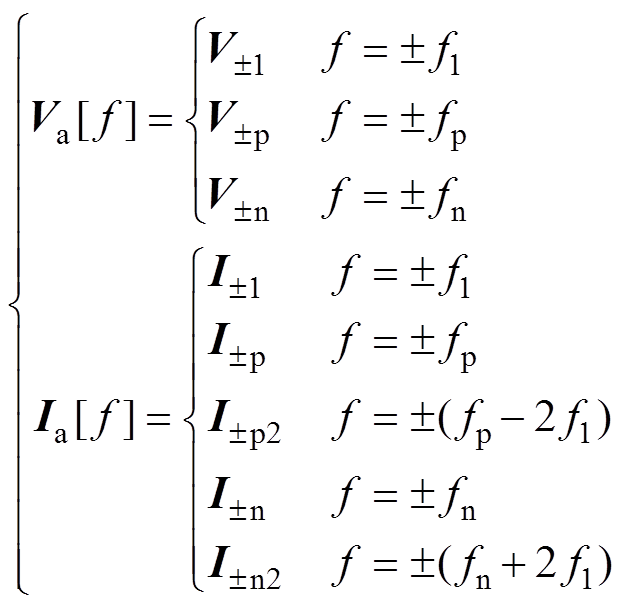 (4)
(4)式中,V±1、V±p和V±n分别为交流电压基波分量、正序扰动分量以及负序扰动分量在频域中的形式;I±1、I±p、I±p2、I±n、I±n2分别为交流电流基波分量、正序电压扰动产生的正序电流扰动分量、正序电压扰动耦合产生的负序电流扰动分量、负序电压扰动产生的负序电流扰动分量以及负序电压扰动耦合产生的正序电流扰动分量在频域中的形式;f1、fp、fp-2 f1、fn、fn+2 f1分别为基波频率、正序扰动频率、正序扰动耦合产生的负序扰动频率、负序扰动频率以及负序扰动耦合产生的正序扰动频率。
从式(2)可以看出,三相调制波与电流相乘求和后,正、负序扰动分量会相互抵消,使直流电流中只剩下直流和零序扰动分量,则直流侧电压在频域中可表示为
 (5)
(5)式中,Vdcr为直流侧电压参考值;V±pdc、V±ndc分别为交流侧正序扰动和负序扰动引起的直流侧电压 扰动。
由于采用谐波线性化方法[24],PWM波ma与采样的交流电流ia、交流电压va以及直流侧电压vdc在频域中可以近似呈线性关系。因此,考虑正、负序扰动及频率耦合,PWM波ma可假设为
 (6)
(6)式中,M±1=(V±1−sLfI±1)/(KmVdcr)为调制波的基波分量在频域中的形式;A(s)、B(s)、C(s)、F(s)分别为交流电流扰动、耦合频率的交流电流扰动、交流电压扰动及直流电压扰动对调制波的影响系数;系数下标p、p2、n、n2分别对应扰动频率fp、fp-2 f1、fn、fn+2 f1。
将式(4)~式(6)代入式(1)~式(3)中,并利用频域卷积定理可得,在正序小信号电压扰动V±p的作用下,得到负荷变换器主电路模型的频域表达式为
频率为fp的正序电流扰动响应为
 (7)
(7)耦合产生的频率为fp-2 f1的负序电流扰动响应为
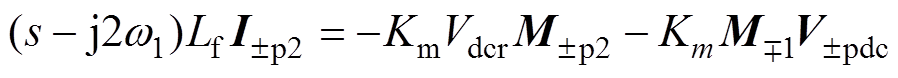 (8)
(8)
频率为fp-f1的直流电压扰动响应为
 (9)
(9)式中,w1为电网额定角频率;M±p、M±p2分别为频率为fp以及fp-2 f1的PWM波扰动分量在频域中的形式。
从式(6)~式(9)中可知,对负荷变换器施加正序电压扰动V±p后,会产生正序电流扰动I±p、负序电流扰动I±p2和直流电压扰动V±pdc,V±pdc又会通过PWM波和主电路模型影响I±p和I±p2。这一扰动传递过程可以表示为信号流如图2所示。

图2 负荷变换器扰动信号流
Fig.2 Disturbance signal-flow graph of load converer
将式(6)中频率为fp和fp-2 f1的扰动分量代入式(7)~式(9)中,可以求得图2中各扰动之间的传递函数为
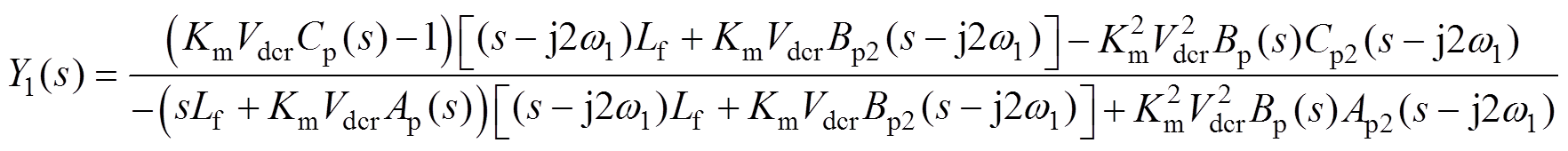 (10)
(10)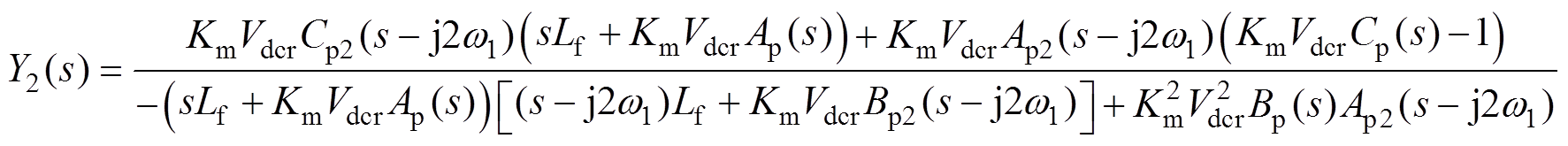 (11)
(11)
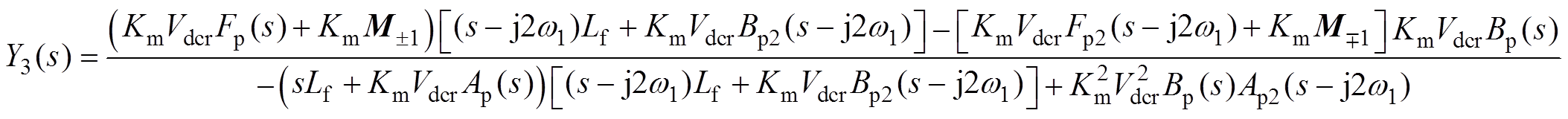 (12)
(12)
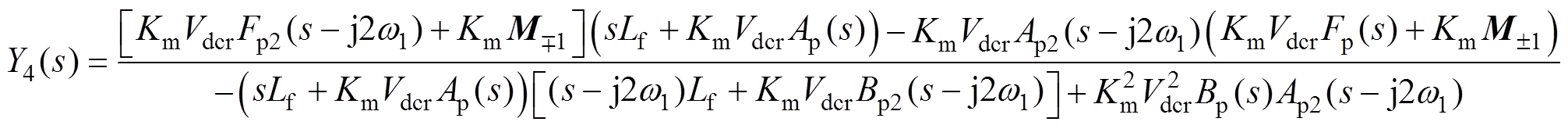 (13)
(13)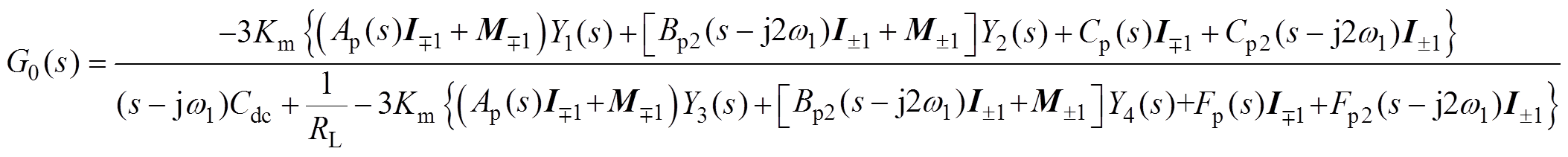 (14)
(14)
根据图2各扰动之间的关系可得,不考虑电网阻抗时,正序电压扰动V±p产生正序电流扰动I±p对应的导纳Ypp(s)以及耦合产生负序电流扰动I±p2对应的导纳Ypn(s)分别为
 (15)
(15) (16)
(16)
考虑电网阻抗Zg(s)影响,则正序电压扰动V±p耦合产生的负序电流扰动I±p2会通过电网阻抗产生负序电压扰动V±p2,V±p2施加在变换器上又会产生I±p2和I±p。这一扰动传递过程可以表示为信号流如图3所示。图中,根据正、负序阻抗之间的共轭关系[33],变换器导纳Ynn(s)和Ynp(s)分别表示为
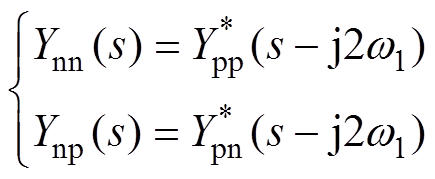 (17)
(17)式中,符号*为复数的共轭。
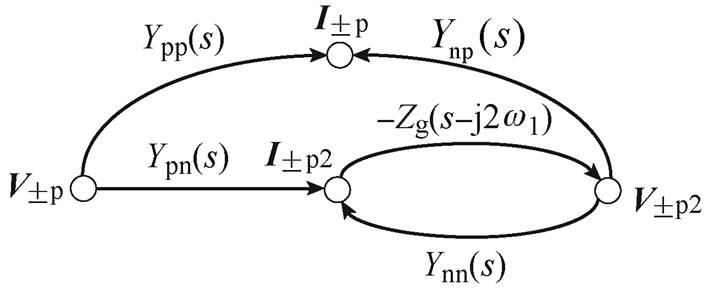
图3 考虑电网阻抗的系统扰动信号流
Fig.3 Disturbance signal-flow graph of system considering grid impedance
根据图3可得,考虑直流电压扰动、频率耦合以及电网阻抗的影响,三相负荷变换器正、负序阻抗计算式分别为
 (18)
(18)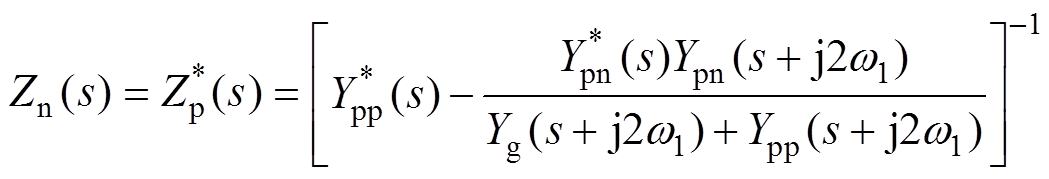 (19)
(19)
因此,对于不同控制方式的负荷变换器,只需计算得到如式(6)形式的PWM波与各采样控制量的关系系数,就能依据通式(10)~式(19)求出变换器的正、负序阻抗模型。
对于同步旋转坐标系下控制的变换器,导致正、负序扰动频率耦合的来源有[31]:①直流电压环; ②锁相环;③dq轴电流控制器参数不相同。因此,在对负荷变换器进行序阻抗建模时,必须考虑直流电压控制对频率耦合的影响。考虑频率耦合的影响后,序阻抗模型会出现正序电压对负序电流影响的阻抗以及负序电压对正序电流影响的阻抗,构成了一个2×2的多输入多输出序阻抗矩阵[31],文献[32]分析了多输入多输出序阻抗与文献[24]中定义的单输入单输出形式的序阻抗之间的转化关系,表明两种序阻抗形式的稳定性分析是完全等价的。因此,为了便于稳定性分析,本文最终推导的是如式(18)和式(19)所示的单输入单输出序阻抗模型。
图4所示为DLCVIC-LC的控制框图[14]。其通过利用直流侧电容吸收/释放能量的特性来模拟同步电机的惯性。图中,虚拟惯性控制系数Kwv将电网频率的变化反馈到直流电压指令上,当电网频率出现波动时,通过动态调节变换器的直流侧电压,利用变换器直流侧电容器中存储的能量来抑制电网频率的波动。同时为了改善虚拟惯性控制的稳定性引入了控制修正系数K。HPLL(s)=Kp_pll+Ki_pll/s为锁相环PI控制器传递函数;Hv1(s)=Kp_v1+Ki_v1/s和Hi(s)=Kp_i+Ki_i/s分别为直流电压和dq轴电流PI控制器传递函数;Kd和Kf分别为电流解耦系数和电压前馈系数;Vdcr为直流侧电压参考值;Iqr为q轴电流参考值;w1为电网额定角频率。
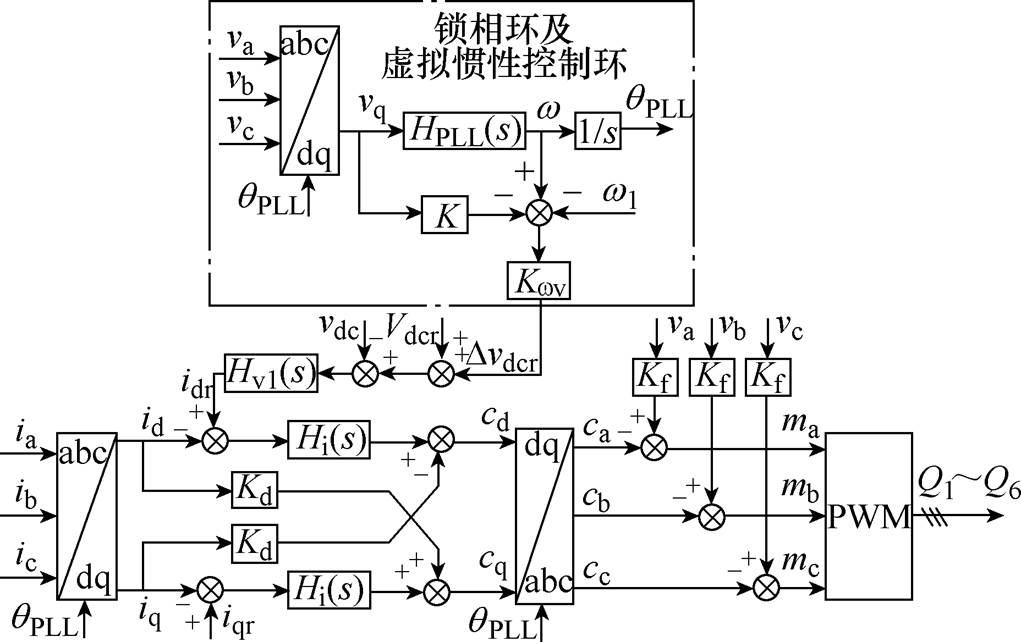
图4 DLCVIC-LC的控制框图
Fig.4 Control diagram of DLCVIC-LC
设锁相环控制输出的相位qPLL=q1+Dq,其中,q1为基波电压相位,Dq为控制输出相位的小信号扰动。根据文献[24],Dq 在频域中的表达式为
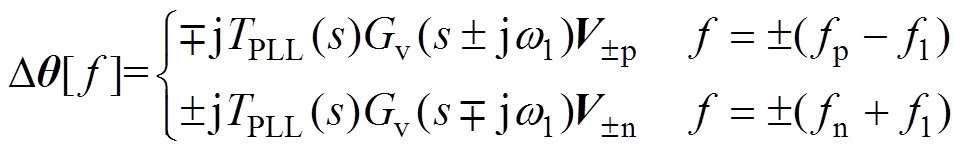 (20)
(20)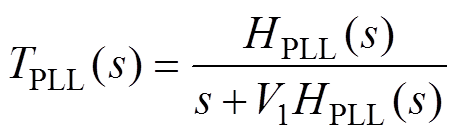 (21)
(21)
式中,Gv(s)=1/(1+sTv)为交流电压采样滤波器传递函数,Tv为交流电压滤波器时间常数;V1为基波电压幅值。
dq坐标变换矩阵T(qPLL)为
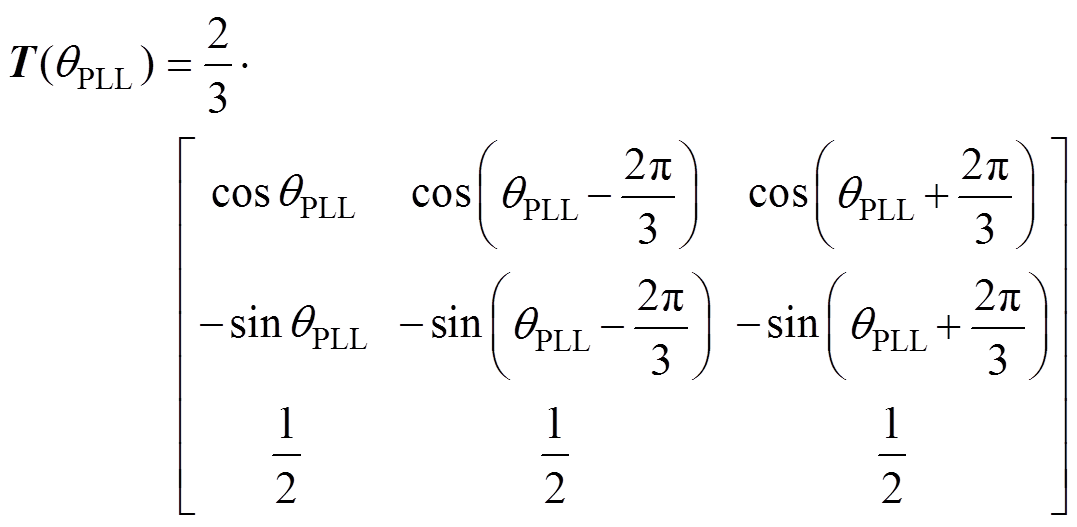 (22)
(22)同步旋转坐标系下id、iq计算式为
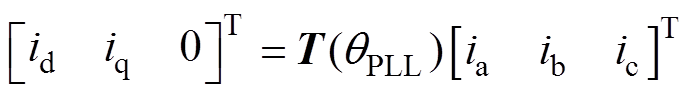 (23)
(23)
坐标变换矩阵中cosqPLL≈cosq1-Dqsinq1,sinqPLL≈sinq1+Dqcosq1。因此,将式(20)~式(22)和式(4)代入式(23)中,并利用频域卷积定理可得id、iq在频域中的表达式为
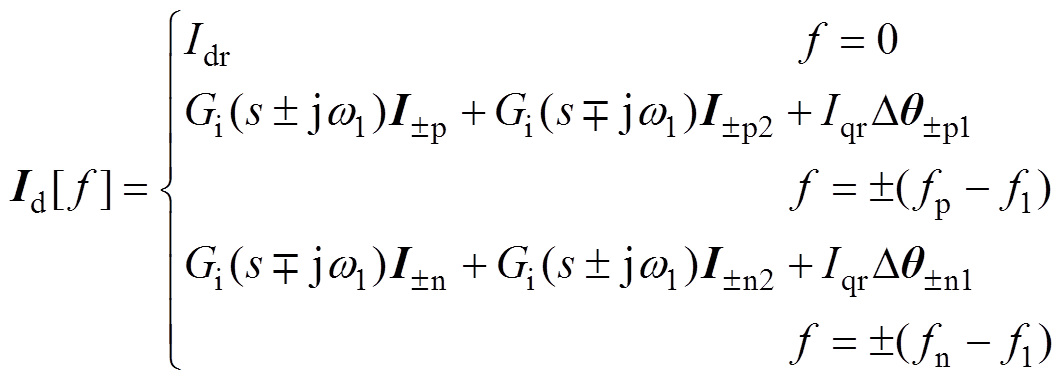 (24)
(24)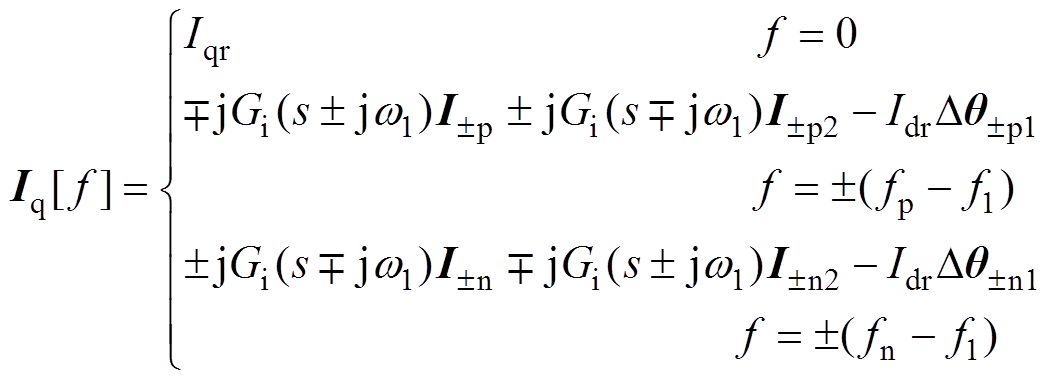 (25)
(25)
式中,Idr为d轴电流参考值;Gi(s)=1/(1+sTi)为交流电流采样滤波器传递函数,Ti为交流电流滤波器时间常数;Dqp1和Dqn1分别为频率是fp-f1和fn-f1的锁相环输出相位扰动。
根据图4,引入虚拟惯性控制后,直流侧电压指令扰动Dvdcr可表示为
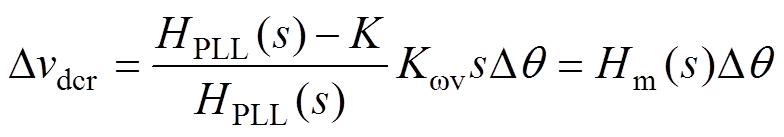 (26)
(26)同步旋转坐标系下调制波cd、cq可以表示为
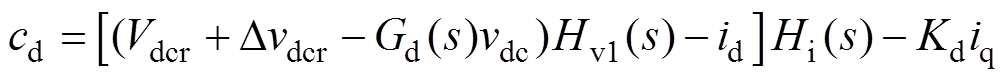 (27)
(27)
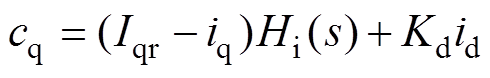 (28)
(28)式中,Gd(s)=1/(1+sTd)为直流电压采样滤波器传递函数,Td为直流电压滤波器时间常数。
cd、cq经过反dq坐标变换与电压前馈控制后得到a相PWM波ma为
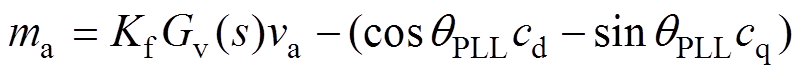 (29)
(29)将式(20)~式(28)代入式(29)中,并利用频域卷积定理可得式(6)中频率为fp和fp-2 f1的扰动关系系数分别为
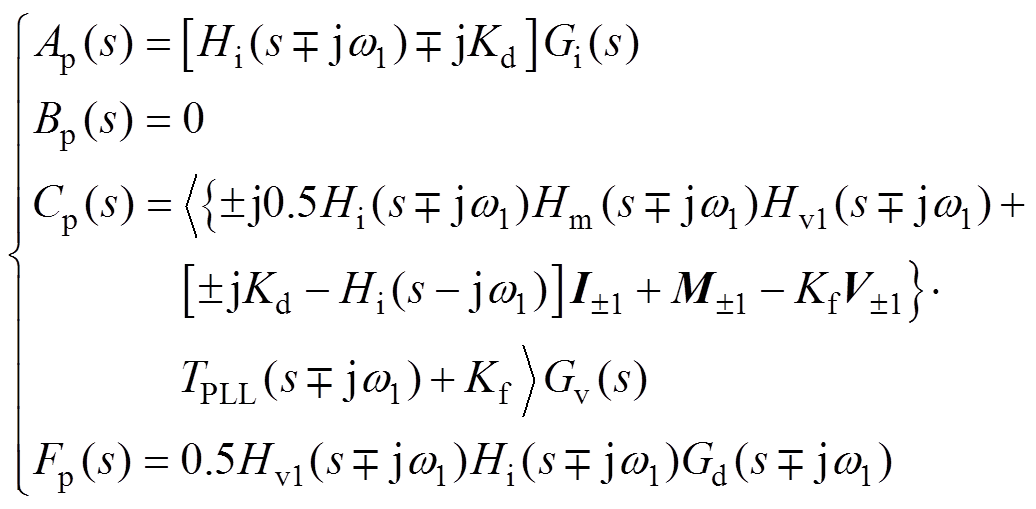 (30)
(30)
 (31)
(31)将式(30)和式(31)代入式(10)~式(14)可计算得到对应DLCVIC-LC的Yc1(s)、Yc2(s)、Yc3(s)、Yc4(s)和Gc0(s),再根据式(15)~式(19)可得DLCVIC- LC的正序阻抗Zcp(s)和负序阻抗Zcn(s)分别为
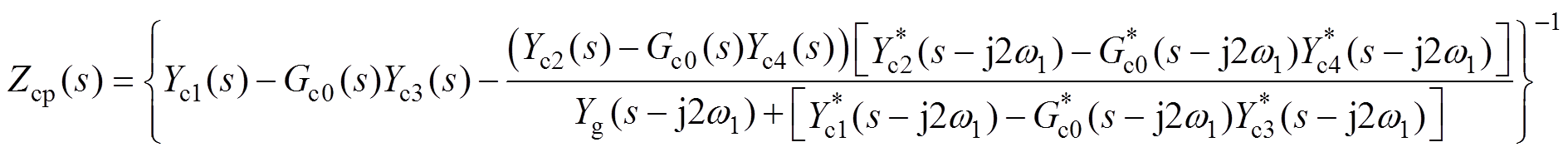 (32)
(32)
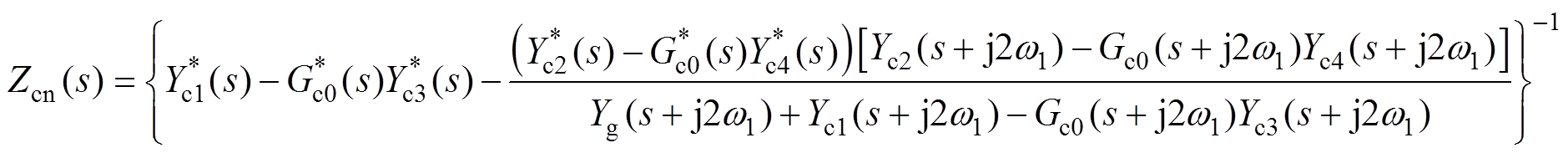 (33)
(33)将Yc1(s)、Yc2(s)、Yc3(s)、Yc4(s)和Gc0(s)代入式(32)和式(33)即可求得Zcp(s)和Zcn(s)。
图5所示为LVSM的控制框图[12]。通过控制模拟传统同步电机的机电暂态方程,使得变换器具有类似的惯性、有功调频和无功调压的特性。同时,为了保证并网电流的质量,根据变换器输出电压指令计算得到并网电流指令,再对输出电流进行准比例谐振(Proportional Resonant, PR)控制。图中,J为虚拟转动惯量;D为阻尼系数;kq、kv分别为无功调节和交流电压调节系数;Hv2(s)=Kp_v2+ Ki_v2/s为直流电压PI控制器传递函数;Hr(s)=-[Krp+Krr/(s2+2wcs+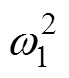 )]为交流电流准PR控制器传递函数;Em为LVSM内电动势幅值参考值;Vr为交流电压幅值参考值;Qr为无功功率参考值;Vdcr为直流侧电压参考值。
)]为交流电流准PR控制器传递函数;Em为LVSM内电动势幅值参考值;Vr为交流电压幅值参考值;Qr为无功功率参考值;Vdcr为直流侧电压参考值。
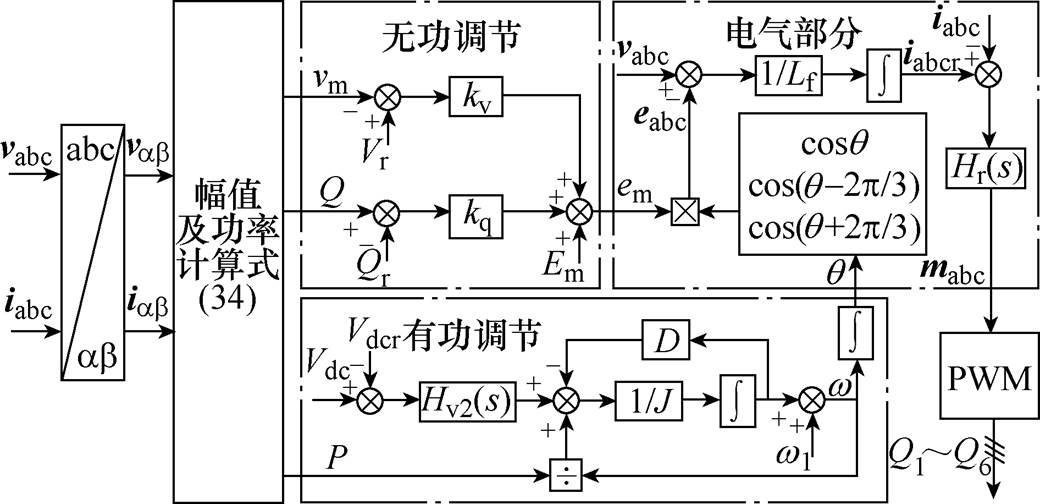
图5 LVSM的控制框图
Fig.5 Control diagram of LVSM
LVSM的有功功率P、无功功率Q以及交流电压幅值vm为
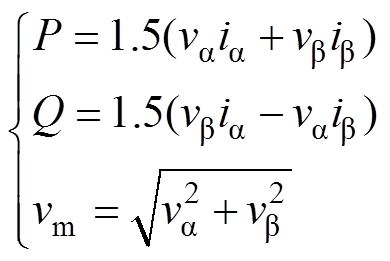 (34)
(34)式中,ia 和ib 为ab 坐标系下LVSM的输入电流;va和vb 为ab 坐标系下LVSM的输入端电压。
在对变换器施加正、负序小信号电压扰动后,电压幅值计算式可利用泰勒公式近似展开为
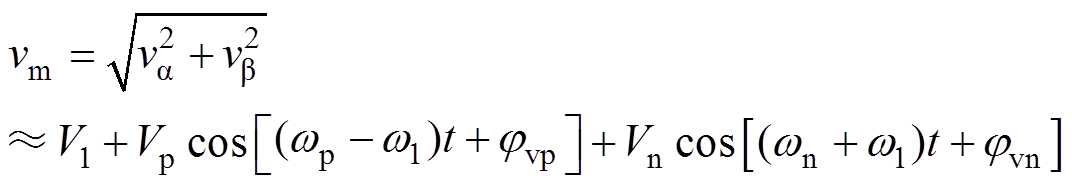 (35)
(35)式中,V1、Vp和Vn分别为基波电压、正序扰动电压和负序扰动电压的幅值;wp和wn分别为正序扰动角频率和负序扰动角频率;jvp和jvn分别为正序扰动电压和负序扰动电压的初相位。
因此,结合式(4),P、Q以及vm在频域中可表示为
 (36)
(36)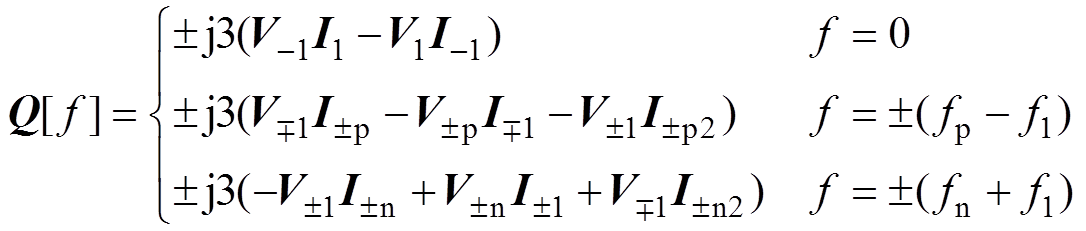 (37)
(37)
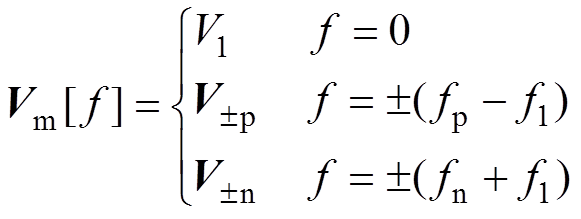 (38)
(38)
根据图5的无功调节控制部分可得LVSM内电动势幅值em在频域中的表达式为
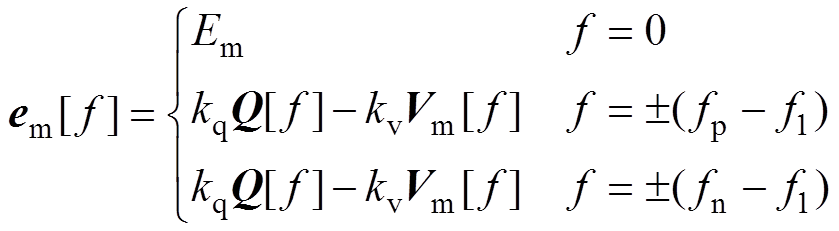 (39)
(39)根据图5的有功调节控制可得LVSM内电动势相位小信号扰动Dq 在频域中的表达式为
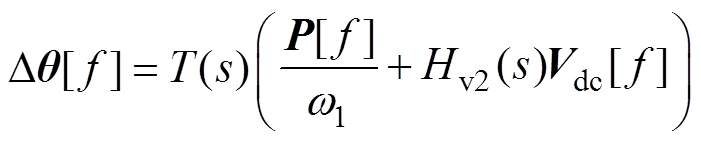 (40)
(40)
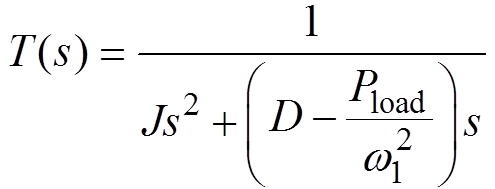 (41)
(41)式中,Pload为LVSM功率稳态值。
LVSM控制中生成的正弦信号为cosq ≈cosq1-Dqsinq1,其中,q1为基波电压相位,再结合式(40)、式(41)和频域卷积定理可得cosq 在频域中的表达式为
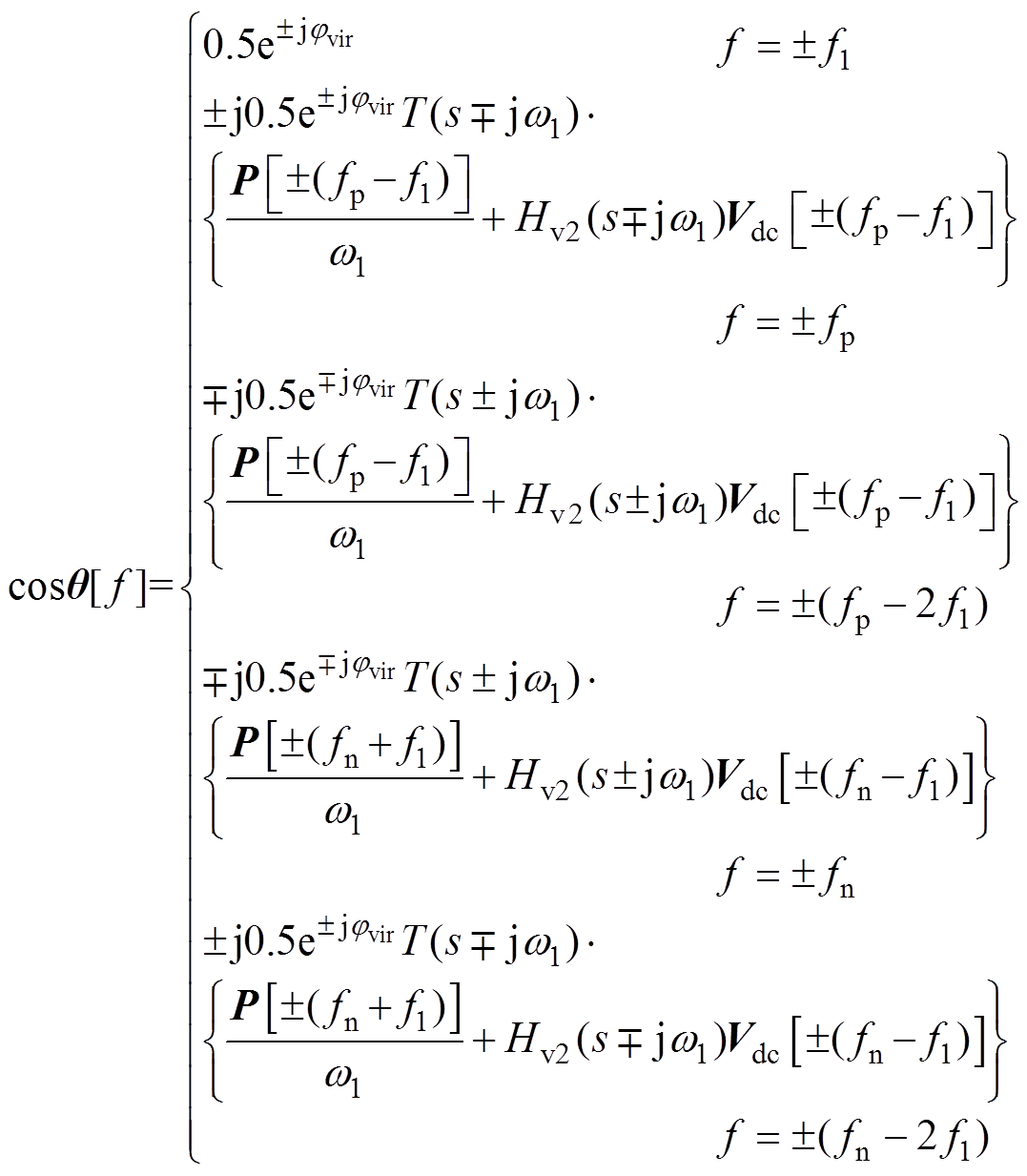 (42)
(42)式中,jvir=-arcsin[2Ploadw1Lf/(3EmV1)]为LVSM内电动势eabc与交流输入电压vabc之间的相位差。
根据图5电气部分控制可得,a相PWM波表达式为
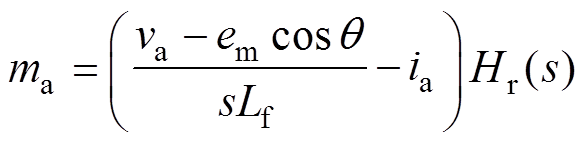 (43)
(43)将式(36)~式(39)和式(42)代入式(43)中,并利用频域卷积定理可得式(6)中频率为fp和fp-2 f1的扰动关系系数分别为
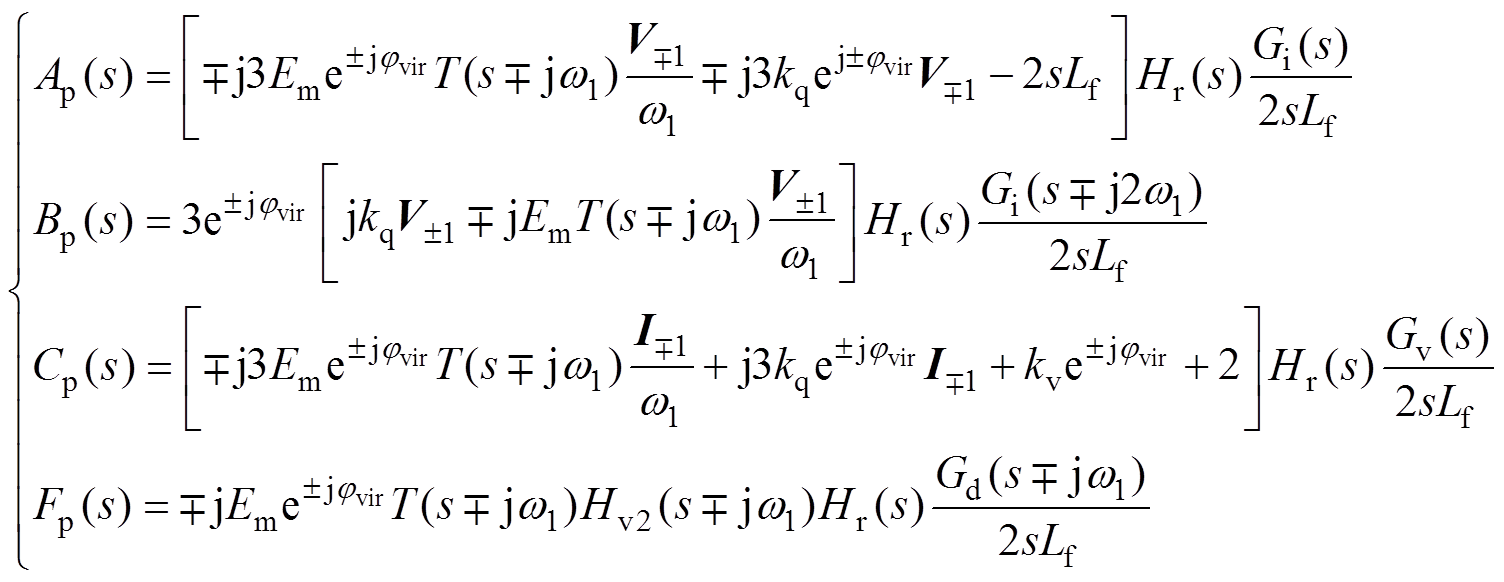 (44)
(44)
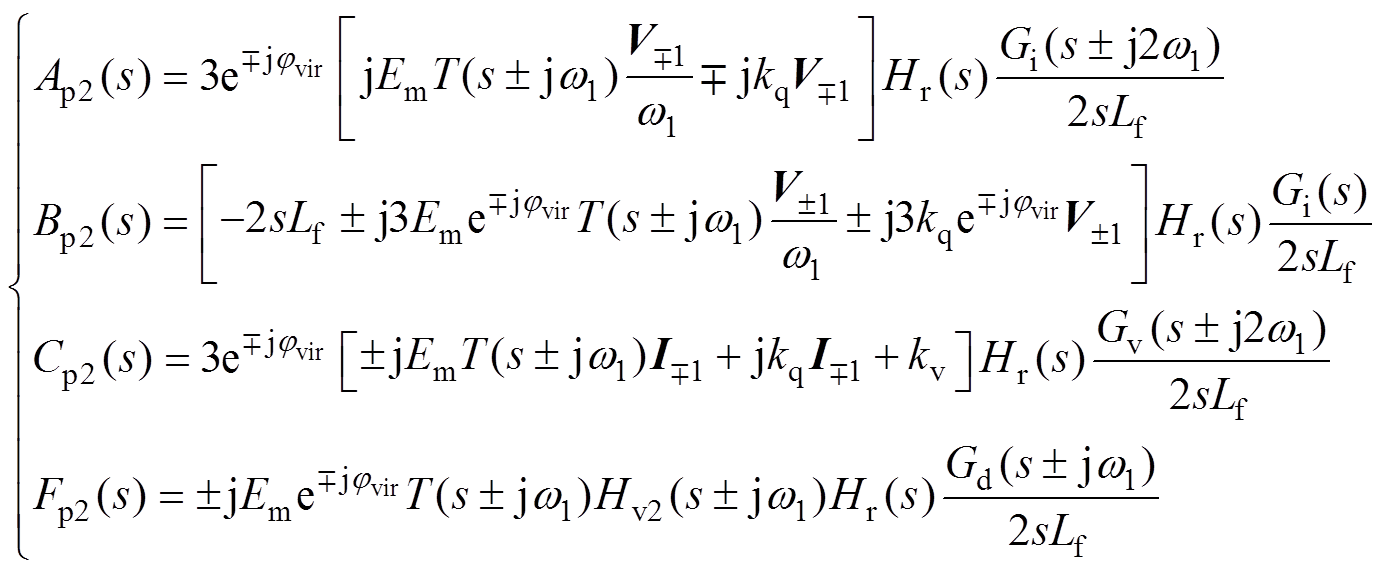 (45)
(45)同理将式(44)和式(45)代入式(10)~式(14)可计算得到对应LVSM的Ym1(s)、Ym2(s)、Ym3(s)、Ym4(s)和Gm0(s),再根据式(15)~式(19)可得LVSM的正序阻抗Zmp(s)和负序阻抗Zmn(s)分别为
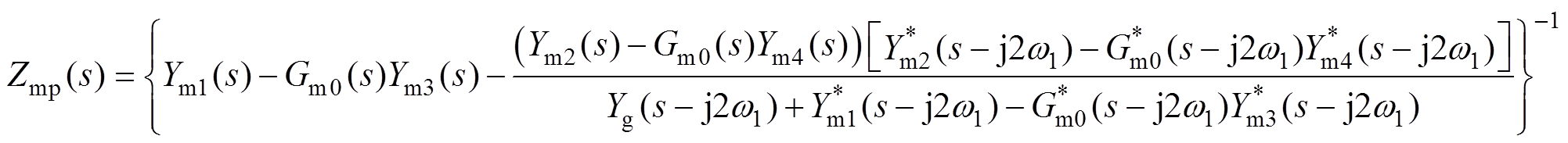 (46)
(46)
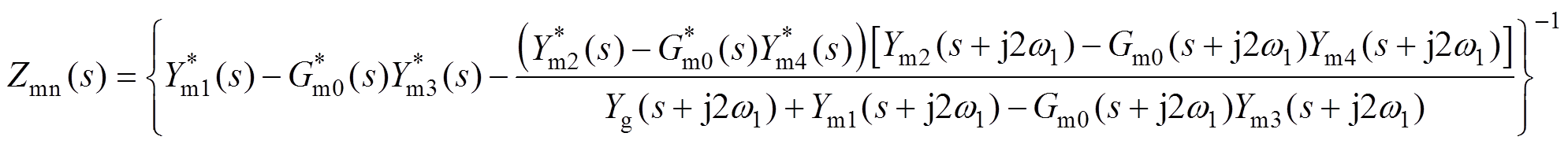 (47)
(47)最后将Ym1(s)、Ym2(s)、Ym3(s)、Ym4(s)和Gm0(s)代入式(46)和式(47)即可计算得到Zmp(s)和Zmn(s)。
为了验证推导的DLCVIC-LC的序阻抗模型,其理论模型频率特性曲线及阻抗仿真测量结果如图6a所示。图中,实线表示电网阻抗Zg(s),虚线和点画线分别表示理论推导的DLCVIC-LC正、负序阻抗模型。方块和圆圈分别表示DLCVIC-LC正、负序阻抗仿真测量结果。阻抗验证所采用的系统参数见表1,其按照文献[14]的参数设计方法计算得到。其中,电流内环控制器的带宽和相位裕度分别为620Hz和75°;直流电压外环的带宽和相位裕度分别为45Hz和77°;锁相环阻尼比设置为0.707,锁相环带宽BWPLL为60Hz;虚拟惯性控制系数Kwv设置为23V/(rad/s);K与锁相环比例系数相同,来增强虚拟惯性控制的稳定性[24]。从图6a中可以看出,测量结果与理论推导结果基本吻合,验证了所建DLCVIC- LC序阻抗模型的正确性。
同样为验证推导的LVSM的序阻抗模型,其理论模型频率特性曲线及阻抗仿真测量结果如图6b所示。图中,实线表示电网阻抗Zg(s),虚线和点画线分别表示理论推导的LVSM正、负序阻抗模型。方块和圆圈分别表示LVSM正、负序阻抗仿真测量结果。LVSM的控制参数按照文献[12]的参数设计方法计算,见表2,其主电路参数与表1一样。从图6b中可以看出,测量结果与理论推导结果基本吻合,验证了所建LVSM序阻抗模型的正确性。

图6 建模及测量的两种负荷变换器序阻抗频率特性
Fig.6 Modeled and measured sequence impedance response of two load converters
表1 DLCVIC-LC的系统参数
Tab.1 System parameters of DLCVIC-LC

参 数数 值参 数数 值 Vdcr/V700Td/ms1 Vg/V220Kp_pll0.833 Lg/mH3.8Ki_pll107.86 Lf/mH2Kp_i0.008 57 Cf/mF22Ki_i1.143 Rd/W1.87Kp_v11 Cdc/mF3Ki_v143 Pload/kW10Kwv/[V/(rad/s)]23 Iqr/A0K0.833 f1/Hz50Kd0.001 8 Tv/ms44Kf0.002 9 Ti/ms44
表2 LVSM的控制参数
Tab.2 Control parameters of LVSM
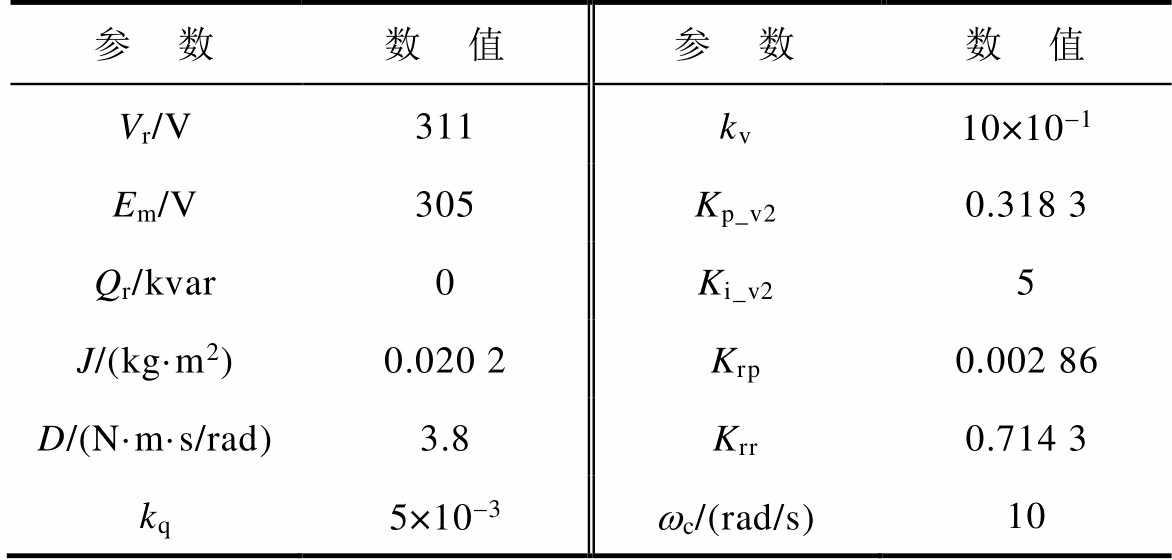
参 数数 值参 数数 值 Vr/V311kv10×10-1 Em/V305Kp_v20.318 3 Qr/kvar0Ki_v25 J/(kg·m2)0.020 2Krp0.002 86 D/(N·m·s/rad)3.8Krr0.714 3 kq5×10-3wc/(rad/s)10
图7和图8分别给出单一参数变化下DLCVIC- LC与LVSM的序阻抗频率特性对比。图中实线和虚线分别表示变换器的正序阻抗和负序阻抗;点线表示电网阻抗。
根据图7和图8可得DLCVIC-LC与LVSM的序阻抗特性对比如下:
1)DLCVIC-LC的正序阻抗在中频段呈负阻容性(相位在-90°~-180°),且随着电网阻抗、虚拟关系控制系数和锁相环带宽的增大,其阻抗幅频曲线在该频段内易与电网的阻抗幅频曲线相交。此 外,电网阻抗Zg(s)在中低频段呈感性特性。因此,DLCVIC-LC的阻抗特性使其在弱电网下易与电网交互作用引发振荡。
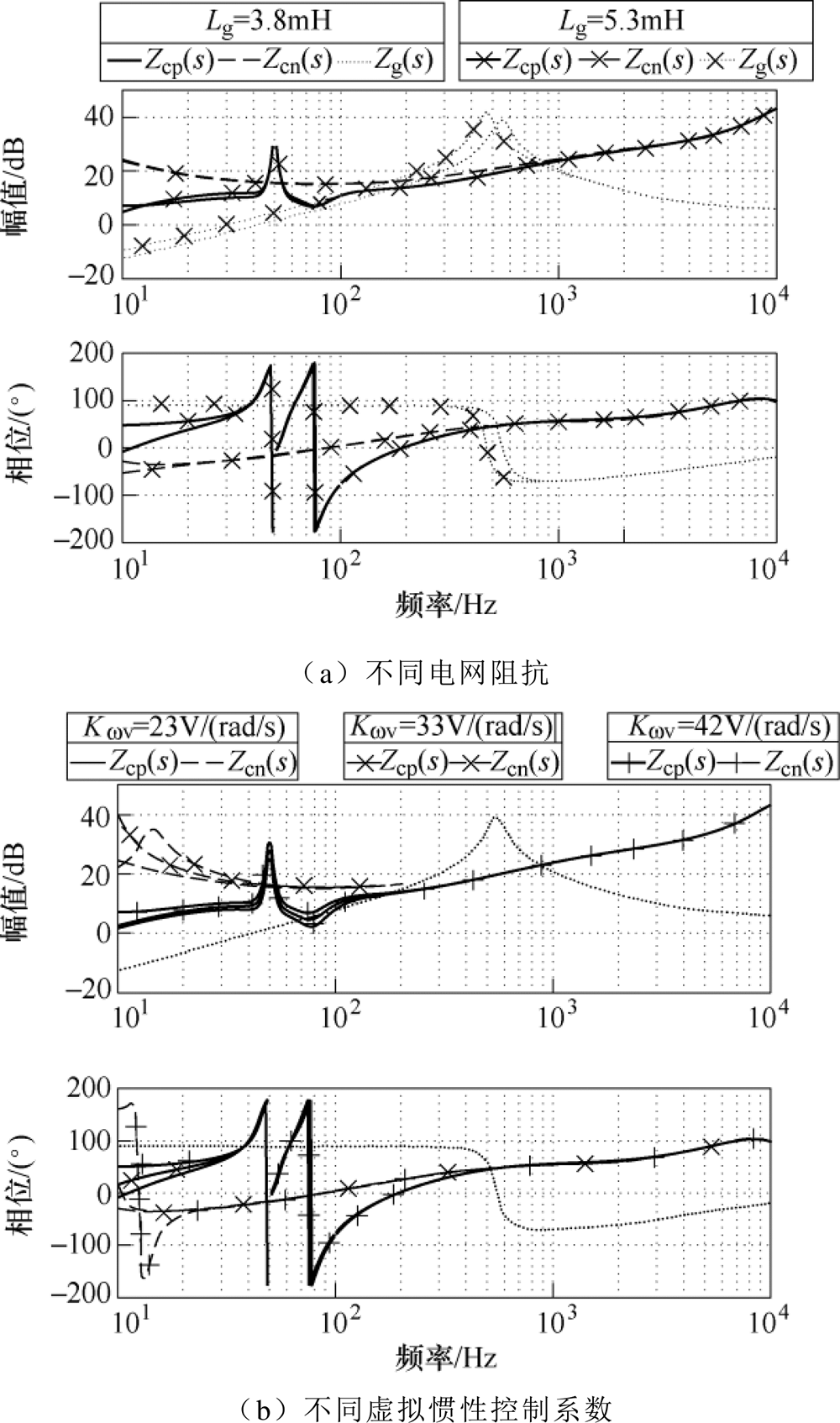
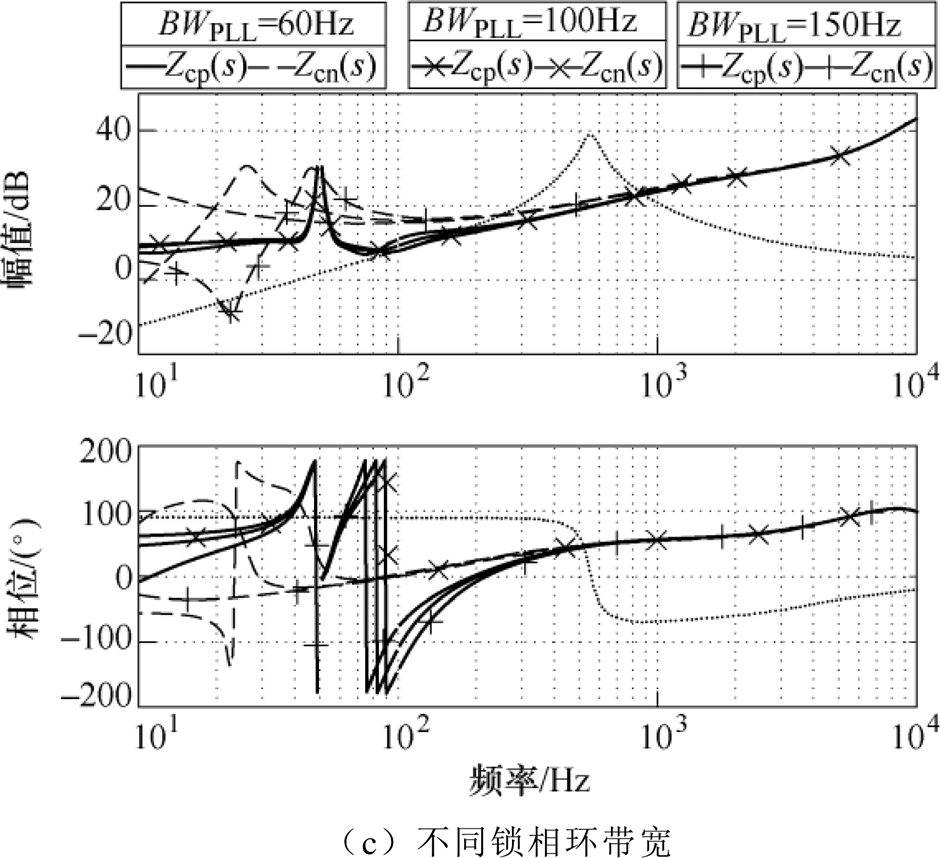
图7 不同参数下DLCVIC-LC的序阻抗频率特性对比
Fig.7 Sequence impedance response comparison of DLCVIC-LC with different parameters

图8 不同参数下LVSM的序阻抗频率特性对比
Fig.8 Sequence impedance response comparison of LVSM with different parameters
2)LVSM的正序阻抗基本呈感性,在中低频段与电网的阻抗特性基本一致,负序阻抗只在低频段呈容性,并且负序阻抗在负阻容性的频段内,阻抗幅值远小于电网阻抗幅值。因此,LVSM具有更优良的阻抗特性以避免在弱电网中发生振荡。
本文采用单输入单输出形式的序阻抗进行稳定性分析,因此可以利用Nyquist稳定判据分别对正、负序阻抗比进行分析。负荷变换器接入电网的小信号等效电路如图9所示。DLCVIC-LC对外等效为电流源与输入阻抗并联的形式,如图9a所示,其输入电流可以表示为
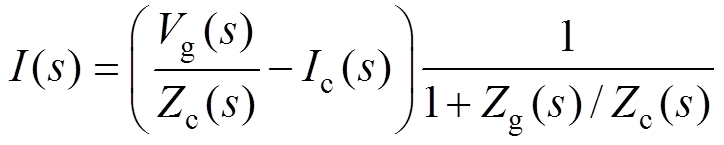 (48)
(48)因理想电网电压Vg(s)稳定且变换器接入理想电网时能保持稳定,即1/Zc(s)无右半平面极点,则系统的稳定性取决于1/(1+Zg(s)/Zc(s)),并且Zg(s)/Zc(s)没有右半平面极点,因此采用阻抗比Zg(s)/Zc(s)进行判稳时只需简单判断Nyquist曲线是否包围 (-1, j0)点。
LVSM对外等效为电压源与输入电阻串联的形式,如图9b所示,其输入电流可以表示为
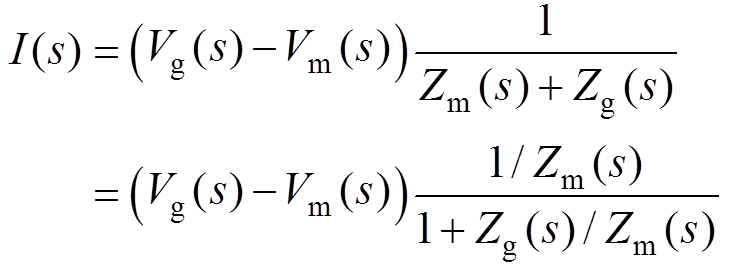 (49)
(49)因理想电网电压Vg(s)与理想变换器电压Vm(s)稳定,则输出电流的稳定性取决于1/(Zm(s)+Zg(s))。考虑到采用Nyquist稳定判据时,通常要求开环传递函数分母的阶数比分子高,使Nyquist曲线不会随着频率的增加而趋于无穷,易于判稳,又由于变换器阻抗Zm(s)的阶数比电网阻抗Zg(s)要高,因此,采用阻抗比Zg(s)/Zm(s)进行判稳。而电网阻抗Zg(s)不会含有右半平面的极点,因此,当Nyquist曲线逆时针包围(-1, j0)点的圈数等于变换器阻抗Zm(s)右半平面零点个数时,系统稳定。
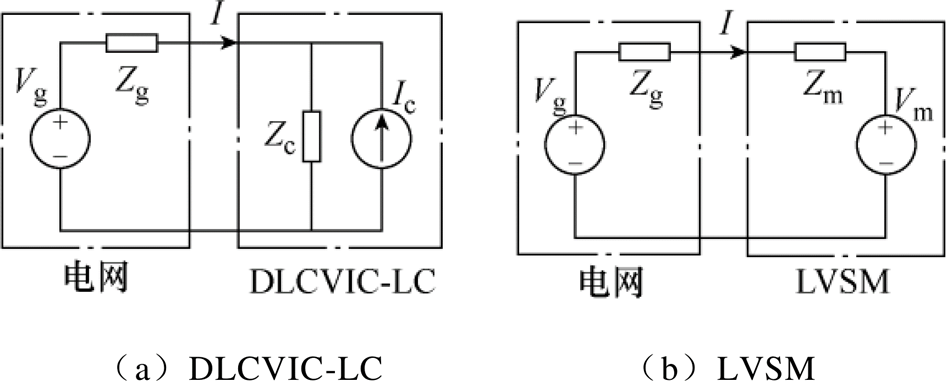
图9 负荷变换器接入电网的小信号等效电路
Fig.9 Small-signal representation of load converter connected to weak grid
图10所示为单一参数变化下DLCVIC-LC判稳阻抗比的Nyquist图(频率从10~105Hz),其余系统参数均见表1。正序阻抗比用实线表示,负序阻抗比用虚线表示。由图10a可知,随着电网强度变弱,Nyquist曲线越容易包围(-1, j0)点,系统越不稳定。当Lg增加至5.3mH时,Nyquist曲线包围了(-1, j0)点,系统出现振荡。由图10b可知,随着虚拟惯性的增强,系统越不稳定,当Kwv增加到42V/(rad/s)时,Nyquist曲线包围(-1, j0)点,系统出现振荡。从图10c可知,锁相环带宽BWPLL越大,系统越不稳定,当BWPLL≥150Hz时,Nyquist曲线包围了(-1, j0)点,系统不稳定。
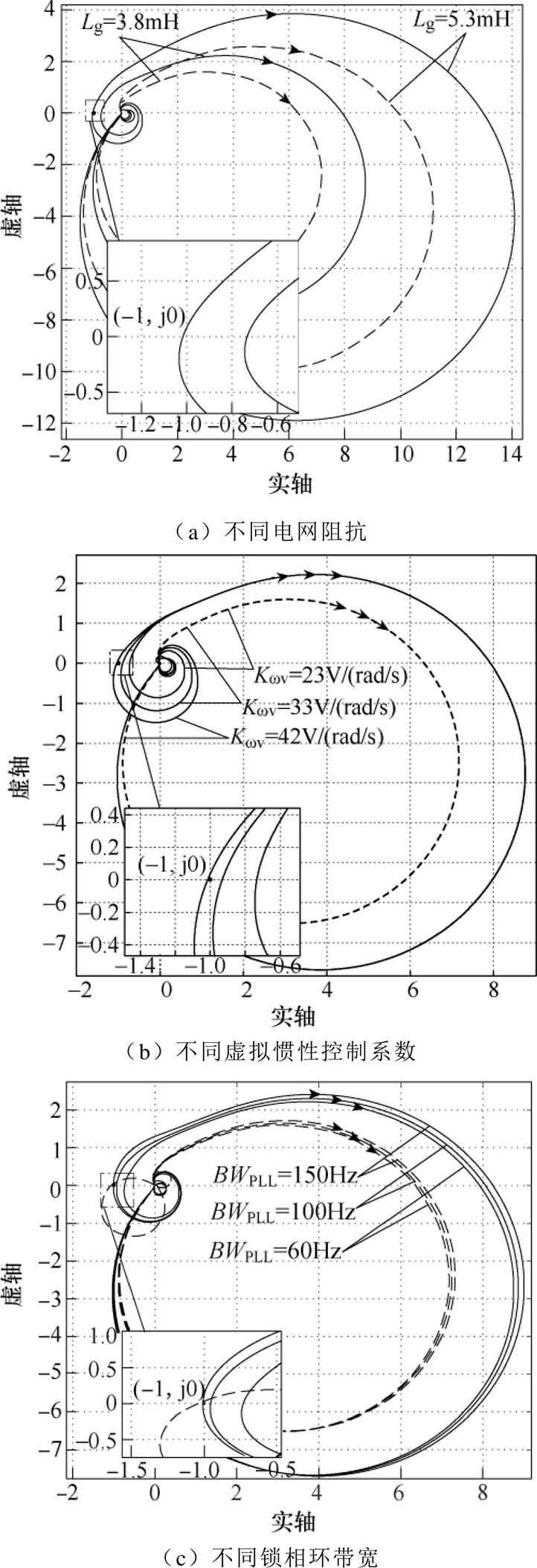
图10 不同参数下DLCVIC-LC判稳阻抗比的Nyquist图
Fig.10 Nyquist plots of DLCVIC-LC impedance ratio for stability assessment with different parameters
图11所示为单一参数变化下LVSM判稳阻抗比Nyquist图(频率从10~105Hz),其余系统参数均见表2。正序阻抗比用实线表示,负序阻抗比用虚线表示。从LVSM序阻抗频率特性曲线上可以看出,其正序阻抗无右半平面零点,负序阻抗包含二阶微分环节,具有一对共轭的右半平面零点。因此,当其正序阻抗比Nyquist曲线不包围(-1, j0)点以及负序阻抗比正频率Nyquist曲线从(-1, j0)左侧正穿越一次时,系统稳定。从图11a中可以看出,随着电网阻抗的增大,LVSM始终能保持稳定。此外,LVSM虚拟转动惯量变化时的Nyquist曲线如图11b所示,从图11b中可以看出,虚拟转动惯量的变化对系统稳定性的影响较小。因此,LVSM具有较强的适应弱电网的能力。
为验证本文理论分析和结论的正确性,在实验室搭建一台10kW的三相负荷变换器原理样机,直流侧所带负荷采用纯电阻负荷。DLCVIC-LC与LVSM具有相同的主电路参数,实验参数见表1和表2。

图11 不同参数下LVSM判稳阻抗比的Nyquist图
Fig.11 Nyquist plots of LVSM impedance ratio for stability assessment with different parameters
图12为不同参数下DLCVIC-LC交流电流波形。由图12a可知,当电网电感Lg由3.8mH增加到5.3mH时,变换器输出电流出现振荡。由图12b可知,当虚拟惯性控制系数Kwv由23V/(rad/s)增加到42V/(rad/s)时,系统也开始振荡。由图12c可知,当锁相环带宽BWPLL从60Hz增加到150Hz时,系统发生振荡。图13为Lg从3.8mH增加至10mH时,LVSM交流电流波形,可以看出,变换器仍然能稳定运行,没有振荡。因此,实验结果与Nyquist稳定判据分析的结果一致,表明在弱电网中LVSM比DLCVIC-LC具有更好的运行稳定性。
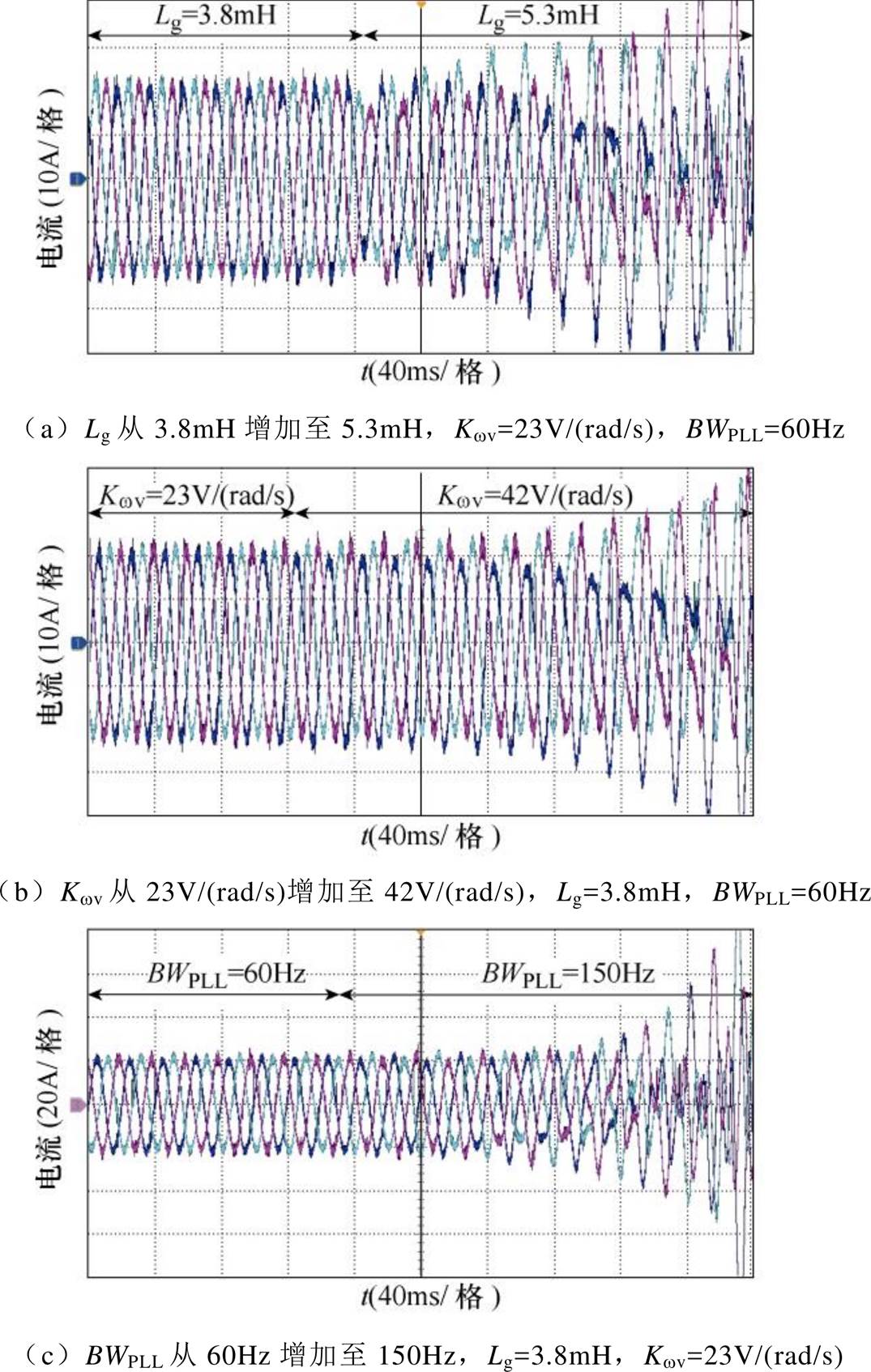
图12 不同参数下DLCVIC-LC三相电流波形
Fig.12 Three-phase current waveforms of DLCVIC-LC with different parameter

图13 不同电网阻抗下LVSM三相电流波形
Fig.13 Three-phase current waveforms of LVSM with different grid impedance
本文从序阻抗的角度分析了DLCVIC-LC及LVSM两种负荷变换器接入弱电网的稳定性问题。在考虑直流电压控制与频率耦合的影响下,推导三相负荷变换器通用序阻抗计算式,并据此建立了两种负荷变换器精确的序阻抗模型。基于所推导的序阻抗模型和Nyquist稳定判据,对比分析了两种负荷变换器在不同电网阻抗以及控制参数下的稳定性。本文所采用的分析方法基于小信号序阻抗模型,适用于分析变换器在不同强度电网条件下与电网的交互稳定性,而在系统故障、电压暂降等大扰动条件下,系统模型不再可以近似为线性,本文的分析方法不再适用。本文得到以下几点结论:
1)LVSM的正序阻抗基本呈感性,在中低频段与电网的阻抗特性基本一致,不易引发负荷变换器与弱电网交互振荡;而由于DLCVIC-LC的正序阻抗在中频段呈负阻容性,且随着电网强度变弱,其幅频曲线越容易在该频段内与电网阻抗的幅频曲线相交,进而引发系统振荡。
2)DLCVIC-LC与电网的交互稳定性受到虚拟惯性控制系数及锁相环带宽的影响,虚拟惯性控制系数或者锁相环带宽越大,越容易发生振荡。
3)LVSM的阻抗特性有利于避免在弱电网中发生谐波振荡;而DLCVIC-LC的阻抗特性使其容易与电网相互作用导致谐波振荡。因此,在弱电网中,LVSM比DLCVIC-LC具有更好的运行稳定性。
参考文献
[1] 郑天文, 陈来军, 陈天一, 等. 虚拟同步发电机技术及展望[J]. 电力系统自动化, 2015, 39(21): 165- 175.
Zheng Tianwen, Chen Laijun, Chen Tianyi, et al. Review and prospect of virtual synchronous generatortechnologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175.
[2] Zhong Qingchang, Weiss G. Synchronverters: inver- ters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[3] 张玉治, 张辉, 贺大为, 等. 具有同步发电机特性的微电网逆变器控制[J]. 电工技术学报, 2014, 29(7): 261-268.
Zhang Yuzhi, Zhang Hui, He Dawei, et al. Control strategy of micro grid converters with synchronous generator characteristic[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 261-268.
[4] 孟建辉, 彭嘉琳, 王毅, 等. 多约束下光储系统的灵活虚拟惯性控制方法[J]. 电工技术学报, 2019, 34(14): 3046-3058.
Meng Jianhui, Peng Jialin, Wang Yi, et al. Multi- constrained flexible virtual inertial control method for photovoltaic energy storage system[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(14): 3046-3058.
[5] Zhong Qingchang, Ma Zhenyu, Ming Wenlong, et al. Grid-friendly wind power systems based on the synchronverter technology[J]. Energy Conversion and Management, 2015, 8(9): 719-726.
[6] Aouini R, Marinescu B, Kilani K B, et al. Synch- ronverter-based emulation and control of HVDC transmission[J]. IEEE Transactions on Power Systems, 2016, 31(1): 278-286.
[7] 钟庆昌. 虚拟同步机与自主电力系统[J]. 中国电机工程学报, 2017, 37(2): 336-348.
Zhong Qingchang. Virtual synchronous machines and autonomous power systems[J]. Proceedings of the CSEE, 2017, 37(2): 336-348.
[8] Zhong Qingchang, Ma Zhenyu, Nguyen P L. PWM- controlled rectifiers without the need of an extra synchronisation unit[C]//IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 2012: 691-695.
[9] 胡文强, 吴在军, 窦晓波, 等. 负荷虚拟同步机及其低电压故障穿越控制[J]. 电力系统自动化, 2018, 43(9): 100-107.
Hu Wenqiang, Wu Zaijun, Dou Xiaobo, et al. Load virtual synchronous machine and its low voltage ride-through control[J]. Automation of Electric Power Systems, 2018, 43(9): 100-107.
[10] 缪惠宇, 梅飞, 张宸宇, 等. 基于虚拟阻抗的虚拟同步整流器三相不平衡控制策略[J]. 电工技术学报, 2019, 34(17): 3622-3630.
Miao Huiyu, Mei Fei, Zhang Chenyu, et al. Three phase unbalanced control strategy for virtual synchronous rectifier based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3622-3630.
[11] 刘其辉, 逯胜建. 参与微电网调频的电动汽车虚拟同步机充放电控制策略[J]. 电力系统自动化, 2018, 42(9): 171-179.
Liu Qihui, Lu Shengjian. Charging and discharging control strategy based on virtual synchronous machine for electrical vehichlesparticipating in frequency regulation of microgrid[J]. Automation of Electric Power Systems, 2018, 42(9): 171-179.
[12] 高丙团, 夏超鹏, 张磊, 等. 基于虚拟同步电机技术的VSC-HVDC整流侧建模及参数设计[J]. 中国电机工程学报, 2017, 37(2): 534-543.
Gao Bingtuan, Xia Chaopeng, Zhang Lei, et al. Modeling and parameters design for rectifier side of VSC-HVDC based on virtual synchronous machine technology[J]. Proceedings of the CSEE, 2017, 37(2): 534-543.
[13] Fang Jingyang, Li Hongchang, Tang Yi, et al. Distri- buted power system virtual inertia implemented by grid-connected power converters[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8488-8499.
[14] Fang Jingyang, Lin Pengfeng, Li Hongchang, et al. An improved virtual inertia control for three-phase voltage source converters connected to a weak grid[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 8660-8670.
[15] Liserre M, Teodorescu R, Blaabjerg F. Stability of photovoltaic and wind turbine grid-connected invertersfor a large set of grid impedance values[J]. IEEE Transa- ctions on Power Electronics, 2006, 21(1): 263-272.
[16] 黄云辉, 宋泽凡, 唐金瑞, 等. 连接弱电网的并网变换器直流电压时间尺度稳定器的设计与分析[J]. 电工技术学报, 2018, 33(增刊1): 185-192.
Huang Yunhui, Song Zefan, Tang Jinrui, et al. Design and analysis of DC-link voltage stabilizer for voltage source converter as connected to weak grid[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 185-192.
[17] 谢志为, 陈燕东, 伍文华, 等. 弱电网下多逆变器并网系统的全局高频振荡抑制方法[J]. 电工技术学报, 2020, 35(4): 885-895.
Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A global high-frequency oscillation suppression method for multi-inverter grid-connected system in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 885-895.
[18] 张学广, 夏丹妮, 陈文佳, 等. 三相并网变流器弱电网下频率耦合抑制控制方法[J]. 电工技术学报, 2019, 34(12): 4559-4571.
Zhang Xueguang, Xia Danni, Chen Wenjia, et al. Frequency coupling suppression control method for three-phase grid-connected converter under weak grid[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 4559-4571.
[19] Wen Bo, Boroyevich D, Burgos R, et al. Small-signal stability analysis of three-phase AC systems in the presence of constant power loads based on measured d-q frame impedances[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5952-5963.
[20] Wen Bo, Boroyevich D, Mattavelli P, et al. Impedance- based analysis of grid-synchronization stability for three-phase paralleled converters[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(1): 26-38.
[21] Lu Dapeng, Wang Xiongfei, Blaabjerg F. Impedance- based analysis of DC-link voltage dynamics in voltage-source converters[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3973-3985.
[22] Li Chi, Burgos R, Wen Bo, et al. Analysis of STATCOM small-signal impedance in the synch- ronous D-Q frame[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1894-1910.
[23] Sun Jian. Small-signal methods for AC distributed power systems: a review[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2545-2554.
[24] Cespedes M, Sun Jian. Impedance modeling and analysis of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1254-1261.
[25] Liu Hanchao, Sun Jian. Voltage stability and control of offshore wind farms with AC collection and HVDC transmission[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(4): 1181-1189.
[26] 张明远, 肖仕武, 田恬, 等. 基于阻抗灵敏度的直驱风电场并网次同步振荡影响因素及参数调整分析[J]. 电网技术, 2018, 42(9): 2768-2777.
Zhang Mingyuan, Xiao Shiwu, Tian Tian, et al. Analysis of SSO influencing factors and parameter adjustment for grid-connected full-converter wind farm based on impedance sensitivity[J]. Power System Technology, 2018, 42(9): 2768-2777.
[27] 刘津铭, 陈燕东, 伍文华, 等. 孤岛微电网序阻抗建模与高频振荡抑制[J]. 电工技术学报, 2020, 35(7): 1538-1552.
Liu Jinming, Chen Yandong, Wu Wenhua, et al. Sequence impedance modeling and high-frequency oscillation suppression method for island micro- grid[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1538-1552.
[28] 伍文华, 陈燕东, 周乐明, 等. 虚拟同步发电机接入弱电网的序阻抗建模与稳定性分析[J]. 中国电机工程学报, 2019, 39(6): 1560-1571.
Wu Wenhua, Chen Yandong, Zhou Leming, et al. Sequence impedance modeling and stability analysis for virtual synchronous generator connected to the weak grid[J]. Proceedings of the CSEE, 2019, 39(6): 1560-1571.
[29] 伍文华, 周乐明, 陈燕东, 等. 序阻抗视角下虚拟同步发电机与传统并网逆变器的稳定性对比分析[J]. 中国电机工程学报, 2019, 39(5): 1411-1420.
Wu Wenhua, Zhou Leming, Chen Yandong, et al. Stability comparison and analysis between the virtual synchronous generator and the traditional grid- connected inverter in the view of sequence impedance[J]. Proceedings of the CSEE, 2019, 39(5): 1411-1420.
[30] Wang Xiongfei, Blaabjerg F, Harmonic stability in power electronic-based power systems: concept, modeling, and analysis[J]. IEEE Transactions on Smart Grid, 2019, 10(3): 2858-2870.
[31] Rygg A, Molinas M, Zhang Chen, et al. A modified sequence-domain impedance definition and its equi- valence to the dq-domain impedance definition for the stability analysis of AC power electronic systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1383-1396.
[32] Rygg A, Molinas M, Zhang Chen, et al. On the equivalence and impact on stability of impedance modelling of power electronic converters in different domains[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(4): 1444-1454.
[33] Wang Xiongfei, Harnefors L, Blaabjerg F. A unified impedance model of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electro- nics, 2018, 33(2): 1775-1787.
Sequence Impedance Modeling and Stability Analysis of Load Converter with Virtual Inertia Control Connected to Weak Grid
Abstract Both load virtual synchronous machine (LVSM) and load converter based on DC-link capacitor virtual inertia control (DLCVIC-LC) can enhance the power system inertia. However, inevitably, there are some interaction problems like harmonic resonance in weak grids. In this paper, considering the DC-link voltage dynamics and frequency-coupling effects, the general sequence impedance formulas for three-phase load converters were derived. Then, the precise sequence impedance models were built for impedance characteristics comparison analysis of LVSM and DLCVIC-LC. The analysis shows that the positive-sequence impedance of LVSM is generally inductive, which is basically consistent with the grid impedance characteristics and hardly causes harmonic resonance. In contrast, the positive-sequence impedance of LCVIC is negative-resistive-capacitive (i.e., phase angle is between -180° and -90°) in the middle-frequency band, which is likely to cause harmonic oscillation in weak grids. Furthermore, based on the derived model and Nyquist stability criterion, the effects of grid impedance and other control parameters on the stability of the two load converters connected to the grid were analyzed. Finally, experiments were performed to validate the analysis.
keywords:Load converter, virtual inertia, sequence impedance modeling, stability analysis, weak grid
中图分类号:TM461
DOI: 10.19595/j.cnki.1000-6753.tces.191697
国家自然科学基金(51907058)和国网湖南省电力有限公司(SGTYHT/18-JS-206)资助项目。
收稿日期 2019-12-02
改稿日期 2020-05-19
刘一锋 男,1994年生,博士研究生,研究方向为电力电子变换器建模与控制。E-mail: 573430757@qq.com
周小平 男,1990年生,博士,研究方向为分布式发电、微电网控制及电能质量控制。E-mail: zxp2011@hnu.edu.cn(通信作者)
(编辑 崔文静)