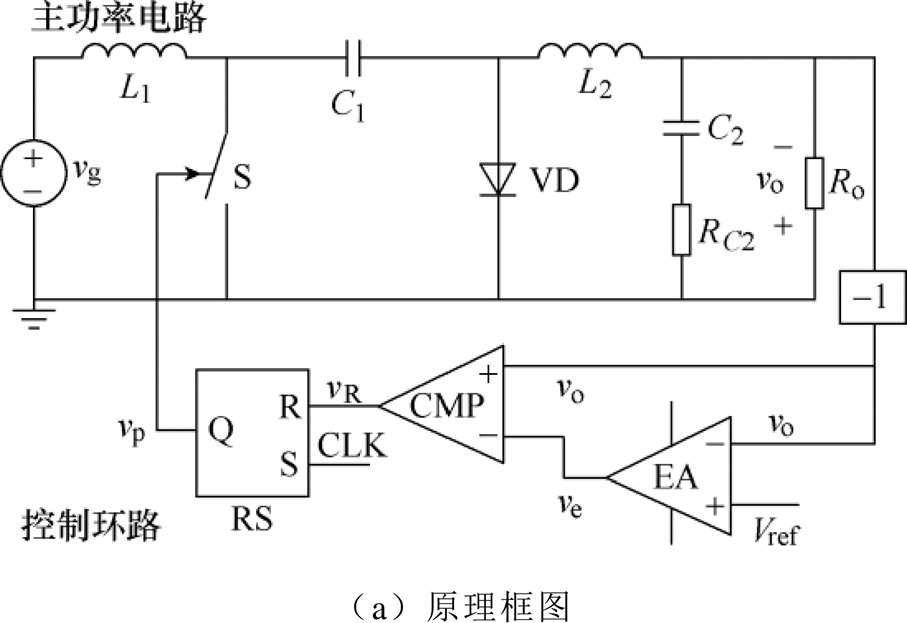
图1 V2控制CCM Cuk变换器
Fig.1 V2 controlled CCM Cuk converter
摘要 将具有快速瞬态响应的V2控制技术应用于Cuk变换器,分析了V2控制Cuk变换器工作于电感电流连续导电模式(CCM)的原理。利用时间平均等效建模方法,推导包含输出电容等效串联电阻(ESR)的CCM Cuk变换器主电路传递函数。在此基础上,建立V2控制和峰值电流控制CCM Cuk变换器的精确小信号模型,详细推导控制-输出传递函数及输出阻抗,并从频域角度对比分析V2控制和峰值电流控制CCM Cuk变换器的瞬态特性。建立V2控制和峰值电流控制CCM Cuk变换器的时域仿真模型和实验电路,通过仿真和实验对比分析两种变换器的稳态和瞬态性能。研究结果表明:V2控制与峰值电流控制CCM Cuk变换器具有相同的稳态性能;相比于峰值电流控制,V2控制CCM Cuk变换器具有更快的负载响应速度。
关键词:V2控制 Cuk变换器 小信号模型 瞬态性能
近年来,随着电力电子技术以及新能源技术的不断发展,DC-DC变换器因具有高功率密度、高效率等特性而得到了广泛的应用[1-3]。在基本的开关变换器中,Buck和Boost变换器因电路结构简单,应用最为广泛。但在一些需要公共接地、正电压输入负电压输出的电路设备和系统中,如运算放大器、电信模块和数据采集系统,Buck和Boost变换器往往不适用[4]。Buck-Boost变换器虽然可以输出负电压,也具有电路结构简单的优点,但其输入电流和输出电流不连续,应用场合受到了限制。
Cuk变换器是一种四阶开关变换器,可以实现负电压输出,且具有实现升压或降压的能力[5]。与Buck、Boost和Buck-Boost变换器不同的是,Cuk变换器的输入、输出电流可以始终保持连续[6]。将Cuk变换器的两个电感进行耦合,通过合理设置电感的耦合系数和匝比,可以实现Cuk变换器的输入、输出电流零纹波[7]。由于Cuk变换器的优良性能较多,它已广泛应用于功率因数校正电路[8]、风能及光伏发电系统[9-10]、发光二极管驱动电路[11]、电机驱动[12]和新能源汽车[13]等领域。
Cuk变换器的控制技术得到了学者的广泛关注。文献[14]将峰值电流控制应用于Cuk变换器,并根据离散迭代映射模型分析了峰值电流控制Cuk变换器的混沌和分叉行为。文献[15]将基于遗传算法的线性二次控制应用至Cuk变换器,在一定程度上提高了变换器的阶跃响应。文献[16]将滑模控制应用至Cuk变换器,降低了基于Cuk变换器的光伏逆变器的设计难度。在对Cuk变换器负载瞬态性能要求较高的应用场合,如当Cuk变换器应用于电动汽车时[17],时刻变化的路面情况要求Cuk变换器具有快速的负载瞬态响应,已有的控制方法很难满足要求。
开关变换器的V2控制技术具有快速的负载响应速度,在学术界和工业界得到了广泛的应用[18-20]。为了提高Cuk变换器的瞬态性能,本文将V2控制技术应用至Cuk变换器,实现V2控制Cuk变换器。以V2控制Cuk变换器工作于电感电流连续导电模式(Continuous Conduction Mode, CCM)为例,在分析其工作原理的基础上,建立包含输出电容等效串联电阻(Equivalent Series Resistance, ESR)的V2控制及峰值电流控制CCM Cuk变换器小信号模型,并推导控制至输出传递函数以及半闭环输出阻抗。从频域的角度对比分析V2控制和峰值电流控制CCM Cuk变换器的瞬态性能,并通过时域仿真和实验样机验证理论分析的正确性。
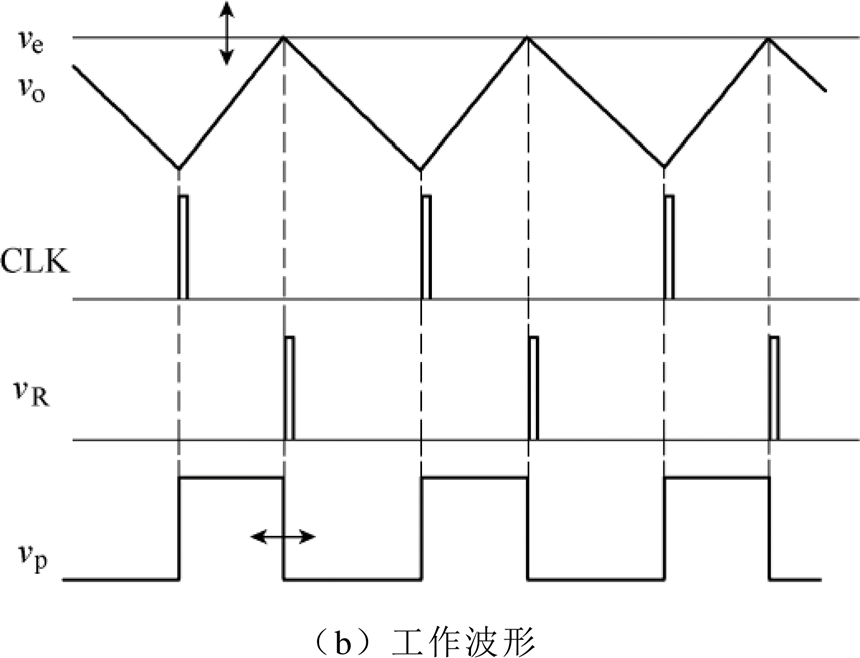
V2控制CCM Cuk变换器如图1所示。图1a所示的原理框图中包含主功率电路和控制环路两部分。主功率电路由输入电压vg、电感L1和L2、开关管S、中间电容C1、二极管VD、输出电容C2、等效串联电阻RC2和负载Ro组成。控制环路主要由误差放大器EA、比较器CMP、时钟CLK和触发器RS组成。在图1b所示的工作波形中,vp为开关管S的驱动波形;ve为控制信号,由输出电压vo与参考电压Vref经过误差放大器EA产生。


图1 V2控制CCM Cuk变换器
Fig.1 V2 controlled CCM Cuk converter
由图1b所示的V2控制CCM Cuk变换器工作波形可知,当时钟脉冲CLK到来时,触发器RS的S端输入高电平,触发器置位,其输出端Q的输出信号vp为高电平,开关管S导通。此时,二极管VD截止,电感电流iL1和iL2增加,输出电压vo增加;当输出电压上升至控制信号ve时,比较器CMP输出高电平,即触发器RS的R端输入高电平,触发器复位,其输出端Q的输出信号vp为低电平,开关管S关断。此时,二极管VD导通,电感电流iL1和iL2下降,输出电压vo下降,直至下一个时钟脉冲的到来。
采用时间平均等效电路建模方法[21],将CCM Cuk变换器中的开关器件用受控电压源和受控电流源进行等效。根据等效后不形成电流源(电感)割集和电压源(电容)回路的原则,将开关管S等效为受控电流源 ,二极管VD等效为受控电压源
,二极管VD等效为受控电压源 ,可以得到CCM Cuk变换器的时间平均等效电路如图2所示。
,可以得到CCM Cuk变换器的时间平均等效电路如图2所示。
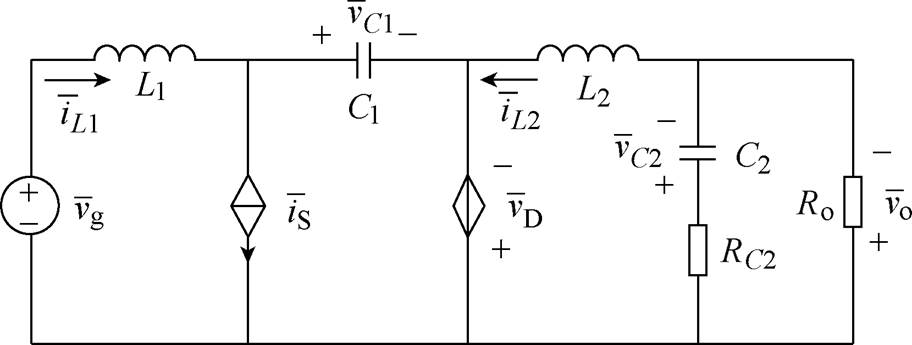
图2 CCM Cuk变换器的时间平均等效电路
Fig.2 Time averaging equivalent circuit of CCM Cuk converter
图2中,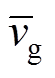 、
、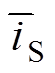 、
、 、
、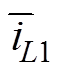 、
、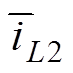 、
、 、
、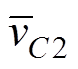 和
和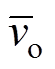 分别是输入电压vg、开关管电流iS、二极管电压vD、电感电流iL1、电感电流iL2、中间电容电压vC1、输出电容电压vC2和输出电压vo的时间平均分量。且满足
分别是输入电压vg、开关管电流iS、二极管电压vD、电感电流iL1、电感电流iL2、中间电容电压vC1、输出电容电压vC2和输出电压vo的时间平均分量。且满足
 (1)
(1)式中,d为开关管S的占空比。
当输入电压或占空比存在小信号扰动时,会引起电路中其他状态变量及等效受控源的小信号扰动。根据式(1),忽略2次及以上小信号分量,有
 (2)
(2)分离式(2)中的直流稳态分量与交流小信号分量,可分别得到CCM Cuk变换器的直流稳态等效电路和交流小信号等效电路,分别如图3和图4所示。图中,Vg、IS、D、IL1、IL2、VD、VC1为直流稳态分量;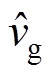 、
、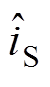 、
、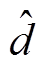 、
、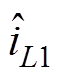 、
、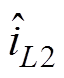 、
、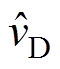 、
、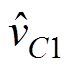 为小信号扰动分量。
为小信号扰动分量。
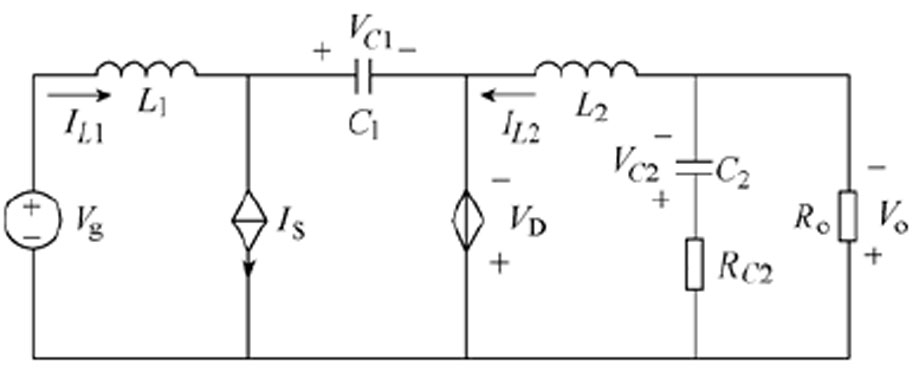
图3 CCM Cuk变换器的直流稳态等效电路
Fig.3 Steady state equivalent circuit of CCM Cuk converter
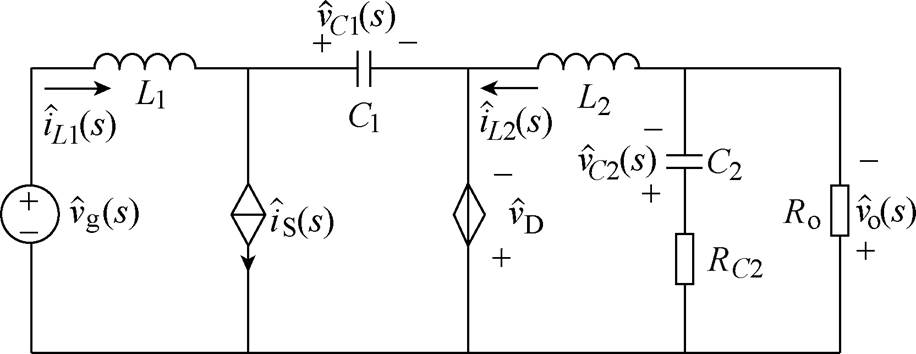
图4 CCM Cuk变换器的交流小信号等效电路
Fig.4 AC small-signal equivalent circuit of CCM Cuk converter
在图3所示的直流稳态等效电路中,存在关系为
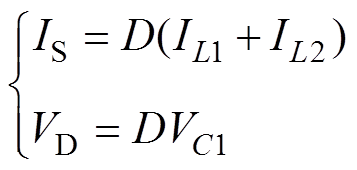 (3)
(3)在分析直流稳态特性时,将图3中的电容C1和C2看作开路,电感L1和L2看作短路。根据基尔霍夫电压定律(Kirchhoff’s Voltage Law, KVL)和基尔霍夫电流定律(Kirchhoff’s Current Law, KCL)可得
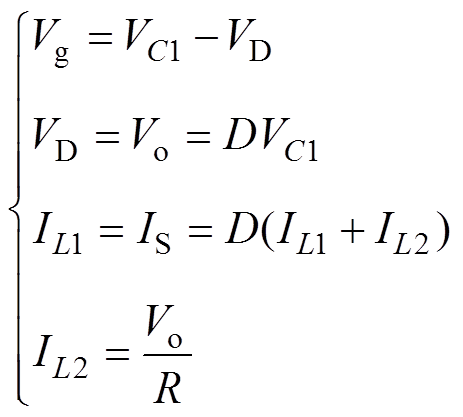 (4)
(4)
联立式(3)、式(4),可求得CCM Cuk变换器的直流电压传输比M以及电感L1与电感L2的电流稳态值之和IL为
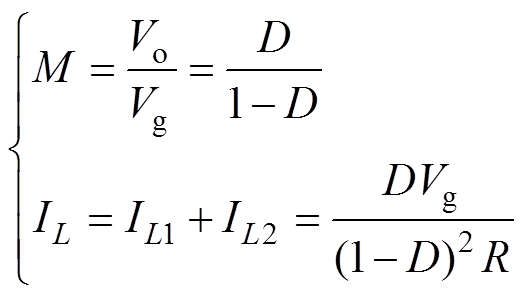 (5)
(5)在图4所示的交流小信号等效电路中,存在关系为
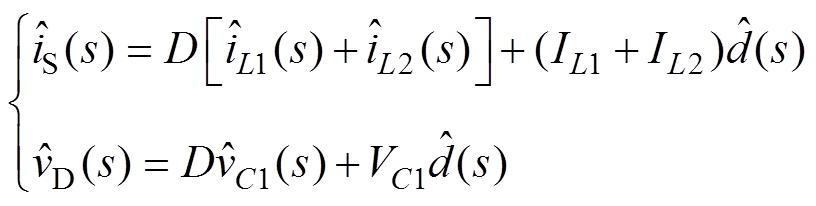 (6)
(6)
根据图4所示的交流小信号等效电路,由KCL及KVL定律可得
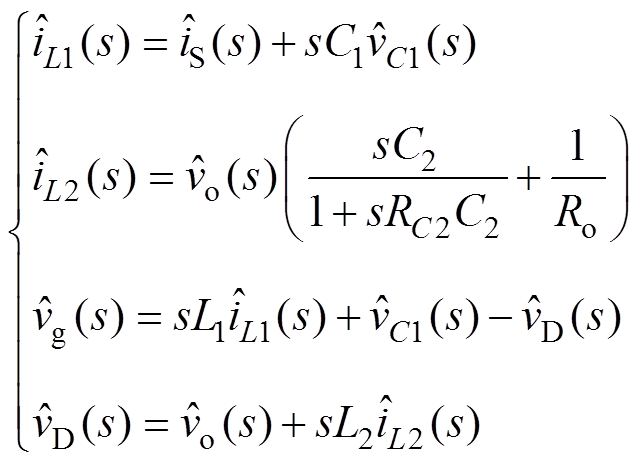 (7)
(7)联立式(6)、式(7),令占空比小信号扰动分量为零,可得CCM Cuk变换器输入-输出传递函数Gvg(s)、输入-中间电容电压传递函数Gv1g(s)和输入-电感电流iL2的传递函数Gi2g(s)分别为
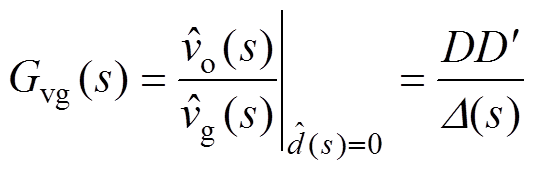 (8)
(8)
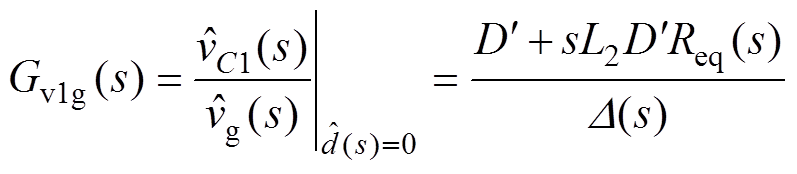 (9)
(9)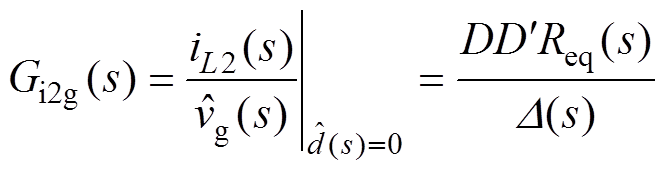 (10)
(10)
其中
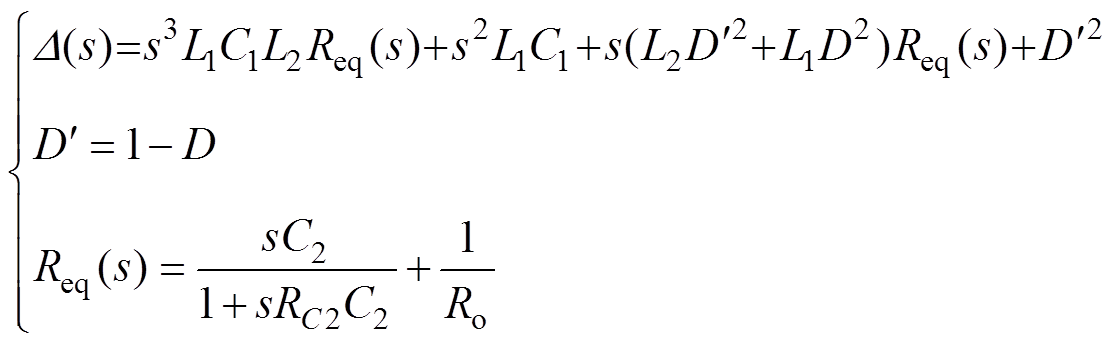
联立式(6)、式(7),令输入电压小信号扰动分量为零,可得CCM Cuk变换器占空比-输出传递函数Gvd(s)、占空比-电感电流iL2的传递函数Gi2d(s)和占空比-中间电容电压传递函数Gv1d(s)分别为
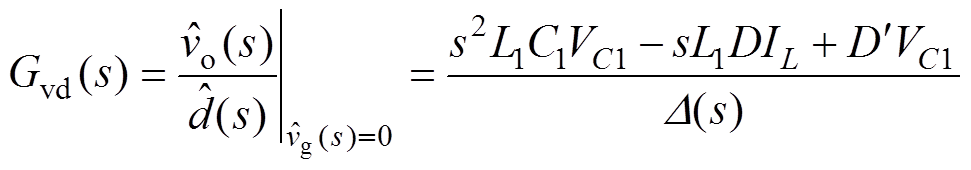 (11)
(11)
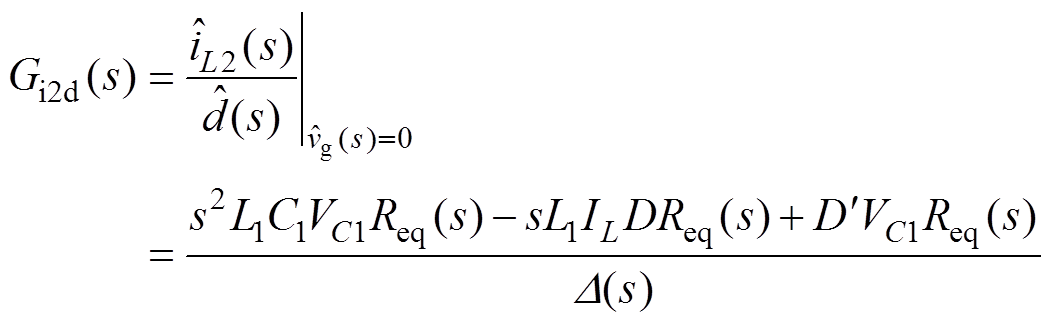 (12)
(12)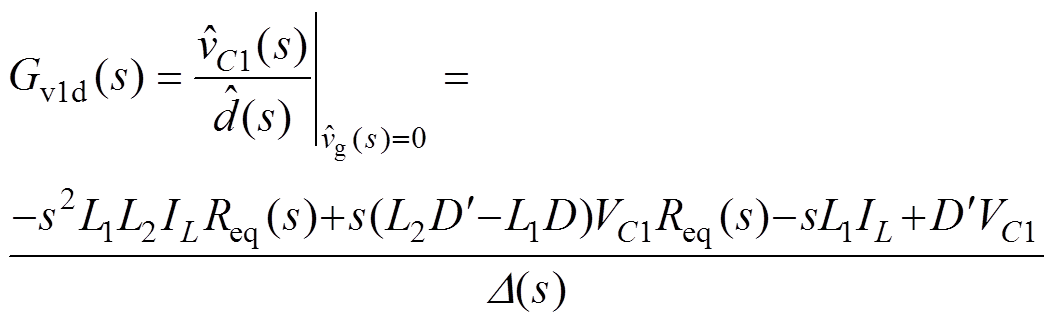 (13)
(13)
令输入电压小信号扰动和占空比小信号扰动均为零,引入输出电流小信号扰动量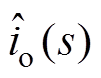 ,式(7)中电感电流iL2的交流小信号表达式为
,式(7)中电感电流iL2的交流小信号表达式为
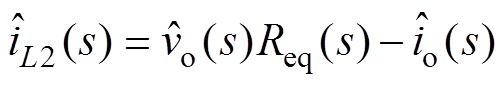 (14)
(14)联立式(6)、式(7)和式(14),可得CCM Cuk变换器输出阻抗Zo(s)、输出电流-中间电容电压传递函数Gv1i(s)和输出电流-电感电流iL2的传递函数Gi2i(s)分别为
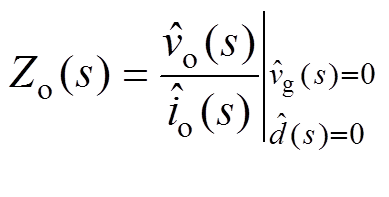
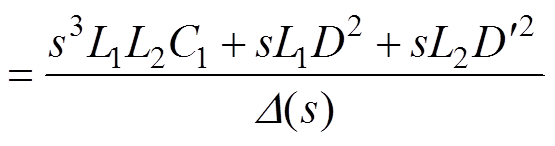 (15)
(15)
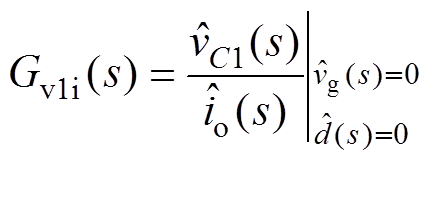
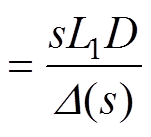 (16)
(16)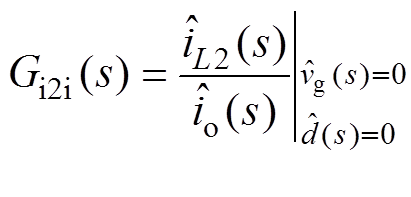
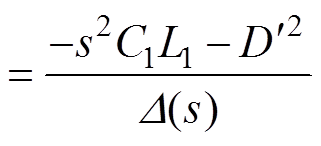 (17)
(17)
图5所示为采用斜坡补偿的V2控制CCM Cuk变换器的输出电压vo与内环电压控制信号ve的关系。
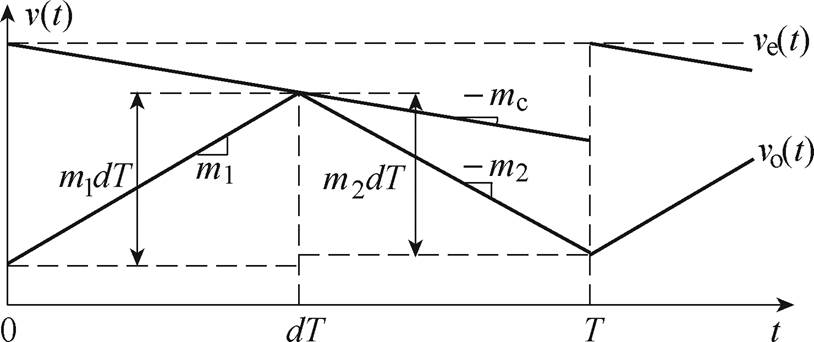
图5 输出电压与电压控制信号的关系
Fig.5 Relation between output voltage and control signal
图中,-mc为斜坡补偿信号的斜率,m1为输出电压纹波的上升斜率,-m2为输出电压纹波的下降斜率。由图5的几何关系可得
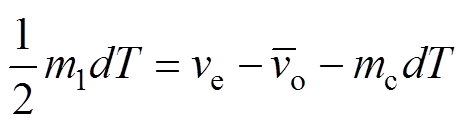 (18)
(18)由式(18)可看出,当输出电压、内环电压控制信号或输出电压纹波上升斜率变化时,会引起占空比的变化。斜坡补偿信号的斜率由外部控制电路决定,认为其恒定,即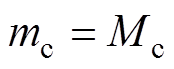 ;在式(18)中引入相关变量的小信号扰动为
;在式(18)中引入相关变量的小信号扰动为
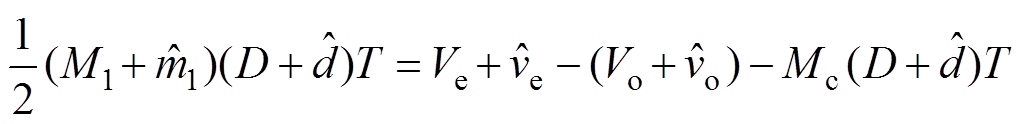 (19)
(19)
式中,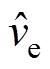 为内环电压控制信号的小信号扰动分量。
为内环电压控制信号的小信号扰动分量。
忽略式(19)中的2次及以上高阶小信号分量,并分离直流分量及小信号扰动分量,可分别解得V2控制CCM Cuk变换器的占空比直流稳态和交流小信号表达式分别为
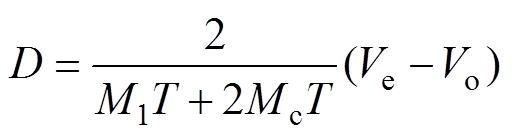 (20)
(20)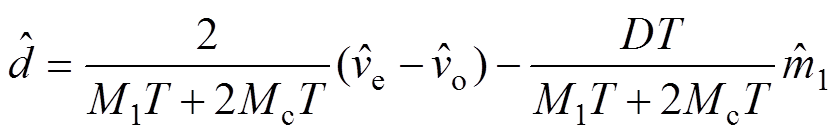 (21)
(21)
对图1所示的V2控制CCM Cuk变换器,可求得输出电压上升斜率的直流稳态及交流小信号表达式分别为
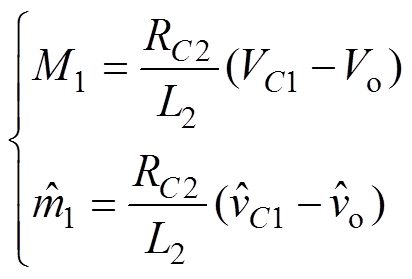 (22)
(22)将式(22)代入式(21),可得V2控制CCM Cuk变换器控制部分的传递函数为
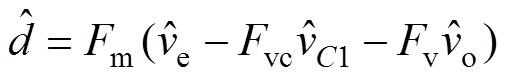 (23)
(23)
其中
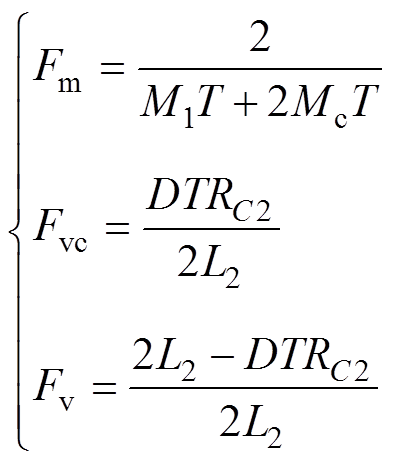
基于式(23),考虑输出电压的采样保持环节,可以建立包含主功率级电路和控制环路的V2控制CCM Cuk变换器的小信号模型,如图6所示。图中,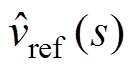 为参考电压,
为参考电压,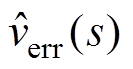 为参考电压与输出电压比较产生的误差电压,Gc(s)为补偿网络传递函数,Hvs(s)为输出电压的采样保持传递函数[22],即
为参考电压与输出电压比较产生的误差电压,Gc(s)为补偿网络传递函数,Hvs(s)为输出电压的采样保持传递函数[22],即
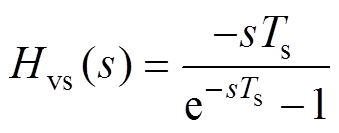 (24)
(24)
令输入电压小信号扰动和输出电流小信号扰动为零,且不考虑补偿环节,可得V2控制CCM Cuk变换器的内环控制环路,如图7所示。
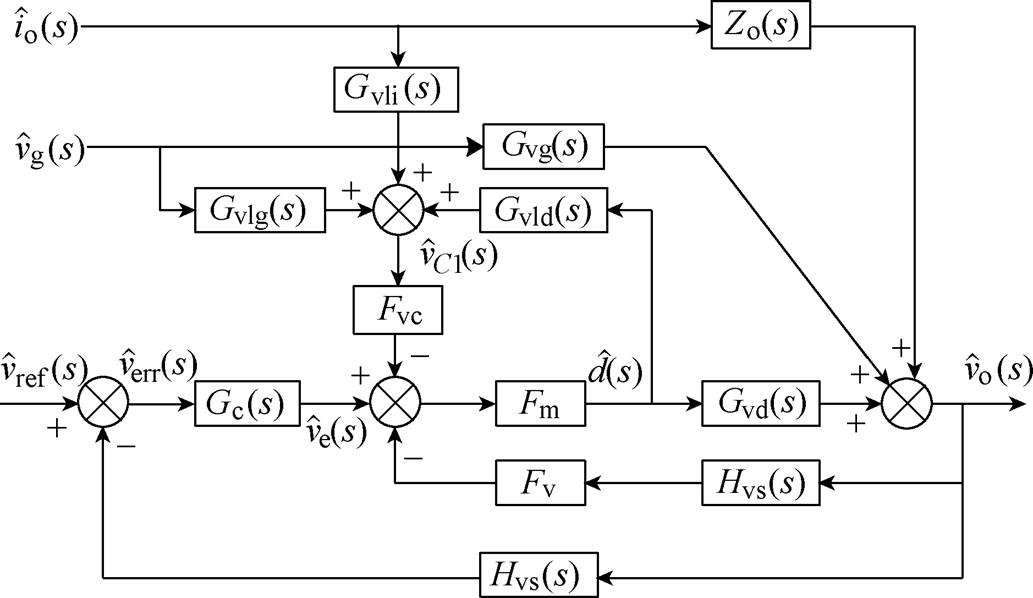
图6 V2控制CCM Cuk变换器的小信号模型
Fig.6 Small signal model of V2 controlled CCM Cuk converter
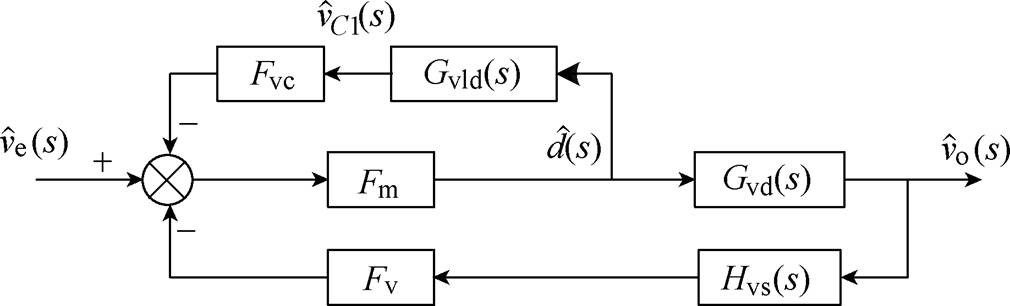
图7 V2控制CCM Cuk变换器的内环控制环路
Fig.7 Inner control loop of V2 controlled CCM Cuk converter
由图7可得,V2控制CCM Cuk变换器的控制-输出传递函数Gvc(s)为
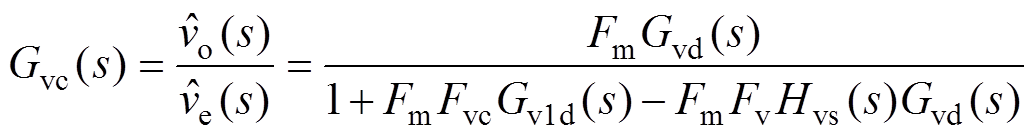 (25)
(25)令输入电压小信号扰动和电压控制信号扰动为零,可得V2控制CCM Cuk变换器的输出阻抗环路,如图8所示。
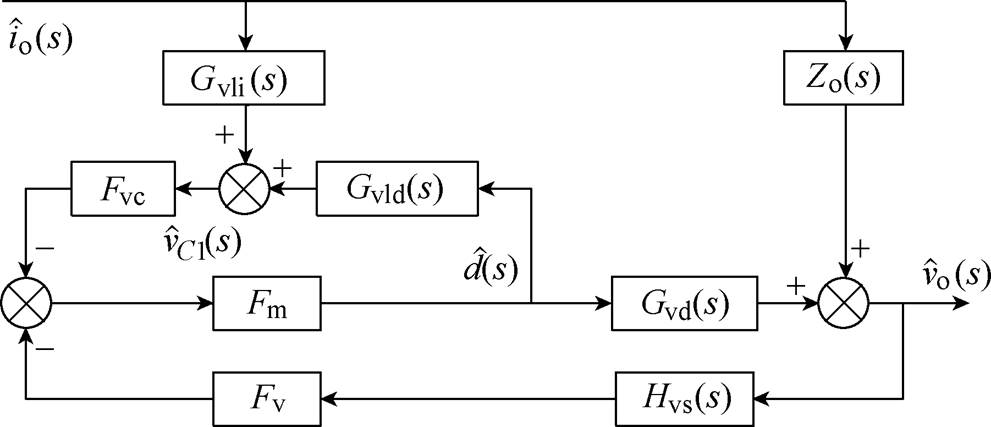
图8 V2控制CCM Cuk变换器的输出阻抗环路
Fig.8 Output impedance loop of V2 controlled CCM Cuk converter
由图8可求得,V2控制CCM Cuk变换器的输出阻抗Zv(s)为
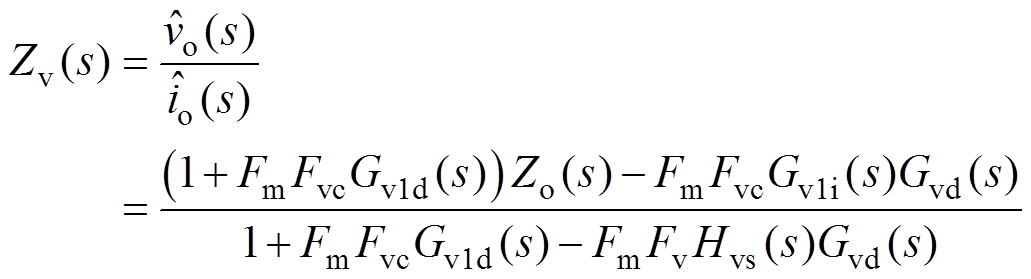 (26)
(26)采用与V2控制CCM Cuk变换器类似的分析方法,可以求得峰值电流控制CCM Cuk变换器占空比与电流控制信号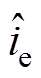 、电感电流
、电感电流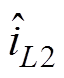 、中间电容电压、输出电压的关系为
、中间电容电压、输出电压的关系为
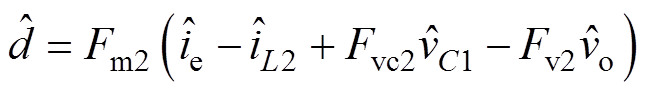 (27)
(27)其中
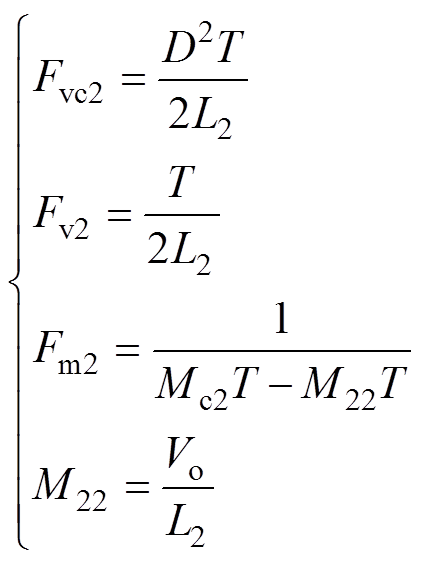
式中,Mc2为电感电流斜坡补偿信号的斜率;M22为电感电流iL2的下降斜率。
基于式(27),考虑电感电流与输出电压的采样保持环节,可以建立包含主功率级电路和控制环路的峰值电流控制CCM Cuk变换器的小信号模型,如图9所示。图中,Gc2(s)为补偿网络传递函数,Hcs(s)为电感电流iL2的采样保持传递函数,表达式与Hvs(s)一致。
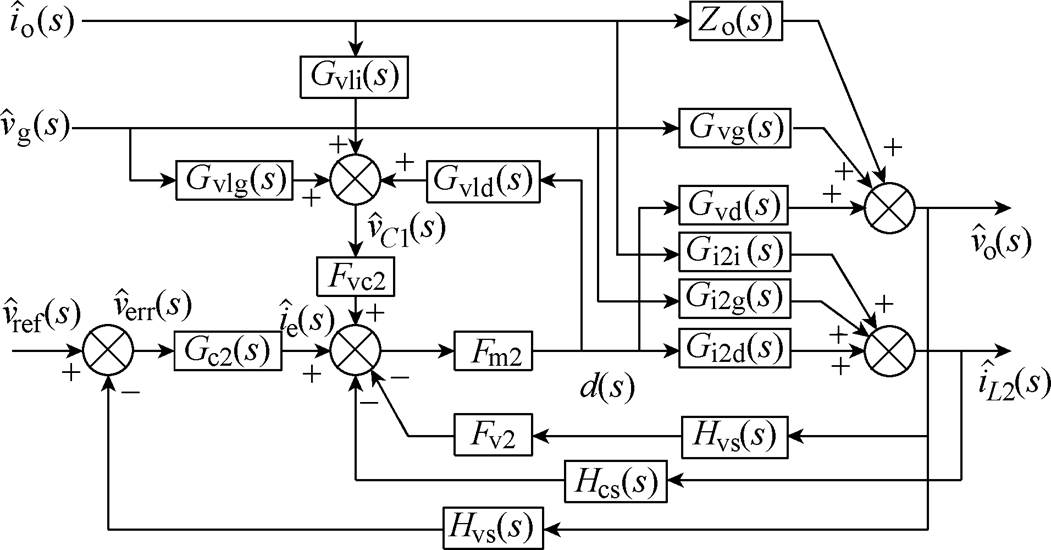
图9 峰值电流控制CCM Cuk变换器的小信号模型
Fig.9 Small signal model of peak current controlled CCM Cuk converter
令输入电压小信号扰动和输出电流小信号扰动为零,且不考虑补偿环节,可得峰值电流控制CCM Cuk变换器的内环控制环路,如图10所示。
由图10可得,峰值电流控制CCM Cuk变换器的控制-输出传递函数Gic(s)为
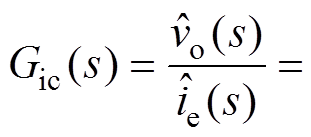
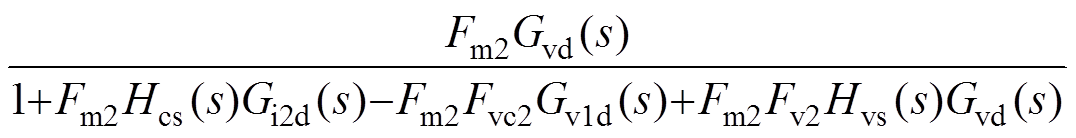 (28)
(28)
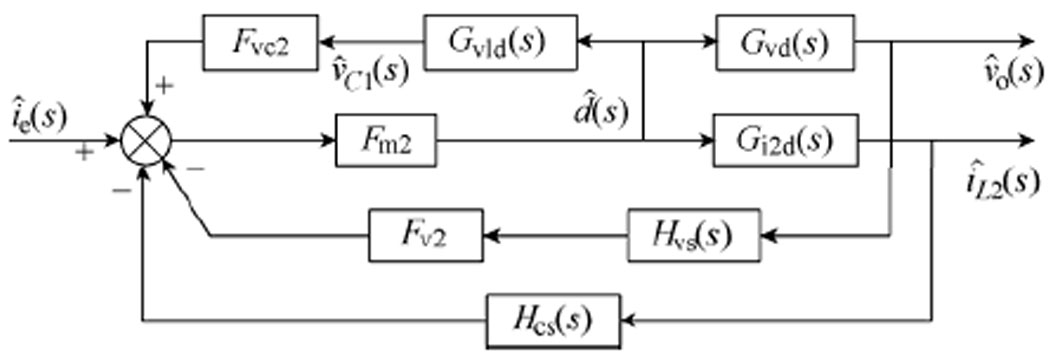
图10 峰值电流控制CCM Cuk变换器的内环控制环路
Fig.10 Inner control loop of peak current controlled CCM Cuk converter
令输入电压小信号扰动和电流控制信号扰动为零,可得峰值电流控制CCM Cuk变换器的输出阻抗环路,如图11所示。
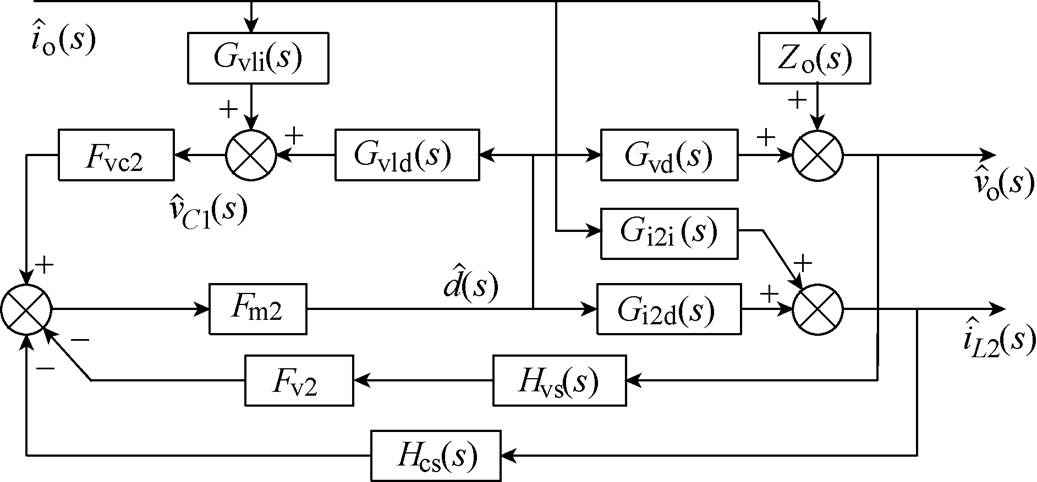
图11 峰值电流控制CCM Cuk变换器的输出阻抗环路
Fig.11 Output impedance loop of peak current controlled CCM Cuk converter
由图11可得,峰值电流控制CCM Cuk变换器的输出阻抗Zi(s)为
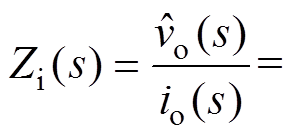
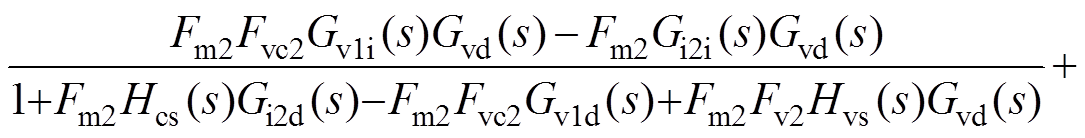
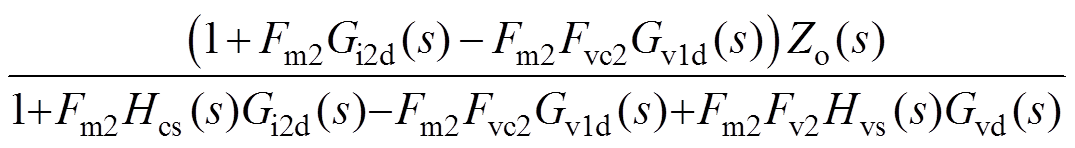 (29)
(29)
为了验证上述控制-输出传递函数及输出阻抗的正确性,选择CCM Cuk变换器电路参数见表1,在SIMPLIS仿真软件中搭建V2控制和峰值电流控制CCM Cuk变换器的仿真电路模型,并进行扫频仿真。
表1 CCM Cuk变换器电路参数
Tab.1 The circuit parameters of CCM Cuk converter

参 数数 值 输入电压Vg/V15 输出电压Vo/V10 电感L1, L2/mH100 电容C1, C2/mF470 等效串联电阻RC2/mW200 负载Ro/W10 开关周期T/ms20
本文主要研究V2控制和峰值电流控制CCM Cuk变换器的瞬态性能;由于在设计的电路参数条件下(占空比小于0.5)可以保证V2控制和峰值电流控制的稳定工作,故在仿真和实验中的斜坡补偿信号均置为0,即Mc=Mc2=0。
图12和图13分别为V2控制和峰值电流控制CCM Cuk变换器的控制-输出传递函数以及输出阻抗的频率响应曲线。从图中可以看出,SIMPLIS仿真与理论的频率响应曲线基本一致,仿真结果验证了理论推导的控制-输出传递函数以及输出阻抗的正确性。此外,由图12和图13还可以看出,相比于峰值电流控制,V2控制CCM Cuk变换器的控制-输出传递函数具有更宽的带宽,且其输出阻抗的低频增益更低,因而具有更快的负载瞬态响应速度。
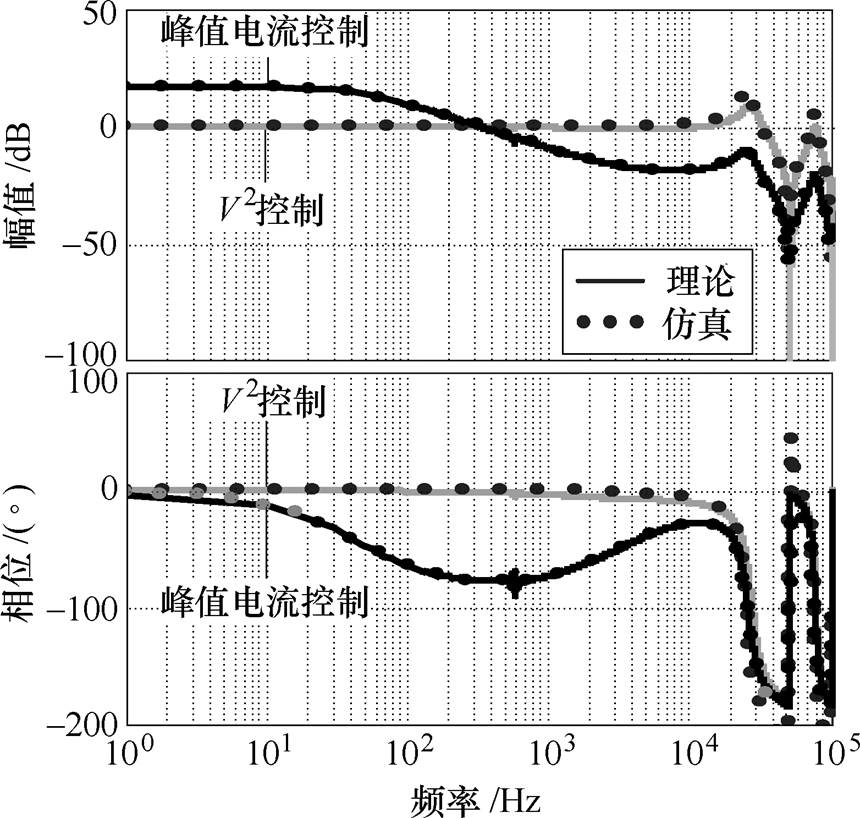
图12 控制-输出传递函数伯德图
Fig.12 Bode plots of control-output transfer functions
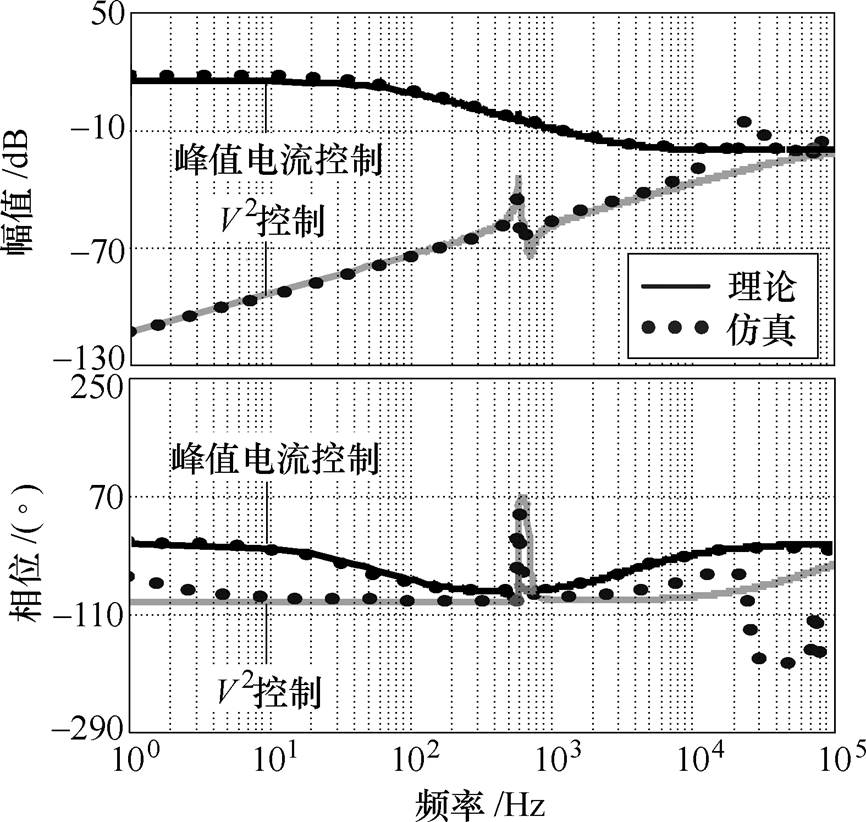
图13 输出阻抗伯德图
Fig.13 Bode plots of output impedance
为了验证V2控制CCM Cuk变换器的负载瞬态响应分析的正确性,采用表1所示的电路参数,在SIMPLIS仿真平台上分别搭建V2控制和峰值电流控制CCM Cuk变换器的时域仿真电路,对比分析两种控制方法下Cuk变换器的负载瞬态响应。
图14所示为负载电流io从1A跳变至2A时,V2控制和峰值电流控制CCM Cuk变换器的瞬态响应仿真波形。由图14可以看出,负载加载时,峰值电流控制CCM Cuk变换器经过3.74ms的调节时间后重新进入稳态,输出电压在调整过程中的超调量为335.6mV;而V2控制CCM Cuk变换器则仅需要0.28ms的调节时间就能重新进入稳态,且输出电压在调整过程中的超调量也仅为142.8mV。
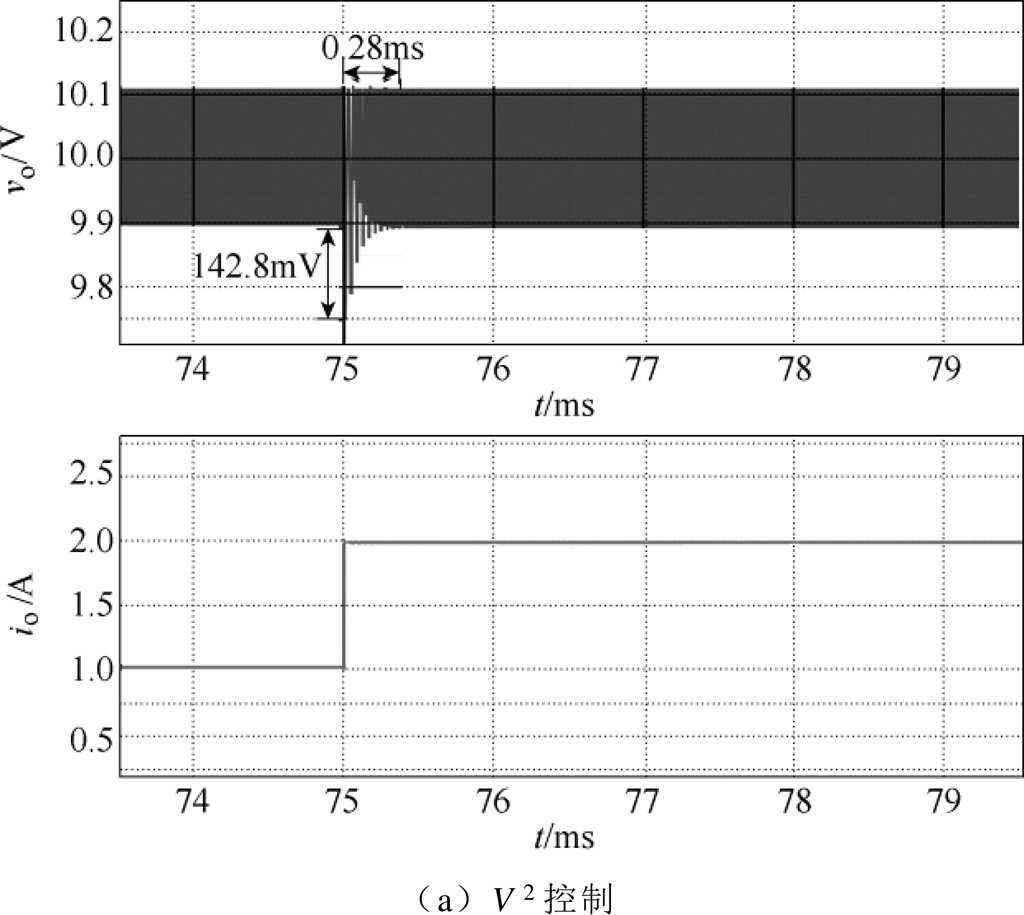
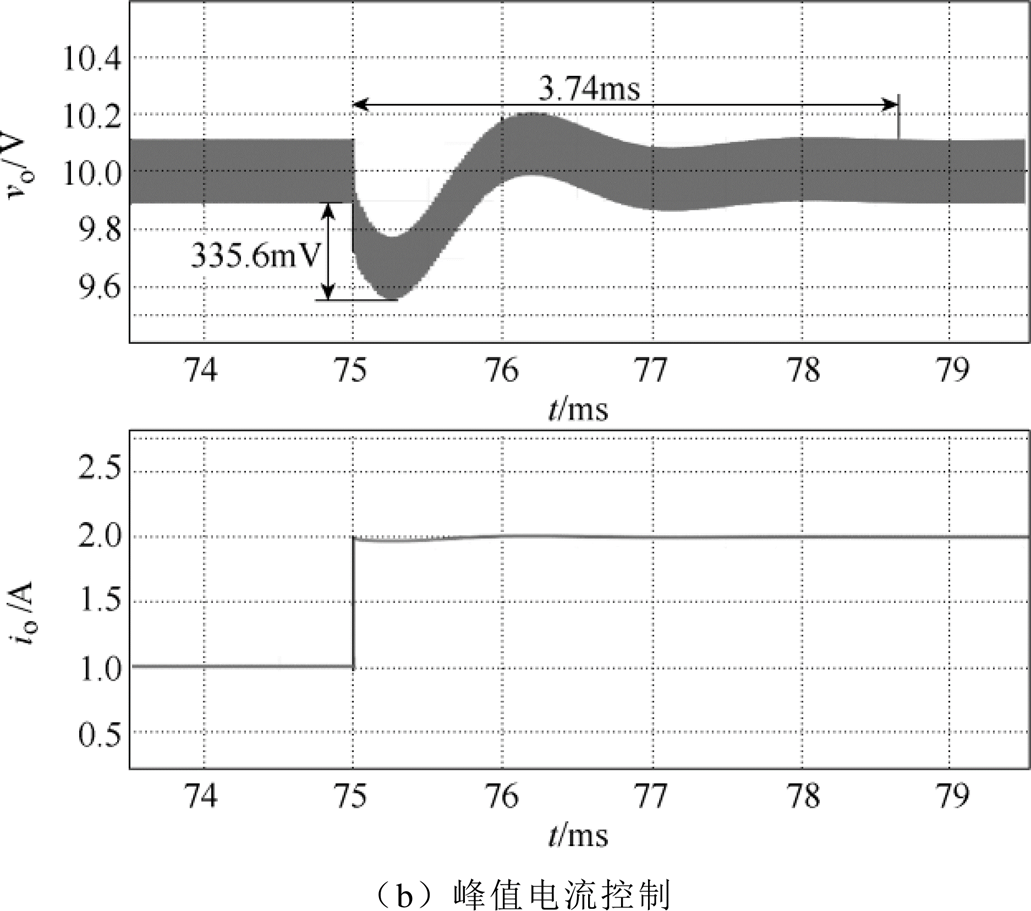
图14 负载加载时CCM Cuk变换器的瞬态仿真波形
Fig.14 Transient simulation waveforms of CCM Cuk converter under load increase
图15所示为负载电流io从2A跳变至1A时V2控制和峰值电流控制CCM Cuk变换器的瞬态响应仿真波形。由图15可以看出,负载减载时,峰值电流控制CCM Cuk变换器经过3.58ms的调节时间后重新进入稳态,输出电压在调整过程中的超调量为337.1mV;而V2控制CCM Cuk变换器则仅需要0.29ms的调节时间就能重新进入稳态,输出电压在调整过程中的超调量也仅为27.8mV。
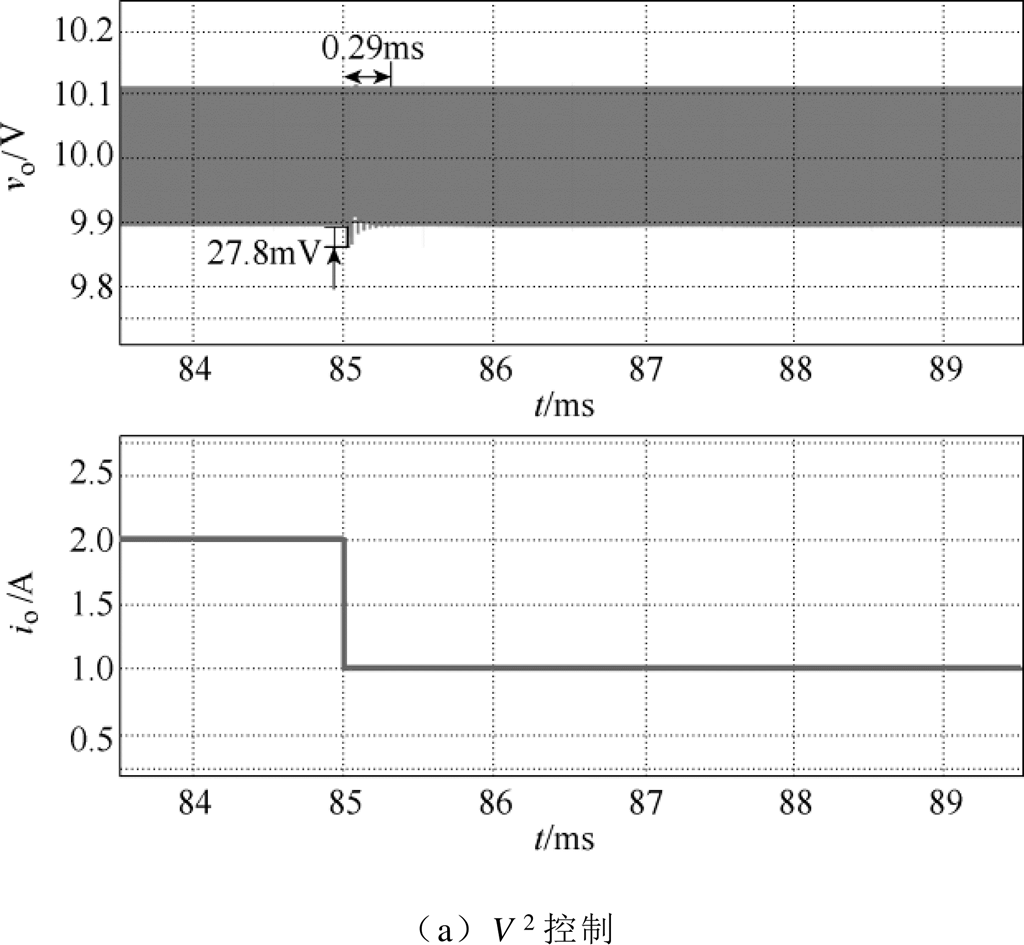
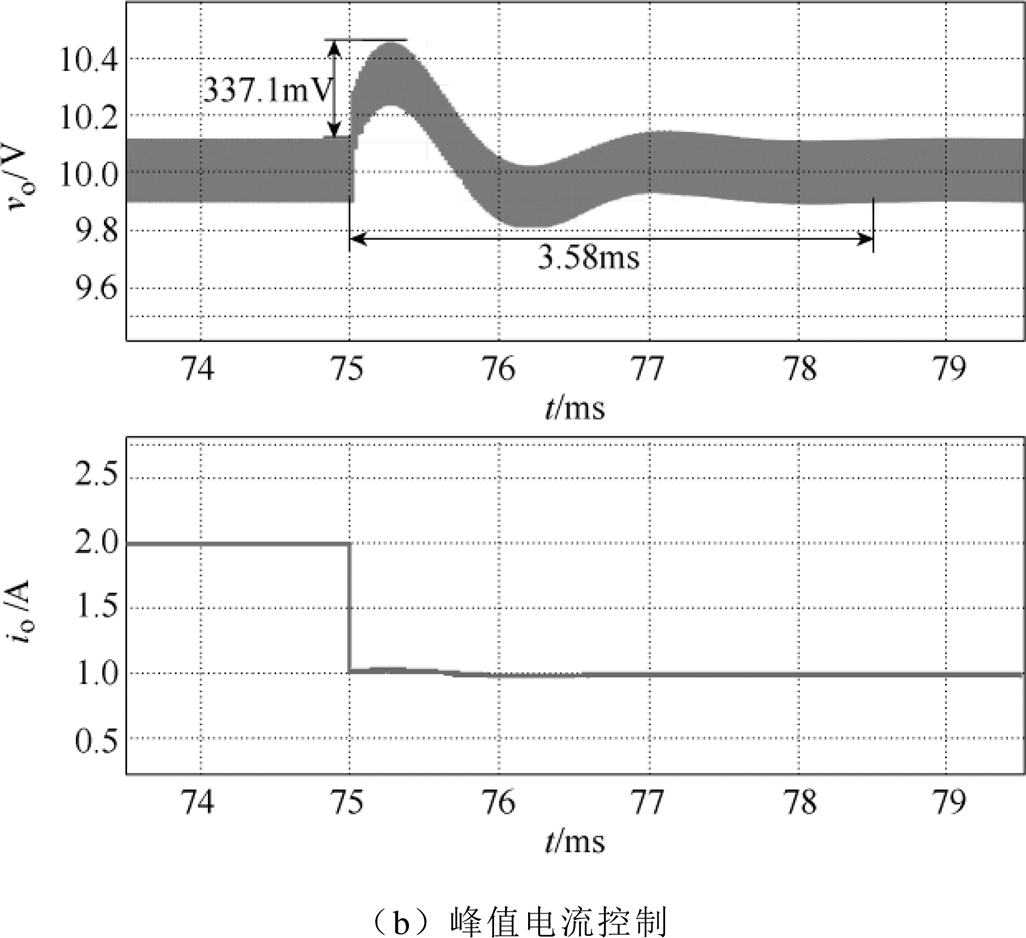
图15 负载减载时CCM Cuk变换器的瞬态仿真波形
Fig 15 Transient simulation waveforms of CCM Cuk converter under load decrease
从上述的瞬态仿真波形可以看出,无论是加载还是减载,V2控制CCM Cuk变换器的瞬态响应时间和超调量都要明显小于峰值电流控制CCM Cuk变换器。时域仿真的结果与频域分析的结果一致,验证了V2控制CCM Cuk变换器理论分析的正确性。
为了进一步验证时域仿真分析的正确性,采用与时域仿真相同的电路参数,搭建V2控制和峰值电流控制CCM Cuk变换器的实验样机,并进行实验验证。
图16所示为V2控制CCM Cuk变换器的样机实物。图中,开关管采用IRF3205场效应管,二极管采用SS54肖特基二极管,采样电路和PI补偿电路均采用LM7171高速运放芯片,比较电路采用LM397单路电压比较器芯片,RS触发电路采用CD4043四路或非R/S锁存器芯片,驱动电路采用A3120光耦芯片。

图16 V2控制CCM Cuk变换器的样机实物
Fig.16 Prototype of V2 controlled CCM Cuk converter
图17和图18分别为V2控制和峰值电流控制CCM Cuk变换器的稳态实验波形,图17a、图18a为输入电压vg,电感电流iL2,输出电压vo和开关管驱动信号vgs的直流信号波形;图17b、图18b为输出电压vo的纹波。从图17和图18可以看出,当输入电压为15V时,V2控制与峰值电流控制CCM Cuk变换器均能使输出电压稳定输出为10V,且二者的稳态性能基本一致,验证了本文将V2控制应用至Cuk变换器的控制方法的可行性。
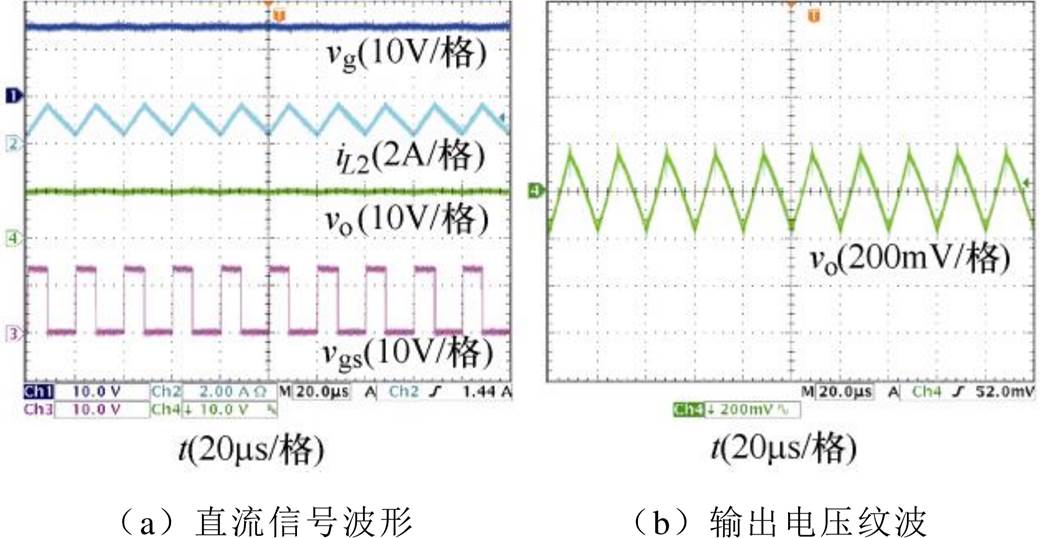
图17 V2控制CCM Cuk变换器的稳态实验波形
Fig.17 Steady-state experimental waveforms of V2 controlled CCM Cuk converter
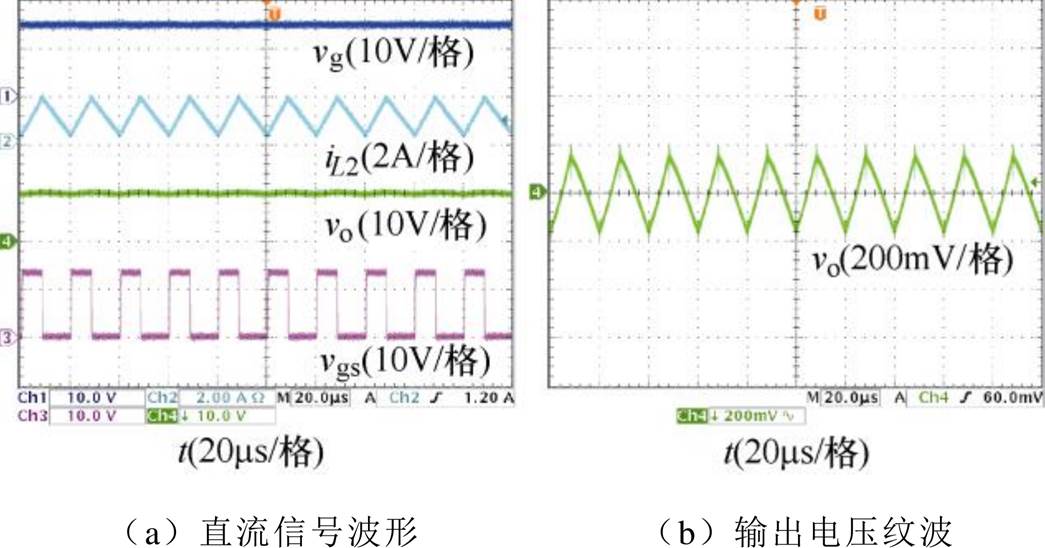
图18 峰值电流控制CCM Cuk变换器的稳态实验波形
Fig.18 Steady-state experimental waveforms of peak current controlled CCM Cuk converter
图19所示为负载加载时,V2控制和峰值电流控制CCM Cuk变换器的瞬态响应实验波形。图19a、图19b分别为V2控制Cuk变换器、峰值电流控制Cuk变换器的输出电压纹波和输出电流波形。从图19可以看出,当输出电流io从1A到2A变化时,峰值电流控制CCM Cuk变换器的输出电压vo经过4.19ms重新进入稳态,超调量为432.0mV;V2控制CCM Cuk变换器的输出电压vo只需0.29ms的调整时间便可重新进入稳态,且超调量仅为171mV。
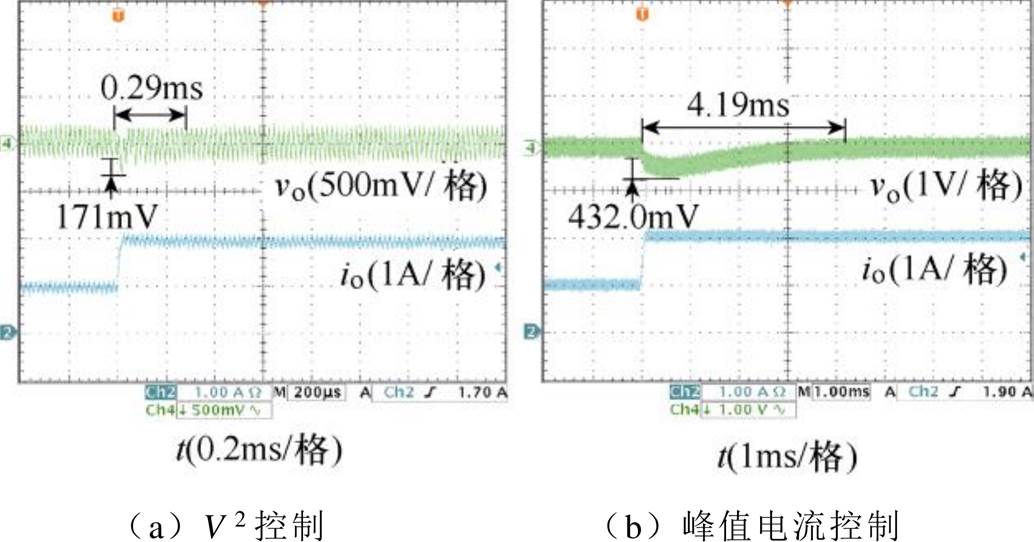
图19 负载加载时,Cuk变换器的瞬态实验波形
Fig.19 The transient experimental waveforms of Cuk converter under load increase
图20所示为负载减载时,V2控制和峰值电流控制CCM Cuk变换器的瞬态响应波形。图20a、图20b分别为V2控制Cuk变换器、峰值电流控制Cuk变换器的输出电压纹波和输出电流波形。从图20可以看出,当输出电流io从2A到1A变化时,峰值电流控制CCM Cuk变换器的输出电压vo经过4.20ms重新进入稳态,超调量为432.4mV;V2控制CCM Cuk变换器的输出电压vo只需0.30ms的调整时间便可重新进入稳态,且超调量极小。由图19和图20所示的实验结果可知,相比于峰值电流控制,无论是加载还是减载,V2控制CCM Cuk变换器都具有更快的瞬态响应速度和更小的超调量。在调整时间和超调量方面,实验波形与理论及仿真结果还存在差异,主要原因是理论及仿真分析中寄生参数的设定与实验中的寄生参数存在差异。综上,实验结果验证了V2控制CCM Cuk变换器的可行性;并证明了相比于电流型控制,V2控制CCM Cuk变换器具有更好的瞬态性能。

图20 负载减载时,Cuk变换器的瞬态实验波形
Fig.20 The transient experimental waveforms of Cuk converter under load decrease
本文将具有快速瞬态响应的V2控制技术应用至Cuk变换器,实现了V2控制CCM Cuk变换器。利用时间平均等效建模方法,推导了包含输出电容ESR的CCM Cuk变换器主功率电路传递函数,在此基础上,建立了V2控制和峰值电流控制CCM Cuk变换器的精确小信号模型,并据此推导了控制-输出传递函数以及输出阻抗。通过伯德图,从频域的角度对比分析了V2控制和峰值电流控制CCM Cuk变换器的瞬态响应速度。研究结果表明,相比于峰值电流控制,V2控制CCM Cuk变换器具有更快的瞬态响应速度。仿真和实验验证了理论分析的正确性。
参考文献
[1] 林雪凤, 许建平, 周翔. 谐振软开关耦合电感高增益DC-DC变换器[J]. 电工技术学报, 2019, 34(4): 747-755.
Lin Xuefeng, Xu Jianping, Zhou Xiang. Soft-switched high step-up DC-DC converter with coupled inductor of resonance[J]. Transactions of China Electro- technical Society, 2019, 34(4): 747-755.
[2] 曾绍桓, 周国华, 周述晗, 等. 电流型控制三态Boost变换器的小信号建模与负载瞬态特性分析[J]. 电工技术学报, 2019, 34(7): 1468-1477.
Zeng Shaohuan, Zhou Guohua, Zhou Shuhan, et al. Small-signal modeling and load transient characteris- tic analysis of current mode controlled tri-state Boost converter[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1468-1477.
[3] 周翔, 许建平, 陈章勇. 高升压增益软开关DC-DC变换器[J]. 电工技术学报, 2016, 31(14): 156-164.
Zhou Xiang, Xu Jianping, Chen Zhangyong. Soft switched DC-DC converter with high voltage gain[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 156-164.
[4] Poorali B, Adib E, Farzanehfard H. Soft switching DC-DC Cuk converter operating in discontinuous capacitor voltage mode[J]. IET Power Electronics, 2017, 10(13): 1679-1686.
[5] Cuk S, Middlebrook R D. A new optimum topology switching DC-DC converter[C]//IEEE Power Electro- nics Specialists Conference, Palo Alto, USA, 1977: 160-179.
[6] Lekić A, Stipanović D M. Hysteresis switching control of the Cuk converter[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2016, 63(11): 2048-2061.
[7] 鲍宁宁. 输出低纹波隔离型Cuk变换器研究[D]. 北京: 北京交通大学, 2014.
[8] Yang H, Chiang H, Chen C. Implementation of bridgeless Cuk power factor corrector with positive output voltage[J]. IEEE Transactions on Industry Applications, 2015, 51(4): 3325-3333.
[9] 李俊. 一种新型直流串联风机并网拓扑结构及其控制策略[D]. 湖南: 湖南大学, 2017.
[10] de Morais J C S, de Morais J L S, Gules R. Photovoltaic AC module based on a Cuk converter with a switched-inductor structure[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(5): 3881- 3890.
[11] Corradini L, Spiazzi G. A high-frequency digitally controlled LED driver for automotive applications with fast dimming capabilities[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6648-6659.
[12] 朱俊杰, 刘浩然, 蒋峰, 等. 无刷直流电机转矩脉动抑制系统的新型拓扑研究[J]. 电工技术学报, 2018, 33(17): 4060-4068.
Zhu Junjie, Liu Haoran, Jiang Feng, et al. A new topology research on torque ripple suppression system of brushless motor[J]. Transactions of China Elec- trotechnical Society, 2018, 33(17): 4060-4068.
[13] Ananthapadmanabha B R, Maurya R, Arya S R. Improved power quality switched inductor Cuk converter for battery charging applications[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9412-9423.
[14] Tse C K, Chan W C Y. Instability and chaos in a current-mode controlled Cuk converter[C]//Proceed- Power Electronics Specialist Conference, Atlanta, USA, 1995: 608-613.
[15] Zaeri A H, Poodeh M B, Eshtehardiha S. Improve- ment of Cuk converter performance with optimum LQR controller based on genetic algorithm[C]// International Conference on Intelligent nd Advanced Systems, Kuala Lumpur, Malaysia, 2007: 917-922.
[16] Knight J, Shirsavar S, Holderbaum W. An improved reliability Cuk based solar inverter with sliding mode control[J]. IEEE Transactions on Power Electronics, 2006, 21(4): 1107-1115.
[17] Xu Wenzheng, Cheng K W E, Chan K W. Application of Cuk converter together with battery technologies on the low voltage DC supply for electric vehicles[C]// International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 2015: 1-5.
[18] 周国华, 许建平. 开关变换器调制与控制技术综述[J]. 中国电机工程学报, 2014, 34(6): 815-831.
Zhou Guohua, Xu Jianping. A review of modulation and control techniques for switching converters[J]. Proceedings of the CSEE, 2014, 34(6): 815-831.
[19] 何圣仲, 周国华, 许建平, 等. 谷值V2控制Boost变换器的精确建模与动力学分析[J]. 物理学报, 2014, 63(17): 79-89.
He Shengzhong, Zhou Guohua, Xu Jianping, et al. Precise modeling and dynamic characteristics of valley V2 controlled Boost converter[J]. Acta Physica Sinica, 2014, 63(17): 79-89.
[20] 王凤岩, 许建平, 许峻峰. V2控制Buck变换器分析[J]. 中国电机工程学报, 2005, 25(12): 67-72.
Wang Fengyan, Xu Jianping, Xu Junfeng. Modeling and analysis of V2 controlled Buck converter[J]. Proceedings of the CSEE, 2005, 25(12): 67-72.
[21] 周国华, 许建平, 吴松荣. 开关变换器建模、分析与控制[M]. 北京: 科学出版社, 2016.
[22] 周国华, 冷敏瑞, 李媛, 等. 开关变换器及其控制环路的建模综述[J]. 中国电机工程学报, 2020, 40(1): 183-199.
Zhou Guohua, Leng Minrui, Li Yuan, et al. A review on modeling of switching converters and their control loops[J]. Proceedings of the CSEE, 2020, 40(1): 183- 199.
Modeling and Transient Performance Analysis of V2 Controlled Cuk Converter
Abstract V2 control technique with fast transient response is applied to Cuk converter, and the principle of V2 controlled Cuk converter operating in continuous conduction mode (CCM) is analyzed. The time-average equivalent circuit modeling approach considering equivalent series resistance (ESR) of output capacitor is used to derive the transfer functions of CCM Cuk converter. Subsequently, the accurate small signal models of V2 controlled CCM Cuk converter and peak current controlled CCM Cuk converter are established, and the control-output transfer function and output impedance are further deduced. The transient characteristics of the two converters are compared in frequency domain, and their time-domain simulation models and experimental circuits are established. Then, the steady-state and transient performance of the two converters are analyzed and compared. The results show that compared with peak current controlled CCM Cuk converter, V2 controlled CCM Cuk converter shares the same steady-state performance, but has better performance in transient response speed.
keywords:V2 control, Cuk converter, small signal model, transient performance
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.191739
国家自然科学基金(61771405)、四川省科技计划(2019JDTD0003)和中央高校基本科研业务费专项资金(2682019YQ02)资助项目。
收稿日期 2019-12-12
改稿日期 2020-06-27
周国华 男,1983年生,教授,博士生导师,研究方向为电力电子变换器建模、调制与控制的基础理论及其在新能源与储能技术领域的应用。E-mail: ghzhou-swjtu@163.com
周述晗 女,1992年生,博士研究生,研究方向为开关变换器拓扑与控制技术。E-mail: shuhan1015@126.com(通信作者)
(编辑 陈 诚)