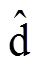与静止坐标系a 轴的估计夹角为
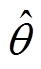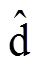，估计直轴与d轴夹角为
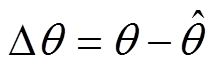。PMSM在dq同步旋转坐标系的数学模型为摘要 针对传统高频信号注入永磁同步电机转子初始位置辨识方法中滤波环节产生的相移影响最终辨识精度的问题，提出一种无滤波器高频脉振信号转子初始位置辨识方法。该方法较传统利用低通滤波器分离高频信号分量方法，改进为利用估计直轴和估计交轴响应电流信号进行解调，去除高频分量，对解调后的信号进行锁相，辨识出转子初始位置。提出利用磁路饱和效应对转子磁极极性进行辨识的方法，提高磁极极性辨识准确性。最后在永磁同步电机矢量控制平台验证了该方法的可行性。
关键词：永磁同步电机 初始位置辨识 高频脉振信号 无滤波器
永磁同步电机（Permanent Magnet Synchronous Machines，PMSM）因具有高功率密度、高效率的特点而被广泛应用于新能源汽车、新能源发电以及航空航天等领域[1-2]。因其不具备自起动能力，在起动前需要获得有效的转子初始位置，如果获得的转子初始位置不准确，会导致无法以最大转矩起动电机，甚至出现电机“反转”现象，从而造成起动失败[3-6]。因此，对初始位置进行准确地辨识是完成永磁同步电机成功起动的关键步骤之一。
针对传感器检测转子初始位置方法存在增加电机复杂度和成本、降低电机系统可靠性的问题[7]，相关学者提出高频信号注入辨识方法。对于表贴式永磁同步电机，可利用高频脉振信号[8-10]所产生的饱和凸极特性完成辨识；对于内嵌式和内埋式永磁同步电机，可利用其本身具有的结构凸极特性，采用高频旋转[11]、高频脉振信号[12-13]进行辨识。
在辨识磁极极性的方法中，通常利用永磁同步电机磁路非线性原理进行判断[14-17]。常见的磁极极性辨识方法有脉冲电压矢量法、响应电流2次谐波法和响应电流幅值法。文献[14]采用注入短脉冲信号以辨识磁极极性的方法，该方法中短脉冲的幅值和脉宽确定不当容易引起电机定子电流过大。文献[15]利用定子响应电流2次谐波分量辨识磁极极性，该方法存在算法复杂的缺陷，且因为电流2次谐波分量本身幅值小而导致采样的电流反馈信号信噪比低，使得转子初始位置信息易受到外界噪声干扰，导致辨识结果鲁棒性较差。
传统的高频信号注入法中，信号处理过程多为利用高频正弦信号与响应电流信号相乘，再通过滤波环节滤除高频信号得到包含转子位置误差信息的直流信号分量。但是滤波环节会对高频信号的幅值和相位产生影响，最终影响转子位置辨识精度[18]。滤波器不仅限制系统带宽，降低转子位置辨识速度，且实现高阶滤波器的计算机程序占用处理器资源[19]。针对传统信号处理过程中滤波环节存在的问题，相关学者提出无滤波器辨识转子位置方法。文献[16]研究了向永磁同步电机定子注入高频旋转信号，对电流响应信号进行移相和傅里叶变换提取出转子磁极轴线初始位置，再利用电机铁心磁饱和特性辨识转子磁极极性。在对电流采样信号处理过程中利用移位方法，代替传统的移相滤波和平波滤波法，虽然此方法能够实现无滤波器转子位置检测，但是其信号处理计算量大。文献[18]中提出利用两次相邻响应电流采样值进行运算分离载波信号的方法，利用矢量叉乘方法解耦位置误差信息，再通过Luenberger位置跟踪器获取转子位置初次辨识值，该方法辨识误差能小于6.9°电角度。
本文提出一种永磁同步电机高频信号注入的转子初始位置无滤波器辨识方法。首先向估计直轴注入高频脉振信号，对估计直轴和估计交轴电流响应信号进行数学处理，无需滤波器分离信号的高频分量，通过位置跟踪器获得转子磁极轴线位置；向辨识的转子轴线位置的正、反方向分两次注入同时包含直流偏置和高频脉振的混合信号，根据两次注入信号和采样的电流响应信号计算得到电感值的不同进而判别磁极极性，最终实现无滤波器精确辨识转子初始位置。
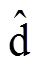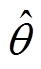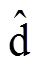假设dq同步旋转坐标系下d轴与静止坐标系a轴的夹角为q，估计直轴与静止坐标系a 轴的估计夹角为，估计直轴与d轴夹角为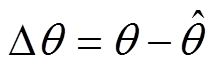。PMSM在dq同步旋转坐标系的数学模型为
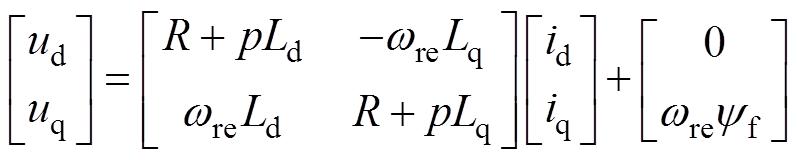（1）式中，ud、uq、id、iq分别为PMSM定子d、q轴电压和电流分量；R为定子相电阻；Ld、Lq分别为d、q轴电感；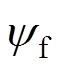
为永磁体主磁链；
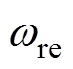为转子电角速度；p为微分算子。
在高频信号作用下，因为永磁同步电机保持静止，其运动反电动势为零，同时定子电阻压降可忽略不计，定子电压方程式（1）简化为
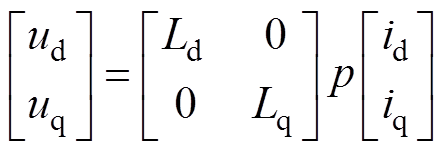（2）将式（2）两侧进行积分，求出电流响应公式，并将dq旋转坐标系中的高频电流响应变换到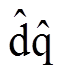
估计坐标系中，即
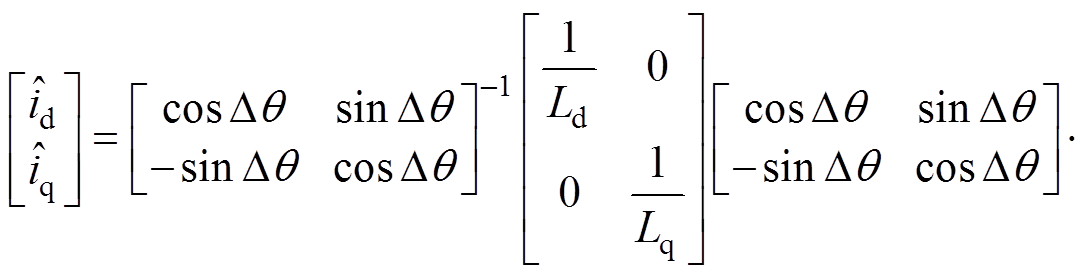
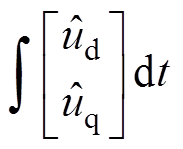（3）对式（3）进行化简得到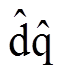估计坐标系中电流响应为
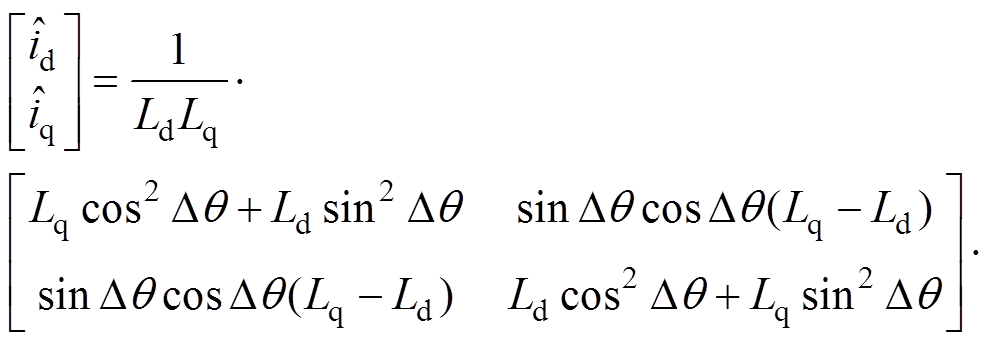
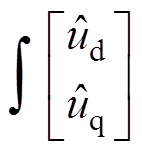（4）进一步化简可得
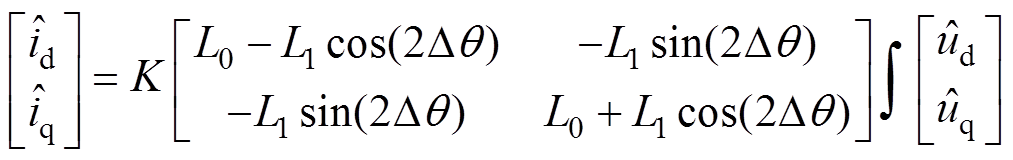（5）
式中，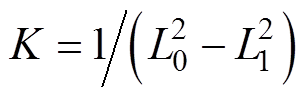
；
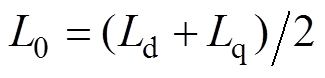为均值电感，
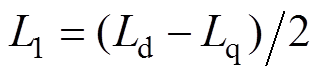为差值电感。
为使得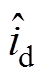
与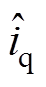
电流解耦和算法简化，在估计坐标系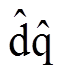中注入高频脉振信号为
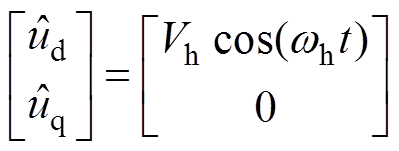（6）式中，Vh为注入高频脉振电压信号的幅值；wh为注入信号电角频率，则在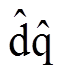估计坐标系中的电流响 应为
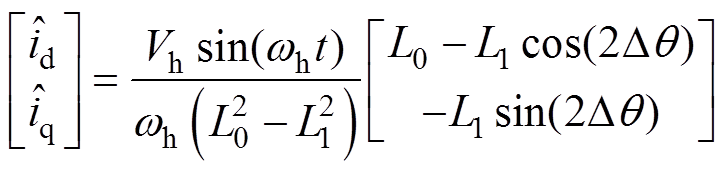（7）
式（7）所示估计坐标系中，估计直轴和估计交轴高频响应电流信号均为角频率wh的高频正弦波，幅值随转子估计位置角度误差Dq 变化，其波形可以看作被转子估计位置误差Dq 调制的正弦量，因此考虑利用估计直轴高频电流响应信号除估计交轴高频电流响应信号，构造出一个不含正弦函数项sin(wht)但包含转子位置估计误差Dq 的新函数为
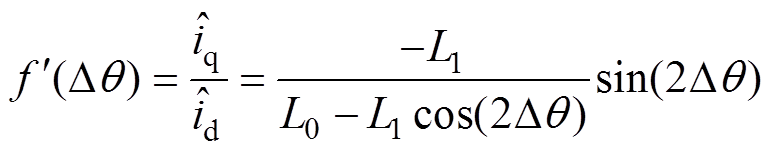（8）当估计角度误差很小时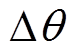
≈0，此时
≈1，令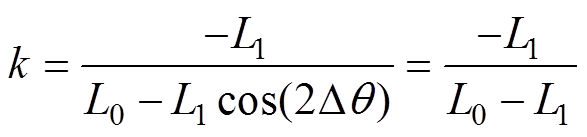
，k近似为常数，则式（8）化简为
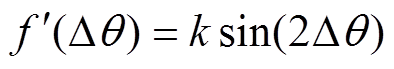（9）函数的值随着估计角度误差呈正弦变化趋势，不需经过带通和低通滤波环节处理，直接进行锁相即可得到转子磁极轴线位置。无滤波器转子初始位置辨识控制框图如图1所示。
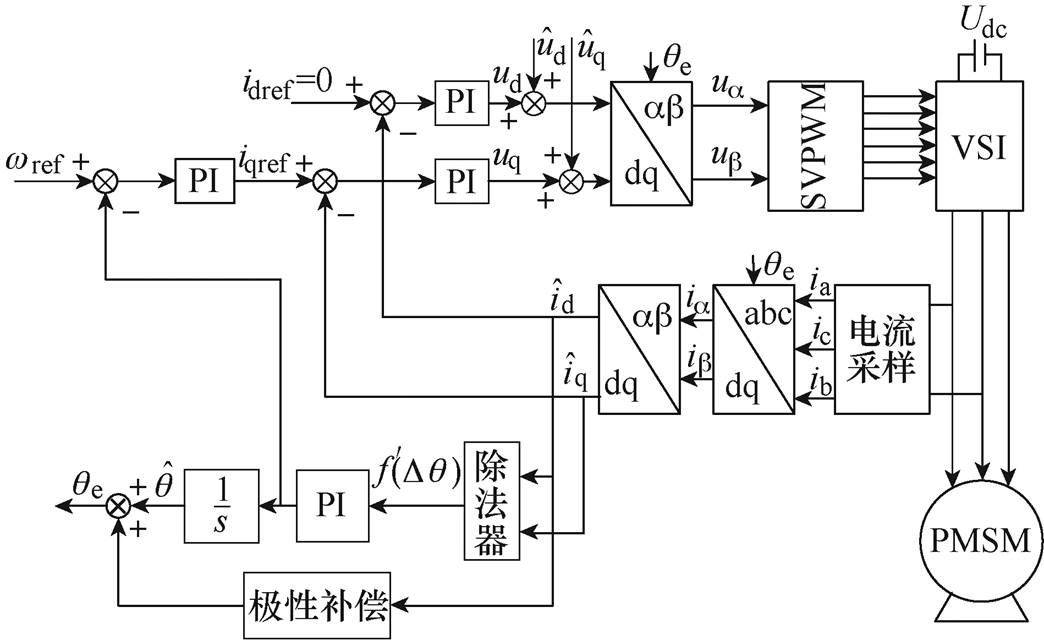
图1 无滤波器转子初始位置辨识控制框图
Fig.1 Scheme of the initial position identification with filterless method
传统有滤波器高频脉振信号注入转子位置辨识方法是：首先利用带通滤波器滤除载波信号和选频输出基波信号，然后将估计q轴电流响应信号与调制信号sin(wht)相乘，再通过低通滤波器滤除信号中高频分量，得到转子位置误差信号为
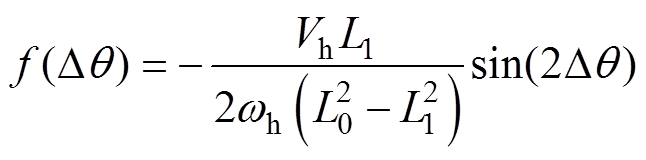（10）对误差信号进行锁相处理得到转子磁极轴线位置，传统信号处理方法如图2所示。
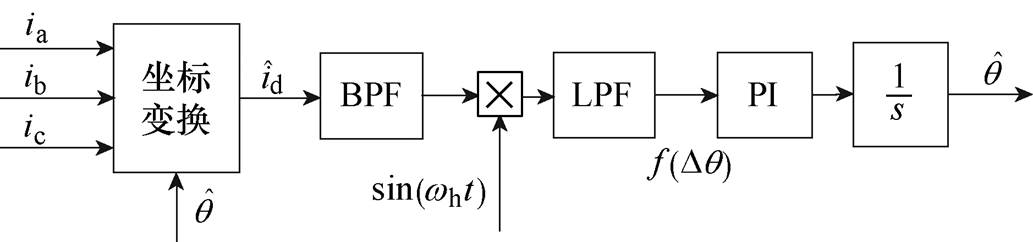
图2 传统信号处理方法
Fig.2 Schematic diagram of conventional signal demodulation method
由于滤波后的电流响应信号幅值和相位发生变化，进而增加了转子位置辨识误差。文中设计的低通滤波器形式为
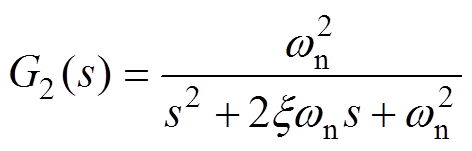（11）通过带通滤波器的高频信号再与高频正弦信号相乘后得到频率升高为注入频率二倍的高频分量（如800Hz），设定低通滤波器自然振荡频率wn= 50Hz，z =0.707，通过相频特性求得滤波器对信号产生的相移为1.627°。设定经过两次滤波环节后含有转子位置估计误差信息的定子电流表达式为
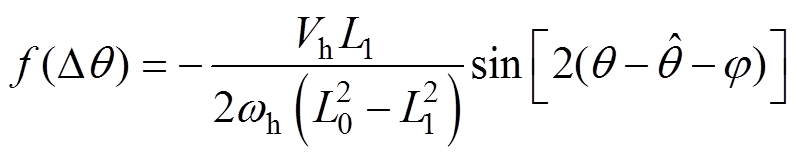（12）
式中，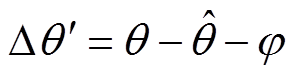
，
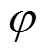为由带通和低通滤波器导致的电流响应信号总相移角度。
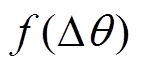信号再经过锁相环节得到磁极轴线辨识值为
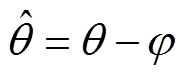。由于滤波器不仅限制系统带宽，降低转子位置辨识速度，且实现高阶滤波器的计算机程序占用处理器资源，同时滤波器产生的相移恶化转子辨识精度。通过比较，无滤波器转子初始位置辨识方法不仅省去滤波环节，使得算法简化，而且消除了滤波器导致的位置检测误差，从而提高转子位置辨识精度。
通过无滤波器高频脉振信号注入方法获得的转子磁极轴线位置既有可能是真实的转子位置电角度q，也可能和q 相差p，若要获取准确的转子位置，需要对磁极极性进行辨识。
为了充分利用永磁体，一般将永磁同步电机磁路设计为接近饱和状态[20]，当磁路未饱和时，磁链与磁化电流呈线性规律，此时等效电感值接近为定值，称此区域为磁链线性区；当磁路饱和时，磁链与磁化电流呈非线性规律，等效电感值随着饱和程度增强而减小，此区域为磁链饱和区，定子磁链与d轴定子电流关系如图3所示。
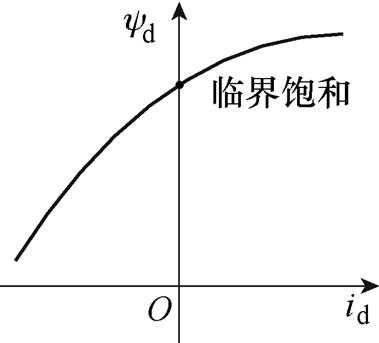
图3 定子磁链与d轴定子电流关系
Fig.3 The relationship between stator flux linkage and d-axis stator current
本文提出一种基于电感量变化的改进磁极极性辨识方法。该方法是在辨识的磁极轴线正、反方向分别施加幅值相同的直流偏置与高频脉振混合信号，不论初次辨识得到的转子磁极轴线与实际磁极轴线是同向还是反向，均能保证有一次直流偏置磁化电流使得永磁同步电机磁路的磁化特性进入饱和状态；下一次直流偏置电流使得电机磁路的磁化特性进入线性区，增大两次直流偏置情况下计算得到的电感差值，从而有效地解决因辨识的电感值接近而误判磁极极性问题。
由于在辨识过程中，电机转子处于静止状态，由式（1）可知，估计直轴电感[21]可以表示为
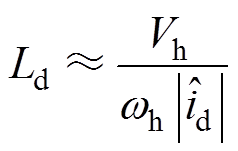（13）式中，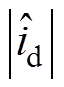
为估计直轴响应电流幅值，其值可利用离散傅里叶变换求取，方法如下
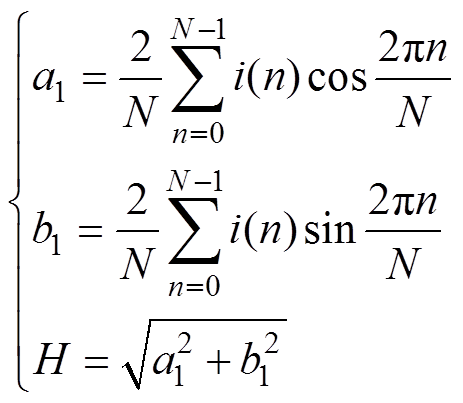（14）
式中，a1、b1分别为基波信号的实部和虚部；N为一个信号周期内的采样数；H为高频信号基波幅值。如果沿着初次辨识的转子轴线位置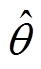方向注入直流偏置计算得到的电感值为Ld1，而沿着
方向注入直流偏置计算得到的电感值为Ld2，当Ld1＜Ld2时，初次辨识转子轴线方向与实际转子磁极方向同向；反之，初次辨识磁极轴线方向与实际转子磁极方向相差p。辨识过程中直流偏置通过d轴设定电流idref给定，为了保证辨识中电机处于静止状态，q轴设定电流iqref始终为0，基于电感差值的磁极极性辨识流程如图4所示。
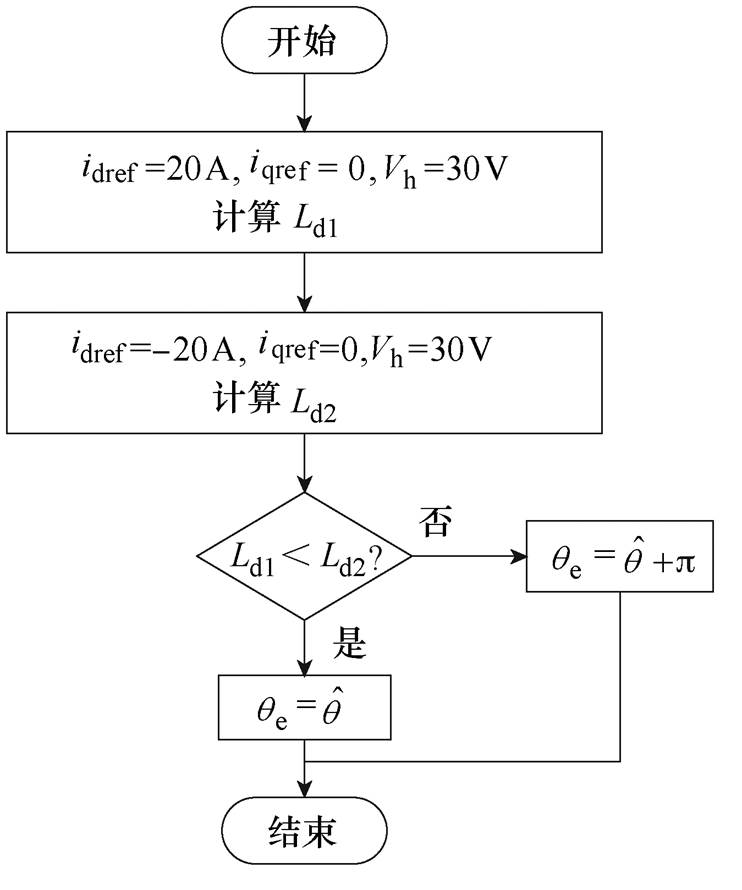
图4 基于电感差值的磁极极性辨识流程
Fig.4 Schematic diagram of polarity identification based on the change of inductance
为了验证所提方法的可行性，利用Matlab仿真软件建立一台内置式永磁同步电机的仿真模型，电机仿真参数见表1。在仿真模型中向电机定子绕组注入的高频电压信号频率为400Hz，永磁同步电机定子绕组所连接逆变器开关频率为8 400Hz，注入的高频旋转电压信号幅值为额定电压的0.3，即108V；磁极极性辨识过程中需要注入的高频信号幅值为额定电压的1/2，即180V，直流偏置给定为20A。两次转子轴线位置辨识角度值平均值误差小于0.01°时，辨识程序进入磁极极性辨识阶段。
表1 电机仿真参数
Tab.1 The simulation parameters of motor
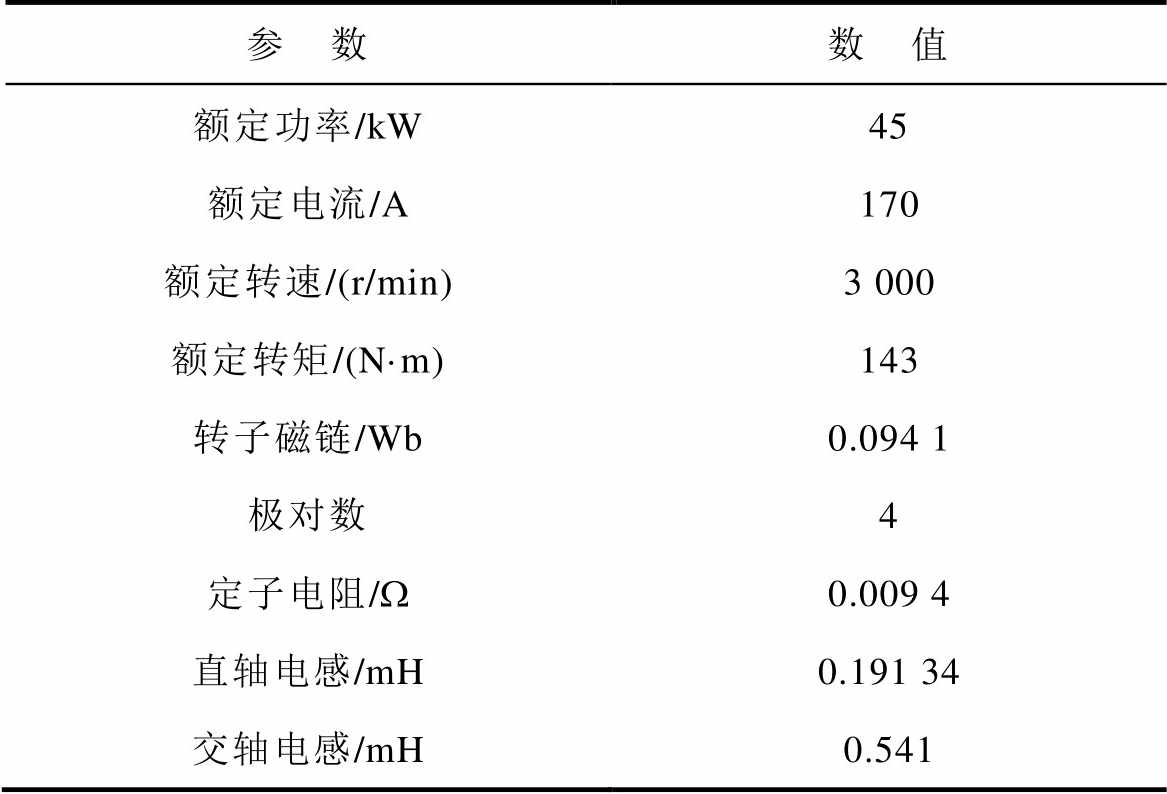
参 数数 值 额定功率/kW45 额定电流/A170 额定转速/(r/min)3 000 额定转矩/(N·m)143 转子磁链/Wb0.094 1 极对数4 定子电阻/W0.009 4 直轴电感/mH0.191 34 交轴电感/mH0.541
无滤波器高频脉振信号注入的永磁同步电机转子初始位置辨识仿真结果如图5和图6所示。图中，q为转子d轴实际位置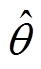，为转子d轴辨识位置。图5a为验证辨识转子轴线位置的仿真曲线，其中转子d轴实际角度q 设定为16°，一方面，转子磁极轴线的辨识角度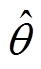曲线经过约2.3s时间收敛到16.4°，实际值与辨识值角度相差0.4°，角度误差很小，可满足电机起动需要；另一方面，由辨识角度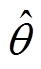曲线可见，转子位置的辨识过程无振荡现象，说明此辨识方法具有渐进稳定的特点。图5b为验证辨识转子磁极极性方法的仿真曲线，由图可知，沿着初次辨识角度方向注入直流偏置信号计算得到的电感值小于沿着相反方向注入直流偏置信号计算得到的电感值，说明初次辨识结果即为转子实际位置，因此不需要对初次辨识结果进行角度补偿，仿真误差为0.6°。
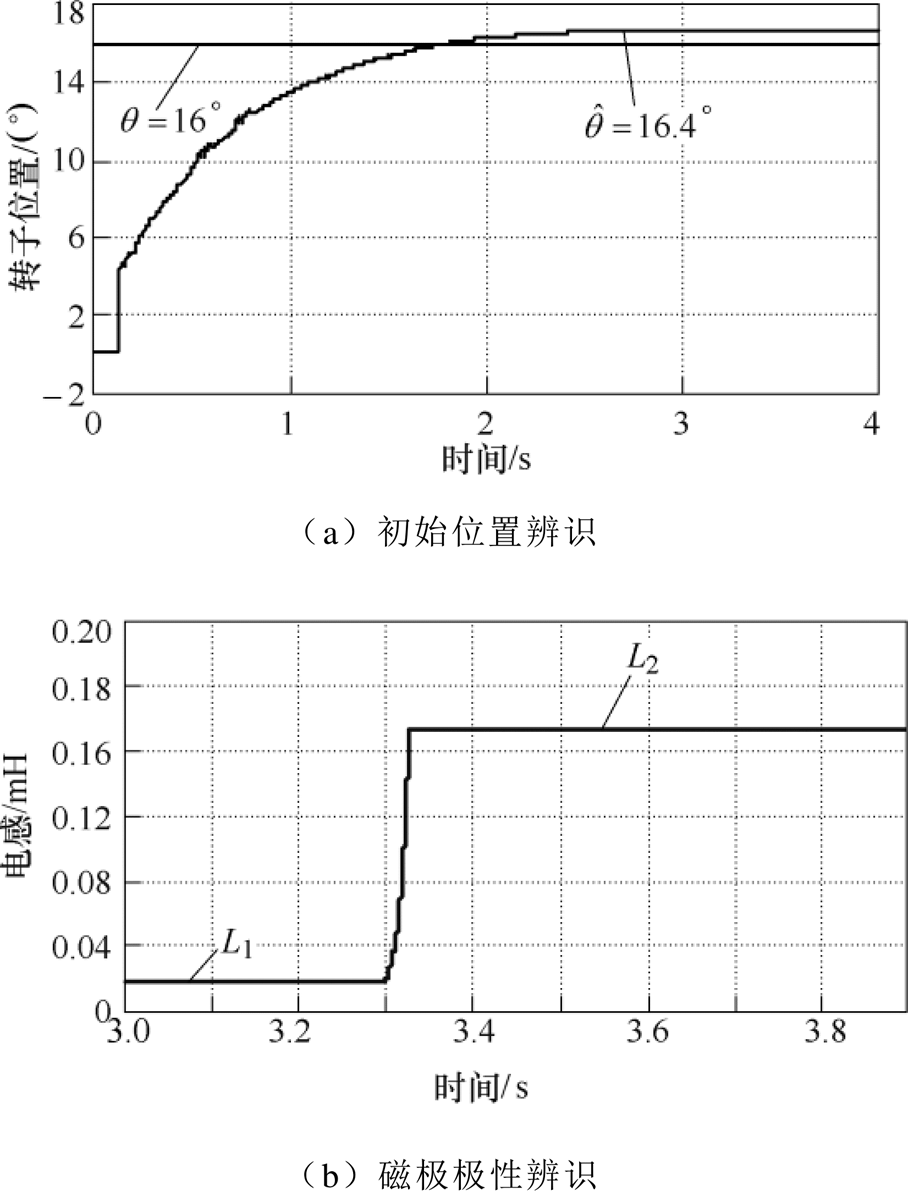
图5 转子位于16°时仿真结果
Fig.5 The simulation results when the rotor is at 16 degree
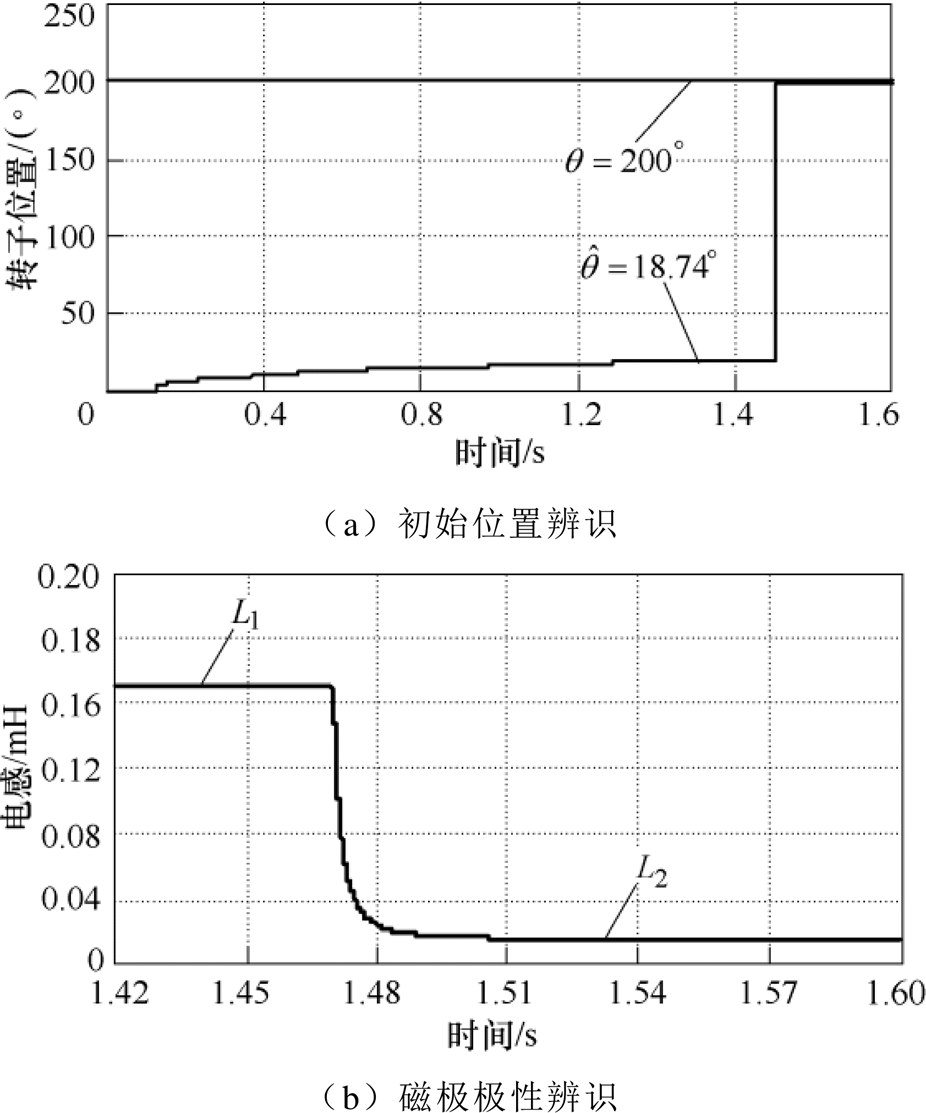
图6 转子位于200°时仿真结果
Fig.6 The simulation results when the rotor is at 200 degree
图6a中，转子实际位置为200°，初次辨识角度为18.74°；图6b中，初次辨识角度方向的电感值大于相反方向的电感值，说明初次辨识结果与转子实际位置相反，因此需要补偿p，补偿后的辨识结果为199.14°，最终误差为0.86°。
为了验证该方法的有效性，利用一台额定功率为16kW的IPMSM进行实验，实验电机参数见表2。实验中，功率管开关频率为8.4kHz，注入高频脉振信号的频率为400Hz，幅值为60V，磁极极性辨识中注入的直流偏置为20A，高频正弦信号幅值为30V，直流母线电压Udc=144V。采用TMS320F28335芯片实现控制算法，辨识结果与安装在IPMSM上的旋转变压器读取的转子位置进行对比。实验平台如图7所示。
表2 实验电机参数
Tab.2 The parameters of experiment motor
参 数数 值 额定功率/kW16 额定电流/A110 额定转速/(r/min)2 400 额定转矩/(N·m)51 转子磁链/Wb0.042 2 极对数4 定子电阻/W0.01 直轴电感/mH0.1 交轴电感/mH0.25
图7 PMSM实验平台
Fig.7 Experimental platform of PMSM
图8为传统磁极极性辨识方法与改进方法的实验对比。图中，t1～t2时间段是转子磁极轴线位置辨识过程，t2～t4时间段是磁极极性辨识过程。图8a中，t2～t3时间段向转子位置初次辨识方向注入直流偏置信号为40A，高频脉振信号频率为400Hz，幅值为30V，系统稳定后求出电感L1并进入到下一阶段；t3～t4时间段沿着相同的方向注入直流偏置信号为60A，高频脉振信号保持不变，稳定后计算电感L2，通过比较L1和L2的大小，判断初次辨识角度是否与转子实际角度相同。转子实际位置为177.48°，初次辨识位置为354.24°，由于直流偏置信号沿着转子实际位置的相反方向注入，使得永磁同步电机磁链进入到线性区，两次直流偏置下的电感值近似相等，造成极性判断失误。
图8b中，为改进磁极极性辨识实验波形，t2～t3时间段向转子位置初次辨识方向注入直流偏置信号为20A，高频脉振信号频率为400Hz，幅值为30V；t3～t4时间段内向初次辨识角度相反方向注入直流偏置信号为20A，高频脉振信号频率为400Hz，幅值为30V的极性辨识信号。由于初次辨识位置与转子实际位置方向相反，沿着初次辨识位置方向注入的直流偏置信号使永磁同步电机磁链进入线性区，电感值较饱和区偏大；沿着初次辨识位置相反方向注入的直流偏置信号使磁链进入饱和区，电感值偏小。由于两次直流偏置信号使磁链位于不同区域，电感值的差值较大，提高了磁极极性辨识的准确度。
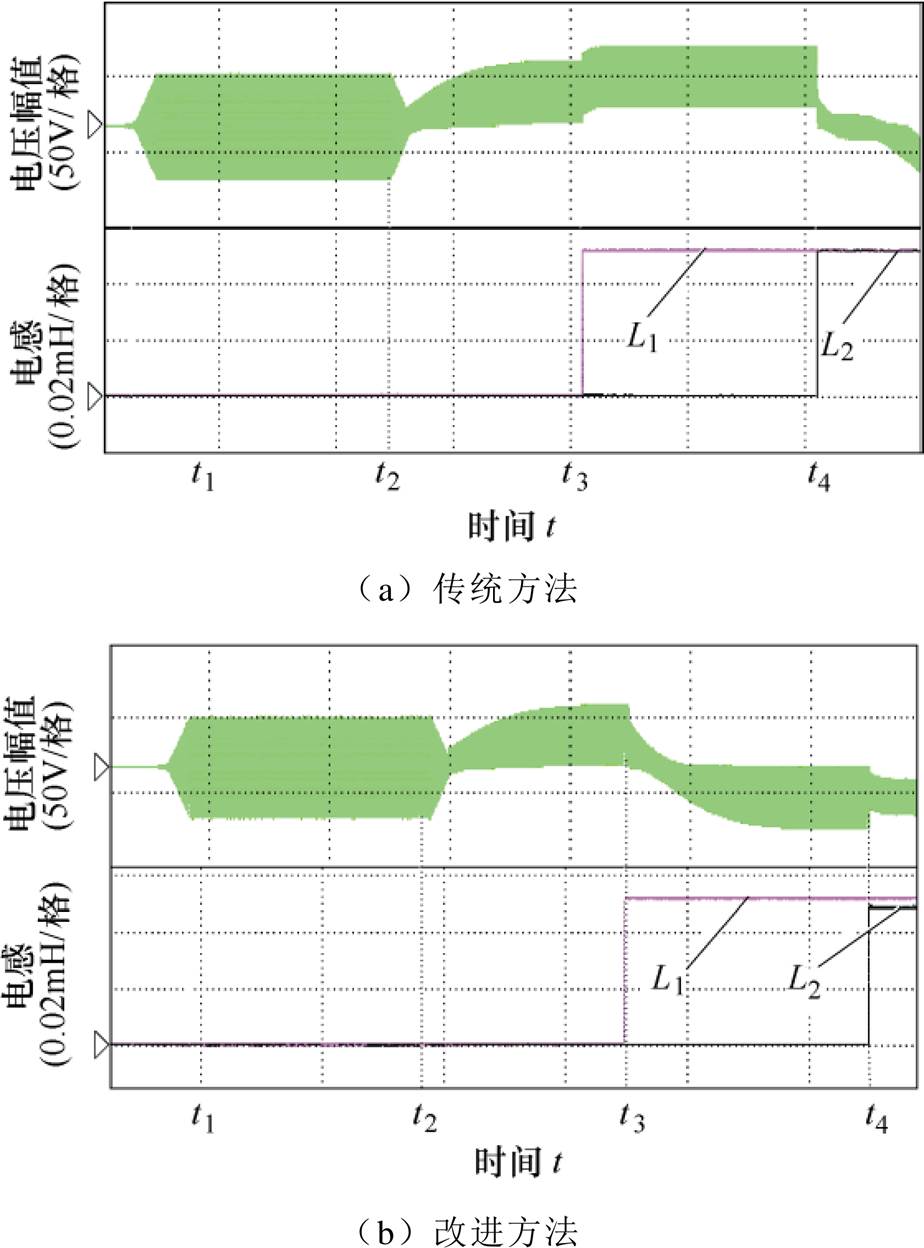
图8 磁极辨识方法实验对比
Fig.8 Experimental comparison of magnetic pole identification methods
图9为转子实际位置为149.76°时的辨识结果，初次辨识结果为329.4°，通过对极性辨识中两次计算得到的电感值判断可知，初次辨识角度与转子实际位置方向相反，对初次辨识角度进行磁极极性补偿后，最终辨识结果为149.4°，辨识误差为0.36°。
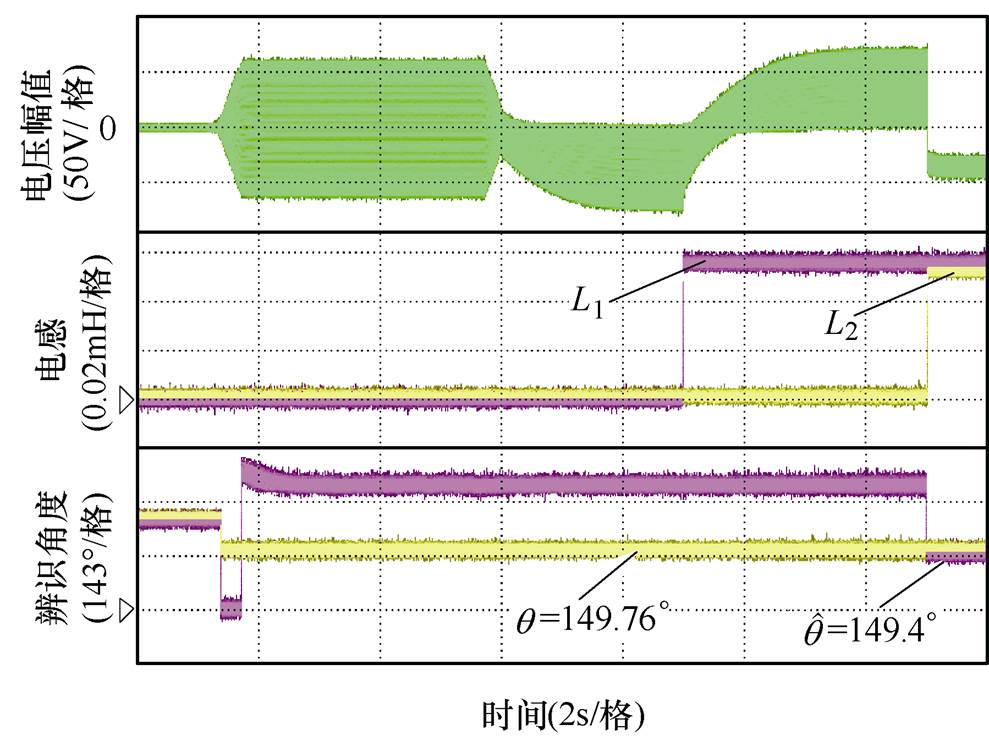
图9 转子位于149.76°时实验结果
Fig.9 Experimental results of the rotor is at 149.76 degree
图10为转子位于329.4°时的实验辨识结果，初次辨识角度为331°，经过磁极极性判断过程可知，初次辨识角度位置与转子实际位置相同，不需要磁极极性补偿，最终辨识角度为331°，辨识误差为1.6°。
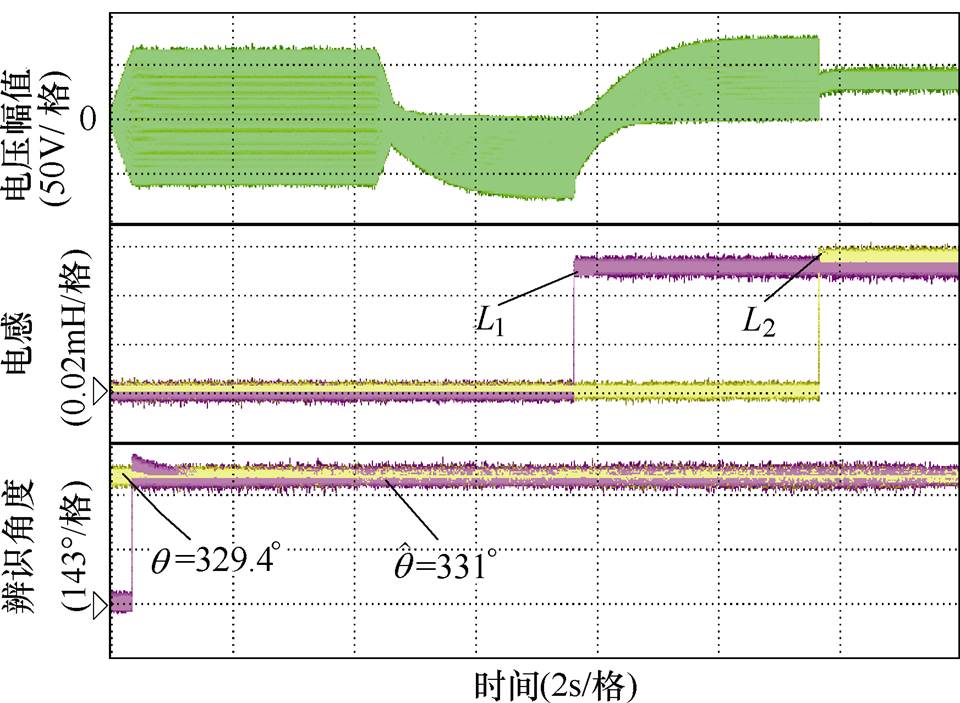
图10 转子位于239.4°时实验结果
Fig.10 Experimental results of the rotor is at 239.4 degree
在永磁同步电机一个电角度周期中取任意角度进行转子位置辨识，辨识过程中改变注入高频脉振信号的幅值和频率，最终辨识误差如图11所示。图11a中，注入高频脉振信号频率为400Hz，幅值为0.4Udc，辨识平均误差为2.63°，最大误差为7.6°；图11b中，注入高频脉振信号频率为400Hz，幅值为0.5Udc，辨识平均误差为2.68°；图11c中，注入高频脉振信号频率为800Hz，幅值为0.4Udc，辨识平均误差为2.75°。对实验数据进行分析可知，注入高频信号的频率和幅值对转子初始位置辨识结果无影响。
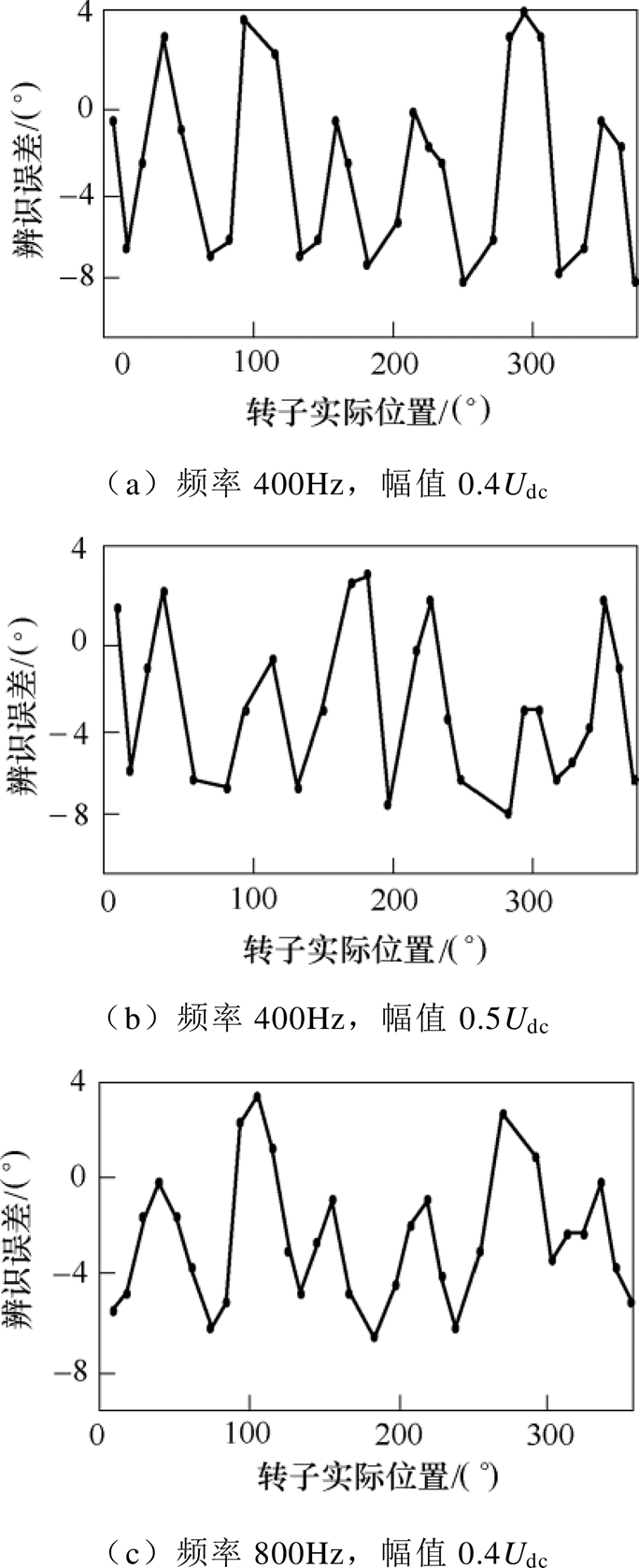
图11 无滤波器辨识方法实验误差
Fig.11 Experimental error of the filterless method
图12为采用传统高频脉振信号法在一个电角度周期内的辨识误差，实验中注入高频信号频率为400Hz，幅值为0.4Udc，最大误差为9.36°，平均误差为4.56°。
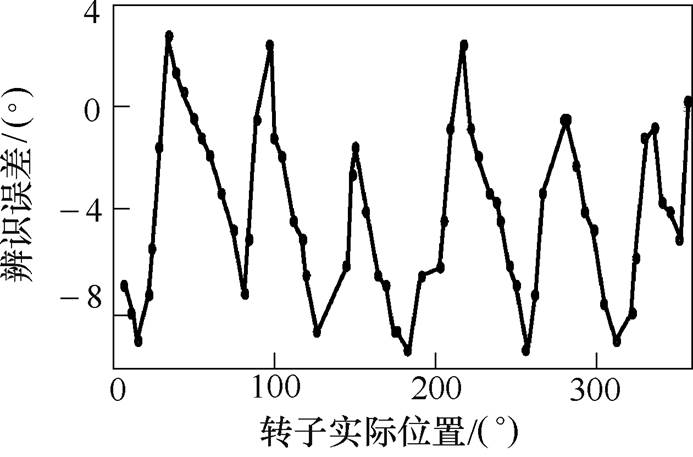
图12 传统辨识方法实验误差
Fig.12 Experimental error of the traditional method
对比传统高频脉振信号法和无滤波器高频脉振信号法在相同注入信号条件下实验误差可知，所提出方法平均实验误差与传统方法相比减小1.93°，最大实验误差减小1.76°，对辨识精度有显著的提高，充分说明无滤波器高频脉振信号法的可行性。
本文对无滤波器高频脉振信号注入永磁同步电机辨识转子初始位置方法进行了研究，仿真和实验结果表明：
1）本文所提出的方法能够在永磁同步电机静止条件下快速、准确地实现转子初始位置辨识，能够有效地克服传统高频脉振信号法中因滤波器相移所导致的辨识精度降低的问题，同时消除注入高频脉振信号幅值对辨识结果的影响。
2）对传统磁极极性辨识方法进行改进，利用正反方向直流偏置下电感大小判断极性，有效地避免了磁链位于线性区时由于电感值近似相等造成的辨识失败情况。
参考文献
[1] 张国强, 王高林, 倪荣刚, 等. 基于自适应线性神经元滤波的内置式永磁电机转子位置观测器[J]. 电工技术学报, 2016, 31(6): 83-89.
Zhang Guoqiang, Wang Gaolin, Ni Ronggang, et al. Adaptive linear element filtering based rotor position observer for interior permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 83-89.
[2] 李旭春, 张鹏, 严乐阳, 等. 具有参数辨识的永磁同步电机无位置传感器控制[J]. 电工技术学报, 2016, 31(14): 139-147.
Li Xuchun, Zhang Peng, Yan Leyang, et al. Sensor- less control of permant magnet synchronous motor with online parameter identification[J]. Transactions of China Eletrotechnical Society, 2016, 31(14): 139- 147.
[3] 田兵, 安群涛, 孙东阳, 等. 基于磁饱和效应的表贴式永磁同步电机初始位置检测方法[J]. 电工技术学报, 2016, 31(1): 155-164.
Tian Bing, An Quntao, Sun Dongyang, et al. Initial position estimation for surface permanent magnet synchronous motors based on magnetic saturation effect[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 155-164.
[4] Diaz R D, Briz F, Blanco C C, et al. Sensorless control of doubly fed induction generators based on rotor high-frequency signal injection[J]. IEEE Transa- ctions on Industry Applications, 2013, 49(6): 2593- 2601.
[5] 黄科元, 陈忠强, 黄守道. 一种基于电感饱和效应的电流差值检测永磁同步电机转子初始位置的方法[J]. 电工技术学报, 2018, 33(7): 1508-1515.
Huang Keyuan, Chen Zhongqiang, Huang Shoudao. A novel initial rotor position estimation method for PMSM based on inductance saturation effect[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1508-1515.
[6] 贾洪平, 贺益康. 基于高频注入法的永磁同步电动机转子初始位置检测研究[J]. 中国电机工程学报, 2007, 27(15): 15-20.
Jia Hongping, He Yikang. Study on inspection of the initial rotor position of a PMSM based on high- frequency signal injection[J]. Proceedings of the CSEE, 2007, 27(15): 15-20.
[7] 刘海东, 周波, 郭鸿浩, 等. 脉振高频信号注入法误差分析[J]. 电工技术学报, 2015, 30(6): 38-44.
Liu Haidong, Zhou Bo, Guo Honghao, et al. Error analysis of high frequency pulsating signal injection method[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 38-44.
[8] 周元钧, 蔡名飞. 改进的永磁同步电机转子初始位置检测方法[J]. 电机与控制学报, 2010, 14(3): 68- 72.
Zhou Yuanjun, Cai Mingfei. Initial rotor position inspection of PMSM based on rotating high frequency voltage signal injection[J]. Electric Machines and Control, 2010, 14(3): 68-72.
[9] Zou Xunhao, Huang Shenghua, Qin Zhuqian, et al. A novel initial rotor position detection method for PM synchronous motors[C]//2015 6th International Con- ference on Power Electronics Systems and Appli- cations (PESA), Hong Kong, 2015: 1-4.
[10] Garcia P, Briz F, Degner M W, et al. Accuracy, bandwidth, and stability limits of carrier-signal- injection-based sensorless control methods[J]. IEEE Transactions on Industry Applications, 2007, 43(4): 990-1000.
[11] 李浩源, 张兴, 杨淑英, 等. 基于旋转高频注入的内置式永磁同步电机初始位置检测算法[J]. 电工技术学报, 2018, 33(8): 1723-1731.
Li Haoyuan, Zhang Xing, Yang Shuying, et al. A detecting algorithm for initial position of interior permanent magnet synchronous motor based on rotating high frequency injection[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1723- 1731.
[12] Raca D, Garcia P, Reigosa D, et al. A comparative analysis of pulsating vs. rotating vector carrier signal injection-based sensorless control[C]//Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 2008: 879-885.
[13] Liu Bing, Zhou Bo, Wei Jiadan, et al. A novel method for polarity detection of nonsalient PMSMs in initial position estimation[C]//2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, 2016: 2754-2758.
[14] 李文真, 刘景林, 陈双双. 基于高频方波信号注入法的永磁同步电机转子位置检测方法[J]. 电工技术学报, 2018, 33(24): 5821-5829.
Li Wenzhen, Liu Jinglin, Chen Shuangshuang. Permanent magnet synchronous motor rotor position detection method based on high-frequency square- wave signal injection[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5821-5829.
[15] Liu Bing, Zhou Bo, Wei Jiadan, et al. A rotor initial position estimation method for sensorless control of SPMSM[C]//IECON 40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, 2014: 354-359.
[16] 何栋炜, 彭侠夫, 蒋学程, 等. 内置式永磁同步电机转子初始位置估计方法[J]. 电机与控制学报, 2013, 17(3): 49-55.
He Dongwei, Peng Xiafu, Jiang Xuecheng, et al. Initial rotor position estimation method for IPMSM[J]. Electric Machines and Control, 2013, 17(3): 49-55.
[17] 刘海东, 周波, 郭鸿浩, 等. 脉振高频信号注入法误差分析[J]. 电工技术学报, 2015, 30(6): 38-44.
Liu Haidong, Zhou Bo, Guo Honghao, et al. Error analysis of high frequency pulsating signal injection method[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 38-44.
[18] 杨健, 杨淑英, 李浩源, 等. 基于旋转高频电压注入的永磁同步电机转子初始位置辨识方法[J]. 电工技术学报, 2018, 33(15): 3547-3555.
Yang Jian, Yang Shuying, Li Haoyuan, et al. Initial rotor position estimation for IPMSM based on high frequency rotating voltage injection[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3547-3555.
[19] 张国强, 王高林, 徐殿国. 基于无滤波器方波信号注入的永磁同步电机初始位置检测方法[J]. 电工技术学报, 2017, 32(13): 162-168.
Zhang Guoqiang, Wang Gaolin, Xu Dianguo. Filter- less square-wave injection based initial position detection for permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 162-168.
[20] 任雷, 崔芮华, 王宗培, 等. 永磁同步电机绕组电感的饱和效应[J]. 电工技术学报, 2000, 15(1): 21-25.
Ren Lei, Cui Ruihua, Wang Zongpei, et al. Saturation effect of PMSM windings inductance[J]. Transactions of China Electrotechnical Society, 2000, 15(1): 21-25.
[21] Wang Gaolin, Wang Ying, Qi Jianbo, et al. Offline inductance identification of PMSM with adaptive inverter nonlinearity compensation[C]//2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, 2015: 2438- 2444.
Initial Position Identification of PMSM with Filterless High Frequency Pulse Signal Injection Method
Abstract A method is proposed to identify the rotor initial angle using high-frequency pulse signal injection into a permanent magnet synchronous motor (PMSM). This method, briefly called filterless high frequency pulse signal injection, is an improvement on the traditional identification of the rotor initial angle. Firstly, the function of rotor initial angle error is calculated from stator current high-frequency response instead of using a low-pass filter, then, the initial rotor angle is obtained through a phase-locked loop. The method of identifying the rotor polarity is also modified using the saturation effect of the magnetic circuit, which improves the polarity identification of the rotor magnet. Finally, the proposed scheme has been verified by experiments on an 16kW interior permanent magnet synchronous motor platform.
keywords：Permanent magnet synchronous motor, initial position identification, high frequency pulse signal, filterless
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.191818
河北省自然科学基金资助项目（E2018203152）。
收稿日期 2019-12-30
改稿日期 2020-05-11
于安博 男，1981年生，博士，研究方向为永磁同步电机控制技术、新能源汽车电驱系统集成技术。E-mail: hbxtyuanbo@163.com
张纯江 男，1961年生，博士，教授，博士生导师，研究方向为电力电子变换器拓扑及控制、可再生能源分布式发电技术、逆变电源及并联并网、微电网及储能功率流控制等。E-mail: zhangcj@ysu.edu.cn（通信作者）
（编辑 陈 诚）