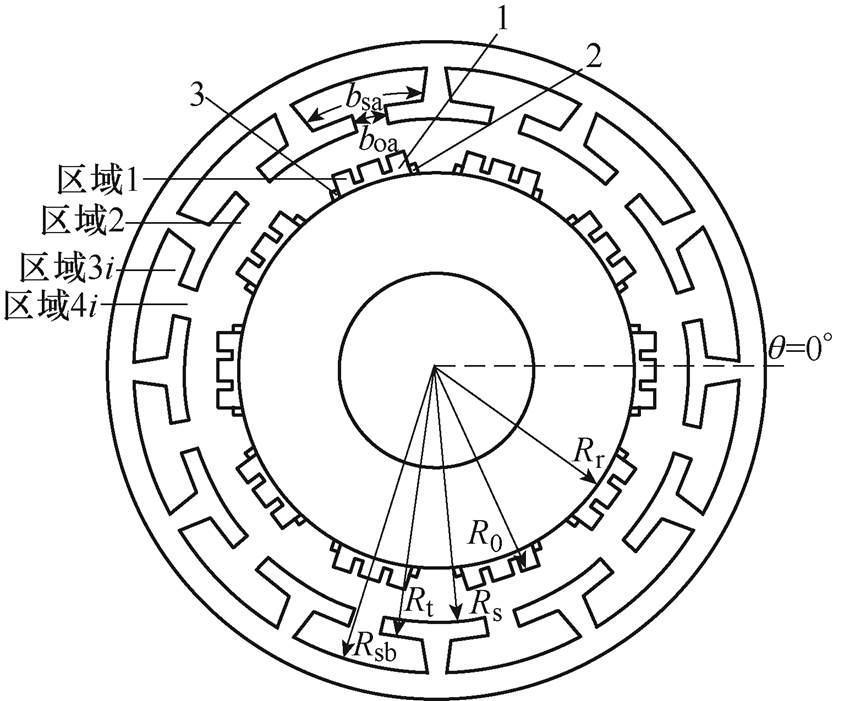
图1 永磁同步电机解析模型
Fig.1 Schematic diagram of PMSM analysis model
摘要 针对高功率密度的永磁同步电机齿槽转矩及永磁体涡流损耗大的问题,设计一种部分分段Halbach结构的表贴式永磁同步电机,永磁体采用Halbach充磁方式,每极分为三段,主磁极采用单侧部分分段,边界磁极与主磁极不等厚且不等宽。采用精确子域模型法,将求解域划分为永磁体、气隙、槽身和槽口四个区域,在二维极坐标下计算电机空载气隙磁通密度及齿槽转矩。建立10极12槽三维电机模型进行电磁仿真分析。结果表明,部分分段Halbach结构降低了永磁体涡流损耗、齿槽转矩及永磁体体积。同时,在有限元应力场中建立三维永磁同步电机求解模型,求得等效应力和总变形,确保部分分段结构永磁体的机械强度维持在允许范围内。
关键词:永磁同步电机 精确子域模型法 部分分段Halbach结构 等效应力
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)由于齿槽物理结构以及钕铁硼永磁材料的广泛应用[1-3],出现了齿槽转矩和永磁体涡流损耗,使电机出现转矩波动以及永磁体温度上升,导致振动、噪声以及电机效率下降[4-7]。
削弱电机齿槽转矩,其中最重要的是分析电机解析模型中开槽对气隙磁场的影响。文献[8]对Halbach永磁电机的建模及气隙磁通密度分布进行分析,但分析对象为未开槽永磁电机。为了考虑定子开槽的影响,文献[9-11]应用数值解析结合法推导了永磁无刷电机的气隙磁场分布表达式,虽然可以精确求解各类复杂槽型,但需要反复迭代,计算时间长。文献[12-13]采用保角变换法并利用复数磁导推导了计及极间间隔Halbach永磁同步电机的气隙磁通密度分布,但无限深单槽模型无法考虑两槽间的相互影响。文献[14-16]采用解析法推导了定子开槽后表贴式PMSM气隙磁通密度分布的表达式,但定子槽开口宽度仅由槽口宽度决定,与实际电机差别较大。
永磁体部分分段使电机磁场发生畸变,增加了计算齿槽转矩的难度。传统磁路法依赖于经验系数对计算结果的修正,而修正系数受到其他参数的影响,难以得到最优解;有限元法计算时间长,难以建立起结构尺寸和气隙磁通密度之间的直接联系。精确子域模型法能考虑到定子槽间相互影响,根据材料属性和电机结构将电机划分为不同的子域,在计算电磁性能方面具有较高的精度。文献[17]采用精确子域模型法,推导了径向及平行充磁时永磁体任意分段数目时的气隙磁通密度分布和齿槽转矩,但未对完全分段的永磁电机进行优化分析。文献[18]采用精确子域模型法推导了表面埋入式PMSM的空载及负载气隙磁通密度分布表达式,但未分析槽口对于表面埋入式电机的影响。文献[19]建立了定子齿上开有辅助槽的表贴式永磁电机的解析模型,采用精确子域模型法推导了空载气隙磁通密度、齿槽转矩等参数的表达式,并对齿槽转矩进行了优化,但采用辅助槽结构优化齿槽转矩的效果并不明显,有待进一步提高。上述文献采用精确子域模型法对于永磁电机的建模仍存在不足之处。
针对永磁体涡流损耗的抑制,最常用的方法是永磁体分段。对于表贴式PMSM,分数槽结构采用永磁体周向均匀分段比整数槽结构更好,整数槽结构更适合采用永磁体非均匀周向分段[20]。文献[21]比较了采用多分段及不分段永磁体结构的效率、涡流损耗和温度,研究了分段数和输入电流对涡流损耗和效率的影响。文献[22]提出一种环形部分分段结构,比较了永磁体单侧、双侧部分分段及单侧、双侧环形部分分段的涡流损耗,并验证了部分分段后永磁体的机械强度。上述文献分别采用永磁体周向非均匀分段、周向均匀分段及部分分段,永磁体部分分段的降耗效果虽然不如完全分段,但完全分段十分复杂,永磁体需要被切割、绝缘以及重新胶合,会增加工艺难度和成本,减小永磁体机械强度。永磁体部分分段的降耗效果虽然不如完全分段,但在保持一定机械强度的基础上,可以保证永磁体的完整性,不需要额外的工艺及成本。
为此,提出了一种部分分段Halbach结构来降低涡流损耗和齿槽转矩,采用精确子域模型法分析定子开槽后对气隙磁场的影响,求解电机空载气隙磁通密度及齿槽转矩表达式,建立10极12槽表贴式PMSM三维模型进行电磁及应力仿真,对电机的空载气隙磁通密度、齿槽转矩、基波幅值、涡流损耗等参数进行分析,并将普通表贴式结构、部分分段结构、等宽等厚Halbach结构以及部分分段Halbach结构的电磁性能进行对比,验证部分分段Halbach结构的优越性。
假设:忽略电机端部效应;铁心磁导率无穷大,忽略电机的饱和效应。
基于精确子域模型法分析定子开槽后的气隙磁场,建立部分分段Halbach PMSM解析模型如图1所示。结构1为径向充磁的主磁极,结构2、3为采用一定充磁角度的两个边界磁极。

图1 永磁同步电机解析模型
Fig.1 Schematic diagram of PMSM analysis model
图1中,Rr为转子外半径;R0为永磁体外半径;Rs为定子铁心内半径;Rt为定子槽顶半径;Rsb为定子槽底半径;boa为槽口对应的圆心角;bsa为槽身对应的圆心角;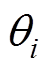 为第i个槽中心的机械角度。将解析模型在二维极坐标系下分成永磁体、气隙、第i个槽身、第i个槽口,四个区域分别为区域1、2、3i、4i。
为第i个槽中心的机械角度。将解析模型在二维极坐标系下分成永磁体、气隙、第i个槽身、第i个槽口,四个区域分别为区域1、2、3i、4i。
为了便于各子域通解及谐波系数的求解[23],定义了函数为
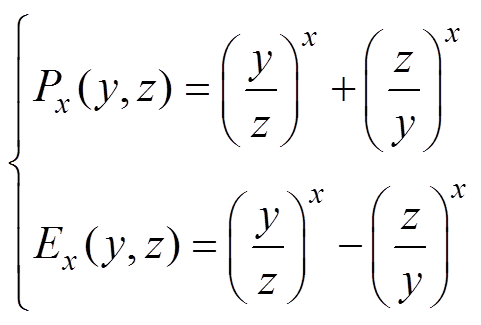 (1)
(1)永磁体子域满足的泊松方程及通解表达式[24-29],有
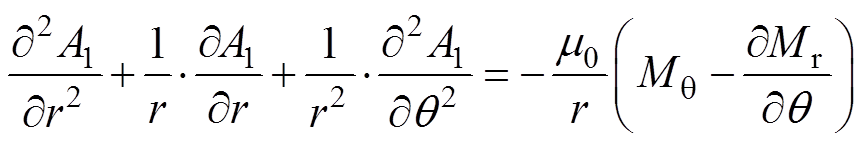 (2)
(2)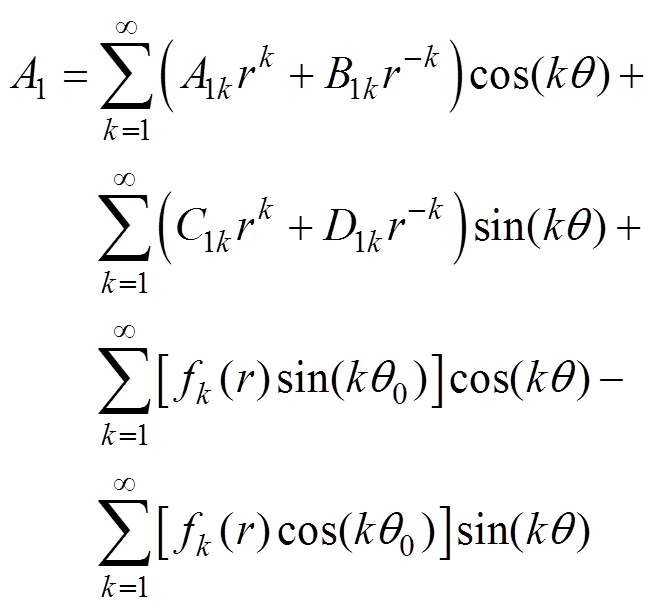 (3)
(3)
其中
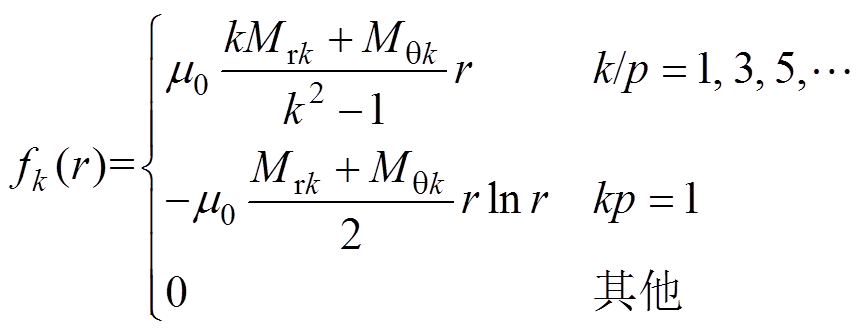 (4)
(4)式中,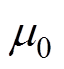 为真空磁导率;
为真空磁导率;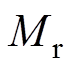 、
、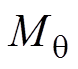 分别为剩余磁化强度的径向及切向分量;k为永磁体及气隙子域矢量磁位的谐波次数;A1k~D1k为永磁体子域矢量磁位的谐波系数;
分别为剩余磁化强度的径向及切向分量;k为永磁体及气隙子域矢量磁位的谐波次数;A1k~D1k为永磁体子域矢量磁位的谐波系数;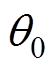 为转子初始位置角。
为转子初始位置角。
在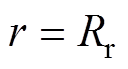 处,永磁体的边界条件为
处,永磁体的边界条件为
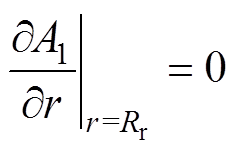 (5)
(5)因此,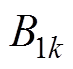 和
和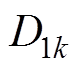 的表达式分别为
的表达式分别为
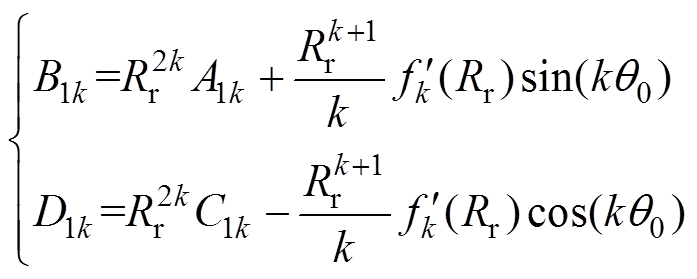 (6)
(6)
又由式(1)可知,可将式(6)转换为
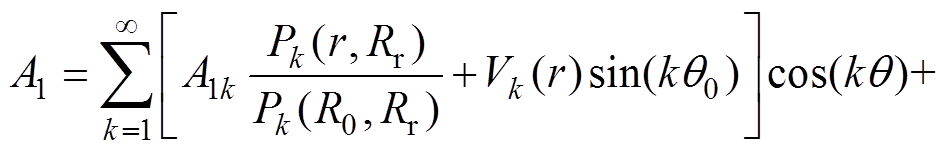
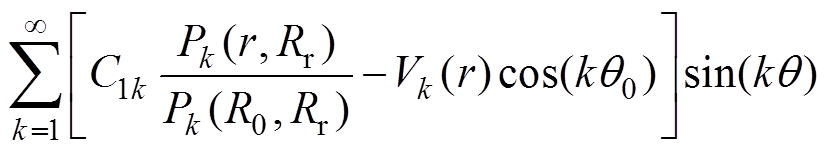 (7)
(7)
其中,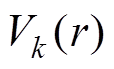 与永磁体磁化方式有关,有
与永磁体磁化方式有关,有
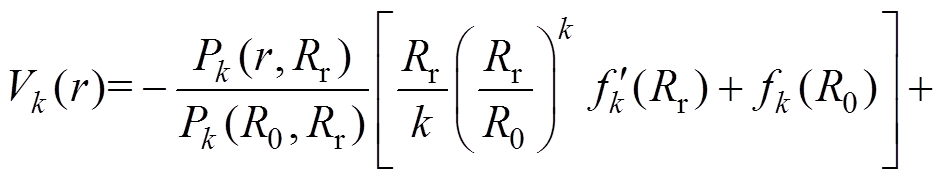
 (8)
(8)
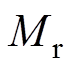 、
、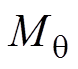 在(0, 2p)内的傅里叶级数展开式为
在(0, 2p)内的傅里叶级数展开式为
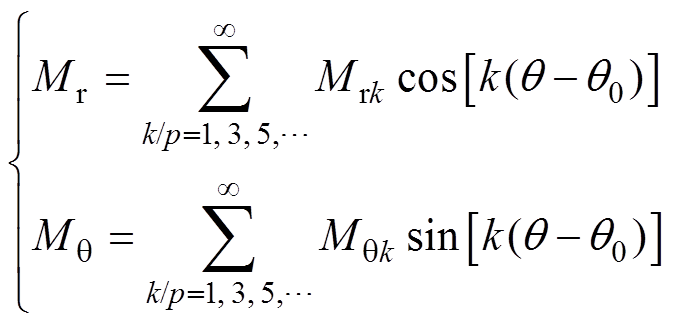 (9)
(9)径向充磁的完全分段永磁体、Halbach充磁的永磁体以及径向充磁的永磁体的每对极下磁化强度分布如附录所示。
对于径向充磁的永磁体,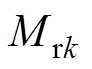 、
、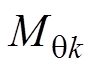 分别为
分别为
 (10)
(10)式中,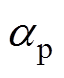 为永磁体极弧系数;
为永磁体极弧系数;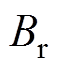 为永磁体剩磁。
为永磁体剩磁。
对于Halbach充磁的永磁体,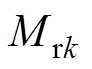 、
、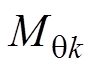 分别为
分别为
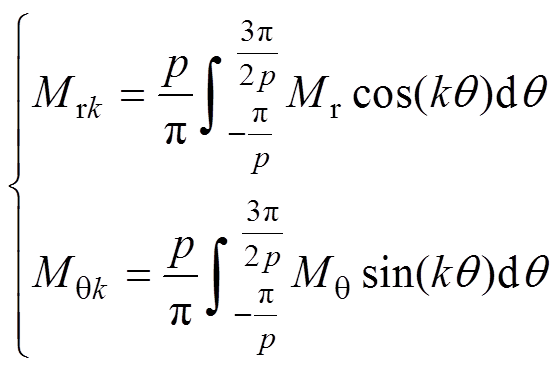 (11)
(11)式中,p为极对数。
对于径向充磁的完全分段永磁体,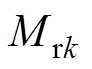 、
、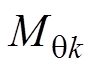 分别为
分别为
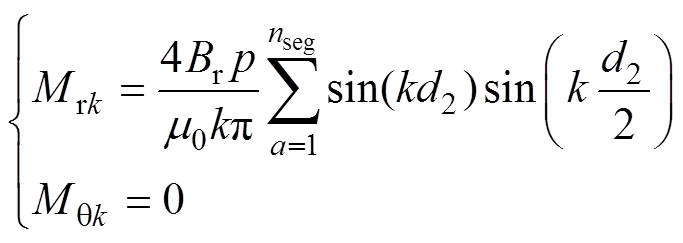 (12)
(12)式中,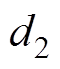 为每块磁块对应的极弧宽度;nseg为每极分段数。
为每块磁块对应的极弧宽度;nseg为每极分段数。
气隙子域满足的拉普拉斯方程及通解表达式分别为
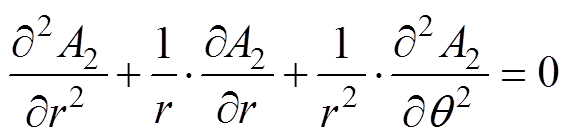 (13)
(13)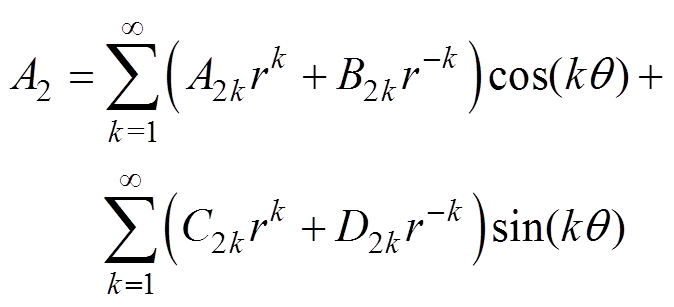 (14)
(14)
由式(1)可知,可将式(14)转换为
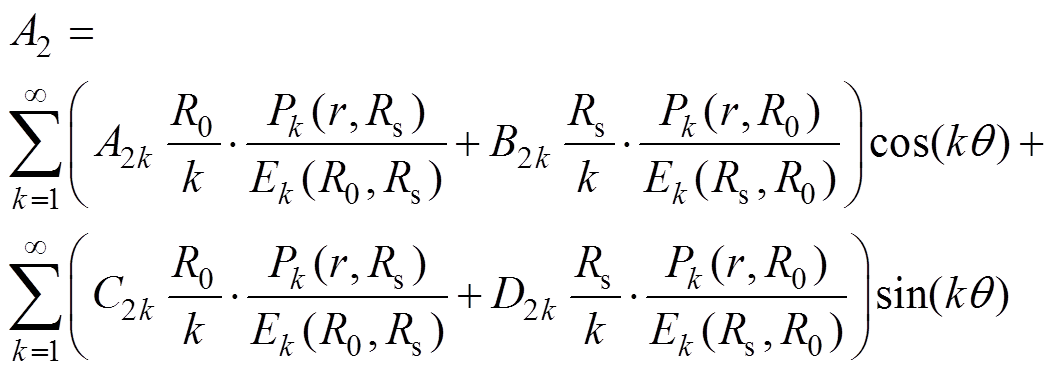 (15)
(15)槽子域满足的拉普拉斯方程及通解表达式分别为
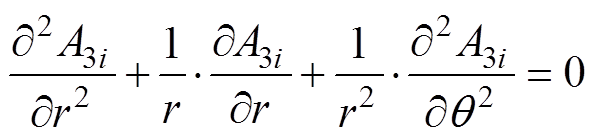 (16)
(16)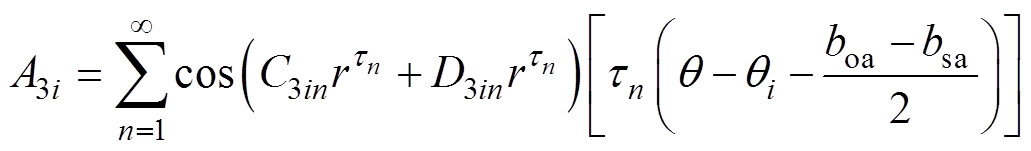 (17)
(17)
式中,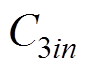 、
、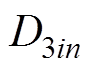 为槽子域谐波系数;
为槽子域谐波系数;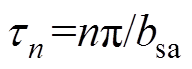 ;Q为定子槽数;
;Q为定子槽数;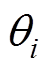 为第i个槽口初始角度,
为第i个槽口初始角度,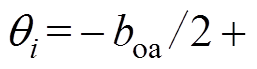
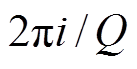 。
。
槽子域满足边界条件为
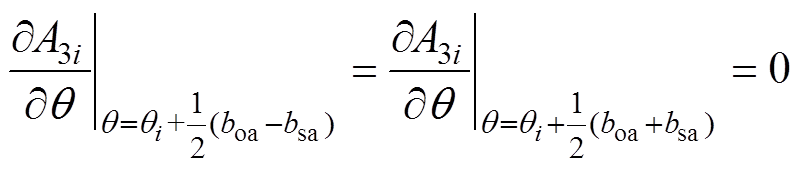 (18)
(18)由式(1)可知,式(17)可转换为
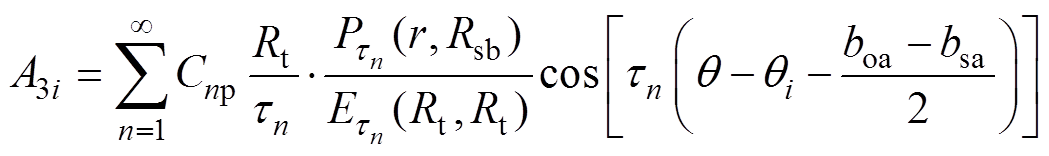 (19)
(19)
式中,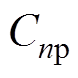 为包含
为包含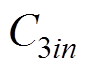 、
、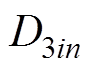 的谐波系数。
的谐波系数。
槽开口子域满足拉普拉斯方程及通解表达式[30-31]分别为
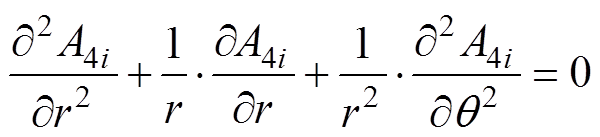 (20)
(20)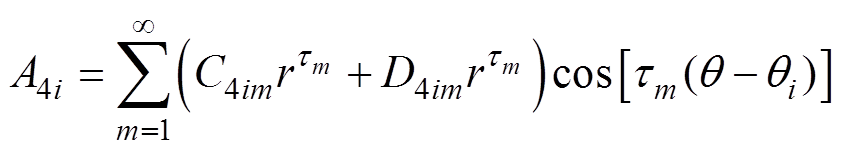 (21)
(21)
由式(1)可知,可将式(21)转换为
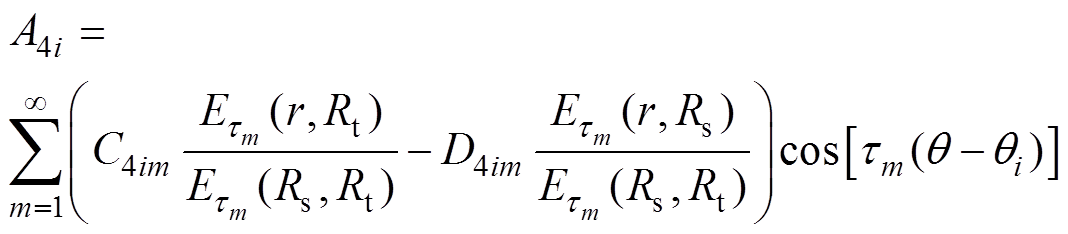 (22)
(22)式中,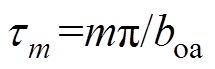 ;
;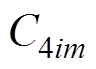 、
、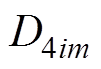 为槽开口子域谐波系数,m为槽开口子域谐波次数。
为槽开口子域谐波系数,m为槽开口子域谐波次数。
在永磁体子域和气隙子域的边界处即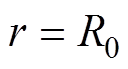 处,边界条件为
处,边界条件为
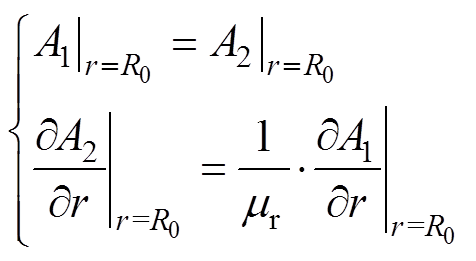 (23)
(23)因此,可得
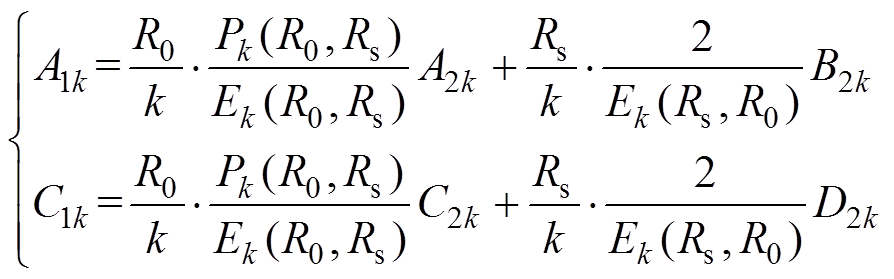 (24)
(24)
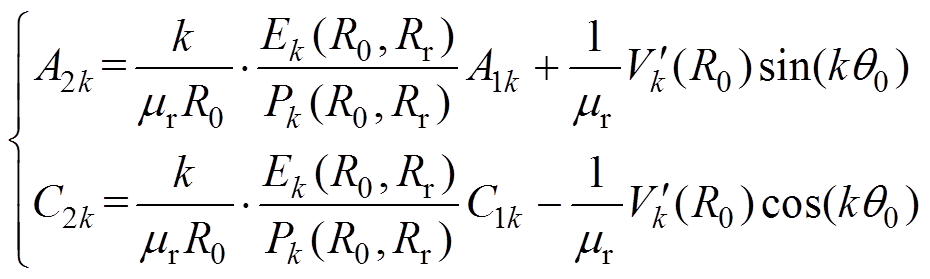 (25)
(25)在槽开口子域和气隙子域的边界,即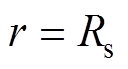 处,边界条件为
处,边界条件为
 (26)
(26)
因此,可得
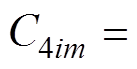
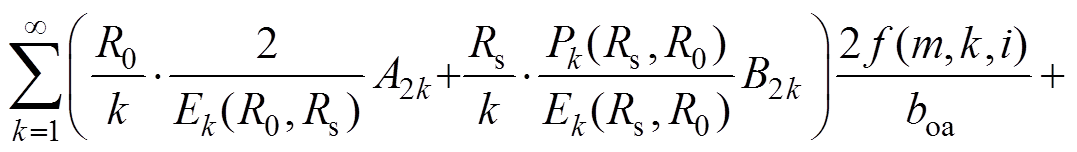
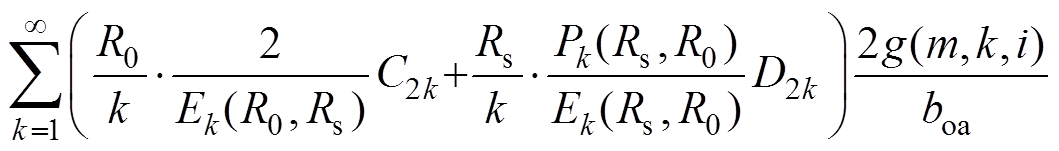 (27)
(27)
 (28)
(28)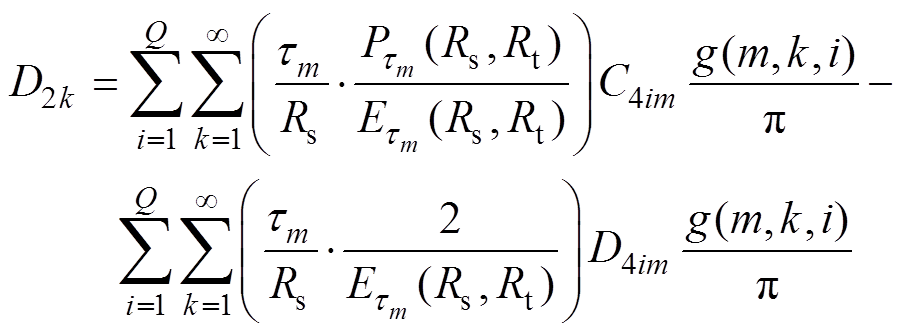 (29)
(29)
其中,当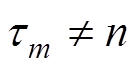 时,有
时,有
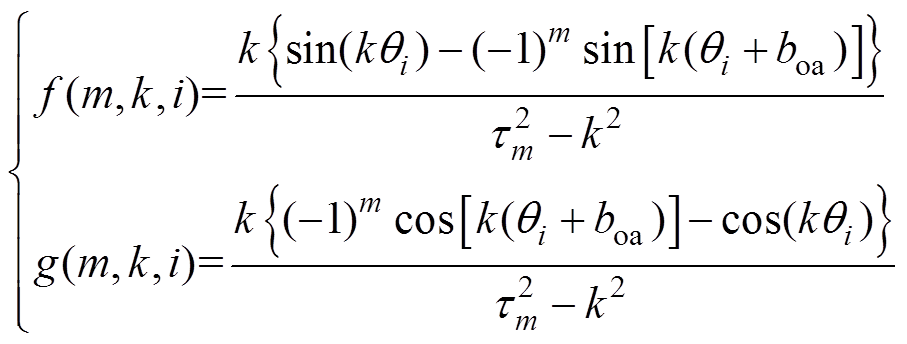 (30)
(30)当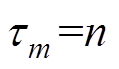 时
时
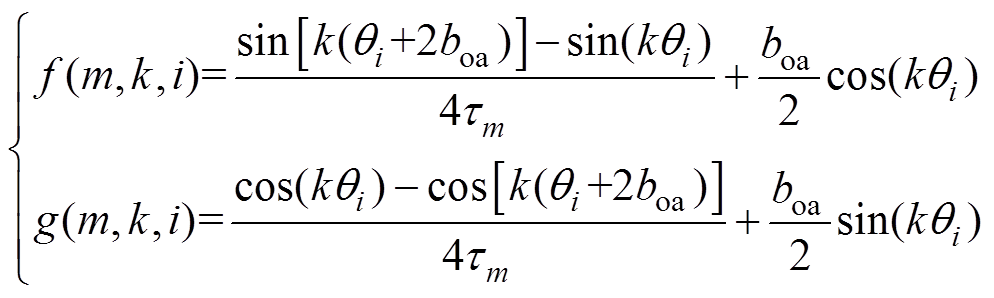 (31)
(31)
在槽开口子域和气隙子域的边界,即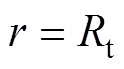 处,边界条件为
处,边界条件为
 (32)
(32)因此,可得
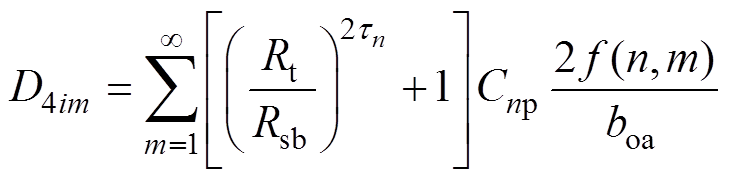 (33)
(33)
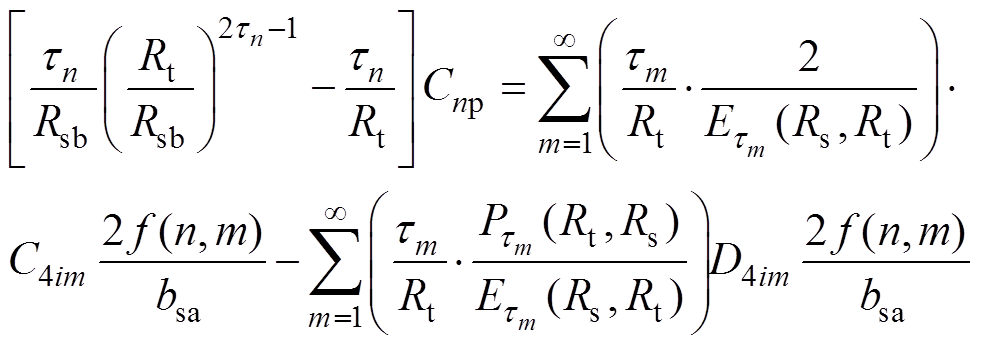 (34)
(34)其中,当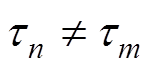 时
时
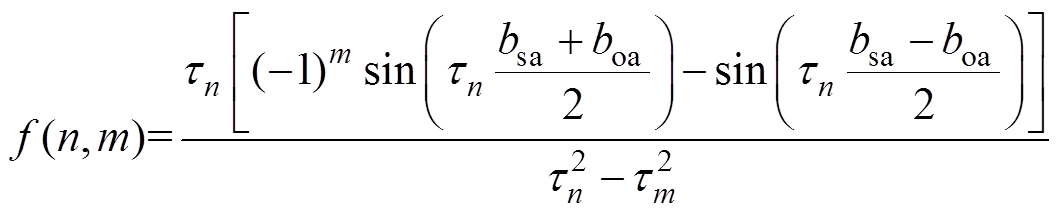 (35)
(35)
当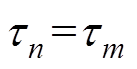 时
时
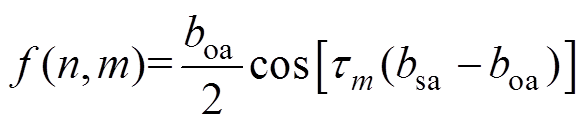 (36)
(36)联立式(24)、式(25)、式(27)~式(29)、式(33)、式(34),可求得四类子域中的各阶次谐波系数: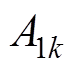 ~
~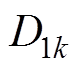 、
、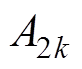 ~
~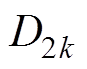 、
、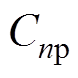 、
、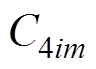 、
、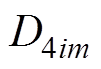 ,具体表达式见附录。
,具体表达式见附录。
采用叠加原理求取部分分段Halbach结构的气隙磁通密度,将图1所示模型的永磁体分解为三部分,分别求取三个部分的气隙磁通密度:第一部分为径向充磁的完全分段永磁体;第二部分为主磁极剩余的两个小永磁体,主磁极结构拆分示意图如图2所示;第三部分为两个边界磁极即结构2、3。图2中,X1为相邻分段间隔,X2为分段处极弧宽度,X3为部分分段深度。

图2 主磁极结构拆分示意图
Fig.2 Main magnetic pole decomposition diagram
对于第一部分径向充磁的完全分段永磁体,将式(12)代入式(7)中,可得第一部分永磁体的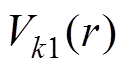 ,即当
,即当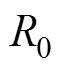 为主磁极外半径
为主磁极外半径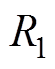 ,
,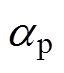 为主磁极极弧系数
为主磁极极弧系数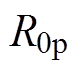 时,再求出径向、切向气隙磁通密度
时,再求出径向、切向气隙磁通密度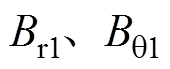 。
。
对于第二部分径向充磁的两个小永磁体,可将其中间部分补齐,求出补齐后永磁体的气隙磁通密度,再减去中间部分永磁体的气隙磁通密度。将式(10)代入式(7)中,可得第二部分永磁体的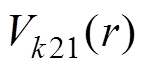 、
、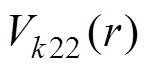 ,即求得永磁体极弧宽度为X1+X2,
,即求得永磁体极弧宽度为X1+X2,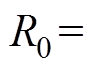
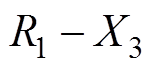 时的
时的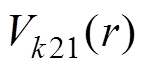 ,以及求得永磁体极弧宽度为X1,
,以及求得永磁体极弧宽度为X1,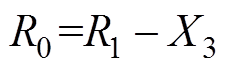 时的
时的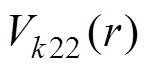 ,再分别求出径向气隙磁通密度
,再分别求出径向气隙磁通密度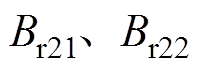 以及切向气隙磁通密度
以及切向气隙磁通密度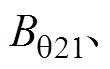
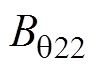 。因此,第二部分的径向气隙磁通密度
。因此,第二部分的径向气隙磁通密度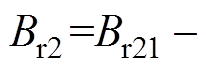
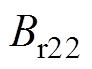 ,切向气隙磁通密度
,切向气隙磁通密度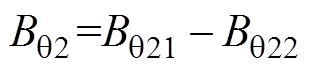 。
。
对于第三部分Halbach充磁的两个边界永磁体,可将其中间部分补齐,如图3所示,求出补齐后永磁体的气隙磁通密度,再减去中间部分径向充磁永磁体的气隙磁通密度。将式(11)代入式(7)中,可得第三部分永磁体的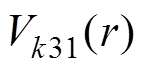 、
、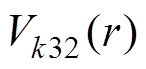 ,即求得永磁体极弧系数为
,即求得永磁体极弧系数为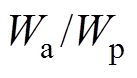 、
、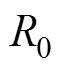 为边界磁极的外半径
为边界磁极的外半径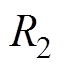 时的
时的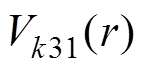 ,以及求得永磁体极弧系数为
,以及求得永磁体极弧系数为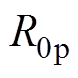 、
、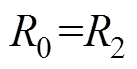 时的
时的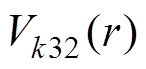 ,再分别求出径向气隙磁通密度
,再分别求出径向气隙磁通密度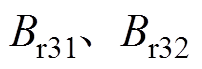 以及切向气隙磁通密度
以及切向气隙磁通密度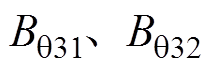 。因此,第三部分的径向气隙磁通密度
。因此,第三部分的径向气隙磁通密度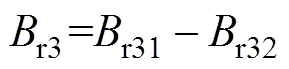 ,切向气隙磁通密度
,切向气隙磁通密度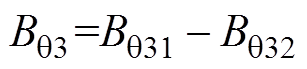 。
。
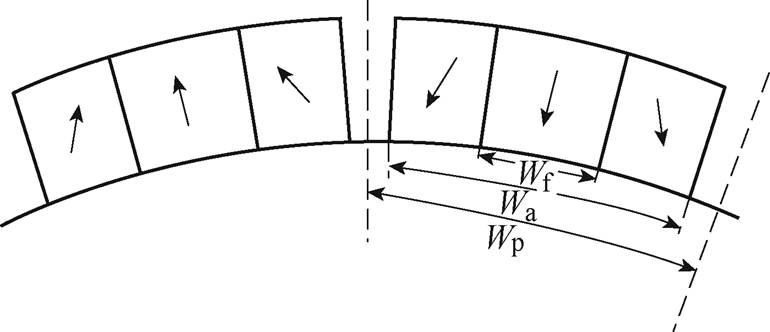
图3 边界磁极模型示意图
Fig.3 Schematic diagram of boundary magnetic pole model
部分分段Halbach PMSM的空载气隙径向磁通密度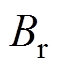 和切向磁通密度
和切向磁通密度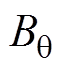 分别为
分别为
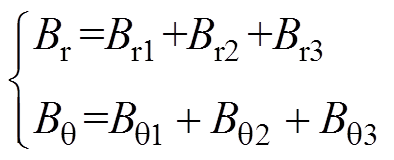 (37)
(37)可以看出,在非永磁体参数一定时,部分分段Halbach PMSM的空载气隙磁通密度仅与三个部分的永磁体外半径和极弧系数有关,即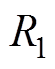 、
、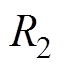 以及
以及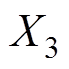 和
和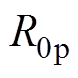 、X1、X2以及
、X1、X2以及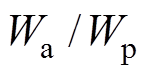 。当主磁极外半径
。当主磁极外半径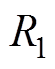 、分段处极弧宽度X2以及极间间隔一定时,空载气隙磁通密度与边界磁极外半径
、分段处极弧宽度X2以及极间间隔一定时,空载气隙磁通密度与边界磁极外半径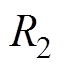 、部分分段深度X3、主磁极极弧系数以及相邻分段间隔有关。因此,对于空载气隙磁通密度的优化主要是对边界磁极厚度h1、部分分段深度X3、边界磁极角度q1以及相邻分段间隔X1的优化。
、部分分段深度X3、主磁极极弧系数以及相邻分段间隔有关。因此,对于空载气隙磁通密度的优化主要是对边界磁极厚度h1、部分分段深度X3、边界磁极角度q1以及相邻分段间隔X1的优化。
由空载气隙磁通密度分布计算结果,利用麦克斯韦应力张量法,齿槽转矩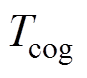 的表达式为
的表达式为
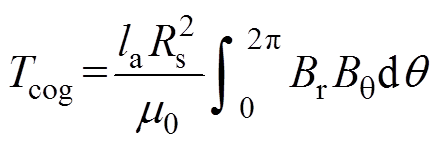 (38)
(38)式中,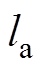 为电机轴向长度。
为电机轴向长度。
如图4所示为PMSM模型示意图。相比于传统表贴式PMSM的磁极,电机永磁体采用Halbach充磁方式,边界磁极与主磁极既不等宽也不等厚,主磁极部分分段。部分分段Halbach结构在Halbach阵列磁场分布正弦度好、磁通密度幅值高等特性的基础上采用主磁极部分分段,使气隙磁通密度波形更加正弦、降低齿槽转矩的同时,可以减小涡流损耗、提高电机性能。子任务设计方案中,轮毂电机为表贴式PMSM,10极12槽,模型电机的主要参数见表1,在Maxwell中进行参数化建模,建立三维PMSM模型,对电机的空载气隙磁通密度、齿槽转矩、涡流损耗等参数进行仿真分析,并比较普通表贴式结构、部分分段结构、普通Halbach结构、部分分段Halbach结构的齿槽转矩、涡流损耗及体积等性能,验证部分分段Halbach结构的有效性及优越性。
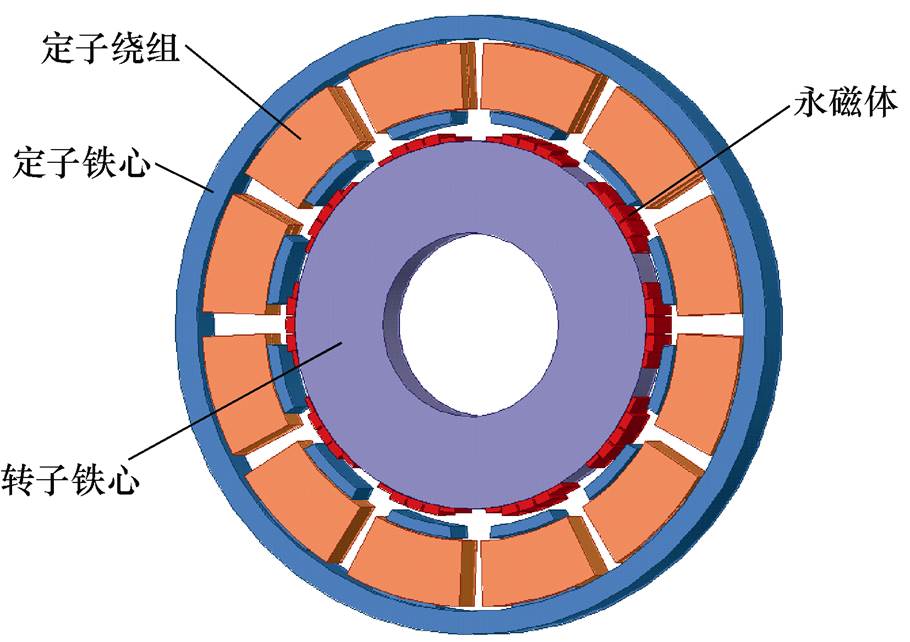
图4 PMSM模型示意图
Fig.4 Schematic diagram of PMSM model
表1 电机模型参数
Tab.1 Parameters of motor model

参 数数 值 定子外半径/mm64 定子内半径Rs/mm40 转子外半径Rr/mm36 主磁极外半径Rm/mm39 定子槽顶半径Rt/mm42.5 定子槽底半径Rsb/mm56.5 主磁极中心厚度/mm3 边界磁极厚度/mm2 极对数5 气隙长度/mm1 定子槽数12 电机转速/(r/min)12 000 永磁体剩磁Br/T1.1 槽口角度boa/(°)6 槽身角度bsa/(°)14 轴向长度/mm41.91
电机空载时气隙中心处的径向磁通密度、切向磁通密度计算结果对比如图5所示。电机齿槽转矩的计算结果对比如图6所示。从图5、图6中可以看出,精确子域模型解析法与有限元结果较为接近,验证了解析公式的正确性,为PMSM模型优化奠定了基础。
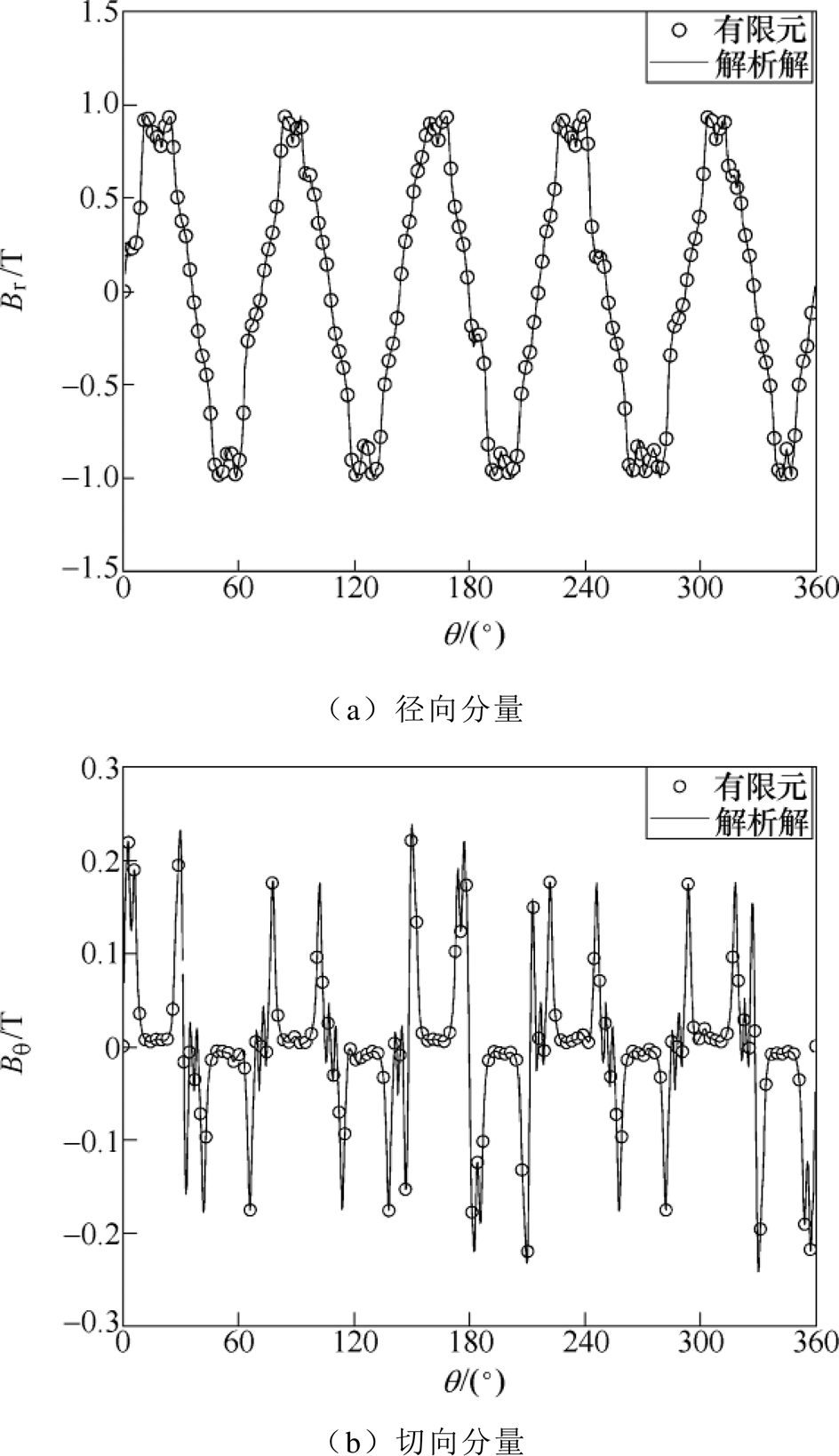
图5 空载气隙径向磁通密度和切向磁通密度的变化曲线
Fig.5 Variation curves of radial magnetic flux density and tangential magnetic flux density of no-load air gap
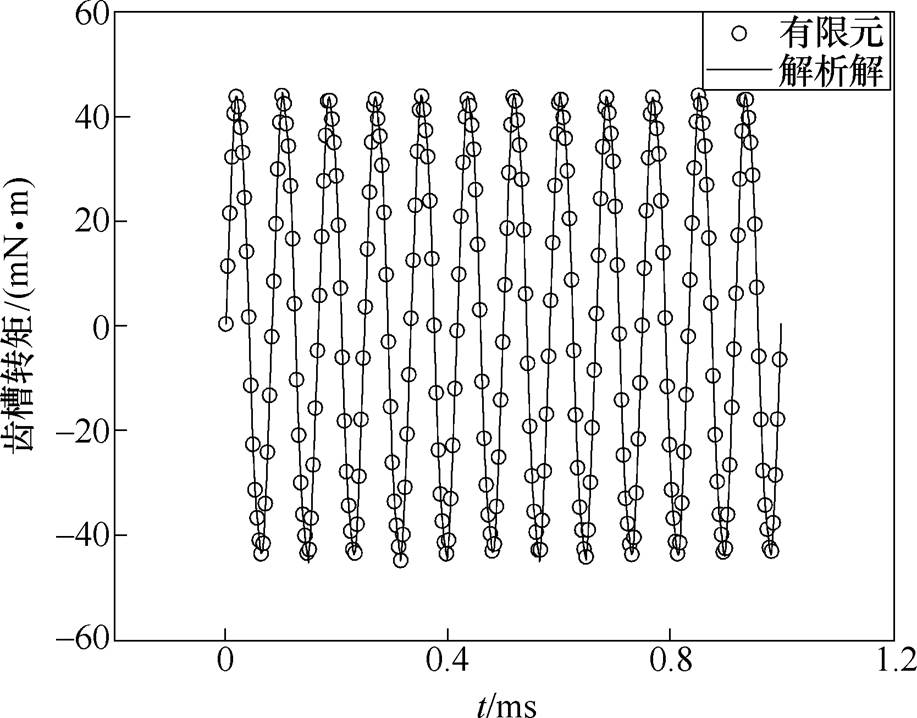
图6 齿槽转矩的变化曲线
Fig.6 Variation curve of cogging torque
改变有限元模型中的主磁极部分分段深度X3,使分段深度X3在0~3mm内,每隔0.2mm取一个值,得到永磁体涡流损耗随X3变化的曲线如图7所示。当X3=0mm时主磁极不分段,即不等厚不等宽的Halbach永磁同步电机。X3=3mm时主磁极为完全分段,从图中可以看出,随着X3的增加,永磁体涡流损耗逐渐减小。考虑到永磁体的完整性及其机械强度,X3不能超过永磁体厚度的65%,即X3= 1.95mm。
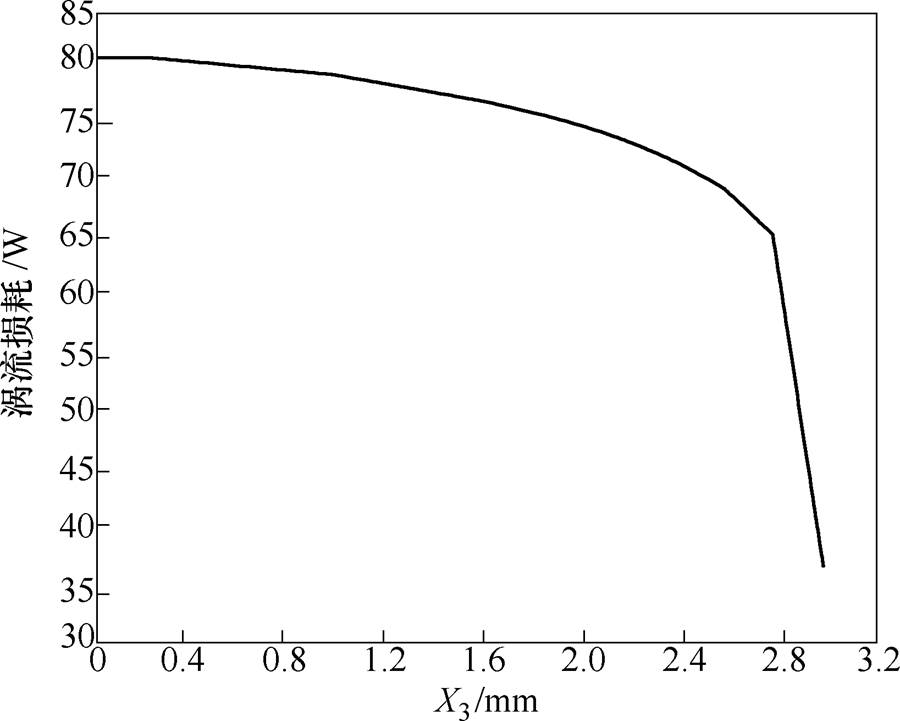
图7 永磁体涡流损耗随X3变化的曲线
Fig.7 Curve of permanent magnet eddy current loss with X3
改变PMSM模型中边界磁极的充磁角度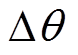 ,在0°~90°内,每隔10°取一个值,得到空载气隙磁通密度谐波畸变率及基波幅值随
,在0°~90°内,每隔10°取一个值,得到空载气隙磁通密度谐波畸变率及基波幅值随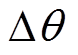 变化的曲线,如图8所示,从图中可以看出,随着
变化的曲线,如图8所示,从图中可以看出,随着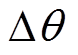 的增大,谐波畸变率先减小再增大,基波幅值先增大再减小,当
的增大,谐波畸变率先减小再增大,基波幅值先增大再减小,当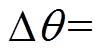 10°时,基波幅值有最大值0.99T,当
10°时,基波幅值有最大值0.99T,当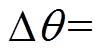 50°时,谐波畸变率有最小值18.27%,基波幅值为0.90T。因此,选取50°的充磁角度对边界磁极进行充磁。
50°时,谐波畸变率有最小值18.27%,基波幅值为0.90T。因此,选取50°的充磁角度对边界磁极进行充磁。
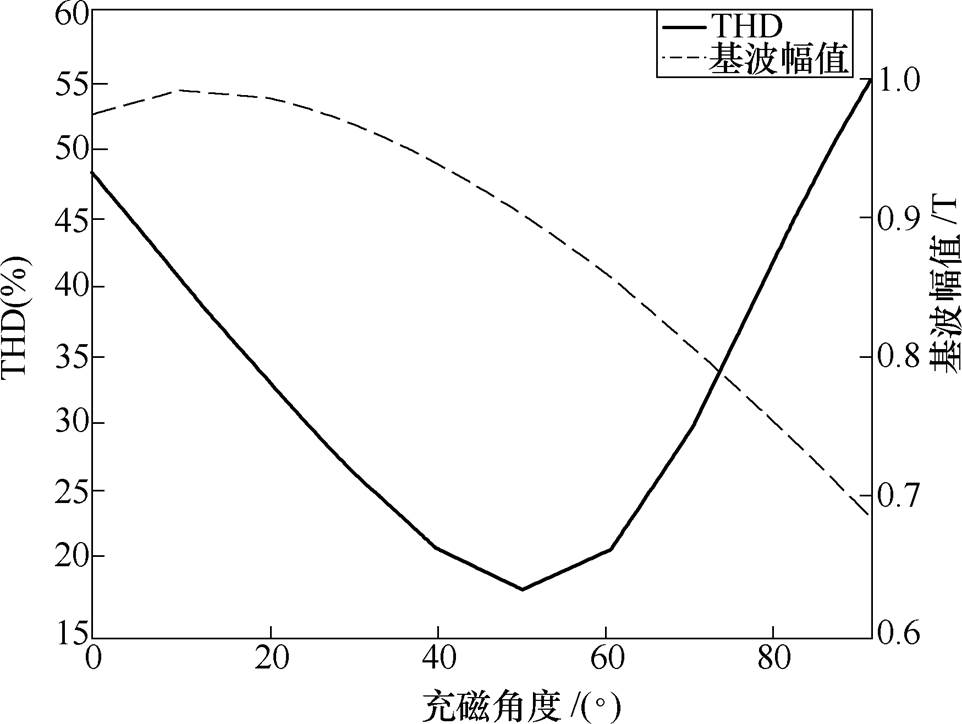
图8 谐波畸变率及基波幅值随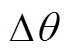 变化的曲线
变化的曲线
Fig.8 Curves of harmonic distortion rate and fundamental wave amplitude with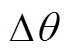
在极间间隔一定时,主磁极与边界磁极所占角度之和为固定值,通过改变边界磁极所占角度,使主磁极角度同时变化。改变边界磁极所占角度q1及边界磁极厚度h1,使q1在0°~8°内,每隔1°取一个值;使h1在1~3mm内,每隔0.5mm取一个值,得到空载气隙磁通密度总谐波畸变率(Total Harmonic Distortion, THD)、齿槽转矩、基波幅值的变化曲线。
空载气隙磁通密度谐波畸变率随边界磁极厚度h1及边界磁极所占角度q1变化的曲线如图9所示,从图中可以看出,当q1=0°时为径向充磁的部分分段PMSM;q1在1°~8°时,随着q1的增大,谐波畸变率先减小再增大;随着h1的增大,谐波畸变率基本符合先减小再增大的趋势。当q1=0°时,THD为25.45%,当h1=2.5mm及q1=6°时,THD有最小值15.27%。
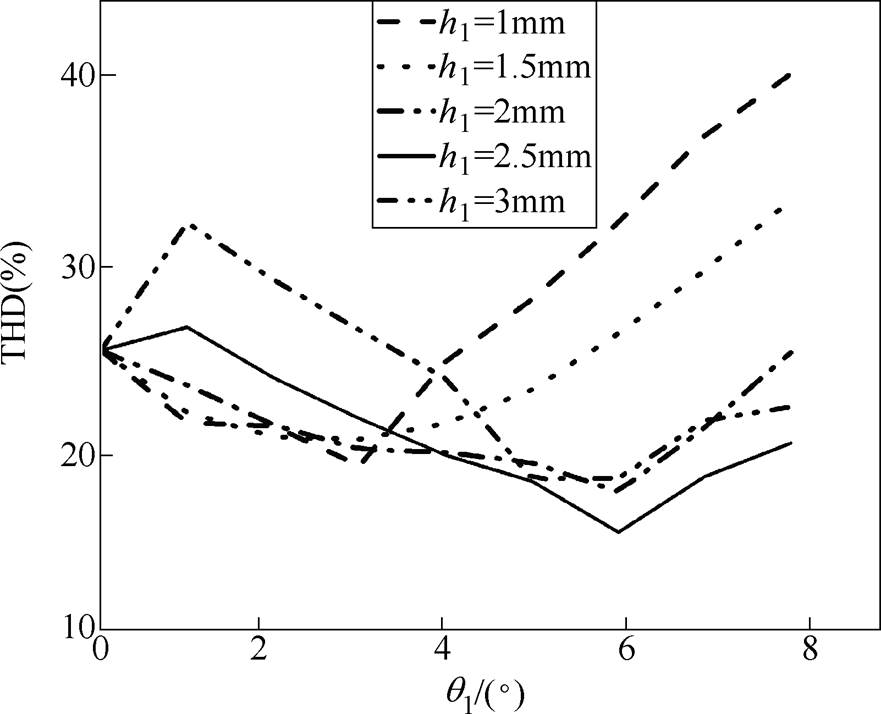
图9 谐波畸变率随边磁厚度及边磁所占角度变化曲线
Fig.9 Curves of THD as a function of edge magnetic thickness and edge magnetic angle
齿槽转矩随边界磁极厚度h1及边界磁极所占角度q1变化的曲线如图10所示,从图中可以看出,随着h1及q1的增大,齿槽转矩先减小再增大,即q1= 6°,h1=2mm时,齿槽转矩有最小值45.0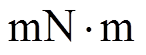 ;当q1=0°时,齿槽转矩为283.2
;当q1=0°时,齿槽转矩为283.2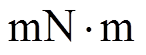 。
。
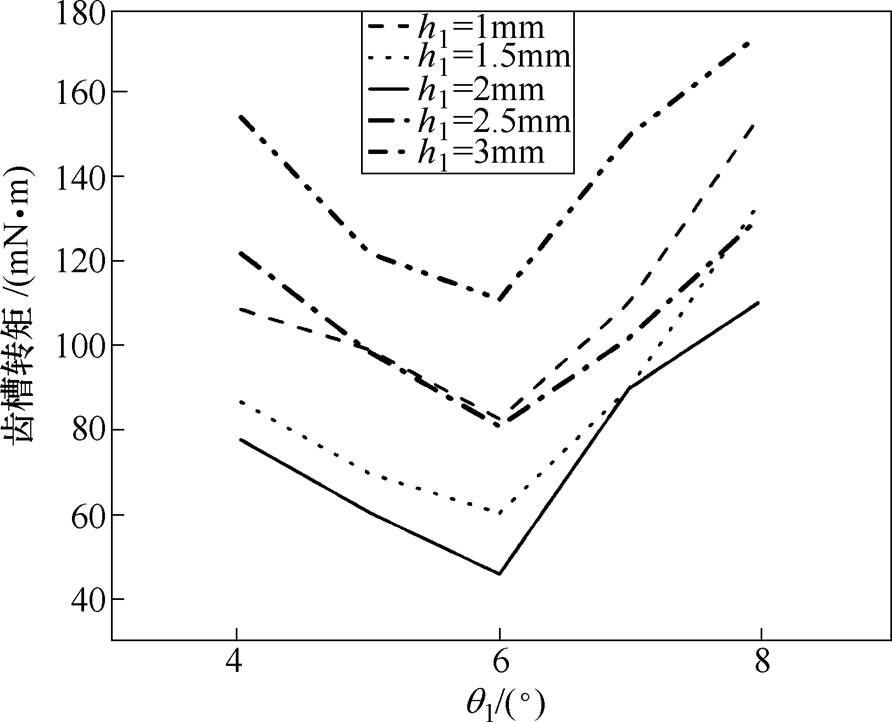
图10 齿槽转矩随边磁厚度及边磁所占角度变化的曲线
Fig.10 Curves of cogging torque as a function of edge magnetic thickness and edge magnetic angle
基波幅值随h1及q1变化曲线如图11所示,从图中可以看出,q1在1°~8°时,随着h1及q1的增大,基波幅值逐渐减小,这是因为气隙磁通密度主要由主磁极建立,随着边界磁极角度的增大,主磁极角度减小,所以基波幅值逐渐降低。当q1=0°时,基波幅值为0.99T,当h1=2mm及q1=6°时,基波幅值为0.84T。
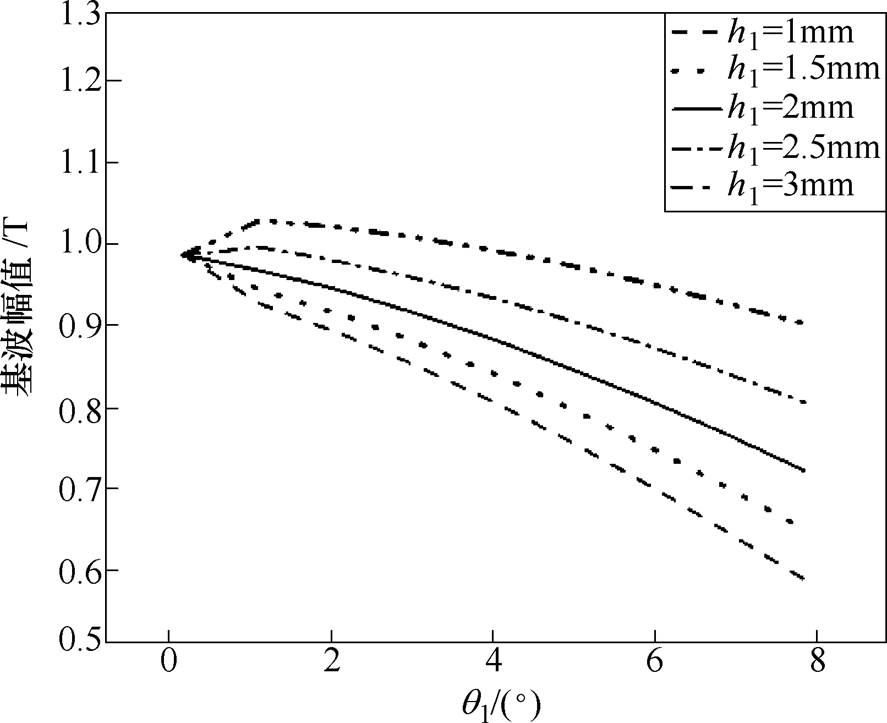
图11 基波幅值随边磁厚度及边磁所占角度变化曲线
Fig.11 Curves of fundamental amplitude as a function of edge magnetic thickness and edge magnetic angle
由图9~图11可知,空载气隙磁通密度谐波畸变率和齿槽转矩随着h1和q1先减小后增大,基波幅值逐渐减小。综合考虑空载气隙磁通密度谐波畸变率、齿槽转矩和基波幅值,h1=2mm及q1=6°为最优解。
优化前后空载气隙磁通密度变化曲线如图12所示,从图中可以看出,普通表贴式PMSM的谐波畸变率为25.79%,部分分段Halbach PMSM的谐波畸变率为19.17%,优化后谐波畸变率减少了6.62%。
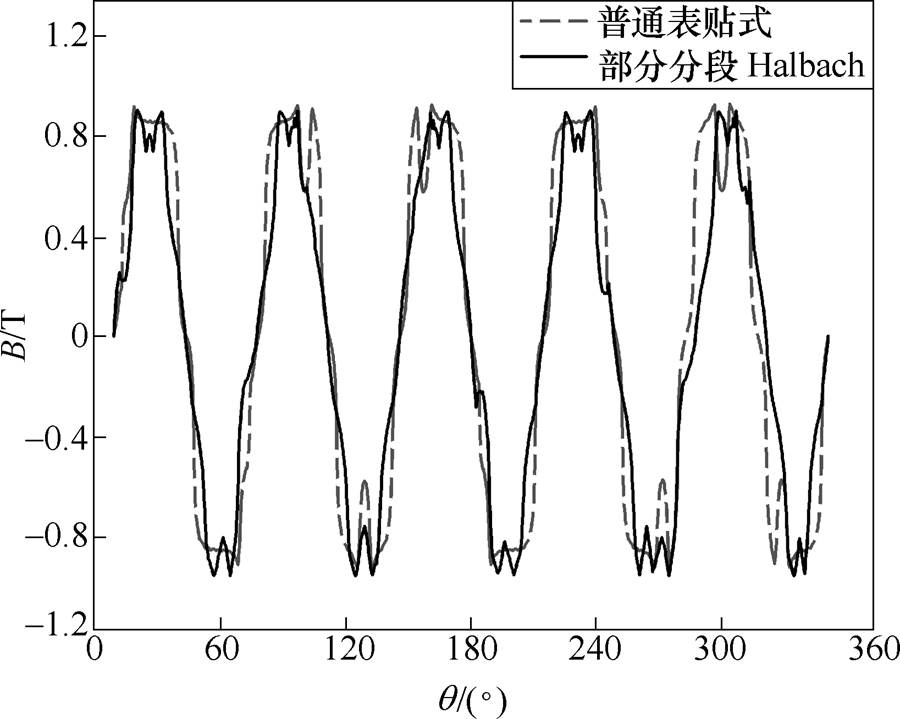
图12 空载气隙磁通密度变化曲线
Fig.12 No-load air gap magnetic density curves
四种结构电机齿槽转矩变化曲线如图13所示,普通表贴式PMSM齿槽转矩为133.1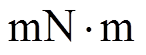 ,等宽等厚的Halbach PMSM齿槽转矩为63.3
,等宽等厚的Halbach PMSM齿槽转矩为63.3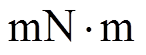 ,部分分段PMSM齿槽转矩为283.2
,部分分段PMSM齿槽转矩为283.2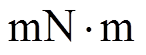 ,部分分段Halbach PMSM齿槽转矩为43.8
,部分分段Halbach PMSM齿槽转矩为43.8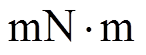 。可以看出,相比于普通表贴式PMSM,部分分段PMSM齿槽转矩大幅度增加,而等宽等厚的Halbach PMSM和部分分段Halbach PMSM齿槽转矩均大幅降低。相比于普通表贴式PMSM,部分分段Halbach PMSM齿槽转矩降低了67.09%。
。可以看出,相比于普通表贴式PMSM,部分分段PMSM齿槽转矩大幅度增加,而等宽等厚的Halbach PMSM和部分分段Halbach PMSM齿槽转矩均大幅降低。相比于普通表贴式PMSM,部分分段Halbach PMSM齿槽转矩降低了67.09%。
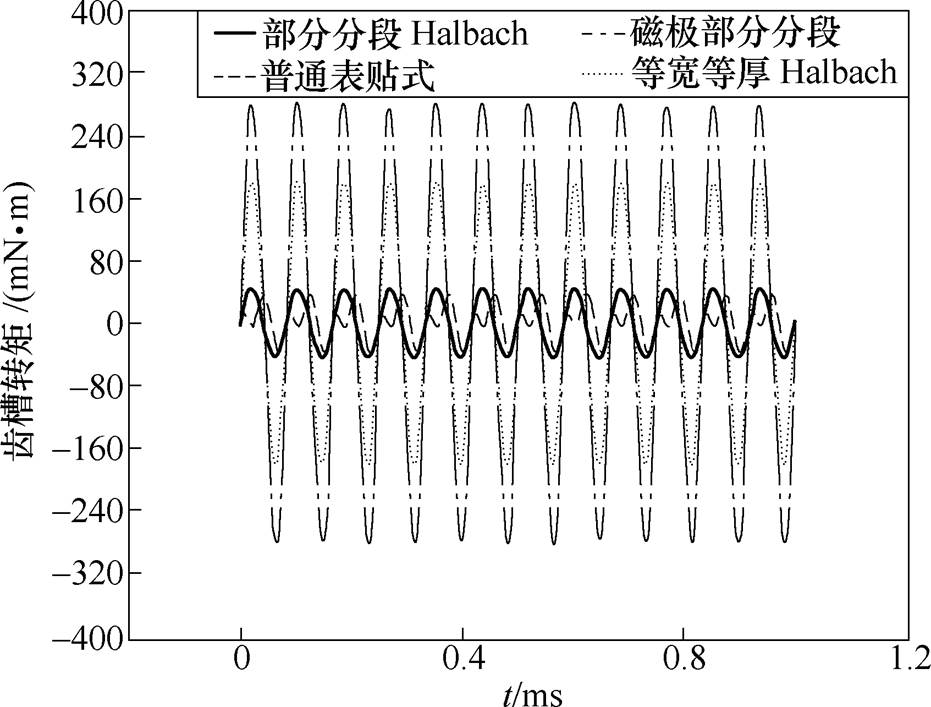
图13 优化后四种结构齿槽转矩变化曲线
Fig.13 Optimized cogging torque curves of four structures
改变有限元模型中的主磁极分段间隔X1,当X3=1.95mm时,使X1在1~6mm内,每隔1mm取一个值,得到永磁体涡流损耗随X1变化的曲线,如图14所示。改变X1的大小,即改变主磁极分段间隔,使主磁极周向不均匀分段。当X1=2.5mm时,涡流损耗有最小值71.61W。
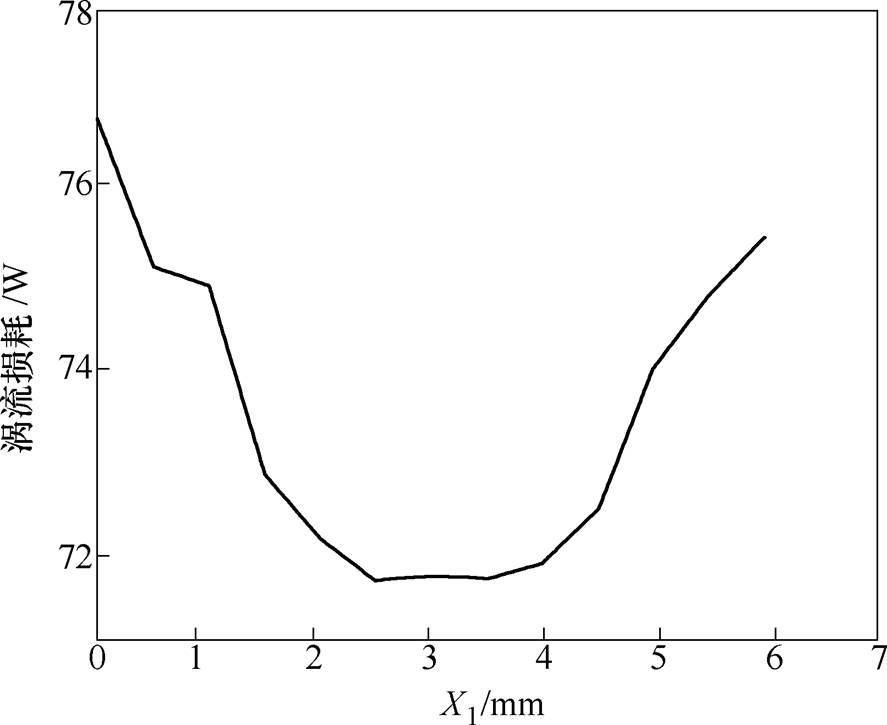
图14 永磁体涡流损耗随X1变化的曲线
Fig.14 Curve of permanent magnet eddy current loss with X1
优化后四种结构涡流损耗变化曲线如图15所示,普通表贴式PMSM永磁体涡流损耗为150.87W,等宽等厚Halbach PMSM涡流损耗为120.03W,部分分段PMSM涡流损耗为54.58W,部分分段Halbach PMSM涡流损耗为52.61W。可以看出,相比于普通表贴式PMSM,其他三种结构均降低了永磁体涡流损耗;相比于普通表贴式PMSM,采用部分分段Halbach结构的PMSM涡流损耗降低了65.14%,单位体积涡流损耗降低了57.97%。
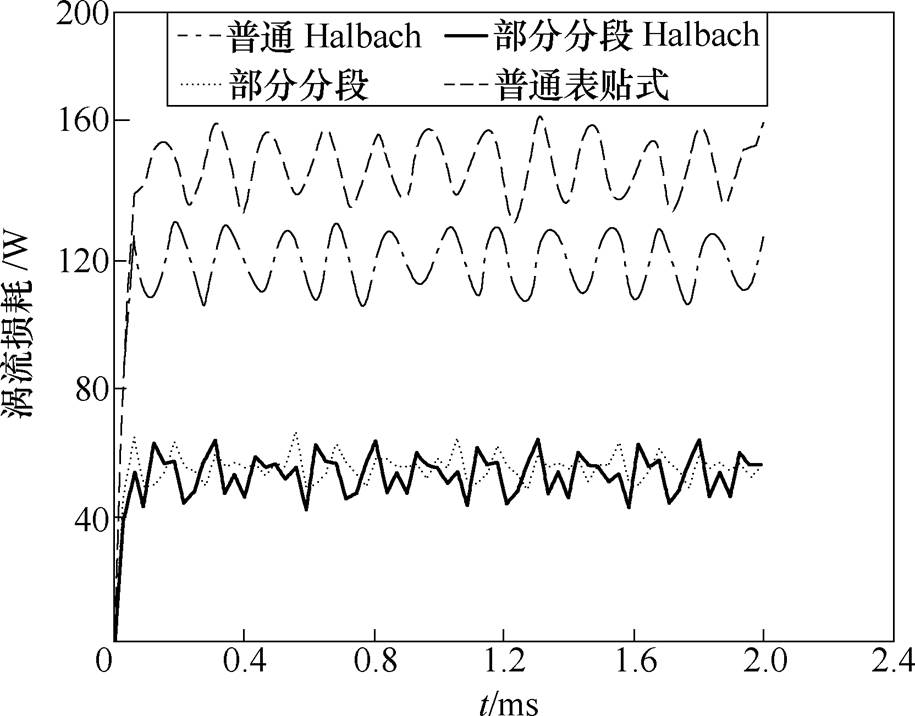
图15 优化后四种结构涡流损耗变化曲线
Fig.15 Optimized eddy current loss curves of four structures
优化后四种结构的齿槽转矩、永磁体涡流损耗、基波幅值以及体积对比见表2,从表中可以看出,Halbach结构对于空载气隙磁通密度谐波畸变率有很大改善,且等宽等厚Halbach结构可以提高基波幅值,部分分段Halbach结构使总的基波幅值降低,但却降低了17.04%的永磁体体积并提高了单位立方厘米的基波幅值,从0.044T/cm3提高到0.050T/cm3。相比于普通表贴式PMSM,部分分段PMSM使涡流损耗大幅度降低,等宽等厚Halbach PMSM使齿槽转矩大幅度降低,而采用部分分段Halbach结构的PMSM结合两者优点,使降低齿槽转矩和涡流损耗的效果有极大提升。
表2 优化后四种结构的参数对比
Tab.2 Comparison of four structural parameters after optimization
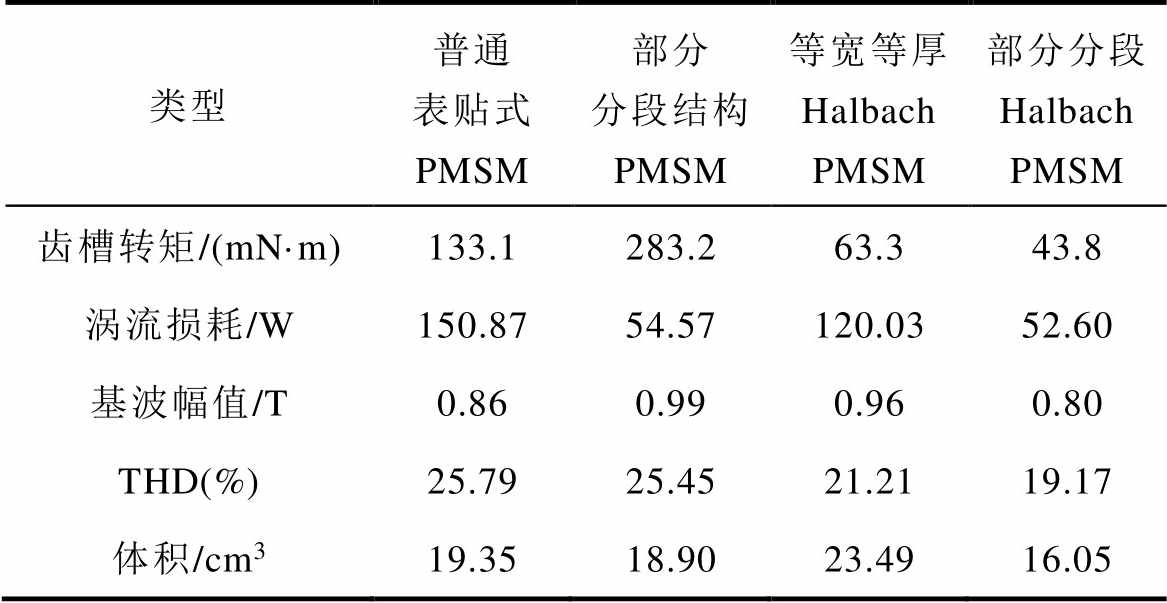
类型普通表贴式 PMSM部分分段结构 PMSM等宽等厚 Halbach PMSM部分分段 Halbach PMSM 齿槽转矩/(mN·m)133.1283.263.343.8 涡流损耗/W150.8754.57120.0352.60 基波幅值/T0.860.990.960.80 THD(%)25.7925.4521.2119.17 体积/cm319.3518.9023.4916.05
在转速为12 000r/min时,在切向离心力和电磁力的作用下,通过Ansys Workbench,仿真得出永磁体总变形和等效应力,如图16和图17所示。
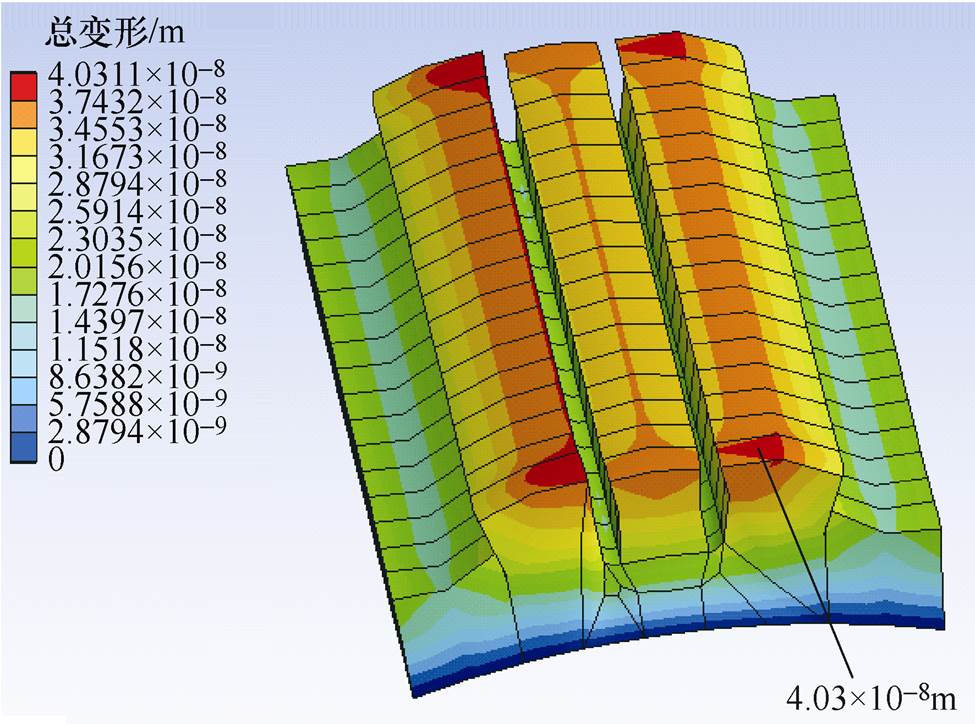
图16 永磁体总变形
Fig.16 Total deformation map of permanent magnets
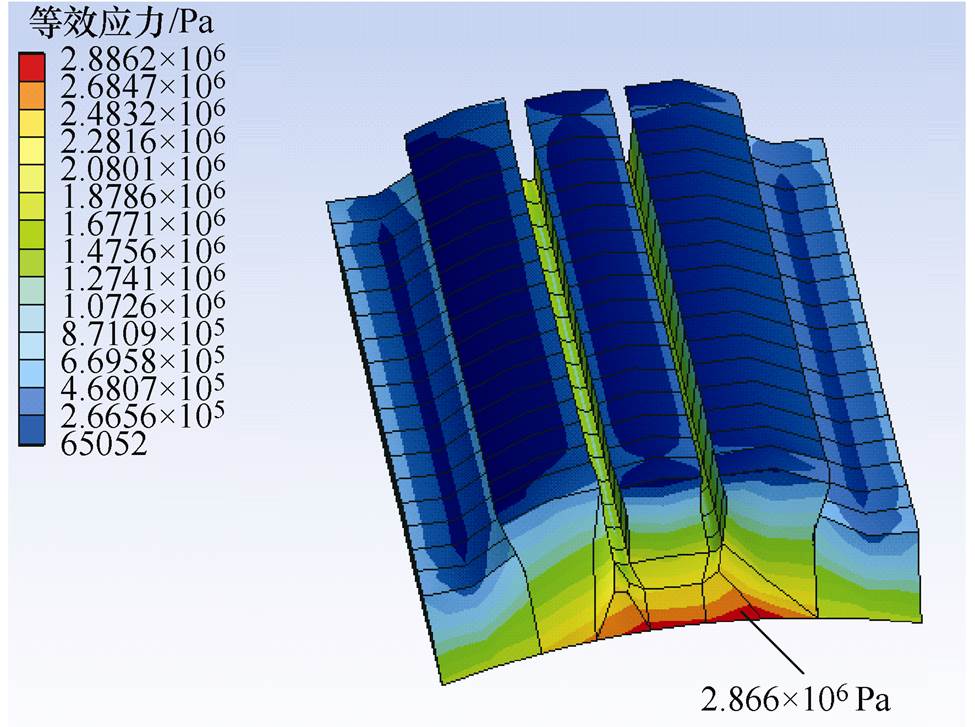
图17 永磁体等效应力
Fig.17 Equivalent stress map of permanent magnets
图16中,显示了永磁体在切向离心力和电磁力的作用下导致的结构变形。可以看出,最大变形发生在永磁体上表面的切口边缘,而发生在永磁体底面结构变形很小,这是因为切口存在于远离轴线的永磁体上表面上,并且永磁体底面附着在转子表面上。
图17中,显示了由切向离心力和电磁力引起的等效应力。可以看出,最大等效应力发生在永磁体底面,这是因为永磁体附着在转子铁心表面上,永磁体最大等效应力为2.886×106Pa,低于永磁体拉伸应力80×106Pa。因此,离心力产生的等效应力不会破坏永磁体的机械结构。
提出一种部分分段Halbach结构,建立了部分分段Halbach PMSM的精确子域模型,通过计算电机空载气隙磁通密度分布,验证了解析方法的正确性。同时,利用有限元软件对电机进行了电磁及应力场仿真分析,在固定极间间隔时,对电机进行了多变量优化,对采用四种结构的PMSM进行了电磁性能对比,结果表明:
1)部分分段Halbach结构结合了Halbach结构和部分分段结构两者的优点,相比于普通表贴式PMSM,大幅度降低了谐波畸变率、单位体积永磁体涡流损耗以及齿槽转矩。
2)相比于等宽等厚Halbach结构,部分分段Halbach结构减小了永磁体体积,节约了成本。相比于完全分段结构,部分分段Halbach结构减小了工艺难度和成本。
3)部分分段Halbach结构永磁体所受拉应力远小于允许值,永磁体机械强度维持在允许范围内。
部分分段Halbach结构节约了制造成本,减小了工艺难度,对涡流损耗和齿槽转矩的优化效果明显,适用于实际工程中,但对于部分分段Halbach永磁同步电机边界磁极结构的多样性有待进一步研究。
径向充磁的完全分段永磁体每对极下磁化强度分布为
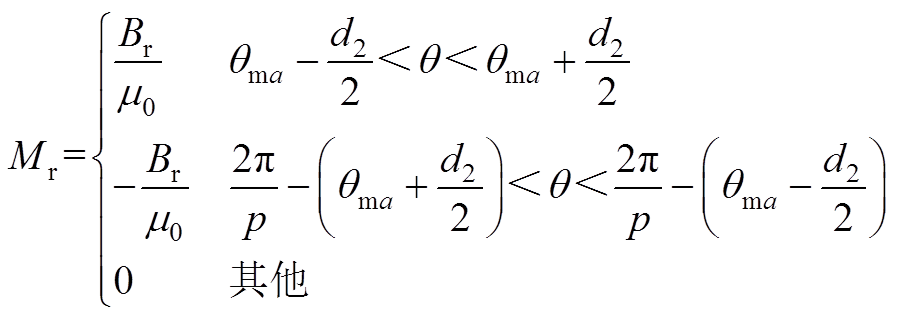 (A1)
(A1)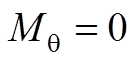 (A2)
(A2)
其中
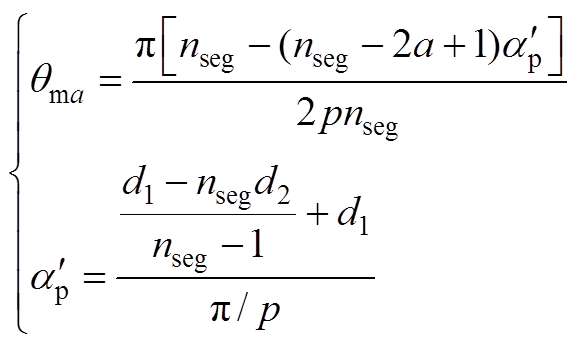 (A3)
(A3)式中,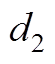 为每极下所有磁块所对应的总极弧宽度;
为每极下所有磁块所对应的总极弧宽度;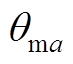 为第a块分段磁块对称轴对应的机械角度。
为第a块分段磁块对称轴对应的机械角度。
径向充磁的永磁体每对极下磁化强度分布为
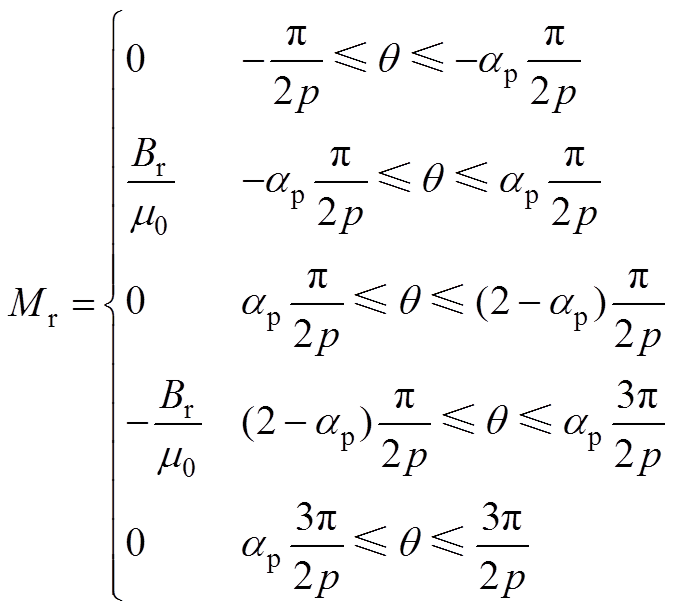 (A4)
(A4)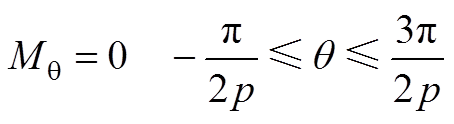 (A5)
(A5)
Halbach充磁的永磁体每对极下磁化强度分布为
 (A6)
(A6) (A7)
(A7)
其中
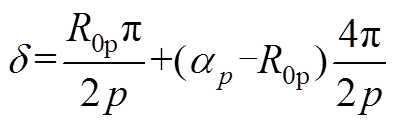
式中,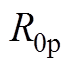 为主磁极极弧系数;
为主磁极极弧系数;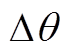 为边界磁极磁化角度。
为边界磁极磁化角度。
空载磁场气隙子域矢量磁位待定系数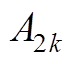 、
、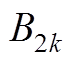 、
、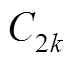 、
、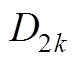 ,表达式分别为
,表达式分别为
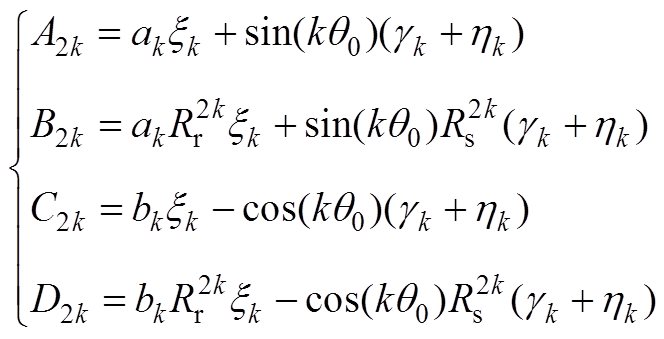 (A8)
(A8)其中
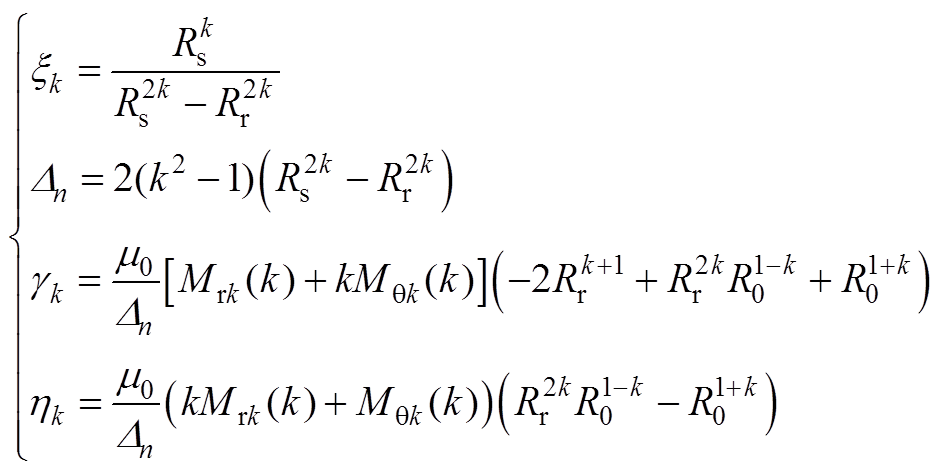 (A9)
(A9)
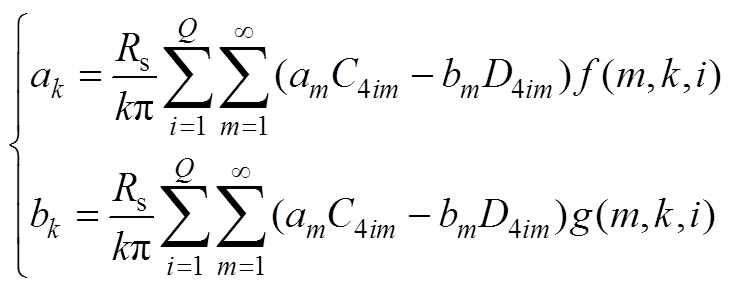 (A10)
(A10)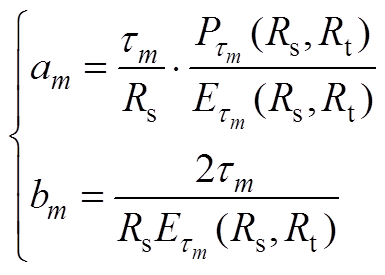 (A11)
(A11)
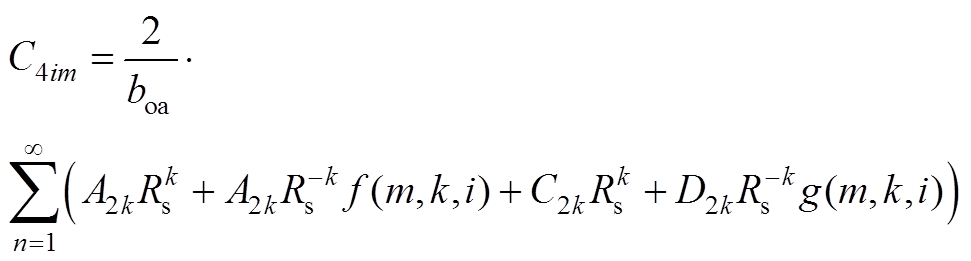 (A12)
(A12)
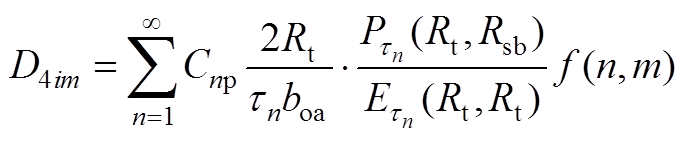 (A13)
(A13)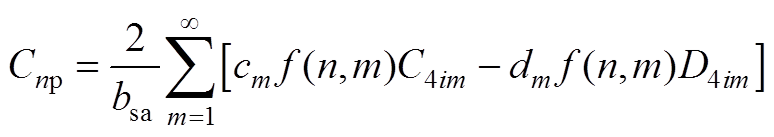 (A14)
(A14)
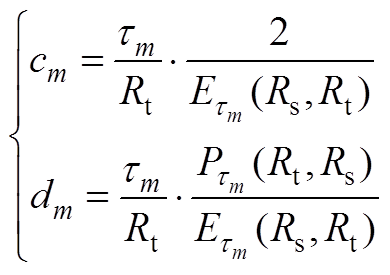 (A15)
(A15)
参考文献
[1] 李勇, 徐兴, 孙晓东, 等. 轮毂电机驱动技术研究概况及发展综述[J]. 电机与控制应用, 2017, 44(6): 1-7, 18.
Li Yong, Xu Xing, Sun Xiaodong, et al. Review and future development of in-wheel motor drive tech- nology[J]. Electric Machines and Control Appli- cations, 2017, 44(6): 1-7, 18.
[2] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 34-46.
Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low speed and large torque permanent magnet direct drive motors[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 34-46.
[3] 孔垂毅, 代颖, 罗建. 电动汽车轮毂电机技术的发展现状与发展趋势[J]. 电机与控制应用, 2019, 46(2): 105-112, 117.
Kong Chuiyi, Dai Ying, Luo Jian. Development status and development trend of electric vehicle wheel motor technology[J]. Electrical and control appli- cations, 2019, 46(2): 105-112, 117.
[4] 黄允凯, 周涛, 董剑宁, 等. 轴向永磁电机及其研究发展综述[J]. 中国电机工程学报, 2015, 35(1): 192-205.
Huang Yunkai, Zhou Tao, Dong Jianning, et al. Overview of axial permanent magnet motor and its research and development[J]. Proceedings of the CSEE, 2015, 35(1): 192-205.
[5] 陈萍, 唐任远, 佟文明, 等. 高功率密度永磁同步电机永磁体涡流损耗分布规律及其影响[J]. 电工技术学报, 2015, 30(6): 1-9.
Chen Ping, Tang Renyuan, Yan Wenming, et al. Permanent magnet eddy current loss and its influence of high power density permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 1-9.
[6] 任庆, 桂祈祯. 基于永磁体温度对车用电机性能影响分析[J]. 机械制造与自动化, 2018, 47(2): 213- 217.
Ren Qing, Gui Qizhen. Influence analysis of tem- perature of permanent magnet on performance of vehicle motor[J]. Mechanical Engineering & Auto- mation, 2018, 47(2): 213-217.
[7] 张磊, 高春侠. 永磁同步电机磁钢涡流损耗模型及其衡量指标[J]. 电机与控制学报, 2013, 17(7): 46-53.
Zhang Lei, Gao Chunxia. Eddy-current loss model and index for magnets of permanent magnet synchronous motors[J]. Journal of Electric Machines and Control, 2013, 17(7): 46-53.
[8] Shi Tingna, Qiao Zhaowei, Xia Changliang, et al. Modelng, analyzing, and parameter design of the magnetic field of a segmented Halbach cylinder[J]. IEEE Transactions on Magnetics, 2012, 48(5): 1890- 1898.
[9] 章跃进, 江建中, 屠关镇. 应用数值解析结合法计算旋转电机磁场[J]. 电工技术学报, 2004, 19(1): 7-11.
Zhang Yuejin, Jiang Jianzhong, Tu Guanzhen. Appli- cation of numerical-nalytical method to magnetic field computation in rotating electric machines[J]. Transactions of China Electrotechnical Society, 2004, 19(1): 7-11.
[10] 章跃进, 江建中, 崔巍. 数值解析结合法提高电机磁场后处理计算精度[J]. 中国电机工程学报, 2007, 27(3): 68-72.
Zhang Yuejin, Jiang Jianzhong, Cui Wei. Accuracy enhancement of post process of magnetic field com- putation for rotational electric machines by numerical- analytical method[J]. Proceedings of the CSEE, 2007, 27(3): 68-72.
[11] 李春江, 章跃进, 卢铁斌, 等. 解析数值结合法在直驱轮毂式永磁无刷电机气隙磁场分析中的应用[J]. 微电机, 2010(12): 26-29, 33.
Li Chunjiang, Zhang Yuejin, Lu Tiebin, et al. Application of analytical numerical method in air gap magnetic field analysis of direct drive hub type permanent magnet brushless motor[J]. Micromotors, 2010(12): 26-29, 33.
[12] 范坚坚, 吴建华. 计及齿槽极间隔断Halbach型磁钢的PMSM气隙磁场解析分析[J]. 中国电机工程学报, 2010, 30(12): 98-105.
Fan Jianjian, Wu Jianhua. Analytical solution and analysis of air-gap magnetic field of PMSM with partition-between-poles Halbach magnet considering effect of slotting[J]. Proceedings of the CSEE, 2010, 30(12): 98-105.
[13] 罗玲, 薛利昆, 吴先宇, 等. Halbach永磁阵列无刷直流电机转矩的解析计算和分析[J]. 电工技术学报, 2017, 32(16): 124-135.
Luo Ling, Xue Likun, Wu Xianyu, et al. Analytical calculation and analysis of torque of Halbach permanent magnet array brushless DC motor[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 124-135.
[14] 李深, 章跃进, 周晓燕, 等. 定子开槽表贴式永磁电机转子偏心空载气隙磁场全局解析法[J]. 电机与控制学报, 2014, 18(10): 27-35.
Li Shen, Zhang Yuejin, Zhou Xiaoyan, et al. Global analytical method for eccentric airborne air gap magnetic field of stator slotted surface-mounted permanent magnet motor[J]. Journal of Electric Machines and Control, 2014, 18(10): 27-35.
[15] Lubin T, Mezani S, Rezzoug A. Exact analytical method for magnetic field computation in the air gap of cylindrical electrical machines considering slotting effects[J]. IEEE Transactions on Magnetics, 2010, 46(4): 1092-1099.
[16] 李节宝, 井立兵, 周晓燕, 等. 表贴式永磁无刷电机直接解析计算方法[J]. 电工技术学报, 2012, 27(11): 83-88.
Li Jiebao, Jing Libing, Zhou Xiaoyan, et al. Exact analytical method for surface-mounted permanent- magnet brushless motors[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 83-88.
[17] 杨思雨, 夏长亮, 王慧敏, 等. 磁极分段型表贴式永磁电机建模与分析[J]. 电工技术学报, 2015, 30(增刊2): 49-55.
Yang Siyu, Xia Changliang, Wang Huimin, et al. Modeling and analysis of magnetic pole segmented surface mount permanent magnet motor[J]. Transa- ctions of Electrical Engineering, 2015, 30(S2): 49-55.
[18] 郭思源, 周理兵. 表面埋入式永磁电机磁场解析[J]. 中国电机工程学报, 2015, 35(3): 710-718.
Guo Siyuan, Zhou Libing. Magnetic field analysis of surface embedded permanent magnet motor[J]. Pro- ceedings of the CSEE, 2015, 35(3): 710-718.
[19] 杨金歌, 邓兆祥, 周忆, 等. 车用永磁轮毂电机解析建模与齿槽转矩削弱[J]. 西安交通大学学报, 2018, 52(1): 84-91, 114.
Yang Jinge, Deng Zhaoxiang, Zhou Yi, et al. Analytical modeling and cogging torque reduction of permanent magnet hub motors for vehicles[J]. Journal of Xi'an Jiaotong University, 2018, 52(1): 84-91, 114.
[20] Madina P, Poza J, Ugalde G, et al. Analysis of nonuniform circumferential segmentation of magnets to reduce eddy-current losses in SPMSM machines[C]// International Conference on Electrical Machines, Marseille, 2012: 79-84.
[21] Lee S H, Oh H S, Kim H S. Experiment research on motor efficiency improvement through the eddy current reduction using segmentation of rotor magnet[C]//IEEE 2017 20th International Conference on Electrical Machines and Systems, Sydney, NSW, 2017: 1-4.
[22] Wang Youhua, Ma J, Liu Chengcheng, et al. Reduction of magnet eddy current loss in PMSM by using partial magnet segment method[J]. IEEE Transactions on Magnetics, 2019, 99: 1-5.
[23] Lubin T, Mezani S, Rezzoug A. 2-D exact analytical model for surface-mounted permanent-magnet motors with semi-closed slots[J]. IEEE Transactions on Magnetics, 2011, 47(2): 479-492.
[24] 杨晨, 白保东, 陈德志, 等. 可变磁通永磁辅助同步磁阻电机设计与性能分析[J]. 电工技术学报, 2019, 34(3): 489-496.
Yang Chen, Bai Baodong, Chen Dezhi, et al. Design and performance analysis of variable flux permanent magnet assisted synchronous reluctance motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 489-496.
[25] 杨定伟, 邓兆祥, 张河山, 等. 永磁轮毂电机磁场解析建模[J]. 电工技术学报, 2019, 34(7): 1423-1433.
Yang Dingwei, Deng Zhaoxiang, Zhang Heshan, et al. Analytical modeling of magnetic field of permanent magnet wheel motor[J]. Transactions of China Elec- trotechnical Society, 2019, 34(7): 1423-1433.
[26] 庞古才, 邓智泉, 张忠明. 基于改进广义磁路法的表贴式永磁电机空载气隙磁场解析计算[J]. 电工技术学报, 2019, 34(22): 4623-4633.
Pang Gucai, Deng Zhiquan, Zhang Zhongming. Analytical calculation of no-load air-gap magnetic field of surface-mounted permanent magnet motor based on improved generalized magnetic circuit method[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4623-4633.
[27] 李琛, 章跃进, 井立兵. Halbach阵列半闭口槽永磁电机全局解析法研究[J]. 中国电机工程学报, 2013, 33(33): 85-94.
Li Chen, Zhang Yuejin, Jing Libing. Global analytical method for semi-closed groove permanent magnet motor with Halbach array[J]. Proceedings of the CSEE, 2013, 33(33): 85-94.
[28] 杨玉波, 刘国鹏, 陈鹏, 等. 基于子域法的游标混合电机电磁性能解析计算[J]. 电机与控制学报, 2019, 23(9): 9-17, 25.
Yang Yubo, Liu Guopeng, Chen Peng, et al. Analytical calculation of electromagnetic performance of cursor hybrid motor based on subdomain method[J]. Journal of Electrical Engineering and Control, 2019, 23(9): 9-17, 25.
[29] 倪有源, 刘跃斌, 王群京. 组合磁极结构的永磁电机解析法建模与分析[J]. 电机与控制学报, 2019, 23(1): 52-62.
Ni Youyuan, Liu Yuebin, Wang Qunjing. Analytical modeling and analysis of permanent magnet motor with combined pole structure[J]. Journal of Motors and Control, 2019, 23(1): 52-62.
[30] 于占洋, 李岩, 井永腾, 等. 基于混合磁场解析法的磁极偏心型表贴式永磁同步电机空载特性分析[J]. 电工技术学报, 2020, 35(18): 3811-3820.
Yu Zhanyang, Li Yan, Jing Yongteng, et al. Analysis of no-load characteristics of magnetic pole eccentric surface mount permanent magnet synchronous motor based on mixed magnetic field analysis method[J]. Transactions of the Chinese Society of Electrical Engineering, 2020, 35(18): 3811-3820.
[31] 张守首, 郭思源. 考虑分段斜极和磁性槽楔的永磁同步电机磁场解析方法[J]. 电工技术学报, 2019, 34(1): 11-22.
Zhang Shoushou, Guo Siyuan. Analytical method for magnetic field of permanent magnet synchronous motor considering segmented slant pole and magnetic slot wedge[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 11-22.
Optimization Design of Partially-Segmented Halbach Permanent Magnet Synchronous Motor
Abstract In order to suppress the cogging torque and reduce the eddy current loss in high power-density permanent magnet synchronous motor, a surface-mounted partially-segmented Halbach structure is designed. The permanent magnets is magnetized with Halbach pattern and each pole is divided into three sections. The main magnetic pole is segmented on single side. The boundary magnetic pole and the main magnetic pole are not equal in thickness and width. A precise subdomain model method is used to divide the solution domain into four regions: permanent magnet, air gap, slot and slot-opening. The magnetic field density of no-load airgap and the cogging torque are calculated under two-dimensional polar coordinates. The 3-D electromagnetic field analysis is carried out with a 10-pole/12-slot permanent magnetic synchronous motor. The simulation results show that the eddy current loss, the cogging torque and the volume of permanent magnet are reduced by partially segmented Halbach structure. Moreover, the equivalent stress and total deformation are calculated based on a 3-D finite element stress model of permanent magnetic synchronous motor, which are also in the tolerant range of mechanical strength.
keywords:Permanent magnet synchronous motor, the precise subdomain model method, partially-segmented Halbach structure, the equivalent stress
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.191554
国家重点研发计划(2018YFB1201602-06)资助。
收稿日期2019-11-19
改稿日期 2020-01-14
高锋阳 男,1970年生,教授级高工,研究方向为电机与电器、电机的优化设计。E-mail: 329365048@qq.com
齐晓东 男,1995年生,硕士研究生,研究方向为永磁同步电机的优化设计。E-mail: 782311500@qq.com(通信作者)
(编辑 崔文静)