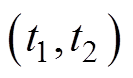 内电压测量值变化、计算电导率分布变化进行重构成像[12-13],可以显著减少误差影响,是一种差分成像方法,目前应用较为广泛。DEIT正问题模型可由麦克斯韦方程推导,将感兴趣区域进行有限元分割,动态电阻抗断层成像线性化正问题可表示为
内电压测量值变化、计算电导率分布变化进行重构成像[12-13],可以显著减少误差影响,是一种差分成像方法,目前应用较为广泛。DEIT正问题模型可由麦克斯韦方程推导,将感兴趣区域进行有限元分割,动态电阻抗断层成像线性化正问题可表示为摘要 大多数电阻抗断层成像算法需要选择较优正则化参数来克服方程病态性,以获得较好的图像质量。该文提出一种基于差分迭代的电阻抗断层成像算法,利用动态线性逼近在不调整正则化参数的情况下提高成像质量。在近似线性变化区域内建立扰动模型,利用梯度法推导出电导率差值迭代关系进行快速重构成像,并将重构图像与基于几种客观正则化参数选取方法的重构图像在位置误差、分辨率、形状误差、环状伪影等性能指标方面进行比较。仿真结果证明,该文提出的差分迭代算法能与常用重构算法保持相似或更优的效果,该方法具有较好的实际应用前景。
关键词:电阻抗断层成像 差分迭代 多目标成像 快速重构算法 正则化参数选取
生物电阻抗断层成像技术(Electrical Impedance Tomography, EIT)是继形态与结构成像后的新一代医学功能成像技术[1],通过在体表电极处施加激励电流及测量激励电压来重构生物体内部阻抗分布的绝对值或变化值,可以在组织/器官尚未达到结构性病变时就根据人体内组织电特性参数分布的变化来进行诊断,具有无损伤无辐射、连续实时动态监测、对组织功能变化敏感、成本低、重复性好等优点。目前,类如CT、MRI和PET等大型医疗成像设备还无法做到动态实时图像监护,因而EIT在脑卒中、肺通气、乳腺癌、腹腔出血等病情的早期诊断与实时监测方面具有广泛的应用前景,可作为实时监护设备为患者临床诊断和治疗争取最佳抢救时机[2-4]。
在电阻抗断层成像技术发展历程中,克服病态性所导致的重构误差一直是相关领域内研究的热点之一[5-7]。病态性即当观测数据发生微小变化时引起解的巨大变化的一种不稳定性质,通常采取各种正则化的方式加以处理,其中最优正则化参数的选取是正则化过程中的重要环节。不同大小的正则化参数会显著地影响图像重构效果,在阻尼最小二乘(Damped Least Squares, DLS)算法中,正则化参数取值越大则图像越显平滑。由定义可知,最优正则化参数应当在正则化解的扰动误差和正则误差之间取得合理的平衡,正则化参数的最优选取是获得较优图像的关键因素之一。
目前已经提出的各种正则化参数选取准则主要分为两类:①基于噪声误差水平等先验信息的先验选取准则;②通过在解中加入定性或定量信息,使得正则化参数选取的噪声误差水平与原始数据相匹配的后验选取准则[8]。通常由于在实际中难以验证先验选取准则成立的条件,使得后验选取准则的应用更加广泛。L型曲线(L-Curve Validation, LCV)法和通用交叉校验(Generalized Cross-Validation, GCV)法等属于后验参数选取方法,虽然被公认是较为可靠的参数选取方法,但也存在着计算方法复杂、实时性差及过拟合的缺点[9-10]。在实际过程中,EIT重建算法更多地倾向于通过主观经验法选择合适的正则化参数,但该方法过于依赖主观经验水平且选取结果不可重复,同样制约了电阻抗成像技术在临床和实验中的应用。本文基于阻尼最小二乘算法提出一种新的无需给定最优正则化参数的电阻抗差分迭代成像算法,通过动态线性逼近实现相近的参数最优选取效果,在保证重构速度的基础上提高了EIT差分成像的重构质量[11]。
动态电阻抗断层成像技术(Dynamic EIT, DEIT)通过计算时间间隔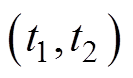 内电压测量值变化、计算电导率分布变化进行重构成像[12-13],可以显著减少误差影响,是一种差分成像方法,目前应用较为广泛。DEIT正问题模型可由麦克斯韦方程推导,将感兴趣区域进行有限元分割,动态电阻抗断层成像线性化正问题可表示为
内电压测量值变化、计算电导率分布变化进行重构成像[12-13],可以显著减少误差影响,是一种差分成像方法,目前应用较为广泛。DEIT正问题模型可由麦克斯韦方程推导,将感兴趣区域进行有限元分割,动态电阻抗断层成像线性化正问题可表示为
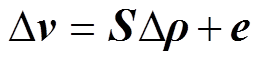 (1)
(1)式中,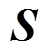 为敏感系数矩阵或称雅可比矩阵;
为敏感系数矩阵或称雅可比矩阵;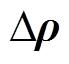 为时间间隔内的离散电导率变化值矩阵;
为时间间隔内的离散电导率变化值矩阵;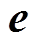 为随机噪声矩阵;
为随机噪声矩阵;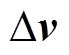 为电压变化值矩阵,定义为
为电压变化值矩阵,定义为
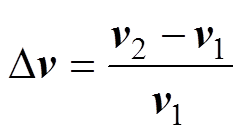 (2)
(2)
式中,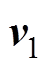 和
和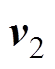 分别为
分别为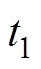 和
和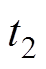 时刻包含所有边界电压测量值的向量。
时刻包含所有边界电压测量值的向量。
通过对代价函数J最小化得方程最优解为
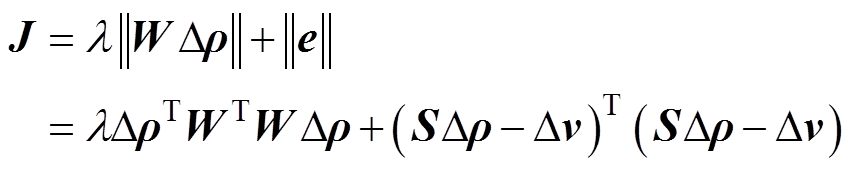 (3)
(3)式中,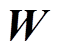 为加权矩阵,令代价函数
为加权矩阵,令代价函数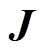 对
对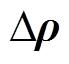 的偏导数等于0得到代价函数极小值,进一步得到阻尼最小二乘解为
的偏导数等于0得到代价函数极小值,进一步得到阻尼最小二乘解为
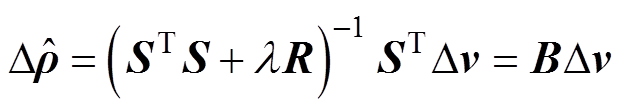 (4)
(4)
式中,R为正则化矩阵,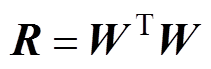 ,用于改善不适定逆问题的条件数[14],常见形式包括
,用于改善不适定逆问题的条件数[14],常见形式包括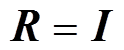 和
和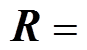
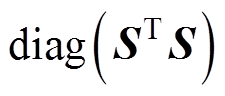 等。
等。
本文提出的基于差分迭代的电阻抗断层成像算法(Differential Iteration EIT, DIEIT),通过差分迭代方式更新电导率变化分布以获得稳定解,假定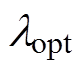 是由客观正则化参数选取方法得到的最优正则化参数,则电导率变化分布直接可解为
是由客观正则化参数选取方法得到的最优正则化参数,则电导率变化分布直接可解为
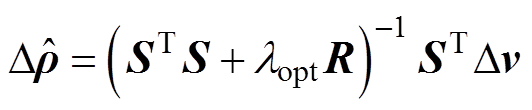 (5)
(5)由于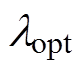 的取值较为困难,考虑设一个比
的取值较为困难,考虑设一个比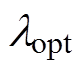 大得多的正则化参数
大得多的正则化参数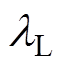 ,
,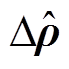 可近似为
可近似为
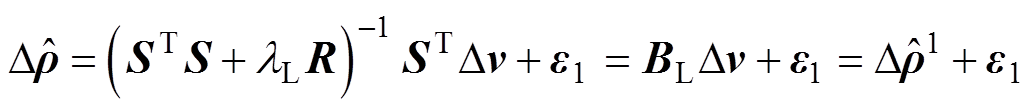 (6)
(6)
式中,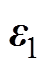 为由于大的正则化参数
为由于大的正则化参数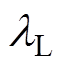 产生的重构误差。令
产生的重构误差。令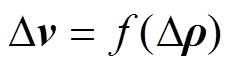 ,
,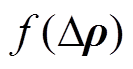 在
在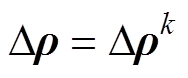 处进行一阶泰
处进行一阶泰
勒公式展开近似[15]为
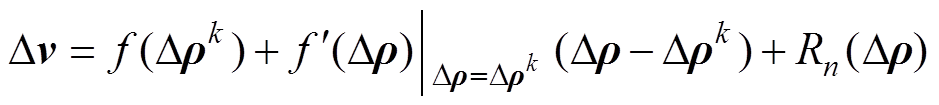 (7)
(7)当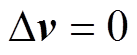 函数存在根
函数存在根
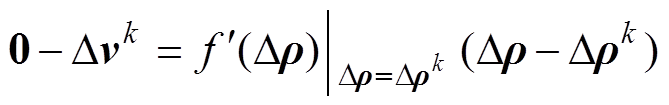 (8)
(8)
根据式(6)与式(9)联立可得
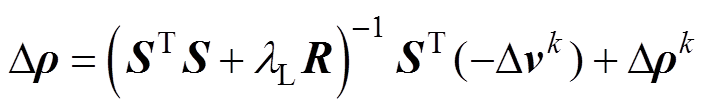 (9)
(9)结合式(7)可得最终解的迭代公式为
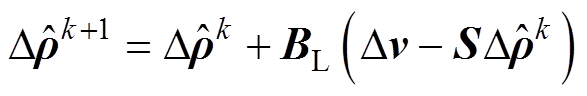 (10)
(10)
式中,k为迭代次数,初始的电导率分布变化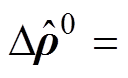
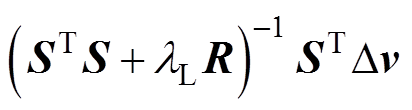 ,可以通过设置差值变化阈值
,可以通过设置差值变化阈值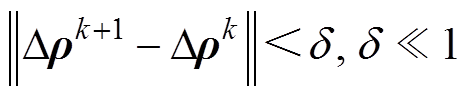 或者限制迭代次数
或者限制迭代次数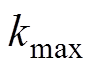 来终止迭代,矩阵
来终止迭代,矩阵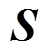 和
和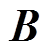 可以通过初始离线计算得到,后续迭代在线计算过程只需计算矩阵乘法,因此迭代算法可以实现实时重建[16]。不失一般性,以下仿真成像中
可以通过初始离线计算得到,后续迭代在线计算过程只需计算矩阵乘法,因此迭代算法可以实现实时重建[16]。不失一般性,以下仿真成像中 取值为10。
取值为10。
(1)仿真模型一。在半径为1、背景电导率为1S/m的圆形仿真域内设置半径为0.2、电导率为2.5S/m的扰动目标由圆心径向直线位移3次至半径0.75处,经EIT正问题模型计算相应的电压测量值后,利用本文提出的差分迭代算法进行图像重构,仿真结果如图1所示。
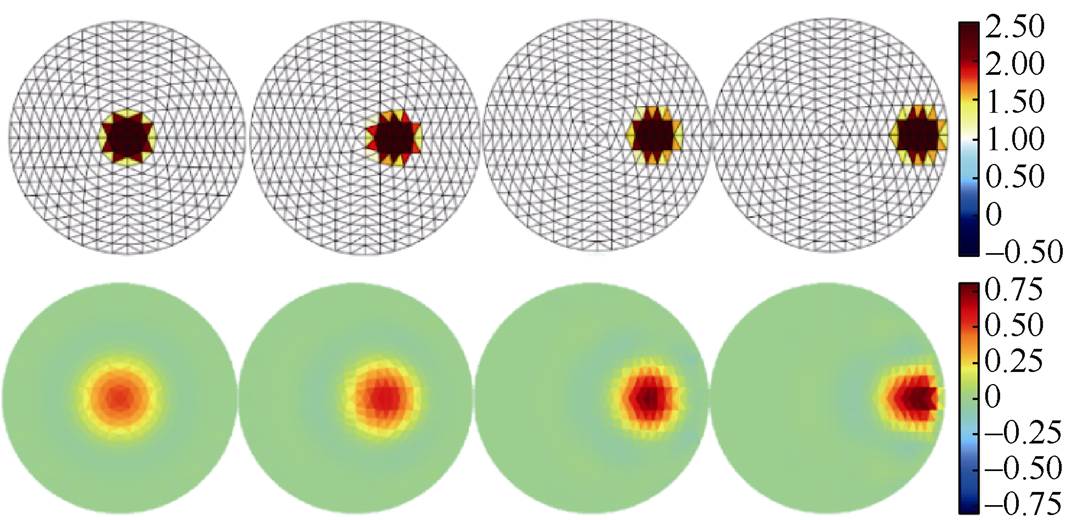
图1 仿真模型一
Fig.1 Simulation model one
(2)仿真模型二。在半径为1、背景电导率为1S/m的圆形仿真域内设置一个半径为0.2、电导率为1.5S/m的扰动目标于下半径0.5处,另设置一个半径为0.2、电导率为1.5S/m的扰动目标在半径0.5处绕上半圆旋转180°,仿真结果如图2所示。
(3)仿真模型三。在半径为1、背景电导率为1S/m的圆形仿真域内设置一个半径为0.2、电导率为1.5S/m的扰动目标于下半径0.5处,另设置一个半径为0.2、电导率为0.5S/m的扰动目标在半径0.5处绕上半圆旋转180°,仿真结果如图3所示。
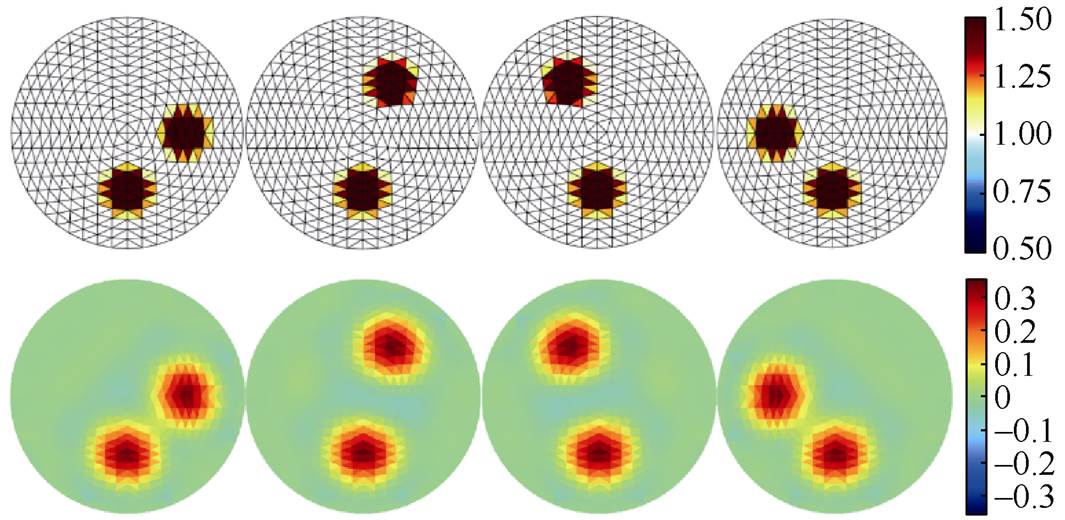
图2 仿真模型二
Fig.2 Simulation model two
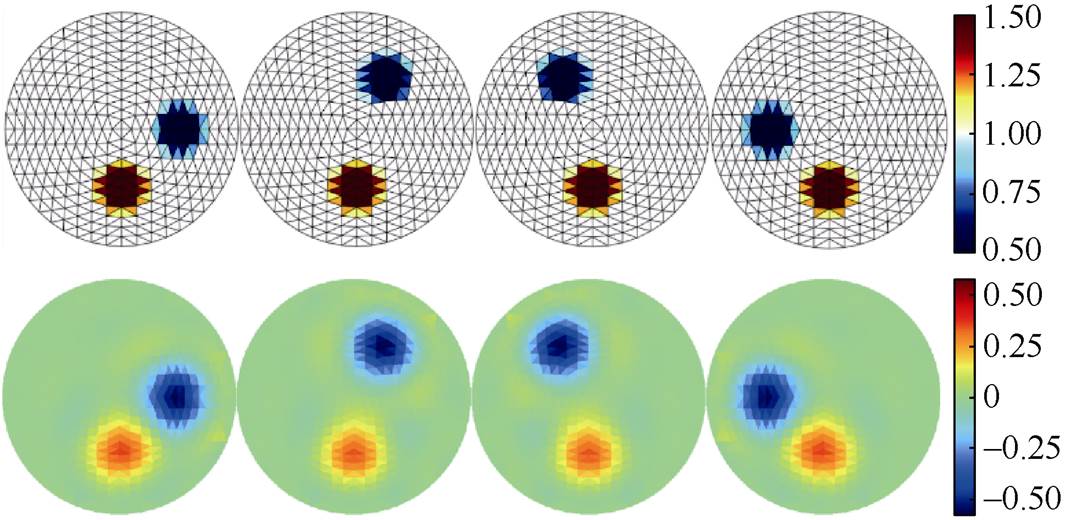
图3 仿真模型三
Fig.3 Simulation model three
仿真实验证明,本文所提出的差分迭代方法可以较好地重构出原始扰动目标图像。在后续章节中将该算法与几种正则化参数选取方法所得到的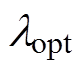 经阻尼最小二乘重建的结果进行客观图像质量对比。
经阻尼最小二乘重建的结果进行客观图像质量对比。
在动态电阻抗断层成像算法研究过程中,为具体客观量化图像重构效果,采用位置误差、分辨率、形状误差、环状伪影等评价指标进行图像评价[17]。
(1)位置误差(Position Error, PE)通过计算重建目标重心与仿真目标重心距离反映重建目标位置偏差程度,有
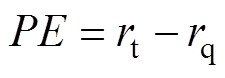 (11)
(11)式中,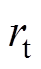 和
和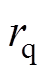 分别为仿真目标重心和重建图像重心到圆形域圆心的距离。
分别为仿真目标重心和重建图像重心到圆形域圆心的距离。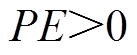 表示重建图像距圆形域比原仿真目标距圆心更近。
表示重建图像距圆形域比原仿真目标距圆心更近。
(2)分辨率(Resolution, RES)通过计算成像目标面积占总面积的百分比反映重建目标大小,有
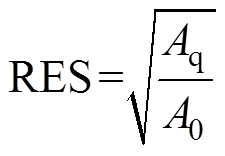 (12)
(12)(3)形状误差(Shape deformation, SD)通过计算成像圆形区域占成像区域的百分比反映重建图像的形状变化,有
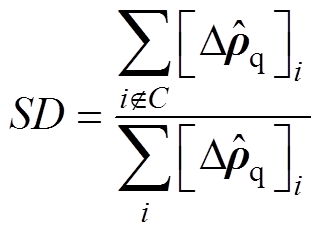 (13)
(13)
式中,C为以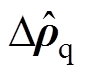 区域重心为圆心与
区域重心为圆心与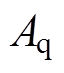 面积相等的圆形域。
面积相等的圆形域。
(4)环状伪影(Ringing, RNG)通过计算重建图像中围绕目标圆形域的电导率相反变化分布与重建图像中圆形域C内电导率变化分布的比值反映重构过程中存在的超调量程度,有
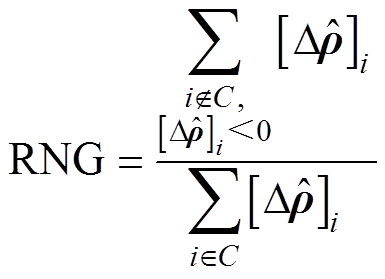 (14)
(14)由正则化原理可知,选取一个良好的正则化参数可以在正则化解中的扰动误差和正则误差之间形成一种合理的平衡,由此重建得到的图像效果较 好[18]。在目前已经提出的各种正则化参数选取策略中,依据是否具有噪声的先验信息可以大致分为两类:①基于对噪声的先验信息进行估计的方法; ②无需噪声先验信息的较优估计方法。本文提出的迭代差分算法无需噪声先验信息,因此选取的实验对照为第二类参数选取方法,包括L型曲线法和广义交叉检验法。
L型曲线法是病态逆问题求解中最常用的客观正则化参数选取方法之一[9]。以残差范数的对数值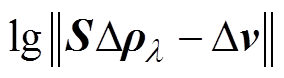 为横坐标,以图像范数的对数值
为横坐标,以图像范数的对数值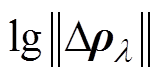 为纵坐标作图,经过曲线拟合得到一条正则化参数曲线,因以
为纵坐标作图,经过曲线拟合得到一条正则化参数曲线,因以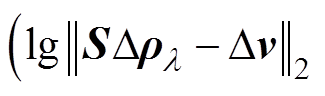 ,
, 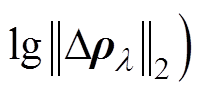 为坐标轴作图形状类似于L形,取名为L型曲线法。L型曲线法的关键是定位曲率最大值为
为坐标轴作图形状类似于L形,取名为L型曲线法。L型曲线法的关键是定位曲率最大值为
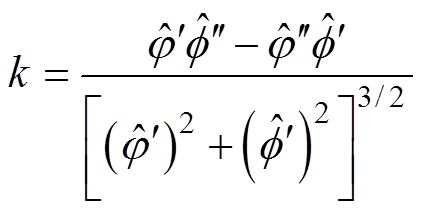 (15)
(15)将曲线拐点对应的参数作为最优正则化参数。该方法具有函数图像变化明显、定位准确、精度较高、适用性较好等特点。
广义交叉检验法与L型曲线法同属后验选取方法,即无需图像相关噪声的先验信息[10]。该方法认为舍弃测量值中的任意一个元素,相应的正则化解应该能够很好地预测该舍弃值,GCV函数可表示为
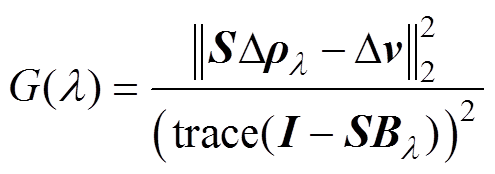 (16)
(16)其中
通过最小化GCV函数选取相应的最优正则化参数。
为使得正则化参数选取过程具有统计学意义,对单目标扰动、双目标同向扰动和双目标反向扰动三种仿真模型的边界电压分别添加50次随机0.1%高斯白噪声,选取结果以均值±标准差的形式给出。L型曲线法和GCV法选取的最优正则化参数经阻尼最小二乘算法进行重构成像,选取的正则化参数仿真结果见表1,重构结果如图4~图6所示。
表1 最优正则化参数选取仿真结果
Tab.1 Optimal regularization parameter selection results

图像序号LCV GCV 单目标双目标同向双目标反向单目标双目标同向双目标反向 10.102±0.0180.034±0.0040.027±0.0050.046±0.0110.029±0.0060.024±0.005 20.084±0.0130.035±0.0070.025±0.0040.050±0.0100.030±0.0070.017±0.008 30.063±0.0080.033±0.0060.030±0.0040.050±0.0080.028±0.0070.018±0.007 40.048±0.0130.031±0.0060.030±0.0050.041±0.0090.033±0.0050.018±0.008 50.056±0.0090.032±0.0050.030±0.0050.041±0.0090.030±0.0080.018±0.007 60.039±0.0060.035±0.0060.029±0.0050.037±0.0070.029±0.0070.017±0.007 70.033±0.0050.036±0.0070.024±0.0040.031±0.0050.029±0.0090.016±0.008 80.040±0.0050.032±0.0050.028±0.0040.040±0.0070.030±0.0050.021±0.007

图4 单目标扰动仿真结果
Fig.4 Simulation results of single target disturbance

图5 双目标同向扰动仿真结果
Fig.5 Simulation results of two same-attribute disturbance targets
单目标扰动仿真结果如图4所示,三种方法的重构效果相似,差分迭代法产生的伪影相对较少,LCV法重构中心位置扰动目标效果较差。双目标同向扰动仿真结果如图5所示,GCV法重构图像更好地区分了临近的两个相同扰动目标,差分迭代法和LCV法也能完成基本的双扰动目标重构成像。双目标反向扰动仿真结果如图6所示,差分迭代法重构表现较好,不仅能够很好地区分两个反向扰动目标,且重构的扰动目标位置和形状都比LCV法和GCV法效果更好。LCV法重构的扰动目标有较为明显的形变失真,同时LCV法和GCV法重构图像产生的伪影较多。
通过计算得到三种仿真扰动模型每帧图像的位置误差、分辨率、形状误差和环状伪影的评价指标结果如图7~图9所示。
由图7可知,在单目标扰动模型中,差分迭代法在位置误差和形状误差方面与LCV法和GCV法保持相近的水平,在环状伪影方面表现相对较优。同时随着扰动目标不断向边界靠近,三种算法重构的位置误差都在不断增大,分辨率都在不断减小,形状误差和环状伪影指标则稳定维持较好的水平。由图8可知,在双目标同向扰动模型中三种方法的表现相近,由于双同向扰动目标在图像序号1和8时最接近,在图像序号4和5时距离最远,三种方法的位置误差和形状误差曲线都呈现出明显的中间高、两边低的形状。差分迭代在形状误差和环状伪影方面表现相对较好,计算均值相比LCV法下降了0.074 6和0.063 9,相比GCV法下降了0.078 7和0.096 4,有效地减少了目标形变及周围反向伪影干扰,体现出明显的成像优势。由图9可知,在双目标反向扰动模型中,GCV法在位置误差与形状误差方面相对表现较差,均值分别达到0.093 2和0.265 5。差分迭代在位置误差方面与LCV法表现相近,两者均差仅为0.001 6。在形状误差和环状伪影方面差分迭代表现最优,均值仅为0.070 1和1.978 9,远小于另外两种方法。考虑到在该扰动模型中环状伪影指标算法可能将反向扰动目标看作伪影,因此和单目标扰动模型及双目标同向扰动模型相比数值偏大。
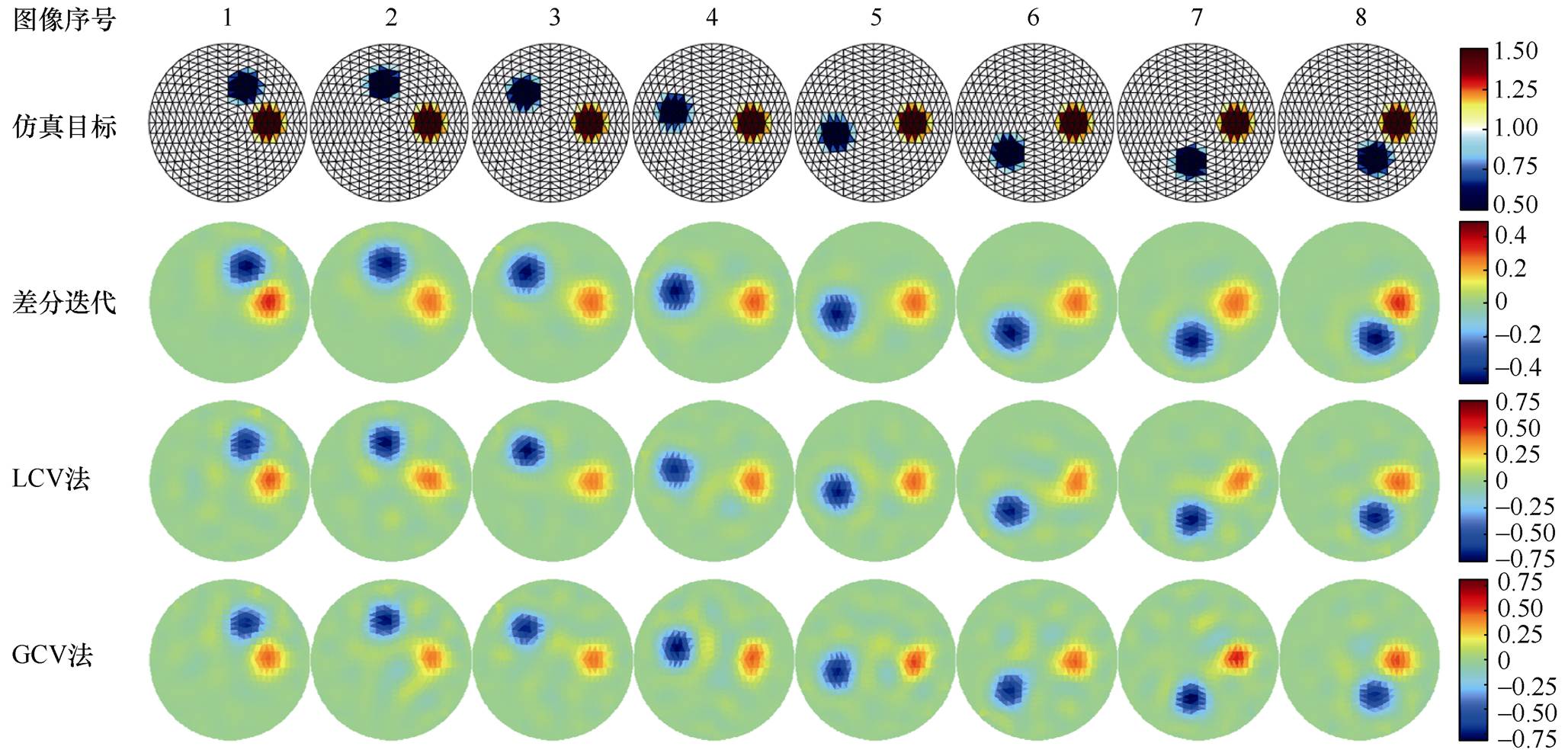
图6 双目标反向扰动仿真结果
Fig.6 Simulation results of two different-attribute disturbance targets


图7 单目标扰动重构图像性能指标对比
Fig.7 Algorithm performance of single target disturbance reconstruction
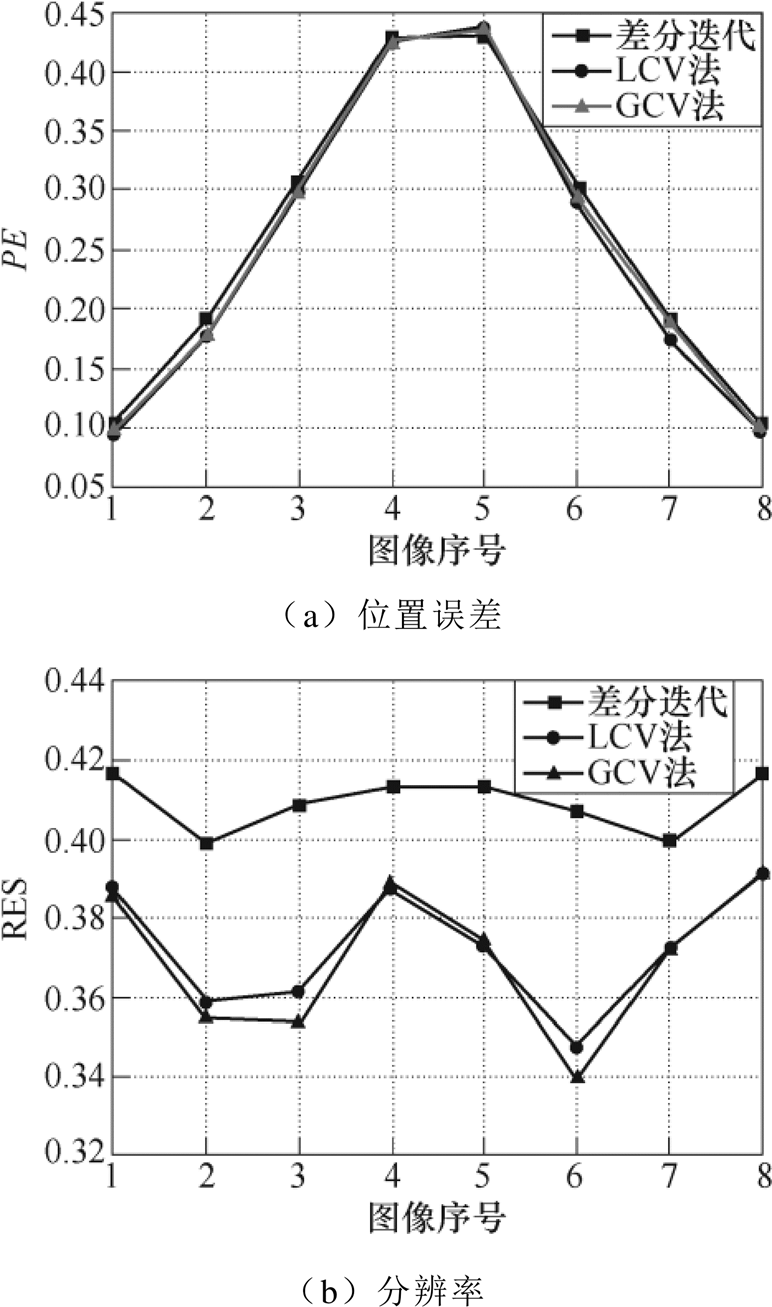
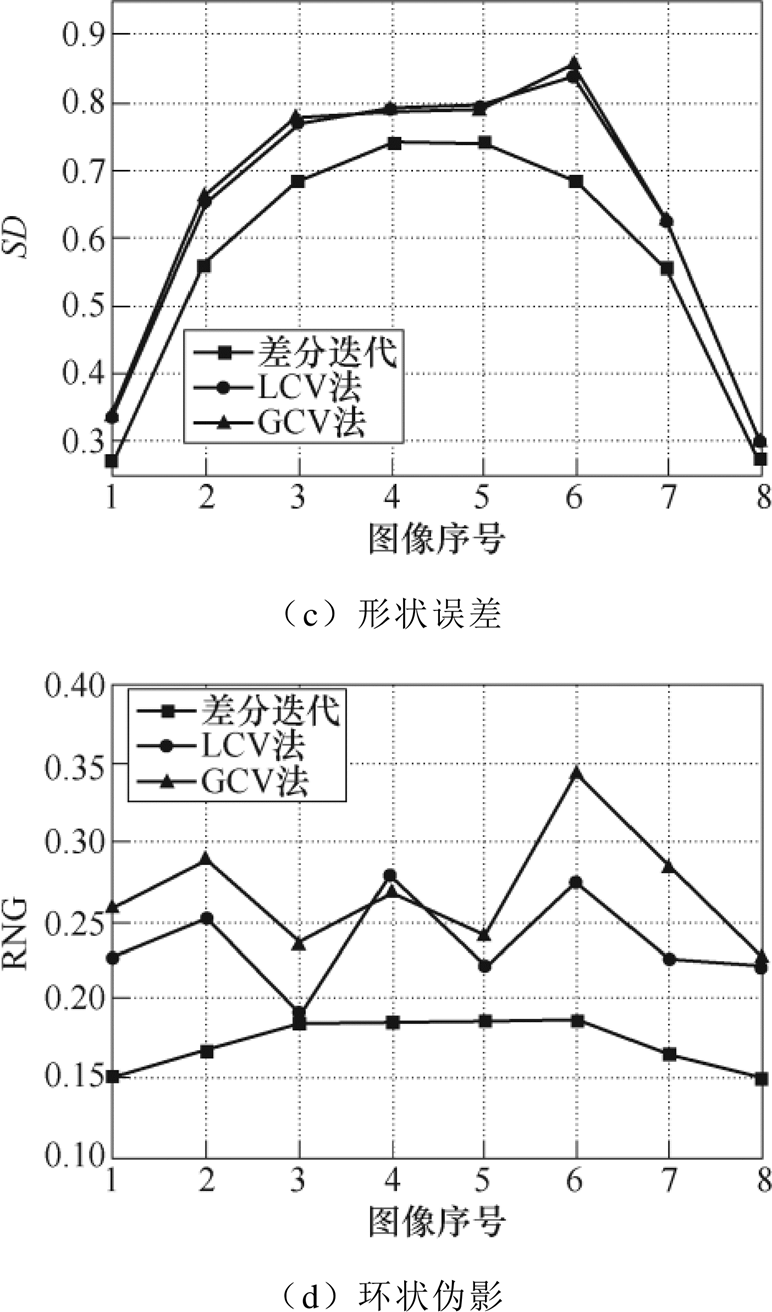
图8 双目标同向扰动重构图像性能指标对比
Fig.8 Algorithm performance of two same-attribute disturbance targets reconstruction
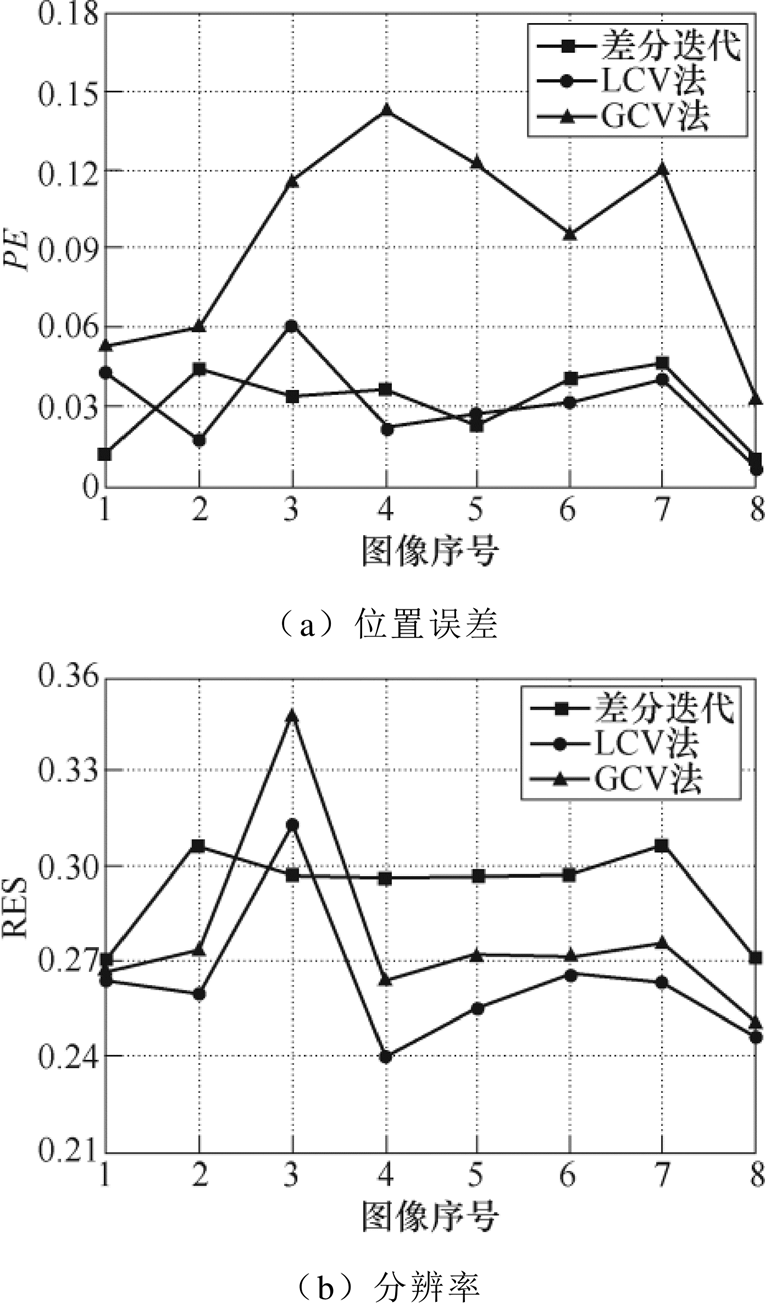
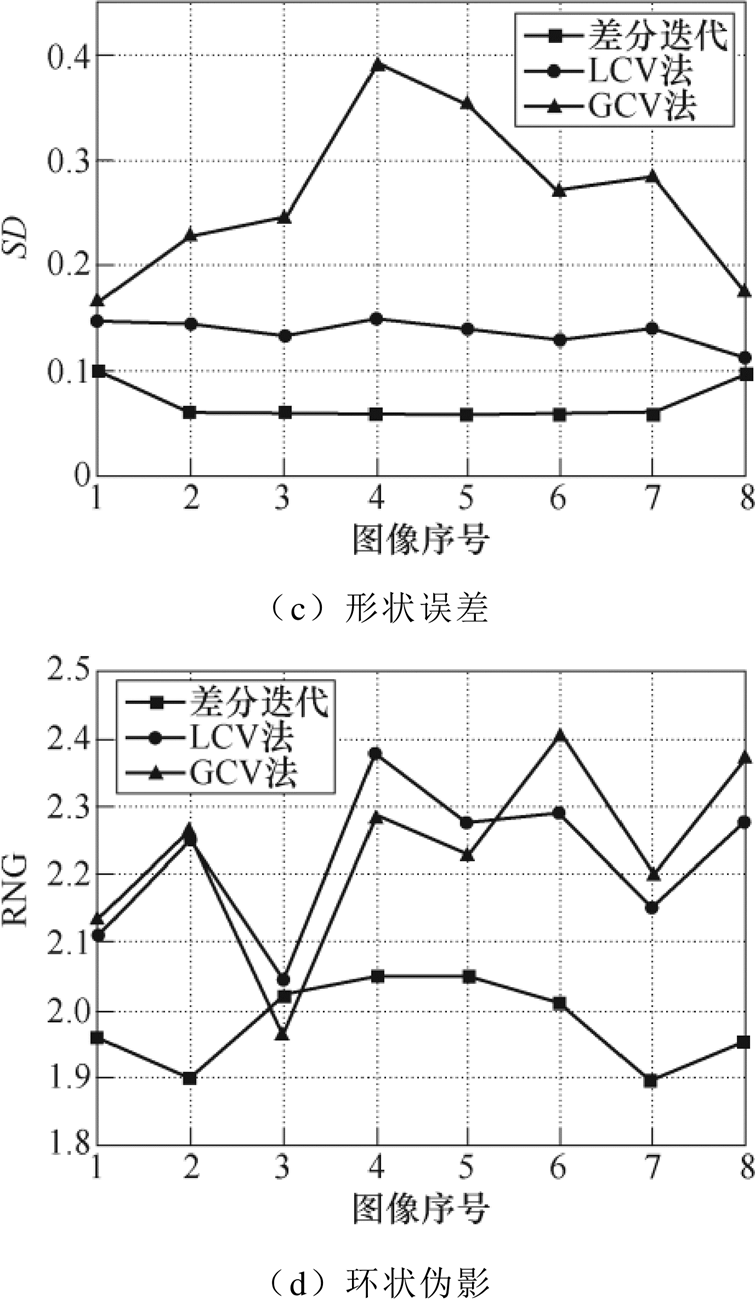
图9 双目标反向扰动重构图像性能指标对比
Fig.9 Algorithm performance of two different-attribute disturbance targets reconstruction
综上所述,在不调整正则化参数的情况下,本文提出的差分迭代算法能够在位置误差、分辨率、形状误差、环状伪影等评价指标方面与基于LCV法和GCV法选取的最优正则化参数经阻尼最小二乘法计算得到的重构图像保持相似甚至更优的效果。
在电阻抗断层成像技术发展历程中,通过选取合适的正则化参数进行正则化求解一直是领域内研究的热点之一,然而经验法选取主观性强、不同实验和使用人员成像一致性不佳、客观参数选取方法实时性差、依赖噪声先验信息,都很难满足EIT在临床与实验中的实际应用。因此本文提出一种基于差分迭代的电阻抗断层成像算法,该算法利用动态线性逼近,在不选择最优正则化参数的情况下提高图像成像质量,且在重构较为快速的同时能够在位置误差、分辨率、形状误差、环状伪影等方面与LCV法和GCV法等常用算法保持相似或更好的重建效果,该方法具有较好的实际应用前景。
参考文献
[1] 徐灿华, 董秀珍. 生物电阻抗断层成像技术及其临床研究进展[J]. 高电压技术, 2014, 40(12): 3738- 3745.
Xu Canhua, Dong Xiuzhen. Advancements in elec- trical impedance tomography and its clinical appli- cations[J]. High Voltage Engineering, 2014, 40(12): 3738-3745.
[2] 董秀珍. 生物电阻抗成像研究的现状与挑战[J]. 中国生物医学工程学报, 2008(5): 641-643, 649.
Dong Xiuzhen. Recent progress and challenges in the study of bioimpedance imaging[J]. Chinese Journal of Biomedical Engineering, 2008(5): 641-643, 649.
[3] 张涛, 安志伟, 刘学超, 等. 脑部电阻抗有限元模型的脑膜结构仿真[J]. 医疗卫生装备, 2020, 41(4): 35-38.
Zhang Tao, An Zhiwei, Liu Xuechao, et al. Brain EIT finite element simulation involving cerebral pia mater structure[J]. Chinese Medical Equipment Journal, 2020, 41(4): 35-38.
[4] 张帅, 李子秀, 张雪莹, 等. 基于时间反演的磁动力超声成像仿真与实验[J]. 电工技术学报, 2019, 34(16): 3303-3310.
Zhang Shuai, Li Zixiu, Zhang Xueying, et al. The simulation and experiment of magneto-motive ultrasound imaging based on time reversal method[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3303-3310.
[5] 张帅, 崔琨, 史勋, 等. 经颅磁声电刺激参数对神经元放电模式的影响分析[J]. 电工技术学报, 2019, 34(18): 3741-3749.
Zhang Shuai, Cui Kun, Shi Xun, et al. Effect analysis of transcranial magneto-acousto-electrical stimulation parameters on neural firing patterns[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3741-3749.
[6] 李文慧, 姜慧, 杨帆, 等. 高频高压激励环形表面介质阻挡放电特性实验研究[J]. 电工技术学报, 2020, 35(16): 3539-3550.
Li Wenhui, Jiang Hui, Yang Fan, et al. Experimental study on ring surface dielectric barrier discharge characteristics of high frequency and high voltage excitation[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3539-3550.
[7] 赵宏晨, 刘晓明, 杨滢璇, 等. 基于分数阶Tikhonov正则化方法的电弧反演研究[J]. 电工技术学报, 2019, 34(1): 84-91.
Zhao Hongchen, Liu Xiaoming, Yang Yingxuan, et al. Research on arc inversion based on fractional Tikhonov regularization method[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 84-91.
[8] Graham B M, Adler A. Objective selection of hyper- parameter for EIT[J]. Physiological Measurement, 2006, 27(5): 65-79.
[9] Hansen P C, Jensen T K, Rodriguez G. An adaptive pruning algorithm for the discrete L-curve criterion[J]. Journal of Computational & Applied Mathematics, 2015, 198(2): 483-492.
[10] Xue Feng, Blu T, Liu Jiaqi, et al. A novel GCV-based criterion for parameter selection in image deconvo- lution[C]//IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 2018: 1403-1407.
[11] Adler A, Guardo R. Electrical impedance tomography: regularized imaging and contrast detection[J]. IEEE Transactions on Medical Imaging, 1996, 15(2): 170- 179.
[12] Liu Xuechao, Li Haoting, Ma Hang, et al. An iterative damped least-squares algorithm for simu- ltaneously monitoring the development of hemorrhagic and secondary ischemic lesions in brain injuries[J]. Medical & Biological Engineering & Computing, 2019, 57(6): 1917-1931.
[13] 王琦, 彭圆圆, 汪剑鸣, 等. 动态电阻抗成像时空相关性重建方法研究[J]. 电子测量与仪器学报, 2018, 32(2): 153-160.
Wang Qi, Peng Yuanyuan, Wang Jianming, et al. Research on spatio-temporal relativity reconstruction method in dynamic electrical impedance tomo- graphy[J]. Journal of Electronic Measurement and Instrumentation, 2018, 32(2): 153-160.
[14] Ho S L, Yang Shiyou. A computationally efficient vector optimizer using ant colony optimizations algorithm for multobjective designs[J]. IEEE Transa- ctions on Magnetics, 2008, 44(6): 1034-1037.
[15] 夏慧, 刘国强, 黄欣, 等. 注入电流式磁声成像平面模型的逆问题研究[J]. 电工技术学报, 2017, 32(4): 147-153.
Xia Hui, Liu Guoqiang, Huang Xin, et al. The inverse problem study of plane model based on magneto- acoustic tomography with current injection[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(4): 147-153.
[16] 李翠环, 汪友华, 耿读艳, 等. 基于双参数模型的ECT图像重构混合算法[J]. 电工技术学报, 2012, 27(4): 24-29.
Li Cuihuan, Wang Youhua, Geng Duyan, et al. Hybrid algorithm based on two-parameter model for electrical capacitance tomography image reconstru- ction[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 24-29.
[17] Adler A, Arnold J H, Bayford R, et al. GREIT: a unified approach to 2D linear EIT reconstruction of lung images[J]. Physiological Measurement, 2009, 30(6): S35-S55.
[18] 李彦东, 杨滨, 徐灿华, 等. 针对脑部电阻抗成像的四种正则参数选取方法的比较研究[J]. 中国医学装备, 2013, 10(11): 4-7.
Li Yandong, Yang Bin, Xu Canhua, et al. Research on comparison of four types of regularization parameter choosing methods for brain electrical impedance tomography[J]. China Medical Equipment, 2013, 10(11): 4-7.
An Algorithm of Electrical Impedance Tomography Based on Differential Iteration
Abstract Most electrical impedance tomography algorithms need to select optimal regula- rization parameters to overcome the ill-conditioned equation and obtain better image quality. This paper proposes an electrical impedance tomography algorithm based on differential iteration, which uses dynamic linear approximation to improve imaging quality without adjusting the regularization parameters. A disturbance model is established in the approximate linear region, and the gradient method is used to derive the conductivity differential iterative relationship for rapid reconstruction. Then, the image reconstructed by this algorithm is compared with the reconstructed image based on several objective regularization parameter selection methods in terms of position error, resolution, shape deformation, ringing, and so on. The simulation results show that the proposed differential iterative algorithm can maintain similar or better results with the commonly used reconstruction algorithms, and has good practical application prospects.
keywords:Electrical impedance tomography, differential iteration, multitarget imaging, fast reconstruction algorithm, regularization parameter selection
中图分类号:TP391.9; R318
DOI: 10.19595/j.cnki.1000-6753.tces.201241
国家自然科学基金(31771073,61771475,51837011)和军委科技委基础加强计划(2019-JCJQ-JJ-096)资助项目。
收稿日期2020-09-18
改稿日期 2020-09-26
章伟睿 男,1996年生,硕士研究生,研究方向生物电阻抗成像。E-mail: 793783799@qq.com
徐灿华 男,1984年生,副教授,硕士生导师,研究方向为生物电磁检测与成像。E-mail: canhuaxu@ fmmu.edu.cn(通信作者)
(编辑 崔文静)