图1 血液导电示意图
Fig.1 Schematic diagram of blood conduction
摘要 脑血液电导率是脑阻抗成像和脑疾病评估的重要参数。为了研究脑部脉动血液电导率变化机理,该文基于Maxwell-Fricke原理建立血液红细胞绝缘孔隙导电模型,以血流动力学参数为指标,研究血流电导率与红细胞绝缘孔隙几何参数之间的数值关系。在此基础上构建具有孔隙导电结构的高分辨率大脑Willis环模型,利用耦合非线性微分方程计算脑动脉血流动力学参数的时空分布,模拟非均匀电导率血液的等效体积电导率。结果表明,与不考虑孔隙取向的定常血流模型电导率相比,一个心动周期内孔隙导电模型的电导率峰值增大27.6%,其余时刻增大约12%,增大比例与心脏泵血时期密切相关。仿真结果与真实脉动血液电导率具有较好的一致性,使用该文所提出的模型能够准确预测不同血液流变条件下的在体血流电导率。
关键词:电导率 脉动血液 孔隙导电模型 大脑动脉模型
人体的血液含量约占体重的8%,血液在体内分布广泛,是影响组织介电性能的重要因素之一。很多生理病理现象都会引起血液成分理化性质的变化,直接影响血液的电导率[1]。研究血液电导率变化机理是基于电导率的人体内部成分测量方法(如电阻抗成像、磁感应成像、磁感应磁声成像等)的基础,对研究电磁场的生物效应、探索生命活动规律、开发新的医学成像方法具有重要意义[2-5]。流变血液电导率的理论计算是基于生理学、血流动力学和电磁学的综合研究,国内外很多学者对此开展了工作。A. E. Hoetink等通过实验证明了定常血流和脉动血流电导率的差别[6]。R. L. Gaw等首次研究了刚性圆柱体中的脉动血流对血液电导率的影响[7-8]。Shen Hua等将血管假设为线弹性圆柱体,使用Maxwell方法计算了血流速度和动脉壁位移对血流电导率的影响,并研究了动脉半径和中心线速度对人颈总动脉脉动流的电导率和电阻抗的影响[9-10]。A. Zhbanov和S. Yang提出了一种基于有效介质理论的血液传导性计算方法,理论计算结果表明,血液电导率随聚集的红细胞数目的增加而降低[11]。
目前的研究主要基于血管是刚性圆柱体这一假设,忽略了血管几何结构对血流速度和剪切应力的影响。线弹性圆柱体的假设与人体动脉存在弯曲和狭窄的结构有一定差异,不能完全反映结构特征对电导率的影响。理论计算结果缺乏一致性和可重复性,计算模型几何形状简单,忽略了血管几何形态对血液红细胞流变的影响以及血流冲击下血管壁周期性运动引起的导体效应。由于解析计算模型与实际生理结构存在差异,相关研究还处于理论研究阶段,极大地限制了该研究在生物阻抗成像方法中的应用和医学临床应用。
为了解决具有真实弹性结构的大脑动脉内部脉动血流在完整心动周期内的血液电导率计算问题,使其更有效地应用于脑阻抗成像研究,利用一名健康受试者的磁共振血管成像(Magnetic Resonance Angiography, MRA)图像建立了人脑动脉树几何模型,利用生理学文献中的颈内动脉血流速和大脑前、中动脉血压数据,建立了大脑动脉Willis环局部血管及血液的数值模型。以Maxwell-Fricke方程为理论基础对血流电导率进行有限元仿真,分析脑动脉Willis环局部血流动力参数的时空特点,以剪切应力计算结果为基准对血液内部划分区域,分析各区域内红细胞绝缘孔隙在血液剪切力作用下的形态变化及对血液电导率的影响,计算电导率数值的变化情况,形成一个完整心动周期内随时间变化的瞬时电导率曲线。
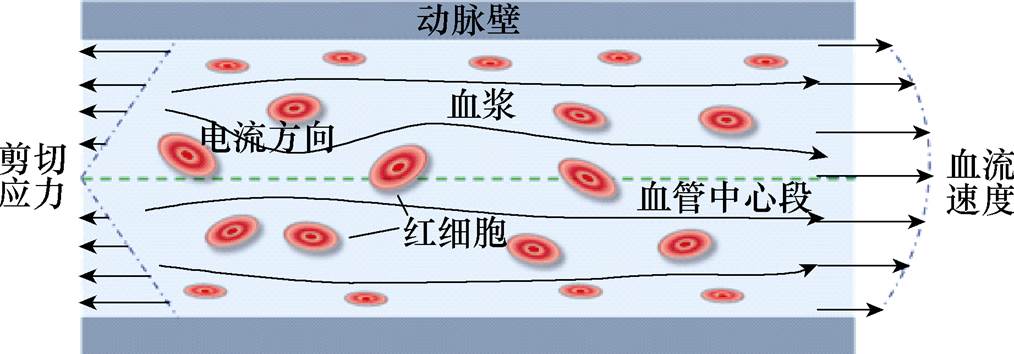
血液由血浆和血细胞组成。血浆是导电液体,成分包括90%的水、7%的血浆蛋白、1%无机质和1%有机质及1%的其他物质。这些物质含量稳定,使血浆具有固定的各向同性电导率。血细胞中的红细胞对电流呈现绝缘性,白细胞、血小板等其他成分对电流走向无明显影响,因此血液可视为存在一定数量的可变形红细胞绝缘孔隙的导电悬浊液。血液孔隙模型内部的电流流向如图1所示。电流沿避开红细胞的方向传播,血液的电导率与红细胞绝缘孔隙的形态、位置和数量有关。

图1 血液导电示意图
Fig.1 Schematic diagram of blood conduction
血流在非大动脉中呈现层流形式,内部由于速度梯度和动力黏度产生了与血流方向相反的内摩擦力,即血流剪切应力t(r),r为该点距血管中心线的垂直距离。红细胞膜是软弹性可变形膜,内部是液态细胞质,红细胞膜在剪切应力作用下发生形态和方向的可逆性改变。
红细胞是双凹形圆盘,具有一个短轴a和两个相等的长轴b。在不同的t(r)范围内,血液中的红细胞呈现不同的形态和方向特性[12]。
(1)低剪切应力区域RL(t(r)<0.03N/m2)内,红细胞不发生形变,在血流中呈现稳定的履带式翻滚,短轴a和长轴b随机平行于血流方向。
(2)中剪切应力区域RM(t(r)>0.1N/m2)内,红细胞脱离翻滚状态并且发生变形,方向逐渐沿受到剪切应力最低的方向变化,即长轴b平行于血液流动方向。
(3)高剪切应力区域RH(0.03N/m2≤t(r)≤0.1N/m2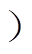 内,红细胞由翻滚逐渐与中轴线对齐,形变由小到大。
内,红细胞由翻滚逐渐与中轴线对齐,形变由小到大。
不考虑细胞膜形变,红细胞取向方向为随机状态定的血流为定常流血液,考虑流动对红细胞形态影响的血液为脉动流血液。红细胞在定常流和脉动流血液中的排列形式分别如图2a和图2b所示。为保持红细胞内外压不变,红细胞膜在血液剪切力的作用下改变轴的长度和旋转方向,使用红细胞短长轴比a/b来描述红细胞变形情况。
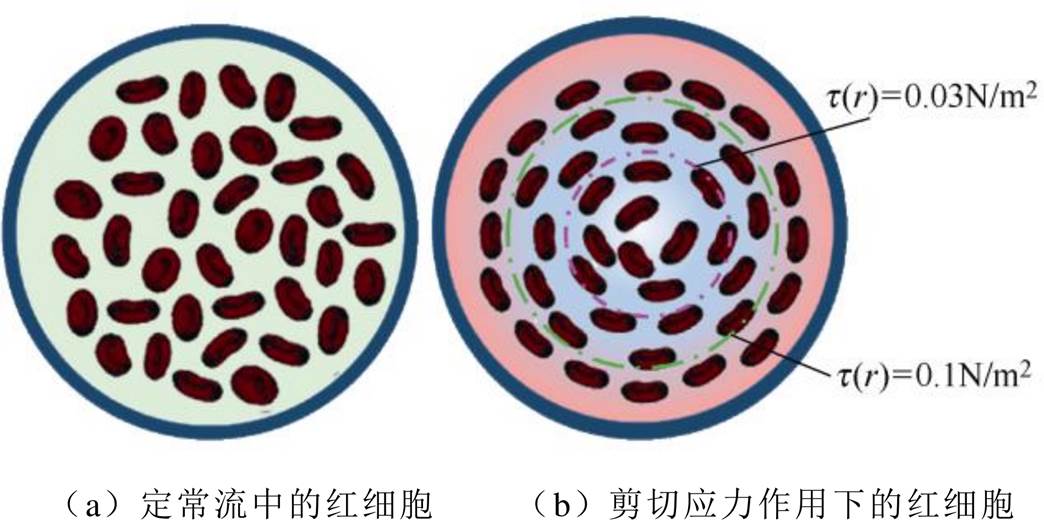
图2 血液中的红细胞形态
Fig.2 The morphology of red blood cells in the blood
血液作为红细胞等血细胞的悬浮液,在非主要动脉中表现出牛顿效应。脑血管直径小于脉搏波每秒传导距离,控制方程[13]为
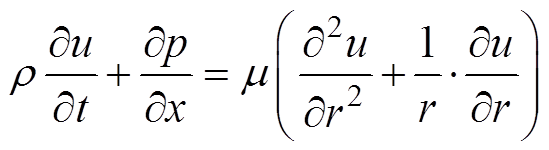 (1)
(1)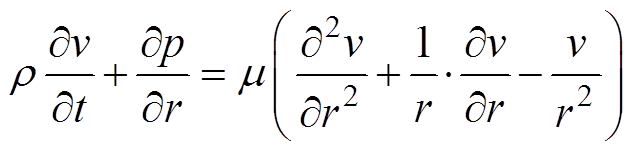 (2)
(2)
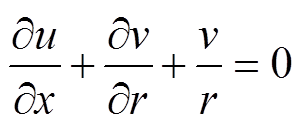 (3)
(3)
式中,r 为血液密度;u、v分别为轴向和径向血流速度;p为血压;x为血管中轴线方向的距离;t为时间;m 为血液的动力黏度;r为径向距离。
将真实血管分成一系列不同直径的小段圆柱体,第i个圆柱体的直径是Di,长度是L,两端的压力分别为p1和p2,圆柱体内部充满动力黏度为m 的血液。设其内部有一个与它同轴的圆柱体,其半径即径向距离r<Di/2。由速度梯度效应产生的剪应力t(r)为
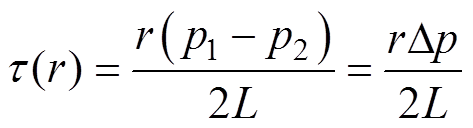 (4)
(4)动脉壁在血管轴向无移动,杨氏模量为E,血管内的位置增量Dr随血压增量Dp的变化及剪切应力t(r)[14]分别为
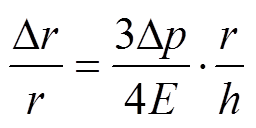 (5)
(5)
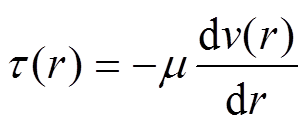 (6)
(6)式中,h为血管壁厚度;。
假设红细胞周围存在长方体的混合体积,由位于中心的红细胞和血浆构成,距离血管中心线径向距离为r处存在着长边为Dr的混合体积,宽边为2pr/k,k是每个圆环上的混合体积个数。由Maxwell混合理论和Fricke方程可得混合体积的电导率[15]为
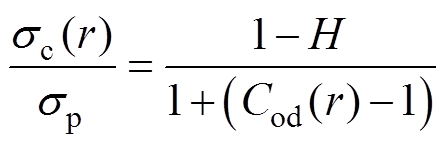 (7)
(7)式中,sc为混合体积电导率;sp为血浆电导率;Cod为红细胞绝缘孔隙的取向系数;H为红细胞比容。在血管直径大于1mm时由血液流动导致的红细胞浓度分布不均可以忽略[16]。
定常血流中红细胞的取向系数为Cods,电导率scs的计算方法为
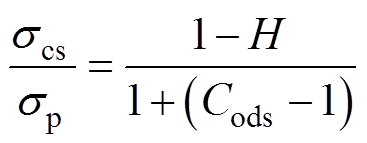 (8)
(8)定常血流中红细胞的一个短轴和两个长轴与电场方向平行的概率相等,红细胞取向系数Cods可描述[6]为
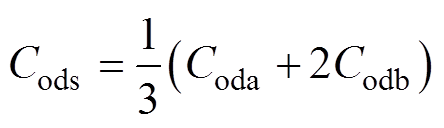 (9)
(9)
式中,Coda、Codb分别为红细胞短半轴a和长半轴b平行于血流方向的取向变形系数。
a0、b0分别为红细胞不受力状态的短、长半轴长度,脉动流中剪切应力作用下短半轴和长半轴分别变化为ad和bd,取向角jdr及变形取向系数Cod(r)与剪切应力之间的关系为
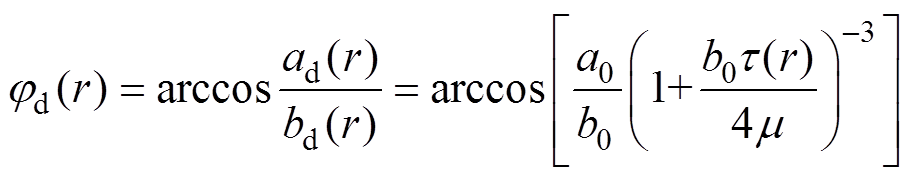 (10)
(10)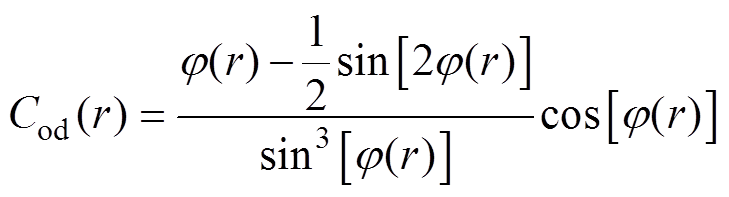 (11)
(11)
设RL、RM、RG三个区域血流电导率分别为sL、sM和sG。3个不同剪切应力区域平行同轴排列,每段圆柱体的电导率sbi的计算公式为
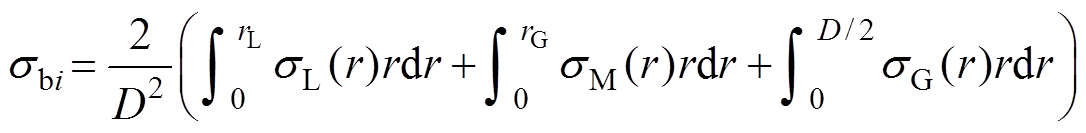 (12)
(12)式中,D为血管直径;rL、rG分别为RL和RM、RM和RG的分界线。
大脑Willis环是重要的侧支循环通路,在调节大脑血液循环中起着显著的作用[17-18]。基于医学图像的三维脑血管模型如图3所示。特定血管的血流动力学效应依赖于血管结构,针对脑血流电导率计算,利用MRA图像建立了具有流体区域和固体区域的两相流脑血管模型,如图3a所示。考虑到血流动力学计算成本和Willis环结构的对称性,选取了Willis环中重要的一部分,包括作为脑血液循环入口的颈内动脉(Internal Carotid Artery, ICA)、为大部分脑区供血的大脑中动脉(Middle Cerebral Artery, MCA)M1段和大脑前动脉(Anterior Cerebral Artery, ACA)起始段,模型如图3b所示。

图3 基于医学图像的三维脑血管模型
Fig.3 3D cerebrovascular model based on medical image
ICA、ACA和MCA的M1段平均直径分别为4.59mm、2.45mm、2.75mm,动脉壁厚度为0.25~0.30mm,平均厚度为0.28mm,模型内部血液体积为197.74mm3,与大脑动脉解剖学数据基本一致[19-21]。
2.2.1 大脑Willis环局部血流动力学仿真
将血管模型进行网格划分,总网格数为56 552,质量为0.63,其中流体区域(血液)网格数为43 935,质量为0.62,固体区域(动脉壁)网格数为12 717,质量为0.65。
血流和血管壁之间没有滑动,即与动脉壁接触的血液的速度随着动脉壁的速度而变化[22-23],血流动力学参数见表1。在Willis环几何模型上使用生理学文献的数据作为仿真条件[24],ICA血流速度、MCA和ACA血压如图4所示。
表1 血流动力学参数
Tab.1 The parameters of hemodynamic

参 数数 值 血液密度[6, 9, 25]rbl/(kg/m3)1 050 血浆动力黏度[6, 9, 25]mpl/(Pa·s)1.35×10−3 全血动力黏度[6, 9, 25]mbl/(Pa·s)mpl(1+2.5H+7.37×10−2H) 红细胞膜剪切模量[6]MRBCs/(N/m)1.5×10−5 血管壁杨氏模量[26]E/MPa0.6
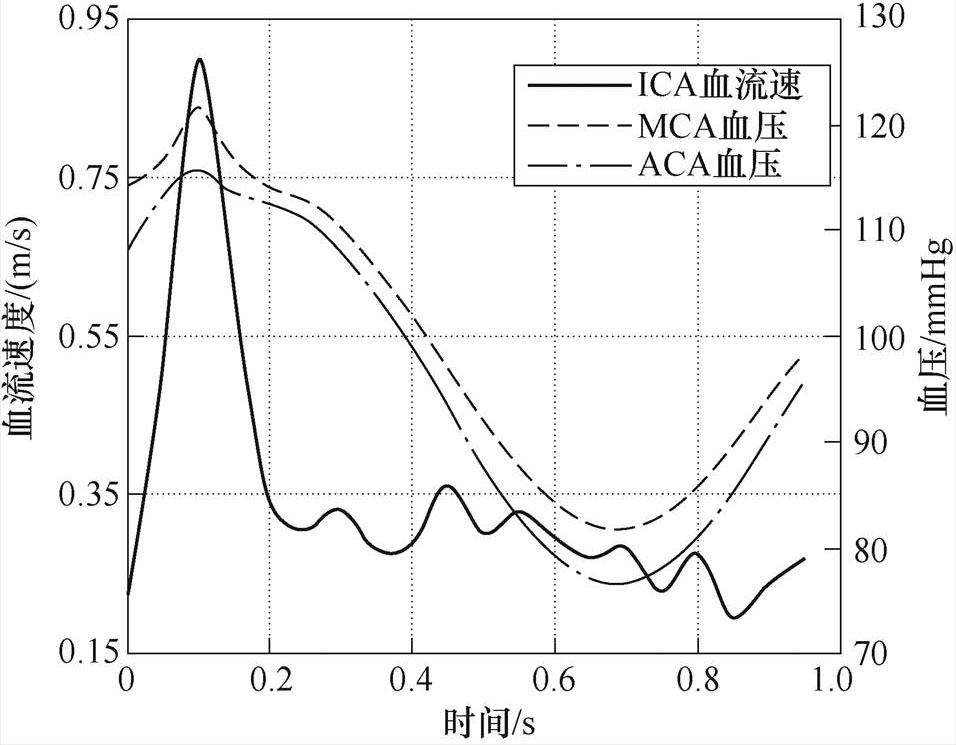
图4 Willis环血流动力学条件
Fig.4 Hemodynamic conditions of circle of Willis
ICA血流速度与心脏活动密切相关,可分为剧烈变化期(t =0~0.2s)和稳定期(t =0.2~1s)。心脏收缩期血流剧烈变化,最大流速为0.9m/s;心脏舒张期血流速度迅速下降,平均流速为0.26m/s。
使用Comsol Multiphysics在Willis环局部血管几何模型上采用流固耦合方法进行仿真[27-28]。采样间隔为0.05s,血流剪切应力仿真结果如图5所示。剪切应力的时间分布特点是最大值出现在心脏收缩期(t =0.05~0.1s),大小为3.58Pa;在心脏舒张期(t =0.15~0.9s)最大值为1.86Pa,剪切应力较小且分布较平均。空间分布特点是在血管宽阔平坦的位置剪切应力较小,狭窄弯曲的位置剪切应力较大。同一截面上,距离血管中心线越远,剪切应力越大。
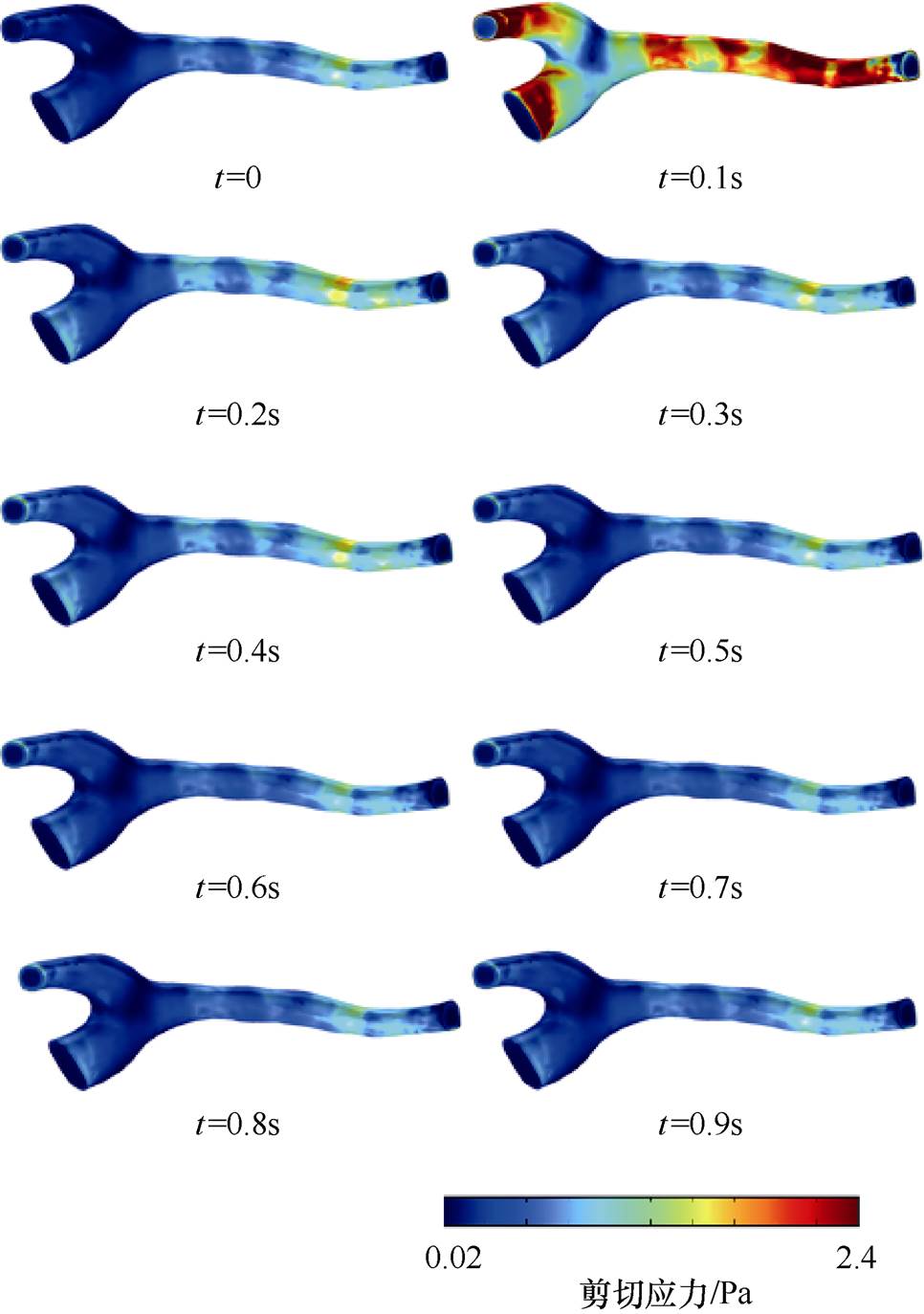
图5 剪切应力分布
Fig.5 Distribution of shear stress
2.2.2 电导率孔隙导电模型仿真
真实血管结构复杂,不能使用传统研究中的解析形式直接求解。将三维血管以血管中心线为轴线分割为一系列等长同轴圆柱体,用数值方法仿真圆柱体中心截面的电导率,作为该圆柱体的电导率,将所有圆柱体串联得到整体血流的电导率。仿真过程中将Willis环局部模型分成407个中心截面。血液总体电导率sbl与每段血液电导率sbi的关系为
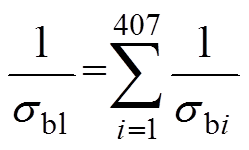 (13)
(13)以血流动力学仿真结果作为计算条件,得到每一个中心截面的sbi(i=1, 2,…,407),RL的取向系数CodL、RM的取向系数CodM和RG的取向系数CodG分别为
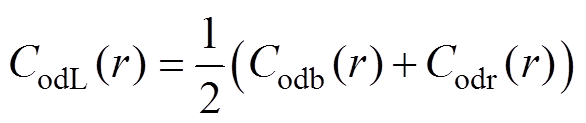 (14)
(14)
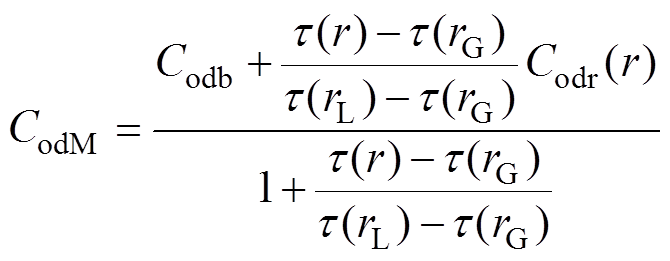 (15)
(15)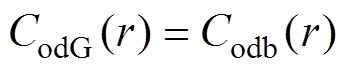 (16)
(16)
Willis环绝缘孔隙电导率模型参数见表2,计算了不同时刻脉动血流的红细胞绝缘孔隙短半轴a和长半轴b平行于电场的变形取向系数Coda和Codb。Coda为2.1~2.4,在0.05~0.10s出现最大值;Codb为1.26~1.31,在心脏舒张的平稳期之后基本保持不变。
表2 电导率模型参数
Tab.2 The parameters for conductivity calculation

参 数数 值 红细胞比容[6, 25]H0.45 红细胞短半轴[7]a0/mm0.2 红细胞长半轴[7]b0/mm0.4 血浆电导率[6-7]sp/(S/m)1.12
使用Comsol Multiphysics仿真得到模型的瞬时电导率,大脑脉动血流瞬时电导率切面如图6所示。

图6 大脑脉动血流瞬时电导率切面
Fig.6 Sectional view of instantaneous conductivity of cerebral pulsating blood flow
脉动血流电导率的时间分布特点是在心脏收缩期(t =0.1s)数值最大,其余时刻电导率小且稳定;空间分布特点是血管中心线的电导率低于血管壁附近,同一时刻的电导率由中心到管壁呈环形增大。
脑动脉血管壁直径增大比例如图7所示。在一个心动周期内,弹性血管壁直径在收缩期内最大位移出现在0.20s,为0.167mm,对应血液中心线最大流速;舒张期直径最小值为0.111mm,舒张期内动脉直径变化不明显。由于脉动血流的影响,血管壁直径的最大变化量分别为3.66%、6.08%和6.83%。
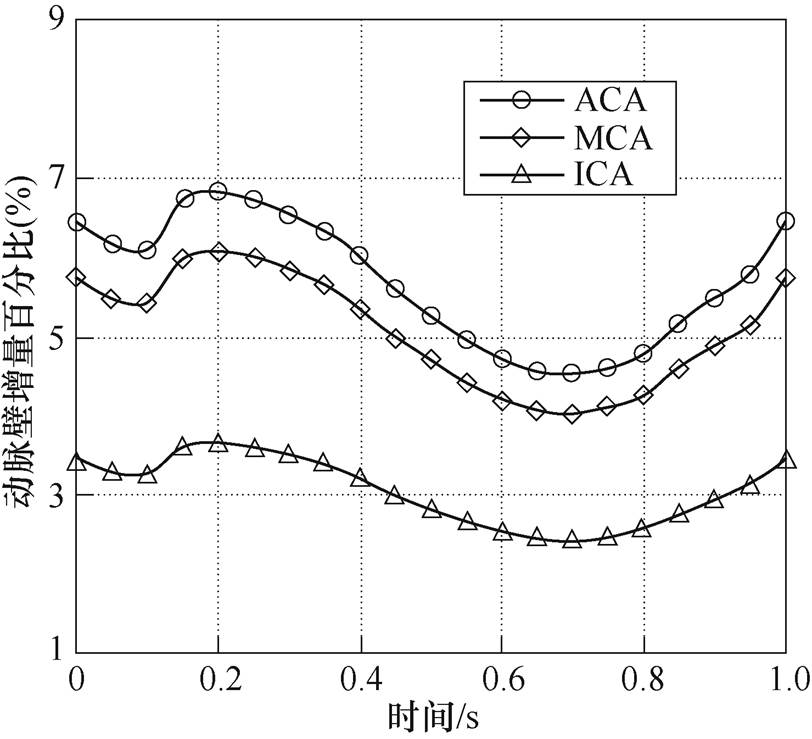
图7 脑动脉直径增大比例
Fig.7 The proportion of increased diameter of cerebral arteries
根据动脉模型几何参数和动脉直径变化计算得,一个心动周期内动脉壁直径变化引起的血容量增量约为4.5ml,与模型的总血量相比增加了2%。
利用式(8)和式(9)计算了定常血流电导率。Codr随着血液中心线速度的增大而增大,血流速度峰值(0.05s)时Codr变化最大。定常血液电导率呈周期性微弱变化,与血流速度波形一致,电导率在0.550s/m左右。一个心动周期之内,在0.10s处出现最大值,电导率为0.557s/m,增加了1.272%,与参考文献中的离体血液电导率数值相符[6, 29]。
RL、RM和RG的平均电导率如图8所示。RG的电导率对脉动血流电导率的贡献最大,平均电导率在0.27~0.47S/m之间,RM的电导率在0.1~0.19S/m之间,RL的平均电导率在0.06~0.25S/m之间。RG的红细胞膜受到挤压最大,红细胞绝缘孔隙最小,对电流的阻碍最小,血流电导率最大。随着血流速度增加,剪切应力增大,原属于RL的一部分血液达到RM,使RL范围减少。血流速度越高,RL的电导率越小,即RL的脑血流电导率与脑血流速度变化趋势相反。同理,高速血流使RM的一部分变为RG,RG电导率增大,表现出与血流速度相同的变化趋势。随着血流速度增大,从RM到RG的区域小于从RL到RM的区域,RM电导率表现出血流速度趋势相同但幅值更平缓的变化特点。
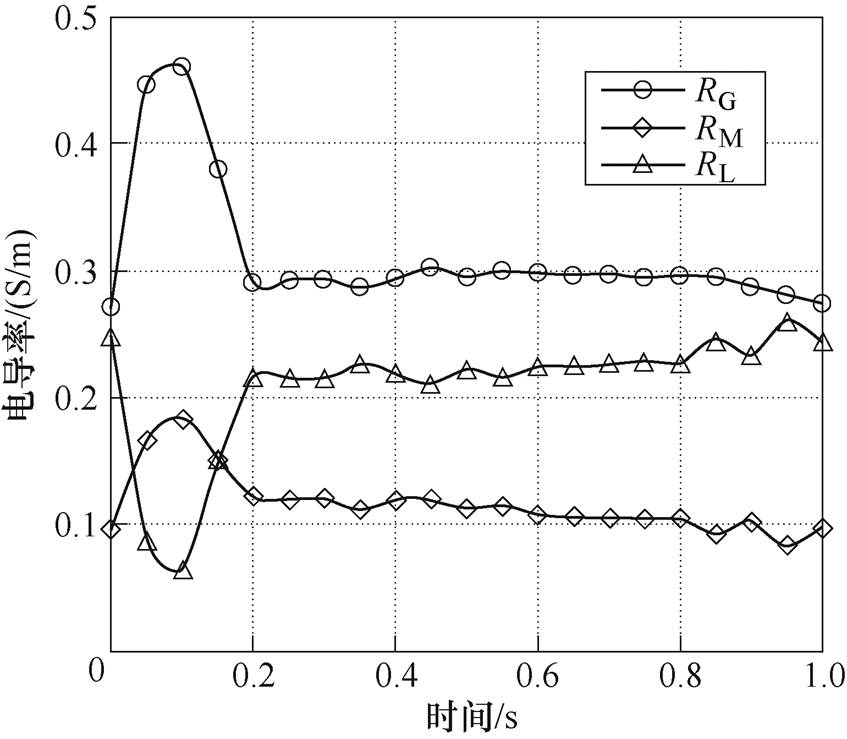
图8 各剪切应力区域平均脉动血流电导率
Fig.8 Average conductivity of pulsating blood flow in different shear stress regions
图9分别显示了脉动血流总体电导率和与定常血流的相对误差。与同一时刻的定常流血液电导率相比,脉动血液电导率在心脏收缩期间(0.05~0.1s)增加了27.6%,其余时刻的增大比例在12%左右。

图9 血液总体电导率和增量百分比
Fig.9 Total electrical conductivity of the blood and the percentage of the increment
图10显示了同一时刻3个区域电导率对整体血液电导率的贡献程度。RG占比最大,在一个心动周期内的占比为44.04%~64.94%,平均占比为49.47%;RM为14.65%~25.87%,平均占比为18.76%;RL为9.20%~40.36%,平均占比为31.79%。
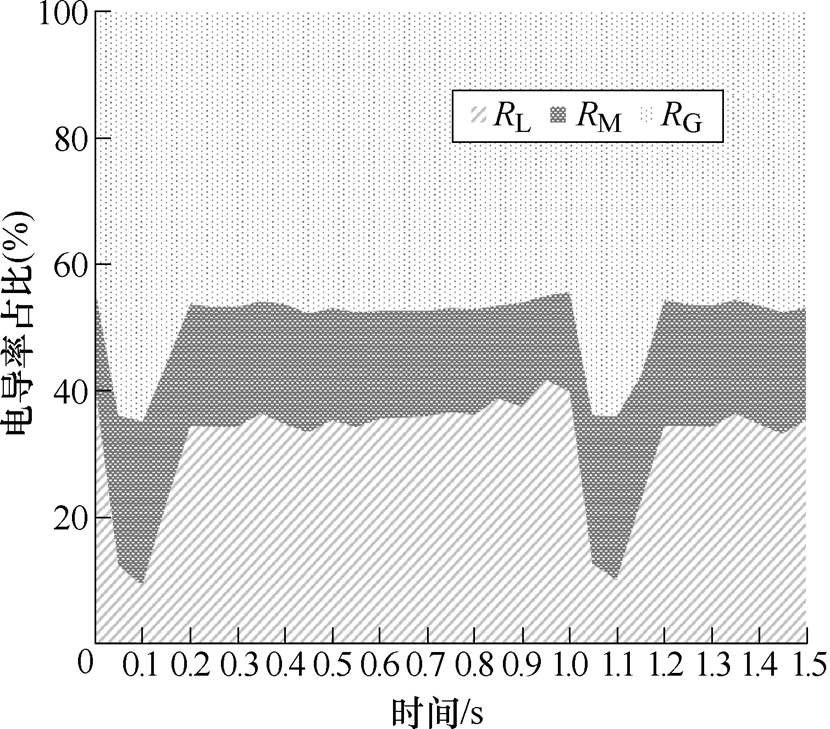
图10 不同剪切应力区域血流电导率占比
Fig.10 Percentage of blood conductivity in different shear stress regions
在其他参数不变的条件下,使动脉壁的杨氏模量E=206GPa,构造四种模型:模型1,刚体血管壁-考虑红细胞变形;模型2,正常血管壁-考虑红细胞变形,即孔隙模型;模型3,刚体血管壁-不考虑红细胞变形;模型4,正常血管壁-不考虑红细胞变形。
四种模型的电导率和模型1、2与模型3、4之间的误差如图11所示。模型1的最大电导率为0.756S/m,比模型2增大了5.6%;模型3的电导率大于模型4,模型3的最大电导率为0.555S/m,比模型4增大了2.2%。结果表明,无论是否考虑红细胞变形,动脉壁的杨氏模量增大都会使血液电导率增大;同理,考虑红细胞变形的模型血液电导率大于不考虑红细胞变形的血液电导率,血液电导率的大小为模型1>模型2>模型>模型4。
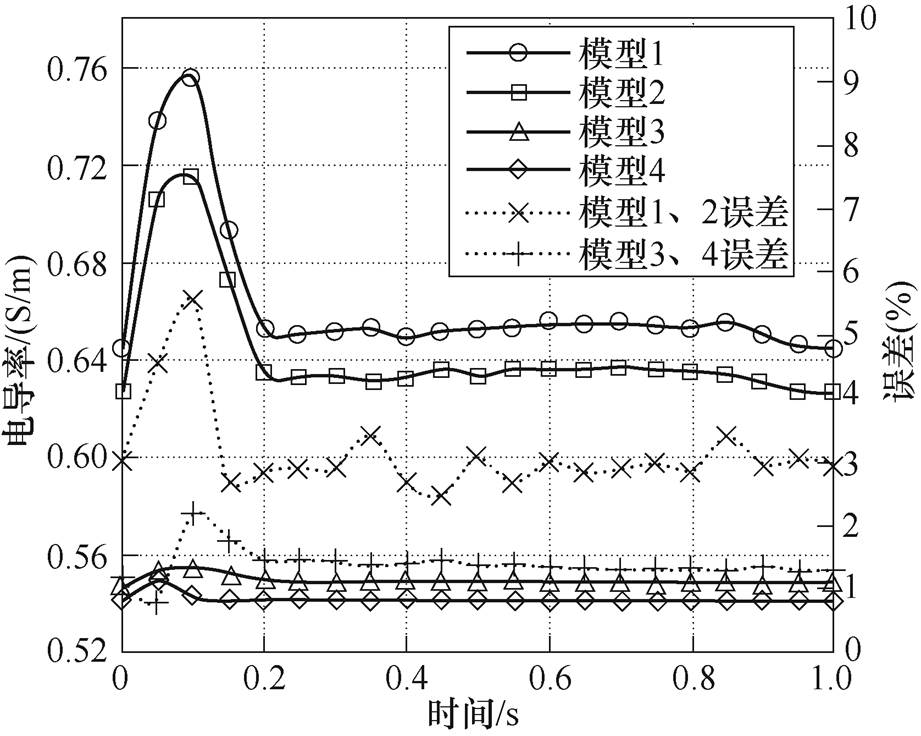
图11 动脉壁力学特性与血液电导率的关系
Fig.11 Relationship between arterial wall structure and blood electrical conductivity
在其他血液理化参数不变的条件下,改变红细胞比容H,使H的范围在0.15~0.85,间隔0.1,利用相同方法计算了不同H下的血流电导率sHi(t),为了便于显示,将电导率进行了尺度变换,变换后的相对电导率为sHI(t),变化公式为
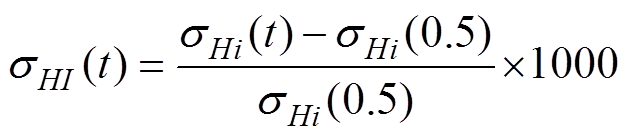 (17)
(17)变换后的相对电导率结果如图12所示。由结果可见,不同H下的血流电导率与健康状态(H=0.45)下的血流电导率趋势一致,幅值都随着心脏收缩期增大,随心脏舒张期稳定变小,整个心动周期内的电导率幅值随H的增大而减小。
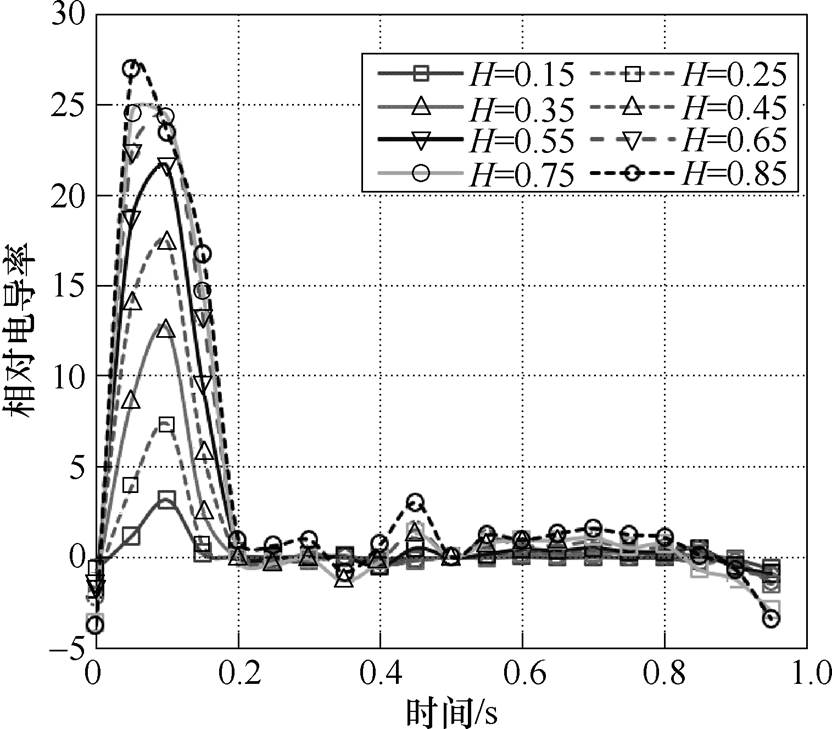
图12 不同红细胞比容的相对血流电导率
Fig.12 Relative blood flow conductivity of different hematocrit
一个心动周期内的平均电导率与红细胞比容H的关系如图13所示,随着H增大,血液平均电导率逐渐减小。
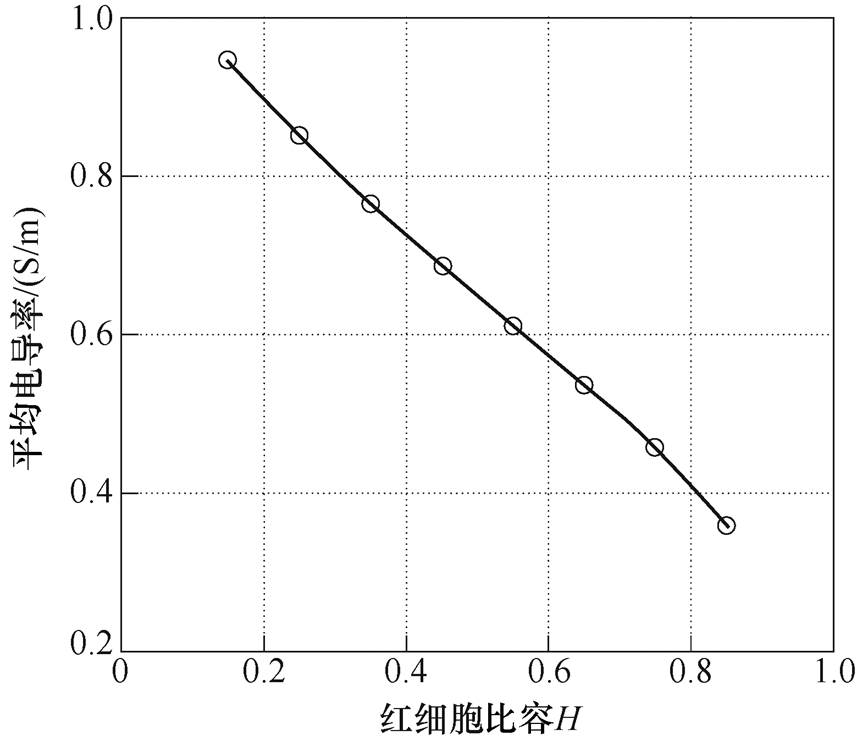
图13 血流平均电导率与红细胞比容关系
Fig.13 Relationship between average conductivity of blood flow and hematocrit
血液平均电导率与H近似呈线性关系,拟合方程为y=-0.814 6x+1.059 2,R2=0.998 3。这是由于H增大使红细胞绝缘孔隙数量增多,绝缘孔隙对电流的阻碍作用增强,血液平均电导率降低。
本文针对脑血流电导率计算问题进行了仿真分析,建立了红细胞绝缘孔隙导电的数值模型并将其应用于大脑动脉Willis环。仿真了Willis环血液内部剪切应力作用下的微观体积电导率,用微观电导率的变化表征了血液流动下的宏观电导率。
仿真结果表明,在一个完整的心动周期内,血液流动速度和血压改变了Willis环动脉壁直径和血液流量,弹性脑血管中的血流电导率变化趋势与血流速一致,高剪切应力区域电导率血流速度正向变化,在总电导率中贡献最大;中剪切应力区域电导率最小,几乎不受血流速度影响;低剪切力区域电导率受血流速度影响最大且与血流速度趋势相反。总体电导率数值随血流速度增大而增大,趋势和心脏泵血时期保持一致,人体血流电导率是三个不同剪切应力区域血液中的绝缘红细胞孔隙受力变形带来的微观电导率变化的总体表现。
根据与离体脉动血流电导率实际值相比较,验证了该绝缘电导率孔隙模型的可靠性。利用该模型仿真了动脉壁结构和红细胞比容对血流电导率的影响。该模型可以灵活地修改各种生理参数,模拟具有不同血流动力学参数、血液理化参数和动脉硬化程度的脑脉动血液并计算其电导率数值,为脑电导率改变的机制研究和脑阻抗精确成像方法提供依据。
参考文献
[1] Pethig R. Dielectric properties of biological materials: biophysical and medical applications[J]. IEEE Transa- ctions on Electrical Insulation, 1984, 19(5): 453-474.
[2] Adler A, Boyle A. Electrical impedance tomography: tissue properties to image measures[J]. IEEE Transa- ctions on Biomedical Engineering, 2017, 64(11): 2494-2504.
[3] Li Xu, Yu Kai, He Bin. Magnetoacoustic tomography with magnetic induction (MAT-MI) for imaging electrical conductivity of biological tissue: a tutorial review[J]. Physics in Medicine & Biology, 2016, 61(18): R249-R270.
[4] Dekdouk B, Ktistis C, Armitage D W, et al. Absolute imaging of low conductivity material distributions using nonlinear reconstruction methods in magnetic induction tomography[J]. Progress in Electromag- netics Research, 2016, 155: 1-18.
[5] 夏慧, 刘国强, 黄欣, 等. 注入电流式磁声成像平面模型的逆问题研究[J]. 电工技术学报, 2017, 32(4): 147-153.
Xia Hui, Liu Guoqiang, Huang Xin, et al. The inverse problem study of plane model based on magneto- acoustic tomography with current injection[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 147-153.
[6] Hoetink A E, Faes T J, Visser K R, et al. On the flow dependency of the electrical conductivity of blood[J]. IEEE Transactions on Biomedical Engineering, 2004, 51(7): 1251-1261.
[7] Gaw R L, Cornish B H, Thomas B J. The electrical impedance of pulsatile blood flowing through rigid tubes: a theoretical investigation[J]. IEEE Transa- ctions on Biomedical Engineering, 2008, 55(2): 721- 727.
[8] Gaw R L. The effect of red blood cell orientation on the electrical impedance of pulsatile blood with implications for impedance cardiography[D]. Brisbane: Queens-land University of Technology, 2010.
[9] Shen Hua, Zhu Yong, Qin Kai-Rong. A theoretical computerized study for the electrical conductivity of arterial pulsatile blood flow by an elastic tube model[J]. Medical Engineering & Physics, 2016, 38(12): 1439-1448.
[10] Shen Hua, Li Siqi, Wang Yu, et al. Effects of the arterial radius and the center-line velocity on the con- ductivity and electrical impedance of pulsatile flow in the human common carotid artery[J]. Medical & Biological Engineering & Computing, 2019, 57(2): 441-451.
[11] Zhbanov A, Yang S. Effects of aggregation on blood sedimentation and conductivity[J]. PLoS One, 2015, 10(6): e0129337.
[12] Cokelet G. Hemorheology and hemodynamics[M]. San Rafael: Morgan & Claypool Publishers, 2011.
[13] Fasano A, Sequeira A. Hemomath: the mathematics of blood[M]. Cham: Springer, 2017.
[14] Brust M, Schaefer C, Doerr R, et al. Rheology of human blood plasma: viscoelastic versus newtonian behavior[J]. Physical Review Letters, 2013, 110(7): 078305.
[15] Grover N, Naaman J, Ben-Sasson S, et al. Electrical sizing of particles in suspensions: i. theory[J]. Bio- physical Journal, 1969, 9(11): 1398-1414.
[16] Sakamoto K, Kanai H. Electrical characteristics of flowing blood[J]. IEEE Transactions on Biomedical Engineering, 1979, 26(12): 686-695.
[17] Donaldson I M. Cerebri anatome: thomas Willis and his circle[J]. The Journal of the Royal College of Physicians of Edinburgh, 2010, 40(3): 277-279.
[18] Iqbal S. A comprehensive study of the anatomical variations of the circle of Willis in adult human brains[J]. Journal of Clinical and Diagnostic Research, 2013, 7(11): 2423-2427.
[19] Tarasów E, Ali A A S, Lewszuk A, et al. Measure- ments of the middle cerebral artery in digital subtraction angiography and MR angiography[J]. Medical Science Monitor, 2007, 13(1): 65-72.
[20] 韩金涛, 乔惠婷, 李选, 等. 应用磁共振血管造影术研究大脑中动脉 M1段形态[J]. 北京大学学报: 医学版, 2015, 47(1): 181-185.
Han Jintao, Qiao Huiting, Li Xuan, et al. Morpho- logical typing of the middle cerebral artery M1 segment by magnetic resonance angiography[J]. Journal of Peking University: Health Sciences, 2015, 47(1): 181-185.
[21] Wright S N, Kochunov P, Mut F, et al. Digital reconstruction and morphometric analysis of human brain arterial vasculature from magnetic resonance angiography[J]. Neuroimage, 2013, 82: 170-181.
[22] Tyfa Z, Obidowski D, Reorowicz P, et al. Numerical simulations of the pulsatile blood flow in the different types of arterial fenestrations: comparable analysis of multiple vascular geometries[J]. Bio- cybernetics and Biomedical Engineering, 2018, 38(2): 228-242.
[23] Lorthois S, Cassot F, Lauwers F. Simulation study of brain blood flow regulation by intra-cortical arterioles in an anatomically accurate large human vascular network. part II: flow variations induced by global or localized modifications of arteriolar diameters[J]. Neuroimage, 2011, 54(4): 2840-2853.
[24] Zarrinkoob L, Ambarki K, Wåhlin A, et al. Blood flow distribution in cerebral arteries[J]. Journal of Cerebral Blood Flow & Metabolism, 2015, 35(4): 648-654.
[25] Gaw R L, Cornish B H, Thomas B J. The electrical impedance of pulsatile blood flowing through rigid tubes: a theoretical investigation[J]. IEEE Transa- ctions on Biomedical Engineering, 2008, 55(2 Pt 1): 721-727.
[26] Akhtar R, Sherratt M J, Cruickshank J K, et al. Characterizing the elastic properties of tissues[J]. Materials Today, 2011, 14(3): 96-105.
[27] 王小飞, 代颖, 罗建. 基于流固耦合的车用永磁同步电机水道设计与温度场分析[J]. 电工技术学报, 2019, 34(增刊1): 22-29.
Wang Xiaofei, Dai Ying, Luo Jian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29.
[28] 朱高嘉, 朱英浩, 朱建国, 等. 基于有限公式法和流固耦合的永磁牵引电动机冷却系统设计与分析[J]. 电工技术学报, 2017, 32(5): 70-77.
Zhu Gaojia, Zhu Yinghao, Zhu Jianguo, et al. Thermal analysis and cooling system design of a permanent magnet traction motor using computational fluid dynamics and cell method[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 70-77.
[29] Trakic A, Akhand M, Wang H, et al. Computational modelling of blood-flow-induced changes in blood electrical conductivity and its contribution to the impedance cardiogram[J]. Physiological Measurement, 2010, 31(1): 13-33.
Simulation on Pore Conductivity Model of Cerebral Pulsating Blood Flow Conductivity
Abstract Cerebral blood conductivity is an important parameter for brain impedance imaging and brain disease assessment. In order to study the change mechanism of brain blood pulsating conductivity, a model of erythrocyte insulation pore conductivity was established based on Maxwell- Fricke principle. Using hemodynamic parameters as reference indicators, the numerical relationship between blood flow conductivity and geometric parameters of erythrocyte insulation pores was analyzed. Then, a high-resolution model of circle of Willis with porous conductive structure was constructed, the coupled nonlinear differential equations were used to calculate the temporal and spatial distribution of cerebral artery hemodynamic parameters, and the equivalent volume conductivity of non-uniform conductivity blood was simulated. Compared with the steady blood flow model without considering the pore orientation, the peak conductivity of the pore conductivity model increases by 27.6% in one cardiac cycle and 12% at the rest of the time, which is closely related to the heart pumping period. The simulation results are in good agreement with the real pulsating blood conductivity, which proves that the model proposed in this paper can accurately predict the in vivo blood conductivity under different hemorheological conditions.
keywords:Electrical conductivity, pulsating blood flow, pore conductivity model, cerebral artery model
中图分类号:TM930
DOI: 10.19595/j.cnki.1000-6753.tces.201253
国家自然科学基金(52077143,51377109)和辽宁省自然科学基金计划(2019-ZD-0204)资助项目。
收稿日期2020-09-20
改稿日期 2020-10-07
丁晓迪 女,1982年生,博士研究生,讲师,研究方向为生物电磁成像。E-mail: bczfy12@126.com
柯 丽 女,1977年生,教授,博士生导师,研究方向为生物电磁成像与智能医疗。E-mail: keli@sut.edu.cn(通信作者)
(编辑 崔文静)