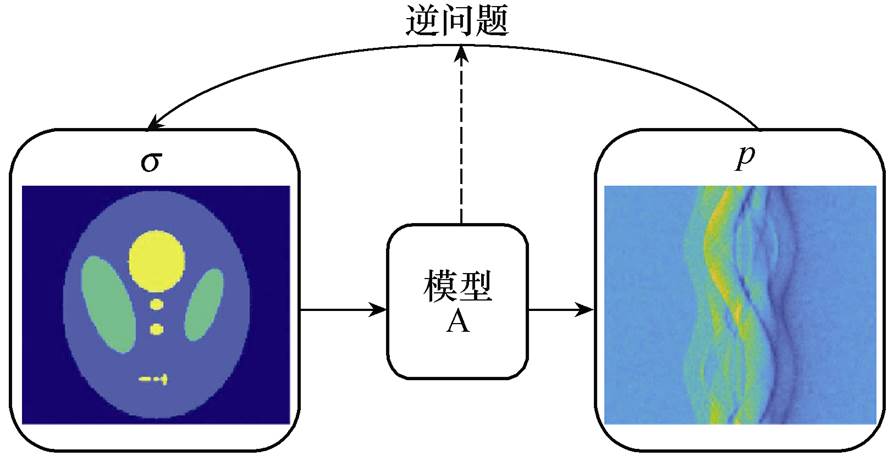
图1 磁声成像系统模型示意图
Fig.1 The system model of MAT
摘要 磁声成像技术是一种利用电磁场及超声场耦合成像的技术，能以超声分辨率来显示生物组织电特性分布参数。为具体分析一些检测条件对磁声成像系统重建的影响，获取高分辨率电导率图像，对磁声成像系统矩阵特征值差异性进行仿真研究。从磁声成像声源产生原理出发，分析磁声声源的特性，并分别针对不同声换能器个数、不同磁声信号接收采样角度及不同带宽换能器的条件，建立磁声成像系统矩阵模型；以矩阵模型为基础，分别计算系统矩阵的特征值，利用截断奇异值方法对各条件下获取的磁声信号进行图像重建。结果表明，换能器个数及换能器带宽特性对电导率信息的重建影响很大，而接收角度对接收电导率信息影响不大，但接收角度会影响求解域，从而造成磁声信号接收不全，重建的电导率图像失真。本研究将对磁声成像实验设计和后续应用提供研究基础。
关键词：磁声成像 逆问题 特征值 系统矩阵 电导率分布
生物组织电特性分布与肿瘤等疾病的发生发展息息相关[1]，如果能对生物组织电特性进行无损成像，将有利于对肿瘤进行早期诊断，为早期治疗创造条件。
磁声成像（Magneto Acoustic Tomography, MAT）技术是一种利用电磁场及超声场的耦合成像技术，能以超声分辨率来显示电特性分布参数[2]。其基本原理是对放置于静磁场中的待成像目标施加短脉冲交变电磁激励，使待成像目标内产生感应电流，感应电流与静磁场相互作用会产生洛仑兹力，形成超声声源，并向外传播超声。通过放置在目标成像体周围的若干个换能器测量超声信号，得到的一组超声信号包含了生物组织电特性的信息，通过重建算法可以重建待成像目标的电特性图像。
近年来，为了提高磁声成像分辨率和磁声信号的信噪比，学者们在磁声成像算法与磁声成像系统的提高与改进上都进行了深入的研究。在成像算法方面，时间反转成像算法[3]、声偶极子源理论方 法[4-5]、矢量声源重建算法[6-8]及基于编码激励的磁声声源重建算法[9-10]相继被提出，为了更加贴近真实模型，提高成像质量，针对生物组织内声速不均匀问题，提出了基于声速不均匀介质的磁声重建算法[11]；为解决理想声换能器接收模型存在的问题，提出了基于真实声换能器的磁感应磁声图像重建算法[12]。在成像系统及实验方法方面，为了提高磁声成像系统信噪比，改善成像质量，中科院电工所对感应式脉冲磁场磁通密度分布及变化规律进行了研究[13]。明尼苏达大学的研究人员分别采用磁共振成像的强磁场和高频功率脉冲源进行了高分辨率的磁声成像研究，结果证明，在7T的强磁场下，可以清楚地分辨电导率为0.65S/m的肌肉组织及0.01S/m的脂肪组织[14]；在1.5MHz高频磁场激励条件下，相比500kHz激励条件电导率边界成像分辨率有了显著提高[15]。此外，为了提高磁声信号信噪比，研究人员还采用了磁纳米粒子作为信号及影像增强剂，设计了相关仿真实验，并分别在凝胶仿体及生物组织中获取了由磁纳米粒子产生的磁声增强信号[16-18]。
目前，对于磁声成像方法的研究，已经逐步以提高磁声信号信噪比，获取高分辨率电导率分布成像为主要目标。随着实验仿体的电导率逐渐降低并接近生物组织，对磁声成像系统的信噪比要求将进一步提高。为具体分析一些检测条件对磁声成像系统的重建影响，进一步提高磁声信号包含的电导率信息的利用率，本研究将基于矩阵特征值分析方法，对各检测条件下的磁声成像系统矩阵的特征值进行对比，从而分析不同检测条件对磁声成像的影响，探索如何最大限度地利用磁声信号提供的电导率信息，实现电导率图像重建。
磁声成像正问题是从待成像组织的电阻抗分布到检测到的超声信号的转换过程，逆问题则是由采集到的超声信号重建待成像组织内部电导率的问题，其系统模型如图1所示。从图1可以看出，系统模型A包含从电导率分布到产生超声信号过程中的各种物理耦合效应、超声换能器特性及磁感应磁声实验系统的设置等参数，是实现信号生成及图像重建的联系纽带。为了研究磁声成像系统的转换过程，建立系统矩阵模型A并对其特性进行分析是电导率参数重建的重要步骤，也是提高超声信号信息提取，完善磁声成像检测方法的重要步骤。
图1 磁声成像系统模型示意图
Fig.1 The system model of MAT
为构建磁声声源矩阵，首先需要从磁声声源项开始研究，由磁声耦合理论，磁场、感应涡流及声压是时间和空间的函数，根据生物组织中电磁场声场的机电耦合机制[19]，声压波动方程可简化为
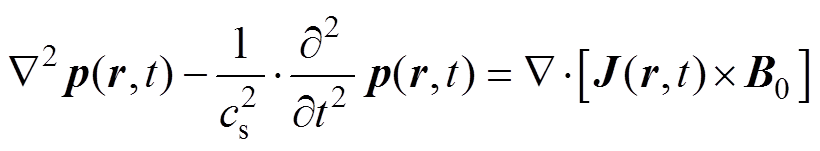（1）式中，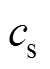
为超声信号在组织中传播的速度；
为声压场的时空分布；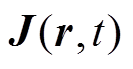
为组织内产生的电流密度分布；
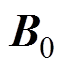为静磁场强度；
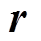为无界空间中的任一点；t为时间；
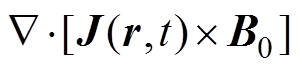为声振源。根据矢量分解公式，该声振源可以分解为两部分，有
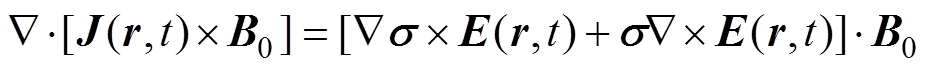（2）
式中，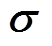
为电导率分布；
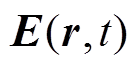为感应电场强度。
进一步地，将第一项声源项离散化可得
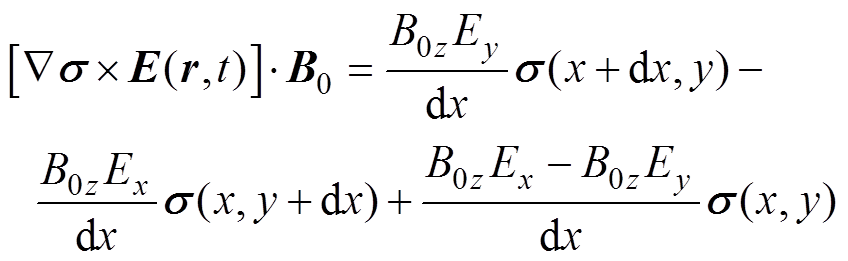（3）其中
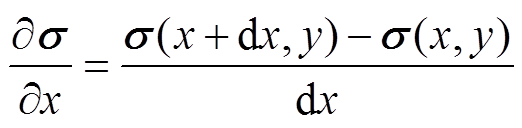
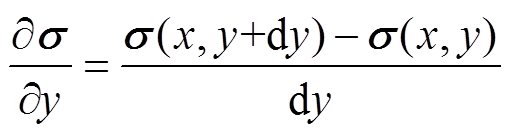
为便于计算和建模，令dx=dy。经过上述转换后，声源项与固定点处电导率及其周边点处电导率之间建立了关系。
对于声源转换为声压的过程，可由自由空间的格林公式方法求解，由此，对于一个具备不同电导率的组织，上述公式证明电导率与电导率的梯度经过一个系统矩阵可以得到相应的超声信号，式（3）与格林公式求解声压过程最终可以抽象为一个矩阵方程的形式，有
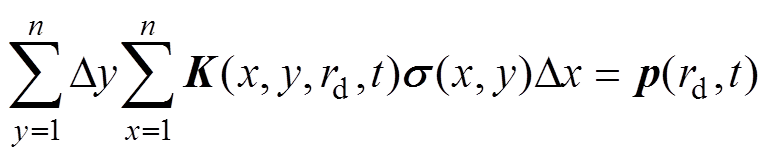（4）式中，
为离散系统矩阵核函数。
对于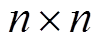
的电导率成像区域，检测换能器个数为
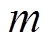，每个换能器的采样点数为
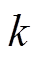。抽象为矩阵形式，有
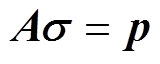（5）式中，A为磁声成像系统矩阵，其矩阵大小为mk×n2；
为待成像区域的电导率分布；p为检测超声信号。
为分析上述矩阵方程，采用特征值分解方法求解矩阵的特征值分布，特征值分解公式为
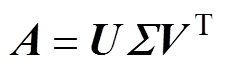（6）式中，U和V为正交矩阵；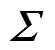
为对角矩阵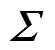，对角线元素为磁声成像系统矩阵的特征值。这些特征值反映了电导率分布与超声声压的线性关系，可以通过这些特征值的分布对系统的抗噪性及稳定性进行初步的评估，从而选择最优参数进行图像重建。
根据特征值方法求得的矩阵定义，可求得矩阵A的逆矩阵为
（7）对于上述矩阵方程，本文采用截断奇异值分解方法（Truncated Singular Value Decomposition, TSVD）[20]进行求解，即将矩阵A分解成特征值与相应的特征向量，其重建电导率分布为
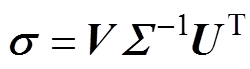p （8）
由式（8）可得，分析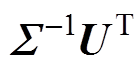
p与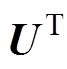
p可以得到特征值的影响及测量声压数据的影响，从而选取用于图像重建的特征值个数。
为实现上述算法，计算不同条件下磁声成像的系统矩阵特征值分布，建立一个模拟肿瘤组织的双椭球原始电导率分布模型，模型内部采用不同大小的椭球，并设定不同的电导率进行区分，外部椭球结构的电导率设定为0.1S/m，内部包括两个电导率分别为0.25S/m和0.35S/m的小椭球结构，该原始电导率分布仿体模型如图2所示。采用稳恒磁场的磁感应强度B0=1T，为保证脉冲激励的均匀性，椭球内部产生的电流密度分布采用赫姆霍兹线圈外部激励磁场产生，该线圈注入电流密度设定为1A/m2，由于仿真过程中激励线圈电流密度幅值与产生感应涡流密度幅值是线性关系，故为了后续计算统一性，将系统矩阵计算中感应电流密度分布进行了归一化操作。
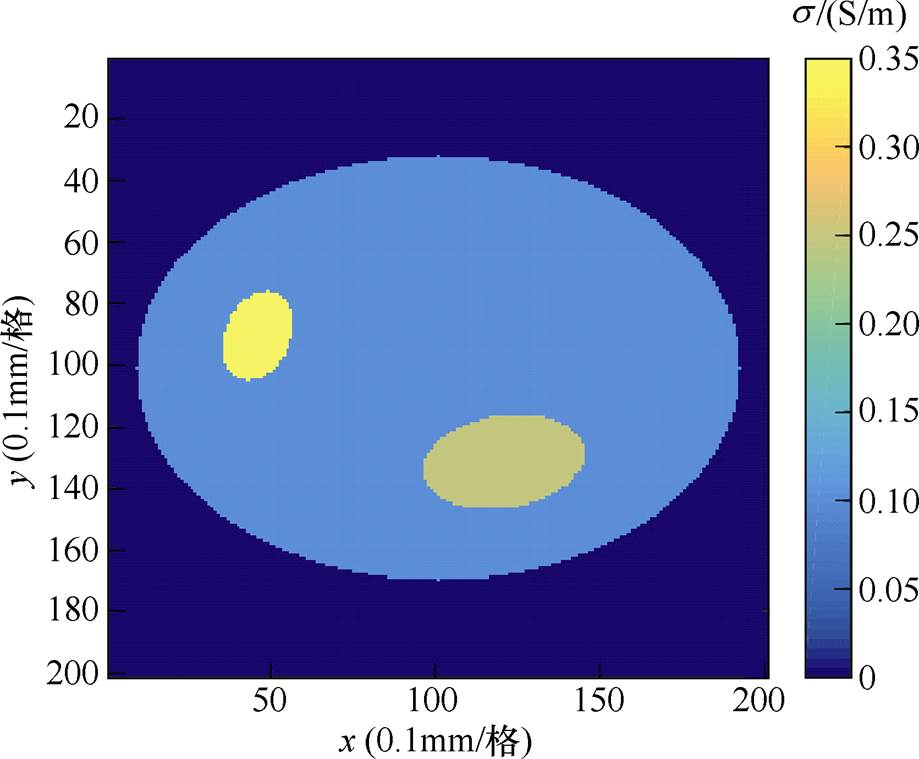
图2 原始电导率分布仿体模型
Fig.2 The phantom of original conductivity distribution
按照式（3），需将求解域离散化，首先假设求解域为一个50mm×50mm的二维求解空间，将该求解空间规则分为501×501的正方形网格，并将待成像模型放置于中心区域201×201的正方体网格中便于计算求解。通过式（4）和式（5）进行系统矩阵的计算，对求解域中的各个磁声声源分别进行有限差分计算并将结果存入Matlab。为分析比较不同换能器接收条件对磁声系统矩阵的影响，进行了三种不同类型的实验设计与比较，具体设置条件如下所示：
（1）不同换能器个数特征值分布比较及重建。设定采集换能器的个数分别为300、200、100及60，这些换能器都均匀分布在360°的圆周上，扫描半径为45mm，每个换能器采样501个点，采样频率为8.333MHz，采用换能器模型为V303，中心频率为1MHz。
（2）不同采样角度特征值分布比较及重建。设定采集换能器的个数为200，换能器都分布在360°（整圆采集）、180°（半圆采集）、120°、60°（弧面采集）的圆周或弧面上，扫描半径同为45mm，每个换能器采样501个点，采样频率为8.333MHz，采用换能器模型为V303，其中心频率为1MHz。
（3）宽频带换能器及窄带换能器特征值分布比较及重建。设定采集换能器为200个，换能器均匀分布在360°的圆周上，扫描半径为45mm，每个换能器采样501个点，采样频率为8.333MHz，分别采用换能器模型为V303及自定义宽带换能器，其中V303为窄带换能器，中心频率为1MHz；自定义宽带换能器中心频率为2.25MHz，截止频率为3.75MHz，且可接收低频及直流声压信号。
利用上述条件可以求解系统矩阵A及其特征值分布，并比较不同条件对磁声信号接收、信息提取及图像重建抗噪性的影响。
为了分析磁声信号噪声的影响，首先对比了信号接收分别在20dB信噪比及40dB信噪比条件下的影响，对比结果通过Picard图显示，如图3所示。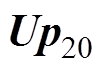
及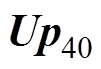
分别表示信噪比在20dB及40dB的条件下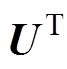p的分布，由于
为单位化的向量，故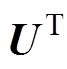p分布给出了接收磁声信号的幅值，随着噪声级别的 增强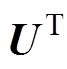，p的数据量级会相应增高。
及
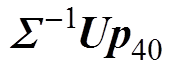则是在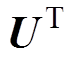
p的基础上，加入了特征值分布的影响，由于V也为单位化的向量，对重建电导率分布量级没有影响，则由式（8）可知，及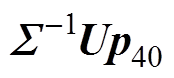
分别表示重建结果的数据量级，该量级分布表示特征值数量对噪声量级的放大作用，同时也可以作为重建算法中特征值个数的选取依据。
从图3可以看出，不同级别噪声的磁声信号的数据量级有很大的差异，20dB信噪比的磁声信号数据量级要远远低于40dB信噪比的磁声信号。因而造成在重建过程中，20dB信噪比的磁声信号可利用的能反映图像重建细节的特征值会变少，同时特征值逆矩阵的幅值变大，噪声信号的影响将逐步被放大，导致重建图像质量下降。目前磁声实验研究得到的磁声信号信噪比极低，无法达到20dB，为了后续不同条件下图像重建算法的验证比较，故而统一选择20dB信噪比进行后续算法比较。
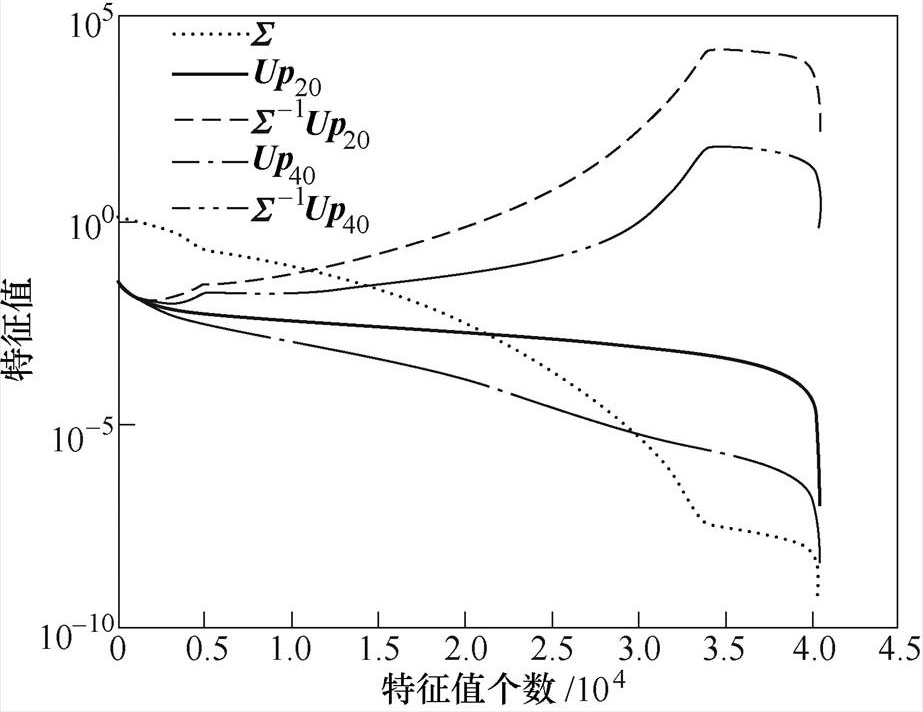
图3 含不同级别噪声磁声信号Picard图
Fig.3 The Picard plot of magneto-acoustic signals with different noise level
分别采用300、200、100及60个声换能器均匀分布在360°的圆周上采集磁声信号，图4给出四种不同磁声系统矩阵A的特征值曲线，其中，N300、N200、N100及N60分别为采用300、200、100及60个声换能器磁声系统的特征值曲线，可以看出，随着声换能器个数的减少，系统矩阵A的特征值下降趋势变得更快，也就是说，在重建过程中，换能器个数减少不仅意味着有用的电导率信息丢失，也意味着其系统总体抗噪声性能的下降。因此声换能器的个数极大地影响了磁声成像系统重建图像分 辨率。
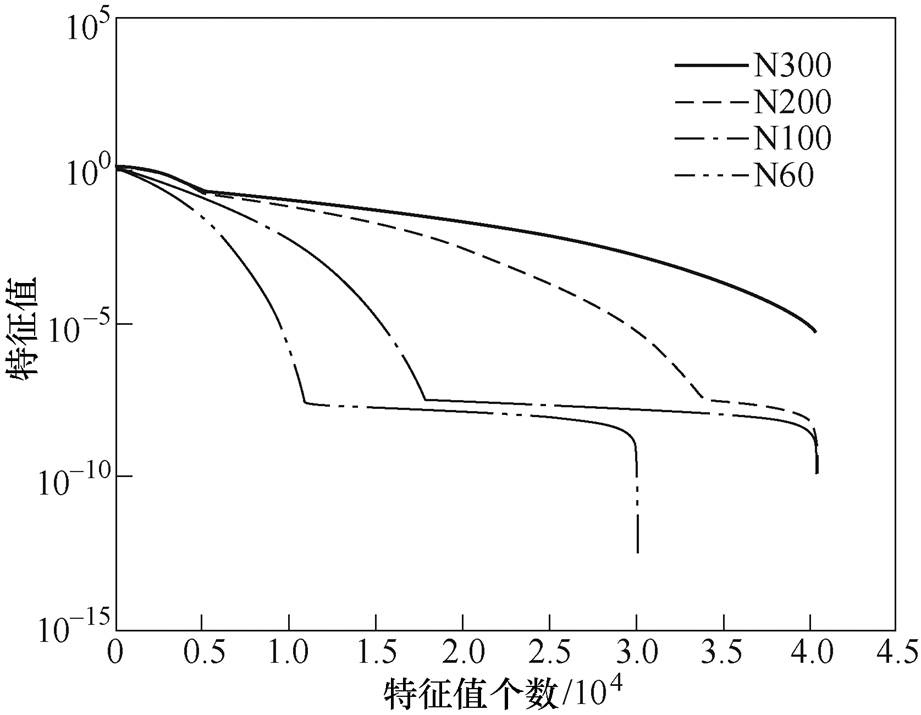
图4 不同换能器个数系统矩阵特征值分布
Fig.4 The eigenvalue curves of system matrix with different transducer numbers
由图4可知，不同特征值条件下可以选取相应数量的特征值进行重建，根据磁声信号的信噪比为20dB，可确定分别采用5 000、7 500、13 000、18 000个特征值进行电导率分布重建。
不同换能器个数重建电导率分布结果如图5所示，给出了使用300、200、100及60个换能器的重建结果，可以得出，使用系统矩阵的特征值越多，重建结果越接近真实电导率分布，由于受到噪声的影响，特征值越小，其受噪声的影响越大。200个换能器与300个换能器重建结果差异相差不大，这是由于后续的特征值越来越小，与系统中噪声级别相当，后续特征值代表了磁声重建图像中的细节部分（或高频成分），受噪声级别影响很大。由上述结果得出，使用系统矩阵方法可以根据实验条件最大限度地利用磁声信号所提供的信息，使重建电导率分布结果最大限度地接近原始电导率分布。
图5 不同换能器个数重建电导率分布结果
Fig.5 Distribution of reconstructive conductivity results with different transducer numbers
采用皮尔逊相关系数方法对重建电导率图像和原始电导率图像进行比较，定义为
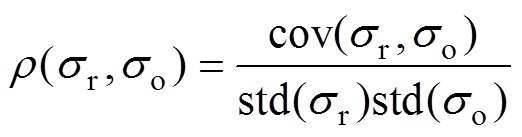（9）式中，cov(x, y)为协方差矩阵；std(x)为标准差；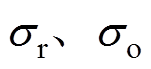
分别为重建图像电导率与原始电导率分布。不同换能器个数皮尔逊相关系数比较见表1，皮尔逊相关系数越接近1，证明相关性越强，也就是重建电导率图像更接近真实电导率分布。
从表1结果可以看出，随着换能器个数的增加，皮尔逊相关系数增大，重建图像更加接近原始图像。但从增加幅度来看，增加换能器个数不能显著提高皮尔逊相关系数，实验中应权衡检测成本、时间和成像质量。且由于均匀电导率分布低频与直流成分较多，重建受声换能器接收特性影响很大，皮尔逊相关系数均低于0.5。
表1 不同换能器个数重建皮尔逊相关系数
Tab.1 The Pearson correlation coefficients with different transducer numbers
换能器个数皮尔逊相关系数 3000.468 2 2000.424 4 1000.375 8 600.229 6
图6给出了不同采样角度系统矩阵特征值分布，从图中可以看出，不同换能器个数、不同角度采样（同为200个换能器），其系统矩阵特征值仅有微弱降低，总体差异不大，在相同换能器个数条件下，可认为磁声成像系统具有相似的重建性能。但是，这并不代表用少量角度磁声信号可以完整重建出电导率图像，由于换能器特性，少量采样角度并不能获取完整整体电导率分布的信息，仅有部分信息会被采集和重建，这点可以通过重建结果图7显示。
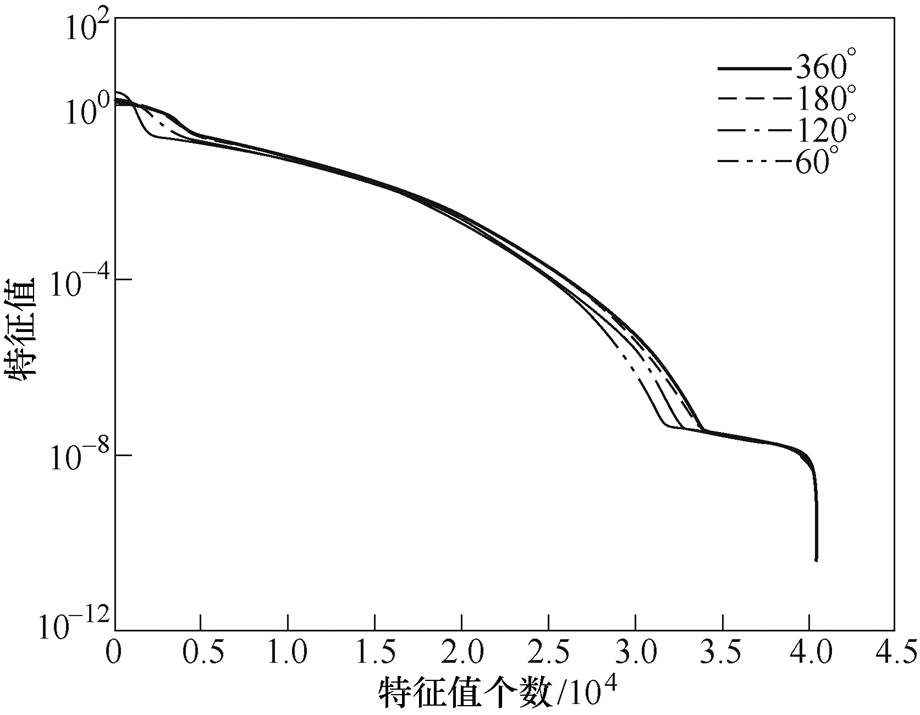
图6 不同采样角度系统矩阵特征值分布
Fig.6 The eigenvalue curves of system matrix with different acquisition angles
图7给出了使用11 000个特征值360°、180°、120°及60°采样角度下（同为200个窄带换能器）的重建结果。可以看出，随着采样角度的增加，电导率信息逐渐被完整覆盖；在不考虑衰减和反射的情况下，180°与360°采集磁声信号所包含的电导率分布信息基本一致。
不同采样角度重建图像的皮尔逊相关系数比较见表2，可以看出，采样角度为360°与180°情况下皮尔逊相关系数很接近，但在120°与60°情况下有明显的下降，说明在120°和60°情况下重建图像存在明显失真。
图7 不同采样角度重建电导率分布结果
Fig.7 Distribution of reconstructive conductivity results with different acquisition angles
表2 不同采样角度重建皮尔逊相关系数
Tab.2 The Pearson correlation coefficients with different acquisition angles
采样角度/(°)皮尔逊相关系数 3600.413 0 1800.401 6 1200.187 9 600.114 8
为比较换能器特性对磁声成像系统矩阵的影响，分别对磁声成像中常用的1MHz V303换能器及中心频率为2.25MHz、截止频率为3.75MHz的宽带换能器分别进行系统矩阵求解计算，磁声系统矩阵特征值比较如图8所示。
从图8可以看出，宽带换能器具有更好的抗噪性能及图像高分辨率重建能力，这是由于宽带换能器对低频电导率信息的接收能力要强于V303，由于V303的换能器特性，磁声信号部分低频电导率分布信息无法被接收，对磁声成像系统造成了很大影响。
在使用不同带宽的换能器条件下，同时采用13 000个特征值的重建结果对比如图9所示。可以明显看出，宽带换能器的重建结果明显优于1MHz 的V303，这也证明了宽带换能器接收的磁声信号包含更多电导率信息，其整体的抗噪性更强。
图8 不同带宽换能器矩阵特征值分布
Fig.8 The eigenvalue curves of system matrix with different bandwidth transducers
图9 不同带宽换能器重建电导率分布结果
Fig.9 Distribution of reconstructive conductivity results with different different bandwidth transducers
表3给出了不同带宽换能器重建电导率分布图像的皮尔逊相关系数的比较，从结果中可以得出，虽然有噪声的影响，但使用宽带换能器进行磁声信号接收及图像重建的相关系数明显高于V303，说明电导率图像重建的质量主要取决于采集的低频分布信号。
表3 不同带宽换能器重建皮尔逊相关系数
Tab.3 The Pearson correlation coefficients with different bandwidcccth transducers
不同带宽换能器皮尔逊相关系数 V3030.424 4 宽带换能器0.895 3
本研究对不同条件下磁声成像系统矩阵的特征值开展研究，并采用特征值分解方法对各种不同条件下的电导率图像重建进行分析比较。仿真结果证明，换能器个数及换能器带宽特性对电导率信息的重建影响很大，而接收角度对接收电导率信息影响不大，但接收角度会影响求解域，从而造成磁声信号接收不全，重建的电导率图像失真。仿真结果也证明了该方法可在一定噪声级别下最大限度地提取磁声信号中的电导率信息，重建电导率分布图像。其中，大特征值可用于电导率边界分布，小特征值受噪声影响较大，可用于重建电导率内部分布及细节。本研究对磁声成像实验设计和后续应用提供研究基础。
参考文献
[1] 张帅, 侯琬姣, 张雪莹, 等. 基于真实乳腺模型的感应式磁声成像正问题[J]. 电工技术学报, 2016, 31(24): 126-133.
Zhang Shuai, Hou Wanjiao, Zhang Xueying, et al. Forward problem in magnetoacoustic tomography with magnetic induction based on real model of breast[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 126-133.
[2] Xu Yuan, He Bin. Magnetoacoustic tomography with magnetic induction (MAT-MI)[J]. Physics in Medi- cine and Biology, 2005, 50(21): 5175-5187.
[3] Li Xu, Xu Yuan, He Bin. Magnetoacoustic tomo- graphy with magnetic induction for imaging electrical impedance of biological tissue[J]. Journal of Applied Physics, 2006, 99(6): 066112.
[4] Sun Xiaodong, Zhang Feng, Ma Qingyu, et al. Acoustic dipole radiation based conductivity image reconstruction for magnetoacoustic tomography with magnetic induction[J]. Applied Physics Letters, 2012, 100(2): 024105.
[5] Ma Qingyu, He Bin. Magnetoacoustic tomography with magnetic induction: a rigorous theory[J]. IEEE Transactions on Biomedical Engineering, 2008, 55(2): 813-816.
[6] Xia Rongmin, Li Xu, He Bin. Reconstruction of vectorial acoustic sources in time-domain tomo- graphy[J]. IEEE Transactions on Medical Imaging, 2009, 28(5): 669-675.
[7] Xia Rongmin, Li Xu, He Bin. Comparison study of three different image reconstruction algorithms for MAT-MI[J]. IEEE Transactions on Biomedical Engineering, 2010, 57(3): 708-713.
[8] Hou Wenjiao, Zhang Shuai, Wang Zhuo, et al. The study of magnetoacoustic tomography with magnetic induction through vector source reconstruction based on real model of breast[C]//Proceedings of the 2016 Asia-Pacific International Symposium on Electro- magnetic Compatibility (APEMC), Shenzhen, 2016: 862-864.
[9] 张顺起, 马任, 王贺, 等. M序列编码激励磁声信号处理方法研究[J]. 医疗卫生装备, 2018, 39(1): 52-57.
Zhang Shunqi, Ma Ren, Wang He, et al. Research on M-sequence coded excitation method for mag- netoacoustic imaging[J]. Chinese Medical Equipment Journal, 2018, 39(1): 52-57.
[10] Zhang Shunqi, Ma Ren, Yin Tao, et al. M-sequence- coded excitation for magneto-acoustic imaging[J]. Medical & Biological Engineering & Computing, 2019, 57(1): 1059-1067.
[11] Zhang Wei, Ma Ren, Zhang Shunqi, et al. Image reconstruction in magnetoacoustic tomography with magnetic induction (MAT-MI) with variable sound speeds[J]. IEEE Transactions on Biomedical Engin- eering, 2016, 63(12): 2585-2594.
[12] Ma Ren, Zhou Xiaoqing, Zhang Shunqi, et al. A 3D reconstruction algorithm for magneto-acoustic tomography with magnetic induction based on ultrasound transducer characteristics[J]. Physics in Medicine and Biology, 2016, 61(24): 8762-8778.
[13] 黄欣, 刘国强, 夏慧, 等. 感应式磁声成像的脉冲磁场研究[J]. 电工技术学报, 2013, 28(2): 67-72.
Huang Xin, Liu Guoqiang, Xia Hui, et al. Study of pulsed magnetic field used in magnetioacoustic tomography with magnetic induction[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 67-72.
[14] Mariappan L, Hu Gang, He Bin. Magnetoacoustic tomography with magnetic induction for high- resolution bioimepedance imaging through vector source reconstruction under the static field of MRI magnet[J]. American Association of Physicists in Medicine, 2014, 41(1): 022902.
[15] Yu Kai, Shao Qi, Ashkenazi S, et al. In vivo electrical conductivity contrast imaging in a mouse model of cancer using high-frequency magneto- acoustic tomography with magnetic induction (hfMAT-MI)[J]. IEEE Transactions on Medical Imaging, 2016, 35(10): 2301-2311.
[16] Hu Gang, He Bin. Magnetoacoustic imaging of magnetic iron oxide nanoparticles embedded in biological tissues with microsecond magnetic stimu- lation[J]. Applied Physics Letters, 2012, 100(1): 013704.
[17] Yan Xiaoheng, Zhang Ying, Liu Guoqiang. Simu- lation research on effect of magnetic nanoparticles on physical process of magneto-acoustic tomography with magnetic induction[J]. Chinese Physics B, 2018, 27(10): 104302.
[18] 张帅, 李子秀, 张雪莹, 等. 基于时间反演的磁动力超声成像仿真与实验[J]. 电工技术学报, 2019, 34(16): 3303-3310.
Zhang Shuai, Li Zixiu, Zhang Xueying, et al. The simulation and experiment of magneto-motive ultra- sound imaging based on time reversal method[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3303-3310.
[19] Roth B J. The role of magnetic forces in biology and medicine[J]. Experimental Biology and Medicine, 2011, 236(2): 132-137.
[20] 周凯, 黄永禄, 谢敏, 等. 短时奇异值分解用于局放信号混合噪声抑制[J]. 电工技术学报, 2019, 34(11): 2435-2443.
Zhou Kai, Huang Yonglu, Xie Min, et al. Mixed noises suppression of partial discharge signal emplo- ying short-time singular value decomposition[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2435-2443.
Simulation Study on the Eigenvalue Difference of the System Matrix in Magneto-Acoustic Tomography
Abstract Magneto-acoustic tomography (MAT) is an imaging technology using the coupling of electromagnetic field and ultrasonic field, which can display the electrical characteristics distribution of biological tissues with ultrasonic resolution. In order to analyze the influence of some detection conditions on the reconstruction of MAT and obtain a high-resolution conductivity image, the eigenvalue difference of MAT is simulated. Based on the principle of acoustic source, the system matrix of MAT is established for different number of acoustic transducers, different acquisition angles and two different bandwidth transducers. Based on the matrix model, the eigenvalues of system matrix are calculated, and the TSVD method is used to reconstruct the conductivity image. The results show that the number of transducers and the bandwidth characteristics of transducers have great influence on the reconstruction of conductivity information, while the acquisition angle has little effect on the conductivity information. However, the acquisition angle will affect the field of image, resulting in incomplete reception of MAT signal and distortion of reconstructed conductivity image. This paper will provide a reference for the experiment design and subsequent applications of MAT.
keywords：Magnetoacoustic tomography, inverse problem, eigenvalues, system matrix, distri- bution of electrical conductivity
中图分类号：TM12
DOI: 10.19595/j.cnki.1000-6753.tces.201266
国家自然科学基金（61701545, 81772004, 81772003, 81927806）、天津市自然科学基金（19JCQNJC12900）和中国医学科学院医学与健康科技创新工程协同创新团队（2017-I2M-3-020）资助项目。
收稿日期 2020-09-21
改稿日期 2020-09-30
马 任 男，1985年生，助理研究员，研究方向为多物理场耦合成像算法。E-mail: likesaber@gmail.com
刘志朋 女，1967年生，研究员，博士生导师，研究方向为磁声耦合效应组织电特性成像方法。E-mail: lzpeng67@163.com（通信作者）
（编辑 崔文静）