0 引言
随着智能电网建设的持续推进,储能技术在电力系统中的应用规模日益增大,是可再生能源发电系统的重要组成部分[1-2]。其中,锂离子电池是应用最广泛的储能电池。锂离子动力电池在电动汽车领域的大规模应用大大促进了产品的快速升级换代,拉动了其在电力储能领域的应用[3]。在削峰填谷典型应用场景中,锂离子电池的工作温度基本可以被控制在适宜的范围内,倍率变化不大。因此,使用区间对电池寿命的影响就变得十分突出,不合理的区间选择容易导致利用率低或滥用加速衰退等情况。虽然电池荷电状态(State of Charge, SOC)的可用范围是 0~100%,但实际中往往仅使用部分SOC区间,很少经历满充-满放过程。储能用锂离子电池的运行工况比车用锂离子电池更加简单,同时考虑到安全裕量和高端 SOC区间段对衰退的影响,锂离子电池的实际应用区间通常限制在一定的范围之内。
现阶段,国内外学者对于不同材料体系的锂离子电池进行了分区间循环寿命的研究。平均SOC和区间宽度或放电深度(Depth of Discharge, DOD)通常用来描述SOC区间对电池衰退的影响[4-8]。文献[4]通过对石墨/钴酸锂电池进行不同 SOC区间和放电倍率下的循环测试,量化了部分充放电区间对电池容量衰退的影响。研究发现,对于前500次等效循环,平均SOC对电池衰退起主导作用,测试后期(600~800次等效循环)SOC区间宽度对容量衰退的影响更大。文献[5]系统地对比了五个20%SOC分区间和全区间循环下容量衰减和阻抗增加情况,并利用容量增量法提取量化锂离子电池不同衰退机理的特征参数,分析各区间下电池的老化原因。文献[6]发现使用高端和低端 SOC区间会包含负极材料的电压平台之间的变换过程,对Li(NiMnCo)O2电池寿命造成较大影响,而在50%SOC附近循环的电池衰退最慢。与以上研究结果相对应的是,文献[4]中指出区间平均SOC越高,SOC区间宽度越大,电池老化越快。另一些研究者则认为SOC区间宽度对锂离子电池的性能衰退没有影响[9-10]。可以看出,以上文献研究结果中存在较多的分歧,究其原因主要是所研究的锂离子电池的材料体系不同,同时测试条件也存在明显差异。
为了量化不同应力因素对电池衰退的影响,模拟电池运行工程中的老化过程,各种电池老化模型不断被提出。电池老化模型可分为理论模型和经验模型两种。理论模型往往关注电池衰退的机理,如固体电解质界面膜的形成和发展、锂离子及活性物质的损失等[11-12]。然而在对锂离子电池部分区间的寿命进行预测时,可利用的信息只有电池的运行工况或循环区间,电池内部发生的微观变化无法获取,这使得理论模型应用困难。相比之下,经验模型更容易与电池寿命预测及控制策略制定相结合。基于实际运行工况,文献[13]针对不同温度、起始 SOC、ΔDODs、放电倍率和再生制动倍率下循环的LiFePO4电池建立了经验模型。文献[4]根据实验数据建立了 Graphite/LiCoO2电池容量幂律衰退模型,但是该模型仅对前500次等效循环和部分区间有效。对于给定的部分SOC区间,以上研究中建立的经验模型忽略了可能加速电池老化的理论因素,如充电截止电压(End of Charging Voltage,EoCV)、区间内恒压充电时间及电池正负极材料的相变过程,导致经验模型精度较低甚至模型无法建立。另外,经验模型对数据具有很强的依赖性,不同材料体系的电池和不同的应用场景下模型适用性较差。目前,结合实验数据和锂离子电池老化机理的半经验模型研究还不够充分。
为了解决以上问题,本文在考虑内部机理的条件下,将电池实际使用过程可能存在的区间和不同反应阶段的SOC区间,按照实用区间、相变区间和20%DOD区间对电池整体使用区间进行了划分。分析区间特征对容量衰退的影响因素,提取多个影响电池老化程度的特征参数,建立了一种基于数据驱动算法的锂离子电池衰退半经验模型。该模型结合电池老化机理和实验结果,能够实现实用区间下电池老化趋势的准确预测。
1 实验设计
本文选用 2.75A·h 18650型号三元材料电池作为研究对象,其基本参数见表 1。其最大充电倍率为 1C,最大放电倍率为 3C。供应商提供的标准充放电方式为:在 25±2℃环境下,以 0.5C的电流恒流充电至上限截止电压4.2V后,转为恒压充电至电流小于0.01C,静置30min后,以1C恒流放电至下限截止电压2.5V。所使用的电池测试平台如图1所示,由电池测试仪器(96通道Maccor充放电设备)、高低温实验箱(含被测电池)和计算机组成。
表1 2.75A⋅h锂离子电池基本参数
Tab.1 The basic parameters of 2.75A⋅h lithium-ion battery
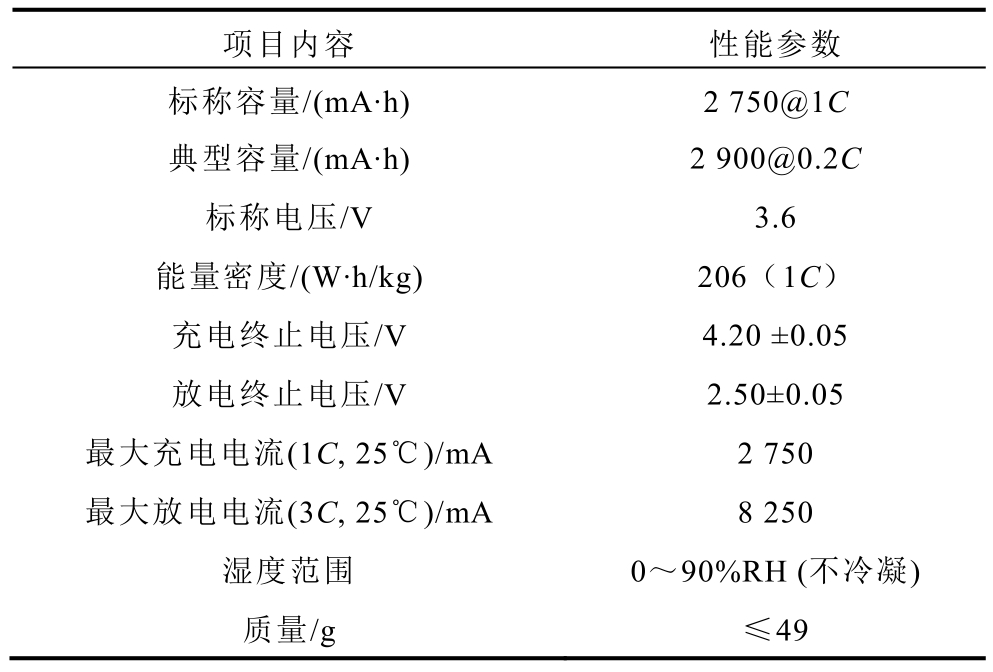
项目内容 性能参数标称容量/(mA·h) 2 750@1C典型容量/(mA·h) 2 900@0.2C标称电压/V 3.6能量密度/(W·h/kg) 206(1C)充电终止电压/V 4.20 ±0.05放电终止电压/V 2.50±0.05最大充电电流(1C, 25℃)/mA 2 750最大放电电流(3C, 25℃)/mA 8 250湿度范围 0~90%RH (不冷凝)质量/g ≤49

图1 锂离子电池测试平台实物图
Fig.1 Lithium-ion battery test platform
为了研究不同充放电区间下锂离子电池的循环寿命特性,本文采用区间循环的方式对锂离子电池进行老化测试,以不同的SOC循环区间对电池容量衰退的影响作为研究目标。现阶段大部分研究对于SOC区间的划分比较随意,没有形成严格的划分原则。考虑锂离子电池在老化过程中的不同反应阶段及其实际运行过程中可能的SOC使用区间,本文分别按照20%SOC区间、相变区间和实用区间对SOC区间进行了划分。
1.1 20% SOC区间
相变区间与20%SOC区间特征对比见表2,首先按照20%SOC原则将0~100%SOC全区间划分为[0, 20%]、[20%, 40%]、[40%, 60%]、[60%, 80%]和[80%, 100%]共五个分区间。所选择的区间具有相同的区间宽度,平均SOC存在差异。在倍率、温度等影响因素相同的前提下,可以突出分析区间平均SOC和电压水平对电池老化的作用。五个分区间之间没有重叠,这将有助于独立分析不同SOC区间下的电池老化机理,为电池SOC使用区间的优化奠定基础。
表2 相变区间与20%SOC区间特征对比
Tab.2 Comparison between phase transition intervals and 20% SOC intervals
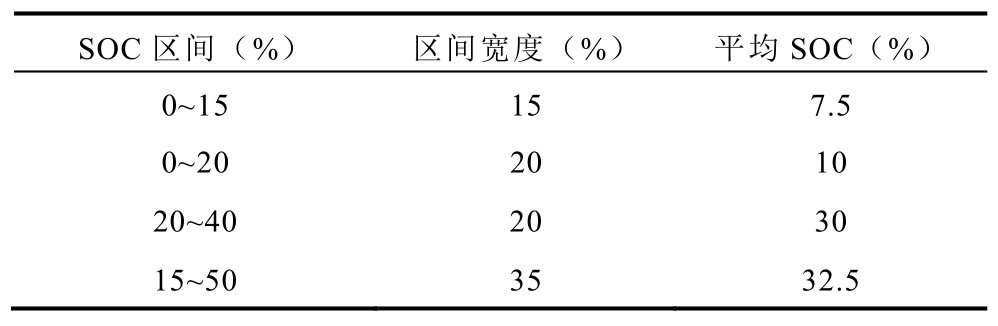
SOC区间(%) 区间宽度(%) 平均SOC(%)0~15 15 7.5 0~20 20 10 20~40 20 30 15~50 35 32.5
1.2 相变区间
锂离子电池的循环寿命还与正负极材料的相变过程相关。容量增量分析(Incremental Capacity Analysis, ICA)法是现阶段进行电池电化学性能分析的有效工具,也被广泛应用于锂离子电池衰退分析中,本文根据容量增量曲线划分电池的相变区间[14]。图2所示为测试目标电池在25℃环境下C/25倍率充放电对应的容量增量曲线。可以看出,目标电池IC曲线中共有四个峰,分别对应不同的电压平台,其中②号峰最明显,③号峰较为平缓。IC曲线峰值之间的低谷对应了充放电平台上电压变化较快的点,体现出不同电压平台的变化。被测电池不同电压平台转换处的SOC分别在15%、50%和83%附近。由于循环过程中采用的充放电倍率远大于ICA特性测试采用的倍率,电池充电至SOC为90%附近时进入恒压阶段,第4个峰消失。因此,根据IC曲线的特征点,现将全区间划分为0~15%、15%~50%、50%~100%三个相变区间进行循环寿命测试。
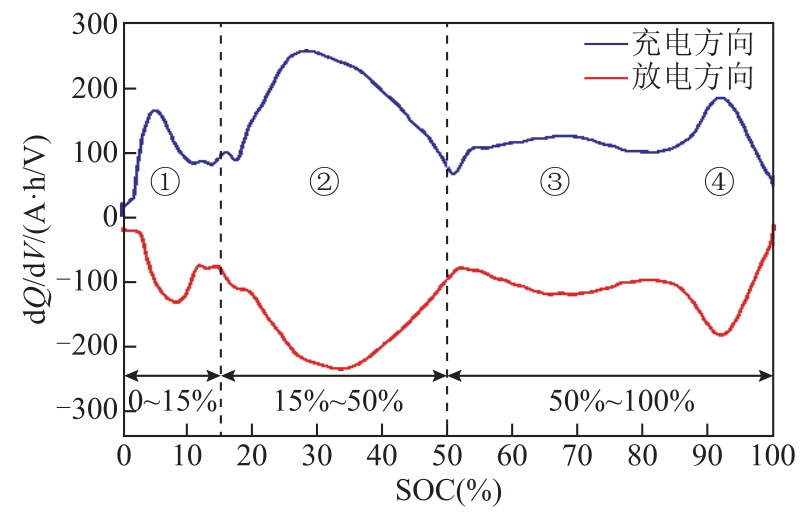
图2 IC曲线及相变区间划分
Fig.2 IC curves and partition of phase transition SOC interval lithium-ion battery test platform
1.3 实用区间
锂离子电池SOC的可用范围是[0, 100%],但为了兼顾锂离子电池的功率能力、使用寿命和安全性,供应商往往建议电池的使用区间控制在一定的范围内。考虑到电池实际应用过程中可能的最大SOC区间,本文选取[5%, 95%]和[15%, 95%]两个实用区间开展循环寿命测试。以[0,100%]全区间作为参考区间,其循环寿命测试结果用于与其他区间测试结果进行对比。同时在利用相变区间和20%SOC区间循环数据建立衰退模型后,较宽的实用区间可作为验证数据对模型精度进行评估。本文中电池的健康状态(State of Health, SOH)用当前容量Qpresent与初始容量Qinitial的百分比来表征,如式(1)所示,本文分析的老化趋势是指电池健康状态随循环次数的变化趋势。

针对以上11个SOC区间,每个独立SOC区间选取同一批次的3个测试单体,来减少随机性的影响,所有单体按照标准充放电方式进行循环测试。从测试起点开始,每完成100次循环寿命测试,进行一次性能测试,包括容量测试、混合功率脉冲特性(Hybrid Power Puls Characteristic, HPPC)测试和容量增量分析(ICA)性能测试,总体流程如图3所示。

图3 循环寿命测试流程
Fig.3 Flow chart of cycle life test
2 电池衰退的影响因素分析
本节将对不同 SOC区间下锂离子电池的容量衰退结果进行分析。由于部分区间宽度差异较大,如上限为100%的SOC区间和实用区间,无法仅根据区间循环次数和容量衰退值对比不同 SOC区间下电池老化速度的快慢。此时需要将分区间循环次数转换成等效全区间循环次数后再进行对比分析。基于容量吞吐量相同的原则,等效全区间循环次数(Equivalent Full Cycles, EFC)的计算式见式(2)。每100次分区间循环的等效全区间循环次数为循环过程中电池的累计放电容量 Qcycle除以上一次性能测试中得到的容量值Capcycle-100。下文中循环次数指各区间的实际循环次数,等效循环次数指等效全区间循环次数。
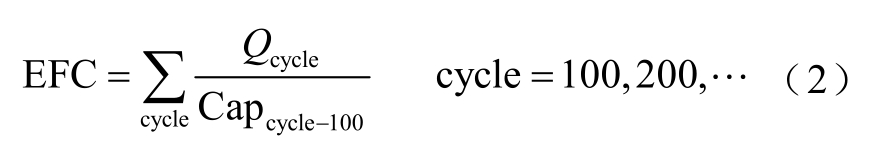
2.1 循环区间宽度对容量衰退的影响分析
以实用区间为例,得到[0, 100%]、[5%, 95%]和[15%, 95%]SOC区间下电池的衰退结果如图 4所示。25℃下,在[0, 100%]区间内循环的电池老化最为显著,900次循环以后SOH达到80%以下。值得注意的是,区间[5%, 95%]和[15%, 95%]下电池的健康状态呈现线性下降的趋势,而区间 0~100%下的电池在600次循环以后出现加速衰退的现象。由结果可以看出,电池使用区间在接近满充满放的状态下,老化前期容量衰减速度基本相同,随着循环次数的增加,SOC循环区间越往中间收缩,电池实际衰退速度越慢。
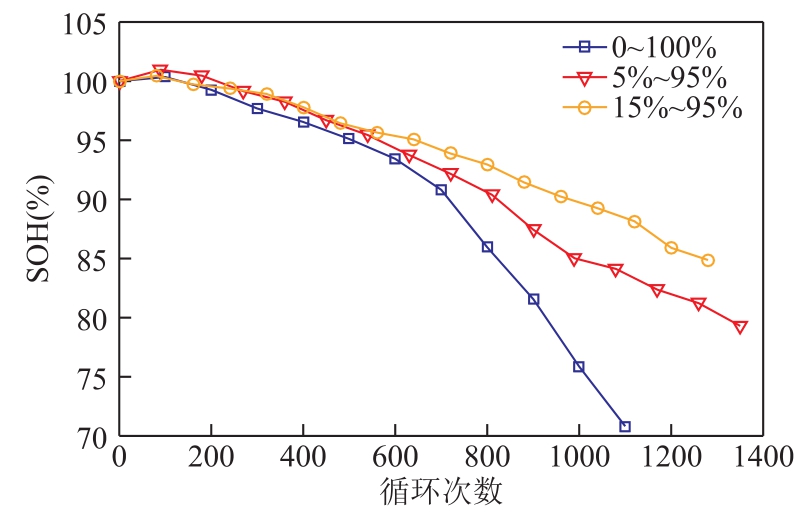
图4 实用区间SOH变化曲线
Fig.4 SOH changing curve of practical SOC intervals
2.2 恒压充电时间对容量衰退的影响分析
本文分别选取[0%, 100%]、[50%, 100%]和[80%,100%]三个上限为 100%的区间来研究恒压充电时间对电池老化的加速作用,得到恒压充电与容量变化关系如图5所示。图5a所示为三块单体的容量均呈现指数衰减趋势。三个区间的电池老化速度由慢到快依次为:[80%, 100%]<[50%, 100%]<[0, 100%],按照容量吞吐量换算至等效循环次数坐标下的衰退结果如图5b所示,三个区间在电池老化初期(<400次等效循环)都是线性衰退的,且衰减速率非常接近。400次等效循环以后,[80%, 100%]的SOC区间最先出现加速衰退现象,随后依次为[50%, 100%]和[0, 100%]区间。可以看出,对于上限SOC为100%的区间而言,区间宽度越小,容量衰退“拐点”出现的越早。
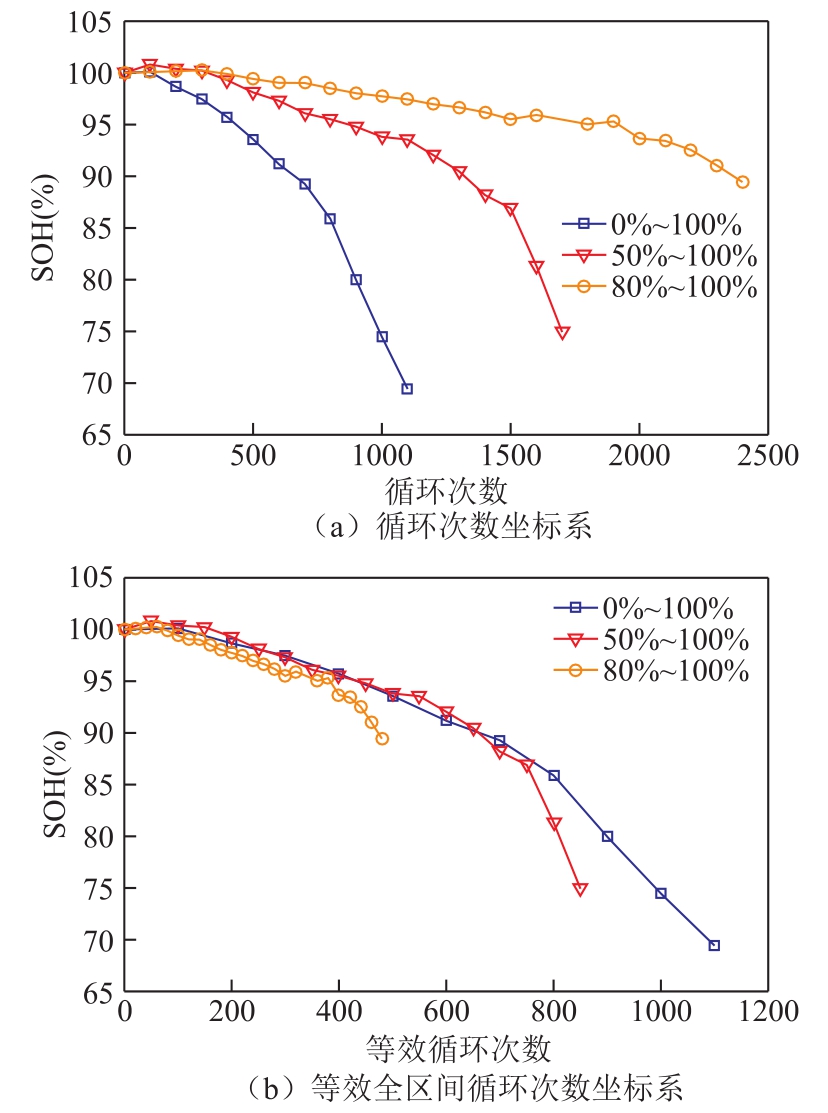
图5 恒压充电与容量变化关系分析
Fig.5 Relationship analysis between constant voltage charging and capacity degredation
以上区间中,[0, 100%]区间的宽度是[80%,100%]区间的5倍,也就是说,在容量吞吐量相同的前提下,[80%, 100%]区间的循环次数是[0, 100%]的5倍。因此在相同容量吞吐量的条件下,恒压充电时间在充电过程的占比大小关系为[0, 100%]<[50%, 100%]<[80%, 100%],区间宽度越小,恒压充电时间在其充电过程中的比例越大。这就意味着[80%, 100%]区间内循环的单体,长时间处于较高的电压水平下,锂离子电池承受的压力急剧增加,容量加速衰退。因此为了提高锂离子电池的循环寿命和使用经济性,在使用过程中,应尽量避免其使用区间中包含过多的恒压充电时间。
2.3 平均SOC对电池容量衰退的影响分析
区间宽度与容量变化关系分析如图6所示。在图6中,区间的宽度固定为20%,平均SOC为变化的参数。为了减少恒压充电时间对分析结果的干扰,使用除[80, 100%]区间之外的四个20%的SOC区间分析区间特征与电池老化的关系。可以看出,[0,20%]区间下电池衰退最慢,[60%, 80%]区间最快。区间[20%, 40%]和[40%, 60%]下电池衰退速度非常接近,所有区间下电池老化速度为[0, 20%]<[20%,40%]<[40%, 60%]<[60%,80%]。根据目前的对比结果可得出结论:在循环区间宽度相同的前提下,区间平均SOC值越高,电池老化速度越快。因此对于电池管理系统来说,在电池达到功率需求的前提下,应尽量避免高SOC区间的使用。

图6 区间宽度与容量变化关系分析
Fig.6 Relationship analysis between interval width and capacity degradation
2.4 相变过程对电池容量衰退的影响分析
由于石墨电极的分级嵌入特征通常伴随着材料性能的变化,电压平台的频繁切换会导致材料膨胀和收缩,从而产生机械应力进而导致石墨材料的破裂损失。因此,当循环区间包含了电压平台之间的转换点时,电池具有更快的老化速度。本研究中选取两个20%SOC区间和两个相变区间来分析相变过程对电池老化的影响,对比结果如图7所示。相变区间与20%SOC区间特征对比见表2。由表2可知,区间[0, 15%]和[15%, 50%]都位于电压平台上,但衰退结果却有很大的差异。如表2所示,[0, 15%]区间具有最小的区间宽度和平均SOC值,衰退速度却是四个区间中最快的。与其相对应的是,[15%, 50%]区间宽度最大,平均SOC值最高,衰退速度却是最慢的。由此可知,锂离子电池区间循环寿命也会受到电池电压平台和区间宽度的影响。但是不同的区间特征和相变过程对电池的老化作用出现重叠,仅从以上数据中很难发现明显的规律。

图7 相变过程与容量变化关系分析
Fig.7 Relationship analysis between phase transition and capacity degradation
3 任意区间老化趋势预测模型
从上文的分析可以看出,区间循环工况下的锂离子电池寿命受多个因素的影响,这使电池老化模型的建立更富挑战性。锂离子电池的数值模型,具有明确的数学表达式,但其建立过程中需要对不同的应力进行解耦,电池测试实验设计及建模任务复杂。数据驱动模型利用机器学习甚至深度学习方法,从实验数据中挖掘电池老化结果与不同影响因子的潜在关系,更适用于老化趋势预测。
3.1 区间特征提取
图8为电池在[0,100%]区间循环过程中IC曲线随循环次数的变化图,IC曲线峰反映电池的相变过程,与充电过程中锂离子在石墨负极中的分层嵌入有关。由于内阻的增加,充电IC曲线整体向上限电压偏移;由于各部分活性材料和锂离子的损失,IC曲线峰值呈下降趋势。IC曲线随电池老化产生的变化趋势在一定程度上反映了电池的衰退状态,是表征电池老化的重要特征。本文建立的电池老化模型主要考虑SOC区间、恒压充电和相变过程的作用机制。

图8 [0,100%]的IC曲线变化图
Fig.8 IC curve variation diagram of [0, 100%]
首先选取区间宽度(ΔSOC)和平均 SOC(SOCmean)两个参数对区间进行量化。其中 SOCmean代表了区间内的电压水平;ΔSOC表示电池循环过程中的放电深度,与电池的容量吞吐量和等效全区间循环次数密切相关。为了体现相变过程对电池老化的影响,分别用区间上限SOCk和区间下限SOCk-1与容量增量特征 SOC点的距离来表述循环区间与电池电压平台之间的包含关系。将区间内是否存在恒压充电阶段作为布尔型输入特征,如果区间内经历恒压充电,该特征取值为1,反之为0。区间上限SOCk到100%的距离(Up2one)说明了区间恒压充电时间的多少,Up2one参数越小,恒压充电时间越长。以区间[20%, 40%]为例,其上、下限SOC与电池第一个相变点(SOC为15%)对应SOC的距离分别是5%和25%。两个数值都为正数,说明第一个相变点位于区间[0, 20%]之内,且数值的大小代表了区间所包含两个电压平台的多少。选取等效全区间循环次数作为时序数据的时间轴,相较于区间循环次数能更好地体现不同区间宽度下电池的衰退情况。每个时间点电池容量体现了当前的老化状态并对下一个时刻的循环结果产生影响,因此将上一个数据点的容量值作为模型特征。所有特征汇总结果见表3。
表3 区间特征汇总表
Tab.3 Summary of SOC interval features

特征名称 特征意义ΔSOC 区间宽度SOCmean 区间平均SOC Peak1_up, Peak1_dn IC曲线1号峰与区间上下限的距离Peak2_up, Peak2_dn IC曲线2号峰与区间上下限的距离Peak4_up, Peak4_dn IC曲线4号峰与区间上下限的距离Valley 1_up, Valley 1_dn IC曲线1号谷与区间上下限的距离Valley2_up, Valley 2_dn IC曲线2号谷与区间上下限的距离Valley3_up, Valley 3_dn IC曲线3号谷与区间上下限的距离Up2one 上限SOCk到100%SOC的距离CV_state 是否存在恒压充电阶段Cycle_eq 等效全区间循环次数Capacity_last 上一个数据点的电池容量值
3.2 数据驱动模型
对于锂离子电池而言,循环衰退过程中出现的容量衰退就是以循环次数为时间轴的时间序列。以第t次循环为例,电池容量Ct与其内阻大小、功率状态等参数密切相关。如式(3)所示,在进行t+1次循环时Ct会影响电池的循环过程进而影响到t+1时刻的容量值 Ct+1。因此锂离子电池的衰退容量值之间存在关联性,可以使用时间序列处理电池的循环寿命问题。
循环神经网络(Recurrent Neural Network,RNN)非常适用于解决具有长期依赖特性的时间序列问题,长短周期记忆网络(Long-Short Term Memory network, LSTM)解决了RNN在长期依赖计算中存在的梯度爆炸或梯度消失问题。本文采用Keras深度学习框架完成了 LSTM RNN网络模型的搭建、调试和评估过程。基于LSTM的锂离子电池区间衰退模型能够在训练数据的基础上,根据区间范围[SOCk-1, SOCk]的不同,输出不同循环次数下的电池容量值,即对电池的衰退曲线进行预测。
基于LSTM的容量时间序列的构建采用了循环迭代的过程。首先采用电池的初始容量和区间特征参数作为第 100次等效循环的模型输入样本,从LSTM衰退模型中输出第100次循环容量预测值。然后将模型输出与区间特征作为第200次等效循环的输入,依此往复,当模型容量预测值达到寿命终点或指定循环次数时迭代停止,整个模型的运行流程如图9所示。

图9 LSTM衰退模型运行流程
Fig.9 Flow chart of battery aging model based on LSTM
本研究中,LSTM RNN网络初始化为双层LSTM结构,每层的神经元数量分别是50个和100个,Dense层用于输出最终的估计结果。所采用的Adam优化方法能基于训练数据自适应更新学习率,在解决深度学习问题中具有高效性。在模型达到最优值或训练损失变化小于规定阈值时,Earlystop函数能够使模型停止训练,有效提高优化效率和防止过拟合,模型参数设置见表4。
表4 LSTM RNN模型参数
Tab.4 LSTM RNN model initialization summary of SOC interval features
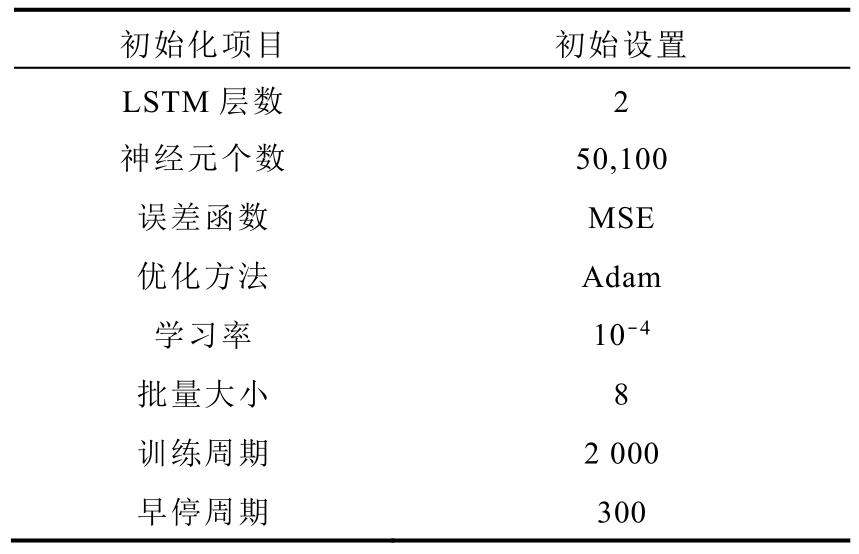
初始化项目 初始设置LSTM层数 2神经元个数 50,100误差函数 MSE优化方法 Adam学习率 10-4批量大小 8训练周期 2 000早停周期 300
3.3 模型验证
选取[0, 100%]、[15%, 95%]、[0, 15%]、[15%,50%]、[50%, 100%]、[0, 20%]、[20%, 40%]、[60%,80%]、[80%, 100%]共九个区间作为模型训练数据,[5%, 95%]、 [40%, 60%]共2个区间作为模型验证数据。即使是同一循环区间下的不同单体也会由于个体差异以及环境因素导致衰退结果不一致。因此本文将相同工况下多个单体的容量平均值作为研究对象,以减小偶然性对研究结果的影响。
图 10所示为模型训练结果,其中图10a为不同优化次数下的训练与验证损失变化曲线,图10b为模型在训练数据集上的表现。LSTM RNN网络能够很好地拟合不同循环区间下电池的容量变化趋势,经过1 516个训练周期后,模型损失降至10-4以下。

图10 模型训练结果
Fig.10 Model training results
根据式(4)计算了预测误差(Error),验证数据的模型预测结果与误差曲线如图 11所示。可以看出,模型预测SOH值与电池实际SOH值匹配度非常高。因此,尽管存在累积误差的影响,该模型可以很好地学习到不同老化因素对电池衰退的作用,从而准确预测任意循环区间下电池的容量变化趋势。

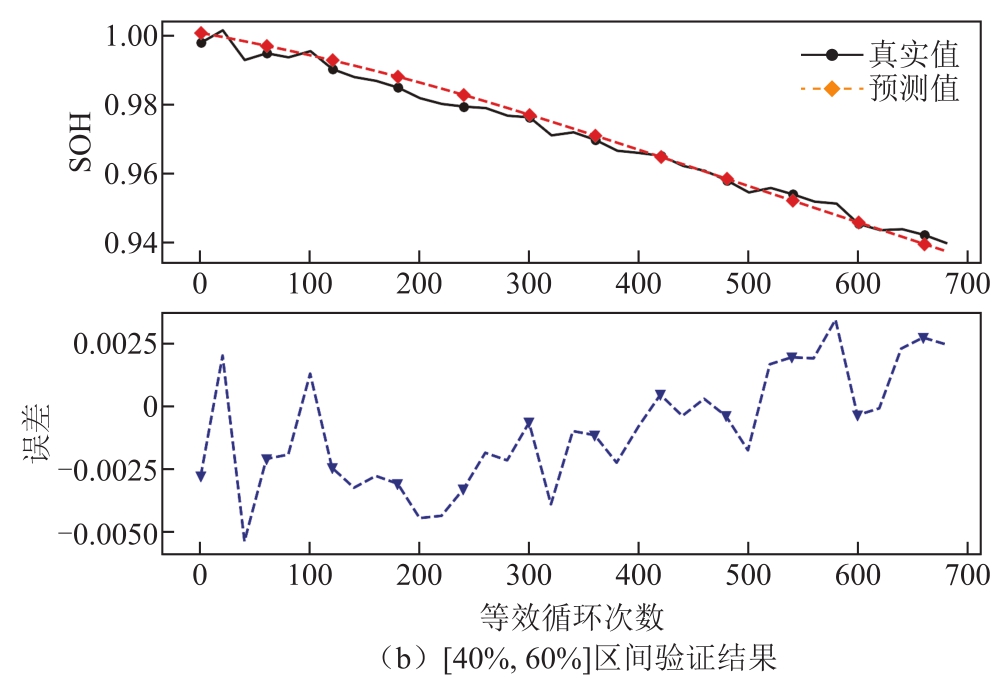
图11 模型在验证数据上的预测结果
Fig.11 Model prediction results of valid data
式中,SOHR、SOHT分别为SOH的预测值和真实值。
为了更好地分析该方法的准确性和可靠性,分别采用误差最大值(Maximum)、平均绝对误差(MAE)、方均根误差(RMSE)和方差(Variance)对误差性能进行评估,详细的统计分析见表 5。区间[5%, 95%]最大预测误差为 0.013 8,平均绝对误差为0.049。
表5 SOH验证误差统计
Tab.5 The statistic list of SOH validation errors
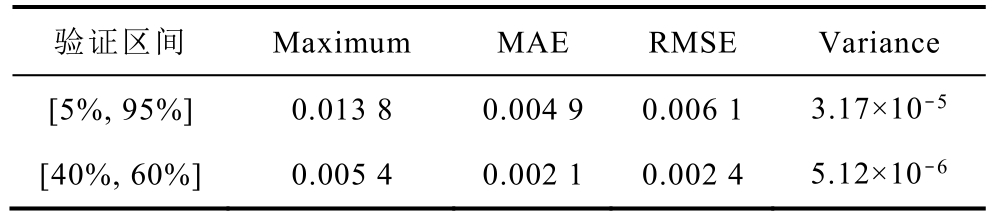
验证区间 Maximum MAE RMSE Variance[5%, 95%]0.013 8 0.004 9 0.006 1 3.17×10-5[40%, 60%]0.005 4 0.002 1 0.002 4 5.12×10-6
从以上分析可以看出,本文提出的电池容量衰退模型,能够很好地预测不同SOC区间下电池的容量变化趋势。这对于电池的运行维护及储能系统中经济计划的制定具有一定的参考意义。
4 结论
本文从循环区间宽度、恒压充电时间、平均SOC及电池相变过程三个方面,对不同区间内的电池容量衰退结果进行了对比分析。结果表明,电池使用区间在接近满充满放的状态下,越往中间收缩,实际衰退速度越慢。恒压充电是导致电池出现衰退加速“拐点”的重要原因。对于上限SOC固定为100%的区间,线性衰退阶段容量下降速率相近,但区间宽度越小“拐点”出现越早。当SOC区间相同时,SOC均值越大,电池老化越快。
结合区间容量衰退结果和衰退机理,提取了部分SOC区间下寿命影响因素的量化特征,采用循环神经网络(LSTM RNN)方法,建立了基于数据驱动方法的锂离子电池SOC区间循环衰退模型。在给定任意SOC区间上、下限前提下,模型输出不同循环次数的容量预测值,通过[5%, 95%]、[40%, 60%]区间进行模型验证,利用平均绝对误差、方均根误差等对模型进行性能评估,发现随着循环次数的增加,预测误差有所增大,但最大误差不超过2%,证明了该预测方法的可行性和有效性。
[1]陈景文, 莫瑞瑞, 党宏社, 等. 储能型光伏系统电池容量优化配置及经济性分析[J]. 科学技术与工程, 2019, 19(28): 165-171.Chen Jingwen, Mo Ruirui, Dang Hongshe, et al.Battery capacity optimal configuration and economical analysis of energy storage photuvataic system[J]. Sciece Technology and Engineering, 2019,19(28): 165-171.
[2]孙丙香, 姜久春, 韩智强, 等. 基于不同衰退路径下的锂离子动力电池低温应力差异性[J]. 电工技术学报, 2016, 31(10): 159-167.Sun Bingxiang, Jiang Jiuchun, Han Zhiqiang, et al.The lithium-ion battery low temperature stress based on different degradation paths[J]. Transactions of China Electrotechnical Society, 2016, 31(10): 159-167.
[3]Guo Binqi, Niu Meng, Lai Xiaokang, et al.Application research on large-scale battery energy storage system under global energy interconnection framework[J]. Global Energy Interconnection, 2018,1(1): 79-86.
[4]Saxena S, Hendricks C, Pecht M. Cycle life testing and modeling of graphite/LiCoO2 cells under different state of charge ranges[J]. Journal of Power Sources,2016, 327: 394-400.
[5]Gao Yang, Jiang Jiuchun, Zhang Caiping, et al.Lithium-ion battery aging mechanisms and life model under different charging stresses[J]. Journal of Power Sources, 2017, 356: 103-114.
[6]Ecker M, Nieto N, Stefan K, et al. Calendar and cycle life study of Li(NiMnCo)O2-based 18650 lithium-ion batteries[J]. Journal of Power Sources, 2014, 248:839-851.
[7]Xu Bolun, Oudalov A, Ulbig A, et al. Modeling of lithium-ion battery degradation for cell life assessment[J]. IEEE Transactions on Smart Grid,2018, 9(2): 1131-1140.
[8]马泽宇, 姜久春, 张维戈, 等. 锂离子动力电池热老化的路径依赖性研究[J]. 电工技术学报, 2014,29(5): 221-227.Ma Zeyu, Jiang Jiuchun, Zhang Weige, et al. Path dependence of thermal aging of Li-ion power battery[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 221-227.
[9]Hu Xiaosong, Xu Le, Lin Xianke, et al. Battery lifetime prognostics[J]. Joule, 2020, 4(2): 310-346.
[10]Li Y, Abdel-Monem M, Gopalakrishnan R, et al. A quick on-line state of health estimation method for Liion battery with incremental capacity curves processed by Gaussian filter[J]. Journal of Power Sources, 2018, 373: 40-53.
[11]Xiong Rui, Tian Jinpen, Mu Hao, et al. A systematic model-based degradation behavior recognition and health monitoring method for lithium-ion batteries[J].Applied Energy, 2017, 207: 372-383.
[12]Hu Xiaosong, Feng Fei, Liu Kailong, et al. State estimation for advanced battery management: key challenges and future trends[J]. Renewable and Sustainable Energy Reviews, 2019, 114: 109334.
[13]Lam L, Bauer P. Practical capacity fading model for li-ion battery cells in electric vehicles[J]. IEEE Transactions on Power Electronics, 2013, 28(12):5910-5918.
[14]薛楠, 孙丙香, 白恺, 等. 基于容量增量分析的复合材料锂电池分区间循环衰退机理[J]. 电工技术学报, 2017, 32(13): 145-152.Xue Nan, Sun Bingxiang, Bai Kai, et al. Different state of charge range cycle degradation mechanism of composite material lithium-ion batteries based on incremental capacity analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 145-152.