0 引言
随着可再生能源（Renewable Energy Source,RES）的渗透率不断提高，RES固有的间歇性对电力系统稳定运行提出新的挑战[1]。近年来电动汽车（Electric Vehicles, EV）的保有量持续大幅增长[2]，EV集群（EV Cluster, EVC）并网将进一步加剧这个挑战[3]。并网EVC作为一种灵活性资源[4]，兼具荷、源双重属性，利用 EVC的灵活性可削弱 RES间歇性对电网运行的不利影响[5]。并网EVC与RES的协同调控已成为提升电网经济性与稳定性的有力手段[6]。
关于EVC与RES的协同优化与控制，已有广泛而深入的研究，且现有成果已证明两者协同优化可提高RES消纳率[7]、降低系统成本[8]、提升电网稳定性[9]等。本质上，EVC与RES的协同优化是不确定环境下极具复杂性的优化问题[10]，首先是RES固有间歇性与EVC功率需求波动的双重不确定性；其次不确定性均具有空间、时间多维度特征，表现为不同区域的RES电站在多时段内的功率波动，EV用户入网区域及并、离网时段的随机性等。针对两者协同优化中的复杂不确定性，可采用随机规划[11]和鲁棒优化[12]两类方法。随机规划须预知不确定变量的概率分布特征，但因实际中其分布特征难以准确获取，且计算复杂度高，随机规划具有明显的应用局限性。鲁棒优化则不需获取不确定变量的分布特征，仅对其采用封闭凸集描述，优化目标对于凸集上的任意点，都能确保鲁棒最优解。
基于鲁棒优化方法，文献[13-14]均考虑风光出力不确定性，并协同EVC有序充电建立鲁棒控制模型，但忽略了 EVC的不确定性；文献[15]考虑 EV的不确定性制定优化调度策略，但未利用 EV的电源属性，且优化策略未与RES协同；文献[16]考虑RES、市场电价的不确定性，提出多重不确定性下的鲁棒优化策略，但未深入讨论EVC的规模及需求的不确定性，适用性有待商榷。文献[17-18]建立的鲁棒优化模型考虑了RES与EVC的双重不确定性，但不适用于大规模EVC的并网场景。现有研究虽已考虑到RES与EVC的双重复杂不确定性，但EVC多局限于小规模，且随着EVC规模的逐渐扩大，集中式优化将难以应对“维度灾难”。此外，EV控制模型在现有研究中均是基于用电需求、充放电约束建立，虽然保证了 EV用户的用电需求，但控制模型显然忽略了用户的需求偏好。实际场景中 EV用户作为高度自主性个体，其 EV不一定参与调度策略，忽略EV用户的偏好与现实场景存在必然矛盾。
基于上述问题，本文初步探索将 EV用户的需求偏好纳入EVC与RES等其他分布式能源协同优化中。首先，考虑用户的需求偏好，将并网EVC细分为额定功率充电、可调节充电及灵活充放电三类并分别建立控制模型；其次，建立时间、空间及功率区间三维多面体不确定性集合描述 EVC功率需求及RES出力的不确定性；最后，构建EVC并网的分布式鲁棒优化模型，并采用交替方向乘子（Alternating Direction Method of Multipliers, ADMM）算法解耦优化模型，实现模型的分布式迭代求解。
1 优化系统构
EV聚合商（EV Aggregator, EVA）作为配网与EV用户的中介[19]，其参与可实现EVC的分布式控制。优化系统的简化结构如图1所示。系统内包含风电、光伏及分布式电源（Distributed Generation,DG），EVC也视为一种特殊的分布式能源。控制中心协调系统内分布式能源，确定最优运行策略。EVA需兼顾用户的需求偏好，在调度策略的引导下对并网EV进行充放电控制；多个EVA对所辖EVC进行独立优化。需要说明的是，因EVC同时具有储能属性，随着EVC的规模不断增大，系统内的储能配置容量将不断减小，因此系统内并未考虑额外的储能配置。
图1 优化系统架构
Fig.1 The framework of optimization system
2 计及用户偏好的EV控制模型
2.1 需求偏好下的EVC划分
EV用户在EVA激励下积极参与优化调度，但考虑到用户的高度自主性且用户具有需求偏好，EV并网需求方式最终取决于用户意愿。
依据 EV储能电池的充放电状态，将 EV的并网需求方式分为三类：额定功率充电、可调节充电及灵活充放电。三类EV依次简称为第1、2和3类EV。第1类EV并网即保持额定功率充电，直至达到期望荷电状态（State of Charge, SOC），之后至离网时段前，EV与充电站保持物理连接但实际中断状态；第2类EV在并网时段内储能电池被禁止处于放电状态，但充电功率可调节；第3类EV在并网时段内储能电池可处于充、放电状态，且充、放电功率均可调节。三类 EV并网时段内储能电池的电能注入轨迹如图2所示。
图2 不同需求方式的电能变化轨迹
Fig.2 The energy trajectory of different grid-connected EV
图2中，El,in为初始电能；El,ex为期望电能；tl,arr为并网时刻；tl,dep为离网时刻。El,cthr、El,dthr分别为功率削减阈值、放电电能阈值。El,cthr、El,dthr的设置可在一定程度上保证 EV突发离网时仍满足电量需求；实际场景中此阈值可由用户设置，体现用户与EVA的互动性。如图2，电能小于El,cthr时，第2、3类EV均等同于第1类EV；电能在El,cthr～El,dthr之间时，第3类EV等同于第2类EV。
三类需求方式映射着 EV用户不同的需求偏好：第1类方式表示用户期望最小化充电时间；第2类方式表示用户期望降低并网费用且不额外增加储能电池损耗（储能电池放电将造成额外损耗[20]）；第 3类方式表示用户期望最小化并网成本。EV并网时，用户可与 EVA交互确定并网需求方式。设EVC中隶属于第 1、2和 3类需求方式的 EV分别构成集合D1、D2和D3；系统内EVA的数量为NA；记 Aj为第 j个 EVA， D i , j (i = 1 ,2,3； j = 1,2,…, N A )为Aj中属于第i类需求方式的EV构成的集合。
2.2 3类并网EV控制模型
对三类并网EV分别建模。
1） ∀ l∈ D 1,j ，且 ∀t∈ t l,in ，车辆l的控制模型为
式中，Pl,t、Sl,t分别为l在t时段的实际充电功率及SOC； 
分别为l的额定充电功率、充电效率、并网时段、初始SOC、离网期望SOC、储能电池容量；Δt为单位时长。
2） ∀ l∈ D 2,j，且 ∀t∈ t l,in ，车辆l的控制模型为
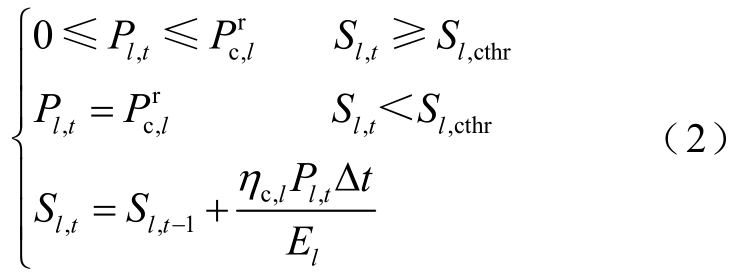
式中，Sl,cthr为功率削减SOC阈值，S l ,cthr = El , c thr/El；式（2）中第二个约束保证储能电量小于El,cthr时，l保持额定功率充电。实际场景中，El,cthr可由用户通过智能终端设置。
3） ∀ l∈ D 3,j，且 ∀t∈ t l,in ，车辆l的控制模型为
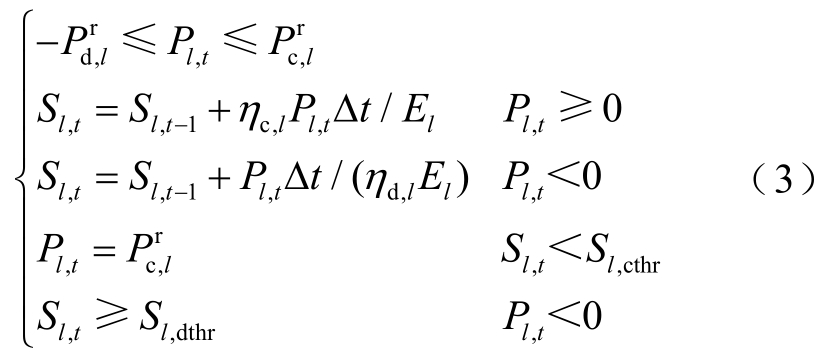
式中，
分别为车辆l的额定放电功率、放电效率；Sl,dthr为放电时的SOC阈值，S l , dthr = El , d thr/El，式（3）中第五个约束保证放电过程中储能电池电量不低于El,dthr。同理，El,dthr可由用户通过智能终端设置。
实际场景中，为激励 EV参与调度策略，EVA针对三类EV须采用差异化计价或其他激励措施。
并网EV需满足如下的其他约束：
1）电量需求约束，EV离网时达到期望 SOC。
式中，Sl,dep为车辆l离网时的SOC。
2）在网时长约束，EV并网时长须不小于最小并网时长。
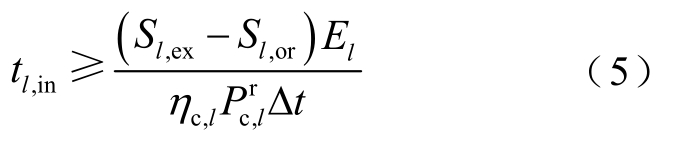
3）所属集的唯一性约束，Aj中的任一EV仅属于一个集合。
4）EV全集约束。
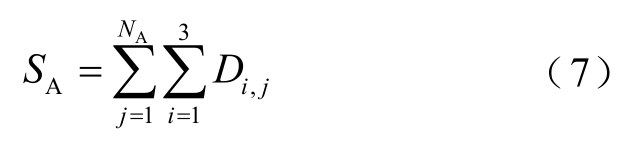
式中，SA为系统内所有EVC构成的全集。
3 分布式鲁棒优化调度模型
3.1 多面体不确定性集合
设系统内RES电站的数量为Ns，N s =Nv +Nw ，Nv 为光伏电站数，Nw为风机电站数。设
表示电站 i (i = 1 ,2,… ,N s )在时段t(t∈T)的功率区间。为平衡鲁棒优化模型的保守度（鲁棒优化模型在3.3节详细论述），引入鲁棒控制系数ΓRS、ΓRT，在空间、时间及功率区间三个维度建立鲁棒条件下的多面体集合ψR，即
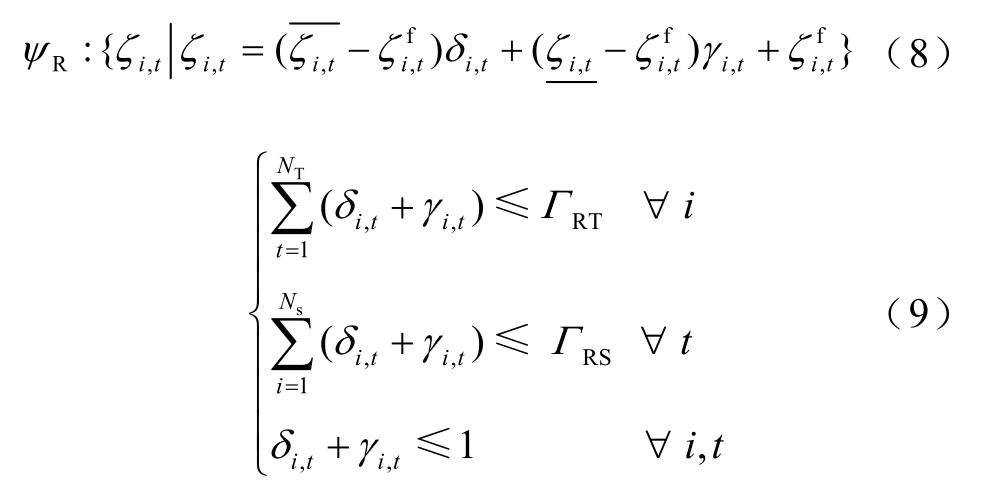
式中，T为优化时域；NT为优化时段数；δi,t、γi,t为布尔变量；ζi,t、
分别为电站i的实际功率、预测功率
分别为ζi,t的下确界、上确界；ΓRS、ΓR T分别为RES空间不确定性控制系数和时间不确定性控制系数。ΓRS和ΓRT共同调节多面体的极点，进而调控模型的保守程度。当ΓRS与ΓRT取值较大时，模型较为保守；取值较小时，模型较为激进[21]。δi, t +γi, t ≤ 1 为鲁棒条件下的极点约束，对应的物理意义为同一电站在同一时段内的实际出力仅能达到上确界和下确界的其中之一。
实际场景中，EVA需要在调度策略制定之前获得T内EV的预测接入信息。随着车联网（Vehicle to Grid, V2G）技术、智能交通等技术的成熟及EV历史并网数据的累积，结合区域特征、智能交通互动系统、历史数据挖掘及智能申报等方法，EVA可获得较准确的 EV需求预测[22]。设
为Aj在t时段的功率区间，类似于RES的不确定性建模方法，构建空间、时间及功率区间三维多面体集合ψA，即
式中，κj,t、υj,t为布尔变量；
分别为Aj的实际功率，预测功率；ΓAS、ΓAT分别为Aj的空间不确定性控制系数和时间不确定性控制系数。κj ,t +υj, t ≤ 1为多面体极点约束，对应的物理意义为同一 EVA在同一时段内的实际功率仅能达到上确界或下确界。
需要说明的是，EVA的不确定性忽略了单台EV不确定细节，如 EV用户并网过程中调整阈值、切换并网方式等，这些多为 EV动态不确定性因素，更适于纳入实时调度策略考虑。
3.2 考虑灵活性差异的确定性优化模型
由第2节可知，用户的需求偏好决定EV的并网需求方式。EVA优化实质是利用EV的灵活性（功率的可调节性）进行最优功率分配。因此在优化角度上，第1、2和3类需求方式EV的灵活性不同，EVA优化本质是计及EVC灵活性差异的优化。
设RES电站仅存在较大建设成本，忽略RES运行成本[23]和系统运行时的功率损耗，则图1的总成本分可为三个部分：DG的运行成本、配网（Distributed Network, DN）与上级电网的功率交互成本、EVC调度补偿成本。其中DG运行成本包括启停成本及燃料成本。以最小化总成本为优化目标，则目标函数为
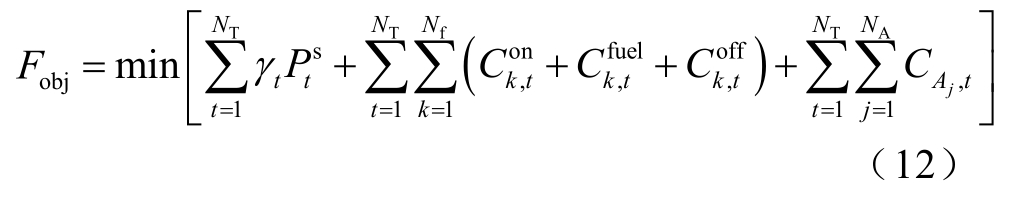
式中，tγ为t时段的市场电价；Nf为DG数量；
为t时段 DN与上级电网的交互功率（下文简称交互功率）；
分别为t时段第k(k = 1 ,2,… ,N f )个DG的启、停及燃料成本； C A j ,t 为t时段Aj中EVC的补偿成本。
由第k个DG的基本参数决定，
由式（13）计算，求解时对
采用分段线性逼近的方法处理[24]。
式中， a k , bk , ck为常系数；Pf,k,t为第k个DG在t时段的发电功率。
式（12）中的 C A j ,t 是EVA对所辖EV进行充电功率削减或调控放电时进行补偿产生的，因此 C A j ,t最终是由t时段Aj所辖的EVC的灵活性决定。依据第 2节计及需求偏好的 EV控制模型，第1类EV不具有灵活性，则D1,j无补偿成本，C A j ,t 实际取决于t时段Aj中的第2类、第3类EV（即D2,j,D3,j内的EVC）。t时段D2,j，D3,j内的EVC总功率分别为
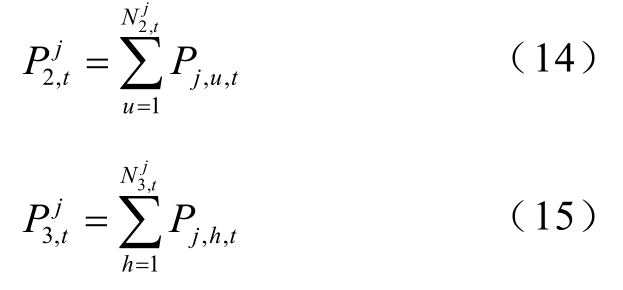
式中，
及P分别为t时段D中EV的总j,u,t2,j功率、EV数量及第 u辆 EV的功率；
及Pj , h,t分别为t时段D3,j集中EV的总功率、EV数量及第 h辆 EV的功率。式（14）中Pj,u,t取值满足式（2）、式（4）～式（6）约束，式（15）中Pj,h,t取值满足式（3）～式（6）约束。
定义t时段Aj的功率削减量
为
式中，
为l的额定充电功率；
为A内EV均j以
充电（即假设D2,j、D3,j中 EV并网功率均为
时在t时段内的EV数量。
t时段Aj的补偿成本 C A j ,t 为
式中，tβ为t时段的补偿系数。
模型须满足的其他约束条件如下。
1）DG的运行约束[25]
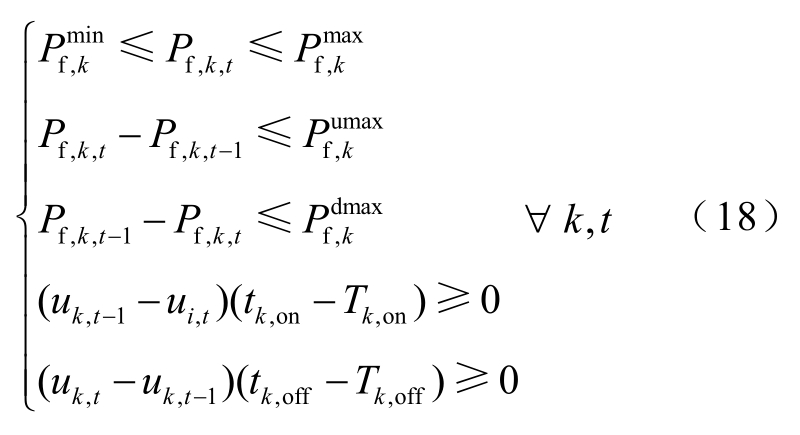
式中，
分别为第k个DG功率的下限、上限；
分别为第k个DG单位时段内最大爬坡功率、下降功率； u k ,t = { 0,1}为t时段第k个DG的启停状态变量；tk,on、tk,off、Tk,on、Tk,off分别为第k个 DG的持续开机、停机时间，最小开机、停机时间。
2）变压器容量约束
式中，Ptr为变压器容量限值。
3）系统功率平衡约束
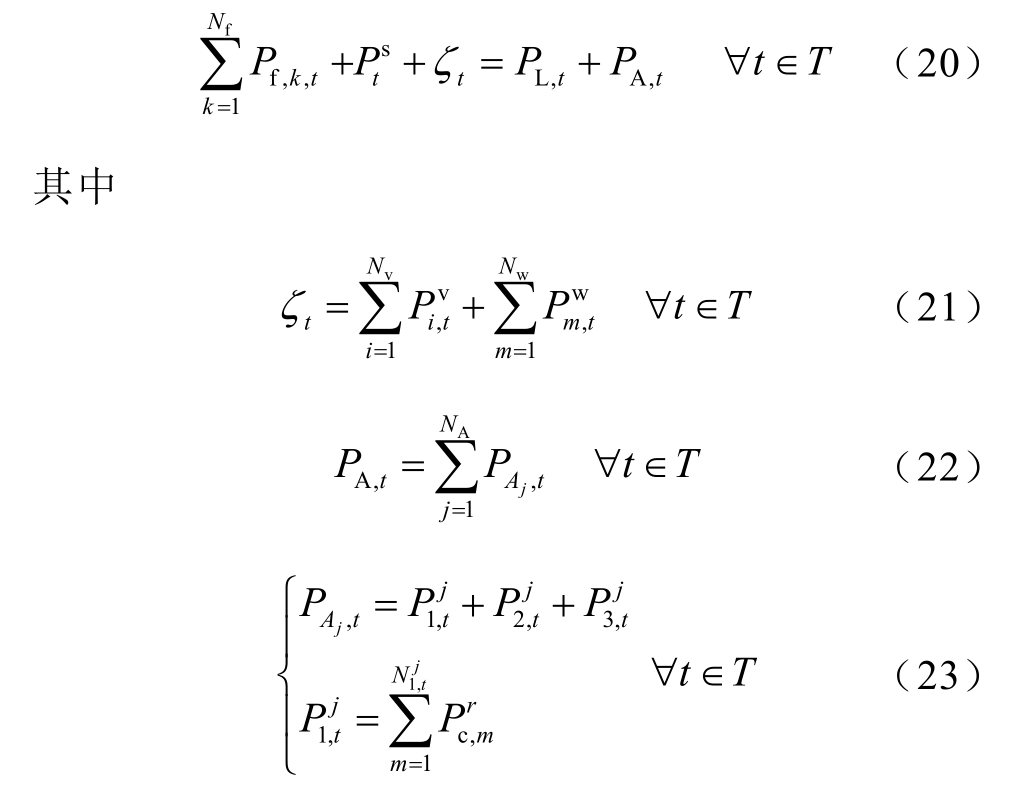
式中，PL,t为系统基负荷（除EVC之外的负荷）；PA,t为t时段NA个EVA的聚合总功率；
为t时段内D1 , j中的EV数量。
需要说明的是，功率平衡式中ζt为RES的实际功率，即考虑RES波动后的功率。ζt高于预测值时，可提高EVA的功率或降低交互功率；ζt低于预测值时，可削减 EVA功率。因此当足够规模的 EVC并网时，将RES实际出力纳入功率平衡，不仅可促进RES的消纳且利于降低系统的运行成本。
3.3 基于多面体集合的鲁棒优化模型
3.2节均基于确定量建立，未考虑RES与EVA功率的波动性。实际中，RES和EVA的协同优化需考虑其多重不确定性，基于 3.1节建立的三维多面体集合，借助最优控制理论中鲁棒优化（Robust Optimization, RO）[26]方法，将3.2节的确定性优化模型转换为鲁棒优化模型。分析式（8）～式（23），ζi,t 与 P A j ,t 的多面体不确定集ψR与ψA对式（20）产生直接影响，进一步影响式（12）。首先将式（20）进行对等转换，得到鲁棒对等式（24）。对等转换的推导过程见附录。
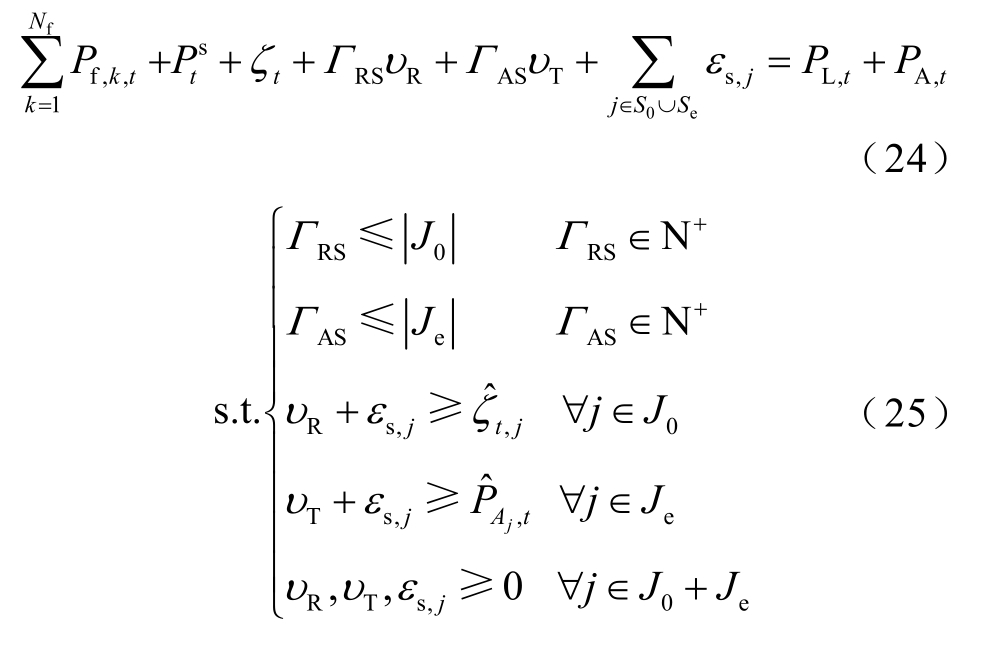
式中，J0为RES电站集合，
为 EVA集合，
对任一时段t(t∈T)，ΓRS和ΓAS分别为控制RES和EVA在同一时段内达到多面体极点的数量；
分别为电站 j、Aj在t时段的最大波动量；Rυ、Tυ、εs,j为鲁棒对等变换引入的对偶变量；N+表示正整数；S0为ΓRS控制下的J0的子集；Se为ΓAS控制下的Je的子集。
鲁棒对等式（24）仅考虑了单一时段内多个RES电站和多个 EVA功率的波动性（空间维度），式（12）为整个优化时域T内的成本最小化，须同时考虑RES电站和EVA功率在多个时段内的波动性（时间维度）。同理，将式（12）进行对等转换，得到鲁棒对等式（26）。转换过程类似于附录的步骤，不再赘述。
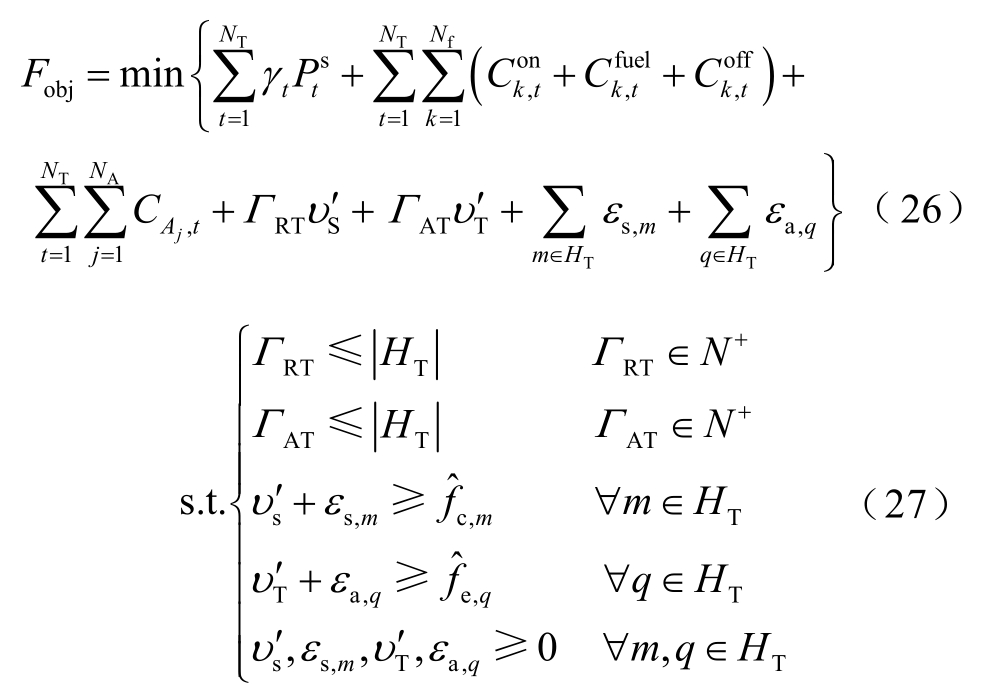
式中，HT为优化时段集合，
ΓRT和ΓAT分别控制RES和EVA功率达到多面体极点的时段数；
为m时段RES功率波动对应的最大成本波动量；
为q时段EVA功率波动对应的最大成本波动量；
为鲁棒对等变换引入的对偶变量。
显然，式（26）需满足第2节建立的EV控制模型约束。式（26）实质是当RES及EVA功率波动时，在满足系统功率需求及功率平衡的前提下，以最小化运行成本优化调整DG出力、EVA功率及交互功率。
3.4 鲁棒优化模型求解
式（26）待求解变量除交互功率及DG功率外，还包括引入的对偶变量及EV功率。随着EVC规模的增大，D2,j、D3,j中EV数量增大，求解复杂度急剧增加。考虑EVA可对所辖EVC独立优化，本文基于ADMM方法，对式（26）进行解耦迭代求解。式（26）为非凸优化，但其非凸性是由包含的DG启停状态的布尔变量导致，文献[27]证明了ADMM算法在解决此类非凸问题时，仍可在有限次迭代后收敛。
引入拉格朗日乘子λ，得到目标函数式（26）的增广拉格朗日模型为
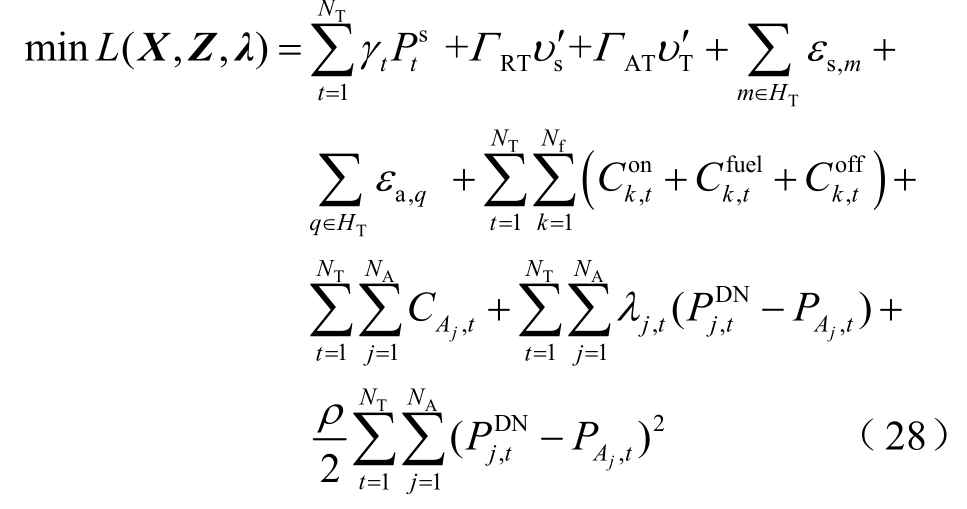
式中，
为新引入变量，表示t时段电网与Aj的交互功率。记变量X包含
记变量Z包含{Pj,u,t,Pj,h,t}。
基于ADMM算法，将式（28）进行如下解耦迭代求解：
式中，λ j, t( r )、PA j ,t (r)为第r次迭代值。Aj的独立优化算式为
联立式（14）～式（17）及式（23），可得与式（31）最优解相同的等价式为
N A个EVA均以式（32）对所辖EVC独立优化。式（32）中
表示t时段D1,j中EV的总功率（D1,j中EV为第1类并网方式，不参与调度优化）。结合式（14）、式（15）可知，式（32）本质是对 P j , u,t ( u ∈D2 , j )、Pj , h,t ( h ∈D3 , j )进行优化。
在NA个EVA均完成优化后，通过式（33）更新第r+1代 P A j ,t ，PA,t值为
式中，
分别为第 j个 EVA在第r+1次迭代时通过式（32）优化得到的第 2类 EV功率、第3类EV功率。
λj, t 的迭代更新算式为
式（29）及式（32）～式（34）即为式（28）的分布式迭代算式。式（35）为迭代收敛判别式，ϑthr为预置常数。
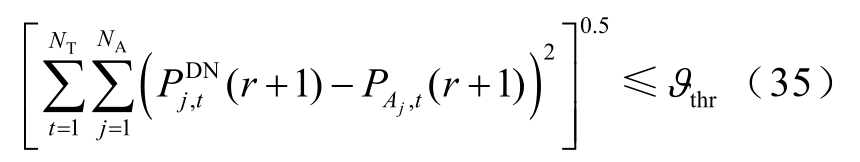
综上分析，EVC并网的分布式鲁棒优化模型求解步骤概述如下：
1）确定优化时域T及优化步长Δt， A j ( j =1,2,… ,N A)读取T内三类EV接入信息（预测值）。Aj计算第1类EV的功率需求并置为首次迭代 P A j ,t 的初始值。
2）设置ρ值，初始化参数λ和ϑthr，置首次迭代r=1。
3）求解式（29）得到第r+1次迭代的变量 X的值，并将
传递给式（32）；NA个EVA均以式（32）对所辖EVC独立优化，求解第r+1次迭代变量Z的值，进而通过式（14）、式（15）和式（33）更新
传递给式（29）。
4）依据式（35）进行收敛判别。若满足式（35），则跳转到步骤6）；若不满足，则通过式（34）更新λj, t( r + 1 )。
5）置迭代次数r=r+1，返回步骤3）。
6）迭代已收敛，迭代结束。
4 算例分析
4.1 数据及实验环境描述
设置优化时域T=24h，优化时段数为24，Δt=1h。系统内包含四个 EVA（ A 1 ～ A4），四个 EVA的 EV最大接入量分别为500、800、1 000、1 300。系统内DG数量为 4，包含两个光伏电站（装机容量均为10MW）和两个风机电站（装机容量均为8MW）。DG参数见附表1。为简化分析，假设接入 A j( j =1,2,3,4)的EV为同一车型，Aj中第1、2和3类EV比例均为1:4:5，EV参数见附表2。鲁棒控制因子ΓRS、ΓRT、ΓAS、ΓAT取值分别为2、8、2、8；βt取γt的50%。γt及PL,t在T内的取值如图3所示。图3中柱状图表示系统内基负荷；曲线表示市场电价；负荷与电价是正相关的，负荷较大时，对应的电价也较高。
图3 基负荷与市场电价
Fig.3 Base load and market price
算例在Matlab 2016a环境下编程求解，并借助YALMIP工具箱调用商用求解器CPLEX。计算机配置为i5-7200U，2.50GHz，8G RAM。
4.2 鲁棒优化结果分析
迭代过程中ρ值的选择决定收敛效率，为确定最优ρ值，测试不同ρ值下的收敛迭代次数，结果见表1。由表1，本文ρ值设定为180，经过6次迭代后收敛。T内RES电站的预测功率如图4所示。对于 3.1节多面体不确定集合中功率的上确界和下确界，本文以预测误差的方式确定RES电站功率及EVA功率区间。设 RES的功率预测误差为 10%，EVA的功率预测误差为5%。则对任一电站i，其功率区间为
对任一A，功率区间为j
实际中可采用深度学习等人工智能方法获得更为精确的上确界和下确界，进一步降低系统的鲁棒成本。
表1 不同ρ值下的迭代次数
Tab.1 The iteration number under differentρvalue
ρ 60 100 140 180 220 260迭代次数 276 166 74 6 24 31
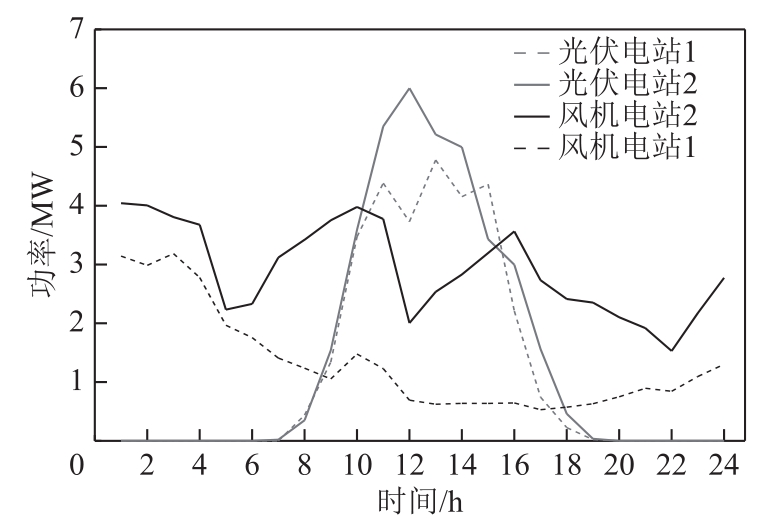
图4 RES预测功率
Fig.4 The predictive power of RES
系统交互功率、DG功率及EVA需求功率的优化结果如图5所示。
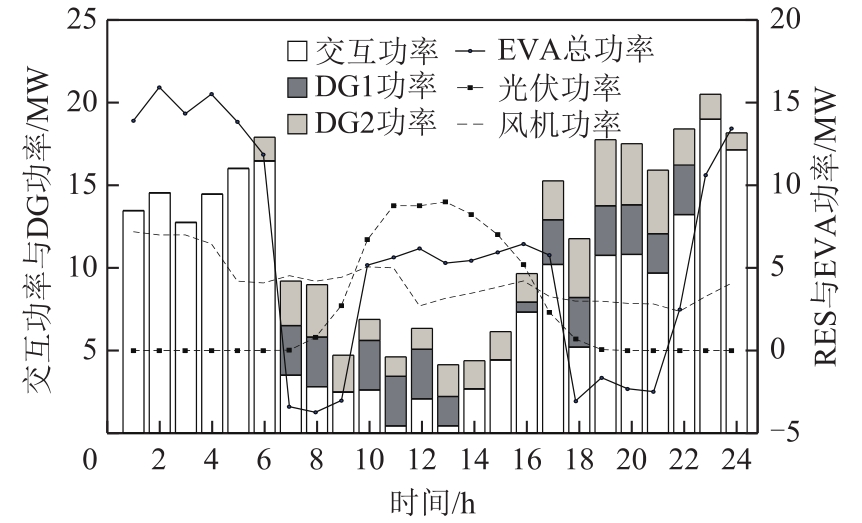
图5 鲁棒优化结果
Fig.5 The results of robust optimization
图 5中 RES的功率曲线是在ΓRS、ΓRT控制下考虑其功率波动后的出力曲线。对照图3和图5可知，在市场电价及基负荷高峰时段，为最小化系统总成本，EVA总功率为负值（EVC整体为放电状态），在市场电价较低时段，EVC功率需求增大，EVA总功率为正值。因此，并网EVC的分布式鲁棒优化，整体上也起到了良好的削峰填谷效果。此外，为降低交互功率成本，市场电价较低时，交互功率较高；市场电价较低时，交互功率较低。在0～6时段，由于市场电价较低，交互功率成本小于系统内DG的发电成本，因而此时段内交互功率较高，系统内DG则处于停机状态。在其他时段，为最小化系统运行成本，DG以最优发电功率补偿系统内的功率需求，从而降低系统交互功率。
DG成本、EVA补偿成本、交互功率成本及系统总成本如图6所示。
图6 系统的鲁棒优化成本
Fig.6 The system cost of robust operation
结合分析图5和图6，在18:00～22:00时段，系统交互功率并不高，但由于市场电价较高，系统为保证此时段内 EVC的功率需求，仍造成了较高的交互功率成本。由图6可知，在电价高峰时段内EVA补偿成本较高，在电价低谷时段内较低，这是由于电价较高时，同时也是基负荷高峰时段，EVA会调控第2类EV充电功率削减，调控第3类EV充电功率削减或进行放电，因此造成较高的 EVC调度补偿成本；相反，在电价低谷时段，EVA调控第2类和第3类EV以接近额定功率充电，调度补偿成本较小。由此可知，本文所提鲁棒优化模型可兼顾D2和D3中 EV用户的利益，有利于降低用户的并网成本。
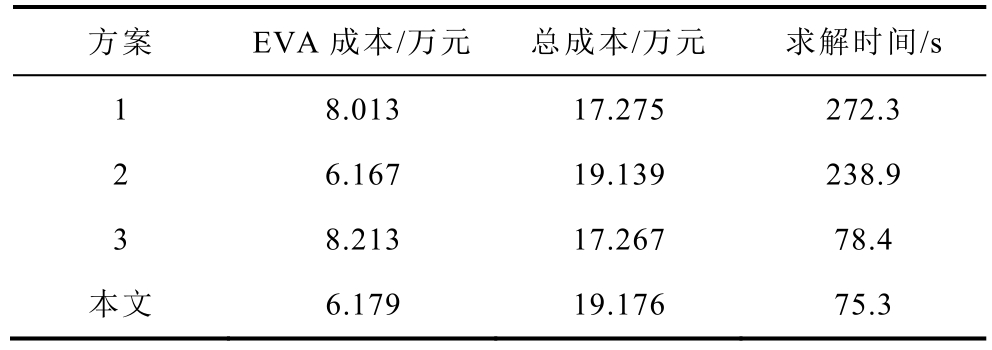
为验证本文所提模型的优势，设置如下三种方案与本文方案对比：方案1，不考虑EVC的灵活性差异（统一视为第3类EV），采用集中式优化。方案 2，考虑 EVC的灵活性差异，采用集中式优化。方案3，不考虑EVC的灵活性差异，采用本文分布式优化模型求解。
上述三种方案的其他参数与本文方案均保持一致。四种方案的鲁棒优化结果见表2。
表2 四种方案下的优化结果
Tab.2 The optimization results under four schemes
方案 EVA成本/万元 总成本/万元 求解时间/s 1 8.013 17.275 272.3 2 6.167 19.139 238.9 3 8.213 17.267 78.4本文 6.179 19.176 75.3
集中式优化即系统内所有EVC统一在配网侧进行优化。附图 2为本文方案与方案 2在每个时段内的EVA优化功率。由附图2及表2可知，集中式与分布式优化的EVA功率存在一定差异，但鲁棒总成本相近，分布式优化具有更高的求解效率；且本文设置的四个EVA所辖EVC规模不同，结合本文分布式优化模型分析，求解效率取决于EVC规模最大的 EVA，当其他三个较小规模的EVC同等扩大至相同的 EVC规模，求解效率不会受到影响。
忽略 EV的灵活性差异，即任一 EV均可参与调度，因此 EVC的灵活性扩大，EVA补偿成本也较高，但系统总成本降低；不考虑EVC的灵活性差异，虽然更具经济性优势，但这显然忽视了 EV用户的需求偏好，与实际场景存在必然矛盾。
4.3 EVA优化结果分析
EVA对所辖EVC独立优化，四个EVA在T内的优化功率如图7所示。
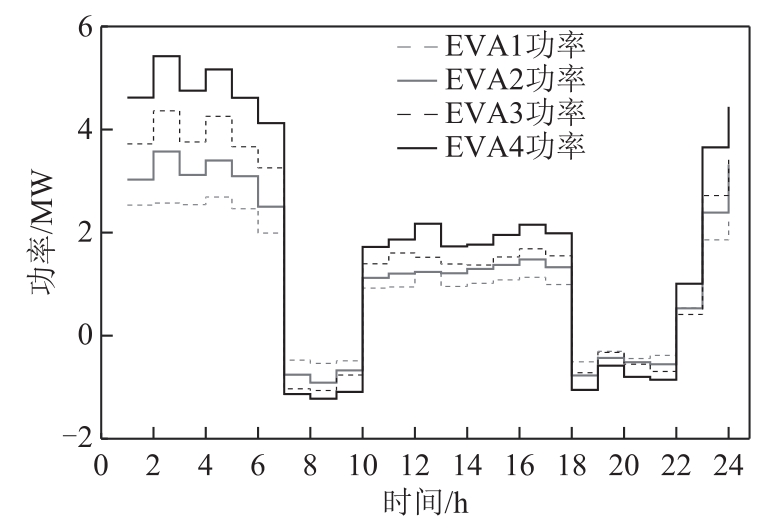
图7 A1 ～ A4在每个时段内的优化功率
Fig.7 The optimal power forA1 −A4in each time period
由图7可知，在 A 1 −A4调控下，并网EVC表现均为电价低谷时段充电，电价高峰时段放电。整体上，EVC规模越大，功率需求也越大；EVC规模较大的 EVA具有更大的灵活性，EVC整体放电时，A1 ～ A4的放电功率依次增大。EVA的实际功率需求及放电能力取决于D2,j、D3,j中EVC的规模及各EV的并、离网时间，若EVA中EVC规模较大，但第2、第3类EV数量较小时，EVA仍具有较小的灵活性。在特定时段内，当EVC规模较大且第2、第3类EV数量也较大时，因EVC的灵活性较大，EVA的实际功率可能较低。 A 1 ～ A4中三类 EV在每个时段内的并网数量如附图1所示。
为直观体现三类 EV并网需求方式的差异，在Di , j (i = 1 ,2,3; j = 1 ,2,3,4)中随机抽取一辆 EV，记为li,j，得到12辆EV的SOC变化曲线如图8所示。
图8 A1 ～ A4中三类EV在并网时段内的SOC变化
Fig.8 The changes of SOC for three EV types in A1 −A4
A1 ～ A4中三类EV离网时的SOC均在0.95以上，保证了EV的用电需求。D1,j中的EV并网功率不可调节，EV无论在高峰时段或低谷时段并网，均以额定功率充电至期望SOC；D2,j和D3,j中任一EV，当SOC低于阈值0.4时，均先保持额定功率充电至0.4以上；当SOC高于阈值时，在负荷及电价高峰时段， A 1 ～ A4调控D2,j中 EV降低充电功率或延缓充电，SOC增长缓慢甚至停滞， A 1 ～ A4调控D3,j中EV放电，SOC降低，但EV放电时保证了SOC在0.4以上。需要注意的是，D2,j与D3,j中的EV在EVA调控下的充、放电状态同时受到用户离网时段的制约，虽然D2,j与D3,j中EV可调度，若EV在网时长较短，为满足用电需求，实际并网功率并不会被削减，如车辆l2,1和车辆l3,4。因此，优化模型充分考虑了用户的需求偏好。
4.4 可变参量对鲁棒优化的影响分析
本文建立的鲁棒优化模型中ζi,t、 P A j ,t 的功率区间和ΓRS、ΓRT、ΓAS、ΓAT的取值及三类 EV占比均对鲁棒优化结果具有直接影响。
4.4.1 ζi,t、 P A j ,t 功率区间对鲁棒优化的影响
ζi,t 、 P A j ,t 的功率区间受预测技术的限制，假设ζi,t 、P A j ,t 的预测值与实际值的误差均在5%～30%内。分别取ζi,t、P A j ,t 预测误差为5%、10%、15%、20%、25%、30%。ΓRS、ΓRT、ΓAS、ΓAT取值及三类EV的占比均保持不变。ζi,t、 P A j ,t 在不同预测误差下的鲁棒总成本如图9所示。
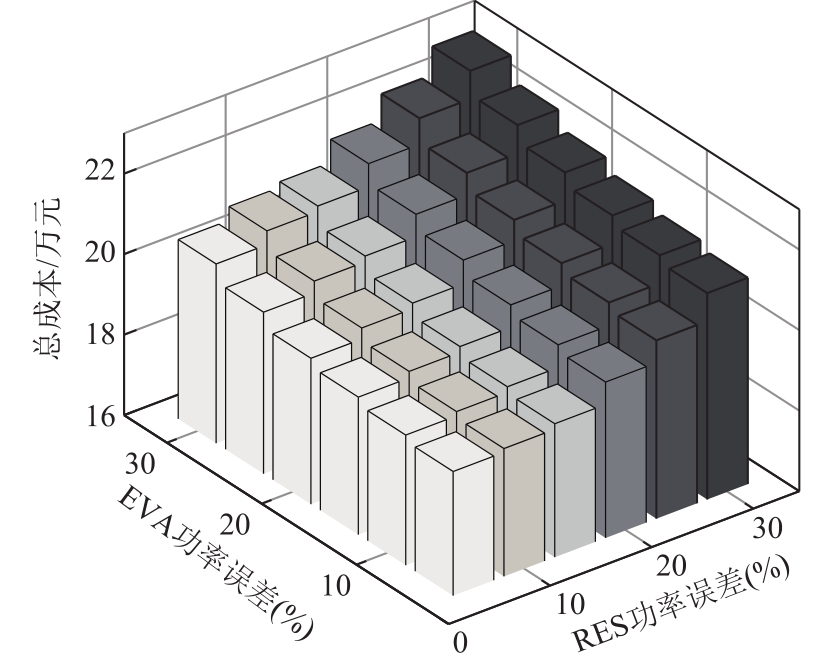
图 9 ζi,t、 P A j ,t 的预测误差与鲁棒成本的关系
Fig.9 The relationship between robust cost and predictive deviation of ζi,t, P A j ,t
随着ζi,t、 P A j ,t 预测误差的增大，系统的鲁棒成本也逐渐增大。当ζi,t与 P Aj ,t 的误差为 5%时，总成本为19.084万元；当ζi,t与 P A j ,t 的误差为30%时，总成本为22.89万元。
4.4.2 鲁棒控制系数对鲁棒优化的影响
ζi,t 、 P A j ,t 的预测误差分别取 10%和 5%且三类EV比例保持不变。系统鲁棒总成本与控制系数（本文取 Γ RS = Γ AS = Γ S，ΓRT = Γ AT = Γ T ）的关系如图10所示。
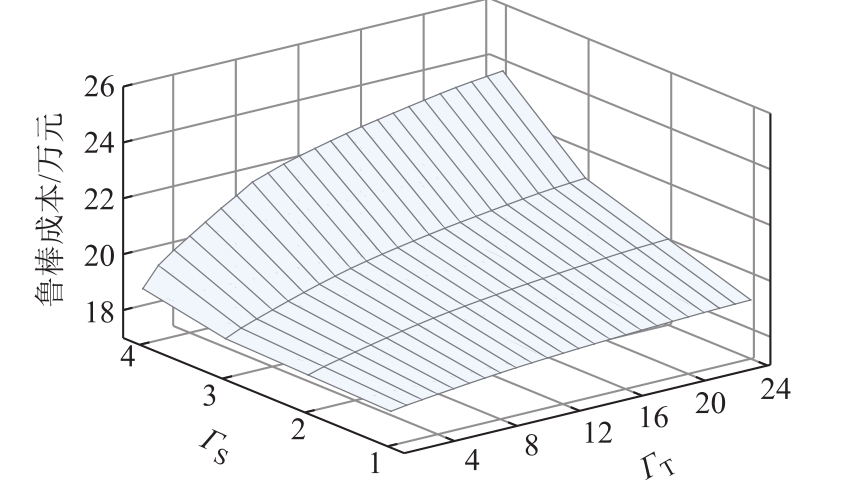
图10 鲁棒总成本与SΓ、TΓ取值的关系
Fig.10 The relationship between robust cost and the value of SΓ,TΓ
ΓS、ΓT取值越大，模型越保守。ΓS、ΓT取值越小，模型越激进。如图10，随着ΓS、ΓT取值的增大，系统鲁棒总成本也逐渐增大。模型最保守（ Γ T = 2 4,Γ S = 4 ）时，系统的鲁棒总成本为 23.671万元。实际应用中，可根据实际需求选取合适的ΓS、ΓT值。
4.4.3 三类EV占比对鲁棒优化的影响
取ζi,t和 P A j ,t 的预测误差分别为10%和5%。ΓS、ΓT取值分别为2和8。第2类和第3类EV占比均在区间[0,0.5]内取值。图11为系统鲁棒总成本与第2类及第3类EV占比的关系。
图11 三类EV不同占比下的鲁棒总成本
Fig.11 The robust cost in different proportion of three types of EV
r2 , j和r3,j的取值步长均为 0.02，第 1类 EV占比为 1 − r 2 , j − r 3,j (r2,j、r3,j分别为第2和第3类EV的占比)。如图11所示，系统总成本随着r2,j和r3,j的减小而增大，当 r2 , j =0、r3 , j=0时，总成本为29.834万元；当 r2 , j = 0 .5、r3 , j = 0 .5时，总成本为18.898万元。因第3类EV灵活性与第2类相比较大，第3类EV占比对系统总成本的影响比第2类显著。
5 结论
本文考虑了RES间歇性及EVA功率波动性，提出了EVC并网的分布式鲁棒优化调度模型，并进行了算例验证。研究可得以下结论：
1）考虑EV用户的偏好，对并网EVC进行细分，建立了计及用户需求偏好的并网EV控制模型。
2）在时间、空间、功率区间三个维度构造表征RES及EVA波动特征的鲁棒多面体不确定集合；并以成本最小为优化目标，通过鲁棒对等转换构建了可解耦迭代求解的鲁棒优化模型。
3）采用ADMM算法实现了模型的分布式迭代求解。算例验证了所提模型在最小化系统成本的同时兼顾了 EV用户的需求偏好；算例分析了模型中可变参量对鲁棒优化模型的影响，给实际应用中模型参数的选择提供了一定指导。
后续研究中将进一步关注单台EV的动态不确定性，如EV用户与EVA的实时互动（用户调整阈值，并网方式切换等），聚焦实时优化调度策略研究。
附 录
DG参数和并网EV参数分别见附表1和附表2。
附表1 DG参数
App.Tab.1 The parameters of DGs
DGs DG1 DG2 P /MW 3 4 max P /MW 0.8 1 a/元 163 169 b/(元/MW) 366 327 c/(元/MW2) 0.0228 0.386 min C /元C /元97 97 ton/h toff/h on off 65 65 1 1 2 2 P /(MW/0.5h)umax P /(MW/0.5h)dmax 1.5 1.5 2 2
附表2 并网EV参数
App.Tab.2 The parameters of grid-connected EV
参 数 数 值额定充电功率 rP /(kW/h) 10 c,l额定放电功率 rP /(kW/h) 10储能电池容量El/(kW·h) 40充电效率ηc,l 0.9放电效率ηd,l 0.9期望荷电水平Sl,ex 0.95放电电能阈值Sl,dthr 0.4功率削减阈值Sl,cthr 0.4 d,l
附图1 A1 ～ A4中3类EV在每个时段的并网数量
App.Fig.1 The number of three types of EV for per period in A1 ～ A4
附图2 集中式与分布式优化下的EVA功率
App.Fig.2 The EVA optimization results of centralized and distributed optimization
[1]张潇, 栗然, 马涛, 等. 基于主从博弈和贪心策略的含电动汽车主动配电网优化调度[J]. 电力自动化设备, 2020, 40(4): 103-110.Zhang Xiao, Li Ran, Ma Tao, et al. Stackelberg game and greedy strategy based optimal dispatch of active distribution network with electric vehicles[J]. Electric Power Automation Equipment, 2020, 40(4): 103-110.
[2]吴赋章, 杨军, 林洋佳, 等. 考虑用户有限理性的电动汽车时空行为特性[J]. 电工技术学报, 2020,35(7): 1563-1574.Wu Fuzhang, Yang Jun, Lin Yangjia, et al. Research on spatiotemporal behavior of electric vehicles considering the users’ bounded rationality[J].Transactions of China Electrotechnical Society, 2020,35(7): 1563-1574.
[3]Zhao Jian, Wan Can, Xu Zhao, et al. Risk-based dayahead scheduling of electric vehicle aggregator using information gap decision in theory[J]. IEEE Transactions on Smart Grid, 2017(8): 1609-1618.
[4]Wei Congying, Xu Jian, Liao Siyang, et al.Aggregation and scheduling models for electric vehicles in distribution networks considering power fluctuations and load rebound [J]. IEEE Transactions on Sustainable Energy, 2020, 11: 2755-2764.
[5]陈吕鹏, 潘振宁, 余涛, 等. 基于动态非合作博弈的大规模电动汽车实时优化调度[J]. 电力系统自动化, 2019, 43(24): 32-40.Chen Lüpeng, Pan Zhenning, Yu Tao, et al. Real-time optimal dispatch for large-scale electric vehicles based on dynamicnon-cooperative game theory[J]. Automation of Electric Power Systems, 2019, 43(24): 32-40.
[6]孔顺飞, 胡志坚, 谢仕炜, 等. 含电动汽车充电站的主动配电网二阶段鲁棒规划模型及其求解方法[J].电工技术学报, 2020, 35(5): 1093-1105.Kong Shunfei, Hu Zhijian, Xie Shiwei, et al. Twostage robust planning model and its solution algorithm of active distribution network containing electric vehicle charging stations[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1093-1105.
[7]杨晓东, 张有兵, 蒋杨昌, 等. 微电网下考虑分布式电源消纳的电动汽车互动响应控制策略[J]. 电工技术学报, 2018, 33(2): 390-400.Yang Xiaodong, Zhang Youbing, Jiang Yangchang, et al. Renewable energy accommodation-based strategy for electric vehicle considering dynamic interaction in micro grid[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 390-400.
[8]Wang Yuntao, Su Zhou, Xu Qichao, et al. A novel charging scheme for electric vehicles with smart communities in vehicular networks[J]. IEEE Transactions on Vehicular Technology, 2019, 68(99):8487-8501.
[9]Zhang Wenjie, Oktoviano G, Quan Hao, et al. A multiagent based integrated volt-var optimization engine for fast vehicle-to-grid reactive power dispatch and electric vehicle coordination[J]. Applied Energy, 2018,229: 96-110.
[10]Hao Ying, Dong Lei, Liang Jun, et al. Power forecasting-based coordination dispatch of PV power generation and electric vehicles charging in microgrid[J]. Renewable Energy, 2020, 155: 1191-1220.
[11]Mazidi M , Rezaei N , Ghaderi A . Simultaneous power and heat scheduling of microgrids considering operational uncertainties: A new stochastic p-robust optimization approach[J]. Energy, 2019, 185: 239-253.
[12]梅生伟, 申铁龙, 刘康志. 现代鲁棒控制理论与应用[M]. 北京: 清华大学出版社, 2003.
[13]Borges N, Soares J, Vale Z. A robust optimization for day-ahead microgrid dispatch considering uncertainties[J]. IFAC Papers On Line, 2017, 50(1):3350-3355.
[14]石文超, 吕林, 高红均, 等. 考虑需求响应和电动汽车参与的主动配电网经济调度[J]. 电力系统自动化, 2020, 44 (11): 41-51.Shi Wenchao, Lü Lin, Gao Hongjun. Economic dispatch of active distribution network with participation of demand response and electric vehicle[J]. Automation of Electric Power Systems,2020, 44(11): 41-51.
[15]Zhou Yaqin, Kumar R, Tang Shaojie. Incentive-based distributed scheduling of electric vehicle charging under uncertainty[J]. IEEE Transactions on Power Systems, 2019, 34(1): 3-11.
[16]Rezaei N, Khazali A, Mazidi M, et al. Economic energy and reserve management of renewable-based microgrids in the presence of electric vehicle aggregators: a robust optimization approach[J]. Energy,2020, 201: 117629.
[17]卢志刚, 王荟敬, 赵号, 等. 含 V2G的虚拟电厂双层逆鲁棒优化调度策略[J]. 电网技术, 2017, 41(4):1245-1252.Lu Zhigang, Wang Huijing, Zhao Hao, et al. Strategy of bilevel inverse robust optimization dispatch of virtual power plant containing V2G[J]. Power System Technology, 2017, 41(4): 1245-1252.
[18]Shi Ruifeng, Li Shaopeng, Zhang Penghui, et al.Integration of renewable energy sources and electric vehicles in V2G network with adjustable robust optimization[J]. Renewable Energy, 2020: 153.
[19]Baringo L, Amaro R S. A stochastic robust optimization approach for the bidding strategy of an electric vehicle aggregator[J]. Electric Power Systems Research, 2017, 146(5): 362-370.
[20]杨晓东, 张有兵, 翁国庆, 等. 基于虚拟电价的电动汽车充放电优化调度及其实现机制研究[J]. 电工技术学报, 2016, 31(17): 52-62.Yang Xiaodong, Zhang Youbing, Weng Guoqing, et al.Virtual time-of-use tariffs based optimal scheduling and implementation mechanism of electric vehicles charging and discharging[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 52-62.
[21]叶畅, 苗世洪, 李姚旺 等. 基于改进不确定边界的主动配电网鲁棒优化调度[J]. 电工技术学报,2019, 34(19): 4084-4095.Ye Chang, Miao Shihong, Li Yaowang. Robust optimal scheduling for active distribution network based on improved uncertain boundary[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4084-4095.
[22]邢强, 陈中, 黄学良, 等. 基于数据驱动方式的电动汽车充电需求预测模型[J]. 中国电机工程学报,2020, 40(12): 3796-3813.Xing Qiang, Chen Zhong, Huang Xueliang, et al.Electric vehicle charging demand forecasting model based on data-driven approach[J]. Proceedings of the CSEE, 2020, 40(12): 3796-3813.
[23]程亦直, 张沛超. 配电网中电动汽车的实时滚动交易式充电管理[J]. 中国电机工程学报, 2019, 39(19):5703-5713, 5898.Cheng Yizhi, Zhang Peichao. Real-time rolling transactive charging management of electric vehicles in distribution network[J]. Proceedings of the CSEE,2019, 39(19): 5703-5713, 5898.
[24]Mazidi M, Monsef H, Siano P, et al. Incorporating price-responsive customers in day-ahead scheduling of smart distribution networks[J]. Energy Conversion and Management, 2016, 115: 103-116.
[25]黄伟, 熊伟鹏, 华亮亮, 等. 基于动态调度优先级的主动配电网多目标优化调度[J]. 电工技术学报,2018, 33(15): 3486-3498.Huang Wei, Xiong Weipeng, Hua Liangliang, et al.Multi-objective optimization dispatch of active distribution network based on dynamic schedule priority[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3486-3498.
[26]Bertsimas D, Sim M. Robust discrete optimization and network flows[J]. Mathematical Programming, 2003,98(1): 49-71.
[27]Li Zhigang, Wu Wenchuan, Zeng Bo, et al. Decentralized contingency-constrained tie-line scheduling for multi-area power grids[J]. IEEE Transactions Power Systems, 2017, 32(1): 354-367.