
图1 自由金属微粒运动观测平台
Fig.1 Observation platform of metal particle movement
摘要 直流GIL中线形金属微粒受力运动极易引发气体间隙击穿或者绝缘子沿面闪络,降低GIL的绝缘性能,严重影响直流输电系统的安全可靠运行。为研究直流GIL中线形金属导电微粒电动力学行为机理,搭建自由微粒实验装置和观测平台,并建立直流下微粒电动力学模型。通过实验与仿真相结合的方法,获得线形金属微粒荷电特性、启举与运动特性以及微粒运动导致的气隙击穿特性,并从微观角度解释了微粒启举与运动现象形成的原因。研究结果表明,线形启举电压只与半径有关,与长度和电压极性无关,随着半径增大,启举电压升高,直流电压极性不影响金属微粒启举电压幅值;线形微粒的运动及导致的气隙击穿与微粒半径、长度和电压极性有关,线形金属微粒半径小、长度增加时容易导致气隙击穿;线形金属微粒形状的不规则使得电场畸变作用加强,极性效应更明显。电晕极性效应导致正负极性下线形微粒的启举与运动及运动致气隙击穿特性呈现出明显的规律,当达到启举电压时,正极性下,线形金属微粒一端抬起后,在下极板小幅跳跃、旋转或者直立,难以贯穿气隙;负极性下,线形金属微粒贯穿气隙运动,极易出现飞萤现象,为直流GIL中线形金属微粒污染防治提供了理论指导。
关键词:直流GIL 线形金属微粒 电动力学行为 启举 运动
气体绝缘金属封闭输电线路(Gas Insulated transmission Line, GIL)因其电压等级高、输送容量大、电磁辐射小、敷设灵活性强等特点具有广阔的发展前景[1-2]。然而,在实际GIL生产、组装、输运和运行过程中将会产生球形、线形等金属微粒,带电微粒受到库仑力、重力、气体黏滞力等作用力,在GIL腔体内部运动或者粘附在绝缘子表面,使周围电场发生畸变,从而引发气体击穿或者绝缘子沿面闪络,降低GIL的绝缘性能,严重影响到直流输电系统的安全可靠运行[3-4]。因此,有必要开展直流GIL中金属微粒的荷电特性、启举与运动特性以及微粒运动导致的气隙击穿特性研究,对GIL绝缘设计以及金属微粒活性抑制措施的制定具有重要意义[5]。
国内外诸多学者针对金属微粒荷电与运动及导致的气隙击穿特性等方面开展了广泛的研究。裸电极下金属微粒带电来源主要有金属电极传导带电、微粒与电极之间进行微放电和微粒尖端电晕放电[6-7]。文献[8-9]推导了静止于平板电极表面金属微粒带电量解析公式。文献[10-12]研究了GIL中不同类型金属微粒的带电及受力机理,在分析微粒碰撞弹性恢复系数的基础上,归纳了电压类型、微粒尺寸与微粒的运动特性和设备绝缘劣化之间的关系和规律。文献[13-14]通过计算得出楔形不均匀直流电场导电金属微粒的启举电压,运用Runge-Kutta方法建立金属微粒运动仿真模型、Monte-Carlo方法模拟金属微粒运动过程中随机变化的施加电压等参数,研究微粒启举及运动特性。文献[15-16]提出了金属微粒运动过程中的带电量及碰撞恢复系数的解析计算方法,实验结合仿真,研究金属微粒运动特性的影响因素。文献[17-18]研究了楔形不均匀直流电场下金属微粒启举前及运动过程中金属微粒表面电场畸变的瞬时情况。
金属微粒的运动在一定条件下会导致气隙击穿。文献[19-21]指出,金属微粒的状态会影响气隙击穿,即自由金属微粒较固定金属微粒更易造成气隙击穿。文献[22]分析了GIS中交直流下自由金属微粒运动导致的气隙击穿,结果表明,交流电压下,金属微粒受到交变的电场力,使得微粒在下极板附近“跳跃”,难以贯穿气隙;在单极性的直流电压下,金属微粒受到单向的电场力,当满足一定条件时,金属微粒会发生贯穿气隙的运动,引起气隙击穿。文献[23-26]指出线形金属微粒因其形成的稳定电晕引发气隙击穿,球形金属微粒造成气隙击穿是由于电子崩发展形成流注。
现有计算模型多为球形微粒,实际上线形金属微粒的危害更大,对设备绝缘性能的威胁也最大[27-30]。对线性微粒的运动特性及其影响因素和运动微粒引起的气隙击穿放电特性的研究多采用实验的方法,缺乏对线性微粒典型运动现象及微粒运动导致气体绝缘击穿机理的微观分析。
本文搭建自由微粒运动实验观测平台,获得线形微粒启举与运动特性以及微粒运动导致的气隙击穿特性。考虑气体中空间电荷的产生、复合、迁移、扩散等,建立多物理场耦合作用下直流线形微粒电动力学行为模型,分析线形金属微粒的荷电机制,探究微粒与空间电荷的协同耦合作用引发电动力学行为机理,从微观角度对典型微粒运动行为和气隙击穿的关联特性进行分析。
由于同轴圆柱结构的GIL内部电场多为稍不均匀电场,仅在如绝缘子支撑、高压导体末端、金属微粒驱赶装置和接头附近等处为不均匀电场,因此,可以用便于分析研究的平板电极来模拟GIL[31]。现有研究结论表明,气压和气体类型对金属微粒的启举电压无影响[32]。因此,本文采用空气中平板电极进行实验。
搭建自由金属微粒运动观测平台如图1所示,平板电极上极板接直流源,下极板接地,采用高速相机(Fastec HiSpec5)观测微粒运动。实验选取半径为0.1mm、0.25mm、0.4mm,长度为2~15mm的铝制线形微粒。每组实验重复5次以上,记录数据。

图1 自由金属微粒运动观测平台
Fig.1 Observation platform of metal particle movement
K. I. Sakai使用势函数法对平行板电极间静电场求解[33],线形微粒的带电量与其位置和形态有关,平躺时微粒的带电量q[34]为
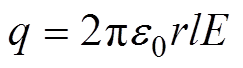 (1)
(1)式中,r为微粒半径;e0为真空介电常数;E为平板电极间电场强度;l为线形微粒长度。
所受库仑力F可表示为
 (2)
(2)式中,k为面电荷引起的镜像修正系数[8]。
线形微粒所受的重力为
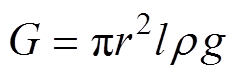 (3)
(3)式中,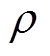 为微粒密度;g为重力加速度。
为微粒密度;g为重力加速度。
微粒运动过程中会受到气体的粘滞阻力和浮力作用,但微粒密度远大于空气密度,可忽略所受到的浮力。气体的粘滞阻力与运动速度有关,初始运动阶段,微粒速度极小,可忽略气体阻力作用。
微粒所受库仑力克服重力时启举,由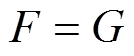 得线形微粒的启举电压为
得线形微粒的启举电压为
 (4)
(4)式中,d为极板间距。
由式(4)可知,线形微粒的启举电压只与半径有关,与长度和电压极性无关。
线形微粒在正负极性电压下不同半径、不同长度线形微粒的启举电压(取每组实验平均值)如图2和图3所示。
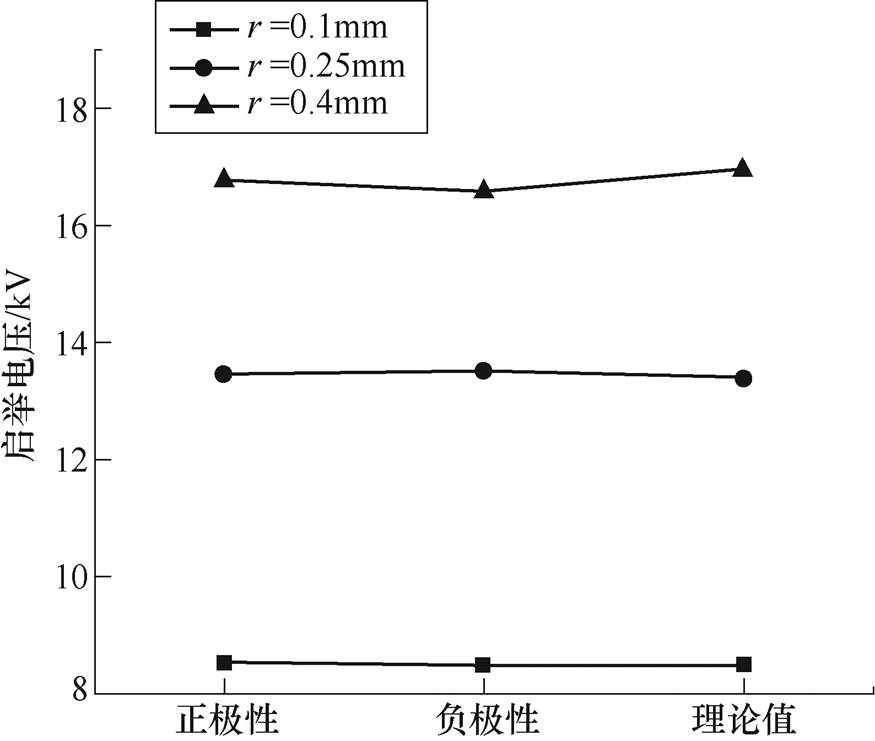
图2 正负极性下不同半径线形微粒启举电压
Fig.2 Lifting voltage of linear particles with different radius under positive and negative polarity

图3 正负极性下不同长度线形微粒启举电压
Fig.3 Lifting voltage of linear particles with different lengths under positive and negative polarity
由图2和图3可知,线形微粒启举电压实验值基本与式(6)理论值预测值相符,启举电压与半径有关,与长度和电压极性无关,随着半径增大,启举电压升高。
实验采用不同长度的半径0.25mm的线形微粒,观测到线形微粒的运动及导致的气隙放电随着长度和电压极性的变化呈现出明显的规律,如图4~图7所示:微粒一端先抬起(见图4a),随着长度增大,正极性下,跳起往返运动、多次碰撞击穿(见图4b、图5a)→下极板旋转、升高电压击穿(见图4c、图5b和图5c)→下极板直立、直接击穿(见图4d、图5d);负极性下,跳起往返运动(见图6a)→“飞萤”(见图6b)→上极板旋转(见图6c)→上极板直立,大概率一运动就击穿(见图6d、图7)。

图4 正极性下不同长度线形微粒运动
Fig.4 Motion of linear particles with different lenghths under positive polarity

图5 正极性下不同长度线形微粒导致气隙放电
Fig.5 Air gap discharge caused by linear particles with different lenghths under positive polarity

图6 负极性下不同长度线形微粒运动
Fig.6 Motion of linear particles with different lenghths under negative polarity

图7 负极性下不同长度线形微粒导致气隙放电
Fig.7 Air gap discharge caused by linear particles with different lenghths under negative polarity
正极性下,微粒长度为5~10mm,随着电压升高,一端先抬起,并伴随着不同程度的以电力线方向为轴心旋转和倾斜等“晃动”,另一端固定不动或也在电极表面作旋转运动,长度越长,旋转转矩越小,倾斜程度越低,轻微晃动后处于相对平衡的“站立”状态;范围内长度越短,晃动越剧烈,继续升高达到启举电压,向上运动,在多次碰撞中发生击穿,长度越长,击穿电压越低。长度大于10mm,微粒一旦启举马上发生击穿,微粒端部伴有剧烈的局部放电,在电极之间形成明亮的流注;微粒长度较短的5mm,一端抬起后,直接跳起,在极板间做无规律旋转的“谐振”运动,直至击穿。
负极性下,长度小于4mm,一端抬起后,直接跳起,在极板间做无规律旋转的“谐振”运动;长度大于4mm,随着长度的增加,飞萤时与上极板间的距离减小,并出现和正极性相似的在上极板“晃动”和“站立”。微粒大概率一运动就发生击穿,两端形成明亮的流注,且运动中存在多次放电。
比较正负极性下不同尺寸线形微粒的启举和击穿电压,如图8所示。
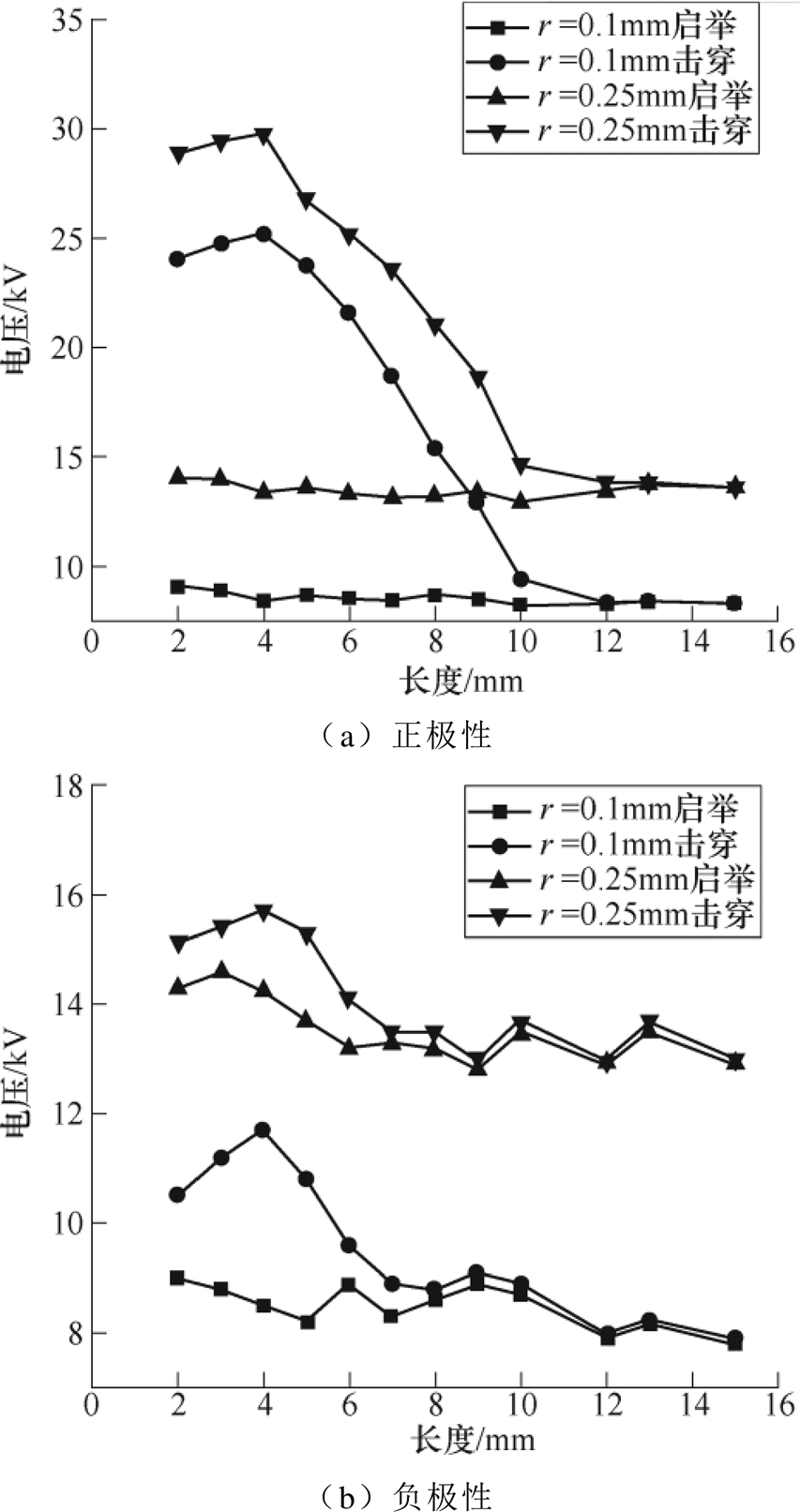
图8 正负极性下不同尺寸线形微粒启举与击穿电压
Fig.8 Lifting and breakdown voltages of linear particles of different sizes under positive and negative polarity
由图8可知,正极性下,长度较小的线形微粒随着长度增加,击穿电压增大,半径越小,启举与击穿电压越低;长度较大的微粒的击穿电压下降幅度随着长度增加明显增大,且微粒的长度越长,击穿电压越接近启举电压,半径越小,启举与击穿电压越低。负极性下,线形微粒长度较小的,随着长度增加,击穿电压增加,半径越小,启举与击穿电压越低;长度较大的,击穿电压逐渐接近启举电压。线形微粒在负极性的击穿电压明显小于正极性,且较短长度的微粒易发生击穿。
线形微粒电动力学模型主要由控制静电场中电势分布的泊松方程、控制空间电荷场中电荷分布的方程及控制流场中速度分布的Navier-Stokes方程构成。
GIL内静电场满足泊松方程,有
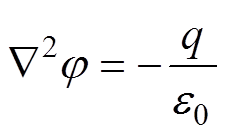 (5)
(5)式中,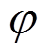 为电势。
为电势。
考虑电场作用下空间电荷的产生、复合及迁移、扩散等物理过程,建立空间电荷输运方程[35]为
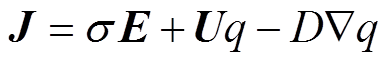 (6)
(6)式中, 为空气电导率;
为空气电导率;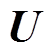 为空气流动速度;D为离子扩散系数;
为空气流动速度;D为离子扩散系数;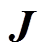 为电流密度。
为电流密度。
平躺时,线形微粒端部电场强度发生畸变,导致电子集中在微粒端部顶点处,与下板接触点存在较大的梯度差。当电压升高至启举电压,微粒所受的库仑力克服重力使微粒微微抬起,悬浮的微粒尖端即会与下极板产生不同程度的电晕放电,放电的随机性,以及线形微粒存在表面粗糙程度不同、质量分布不均等因素,导致微粒电荷量及电荷分布存在随机性,随机的旋转力矩迫使微粒一端先抬起,即出现一个较小的偏角。
极板内空气可以看作不可压缩流体[35],其控制方程为Navier-Stokes方程,有
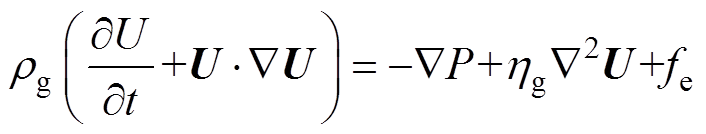 (7)
(7)式中,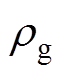 为空气密度;P为气体压力;
为空气密度;P为气体压力;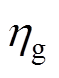 为空气动力学黏度;fe为体积力。
为空气动力学黏度;fe为体积力。
空气放电过程较为复杂,为了简化计算,将空气简化为N2和O2的混合气体,N2 O2=4
O2=4 1。基本模型包括电子连续性方程、重粒子多组分扩散运输方程、动量平衡方程、能量约束方程耦合泊松方程。并利用Maxwell电子能量分布函数作为Boltzmann方程的解,计算电子迁移率、扩散系数和碰撞速率系数[36-38]。
1。基本模型包括电子连续性方程、重粒子多组分扩散运输方程、动量平衡方程、能量约束方程耦合泊松方程。并利用Maxwell电子能量分布函数作为Boltzmann方程的解,计算电子迁移率、扩散系数和碰撞速率系数[36-38]。
电子连续性方程[36]为
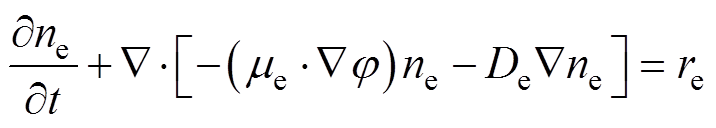 (8)
(8)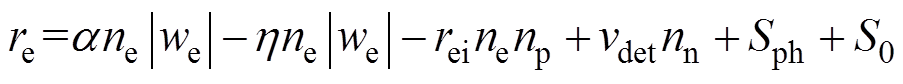 (9)
(9)
式中,ne为电子的数密度;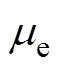 为电子迁移率;De为电子扩散系数;re为产生电子的净速率;we为电子漂移速度;
为电子迁移率;De为电子扩散系数;re为产生电子的净速率;we为电子漂移速度;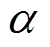 为电离系数;
为电离系数; 为附着系数;rei为电子-离子复合系数;np为正离子的数密度;vdet为解离系数;nn为负离子的数密度;Sph为光电离速率;S0为初始电子出现率。
为附着系数;rei为电子-离子复合系数;np为正离子的数密度;vdet为解离系数;nn为负离子的数密度;Sph为光电离速率;S0为初始电子出现率。
重粒子(正离子、负离子和中性粒子)多组分输运方程[37]表示为
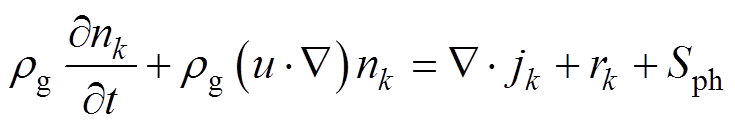 (10)
(10)式中,u为流体平均速度;nk为粒子k的数密度;jk为粒子k的扩散通量;rk为粒子k的化学反应速率。
电子能量约束方程[38]为
 (11)
(11)式中,kB为Boltzmann常数;Te为电子温度;x为电极间的轴向距离;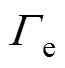 为电子通量;e为元电荷;
为电子通量;e为元电荷;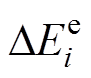 为气体反应i中发生非弹性碰撞的每个电子的能量损失;ri为反应i的进度;me和mk分别为电子和粒子k的质量;ve为电子动量传递碰撞频率;Qe为电子热流。
为气体反应i中发生非弹性碰撞的每个电子的能量损失;ri为反应i的进度;me和mk分别为电子和粒子k的质量;ve为电子动量传递碰撞频率;Qe为电子热流。
重粒子动量方程[39]为
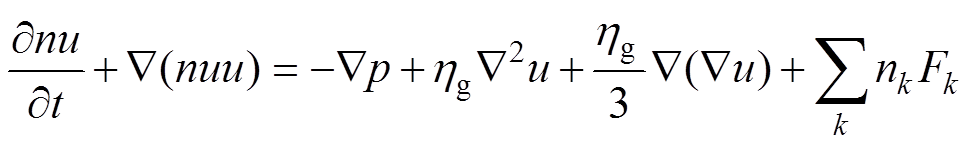 (12)
(12)式中,n为重粒子的数密度;p为重粒子所有分压的总和;Fk为作用在粒子k上的体积力。
简化的模型方程[40]为
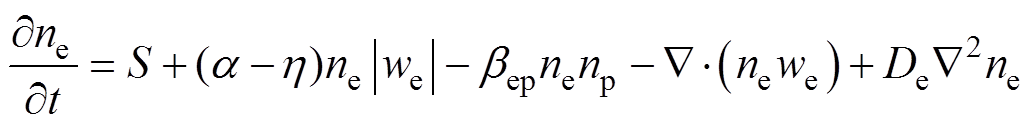 (13)
(13)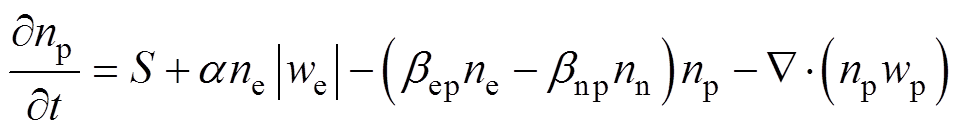 (14)
(14)
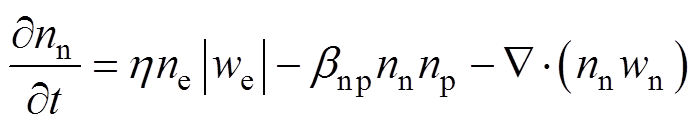 (15)
(15)
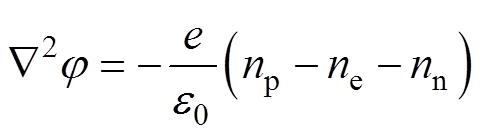 (16)
(16)式中,S为光电离引起的浓度变化量;we、wp和wn分别为电子、正离子和负离子的漂移速度;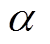 、
、 分别为电离系数、附着系数;
分别为电离系数、附着系数;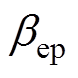 、
、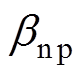 分别为电子和负离子的复合系数[41]。
分别为电子和负离子的复合系数[41]。
仿真选取半径0.25mm,长度5mm的铝制线形微粒,缓慢升高电压至式(4)理论启举电压,此时,平躺在下极板中心位置线形微粒周围电场强度如图9所示。
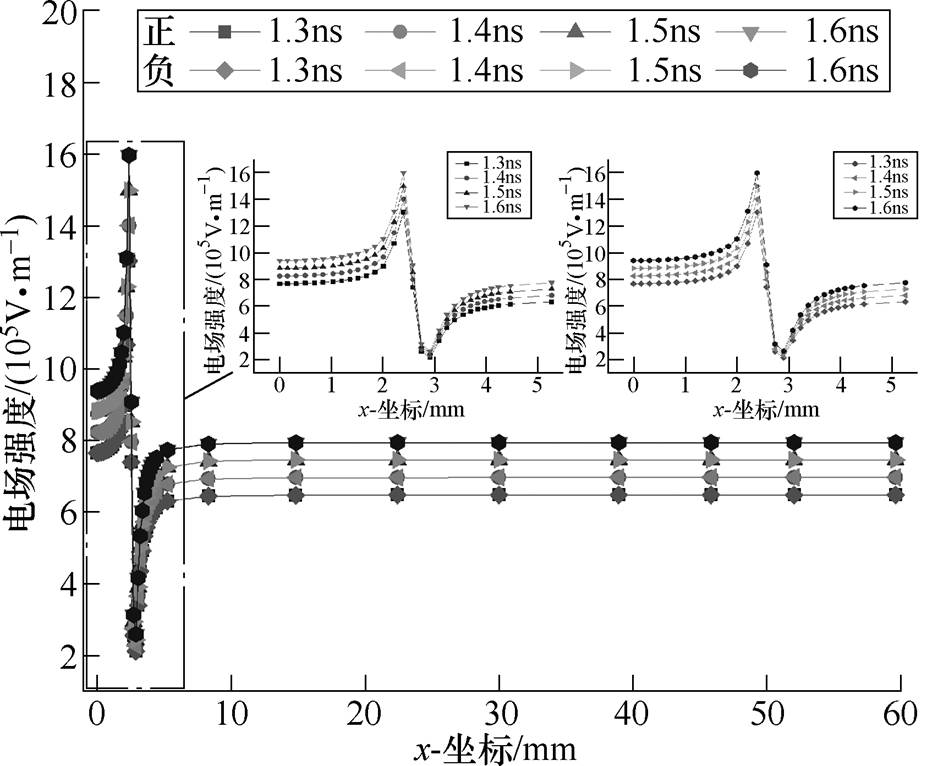
图9 线形微粒沿轴线方向电场强度
Fig.9 The electric field intensity along the axis of linear particles
平躺时,线形微粒端部电场强度发生畸变,导致电子集中在微粒端部顶点处,与下板接触点存在较大的梯度差。当电压升高至启举电压,微粒所受的库仑力克服重力使微粒微微抬起,悬浮的微粒尖端即会与下极板产生不同程度的电晕放电,放电的随机性,以及线形微粒存在表面粗糙程度不同、质量分布不均等因素,导致微粒电荷量及电荷分布存在随机性,随机的旋转力矩迫使微粒一端先抬起,即出现一个较小的偏角[6]。
设置偏角为1°,对比平躺和存在1°偏角线形微粒表面电荷和电场分布,线形微粒沿轴线方向表面电荷密度和电场强度如图10所示。可知,平躺在下极板,即偏角为0°时,微粒表面电荷主要集中在两端,呈近梯形的对称分布;即使是较小的1°偏角也会导致微粒表面的电荷呈现左右不均的情况,抬起端电荷分布较多,所受电场力较大,更易抬起。这就解释了施加电压后,与半径、长度和电压极性无关,线形微粒均出现如图4a所示的实验现象。因此线形微粒在启举过程时,往往是一端先抬起。

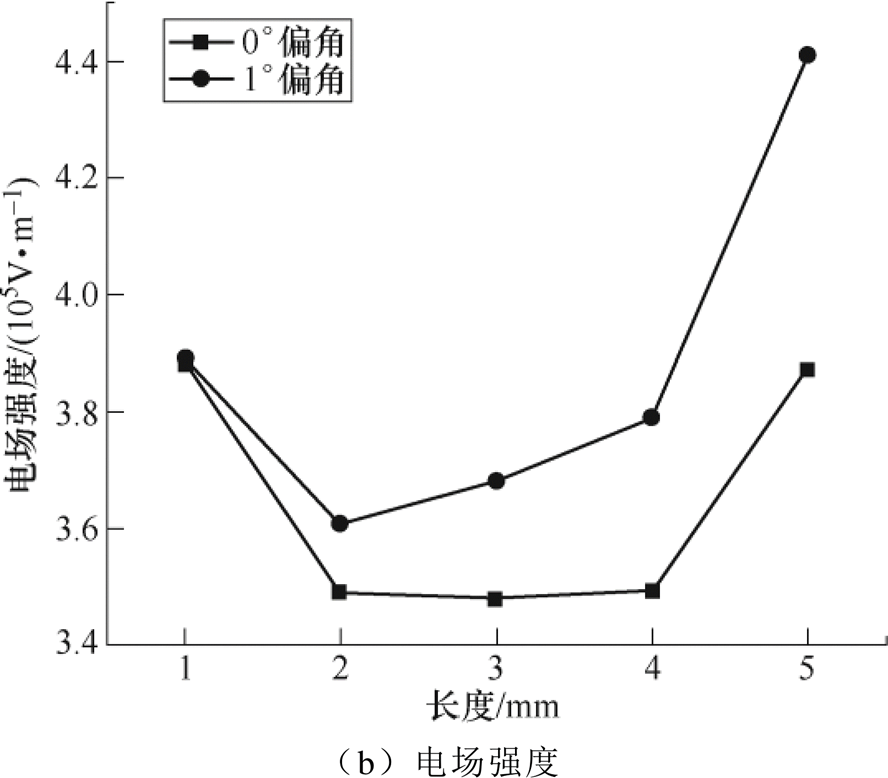
图10 线形微粒沿轴线方向表面电荷密度和电场强度
Fig.10 The surface charge density and electric field intensity along the axis of linear particles
达到启举电压,线形微粒一端抬起,另一端与下极板存在微小间隙。微小间隙产生严重的电场畸变,使得微粒底端与下极板产生微放电而等电位[10]。因此,可将微粒当作极板上的突起,等效为“站立”的微粒。
初始阶段,随着电压升高,正负极性下电极轴线处电场分布如图11所示。可知,随着电压升高,正极性下,1.7ns即有明显的起晕现象,负极性下1.9ns时才出现电晕,且相同时间正极性下微粒附近电场强度大于负极性。分析原因:电极间存在空间电荷效应,空气电离、解离产生大量正、负离子(电子),在电场作用下定向移动,而负离子的迁移率大于正离子。正极性时,微粒带负电,表面形成电子立即进入强电场,造成电子崩,速度较慢的正离子向微粒运动,因此,在微粒附近的正空间电荷较为集中,使其电场发生畸变,易于满足自持放电条件并转为流注而形成电晕放电。负极性时,微粒附近的正空间电荷对其电场起屏蔽作用,削弱电场强度,使电晕难以形成。从场致发射角度分析,Schottky效应使得金属中部分处于导带的电子从外电场获得能量,金属表面势垒畸变并产生隧道效应,发生势垒贯穿进而使电子脱离其表面,即形成场致发射[41]。正负极性下,微粒顶端电场畸变最为严重,因此,正极性下,微粒带负电,电场强度畸变最严重的端部的势垒壁很薄,电子容易透过势垒而脱离表面形成场致发射,在强电场作用下进而产生电子崩,出现电晕放电。根据Townsend放电理论[42],正负极性下a电离和b电离基本相同,正极性的g电离作用远强于负极性。电晕放电使得微粒电荷量和电荷在微粒上重新分布,旋转力矩迫使微粒运动,电晕效果越强,电荷分布越不均匀,微粒运动越明显。综上所述,正极性下电晕较负极性易发生。这就导致出现2.3节实验中,正极性下,随着电压升高,一端先抬起,并伴随着不同程度的以电力线方向为轴心旋转和倾斜等“晃动”,另一端固定不动或也在电极表面作旋转运动;而负极性下,达到启举电压前,微粒则保持相对静止状态,即电压升高初始阶段,正极性下的微粒相较于负极性就有较大幅度的“振动”。
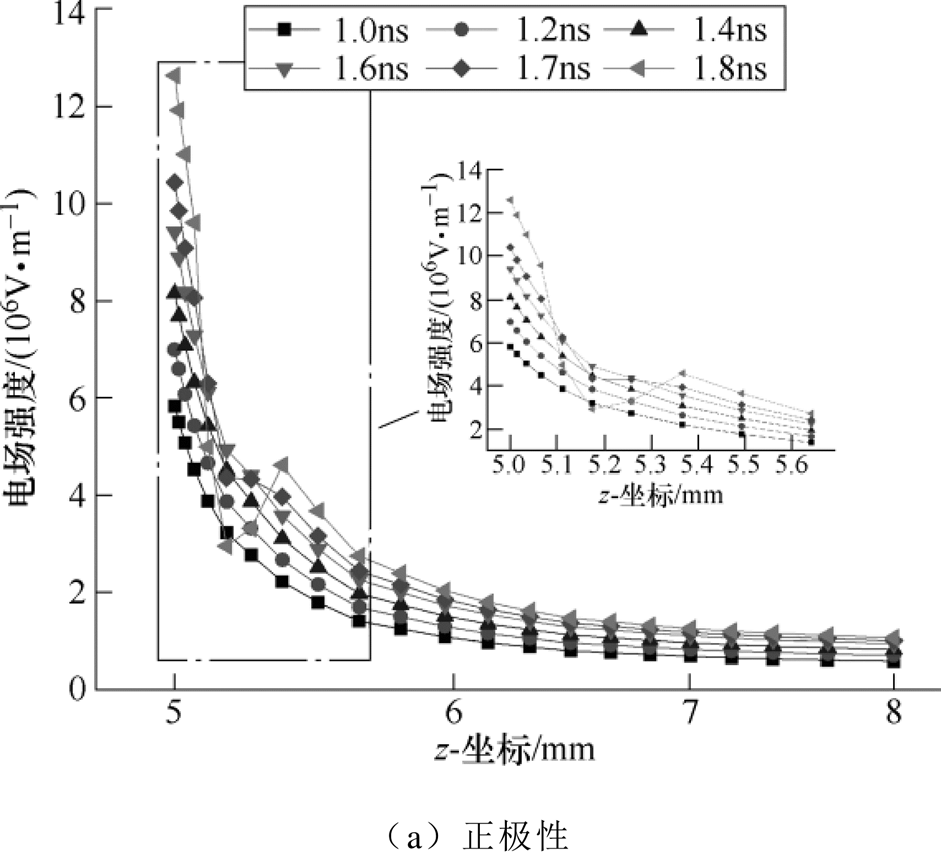
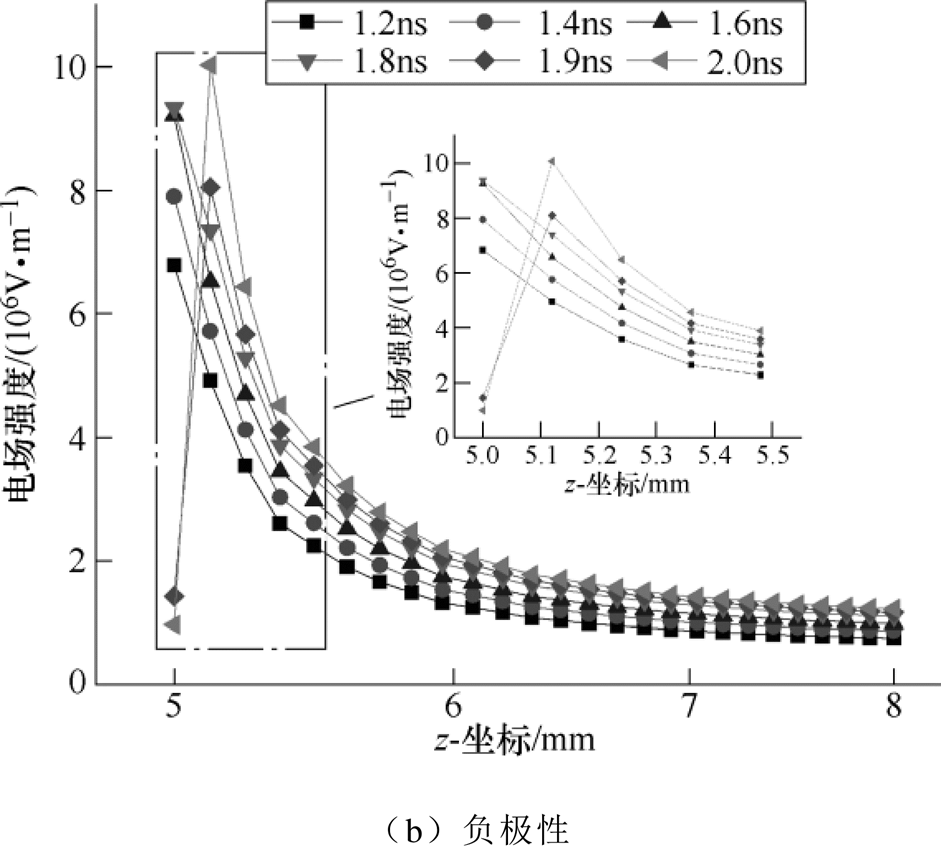
图11 初始阶段沿电极轴线方向电场强度
Fig.11 The electric field intensity along the axis of electrode in the initial stage
继续增加电压,电晕极性效应增强。发展阶段沿电极轴线方向电场强度如图12所示。
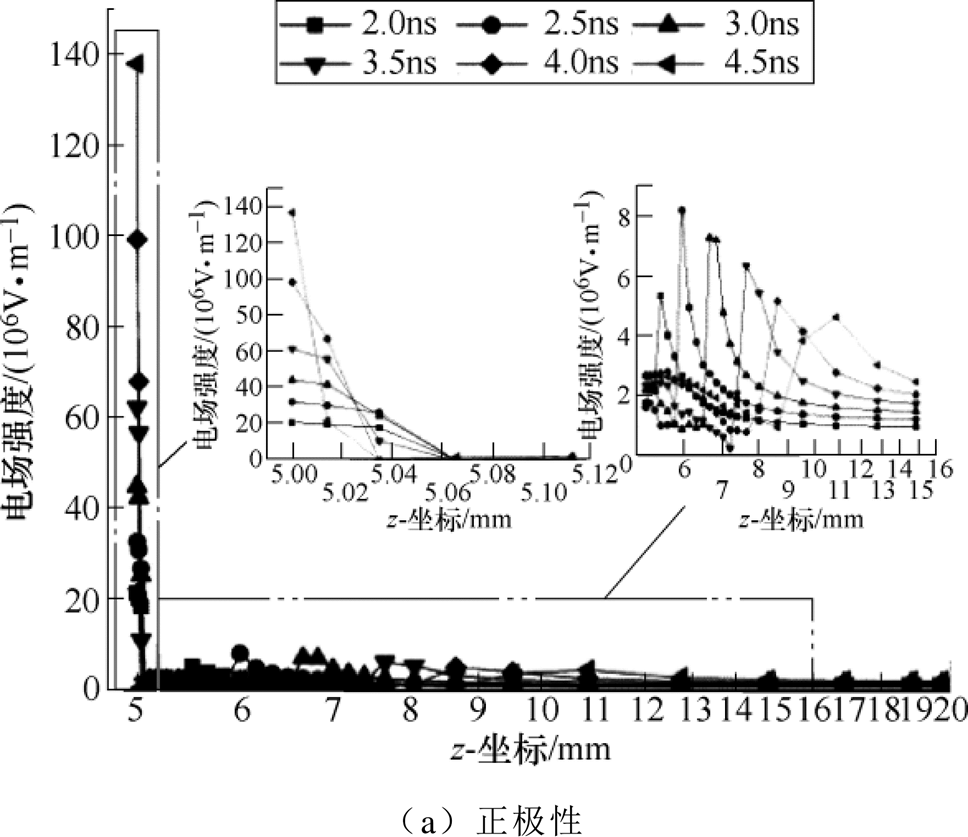

图12 发展阶段沿电极轴线方向电场强度
Fig.12 The electric field intensity along the axis of electrode in the development stage
正极性下微粒带负电,当电压达到起晕电压,随着电压升高,微粒顶端发生严重的电场畸变,强烈的电离产生大量的电子崩,集中在微粒尖端,与正极性空间电荷形成扩散状分布的流注等离子体层,相当于增大了顶端流注的曲率半径,使得前沿电场整体削弱,因此,正极性时微粒易出现如图4c和图4d所示的在下极板“站立”和出现文献[43]正极性实验的点状发光的现象;负极性下微粒带正电,微粒顶端流注的等离子体头部产生正极性空间电荷,使得等离子体中的电场削弱,而其头部的电场加强,促使电离继续发展,产生新的电子崩,加强并延伸了顶端的流注通道,使得电晕更加强烈,因此,负极性下在下极板更易起跳,如图5a所示,并出现如图5c和图5d所示的在上极板站立和出现文献[43]负极性实验的刷状发光的现象。
本文研究了线形微粒启举特性、运动特性以及微粒导致的气隙击穿特性,分析了线形金属微粒的荷电机制,探究微粒与空间电荷的协同耦合作用引发电动力学行为机理,从微观角度分析微粒运动行为和气隙击穿的关联特性,得出以下结论:
1)线形启举电压只与半径有关,与长度和电压极性无关,随着半径增大,启举电压升高。
2)线形微粒的运动及导致的气隙击穿随着长度和电压极性的变化呈现出明显的规律:微粒一端先抬起,随着长度增大,正极性下,跳起往返运动、多次碰撞击穿→下极板旋转、升高电压击穿→下极板直立、直接击穿;负极性下,跳起往返运动→“飞萤”→上极板旋转→上极板直立,大概率一运动就击穿。线形微粒在负极性的击穿电压明显小于正极性,且较短长度的微粒易发生击穿。
3)线形微粒出现一端抬起、“站立”等启举与运动现象以及碰撞击穿、直接击穿等运动致气隙击穿现象与电晕的极性效应有关。
参考文献
[1] Cookson A H, Farish O, Sommerman G M. Effect of conducting particles on AC corona and breakdown in compressed SF6[J]. IEEE Transactions on Power Apparatus and Systems, 1972, 91(4): 1329-1338.
[2] 罗毅, 唐炬, 潘成, 等. 直流GIS/GIL盆式绝缘子表面电荷主导积聚方式的转变机理[J]. 电工技术学报, 2019, 34(23): 5039-5048.
Luo Yi, Tang Ju, Pan Cheng, et al. The transition mechanism of surface charge accumulation dominating way in DC GIS/GIL[J]. Transactions of China Elec- trotechnical Society, 2019, 34(23): 5039-5048.
[3] Xiao Song, Zhang Xiaoxing, Zhuo Ran, et al. The influence of Cu, Al and Fe free metal particles on the insulating performance of SF6 in C-GIS[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(4): 2299-2305.
[4] 孙秋芹, 罗宸江, 王峰, 等. 直流GIL导体表面金属颗粒跳跃运动特性研究[J]. 电工技术学报, 2018, 33(22): 5206-5216.
Sun Qiuqin, Luo Chenjiang, Wang Feng, et al. Jumping characteristics of metal particle on the surface of DC gas insulated transmission line conductor[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5206-5216.
[5] 范建斌, 李鹏, 李金忠, 等. ±800kV特高压直流GIL关键技术研究[J]. 中国电机工程学报, 2008, 28(13): 1-7.
Fan Jianbin, Li Peng, Li Jinzhong, et al. Study on key technology of ±800kV UHVDC GIL[J]. Proceedings of the CSEE, 2008, 28(13): 1-7.
[6] 张连根, 路士杰, 李成榕, 等. GIS中线形和球形金属微粒的运动行为和危害性[J]. 电工技术学报, 2019, 34(20): 4218-4225.
Zhang Liangen, Lu Shijie, Li Chengrong, et al. Motor behavior and hazard of spherical and linear particle in gas insulated switchgear[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4218-4225.
[7] 贾江波, 陈姝敏, 杨兰均, 等. GIS中绝缘子附近自由导电微粒无害化研究[J]. 高压电器, 2004, 5(1): 370-372.
Jia Jiangbo, Chen Shumin, Yang Lanjun, et al. Study of deactivation of free conducting particle near spacer in GIS[J]. High Voltage Apparatus, 2004, 5(1): 370-372.
[8] Lebedev N N, Skal Skaya I P. Force acting on a conducting sphere in the field of a parallel plane condenser[J]. Soviet Physics-Technical Physics, 1962, 7(3): 268-270.
[9] Sakai K I, Abella D L, Khan Y, et al. Experimental studies of free conducting wire particle behavior between nonparallel plane electrodes with AC voltages in air[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2003, 10(3): 418-424.
[10] 李庆民, 王健, 李伯涛, 等. GIS/GIL中金属微粒污染问题研究进展[J]. 高电压技术, 2016, 42(3): 849-860.
Li Qingmin, Wang Jian, Li Botao, et al. Review on metal particle contamination in GIS/GIL[J]. High Voltage Engineering, 2016, 42(3): 849-860.
[11] 李庆民, 刘思华, 王健, 等. 直流气体绝缘线路中自由金属微粒的局部放电特性与影响因素[J]. 高电压技术, 2017, 43(2): 367-374.
Li Qingmin, Liu Sihua, Wang Jian, et al. Characteri- stics of partial discharges caused by free metal particle and influencing factors in DC gas insulated line[J]. High Voltage Engineering, 2017, 43(2): 367- 374.
[12] 王健, 李庆民, 李伯涛, 等. 考虑非弹性随机碰撞与SF6/N2混合气体影响的直流GIL球形金属微粒运动行为研究[J]. 中国电机工程学报, 2015, 35(15): 3971-3978.
Wang Jian, Li Qingmin, Li Botao, et al. Motion analysis of spherical conducting particle in DC GIL considering the influence of inelastic random collisions and SF6/N2 gaseous mixture[J]. Proceedings of the CSEE, 2015, 35(15): 3971-3978.
[13] 贾江波, 陶风波, 杨兰均, 等. GIS中不均匀直流电场下球状自由导电微粒运动分析[J]. 中国电机工程学报, 2006, 26(8): 106-111.
Jia Jiangbo, Tao Fengbo, Yang Lanjun, et al. Motion analysis of spherical free conducting particle in non- uniform electric field of GIS under DC voltage[J]. Proceedings of the CSEE, 2006, 26(8): 106-111.
[14] 贾江波, 查玮, 张乔根, 等. 交流电压下预埋电极对绝缘子附近导电微粒运动的影响[J]. 中国电机工程学报, 2008, 28(10): 136-141.
Jia Jiangbo, Zha Wei, Zhang Qiaogen, et al. Influence of metal inserted polytetrafluorethylene spacer on the motion of conducting particle under AC voltage[J]. Proceedings of the CSEE, 2008, 28(10): 136-141.
[15] 孙继星, 戴琪, 边凯, 等. 自由导电微粒受迫运动过程与振动特性[J]. 电工技术学报, 2018, 33(22): 5224-5232.
Sun Jixing, Dai Qi, Bian Kai, et al. Forced movement process and vibration characteristics of free con- ductive particle[J]. Transactions of China Elec- trotechnical Society, 2018, 33(22): 5224-5232.
[16] 孙继星, 陈维江, 李志兵, 等. 直流电场下运动金属微粒的带电估算与碰撞分析[J]. 高电压技术, 2018, 44(3): 779-786.
Sun Jixing, Chen Weijiang, Li Zhibing, et al. Charge estimating and impact analysis of moving metal particle under DC electric field[J]. High Voltage Engineering, 2018, 44(3): 779-786.
[17] 律方成, 刘宏宇, 李志兵, 等. 直流电压下SF6气体中电极覆膜对金属微粒启举的影响机理[J]. 电工技术学报, 2017, 32(13): 239-247.
Lü Fangcheng, Liu Hongyu, Li Zhibing, et al. Influence mechanism of dielectric coated electrodes on metallic particle lift-off in SF6 gas under DC voltage[J]. Proceedings of the CSEE, 2017, 32(13): 239-247.
[18] 律方成, 刘宏宇, 阴凯, 等. 直流GIL不均匀场中金属微粒运动的数值模拟及放电特性分析[J]. 中国电机工程学报, 2017, 37(10): 2798-2806.
Lü Fangcheng, Liu Hongyu, Yin Kai, et al. Numerical simulation and discharge characteristic analysis of metallic particle motion in non-uniform electric field of DC GIL[J]. Proceedings of the CSEE, 2017, 37(10): 2798-2806.
[19] Rizk F M, Comsa R P. Particle-initiated breakdown in SF6 insulated systems under high direct voltage[J]. IEEE Transactions on Power Apparatus and Systems, 1979, 98(3): 825-836.
[20] Budiman F N, Khan Y, Arainy A A, et al. Estimation of particle initiated PD inception voltage around spacer in GIS[C]//4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, 2013: 517-521.
[21] 张连根, 路士杰, 李成榕, 等. 气体绝缘组合电器中微米量级金属粉尘运动和放电特征[J]. 电工技术学报, 2020, 35(2): 444-452.
Zhang Liangen, Lu Shijie, Li Chengrong, et al. Movement and discharge characteristics of micron- scale metal dust in gas insulated switchgear[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 444-452.
[22] 汪沨, 邱毓昌. 直流气体绝缘开关装置绝缘设计的探讨[J]. 中国电力, 2002, 11(1): 50-53.
Wang Feng, Qiu Yuchang. Discussion on the electrical insulation design of the HVDC gas insulated switchgear[J]. Electric Power, 2002, 11(1): 50-53.
[23] Hara M, Akazaki M. A method for prediction of gaseous discharge threshold voltage in the presence of a conducting particle[J]. Journal of Electrostatics, 1977, 2(3): 223-239.
[24] Pedersen A, Lebeda J, Vibholm S. Analysis of spark breakdown characteristics for sphere gaps[J]. IEEE Transactions on Power Apparatus and Systems, 1967, 8(1): 975-978.
[25] Hara M, Negara Y, Setoguchi M, et al. Particle- triggered pre-breakdown phenomena in atmospheric air gap under AC voltage[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2005, 12(5): 1071-1081.
[26] 武占成, 张希军, 胡有志. 气体放电[M]. 北京: 国防工业出版社, 2012.
[27] 黄旭炜, 倪潇茹, 王健, 等. 苯硫醚聚酰亚胺电极覆膜材料合成及直流应力下对金属微粒运动特性的抑制作用[J]. 电工技术学报, 2018, 33(20): 4712- 4721.
Huang Xuwei, Ni Xiaoru, Wang Jian, et al. Synthesis of phenyl-thioether polyimide as the electrode coating film and its suppression effect on motion behavior of the metal particles under DC stresses[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4712-4721.
[28] 姚雨杭, 潘成, 唐炬, 等. 交直流复合电压下流动变压器油中金属微粒运动规律和局部放电特性研究[J]. 电工技术学报, 2021, 36(15): 3101-3112.
Yao Yuhang, Pan Cheng, Tang Ju, et al. Motion behaviors and partial discharge characteristics of metallic particles in moving transformer oil under AC/DC composite voltage[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3101-3112.
[29] 王渊, 马国明, 周宏扬, 等. SF6/N2混合气体中直流叠加雷电冲击复合电压作用下绝缘子闪络特性[J].电工技术学报, 2019, 34(14): 3084-3092.
Wang Yuan, Ma Guoming, Zhou Hongyang, et al. Flashover characteristics of spacers in SF6/N2-filled under composite voltage of DC and lightning impulse[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3084-3092.
[30] 张博雅, 张贵新. 直流GIL中固-气界面电荷特性研究综述Ⅰ: 测量技术及积聚机理[J]. 电工技术学报, 2018, 33(20): 4649-4662.
Zhang Boya, Zhang Guixin. Review of charge accumulation characteristics at gas-solid interface in DC GIL, part I: measurement and mechanisms[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4649-4662.
[31] 周远翔, 赵健康, 刘睿, 等. 高压/超高压电力电缆关键技术分析及展望[J]. 高电压技术, 2014, 40(9): 2593-2612.
Zhou Yuanxiang, Zhao Jiankang, Liu Rui, et al. Key technical analysis and prospect of high voltage and extra-high voltage power cable[J]. High Voltage Engineering, 2014, 40(9): 2593-2612.
[32] 张乔根, 游浩洋, 马径坦, 等. 直流电压下SF6中自由线形导电微粒运动特性[J]. 高电压技术, 2018, 44(3): 696-703.
Zhang Qiaogen, You Haoyang, Ma Jingtan, et al. Motion behavior of free conducting wire-type particles in SF6 gas under DC voltage[J]. High Voltage Engineering, 2018, 44(3): 696-703.
[33] Sakai K I, Labrado A D, Suehiro J, et al. Charging and behavior of a spherically conducting particle on a dielectrically coated electrode in the presence of electrical gradient force in atmospheric air[J]. IEEE Transactions Dielectrics and Electrical Insulation, 2002, 9(4): 577-588.
[34] Asano K, Anno K, Higashiy Y. The behavior of charged conducting particles in electric fields[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1997, 33(3): 679-686.
[35] 高丽娟. 考虑等离子体-静电耦合场的复合绝缘子均匀电晕老化电极设计[D]. 北京: 华北电力大学, 2018.
[36] Neufeld P D, Janzen A R, Aziz R A. Empirical equations to calculate 16 of the transport collision integrals W(l, s)* for the lennard-jones (12-6) potential[J]. The Journal of Chemical Physics, 1972, 57(3): 1100-1102.
[37] Yuan Xiaohui, Raja L L. Computational study of capacitively coupled high-pressure glow discharges in helium[J]. IEEE Transactions on Plasma Science, 2003, 31(4): 495-503.
[38] Hsu C P, Jewell L N E, Krichtafovitch I A. Miniaturization of electrostatic fluid accelerators[J]. Journal of Microelectromechanical Systems, 2007, 16(4): 809-815.
[39] Georghiou G E, Morrow R, Metaxas A C. The effect of photoemission on the streamer development and propagation in short uniform gaps[J]. Journal of Physics D: Applied Physics, 2001, 34(2): 200-208.
[40] Morrow R, Lowke J J. Streamer propagation in air[J]. Journal of Physics D: Applied Physics, 1997, 30(4): 614-627.
[41] 杨津基. 气体放电[M]. 北京: 科学出版社, 1983.
[42] 胡孝勇. 气体放电[M]. 哈尔滨: 哈尔滨工业大学出版社, 1994.
[43] 王健, 李庆民, 李伯涛, 等. 直流GIL中自由线形金属微粒的运动与放电特性[J]. 中国电机工程学报, 2016, 36(17):4793-4800.
Wang Jian, Li Qingmin, Li Botao, et al. Motion and discharge behavior of the free conducting wire-type particle within DC GIL[J]. Proceedings of the CSEE, 2016, 36(17): 4793-4800.
Study on the Electrodynamic Behavior of Linear Metal Particles in DC Gas Insulated Transmission Line
Abstract The stress motion of linear metal particles in DC GIL can easily cause gas gap breakdown or surface flashover of insulators, which reduces the insulation performance of GIL and seriously affects the safe and reliable operation of the DC transmission system. In order to study the electrodynamic behavior mechanism of linear metal particles in DC GIL, the free particle experiment device and observation platform are built, and the particle electrodynamic model under DC is established. Through experiments and simulations, the characteristics of the linear particle lifting, motion and gas gap breakdown caused by particles are obtained, and the reasons of the particle lifting and motion are analyzed from the microscopic view. The results show that the lifting voltage is related to the radius and independent of length and voltage polarity. The voltage polarity does not affect the lifting voltage amplitude of metal particles. The particle motion and the resulting air gap breakdown are related to the particle radius, particle length and voltage polarity. The smaller the radius and the longer the length of the linear metal particles, the easier it is to cause the air gap to breakdown; the irregular shape of the linear metal particles strengthens the electric field distortion, and the polarity effect is more obvious. The effect of corona polarity leads to the lifting and motion of the particles under positive and negative polarities and the gas gap breakdown characteristics caused by motion show obvious laws. If the particles are lifted, under the DC positive polarity voltage, the linear metal particles will jump, rotate or standing upright near the lower electrode, and it is difficult to penetrate the air gap; under the negative polarity voltage, the particles will move through the air gap, and the phenomenon of flying firefly is easy to appear. It provides theoretical guidance for the prevention and control of the linear metal particle pollution in DC GIL.
keywords:DC GIL, linear metal particles, electrodynamic behavior, lifting, motion
DOI: 10.19595/j.cnki.1000-6753.tces.L90137
中图分类号:TM85
收稿日期 2020-06-29
改稿日期 2020-09-22
程 涵 女,1997年生,硕士研究生,研究方向为直流GIL金属微粒电动力学行为及防治措施建模。E-mail: 17854160922@163.com
张 黎 男,1979年生,副教授,博士生导师,研究方向为高电压与绝缘技术。E-mail: zhleee@sdu.edu.cn(通信作者)
(编辑 崔文静)