
图1 基于集成变压器的输入串联型反激式变换器
Fig.1 Input-series flyback converter based on integrated-transformer
摘要 基于变压器集成的输入串联型变换器具有各串联电路自然均压、结构简单的优势,适合高压输入多输出场合应用。在高压场合,集成变压器的分布电容储能对变换器影响较大。以该类输入串联型双开关反激式变换器为研究对象,对集成变压器分布电容的影响进行深入研究。在对集成变压器一次绕组各类分布电容储能进行分析的基础上,提出一种可有效抑制分布电容影响的该类集成变压器绕组布局方法。最后,在已搭建的该类输入串联型变换器实验平台上进行实验研究,实验结果验证了理论分析的正确性以及所提方法的可行性。
关键词:输入串联 集成变压器 分布电容 绕组布局
近年来,随着高压场合的逐渐增多,各种高压变换器得到了广泛的研究,而如何降低各器件电压应力一直是该类变换器的研究重点。目前,降低变换器电压应力的常用方法有三种:①采用多电平技术;②采用开关管串联;③采用多个电路在输入侧串联[1-3]。随着电平数量的增加,多电平直流变换器结构的复杂程度将显著增加,因此,多电平技术通常应用于中、大功率场合;采用开关管串联时,相关功率器件的电压应力可以得到有效抑制,而变换器中磁性器件的高压问题并未得到解决;采用多个电路在输入侧串联时,每个串联电路均分输入电压,各电路中功率器件和磁性器件的电压应力均得到有效抑制。
确保每个串联电路间电压与电流的均衡是各类输入串联型变换器研究的重要任务。多年来,研究人员针对各类输入串联型变换器提出了大量专门的均压、均流控制环节,有效实现了各电路间电压与电流的均衡[3-8]。然而,引入各种专门的控制环节后,变换器控制系统的复杂程度显著增加,因此,目前已有的各种均压、均流环节一般都在中、大功率场合应用。此外,研究人员还对一些具有自然均压、均流能力的输入串联型变换器进行了一定的研 究[9-11]。其中,各串联电路同步工作,且共用一套控制电路,在不增加任何控制环节的情况下,即可实现各电路间电压与电流的均衡。该类变换器的应用视其拓扑本身而定,如各串联电路采用正激、反激等拓扑,则适合中、小功率场合。然而,由于各串联电路采用输出并联或串联的方式,该类变换器不适合要求多路输出的应用场合。文献[12-13]提出输入串联多输出型变换器,然而,该类变换器的输入均压效果受多路负载的影响较大,因此,主要应用在一些多路负载一致性较好的场合,如作为模块化输入串联型变换器的多输出辅助电源。
近年来,研究人员还对一类基于变压器集成方式的输入串联型变换器进行了一定的研究。其中,各串联电路共用一个集成变压器,通过增加变压器二次绕组的方式即可实现该类变换器的多路输出。按各串联电路工作模式的不同,该类变换器有交错式和同步式两种,其典型研究如下:文献[14-15]提出一种输入串联交错式变换器,其中,两个正激式串联电路交错运行,集成变压器双向励磁,具有磁心利用率高的优势;文献[16-19]针对一系列输入串联同步式变换器进行研究,其中,各串联电路(分别采用正激、反激及全桥拓扑)同步工作,通过集成变压器各一次绕组的耦合实现自然均压,且均压效果不受各输出电路的影响。目前,对于该类变换器的研究主要集中在输入均压效果的分析与优化等方面,尚未有专门针对该类集成变压器设计、制造等方面研究的报道。
在实际中,各类变换器均不同程度地受到高频变压器寄生参数的影响。高频变压器的寄生参数主要包括漏感和分布电容,在变压器的设计过程中,通常对变压器漏感的影响非常重视,而对分布电容的影响考虑较少[20-21]。分布电容寄生在变压器各绕组的匝间与层间,在变换器的运行过程中,由于各绕组电压不断变化,使得分布电容的储能在每个开关周期内均有变化。分布电容储能的变化导致了分布电容与主电路及变压器本身均发生高频谐振,造成功率器件和变压器损耗的增加,降低了变换器运行的可靠性[22-25]。由于分布电容的储能随着变换器电压等级的增加而增加,因此,在高压场合,变压器分布电容的影响不容忽视。
基于变压器集成的输入串联型变换器主要应用于高压场合,因此,集成变压器的分布电容储能对该类变换器的影响较大。为此,本文以该类输入串联型双开关反激式变换器为研究对象,对集成变压器分布电容的影响进行深入研究,在对集成变压器一次绕组各类分布电容储能进行分析的基础上,提出一种可有效抑制分布电容储能的该类集成变压器绕组布局方法。
基于集成变压器的输入串联型反激式变换器如图1所示,图中,N(N≥1)个串联电路具有相同的元器件及参数,如开关管(S11, S12, S21, S22,…, SN1, SN2)、二极管(VD11, VD12, VD21, VD22,…, VDN1, VDN2)以及电容(Ci1=Ci2=…=CiN),各串联电路共用一个集成变压器与n(n≥1)个输出电路。集成变压器各一次绕组(PW1, PW2,…, PWN)具有相同的自感(Lp1=Lp2=…=LpN)与匝数(Wp1=Wp2=…= WpN=Wp/N, Wp为N个一次绕组总匝数);Llk1, Llk2,…, LlkN为等效漏感;Ws1, Ws2,…,Wsn为各二次绕组(SW1, SW2,…, SWn)匝数;Co1, Co2,…,Con为输出滤波电容。该变换器各串联电路同步工作,通过集成变压器各一次绕组的耦合实现自然均压,其均压效果不受各输出电路的影响。

图1 基于集成变压器的输入串联型反激式变换器
Fig.1 Input-series flyback converter based on integrated-transformer
下面以N=2和n=2为例介绍该变换器的工作过程。这里假设:①电路中元器件均为理想元器件;②输出滤波电容足够大,分析中认为输出电压恒定;③忽略各串联电路间的电压、电流差异。在一个开关周期内,变换器主要有三个工作阶段。阶段1和2的等效电路如图2所示。
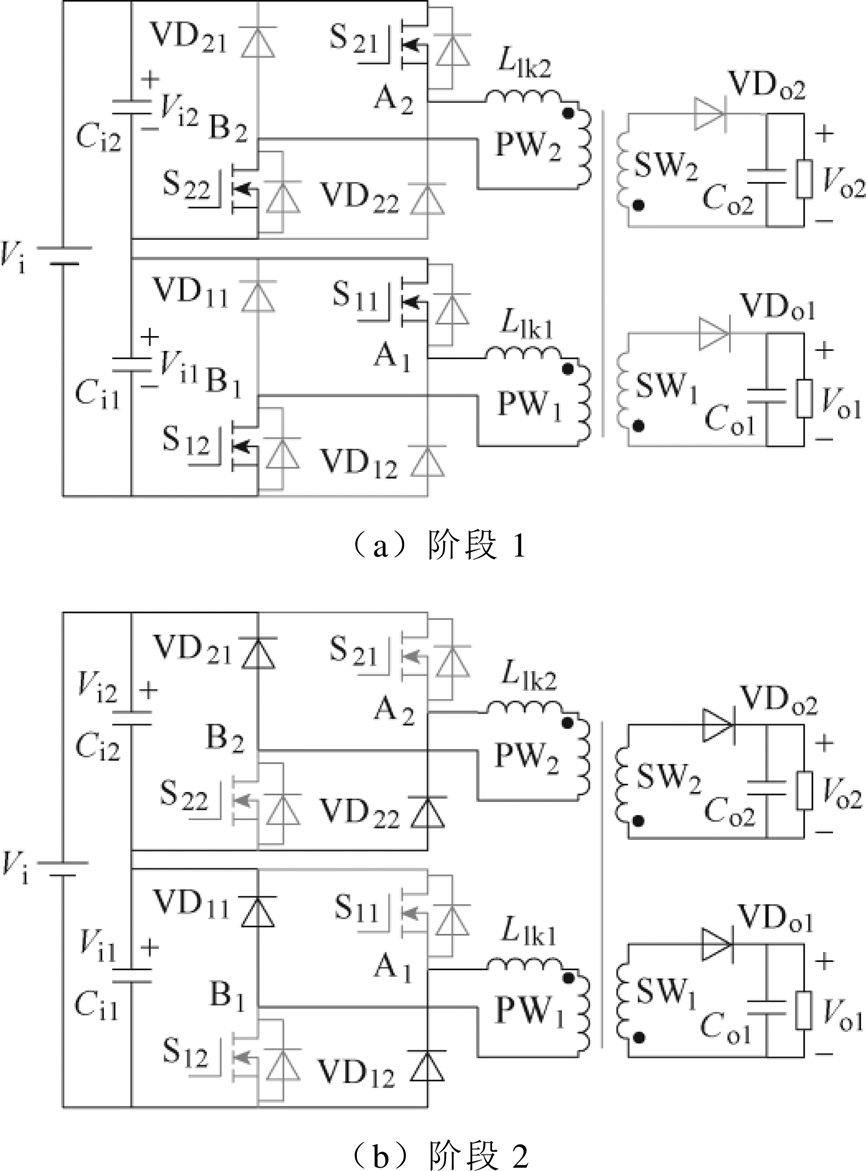
图2 阶段1和2的等效电路
Fig.2 Equivalent circuits of stages 1 and 2
阶段1(t0, t1):变换器的等效电路如图2a所示。t0时刻,所有开关管导通,集成变压器各一次侧电感储能逐渐增加。本阶段,各一次绕组电压为VA1-B1=VA2-B2=Vi/2。
阶段2(t1, t2):变换器的等效电路如图2b所示。t1时刻,所有开关管关断,集成变压器一次侧电感能量转移至二次侧,并向负载传输。另外,集成变压器漏感能量向输入侧回馈,该过程于t2时刻结束。本阶段,各一次绕组电压为:VA1-B1=VA2-B2=-Vi/2。
阶段3(t2, t3):t2时刻以后,集成变压器一次电流为零,二次侧电感能量继续向负载传输,各一次绕组电压为VA1-B1=VA2-B2=-Vo1Wp1/Ws1。到t3时刻,开关管再次导通,变换器进入下一个开关周期的工作中。如果变换器工作于电流断续模式,则本阶段在二次侧电感电流降为零后,各一次绕组电压变为VA1-B1=VA2-B2=0。
图1中的反激式集成变压器主要有五种分布电容:①单个一次绕组分布电容;②一次、二次绕组之间分布电容;③一次绕组之间分布电容;④单个二次绕组分布电容;⑤二次绕组之间分布电容。该变换器的输出电压一般远低于输入电压,因此,在集成变压器的设计中,二次绕组上各类分布电容(单个二次绕组分布电容和二次绕组之间分布电容)的影响通常可以忽略,而与一次绕组相关的各类分布电容必须考虑。
单个一次绕组分布电容与一次、二次绕组之间分布电容同样存在于其他常规变压器中,它们的特征为:
(1)单个一次绕组分布电容通常包括匝间和层间电容两部分(由于电压较高,绕组一般采用多层结构),二者分别分布在每层绕组的匝与匝之间,以及绕组的层与层之间,由于此类电容的存在,相当于每个一次绕组都并联一个等效电容,目前针对该类电容的研究主要围绕其储能展开[23-25]。
(2)一次、二次绕组之间分布电容分布在一次和二次绕组之间,通常由开关电路产生的共模噪声通过此类电容向变换器输出侧传输,一般采用在一次、二次绕组间增加屏蔽层的方法可限制该噪声的传输[26-27]。
一次绕组之间分布电容是该集成变压器所特有的,该类电容分布在集成变压器多个一次绕组之间。由于各一次绕组之间存在电位差,此类电容也将存储一定能量。下面借鉴单个一次绕组分布电容的等效建模方式,以N=2为例对此类电容进行集中化建模。为了简化分析,这里首先考虑每个一次绕组采用单层绕制的情况。
单层一次绕组PW1和PW2有两种基本布局方式:同向和反向布局,PW1和PW2之间的集中电容模型如图3所示。在绕组端部利用两个电容代替分布电容,得到用来表征PW1和PW2之间分布电容的4个集中等效电容(C11、C12、C21、C22)。经过对单个一次绕组分布电容以及一次绕组之间分布电容进行集中化建模之后的反激式集成变压器如图4所示,图中,C1和C2为单个一次绕组分布电容的集中等效电容。在变换器的运行过程中,近似地认为单个一次绕组分布电容和一次绕组之间分布电容的能量分别存储于电容C1、C2和C11、C12、C21、C22上。
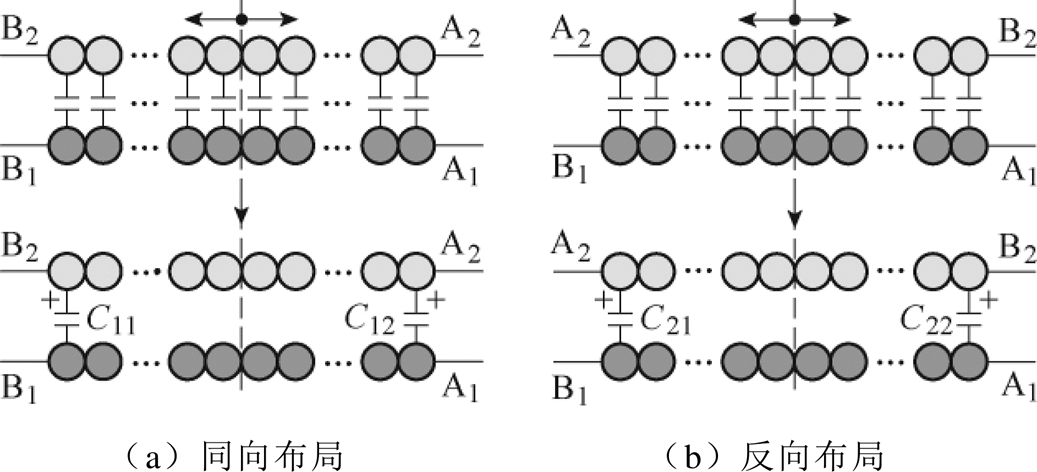
图3 PW1和PW2之间的集中电容模型
Fig.3 Lumped capacitors models between PW1 and PW2
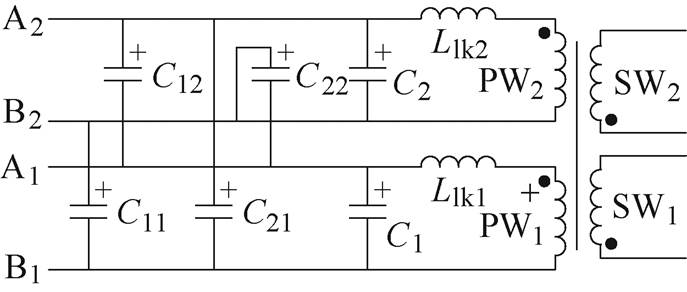
图4 带分布电容的反激式集成变压器
Fig.4 Flyback integrated-transformer with the stray capacitances
由图2和图4可以得到,在变换器运行的各个阶段,C1、C2和C11、C12、C21、C22的电压变化情况,见表1。表中,Vi/2≥Vo1Wp1/Ws1。可以看出,在每个开关周期内,C1、C2和C21、C22的电压变化较大,其储能变化对变换器造成一定影响,而C11、C12的电压不变,其储能对变换器不造成影响。
表1 各电容的电压变化情况
Tab.1 Voltage varying of each capacitor

电容阶段1阶段2阶段3 C1, C2Vi/2-Vi/2-Vo1Wp1/Ws1 C11, C12Vi/2Vi/2Vi/2 C21Vi0Vi/2-Vo1Wp1/Ws1 C220ViVi/2+Vo1Wp1/Ws1
结合该变换器的工作过程可以得出,C1、C2和C21、C22对变换器的影响主要发生在各开关管的导通与关断时刻:开关管导通时,由于各电容的快速充、放电(分布电容与主电路发生高频谐振),各开关管出现较大的电流尖峰;开关管关断时,电容与集成变压器一次侧各电感发生谐振,导致损耗增加。上述影响主要由各电容的储能变化决定,C1、C2和C21、C22的储能越大,变换器受到的影响就越严重。在高压场合,由于分布电容的储能较大,对变换器的影响也相对较大。
在高压场合,集成变压器各一次绕组一般采用多层结构。N个多层一次绕组有两种基本的布局方式:集中式布局和交错式布局。N个多层一次绕组的布局方式如图5所示(这里以两层结构为例给出,并考虑绕组为紧密绕制的情况)。由文献[17]可知,该类变换器通过集成变压器各一次绕组的耦合实现自然均压,各串联电路的电压、电流差异随着各电路间器件参数误差的增加而增大。相比之下,集中式布局的一次绕组耦合较差,另外,由于各绕组绕制在绕线骨架的不同层,它们之间的长度、内阻以及与二次绕组之间的漏感等参数均有一定的差异。因此,集中式布局不适合该集成变压器的N个一次绕组,下面主要针对图5中层层交错式布局的一次绕组进行分析。

图5 N个多层一次绕组的布局方式
Fig.5 Layout schemes of N multiple-layer primary windings
对于多层一次绕组而言,由于绕组匝数较多,匝间电压较低,匝间电容储能通常远小于层间电容储能,因此,这里主要对其层间电容储能进行分析。
多层绕组有两种基本结构:C形和Z形。如图6所示为PW1的相邻两层结构及其层间电压分布,其中,两种结构绕组的层间电压分别为
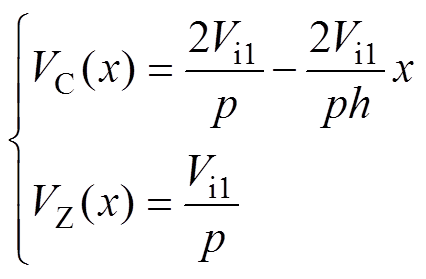 (1)
(1)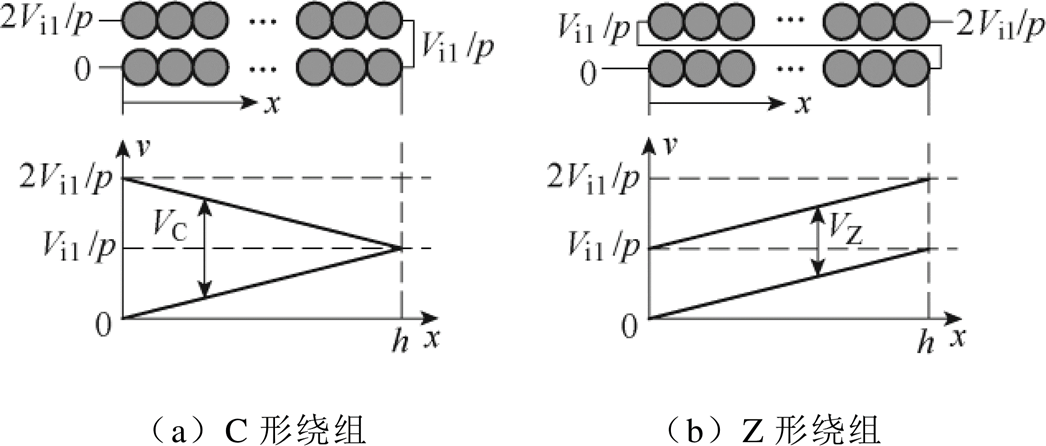
图6 两种多层绕组结构及其相邻层间电压分布
Fig.6 Two multiple-layer winding structures and their voltage distribution within the adjacent layers
式中,p为绕组层数;h为每层绕组高度。
由式(1)可得两种结构PW1层间电容储能为
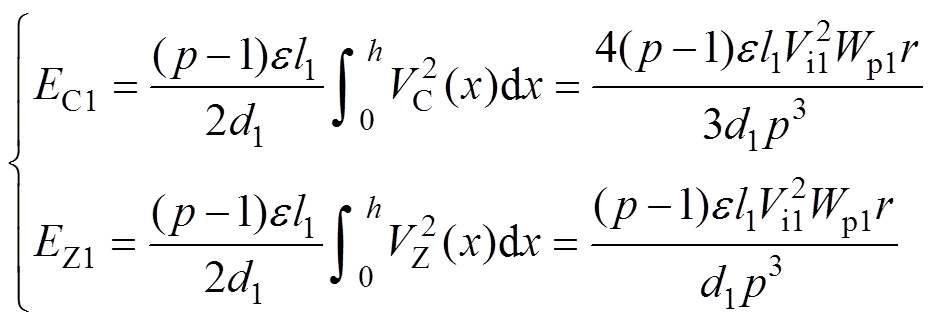 (2)
(2)式中,e 为绝缘材料的介电常数;l1为绕组平均匝长;d1为平均层间距;r为导线半径,r=ph/(2Wp1)。
这里考虑N个一次绕组结构相同,由式(2)可得,两种结构的N个一次绕组总的层间电容储能分别为
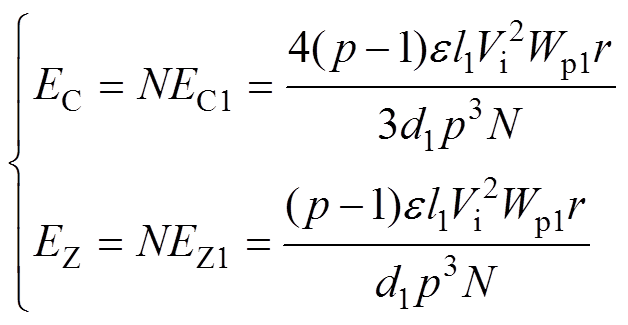 (3)
(3)式中,Vi=NVi1(忽略各串联电路的输入电压差异)。
由式(2)和式(3)可以得出,由于层间电容储能相对较小,Z形结构更加适合各一次绕组;层间电容储能随着输入串联电路数N的增加而减少。
图7为层层交错式布局的一次绕组,图中,每个绕组(p层)采用Z形结构,N个绕组每层采用同向布局的方式,a为每层绕组匝数,a=Wp1/p。为了简化说明,图中只给出变压器绕线骨架的一半截面,另外,此处暂不考虑二次绕组的布局。图8为N个一次绕组每层的连接方式及其电位分布。由变换器的工作过程可知,各一次绕组的最大正向、反向电压分别出现在阶段1和2中,因此,下面以两个阶段为例分析N个一次绕组之间分布电容储能变化情况。
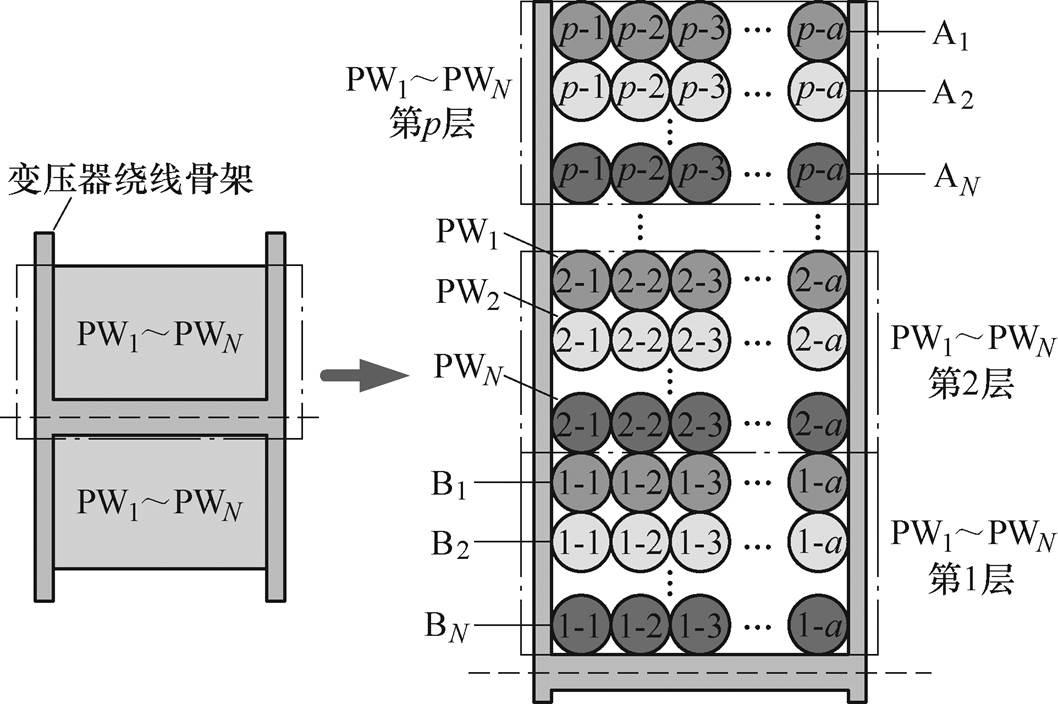
图7 层层交错式布局的一次绕组
Fig.7 Layer-by-layer interleaved layout primary windings
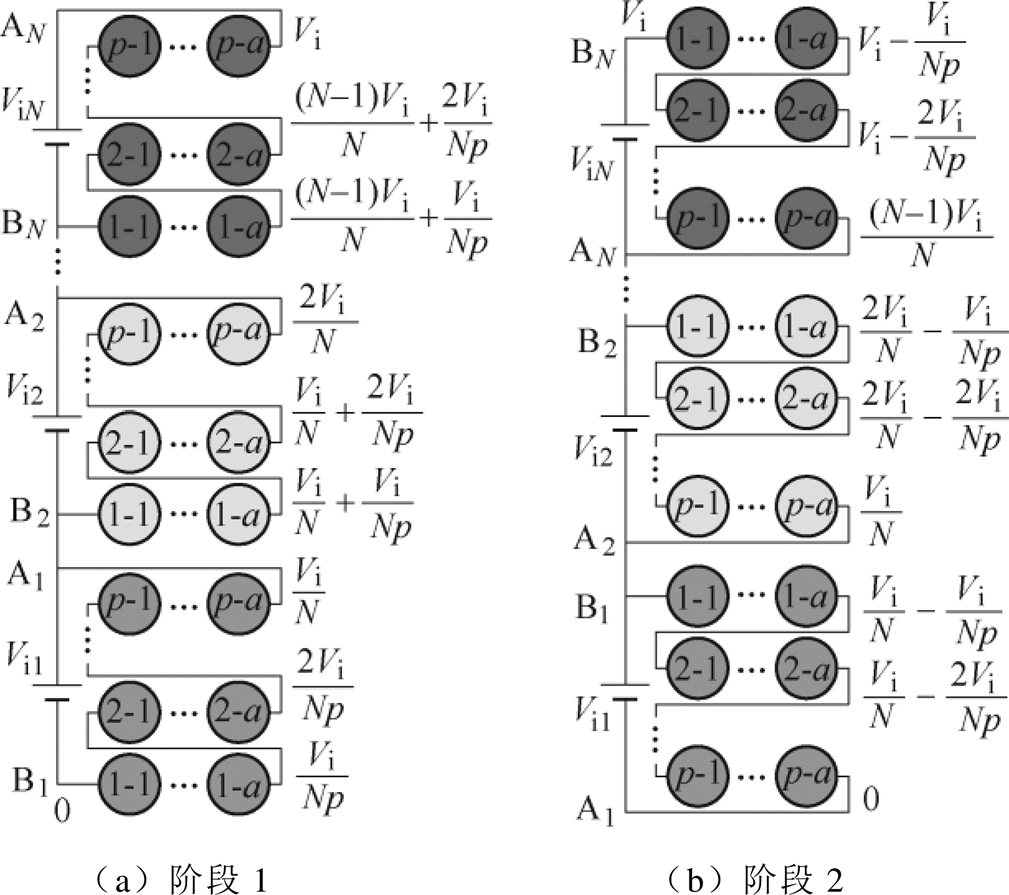
图8 一次绕组每层的连接方式与电位分布
Fig.8 Connection scheme and electric potential in each layer of the primary windings
按照图7所示的布局方式,可将集成变压器的一次绕组之间分布电容分为两个类型:
(1)类型1:分布在N个一次绕组相同层之间的分布电容,例如,分布在PW1和PW2第1层绕组之间的分布电容C12-11,如图9a所示。
(2)类型2:分布在N个一次绕组不同层之间的分布电容,例如,分布在PW1第1层绕组和PWN第2层绕组之间的分布电容C1N-12,如图9b所示。
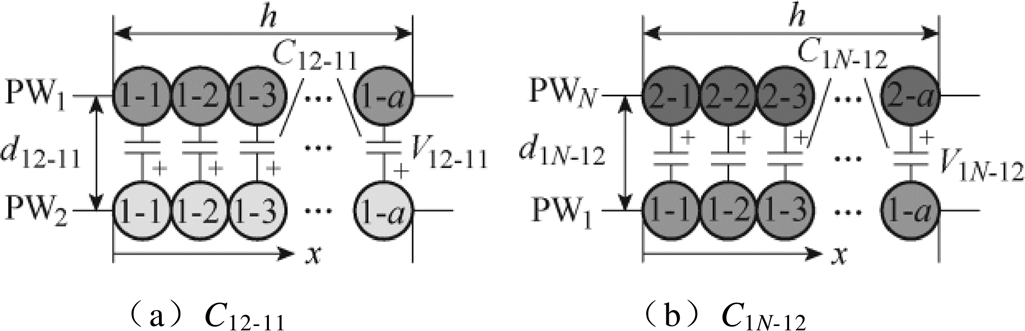
图9 两类一次绕组之间分布电容
Fig.9 Two types of the inter-primary-winding capacitances
C12-11和C1N-12的电压分布如图10所示。结合图8所示电位分布可以得到,C12-11在阶段1和2的电压分布情况,如式(4)和图10a所示;C1N-12在阶段1和2的电压分布情况,如式(5)和图10b所示。
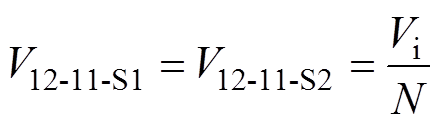 (4)
(4)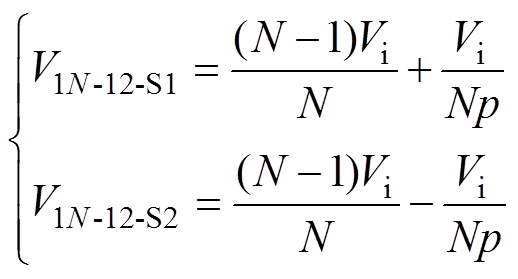 (5)
(5)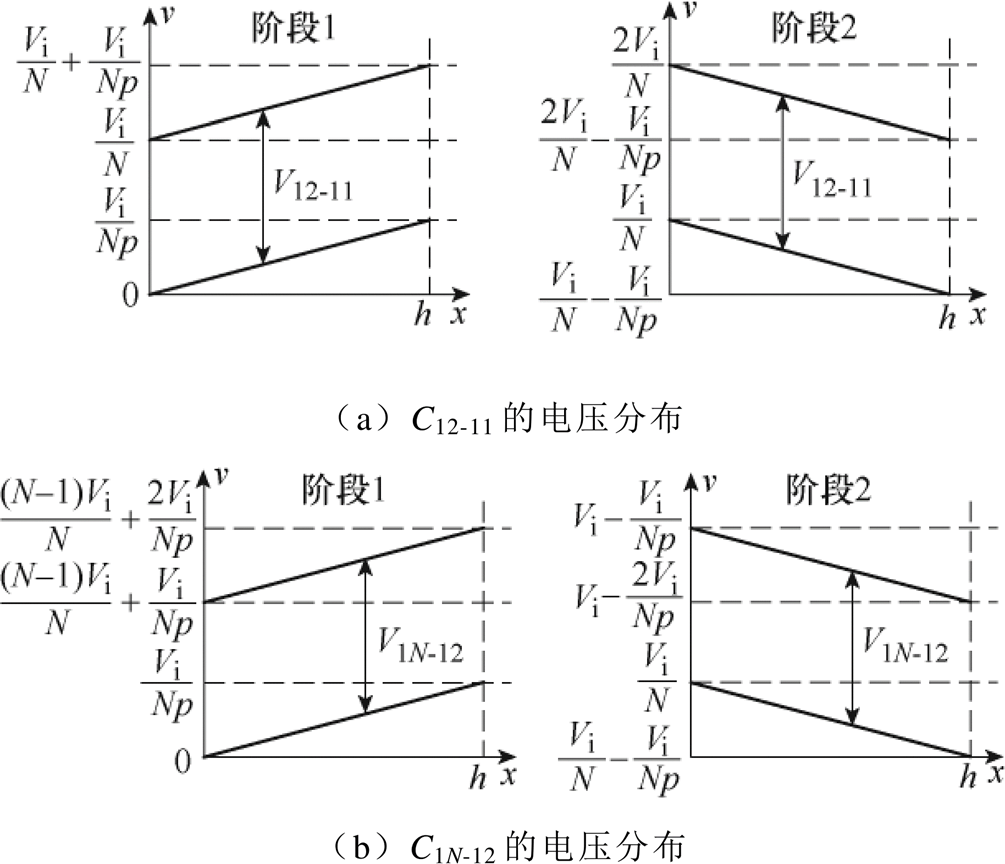
图10 C12-11和C1N-12的电压分布
Fig.10 Voltage distribution of C12-11 and C1N-12
由式(4)和式(5)可以得到,C12-11和C1N-12在阶段1和2之间的储能变化情况分别为
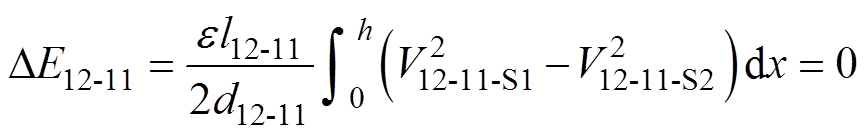 (6)
(6)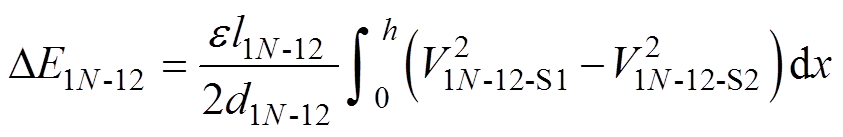
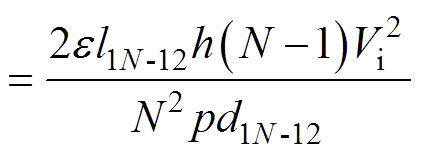 (7)
(7)
式中,l12-11和l1N-12为相应层的绕组平均匝长;d12-11和d1N-12为相应层的平均层间距。
由上述分析可以得出如下结论(上述分析以C12-11和C1N-12为例进行,如果对两个类型中的其他分布电容进行储能分析,可得到相同的结果):
(1)以C12-11为代表的N个一次绕组之间分布电容(类型1)在每个开关周期内储能不变,因此,该类分布电容对变换器的运行不产生影响,在分布电容的等效模型中,相当于图4中的C11和C12。
(2)以C1N-12为代表的N个一次绕组之间分布电容(类型2)在每个开关周期内储能变化,因此,该类分布电容对变换器的运行产生影响,在分布电容的等效模型中,相当于图4中的C21和C22。
集成变压器的单个一次绕组分布电容与一次绕组之间分布电容储能对变换器的影响在高压场合不容忽视。为了抑制分布电容影响,下面对集成变压器绕组布局的优化设计进行研究。
由式(3)和式(7)可知,增加集成变压器N个一次绕组不同层之间的层间距可有效抑制其单个一次绕组分布电容以及一次绕组之间分布电容(类型2)的储能。这种方法原理简单,直接在相关层间进行绝缘填充即可实现,然而,这将造成变压器磁心窗口利用率的下降。
如果集成变压器的N个一次绕组采用单层绕制结构(p=1),单层一次绕组及其匝间电容如图11所示,则每个一次绕组不存在层间电容,一次绕组之间分布电容(类型2)也不存在。此时,由于一次绕组之间分布电容(类型1)对变换器不产生影响,因此,只有每个绕组的匝间电容储能对变换器的运行有一定影响。在各绕组紧密绕制的情况下,匝间电容几乎恒定,如图中Ctt-1, Ctt-2,…,Ctt-N(Ctt-1>Ctt-2>…>Ctt-N,通常外层绕组的匝间面积较大,因此,匝间电容也较大)。各绕组的匝间电容储能(以PW1在阶段1为例)为
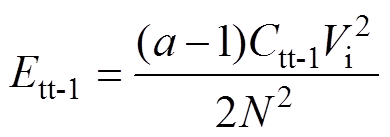 (8)
(8)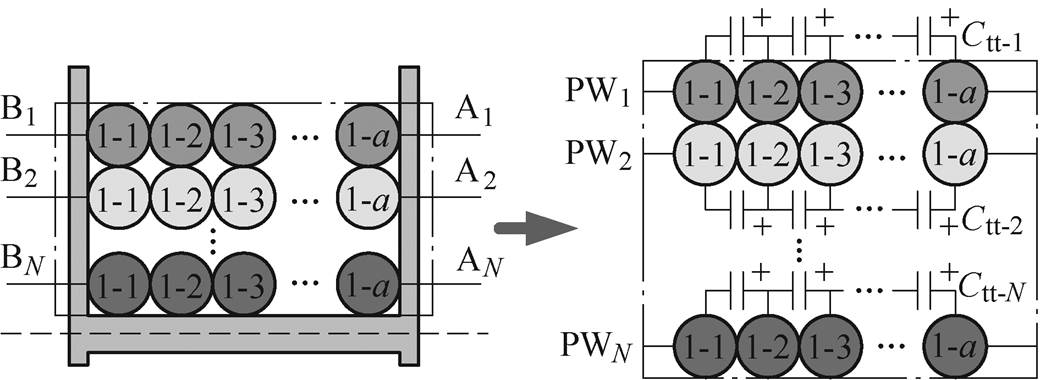
图11 单层一次绕组及其匝间电容
Fig.11 One-layer primary windings and their turn-to-turn capacitances
由于匝间电容储能通常远小于层间电容储能,因此,图11中的单层一次绕组具有最小的分布电容储能影响。然而,该方案也存在明显的不足:由于N个一次绕组的总匝数(Wp)较多,受磁心尺寸的限制,每层绕组的绕制匝数(a)不能随意增加,因此,在N相对较小的情况下,很难实现每个一次绕组的单层绕制。而串联电路数N主要依据各串联电路的电压应力而定,在设计中不能随意改变。
对于常规的反激式变压器,其一次、二次绕组有两种基本布局方式:①集中式布局,如依次将一次、二次绕组绕制在变压器绕线骨架的里层和外层;②交错式布局,将一次、二次绕组的每层或者每几层交错地绕制在绕线骨架上。
为了克服图11中单层一次绕组布局的不足,这里借鉴常规反激式变压器绕组的交错式布局方法,提出一种适合该类集成变压器的交错式单层一次绕组布局方法。图12a为当N个一次绕组采用两层结构(p=2)时集成变压器的交错式单层一次绕组布局方法。其中,将N个一次绕组分成结构相同的两部分,每部分相当于单层结构,将二次绕组(SW1~SWn)集中绕制在两部分一次绕组中间以增加其间距。所提方法还有另一种实现方案,如图12b所示,其中,每部分一次绕组仍然相当于单层结构。与方案1相比,方案2的特点为:①每个一次绕组的长度几乎相等(在方案1中,处于外层的PW1长度最大),因此,每个一次绕组的匝间电容及其储能也几乎相等;②每个一次绕组的层间距不同(PW1的层间距最小),因此,每个一次绕组的层间电容储能不同。

图12 交错式单层一次绕组
Fig.12 Interleaved one-layer primary windings
由于该变换器主要应用于高压输入、小功率场合,集成变压器一次绕组的线径通常很小,因此两种实现方案的差异也很小。相比于图7中层层交错式布局的一次绕组,图12中两种交错式单层一次绕组具有更小的分布电容储能影响。
图12中的交错式单层一次绕组布局方法以两层结构(p=2)为例给出。如果绕组采用三层结构,则可将N个一次绕组分成结构相同的三部分,将二次绕组一分为二,分别绕制在三部分一次绕组之间,这样每部分一次绕组仍然相当于单层绕制结构。当绕组采用四层及以上结构时,处理方法相同。
为了验证理论分析以及所提方法的正确性,在已搭建的该类变换器实验平台上进行实验研究,如图13a所示[17]。该平台包括3个双开关反激式串联电路(N=3)和两个输出电路(n=2),主要器件参数为:Ci1=Ci2=Ci3=0.1μF;S11, S12, S21, S22, S31, S32采用型号K1271,开关频率为50kHz;VD11, VD12, VD21, VD22, VD31, VD32采用型号BYV26G;VDo1, VDo2采用型号MUR1520;Co1=Co2=1 000μF;Vo1= Vo2=24V, Io1= 1.5A, Io2=1A。
为了验证所提方法,此处设计了三个绕组布局不同的反激式集成变压器(T1~T3),其共性参数为:磁心采用型号ETD40;一次绕组采用三层绝缘线(直径0.25mm):Lp1=Lp2=Lp3=6.4mH,Wp1=Wp2= Wp3=112,p=2;二次绕组采用常规漆包线:Ws1= Ws2=7。图13b为T1~T3的绕线骨架照片(不带磁心)。其中,T1的一次绕组(PW1, PW2, PW3)采用图7中的层层交错式布局方式,并绕制在绕线骨架的里层,二次绕组(SW1, SW2)绕制在外层;T2和T3分别采用图12a和图12b中的交错式单层一次绕组布局方法。
图14~图16为输入电压1 500V、依次采用T1~T3时,该变换器各串联电路的开关管驱动、电压和电流波形,可以看出,各开关管在开通时刻存在一个明显的电流尖峰,其中:采用T1时,开关管S12、S22和S32的电流尖峰分别约为0.32A、0.36A和0.48A;采用T2时,S12、S22和S32的电流尖峰分别约为0.28A、0.26A和0.26A;采用T3时,S12、S22和S32的电流尖峰分别约为0.32A、0.32A和0.2A。对比图14~图16中的结果可以看出,与T2和T3相比,采用T1时各开关管开通后瞬间的电流振荡更加明显。上述结果说明,与T1相比,T2和T3的分布电容储能影响更小,证明了文中关于集成变压器绕组布局优化方面的分析。另外,在各开关管关断时刻,分布电容与各电感的谐振发生在集成变压器内部,且谐振周期远大于开关管导通时分布电容与主电路间的谐振周期,因此,相关结果并没有在各开关管的电压、电流波形中明显体现。

图13 实验平台以及T1~T3的绕线骨架照片
Fig.13 Photos of the experimental prototype and the transformer bobbins of T1~T3
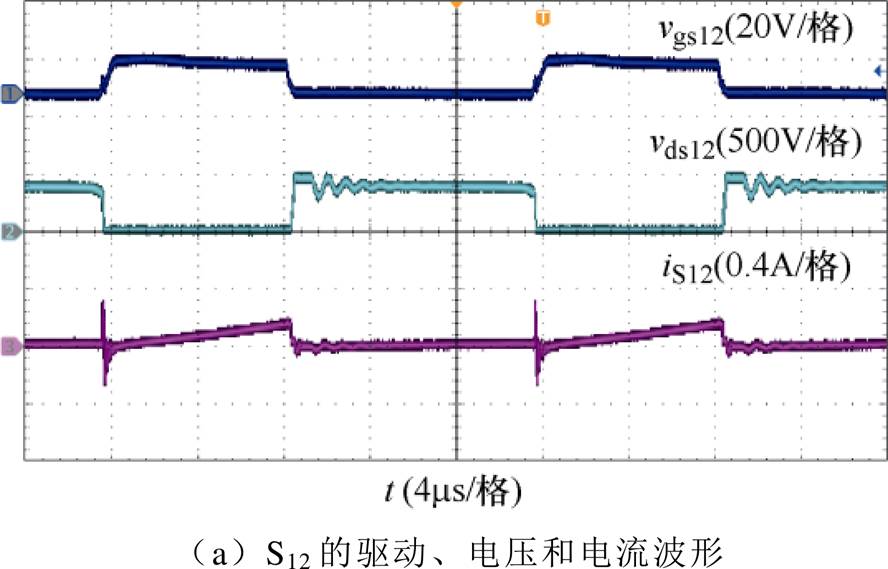
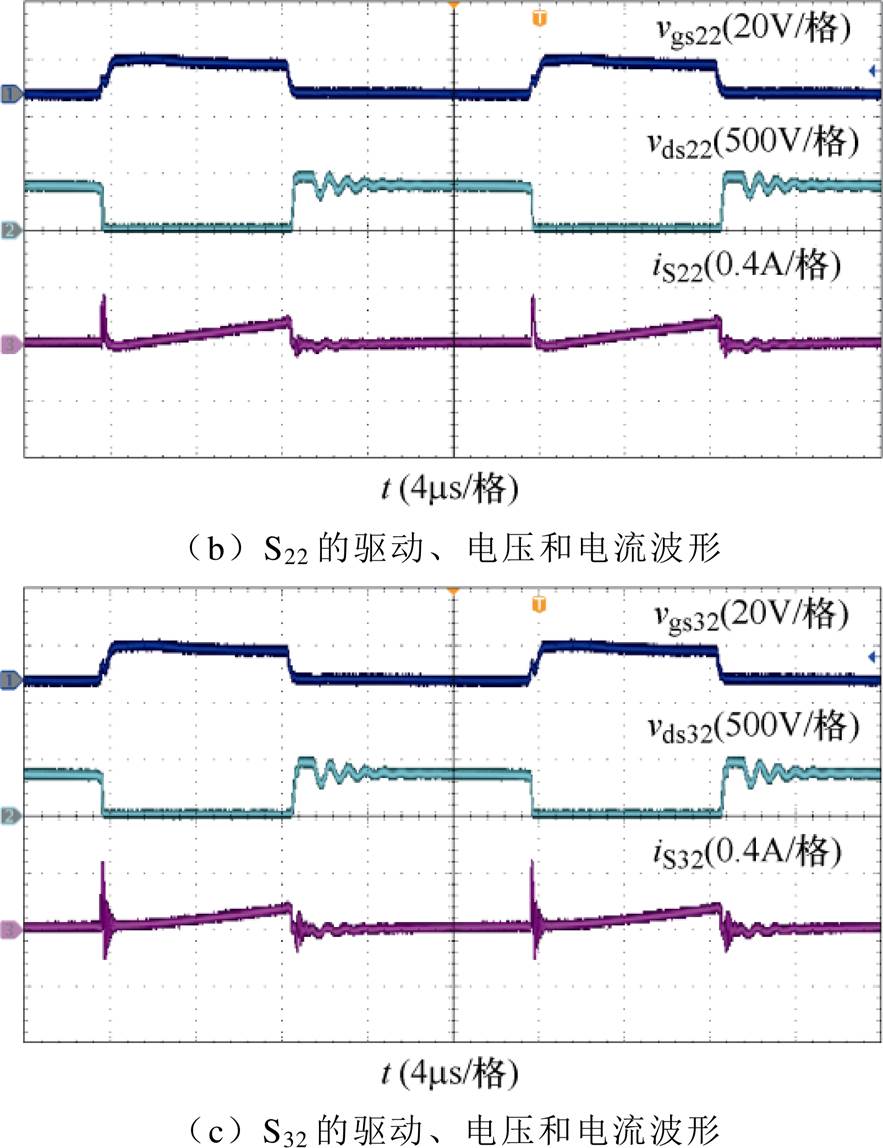
图14 采用T1时的实验结果(Vi=1 500V)
Fig.14 Experimental results when T1 is adopted (Vi=1 500V)

图15 采用T2时的实验结果(Vi=1 500V)
Fig.15 Experimental results when T2 is adopted (Vi=1 500V)
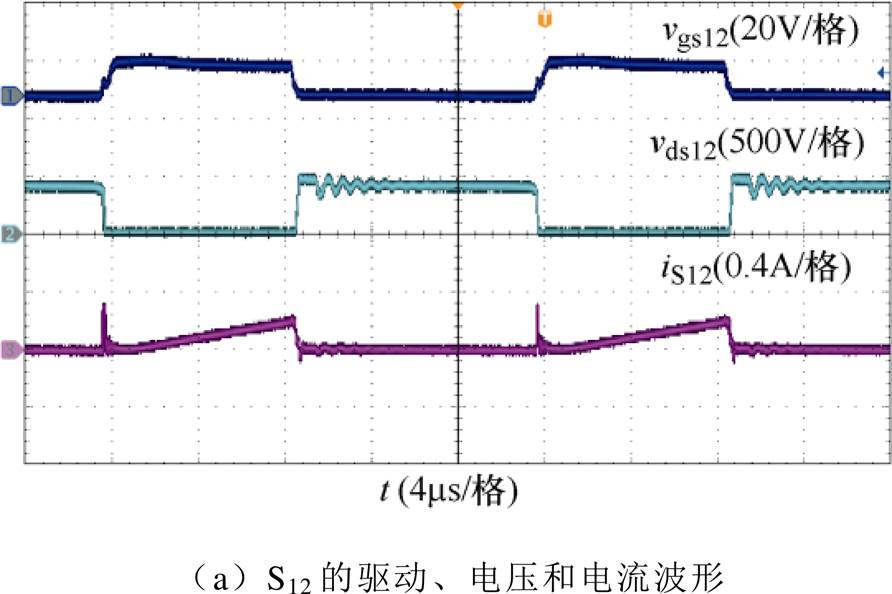
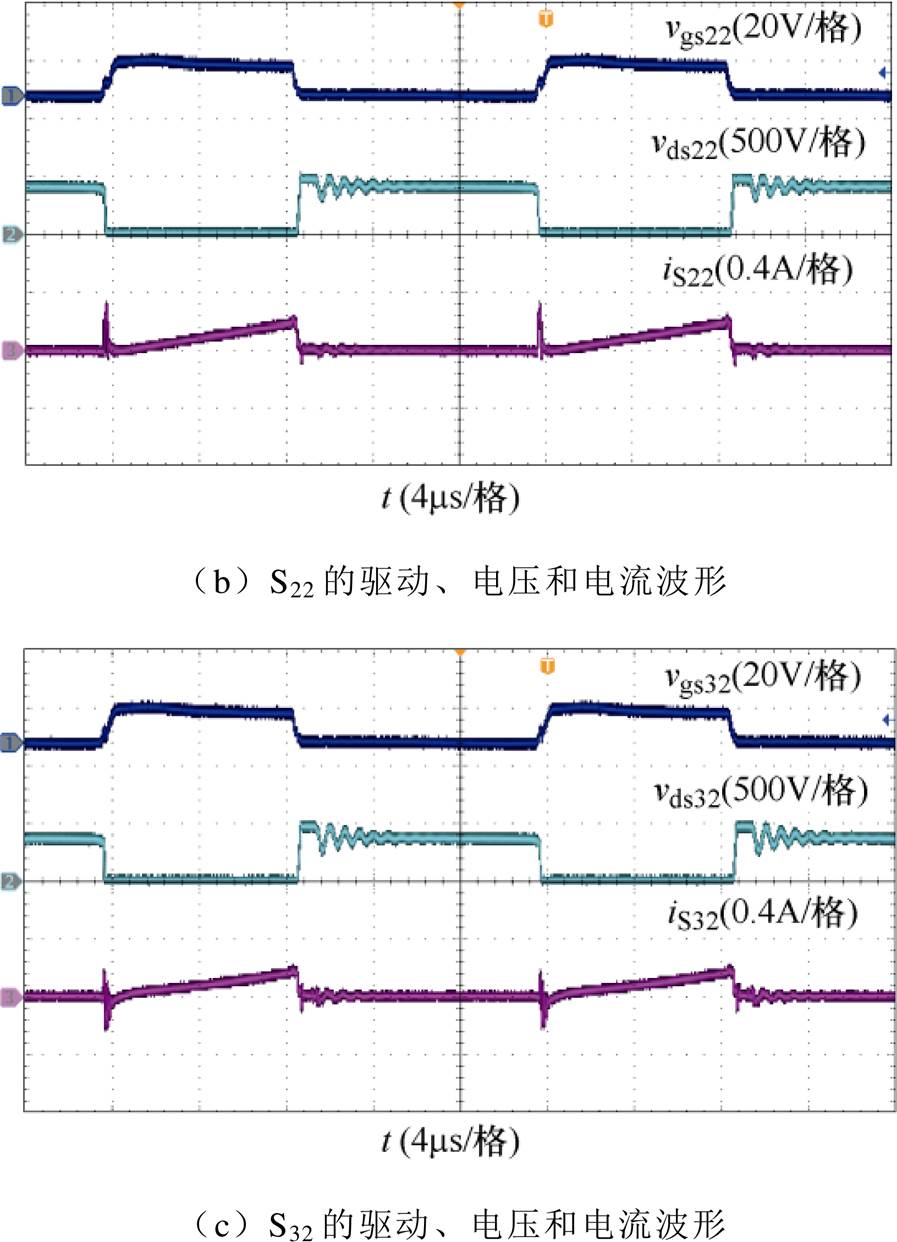
图16 采用T3时的实验结果(Vi=1 500V)
Fig.16 Experimental results when T3 is adopted (Vi=1 500V)
对比图15和图16中的结果还可以看出,与T2相比,采用T3时,S12的电流尖峰略大,而S32的电流尖峰略小。这是由于与T2相比,T3中一次绕组PW1的层间距较小,而PW3的层间距较大,造成单个一次绕组分布电容储能差异,与文中分析相符。
由此可见,每个开关管的电流尖峰并不完全相同,这是由于各串联电路开关管的导通过程无法完全同步,造成各串联电路在开关管导通时刻出现少量的输入电压差异,进而引发各串联电路在该时刻出现少量的环流(相关分析见文献[18])。分别采用T1~T3时,上述问题对变换器的影响基本相同,对实验中T1~T3分布电容影响的对比结果不造成影响。另外,文献[18]中各开关管电流波形是在集成变压器未经绕组布局优化的情况下获得的,与之相比可以看出,经过绕组布局优化后的集成变压器T2和T3具有更小的分布电容储能影响。
表2为输入电压1 500V、依次采用T1~T3时,该变换器的效率测试结果。可以看出,采用T2或T3时,变换器的效率h2或h3明显高于采用T1时的h1。此处效率的提升有以下两方面原因:
表2 变换器的效率测试结果
Tab.2 Efficiency results of the converter

输出功率/W效率(%) h1h2h3 1680.7181.5481.35 3884.3385.4885.31 6085.8987.2787.01
(1)经过绕组布局优化后的集成变压器T2和T3具有更小的分布电容储能影响。
(2)采用一次、二次绕组交错布局的集成变压器T2和T3具有更小的漏感(相关原理已广泛研究,这里不再解释)。该变换器主要面向高压输入、小功率场合,与其他变换器相比,该集成变压器的分布电容储能更大,漏感储能更小。另外,各串联电路采用双开关反激式结构,在变换器的运行中可有效实现漏感能量向输入侧的回馈。因此,本实验中,集成变压器漏感造成的影响相对较小,表2中的效率对比证明了文中关于集成变压器绕组布局优化方面的分析。
本文针对输入串联型变换器集成变压器的分布电容影响与绕组布局方法展开研究。以该类双开关反激式变换器为研究对象,对集成变压器的分布电容进行集中化建模,分析得出集成变压器的单个一次绕组分布电容以及一次绕组之间分布电容储能在高压场合对变换器影响较大。通过对集成变压器交错式布局的一次绕组分布电容储能进行分析,得出:
1)各绕组采用Z形结构时,单个一次绕组分布电容储能相对较小。
2)一次绕组之间分布电容分为两类:对于各一次绕组相同层之间的分布电容(类型1)而言,如各层绕组采用同向布局,则该类型分布电容的储能对变换器不产生影响;而各一次绕组不同层之间的分布电容(类型2)储能对变换器产生影响。在此基础上,对集成变压器绕组布局的优化方法进行分析,提出一种交错式单层一次绕组的布局方法。实验结果表明,采用所提绕组布局方法后,集成变压器分布电容储能对变换器的影响得到了有效的 抑制。
参考文献
[1] 杨超, 许海平, 袁志宝, 等. 双PWM控制下三电平半桥隔离型双向DC-DC变换器的全局最小峰值电流研究[J]. 电工技术学报, 2020, 35(8): 1679-1689.
Yang Chao, Xu Haiping, Yuan Zhibao, et al. Global minimum peak current control of the three level isolated half-bridge bi-directional DC-DC converters with PWM-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1679- 1689.
[2] Chen Xiliang, Chen Wenjie, Yang Xu, et al. Research on a 4000V ultrahigh input switched mode power supply using series connected MOSFETs[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5995-6011.
[3] 杨博, 葛琼璇, 赵鲁, 等. 基于输入串联输出并联的双向全桥串联谐振DC-DC变换器系统控制策略研究[J]. 电工技术学报, 2020, 35(12): 2574-2584.
Yang Bo, Ge Qiongxuan, Zhao Lu, et al. Control strategy of dual bridge series resonant DC-DC converter system based on input series output parallel connection[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2574-2584.
[4] 方天治, 张先云, 黄淳, 等. 输入串联输出并联LCL型并网逆变器系统的目标多重化控制策略[J]. 电工技术学报, 2019, 34(6): 1189-1200.
Fang Tianzhi, Zhang Xianyun, Huang Chun, et al. Control strategy to reach multiple objectives for input-series-output-parallel LCL-type grid-connected inverter system[J]. Transactions of China Electro- technical Society, 2019, 34(6): 1189-1200.
[5] Qu Lu, Zhang Donglai, Zhang Bohan. Input voltage sharing control scheme for input series and output parallel connected DC-DC converters based on peak current control[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 429-439.
[6] Chen Wu, Fu Xinghe, Xue Chenyang, et al. Indirect input-series output-parallel DC-DC full-bridge con- verter system based on asymmetric pulsewidth modulation control strategy[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3164-3177.
[7] 黄先进, 赵娟, 游小杰, 等. 一种基于输入串联输出并联移相全桥变换器的改进交错控制方法[J]. 电工技术学报, 2020, 32(增刊1): 81-90.
Huang Xianjin, Zhao Juan, You Xiaojie, et al. An improved interlace control method based on input series output parallel phase-shift full-bridge con- verter[J]. Transactions of China Electrotechnical Society, 2020, 32(S1): 81-90.
[8] 谷恭山, 郑祥杰, 高明, 等. 两级结构模块化ISOP组合的DC-DC变换器均压控制策略[J]. 电工技术学报, 2019, 34(15): 3175-3185.
Gu Gongshan, Zheng Xiangjie, Gao Ming, et al. Research on voltage sharing control strategy of a combined two-stage modular input series output parallel DC-DC converter[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3175-3185.
[9] Giri R, Choudhary V, Ayyanar R, et al. Common duty ratio control of input-series connected modular DC-DC converters with active input voltage and load current sharing[J]. IEEE Transactions on Industry Applications, 2006, 42(4): 1101-1111.
[10] Pagliosa M, Lazzarin T, Barbi I. Modular two switch flyback converter and analysis of voltage balancing mechanism for input-series and output series con- nection[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 8317-8328.
[11] 石健将, 罗劼, 何湘宁. 相同移相角控制的串-并型移相全桥组合变换器[J]. 中国电机工程学报, 2012, 32(21): 23-30.
Shi Jianjiang, Luo Jie, He Xiangning. Input series output parallel connected phase shifted full bridge converter with common phase shift control[J]. Proceedings of the CSEE, 2012, 32(21): 23-30.
[12] Hu Qingcong, Zane R. LED driver circuit with series-input-connected converter cells operating in continuous conduction mode[J]. IEEE Transactions on Power Electronics, 2010, 25(3): 574-582.
[13] 张志杰, 杨威, 杨世彦. 模块化输入串联输出独立辅助电源系统及其输入均压控制策略[J]. 电工技术学报, 2017, 32(增刊2): 156-163.
Zhang Zhijie, Yang Wei, Yang Shiyan. Input series output independent auxiliary power supply system and its input voltage sharing control strategy[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 156-163.
[14] Bascope R, Barbi I. A double ZVS PWM active clamping forward converter: analysis, design, and experimentation[J]. IEEE Transactions on Power Electronics, 2001, 16(6): 745-751.
[15] Ghodke D, Muralikrishnan K. ZVZCS dual two transistor forward DC-DCconverter with peak voltage of Vin/2, high input and high power application[C]// IEEE Power Electronics Specialists Conference, Cairns, Old, Australia, 2002: 1853-1858.
[16] Meng Tao, Ben Hong, Song Yilin, et al. Analysis and design of an input series two transistor forward converter for high input voltage multiple output applications[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 270-279.
[17] Meng Tao, Song Yilin, Wang Zhongxian, et al. Investigation and implementation of an input series auxiliary power supply scheme for high input voltage low power applications[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 437-447.
[18] Meng Tao, Ben Hongqi, Song Yilin, et al. Analysis and suppression of the circulating current influence in the input series auxiliary power supply for high input voltage applications[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6533-6543.
[19] Choi S, Lee J, Lee J. High efficiency portable welding machine based on full bridge converter with ISOP connected single transformer and active snubber[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 4868-4877.
[20] Thummala P, Schneider H, Zhang Z, et al. Efficiency optimization by considering the high voltage flyback transformer parasitics using an automatic winding layout technique[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5755-5768.
[21] Hong S, Ji S, Jung Y, et al. Analysis and design of a high voltage flyback converter with resonant elements[J]. Journal of Power Electronics, 2010, 10(2): 107-114.
[22] Thummala P, Schneider H, Zhang Zhe, et al. Investigation of transformer winding architectures for high voltage (2.5kV) capacitor charging and dis- charging applications[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5786-5796.
[23] Biela J, Kolar J. Using transformer parasitics for resonant converters a review of the calculation of the stray capacitance of transformers[J]. IEEE Transa- ctions on Industry Applications, 2008, 44(1): 223- 233.
[24] Meng Xianzeng, Li Chunyan, Meng Tao, et al. Analysis and design of transformer windings schemes in multiple output flyback auxiliary power supplies with high input voltage[J]. Journal of Power Elec- tronics, 2019, 19(5): 1122-1132.
[25] 赵志英, 龚春英, 秦海鸥. 高频变压器分布电容的影响因数分析[J]. 中国电机工程学报, 2008, 28(9): 55-60.
Zhao Zhiying, Gong Chunying, Qin Haiou. Effect factors on stray capacitances in high frequency transformers[J]. Proceedings of the CSEE, 2008, 28(9): 55-60.
[26] Fu Dianbo, Wang Shuo, Kong Pengju, et al. Novel techniques to suppress the common mode EMI noise caused by transformer parasitic capacitances in DC-DC converters[J]. IEEE Transactions on Industrial Elec- tronics, 2013, 60(11): 4968-4977.
[27] Zhang Huan, Wang Shuo, Li Yiming, et al. Two capacitor transformer winding capacitance models for common mode EMI noise analysis in isolated DC-DC converters[J]. IEEE Transactions on Power Electro- nics, 2017, 32(11): 8458-8469.
Stray Capacitances Influences and Windings Layout of the Integrated-Transformer in the Input-Series Converter
Abstract The input-series converters based on transformer-integration have the advantages of active input voltage sharing of each series-module and simple structure, which are suitable for high-input voltage multiple-output applications. In the high voltage applications, these converters can be affected seriously by the energy stored in their integrated-transformers’ stray capacitances. Taking this type of input-series two-transistor flyback converter as the object, the influence of the integrated-transformer’s stray capacitances was investigated. Energy storage of stray capacitances in the primary windings of the integrated-transformer was analyzed, and a winding layout scheme of the integrated-transformer was proposed to suppress the influence of stray capacitances. Finally, experiments were carried out on an experimental prototype of this type of input-series converter, which verified the theoretical analysis and feasibility of the proposed scheme.
keywords:Input-series, integrated-transformer, stray capacitance, windings layout
DOI: 10.19595/j.cnki.1000-6753.tces.L90145
中图分类号:TM46
国家自然科学基金(51677056)、黑龙江省博士后基金(LBH-Q17145)和黑龙江省高校基本科研业务费黑龙江大学专项基金(RCYJTD201802, KJCX201915)资助项目。
收稿日期 2020-06-30
改稿日期 2020-11-21
孟 涛 男,1980年生,博士,教授,研究方向为高频AC-DC、DC-DC功率变换技术。E-mail: mengtaohit@126.com(通信作者)
安彦桦 男,1994年生,硕士研究生,研究方向为高频功率变换技术。E-mail: anyanhua186@126.com
(编辑 陈 诚)