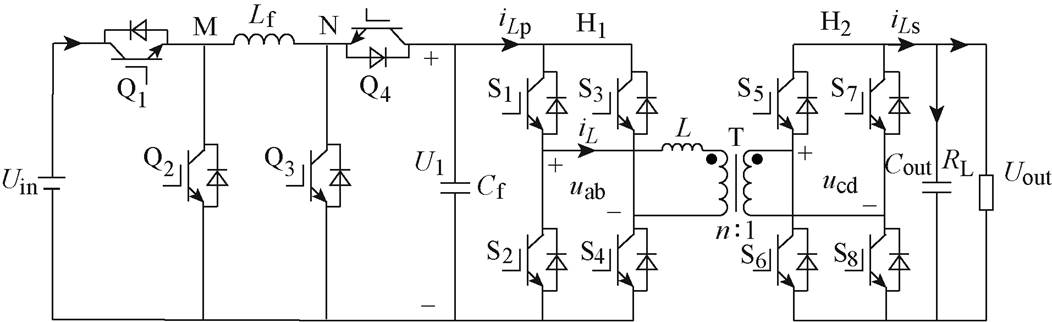
图1 VAU-DAB级联系统拓扑
Fig.1 Topology of VAU-DAB cascade system
摘要 具有电压调整单元(VAU)的双有源桥(DAB)直流变换器是解决宽电压输入时电感电流应力问题的方案之一,然而VAU-DAB存在级联稳定性问题。该文分别推导前级VAU输出阻抗模型和后级DAB输入阻抗模型,在复频域下根据禁区概念阻抗稳定性判据分析级联系统阻抗比,研究阻抗特性对级联系统稳定性的影响。由于VAU输出阻抗谐振峰值与DAB输入阻抗存在交叉点,使级联系统由于阻抗不匹配而导致系统电压振荡失稳。在此基础上,该文基于阻抗匹配准则,提出一种基于超前-滞后的阻抗优化调节器用以抑制VAU输出阻抗谐振尖峰,使级联系统阻抗比满足稳定性判据,提升了系统运行可靠性,并优化了电流应力。最后通过仿真验证了该文提出阻抗优化调节策略的有效性及可行性。
关键词:双有源桥 电压调整 稳定性分析 输入/输出阻抗 级联系统
随着能源革命的不断推进,能源互联网作为分布式电源接入电网的有效途径得到了国内外学者的广泛关注[1-4]。其中,双有源桥(Dual Active Bridge, DAB)直流变换器因其具有高效率、能量双向传输及电气隔离等优势,被广泛应用于储能设备、电动汽车、光伏及能量路由器等场合[5-7],成为能源互联网的研究热点之一。
储能装置如蓄电池、超级电容,分布式电源如光伏等,大多都是输出直流且电压变化范围大,为保证DAB在调压范围较大时仍具有较低电流应力,目前主要有单级式和级联式两种解决方案。单级式解决方案为传统DAB拓扑采用改进的优化控制策略降低电流应力,但如何设计和选择控制变量是具体实现的难点[8]。相关学者先后提出了包括双重移相[9]、扩展移相[10]及三重移相控制[11]在内的一系列改进型移相控制方法。文献[12]基于扩展移相控制提出一种电感电流应力优化算法,在一定程度上减小了DAB电流应力,然而该方法无法在全功率范围内实现优化控制。文献[13]在双重移相控制基础上通过对DAB电流应力以及软开关范围分析,采用查表法获取最优的移相角组合,但该方法不易扩展至其他移相控制中。文献[14-15]提出了基于三重移相的优化控制策略,但涉及12种工作模态,导致模态切换和优化算法相对复杂。上述方案不仅一定程度上增加了DAB变换器控制的复杂性,同时限制了优化电感电流应力的程度[16]。
级联式方案通过在DAB变换器两端引入其他结构,从而在硬件上实现DAB的宽调压和低电流应力。文献[17]提出一种基于双阻抗网络的级联结构,在DAB变换器的两端级联Z源网络结构,系统可同时通过阻抗网络和变压器电压比调节电压,拓展了调压范围。文献[18]将二级准Z源结构与DAB级联,解决了开关管死区问题,提高了系统运行可靠性。但上述文献没有进一步对宽输入电压时DAB电感电流应力进行分析与优化。文献[19]提出了一种四开关变换器,其不仅具有升降压功能,与常规Buck-Boost、Cuk、Zeta、Sepic等变换器相比,还具有拓扑单元结构简单、无源器件少和输入输出电压极性相同等优点。与DAB级联之后,组成具有电压调整单元(Voltage Adjustment Unit, VAU)的DAB变换器,简称VAU-DAB,且该级联系统控制器的设计依然各自独立,便于实现。
此外,级联式方案的稳定性问题也得到了学者们的关注[20-21]。两个变换器组成的级联系统中,前级称为源变换器,后级称为负载变换器。尽管两者工作相对独立,但由于源变换器和负载变换器间存在耦合,阻抗不匹配会引起级联系统的不稳定[22]。Middlebrook阻抗匹配准则是判断直流级联系统中阻抗稳定性的经典方法之一[23],方法简单,但是条件过于苛刻,会导致系统设计过于保守。因此,有学者基于此提出禁区概念的阻抗比判据[24-25],同时考虑了相位和幅值增益条件,直观且更具有实用性。阻抗判据可以判断系统的稳定性,并且可为直流系统中变换器的设计提供理论支撑。
本文基于VAU-DAB级联系统,采用小信号线性化分析法,推导了VAU的输出阻抗和DAB变换器的输入阻抗,建立VAU-DAB级联系统阻抗模型。进而根据基于禁区的阻抗稳定性判据,分析前后级变换器等效阻抗之间的交互特性,揭示该级联系统的振荡失稳机理。在此基础上提出了用于抑制VAU输出阻抗谐振尖峰的基于超前-滞后的阻抗优化调节器,使级联系统阻抗比满足稳定性判据,进而通过稳定级联母线电压使后级DAB变换器始终工作于匹配状态,在提升级联系统的功率传输能力以及稳定性的同时优化了电感电流应力。最后通过仿真结果验证了本文理论分析的正确性及可行性。
图1为VAU-DAB级联系统拓扑。前级VAU为四开关Buck-Boost变换器,Q1与Q2为Buck单元,Q3与Q4为Boost单元,可工作在降压和升压工作模式,图中,Uin和U1分别为前级VAU输入和输出电压。后级DAB变换器包括一次侧桥H1、二次侧桥H2和隔离变压器T三部分。U1和Uout分别为后级DAB输入和输出电压,iLp和iLs为一次侧桥输入电流和二次侧桥输出电流;iL为电感电流,uab和ucd为二次侧桥输出电压和二次侧桥输入电压。规定图1中箭头方向为电流正方向,L为变压器漏感和辅助电感之和,Cout为输出电容,RL为负载等效电阻,n为变压器电压比。

图1 VAU-DAB级联系统拓扑
Fig.1 Topology of VAU-DAB cascade system
该拓扑中,前后级通过支撑电容Cf级联,前级VAU用于将宽范围的输入电压Uin调节为一个稳定的级联母线电压U1。从而保证当输入电压Uin变化时,后级DAB始终处在电压匹配状态。因此,VAU-DAB级联系统可实现优化DAB变换器的电感电流应力,同时实现宽输入电压范围的效果。
定义D1、D2分别为Q1、Q3占空比,则图1中M、N两点的平均电压可分别表示为
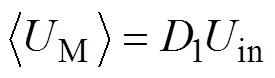 (1)
(1)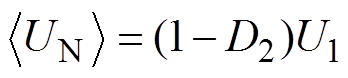 (2)
(2)
根据电感Lf伏秒平衡,可得DAB一次侧桥输入电压U1为
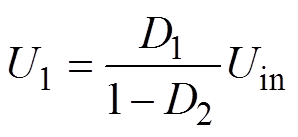 (3)
(3)VAU控制方式有单模式控制、双模式控制和三模式控制[26],其中单模式控制下变换器效率较低;双模式控制未考虑输入电压Uin在额定级联母线电压UN附近频繁变化所导致的变换器可靠性降低问题,因此,本文VAU采用三模式控制方式。设UN为后级DAB额定输入电压,当Uin<UN-DU时,VAU工作在升压模式;当Uin>UN+DU时,VAU工作在降压模式;当Uin在[UN-DU, UN+DU]内时,VAU工作在升-降压模式。由式(3)知,当输入电压一定时,U1为D1、D2的函数,D2越小,则D1越大;当Uin<UN-DU时,Q1、Q3占空比满足D1+D2≥1,为尽可能减小开关损耗,此时调节D1取最大值1,调节D2以改变输出U1值,VAU处于升压工作模式,根据式(3)可以得出该模式下D2的表达式为
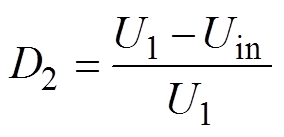 (4)
(4)
当Uin>UN+DU时,Q1、Q3的占空比满足D1+D2< 1,同理,此时D2取最小值0,调节D1可调节输出电压,VAU处于降压工作模式,该模式下D1的表达式为
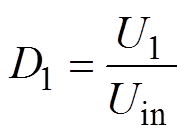 (5)
(5)当Uin在[UN-DU, UN+DU]内时,选择D1工作于一个固定的最大占空比Dm,调节D2控制VAU输出稳压。由于开关器件并非理想器件,开通与关断都需要一定的时间,因此,开关管最小开通和关断时间都应作限制,即最大和最小占空比有一定的范围限制[27]。本文从开关器件特性和驱动电路实现考虑,取D1max=0.9,D2min=0.1。而根据式(3)知,当D1=Dm确定时,输入电压最高对应于D2取最小,即
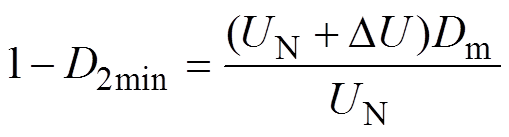 (6)
(6)
由D2min=0.1,可得
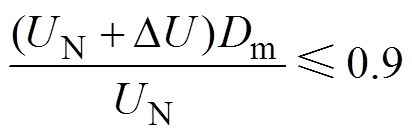 (7)
(7)由式(7)可以得到,Dm与DU关系曲线如图2所示。DU的选择需要综合考虑。即太大会影响后级DAB的优化设计,过小则会造成频繁的工作模式切换。因此,由图2以及实际设计需求,本文选择DU=5V,并根据式(7)可近似得到Dm=0.875。
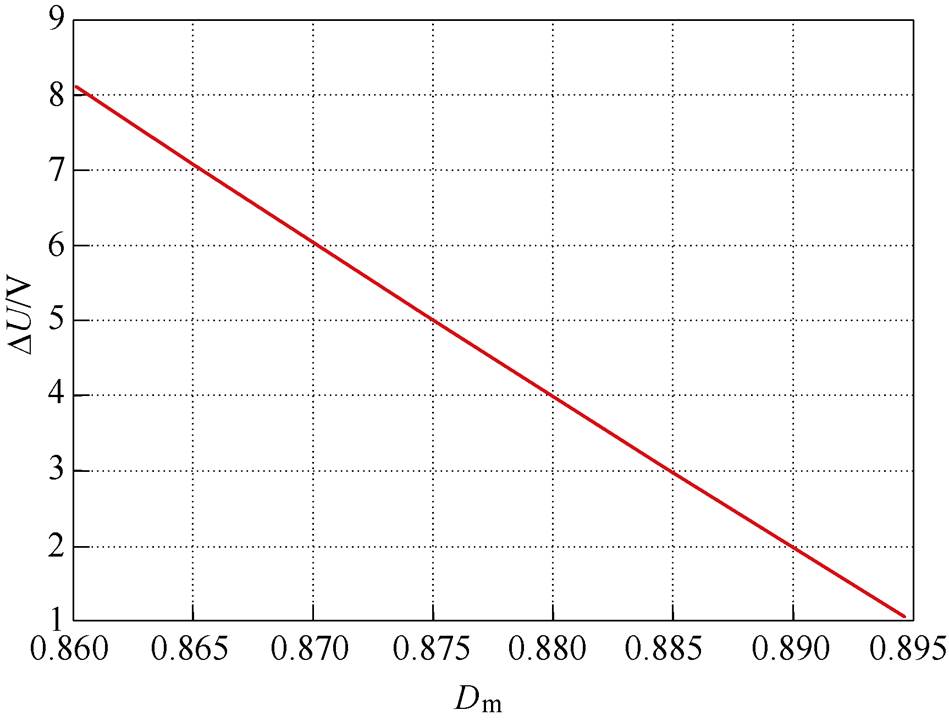
图2 Dm与DU关系曲线
Fig.2 The relationship curve between Dm and DU
由此可以得到,VAU在三模式控制下占空比D1、D2取值见表1。
表1 VAU工作于不同模式时D1、D2占空比
Tab.1 The D1, D2 value of VAU in different modes
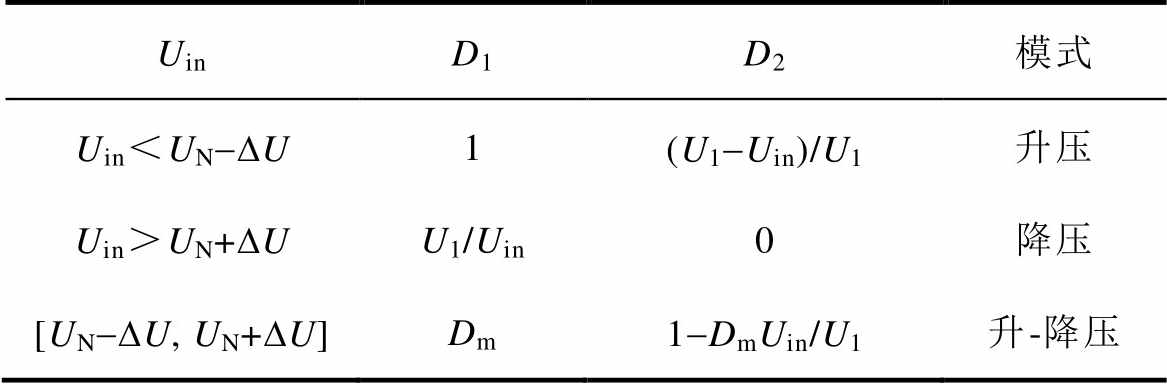
UinD1D2模式 Uin<UN-DU1(U1-Uin)/U1升压 Uin>UN+DUU1/Uin0降压 [UN-DU, UN+DU]Dm1-DmUin/U1升-降压
本文中VAU采用电压负反馈闭环控制,图3为控制框图。图中,Gud(s)为控制d(s)至输出U1(s)的传递函数,Gm(s)为PWM传递函数,Hs(s)为采样器传递函数,Gc(s)为控制补偿网络传递函数。开关变换器输出电压U1(s)经过采样器得到反馈电压信号,与参考信号U1ref(s)相减得到误差信号E(s),输入至控制补偿网络得到控制量Uc(s),经PWM将控制量转化为占空比为d(s)的调制波,最后输入至VAU电路。
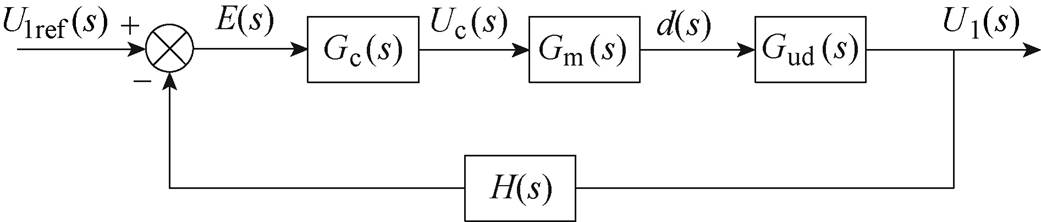
图3 VAU电压负反馈闭环控制框图
Fig.3 Voltage feedback control diagram of VAU
根据三模式控制思路,对VAU进行小信号建模,可得VAU电压型控制闭环电路通用模型如图4所示,图中,输入电压、输出电压以及控制量用s域交流小信号分量表示。
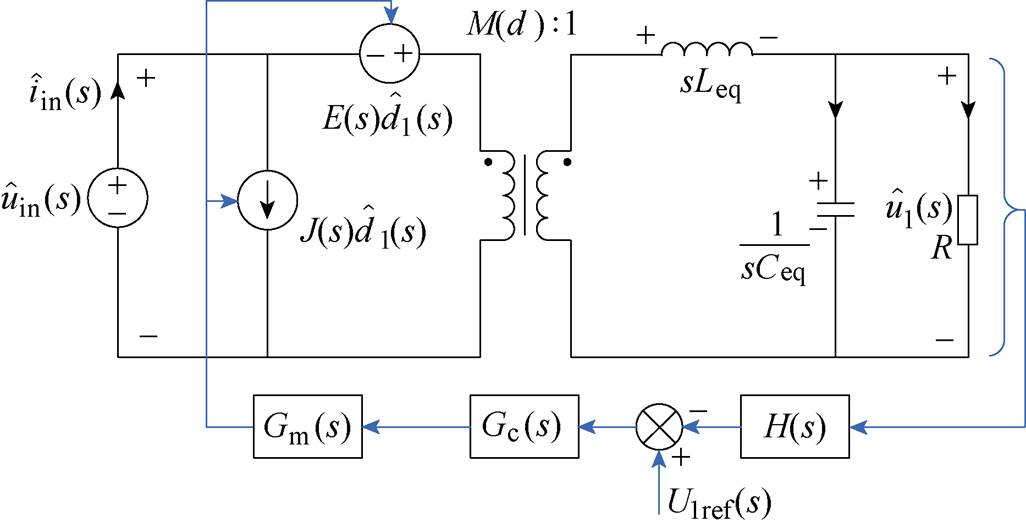
图4 VAU电压型控制闭环电路通用模型
Fig.4 General model of VAU under voltage closed-loop control
VAU电压型闭环控制电路小信号通用模型参数见表2。表中,M(d)为变换器稳态工作点处占空比d的函数,不同工况下表达式不相同;E(s)和J(s)分别为通用模型下受控电压源和受控电流源的控制系数。
表2 VAU电压型闭环控制电路小信号通用模型参数
Tab.2 Parameters of VAU voltage-type closed-loop control general model
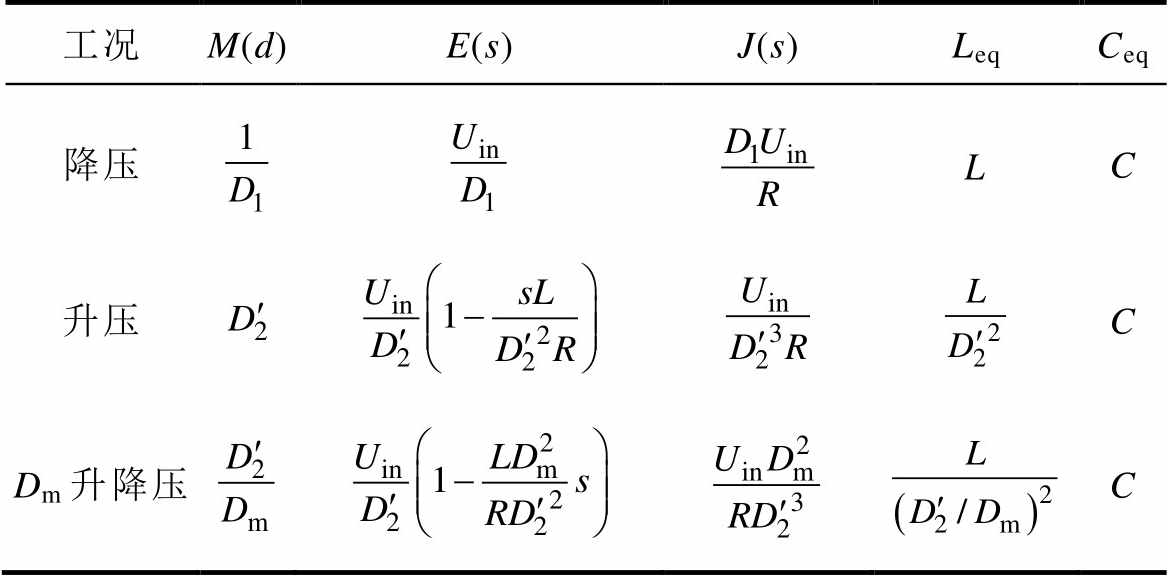
工况M(d)E(s)J(s)LeqCeq 降压C 升压C Dm升降压C
由图4可得,VAU控制-输出传递函数Gud(s)为
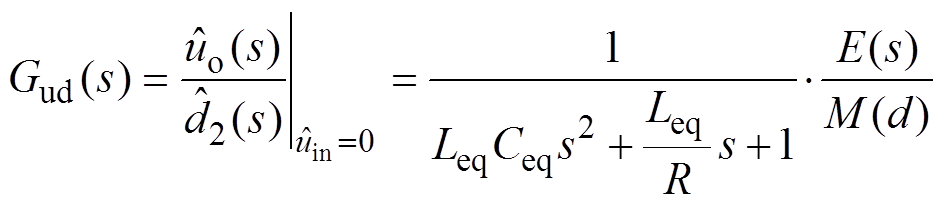 (8)
(8)式中,Leq、Ceq分别为VAU电路小信号模型等效电感和等效电容。
开环输出阻抗Zo_VAUOL(s)通用表达式为
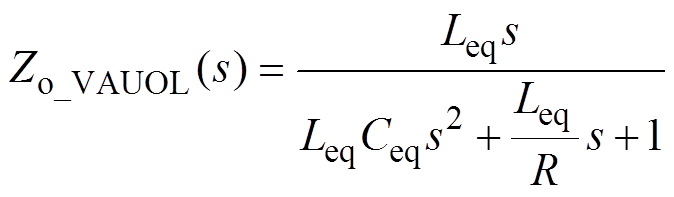 (9)
(9)因此,可得闭环输出阻抗Zo_VAUCL(s)通用表达式为
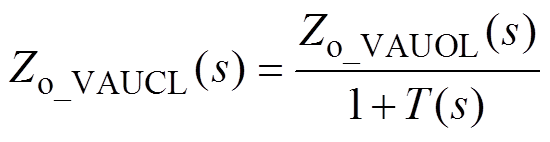 (10)
(10)
式中,T(s)为开环回路增益,有
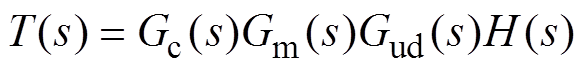 (11)
(11)DAB变换器在单移相(Single Phase Shift, SPS)控制下的工作波形如图5所示。
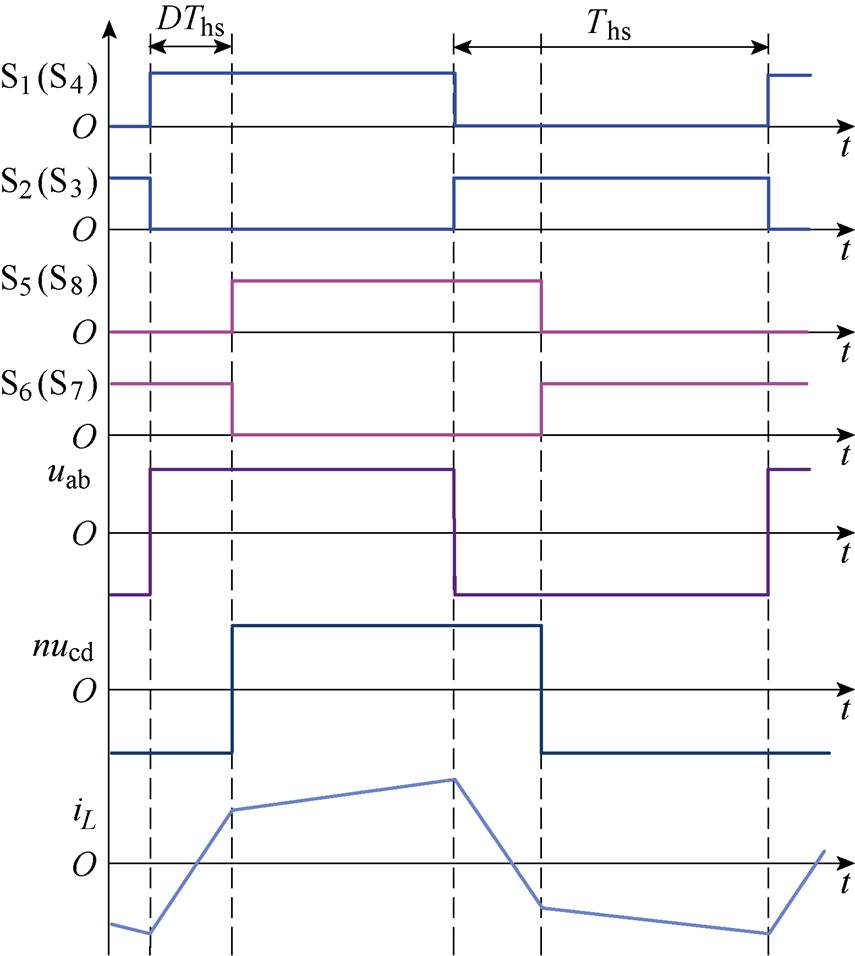
图5 SPS控制下DAB变换器工作波形
Fig.5 Waveforms of DAB converter under SPS control
图5中,定义Ths为半个开关周期,D为H1与H2之间的移相比,0≤D≤1。DAB变换器的传输功率Pt与移相比D之间的数学表达式[28]为
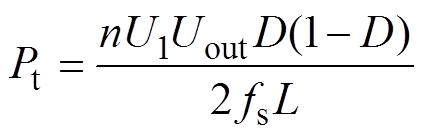 (12)
(12)电流应力Imax与移相比D之间的数学表达式为
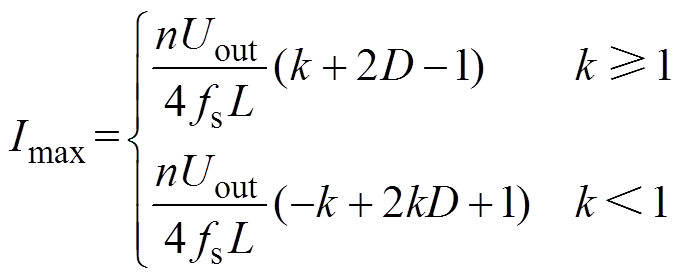 (13)
(13)
式中,k为电压转换比,表征DAB变换器输入输出端电压匹配程度,k=U1/(nUout)。
设变换器平均传输功率和电流应力的额定值分别为其在SPS控制下的最大传输功率PN和最大平均输入电流IN,即
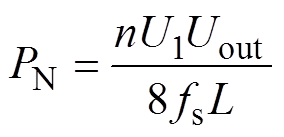 (14)
(14) (15)
(15)
则DAB变换器的传输功率标幺值pt和电流应力标幺值imax分别表示为
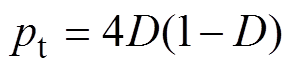 (16)
(16)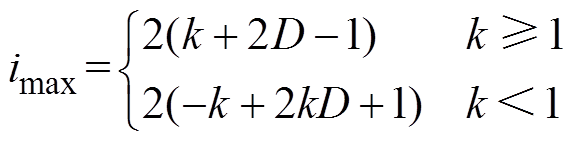 (17)
(17)
根据式(17)可以得到电感电流应力imax与电压转换比k以及移相比D的关系如图6所示。可见,在SPS控制下,DAB变换器在k=1时电流应力imax最小,同时电流应力会随着电压转换比k的增加而增加,这不仅会损坏功率开关器件,也增加了DAB变换器的损耗。
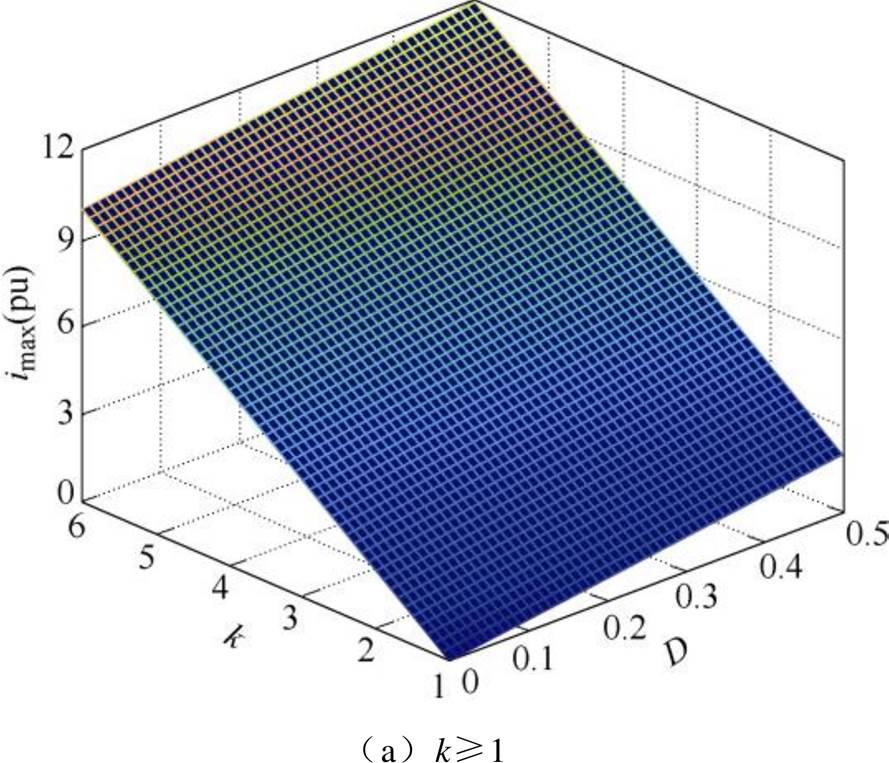
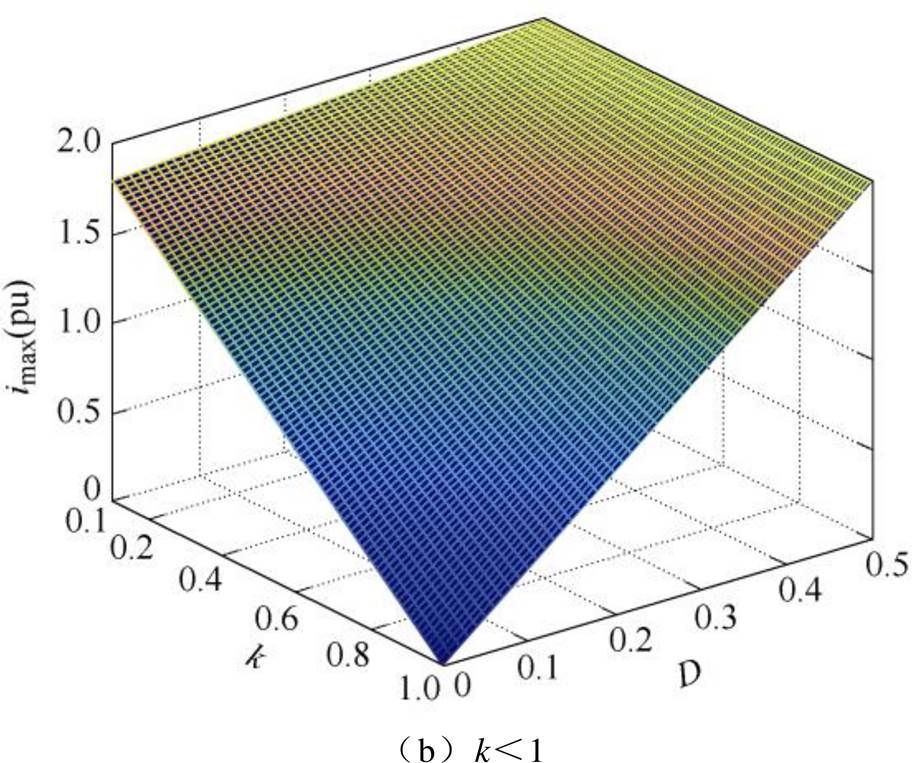
图6 电流应力imax与电压转换比k及移相比D的关系
Fig.6 The relationship between current stress imax, voltage conversion ratio k and phase shift D
假设DAB变换器工作在某一稳态工作点,占空比d(t)=D,输入电压u1(t)稳态值为U1。通过对DAB变换器一次电流iLp平均化,可得在一个开关周期内,平均输入电流ILp可表示为
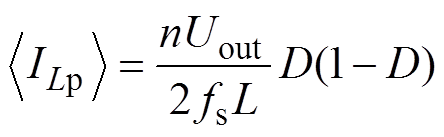 (18)
(18)同理,可得一个开关周期内,二次侧平均输出电流ILs可表示为
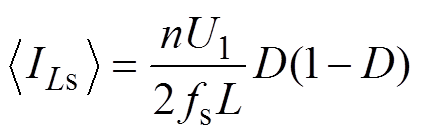 (19)
(19)
根据小信号扰动法,对占空比d1(t)施加一个低频小扰动,即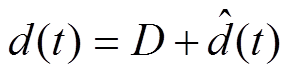 ,DAB变换器中各状态变量由于受到小扰动而发生微小变化,代入式(18)和式(19),并进行拉氏变换,可得到复频域下DAB变换器的小信号数学模型分别为
,DAB变换器中各状态变量由于受到小扰动而发生微小变化,代入式(18)和式(19),并进行拉氏变换,可得到复频域下DAB变换器的小信号数学模型分别为
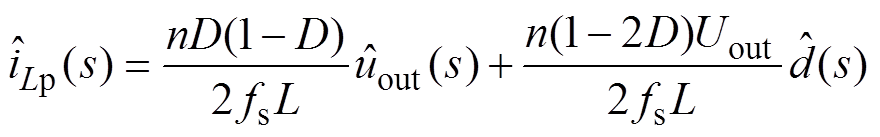 (20)
(20)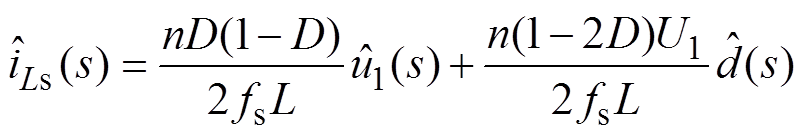 (21)
(21)
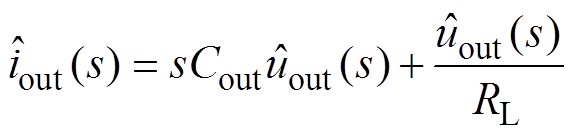 (22)
(22)
式中,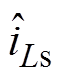 和
和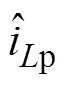 分别为一次、二次电流的扰动分量;
分别为一次、二次电流的扰动分量;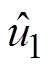 和
和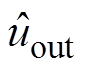 分别为一次、二次侧电容电压的扰动分量;Cout为DAB输出电容。由此可得DAB变换器的小信号模型如图7所示。
分别为一次、二次侧电容电压的扰动分量;Cout为DAB输出电容。由此可得DAB变换器的小信号模型如图7所示。
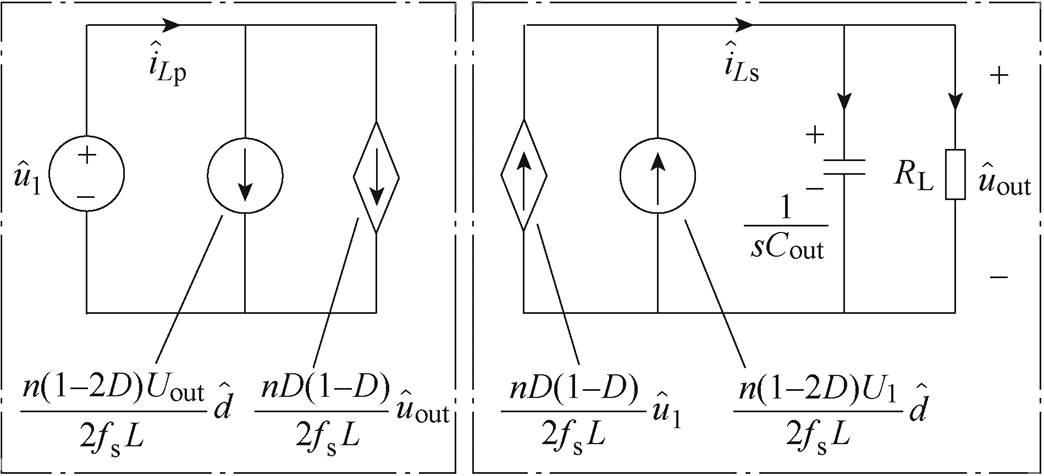
图7 DAB变换器小信号模型
Fig.7 Small signal model of DAB converter
根据图7可得到DAB变换器的开环小信号输出阻抗ZoDAB_OL(s)为
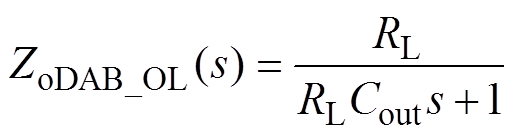 (23)
(23)本文对DAB变换器采用单电压闭环控制,其小信号模型控制框图如图8所示,图中,Gc_DAB(s)为输出电压控制器。
根据图8可推导出闭环控制下DAB变换器的输入阻抗ZiDAB_CL(s)为
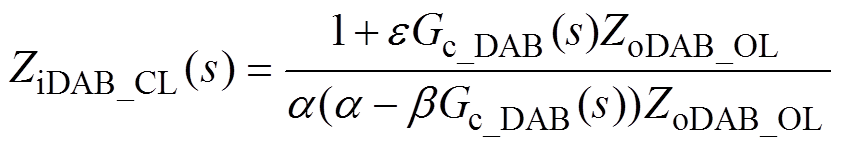 (24)
(24)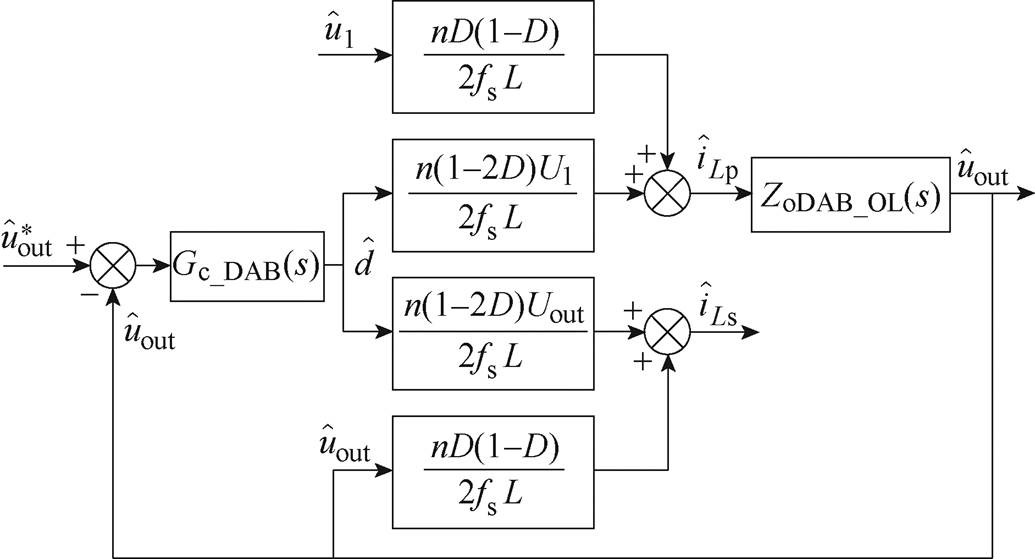
图8 DAB变换器电压闭环控制框图
Fig.8 Voltage closed-loop control diagram of DAB
其中
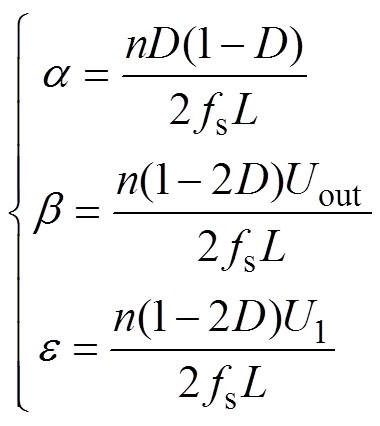 (25)
(25)图9为VAU-DAB级联系统的简化,图中,VAU为源变换器,Zo_VAU为输出阻抗,G1(s)、G2(s)为电压增益;DAB变换器为负载变换器,Zi_DAB为输入阻抗。
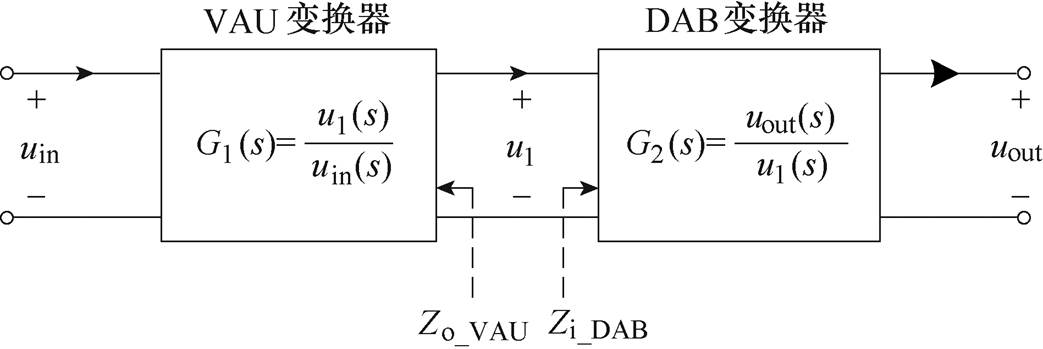
图9 VAU-DAB级联系统简化
Fig.9 Simplified diagram of VAU-DAB system
级联系统输入端至输出端传递函数G(s)可以表示为
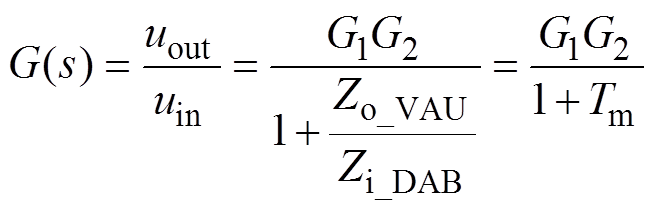 (26)
(26)式中,Tm=Zo_VAU/Zin_DAB为源变换器输出阻抗和负载变换器输入阻抗之比,以下简称阻抗比。
为方便判断级联系统的阻抗稳定性,结合Middlebrook判据,本文采用文献[24]提出了基于禁区概念的阻抗比判据。禁区是指在极坐标设立一个区域,基于禁区概念的阻抗比判据如图10所示。
其禁区范围可表示为
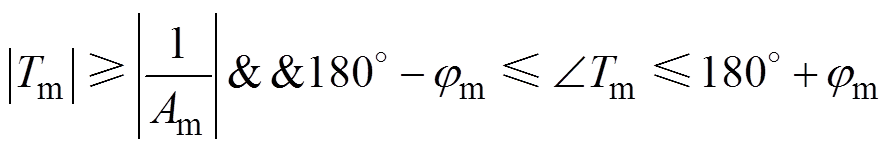 (27)
(27)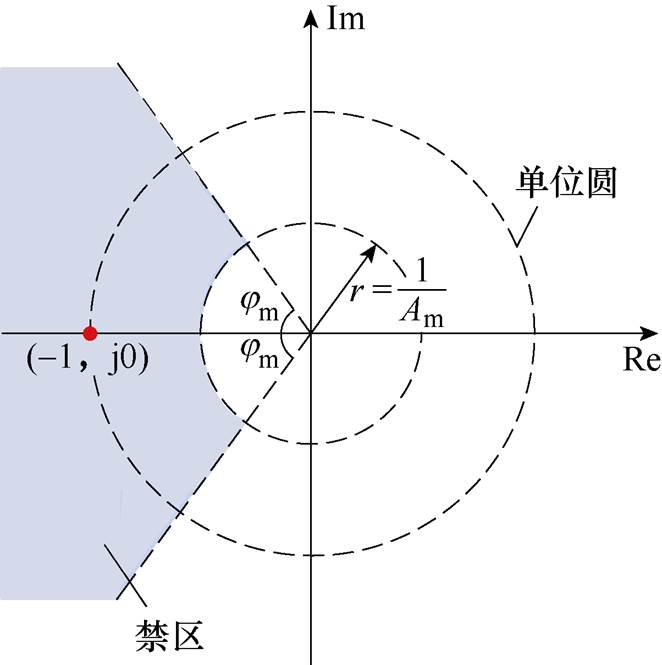
图10 基于禁区概念的阻抗比判据
Fig.10 Impedance criterion with forbidden region
只要阻抗比Tm不进入该区域,就认为系统是稳定的,且系统具有所期望的jm和Am。对阻抗比的要求可以表示为
 (28)
(28)在实际工程应用中,考虑到实际参数的变化,一般要求相位裕度jm在60°左右,幅值裕度在6dB以上(即Am≥2)[24]。式(28)表明,当阻抗比Tm幅值曲线在全频率范围内低于-6dB时,级联系统阻抗稳定;当幅值曲线穿越-6dB时,则需考虑相位曲线是否在稳定裕度内。
综上可知,基于禁区概念的新判据实际上是将Middlebrook判据规定的禁区进行缩小,从而增大了系统参数设计的自由度。从系统阻抗稳定性角度而言,级联系统中源变换器的输出阻抗幅值越小越好,而负载变换器的输入阻抗越大越好。同时,为了满足负载变换器并联扩容或负载分布的需求,变换器阻抗比应尽可能满足上述禁区要求。本文以文献[24]禁区判据对VAU-DAB变换器稳定性的优化进行讨论,其中幅值裕度取Am=2,相位裕度jm=60°。
为分析级联系统稳定性,采用基于禁区的稳定判据分析方法,其充分必要条件是系统输出和输入阻抗比的奈奎斯特曲线不通过图10所示的禁区。VAU-DAB级联系统主电路参数见表3。
图11给出了优化前级联系统在不同工况下VAU开环输出阻抗Zo_VAUOL和DAB变换器输入阻抗Zin_DABCL幅值特性曲线。
VAU等效LC滤波器增大了开环输出阻抗Zo_VAUOL幅值曲线,所形成的谐振峰值使其与DAB闭环输入阻抗Zin_DABCL存在交叉点,降低了级联系统的稳定裕度,故母线电压可能产生Zo_VAUOL谐振峰值频率附近的振荡(谐振频率可根据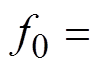
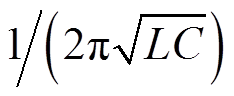 计算)。得到升压工况、降压工况、Dm升降压工况谐振频率分别约为39.2Hz、68.5Hz和66.5Hz。
计算)。得到升压工况、降压工况、Dm升降压工况谐振频率分别约为39.2Hz、68.5Hz和66.5Hz。
表3 VAU-DAB级联系统主电路参数
Tab.3 Parameters of VAU-DAB cascade system
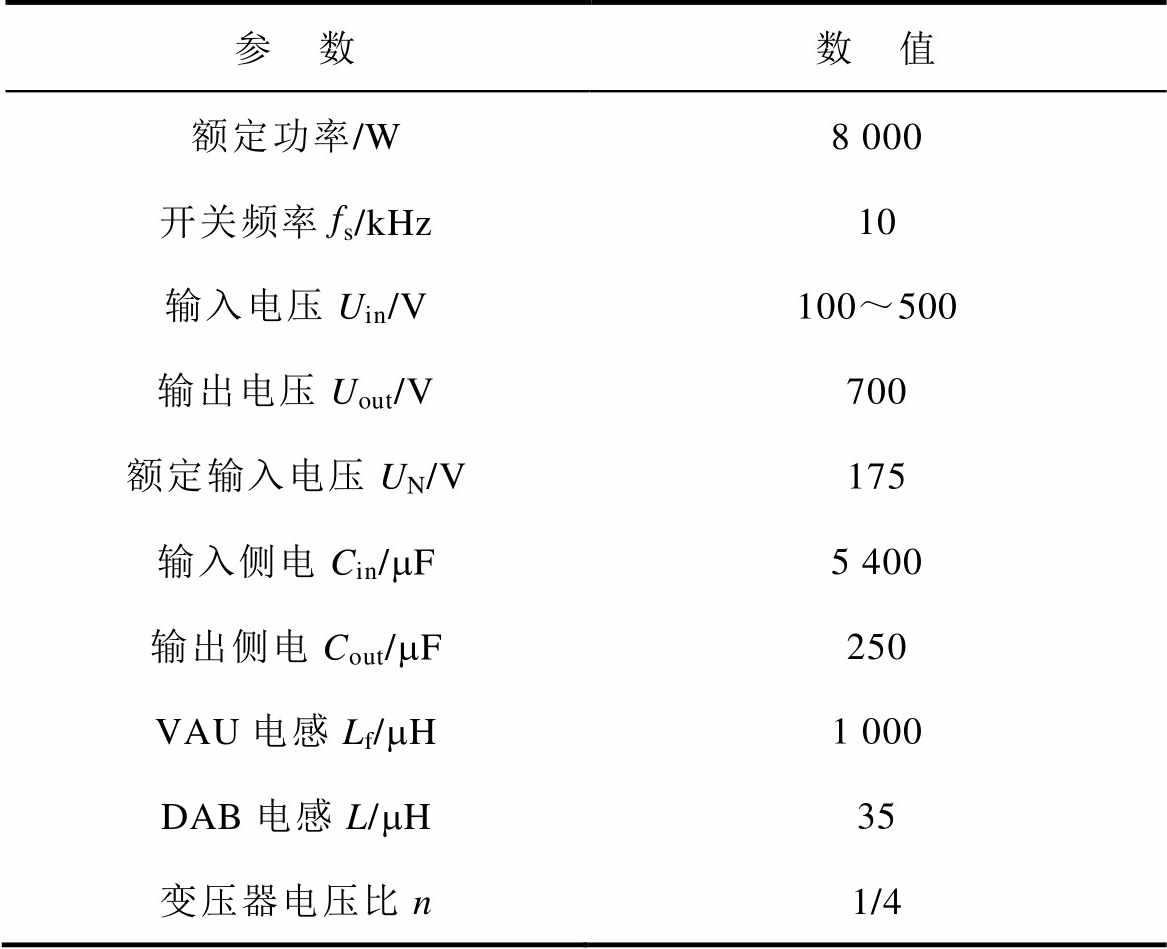
参 数数 值 额定功率/W8 000 开关频率fs/kHz10 输入电压Uin/V100~500 输出电压Uout/V700 额定输入电压UN/V175 输入侧电Cin/mF5 400 输出侧电Cout/mF250 VAU电感Lf/mH1 000 DAB电感L/mH35 变压器电压比n1/4
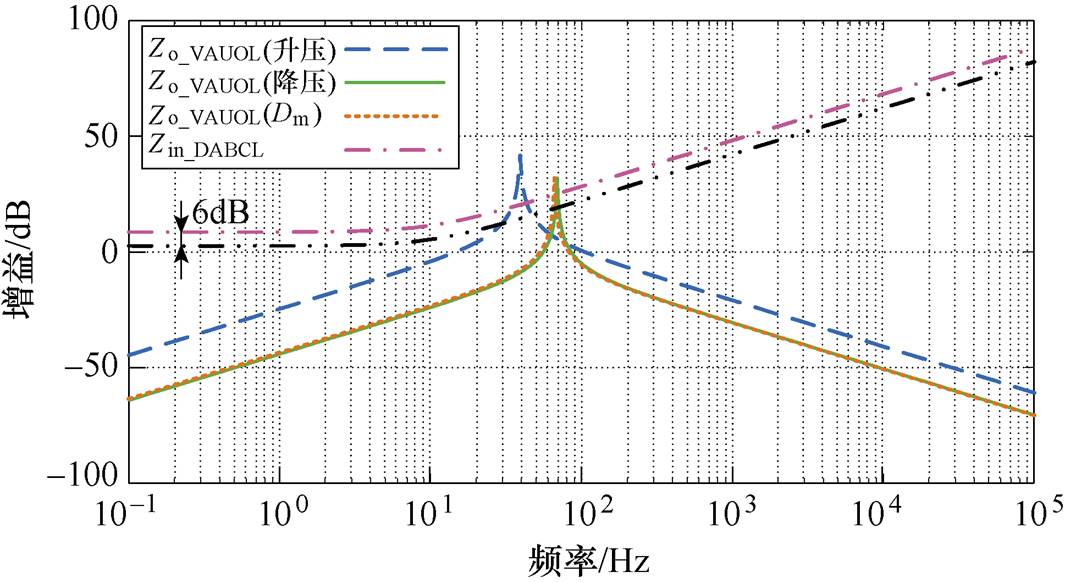
图11 优化前VAU各工况下输出阻抗和DAB输入阻抗幅值特性曲线
Fig.11 Amplitude plot of VAU output impedance and DAB input impedance before optimization
图12给出了级联系统在不同工况下阻抗比Tm伯德图和奈奎斯特图。由伯德图可知,各工况下系统阻抗比幅值曲线均与判据要求的幅值裕度Am有交点;且阻抗比曲线穿越-6dB时的相位曲线没有在稳定裕度内;由奈奎斯特图知,阻抗比曲线进入禁区,从另一个角度验证了未进行阻抗优化调节时VAU-DAB级联系统阻抗特性较差。
根据以上分析可知,VAU等效LC滤波器使开环输出阻抗Zo_VAUOL幅值曲线存在谐振尖峰,导致VAU-DAB级联系统阻抗不匹配,大大降低了级联系统的稳定裕度。
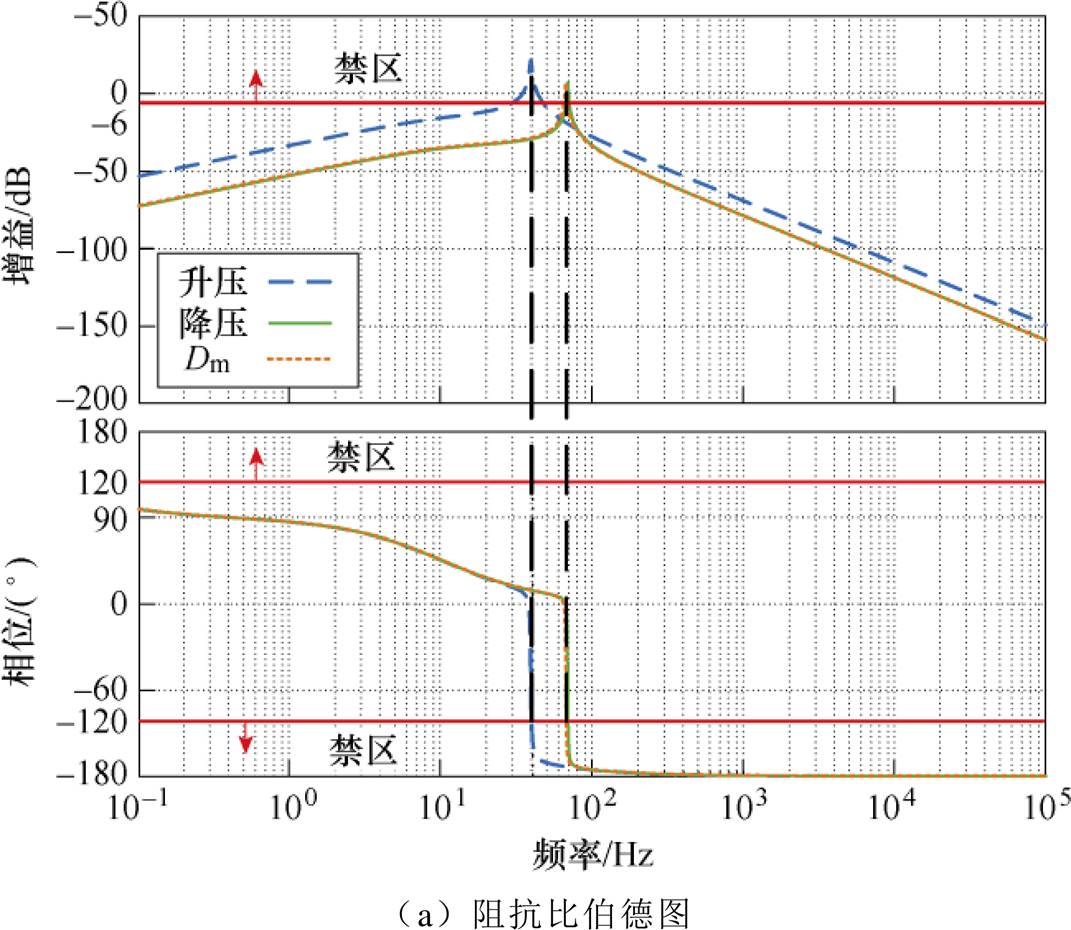
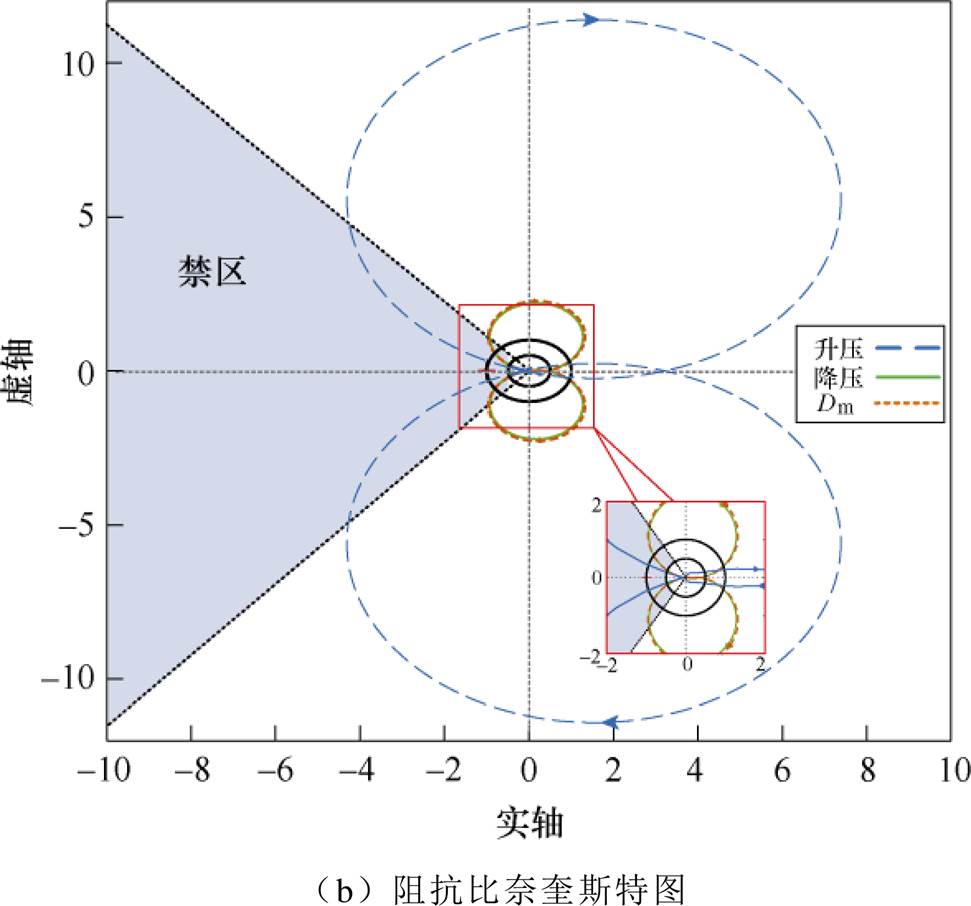
图12 优化前VAU-DAB级联系统各工况下阻抗比伯德图和奈奎斯特图
Fig.12 Bode plot and nyquist plot of VAU-DAB cascade system
为实现级联系统阻抗特性的优化,需对VAU输出阻抗在谐振频率点尖峰进行抑制,使阻抗比满足稳定性判据。由式(10)可知,闭环回路对截止频率以下的输出阻抗具有抑制作用,因此需要对开环回路增益T(s)进行合理设置。T(s)由四部分组成:脉宽调制器Gm(s)和采样器Hs(s)均为典型比例环节,为方便分析,其值均设为1。控制-输出传递函数Gud(s)由电路参数决定,而补偿网络Gc(s)是闭环系统设置的关键环节。
由于级联系统工作于多个模式,在实际电路中一般情况下三种工况共用一个控制器[26]。由图12可知,当其工作在升压工况时,阻抗比Tm与禁区交截面积最大,因此相对于其余两个工况,升压工况下稳定裕度较低。所以,阻抗优化调节器应按照升压模式的需求设计。
为使闭环阻抗满足稳定性要求,同时提高变换器动态特性,本文采用滞后-超前补偿网络。Gc(s)零极点表示为
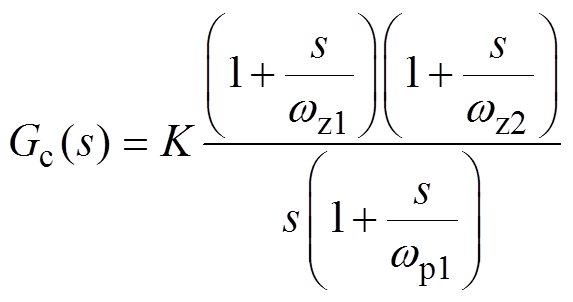 (29)
(29)传递函数中存在两个极点和两个零点,其中补偿系统设计中需要配置的是零点z1、z2和极点p1。第一个零点频率wz1与位于原点的极点组成比例积分(Proportion Integration, PI)补偿网络,用于缓和PI控制器对系统稳定性产生的不利影响,设在原始系统转折频率w0的1/2~1/4处。第二个零点频率设置在原始系统转折频率w0附近,用于抵消原始系统转折频率。为提高系统高频抑制能力,极点频率wp1位置应设在校正后系统截止频率wc的1.5倍以上,而一般将校正后系统截止频率wc设置在1/5~1/20开关频率处,变换器开关频率fs=10kHz,因此本文取fc=1kHz。K的大小调整可以实现Gc(s)对数幅频在垂直方向上下的位置,以满足fc=1kHz。通过以上分析,最后得到阻抗优化控制补偿网络Gc(s)为
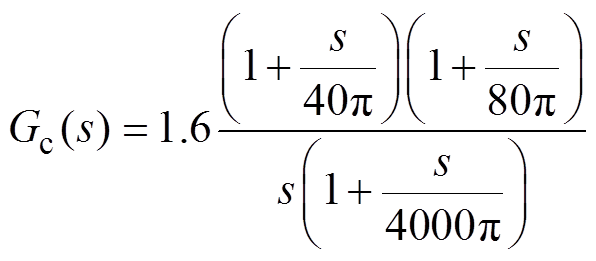 (30)
(30)
综上可得,VAU-DAB级联系统阻抗优化控制框图如图13所示,图中,b 为考虑开关管的压降及开通关断延迟、元件参数测量误差、变换器死区时间以及控制系统的采样传输延迟等因素的影响而引入误差校正因子。
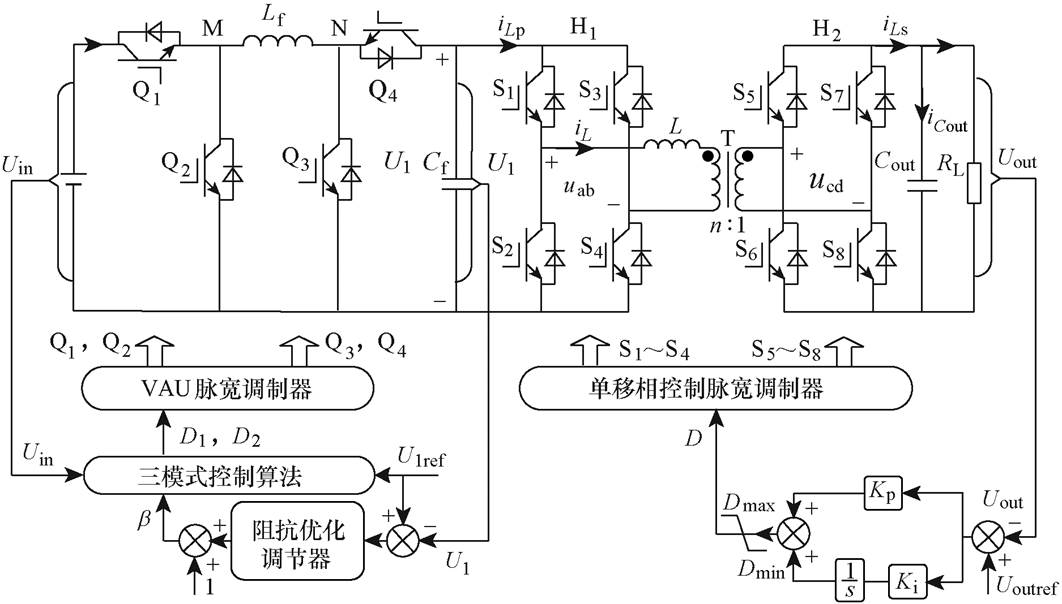
图13 VAU-DAB级联系统阻抗优化控制框图
Fig.13 Impedance optimization control block diagram VAU-DAB cascade system
当采用阻抗优化调节器后,可得级联系统在不同工况下VAU输出阻抗Zo_VAUOL和DAB变换器输入阻抗Zin_DABCL幅值特性曲线如图14所示。
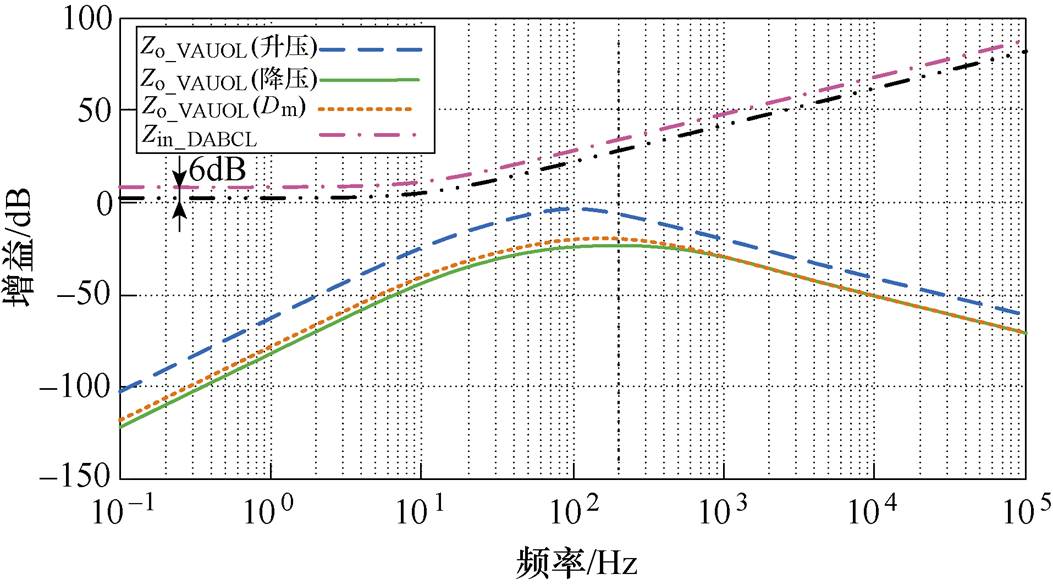
图14 优化后VAU各输出阻抗和DAB输入阻抗幅值特性曲线
Fig.14 Amplitude plot of VAU output impedance and DAB input impedance after optimization
由图14可知,当采用阻抗优化调节器后,VAU的输出阻抗的谐振尖峰得到了抑制,在全频率范围内输入和输出阻抗的幅频特性曲线没有交叉点。
图15为加入阻抗优化调节器后级联系统在不同工况下阻抗比Tm伯德图和奈奎斯特图。从伯德图可知,系统阻抗比幅值曲线峰值远低于禁区边界-6dB,达到稳定性判据所要求的Am=2的幅值裕度;此外,从奈奎斯特图也可看出,级联系统各工况下阻抗比曲线均在r=1/Am圆内,穿越禁区的现象消失。
综上所述,本文所提阻抗优化调节器改善了系统的阻抗特性,从阻抗匹配的角度优化了系统性能,提升了系统的运行可靠性。
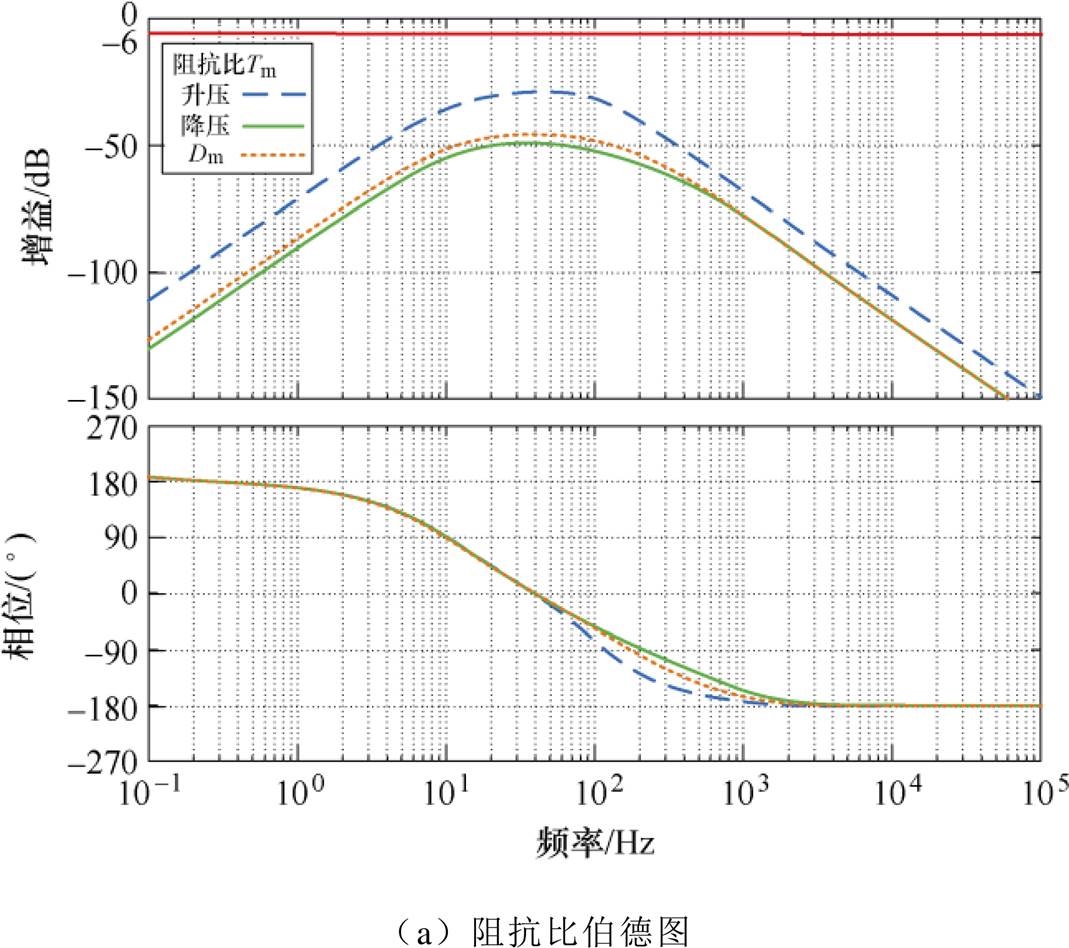
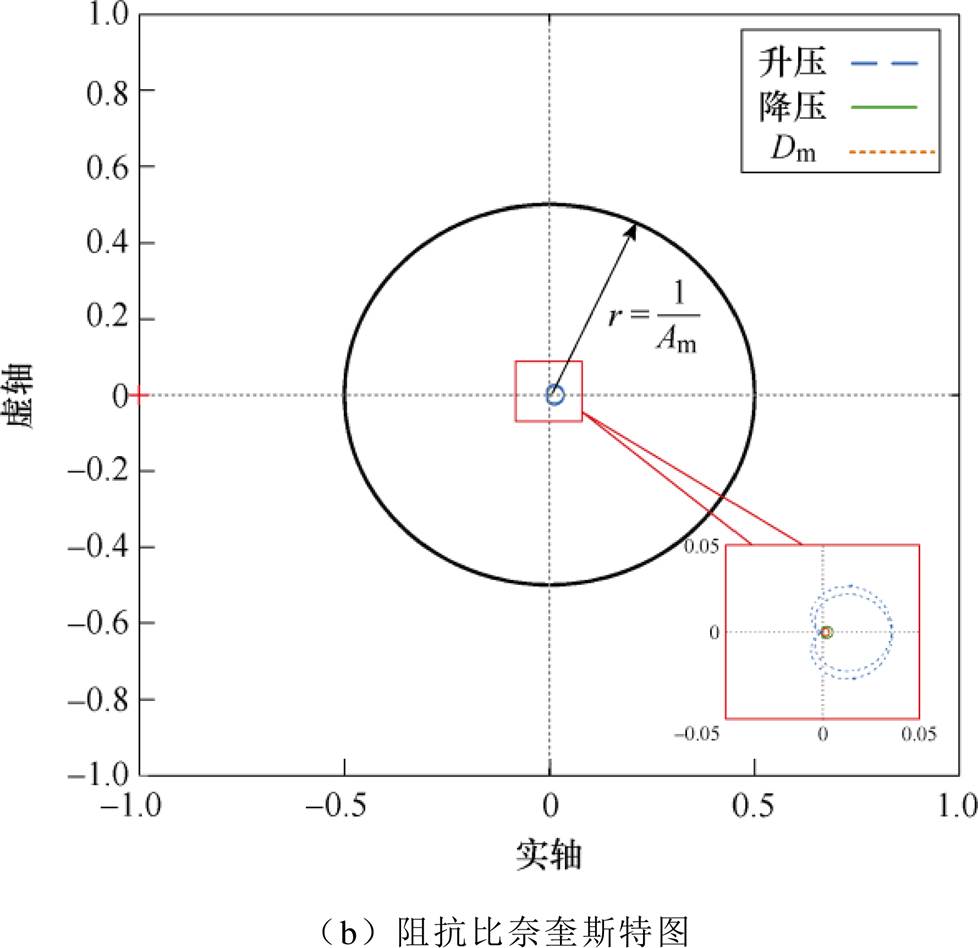
图15 优化后VAU-DAB级联系统各工况下阻抗比伯德图和奈奎斯特图
Fig.15 Bode plot and nyquist plot of VAU-DAB cascade system impedance ratio after optimization
为了验证本文所提分析方法控制策略的有效性,在Matlab/Simulink中搭建图1所示的VAU-DAB仿真平台,级联系统参数见表3。
额定功率运行时,令输入侧直流电压Uin给定从100V到170V,再从170V到300V变化,验证级联系统在宽电压输入时的运行效果。
图16a和图16b分别为未加入和加入阻抗优化调节器后的电压仿真波形。由图可知,当系统未加以阻抗匹配调节时,各工况下级联接口侧直流母线电压U1和输出母线电压Uout都会产生明显振荡。其中,U1振荡峰值分别为277V、272V和224V,Uout振荡峰值分别为915V、788V和745V,均大大超出额定值,系统运行状况较差;而采用所提控制方法后,电压能稳定在额定值。因此,本文所提方法能抑制系统振荡,提高系统稳定性。
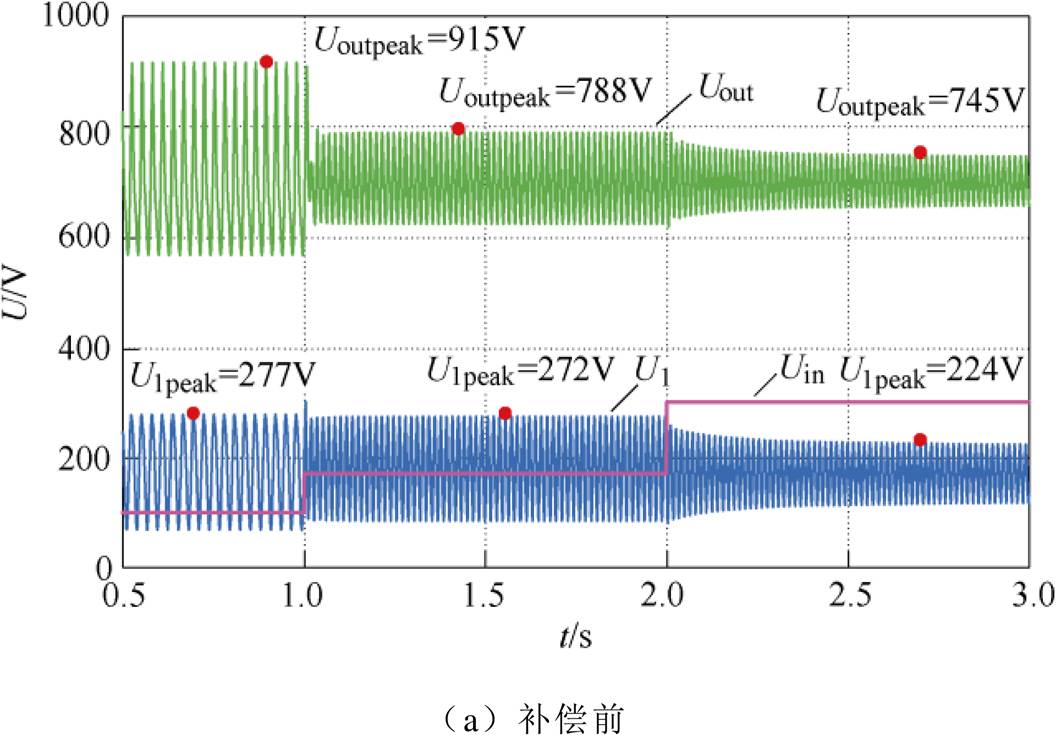
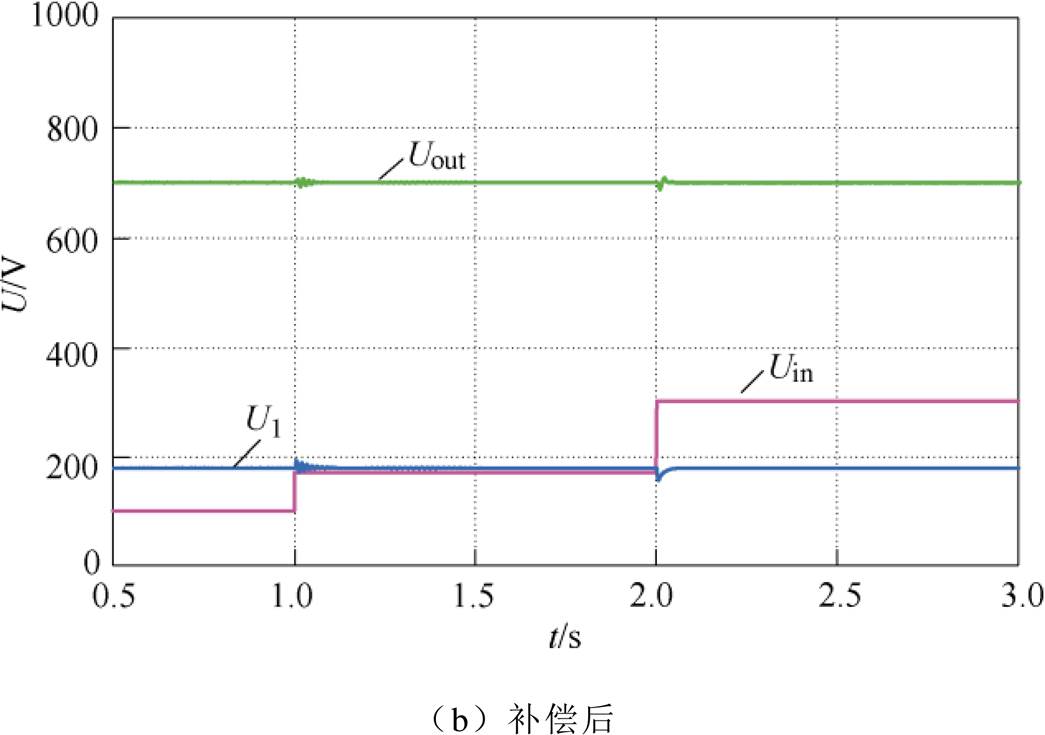
图16 宽电压输入电压U1和Uout仿真波形
Fig.16 Wide input voltage U1和Uout simulation waveforms
图17为对应的级联接口侧直流母线电压U1和输出母线电压Uout的频谱。由图17a和图17b可得系统在未加阻抗调节器时母线电压的振荡频率。其中,升压工况振荡频率约为35Hz,降压工况振荡频率约为65Hz,升降压工况振荡频率约为62.5Hz,振荡频率均在谐振频率附近,与第2节理论分析基本相对应。并且从图17c和图17d可以看出,通过阻抗优化调节,母线电压的振荡谐波均已得到抑制。
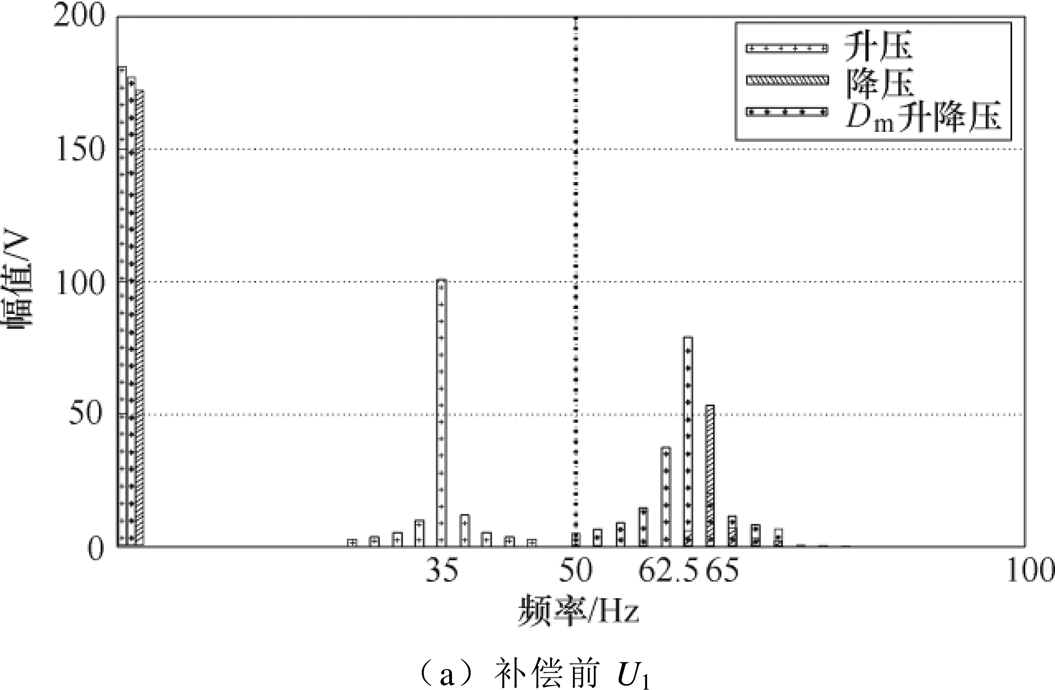
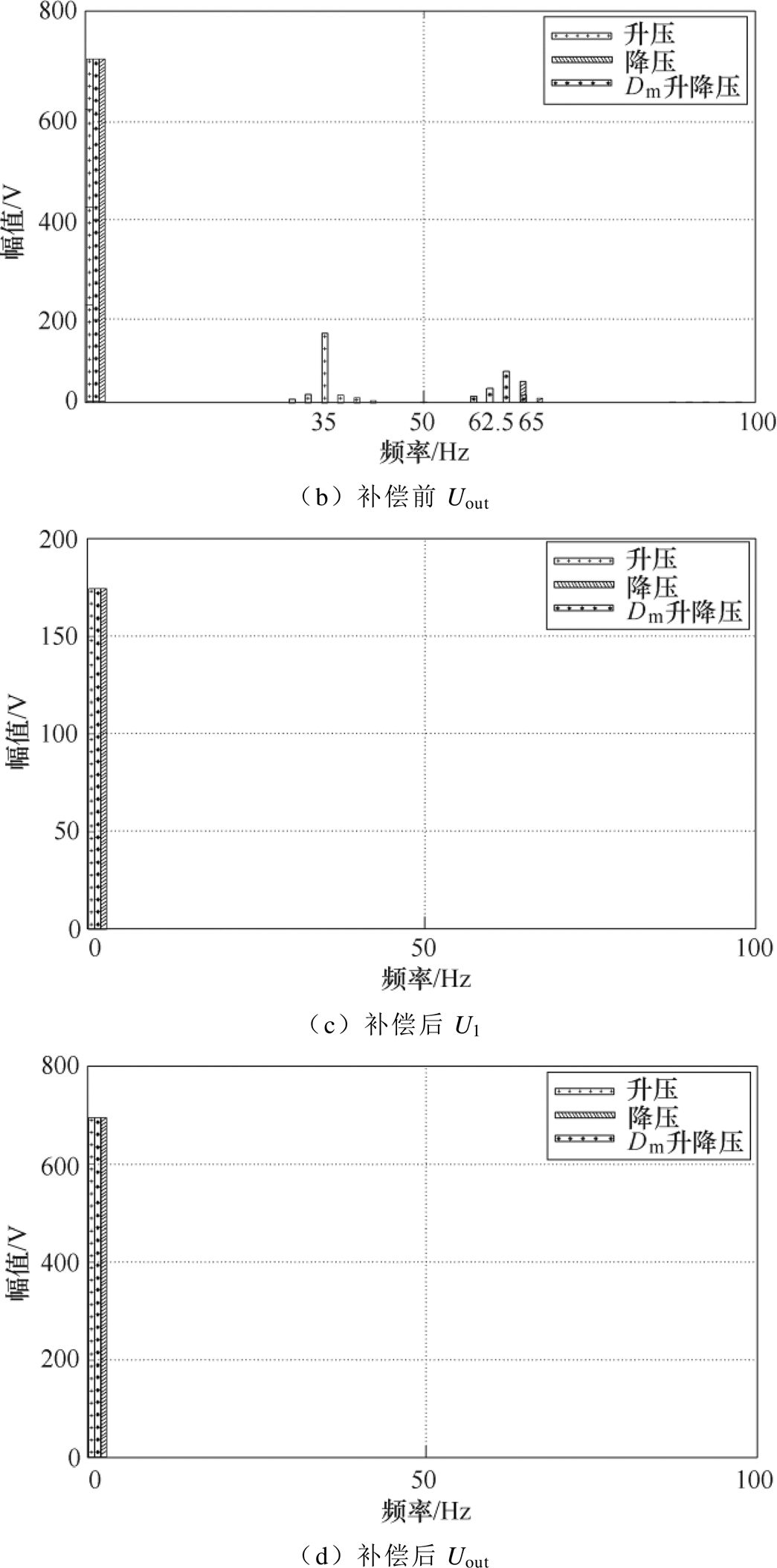
图17 电压U1和Uout频谱分析波形
Fig.17 FFT analysis waveforms of U1 and Uout
令级联系统工作在输入电压Uin=300V工况,负荷功率由2.5kW突增至5kW。
图18为DAB变换器辅助电感电流iL、级联接口母线电压U1和输出电压Uout仿真波形。由图可知,未加阻抗调节器时,由于母线电压存在振荡现象,系统运行状况较差。负荷功率为5kW时,由于DAB等效输入阻抗幅值曲线下移,导致阻抗不匹配情况加剧,振荡幅值较大,其中U1超出额定值78.9%,Uout超出额定值15.3%,电感电流峰值可达到164A。系统从2.5kW切换到5kW时,需较长时间才进入稳态,动态响应慢。进行阻抗优化控制后,母线电压的振荡得到抑制,电感电流峰值大大降低;切载时电压冲击小,且很快恢复到额定值。因此,所提阻抗优化调节器不仅提高了系统的稳态特性,同时也提升了系统暂态特性。
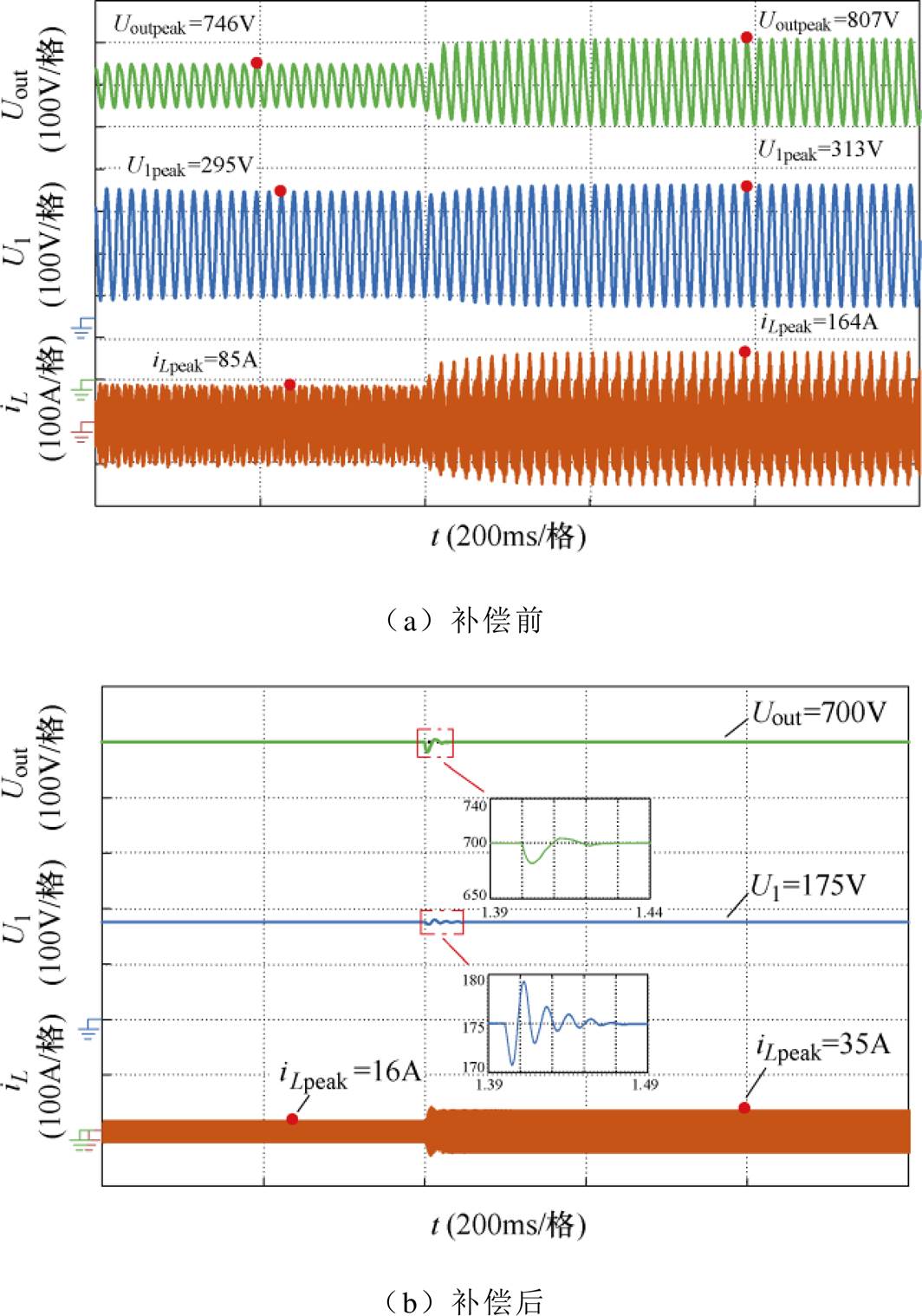
图18 切载试验电压电流仿真波形
Fig.18 Change load simulation waveforms of voltage and current
图19a和图19b分别为输入电压从150V到450V变化时,传统DAB和VAU-DAB电感电流有效值iLRMS以及最大值iLpeak随输入电压Uin变化对比波形。
由图19可知,VAU-DAB电感电流有效值和峰值曲线均在传统DAB的下方,两者在级联接口母线电压为额定值(Uin=175V)最低点重合。这表明在宽电压输入时,VAU-DAB对电感电流应力的优化效果明显。
本文基于具有电压自调节特性的VAU-DAB级联系统,采用基于禁区的阻抗稳定性判据,分析了其阻抗稳定性,并同时提出一种阻抗优化控制来抑制级联系统的振荡,提升系统稳定性。理论分析和仿真结果表明:

图19 宽输入电压电流应力对比波形
Fig.19 Current stress comparison waveforms of wide input voltage
1)VAU即四开关变换器采用小信号通用模型时,等效LC滤波器会增大开环输出阻抗Zo_VAUOL幅值曲线,所形成的谐振峰值在一定情况下会使其与DAB闭环输入阻抗Zin_DABCL存在交叉点,故母线电压可能产生Zo_VAUOL谐振峰值频率附近的振荡。
2)根据阻抗匹配准则,提出一种基于超前-滞后的阻抗优化控制,抑制了VAU输出阻抗谐振尖峰现象,使级联系统阻抗比满足稳定性判据,提升了级联系统的鲁棒性及稳定性。
3)VUA-DAB级联系统在能够实现宽输入电压的同时,对电感电流应力的优化效果明显。
参考文献
[1] 赵海, 蔡巍, 王进法, 等. 能源互联网架构设计与拓扑模型[J]. 电工技术学报, 2015, 30(11): 34-40.
Zhao Hai, Cai Wei, Wang Jinfa, et al. An architecture design and topological model of intergrid[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(11): 34-40.
[2] 余晓丹, 徐宪东, 陈硕翼, 等. 综合能源系统与能源互联网简述[J]. 电工技术学报, 2016, 31(1): 1-13.
Yu Xiaodan, Xu Xiandong, Chen Shuoyi, et al. A brief review to integrated energy system and energy internet[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 1-13.
[3] 冯高辉, 赵争鸣, 袁立强. 基于能量平衡的电能路由器综合控制技术[J]. 电工技术学报, 2017, 32(14): 34-44.
Feng Gaohui, Zhao Zhengming, Yuan Liqiang. Synthetical control technology of electric energy router based on energy balance relationship[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 34-44.
[4] Huang A Q, Crow M L, Heydt G T, et al. The future renewable electric energy delivery and management (FREEDM) system: the energy internet[J]. Pro- ceedings of the IEEE, 2011, 99(1): 133-148.
[5] 雷志方, 汪飞, 高艳霞, 等. 面向直流微网的双向DC-DC变换器研究现状和应用分析[J]. 电工技术学报, 2016, 31(22): 141-151.
Lei Zhifang, Wang Fei, Gao Yanxia, et al. Research status and application analysis of bidirectional DC-DC converters in DC micro-grids[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 141-151.
[6] 涂春鸣, 孟阳, 肖凡, 等. 一种交直流混合微网能量路由器及其运行模态分析[J]. 电工技术学报, 2017, 32(22): 176-188.
Tu Chunming, Meng Yang, Xiao Fan, et al. An AC-DC hybrid microgrid energy router and oper- ational modal analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 176-188.
[7] 卢林煜, 王鲁杨, 柏扬, 等. 面向能源互联网的固态变压器中双有源桥直流变换器研究[J]. 电力系统保护与控制, 2019, 47(6): 141-150.
Lu Linyu, Wang Luyang, Bai Yang, et al. Research on dual-active-bridge DC-DC converter in solid state transformer for energy internet[J]. Power System Protection and Control, 2019, 47(6): 141-150.
[8] Hou Nie, Li Yunwei. Overview and comparison of modulation and control strategies for a nonresonant single-phase dual-active-bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 3148-3172.
[9] Hirose T, Matsuo H. A consideration of bidirectional superposed dual active bridge DC-DC converter[C]// The 2nd International Symposium on Power Elec- tronics for Distributed Generation Systems, Hefei, China, 2010: 39-46.
[10] Oggier G G, Leidhold R, Garcia G O, et al. Extending the ZVS operating range of dual active bridge high- power DC-DC converters[C]//2006 37th IEEE Power Electronics Specialists Conference, Jeju, South Korea, 2006: 1-7.
[11] Wu Kuiyuan, De Silva C W, Dunford W G. Stability analysis of isolated bidirectional dual active full- bridge DC-DC converter with triple phase-shift control[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 2007-2017.
[12] Zhao Biao, Yu Qingguang, Sun Weixin. Extended- phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4667-4680.
[13] Kim M, Rosekeit M, Sul S K, et al. A dual-phase-shift control strategy for dual-active-bridge DC-DC converter in wide voltage range[C]//8th International Conference on Power Electronics-ECCE Asia, Jeju, 2011: 364-371.
[14] 侯聂, 宋文胜. 全桥隔离DC/DC变换器的三重相移控制及其软启动方法[J]. 中国电机工程学报, 2015, 35(23): 6113-6121.
Hou Nie, Song Wensheng. Full-bridge isolated DC/DC converters with triple-phase-shift control and soft starting control method[J]. Proceedings of the CSEE, 2015, 35(23): 6113-6121.
[15] 谷庆, 袁立强, 聂金铜, 等. 基于开关组合规律的双有源桥DC-DC变换器传输功率特性[J]. 电工技术学报, 2017, 32(13): 69-79.
Gu Qing, Yuan Liqiang, Nie Jintong, et al. Trans- mission power characteristics of dual-active-bridge DC-DC converter based on the switching combination rules[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 69-79.
[16] 阚加荣, 吴云亚, 谢少军, 等. 基于高频交流升降压原理的双有源桥双向变换器[J]. 中国电机工程学报, 2017, 37(6): 245-256,
Kan Jiarong, Wu Yunya, Xie Shaojun, et al. Dual- active-bridge bidirectional DC/DC converter based on high-frequency AC Buck-Boost theory[J]. Proceedings of the CSEE, 2017, 37(6): 245-256.
[17] 赵彪, 于庆广, 王立雯. Z源双向DC-DC变换器及其移相直通控制策略[J]. 中国电机工程学报, 2011, 31(9): 43-49.
Zhao Biao, Yu Qingguang, Wang Liwen. A Z-source bi-directional DC-DC converter and its phase shifting-short control strategy[J]. Proceedings of the CSEE, 2011, 31(9): 43-49.
[18] 杨林涛, 傅兴华. 二级准Z源双向直流变换器的设计与仿真[J]. 电子设计工程, 2013, 21(24): 90-92, 97.
Yang Lintao, Fu Xinghua. Design and simulation of two level quasi-source bidirectional DC-DC con- verter[J]. Electronic Design Engineering, 2013, 21(24): 90-92, 97.
[19] 任小永, 唐钊, 阮新波, 等. 一种新颖的四开关Buck-Boost变换器[J]. 中国电机工程学报, 2008, 28(21): 15-19.
Ren Xiaoyong, Tang Zhao, Ruan Xinbo, et al. A novel four switch Buck-Boost converter[J]. Proceedings of the CSEE, 2008, 28(21): 15-19.
[20] 温振霖, 阮新波, 任小永, 等. 高压输入低压多路输出的两级式变换器[J]. 电工技术学报, 2010, 25(1): 90-96.
Wen Zhenlin, Ruan Xinbo, Ren Xiaoyong, et al. Two-stage converter of high voltage input low voltage multi-output[J]. Transactions of China Electro- technical Society, 2010, 25(1): 90-96.
[21] 朱成花, 石健将, 严仰光. 直/直变换器输入滤波器的设计[J]. 电工技术学报, 2004, 19(1): 85-90, 94.
Zhu Chenghua, Shi Jianjiang, Yan Yangguang. Design of input filter for DC/DC converter[J]. Transactions of China Electrotechnical Society, 2004, 19(1): 85-90, 94.
[22] Choi B. Dynamics and control of switch mode power conversions in distributed power systems[D]. Blacksburg: Virginia Polytechnic Institute and State University, 1992.
[23] Middlebrook R D. Input filter considerations in design and application of switching regulators[C]// IEEE Power Electronics Specialists Conference, Chicago, lllionios, 1976: 366-382.
[24] Carl M Wildrick, Fred C Lee, Bo H Cho, et al. A method of defining the load impedance specification for a stable distributed power system[J]. IEEE Transa- ctions on Power Electronics, 1995, 10(3): 280-285.
[25] Feng Xiaogang, Liu Jinjun, Lee F C. Impedance specifications for stable DC distributed power systems[J]. IEEE Transactions on Power Electronics, 2002, 17(2): 157-162.
[26] 李山, 宋立风, 章治国. 四开关Buck-Boost变换器的三模式控制方法研究[J]. 电源学报, 2019, 17(3): 111-119.
Li Shan, Song Lifeng, Zhang Zhiguo. Study on three-mode control method for four-switch Buck- Boost converter[J]. Journal of Power Supply, 2019, 17(3): 111-119.
[27] Wang Xiaopeng, Yao Ruoping, Rao Fangquan. Subsystem-interaction restraint in the two-stage DC distributed power systems with decoupling-controlled- integration structure[J]. IEEE Transactions on Industrial Electronics, 2005, 52(6): 1555-1563.
[28] 安峰, 杨柯欣, 王嵩, 等. 基于模型前馈的双有源全桥DC-DC变换器电流应力优化方法[J]. 电工技术学报, 2019, 34(14): 2946-2956.
An Feng, Yang Kexin, Wang Song, et al. Current stress optimized scheme with model-based feed- forward for dual-active-bridge DC-DC converters[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2946-2956.
Optimal Design of Impedance Matching for Voltage Adjustment Unit-Dual Active Bridge Cascade System
Abstract The dual active bridge (DAB) DC-DC converter with voltage adjustment unit (VAU) is one of the solutions to reduce current stress in wide input voltage range.However, the impedance stability of the VAU-DAB cascade system is poor. This paper firstly deduces the output impedance model of the VAU and the input impedance model of the DAB, and analyzes the impedance ratio in the complex frequency domain according to the impedance stability criterion concept of the forbidden region. Because of the existing crossing point between the resonance peak of the VAU output impedance amplitude curve and DAB input impedance, the cascaded system is likely to cause system voltage oscillation instability due to impedance mismatch. Then, according to the impedance matching criteria, an impedance optimization controller based on lead-lag is proposed. By suppressing the convexity of the VAU output impedance, the cascade system meets the stability criterion, the system reliability is improved, and the current stress is reduced. Finally, the simulation verifies the proposed strategy.
keywords:Dual active bridge, voltage adjustment, stability analysis, input/output impedance,cascade system
DOI: 10.19595/j.cnki.1000-6753.tces.L90232
中图分类号:TM46
国家重点研发计划资助项目(2016YFE0131700)。
收稿日期 2020-07-04
改稿日期 2020-11-07
农仁飚 男,1994年生,硕士,研究方向为双有源桥DC-DC变换器控制技术与应用。E-mail: 19121481@bjtu.edu.cn
杨晓峰 男,1980年生,副教授,博士生导师,研究方向为多电平变换器技术、柔性直流输电技术、电力电子技术在轨道交通中的应用。E-mail: xfyang@bjtu.edu.cn(通信作者)
(编辑 陈 诚)