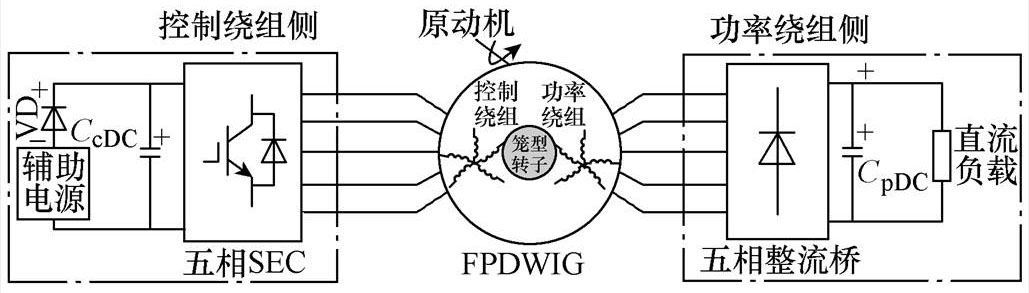
图1 FPDWIG系统
Fig.1 FPDWIG system
摘要 双绕组感应发电机系统采用磁链定向控制策略可以分别对控制绕组有功电流与无功电流进行调节，从而获得控制绕组与功率绕组两端直流电压的稳定控制。然而，该控制策略需采用多个调节器，使得控制器设计困难，也制约了双绕组感应发电机系统的进一步发展与应用。针对该问题，提出双绕组感应发电机系统的无差拍电流预测控制策略，建立发电机系统的预测模型，在一个控制周期内以消除被控量的误差为目标，直接计算得到所需的控制量，又分析模型参数失配带来的电流误差问题，对该控制策略做了误差补偿。该文所提出的电流预测控制策略避免了繁琐的调节器参数整定过程，同时具有优秀的控制性能，实现了电流的无误差跟踪。样机仿真与实验结果验证了双绕组感应发电机系统无差拍电流预测控制的正确性与可行性。
关键词：双绕组感应发电机 电流预测控制 磁链定向控制 误差补偿
随着电气化进程的加速推进，独立电源系统向着大容量、高功率密度、高可靠性、高动态性能的方向发展。在众多独立电源系统中，高压直流电源系统在满足上述要求方面具有较大优势，成为独立电源系统的重要发展方向。现有研究表明，同步发电机、开关磁阻发电机、双凸极发电机、感应发电机等是独立电源系统常采用的几种发电机[1-6]。这些发电机各有优势，其中，感应发电机因其噪声小、转矩平稳、成本低、可靠性高等优点近年来得到了广泛关注，具有良好的应用前景。然而，它的变换器需要同时控制发电机的有功功率和无功功率，导致其变换器容量较大，控制较困难。
因此，有必要对其进行改进，为克服传统感应发电机系统的不足，研究人员提出双绕组感应发电机系统，它继承了传统感应发电机的优点，克服了其缺点和不足。该发电机的转子为笼型，是天然无刷结构，简单坚固，定子上布置有两套绕组，一套称为功率绕组，专门为负载供电；另一套称为控制绕组，接有励磁变换器，用以调节发电机励磁[7-8]。
要充分发挥双绕组感应发电机的优势，就离不开它所采用的控制策略。由于其拥有两套绕组，需要同时对两端电压进行控制，这使得控制策略变得相对较复杂。目前，该发电机最常用的控制策略为磁链定向控制策略[9-11]，该控制策略将电流矢量定向于磁链矢量方向，通过调节有功电流、无功电流来分别调节控制绕组直流电压、功率绕组直流电压。文献[9]对比分析了多种双绕组感应发电机控制策略，指出磁链定向控制具有开关频率固定、电流纹波较小的优势，却给整个系统引入了4个比例-积分（Proportional-Integral, PI）调节器，增加了控制器的设计难度。文献[10]采用磁链定向控制实现了发电机系统突加额定负载下的稳定运行，但这个过程却需要设置多组PI参数，导致实际应用中控制器设计过程繁琐，且不易进行参数优化，这无疑为双绕组感应发电机的进一步发展增加了困难。因此，如何简化控制器设计，降低控制策略的复杂度，成为一个需要深入研究的问题。
为此，很多研究人员做出了大量的努力，其中，PI参数整定法是最常见的方法。文献[12]根据旋转坐标系下的双绕组感应发电机数学模型，建立了系统的传递函数，运用零极点对消法设计了电压外环PI调节器的参数，但这个过程中却多处进行了简化等效，与实际系统不符，并且没有对整定难度更大的电流内环进行参数设计。文献[13-14]采用模型预测控制代替原有的电流环，避免了复杂的参数整定过程，但是模型预测控制在线实时计算量偏大，而且由于缺少调制环节，其开关频率变化较大。文献[15-18]采用无差拍电流预测控制与空间矢量脉宽调制相结合，应用于PWM整流器、并网逆变器与永磁同步电机中，主要思想是根据系统模型建立预测模型，以下一控制周期实际电流跟上给定值为目标，从而计算得到最优的控制电压矢量，具有实现简单、响应快速、控制精确的优点，其控制思想十分适合本文所研究的双绕组感应发电机系统，但目前暂未有研究人员对其开展研究。
本文对双绕组感应发电机系统的无差拍电流预测控制技术开展了相关的基础研究，并针对参数不准确导致产生电流静态误差的情况，分析了不同参数变化带来的影响，对电流预测控制进行了误差补偿的改进，从而为高性能双绕组感应发电机系统的研究奠定基础。
相比于三相双绕组感应发电机，五相双绕组感应发电机（Five Phase Dual Winding Induction Gen- erator, FPDWIG）的功率密度相对较高，且具有容错运行能力[10, 12]。FPDWIG系统如图1所示。其转子为笼型无刷结构，简单坚固。其定子上有两套五相绕组，极对数相同，且均采用星形集中整距绕组结构，一套为控制绕组，接有五相励磁变换器（Static Excitation Converter, SEC），用来调节发电机励磁来保证输出电压稳定；另一套为功率绕组，经五相不控整流桥输出直流电能。两套绕组除容量不同外，极对数及绕组形式均一样，其在电气上没有直接连接，仅通过磁场耦合，电磁兼容性较好，功能分开，易于实现高性能控制和输出高品质电能。
图1 FPDWIG系统
Fig.1 FPDWIG system
FPDWIG系统传统的磁链定向控制策略的矢量如图2所示。
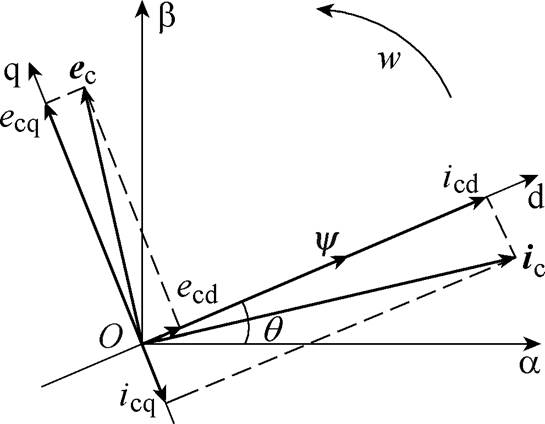
图2 磁链定向矢量
Fig.2 Vector illustration of flux orientation
该控制策略中，电流在d轴上的投影分量为无功电流，在q轴上的投影分量为有功电流。控制绕组的电压矢量为
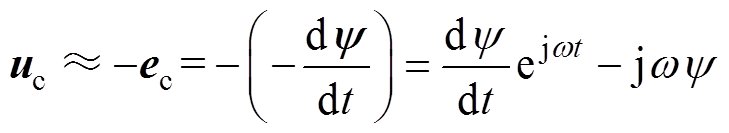（1）式中，uc为控制绕组电压矢量；ec为控制绕组的反电动势矢量；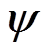
为磁链矢量；
为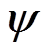的幅值；w 为同步角速度。uc的幅值uc可表示为
（2）
式中，ucd、ucq分别为控制绕组电压矢量d轴、q轴分量。在系统稳定时，磁链幅值不变，根据瞬时功率理论，可以将控制绕组瞬时有功功率p和瞬时无功功率q分别表示为
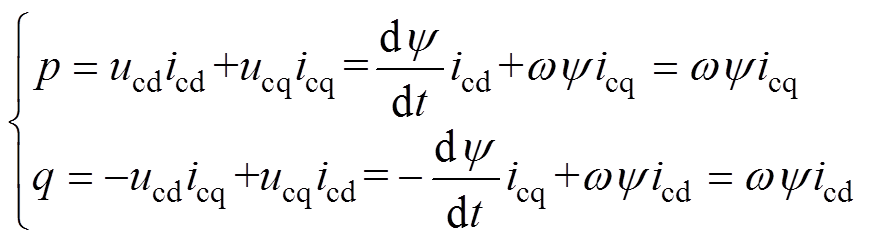（3）式中，icd、icq分别为控制绕组电流矢量d轴、q轴分量。可以看出，此时FPDWIG系统有功与无功分别与icd、icq呈线性关系，可以直接通过PI调节器分别对有功与无功进行调节。
五相整流桥输出的直流母线电压UpDC约为
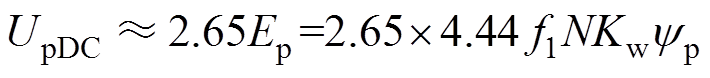（4）式中，Ep为功率绕组感应电动势有效值；f1为同步频率；N为功率绕组的匝数；Kw为绕组系数；yp为功率绕组每极磁通，它的大小与励磁无功呈正相关[11]。
所以，可以通过调节无功电流，控制五相SEC向发电机提供的励磁无功，来调节气隙磁通，从而达到调节UpDC的目的。
而对于控制绕组一侧的直流母线电压UcDC，关于电磁转矩有
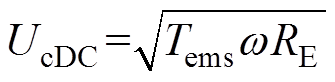（5）式中，RE为SEC线路电阻和开关损耗的等效电阻；Tems为电磁转矩，它与FPDWIG的有功功率呈线性关系[11]。
所以，可以通过调节有功电流控制有功功率，来改变控制绕组电磁转矩Tems，从而实现对控制侧直流母线电压UcDC的调节。
综合上述分析，得到如图3所示的磁链定向控制策略框图。
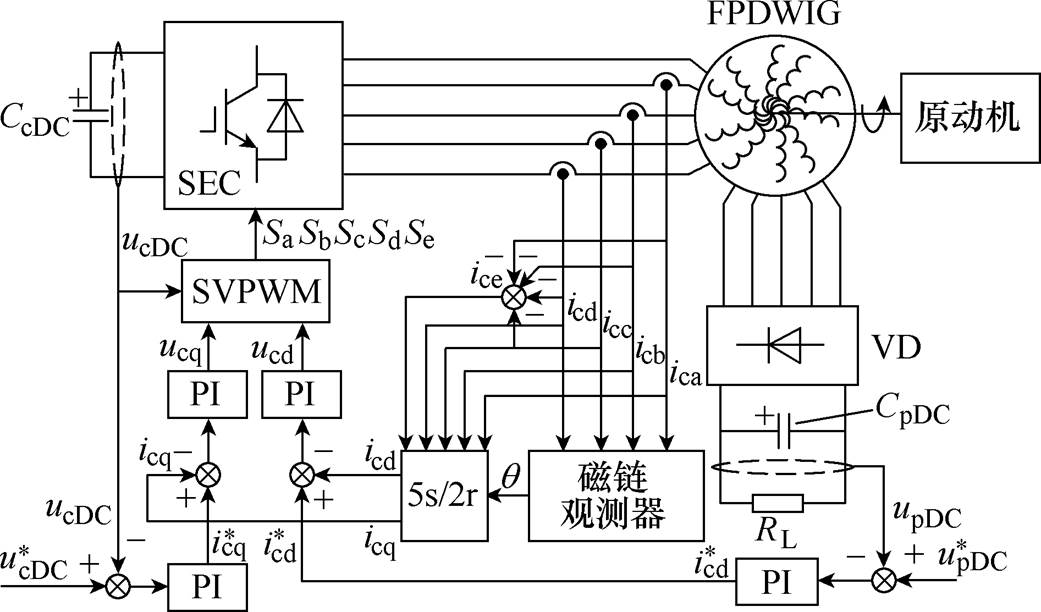
图3 磁链定向控制策略框图
Fig.3 Block diagram of flux-oriented control strategy
然而，磁链定向控制的推导建立在系统稳定运行的情况之下。在实际应用中，工况更为复杂。如在突加负载瞬间，磁链幅值会发生突变，此时式（3）中瞬时有功p和瞬时无功q分别表示为
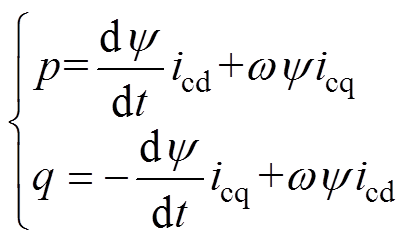（6）式中，dy/dt一项不再为零，与此同时，y 的大小也会受到icd、icq变化的影响，有
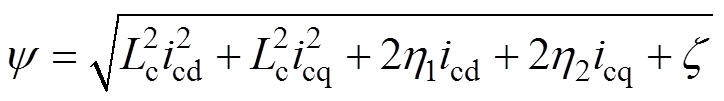（7）
其中
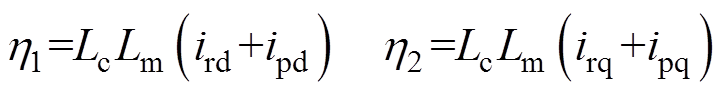
z=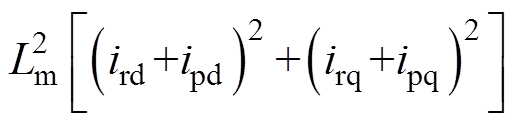
这导致整个磁链定向控制系统的变量之间表现出复杂的非线性耦合关系。而PI调节器本质上是一种线性控制器，图3的磁链定向控制框图中嵌入了4个PI调节器，在提升控制器复杂度的同时，忽略了系统动态过程中的磁链幅值变化，将其近似为线性系统进行控制，虽然能够得到较好的稳态控制性能，却致使系统在发生动态变化时，调节器参数的整定难度更大，有时甚至需要在不同的负载情况下设置多组PI参数，导致实际应用中控制器设计过程繁琐，且不易进行参数优化。
无差拍电流预测控制是一种简单有效的离散化控制方法，该方法根据系统模型建立了预测模型，以下一控制周期实际电流跟上给定值为目标，计算得到最优的控制电压矢量，具有计算量小、响应快速等优点。本文提出FPDWIG系统的无差拍电流预测控制，旨在有效解决传统的磁链定向控制策略中调节器参数整定困难、控制策略复杂的问题，提升电流的控制性能。下面对其进行推导与分析。
根据数学模型中转子磁链表达式可得
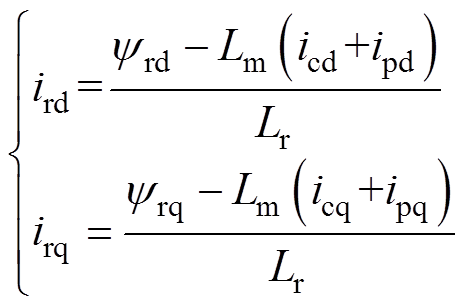（8）将式（8）代入控制绕组磁链方程和转子电压方程，分别得到
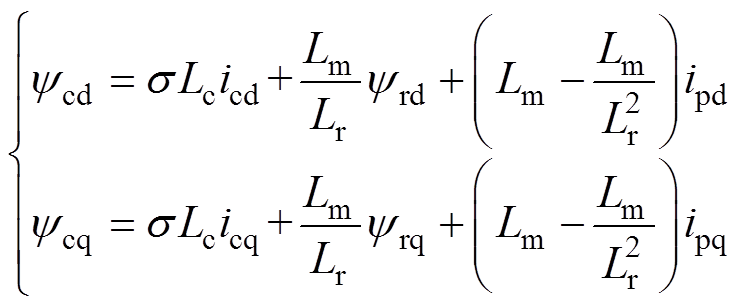（9）
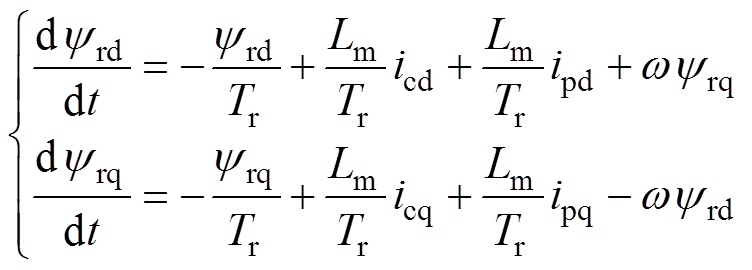（10）其中
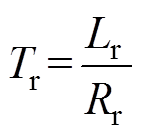
将式（9）和式（10）代入控制绕组电压方程得到
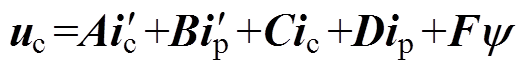（11）其中
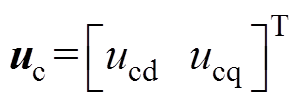
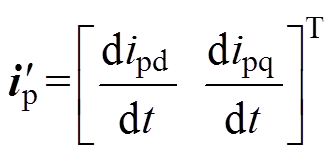
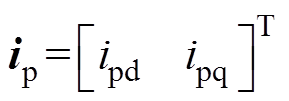
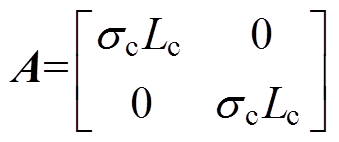
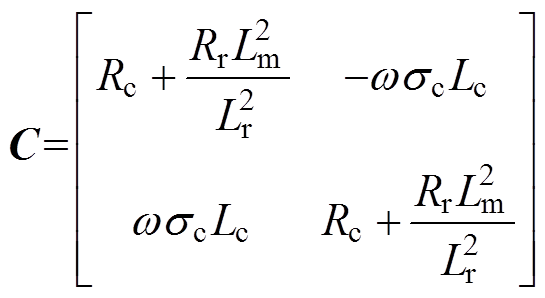
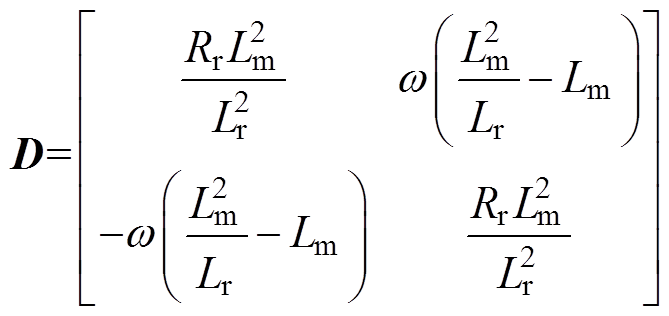
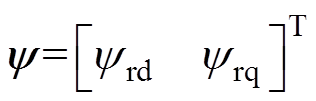sc=
式中，L为电感；R为磁链；下标c表示控制绕组，下标p表示功率绕组，下标r表示转子等效绕组，下标d表示d轴分量，下标q表示q轴分量；wr为转差角频率。
为方便计算，忽略几乎为零的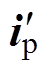
一项，对式（11）在Ts的采样时间下进行离散化，有
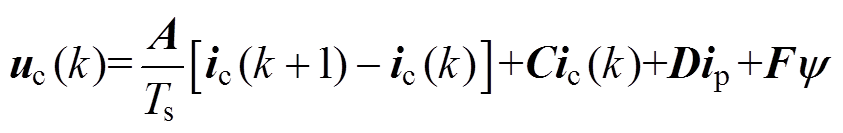（12）由式（12）得到下一控制周期电流预测值表达式为
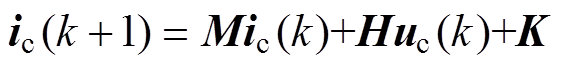（13）
其中
M=E-TsA-1C H=TsA-1 K=-TsA-1Dip-TsA-1Fy
由于数字控制系统延迟的存在，k时刻计算得到的电压矢量需要在k+1时刻才加载于励磁变换器上，合成的电流矢量在k+2时刻才能被采集到，所以还需要进一步对k+2时刻的电流进行预测计算，用它代替k+1时刻的电流值，以此来补偿FPDWIG控制系统中的延时，有
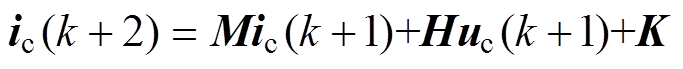（14）由于两个控制周期的时间间隔极小，所以将发电机参数视为常数，可以得到k+1时刻产生的控制电压uc(k+1)为
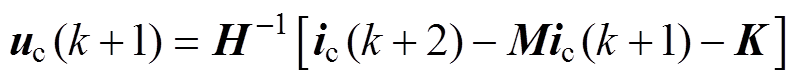（15）
控制延时得到补偿之后，可以认为k+2时刻的电流实际值与给定值之差为零，即此时可以用电流给定值代替电流实际值，表示为
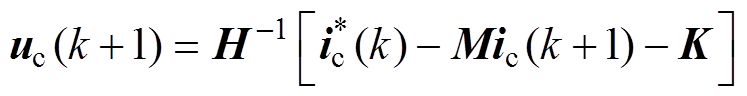（16）将电流预测值表达式（13）代入式（16）中，得到FPDWIG电流预测控制电压矢量的表达式为
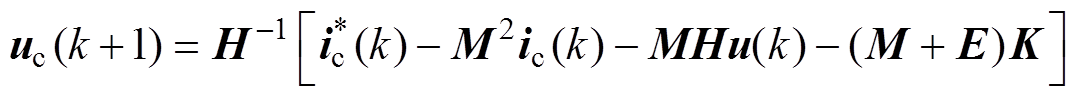（17）
式中，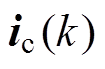
为当前时刻采集的控制绕组电流；
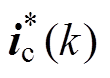为当前时刻的控制绕组电流给定；uc(k)为当前时刻作用发电机的电压矢量；E为单位矩阵。
由本小节的推导得到无差拍电流预测控制策略框图如图4所示，其中，电流控制流程如图5所示。由图5可以看出，控制流程可以分为两步，预测电流计算和电压矢量计算。由于其计算涉及的参数均为已知的发电机参数，不需要传统磁链定向控制中繁琐的参数整定过程，实现起来更加简单方便。
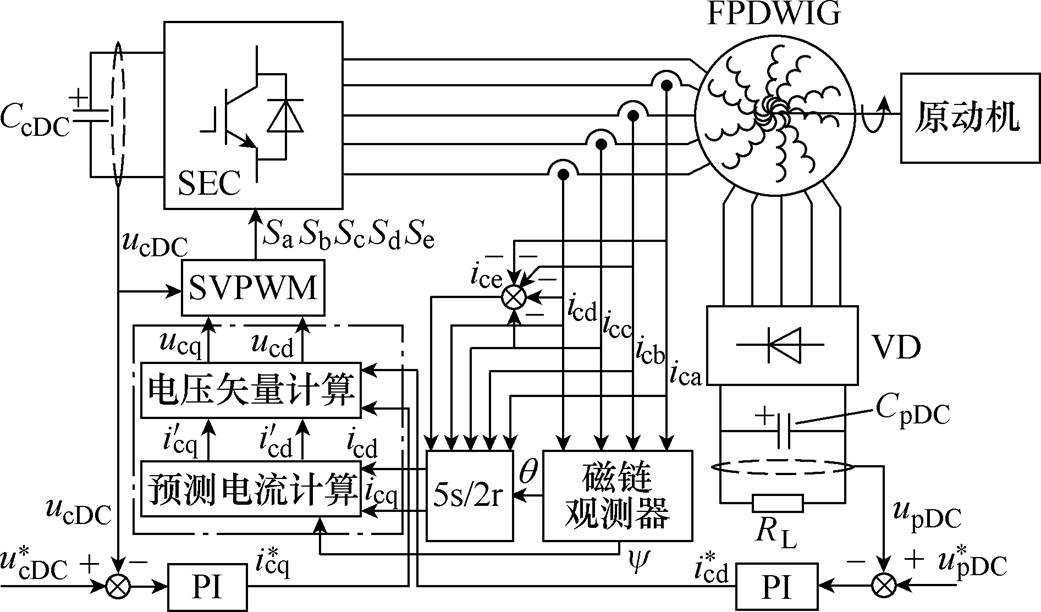
图4 无差拍电流预测控制框图
Fig.4 Block diagram of deadbeat predictive current control
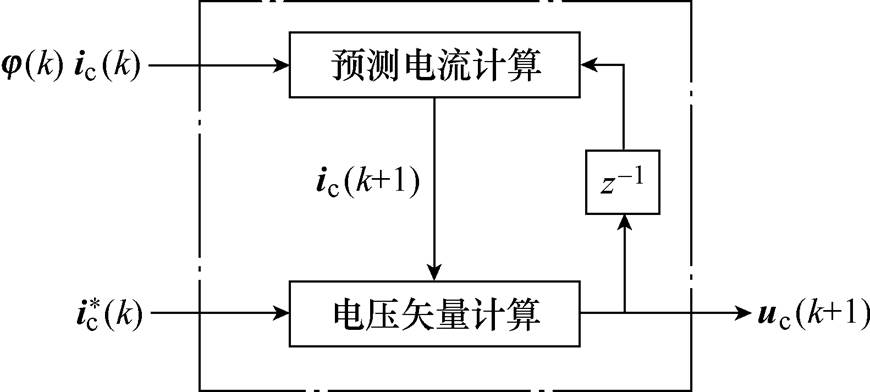
图5 电流控制流程
Fig.5 Block diagram of current control process
基于上述推导可得到如图6所示的无差拍电流预测控制系统模型。
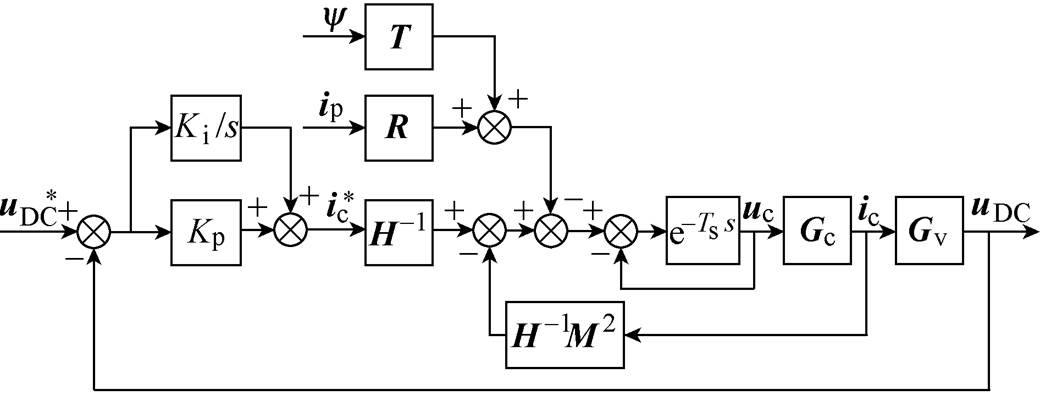
图6 无差拍电流预测控制系统模型
Fig.6 Deadbeat predictive current control system model
图6中，T=-A(M+E)A-1F，R= -A(M+E)A-1D，Gc为电流控制对象，Gv为电压控制对象，它们分别可表示为
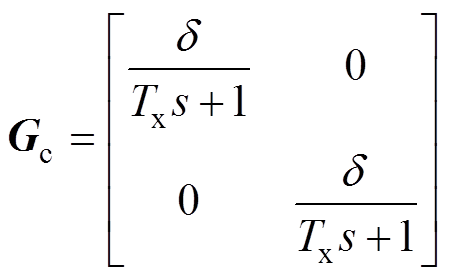
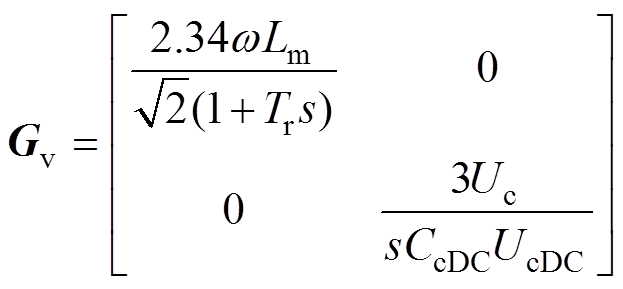
其中
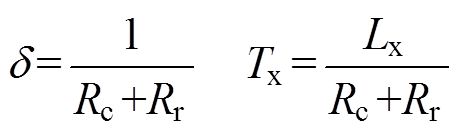
式中，Lx为总漏感。
根据无差拍电流预测控制系统模型，绘制出FPDWIG在两种控制方法下电流的闭环幅频与相频特性曲线，如图7所示。控制系统带宽反映了系统响应的快速性，可以看出，采用无差拍电流预测控制策略后，控制带宽增大，系统快速性得到一定提升。
FPDWIG的无差拍电流预测控制中预测模型是依靠发电机模型推导得来的。在实际系统中，发电机模型参数与理论计算值有所偏差时，可能会影响电流预测控制系统的稳定性[19]。
图7 幅频与相频特性曲线
Fig.7 Amplitude-frequency and phase-frequency characteristic curves
为了分析不同发电机参数偏差对FPDWIG电流预测控制的影响，本文分别对FPDWIG发电机模型中最主要的三种参数，励磁电感、控制绕组电阻、转子等效绕组电阻，其误差对电流预测控制产生的影响进行分析。
当电流预测控制器的电感值与实际电感值发生偏差时，令发电机励磁电感值为Lm，而电流预测控制器电感值为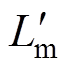
=Lm+DL，DL为电感偏差值，得到k+1时刻预测电流表达式为
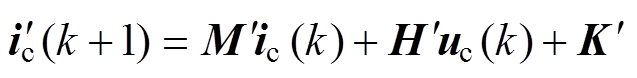（18）此时计算电压矢量的表达式为
（19）
其中
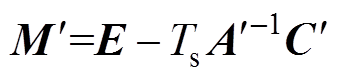
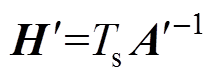
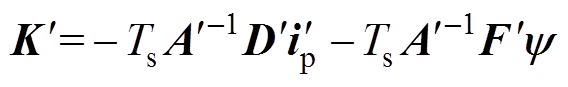
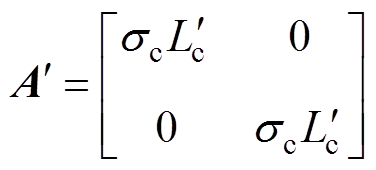
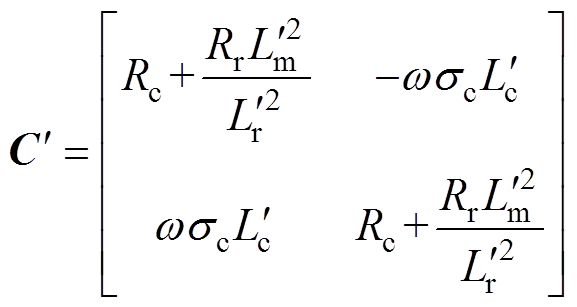
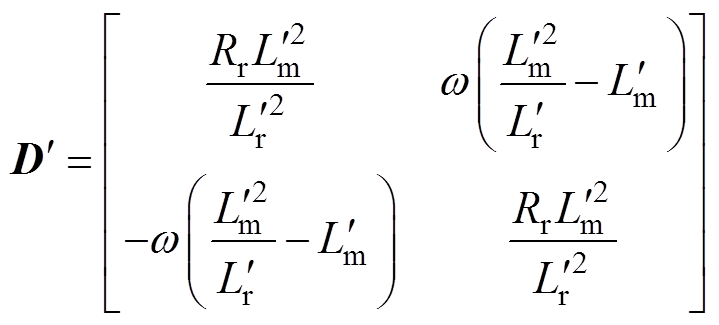
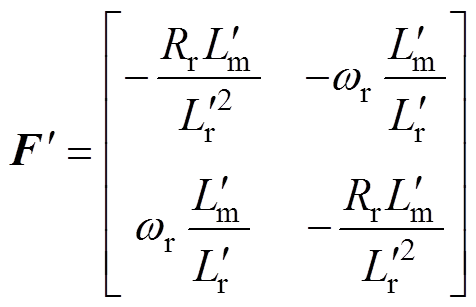
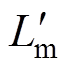=Lm+DL 
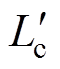=Lc+DL 
=Lr+DL将式（13）与式（18）相减，得到当控制器发电机模型电感参数出现误差时，下一时刻计算得到的预测电流偏差值为
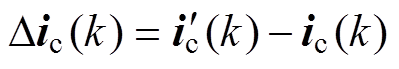（20）
由3.1节分析可知，电流预测控制根据预测的电流值计算控制电压，当预测电流发生以上偏差时，控制电压的偏差值为
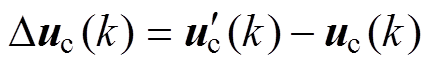（21）文献[20]指出励磁电感参数变化至2倍大小时，会导致系统的不稳定，所以本文分析励磁电感误差时，使励磁电感在[0.5Lm, 2Lm]范围内变化，即电感偏差值DL在[-0.005, 0.01]H范围内变化，绘制出电流偏差值Dic(k)与控制电压偏差值Duc(k)关于电感偏差值DL变化的曲线，如图8所示。同样地，为了与励磁电感形成对比，使得控制绕组电阻与转子等效绕组电阻0.5～2倍范围内变化，其分析方法与励磁电感相同，不再赘述。绘制出电流电压偏差值关于电阻偏差值变化的曲线，如图9与图10所示。
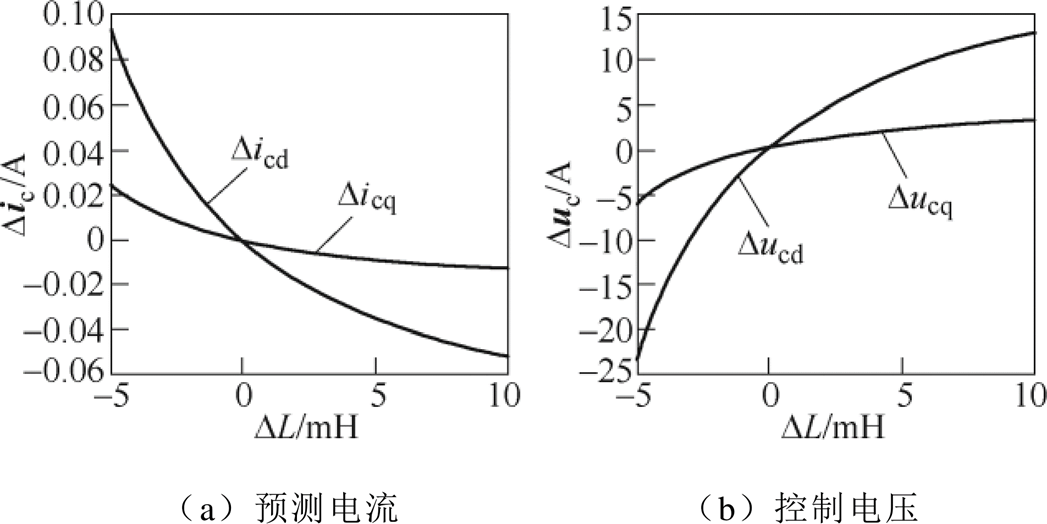
图8 预测电流与控制电压偏差关于电感偏差值的曲线
Fig.8 Curves of predictive current and control voltage errors with respect to inductor error
由图8可以看出，两曲线均相交于（0, 0），此时电感参数没有误差。在励磁电感由0.5Lm逐渐变化至2Lm的过程中，Dic(k)逐渐变小，Duc(k)逐渐变大，其中，参数偏差对d轴电流电压的影响更大，相较而言对q轴电流电压的影响可以忽略不计。而Dic(k)与Duc(k)曲线斜率相反是因为当预测电流值低于理想值时，会导致控制器在电压矢量计算时低估电流的跟踪性能，从而发出更高的控制电压。当预测电流值低于理想值时同理。这也是FPDWIG电流预测控制中，参数不准确会产生电流静态误差的原因所在，发出了更高的控制电压之后，将会导致电流实际值略高于电流给定，而一旦控制电压低于理想值，也会导致电流实际值略低。
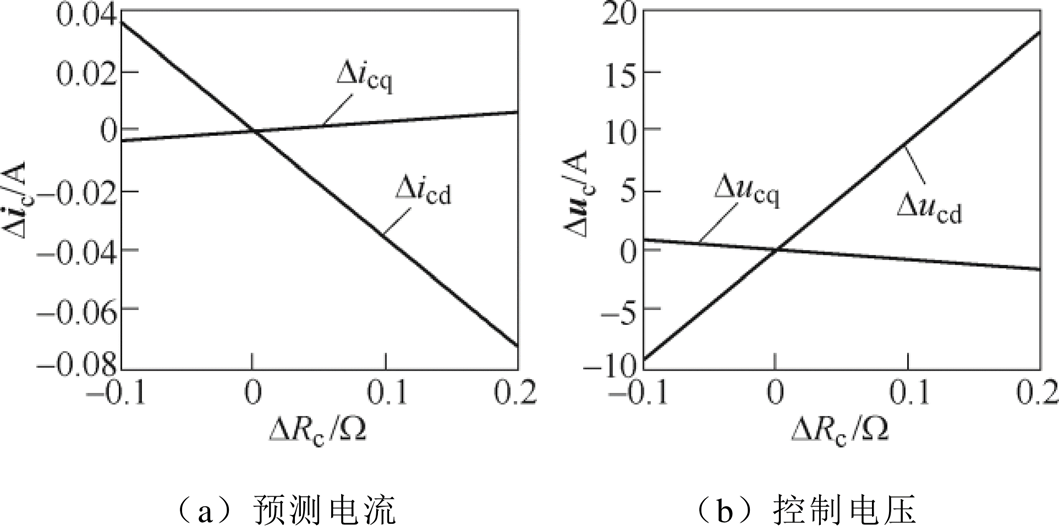
图9 预测电流与控制电压偏差关于控制绕组电阻 偏差值的曲线
Fig.9 Curves of predictive current and control voltage errors with respect to error of control winding resistor
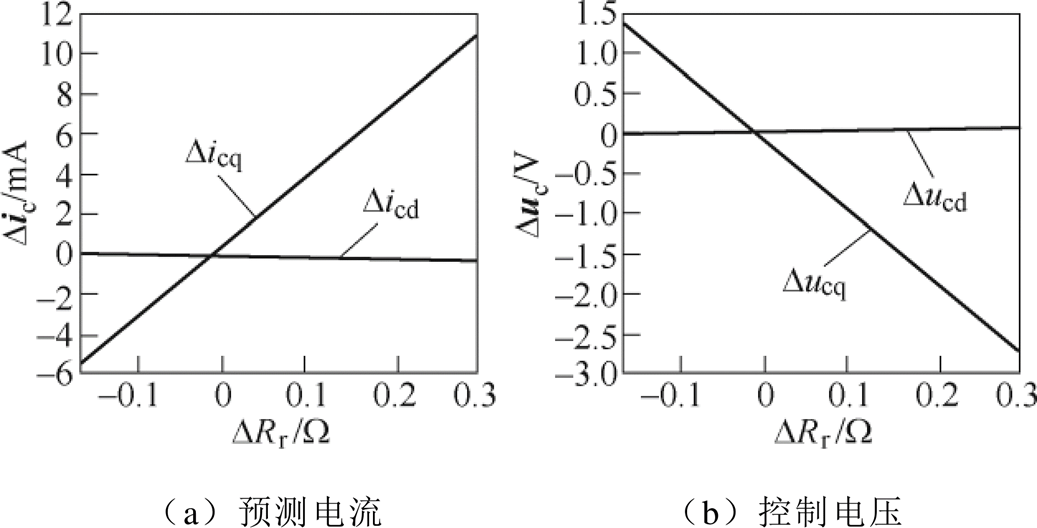
图10 预测电流与控制电压偏差关于转子绕组等效电阻偏差值的曲线
Fig.10 Curves of predictive current and control voltage errors with respect to error of rotor resistor
图9中，当阻值由0.5Rc逐渐变化至2Rc的过程中，Dicd逐渐变小且斜率较大，而Dicq同样受DRc影响很小；同样地，图9b中，Ducd与Ducq的斜率分别与Dicd和Dicq相反，造成的原因与电感参数变化时相同。
图10中，相比于励磁电感与控制绕组电阻，转子等效绕组电阻参数的变化对于电流预测控制的影响要小得多，几乎可以忽略不计。
为了提高FPDWIG无差拍电流预测控制策略的参数鲁棒性，本节对FPDWIG无差拍电流预测控制策略进行了改进，加入了误差补偿环节，即使模型参数有所偏差时，d、q电流仍然能够实现快速无误差的跟踪。
图11给出基于误差补偿的电流预测控制框图，图中，
为电流给定修正值，
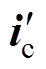为电流预测值，it为低通滤波器的输出。
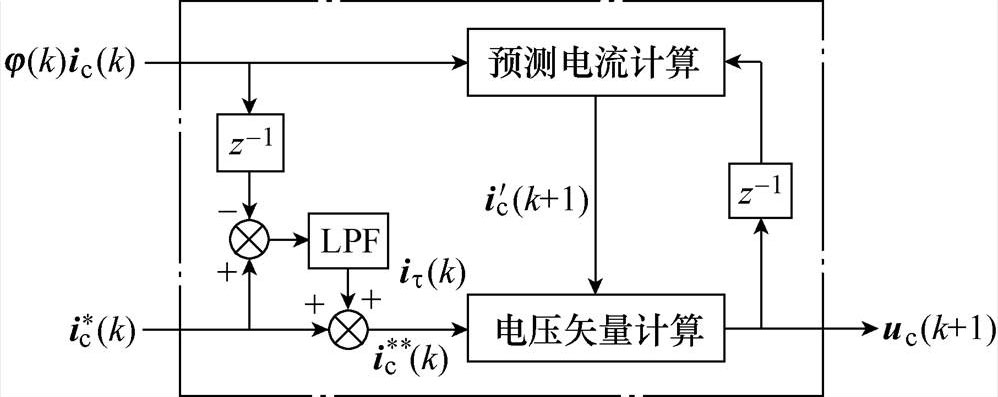
图11 基于误差补偿的电流预测控制框图
Fig.11 Block diagram of current predictive control based on error compensation
当控制器中发电机模型参数准确时，实际电流与给定电流无静态误差，此时it为零，给定电流的修正值与给定电流相同，即
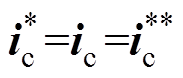（22）当控制器中发电机模型参数开始出现偏差，由于低通滤波器的滞后特性，此时it暂时还为零，电流给定值并未及时修正，导致实际电流开始与给定电流出现静态误差。参数不准确带来的电流偏差值可以视为电流误差的低频分量，而由于开关信号的原因，高频次信号也存在于电流误差之中。因此，产生的电流误差可以表示为
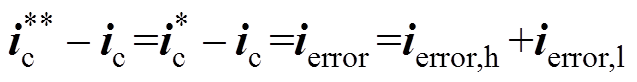（23）式中，ierror为电流跟踪误差；ierror,h为其高频分量；ierror,l为其低频分量。
当电流跟踪误差出现之后，低通滤波器开始作用，实际电流值与给定值之差经过低通滤波器之后输出，补偿到原有的电流给定上。此时低通滤波器的输出可以表示为
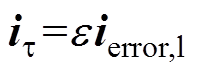（24）式中，e 为低通滤波器的低频增益。
若实际电流值小于给定值，则低通滤波器的输出it将变为大于零且逐渐增大，补偿到电流给定上使得i**逐渐增大。由式（23）可知，电流预测器的修正给定输入的增大，将导致实际电流也随之增大。当实际电流增大至与电流给定值相当时，低通滤波器的输出不再发生改变，此时电流给定值修正完成，电流的静态误差被消除，参数不准确带来的误差得到补偿。若实际电流值小于给定值，则情况与之相反，不再赘述。
为验证本文所提出的FPDWIG系统无差拍电流预测控制策略的有效性和可行性，在Matlab/ Simulink软件中搭建仿真模型，对无差拍电流预测控制策略进行对比仿真，并在FPDWIG发电机系统实验平台上进行实验对比研究。实验平台的相关参数见表1。
表1 实验平台参数
Tab.1 Platform parameters
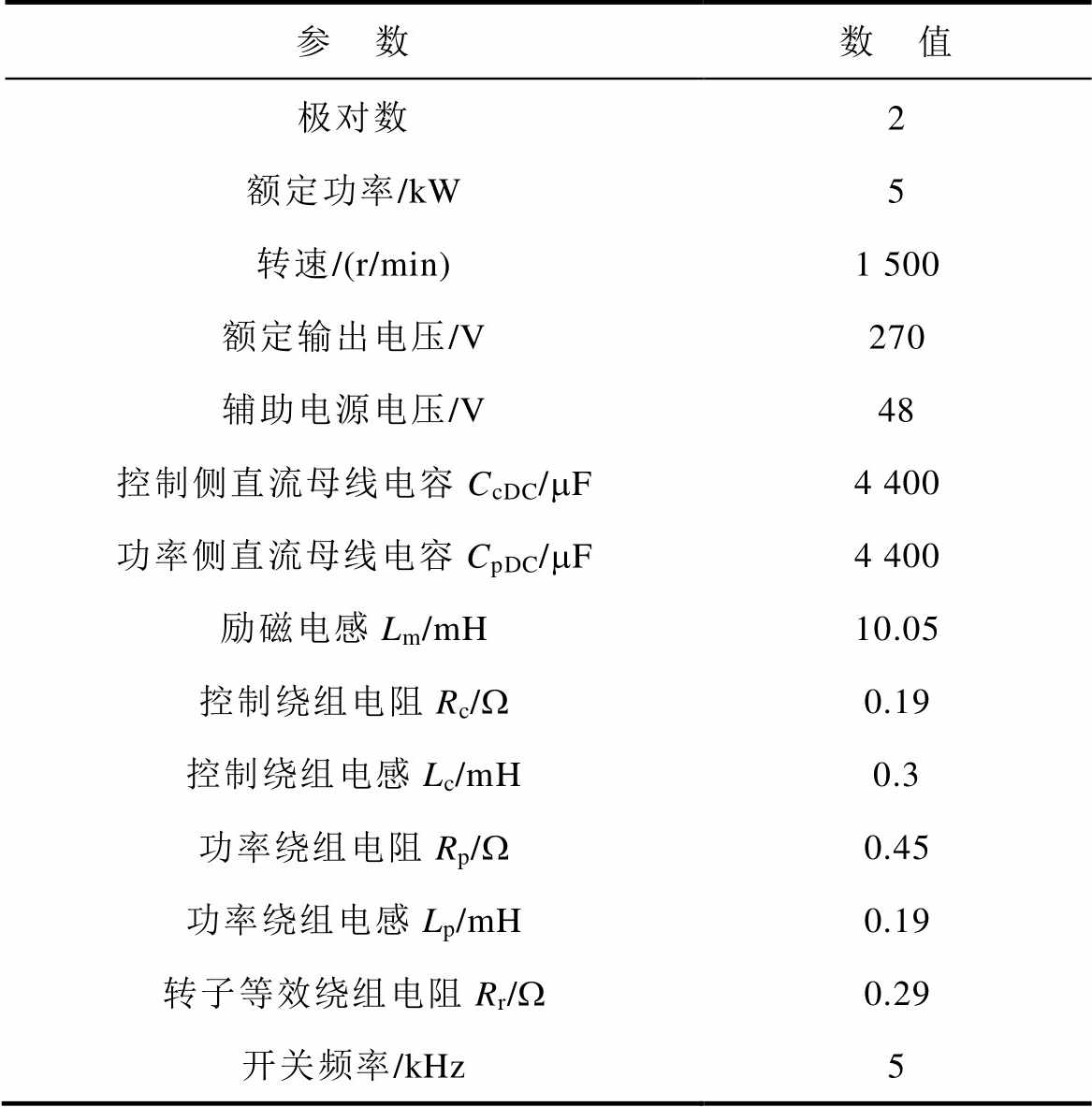
参 数数 值 极对数2 额定功率/kW5 转速/(r/min)1 500 额定输出电压/V270 辅助电源电压/V48 控制侧直流母线电容CcDC/mF4 400 功率侧直流母线电容CpDC/mF4 400 励磁电感Lm/mH10.05 控制绕组电阻Rc/W0.19 控制绕组电感Lc/mH0.3 功率绕组电阻Rp/W0.45 功率绕组电感Lp/mH0.19 转子等效绕组电阻Rr/W0.29 开关频率/kHz5
为验证无差拍电流预测控制的电流控制性能，仿真得到图12a所示的突加负载情况下电流预测控制电流波形。从图中可以看出，实际电流的控制效果确实与预测计算的电流值几乎一致，它们都能够快速精确地跟上给定电流，这是建立了正确的预测模型带来的结果，也是电流预测控制中实际电流能够快速跟踪上给定的原因。
为观察无差拍电流预测控制的控制输出是否超限，仿真得到图12b所示的突加负载情况下控制输出电压波形。从图中可以看出，ucd最大值为37V左右，ucq最大值为195V左右。五相SVPWM的最大线性调制比为1.05，由于本文实验平台中控制绕组直流母线电压为400V，无差拍电流预测控制输出限幅设定为210V。可以看出，在突加额定负载的工况下，无论是ucd或是ucq均没有超限，一直处于线性调制区间内，控制效果较好。
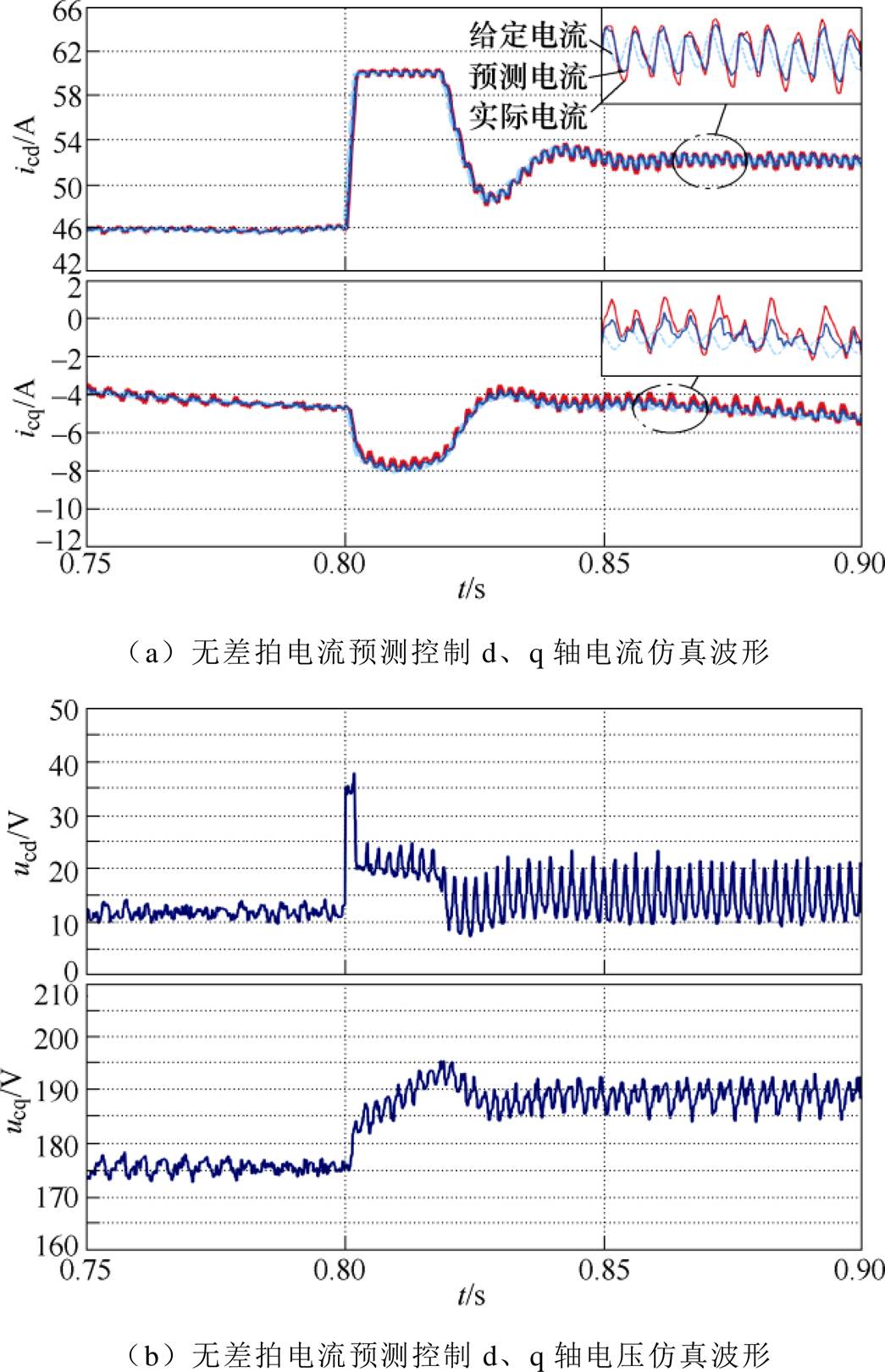
图12 无差拍预测控制d、q轴电流和电压仿真波形
Fig.12 Simulation waveforms of currents and voltages of d and q axis for deadbeat predictive control
为对比FPDWIG系统的无差拍电流预测控制与磁链定向控制的控制性能，仿真分别得到如图13所示的突加额定负载波形。从图中可以看出，磁链定向控制的功率侧直流电压恢复时间约为62ms，其加载瞬间电压跌落约为16V，而采用无差拍电流预测控制，功率侧直流电压仅需要约48ms的恢复时间，电压跌落约为15V；磁链定向控制策略下加载之后的d轴电流需要约86ms恢复稳定，而电流预测控制则仅需要约73ms，且它的q轴电流恢复至稳态所需时间也更短；磁链定向控制下的控制绕组相电流ica总谐波畸变率（Total Harmonic Distortion, THD）为12.08%，无差拍电流预测控制下的控制绕组相电流THD=13.38%，后者略大，但它们的差距不明显。由此可见，无差拍电流预测控制用更加简单的实现方式，在仿真中得到了优秀的动态性能与静态性能。
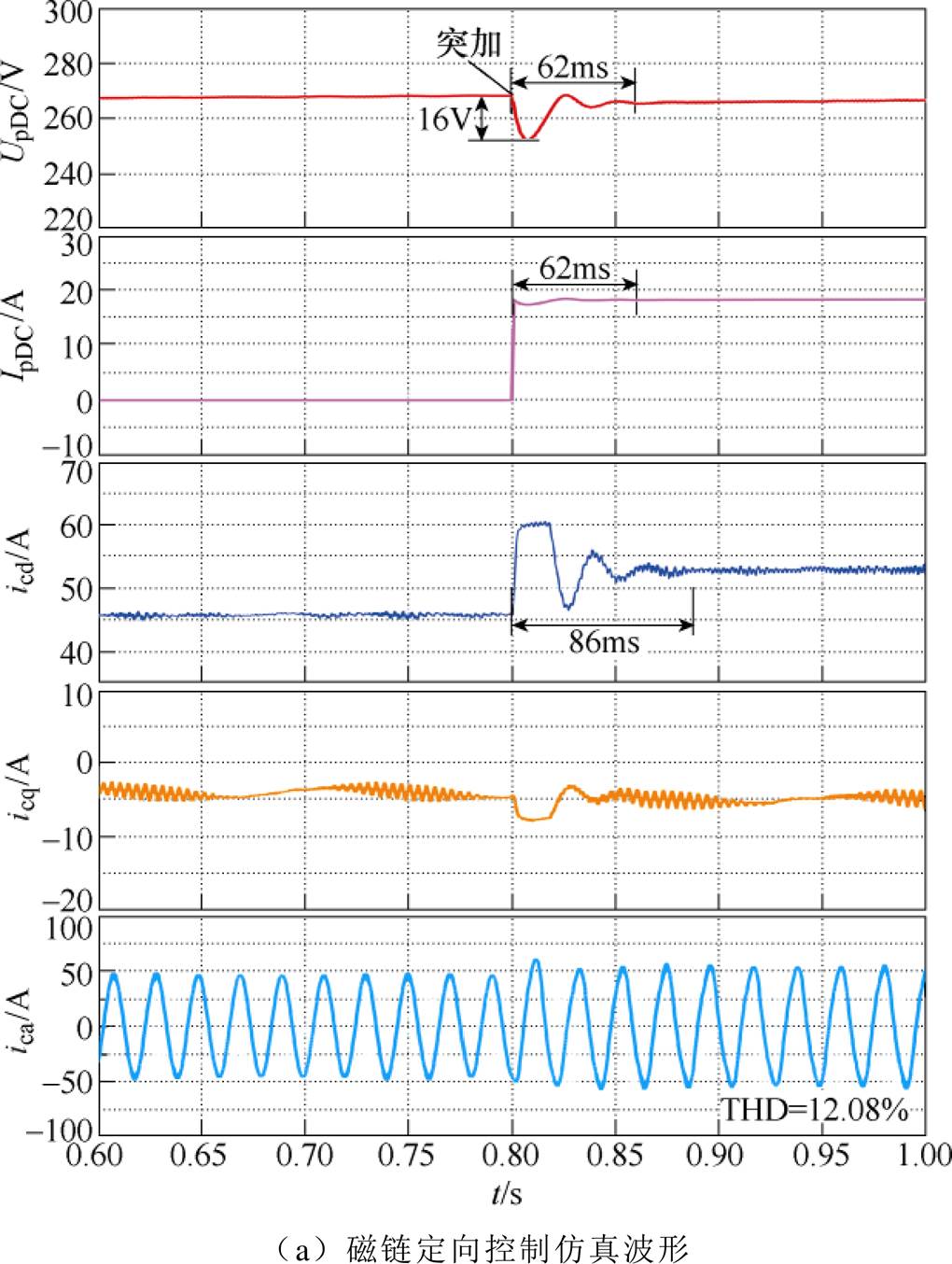
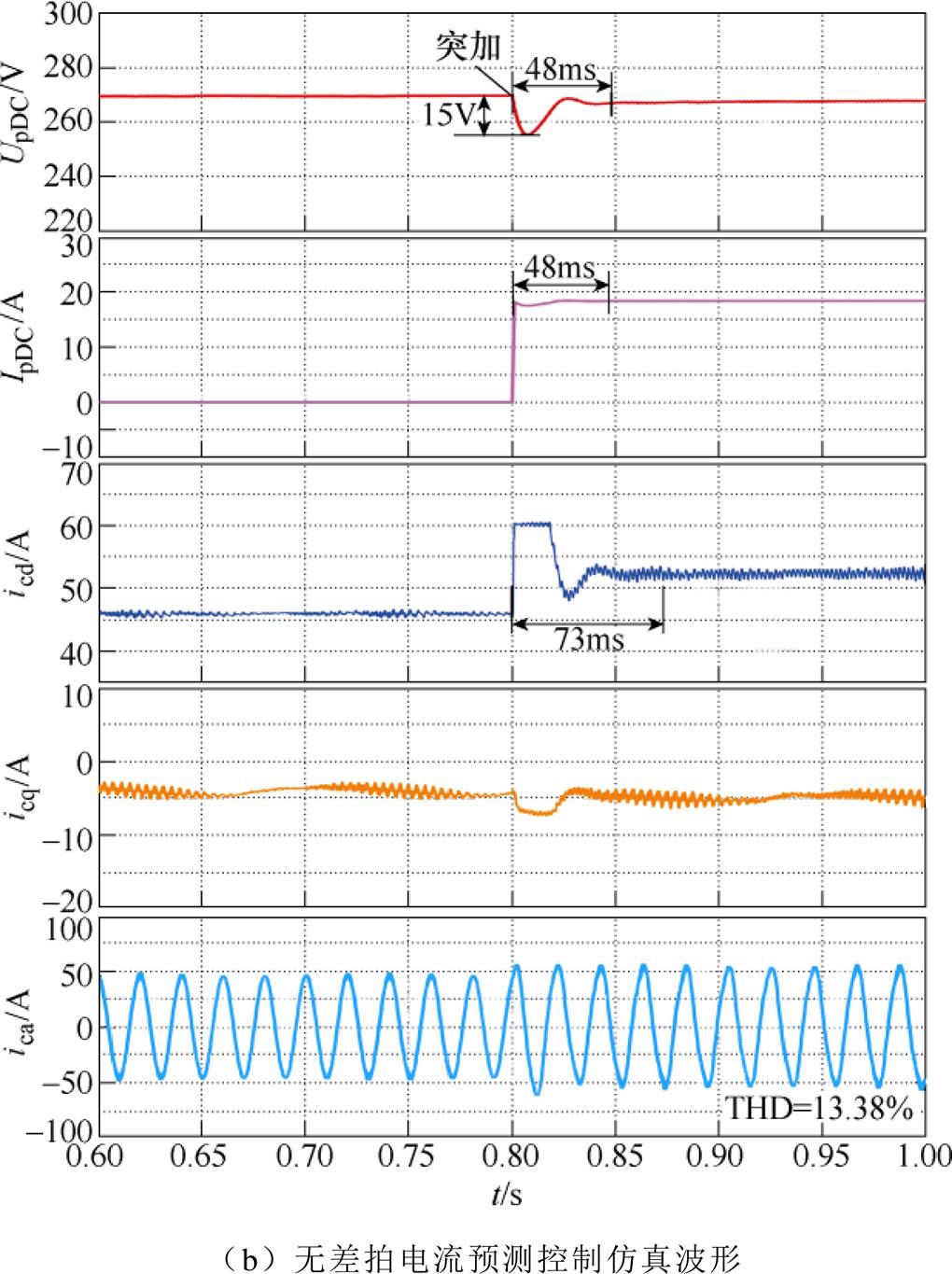
图13 两种控制策略的对比仿真波形
Fig.13 Comparative simulation waveforms of two control strategies
从3.2节分析可知，转子等效绕组电阻参数的偏差对电流预测控制的影响极小，可忽略不计，故选取典型值分别为
=2Lm、=0.5Lm、
=2Rc、=0.5Rc情况进行仿真，获得了加入误差补偿前后的仿真波形如图14所示。可以看出，四种情况下分别产生了+1.2A、-1.8A、+1.4A、-0.7A的电流误差，误差变化趋势与3.2节分析相同。而加入误差补偿的电流预测控制能够有效消除误差，实现无误差跟踪。
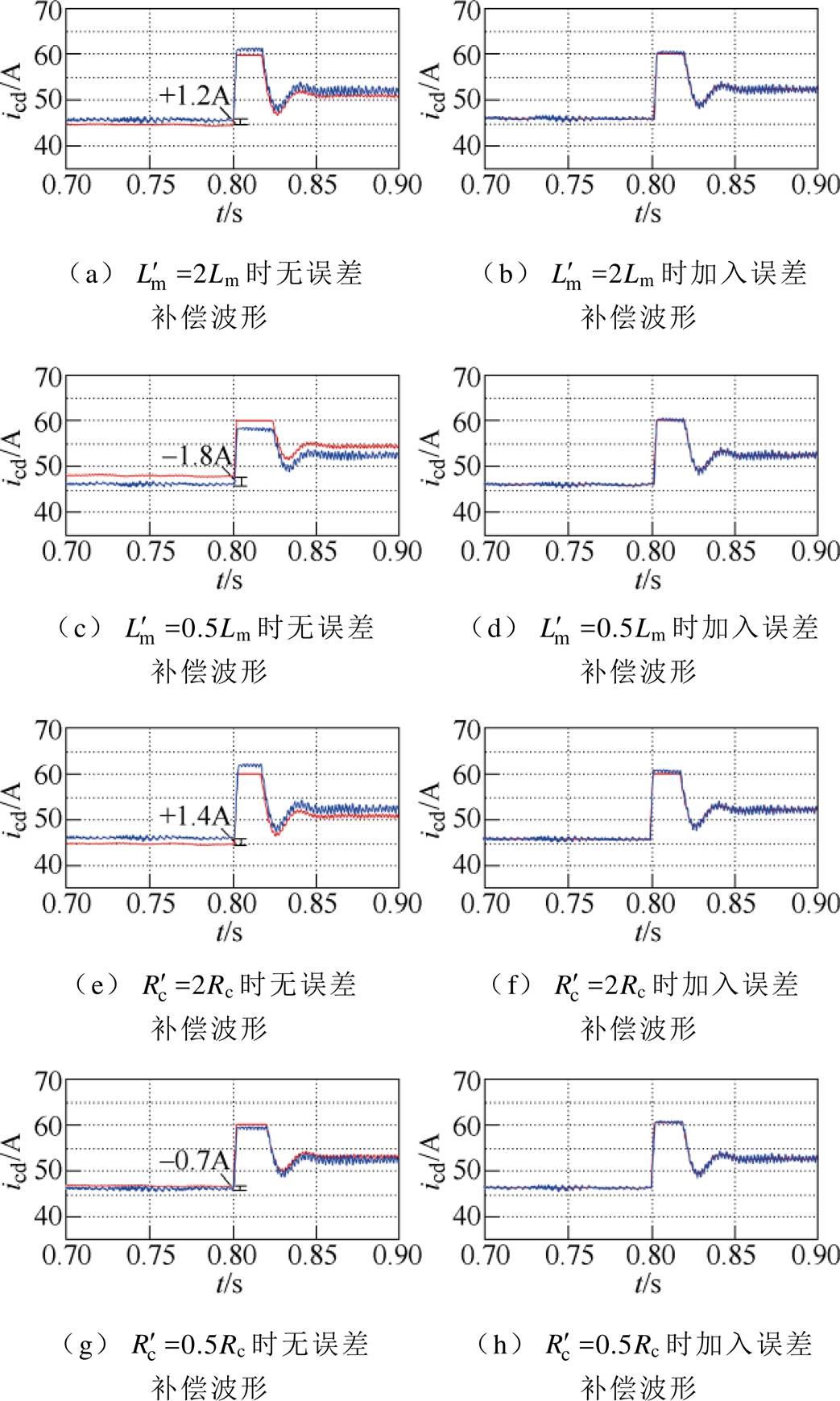
图14 加入误差补偿前后的电流预测控制的仿真波形
Fig.14 Simulation waveforms of current predictive control before and after error compensation
为了对本文所提出的无差拍电流预测控制进行实验验证，搭建了如图15所示的FPDWIG直流发电系统实验平台，主要包括FPDWIG、五相静止励磁变换器、数字控制板、采样调理板、5kW直流负载、原动机（三相普通感应电动机）、机械特性模拟装置等。其中，机械特性模拟装置主要由变频器和上位机两大部分组成，用于控制三相普通感应电动机的转速、转矩等，以模拟实际原动机（一般为发动机）的机械特性，本文中该机械特性模拟装置根据负载工况需求，控制三相普通感应电动机在1 500r/min下恒速运行。
图16a、图16b分别为FPDWIG采用两种控制方法的动态对比实验结果。从图中可以看出，在功率侧直流母线电压给定值为270V的情况下，突加额定负载后，两种控制方法的功率侧直流母线电压均能及时稳定在270V。其中，采用磁链定向控制时电压跌落约为49V，功率侧直流母线电压恢复时间约为135ms。采用无差拍电流预测控制时，功率侧直流母线电压跌落约为45V，功率侧直流母线电压恢复时间约为118ms。实验结果表明，FPDWIG采用电流预测控制功率绕组侧直流母线电压跌落幅度更小，系统动态性能有所提升。图16c、图16d分别为FPDWIG采用两种控制方法的稳态对比实验结果。从图中可以看出，磁链定向控制时控制绕组相电流THD略小，这是因为该控制方法中积分器的存在，导致其控制量输出的波动较小于无差拍电流预测控制方法。两种控制方法下，功率绕组直流母线电压均稳定在270V，与母线电压给定值一致，电压波动较小，均不足5V；控制绕组相电流幅值约为42A，功率绕组直流母线电流约为21A。实验结果表明，无差拍电流预测控制实现了系统优秀动态性能的同时，也保持了稳态性能优秀。
图15 FPDWIG直流发电系统实验平台的实物
Fig.15 Figure of FPDWIG DC power generation system experiment platform
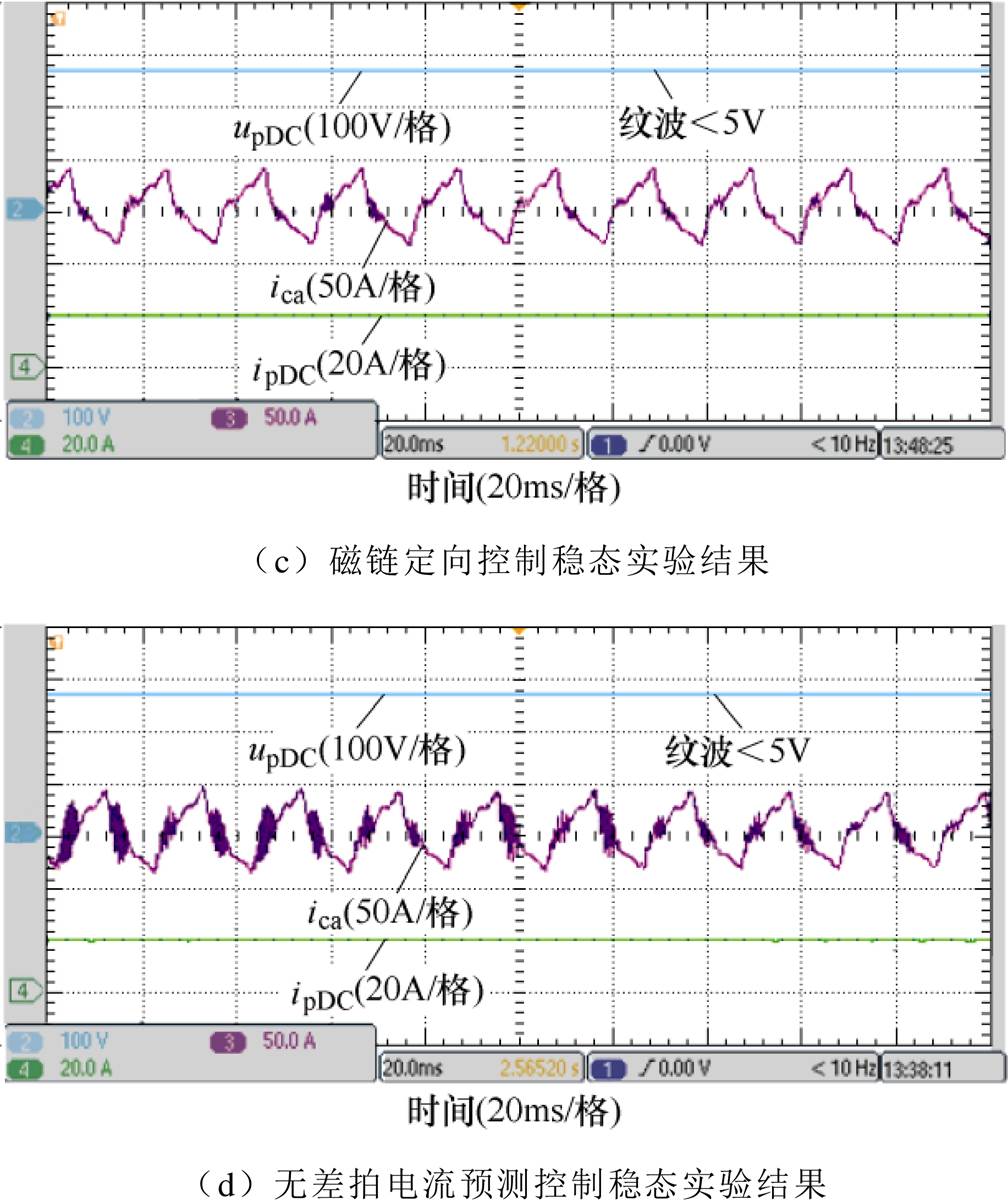
图16 磁链定向控制与无差拍电流预测控制的对比实验
Fig.16 Comparative experiment of flux-oriented control and predictive current control
实验中同样选取了=2Lm、=0.5Lm、= 2Rc、=0.5Rc四种典型情况，得到如图17所示的无差拍电流预测控制参数误差补偿实验波形。从图中可以看出，没有加入误差补偿之前，四种情况分别产生了+2.6A、-2A、+2.3A、-1.6A的误差，其误差变化趋势与3.2节分析相同。加入误差补偿之后，二者的静态误差都几乎被消除。实验结果表明，加入电流误差补偿的电流预测控制在保证了传统无差拍电流预测控制快速性的基础上，实现了参数不准确条件下电流的无误差跟踪。
（a）=2Lm时无误差补偿波形（b）=2Lm时加入误差补偿波形 （c）=0.5Lm时无误差补偿波形（d）=0.5Lm时加入误差补偿波形 （e）=2Rc时无误差补偿波形（f）=2Rc时加入误差补偿波形 （g）=0.5Rc时无误差补偿波形（h）=0.5Rc时加入误差补偿波形
图17 加入误差补偿前后的电流预测控制的实验波形
Fig.17 Experimental waveforms of current predictive control before and after error compensation
本文提出了五相双绕组感应发电机系统的无差拍电流预测控制，并在此基础上，针对模型参数不准确导致电流产生误差的情况，分析了不同参数偏差带来的影响，同时对电流预测控制进行了误差补偿的改进，在五相双绕组感应发电机系统仿真与实验平台上，开展了相关验证，获得以下结论：
1）无差拍电流预测控制根据双绕组感应发电机系统的预测模型，在一个控制周期内以消除被控量的误差为目标，分两步进行计算得到所需控制量，实现简单，不需要繁琐的参数整定过程，控制性能优秀，且易于数字化。
2）加入了误差补偿的双绕组感应发电机系统电流预测控制能够有效消除由参数误差带来的电流跟踪误差，实现参数不准确情况下的电流无误差跟踪。
参考文献
[1] Liu Xiao, Wang Chao, Chen Zhe. Characteristics analysis of an excitation assistance switched relu- ctance wind power generator[J]. IEEE Transactions on Magnetics, 2015, 51(11): 1-4.
[2] Zhang Zhuoran, Yu Li, Wang Yuting, et al. Overview and design methodology of doubly salient brushless DC gener- ators with stator-field winding[J]. IET Electric Power Applications, 2017, 11(2): 197-211.
[3] Wei Xinchi, Cheng Ming, Wang We, et al. Direct voltage control of dual-stator brushless doubly fed induction generator for stand-alone wind energy con- version systems[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-4.
[4] Chen Jiansheng, Zhang Wei, Chen Bojian, et al. Improved vector control of brushless doubly fed induction generator under unbalanced grid conditions for offshore wind power generation[J]. IEEE Transa- ctions on Energy Conversion, 2016, 31(1): 293-302.
[5] 王涛, 诸自强, 年珩. 非理想电网下双馈风力发电系统运行技术综述[J]. 电工技术学报, 2020, 35(3): 455-471.
Wang Tao, Zhu Ziqiang, Nian Heng. Review of operation technology of doubly-fed induction generator- based wind power system under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 455-471.
[6] 许利通, 程明, 魏新迟, 等. 考虑损耗的无刷双馈风力发电系统功率反馈法最大功率点跟踪控制[J]. 电工技术学报, 2020, 35(3): 472-480.
Xu Litong, Cheng Ming, Wei Xinchi, et al. Power signal feedback control of maximum power point tracking control for brushless doubly-fed wind power generation system considering loss[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 472- 480.
[7] Ojo O, Davidson I E. PWM-VSI inverter-assisted stand-alone dual stator winding induction generator[J]. IEEE Transactions on Industry Applications, 2000, 36(6): 1604-1611.
[8] 吴新振. 带整流负载双绕组多相高速异步发电机系统的研究[D]. 北京: 清华大学, 2006.
[9] Xu Haijun, Bu Feifei, Huang Wenxin, et al. Analysis, comparison, and discussion of control strategies for dual stator-winding induction generator DC generating system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(3): 1007-1014.
[10] Xu Haijun, Bu Feifei, Huang Wenxin, et al. Control and performance of five-phase dual stator-winding induction generator DC generating system[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 5276-5285.
[11] 李勇, 胡育文, 黄文新, 等. 变速运行的定子双绕组感应电机发电系统控制技术研究[J]. 中国电机工程学报, 2008, 28(20): 124-130.
Li Yong, Hu Yuwen, Huang Wenxin, et al. Research on the dual stator-winding induction generator with variable speed operation[J]. Proceedings of the CSEE, 2008, 28(20): 124-130.
[12] 许海军. 双绕组五相异步发电系统的控制技术及容错运行[D]. 南京: 南京航空航天大学, 2018.
[13] 梁营玉, 杨奇逊, 刘建政, 等. 电网电压不平衡时MMC-HVDC的无差拍直接功率控制[J]. 电工技术学报, 2015, 30(15): 15-25.
Liang Yingyu, Yang Qixun, Liu Jianzheng, et al. Deadbeat direct power control for MMC-HVDC under unbalanced grid voltages[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 15-25.
[14] 杨惠, 晁凯悦, 孙向东, 等. 基于矢量作用时间的双向DC-DC变换器预测电流控制方法[J]. 电工技术学报, 2020, 35(增刊1): 70-80.
Yang Hui, Chao Kaiyue, Sun Xiangdong, et al. Predictive current control method for bidirectional DC-DC converter based on optimal operating time of vector[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 70-80.
[15] 张晓, 谭力, 鲜嘉恒, 等. LCL并网逆变器预测电流控制算法[J]. 电工技术学报, 2019, 34(增刊1): 189-201.
Zhang Xiao, Tan Li, Xian Jiaheng, et al. Predictive current control algorithm for grid-connected inverter with LCL filter[J]. Transactions of China Electro- technical Society, 2019, 34(S1): 189-201.
[16] Reza S D, Mohammad A A, Hadi S, et al. Perfor- mance improvement of permanent-magnet synchronous motor using a new deadbeat-direct current con- troller[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3530-3543.
[17] Judewicz M G, González S A, Fischer J R, et al. Inverter-side current control of grid-connected voltage source inverters with LCL filter based on generalized predictive control[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 1732-1743.
[18] 李景灏, 吴爱国. 基于离散趋近律与无差拍双闭环结构的单相LCL型PWM整流器控制策略[J]. 电工技术学报, 2021, 36(6): 1290-1303.
Li Jinghao, Wu Aiguo. A double closed-loop control method for single-phase PWM rectifiers with LCL filter based on discrete reaching law and deadbeat algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1290-1303.
[19] 孙建业, 王志强, 谷鑫, 等. 高速低载波比下永磁同步电机预测电流控制[J]. 中国电机工程学报, 2020, 40(11): 3663-3673.
Sun Jianye, Wang Zhiqiang, Gu Xin, et al. Predictive current control of PMSM with high speed and low- frequency-ratio[J]. Proceedings of the CSEE, 2020, 40(11): 3663-3673.
[20] 姜卫东, 汪磊, 皋艳, 等. 一种实现内环电流跟踪的改进无差拍控制方法[J]. 中国电机工程学报, 2017, 37(8): 2370-2383.
Jiang Weidong, Wang Lei, Gao Yan, et al. An improved deadbeat control method to implement current tracking for inner loop[J]. Proceedings of the CSEE, 2017, 37(8): 2370-2383.
Deadbeat Predictive Current Control Strategy of Dual Winding Induction Generator System
Abstract The dual winding induction generator system adopts the flux-oriented control strategy to adjust the active current and the reactive current separately, so as to obtain stable control of the DC voltage at both ends of the control winding and the power winding. However, the control strategy is relatively complicated, and multiple regulators bring difficulties in the design of the controller, which restricts the further development and application of the dual winding induction generator system. Therefore, a deadbeat predictive current control strategy for the dual-winding induction generator system is proposed, and a predictive model of the generator system is established. In a control cycle, with the goal of eliminating the error of the controlled quantity, the required control quantity is directly calculated. The current error caused by the model parameter mismatch is analyzed, and error compensation is made for the control strategy. The proposed deadbeat predictive current control strategy avoids the cumbersome adjustment process of regulator parameters, has excellent control performance, and achieves error-free current tracking. The prototype simulation and experimental results verify the correctness and feasibility of the predictive current control of the dual winding induction generator system.
keywords：Dual winding induction generator, predictive current control, flux-oriented control, error compensation
DOI: 10.19595/j.cnki.1000-6753.tces.210430
中图分类号：TM346
国家自然科学基金资助项目（52177050）。
收稿日期 2021-03-29
改稿日期 2021-08-10
卜飞飞 男，1984年生，副教授，硕士生导师，研究方向为航空电源、新能源发电、伺服驱动、电机及其控制等。E-mail: bufeifei1984@163.com（通信作者）
罗 捷 男，1996年生，硕士，研究方向为电力电子与电力传动。E-mail: luo_jie@nuaa.edu.cn
（编辑 崔文静）