
图1 电池老化过程充电电压曲线
Fig.1 Charging voltage curves during battery degradation
摘要 锂离子电池健康状态(SOH)的准确估计是电池管理系统(BMS)的关键技术。该文提出一种基于数据驱动与经验模型组合的在线SOH预测方法。通过电池容量增量分析(ICA),找出与SOH相关性较高的两个电压升片段下所耗时间作为电池外部健康特征(HF),并使用高斯过程回归(GPR)的方法建立电池老化的数据驱动模型。利用数据驱动模型对电池工作初期的SOH进行预测,并使用预测值拟合指数经验模型。之后,电池各循环下的SOH用指数经验模型来预测,并且每隔固定循环次数使用观测器对指数模型参数进行一次修正,以保证电池SOH预测的准确性。实验结果表明,该文所提的方法可以在减轻电池监测设备负担的前提下将预测精度保持在较高水平。
关键词:锂离子电池 健康状态 指数模型 高斯过程回归 观测器
锂电池作为一种清洁能源,以其体积小、能量密度高、寿命长等优点,被广泛应用于生活用电子产品、电动汽车、通信基站,甚至航天、军事等多个领域[1]。电池管理系统(Battery Management System, BMS)可以对电池状态进行评估,给出风险预警,保证电池长期安全稳定运行。其中,准确的电池状态估计是BMS运维的关键[2]。电池健康状态(State of Health, SOH)是表征电池老化程度与健康状况的关键指标,其通常定义为当前可用最大容量与出厂额定容量之间的比值[3]。随着电池老化程度的加深,SOH逐渐降低,在SOH下降到80%时[4],电池衰减至寿命终止。
国内外对电池SOH预测进行了广泛的研究,主要包括直接测量法、基于模型的方法与基于数据驱动的方法。直接测量法是一种离线方法,通过对电池容量、内阻、电化学阻抗谱等与电池老化直接相关的参数进行测量,采用简单的函数映射得到SOH。如文献[5]中采用了库伦计数法求得电池最大可释放容量来评估SOH;文献[6]中指出商用18650电池在316Hz下的阻抗响应可以反映出其SOH;文献[7]中采用电化学阻抗谱技术对锂聚合物锂电池的老化特性进行研究。该类方法原理简单,对不同电池都有着很强的适应性,但是对传感器等测量设备要求较高,脱离实验室环境后难以应用到实际当中。目前,关于SOH研究的主流方向还是基于模型的方法与基于数据驱动的方法。常用的模型种类有等效电路模型、电化学模型以及经验衰退模型。等效电路模型是由常见的电路元件对电池内部的工作状态进行模拟所得。该方法通过对元件参数进行辨识,利用辨识结果进行SOH预测。如文献[8]建立二阶RC等效电路模型,通过使用自适应无迹卡尔曼滤波算法对电池欧姆内阻进行实时估算,并根据欧姆内阻与电池SOH的映射关系来预测SOH。这类模型具有结构简单、计算量小等优点,但是其适应性较差,存在模型参数准确辨识困难的问题。电化学模型从电池内部工作机理出发,利用偏微分方程组来刻画电池的容量衰退机理,如基于多孔电极理论搭建的准二维多孔电极模型(Pseudo Two- Dimensional model, P2D model)[9]。该类模型过于复杂,难以应用于在线估计。经验模型可以对电池完整的循环周期进行建模,拟合电池健康状态的衰退趋势。如文献[10]从阿伦尼乌斯定律出发,推导出含有温度参数的关于循环次数的幂律电池老化模型。虽然该经验模型考虑了温度对电池衰退速率的影响,但是仍存在由电池个体差异造成的预测初期模型参数难以准确确定的问题。这类方法虽然计算简单,但是适应性差、准确度受限。目前,常常将经验模型与其他方法组合建模。文献[11]通过粒子滤波算法将双指数模型与人工神经网络相结合,较好地拟合了电池衰退曲线。但是,由于神经网络的引入反而增加了模型的复杂度,并没有体现出经验模型简单易用的优势。基于数据驱动的方法不需要研究电池内部老化机理,而是通过机器学习算法,如向量机[12]、高斯过程回归[13]、神经网络[14-16]等建立外部健康特征(Health Feature, HF)[17]与电池SOH之间的非线性映射关系。文献[18]从电池充电曲线中提取了8个有效健康特征后通过主成分分析得到间接健康特征,并利用相关向量机建立SOH的预测模型;文献[19]从电池恒流充电阶段温度差分曲线提取健康特征,使用支持向量机进行容量衰退预测;文献[20]使用深度学习的方法,以电压、电流、温度的采样序列为输入,训练卷积神经网络来预测SOH。这类方法简单易实现,且在训练集可靠的前提下可以获得较高的预测精度,但是存在健康特征选取困难与对设备算力要求苛刻的问题。特别是在多电池同时监测的情景中,监测设备面临的计算压力会进一步体现。
为了减轻电池监测设备的负担,同时保证SOH在线预测具有较高的精度,本文提出一种利用观测器[21-22]将高斯过程回归与指数经验模型组合的在线SOH预测方法。该方法分为离线与在线两个阶段,在离线阶段以同类型电池的历史使用数据为训练集,利用高斯过程回归建立数据驱动模型。在在线阶段,首先使用数据驱动模型对电池初始部分循环下的SOH进行预测;然后利用预测所得数据建立指数模型;最后使用指数模型对后续循环下的SOH进行预测,并每隔固定循环次数使用观测器对指数模型参数进行修正,以保证SOH预测的准确性。本文通过对牛津大学电池老化数据集(Oxford Battery Degradation Dataset, OBDD)[23]的多个电池进行实验,结果表明所提方法较好地结合了经验模型与数据驱动模型的优点。
健康特征的提取与机器学习方法的选择是数据驱动模型建立的关键。
本文使用牛津大学电池老化数据集进行实验,该数据集共含编号为Cell1, Cell2, …, Cell8的8块Kokam的钴酸锂离子袋装电池的测试数据。电池的额定容量为740mA·h,在40℃环境温度下重复进行2C(1.48A)恒流充电,模拟Artemis市区行驶工况动态放电的老化实验。并每隔100个充放电循环以1C恒流放电进行容量标定。为便于后续的实验,规定每进行一次容量标定表示一次工作周期循环的完成。该数据集提供了各个电池全生命周期下的标定数据,适合进行SOH预测实验。
对于健康特征的选取,除了需要考虑特征的强相关性,还应当考虑提取的便捷性、合理性与实用性。随着电池老化程度的加剧,其充放电曲线也会随之发生改变。在实际中,由于工况的不确定性,放电曲线也会有所不同,而充电工况往往是固定的,通常为恒流恒压充电模式。相比复杂多变的放电曲线,充电电压曲线相对来说较为平稳,更易于提取特征。数据集中电池Cell1全周期恒流阶段充电曲线如图1所示,电池老化越严重,曲线的颜色越深。观察图1可知,不同老化程度的电池在恒流充电阶段曲线有着明显的差异,随着电池不断的老化,曲线整体向上平移,越早地进入电压平台期,并且越早地结束恒流充电的过程。为了更好地体现电池容量的衰退对充电电压曲线造成的变化,本文采用了容量增量分析[24-25](Incremental Capacity Analysis, ICA)的方法。同时为了可以更好展示容量增量曲线的特性,使用卡尔曼滤波器对其进行了滤波处理,电池Cell1容量增量曲线如图2所示。观察图2可知,随着电池的不断老化,ICA曲线两个峰的峰值在不断下降。而且曲线在电压区间[3.55, 3.75]V与区间[3.80, 4.15]V内有着较大的差异,与电池容量衰退有着很强的相关性。为便于后文的讨论,记这两个区间为[A1, B1]和[A2, B2]。

图1 电池老化过程充电电压曲线
Fig.1 Charging voltage curves during battery degradation
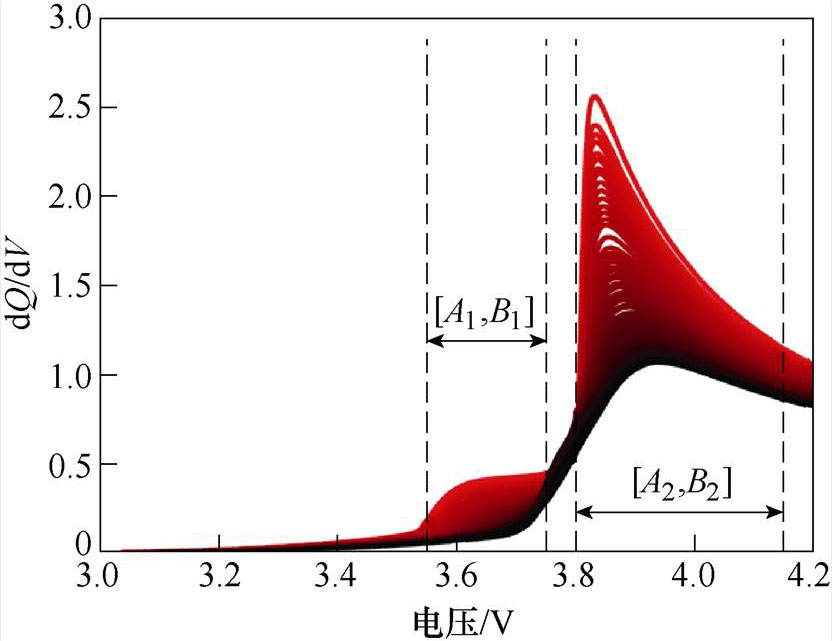
图2 电池老化过程容量增量曲线
Fig.2 Capacity increment curves during battery degradation
为了量化在上述区间下不同ICA曲线的差异性,可以从峰值大小或曲线与x轴所围成的面积等方面进行考虑。本文从面积这一方面进行分析。在电压区间[A, B]上,对ICA曲线进行积分,有
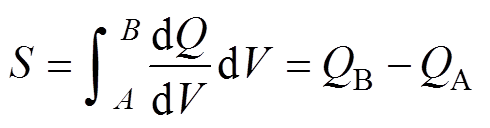 (1)
(1)式中,S为积分面积;Q为电荷量;V为电压。可知,面积S的物理含义为,电池电压V从A上升至B时获得的电荷量。电荷量Q的计算公式为
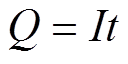 (2)
(2)
式中,I为充电电流,在恒流充电阶段为常数;t为充电时间。可知,电荷量与时间之间成正比关系,故可用电压区间[A, B]内对应的时间变化量Dt代替该区间下ICA曲线的面积S来做为电池的健康特征,记该特征名称为dV-dt。为了量化该健康特征与SOH之间相关程度,本文采用Pearson和Spearman相关系数进行衡量,计算公式分别为
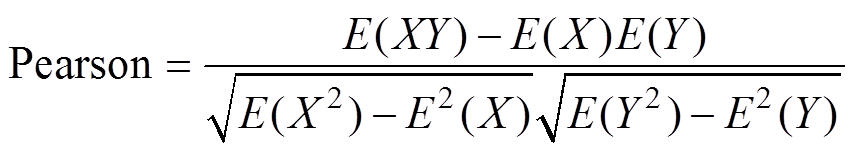 (3)
(3)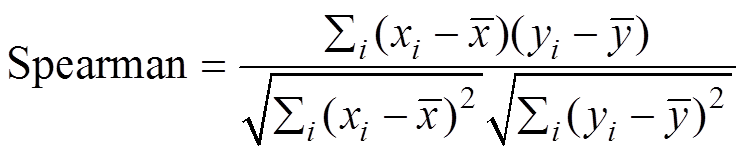 (4)
(4)
式中,X和Y为样本总体;xi和yi为样本个体。
Pearson和Spearman相关系数常用于刻画两个变量之间的相关程度,绝对值越接近1,表明相关性越强,当绝对值为1时表明两个变量完全相关。在满足连续数据、正态分布、线性关系时,用Pearson相关系数最为恰当,若上述有任一条件不满足时,Spearman相关系数则更加可靠,所以本文采用两者来对健康特征进行综合考察。dV-dt与SOH相关性系数见表1和表2。分析表中数据可知,各电池在两个电压区间对应的健康特征dV-dt1和dV-dt2,与SOH之间的Pearson相关系数和Spearman相关系数均超过0.97,有着极强的相关性;同时该健康特征还具有物理意义明确、易于提取的优点。
表1 HF的Pearson相关系数
Tab.1 Pearson correlation coefficient of HF

特征区间Pearson相关系数 Cell1Cell2Cell3Cell4Cell5Cell6Cell7Cell8 dV-dt1[3.55, 3.75]V0.999 00.995 80.998 50.998 90.976 90.998 50.998 90.998 7 dV-dt2[3.8, 4.15]V0.999 50.997 00.999 50.998 10.999 00.995 00.999 20.999 0
表2 HF的Spearman相关系数
Tab.2 Spearman correlation coefficient of HF

特征区间Spearman相关系数 Cell1Cell2Cell3Cell4Cell5Cell6Cell7Cell8 dV-dt1[3.55, 3.75]V0.999 20.994 40.998 30.999 30.998 80.999 10.998 90.998 7 dV-dt2[3.8, 4.15]V0.999 80.997 50.999 70.999 80.999 80.999 50.999 70.999 7
GPR模型是一种使用高斯过程(Gaussian Process, GP)先验对数据进行回归分析的非参数模型。高斯过程是定义在连续域上的无限多个高斯随机变量所组成的随机过程。设有训练集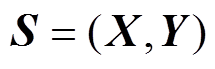 ,其中,
,其中,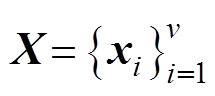 ,
, ,
,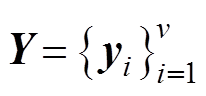 ,
, ;测试集
;测试集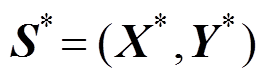 ,其中,
,其中,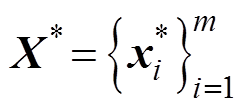 ,
,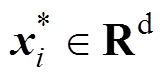 ,
,
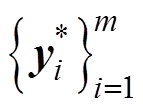 ,
,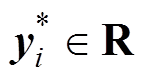 。GPR模型可以在训练集S上学习到X与Y之间的映射函数
。GPR模型可以在训练集S上学习到X与Y之间的映射函数 ,并且通过这一函数给出测试集S*中输入为
,并且通过这一函数给出测试集S*中输入为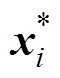 时的预测值
时的预测值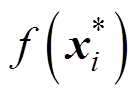 。GPR模型可以在权重空间和函数空间下进行推导。其中,在函数空间的推导方式更加简单,也更容易理解,推导过程如下。
。GPR模型可以在权重空间和函数空间下进行推导。其中,在函数空间的推导方式更加简单,也更容易理解,推导过程如下。
在训练集中,输入矩阵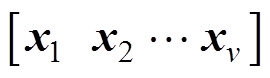 对应的输出向量
对应的输出向量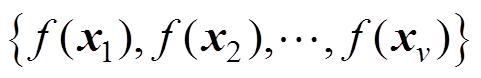 是一个高斯随机变量的集合。这些高斯变量组成的随机过程也就是高斯过程。高斯过程可以由其均值函数
是一个高斯随机变量的集合。这些高斯变量组成的随机过程也就是高斯过程。高斯过程可以由其均值函数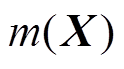 与协方差函数Cov(X, X)来确定,有
与协方差函数Cov(X, X)来确定,有
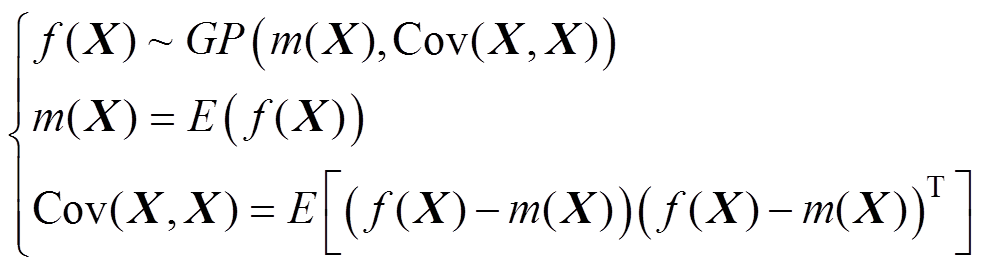 (5)
(5)式中,X为输入矩阵; 为X的映射向量。通过数据预处理使均值函数取值为0,并将协方差函数设置为核函数的形式。本文选用二次方指数函数作为核函数,其形式为
为X的映射向量。通过数据预处理使均值函数取值为0,并将协方差函数设置为核函数的形式。本文选用二次方指数函数作为核函数,其形式为
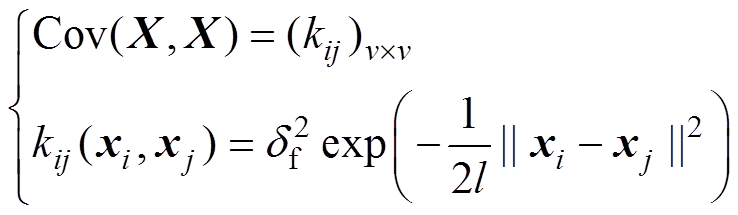 (6)
(6)
式中,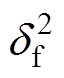 为信号方差;l为特征长度尺度。
为信号方差;l为特征长度尺度。
考虑到在实际中噪声是不可避免的,故在模型中加入独立同分布的高斯噪声,具体形式为
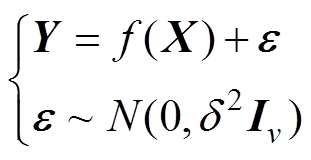 (7)
(7)则模型的先验分布为
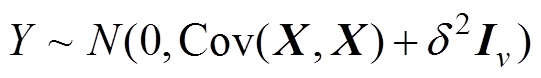 (8)
(8)
已知在训练集S中,Y服从高斯分布,在测试集中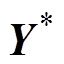 也服从高斯分布,将Y与
也服从高斯分布,将Y与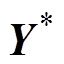 拼接成一个向量,其联合先验分布为
拼接成一个向量,其联合先验分布为
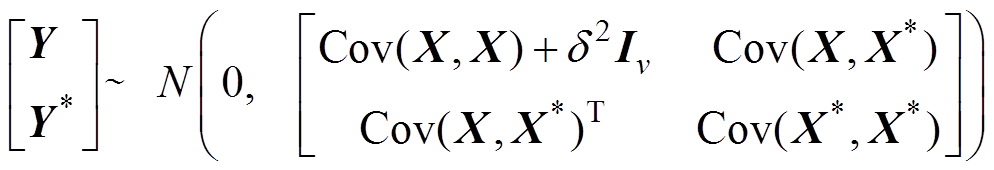 (9)
(9)则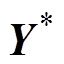 的后验分布为
的后验分布为
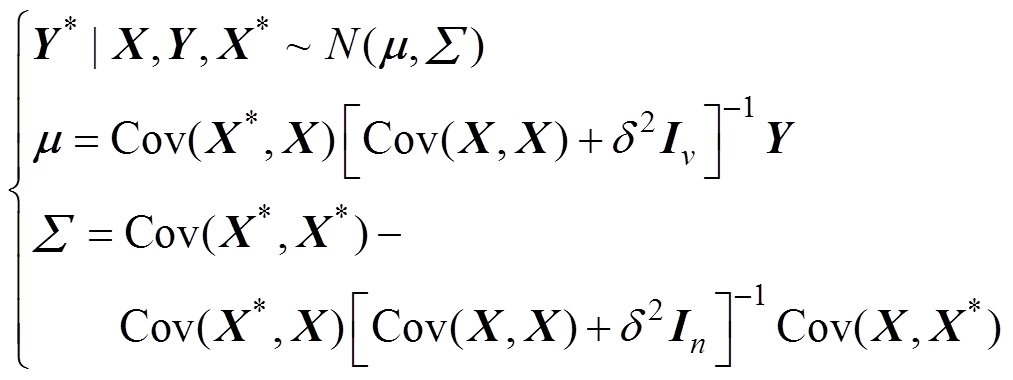 (10)
(10)
超参数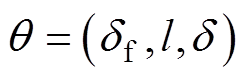 ,可通过最小化负对数似然(Negative Log Marginal Likelihood, NLML)函数来求解,求解步骤一般为先对似然函数求偏导,再使用共轭梯度法来求解,这里不再给出详细推导过程。超参数求解完成后,即可得到GPR模型。GPR模型95%置信区间预测结果为
,可通过最小化负对数似然(Negative Log Marginal Likelihood, NLML)函数来求解,求解步骤一般为先对似然函数求偏导,再使用共轭梯度法来求解,这里不再给出详细推导过程。超参数求解完成后,即可得到GPR模型。GPR模型95%置信区间预测结果为
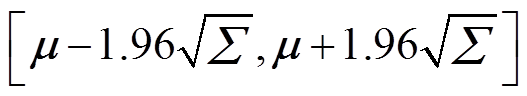 (11)
(11)数据驱动老化模型建立的实施步骤如下:
(1)测量并记录同种类多个电池的全生命周期下循环充放电数据。并通过ICA曲线分析得到电池健康特征dV-dt所对应电压区间。
(2)将离线历史数据作为训练集,以健康特征dV-dt1与dV-dt2序列作为GPR模型的输入,SOH序列作为输出,训练得到GPR电池老化模型。
(3)在线预测时需要实时采集特征dV-dt1与dV-dt2,输入到训练好的GPR模型中来获得此刻电池的SOH,并给出相应的置信区间。
描述电池衰退趋势的经验模型常为SOH与循环次数n之间的函数,其一般形式为
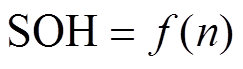 (12)
(12)指数函数由于有结构简单、拟合电池衰退趋势效果好的优点,得到了广泛的应用,其函数形式为
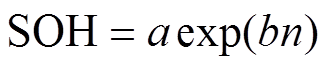 (13)
(13)
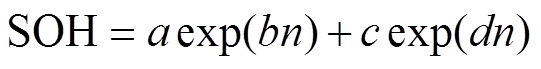 (14)
(14)式中,a, b, c, d为指数模型的参数。
本文选用单指数函数来对容量衰退进行拟合。指数模型拟合结果如图3所示,相比于双指数模型,其对电池循环全周期的拟合效果并不是十分出色。但是,分区间单指数模型拟合结果如图4所示,每隔20个循环周期,对不同区间的真实曲线独立拟合,同样可以获得较好的效果,各区间参数辨识结果见表3。单指数模型具有参数个数少的优点,辨识会更加容易,同时也更易于修正,这与本文提出的利用观测器修正模型参数的方法十分契合。

图3 指数模型拟合结果
Fig3 Results of exponential model fitting
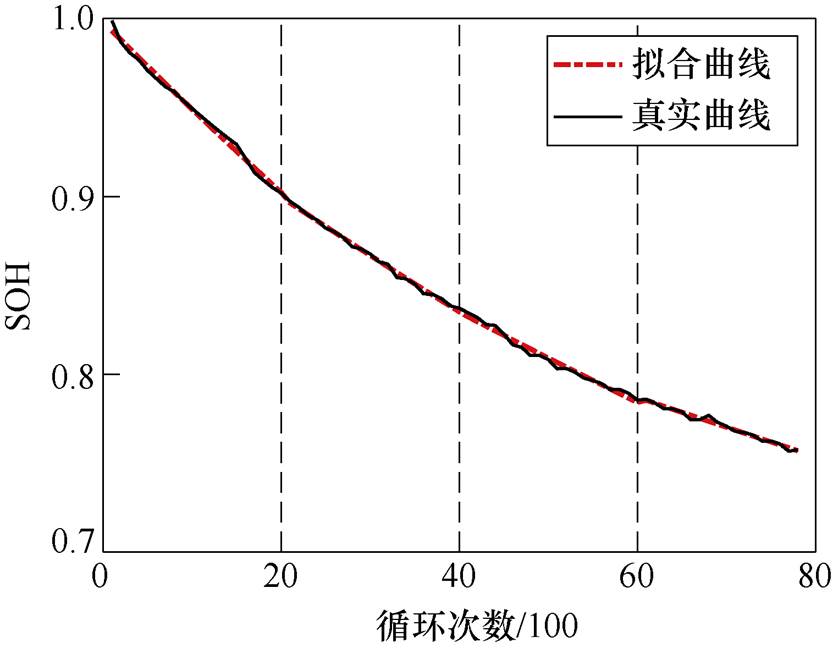
图4 分区间单指数模型拟合结果
Fig.4 Results of single exponential model fitting in fragment
表3 单指数模型参数辨识结果
Tab.3 Parameter identification results of single exponential model
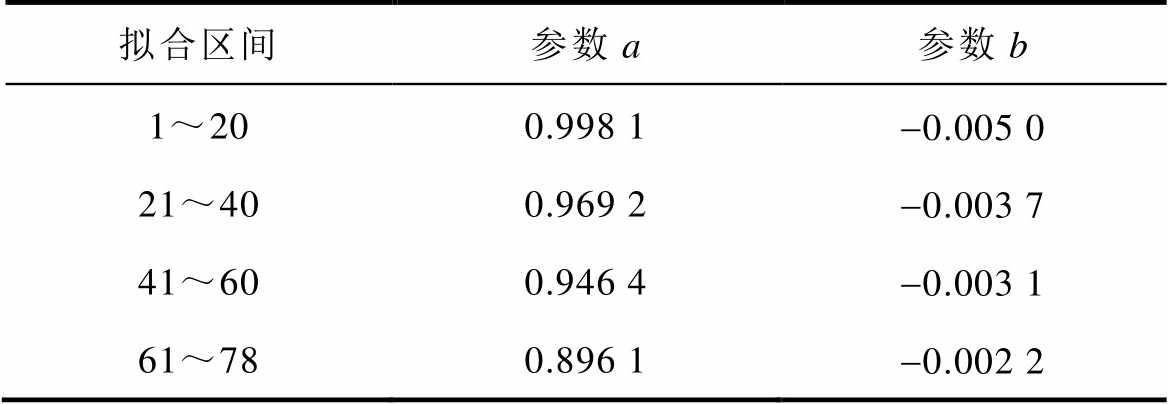
拟合区间参数a参数b 1~200.998 1-0.005 0 21~400.969 2-0.003 7 41~600.946 4-0.003 1 61~780.896 1-0.002 2
如式(13)所示,一般的指数模型是连续函数,当观测器得到真实值时,会难以实现对指数模型起始点的校正,同时对模型参数的修正也存在一定的困难,所以必须要对指数模型进行离散化。对式(13)进行求导,有
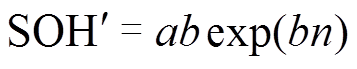 (15)
(15)则离散化后的模型为
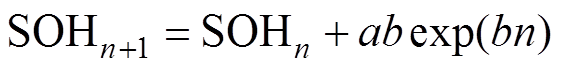 (16)
(16)
更一般地,假设在n=np处获得观测值 ,并将模型参数a和b矫正为ap和bp,则更新之后的指数模型表示为
,并将模型参数a和b矫正为ap和bp,则更新之后的指数模型表示为
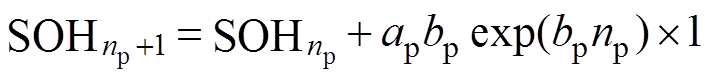 (17)
(17)进一步推导,有
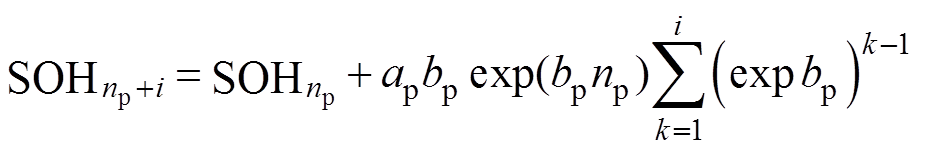
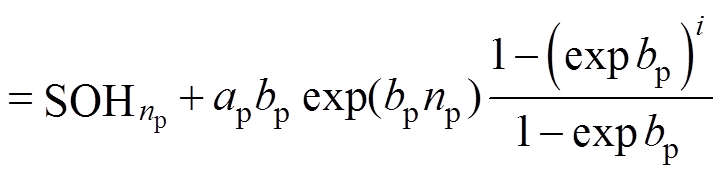 (18)
(18)式中,i为指数模型更新后第i个循环的预测。
在下一次观测值到来之前,SOH一直使用由上一次观测器修正过后的指数模型进行预测。
在实际应用系统中,并不是所有参数都是可观或直接可测的,但是可以利用观测器将这些系统对象进行模拟,进而较为容易地获取这些内部变量。电池老化模型是一个黑箱模型,在任意时刻下模型参数是难以根据已知条件直接获取的。但可以先假设电池老化模型为指数模型,由第2节分析,该假设是合理的。同时将一已知可观的指数模型作为实际电池老化模型的观测器,则可以通过该可观的指数模型近似获得实际老化模型的内部参数。
为了使指数老化模型能更贴合实际模型,需要对模型的参数不断修正,相关流程如图5所示。假设在第n次循环下由实际电池老化模型输出SOH的真实值,此时,指数模型输出该循环下SOH的估计值。令真实值减去估计值获得估计误差e。将估计误差e与增益K相乘,并与现有指数模型的参数a、b相加,从而得到新的模型参数anew、bnew,有
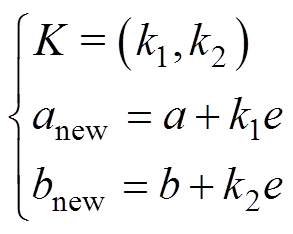 (19)
(19)式中,k1、k2为K的分量。
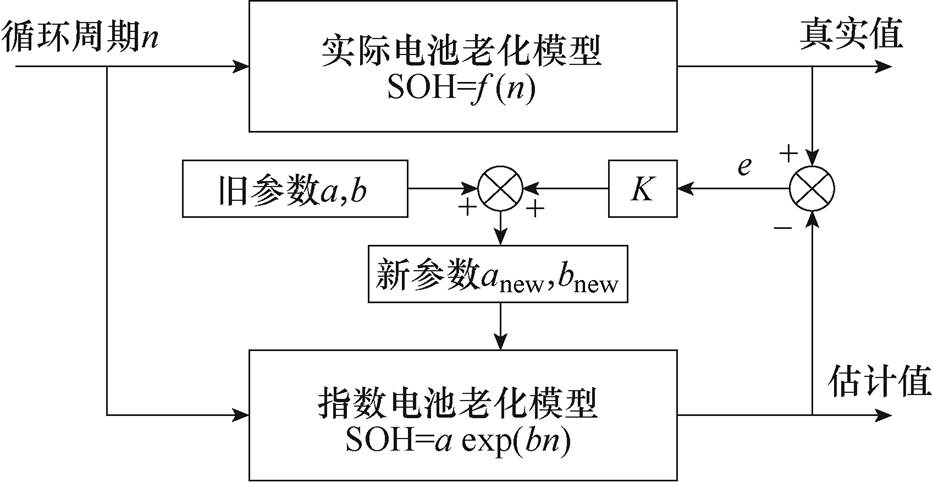
图5 参数校正框图
Fig.5 Parameter correction block diagram
同种类不同电池个体之间,虽然会在容量衰退轨迹的细节上表现出一定的差异性,但是在整体趋势上还是以一致性为主。所以,电池Cell1对应增益K的筛选值同样适用于同种类的其他电池。增益K的选取方法如下:
(1)粗筛范围。由表3各个区间拟合数据计算可得,相邻两个区间参数a与参数b变化量的比值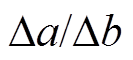 分别约为-22,-38,-55,取其平均值为-38,粗略认为每次参数更新
分别约为-22,-38,-55,取其平均值为-38,粗略认为每次参数更新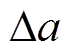 为
为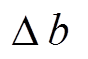 的-38倍,对应有k1=-38k2。按此比例关系将增益K的一个变量消去后,以全周期预测平均绝对误差最小为目标,由试探法确定出k2的一个合适取值0.04,对应此时增益K为(-1.52, 0.04)。
的-38倍,对应有k1=-38k2。按此比例关系将增益K的一个变量消去后,以全周期预测平均绝对误差最小为目标,由试探法确定出k2的一个合适取值0.04,对应此时增益K为(-1.52, 0.04)。
(2)精筛范围。使用遍历法对上一步确定出的K值附近邻域进行搜寻,筛选出一个更为合适的增益K为(-1.8, 0.03)。
经实验测试,本文在第1节提出的数据驱动模型SOH的预测相对误差基本在1%以内,具有较高的精度,所以可以将该模型的预测值近似视作观测器中需要的真实值。整体SOH预测框架如图6所示,t为校正间隔周期数。将电池在线监测工作过程分为“磨合期”与“工作期”两个阶段。首先在电池开始工作的前n个周期,通过传感器提取特征,使用数据驱动模型对电池SOH进行预测,利用预测值对单指数模型进行拟合,获得指数模型初始参数,这一阶段称为“磨合期”;接着使用指数模型对后续循环周期电池SOH预测,并在后续的循环过程中每隔t次循环利用观测器对指数模型参数进行修正,观测器中真实值用数据驱动模型预测值代替,把这一阶段称为“工作期”。在电池监测系统进入“工作期”后,电池组同一循环周期下只需要对一个或部分电池的指数模型进行参数校正,其余电池使用指数模型直接预测,在此基础上实现各个电池模型参数的轮流校正。通过该方法可以有效减少传感器与计算设备的压力。
本文在CPU型号为i5-8300h,RAM内存16GB的计算机设备上进行实验。首先应对建立的数据驱动电池老化模型的准确性进行校验,因为核验了该模型的准确性,后续指数模型的参数校正才会有意义;其次再对数据驱动与指数模型相结合方法的准确性进行检验。实验中用于SOH预测性能评估的指标有相对误差百分比(Relative Percentage Error, RPE)、平均绝对误差(Mean Absolute Error, MAE)和方均根误差(Root Mean Squared Error, RMSE),其中,xi和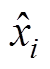 分别为SOH真实值和预测值。
分别为SOH真实值和预测值。
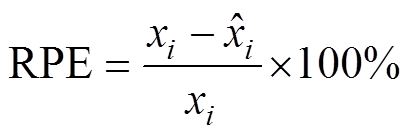 (20)
(20)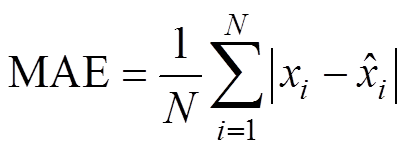 (21)
(21)
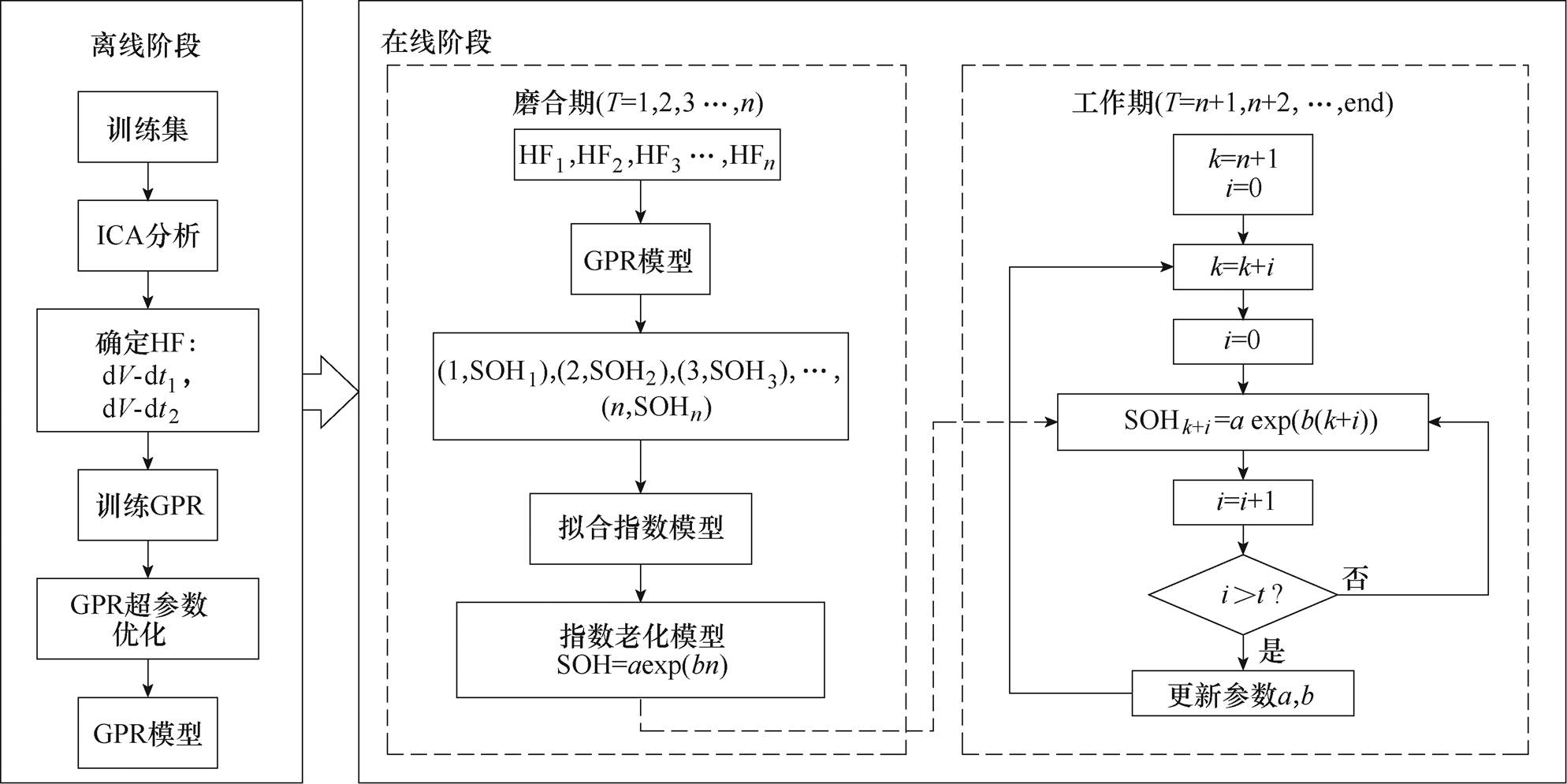
图6 SOH预测方法流程
Fig6 Flow chart of SOH prediction method
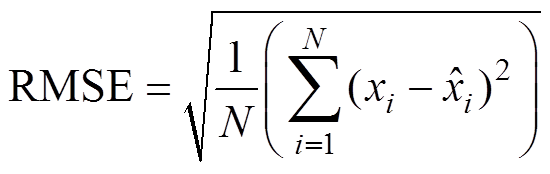 (22)
(22)为充分利用牛津数据集中的数据,每次选择1个电池数据做测试集,其余7个电池数据做训练集来进行实验,使得每一个电池都可以得到验证。实验测试得到,GPR模型每进行一次预测计算耗时约为0.046 1s。各电池的SOH预测结果和相对误差百分比如图7所示。
图7中,实线表示SOH的真实值曲线,虚线表示SOH预测值曲线,阴影区域表示预测值的95%置信区间。一般地,置信区间越窄,代表模型可靠性越高。可以观察到,8个电池的置信区间宽度均比较窄,且SOH真实值除极个别点外,基本落在置信区间内部,可以说明,所提出老化模型具有较高的准确度。由相对误差结果可以观察到,各电池相对误差基本在1%以内,均维持在较低水平。表4给出MAE和RMSE的计算结果,SOH估计的MAE和RMSE基本小于0.01。实验所用的8块电池老化速率并不完全相同,电池数据包含的循环次数也有着较大差异,如Cell1包含78个工作循环周期,Cell4只含有46个工作循环周期,但是该模型对所有电池都有较好的预测结果,这进一步表明了GPR老化模型具有较强的适应性和较高的可靠性。
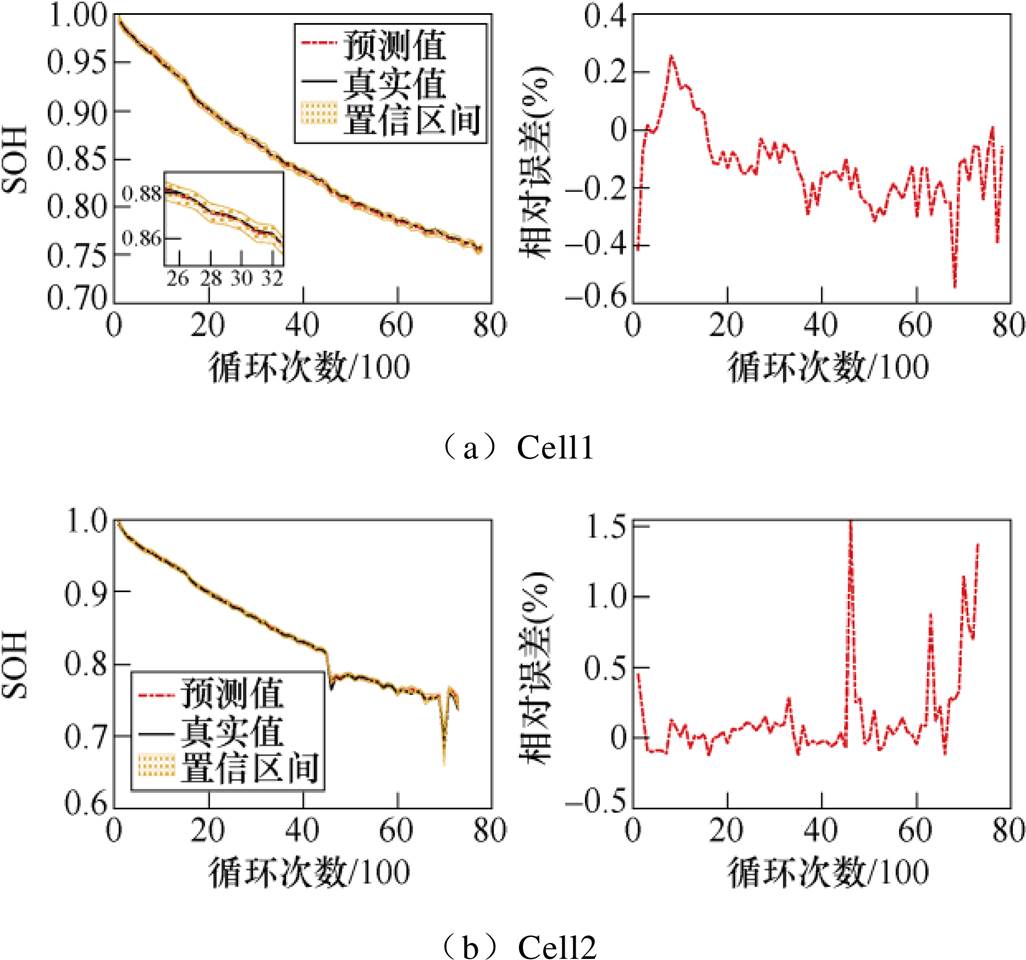
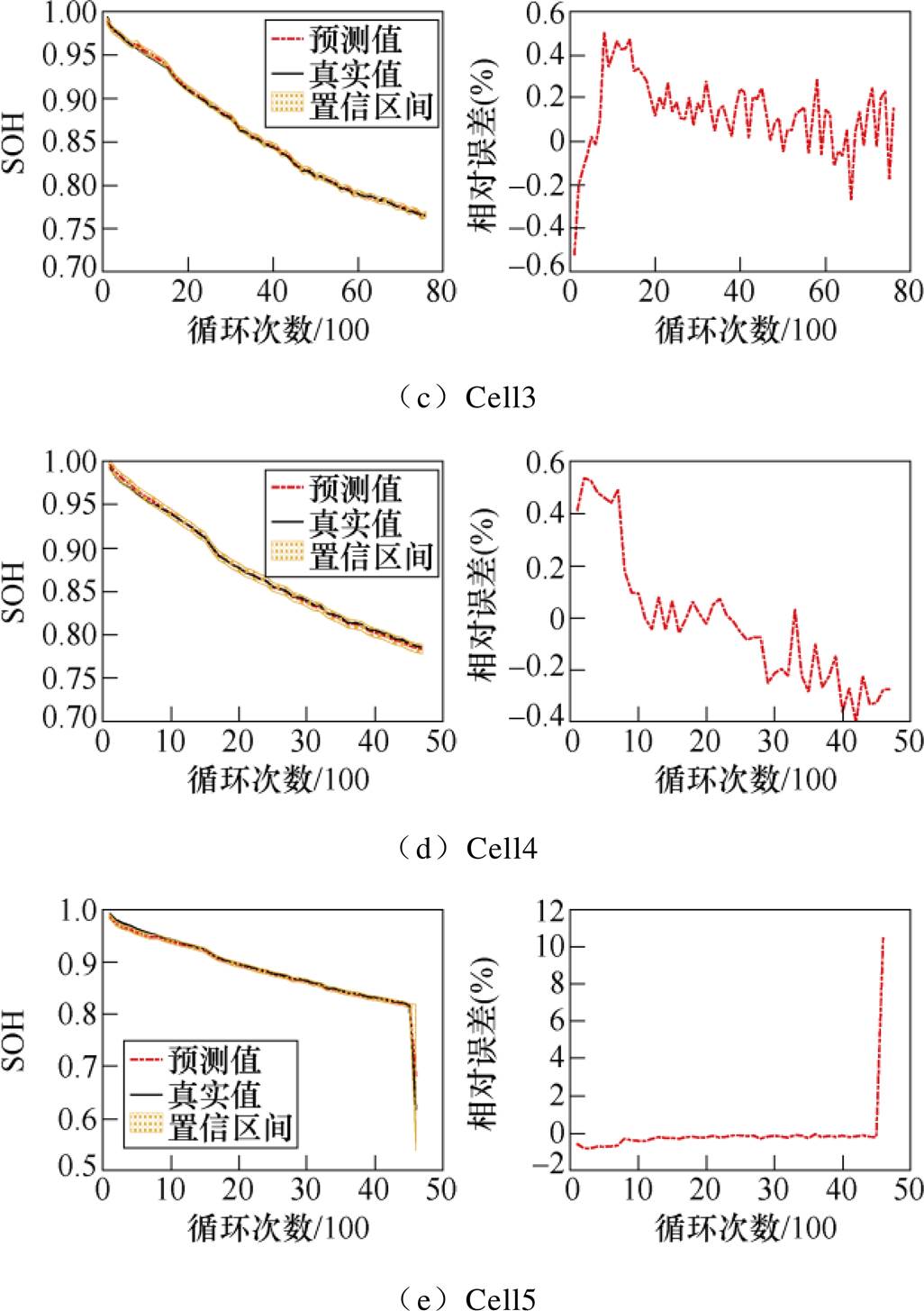
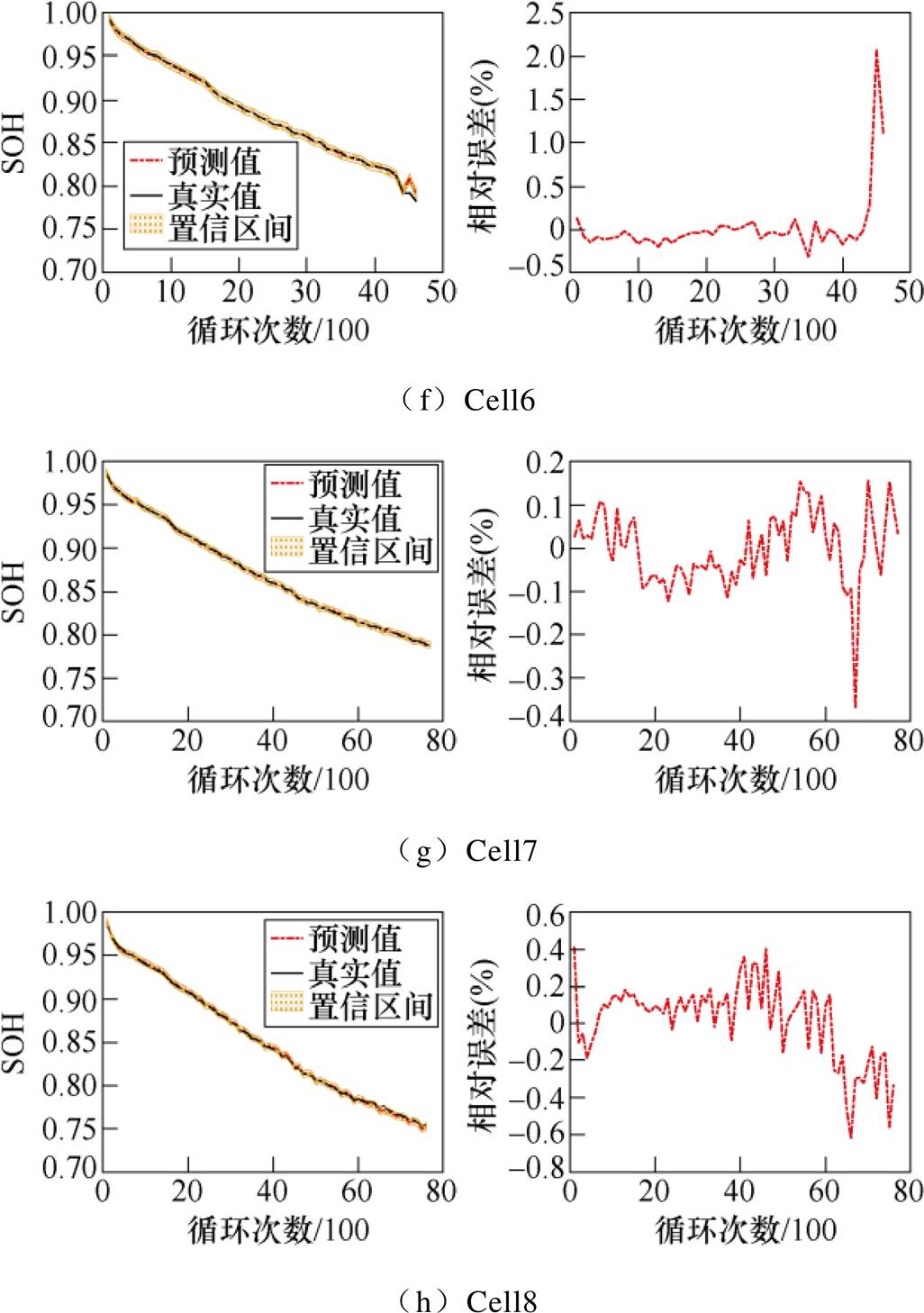
图7 GPR模型SOH估计结果
Fig.7 SOH estimation results with GPR model
表4 SOH估计误差结果
Tab.4 Results of SOH estimation error

电池Cell1Cell2Cell3Cell4Cell5Cell6Cell7Cell8 MAE0.001 30.001 40.001 50.001 70.004 00.001 30.000 60.001 4 RMSE0.001 50.002 60.001 90.002 30.010 10.002 90.000 70.001 7
在组合模型预测的实验中,使用GPR模型对前15个周期下的电池SOH进行预测,并利用最小二乘法对得到的预测值进行指数模型的拟合,获得指数模型参数的初始值。由于后续利用观测器进行参数校正的间隔周期数对组合模型的预测精度有所影响,本文对不同间隔周期t的影响进行讨论。分别令t =5,t =10,t =15来进行实验。实验测试得到,指数经验模型每次预测计算耗时约为0.003 7s;在t =5时,组合模型平均每次计算耗时约为0.010 8s。实验结果如图8所示。
图8中,指数模型曲线表示由前15个周期建立的初始指数模型,该曲线可以刻画出电池SOH的衰退趋势,但是与实际衰退曲线还是有所差异。图中还包括了校正间隔周期为t =5,t =10,t =15下的实验结果,可以看到,t取值越小,对指数模型参数的修正越频繁,预测曲线对实际曲线的跟随效果越好。在t =5时,除了Cell2电池外,其余电池的估计相对百分比误差基本可以维持在1%以内,具有很高的精度。但是如果在精度要求不那么苛刻的条件下,适当延长t,也能获得不错的预测效果,在t =15时,同样除了Cell2电池效果不好外,其余电池的估计相对百分比误差基本可以维持在3%以内。这表明,在进入“工作期”后,只需每隔15个工作循环周期提取一次特征即可获得不错的预测精度。在实际应用中,可以根据对精度的具体要求,来对间隔周期t灵活选取。在满足精度的前提下,尽可能地增加t的取值,以减少监测设备的工作负担。


图8 组合模型SOH估计结果
Fig.8 SOH estimation results with combined model
表5给出MAE和RMSE的计算结果,计算区间从第16个周期开始。除Cell2与Cell5电池以外,SOH估计的MAE和RMSE均小于0.01。这两块电池之所以实验效果不佳,是因为该电池的退化轨迹发生了突变,特别是Cell5在最后一个周期出现了剧烈突变,而指数模型并没有很好地刻画突变的能力,造成在突变处误差较大的结果。但是观察Cell2的结果图像可知,在SOH发生突变后,只有后续少数几个周期下估计误差较大。在到达实施校正的周期时,指数模型参数会得到更新,进而迅速对实际曲线实现跟随,这表明本文提出的方法具有较好的适应性与鲁棒性。同时由于观测器对模型参数的更新,该方法基本不会对误差造成累计,具有不错的可靠性。
表5 SOH估计误差结果
Tab.5 Results of SOH estimation error

电池Cell1Cell2Cell3Cell4Cell5Cell6Cell7Cell8 MAEt =50.002 60.008 80.002 60.004 90.009 40.004 30.001 60.002 6 t =100.004 30.008 10.004 40.008 10.011 10.006 30.002 10.003 3 t =150.005 30.009 70.006 10.008 10.009 50.004 40.003 10.002 6 RMSEt =50.003 30.019 10.003 50.005 80.035 50.006 40.002 00.003 3 t =100.005 20.013 90.005 40.009 10.035 80.007 80.002 50.004 6 t =150.006 60.014 40.007 20.009 60.035 60.006 50.004 00.003 4
经上述实验检验,组合模型的方法与纯数据驱动方法相比,不仅预测精度没有出现明显的下降,而且节省了特征提取的次数,同时计算耗时大幅度减少,监测设备工作负担也有所减轻。
本文提出一种基于数据驱动与经验模型相结合的在线SOH预测方法。在离线阶段,通过电池容量增量分析,提取与SOH相关性较高的两个电压升片段下所耗的时间dV-dt1与dV-dt2作为外部健康特征,并使用高斯过程回归的方法对电池SOH的衰退进行建模。将在线阶段分为两部分,在“磨合期”通过GPR模型对电池前部分周期的SOH进行预测,利用预测所得数据拟合指数模型,得到指数模型参数的初值;在“工作期”使用指数模型进行SOH预测,并利用观测器每隔固定循环次数对指数模型的参数进行修正。实验结果表明,本文提出的组合模型方法较好地结合了经验模型与数据驱动模型的优点,可以在减轻监测设备负担的前提下,将预测结果保持在较高的精度,比较适合电池组中多电池健康状态同时监测的应用场景。
参考文献
[1] Sarmah S B, Kalita P, Garg A, et al. A review of state of health (SoH) estimation of energy storage systems: challenges and possible solutions for futuristic applications of Li-ion battery packs in electric vehicles[J]. Journal of Electrochemical Energy Conversion and Storage, 2019, 16(4): 040801.
[2] Rahimi-Eichi H, Ojha U, Baronti F, et al. Battery management system: an overview of its application in the smart grid and electric vehicles[J]. IEEE Indu- strial Electronics Magazine, 2013, 7(2): 4-16.
[3] 孙丙香, 任鹏博, 陈育哲, 等. 锂离子电池在不同区间下的衰退影响因素分析及任意区间的老化趋势预测[J]. 电工技术学报, 2021, 36(3): 666-673.
Sun Bingxiang, Ren Pengbo, Chen Yuzhe, et al. Analysis of influencing factors of degradation under different interval stress and prediction of aging trend in any interval for lithium-ion battery[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(3): 666-673.
[4] 焦自权, 范兴明, 张鑫, 等. 基于改进粒子滤波算法的锂离子电池状态跟踪与剩余使用寿命预测方法[J]. 电工技术学报, 2020, 35(18): 3979-3992.
Jiao Ziquan, Fan Xingming, Zhang Xin, et al. State tracking and remaining useful life predictive method of Li-ion battery based on improved particle filter algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3979-3992.
[5] Ng K S, Moo C S, Chen Y P, et al. Enhanced coulomb counting method for estimating state-of- charge and state-of-health of lithium-ion batteries[J]. Applied Energy, 2009, 86(9): 1506-1511.
[6] Love C T, Virji M B V, Rocheleau R E, et al. State-of- health monitoring of 18650 4S packs with a single point impedance diagnostic[J]. Journal of Power Sources, 2014, 266: 512-519.
[7] Galeotti M, Cinà L, Giammanco C, et al. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy[J]. Energy, 2015, 89: 678- 686.
[8] 颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3948.
Yan Xiangwu, Deng Haoran, Guo Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Elec- trotechnical Society, 2019, 34(18): 3937-3948.
[9] Han Xuebing, Ouyang Minggao, Lu Languang, et al. Simplification of physics-based electrochemical model for lithium-ion battery on electric vehicle. part II: pseudo-two-dimensional model simplification and state of charge estimation[J]. Journal of Power Sources, 2015, 278: 802-813.
[10] Han Xuebing, Ouyang Minggao, Lu Languang, et al. A comparative study of commercial lithium ion battery cycle life in electric vehicle: capacity vehicle: capacity loss estimation[J]. Journal of Power Sources, 2014, 268: 658-669.
[11] Qin Wei, Lü Huichun, Liu Chengliang, et al. Remaining useful life prediction for lithium-ion batteries using particle filter and artificial neural network[J]. Industrial Management & Data Systems, 2020, 120(2): 312-328.
[12] 张婷婷, 于明, 李宾, 等. 基于Wavelet降噪和支持向量机的锂离子电池容量预测研究[J]. 电工技术学报, 2020, 35(14): 3126-3136.
Zhang Tingting, Yu Ming, Li Bin, et al. Capacity prediction of lithium-ion batteries based on Wavelet noise reduction and support vector machine[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3126-3136.
[13] Liu Jian, Chen Ziqiang. Remaining useful life prediction of lithium-ion batteries based on health indicator and Gaussian process regression model[J]. IEEE Access, 2019, 7: 39474-39484.
[14] Lin Mingqiang, Zeng Xianping, Wu Ji. State of health estimation of lithium-ion battery based on an adaptive tunable hybrid radial basis function net- work[J]. Journal of Power Source, 2021, 504: 230063.
[15] 韦海燕, 陈孝杰, 吕治强, 等. 灰色神经网络模型在线估算锂离子电池SOH[J]. 电网技术, 2017, 41(12): 4038-4044.
Wei Haiyan, Chen Xiaojie, Lü Zhiqiang, et al. Online estimation of lithium-ion battery state of health using grey neural network[J]. Power System Technology, 2017, 41(12): 4038-4044.
[16] Chang Chun, Wang Qiyue, Jiang Jiuchun, et al. Lithium-ion battery state of health estimation using the incremental capacity and Wavelet neural networks with genetic algorithm[J]. Journal of Energy Storage, 2021, 38: 102570.
[17] Liu Datong, Zhou Jianbao, Liao Haitao, et al. A health indicator extraction and optimization frame- work for lithium-ion battery degradation modeling and prognostics[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2015, 45(6): 915-928.
[18] Guo Peiyao, Cheng Ze, Yang Lei. A data-driven remaining capacity estimation approach for lithium- ion batteries based on charging health feature extraction[J]. Journal of Power Sources, 2019, 412: 442-450.
[19] Tian Jinpeng, Xiong Rui, Shen Weixiang. State-of- health estimation based on differential temperature for lithium ion batteries[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10363-10373.
[20] 李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J]. 电工技术学报, 2020, 35(19): 4106-4119.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(19): 4106-4119.
[21] 周娟, 孙啸, 刘凯, 等. 联合扩展卡尔曼滤波的滑模观测器SOC估算算法研究[J]. 中国电机工程学报, 2021, 41(2): 692-703.
Zhou Juan, Sun Xiao, Liu Kai, et al. Research on the SOC estimation algorithm of combining sliding mode observer with extended Kalman filter[J]. Proceedings of the CSEE, 2021, 41(2): 692-703.
[22] 孙冬, 陈息坤. 基于离散滑模观测器的锂电池荷电状态估计[J]. 中国电机工程学报, 2015, 35(1): 185-191.
Sun Dong, Chen Xikun. Charge state estimation of Li-ion batteries based on discrete-time sliding mode observers[J]. Proceedings of the CSEE, 2015, 35(1): 185-191.
[23] Birkl C R. Diagnosis and prognosis of degradation in lithium-ion batteries[D]. Oxford: University of Oxford, 2017.
[24] He Jiangtao, Wei Zhongbao, Bian Xiaolei, et al. State-of-health estimation of lithium-ion batteries using incremental capacity analysis based on voltage- capacity model[J]. IEEE Transactions on Trans- portation Electrification, 2020, 6(2): 417-426.
[25] 杨胜杰, 罗冰洋, 王菁, 等. 基于容量增量曲线峰值区间特征参数的锂离子电池健康状态估算[J]. 电工技术学报, 2021, 36(11): 2277-2287.
Yang Shengjie, Luo Bingyang, Wang Jing, et al. State of health estimation for lithium-ion batteries based on peak region feature parameters of incremental capacity curve[J]. Transactions of China Electro- technical Society, 2021, 36(11): 2277-2287.
An Online State of Health Prediction Method for Lithium Batteries Based on Combination of Data-Driven and Empirical Model
Abstract The accurate estimation of the state of health (SOH) of lithium-ion batteries is a key technology in battery management system (BMS). This paper presents an online SOH prediction method combined with data-driven and empirical models. Through incremental capacity analysis (ICA), the time spent under two voltage rise segments with high correlation with SOH was identified as the external health factor (HF) of the battery, and a data-driven model of battery aging was established using gaussian process regression (GPR). The data-driven model was used to predict the SOH of the battery in the initial working period, and the exponential empirical model was fitted with the predicted values. Then the SOH of the subsequent cycle was predicted by the exponential model. And the parameters of the exponential model were modified by the observer every fixed number of cycles to ensure the accuracy of SOH prediction. The experimental results show that the proposed method can keep the prediction accuracy at a high level while reducing the burden of battery monitoring equipment.
keywords:Lithium-ion battery, state of health, exponential model, Gaussian process regression, observer
DOI: 10.19595/j.cnki.1000-6753.tces.210385
中图分类号:TM912
国家自然科学基金资助项目(61873180)。
收稿日期 2021-03-22
改稿日期 2021-07-27
王 萍 女,1959年生,教授,博士生导师,研究方向为电能质量、智能检测与控制等。E-mail: pingW@tju.edu.cn
程 泽 男,1959年生,教授,博士生导师,研究方向为现代电力电子技术等。E-mail: chengze@tju.edu.cn(通信作者)
(编辑 崔文静)