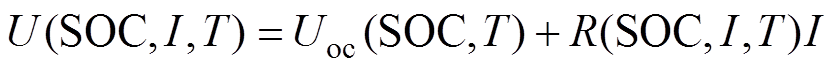（1）工程常用安时积分法[9, 12]描述SOC变化过程，有
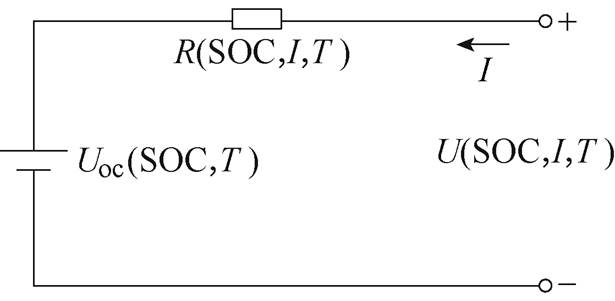
图1 直流内阻模型
Fig.1 DC internal resistance model
摘要 锂离子电池（LiB）的开路电压Uoc和内阻R是对LiB进行特性评估的重要参数。由于两者与LiB的荷电状态（SOC）、电流I及温度T呈非线性耦合关系，难以为工程应用建立一个参数（Uoc, R）相对于这些变量的准确的解析模型。该文提出一种工程性建模方法，旨在建立参数（Uoc, R）与LiB常用恒流工况范围内的变量（SOC, I, T）之间的映射关系。该方法首先在LiB常用工况范围内设计多个恒流工况实验以获取包含变量（SOC, I, T）典型信息的实验数据；其次采用一套数据处理方法解决LiB运行中SOC与T同时变化问题，并测算典型工作点{SOC, I, T}下的（Uoc, R）；最后分析SOC、I、T到Uoc及R的映射关系，并构建开路电压模型Uoc(SOC, T)和内阻模型R(SOC, I, T)。与现有方法相比，该方法建立的模型涉及的工况全面、实验时间短、参数估计精度高，适用于LiB工程应用和特性研究。实验结果验证了该方法的有效性。
关键词：锂离子电池 开路电压模型 内阻模型 温度 荷电状态 电流
锂离子电池（Lithium-ion Battery, LiB）的开路电压和内阻是评估其性能的两个重要参数，工程上可用来评估电极材料[1]、荷电状态（Stage of Charge, SOC）[2-3]、健康状态（Stage of Health, SOH）[4-6]、功率状态（Stage of Power, SOP）[7]、一致性[8]等LiB状态。目前，工程上一般基于图1所示的直流内阻模型[8-12]描述LiB恒流工况，图中，I为工作电流、T为LiB温度、U为电池端电压、Uoc为开路电压、R为电池内阻，并据此模型估计LiB的Uoc和R。Uoc和R与LiB的SOC、I、T的关系[9-15]如图2所示，图中，TA为电池所处的环境温度，DU为R两端的压降，以上各量关系满足
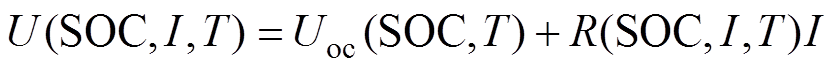（1）工程常用安时积分法[9, 12]描述SOC变化过程，有
图1 直流内阻模型
Fig.1 DC internal resistance model
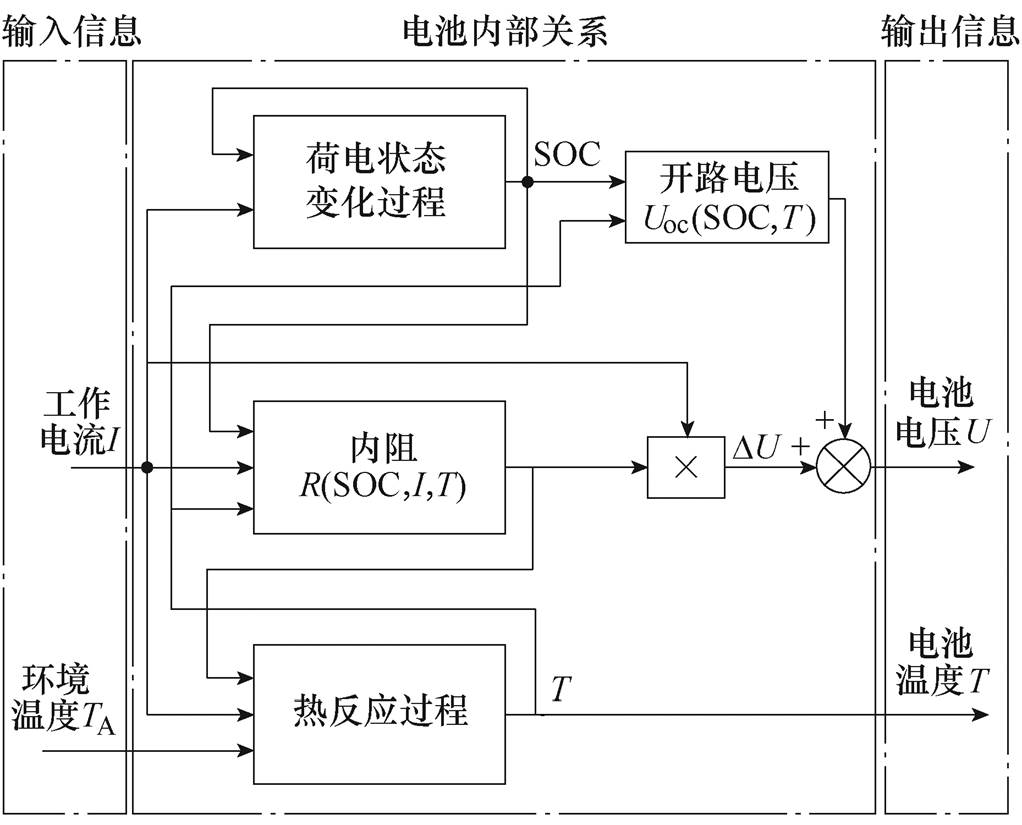
图2 LiB内部各量关系
Fig.2 The internal relationships in LiB
（2）式中，ts、tf分别为起始和终止时刻（h）；Crated为LiB的额定容量（A·h），即以电池厂规定标准方式充入的容量。
本文将SOC、I、T的某个运行状态组合{SOC, I, T}定义为运行工作点，简称工作点（即用“{ }”描述工作点）；此外，用“（）”描述变量名称。文中，Uoc、R为因变量，SOC、I、T为自变量。
由于参数（Uoc, R）与变量（SOC, I, T）呈非线性和耦合（如在LiB运行中SOC和T同时变化）关系，电池运行时不能在工作点准确地辨识参数（Uoc, R），更难以给出Uoc和R相对于（SOC, I, T）的解析模型。而从多数LiB工程应用出发，要求LiB模型应具有以下特征：①模型应能反映LiB的运行/工作的典型路径，也即不同工作点{SOC, I, T}下的LiB特性；②模型具有（SOC, I, T）到Uoc和R的映射关系，也即要给出子模型Uoc(SOC, T)和R(SOC, I, T)，以便基于式（1）进行工程应用。
为辨识参数（Uoc, R），现有测试方法主要有：①电压静置法[2, 16]，仅能辨识Uoc，在工作点{SOC, T}下静置以消除极化过电压，将此时端电压U作为Uoc{SOC, T}，此方法每次仅能获取单个工作点下的Uoc，并且因静置时间长而十分耗时；②电压平均 法[17-18]，仅能辨识Uoc，使用小电流进行充/放电并取电压的平均值作为Uoc，此方法可获得整条的Uoc- SOC曲线，但忽略LiB温升且耗时严重；③电流阶跃测试法[14, 19]，仅能辨识R，基于恒流以及工作点{SOC}下电流阶跃工作点{I1, I2}的实验数据，辨识电流阶跃点（考虑了I对R的影响）下的R-SOC数据，实验耗时随工作点增多而加大，且未解决SOC与T同时变化的问题；④电流脉冲测试法[7, 20-22]，同时辨识Uoc和R，是常见的一种工程方法，在工作点{SOC, T}下进行短时间的静置以使LiB温度等于环境温度，取U作为Uoc，然后施加数十秒的电流脉冲激励，用基于公式的数据拟合辨识R（未考虑I对R的影响），工作点增多将消耗大量实验时间，当SOC或T较低、激励时间长、SOC估计偏差等情况出现时参数辨识误差将变大；⑤未考虑T的恒流实验测试法[10-11]，仅能辨识R，基于多个恒流实验数据，将SOC进行归一化处理，同时获取不同I（考虑了I对R的影响）下的R-SOC数据且缩短实验时间，因其未考虑温升问题而降低辨识精度； ⑥考虑T的恒流实验测试法[9, 12]，同时辨识Uoc和R，基于多个恒流工况实验及数据处理，解决了SOC与T同时变化的问题，并辨识出设定工作点{SOC, I, T}下的Uoc和R，明显缩短了实验时间。
为建立参数解析模型，现有方法主要有：文献[2, 16]用曲线拟合或插值方法仅建立模型Uoc(SOC)，未考虑T到Uoc的映射；文献[17-18]用插值方法仅建立模型Uoc(SOC, T)，但未据Uoc-T特性进行建模；文献[14, 19]仅建立R关于SOC、(I1, I2)的函数，对典型工作点{SOC}下的R(I1, I2)数据进行曲面拟合，并同时对典型工作点{I1, I2}下的R-SOC数据进行曲线拟合，建模所需实验数据多且未考虑T到R的映射；文献[20-22]用曲线拟合或插值方法仅建立模型Uoc(SOC)、R(SOC)，未考虑I、T到Uoc及R的映射；文献[7]基于Arrhenius方程用曲线拟合方法仅建立模型R(T)，未考虑SOC、I到R的映射；文献[11]用曲线拟合方法仅建立模型R(SOC, I)，未考虑T到R的映射；文献[9, 12]仅提出了一种考虑SOC、I、T的开路电压和内阻测试方法，未建立参数模型，无法准确估计典型工作点以外的Uoc和R。
综上所述，迄今仍然缺少一种描述LiB常用恒流工况特性的面向工程的简单实用方法。这里的常用恒流工况，指LiB正常使用时电流范围、温度范围内的恒流工况；特性，指LiB的常用工作路径变量（SOC, I, T）到参数（Uoc, R）的映射关系；简单实用，指采用简单设备、有限实验即可获取该特性。
设计具有该特征方法的一个典型思路是，选取典型工况或工作路径并求取这些路径上变量（SOC, I, T）到参数（Uoc, R）的映射关系，然后据此求得上述映射的完整表达。为此，本文提出一种具有上述特征的工程方法。其要点为：①根据LiB特性及需求，设计多个恒流工况的关键实验并采集数据；②解决LiB运行中SOC与T同时变化问题，估计典型工作点{SOC, I, T}（即对应于实验设定条件）下LiB的U，据电池U-I特性推算典型工作点{SOC, T}下的Uoc，并据式（1）测算典型工作点{SOC, I, T}下的R；③分析SOC、T到Uoc的映射，据此用合适的方式及数据处理方法构建关于SOC、T的解析模型Uoc(SOC, T)；④分析SOC、I、T到R的映射，据此用合适的方式及数据处理方法构建关于SOC、I、T的解析模型R(SOC, I, T)。通过多个恒流工况下的实验，从多方面对比LiB模型的输出效果，验证该方法的合理性、有效性、准确性。相较于其他方法，该方法能够基于有限、关键的实验数据同时获取使用恒流工况范围内任意工作点{SOC, I, T}下的Uoc和R，具有实验时间短、工况全面、参数估计精度高等优势。
本方法四个要点的关系及作用如图3所示。图中，U{SOC, I, T}、Uoc{SOC, T}、R{SOC, I, T}分别表示在工作点{SOC, I, T}下LiB的端电压、开路电压和内阻，其值均为离散值；Uoc(SOC, T)、R(SOC, I, T)分别表示关于变量(SOC, I, T)的连续函数，即参数模型；“开路电压特性”和“内阻特性”分别指Uoc和R相对于各变量（SOC, I, T）的变化规律。LiB恒流工况运行中，因温升和电荷积累而使T与SOC同时变化，无法获取特定工作点{SOC, I, T}下的端电压数据，难以进一步测算Uoc{SOC, T}及R{SOC, I, T}，故需先解决此问题；而模型Uoc(SOC, T)及R(SOC, I, T)为涉及多个变量的函数，采用何种解析式及如何构造是本方法需要解决的重点问题。以下按图示顺序说明各部分内容。
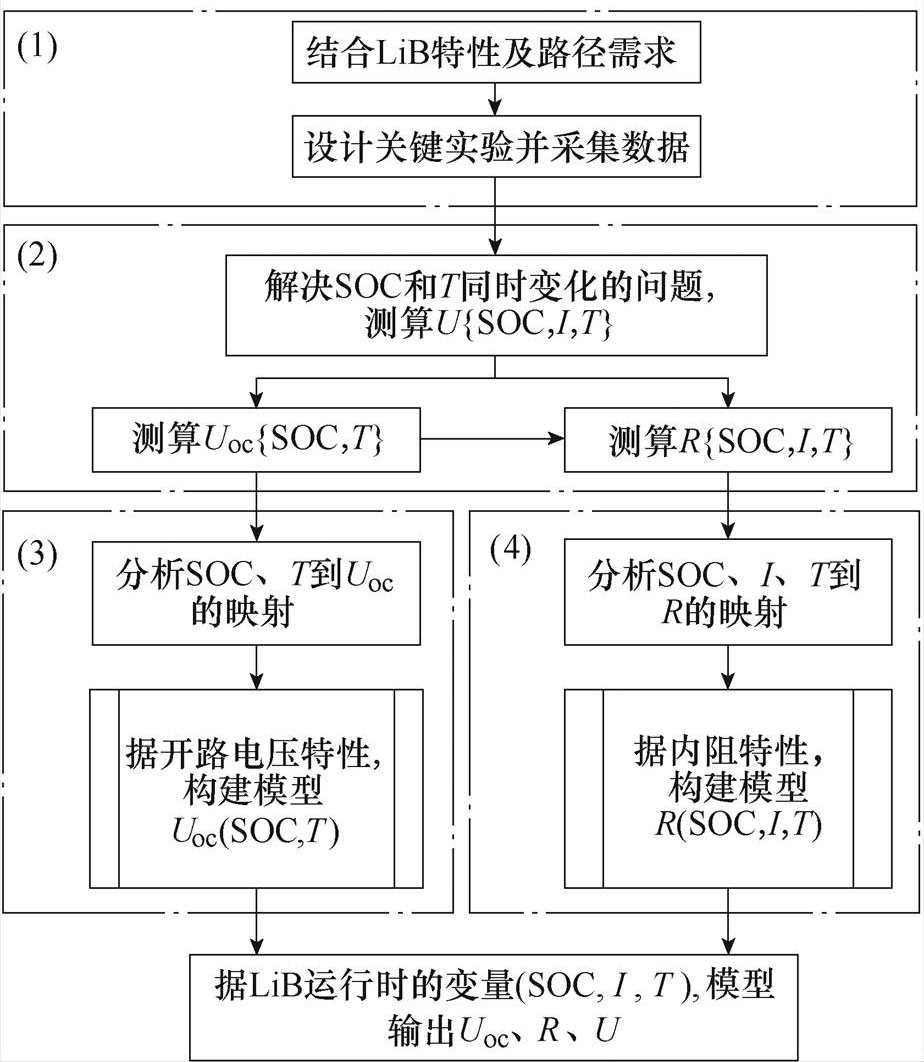
图3 方法的构架、要点以及关系
Fig.3 Configuration and key-points of the method
结合LiB特性及运行/工作路径需求，设计有限、充足的关键实验，以减少实验时间。SOC与U、Uoc及R的映射关系呈非线性[9-11, 16-22]，实验设计应密集选取工作点{SOC}以减少非线性误差；T到U、Uoc及R的映射呈非线性且单调[7, 9, 12, 15]，实验设计可分散选取运行温度范围内的环境温度工作点{TA}；I到U及R的映射也呈单调性[9-12]，且U和R对电流I的敏感程度波动不大，故实验设计可均匀分散覆盖工作点{I}。
因此，本方法分别在m个环境温度条件下进行n个恒流工况实验（本文仅以充电工况为例，放电工况类似，不再赘述），可获取运行中SOC变化范围内的全部实验数据并减少实验时间，实验设定取值为
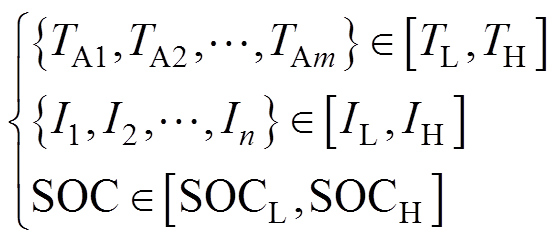（3）式中，“[ ]”为变量取值闭区间；各变量的下标L、H分别为最小值和最大值，其值应在电池厂规定范围内；下标m、n为离散变量序号，据常用工况设定m、n的数量及分布，且相应变量值随序号递增。
实验具体步骤如下：
（1）步骤E1：设计实验环境温度为{TA1, TA2, …, TAm}、工作电流为{I1, I2, …, In}；定义Tref为参考温度，其值结合电池厂要求设定；将LiB近似为一个质点（不考虑其三维空间温度场），因无法在其内部植入温度传感器，故用正极温度近似代表电池温度，即在LiB正极放置一个热电偶[23]以采集LiB温度T。
（2）步骤E2：设置环境温度为Tref，静置1h以使LiB的物理化学状态达到稳态[12]，此时，LiB内外温度近似相等[23]（即T=Tref），然后用标准电流I0对LiB进行放电，直至U达到放电截止电压UDend（此值由电池厂规定），定义此时SOC=0，以保障每次充电开始时LiB的初始状态一致。
（3）步骤E3：设置环境温度
∈{TA1, TA2, …, TAm}（上标*代表具体工作点），静置1h以使T=，然后设置I*∈{I1, I2, …, In}，对LiB进行恒流充电，当U达到充电截止电压UCend（此值由电池厂规定）时，充电过程结束。
（4）步骤E4：遍历∀I∈{I1, I2, …, In}，重复步骤E2和步骤E3，完成环境温度下的所有充电实验，即共进行n个恒流工况实验。
（5）步骤E5：遍历∀TA∈{TA1, TA2, …, TAm}，重复步骤E4，完成所有{I, TA}下的充电实验，即共进行m×n个恒流工况实验并全程采集运行时间t、TA、T、I、U等实验数据，将实验设定条件的组合{SOC, I, T}定义为LiB的典型工作点。
据式（1）可知，在任意工作点{SOC*, T*}下，当电流无限小时，可近似认为LiB的U=Uoc，然而这会增加大量实验时间。本文采用求极限的方法测算开路电压，该方法可减小LiB的电压滞回现象对U预测的影响[23]，有
（4）式中，U(SOC*, I, T*)为工作点{SOC*, T*}下U-I函数（I为自变量，U为因变量）。
在恒流工况运行中，T与SOC同时变化，无法通过实验获取工作点{SOC*, T*}下的U-I数据，故不能基于式（4）测算Uoc{SOC*, T*}。因U-T存在单调函数关系[12, 15]，故本方法用数据处理的方法解决此问题（此过程在本文被称为“电压的测算”）。
电压的测算及开路电压建模详细步骤如下：
（1）步骤U1：基于I*∈{I1, I2, …, In}、SOC*∈[SOCL, SOCH]下的实验数据，可用曲线拟合方法获得工作点{SOC*, I*}下的U-T函数U(SOC*, I*, T)，有
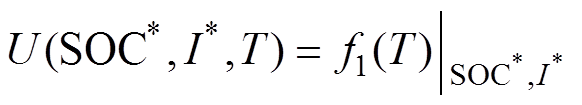（5）式中，f1(T)为关于T的多项式，其次数依数据特点及需要而定，因任何函数式按级数展开后均可近似为多项式，故采用特定次数的多项式近似表示某种函数是合理、可行的工程方法。
（2）步骤U2：据式（5），分别估计∀T∈{TA1, TA2, …, TAm}时{SOC*, I*}下U{SOC*, I*, T}。
（3）步骤U3：遍历∀SOC∈[SOCL, SOCH]，重复步骤U1和步骤U2，可获取工作点{I*}下任意U{SOC, I*, T}数据，即估计出“LiB恒温恒流”时的U-SOC曲线。
（4）步骤U4：遍历∀I∈{I1, I2, …, In}，重复步骤U3，可获取∀SOC∈[SOCL, SOCH]、∀I∈{I1, I2, …, In}、∀T={TA1, TA2, …, TAm}（即典型工作点）下的U{SOC, I, T}，即解决了T与SOC同时变化的问题，并获取U测算数据。
（5）步骤U5：基于任意工作点{SOC*, T*}下的U-I数据，用曲线拟合方法获取U-I函数U(SOC*, I, T*)，有
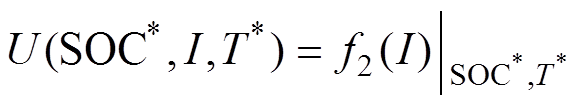（6）式中，f2(I)为关于I的多项式，其次数依数据特点及需要而定。
（6）步骤U6：据式（6），求取I=0处的U，即可近似测算{SOC*, T*}下的Uoc{SOC*, T*}，有
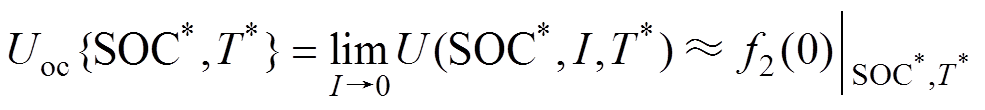（7）（7）步骤U7：遍历∀SOC∈[SOCL, SOCH]、∀T∈{TA1, TA2, …, TAm}，重复步骤U5和步骤U6，可测算典型工作点{SOC, T}下的Uoc{SOC, T}，即获取m条不同T下的Uoc-SOC曲线，其中，SOC为[SOCL, SOCH]范围内的任意值，T仅为m个离散值，Uoc也仅为典型工作点下的离散值，将其作为开路电压建模工作的原始数据。
（8）步骤U8：用控制变量法分别分析SOC、T到Uoc的映射，获取开路电压特性，据此开展建模工作。
（9）步骤U9：基于SOC*∈[SOCL, SOCH]下的Uoc-T数据，因Uoc-T是单调函数且变化率不大[15, 24]，可用曲线拟合方法构建工作点{SOC*}下的Uoc-T函数Uoc(SOC*, T)，有
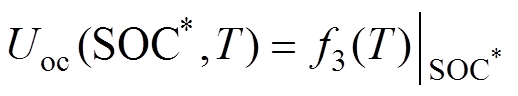（8）式中，f3(T)为q次多项式，q值据Uoc-T特性及需要选定，以近似SOC、T对Uoc的非线性关系，即
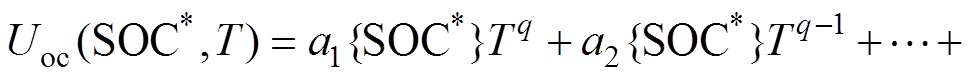
（9）式中，ai{SOC*}（i=1, 2, …, q, q+1）为f3(T)的拟合系数，其值与工作点{SOC*}有关。
（10）步骤U10：遍历∀SOC∈[SOCL, SOCH]，重复步骤U9，可获取任意工作点{SOC}下的系数ai，此时ai为关于变量SOC的离散值。
（11）步骤U11：分别对ai-SOC进行曲线拟合或插值运算，即可获得系数函数a1(SOC)、a2(SOC)、…、aq(SOC)、aq+1(SOC)，因在[SOCL, SOCH]范围内的原始数据较多，故各系数函数能在式（9）中准确反映SOC到Uoc的映射。
（12）步骤U12：将各系数函数回归式（9），则完成模型Uoc(SOC, T)的构建，该模型可表示变量（SOC, T）到Uoc的映射。有
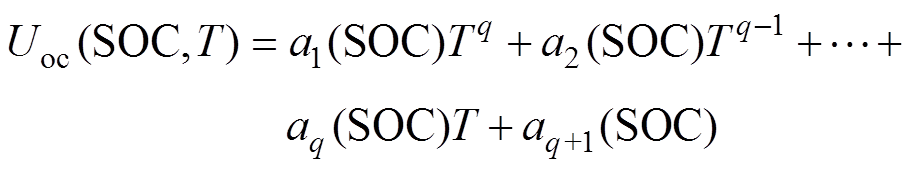（10）式中，SOC、T均为连续变量。据式（10）可估计LiB使用范围[SOCL, SOCH]、[TA1, TAm]内任意工作点{SOC, T}下的Uoc。
1.3.1 内阻的测算
为有效、准确、全面地描述SOC、I、T到R的映射，内阻建模需要充足的原始数据，故仅依靠实验则需要消耗大量的时间。因LiB的U-I呈单调关系，在典型工作点{SOC, T}下基于式（6）可获取∀I∈[I1, In]时的U(I)数据，故可用U-I数据处理的方式减少恒流工况实验数量，即获取实验设定以外的电流所对应的电压数据，从而进一步减少实验 时间。
基于1.2节方法，获取∀SOC∈[SOCL, SOCH]、∀I∈[I1, In]、∀T={TA1, TA2, …, TAm}下的U{SOC, I, T}和Uoc{SOC, T}数据，可据式（11）测算典型工作点{SOC, I, T}下的R{SOC, I, T}（此过程在本文被称为“内阻的测算”），该数据作为构建内阻解析模型的原始数据。
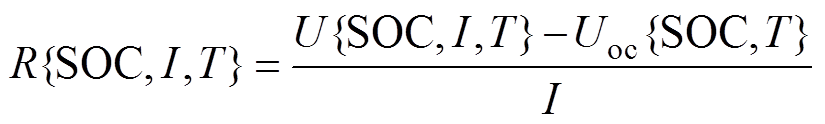（11）1.3.2 内阻建模
内阻建模的重点是构建R关于SOC、I、T的连续变化模型R(SOC, I, T)，以使其在LiB使用范围[SOCL, SOCH]、[I1, In]、[TA1, TAm]内准确估计任意工作点{SOC, I, T}下的内阻R。
内阻建模具体步骤如下：
（1）步骤R1：采用控制变量法分别分析SOC、I、T到R的映射，获取内阻特性，据此开展建模工作。
（2）步骤R2：由于Butler-Volmer方程表明R-T关系单调递减[15, 7]，基于SOC*∈[SOCL, SOCH]、I*∈[I1, In]时的R-T数据，可用曲线拟合构建工作点{SOC*, I*}下的R-T函数R(SOC*, I*, T)，有
（12）式中，g(T)为k次多项式，k值根据R-T特性及需要选定，以近似SOC、I、T对R的非线性关系，即
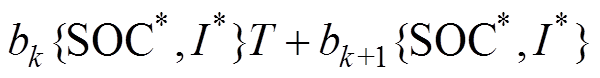（13）式中，bj{SOC*, I*}（j=1, 2, …, k, k+1）为g(T)的拟合系数，其值与工作点{SOC*, I*}有关。
（3）步骤R3：遍历∀SOC∈[SOCL, SOCH]、∀I∈[I1, In]，重复步骤R2，可获取典型工作点{SOC, I}下的系数bj{SOC, I}，其中，bj为关于SOC、I的离散值。
（4）步骤R4：分别对各系数数据bj{SOC, I}进行曲面拟合或插值运算（bj为因变量，SOC、I为自变量），即可获得系数函数b1(SOC, I)、b2(SOC, I)、…、bk(SOC, I)、bk+1(SOC, I)。
（5）步骤R5：将各系数函数回归式（13），则构建了内阻模型R(SOC, I, T)，该模型可表示变量（SOC, I, T）到R的映射。有
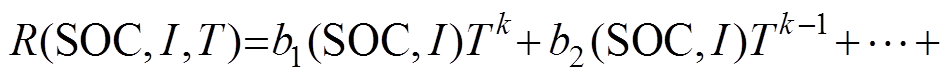
（14）
综上，本节用数据拟合构建了R-T函数式，并将SOC、I对R的定量影响体现于该式的系数，因[SOCL, SOCH]和[I1, In]范围内内阻原始数据（即测算数据）较多，故步骤R5中的各系数函数能够在式（14）中准确反映SOC、I到R的映射。
本节给出了一个磷酸铁锂电池的建模实例，并对建模结果进行讨论，以说明该建模方法的准确性。
LiB具体参数见表1，实验设备包括充放电测试仪以及恒温箱，测试条件见表2。
表1 LiB参数
Tab.1 LiB parameters
参 数数 值(型号) LiBHX1865130AF 电极材料LiFePO4/Graphite 额定容量/(A·h)10 最大充电电流/A10（1C） 最大持续放电电流/A20（2C）
注：C代表C率，即对于该电池1C=10A。
本节以正常使用温度范围（15～45℃）内电池恒流工况为例，描述本方法的实施过程，温度设定值采用等间距设定。
表2 测试条件
Tab.2 Test conditions
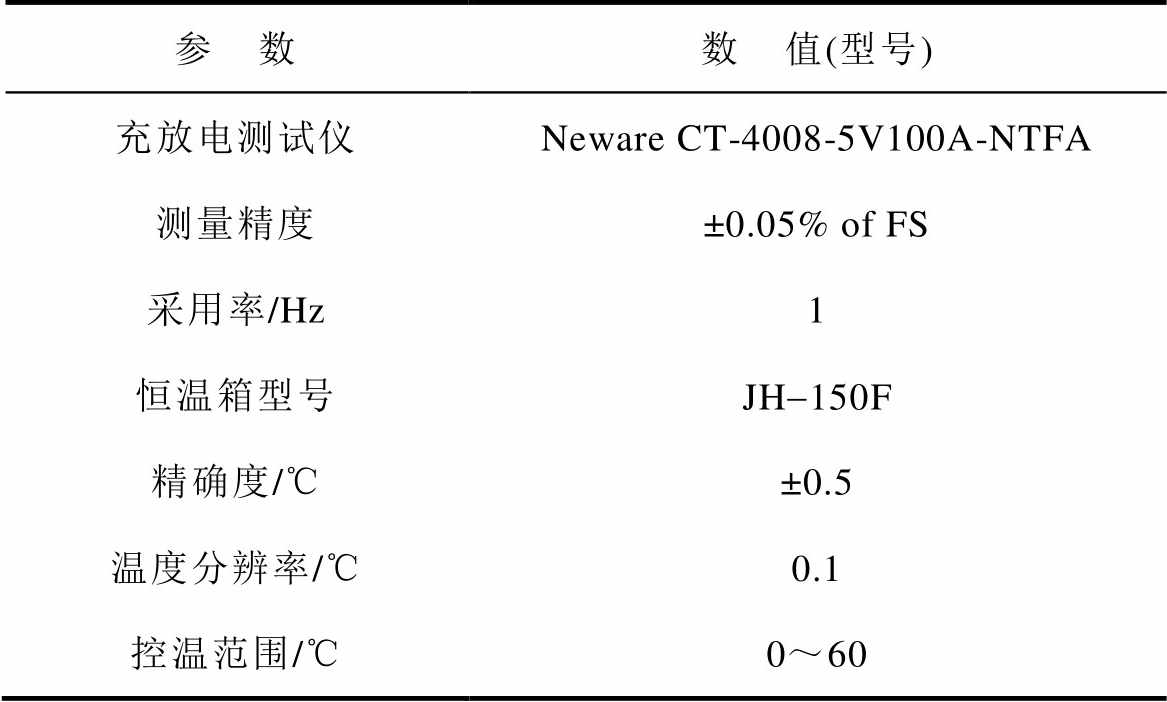
参 数数 值(型号) 充放电测试仪Neware CT-4008-5V100A-NTFA 测量精度±0.05% of FS 采用率/Hz1 恒温箱型号JH-150F 精确度/℃±0.5 温度分辨率/℃0.1 控温范围/℃0～60
结合LiB参数和测试条件，实验设定取值为
说明：①在本节，工作点{SOC, I, T}表述中会出现具体数值及单位，其中，SOC为荷电状态，无量纲；I为工作电流（C）；T为LiB温度（℃）；②温度范围为[TA1, TAm]=[15℃, 45℃]，电流范围为[I1, In]= [0.2C, 1.0C]；③在任意温度下，经计算所有电流下的SOC均能达到94%以上，故本实例中选定SOC范围为[SOCL, SOCH]=[0, 0.94]；④实验实施过程按照1.1小节所述实验具体步骤开展。
LiB运行中，T与SOC同时发生变化，且电流越大造成的LiB温升越大，进而影响U越明显。此外，因工业用恒温箱的控制精度误差以及箱内温度的差异，很难保证电池所处的实验环境温度被精确地控制在设定温度值，故需要采用数据处理的办法解决LiB温升以及环境温度控制不准确等问题。基于∀SOC∈[0, 0.94]、∀I∈{0.2C
0.2C1.0C}下的U-T数据和式（5），可在任意工作点{SOC, I}下拟合得到U-T关系（本实例f1(T)选取3次多项式）。
图4仅以工作点{SOC=0.1, I=0.6C}下的U-T数据为例，说明该数据处理过程以及拟合结果，其中，“原始电压”为实际测量的LiB端电压，“测算电压”为式（5）的测算电压。结果说明，U-T确实存在单调函数关系且拟合效果好（拟合系数R-square为0.999 5），据式（5）估计∀T∈{15℃5℃45℃}下U(T)。遍历∀SOC∈[0, 0.94]、∀I∈{0.2C0.2C1.0C}，可测得任意典型工作点{SOC, I, T}下的U。
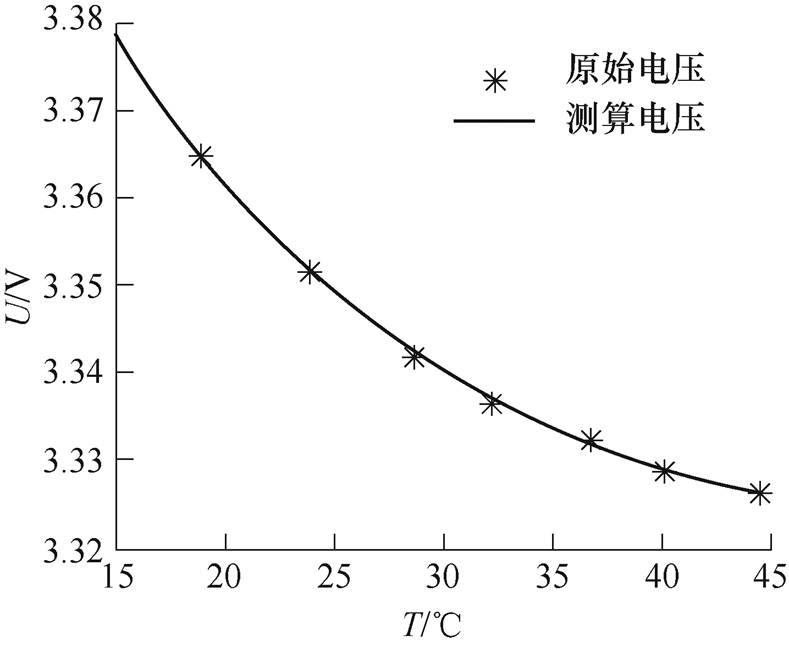
图4 U-T测算结果
Fig.4 U-T calculation results
图5仅以TA=20℃、I∈{0.2C, 0.6C, 1.0C}时的测算电压曲线为例，展示采用上述方法后获取“LiB恒温恒流”时的U-SOC曲线，如图中“测算”所示；图中“原始”表示实验中实测的包含了温升影响的电池端电压。
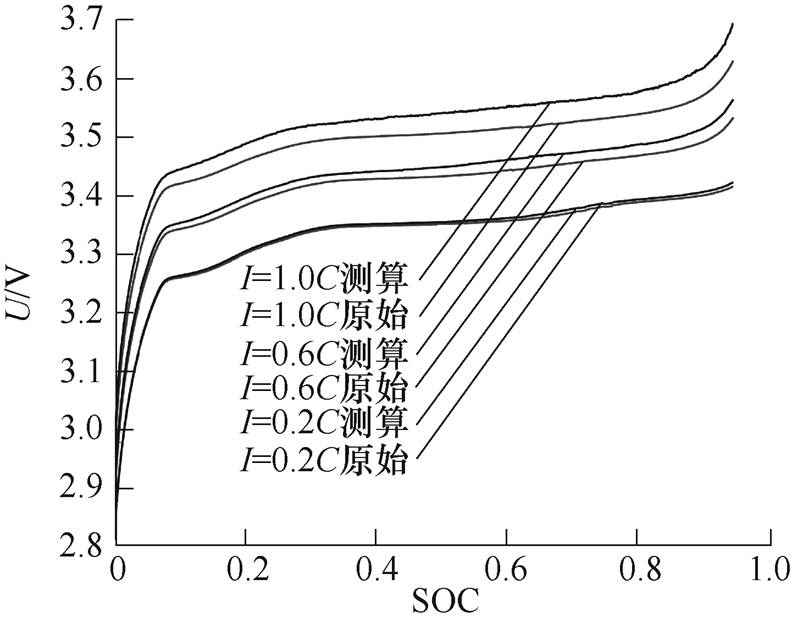
图5 原始电压与测算电压对比
Fig.5 The comparison of original and calculated voltage
图5表明电流越大，原始电压与测算电压差值越大，这是因为大电流造成R上的电压差较大，以及产生更大的LiB温升而使电压差值进一步增加，故采用式（5）对原始电压进行测算是合理且必要的，这样可以解决T与SOC同时发生变化的问题，为开路电压和内阻的测算提供准确的电压数据。
基于任意工作点{SOC, T}下的U-I数据，本实例选f2(I)为2次多项式对U-I数据进行曲线拟合，获取Uoc{SOC, T}。为了说明本文方法测算的开路电压的准确性，本节采用工程上常用的混合功率脉冲特性（Hybrid Pulse Power Characteristics, HPPC）方法获取开路电压（具体获取过程请参考文献[10, 12, 23]，将其结果作为真值），并将其与本文方法测算的开路电压进行对比，结果如图6所示。图6仅以电池温度为25℃条件下的开路电压数据为例进行展示，其中，“HPPC方法”表示HPPC方法获取的开路电压，“本文方法”表示采用本文方法测算的开路电压。结果表明，本文方法的相对误差低于5‰。若此误差在允许范围内，则可用本文方法替代传统开路电压的测试方法，以避免搁置时间，进而减少实验时间及快速测算内阻。由文献[12]可知，若想进一步减少开路电压测算误差，可以给本文方法测算开路电压的结果加上一个修正系数。
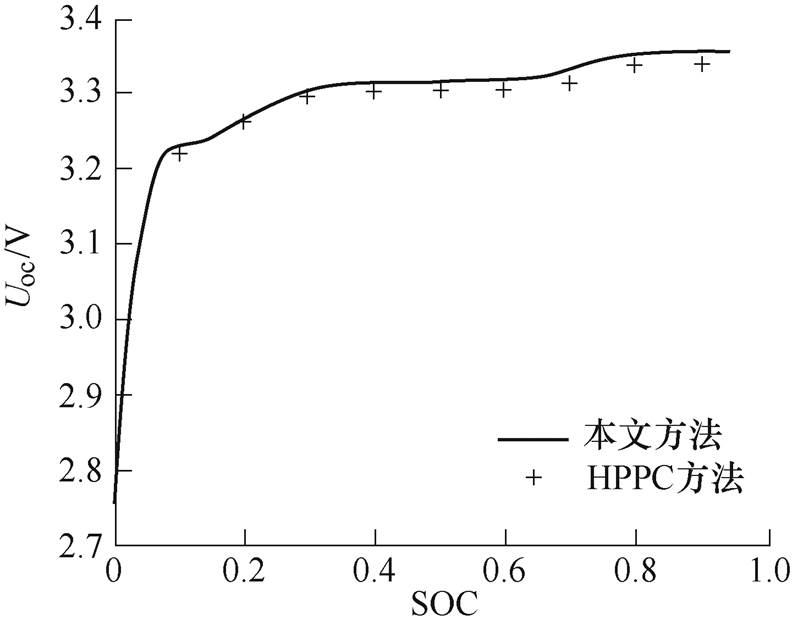
图6 开路电压对比
Fig.6 The comparison of open circuit voltage
基于开路电压测算数据及建模方法，本实例选用f3(T)为3次多项式对Uoc-T数据进行拟合（R- square均为1），并且f3(T)的系数函数a1(SOC)、a2(SOC)、a3(SOC)、a4(SOC)采用插值的办法获取，即得到开路电压与SOC的映射关系。模型Uoc(SOC, T)为
（15）系数函数ai(SOC)（i=1, 2, 3, 4）如图7所示。
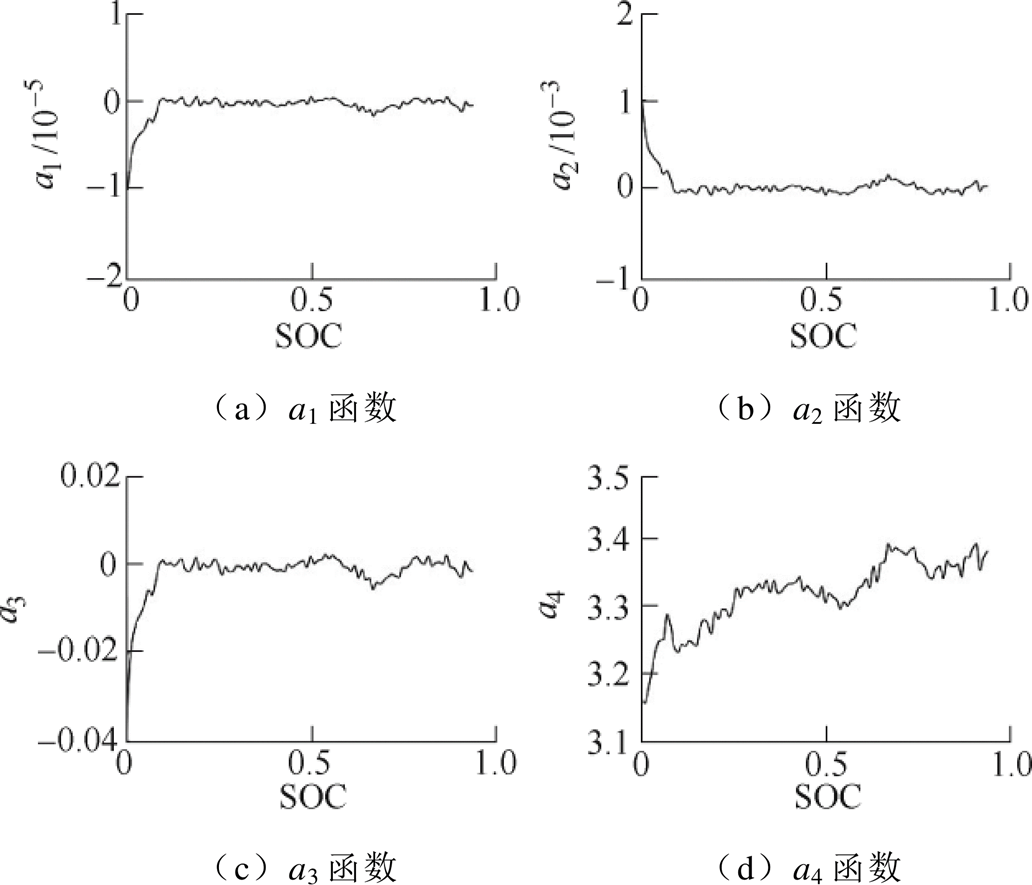
图7 系数函数ai(SOC)
Fig.7 The coefficient function of ai(SOC)
为了验证式（15）能准确地描述变量（SOC, T）到Uoc的映射关系，将模型结果与原始数据进行了对比，如图8所示。图中，“
”为开路电压原始数据（即Uoc测算数据，其为构建开路电压解析模型的真值），“曲面”为模型Uoc(SOC, T)输出数据。图8表明，在任意工作点{SOC}下，Uoc-T变化率较小[24]，采用3次多项式足以精确地描述Uoc-T函数关系，且本文所用SOC范围内的数据量充足，系数函数ai(SOC)也能够描述Uoc-SOC函数关系。
图8 模型Uoc(SOC, T)
Fig.8 The graph of Uoc(SOC, T)
为了在不额外增加实验的同时扩大内阻建模的数据量，以提高内阻建模中R-I估计精度，本实例基于任意工作点{SOC, T}下的U-I数据，用式（6）对U-I数据进行曲线拟合（R-square均为0.999 5以上），可获取∀I∈[0.2C, 1.0C]范围内U-I数据，本实例仅以获取∀I∈{0.2C0.1C1.0C}为例进行说明。
基于LiB的U{SOC, I, T}和Uoc{SOC, T}数据，用式（11）可测算
下的R{SOC, I, T}，这些均为内阻离散数值。据此，在任意工作点{SOC, I}下，本实例据式（12）选g(T)为3次多项式对R-T数据进行拟合，图9仅以工作点{SOC=0.1, I=0.6C}下的R-T数据为例，描述该数据处理过程以及拟合结果，其中，“原始内阻”为内阻原始数据（即R测算数据，其为构建内阻解析模型的真值），“估计内阻”为拟合后的模型R(T)曲线。结果说明，R-T确实存在单调函数关系且拟合效果好（R-square为1），此时R(T)能准确描述R-T关系。此过程与2.2节U-T数据处理的过程类似（见图4），其原因是U-R满足式（1），并且Uoc相对T的变化率较小，故U-T关系与R-T关系本应一致。
图9 R-T拟合结果
Fig.9 R-T fitting result
遍历∀SOC∈[0, 0.94]、∀I∈{0.2C0.2C1.0C}后可获取相应工作点{SOC, I}下g(T)的系数bj{SOC, I}（j=1, 2, 3, 4），用曲面插值方法求取各系数函数bj(SOC, I)，并将其回归式（14），则获得内阻模型R(SOC, I, T)为
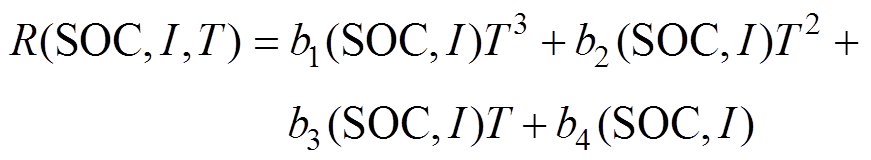（16）系数函数bj(SOC, I)如图10所示。
图10 系数函数bj(SOC, I)
Fig.10 The coefficient function of bj(SOC, I)
为了验证式（16）能准确、完整地描述变量（SOC, I, T）到R的映射关系，图11～图13分别给出不同视域时的模型R(SOC, I, T)结果，并将其结果与原始数据对比，图中，“
”为内阻原始数据，“曲面”为模型R(SOC, I, T)输出数据。图11仅以SOC分别为0.1、0.6时为例，展示模型R(I, T)。图12仅以I分别为0.4C、0.8C时为例，展示模型R(SOC, T)。图13仅以T分别为20℃、40℃时为例，展示模型R(SOC, I)。
图11～图13仅以特定视域时为例展示内阻模型的结果及其反映原始数据的效果，其他视域时类似，不再赘述，故由图11～图13可知：
（1）当工作点{SOC, I}固定时，R-T呈非线性关系且单调递减，故用3次多项式g(T)对R-T进行数据拟合（R-square均为1）可准确描述内阻关于温度的变化规律。
（2）当工作点{I, T}固定时，R-SOC呈非线性波动变化关系，且在SOC∈[0.6, 0.7]范围内，内阻具有明显上凸波形（由LiB机理决定，本文不作讨论），本方法将SOC对R的映射体现在g(T)的系数中，且选取的工作点{SOC}数据较多并用插值方法构建，该数据处理过程具有一定的合理、有效性，能够描述R-SOC之间的非线性关系。
（3）当工作点{SOC, T}固定时，R-I呈近似单调关系，在SOC
[0.6, 0.7]且T较高时，R-I基本为定值，但在SOC∈[0.6, 0.7]且温度T较低时，R-I具有一定的非线性波动性，由数据可知，I对R的影响比SOC或T的影响小，故内阻建模过程中将I对R的映射体现在g(T)的系数中，也同样具有一定的合理性。
图11 SOC=定值时模型R(I, T)
Fig.11 The graphof R(I, T) at SOC=Const
图12 I=定值时模型R(SOC, T)
Fig.12 The graphof R(SOC, T) at I=Const
图13 T=定值时模型R(SOC, I)
Fig.13 The graphof R(SOC, I) at T=Const
综上所述，本内阻建模方法能够在LiB使用范围（SOC∈[SOCL, SOCH]、I∈[I1, In]、T=[TA1, TAm]）内完整、详细、准确地描述变量（SOC, I, T）到R的映射，而无需额外增加实验时间。
为说明本文建模方法能够在计及SOC、I、T的综合影响后客观、准确地估计LiB的开路电压、内阻及端电压，实验验证部分需要在多个环境温度TA、电流I下分别验证R-SOC、端电压U-SOC曲线的模型输出效果。由于在运行过程中LiB温度T在环境温度TA的基础上实时变化，故本节采用Bernardi模型[23, 25-26]作为LiB的热模型，用以实时估计T，有
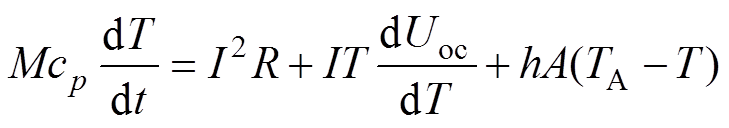（17）式中，M为电池质量（kg）；cp为比定压热容[J/(kg·℃)]；h为热传递系数[W/(m2·℃)]；A为电池表面积（m2）。
因本文篇幅所限及主题所需，Bernardi模型的参数辨识等方面的内容不再展开叙述，具体辨识过程请参照文献[23, 26]。将Bernardi模型估计的T引入模型Uoc(SOC, T)及R(SOC, I, T)，即式（15）和式（16），进而根据变量（SOC, I, T）的实时值估计LiB的Uoc、R及U。
本节所述的“LiB模型”包括构建的开路电压模型、内阻模型、Bernardi模型，本节假设Bernardi模型能够准确估计T，由其造成的误差计入实验误差内。
鉴于篇幅限制，结合建模实例的实施条件，本节仅以TA∈{23℃, 36℃}、I∈{0.3C, 0.5C, 0.8C}条件下的实验结果为例，对本文构建的LiB模型进行综合验证，包括内阻验证和电压验证。
2.4.1 内阻验证与分析
图14、图15分别展示了当TA=23℃、36℃时，I分别为0.3C、0.5C、0.8C时的R-SOC曲线，其中，实测内阻为据LiB的实际端电压测算的内阻（其中测算所需Uoc(SOC, T)为LiB运行中开路电压模型输出值，前提假设其能准确反映真值）；仿真内阻为本文建模实例中LiB模型的输出内阻；实测内阻和仿真内阻中的R-SOC曲线均包含LiB温升的影响。为表明本LiB模型能够根据LiB的实时温度估计内阻，本节以假定运行过程中LiB温度恒定（即T=TA）时的模型输出内阻作为对比，在图中称之为对比 内阻。
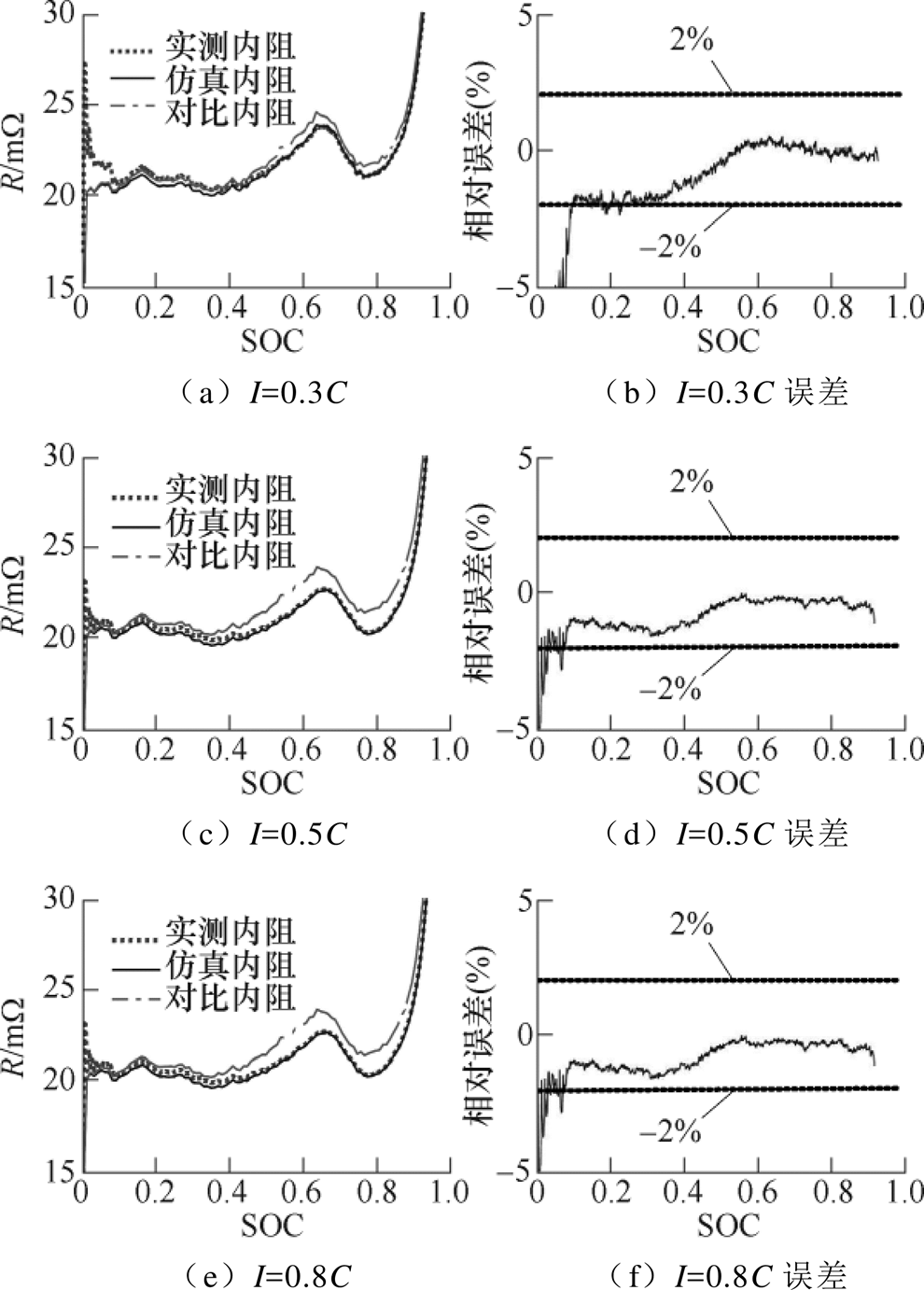
图14 对内阻的验证（TA=23℃）
Fig.14 R verification result at TA=23℃
图15 对内阻的验证（TA=36℃）
Fig.15 R verification result at TA=36℃
由图14和图15可知：
（1）在SOC＜0.1时，磷酸铁锂电池的电压上升率较大，SOC、I的非线性影响更加突出，故内阻估计误差相对较大。
（2）除个别数据外，不同电流下的模型输出内阻相对误差均低于2%。
（3）环境温度越高，模型输出内阻精度越高，其原因是开路电压和内阻随LiB温度升高而对温度敏感度降低。
（4）在SOC∈[0.6, 0.7]且温度T较低时，虽然R-I具有一定的非线性波动性（2.3节已说明），但本方法也可准确地估计内阻。
（5）对比内阻表明LiB运行过程中温升对Uoc及R确实存在较大影响，且环境温度越低、电流越大，该影响越大，而模型Uoc(SOC, T)及模型R(SOC, I, T)根据实时变量值可准确估计LiB参数。
2.4.2 电压验证与分析
为更加直观地验证本文建模方法，本节用LiB的端电压验证模型的准确性。据式（1）可知，在恒流工况下若Uoc和R估计准确，则U必然准确。
图16～图21分别展示了当TA=23℃、36℃时，I分别为0.3C、0.5C、0.8C时LiB的U-SOC曲线，其中，实测电压为LiB实际测量的端电压；仿真电压为LiB模型的输出电压；本节同样以假定运行过程中LiB温度恒定（即T=TA）时的模型输出电压作为对比，在图中称之为对比电压。
图16 TA=23℃、I=0.3C时电压验证结果
Fig.16 Voltage verification result at TA=23℃, I=0.3C
图17 TA=23℃、I=0.5C时电压验证结果
Fig.17 Voltage verification result at TA=23℃, I=0.5C
图18 TA=23℃、I=0.8C时电压验证结果
Fig.18 Voltage verification result at TA=23℃, I=0.8C
图19 TA=36℃、I=0.3C时电压验证结果
Fig.19 Voltage verification result at TA=36℃, I=0.3C
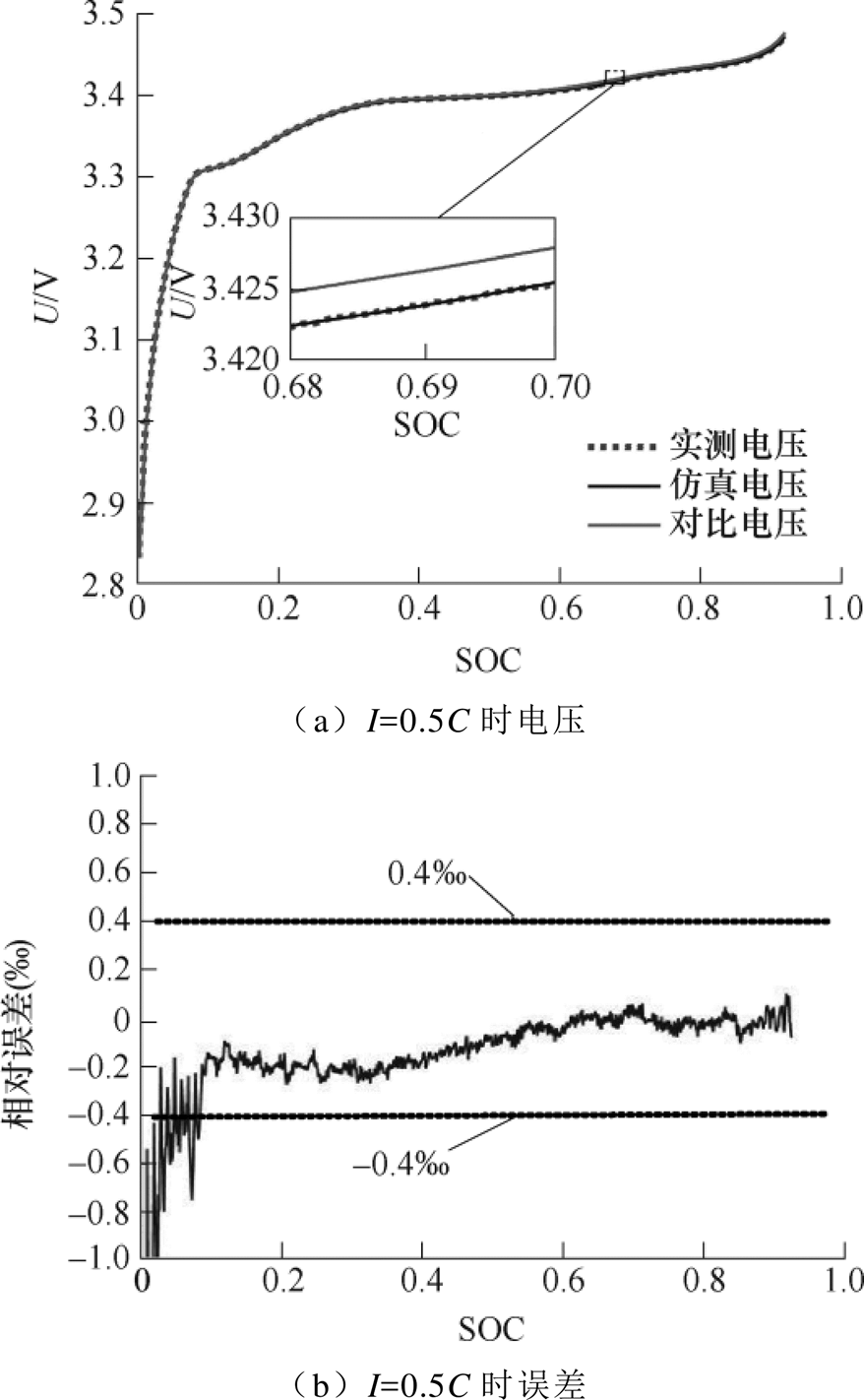
图20 TA=36℃、I=0.5C时电压验证结果
Fig.20 Voltage verification result at TA=36℃, I=0.5C
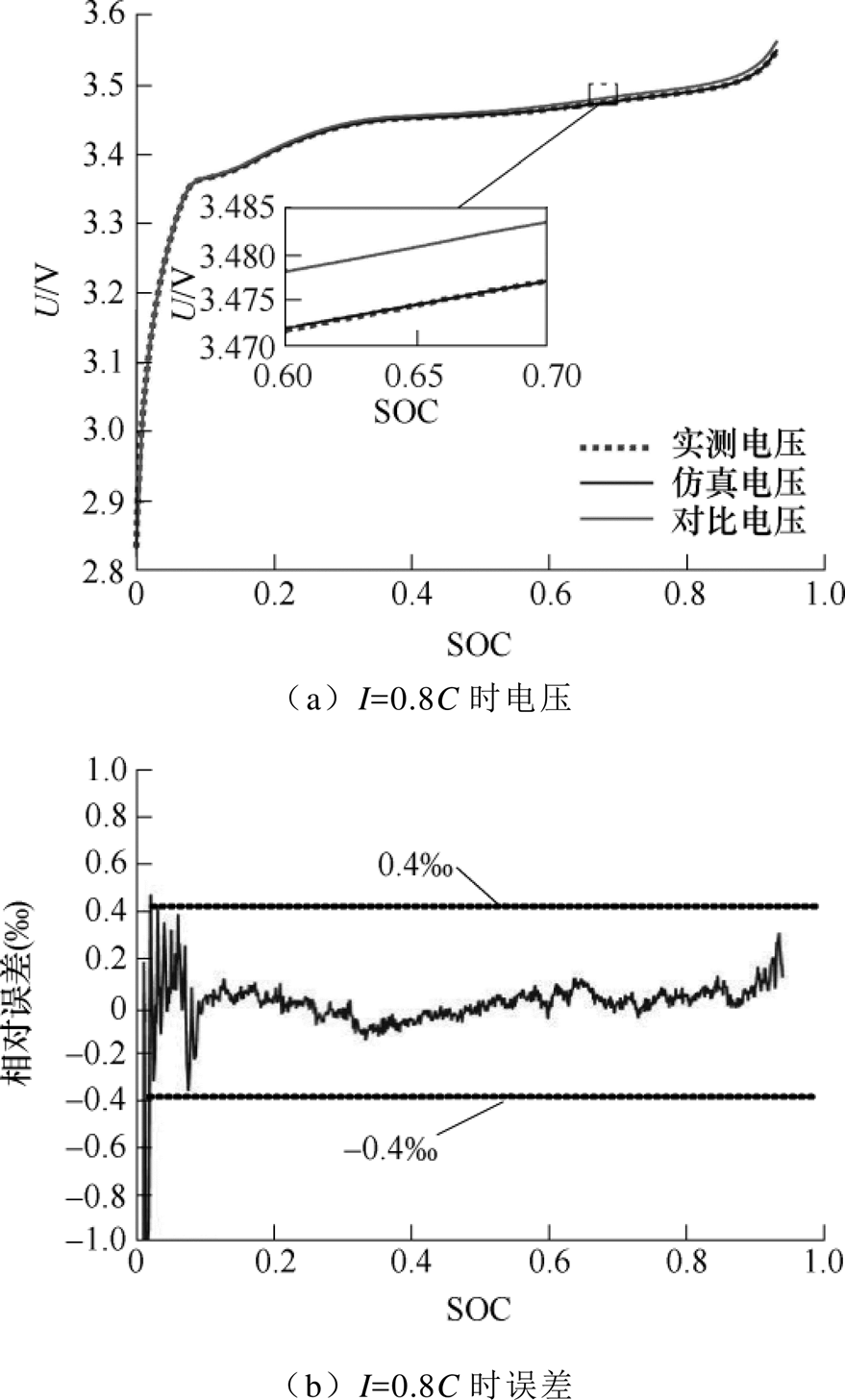
图21 TA=36℃、I=0.8C时电压验证结果
Fig.21 Voltage verification result at TA=36℃, I=0.8C
由图16～图21可知，在SOC＜0.1时，磷酸铁锂电池的电压上升率较大；除个别数据外，模型输出电压相对误差均低于0.4‰；LiB温度越高，模型输出电压精度越高；对比电压表明，LiB运行过程中温升对电压确实存在影响，其根本原因是温升影响了开路电压和内阻，进而影响了LiB端电压。以上现象的原因与内阻验证部分一致。
鉴于文献[12]与本文均采用“考虑T的恒流实验测试法”，该测试方法相比较其他测试方法的优势已详述[12]，本文不再赘述。与文献[12]方法相比，本方法主要优势：①实验时间更短，文献[12]仅是一种基于实验数据的“测试方法”，其无法准确估计实验测试工作点以外的Uoc和R，其所需实验数量及时间随着工作点递增，而本方法属于“建模方法”，所需实验时间固定，不再额外增加；②参数估计精度高，文献[12]对磷酸铁锂电池的端电压估计精度低于1.7‰（电流为3.6A），而本方法估计精度低于0.4‰（电流为8A），实验对象为同类型LiB，本实例所用电流大而误差反而小，故说明本方法参数估计精度更高。
本文提出的LiB建模方法由两个内容组成：①考虑LiB运行/工作路径的有限关键实验设计；②一套准确描述参数（Uoc, R）与变量（SOC, I, T）之间映射关系的数据处理方法。
本方法的特征为：①基于多个恒流工况实验及数据处理，获取了同时包含变量（SOC, I, T）等信息的实验数据，解决了SOC和T同时变化以及对参数的非线性影响问题；②通过数据拟合，新增了测算R所需的U(I)数据，减少了实验时间；③将变量（SOC, I, T）到Uoc及R的映射关系以解析模型的形式进行定量描述，可准确、全面、实时估计工作范围内任意Uoc及R；④无需特殊设备，数据处理过程简单易行。因此，与其他方法相比，本方法主要优势为：①实验时间短；②可获取详细和全面的模型Uoc(SOC, T)及R(SOC, I, T)；③参数估计精度高，内阻估计误差低于2%，端电压估计误差低于0.4‰。
参考文献
[1] Ven A D, Bhattacharya J, Belak A A. Under- standing Li diffusion in Li-intercalation com- pounds[J]. Accounts of Chemical Research, 2013, 46(5): 1216-1225.
[2] Yang Jufeng, Huang Wenxin, Xia Bing, et al. The improved open-circuit voltage characterization test using active polarization voltage reduction method[J]. Applied Energy, 2019, 237: 682-694.
[3] Ovejas V J, Cuadras A. State of charge dependency of the overvoltage generated in commercial Li-ion cells[J]. Journal of Power Sources, 2019, 418: 176- 185.
[4] 石琼林, 郭东旭, 杨耕, 等. 具有磷酸铁锂电池负极特征的SOC区间的确定方法[J]. 电工技术学报, 2020, 35(19): 4097-4105.
Shi Qionglin, Guo Dongxu, Yang Geng, et al. A method to determine characteristic region of negative electrode with state of charge for lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4097-4105.
[5] 韩乔妮, 姜帆, 程泽. 变温度下IHF-IGPR框架的锂离子电池健康状态预测方法[J]. 电工技术学报, 2021, 36(17): 3705-3720.
Han Qiaoni, Jiang Fan, Cheng Ze. State of health estimation for lithium-ion batteries based on the framework of IHF-IGPR under variable temper- ature[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3705-3720.
[6] 孙丙香, 刘佳, 韩智强, 等. 不同区间衰退路径下锂离子电池的性能相关性及温度适用性分析[J]. 电工技术学报, 2020, 35(9): 2063-2073.
Sun Bingxiang, Liu Jia, Han Zhiqiang, et al. Performance correlation and temperature appli- cability of Li-ion batteries under different range degradation paths[J]. Transactions of China Electro- technical Society, 2020, 35(9): 2063-2073.
[7] 刘新天, 何耀, 曾国建, 等. 考虑温度影响的锂电池功率状态估计[J]. 电工技术学报, 2016, 31(13): 155-163.
Liu Xintian, He Yao, Zeng Guojian, et al. State- of-power estimation for Li-ion battery considering the effect of temperature[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 155-163.
[8] 王帅, 尹忠东, 郑重, 等. 电池模组一致性影响因素在放电电压曲线簇上的表征[J]. 电工技术学报, 2020, 35(8): 1836-1847.
Wang Shuai, Yin Zhongdong, Zheng Zhong, et al. Representation of influence factors for battery module consistency on discharge voltage curves[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1836-1847.
[9] Chen Yingjie, Yang Geng, Liu Xu, et al. A time-efficient and accurate open circuit voltage estimation method for lithium-ion batteries[J]. Energies, 2019, 12(9): 1803.
[10] 何志超, 杨耕, 卢兰光, 等. 基于恒流外特性和SOC的电池直流内阻测试方法[J]. 清华大学学报(自然科学版), 2015, 55(5): 532-537.
He Zhichao, Yang Geng, Lu Languang, et al. Battery DC internal resistance test method based on the constant current external characteristics and SOC[J]. Journal of Tsinghua University (Science & Techno- logy), 2015, 55(5): 532-537.
[11] 刘伟, 吴海桑, 何志超, 等. 一种均衡考虑锂电池内部能量损耗和充电速度的多段恒流充电方法[J]. 电工技术学报, 2017, 32(9): 112-120.
Liu Wei, Wu Haisang, He Zhichao, et al. A multi- stage current charging method for Li-ion battery considering balance of internal consumption and charging speed[J]. Transactions of China Electro- technical Society, 2017, 32(9): 112-120.
[12] 陈英杰, 杨耕, 祖海鹏, 等. 基于恒流实验的锂离子电池开路电压与内阻估计方法[J]. 电工技术学报, 2018, 33(17): 3976-3988.
Chen Yingjie, Yang Geng, Zu Haipeng, et al. An open circuit voltage and internal resistance estimation method of lithium-ion batteries with constant current tests[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3976-3988.
[13] 庞辉, 郭龙, 武龙星, 等. 考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算[J]. 电工技术学报, 2021, 36(10): 2178-2189.
Pang Hui, Guo Long, Wu Longxing, et al. An improved dual polarization model of Li-ion battery and its state of charge estimation considering ambient temperature[J]. Transactions of China Electro- technical Society, 2021, 36(10): 2178-2189.
[14] He Zhichao, Yang Geng, Lu Languang. A parameter identification method for dynamics of lithium iron phosphate batteries based on step-change current curves and constant current curves[J]. Energies, 2016, 9(6): 444.
[15] Bard A J, Faulkner L R. Electrochemical methods: fundamentals and applications[M]. New York: Wiley, 1980.
[16] Farmann A, Sauer D U. A study on the dependency of the open-circuit voltage on temperature and actual aging state of lithium-ion batteries[J]. Journal of Power Sources, 2017, 347: 1-13.
[17] Xing Yinjiao, He Wei, Pecht M, et al. State of charge estimation of lithium-ion batteries using the open- circuit voltage at various ambient temperatures[J]. Applied Energy, 2014, 113: 106-115.
[18] Zheng Fangdan, Xing Yinjiao, Jiang Jiuchun, et al. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries[J]. Applied Energy, 2016, 183: 513-525.
[19] 何志超, 杨耕, 卢兰光, 等. 一种动力电池动态特性建模[J]. 电工技术学报, 2016, 31(11): 194- 203.
He Zhichao, Yang Geng, Lu Languang, et al. A modeling method for power battery dynamics[J]. Transactions of China Electrotechnical Society, 2016, 31(11): 194-203.
[20] 潘海鸿, 张沫, 王惠民, 等. 基于多影响因素建立锂离子电池充电内阻的动态模型[J]. 电工技术学报, 2021, 36(10): 2199-2206.
Pan Haihong, Zhang Mo, Wang Huimin, et al. Establishing a dynamic model of lithium-ion battery charging internal resistance based on multiple factors[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2199-2206.
[21] Waag W, Käbitz S, Sauer D U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application[J]. Applied Energy, 2013, 102: 885-897.
[22] 颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3948.
Yan Xiangwu, Deng Haoran, Guo Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Electro- technical Society, 2019, 34(18): 3937-3948.
[23] 陈英杰, 杨耕, 刘旭. 恒流环境下锂离子电池热参数估计[J]. 电机与控制学报, 2019, 23(6): 1-9.
Chen Yingjie, Yang Geng, Liu Xu. Thermal para- meters estimation of lithium-ion batteries under constant current conditions[J]. Electric Machines & Control, 2019, 23(6): 1-9.
[24] Pattipati B, Balasingam B, Avvari G V, et al. Open circuit voltage characterization of lithium-ion batteries[J]. Journal of Power Sources, 2014, 269: 317-333.
[25] Bernardi D, Pawlikowski E, Newman J. A general energy balance for battery systems[J]. Journal of the Electrochemical Society, 1984, 132(1): 5-12.
[26] Hariharan K S. A coupled nonlinear equivalent circuit-thermal model for lithium ion cells[J]. Journal of Power Sources, 2013, 227: 171-176.
Modeling Method of Lithium-Ion Battery Considering Commonly Used Constant Current Conditions
Abstract The open circuit voltage Uoc and internal resistance R of Lithium-ion battery (LiB) are important parameters for the feature evaluation of LiB. Because Uoc and R are in non-linear and coupling relationships with the state of charge (SOC), current I and temperature T ofaLiB, it is difficult to formulate an accurate mathematical model of the parameters (Uoc, R) relative to the variables for engineering applications. This paper proposes an engineering modeling method to establish a mapping relationship between the parameters (Uoc, R) and the variables (SOC, I, T) of LiB in the concerned application range. This method firstly designed multiple constant-current experiments within the range of LiB common operating conditions, and obtained experimental data containing typical information of variables (SOC, I, T). Secondly, a designed data process was used to solve the SOC simultaneous change problem with the temperature T during operation and calculate (Uoc, R) under the typical operating points {SOC, I, T}. Finally, the method gave the mapping of SOC, I, T to (Uoc, R), and then established the Uoc model and R model, respectively. Compared with existed models, this model involves comprehensive working conditions, short experiment time and better parameter estimation accuracy, which is suitable for LiB engineering applications and characteristics research. The experimental results verify the effectiveness of the method.
keywords：Lithium-ion battery, open circuit voltage model, internal resistance model, temperature, state of charge (SOC), current
DOI: 10.19595/j.cnki.1000-6753.tces.210297
中图分类号：TM911
国家重点研发计划（2016YFB0900302）、沧州师范学院校内科研基金（xnjjl1917）和沧州市重点研发计划指导（192103005）资助项目。
收稿日期 2021-03-11
改稿日期 2021-08-23
刘 伟 男，1990年生，讲师，研究方向为动力电池管理系统。E-mail: liuw0214@sina.com（通信作者）
杨 耕 男，1957年生，教授，博士生导师，研究方向为电力电子系统、可再生能源系统以及微电网的控制、动力电池的老化模型。E-mail: yanggeng@tsinghua.edu.cn
（编辑 崔文静）