 ,将决策树作为基分类器[17],有
,将决策树作为基分类器[17],有摘要 行驶工况下电动汽车锂离子电池剩余使用寿命(RUL)衰退情况复杂,准确的RUL预测可为电池的定期维护和安全稳定运行提供指导,避免安全隐患。为此,该文提出一种适用于行驶工况下电动汽车电池的RUL预测方法。首先,针对行驶工况,提出一种基于轻量型梯度提升机(LightGBM)的RUL预测模型,利用元学习超参数优化方法对其进行超参数调优;其次,搭建行驶工况下电池全生命周期容量测试系统,模拟行驶工况下电池所受振动应力、充放电应力环境和测试电池容量衰退情况;然后,基于动态时间规整对容量衰退的相似性分析结果,使用生成对抗网络(GAN)生成新的容量序列;最后,通过实验数据验证所提模型和生成容量序列的有效性。
关键词:电动汽车 行驶工况 锂离子电池 剩余使用寿命 轻量型梯度提升机
现如今的电池市场上,动力电池主要包括铅酸电池、镍氢电池和锂离子电池等。其中,锂离子电池因其在能量密度、循环寿命、自放电率、充放电性能、工作温度范围等性能方面的优良表现,在电动汽车(Electric Vehicle, EV)或者混合电动汽车(Hybrid Electric Vehicle, HEV)等领域得到广泛应用[1]。然而,随着锂离子电池循环充放电次数的增加,电池内部的电化学反应加剧,除了锂离子脱嵌发生的氧化还原反应外,还存在许多的副反应,如电解液分解、活性物质溶解、金属锂沉积等,这些副反应导致电池容量衰减[2]。在电动汽车实际行驶工况下,电池的工作环境和性能衰退情况复杂,电池剩余使用寿命(Remaining Useful Life, RUL)的准确预测可为电池的定期维护和安全稳定运行提供指导[3]。
电池剩余使用寿命是电池可用容量衰减至标准容量的70%~80%(电池服役结束)前所经历的充放电循环次数。目前,国内外学者和企业已对电池RUL预测方法展开研究[4],如基于模型驱动的粒子滤波[5]、卡尔曼滤波[6]、退化机理模型[7]、经验老化模型[8-9];基于数据驱动的支持向量机[10-11]、支持向量回归[12]、神经网络[13]、高斯回归[14]、蒙特卡洛模拟[15]和极限梯度提升(eXtreme Gradient Boosting, XGBoost)[16]等。基于模型驱动的预测效果取决于电池模型,但电池模型无法完全反映内部复杂的电化学动态特性,在一定程度上影响预测效果。基于数据驱动的预测方法可以摆脱对电池模型的依赖性,提升泛化能力。
在基于模型驱动的RUL预测方面,文献[5]应用粒子滤波算法将不可观测的状态量与物理模型相结合进行RUL预测,考虑预测的不确定性;文献[6]应用卡尔曼滤波算法观测电池状态,预测剩余使用寿命,但以上两种预测方法均未能考虑可变负载工况。文献[7]探究不同温度应力下电池容量退化规律,构建电池退化机理模型进行RUL预测;文献[8-9]分别利用电池全生命周期测试数据和电化学交流阻抗谱构建电池经验退化模型,完成RUL预测,以上两种预测模型均能考虑电池性能衰减和老化的关键因素,但这两种预测方法需要庞大的计算量和复杂的物理模型。
基于数据驱动的RUL预测方面,文献[11-12]分别利用支持向量机(Support Vector Machine, SVM)和支持向量回归(Support Vector Regression, SVR)等相关向量机算法解决RUL预测过程中的非线性数据处理和时间序列预测问题,但未能考虑充放电应力和外界因素等应力条件。文献[13]利用非线性自回归神经网络,通过捕捉电压下降趋势和电压分线性变化对RUL进行预测;文献[14]基于高斯回归模型,结合模糊理论,解决RUL预测中的不确定性问题;文献[15]利用蒙特卡洛模拟算法,避免设计老化试验的困难,但上述三种预测方法均需要大量历史数据。文献[16]从放电曲线提取特征值,利用XGBoost算法构建电池状态非线性模型,但XGBoost采用的是传统的Boosting集成学习方式,即需要在预测时多次遍历整个训练集,选取最佳的分割点,效率较低。
综上所述,基于模型驱动的预测方法受限于庞大的计算量和复杂的物理模型,难以满足复杂工况下RUL预测的需求。基于数据驱动的预测方法能够摆脱对模型的依赖,有效应对非线性数据,在时间序列预测方面有较好表现。但是,现有预测方法在预测时需遍历整个训练集,计算效率较低,内存消耗较大。在不牺牲速度的前提下,为充分利用数据,轻量型梯度提升机(Light Gradient Boosting Machine, LightGBM)[17]和随机森林(Random Forest, RF)采用Bagging集成学习方式,能够提升训练效率,降低时间复杂度,通过直方图优化、单边梯度采样(Gradient-based One-Side Sampling, GOSS)、互斥稀疏特征绑定(Exclusive Feature Bundling, EFB),以及深度限制的按叶子生长(leaf-wise)方式,可降低样本和特征维度,减小内存使用率,进一步降低时间复杂度。
因此,为准确预测行驶工况下电池剩余使用寿命,本文基于LightGBM回归模型,构建行驶工况下电池RUL预测模型,采用元学习超参数优化方法(Hyper-parameter optimization, Hyperopt)对预测模型进行超参数调优,减轻人工调参负担。本文利用行驶工况下电池全生命周期容量测试数据,从容量回弹处预测效果、时间复杂度、内存使用率和预测准确度等方面评估预测效果,验证所建RUL预测模型的有效性。最后,本文通过LightGBM模型验证生成对抗网络(Generative Adversarial Networks, GAN)生成的容量序列的可行性,以期减少实验周期,节约实验成本。
LightGBM实际是基于梯度提升决策树(Gradient Boosting Decision Tree, GBDT)的集成回归树近似最终模型 ,将决策树作为基分类器[17],有
,将决策树作为基分类器[17],有
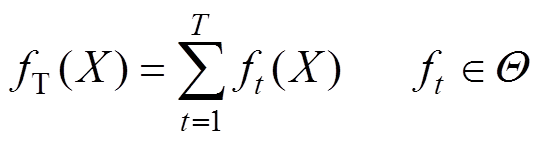 (1)
(1)式中,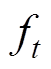 为第t棵决策树;
为第t棵决策树; 为所有树的集合空间。
为所有树的集合空间。
LightGBM使用决策树来得到一个从输入空间Xs到梯度空间G的映射函数。假设有一个数据量为n的训练集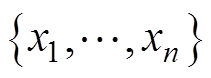 ,其中,xi为空间xs中第i个维度为s的向量。
,其中,xi为空间xs中第i个维度为s的向量。
构造损失函数 ,其中,
,其中,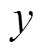 为输出,
为输出, 为估计函数。找到使得损失函数期望最小的函数
为估计函数。找到使得损失函数期望最小的函数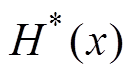 ,有
,有
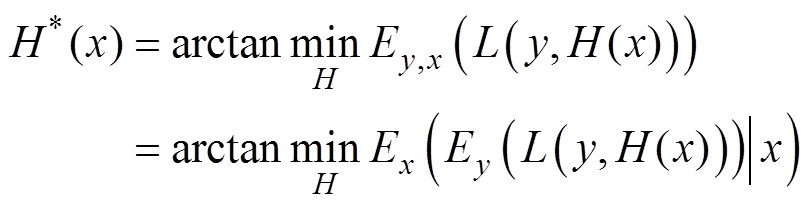 (2)
(2)每次梯度提升迭代中,当前模型损失函数负梯度输出值为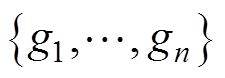 ,其中,
,其中, 为
为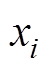 对应的损失函数负梯度在当前模型输出的值。弱学习器在信息增益最大的特征分裂点处进行分割,而信息增益通过分裂后方差度量。
对应的损失函数负梯度在当前模型输出的值。弱学习器在信息增益最大的特征分裂点处进行分割,而信息增益通过分裂后方差度量。
设O为基模型一个固定节点内的数据集。此节点j处特征在分割点d的方差增益定义为
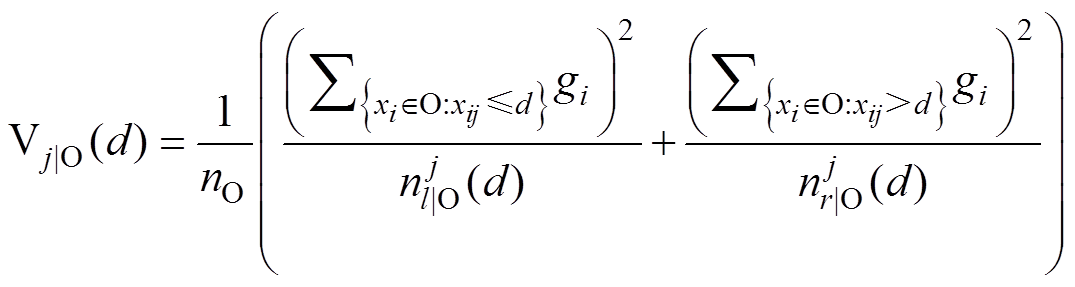 (3)
(3)式中,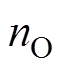 为某个固定叶子节点的训练集样本数,且
为某个固定叶子节点的训练集样本数,且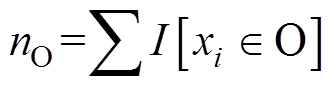 ;
;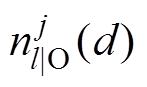 为第
为第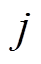 个特征中值小于等于
个特征中值小于等于 的样本数,且
的样本数,且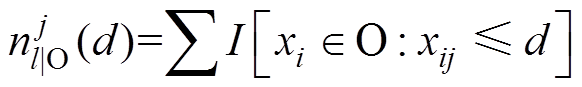 ;
; 为第
为第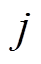 个特征中值大于
个特征中值大于 的样本数,且
的样本数,且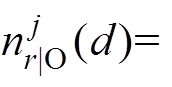
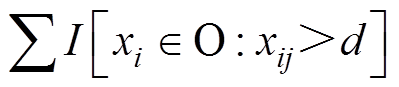 。
。
遍历每个特征的每个分裂点,找到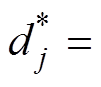
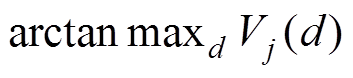 ,计算对应的最大信息增益
,计算对应的最大信息增益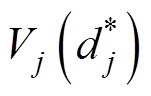 ,根据分裂点
,根据分裂点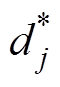 将数据分为左右子节点。
将数据分为左右子节点。
LightGBM和XGBoost是基于GBDT的框架进行优化发展而来的,本文对三者进行比较,其区别见表1。
表1 LightGBM与GBDT和XGBoost对比情况
Tab.1 Comparison between LightGBM and GBDT with XGBoost

算法GBDTXGBoostLightGBM 损失函数一阶导数一阶导数二阶导数一阶导数二阶导数 基分类器分类回归树基于预排序的分类回归树基于直方图的分类回归树 分裂方式遍历全部数据按层生长按叶生长 数据处理负梯度划分预排序GOSS和EFB 学习方式BoostingBoostingBagging 内存使用率迭代次数*#data2*#data*#features*4Bytes#data*#features*1Bytes 计算时间迭代次数*#data#data*#featuresk*#bin*#features
LightGBM所采用的直方图优化策略是一种数据离散化处理方法,其基本思想:针对每一维特征,将连续的浮点型数据划分进离散的k个范围内,得到k个“桶”(bin),构造一个宽度为k的直方图,如图1所示。遍历数据时,在直方图的每个“bin”中对作为索引的离散值进行累积。遍历一次数据后,得到每个“bin”内的累积量。由此,在寻找决策树最优分割点时,无需对特征值进行逐个对比,从而大大减少运算量,提高训练速度。此外,针对含有噪声的数据(真实值附近存在小范围内波动),如果模型拥有较强的逼近能力,将会学习到这些波动,以至于出现过拟合现象。应用直方图优化策略,处于一定区间内每维特征会被划分进同一个“bin”,从而获得同样的索引,因此,可以显著改善噪声引起的过拟合现象。
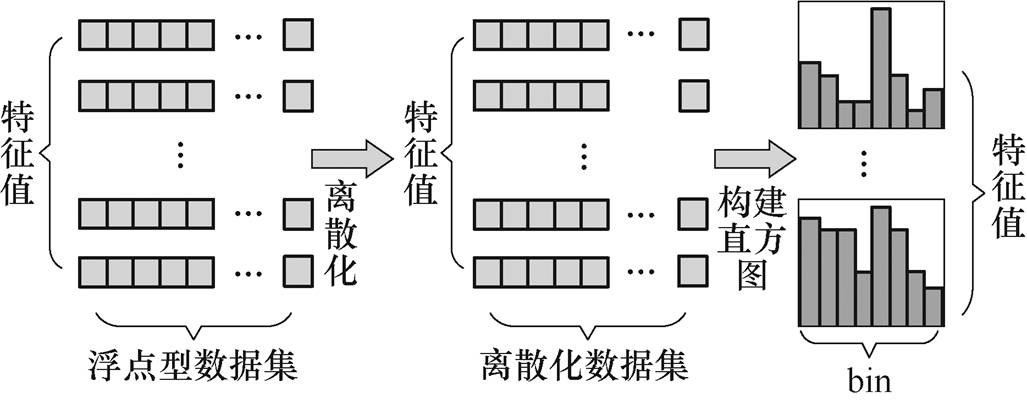
图1 直方图优化方式示意图
Fig.1 Schematic diagram of histogram optimization
原始的GBDT采用“损失函数的负梯度近似等于残差”的处理方式,与LightGBM的Bagging相比,其他基于Boosting方式的树模型算法在每一次构建决策树时,采用随机采样策略抽取一定数量的样本参与决策树的构建,进行梯度更新。而LightGBM算法采用梯度单边采样策略,有针对性地将梯度较大的样本用于构建决策树,同时将随机采样梯度较小的样本进行放大后也用于构建决策树,从而保证样本的数据分布的完整性。
GOSS处理流程如图2所示。
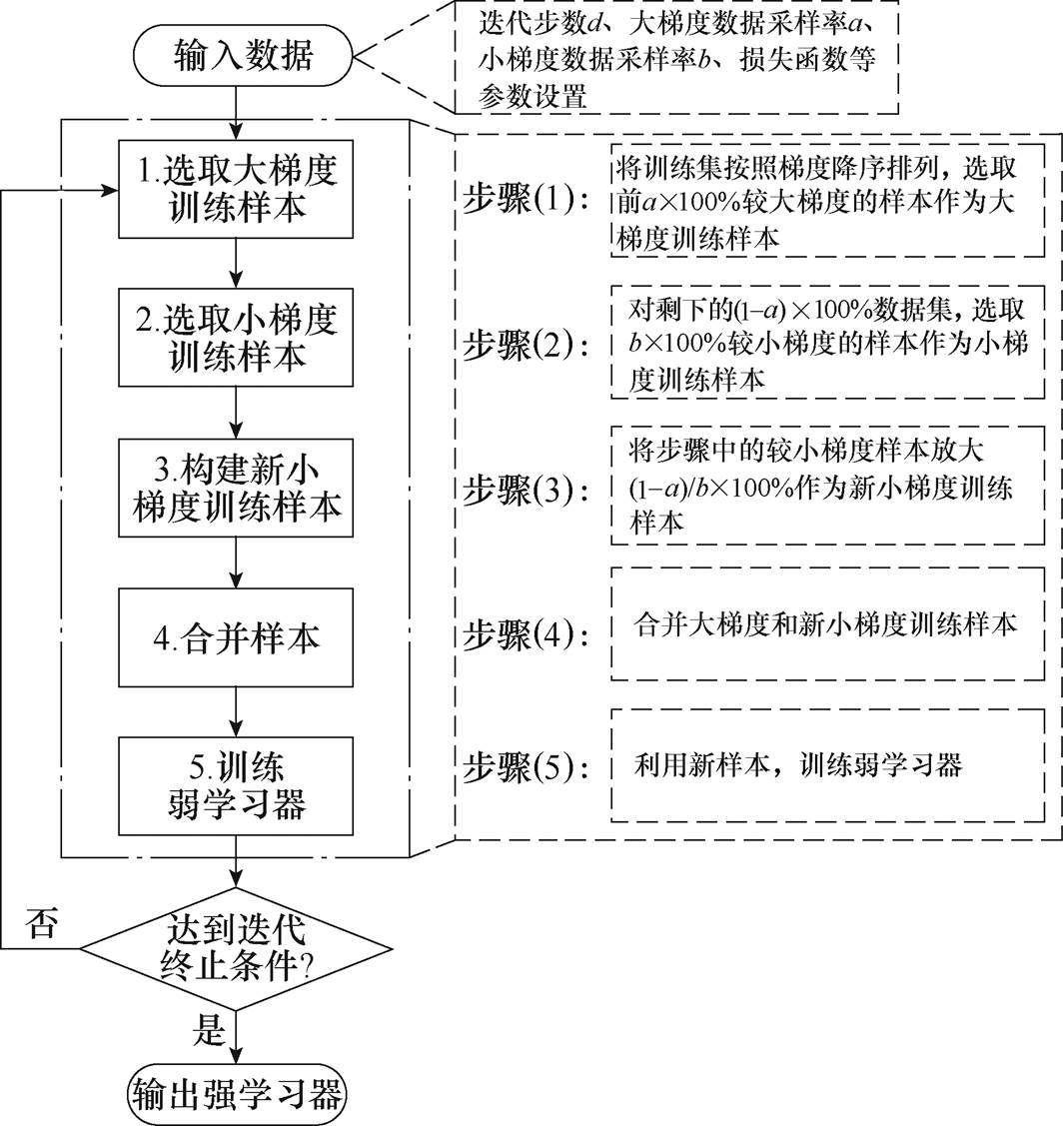
图2 GOSS处理流程
Fig.2 Flowchart of GOSS process
按层生长(Level-wise)和按叶生长的两种方式示意图如图3所示。传统的决策树采用按层生长的生长方式,很多节点分裂后只能获得很低的信息增益,对分类结果影响较小,全部分裂会带来庞大的运算量,降低模型训练速度。而LightGBM使用按叶生长的生长方式是在每一次节点分裂时,选择增益最大的叶子节点进行生长,限制模型的复杂度,提升训练速度,避免出现过拟合。
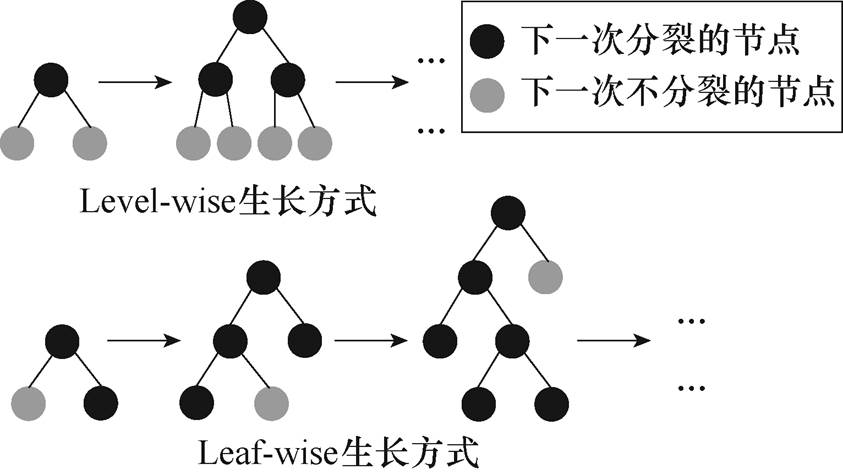
图3 Leaf-wise生长方式示意图
Fig.3 Schematic diagram of Leaf-wise growth
人工调参不仅耗时而且效果不好,基于Hyperopt超参数优化框架可实现序列预测模型的超参数优化,减轻人工调参负担,提升准确性。Hyperopt- LightGBM模型预测具体步骤如下:
(1)数据处理:基于多线程并行直方图的训练方式和GOSS处理方式,对数据进行预处理,降低样本数据和特征维度,然后分别将数据集的40%、50%和60%设置为训练集。
(2)LightGBM模型构建:选取模型参数:'bagging_fraction' 'num_threads', 'feature_fraction', 'max_depth', 'lambda_l1', 'lambda_l2', 'learning_rate', 'num_leaves', 'min_data_in_leaf', 'min_sum_hessian_ in_leaf','num_trees';基于Leaf-wise生长方式,对决策树的深度进行限制,从而降低模型复杂度。
(3)Hyperopt获取LightGBM最佳模型:基于Hyperopt,对步骤(2)中的模型参数进行参数空间定义;创建LightGBM模型工厂和分数获取器,模型工厂用于“生产”所需模型,分数获取器则是用于解耦;通过迭代,获得模型最佳参数。调优后的LightGBM模型和其他模型超参数设置情况见表2。
表2 各模型超参数设置情况
Tab.2 Parameters of different RUL prediction models

模型超参数 LightGBM'bagging_fraction': 0.56, 'num_threads': 2,'feature_fraction': 0.112, 'max_depth': 18,'lambda_l1': 0.0001, 'lambda_l2': 0.0511,'learning_rate': 0.0511, 'num_leaves': 46,'min_data_in_leaf': 34, 'num_trees': 588,'min_sum_hessian_in_leaf': 0.0511 XGBoost'alpha': 0.0512, 'learning_rate': 0.0510,'min_child_weight': 4, 'n_estimators': 550,'max_depth': 20, 'subsample': 0.59,'num_threads': 2, 'gamma': 0.0, 'lambda': 0.0511 GBDT'alpha': 0.9, 'min_samples_leaf': 57,'max_depth': 7, 'learning_rate': 0.01,'min_samples_split': 200, 'subsample': 0.8,'n_estimators': 100, 'random_state': 10,'tol': 0.0001, 'validation_fraction': 0.1 RF'n_estimators': 600, 'min_samples_leaf': 4,'min_samples_split': 10, 'max_depth': 100
(4)设置评价标准:使用实际容量和预测容量之间的方均根误差(Root Mean Square Error, RMSE)作为评价标准,有
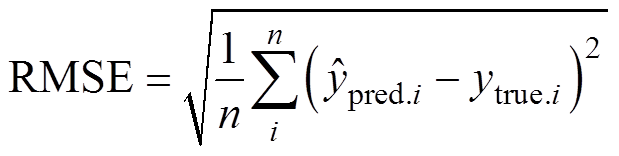 (4)
(4)式中,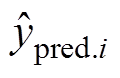 为第i次循环的预测容量;
为第i次循环的预测容量;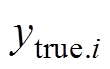 为第i次循环的实际容量。
为第i次循环的实际容量。
(5)RUL预测:利用测试集验证已经修正的模型,预测行驶工况下动力电池的剩余使用寿命。
为模拟行驶工况下电动汽车电池所受振动应力和充放电应力,本文搭建行驶工况下电池全生命周期容量测试系统,该系统由航天希尔振动测试系统和蓝电CT2014F电池充放电系统组成,如图4所示。

图4 行驶工况下电池全生命周期容量测试系统
Fig.4 Experimental bench of battery life cycle capacity under driving conditions
本文选择的研究对象是磷酸铁锂(LiFePO4)电池,其正极材料是LiFePO4,负极材料是石墨,隔膜材料是PP/PE/PP聚烯烃(用以隔离正、负极,阻止电子,通过锂离子)。其参数为:额定容量1.35A·h,标称电压3.3V,充电截止电压3.7V。在对磷酸铁锂电池进行充放电的过程中,其主要反应式为
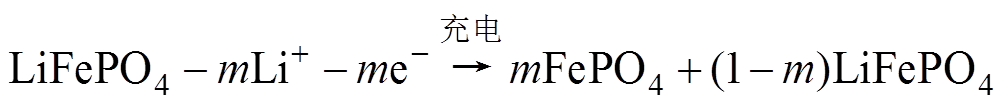 (5)
(5) (6)
(6)
根据城市行驶工况(Urban Driving Condition, UDC)[3],为模拟行驶工况下电池所受充放电应力,本文设置锂离子电池充放电测试曲线如图5所示。
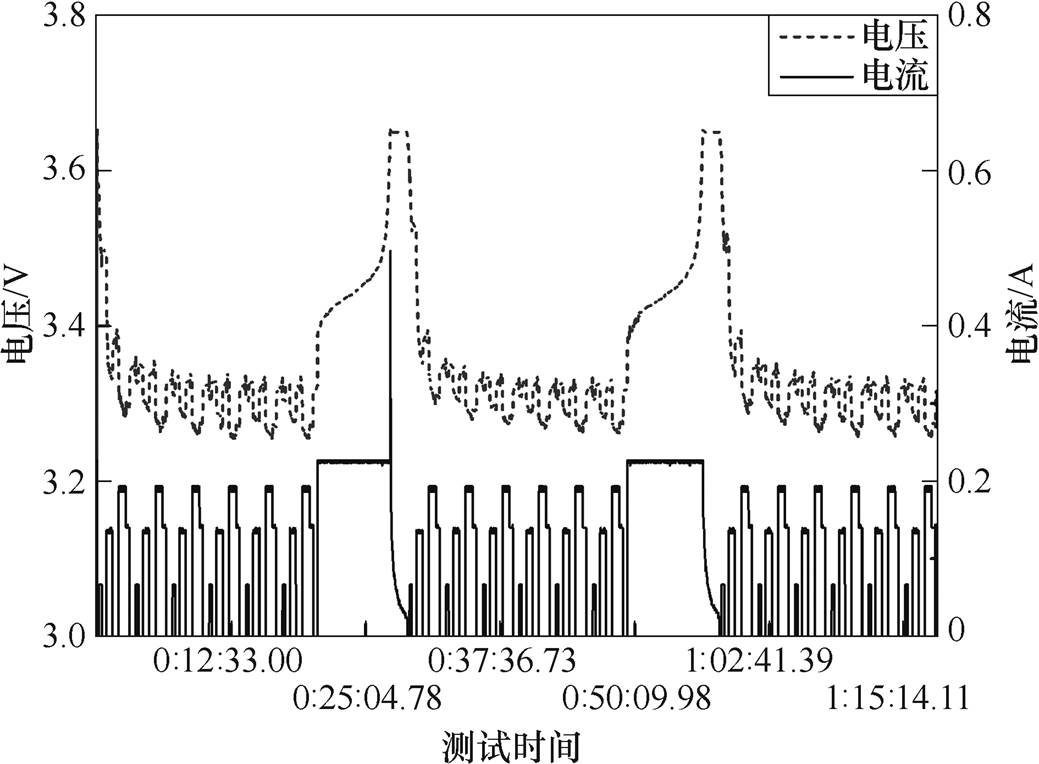
图5 行驶工况下电池充放电测试曲线
Fig.5 Charge-discharge curves of battery under driving conditions
为模拟行驶工况下电池所受振动应力,加速度目标谱参数设置见表3,振动目标谱参数具体设置见表4。
表3 锂离子电池加速度目标谱参数
Tab.3 Acceleration target spectrum parameters of lithium-ion battery
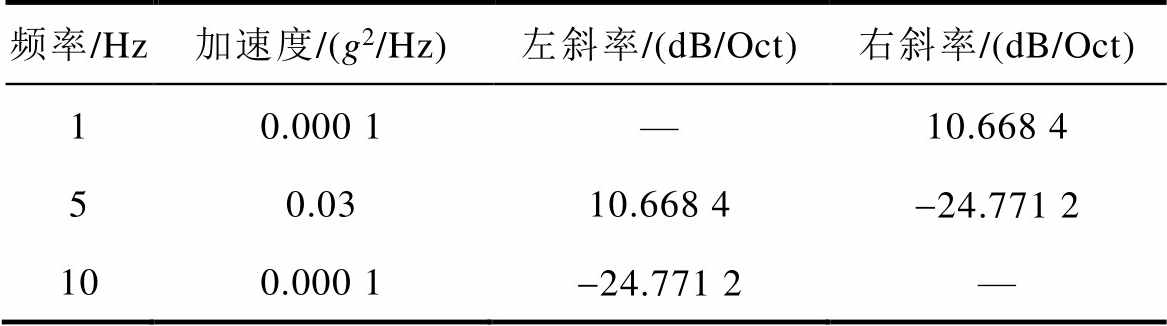
频率/Hz加速度/(g2/Hz)左斜率/(dB/Oct)右斜率/(dB/Oct) 10.000 1—10.668 4 50.0310.668 4-24.771 2 100.000 1-24.771 2—
表4 锂离子电池振动目标谱参数
Tab.4 Vibration target spectrum parameters of lithium-ion battery
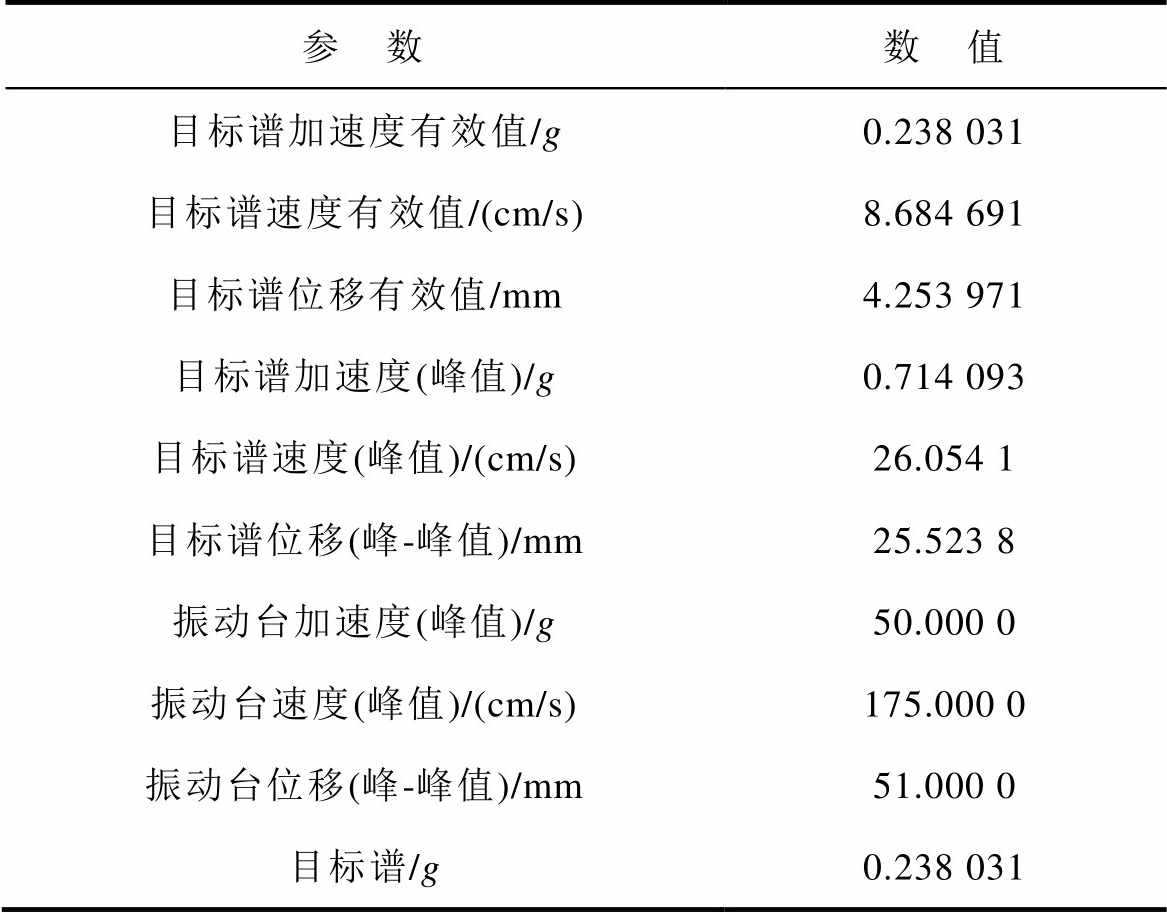
参 数数 值 目标谱加速度有效值/g0.238 031 目标谱速度有效值/(cm/s)8.684 691 目标谱位移有效值/mm4.253 971 目标谱加速度(峰值)/g0.714 093 目标谱速度(峰值)/(cm/s)26.054 1 目标谱位移(峰-峰值)/mm25.523 8 振动台加速度(峰值)/g50.000 0 振动台速度(峰值)/(cm/s)175.000 0 振动台位移(峰-峰值)/mm51.000 0 目标谱/g0.238 031
针对本文所选的锂离子电池(LiFePO4),在充放电过程中,除了锂离子脱嵌发生的氧化还原反应外,还存在许多的副反应,如电解液分解、活性物质溶解、金属锂沉积等,这些副反应导致电池容量衰减。当行驶工况(实验组)和静置工况(对照组)下电池循环充放电至剩余容量为标称容量的80%时,认定电池寿命终止(End of Life, EOL),则停止实验。两种工况下电池容量衰退情况如图6所示。
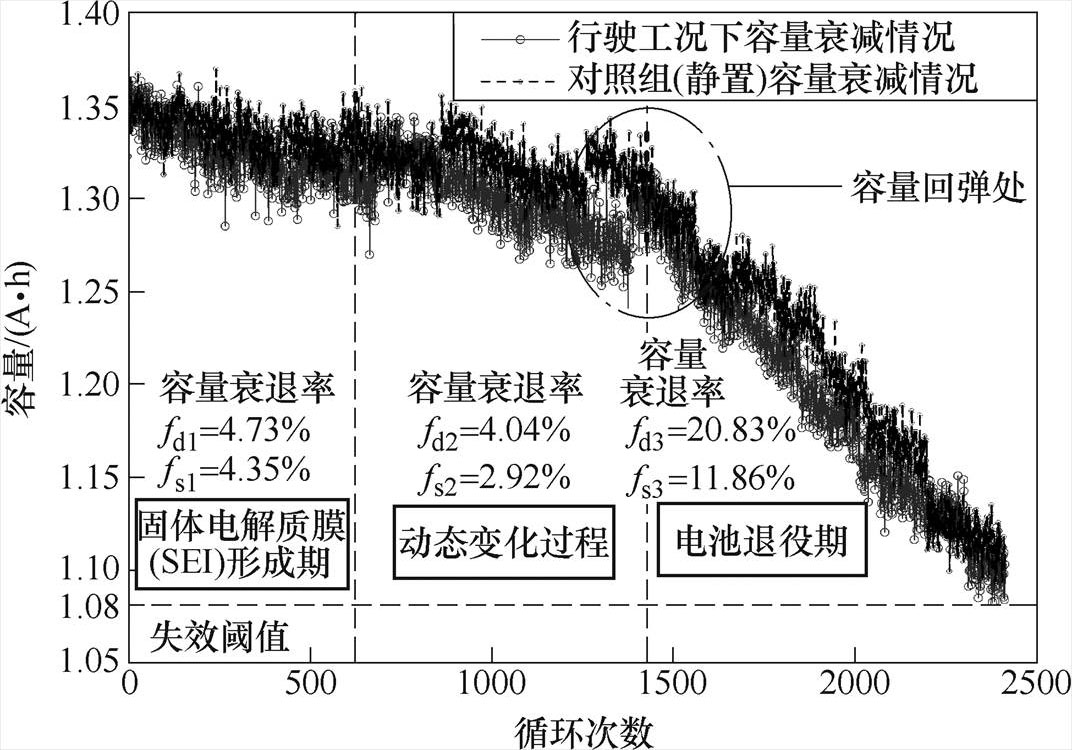
图6 锂离子电池容量衰退情况
Fig.6 Degradation of lithium-ion battery capacity
根据实验结果,行驶工况下的电池在2 414次循环充放电后到达EOL,而静置工况下的电池尚未到达EOL。根据容量衰减率,将电池全生命周期大致划分为三个阶段:固体电解质膜(Solid Electrolyte Interphase, SEI)形成期、动态变化过程和电池退役期,图6中以拟合曲线示意显示每个阶段。
根据图6所示,在700~1 000次循环和1 400~ 1 600次循环间容量衰退曲线出现了突变点,即在容量衰减的趋势下,部分充放电过程中电池容量出现突然上升的情况,原因是在试验过程中锂离子电池出现了自充电现象[9]。在容量回弹后,容量衰退速率明显加剧,造成该现象的主要原因是随着充放电循环次数增加,SEI增厚和负极锂沉积。700~1 000次循环是电池容量动态变化过程,1 400~1 600次循环是动态变化过程到电池退役期转换过程,包含容量衰退加剧的转折点[18]。因此,本文重点关注1 400~1 600次循环间容量回弹处的预测效果问题。
从图6中可以看出,两种工况下锂离子电池全生命周期容量呈现类似衰退的趋势,由于两个容量序列的长度不同,无法通过曼哈顿距离或者欧氏距离计算两个容量序列间的距离,也就无法分析其相似性。因此,选择动态时间规整(Dynamic Time Warping, DTW)算法对两种工况下电池容量序列的相似性进行定量分析,为2.5节提供先验分析。
根据DTW原理[19],定义规整路径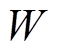 为
为
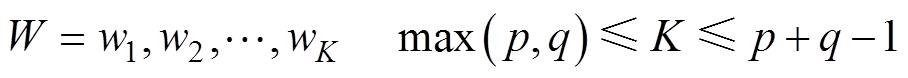 (7)
(7)其规整代价最小的路径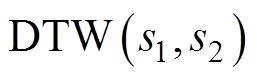 表示为
表示为
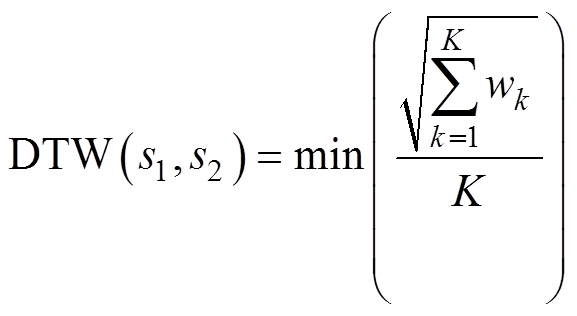 (8)
(8)
式中,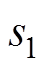 和
和 分别为两种工况下容量序列。
分别为两种工况下容量序列。
根据式(9),通过累计距离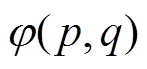 的递归求解,获得两个电池容量序列的最小规整距离,用以定量分析两者的相似性。
的递归求解,获得两个电池容量序列的最小规整距离,用以定量分析两者的相似性。
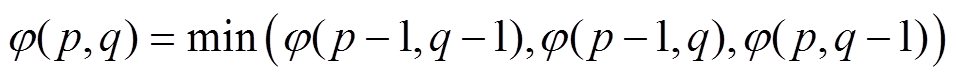 (9)
(9)通过DTW计算可知,两种工况下电池容量序列的最小规整距离为0.009 6,约为容量序列量级的0.7%左右,因此,两个容量序列具有一定的相似性。
根据2.3节内容,虽然电池在实际工况中会出现具有独特性的差异变化,但是在相同或类似工况下,同种电池在相同充放电循环过程中的性能退化情况是相似的,例如,城市行驶工况下的锂离子电池,在每辆车的行驶环境(振动工况和静置工况)相差不大的情况下,电池性能的退化过程从整体上来看相差不大。但是为了得到相同或相似工况下电池全生命周期容量序列,至少需要长达约3~6个月的实验时间,耗费大量的实验成本,且设计老化实验困难。因此,本文依据行驶工况下电池全生命周期容量衰退情况,利用GAN生成新的容量序列[20],其可行性在后续章节讨论。
新容量序列生成情况如图7所示,GAN生成过程本质上是一个极大极小优化问题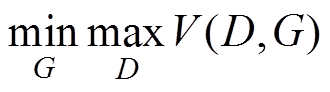 ,其中,G为生成器,D为判别器,有
,其中,G为生成器,D为判别器,有
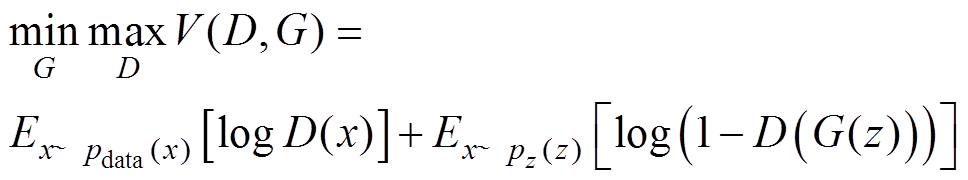 (10)
(10)式中,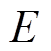 为求解期望值;
为求解期望值;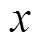 为实际容量序列;
为实际容量序列;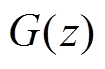 为由噪声
为由噪声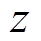 生成的容量序列;
生成的容量序列;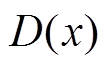 为
为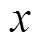 的概率;
的概率;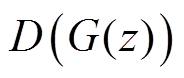 为
为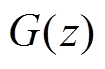 的概率;
的概率; 用于衡量生成的容量序列真实的程度(对于
用于衡量生成的容量序列真实的程度(对于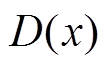 来说,越接近1越好),所以,底数对结果无影响,取值合理即可。
来说,越接近1越好),所以,底数对结果无影响,取值合理即可。
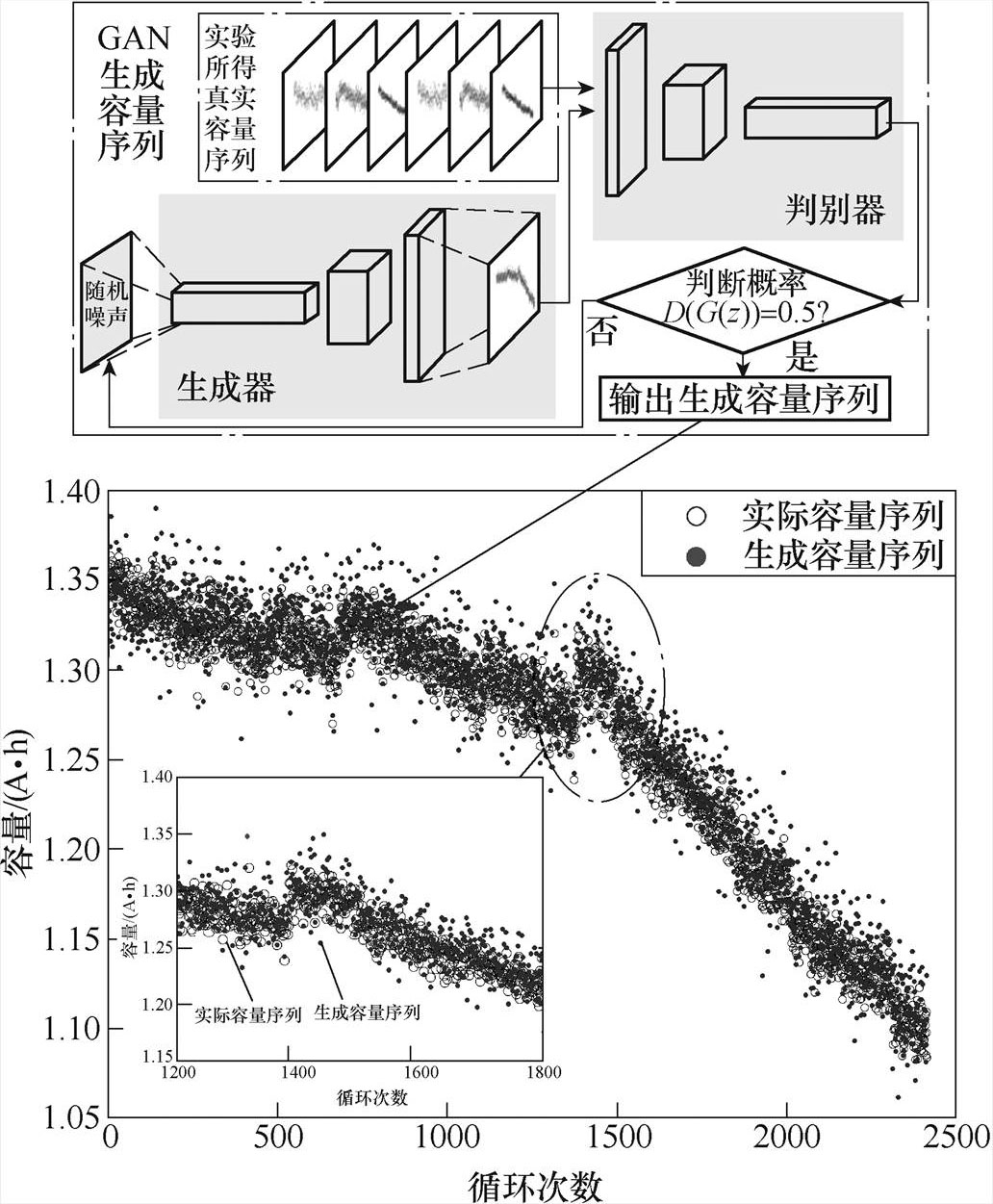
图7 新容量序列生成情况
Fig.7 Results of generated new capacity sequences
通过更新迭代,尽可能减小生成样本与真实样本之间的差距,最终使得判别器无法判别样本来自于生成器还是真实样本,即判别概率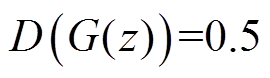 。
。
预测效果评估的性能指标有很多[4, 13, 16],除了方均根误差外,本文重点关注以下性能指标:
(1)容量回弹处预测效果:在对RUL进行线性回归预测时,电池全生命周期容量衰退过程出现的容量回弹(见图6)会影响后续容量预测。
(2)时间复杂度:训练时间和预测时间的总和。较高的时间复杂度会在一定程度上影响其实际应用效果,降低时间复杂度有助于完成快速、有效的RUL预测。
(3)内存使用率:随着数据量的增加,内存资源被大量占用,增加内存负担。减少内存使用率,有助于节省硬件成本,提升效率。
因此,选择容量回弹处预测效果、时间复杂度、内存使用率和方均根误差作为预测效果评估的性能评估标准。
为验证LightGBM预测模型有效性,选用行驶工况下的电池全生命周期容量实验数据作为数据集,分别以总循环次数的40%、50%和60%作为循环起点进行剩余使用寿命预测,以全面展示LightGBM预测模型的RUL预测效果。
LightGBM、XGBoost、RF和GBDT四种模型预测效果(包括容量回弹处预测效果)对比情况如图8所示。其中,图8a~图8c分别展示了训练样本占数据集的40%、50%、60%情况下的预测效果。
从图8可以看出,LightGBM和XGBoost不论在整体预测还是容量回弹处预测效果均优于RF和GBDT,在电池退役期阶段末期(约2 000次循环后)RF和GBDT的预测效果明显下降,而LightGBM和XGBoost仍能保持稳定良好的预测效果。
为了进一步验证所建LightGBM预测模型的性能,从时间复杂度、内存使用率和方均根误差三方面与现有预测模型进行对比,结果如图9~图11 所示。
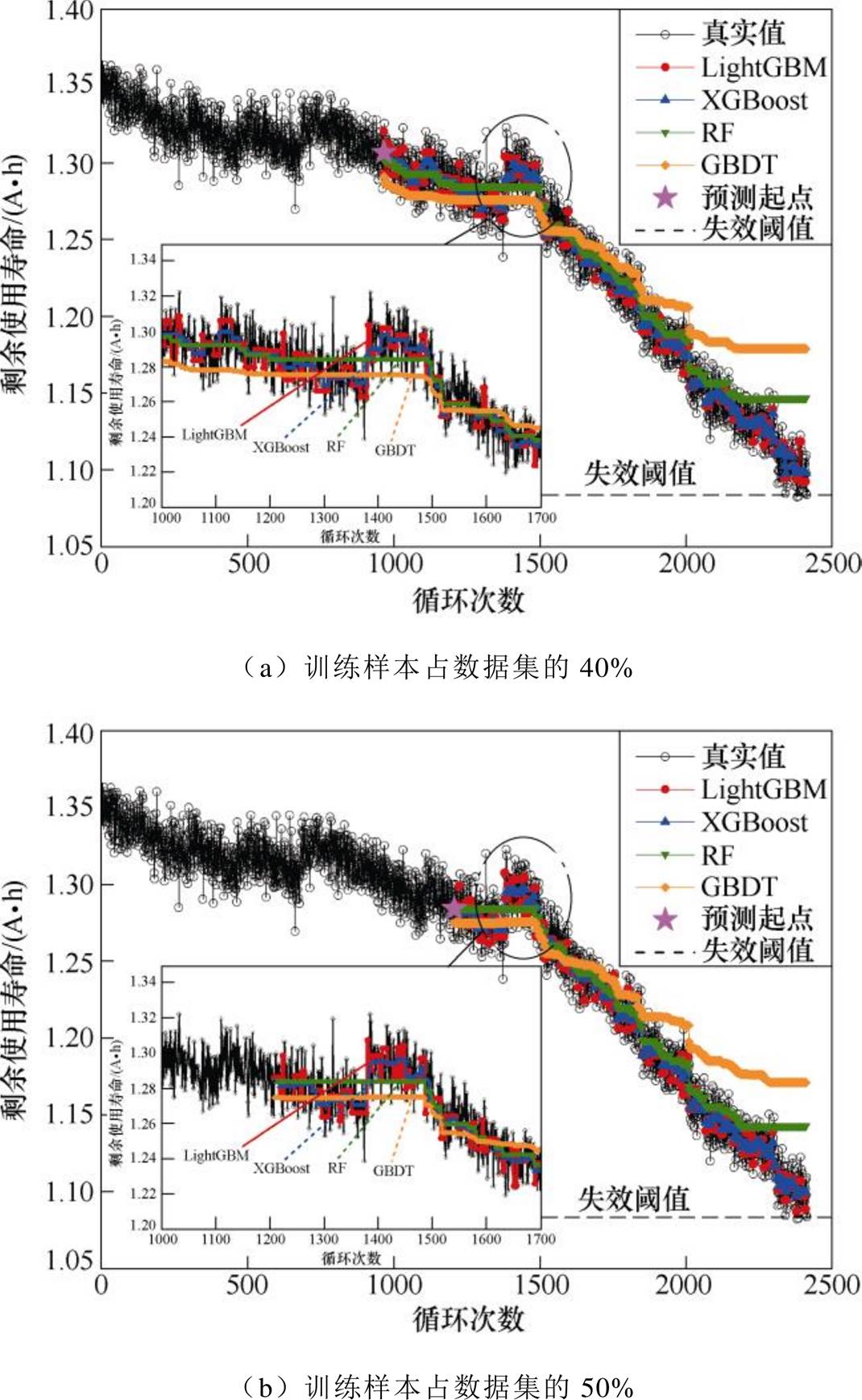
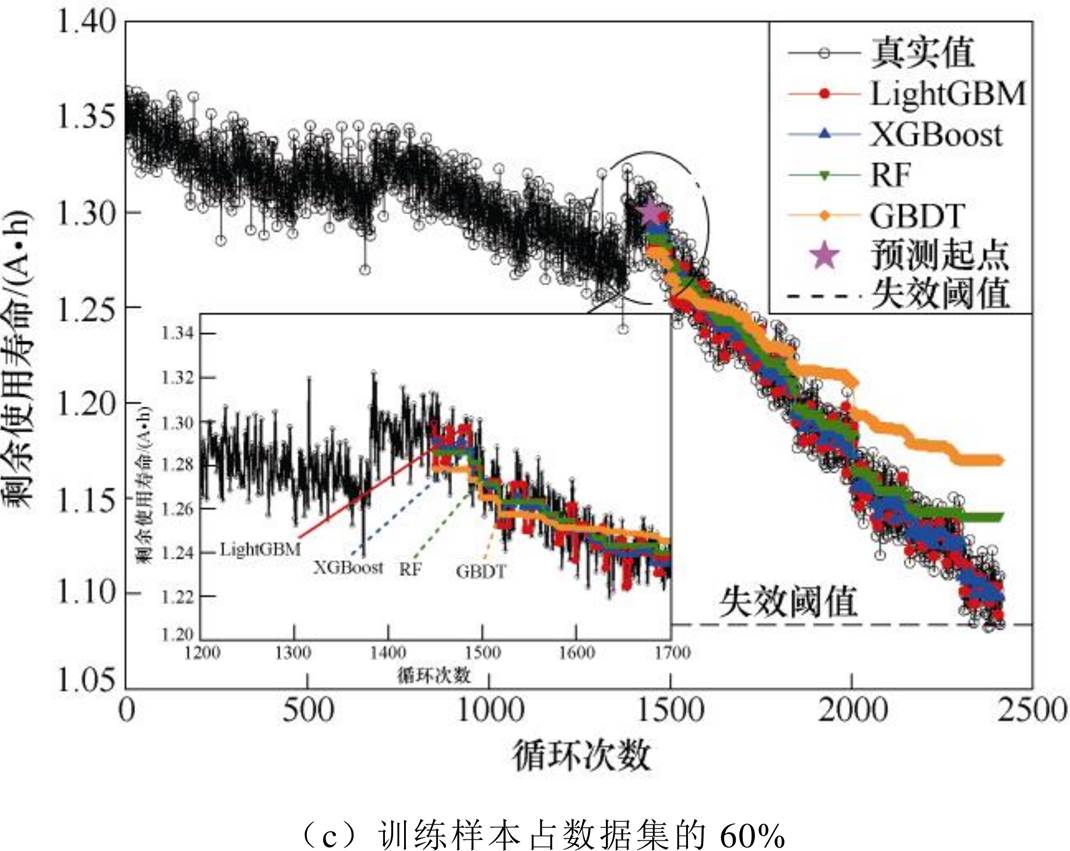
图8 不同训练样本比例下的RUL预测结果
Fig.8 RUL prediction results based on different methods using different proportion of training samples
不同算法时间复杂度对比情况如图9所示。从图9可得出,GBDT的时间复杂度远低于其他三种预测模型,而RF的时间复杂度远高于其他三种预测模型,LightGBM的时间复杂度低于XGBoost。随着训练样本量的增加,LightGBM、XGBoost、RF和GBDT四种RUL预测模型的时间复杂度呈现不同程度的增长,其中,RF预测模型的时间复杂度受训练样本量的影响较大,LightGBM受训练样本量的影响较小。
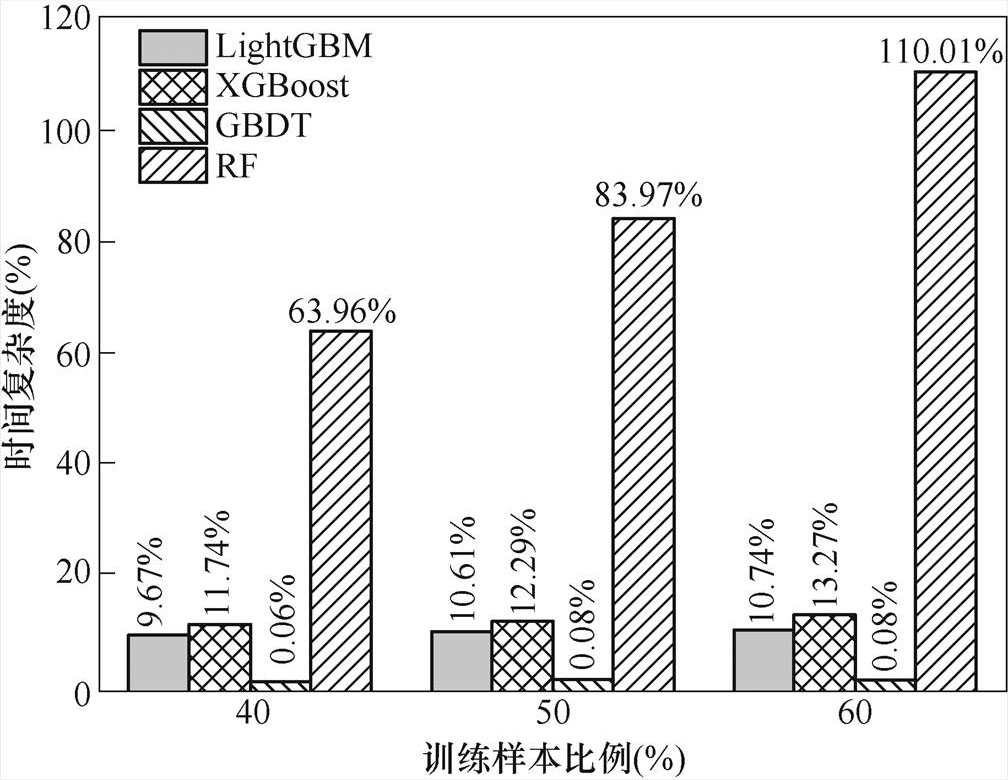
图9 不同算法时间复杂度对比情况
Fig.9 Comparison of calculation time based on different methods
不同算法内存使用率对比情况如图10所示。从图10可得出,四种预测模型的内存使用率相差不大,由于使用直方图优化、单边梯度采样和深度限制的按叶生长方式,LightGBM的内存使用率低于其他三种预测模型。随着训练样本量的增加,LightGBM、XGBoost、RF和GBDT四种RUL预测模型的内存使用率呈现相似程度的增长。

图10 不同算法内存使用率对比情况
Fig.10 Comparison of memory usage based on different methods
图11展示了不同算法方均根误差的对比情况,可以看出,LightGBM和XGBoost预测结果的方均根误差最小,且两者相差不大,而GBDT预测结果的误差较大。随着训练样本量的增加,LightGBM、XGBoost、RF和GBDT四种RUL预测模型的方均根误差呈现不同程度的减小。
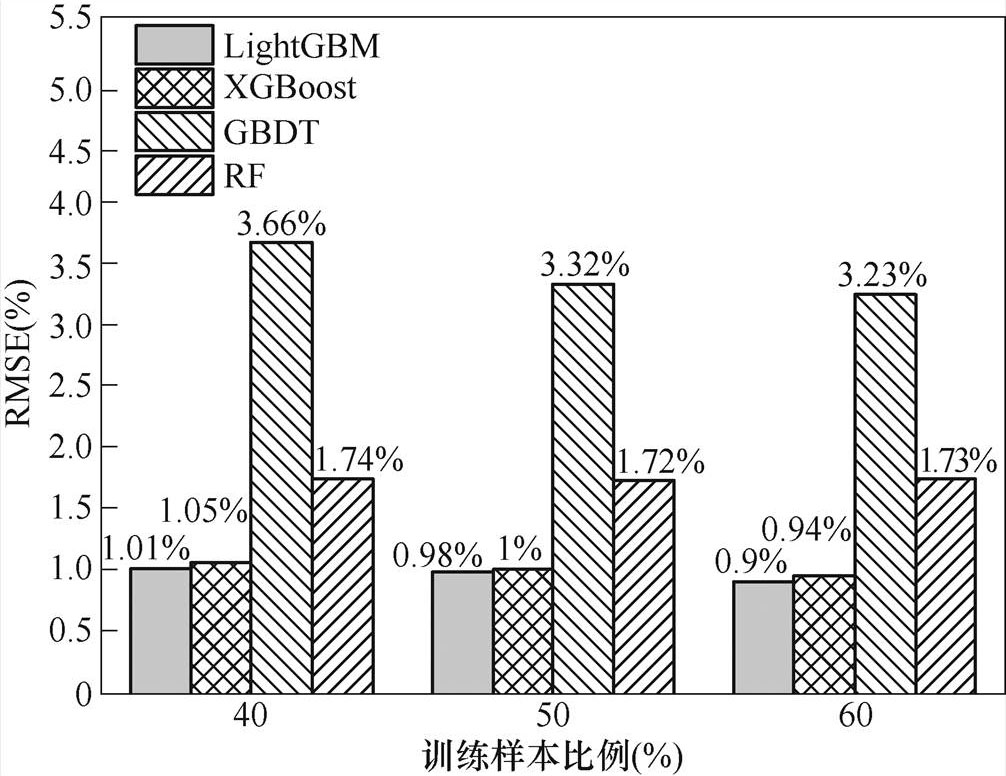
图11 不同算法RMSE对比情况
Fig.11 Comparison of RMSE based on different methods
综上所述,虽然在时间复杂度和内存使用率方面GBDT有良好的表现,但是以牺牲预测准确性为代价。从容量回弹处预测效果、时间复杂度、内存使用率和方均根误差四方面综合评估预测性能,LightGBM模型在容量回弹处具有较好的预测效果,且与XGBoost、GBDT和RF模型相比,LightGBM模型时间复杂度低于11s,内存使用率低于27%,RMSE低于1.01%。因此,LightGBM预测模型的有效性得以验证。
在3.2节中,LightGBM预测模型有效性验证完毕,下面利用LightGBM预测模型验证GAN生成容量序列的可行性。
选取行驶工况下实际容量序列和GAN生成容量序列作为样本集进行对比测试,测试结果如图12所示(仅以样本集的40%作为训练样本进行测试)。虽然生成容量序列训练下的RUL预测效果(RMSE= 1.03%)不如实际容量序列,但是整体预测效果和容量回弹处预测效果基本满足预期需求,因此,GAN生成新容量序列的可行性得以验证。

图12 生成容量序列的RUL预测效果
Fig.12 RUL prediction results using the generated capacity sequences
本文构建了基于LightGBM的RUL预测模型,利用元学习Hyperopt对LightGBM模型进行参数优化,完成了行驶工况下锂离子电池RUL预测;通过行驶工况下锂离子电池全生命周期容量测试实验数据,验证了所提RUL预测模型的有效性;利用DTW量化相似性,验证了所生成容量序列的可行性,得出以下结论:
1)LightGBM模型在容量回弹处具有较好的预测效果,且与XGBoost、GBDT和RF模型相比,LightGBM模型时间复杂度低于11s,内存使用率低于27%,RMSE低于1.01%,其有效性得以验证。
2)采用DTW对行驶工况和静置工况下的电池容量序列进行相似性分析,得出同种电池在相同或类似充放电循环过程中容量衰退情况相似。
3)基于GAN生成容量序列,测试结果表明,利用生成容量序列预测的RMSE为1.03%,虽然预测效果不如实际容量序列,但基本满足预测需求,能够在一定程度上减轻实验负担。
本文建立的行驶工况下锂离子电池剩余使用寿命预测模型仅考虑单体电池的预测,未能对行驶工况下电动汽车中整个电池组剩余使用寿命进行预测,后续将重点关注电池组的剩余使用寿命预测研究。
参考文献
[1] Hu Xiaosong, Liu Wenxue, Lin Xianke, et al. A control-oriented electrothermal model for pouch-type electric vehicle batteries[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 5530-5544.
[2] Meng Jinhao, Store Daniel-loan, Ricco Mattia, et al. A simplified model-based state-of-charge estimation approach for lithium-ion battery with dynamic linear model[J]. IEEE Transactions on Industrial Infor- matics, 2019, 66(10): 7717-7727.
[3] Li Wenhua, Jiao Zhipeng, Xiao Qian, et al. A study on performance characterization considering six- degree-of-freedom vibration stress and aging stress for electric vehicle battery under driving con- ditions[J]. IEEE Access, 2019, 7: 112180-112190.
[4] 徐佳宁, 倪裕隆, 朱春波. 基于改进支持向量回归的锂电池剩余寿命预测[J]. 电工技术学报, 2021, 36(17): 3693-3704.
Xu Jianing, Ni Yulong, Zhu Chunbo. Remaining useful life prediction for lithium-ion batteries based on improved support vector regression[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(17): 3693-3704.
[5] 焦自权, 范兴明, 张鑫, 等. 基于改进粒子滤波算法的锂离子电池状态跟踪与剩余使用寿命预测方法[J]. 电工技术学报, 2020, 35(18): 3979-3993.
Jiao Ziquan, Fan Xingming, Zhang Xin, et al. State tracking and remaining useful life predictive method of Li-ion battery based on improved particle filter algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3979-3993.
[6] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698- 707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[7] Cong Xinwei, Zhang Caiping, Jiang Jiuchun, et al. A hybrid method for the prediction of the remaining useful life of lithium-ion batteries with accelerated capacity degradation[J]. IEEE Transactions on Vehicular Technology, 2020, 69(11): 12775-12785.
[8] Hu Jiawen, Sun Qiuzhuang, Ye Zhisheng, et al. Joint modeling of degradation and lifetime data for RUL prediction of deteriorating products[J]. IEEE Transa- ctions on Industrial Informatics, 2021, 17(7): 4521- 4531.
[9] Zhang Yunwei, Tang Qiaochu, Zhang Yao, et al. Identifying degradation patterns of lithium ion bat- teries from impedance spectroscopy using machine learning[J]. Nature Communications, 2020, 11(1): 1706.
[10] Ng Man-Fai, Zhao Jin, Yan Qingyu, et al. Predicting the state of charge and health of batteries using data-driven machine learning[J]. Nature Machine Intelligence, 2020(2): 161-170.
[11] 张婷婷, 于明, 李宾, 等. 基于Wavelet降噪和支持向量机的锂离子电池容量预测研究[J]. 电工技术学报, 2020, 35(14): 3126-3136.
Zhang Tingting, Yu Ming, Li Bin, et al. Capacity prediction of lithium-ion batteries based on Wavelet noise reduction and support vector machine[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3126-3136.
[12] 王瀛洲, 倪裕隆, 郑宇清, 等. 基于ALO-SVR的锂离子电池剩余使用寿命预测[J]. 中国电机工程学报, 2021, 41(4): 1445-1457, 1550.
Wang Yingzhou, Ni Yulong, Zheng Yuqing, et al. Remaining useful life prediction of lithium-ion batteries based on support vector regression opti- mized and ant lion optimizations[J]. Proceedings of the CSEE, 2021, 41(4): 1445-1457, 1550.
[13] 曹洋. 基于模型驱动的锂离子电池剩余寿命预测方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
[14] Kang Weijie, Xiao Jiyang, Xiao Mingqing, et al. Research on remaining useful life prognostics based on fuzzy evaluation-Gaussian process regression method[J]. IEEE Access, 2020(8): 71965-71973.
[15] Zhang Yongzhi, Xiong Rui, He Hongwen, et al. Lithium-ion battery remaining useful life prediction with Box-Cox transformation and monte carlo simulation[J]. IEEE Transactions on Industrial Electronics, 2018, 66(2): 1585-1597.
[16] Jiang Fu, Yang Jiajun, Cheng Yijun, et al. An aging- aware SOC estimation method for lithium-ion batteries using xgboost algorithm[C]//2019 IEEE International Conference on Prognostics and Health Management (ICPHM), San Francisco, CA, USA, 2019: 1-8.
[17] 颜诗旋, 朱平, 刘钊. 基于改进LightGBM模型的汽车故障预测方法研究[J]. 汽车工程, 2020, 42(6): 815-819, 825.
Yan Shixuan, Zhu Ping, Liu Zhao. Research on vehicle fault prediction scheme based on improved LightGBM model[J]. Automotive Engineering, 2020, 42(6): 815-819, 825.
[18] Lu Languang, Han Xuebing, Li Jianqiu, et al. A review on the key issues for lithium-ion battery management in electric vehicles[J]. Journal of Power Sources, 2013, 226: 272-288.
[19] Bai Lu, Cui Lixin, Zhang Zhihong, et al. Entropic dynamic time warping kernels for co-evolving financial time series analysis[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, DOI: 10.1109/TNNLS.2020.3006738.
[20] Gao Yuan, Liu Yingchao, Wang Yuanyuan, et al. A universal intensity standardization method based on a many-to-one weak-paired cycle generative adversa- rial network for magnetic resonance images[J]. IEEE Transactions on Medical Imaging, 2019, 38(9): 2059-2069.
LightGBM Based Remaining Useful Life Prediction of Electric Vehicle Lithium-Ion Battery under Driving Conditions
Abstract The degradation of the remaining useful life (RUL) for EV lithium-ion battery under driving conditions is complicated. The appropriate prediction of RUL can provide guidance for the periodic maintenance and stable operation to avoid the risks. Therefore, a RUL prediction method for driving conditions is proposed in this paper. Firstly, a light gradient boosting machine (LightGBM) based RUL prediction model is constructed, and the coefficients are obtained by the hyper parameter optimization (Hyperopt). Secondly, the experimental bench of battery cycle life capacity is established to simulate the vibration stress and charge-discharge stress, and the RUL degradation of battery under driving conditions is measured. Then, based on the dynamic time warping (DTW), the similarity of RUL degradation between driving conditions and static conditions is analyzed, and a new capacity sequence can be generated by the generative adversarial networks (GAN). Finally, experimental results verify the effectiveness of the proposed model and the generated capacity sequence.
keywords:Electric vehicle, driving conditions, lithium-ion battery, remaining useful life, light gradient boosting machine (LightGBM)
DOI: 10.19595/j.cnki.1000-6753.tces.201653
中图分类号:TM911
国家自然科学基金(U2066213, 52107121)和中国博士后科学基金(2020M680880)资助项目。
收稿日期 2020-12-17
改稿日期 2021-03-26
肖 迁 男,1988年生,博士,讲师,博士生导师,研究方向为分布式能源与微电网、直流配电网、电力电子技术及其在智能电网和综合能源系统中的应用、电池储能系统。E-mail: xiaoqian@tju.edu.cn
焦志鹏 男,1993年生,硕士,研究方向为电动汽车储能技术。E-mail: 18722518050@163.com(通信作者)
(编辑 崔文静)