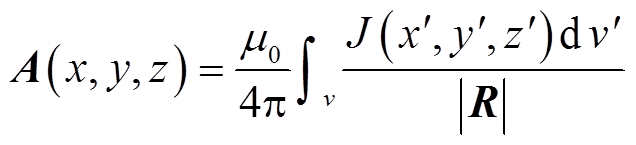 (1)
(1)摘要 在磁耦合谐振式动态无线电能传输系统中,发射线圈与接收线圈之间的相对水平偏移距离将达到发射线圈边长的一半,此时线圈间互感波动非常剧烈,导致系统无法正常工作。为此该文提出了一种多接收线圈正反串联结构来减小互感波动率。首先,提出了一种矩形线圈互感计算方法,运用提出的互感计算方法,分析了该线圈结构的互感特性;其次,给出了一种互感优化方法,运用提出的优化方法,得到了满足设计要求的各线圈参数;最后,根据得到的线圈参数,研制了一套基于多接收线圈正反串联结构的无线电能传输系统,通过仿真和实验验证了所提结构与方法的正确性。结果显示,运用提出的结构,其线圈间的偏移距离在发射线圈边长一半范围内变化时,线圈间最大互感波动率仅为3.81%。
关键词:动态无线电能传输系统 互感计算 互感优化 多接收线圈正反串联结构
磁耦合谐振式动态无线电能传输技术(Dynamic Wireless Power Transfer, DWPT)受到国内外学者广泛关注[1],该技术可应用于自动导引车(Automatic Guided Vehicles, AGV)和电动汽车(Electric Vehicles, EV)的供电系统[2-5]。它的主要优点是可以消除AGV或EV对电池的依赖,因为AGV或EV使用DWPT系统时,可以在行驶时充电。然而在DWPT系统中,发送线圈和接收线圈沿运动方向不可避免地会产生水平偏移,从而导致其互感变化。值得注意的是,在DWPT系统中,沿运动方向的水平偏移可能会至少达到传输线圈边长(或外径)的一半。在此极限偏移下,互感的变化非常剧烈,严重影响DWPT系统的稳定性。目前主要有两种方法来解决线圈偏移对无线电能传输系统稳定性的影响,即阻抗匹配方法[6-19]和新线圈结构的设计与优化[20-31]。
阻抗匹配方法主要有阻抗补偿网络法和调节变量法。阻抗补偿网络类型主要包括SPS阻抗补偿网络[4]、LC阻抗补偿网络[7]、T型[8-9]、π型阻抗补偿网络[10]、LCC型阻抗补偿网络[11-12]、LCL型补偿网络[13]、LCL和 CL混合型补偿网络[14]、LCC-C型补偿网络[15]和DC-DC型补偿网络[16]等。调节变量法主要有调节系统工作频率法[17-18]和调节开关器件的占空比法[19]。以上方法都可以提升线圈的有效偏移距离,然而以上方法抗偏移能力有限,很难胜任互感波动较大时的情况。
线圈本体结构设计与优化方法是解决线圈偏移时互感变化的一个有效方法。目前线圈本体结构设计与优化方法主要有:线圈自身结构设计与优化方法和线圈组合结构设计与优化方法。
在线圈自身结构设计与优化方面:韩国高等科学技术学院的Chun T. Rim等学者相继研制了E型、U型、W型、I型和S型磁心的长导轨型线圈结构[20]。上述线圈结构提升了线圈的偏移距离,然而该接收线圈只能覆盖长导轨线圈(发射线圈)的一部分,不可避免地降低了接收线圈和发射线圈之间的耦合系数,导致系统效率降低。新西兰奥克兰大学的J. T. Boys等学者[21]提出了双极性矩形平面线圈结构(Double D, DD),提高了线圈之间的耦合系数,且DD线圈结构在Y轴方向有较好的抗偏移能力,然而该结构在X轴方向的抗偏移能力较差。奥克兰大学M. Budhia等学者[22]在DD线圈的基础上增加一个正交Q线圈,从而形成了DDQ线圈,弥补了DD线圈的不足。重庆大学孙跃等学者在DD线圈的基础上提出一种DLDD(double layer double D)型线圈结构,进一步提升了系统抗偏移能力[23]。文献[24]基于一种不对称线圈结构,通过优化发射线圈和接收线圈的直径和匝数,提升了系统的抗偏移能力。实验表明:当偏移距离在10cm之内时,线圈的互感基本保持不变。
在线圈组合结构设计与优化方面,H. R. Ahn等学者[25]使用多个接收线圈,提高了线圈偏移时的传输效率。J. P. W. Chow等学者[26]提出了一种T型接收线圈结构,该接收线圈结构由两个互相垂直的线圈构成,该结构可以有效提升角度的偏移能力。然而T型线圈结构在X轴方向偏移能力不强。为此,S. Y. Choi等学者[27]提出了一种双接收线圈结构,该结构在一定程度上增加了X轴方向的偏移距离。哈尔滨工业大学宋凯和朱春波等学者[28]研究一种基于多发射线圈并联方式的无线供电系统,与单收发线圈结构相比,功率提升了25%,效率提升了7%。天津大学张镇等学者[29]提出了一种空心多发射线圈结构,当接收线圈在发射矩阵上移动时,它们之间磁场分布基本均匀,系统效率基本不变。Chris Mi等学者[30]研究了一种六个空心发射线圈对单个接收线圈结构,实验结果表明:当系统运动方向发生偏移时,输出功率的波动为±7.5%。西南交通大学麦瑞坤等学者提出了一种在发射线圈上加入一个线圈的组合结构,偏移距离在发射线圈直径的40%范围内,该结构的互感变化率仅为2.8%。然而偏移距离在发射线圈直径的44.4%范围内时,该结构互感变化率增加到了6.4%[31]。综观现有文献,当偏移距离在发射线圈直径或边长的一半范围内变化时,互感波动率较大的问题仍然没有解决。
本文提出了一种多接收线圈正反串联结构来减小沿运动方向的互感波动率。该接收线圈结构由三个接收线圈串联而成,当线圈偏移时,其中一个接收线圈与发射线圈之间的互感会增加,另外两个接收线圈与发射线圈之间的互感会减小。由于以上特点,相比传统的线圈结构,该结构的互感波动率很小。另外提出了一种互感计算方法和互感优化方法,通过优化各线圈参数,进一步减小了互感波动率。最后通过仿真和实验验证了所提结构与方法的正确性。结果显示,线圈间的偏移距离在发射线圈边长一半范围内变化时,线圈间互感基本不变。
为了减小动态无线电能传输系统线圈间的互感波动率,本节首先提出一种基于矢量磁位的矩形线圈互感计算方法,使用提出的互感计算方法,可以计算出多接收线圈正反串联结构与发射线圈之间的互感;其次,基于提出的互感计算方法,分析多接收线圈正反串联结构的互感特性,得出了该结构的互感变化规律;最后,基于互感计算方法和互感变化规律,根据设定的约束条件,通过调节多接收线圈的参数,对提出结构的互感进行了优化,当线圈偏移范围在发射线圈的半边长范围内变化时,满足了低互感波动率的要求。
在本小节中,提出了一种基于矢量磁位的矩形线圈互感计算方法。图1显示了两个矩形线圈Coil1和Coil2的示意图。a1和a2是Coil1的长度和宽度,b1和b2是Coil2的长度和宽度。Coil1分为四个部分(l1、l2、l3和l4),s1是O和O1之间的垂直距离,s2是O和O2之间的垂直距离,参数I表示流过Coil1的电流。在图1中设定空间任意一点P(x, y, z),其矢量磁位表达式为[32]
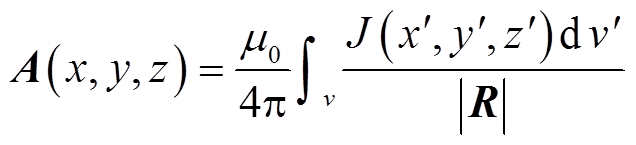 (1)
(1)式中,J为电流密度;v为Coil1的电流分布;R为源点(x', y', z')到空间中任意一点P (x, y, z)的距离矢量,其表达式为
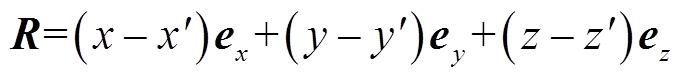 (2)
(2)式中,ex,ey和ez分别为X轴、Y轴和Z轴方向单位矢量。
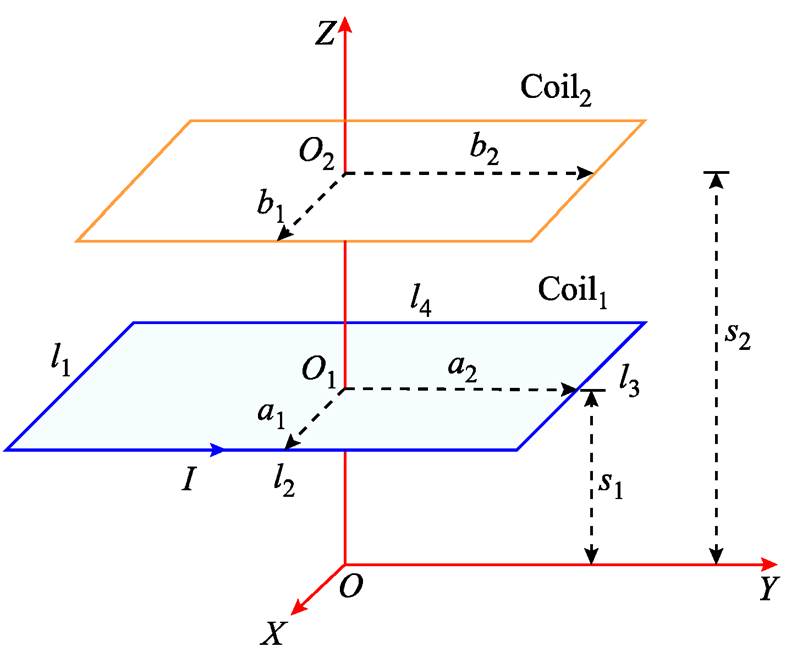
图1 两个矩形线圈示意图
Fig.1 Schematic diagram of two rectangular
双傅里叶变换及其逆变换被引入来求解式(1)[33],得到
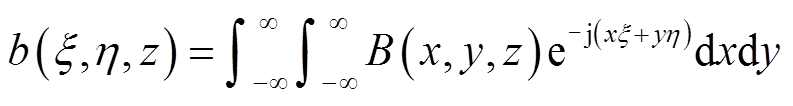 (3)
(3)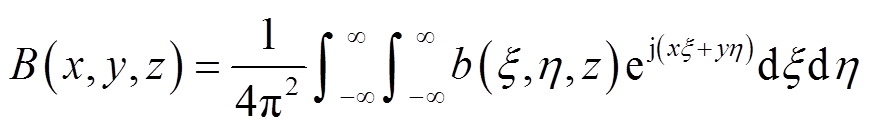 (4)
(4)把式(1)代入式(3)可以得到运用双傅里叶变换后的矢量磁位表达式为
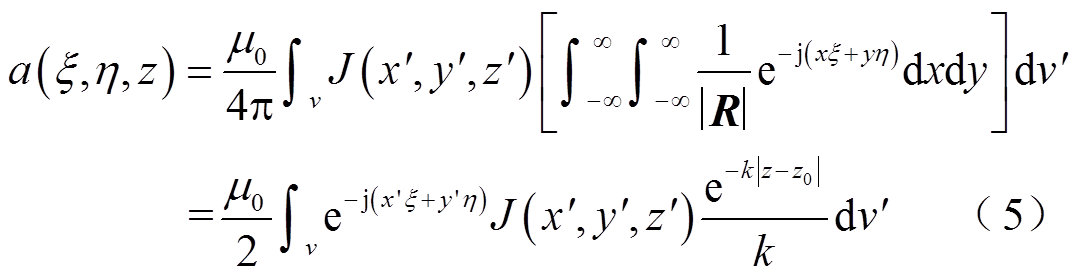
其中
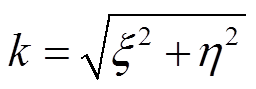 (6)
(6)根据矢量磁位,可以求出磁通密度B的表达式为
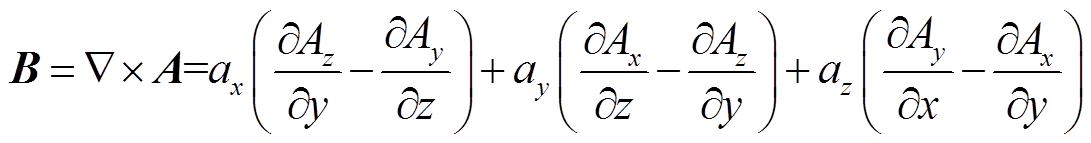 (7)
(7)令
 (8)
(8)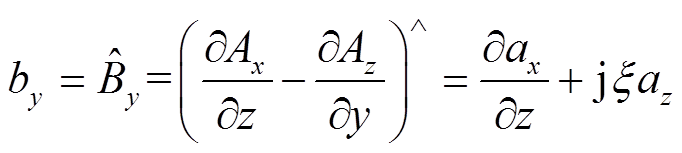 (9)
(9) (10)
(10)式中,符号“^”表示双傅里叶变换运算。
从图1可以看出,ax可以通过平行于X轴的电流获得,ay可以通过平行于Y轴的电流获得,az等于零。式(8)、式(9)和式(10)可以简化为
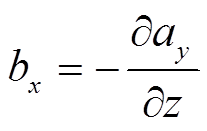 (11)
(11)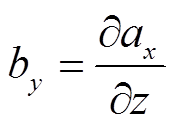 (12)
(12)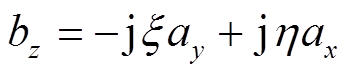 (13)
(13)假设a1x由线l1的电流产生,而a2x由线l3的电流产生,可以得到a1x和a2x的表达式为
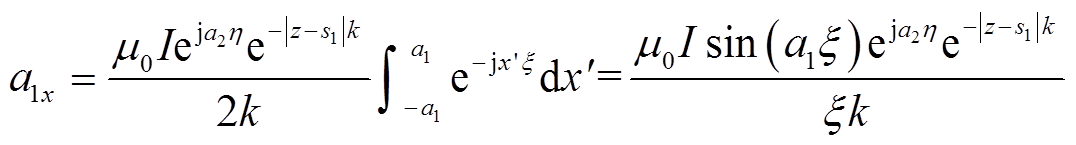 (14)
(14)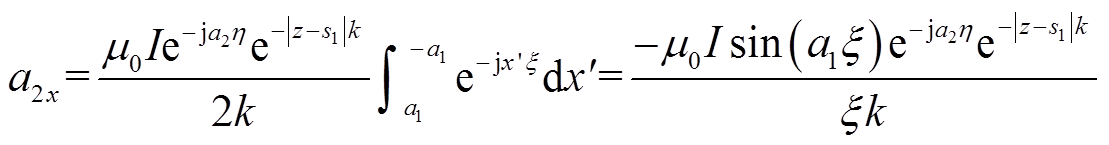 (15)
(15)根据式(14)和式(15),可以得到ax为
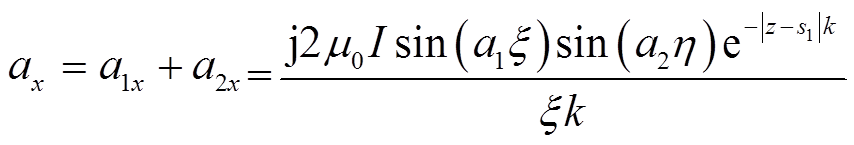 (16)
(16)假设a1y由线l2的电流产生,而a2y由线l4的电流产生,可以得到a1y和a2y的表达式为
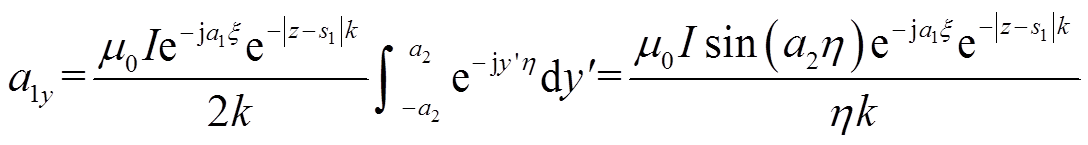 (17)
(17)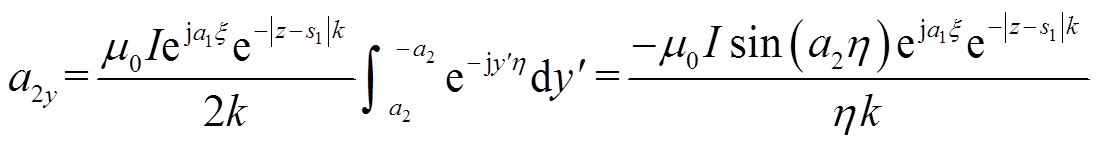 (18)
(18)根据式(17)和式(18),可以得到ay为
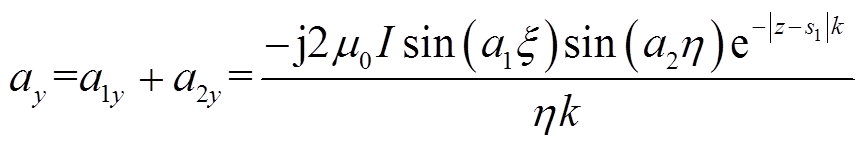 (19)
(19)将式(16)和式(19)代入式(11)、式(12)和式(13),可以得到
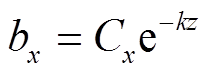 (20)
(20)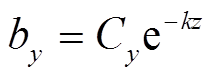 (21)
(21)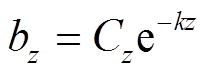 (22)
(22)式中
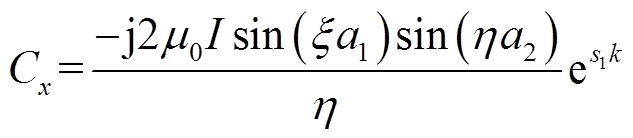 (23)
(23)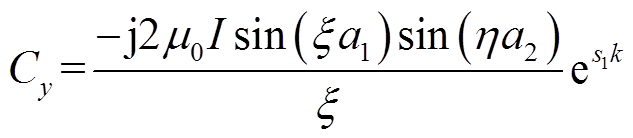 (24)
(24) (25)
(25)将式(20)~式(22)代入式(4),可以得到磁通密度B的表达式为
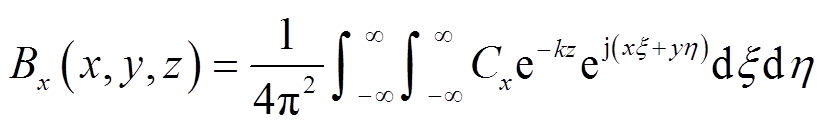 (26)
(26)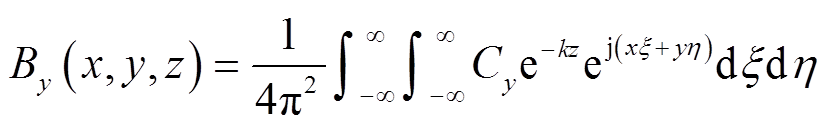 (27)
(27)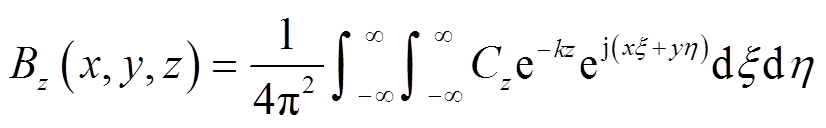 (28)
(28)根据式(26)~式(28),可以获得单匝矩形线圈之间的互感表达式为

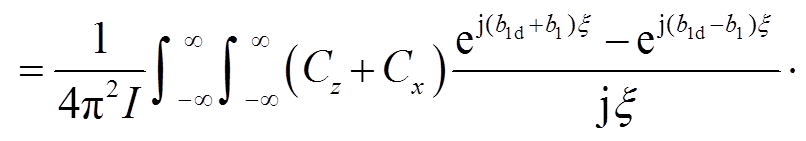
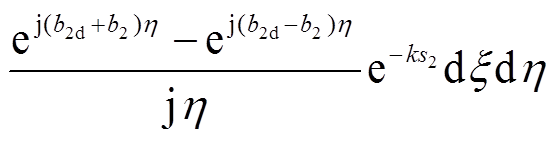 (29)
(29)式中,b1d和b2d分别为X轴和Y轴的偏移距离。
根据式(29),可以得到多匝矩形线圈之间的互感计算式为[34]
 (30)
(30)式中,N1为Coil1的匝数;N2为Coil2的匝数;m为Coil1的第m匝;n为Coil2的第n匝。该互感计算方法为下一节中多接收线圈正反串联结构的互感计算、互感特性分析和互感优化提供理论基础。
为了在线圈极限偏移时仍获得较低的互感波动率,本文运用局部变化而整体不变的思想,提出了一种新型的线圈结构,它由一个发射线圈Tx和一个接收线圈Rx构成,其中接收线圈由Rx1和Rx2正向串联,然后再反向串联Rx3而成。Rx1和Rx2关于Z轴对称,Rx3放置于Rx1和Rx2的中间,Tx和Rx3中心对称,如图2所示。与传统的线圈结构相比,该线圈结构有两个显著的特点:①接收线圈由三个线圈正反串联而成,在线圈极限偏移时,单个发射线圈与单个接收线圈之间的互感可能变化,然而整个接收线圈与发射线圈之间的互感可能不变;②发射线圈的尺寸略小于接收线圈的尺寸,以便进一步降低互感波动率。多接收线圈正反串联结构如图3所示,它由Rx1、Rx2和Rx3构成。Rx1和Rx2采用正向串联方式,Rx3采用反向串联方式。根据纽曼公式,可以得到新型线圈结构的互感表达式为
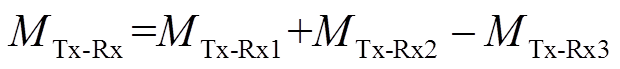 (31)
(31)式中,MTx-Rx为发射线圈Tx和接收线圈Rx之间的互感;MTx-Rx1为Tx和Rx1之间的互感; MTx-Rx2为Tx和Rx2之间的互感;MTx-Rx3为Tx和Rx3之间的互感。根据式(29)和式(30),可以计算各接收线圈与发射线圈间的互感。
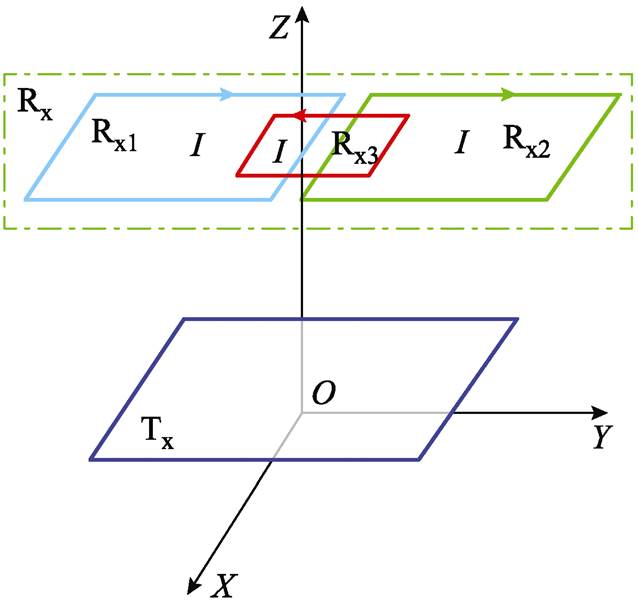
图2 单发射多接收正反串联线圈结构示意图
Fig.2 Multi-receiving coil positive and negative series structure
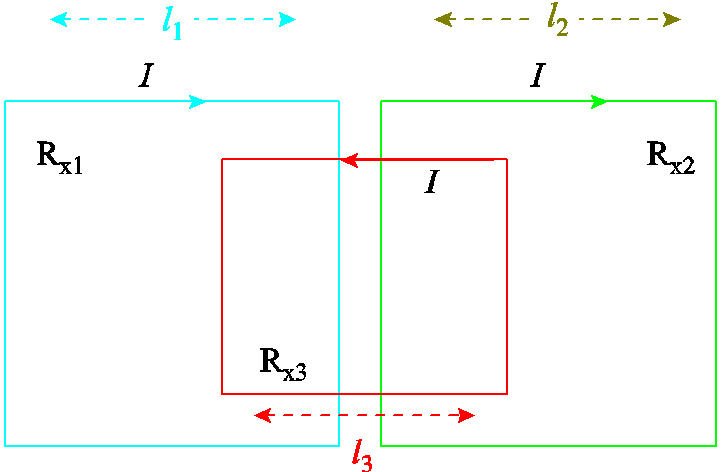
图3 接收线圈俯视图
Fig.3 Top view of the receiving coil structure
结合新型线圈结构两个特点及其互感表达式进行分析可知,当接收线圈沿Y轴方向水平偏移时,MTx-Rx1的互感可能会增加,而MTx-Rx2的互感可能会减小,MTx-Rx3的互感也有可能会减小。只要MTx-Rx1的增加量等于MTx-Rx2和MTx-Rx3的减小量,MTx-Rx就有可能保持基本不变,不受线圈偏移的影响。
本小节根据提出的矩形线圈互感计算公式,对新型线圈结构的参数进行优化,以达到互感基本恒定的目标。互感优化方法流程如图4所示。
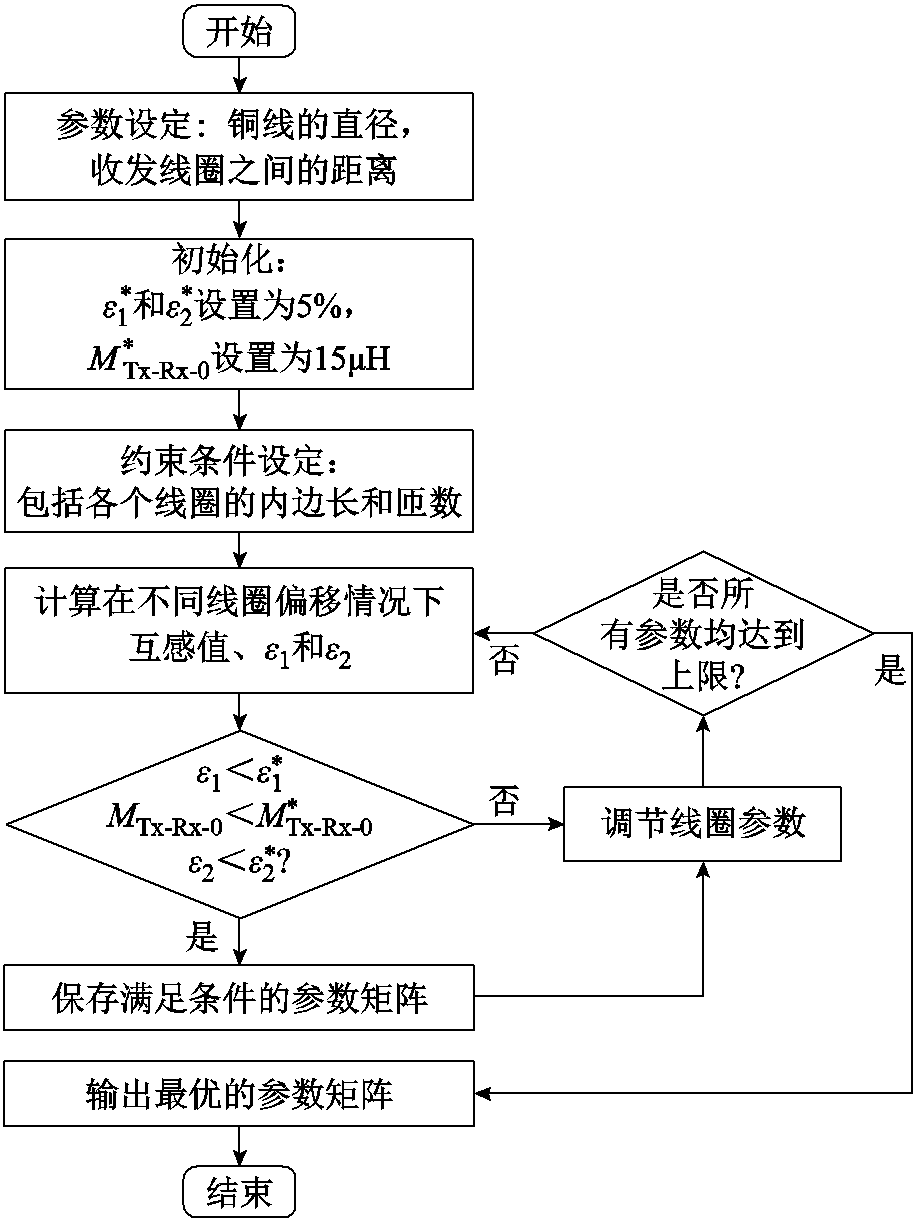
图4 互感优化方法流程
Fig.4 Flow chart of the optimization method of the mutual inductance
根据式(29)和式(30),互感与矩形线圈的长度、宽度、匝数和相对位置有关。当线圈偏移范围在传输线圈长度的一半以内时,可以通过优化每个线圈的参数(例如长度、宽度、匝数等)来使互感保持恒定。具体的互感优化方法的步骤如下:
(1)参数设置和初始化:发射线圈与接收线圈之间的传输距离设置为15cm。铜线的直径为5mm。 和
和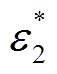 设置为5%。
设置为5%。 设置为15μH。沿Y轴方向的互感波动率定义为
设置为15μH。沿Y轴方向的互感波动率定义为
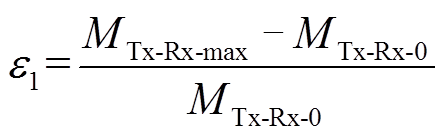 (32)
(32)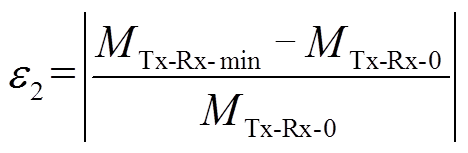 (33)
(33)式中,MTx-Rx-0为Δ=0 cm时Tx和Rx之间的互感(Δ表示沿运动方向Y轴的偏移距离);MTx-Rx-max为Tx和Rx之间的最大互感;MTx-Rx-min为Tx和Rx之间的最小互感。
(2)设置约束条件:可以根据实际应用情况来设置约束条件。在本文中,Rx1的内边长l1-inner范围为10~14cm。Rx2内边长l2-inner范围为10~14cm。Rx3内边长l3-inner范围为25~29cm。Tx的内边长l4-inner范围是32~36cm。Rx1的匝数N1为18~20匝。Rx2的匝数N2是18~20匝。Rx3的匝数N3范围是5~8匝。Tx的匝数N4为12~14匝。匝数的步长为1匝。边长的步长均为2cm。边长的步长越小,得到的结果就越多。然而,步长越小,计算时间也就越长。因此要根据实际应用需求,选择合适的步长。
(3)计算互感、ε1和ε2:根据式(29)和式(30),可以计算出在不同线圈偏移情况下Tx和Rx之间的互感。根据式(32)和式(33),可以计算出ε1和ε2。MTx-Rx-0表示Δ=0cm时的互感。MTx-Rx-1表示Δ=55%× (l4-outer /2)时的互感。MTx-Rx-2表示Δ=60%´(l4-outer/2)时的互感,MTx-Rx-3表示Δ=65%´(l4-outer/2)时的互感,MTx-Rx-4表示Δ=70%´(l4-outer/2)时的互感,MTx-Rx-5表示Δ=100%´(l4-outer/2)时的互感,式中l4-outer表示Tx的外边长。
(4)条件判断:为了使互感基本恒定,必须满足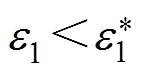 和
和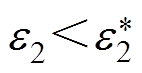 这个条件。为了保证系统的高效率,必须满足MTx-Rx-0>
这个条件。为了保证系统的高效率,必须满足MTx-Rx-0>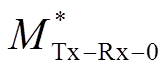 的条件。如果结果符合以上两个条件,则将结果保存;否则,将不保存结果,继续优化线圈参数。如果所有线圈参数均达到上限,结束互感优化程序;否则,程序跳至步骤(3)。
的条件。如果结果符合以上两个条件,则将结果保存;否则,将不保存结果,继续优化线圈参数。如果所有线圈参数均达到上限,结束互感优化程序;否则,程序跳至步骤(3)。
(5)输出找到的解决方案:保存并输出满足所有设置条件的结果。
本节从计算、仿真和实验三方面得到了新型线圈结构的互感值,互感实测值和计算与仿真值一致,从而验证了所提互感计算方法、新型线圈结构与参数优化方法的正确性。
根据参数优化方法,得到了满足条件的线圈尺寸参数,详细的线圈尺寸参数见表1。根据表1中的参数,研制了一套新型线圈结构实物模型,所有线圈的利兹线规格为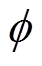 0.1mm´1 200股。实物模型包括一个发射线圈与一个接收线圈,如图5a所示,发射线圈如图5b所示,接收线圈如图5c所示,线圈的详细物理参数见表2。
0.1mm´1 200股。实物模型包括一个发射线圈与一个接收线圈,如图5a所示,发射线圈如图5b所示,接收线圈如图5c所示,线圈的详细物理参数见表2。
表1 线圈尺寸参数
Tab.1 Dimensions of each coil
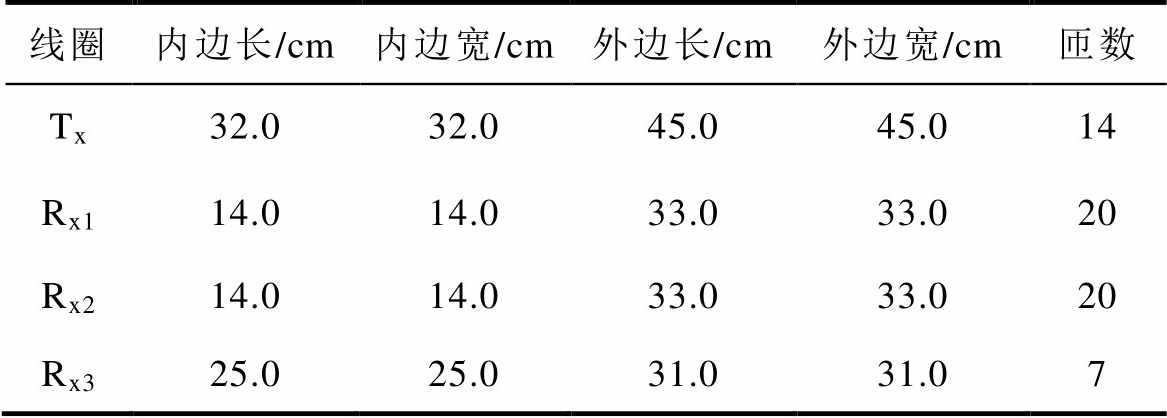
线圈内边长/cm内边宽/cm外边长/cm外边宽/cm匝数 Tx32.032.045.045.014 Rx114.014.033.033.020 Rx214.014.033.033.020 Rx325.025.031.031.07


图5 实验装置图
Fig.5 Experimental setup
表2 线圈的测量参数
Tab.2 Measured parameters of the resonance coils

参数物理意义数值 L1/μH发射线圈的自感146.98 L2/μH接收线圈的自感204.77 C1/nF发射线圈的补偿电容16.86 C2/nF接收线圈的补偿电容12.10 R1/mΩ发射线圈的寄生电阻122.15 R2/mΩ接收线圈的寄生电阻304.80 f0/kHz谐振频率101.1
首先根据式(29)和式(30),运用Matlab软件,计算出了新型线圈结构互感值Mc;其次,运用Ansys Maxwell软件,画出了新型线圈结构的有限元模型,如图6所示,依据仿真模型,可以得到新型线圈结构互感仿真值Ms;最后,使用日置IM3536阻抗分析仪,测量了新型线圈结构的互感值Me。互感仿真与计算值之间的误差定义为εs,互感实测与计算值之间的误差定义为εe,两者表达式为
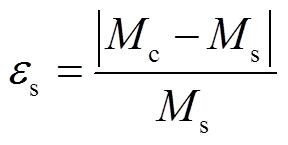 (34)
(34)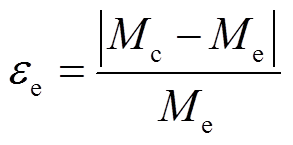 (35)
(35)
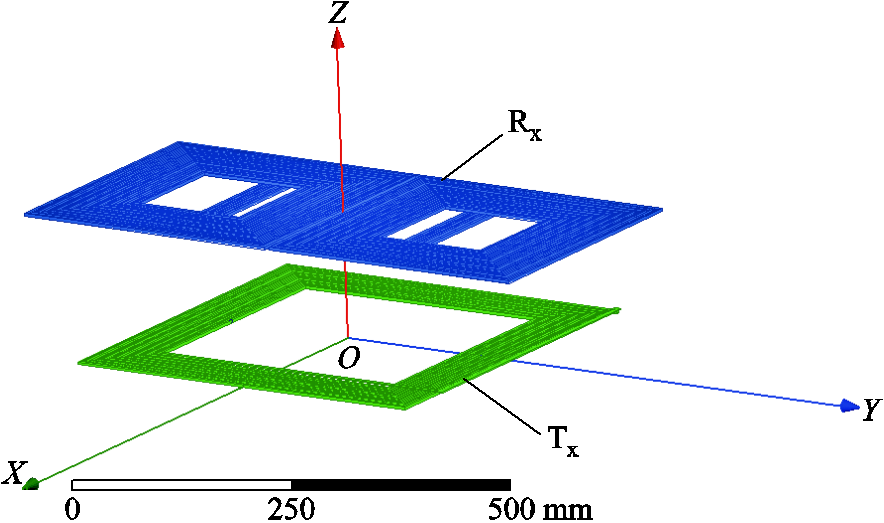
图6 仿真模型
Fig.6 Simulation model
新型发射与接收线圈结构之间的互感测量方法如下。
(1)当发射线圈与接收线圈异名端相连时,可以通过阻抗分析仪测量Lp的值,如图7a所示,L1为发射线圈的自感,L2为接收线圈的自感,M为发射线圈与接收线圈之间的互感。
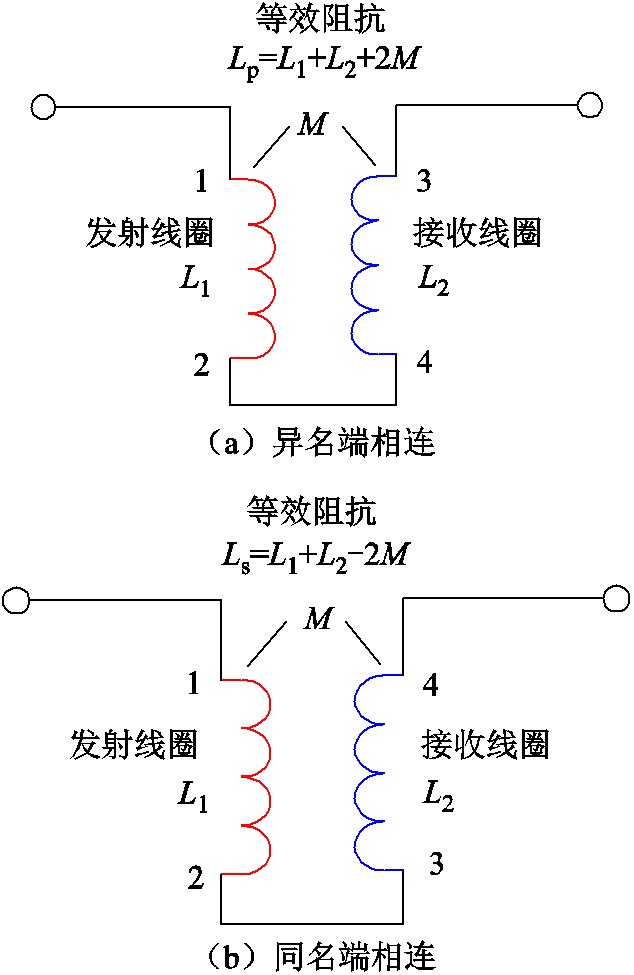
图7 线圈间互感测量方法
Fig.7 Measuring method of mutual inductance
(2)当发射线圈与接收线圈同名端相连时,可以通过阻抗分析仪测量Ls的值,实测的互感模型如图7b所示。
(3)根据M=|Lp-Ls|/4可以求得互感测量值Me,见表3和表4。在测量中两个线圈不可避免地使用较长的接线端子连接到IM3536阻抗分析仪上。对两个接线端子进行缠绕可以减小接线端子对互感的影响。另外,为了减少周围环境对互感的影响,获得精确的测量结果,测量过程是在木桌和亚克力实验框架上进行的,木材和亚克力是非磁性材料,对互感影响可以忽略不计。
表3 沿Y轴正方向互感计算、仿真、实测值和互感误差率
Tab.3 Calculated, simulated, and measured value of mutual inductance and relative error of mutual inductance along the positive direction of Y axis
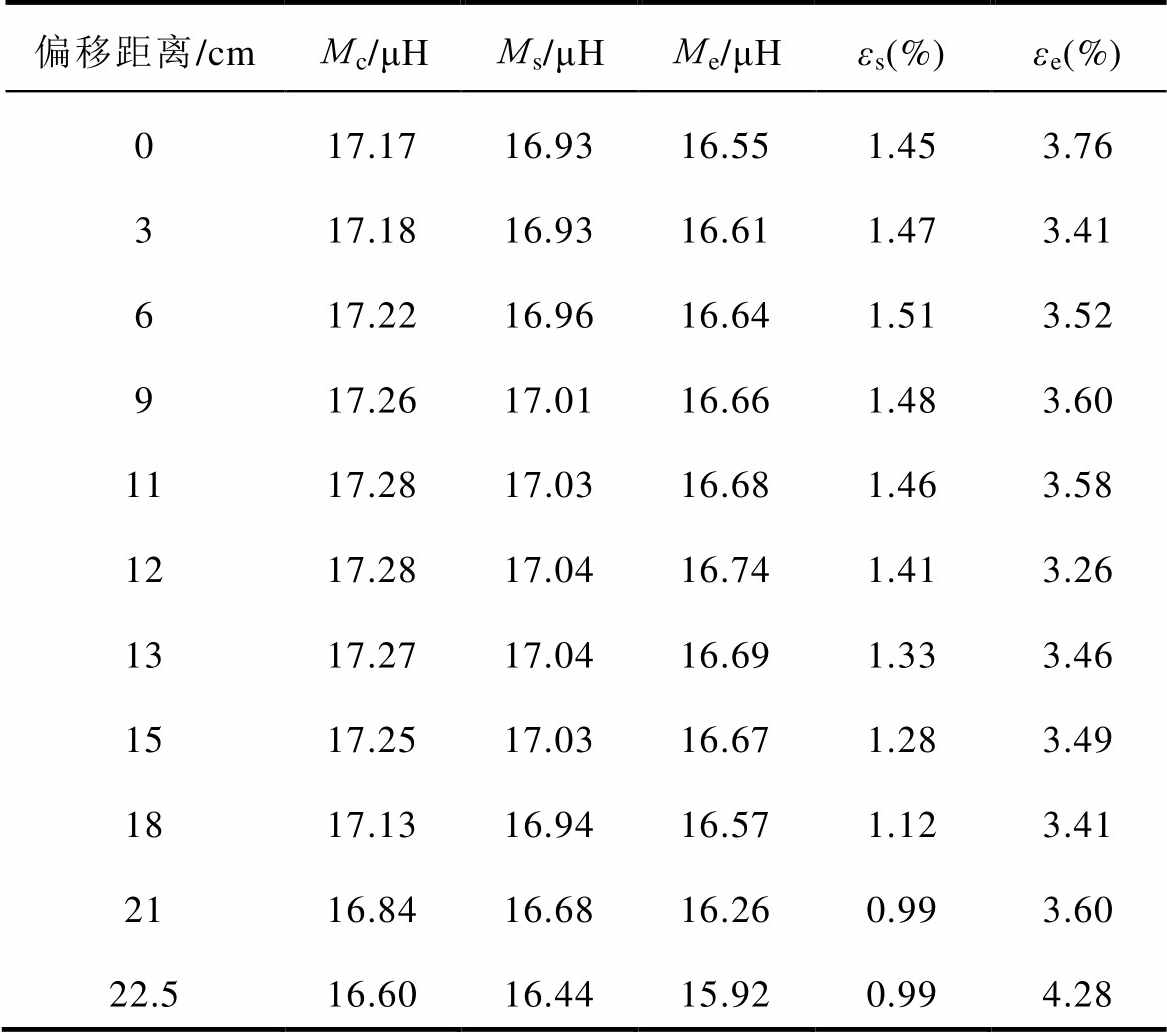
偏移距离/cmMc/μHMs/μHMe/μHεs(%)εe(%) 017.1716.9316.551.453.76 317.1816.9316.611.473.41 617.2216.9616.641.513.52 917.2617.0116.661.483.60 1117.2817.0316.681.463.58 1217.2817.0416.741.413.26 1317.2717.0416.691.333.46 1517.2517.0316.671.283.49 1817.1316.9416.571.123.41 2116.8416.6816.260.993.60 22.516.6016.4415.920.994.28
表4 沿Y轴负方向互感计算、仿真、实测值和互感误差率
Tab.4 Calculated, simulated, and measured value of mutual inductance and relative error of mutual inductance along the negative direction of Y axis

偏移距离/cmMc/μHMs/μHMe/μHεs(%)εe(%) 017.1716.9316.551.453.76 -317.1816.9616.611.323.44 -617.2217.0116.641.213.50 -917.2617.0816.651.083.64 -1117.2817.1016.701.033.50 -1217.2817.1116.720.983.37 -1317.2717.1216.690.883.48 -1517.2517.1116.670.813.50 -1817.1317.0216.590.623.26 -2116.8416.7616.270.483.49 -22.516.6016.5615.910.244.34
表3显示了多接收线圈正反串联结构沿Y轴正方向互感计算、仿真、实测值和互感波动率值。从表3中可以看出,互感仿真与计算值之间的最大误差εs为1.51%,互感实测与计算值之间的最大误差εe为4.28%,验证了所提矩形线圈间互感计算方法的正确性。从表中还可以看出,与传统线圈结构的互感值随偏移距离单调下降不同,新型线圈结构的互感值随偏移距离先增大而后减小。当偏移距离为12cm,互感最大值等于16.74μH;当偏移距离为22.5cm(即发射线圈边长的一半),互感最小值等于15.92μH;当偏移距离为0cm,互感值等于16.55μH。根据式(32)和式(33),可以计算出互感波动率ε1=0.01%和ε2=3.81%,说明互感值基本不随偏移距离的变化而变化,达到了准恒定互感的目标。
表4显示了多接收线圈正反串联结构沿Y轴负方向互感计算、仿真、实测值和互感波动率值,其互感和互感波动率的变化情况与沿Y轴正方向时的互感和互感波动率的变化情况基本一致。为了便于观察互感和耦合系数的变化趋势,根据表2~表4的数据,得到了互感和耦合系数随偏移距离的变化曲线,如图8和图9所示。从图中可以看出,互感和耦合系数基本恒定,而且耦合系数值基本恒定在0.1,系统可以实现高效率的能量传输。
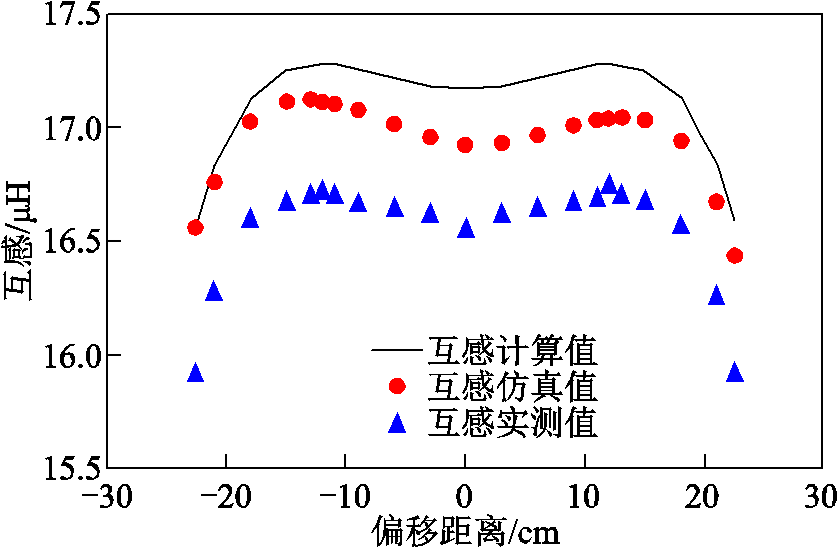
图8 新型线圈结构互感的计算、仿真与实测值
Fig.8 Calculated, simulated, and measured value of mutual inductance with the new structure
通过对比优化参数前所提线圈结构与普通矩形线圈的耦合系数,进一步验证本文所提线圈结构和参数优化方法的有效性。为了保证对比实验的公平性,优化参数前所提线圈结构的最大尺寸与优化参数后所提线圈的最大尺寸一致。同理,普通矩形线圈的最大尺寸也与参数优化后所提线圈的最大尺寸一致。
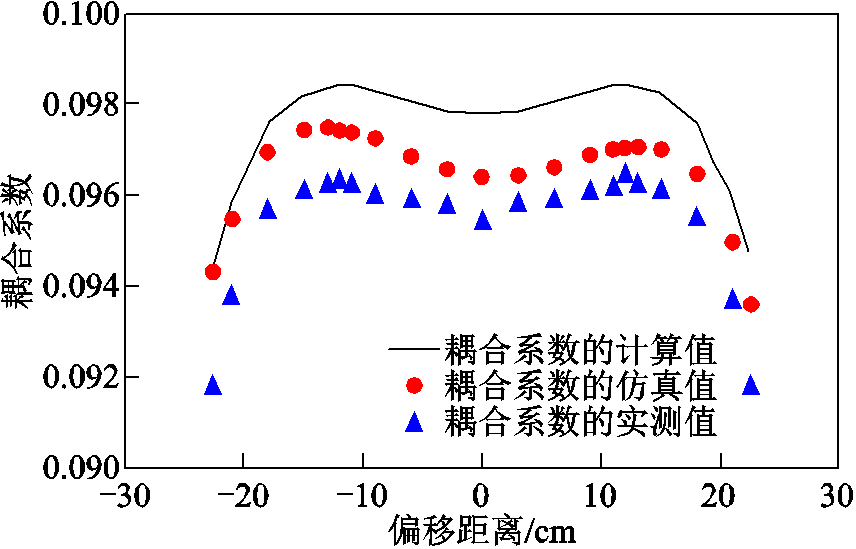
图9 新型线圈结构耦合系数的计算、仿真与实测值
Fig.9 Calculated, simulated, and measured value of coupling coefficient with the new structure
图10显示了优化参数前所提线圈结构的耦合系数。从图10中可以看出,随着偏移距离的增加,耦合系数逐渐减少。当发射线圈与接收线圈之间没有偏移时,耦合系数0.15;当线圈间偏移距离为发射线圈边长的一半时,耦合系数0.109。优化参数前所提线圈结构的耦合系数波动率达到了27.3%。
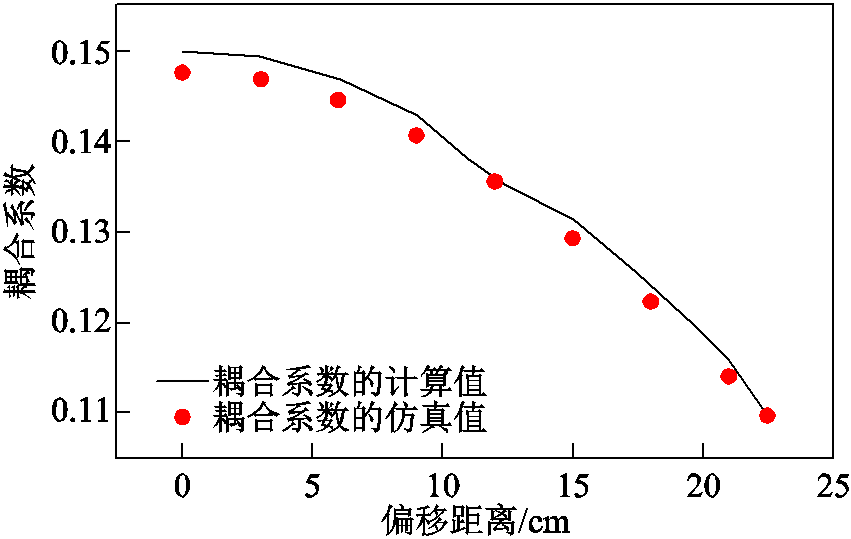
图10 优化参数前新型线圈结构的耦合系数的计算和仿真值
Fig.10 Calculated and simulated value of coupling coefficient with new coil structure before optimized parameters
图11显示了普通矩形线圈结构的耦合系数,从图11中可以看出,随着偏移距离的增加,耦合系数也逐渐减少。当发射线圈与接收线圈之间没有偏移时,耦合系数0.183;当线圈间偏移距离为发射线圈边长的一半时,耦合系数0.117。普通矩形线圈结构的耦合系数波动率高达36.0%。
为了进一步测试在不同偏移距离下多接收线圈正反串联结构的输出功率和效率,搭建了一套无线电能传输系统,实验装置如图5所示。包括功率放大电源、发射线圈、接收线圈和负载。功率放大电源型号为Aigtek ATA—3090,放大倍数设置为15,负载电阻RL设置为20Ω,发射线圈和接收线圈之间的传输距离D设置为15cm,谐振线圈的测量参数见表2。使用横河WT5000功率分析仪,测试了发射侧的输入电压、输入电流、负载上的输出电压和输出电流。
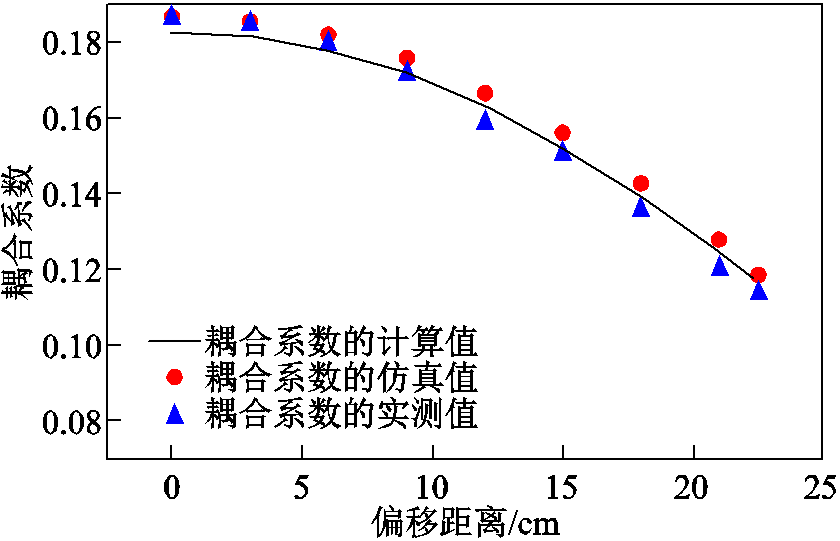
图11 普通矩形线圈结构耦合系数的计算、仿真与实测值
Fig.11 Calculated, simulated, and measured value of coupling coefficient with traditional structure
图12显示了输出功率和传输效率与偏移距离之间的关系。从图12中可以看出,新型线圈结构的最高传输效率约97.0%,随着偏移距离的增加,效率呈现出先增加后减小的趋势,这与图8和图9展现的互感与耦合系数的变化趋势一致。在偏移距离为12cm时,效率最高,这是因为此时互感与耦合系数最大。总体来说效率几乎不受线圈偏移距离的影响。从图12中还可以看出,新型线圈结构的输出功率也基本不随线圈偏移距离的变化而变化,最大输出功率波动率仅为5.88%,这也得益于所提出的新型准恒定互感线圈结构。
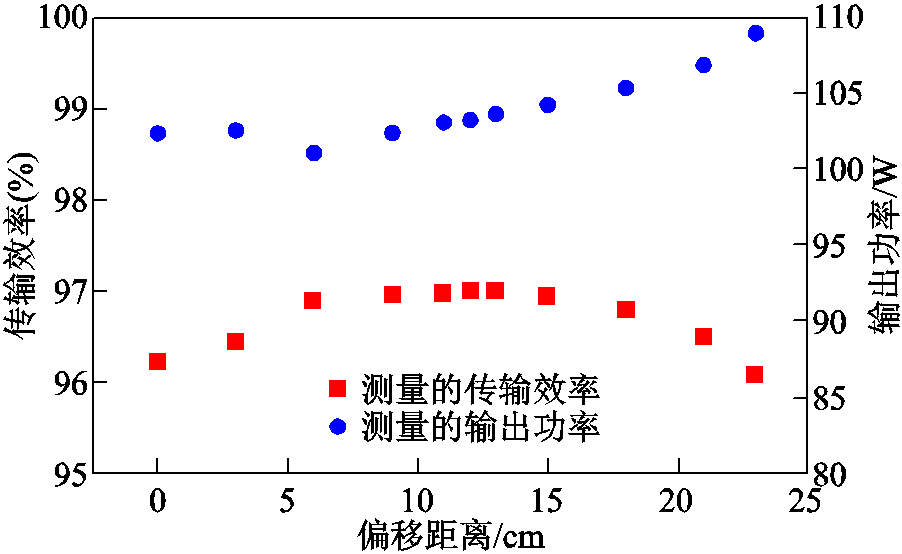
图12 新型线圈结构输出功率和传输效率测试结果
Fig.12 Measured output power and transmission efficiency with the new structure
为了进一步对比不同线圈结构间的性能,测试了普通矩形线圈结构发射线圈上的输入电压和电流、接收线圈上的输出电压和电流。普通矩形线圈结构的测试电源值和所用负载值与新型线圈结构测试中的设备值一致。图13显示了普通矩形线圈结构的输出功率和传输效率。从图13中可以看出,普通矩形线圈结构的最高传输效率为98.2%,而新型线圈结构的最高传输效率为97.0%,仅仅比新型线圈结构的效率高1.2%;随着偏移距离的变化,普通矩形线圈结构的输出功率从19.2W到44.1W变化,输出功率的波动率高达129.7%。而从图12中可知,新型线圈结构的输出功率的波动率仅为5.88%。值得一提的是,过大的耦合系数导致系统发生了功率分裂[35],所以普通矩形线圈结构在原始谐振频率点的输出功率反而下降。随着偏移距离的增加,耦合系数逐渐减小,输出功率反而会逐渐增大,如图13所示。
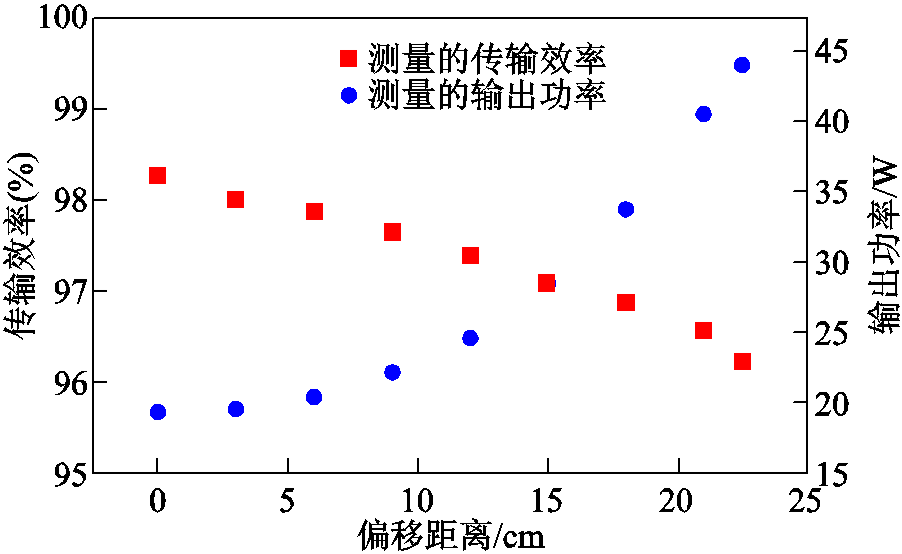
图13 普通矩形线圈结构的输出功率和传输效率测试结果
Fig.13 Measured output power and transmission efficiency with traditional structure
本文提出了一种多接收线圈正反串联结构,结合提出的互感计算方法和互感优化方法,当发射线圈与接收线圈之间的水平偏移距离在发射线圈边长一半范围内变化时,保证了其线圈间互感基本恒定。实验结果表明,当线圈间水平偏移距离在22.5cm之内变化时,线圈间的互感波动率仅为3.81%。该结构非常适合于电动汽车或AGV小车的动态无线电能传输系统,可以极大简化其动态无线电能传输系统的恒功率或恒流控制策略。本文只研究了该线圈结构在运动方向的水平偏移对互感的影响,未来需研究侧向水平偏移和运动方向的水平偏移同时变化时,如何保证线圈互感也基本恒定。
参考文献
[1] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[2] 罗成鑫, 丘东元, 张波, 等. 多负载无线电能传输系统[J]. 电工技术学报, 2020, 35(12): 2499-2516.
Luo Chengxin, Qiu Dongyuan, Zhang Bo, et al. Wireless power transfer system for multiple loads[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2499-2516.
[3] 廖志娟, 孙跃, 叶兆虹, 等. 无线电能传输系统共振机理及共振点分布特性研究[J]. 电工技术学报, 2020, 35(2): 215-224.
Liao Zhijuan, Sun Yue, Ye Zhaohong, et al. Research on resonance mechanism and resonant point distri- bution characteristic of magnetic coupling wireless power transfer systems[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 215-224.
[4] Fang Chen, Zhao Xiaojin, Xu Qin, et al. Aggregator- based demand response mechanism for electric vehicles participating in peak regulation in valley time of receiving-end power grid[J]. Global Energy Inter- connection, 2020, 3(5): 453-463.
[5] Zhang Jing, Liu Chang, Yuan Ruiming, et al. Design scheme for fast charging station for electric vehicles with distributed photovoltaic power generation[J]. Global Energy Interconnection, 2019, 2(2): 150-159.
[6] 贾金亮, 闫晓强. 磁耦合谐振式无线电能传输特性研究动态[J]. 电工技术学报, 2020, 35(20): 4217- 4231.
Jia Jinliang, Yan Xiaoqiang. Research tends of magnetic coupling resonant wireless power transfer characteristics[J]. Transactions of China Electrotech- nical Society, 2020, 35(20): 4217-4231.
[7] 赵鱼名, 王智慧, 苏玉刚, 等. 基于T型CLC谐振网络的恒压型电场耦合电能传输系统负载自适应技术[J]. 电工技术学报, 2020, 35(1): 106-114.
Zhao Yuming, Wang Zhihui, Su Yugang, et al. Load adaptive technology of constant voltage electric-field coupled power transfer system based on T-CLC resonant network[J]. Transactions of China Electro- technical Society, 2020, 35(1): 106-114.
[8] 赵锦波, 蔡涛, 段善旭, 等. 适用于分段式动态无线充电的T型抗偏移补偿拓扑[J]. 电工技术学报, 2017, 32(18): 1-7.
Zhao Jinbo, Cai Tao, Duan Shan, et al. A T-type high misalignment tolerant compensated topology for sectional track-based dynamic wireless power trans- mission system[J]. Transactions of China Electro- technical Society, 2017, 32(18): 1-7.
[9] 陈庆彬, 张伟豪, 叶逢春, 等. 结合变压器T网络模型的具有可变恒压增益特性的补偿网络参数确定新方法[J]. 中国电机工程学报, 2017, 37(15): 4483-4494, 4590.
Chen Qingbin, Zhang Weihao, Ye Fengchun, et al. A new compensation network parameters design method with variable constant voltage gain characteristics based on transformer T model[J]. Proceedings of the CSEE, 2017, 37(15): 4483-4494, 4590.
[10] 李阳, 张雅希, 闫卓, 等. 磁耦合谐振式无线电能传输系统阻抗分析与匹配电路设计方法[J]. 电工技术学报, 2016, 31(22): 12-18.
Li Yang, Zhang Yaxi, Yan Zhuo, et al. Impedance analysis and design of matching circuit in wireless power transfer system via coupled magnetic reso- nances[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 12-18.
[11] 高键鑫, 吴旭升, 高嵬, 等. 基于LCC的磁谐振无线电能传输发射端补偿技术[J]. 电工技术学报, 2016, 31(增刊1): 9-15.
Gao Jianxin, Wu Xusheng, Gao Wei, et al. Com- pensation technology of magnetic resonant wireless power transfer transmitter based on LCC[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(S1): 9-15.
[12] Lu Fei, Zhang Hua, Hofmann H, et al. A dual-coupled LCC-compensated IPT system to improve misalign- ment performance[C]//2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqing, China, 2017, 1-8.
[13] 孙跃, 张欢, 唐春森, 等. LCL型非接触电能传输系统电路特性分析及参数配置方法[J]. 电力系统自动化, 2016, 40(8): 103-107.
Sun Yue, Zhang Huan, Tang Chunsen, et al. Circuit characteristic analysis and parameter configuration method of LCL type contactless power transfer system[J]. Automation of Electric Power Systems, 2016, 40(8): 103-107.
[14] Zhao L, Thrimawithana D J, Madawala U K, et al. Hybrid bidirectional wireless EV charging system tolerant to pad misalignment[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7079-7086.
[15] Xiao Chunyan, Cheng Dingning, Wei Kangzheng. An LCC-C compensated wireless charging system for implantable cardiac pacemakers: theory, experiment, and safety evaluation[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 4894-4905.
[16] Sample A P, Waters B H, Wisdom S T, et al. Enabling seamless wireless power delivery in dynamic environments[J]. Proceedings of the IEEE, 2013, 101(6): 1343-1358.
[17] Tan Linlin, Yan Changxin, Huang Xueliang, et al. Online frequency and power regulation scheme of magnetic coupled resonant wireless power transfer[J]. Journal of Southeast University (English Edition), 2016, 32(2): 187-194.
[18] Gati E, Kampitsis G, Manias S. Variable frequency controller for inductive power transfer in dynamic conditions[J]. IEEE Transactions on Power Electro- nics, 2017, 32(2): 1684-1696.
[19] Fu Minfan, Yin He, Zhu Xinen, et al. Analysis and tracking of optimal load in wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3952-3963.
[20] Choi S Y, Gu B W, Jeong S Y. et al. Advances in wireless power transfer systems for roadway-powered electric vehicles[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(1): 18-36.
[21] Covic G A. Boys J T. Modern trends in inductive power transfer for transportation applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2013, 1(1): 28-41.
[22] Budhia M, Boys J T, Covic G A, et al. Development of a single-sided flux magnetic coupler for electric vehicle IPT charging systems[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 318-328.
[23] 胡超. 电动汽车无线供电电磁耦合机构能效特性及优化方法研究[D]. 重庆: 重庆大学, 2015.
[24] Li Zhongqi, Cheng Wangyang, Yi Jiliang, et al. Design and optimization of quasi-constant mutual inductance for asymmetric two-coil wireless power transfer system with lateral misalignments[J]. Pro- gress in Electromagnetics Research M, 2018, 69: 207-217.
[25] Ahn H R, Kim M S, Kim Y J. Inductor array for minimising transfer efficiency decrease of wireless power transmission components at misalignment[J]. Electronics Letters, 2014, 50(5): 393-394.
[26] Chow J P W, Chen N, Chung H S H, et al. An investigation into the use of orthogonal winding in loosely coupled link for improving power transfer efficiency under coil misalignment[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5632-5649.
[27] Choi S Y, Jeong S Y, Lee E S, et al. Generalized models on self-decoupled dual pick-up coils for large lateral tolerance[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6434-6445.
[28] 宋凯, 朱春波, 李阳, 等. 用于电动汽车动态供电的多初级绕组并联无线电能传输技术[J]. 中国电机工程学报, 2015, 35(17): 4445-4453.
Song Kai, Zhu Chunbo, Li Yang, et al. Wireless power transfer technology for electric vehicle dynamic charging using multi-parallel primary coils[J]. Pro- ceedings of the CSEE, 2015, 35(17): 4445-4453.
[29] Zhang Zhen, Chau K T. Homogeneous wireless power transfer for move-and-charge[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6213-6220.
[30] Lu Fei, Zhang Hua, Hofmann H, et al. A dynamic charging system with reduced output power pulsation for electric vehicles[J]. IEEE Transactions on Indu- strial Electronics, 2016, 63(10): 6580-6590.
[31] Chen Yang, Mai Ruikun, Zhang Youyuan, et al. Improving misalignment tolerance for IPT system using a third-coil[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3009-3013.
[32] Carretero C, Acero J, Alonso R J, et al. Modeling mutual impedances of loaded non-coaxial inductors for induction heating applications[J]. IEEE Transa- ctions on Magnetics, 2008, 44(11): 4115-4118
[33] Luo Zhichao, Wei Xuezhe. Analysis of square and circular planar spiral coils in wireless power transfer system for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 331-341.
[34] 吴德会, 何天府, 王晓红, 等. 感应电能传输中矩形螺线线圈互感耦合的解析建模与分析[J]. 电工技术学报, 2018, 33(3): 680-688.
Wu Dehui, He Tianfu, Wang Xiaohong, et al. Analytical modeling and analysis of mutual Indu- ctance coupling of rectangular spiral coils in inductive power transfer[J]. Transactions of China Electro- technical Society, 2018, 33(3): 680-688.
[35] 李中启, 黄守道, 易吉良, 等. 磁耦合谐振式无线电能传输系统频率分裂抑制方法[J]. 电力系统自动化, 2017, 41(2): 21-27.
Li Zhongqi, Huang Shoudao, Yi Jiliang, et al. Frequency splitting suppression method of wireless power transfer via magnetic resonance coupling[J]. Automation of Electric Power Systems, 2017, 41(2): 21-27.
Mutual Inductance Calculation and Optimization of Multi-Receiver Positive and Negative Series Coil Structure in Dynamic Wireless Power Transfer Systems
Abstract In dynamic wireless power transfer (DWPT) system via magnetic coupling resonance, the misalignment between the transmission and the receiving coils can reach half of the side length of the transmission coil. At this moment, the variations in mutual inductance are very large. These variations in mutual inductance may harm the stability of the DWPT systems. This paper proposes a multi-receiving positive and negative series coil structure to reduce the fluctuation rate of the mutual inductance. First, a method of calculating the mutual inductance of a rectangular coil is proposed, and the mutual inductance characteristics of the proposed structure are analyzed by using the formula of the mutual inductance calculation. Secondly, an optimization method of the mutual inductance is presented. The parameters of the proposed structure that meet the design requirements are obtained by using the proposed optimization method. Finally, a wireless power transfer system based on the multi-receiving positive and negative serial coil structure is developed according to the obtained parameters. And the correctness of the proposed structure and method is verified through simulation and experiment results. These results show that the maximum fluctuation rate of the mutual inductance between the coils is 3.81% by using the proposed structure when the misalignment between the coils is changed within half of the side length of the transmission coil.
keywords:Dynamic wireless power transfer system, mutual inductance calculation, mutual inductance optimization, multi-receiving positive and negative series coil structure
DOI: 10.19595/j.cnki.1000-6753.tces.211082
中图分类号:TM724
国家自然科学基金(11901188)、湖南省教育厅项目(20B186, 18A272)和湖南省自然科学基金(2019JJ60055)资助。
收稿日期 2021-07-19
改稿日期 2021-08-11
李中启 男,1985年生,博士,研究生导师,研究方向为无线电能传输系统。E-mail:lizhongqi@hnu.edu.cn
黄守道 男,1962年生,博士,教授,博士生导师,研究方向为特种电机设计及驱动和无线电能传输系统。E-mail:hsd1962@hnu.edu.cn(通信作者)
(编辑 郭丽军)