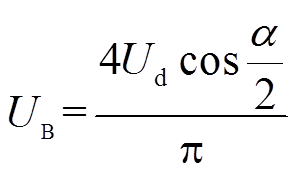（1）式中，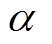
为逆变器移相角；Ud为逆变器输入侧电压。
图1 基于LCL-S型拓扑结构系统的等效电路
Fig.1 The equivalent circuit based on LCL-S topological structure system
摘要 无线电能传输（WPT）系统具有高阶、非线性及强耦合的特点。为准确描述WPT系统动态响应，进而实现控制系统的优化设计与分析，该文以LCL-S电路拓扑为研究对象，利用广义状态空间平均建模方法得到WPT系统的大信号模型，在此基础上建立系统高阶小信号模型。同时，为简化系统控制器设计，采用拉盖尔多项式展开与平衡理论相结合的方法，对高阶小信号模型进行降阶处理，即将11阶系统降为3阶。仿真与实验结果表明，降阶系统与全阶系统具有相似的动态响应及小扰动稳定性，验证了降阶模型的有效性与准确性，为WPT控制系统的设计奠定了模型基础。
关键词：无线电能传输 小信号模型 平衡实现 模型降阶
无线电能传输（Wireless Power Transfer, WPT）技术通过高频磁场构建能量传输通道，能在非导电介质之间传输电能，避免了机械式的连接方式，且具有耐高温、耐腐蚀、安全可靠性高等诸多优点，近年来在电动汽车、医疗植入设备、自主式水下机器人（Autonomous Underwater Vehicle, AUV）等领域得到了广泛研究[1-6]。
由于无线电能传输系统通过松耦合变压器实现气隙传能，为最大限度地减少漏磁及满足直流负载需求，需引入谐振与不控整流环节，使得系统具有高阶、非线性及强耦合的特点，极大地增加了控制器的设计难度与复杂性。目前针对WPT系统控制器设计，主要基于建模与控制算法的研究，且为了获取系统优良的动态性能，系统建模应最大限度地接近于实际。为满足这一需求，现有针对WPT系统的建模方法主要有状态空间平均（State Space Average, SSA）、广义状态空间平均（Generalized SSA, GSSA）、频闪映射方法[7]和拓展描述函数法。其中，广义状态空间平均法能够精确地描述15阶以下变换器系统各状态变量的动态响应，文献[8]基于此方法建立了双向WPT系统状态空间模型。文献[9-10]使用拓展函数法，对于SS拓扑的WPT系统进行建模，得到了一个9阶的小信号模型。
然而系统阶数过高会增加控制系统设计的难度。因此针对系统模型降阶的研究得以重视。模型降阶即在保证动态特性及稳定性与原系统相似的条件下，利用低阶模型代替原高阶系统，采用该方法可极大地简化系统控制器设计。文献[11]采用Krylov子空间的降阶方法对配电网络进行降阶，但缺点在于算法较为复杂，且无法保证系统的可控与可观性。文献[12]运用平衡理论的方法将电力系统模型进行降阶，得到的降阶系统很好地保留了原系统的动态过程和稳定性。文献[13]同样采用平衡理论的方法针对模块化多电平变换器进行降阶并设计控制器，为预估与改善系统的不稳定性提供了便捷。目前，系统降阶在无线电能传输领域中研究较少，如文献[14]针对WPT系统进行小信号建模，为了验证所设计控制器性能，仅对模型的零极点分布进行了研究，但整体的控制仿真系统仍采用阶数较高的小信号模型结构。文献[15]将WPT系统中LC谐振部分视作一个电感元件，采用场振幅与场相位对等效电感元件进行描述，从而成功地将9阶小信号模型降为5阶系统，但该方法理论体系较为复杂，缺乏一定的适用性，且系统所降阶次仍然较高。文献[16]采用闭环主导极点法，将WPT系统由11阶等效为2阶系统，由于只考虑了主导极点，在动态特性与稳态误差上无法保证与原系统高度匹配，同时闭环主导极点法源于经典控制理论，故仅针对单输入单输出系统，应用上具有一定的局限性。
本文首先基于LCL-S拓扑结构的WPT系统进行小信号建模，采用拉盖尔多项式展开与平衡理论相结合，对全阶小信号模型进行了降阶处理；然后针对降阶后不同阶数与全阶系统进行对比分析，得出有利于控制器设计的等效三阶模型；最后，通过仿真与实验验证了降阶后小信号模型与全阶系统高相似度的特点。
图1所示为LCL-S拓扑结构的WPT系统的等效电路。其中，R1、Rp和Rs分别是L1、Lp和Ls的内阻，Cf是输出侧滤波电容,uH为逆变器输出电压，对其进行傅里叶级数展开，得到基波幅值UB，其值为
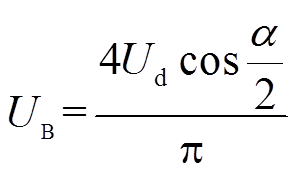（1）式中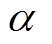，为逆变器移相角；Ud为逆变器输入侧电压。
图1 基于LCL-S型拓扑结构系统的等效电路
Fig.1 The equivalent circuit based on LCL-S topological structure system
通过LCL-S型拓扑结构的滤波后，逆变器输出电压的基波分量uB提供了主要功率输出的功能，所以采用uB代替逆变器输出电压。此外，用方波电压源urec与电流源irec来等效表示整流电路部分[17]。
选取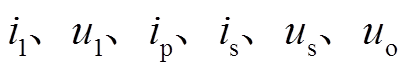
为状态变量，根据图1的系统等效电路可建立系统的微分方程为
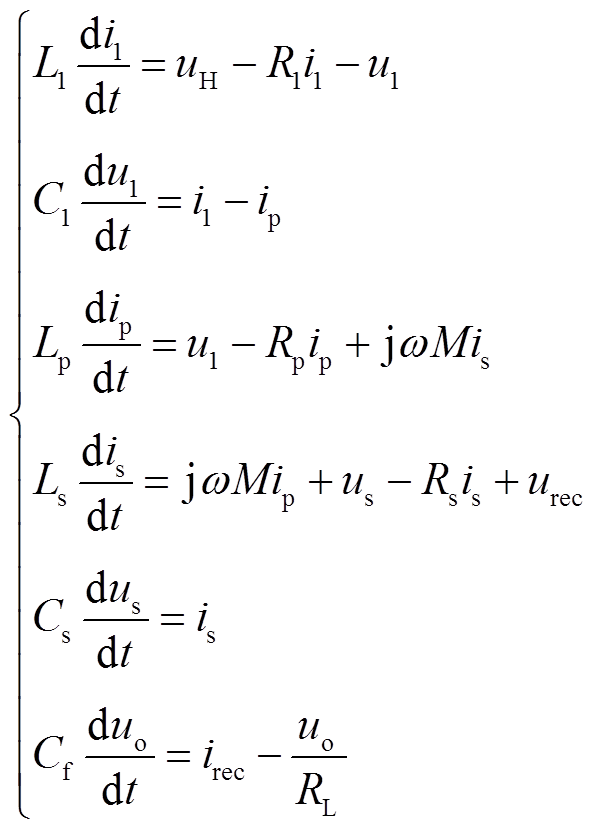（2）以逆变器输出电压为零相位参考，逆变器输出电压和其他状态变量[18]可表示为
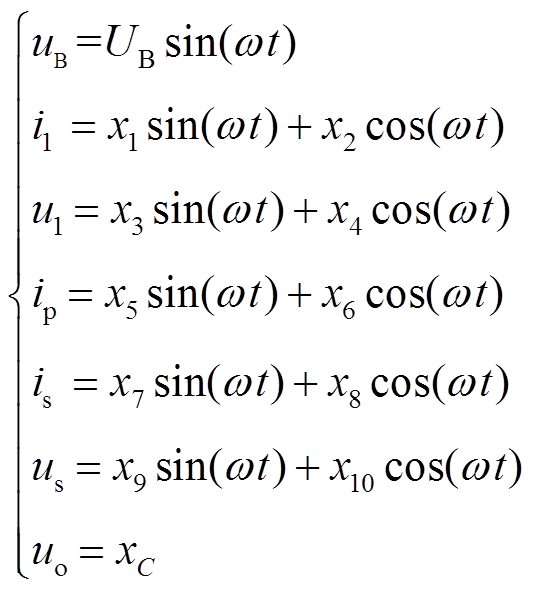（3）式中，奇数项为正弦分量幅值；偶数项为余弦分量幅值；xC为滤波电容的电压有效值。
由于WPT系统副边谐振网络工作在额定频率附近，且urec为方波信号，通过傅里叶展开可得无数的奇次谐波，因此可将3次及以上谐波滤除[19]，其基波分量为
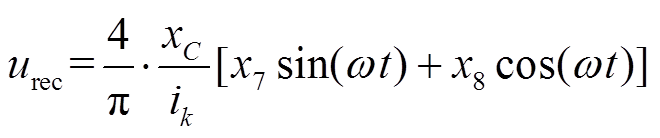（4）由于整流桥的输入输出功率守恒，可得整流部分输出电流irec为
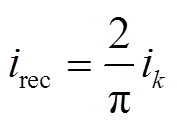（5）其中，ik的表达式为
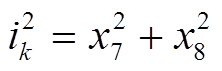（6）选取状态变量
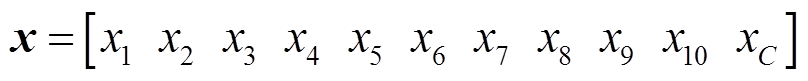
将式（3）～式（6）代入式（2）可建立系统的广义状态空间平均模型为
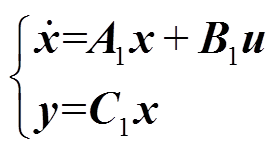（7）式中，A1∈R11×11，B1∈R11×1，C1∈R1×11，其值分别为附录中式（A1）、式（A2）与式（A3）。式（7）即为谐振电路大信号模型，令微分项为零可得到系统在稳态点时各个状态变量的幅值大小。
在非线性系统中，若各物理量只在稳态点产生较小的变化，则非线性模型就可以在此稳态点下表示为线性模型，进而可利用小信号模型来设计系统的控制器。在系统的稳态点（UB,ss, Xi,ss）下使逆变器输出电压产生一个扰动，进而各状态变量会相应地产生一个扰动（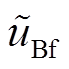
, 
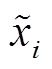），即
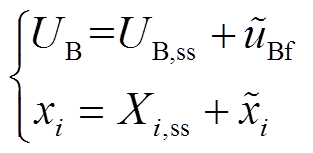（8）由于系统模型中存在非线性部分，即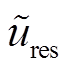
与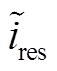
，可利用泰勒公式，将式（8）中非线性部分在稳态点进行线性化处理为
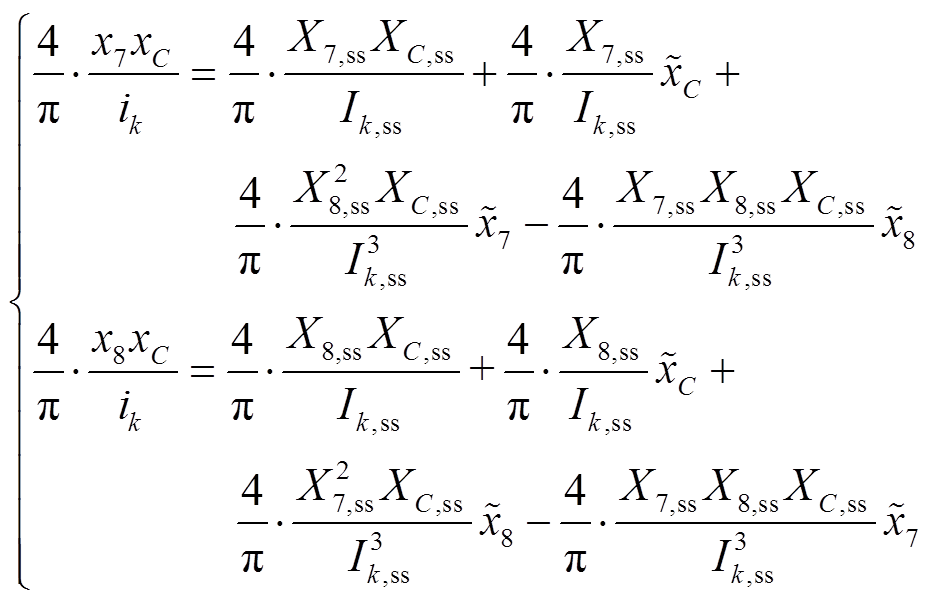（9）其中
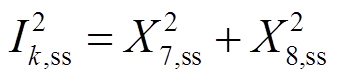（10）将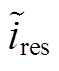
进行线性化处理
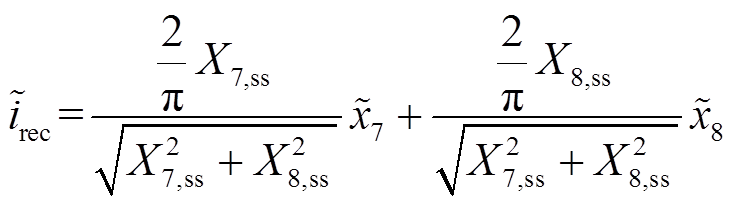（11）将式（8）～式（11）与式（7）结合，现以x=[x1x2x3x4x5x6x7 x8x9x10xC]为状态变量建立小信号模型，即
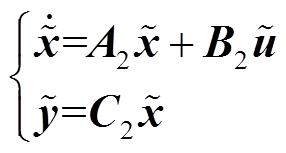（12）式中，A2∈R11×11，B2∈R11×1，C2∈R1×11，A2、B2、C2值分别为附录中式（A4）、式（A2）和式（A3）；参数ki（i=1,…,5）见附录式（A5）。
本文基于平衡理论和Hankel奇异值降阶思想对系统模型进行降阶，在保证系统动态特性基本不变的条件下，利用低阶系统代替原高阶系统。
平衡实现是将原高阶系统模型转换为平衡系统后，通过奇异值分解得到降阶模型，即通过选取适当映射子空间得到高性能降阶模型的降阶方法[20]。
式（12）所表示的WPT系统高阶小信号模型可描述为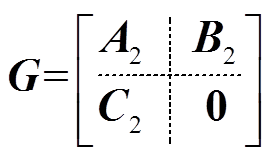
，且假设系统是稳定的，则其可控格兰姆矩阵Wc和可观格兰姆矩阵Wo是正定的，分别定义为
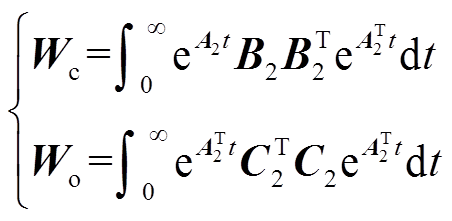（13）通过非奇异变换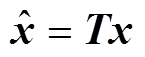
得到
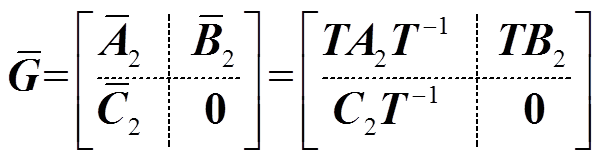（14）若系统同时满足式（15），则可认为式（14）是WPT系统小信号模型的平衡系统。
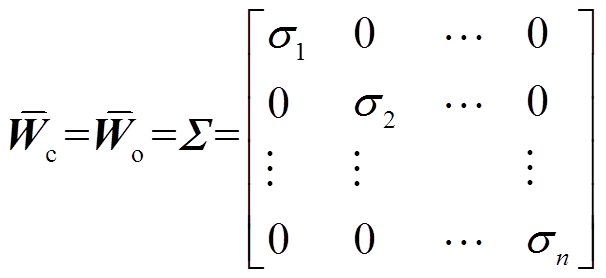（15）式中，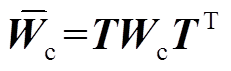
；
；
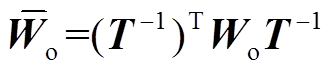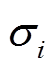为该系统的Hankel奇异值，且
。
对于平衡系统，其Hankel奇异值代表了各状态的重要性[21]，系统中最大奇异值的状态影响系统输入输出行为最大，因此可根据条件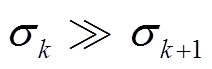
，对Hankel奇异值进行区分，从而可将平衡系统用分块形式进行描述为
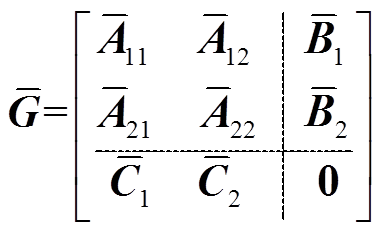（16）平衡截断法是将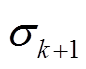
之前的状态变量保留，余下部分直接消去，最终降阶系统模型为
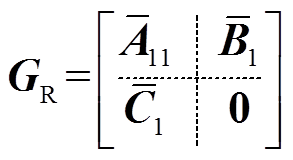（17）式中，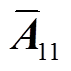
∈Rk×k；
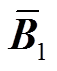∈Rk×1；
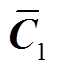∈R1×k。
上述平衡截断法是通过求解Lyapunov方程来得到系统的可控格兰姆矩阵Wc和可观格兰姆矩阵Wo，存在计算复杂度高，求解过程时间长的缺点。鉴于拉盖尔多项式展开法在满足一定精度的条件下可将矩阵指数进行近似求解，具有求解过程高效的优点，故本文采用该方法解决问题。
系统的状态转移矩阵又称作矩阵指数，即eAt。本文采用的方法是基于拉盖尔多项式将eAt进行展开，从而简化平衡截断方法中可控格兰姆矩阵Wc与可观格兰姆矩阵Wo的求解。
拉盖尔多项式可表示为
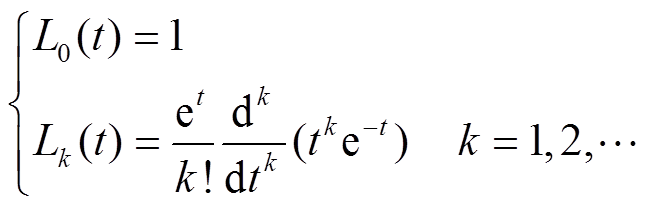（18）对指数函数eat进行拉盖尔多项式级数展开可得
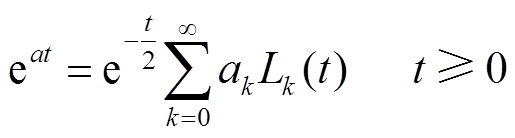（19）其中，ak满足
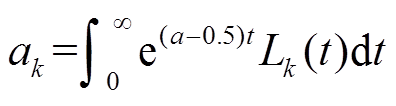（20）将拉盖尔多项式进行拉普拉斯变换可得[22]
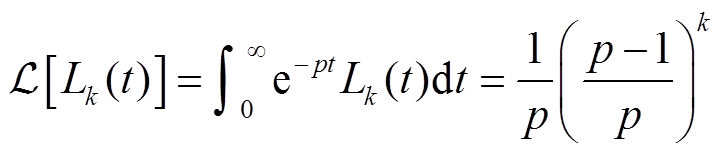（21）令p=-(a-0.5)，代入式（21）能够得到递归形式为
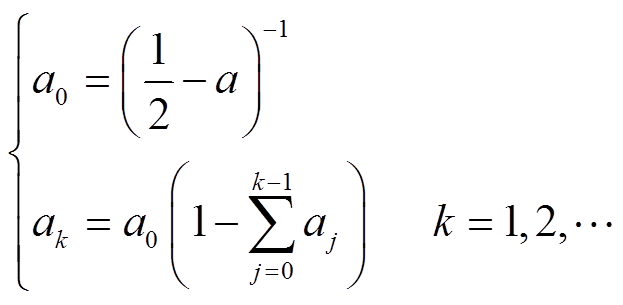（22）进行上述推导后，所得递归形式可类似地应用于全阶小信号系统的状态转移矩阵。
基于拉盖尔多项式展开的求解方法，首先对式（13）中的矩阵eA2t进行近似展开为
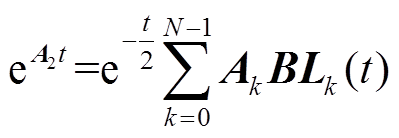（23）由2.2节可知，其中
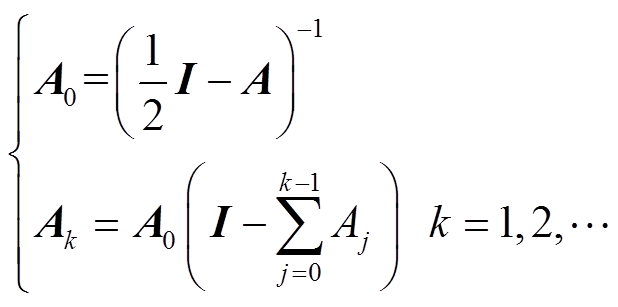（24）将式（23）与式（24）代入到式（13）中可得
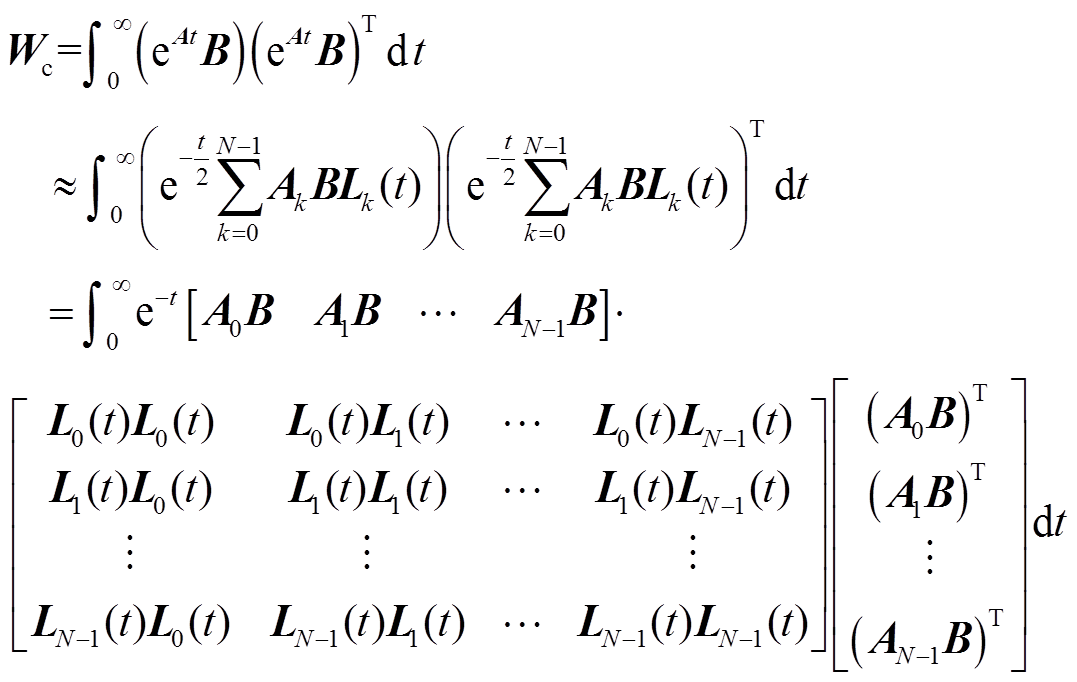
由拉盖尔多项式的正交性，可以得到系统可控格兰姆矩阵的低秩分解为
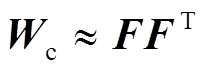（25）式中，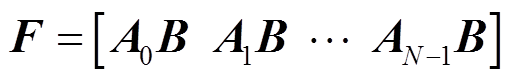
。
同理，可观格兰姆矩阵能够得到低秩分解为
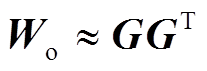（26）式中，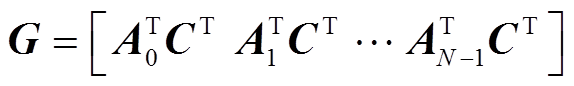
，后通过奇异值分解UΣVT=GTF，计算正定对角矩阵
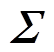和正交矩阵U、V。令矩阵P、Q为
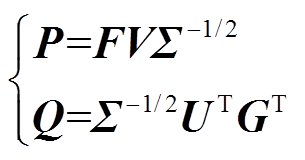（27）通过投影变换得到平衡系统
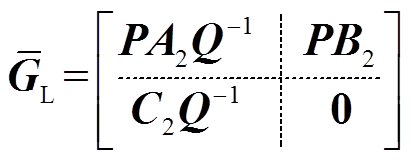（28）用平衡截断法对平衡系统进行截断处理，保留对系统输入输出影响较大的状态变量，舍去冗余部分，即可得到基于拉盖尔多项式展开方法的小信号模型降阶系统。
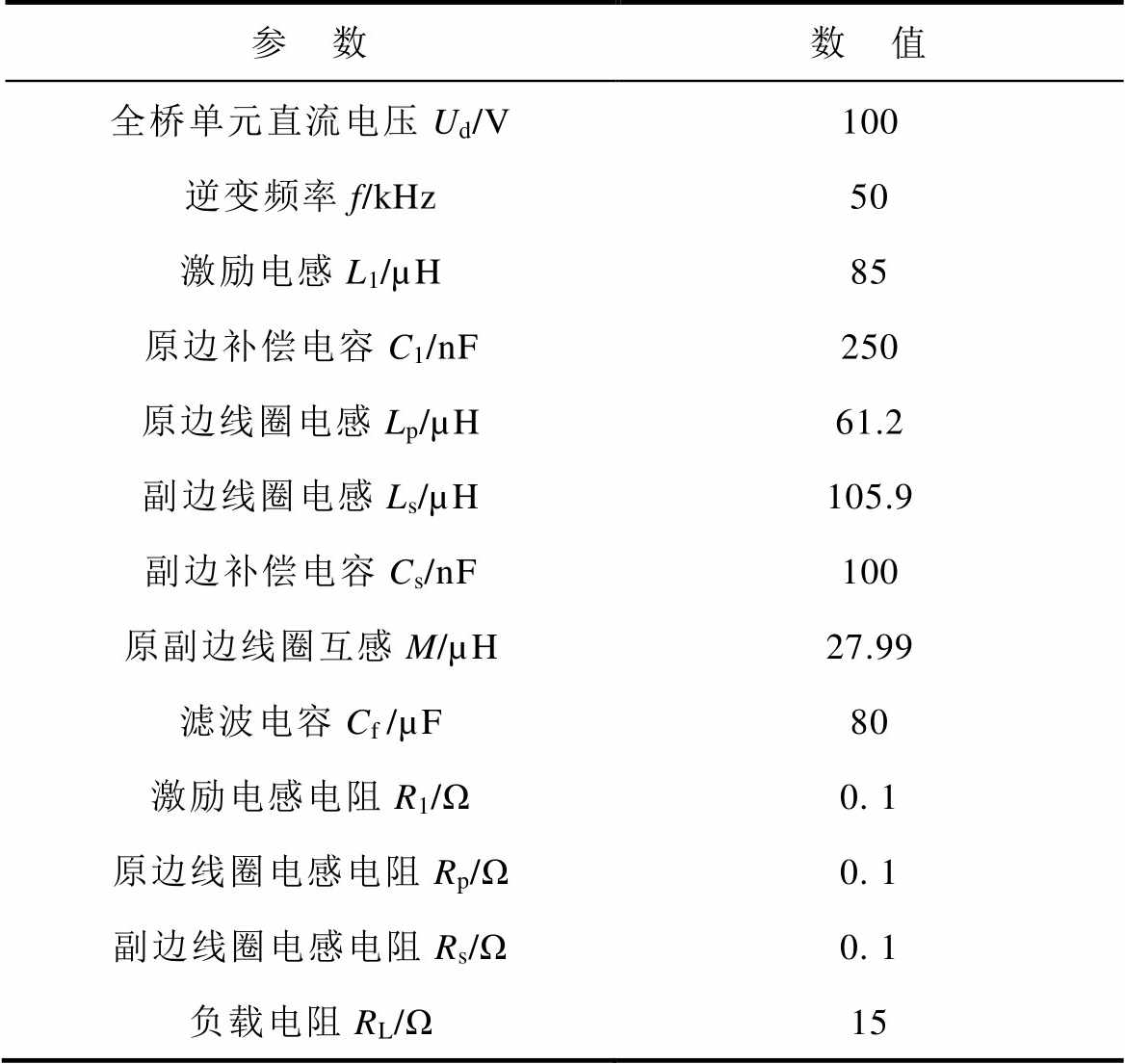
本文以LCL-S拓扑的WPT系统为研究对象，其仿真模型参数见表1。
表1 WPT系统仿真参数
Tab.1 Simulation parameters of the WPT system
参 数数 值 全桥单元直流电压Ud/V100 逆变频率f/kHz50 激励电感L1/µH85 原边补偿电容C1/nF250 原边线圈电感Lp/µH61.2 副边线圈电感Ls/µH105.9 副边补偿电容Cs/nF100 原副边线圈互感M/µH27.99 滤波电容Cf/µF80 激励电感电阻R1/Ω0. 1 原边线圈电感电阻Rp/Ω0. 1 副边线圈电感电阻Rs/Ω0. 1 负载电阻RL/Ω15
根据所给参数，采用上述理论分析对系统进行降阶，全阶小信号模型的阶数为11阶，降阶处理后得到系统阶数与Hankel奇异值对应关系如图2所示。显然，前5个状态占了系统总信息99%以上，后6个状态的Hankel奇异值远远小于前5个状态的奇异值。因此，以下仿真中将分别针对1～5阶系统，从时域与频域等方面进行分析，比较各阶数系统与全阶系统的匹配程度。
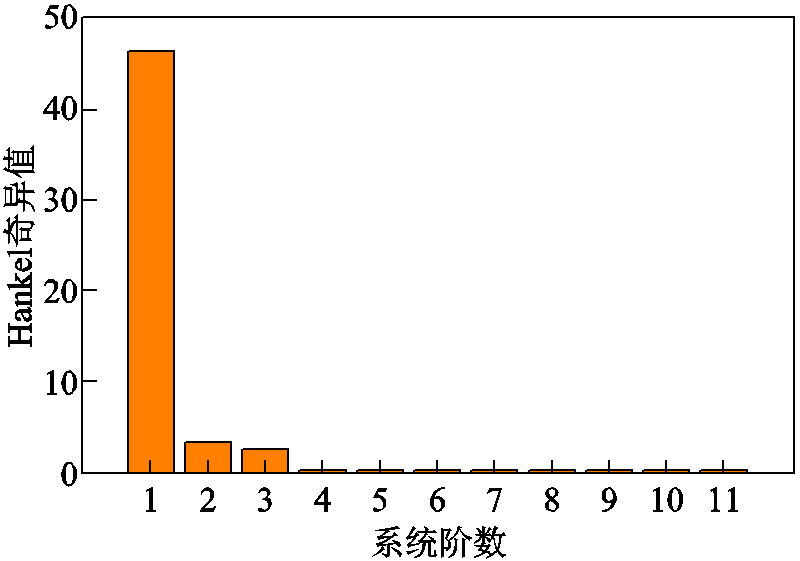
图2 Hankel奇异值
Fig.2 Hankel singular value
采用表1所示参数，移相角α从180°阶跃至 0°的条件下，从时域角度对原系统与降阶系统的输出动态行为与稳态值进行分析，响应如图3所示。
图3 全阶与各降阶系统的阶跃响应曲线
Fig.3 Step response curves of full-order and reduced-order systems
由图3可以看出，5阶系统与全阶系统的系统响应曲线基本一致，3、4阶系统的输出响应较原系统曲线误差也较小，偏差在0.6V以下。而1、2阶系统的稳态时误差相对较大。
为了定量地分析各降阶系统与原系统的匹配程度，本文采用皮尔逊相关系数来进行计算与分析，其取值在-1～1之间，绝对值越大，说明二者相关性越强，其公式为
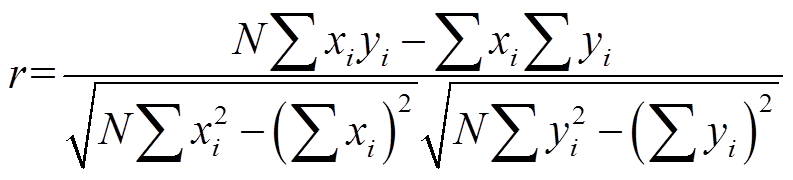（29）式中，N为数据点个数；xi、yi分别为第i个节点数据；r为皮尔逊相关系数。
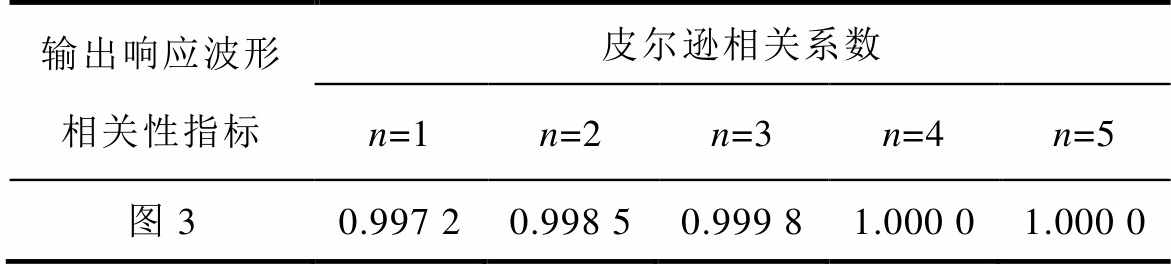
各降阶系统与全阶小信号系统动态响应波形的皮尔逊相关系数见表2，由数据可以看出3～5阶系统的响应曲线与全阶系统的匹配程度较高。
表2 降阶系统动态响应皮尔逊相关系数
Tab.2 Pearson correlation coefficient of dynamic response of reduced-order system
输出响应波形相关性指标皮尔逊相关系数 n=1n=2n=3n=4n=5 图30.997 20.998 50.999 81.000 01.000 0
为了进一步分析3～5阶系统与全阶系统的匹配程度，图4与图5分别给出降阶前后模型的极点分布与伯德图。
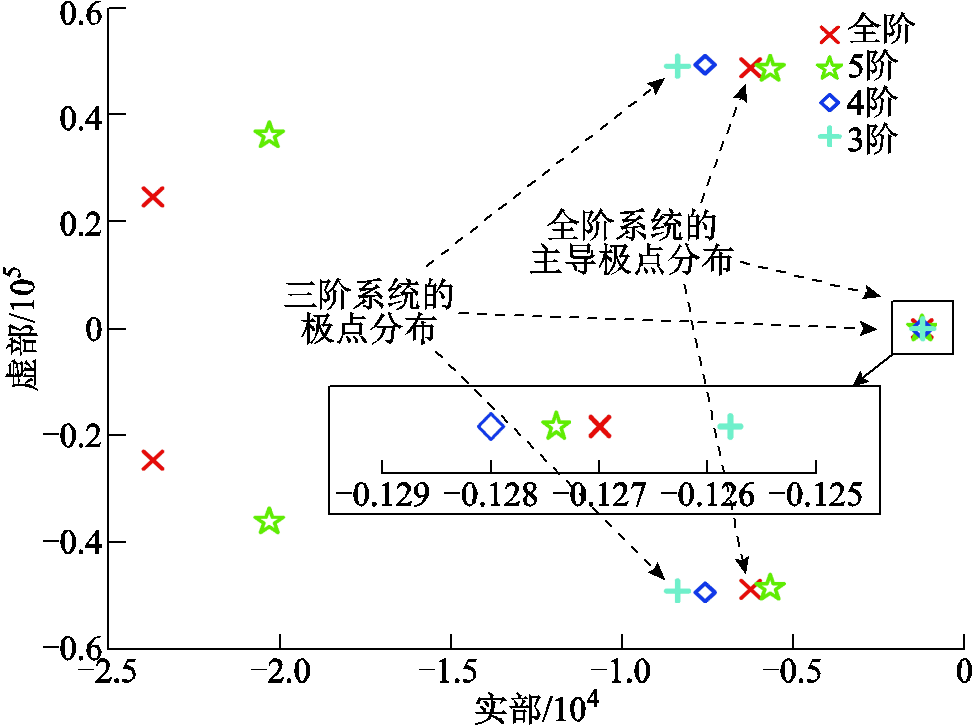
图4 全阶与3～5阶系统极点分布
Fig.4 Pole distribution diagram of full-order and 3～5 order systems
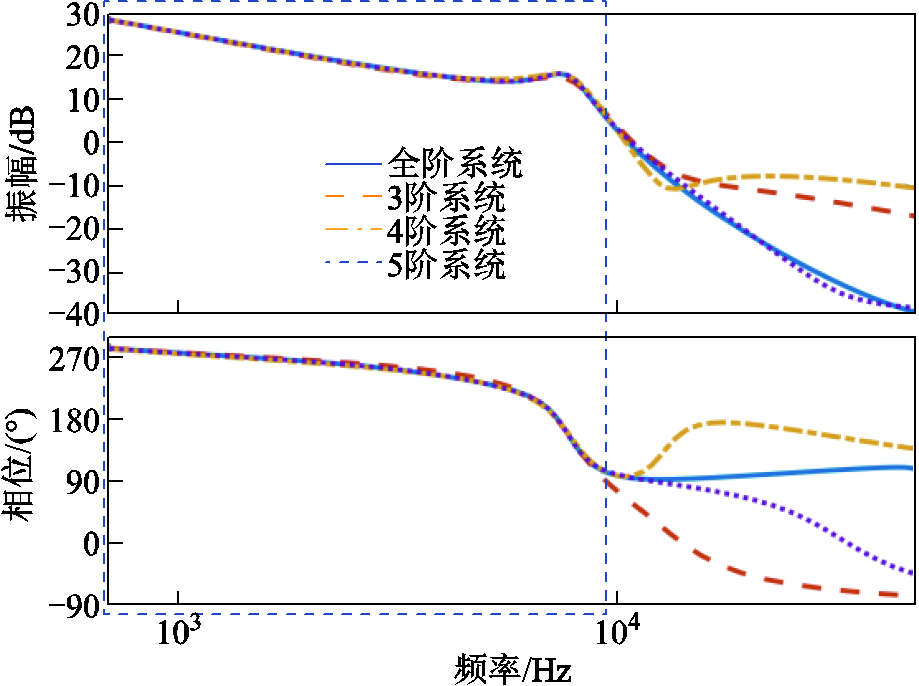
图5 全阶与3～5阶系统的伯德图
Fig.5 Bode plots of full order and 3～5 order systems
由图4可知，3阶降阶系统与全阶系统主导极点具有较高的相似性，即瞬态响应趋于一致，且从伯德图中可以看出，降阶系统与全阶系统重叠的部分接近10kHz。因此，为了大大简化一定频率范围内控制器的分析和设计，可将全阶系统用3阶降阶系统来表征与模拟。
为验证所得模型的可靠性，现搭建如图6所示基于LCL-S拓扑结构的无线电能传输实验平台。
图6 无线充电装置实验平台
Fig.6 Experimental platform of wireless charging device
图7是输入直流电压100V，负载为15Ω，移相角为0°时原边逆变与副边整流输出电压与电流波形，可以看出系统逆变侧输出电流滞后于移相电压，处于弱感性状态，这为系统能够工作在软开关状态下提供了条件。
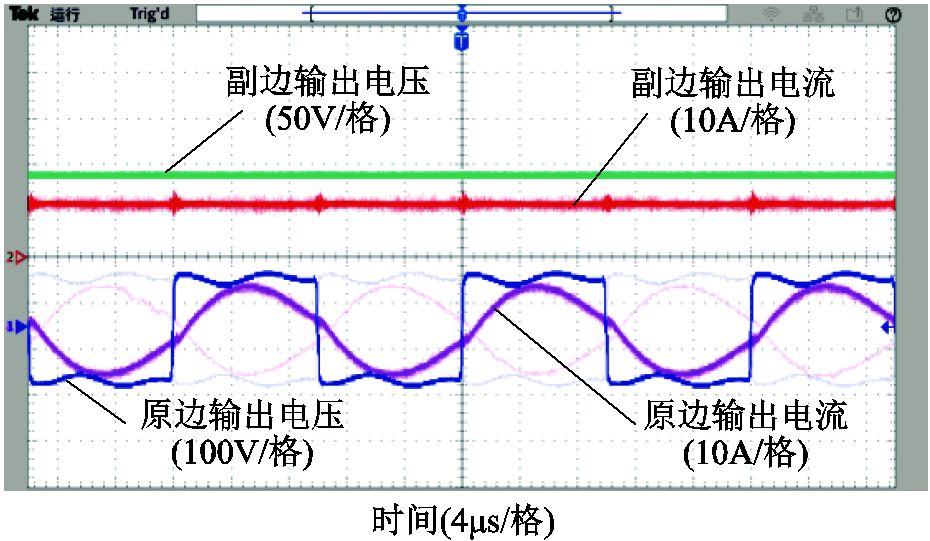
图7 原边逆变与副边整流输出电压与电流波形
Fig.7 Output voltage and current waveforms of primary side inverter and secondary side rectifier
图8是移相角从180°阶跃至0°时实验平台的负载电压与三阶系统仿真波形的对比，其稳态误差仅为1.71V，可满足基本精度需求。二者的皮尔逊相关系数为0.792 2（系数在±(0.5～1)以内即为强相关）。因此认为降阶模型能够有效地模拟全阶系统。
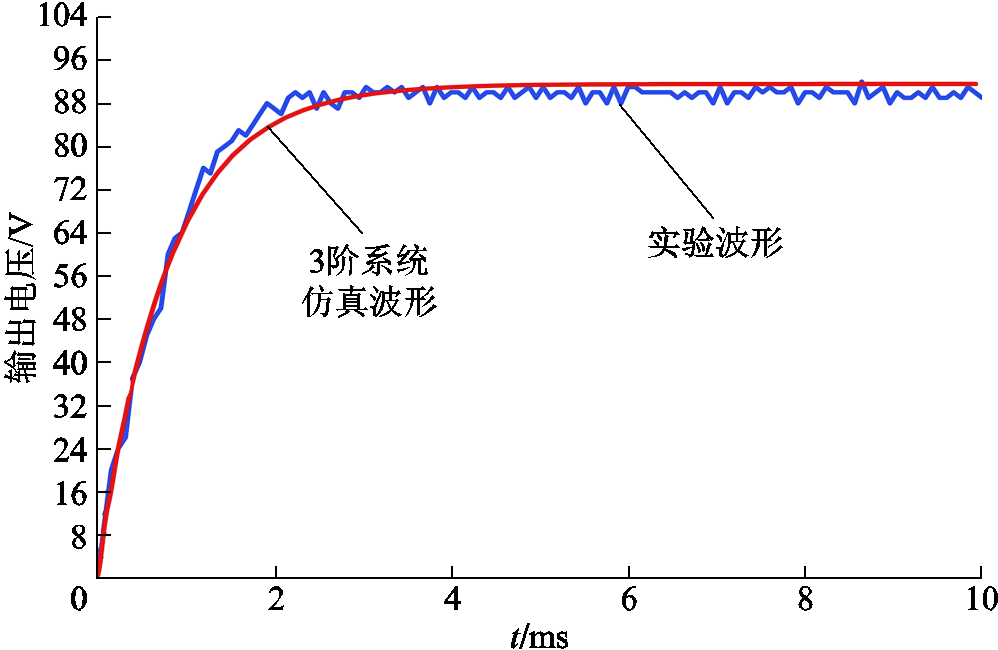
图8 降阶模型仿真与实验波形
Fig.8 Reduced-order model simulation and experimental waveforms
为验证降阶系统在频域上的匹配程度，采用数字控制方法，通过控制器产生稳态移相角的同时叠加幅值一定但频率不同的小信号移相角，而后通过示波器的FFT分析采集统一频率下的输出响应与小信号移相角的信号增益大小，从而绘制出仿真全阶、3阶系统和实验平台的开环伯德图如图9所示。由图9可以看出，实际与仿真系统的幅频响应吻合较好，但存在一定的偏差。降阶模型与实验平台在时域和频域均存在一定误差，造成这种偏差的原因为：实验平台中的器件可能存在杂散参数，在运行过程中影响系统的动态特性；在小信号模型分析建模时所采用的线性化方法使得系统存在一部分的失真。
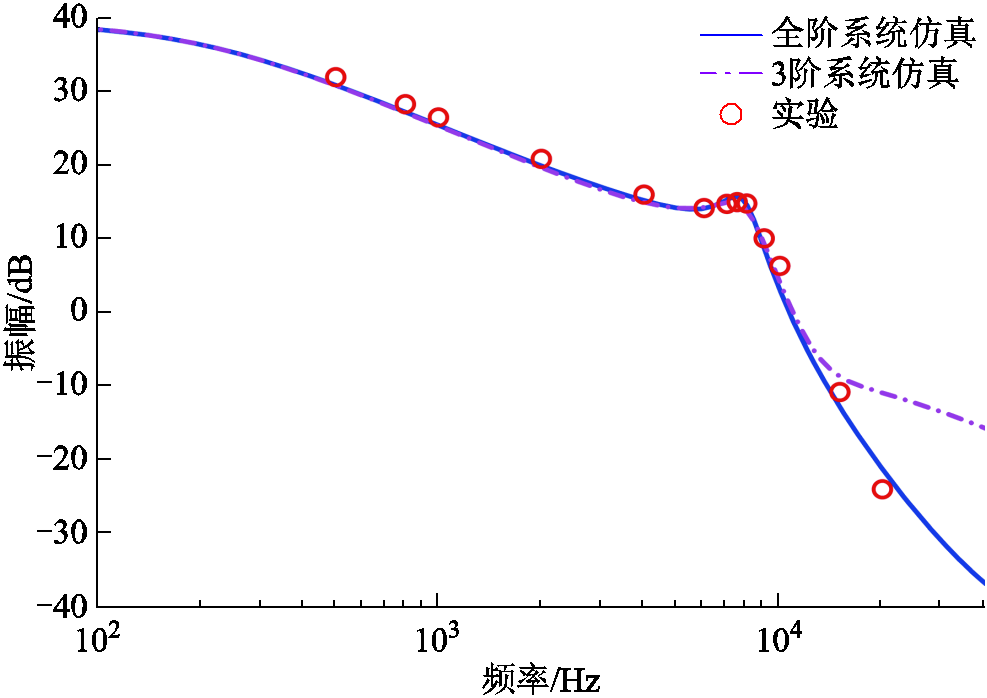
图9 仿真与实验系统伯德图
Fig.9 Bode plot of simulation and experiment system
1）本文建立了基于LCL-S电路拓扑的无线电能传输系统小信号模型，采用拉盖尔多项式展开与平衡截断相结合的方法，使原11阶系统降至3阶系统，通过仿真对比了全阶系统、1～5阶系统在稳态工作点处的动态阶跃响应。结果表明，5阶与全阶系统响应曲线基本一致，3、4阶系统的输出响应较原系统偏差也仅在0.6V以下。验证了降阶模型的有效性和准确性。
2）针对本文所设计的无线电能传输系统，3阶降阶系统与全阶系统主导极点具有较高的相似性，使得3阶模型基本保留原模型的动态特性，并且最终都趋于平稳，达到降阶且保持原系统性能近似不变的目的。因此，可将全阶系统用3阶降阶系统来表征与模拟全阶系统，进而极大地简化一定频率范围内控制系统的分析和设计。
3）本文所采用的小信号建模及与之相对应的降阶方法，可应用于不同电路拓扑的无线电能传输控制系统的设计，具有一定的普适性。
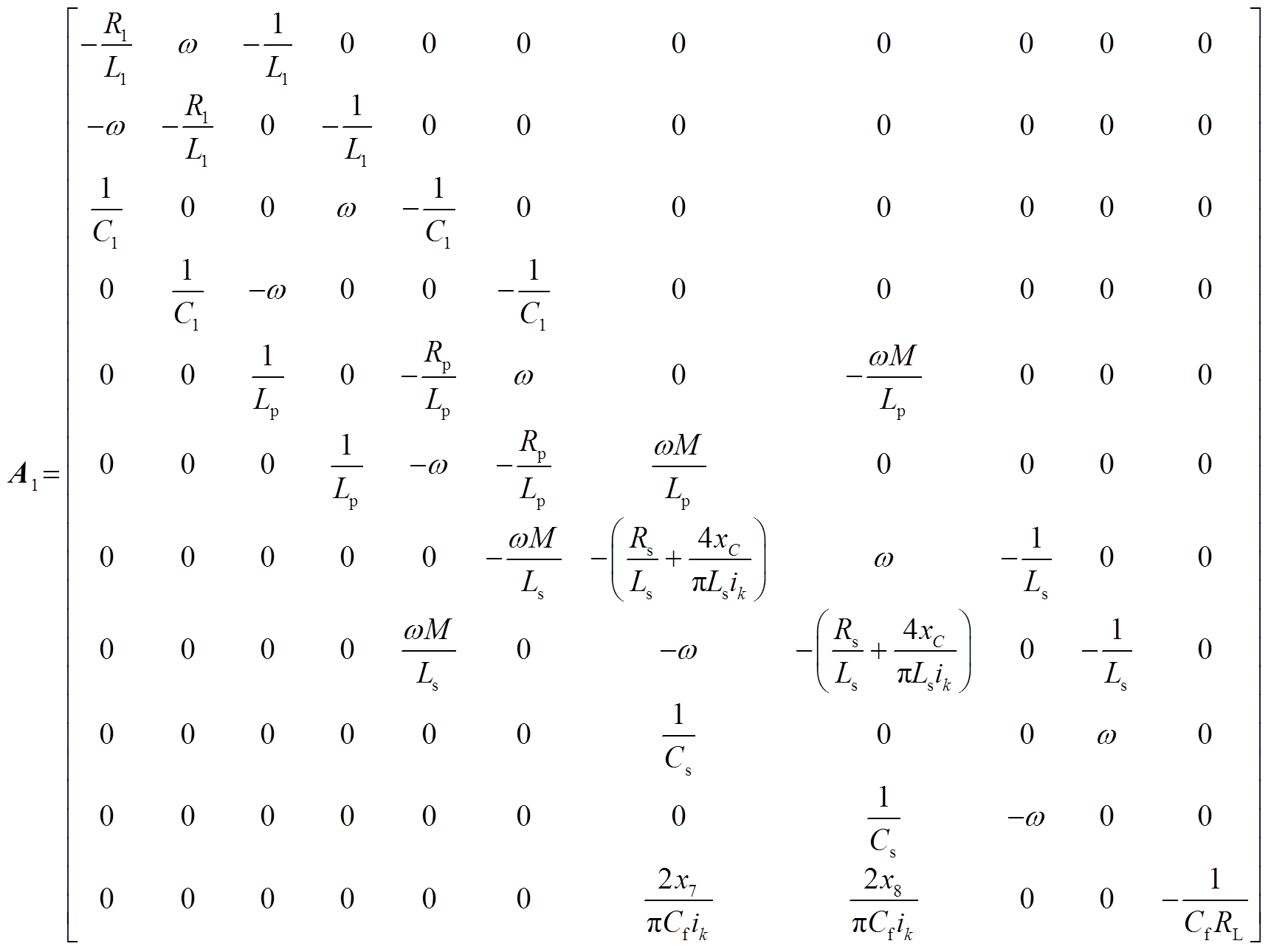（A1）B1、B2表达式为
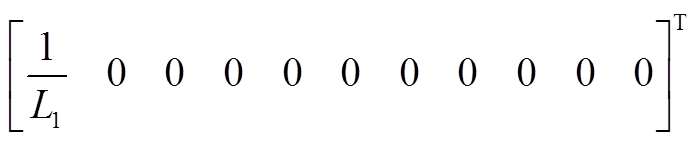（A2）C1、C2表达式为
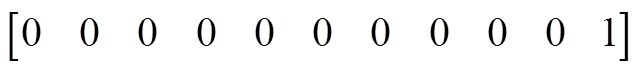（A3）
（A4）
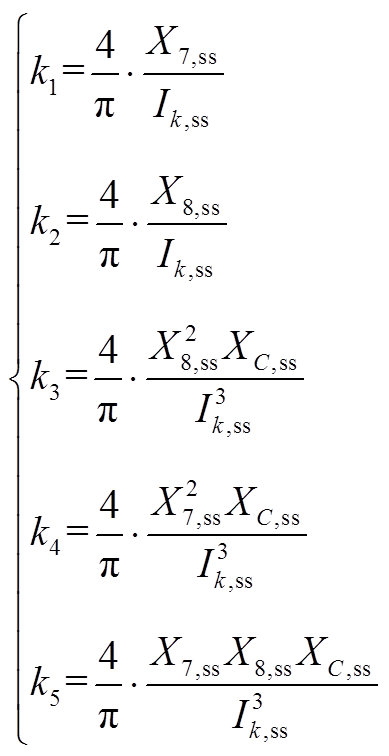（A5）参考文献
[1] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[2] 范兴明, 高琳琳, 莫小勇, 等. 无线电能传输技术的研究现状与应用综述(英文)[J]. 电工技术学报, 2019, 34(7): 1353-1380.
Fan Xingming, Gao Linlin, Mo Xiaoyong, et al. Overview of research status and application of wireless power transmission technology[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(7): 1353-1380.
[3] 张献, 任年振, 杨庆新, 等. 电动汽车无线充电自整定控制[J]. 电工技术学报, 2020, 35(23): 4825- 4834.
Zhang Xian, Ren Nianzhen, Yang Qingxin, et al. Research on self-tuning control strategy of wireless charging for electric vehicles[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4825- 4834.
[4] Zhen Z, Pang H, Georgiadis A, et al. Wireless power transfer—an overview[J]. IEEE Transactions on Industrial Electronics, 2018, 66(2): 1044-1058.
[5] 蔡春伟, 武帅, 张言语, 等. 基于弧形线圈结构的无线充电系统能量传输与控制[J]. 电工技术学报, 2020, 35(14): 2959-2968.
Cai Chunwei, Wu Shuai, Zhang Yanyu, et al. Power transfer and control of wireless charging system based on an arc coil structure[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 2959- 2968.
[6] 卿晓东, 苏玉刚. 电场耦合无线电能传输技术综述[J]. 电工技术学报, 2021, 36(17): 3649-3663.
Qing Xiaodong, Su Yugang. An overview of electric- filed coupling wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3649-3663.
[7] 代云中, 何凯瑞, 杜程茂, 等. LC滤波H6结构逆变器离散模型简化与动力学行为[J]. 高电压技术, 2017, 43(10): 3313-3321.
Dai Yunzhong, He Kairui, Du Chengmao, et al. Discrete model simplification and dynamic behavior of LC-filter-based inverter with H6 type[J]. High Voltage Engineering, 2017, 43(10): 3313-3321.
[8] Hu A P. Modeling a contactless power supply using GSSA method[C]//Proceedings of the 2009 IEEE International Conference on Industrial Technology, Churchill, VIC, Australlia, 2009: 10-13.
[9] Zahid Z U, Dalala Z M, Cong Z. Modeling and control of series–series compensated inductive power transfer system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(1): 111-123.
[10] Huang Zhicong, Wong Siu-Chung, Tse C K. Control design for optimizing efficiency in inductive power transfer systems[J]. IEEE Transactions on Power Electronics, 2017, 33(5): 4523-4534.
[11] 李鹏, 于浩, 王成山, 等. 基于Krylov子空间的大规模配电网络模型整体化简方法[J]. 电网技术, 2013, 37(8): 2343-2348.
Li Peng, Yu Hao, Wang Chengshan, et al. Model order reduction of large scale distribution grid based on Krylov subspace method[J]. Power System Tech- nology, 2013, 37(8): 2343-2348.
[12] 张喆, 赵洪山, 李志为, 等. 平衡格莱姆方法在电力系统线性模型降阶中的应用[J]. 电工技术学报, 2013, 28(6): 201-207.
Zhang Zhe, Zhao Hongshan, Li Zhiwei, et al. Power system linear model reduction based on the balanced gramian method[J]. Transactions of China Electrote- chnical Society, 2013, 28(6): 201-207.
[13] 李正, 郝全睿, 尹晓东, 等. 模块化多电平换流器的降阶小信号模型研究[J]. 中国电机工程学报, 2018, 38(12): 3638-3650.
Li Zheng, Hao Quanrui, Yin Xiaodong, et al. Research on reduced-order small-signal model of modular multilevel converter[J]. Proceedings of the CSEE, 2018, 38(12): 3638-3650.
[14] Aditya K, Williamson S S. Simplified mathematical modelling of phase-shift controlled series-series compensated inductive power transfer system[C]// 2016 IEEE 25th International Symposium on Indu- strial Electronics (ISIE), Santa Clara, CA, USA, 2016: 8-10.
[15] Li Hongchang, Wang Kangping, Huang Lang, et al. Dynamic modeling based on coupled modes for wireless power transfer systems[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(11): 6245- 6253.
[16] Feng H, Lukic S M. Reduced-order modeling and design of single stage LCL compensated IPT system for low voltage vehicle charging applications[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 3728-3739.
[17] Zahid Z U, Dalala Z M, Cong Z, et al. Modeling and control of series–series compensated inductive power transfer system[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2015, 3(1): 111-123.
[18] Sanders S R, Noworolski J M. Generalized averaging method for power conversion circuits[J]. IEEE Transactions on Power Electronics, 1991, 6(2): 251-259.
[19] Borage M, Tiwari S, Kotaiah S. Analysis and design of an LCL-T resonant converter as a constant-current power supply[J]. IEEE Transactions on Industrial Electronics, 2005, 52(6): 1547-1554.
[20] Moore B. Principal component analysis in linear systems: controllability, observability, and model reduction[J]. IEEE Transactions on Automatic Control, 1981, 26(1): 17-32.
[21] Chang W, Smith R C. Model reduction based on modal Hankel singular values[J]. International Society for Optics and Photonics, 2004, 5383: 433-444.
[22] Moore G. Orthogonal polynomial expansions for the matrix exponential[J]. Linear Algebra and Its Appli- cations, 2011, 435(3): 537-559.
Research on Order Reduction of Small Signal Model of Wireless Power Transmission System
Abstract The wireless power transmission system has the characteristics of high level, nonlinearity, and strong coupling. To describe the dynamic response of the WPT system accurately to realize the optimal design and analysis of the control system, the report takes the LCL-S circuit topology as a research subject. Firstly, the large-signal model of the WPT system is obtained by the generalized state-space average modelling method. On the basis to establish a high-level small-signal model of the system. Also, Laguerre's expansion and balancing realization were used to reduce the level of the high-level small-signal model to obtain the low-order model and to simplify the design of the system controller. So, the third level was reduced by the eleventh level system. Simulation and experimental results show that the level-reduced system and full-level system have a similar dynamic response and small disturbance stability, which verifies the effectiveness and accuracy of the level-reduced model. And it builds a model foundation for the design of the WPT control system.
keywords：Wireless power transfer, small-signal model, balanced realization, model reduction
DOI: 10.19595/j.cnki.1000-6753.tces.211079
中图分类号：TM712
国家自然科学基金资助项目（5187070548）。
收稿日期 2021-07-15
改稿日期 2021-09-09
程志远 男，1977年生，博士，高级工程师，研究方向为无线电能传输、高压电缆无线取电。E-mail：chengzhiyuan@126.com
李东东 男，1976年生，博士，教授，研究方向为风力发电与电力系统稳定控制、智能用电等。E-mail：powerldd@163.com（通信作者）
（编辑 郭丽军）