推挽型隔离DC-DC变换器软开关条件分析
阚志忠1 冯建兴1 孟宪慧1,2 王晓寰1 张纯江1
(1. 燕山大学电气工程学院 秦皇岛 066000 2. 唐山学院机电工程系 唐山 063000)
摘要 电流型隔离DC-DC变换器具有电流脉动小的优点,有利于延长储能系统锂电池的使用寿命;同时,减小开关损耗是提高功率变换效率的关键技术之一。因此该文讨论利用电流型推挽隔离DC-DC变换器开关管的寄生电容进行谐振,满足开关管的软开关条件。首先分析变换器的增益特性和工作模态;其次基于变换器的等效电路模型,详细分析推挽型隔离DC-DC变换器的软开关瞬态过程,推导出变换器全部开关管软开关条件的参量表达式;最后通过仿真和实验结果验证了软开关条件的正确性。
关键词:DC-DC变换器 软开关 推挽型 隔离
0 引言
由于具有较高的安全性、较好的保护性和较小的体积,隔离型DC-DC变换器在电动汽车、新能源发电等方面得到广泛应用[1-4],且智能电网和能源互联网中电能路由器的研究给这类变换器提出了新要求[5-8]。本文研究适用于电能路由器储能接口的推挽隔离型DC-DC变换器,用于锂离子电池和电能路由器直流母线之间能量传输。作为储能接口的DC-DC变换器需满足如下要求:①能够实现功率双向传输;②高效率;③宽电压范围;④电池侧低电流纹波。为此,许多学者开展了大量研究工作。
高效率是储能接口隔离型DC-DC变换器的重要指标,简化变换器结构、减小变换器的回流功率和实现软开关为高效率变换器研究的三个典型方向。文献[9-10]研究了一种隔离型双半桥DC-DC变换器拓扑及其工作原理。与全桥变换器相比,该变换器功率器件数量减少一半,且无需额外的开关器件和谐振元件,可实现软开关条件下的双向功率流动。文献[11]讨论了输入电感、移相角与占空比对双半桥DC-DC变换器软开关条件的影响。文献[12]分析了传统的移相全桥DC-DC变换器的功率回流现象和回流功率对电流应力的影响。文献[13]分析了PWM+移相控制下双半桥DC-DC变换器传输电感电流变化区间,通过占空比控制限制传输电感电流尖峰减小回流功率。文献[14]在建立推挽型隔离DC-DC变换器的状态平均模型的基础上,采用PWM加移相方式达到降低传输电感电流、减小回流功率和提高传输效率的目的。文献[15]重点讨论利用开关管占空比、移相比和变换器增益之间的关系优化变换器的软开关区间。本文针对电流型输入推挽隔离DC-DC双向变换器实现全部软开关问题,逐一分析开关管的软开关瞬态工作过程;建立每一个软开关瞬态过程的等效电路模型,详细推导出与每个开关对应的软开关工作条件,同时分析传输电感和开关管输出电容对软开关的影响。
1 变换器的工作原理
1.1 拓扑结构及增益
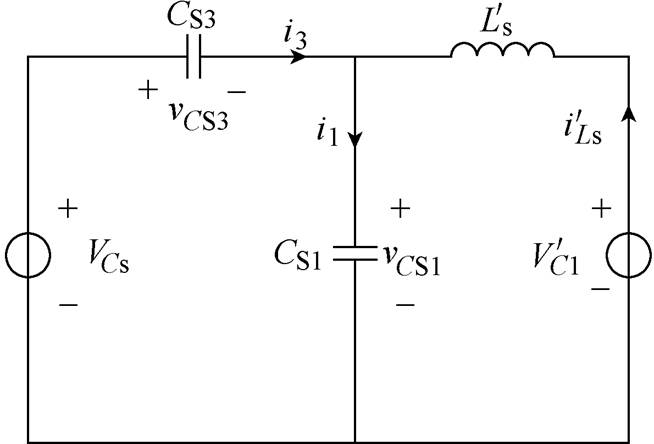
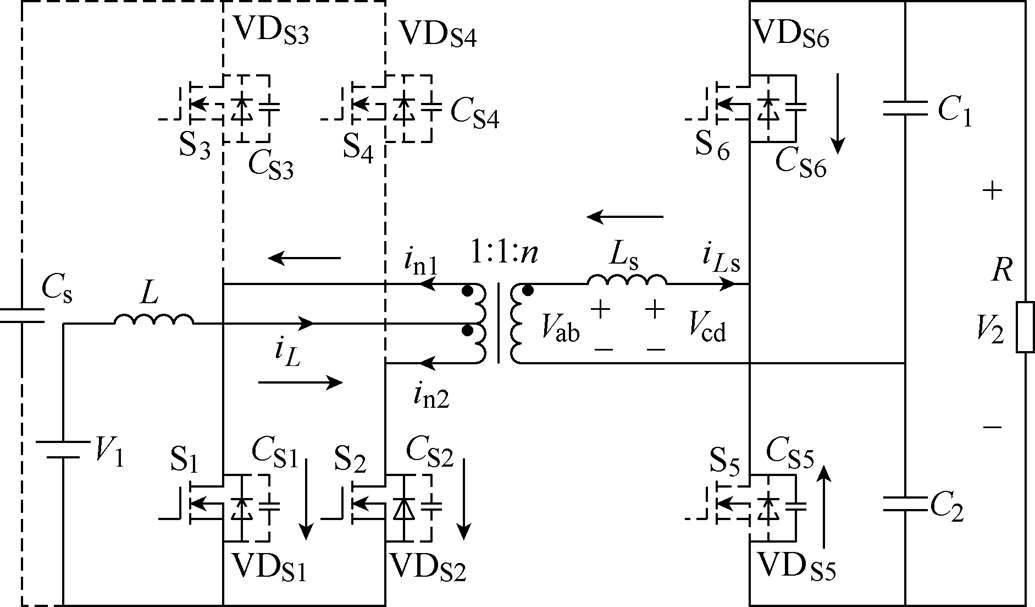
电流输入推挽型隔离DC-DC变换器如图1所示,其具有如下特点:可实现高效率双向传输功率;适合宽输入电压范围;电源V1侧电流连续且纹波较低。图1中,V1和V2分别为低压侧和高压侧输出电压,L和Ls分别为一次侧输入升压电感和二次侧传输电感,Cs为一次侧钳位电容,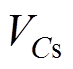 为钳位电容电压,C1和C2为二次侧倍压电容,
为钳位电容电压,C1和C2为二次侧倍压电容,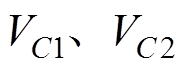 分别为C1和C2电压,图1中箭头方向分别为隔离变压器一次、二次电流的参考方向,定义
分别为C1和C2电压,图1中箭头方向分别为隔离变压器一次、二次电流的参考方向,定义 为变压器二次电压,
为变压器二次电压,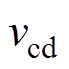 为开关管S5和S6之间的桥臂电压,
为开关管S5和S6之间的桥臂电压, 分别为开关管S1~S6的漏极电流,
分别为开关管S1~S6的漏极电流,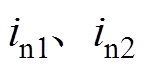 分别为变压器一次侧上、下绕组电流,
分别为变压器一次侧上、下绕组电流,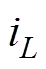 为升压电感L的电流。
为升压电感L的电流。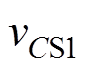 、
、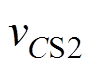 、
、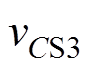 、
、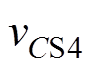 、
、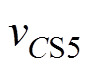 、
、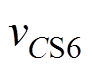 为电容
为电容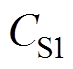 、
、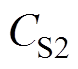 、
、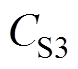 、
、 、
、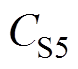 、
、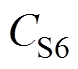 两端电压。S1和S2为变换器一次侧主开关管,且每个开关管的导通占空比均为D,S1开关管的驱动脉冲相位超前于S2开关管的脉冲相位180°;S3和S4为钳位开关管,且开关管S3和S1互补导通,开关管S4和S2互补导通。在二次侧,定义j 为S1和S5之间的移相比,即移相角/ (2π),S1超前于S5;开关管S5和S6的占空比D固定为0.5,则能够实现变换器二次有源倍压直流输出,倍压电容C1和C2容值相同且承受电压相等。
两端电压。S1和S2为变换器一次侧主开关管,且每个开关管的导通占空比均为D,S1开关管的驱动脉冲相位超前于S2开关管的脉冲相位180°;S3和S4为钳位开关管,且开关管S3和S1互补导通,开关管S4和S2互补导通。在二次侧,定义j 为S1和S5之间的移相比,即移相角/ (2π),S1超前于S5;开关管S5和S6的占空比D固定为0.5,则能够实现变换器二次有源倍压直流输出,倍压电容C1和C2容值相同且承受电压相等。 、
、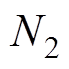 、
、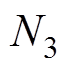 分别为变压器绕组匝数,变压器电压比为1
分别为变压器绕组匝数,变压器电压比为1 1
1 n。
n。
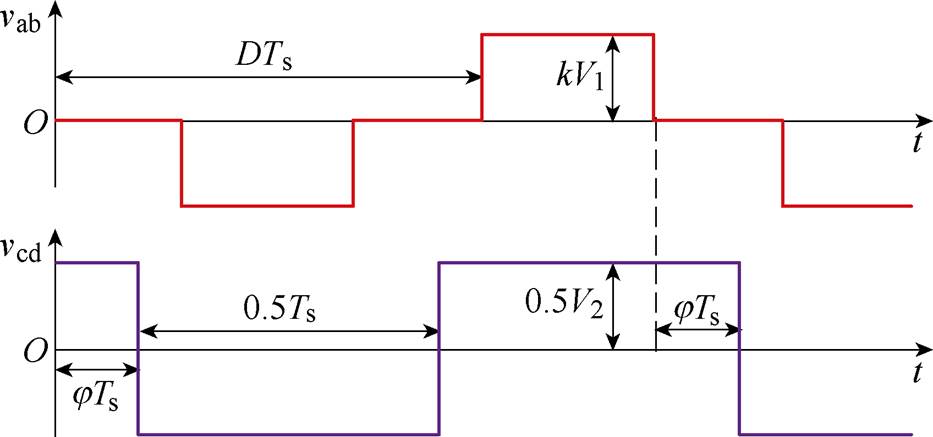
推挽型隔离DC-DC变换器的等效电路如图2所示,变压器一次侧折射到二次电压 、二次侧桥臂电压
、二次侧桥臂电压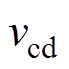 波形如图3所示,
波形如图3所示, 为传输电感Ls的电流。结合图2和图3可知,
为传输电感Ls的电流。结合图2和图3可知,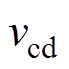 的幅值
的幅值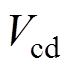 =0.5V2,为了减少变换器的回流功率,通过PWM控制将
=0.5V2,为了减少变换器的回流功率,通过PWM控制将 的正、负幅值与
的正、负幅值与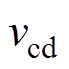 的正、负幅值分别对应相等使传输电感Ls两侧电压幅值匹配。
的正、负幅值分别对应相等使传输电感Ls两侧电压幅值匹配。
为保持在一个开关周期内输入升压电感L及变压器的伏秒平衡,可得
可知一次侧钳位电容电压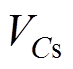 为
为
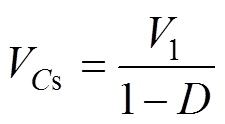 (2)
(2)
当变换器稳态运行时,变压器二次侧传输电感Ls两侧电压的幅值分别为
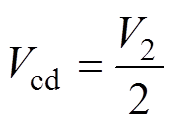 (4)
(4)
由于传输电感值很小,若其两端的电压幅值差较大将导致在很短的时间内流过电感的电流 上升到很大的值,最终导致环流功率增加。为了降低环流功率,通过PWM控制,使得传输电感Ls两侧的方波电压幅值相等,即
上升到很大的值,最终导致环流功率增加。为了降低环流功率,通过PWM控制,使得传输电感Ls两侧的方波电压幅值相等,即
则输入电压V1与输出电压V2的电压转换比为
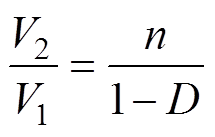 (6)
(6)
由于设定变压器绕组匝数 、
、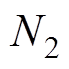 、
、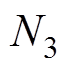 关系为
关系为
根据图1中变压器的一次电流KCL方程和变压器磁动势平衡关系可得
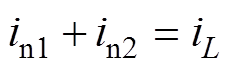 (8)
(8)
将式(7)~式(9)联立,可以解出
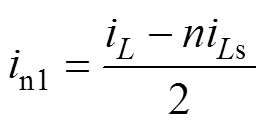 (10)
(10)
1.2 工作模式分析
一个开关周期中推挽型隔离DC-DC变换器共有18个工作模态,变换器一个开关周期内的工作波形如图4所示。
在t0~t6表示的一个开关周期内对其工作模态分析如下。假设t0时刻以前,开关管S2和S6导通,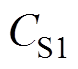 、
、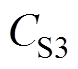 与Ls谐振,工作模态波形如
与Ls谐振,工作模态波形如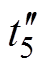 ~t6时间段所示。
~t6时间段所示。
模态1 [t0, 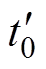
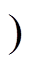 :t0时刻以前,开关管S2和S6处于导通状态,
:t0时刻以前,开关管S2和S6处于导通状态,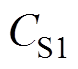 、
、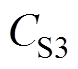 与Ls谐振。t0时刻,
与Ls谐振。t0时刻,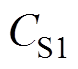 、
、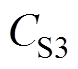 与Ls谐振结束,VDS1导通,开关管S1实现零电压开通。变压器二次侧电路状态不发生改变,电流
与Ls谐振结束,VDS1导通,开关管S1实现零电压开通。变压器二次侧电路状态不发生改变,电流 为正值,电流
为正值,电流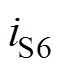 为负值。
为负值。
模态2 [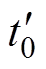 ,
, 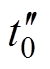
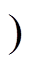 :
: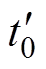 时刻,
时刻,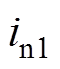 从负值增大至零,此后开始正向增加。
从负值增大至零,此后开始正向增加。
模态3 [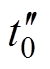 ,
, 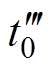
 :
: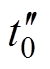 时刻,传输电感电流
时刻,传输电感电流 降为零,此后变为负值且继续减少,输入侧升压电感电流
降为零,此后变为负值且继续减少,输入侧升压电感电流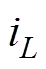 、电流
、电流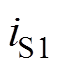 、
、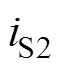 、
、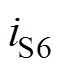 、
、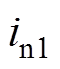 和
和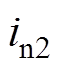 皆为正值。
皆为正值。
模态4 [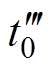 , t1
, t1 :
: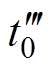 时刻,开关管S6关断,S5、S6的寄生电容
时刻,开关管S6关断,S5、S6的寄生电容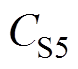 和
和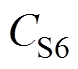 和传输电感Ls谐振,
和传输电感Ls谐振,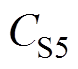 两端电压
两端电压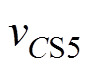 从V2下降,
从V2下降,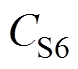 两端电压
两端电压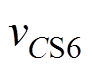 从零开始上升。直至t1时刻,
从零开始上升。直至t1时刻,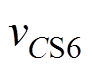 升到V2,
升到V2,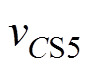 下降到零,谐振过程结束。
下降到零,谐振过程结束。
模态5 [t1, 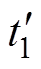
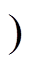 :t1时刻,谐振过程结束且给开关管S5加驱动信号。由于感性电流
:t1时刻,谐振过程结束且给开关管S5加驱动信号。由于感性电流 不能突变,则传输电感电流
不能突变,则传输电感电流 经过开关管S5的寄生二极管
经过开关管S5的寄生二极管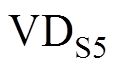 导通而形成回路,实现了S5的零电压开通。
导通而形成回路,实现了S5的零电压开通。
模态6 [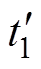 , t2
, t2 :
: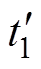 时刻,开关管S2关断。此时电容
时刻,开关管S2关断。此时电容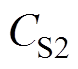 、
、 与电感Ls谐振,
与电感Ls谐振,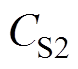 两端电压
两端电压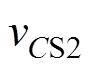 从零开始上升,
从零开始上升, 两端电压
两端电压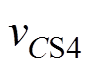 从
从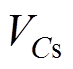 开始下降。直至t2时刻,
开始下降。直至t2时刻,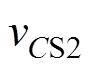 上升到
上升到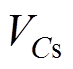 ,
,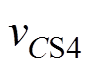 下降到零,谐振结束。
下降到零,谐振结束。
模态7 [t2, 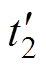
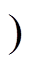 :t2时刻,给S4施加驱动脉冲,S4导通,由于感性电流
:t2时刻,给S4施加驱动脉冲,S4导通,由于感性电流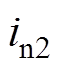 不能突变并通过开关S4的寄生体二极管
不能突变并通过开关S4的寄生体二极管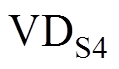 进行续流,开关管S4实现零电压开通。
进行续流,开关管S4实现零电压开通。
模态8 [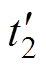 ,
, 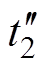
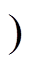 :开关管S4的电流
:开关管S4的电流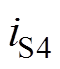 从负值变为零,此后为正值且继续增加。
从负值变为零,此后为正值且继续增加。
模态9 [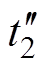 , t3
, t3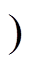 :
: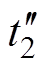 时刻,开关管S4关断,此时
时刻,开关管S4关断,此时 、
、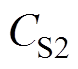 与传输电感Ls谐振,
与传输电感Ls谐振, 两端电压
两端电压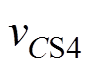 从零开始上升,
从零开始上升,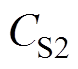 两端电压
两端电压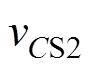 从
从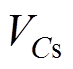 开始下降。直至t3时刻,
开始下降。直至t3时刻,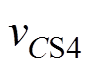 上升到
上升到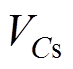 ,
,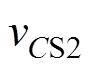 下降到零,谐振过程结束。在t3时刻S2导通,此时推挽型隔离DC-DC变换器工作了半个开关周期。
下降到零,谐振过程结束。在t3时刻S2导通,此时推挽型隔离DC-DC变换器工作了半个开关周期。
从t3~t6时间段为后半个开关周期,其工作模态与t0~t3时间段类似,在此不再进行赘述。
2 软开关过程分析
通过对第1节工作原理分析可发现,推挽型隔离DC-DC变换器实现零电压开通,在开关管开通、关断过程中开关管的寄生电容与变压器传输电感Ls进行谐振,并在开关管开通前其两端电压下降到零,使反向并联二极管导通。下面通过分析谐振过程推导出推挽型DC-DC变换器的软开关条件。
推挽型隔离DC-DC变换器谐振过程的工作模态分别为模态4 [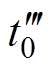 , t1
, t1 、模态6 [
、模态6 [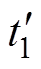 , t2
, t2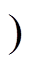 、模态9 [
、模态9 [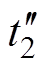 , t3
, t3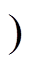 、模态13 [
、模态13 [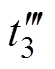 , t4
, t4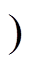 、模态15 [
、模态15 [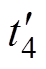 , t5
, t5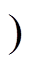 、模态18 [
、模态18 [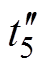 , t6
, t6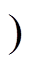 。模态4中
。模态4中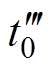 时刻,开关管S6关断,S5实现零电压开通;模态6中
时刻,开关管S6关断,S5实现零电压开通;模态6中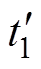 时刻,开关管S2关断,S4实现零电压开通;模态9中
时刻,开关管S2关断,S4实现零电压开通;模态9中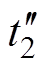 时刻,S4关断,S2实现零电压开通;模态13中
时刻,S4关断,S2实现零电压开通;模态13中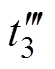 时刻,S5关断,S6实现零电压开通;模态15中
时刻,S5关断,S6实现零电压开通;模态15中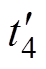 时刻,S1关断,S3实现零电压开通;模态18中
时刻,S1关断,S3实现零电压开通;模态18中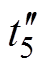 时刻,S3关断,S1实现零电压开通。
时刻,S3关断,S1实现零电压开通。
在推挽型隔离DC-DC变换器中,桥臂S1和S2、桥臂S3和S4、桥臂S5和S6的工作方式完全对称,不存在超前滞后现象。因此,只要实现了开关管S1、S3和S5的零电压开通,即可实现所有开关管的零电压开通。因此,将对开关管S1(模态18)、S3(模态15)、S5(模态4)进行软开关分析。
软开关分析前,把传输电感折算到变压器一次侧,折算后的传输电感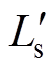 与传输电感Ls的比例为
与传输电感Ls的比例为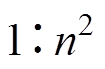 ;流过电感
;流过电感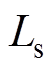 的电流
的电流 折算后为
折算后为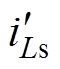 ,折算到变压器一次侧后的倍压电容电压
,折算到变压器一次侧后的倍压电容电压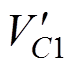 与倍压电容电压VC1的比例为
与倍压电容电压VC1的比例为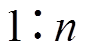 。
。
2.1 开关管S1软开关分析
在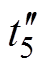 时刻,开关管S3关断,此时
时刻,开关管S3关断,此时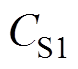 、
、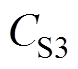 与传输电感Ls谐振,
与传输电感Ls谐振,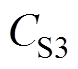 两端电压
两端电压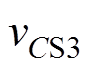 从零开始上升,
从零开始上升,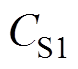 两端电压从VCs开始下降。直至t6时刻,
两端电压从VCs开始下降。直至t6时刻,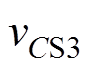 上升到VCs,
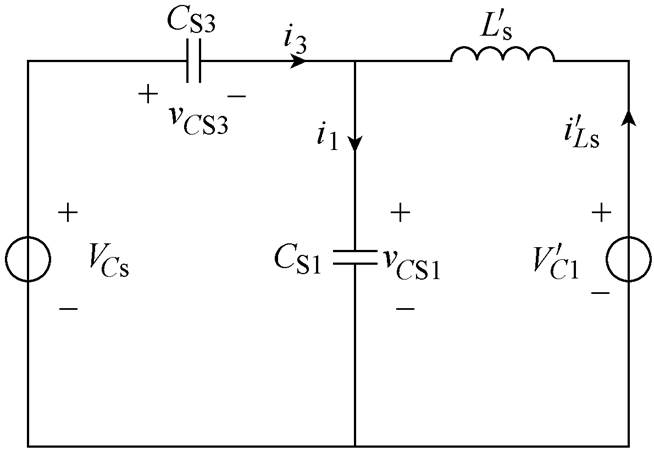
上升到VCs,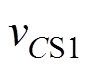 下降到零,谐振过程结束。S1零电压开通,此状态的电路如图5所示,其等效电路如图6所示。
下降到零,谐振过程结束。S1零电压开通,此状态的电路如图5所示,其等效电路如图6所示。
根据图6等效电路可列方程式为
由于开关器件寄生参数的一致性,则假设
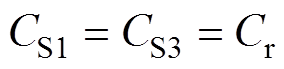 (13)
(13)
解式(12)可得
在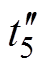 时刻,开关管S3关断时,根据稳态过程可得电流
时刻,开关管S3关断时,根据稳态过程可得电流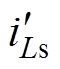 的初值
的初值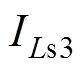 为
为
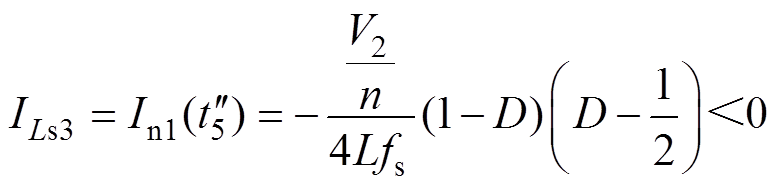 (15)
(15)
此时,0.5<D<1,联立式(13)、式(14)可解得
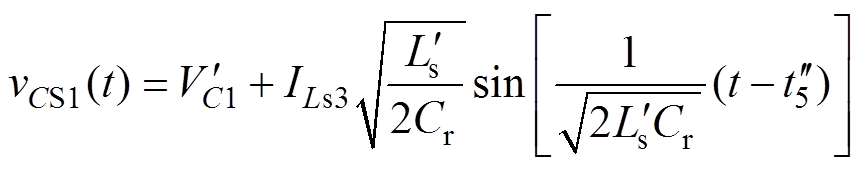 (17)
(17)
式中,Zr为谐振电路特征阻抗,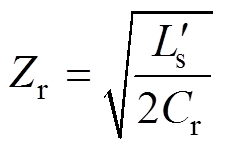 ;wr为谐振频率,
;wr为谐振频率, 。则电压
。则电压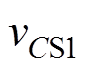 瞬时值为
瞬时值为
由式(18)可分析开关管S1两端电压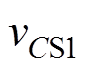 的变化。当
的变化。当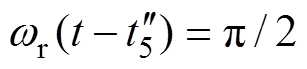 时,电压
时,电压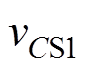 达到最小值,即
达到最小值,即
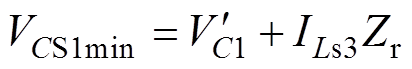 (19)
(19)
由于要实现开关管S1的零电压开通,因此在模态18结束时要将S1两端电压降到零,使VDS1导通。即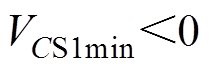 。
。
同时式(20)还可写成
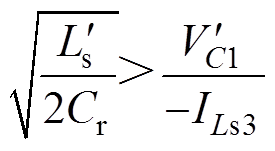 (21)
(21)
由此可看出,当传输电感固定不变时,在一定范围内寄生电容Cr越小,S1越容易实现软开关。
当寄生电容充放电完成时,电流将以斜率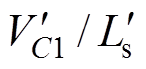 下降,当CS1过小时,将使电压
下降,当CS1过小时,将使电压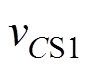 提前下降到零,而此时S1的驱动脉冲尚未到来,使得寄生电容CS1被充电失去软开关机会,因此需要对S1、S3的死区时间Td进行设计(通常取死区时间Td= Tr/4,Tr为谐振周期,Tr=2p/wr),使电压vCS1满足最小值要求,又不致使电容CS1被重新充电。
提前下降到零,而此时S1的驱动脉冲尚未到来,使得寄生电容CS1被充电失去软开关机会,因此需要对S1、S3的死区时间Td进行设计(通常取死区时间Td= Tr/4,Tr为谐振周期,Tr=2p/wr),使电压vCS1满足最小值要求,又不致使电容CS1被重新充电。
2.2 开关管S3软开关分析
在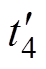 时刻,开关管S1关断。此时电容CS1、CS3与电感Ls谐振,CS1两端电压
时刻,开关管S1关断。此时电容CS1、CS3与电感Ls谐振,CS1两端电压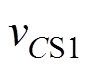 从零开始上升,CS3两端电压
从零开始上升,CS3两端电压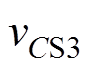 从
从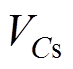 开始下降。直至t5时刻,
开始下降。直至t5时刻,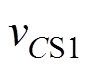 上升到
上升到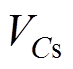 ,
,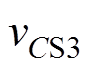 下降到零,谐振结束。开关管S1关断,S3实现零电压开通,此软开关过程电路如图7所示,等效电路如图8所示。
下降到零,谐振结束。开关管S1关断,S3实现零电压开通,此软开关过程电路如图7所示,等效电路如图8所示。
根据等效电路可列方程式为
由于开关器件寄生参数一致性,则假设
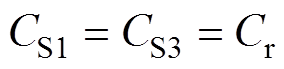 (23)
(23)
在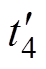 时刻,开关管S1关断时,根据稳态过程可得电流
时刻,开关管S1关断时,根据稳态过程可得电流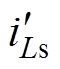 的初值ILs1为
的初值ILs1为
则可解出
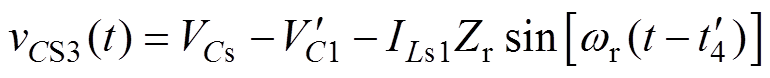 (25)
(25)
由式(25)分析可知,开关管S3两端电压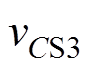 随时间变化的关系。当
随时间变化的关系。当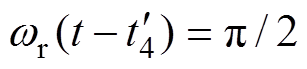 时,电压
时,电压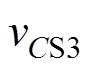 达到最小值
达到最小值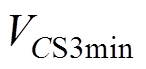 。
。
为保证实现开关管S3零电压开通,需要在模态15结束时将S3两端电压降到零,使VDS3导通。即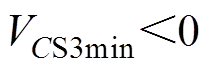 。
。
由式(26)可得,当传输电感固定时,在一定范围内寄生电容值Cr越小,S3越容易实现软开关。
当寄生电容充放电完成时,电流将以斜率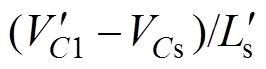 下降,当CS3过小时将使电压vCS3提前下降到零,而此时S3驱动信号尚未到来,使得寄生电容CS3被充电失去软开关机会,因此需要对死区时间Td进行设计,使电压
下降,当CS3过小时将使电压vCS3提前下降到零,而此时S3驱动信号尚未到来,使得寄生电容CS3被充电失去软开关机会,因此需要对死区时间Td进行设计,使电压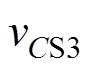 满足最小值要求,又不致使电容CS3被重新充电。
满足最小值要求,又不致使电容CS3被重新充电。
2.3 开关管S5软开关分析
在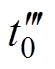 时刻,开关管S6关断,S5、S6的寄生电容CS5、CS6和传输电感Ls谐振,CS5两端电压
时刻,开关管S6关断,S5、S6的寄生电容CS5、CS6和传输电感Ls谐振,CS5两端电压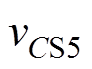 从V2下降,CS6两端电压
从V2下降,CS6两端电压 从零开始上升。直至t1时刻,
从零开始上升。直至t1时刻, 上升到V2,
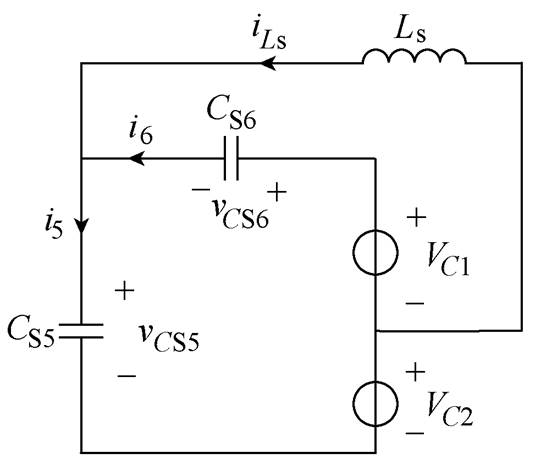
上升到V2,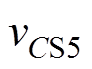 下降到零,谐振过程结束。S6关断继而S5实现零电压开通,此软开关过程的电路如图9所示,等效电路如图10所示。根据开关器件参数一致性,假设寄生电容CS5、CS6满足
下降到零,谐振过程结束。S6关断继而S5实现零电压开通,此软开关过程的电路如图9所示,等效电路如图10所示。根据开关器件参数一致性,假设寄生电容CS5、CS6满足
图10中,电容CS5、CS6电流分别为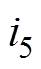 、
、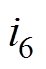 。由图10可列方程式为
。由图10可列方程式为
在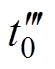 时刻,开关管S6关断时,根据稳态过程可得电流
时刻,开关管S6关断时,根据稳态过程可得电流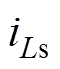 的初值ILs6为
的初值ILs6为
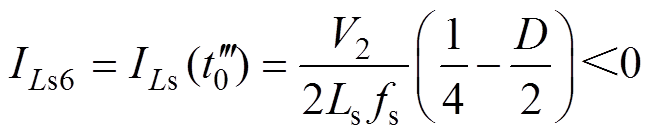 (29)
(29)
则可解出电容CS5两端电压为
由式(30)可见,开关管S5两端电压VCS5随时间变化的关系。当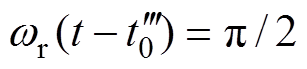 时,电压
时,电压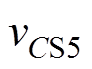 达到最小值
达到最小值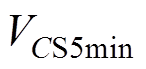 。由于要实现开关管S5的零电压开通,因此在模态4结束时要将S5两端电压降到零,使VDS5导通,即
。由于要实现开关管S5的零电压开通,因此在模态4结束时要将S5两端电压降到零,使VDS5导通,即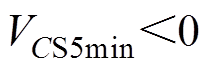 。
。
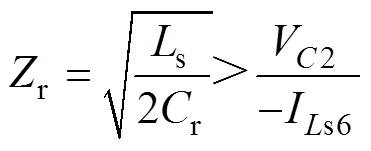 (31)
(31)
由式(31)可以看出,当传输电感固定时,在一定范围内寄生电容Cr越小,S5越容易实现软开关。
当寄生电容充放电完成时,电流将以斜率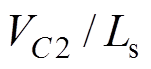 下降,当CS5过小时将使电压
下降,当CS5过小时将使电压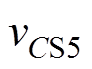 提前下降到零,而此时驱动信号并没有到来,使得寄生电容CS5被充电失去软开关机会,因此需要对死区时间Td进行设计,使电压vCS5满足最小值要求,又不致使电容CS5被重新充电。
提前下降到零,而此时驱动信号并没有到来,使得寄生电容CS5被充电失去软开关机会,因此需要对死区时间Td进行设计,使电压vCS5满足最小值要求,又不致使电容CS5被重新充电。
3 仿真与实验结果分析
为验证理论分析的正确性,采用Matlab仿真软件建立仿真模型进行验证,变换器主电路的仿真与实验参数见表1。
3.1 仿真分析
3.1.1 全周期软开关仿真分析
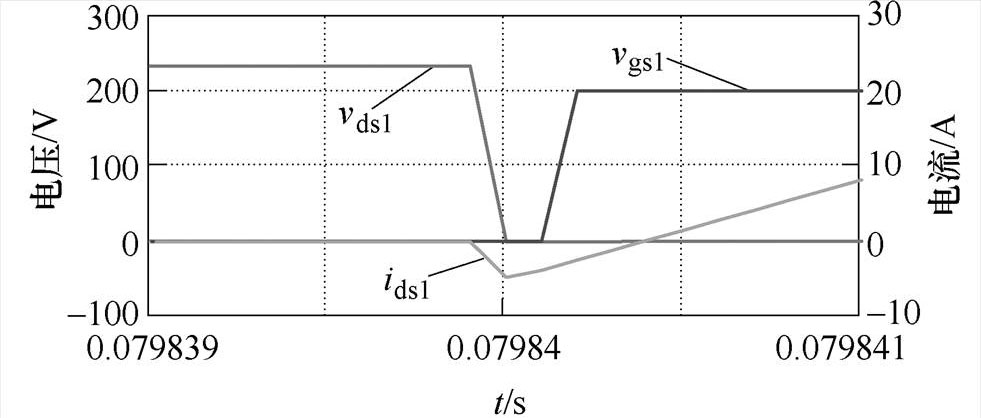
开关管S1开通的仿真波形如图11所示,由图11可见,从SiC MOSFET开通时刻到S1的漏源电压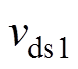 下降到零的时间段,电流
下降到零的时间段,电流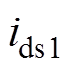 一直为负值,说明电流一直流经开关管S1的寄生二极管,开关管S1实现零电压开通。
一直为负值,说明电流一直流经开关管S1的寄生二极管,开关管S1实现零电压开通。
表1 主电路参数
Tab.1 main circuit parameters
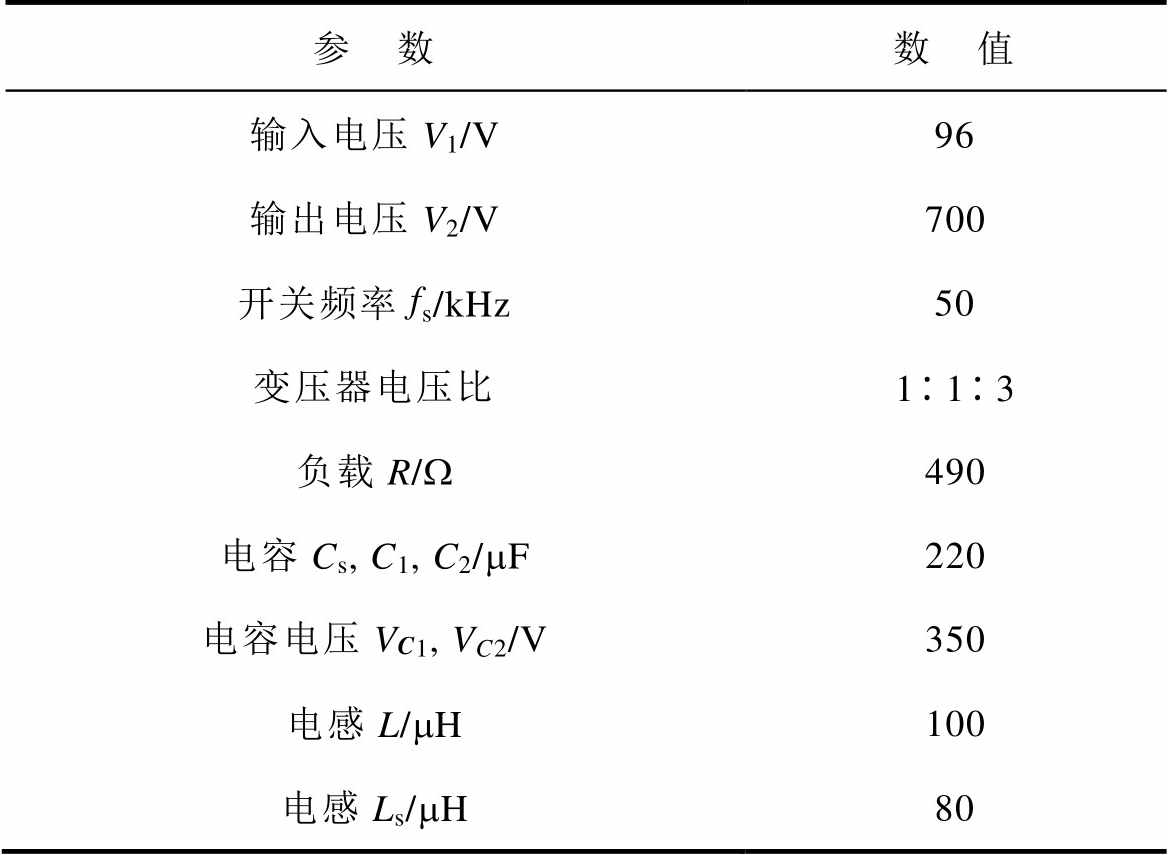
参 数数 值 输入电压V1/V96 输出电压V2/V700 开关频率fs/kHz50 变压器电压比113 负载R/W490 电容Cs, C1, C2/mF220 电容电压VC1, VC2/V350 电感L/mH100 电感Ls/mH80
根据开关管S1的软开关过程分析,代入相应数值后可得:ILs3=-5A,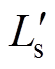 =80/9mH,
=80/9mH,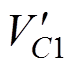 =350/3V。根据式(21)可得,Cr<8.166nF。开关管S1的寄生电容为60pF,符合软开关寄生电容的数值范围,因此开关管S1达到了软开关条件。
=350/3V。根据式(21)可得,Cr<8.166nF。开关管S1的寄生电容为60pF,符合软开关寄生电容的数值范围,因此开关管S1达到了软开关条件。
图12为开关管S3开通的仿真波形,由图12可见,从SiC MOSFET开通时刻到漏源电压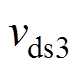 降到零区间,电流
降到零区间,电流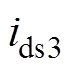 一直保持负值,说明电流一直经过开关管S3的寄生二极管,开关管S3实现零电压开通。
一直保持负值,说明电流一直经过开关管S3的寄生二极管,开关管S3实现零电压开通。
根据开关管S3软开关过程的原理分析,代入相应数值后可得:ILs1=5.07A,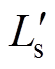 =80/9mH,
=80/9mH,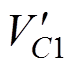 =350/3V,VCs=700/3V。根据式(26)可得,Cr<8.4nF。开关管S3的寄生电容为120pF,参数满足软开关条件。
=350/3V,VCs=700/3V。根据式(26)可得,Cr<8.4nF。开关管S3的寄生电容为120pF,参数满足软开关条件。
图13为开关管S5开通的仿真波形,由图13可见,在SiC MOSFET开通时刻到漏源电压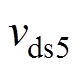 降到零时刻的区间内电流
降到零时刻的区间内电流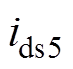 一直保持负值,说明电流一直经过开关管S5的寄生二极管,开关管S5可实现零电压开通。
一直保持负值,说明电流一直经过开关管S5的寄生二极管,开关管S5可实现零电压开通。
根据开关管S5软开关过程原理,代入相应数值后可得:ILs6=-7A,Ls=80mH,VC2=350V。根据式(31)可得,Cr<16nF。开关管S5的寄生电容为130pF,该参数符合软开关寄生电容的数值范围,满足开关管S5软开关条件。
3.1.2 寄生电容对软开关的影响
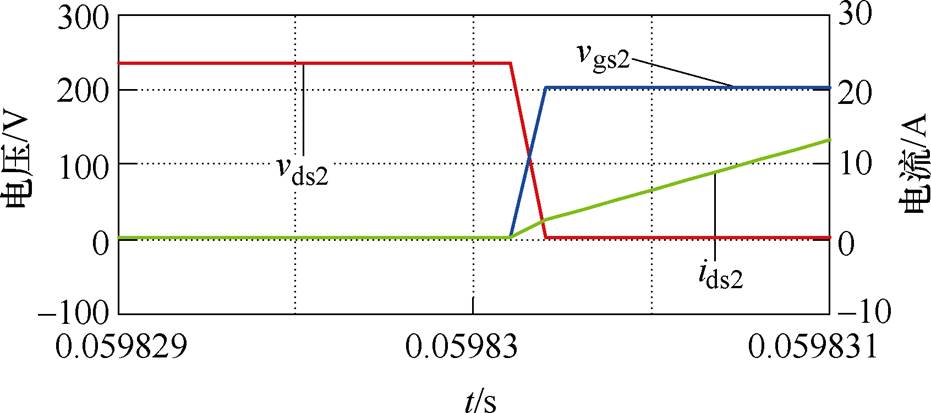
在验证变换器所有开关管零电压开通的基础上,S2的寄生电容增加0.1mF,进一步验证软开关条件,图14为增加了0.1mF寄生电容开通过程仿真波形。
由图14可以看出,在开关管两端并联0.1mF寄生电容后,在SiC MOSFET的漏源极电压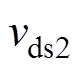 降到零之前,驱动信号
降到零之前,驱动信号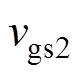 已经加在栅源极间,流过开关管的漏极电流ids2为正值,在开通时刻开关管电压
已经加在栅源极间,流过开关管的漏极电流ids2为正值,在开通时刻开关管电压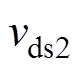 与电流
与电流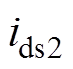 存在交叠区域,产生了开通损耗。
存在交叠区域,产生了开通损耗。
由3.1.1节可知,开关管寄生电容范围Cr<8.166nF,开关管两端寄生电容要在此范围内,否则推挽型隔离DC-DC变换器将不能满足零电压开通条件。
3.2 实验分析
图15为开关管S2的软开关实验波形。图15中,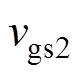 为栅源极间电压,
为栅源极间电压,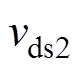 为漏源极间电压,in2为变压器一次侧下绕组电流,此时开关管S2的电流
为漏源极间电压,in2为变压器一次侧下绕组电流,此时开关管S2的电流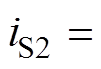
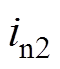 。由图中可见,在开关管S2开通前,流过S2的电流已经为负值,说明电流iS2流经开关管S2的寄生体二极管,S2实现零电压开通。
。由图中可见,在开关管S2开通前,流过S2的电流已经为负值,说明电流iS2流经开关管S2的寄生体二极管,S2实现零电压开通。
图16为开关管S3的软开关实验波形。图16中,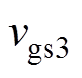 为S3的栅源极间电压,
为S3的栅源极间电压,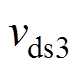 为S3的漏源极间电压,
为S3的漏源极间电压,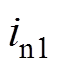 为变压器上绕组电流,此时
为变压器上绕组电流,此时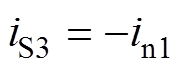 。由图中可见,在开关管S3的栅源极间电压
。由图中可见,在开关管S3的栅源极间电压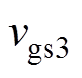 从-2V变为18V过程中,电流
从-2V变为18V过程中,电流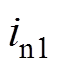 为正值,则流过开关管S3的电流为负值,说明此时电流
为正值,则流过开关管S3的电流为负值,说明此时电流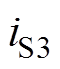 流经S3的寄生体二极管,实现了S3的零电压开通。
流经S3的寄生体二极管,实现了S3的零电压开通。
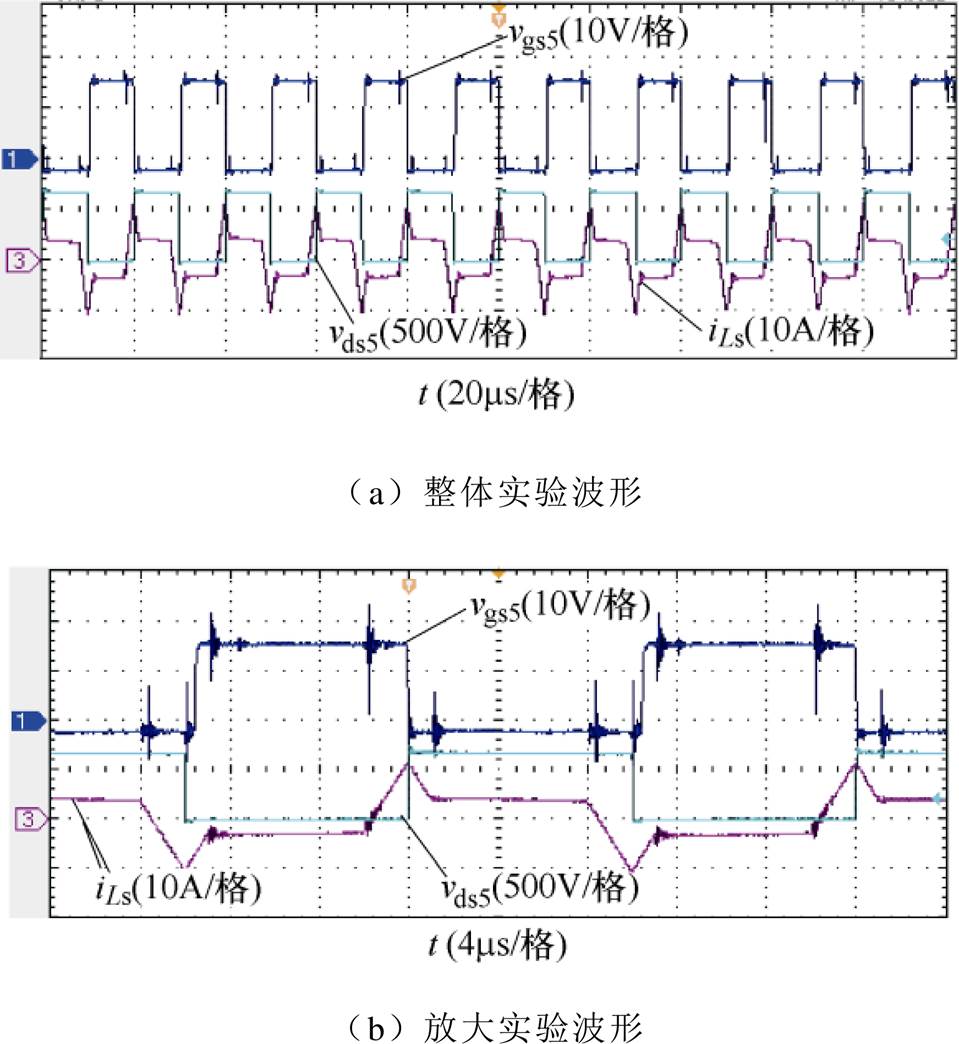
图17为开关管S5的软开关实验波形。图17中,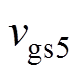 为开关管S5的栅源极间电压,
为开关管S5的栅源极间电压,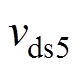 为S5的漏源极间电压,
为S5的漏源极间电压,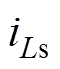 为流过传输电感的电流,当开关管S5工作时
为流过传输电感的电流,当开关管S5工作时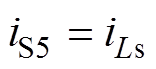 。由图中可见,当开关管S5的漏源极间电压由高压变为低压前,传输电感的电流已经为负值,即流过S5的电流为负值,此时电流iS5经过S5的寄生体二极管进行流通,实现了S5的零电压开通。
。由图中可见,当开关管S5的漏源极间电压由高压变为低压前,传输电感的电流已经为负值,即流过S5的电流为负值,此时电流iS5经过S5的寄生体二极管进行流通,实现了S5的零电压开通。
4 结论
电流型推挽隔离DC-DC变换器具有适合宽电压范围、电池侧低电流纹波的特点。本文首先分析了其工作原理,重点分析了变换器软开关过程,尤其是分析了寄生参数对软开关的影响,推导了推挽隔离DC-DC变换器中各个开关管达到软开关条件的参数表达式。在仿真和实验中通过设置不同的谐振电容值,进一步验证了软开关条件理论分析的正确性与有效性。
参考文献
[1] 李广地, 阮杰, 王昆, 等. 一种混合调制型三路输出DC-DC变换器[J]. 电工技术学报, 2019, 34(22): 4719-4727.
Li Guangdi, Ruan Jie, Wang Kun, et al. A hybrid modulated triple-output DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(22): 4719-4727.
[2] 余雪萍, 涂春鸣, 肖凡, 等. 三端口隔离DC-DC变换器的暂态直流偏置机理及抑制策略[J]. 电工技术学报, 2020, 35(9): 1962-1972.
Yu Xueping, Xu Chunming, Xiao Fan, et al. Transient DC bias mechanism and suppression strategy of the three-port isolated DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1962- 1972.
[3] 杨超, 许海平, 袁志宝, 等. 双PWM控制下三电平半桥隔离型双向DC-DC变换器的全局最小峰值电流研究[J]. 电工技术学报, 2020, 35(8): 1679-1689.
Yang Chao, Xu Haiping, Yuan Zhibao, et al. Global minimum peak current control of the three level isolated half-bridge bi-directional DC-DC converters with PWM-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1679- 1689.
[4] 殷晓东, 罗登, 李祖勇, 等. 一种双向隔离DC-DC变换器二次纹波电压抑制方法[J]. 电工技术学报, 2018, 33(6): 1356-1363.
Yin Xiaodong, Luo Deng, Li Zuyong, et al. A second-order ripple voltage suppression algorithm of bidirectional isolation DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(6): 1356-1363.
[5] Wu Runze, Wang Bixiao, Zou Yingjie, et al. Energy router interface model based on bidirectional flow control for intelligent park[C]//43rd Annual Con- ference of the IEEE Industrial Electronics Society, Beijing, 2017: 7771-7776.
[6] Li Zhen, Li Penghua, Sheng Wanxing, et al. Research on a household energy router for energy internet[C]// Conference on Industrial Electronics and Applications, Wuhan, 2018: 952-957.
[7] Wang Kaixuan, Liu Xiaosheng, Zhao Liang, et al. Research on structure and energy management strategy of household energy router based on hybrid energy storage[C]//2019 IEEE Power & Energy Society Innovative Smart Grid Technologies Con- ference (ISGT), Washington, DC, 2019: 1-5.
[8] Qin Yuchao, Hua Haochen, Cao Junwei. Short-term energy cache regulation for energy router: a robust h-infinity approach[C]//2019 IEEE International Con- ference on Energy Internet (ICEI), Nanjing, 2019: 161-166.
[9] Li Hui, Peng Fangzheng, Lawler J S. A natural ZVS medium-power bidirectional DC-DC converter with minimum number of devices[J]. IEEE Transactions on Industry Applications, 2003, 39(2): 525-535.
[10] Peng Fangzheng, Li Hui, Su Guijia, et al. A new ZVS bidirectional DC-DC converter for fuel cell and battery application[J]. IEEE Transactions on Power Electronics, 2004, 19(1): 54-65.
[11] Hamid Daneshpajooh, Alireza Bakhshai, Praveen Jain. Design of DC-DC converter with phase shift and duty cycle control for full range soft switching[C]//2011 IEEE 33rd International Telecommunications Energy Conference (INTELEC), Amsterdam, 2011: 1-6.
[12] Zhao Biao, Yu Qingguang, Sun Weixin. Extended- phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4667-4680.
[13] Kang Xiangli, Li Shouxiang, Keyue Ma Smedley. Decoupled PWM plus phase-shift control for a dual-half-bridge bidirectional DC-DC converter[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 7203-7213.
[14] Kang Xiangli, Li Shouxiang, Keyue Ma Smedley. Analysis and modelling of a bidirectional push-pull converter with PWM plus phase-shift control[C]// 42nd Annual Conference of the IEEE Industrial Electronics, Florence, 2016: 1268-1273.
[15] Li Shouxiang, Kang Xiangli, Keyue Ma Smedley. A control map for a bidirectional PWM plus phase- shift-modulated push-pull DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 8514-8524.
Analysis of Soft Switching Conditions of Push-Pull Isolated DC-DC Converter
Kan Zhizhong1 Feng Jianxing1 Meng Xianhui1,2 Wang Xiaohuan1 Zhang Chunjiang1
(1. School of Electrical Engineering Yanshan University Qinhuangdao 066000 China 2. Department of Mechanical And Electrical Engineering Tangshan University Tangshan 063000 China)
Abstract The current source isolated (CSI) DC-DC converter has the advantage of low current ripple, and it is beneficial to the service life of the lithium battery of the energy storage system. At the same time, reducing the switching loss is one of the key technologies to improve the power conversion efficiency. Therefore, this paper discusses the method of using the parasitic capacitance of the push-pull CSI DC-DC converter switch tube to perform resonance to meet the soft-switching conditions of the switch tube. Firstly, the gain characteristics and operating mode of the converter are analyzed. Secondly, based on the converter’s equivalent circuit model, the soft-switching transient process of the push-pull CSI DC-DC converter is analyzed in detail, and the parametric expressions of the soft-switching conditions of all switches of the converter are derived. Finally, the simulation and experimental results verify the correctness of the soft-switching conditions.
keywords:DC-DC converter, soft-switching, push-pull, isolation
DOI: 10.19595/j.cnki.1000-6753.tces.L90349
中图分类号:TM46
国家自然科学基金资助项目(51877187)。
收稿日期 2020-07-09
改稿日期 2020-12-09
作者简介
阚志忠 男,1970年生,博士,副教授,研究方向为新能源变换技术。E-mail: kanzhizhong@126.com
张纯江 男,1961年生,教授,博士生导师,研究方向为可再生能源分布式发电及控制、逆变电源及并联并网技术、储能系统功率流控制。E-mail: zhangcj@ysu.edu.cn(通信作者)
(编辑 陈 诚)
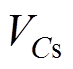 为钳位电容电压,C1和C2为二次侧倍压电容,
为钳位电容电压,C1和C2为二次侧倍压电容,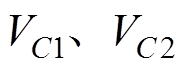 分别为C1和C2电压,图1中箭头方向分别为隔离变压器一次、二次电流的参考方向,定义
分别为C1和C2电压,图1中箭头方向分别为隔离变压器一次、二次电流的参考方向,定义 为变压器二次电压,
为变压器二次电压,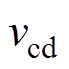 为开关管S5和S6之间的桥臂电压,
为开关管S5和S6之间的桥臂电压, 分别为开关管S1~S6的漏极电流,
分别为开关管S1~S6的漏极电流,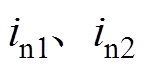 分别为变压器一次侧上、下绕组电流,
分别为变压器一次侧上、下绕组电流,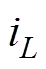 为升压电感L的电流。
为升压电感L的电流。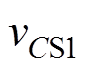 、
、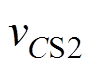 、
、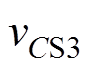 、
、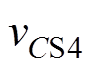 、
、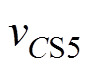 、
、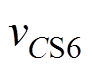 为电容
为电容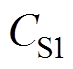 、
、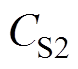 、
、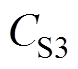 、
、 、
、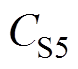 、
、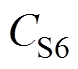 两端电压。S1和S2为变换器一次侧主开关管,且每个开关管的导通占空比均为D,S1开关管的驱动脉冲相位超前于S2开关管的脉冲相位180°;S3和S4为钳位开关管,且开关管S3和S1互补导通,开关管S4和S2互补导通。在二次侧,定义j 为S1和S5之间的移相比,即移相角/ (2π),S1超前于S5;开关管S5和S6的占空比D固定为0.5,则能够实现变换器二次有源倍压直流输出,倍压电容C1和C2容值相同且承受电压相等。
两端电压。S1和S2为变换器一次侧主开关管,且每个开关管的导通占空比均为D,S1开关管的驱动脉冲相位超前于S2开关管的脉冲相位180°;S3和S4为钳位开关管,且开关管S3和S1互补导通,开关管S4和S2互补导通。在二次侧,定义j 为S1和S5之间的移相比,即移相角/ (2π),S1超前于S5;开关管S5和S6的占空比D固定为0.5,则能够实现变换器二次有源倍压直流输出,倍压电容C1和C2容值相同且承受电压相等。 、
、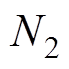 、
、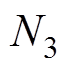 分别为变压器绕组匝数,变压器电压比为1
分别为变压器绕组匝数,变压器电压比为1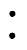 1
1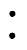 n。
n。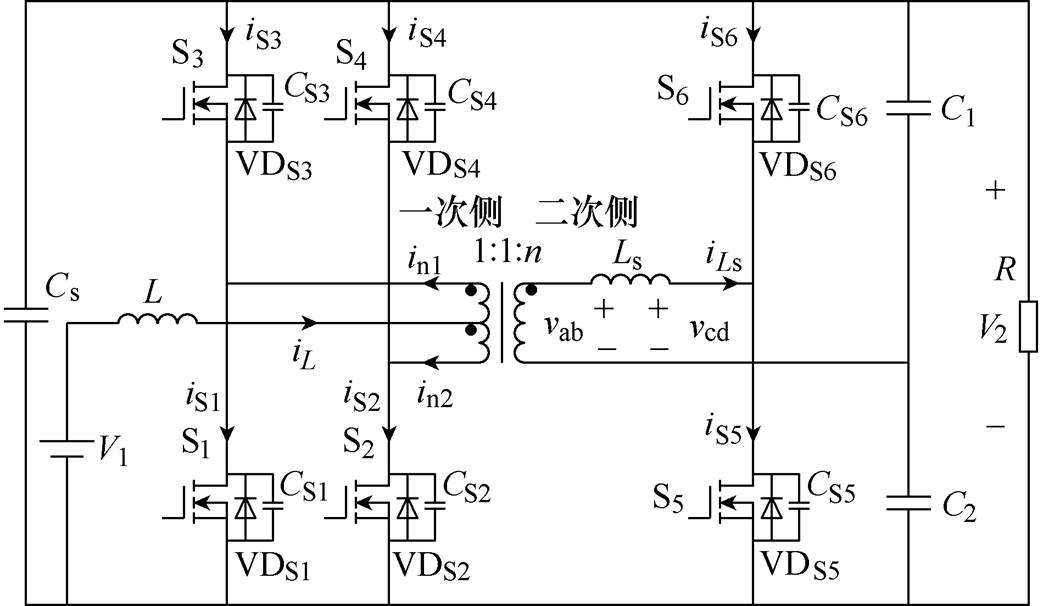
 为传输电感L
为传输电感L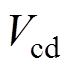 =0.5V
=0.5V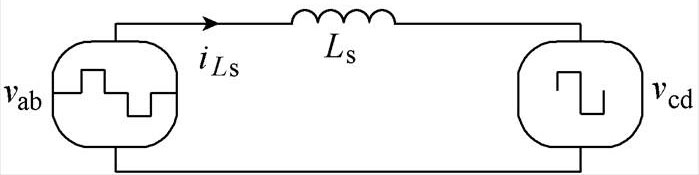
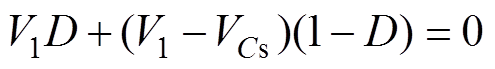 (1)
(1)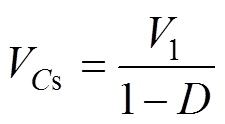 (2)
(2)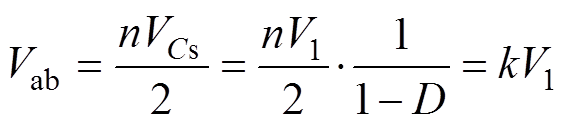 (3)
(3)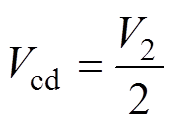 (4)
(4)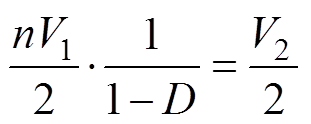 (5)
(5)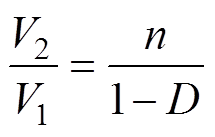 (6)
(6)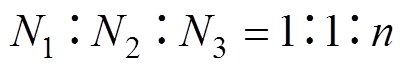 (7)
(7)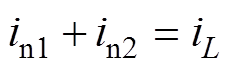 (8)
(8)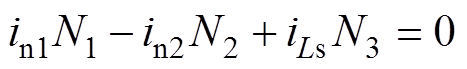 (9)
(9)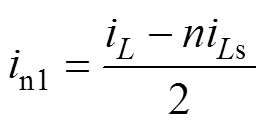 (10)
(10)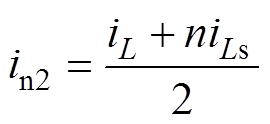 (11)
(11)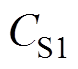 、
、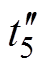 ~t
~t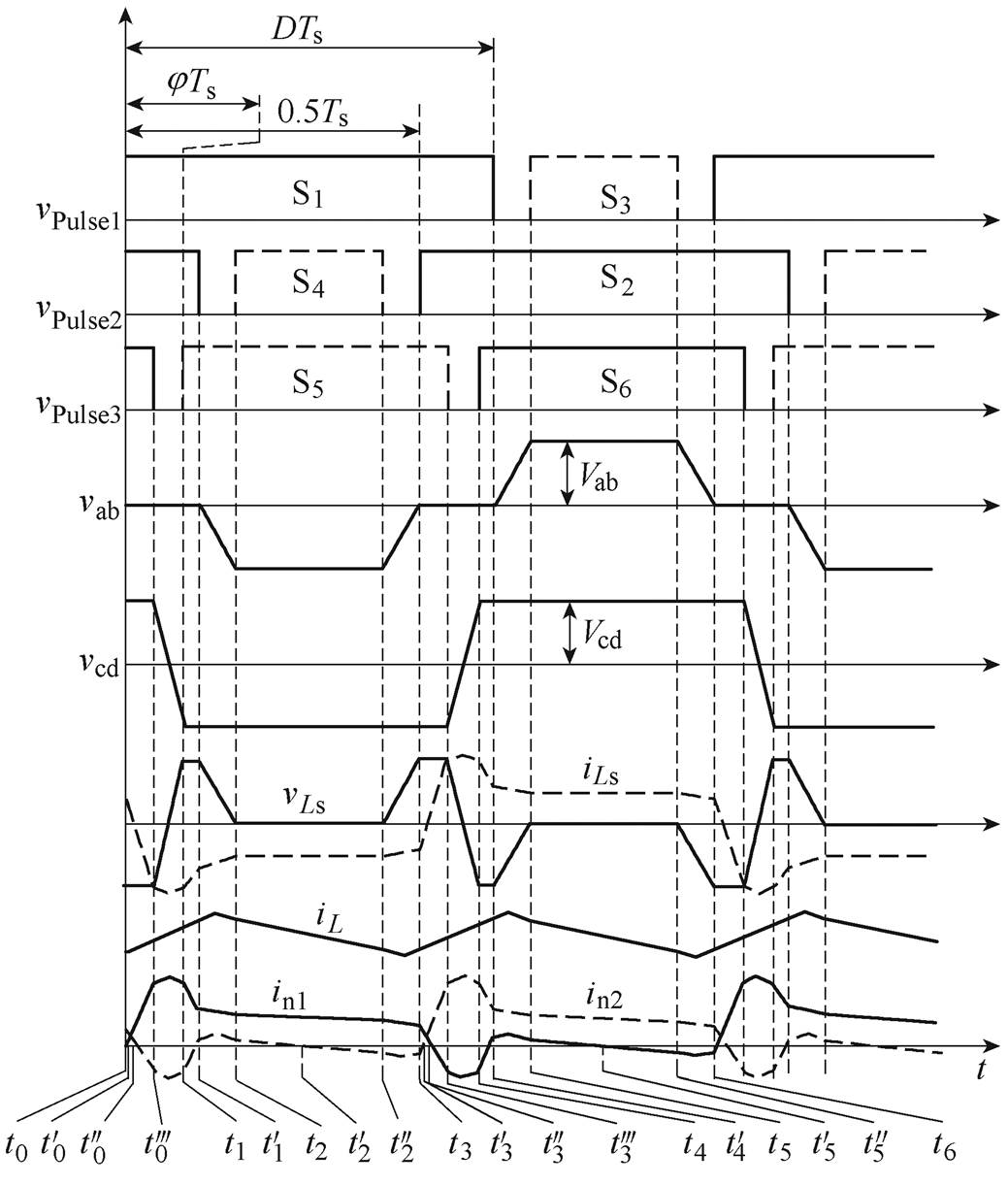
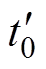
 :t
:t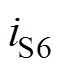 为负值。
为负值。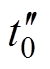
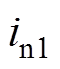 从负值增大至零,此后开始正向增加。
从负值增大至零,此后开始正向增加。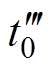
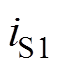 、
、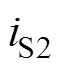 、
、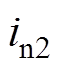 皆为正值。
皆为正值。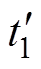
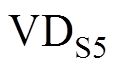 导通而形成回路,实现了S
导通而形成回路,实现了S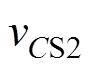 从零开始上升,
从零开始上升,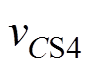 从
从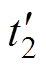
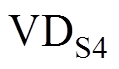 进行续流,开关管S
进行续流,开关管S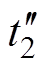
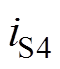 从负值变为零,此后为正值且继续增加。
从负值变为零,此后为正值且继续增加。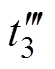 , t
, t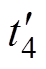 , t
, t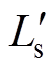 与传输电感L
与传输电感L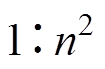 ;流过电感
;流过电感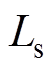 的电流
的电流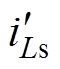 ,折算到变压器一次侧后的倍压电容电压
,折算到变压器一次侧后的倍压电容电压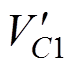 与倍压电容电压V
与倍压电容电压V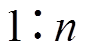 。
。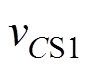 下降到零,谐振过程结束。S
下降到零,谐振过程结束。S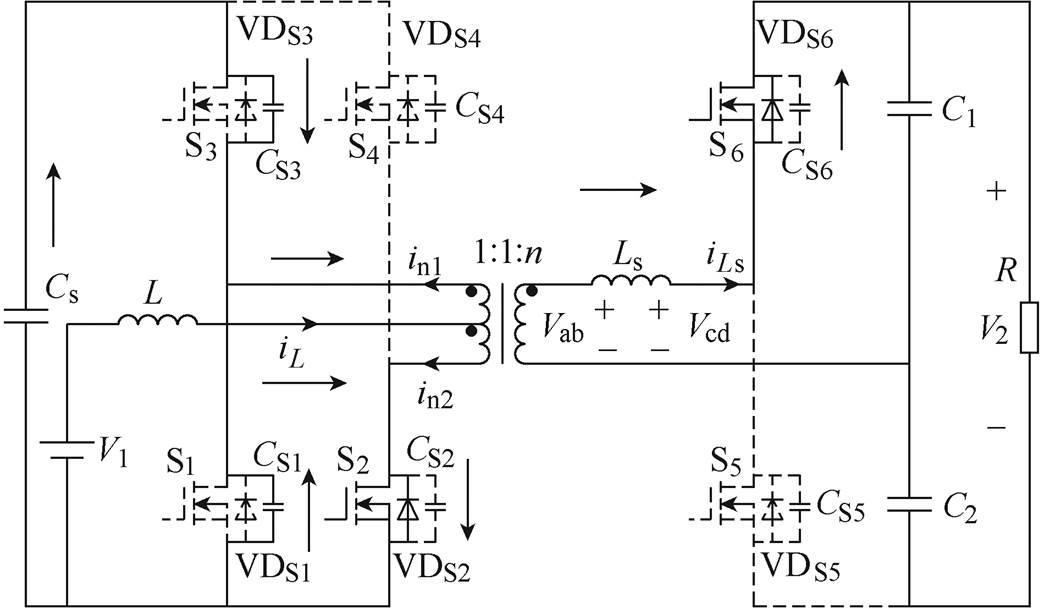
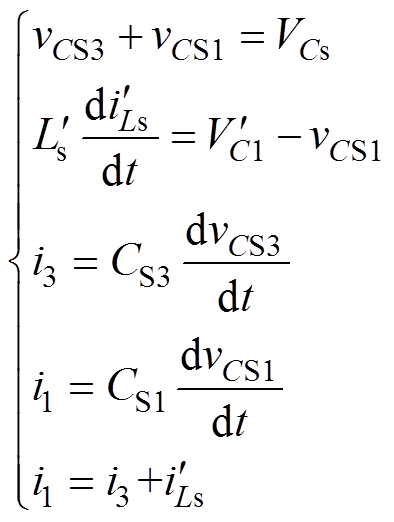 (12)
(12)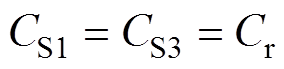 (13)
(13)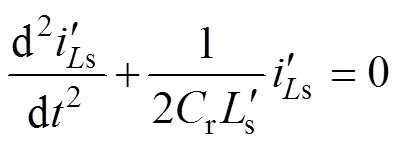 (14)
(14)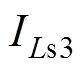 为
为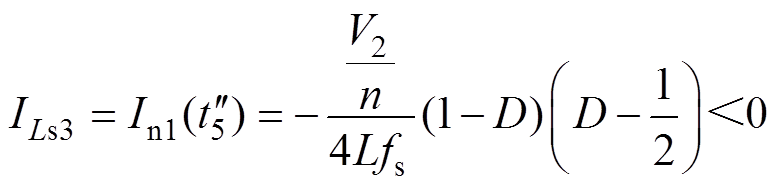 (15)
(15)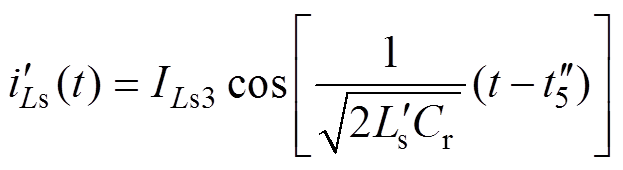 (16)
(16)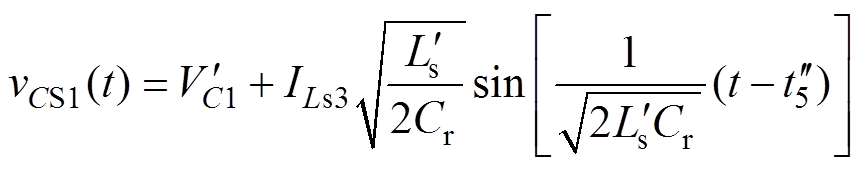 (17)
(17)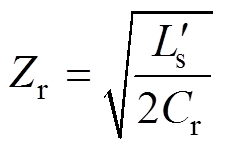 ;
; 。则电压
。则电压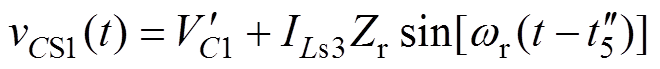 (18)
(18)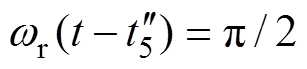 时,电压
时,电压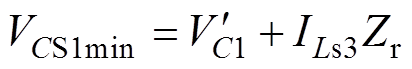 (19)
(19)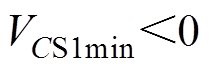 。
。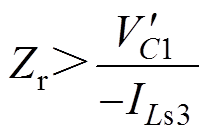 (20)
(20)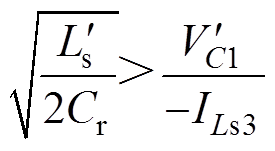 (21)
(21)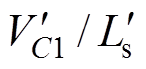 下降,当C
下降,当C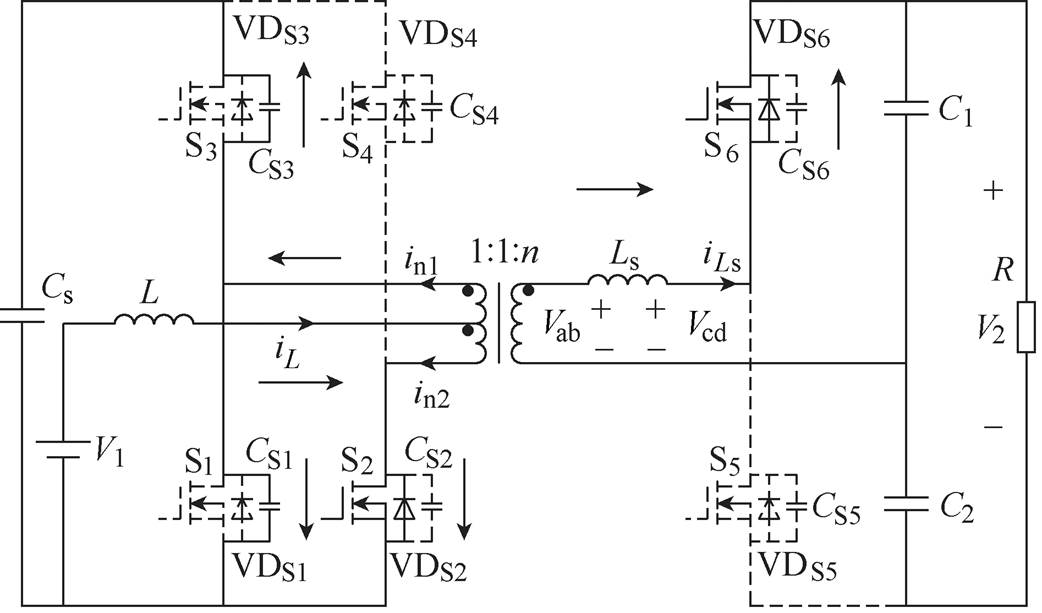
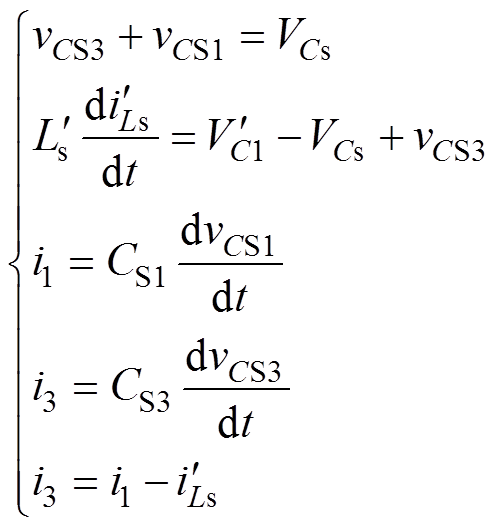 (22)
(22)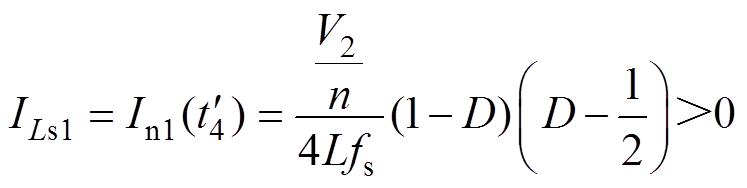 0.5<D<1(24)
0.5<D<1(24)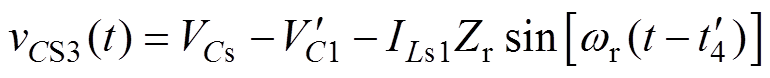 (25)
(25)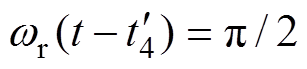 时,电压
时,电压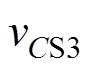 达到最小值
达到最小值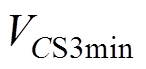 。
。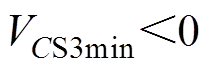 。
。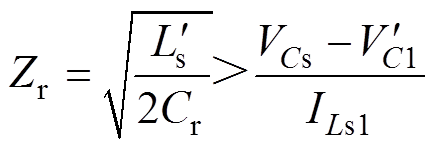 (26)
(26)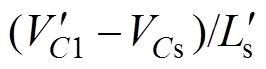 下降,当C
下降,当C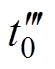 时刻,开关管S
时刻,开关管S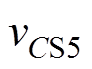 从V
从V 从零开始上升。直至t
从零开始上升。直至t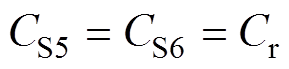 (27)
(27)
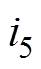 、
、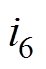 。由图10可列方程式为
。由图10可列方程式为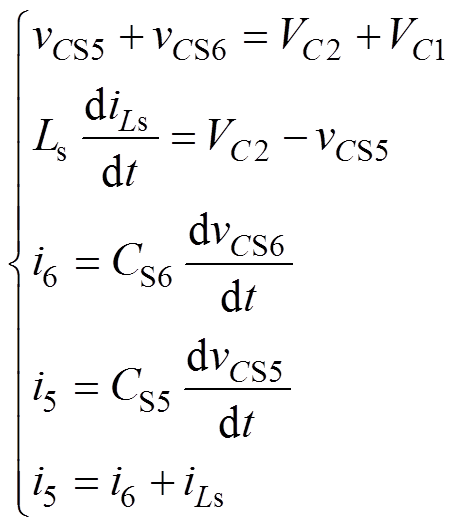 (28)
(28)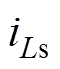 的初值I
的初值I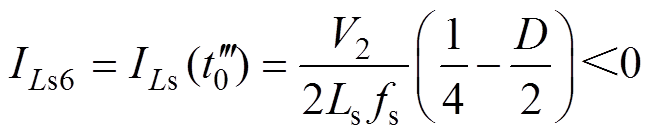 (29)
(29)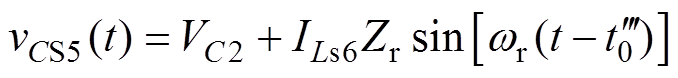 (30)
(30)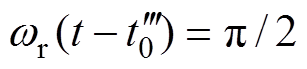 时,电压
时,电压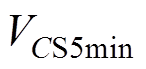 。由于要实现开关管S
。由于要实现开关管S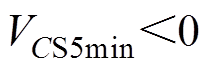 。
。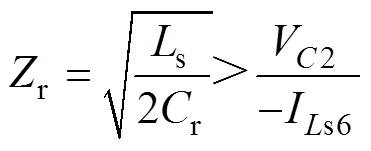 (31)
(31)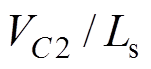 下降,当C
下降,当C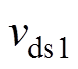 下降到零的时间段,电流
下降到零的时间段,电流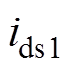 一直为负值,说明电流一直流经开关管S
一直为负值,说明电流一直流经开关管S
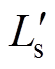 =80/9
=80/9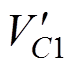 =350/3V。根据式(21)可得,C
=350/3V。根据式(21)可得,C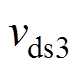 降到零区间,电流
降到零区间,电流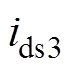 一直保持负值,说明电流一直经过开关管S
一直保持负值,说明电流一直经过开关管S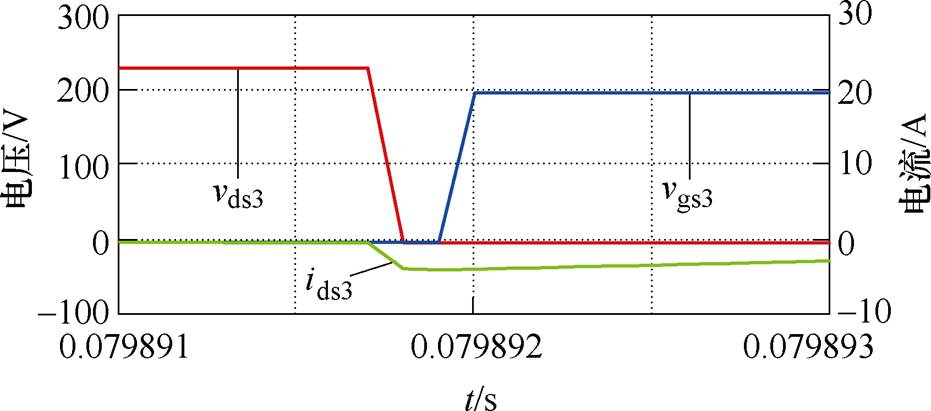
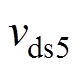 降到零时刻的区间内电流
降到零时刻的区间内电流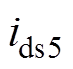 一直保持负值,说明电流一直经过开关管S
一直保持负值,说明电流一直经过开关管S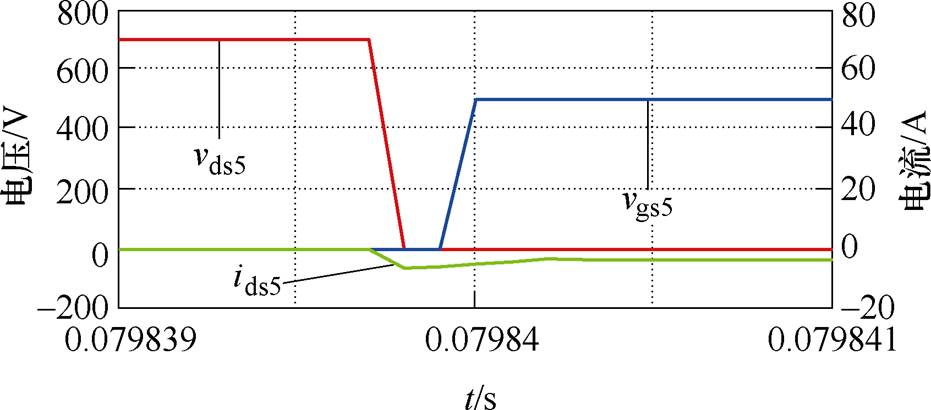
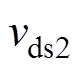 降到零之前,驱动信号
降到零之前,驱动信号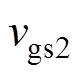 已经加在栅源极间,流过开关管的漏极电流i
已经加在栅源极间,流过开关管的漏极电流i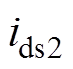 存在交叠区域,产生了开通损耗。
存在交叠区域,产生了开通损耗。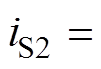
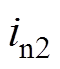 。由图中可见,在开关管S
。由图中可见,在开关管S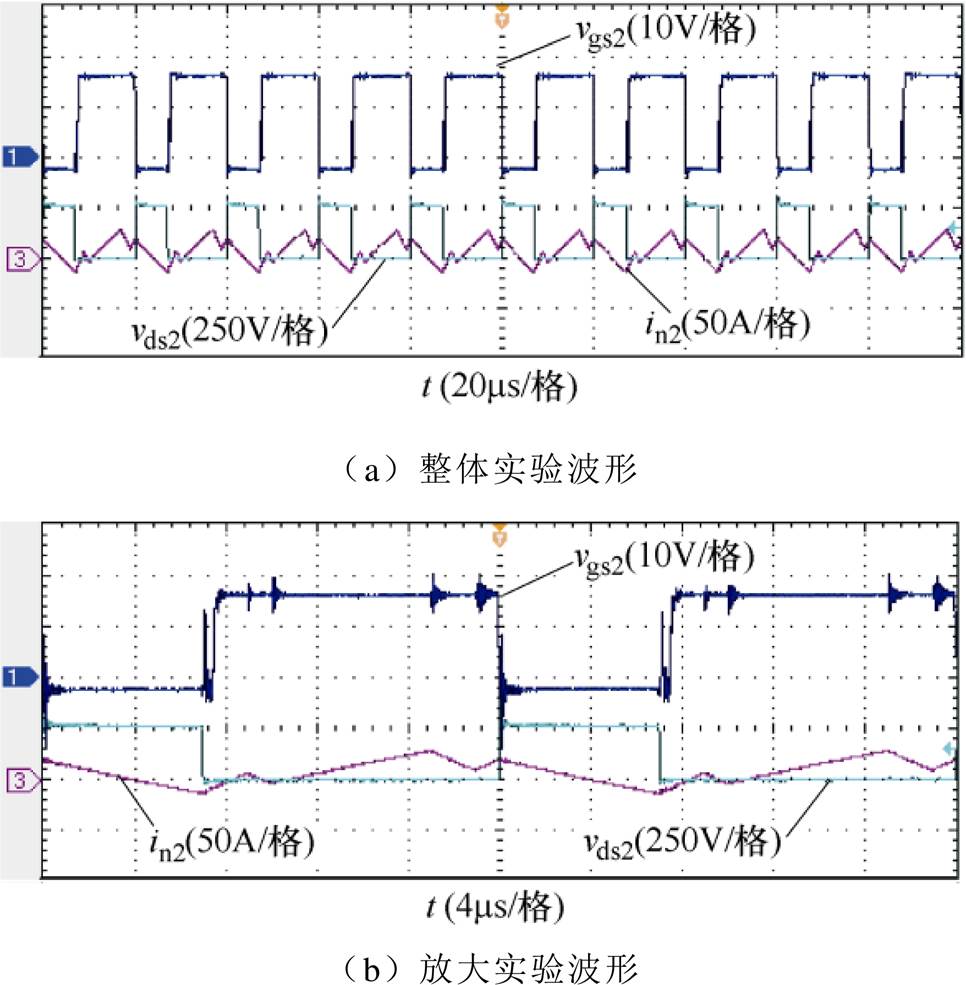
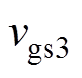 为S
为S 为变压器上绕组电流,此时
为变压器上绕组电流,此时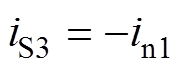 。由图中可见,在开关管S
。由图中可见,在开关管S 流经S
流经S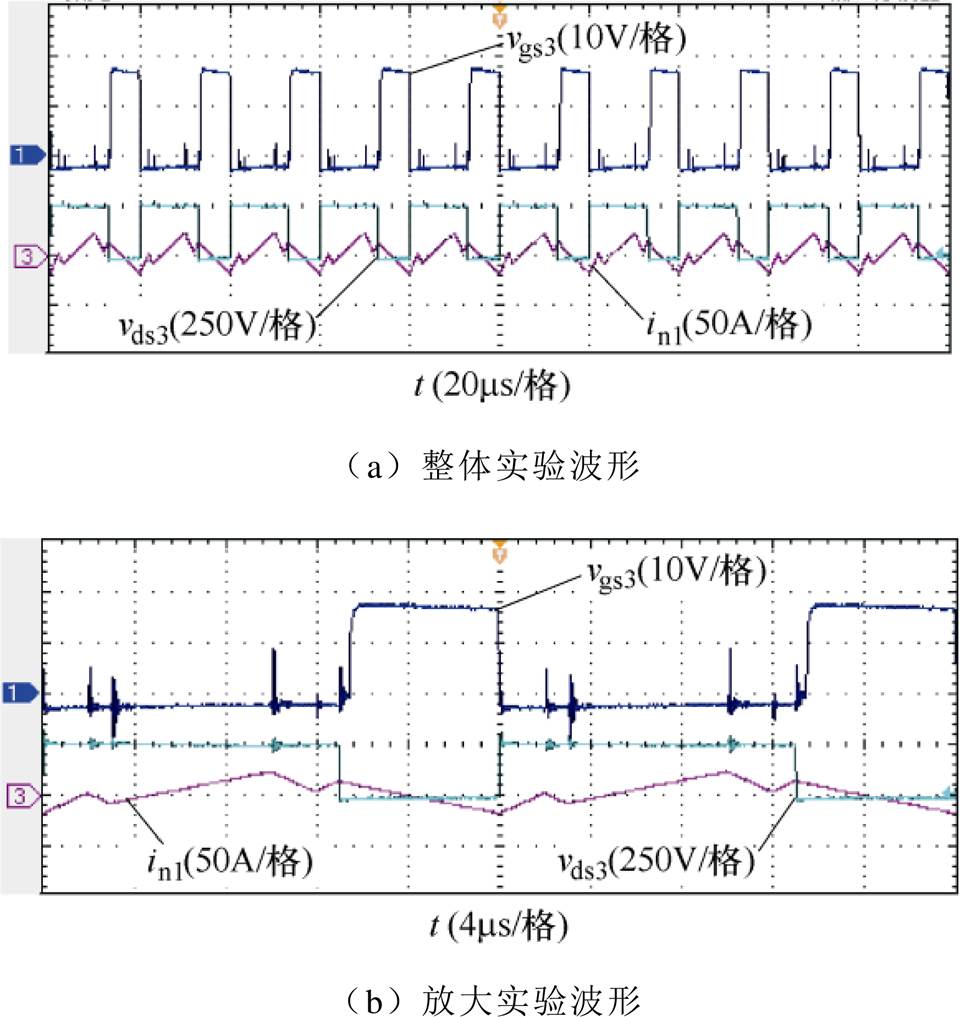
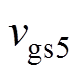 为开关管S
为开关管S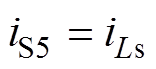 。由图中可见,当开关管S
。由图中可见,当开关管S