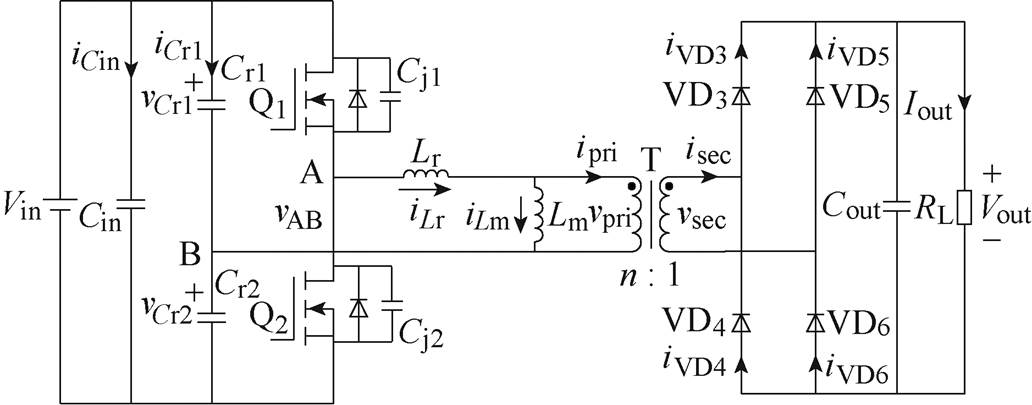
图1 对称半桥LLC谐振变换器拓扑示意图
Fig.1 Topology diagram of symmetrical half-bridge LLC resonant converter
摘要 在LLC谐振变换器中,对谐振电流的精确解析可以实现变换器的损耗计算。该文基于谐振电流近似拟合法提出一种改进型LLC谐振变换器电流解析方法,分析死区时间内的开关管结电容充放电过程、谐振电流的变化过程,通过对表达式中初始值的计算方法进行修正,该方法计算得到的谐振电流在死区时间内的变化情况更加准确。仿真结果表明,所提出的改进解析式相比原有的方法,在死区时间范围内可以准确描述谐振电流变化过程,相较于其他方法获得的初始值和励磁电流峰值,所提出方法的计算结果误差更小。实验结果进一步证明该文所提出的谐振电流解析方法的有效性和正确性。
关键词:LLC谐振变换器 谐振电流 改进解析法 死区时间 初始值计算
LLC谐振变换器具有一系列优良性能:实现一次侧开关管零电压开通和二次侧整流桥二极管的零电流关断;一次侧和二次侧实现电气隔离;宽范围的电压调节性能,既能实现升压,也能实现降压等,在轨道交通牵引电力电子变压器[1-2]、新能源汽车充电装置[3-4]、服务器电源[5-6]及其他工业电源[7]等场合得到广泛应用。LLC谐振变换器的效率提升和参数优化设计是当前一个重要研究方向,文献[8-10]通过改进变换器拓扑结构、设计最优参数、优化控制方法等方面提升了LLC谐振变换器的效率。
在LLC谐振变换器的参数设计过程中,不仅需要考虑变换器的总损耗,而且需要通过变换器各部分电流的具体变化情况对开关器件和其他部件进行合理选型。利用仿真软件直接计算损耗存在计算量大、费时等缺点,而通过电流解析表达式结合变换器的损耗模型计算损耗的方法则具有计算速度快的优势。另外,通过利用电流解析表达式和系统损耗模型对不同参数条件下的变换器的损耗进行计算和比较,可以对变换器参数进行最优设计,而利用仿真软件直接计算损耗则不利于大规模的参数选取和变换器参数优化设计。所以对LLC谐振变换器的谐振电流进行精确解析是十分必要的。现有文献中对谐振电流的解析式计算主要包括两大类:
第一类是列写谐振电流和谐振电感电压的微分方程,通过求解微分方程的方法,直接计算出谐振电流和谐振电感电压的表达式。文献[11-13]通过时间分段,列写电流、电压微分方程,然后求解微分方程,得到比较精确的相关变量解析表达式。但是该方法的准确性易受到参数变化的影响,并且方程式中包含的三角函数较多,计算量较大。该方法的准确性依赖于初始值求解的准确性,当求解初值不正确时会导致分段函数不连续,从而不能准确描述谐振电流的变化过程。文献[14-15]采用了列写LLC微分方程的方法求解谐振电流,除了最终电流表达式比较繁琐外,为了简化分析过程,这些方法没有进一步对死区时间内谐振电流的变化情况做出 分析。
第二类是在不同时间段上直接分析和求解谐振电流解析式的方法,也称为电流近似拟合法。文献[16-17]中将励磁电流近似等效为三角波,假设其在前后半周期中分别保持斜率不变,将二次侧整流桥二极管的波形近似等效为正弦电流,通过叠加折算到一次侧的整流桥二极管电流和励磁电流得到谐振电流。该方法的问题在于,没有考虑LC两谐振阶段和LLC三谐振阶段的励磁电流斜率变化,并且没有考虑死区时间对谐振电流和励磁电流产生的影响。文献[18]在此基础上,采取分段解析法,进一步考虑不同谐振阶段励磁电流斜率变化,但是该方法仅考虑励磁电流和谐振电流在死区时间内保持不变,没有考虑开关管结电容的充放电过程对励磁电流、谐振电流的影响,对死区时间和结电容充放电时间没有做出区分,这样会对LLC软开关的分析和体二极管损耗计算的准确性产生影响。文献[19]比较了频域分析法和时域分段解析法对LLC变换器增益和参数设计的影响,为了简化分析,文献[19]中忽略了死区时间的作用。
本文提出一种改进型LLC电流解析式的方法,基于谐振电流近似拟合法,进一步研究死区时间内LLC电流的变化情况。首先,按分段解析的方法列写不同时间段LLC励磁电流和谐振电流的解析式。然后,通过对死区时间内开关管结电容充放电过程中结电容两端电压的分析,对谐振电流和励磁电流的电流变化率进行研究,得到更加准确的死区时间内的谐振电流、励磁电流解析式。最后,根据所列写的电流解析式,通过电流对称性和电流增量的精确分析,研究了精确的初始值计算方法。仿真结果和实验结果表明,本文所提方法得到谐振电流初值比解析表达式计算得到的电流值更加精确,并可以利用该表达式更准确地分析系统损耗模型。
图1给出了对称半桥LLC谐振变换器拓扑示意图。图1中,Vin和Vout为变换器输入电压和输出电压。Cin为输入电容,iCin为输入电容电流。Cr1和Cr2为谐振电容,iCr1和iCr2为流过Cr1和Cr2上的电流,vCr1和vCr2为Cr1和Cr2两端的电压。Q1和Q2为两个开关管。Cj1和Cj2为开关管的输出侧结电容。vAB为变压器T的一次电压。Lr为谐振电感,iLr为谐振电流。Lm为励磁电感,iLm为励磁电流。vpri和ipri为理想变压器一次电压和一次电流。vsec和isec为理想变压器的二次电压和二次电流。n为变压器电压比。VD3~VD6为二次侧整流桥的四个二极管,iVD3~iVD6为流经四个整流桥二极管的电流。Cout为输出电容,RL为负载电阻,Iout为负载电流。首先针对励磁电流iLm的解析式进行推导,得到改进的励磁电流表达式。然后考虑在励磁电流的基础上叠加变压器一次电流ipri,最终得到改进的谐振电流iLr表达式。

图1 对称半桥LLC谐振变换器拓扑示意图
Fig.1 Topology diagram of symmetrical half-bridge LLC resonant converter
图2给了LLC谐振变换器主要波形。图2中,第一通道为谐振电流iLr和励磁电流iLm,第二通道为流经两个开关管的电流iQ1和iQ2,第三通道为两个开关管的驱动脉冲vgs1和vgs2,其中,1和0分别表示高、低电平,对应开关管开通和关断状态。
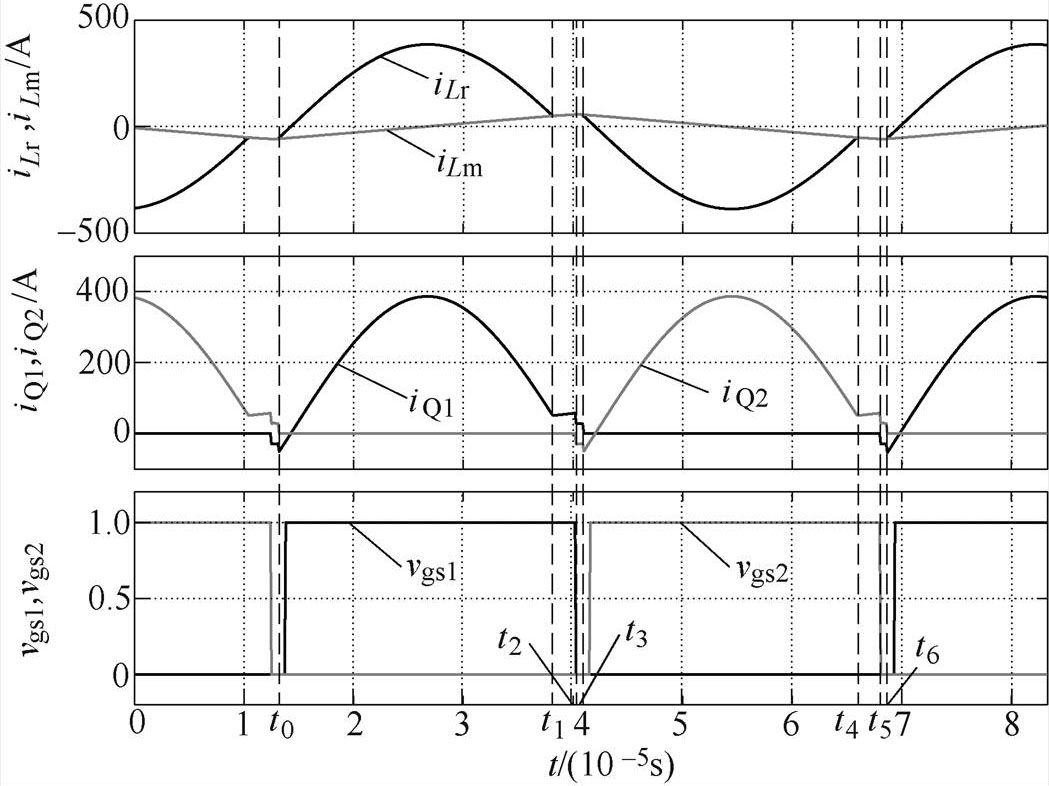
图2 LLC谐振变换器主要波形
Fig.2 Main waveforms of LLC resonant converter
图2中标注的t0~t6各时刻的值具体为
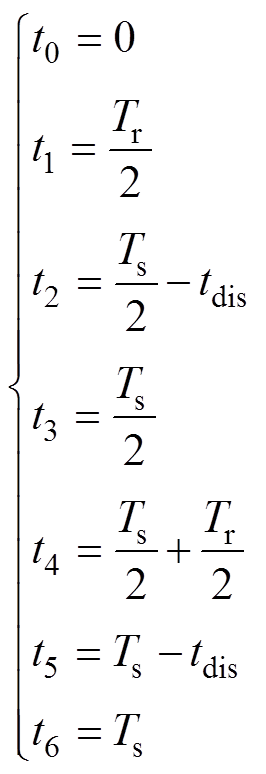 (1)
(1)式中,t0为前半个周期LC谐振起始时刻;Ts=1/fs为开关周期,fs为变换器的开关频率;tdis为开关管输出结电容的放电时间(下半周期预开通开关管的结电容放电时间,也是当前正关断的开关管的结电容充电时间);Tr=1/fr为谐振周期,fr为变换器的LC两元件谐振时的谐振频率,即
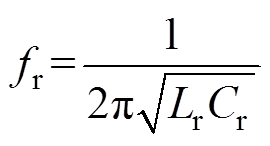 (2)
(2)
图3为在死区时间td附近的谐振电流iLr和励磁电流iLm,以及两个开关管的驱动脉冲vgs1和vgs2波形。t1~t3的具体值在式(1)中给出。可以看出,t2时刻上管Q1关断,变换器进入死区时间。
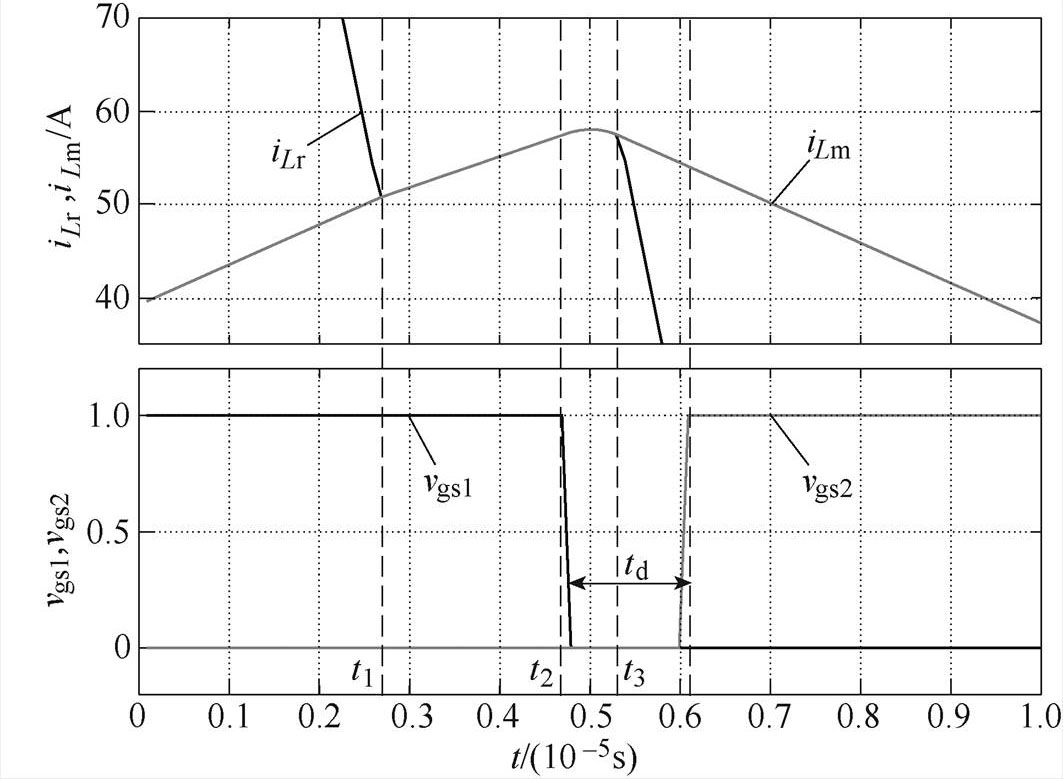
图3 死区时间附近谐振电流、励磁电流波形和开关管驱动脉冲波形
Fig.3 The waveforms of resonant current, magnetizing current and driving pulses of switches near the dead-time
首先将LLC谐振变换器二次侧整流桥二极管中流经的电流近似考虑为正弦波,可以得到整流桥二极管的电流iVD3,6和iVD4,5分别为
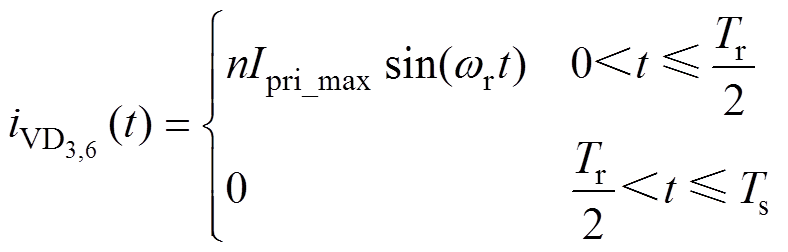 (3)
(3) (4)
(4)
式中,Ipri_max为变压器一次电流的峰值;wr=2p fr为谐振频率对应的角频率。
为了求得整流桥二极管电流的峰值,此处令整流桥流经电流的平均值等于输出电流。得到
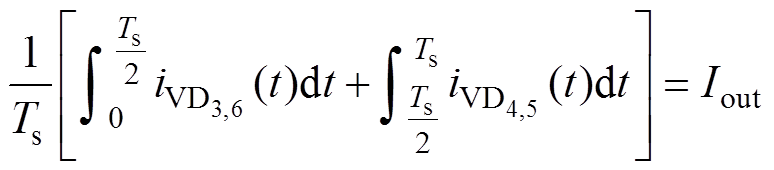 (5)
(5)解得
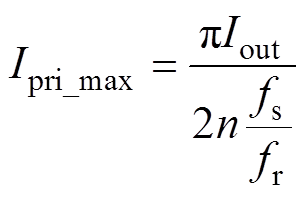 (6)
(6)
变压器一次电流ipri(t)与二次侧整流桥二极管的电流iVD(t)关系为
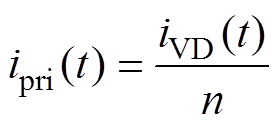 (7)
(7)考虑电流方向后,ipri(t)最终可以表示为
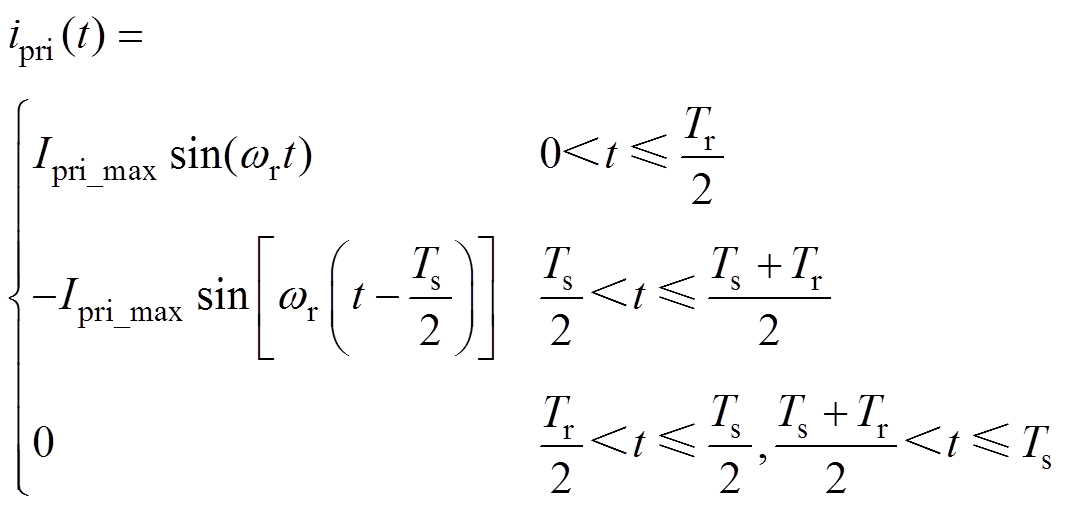 (8)
(8)
如图2所示,励磁电流的变化过程主要可分为6个时间段。因为前半个周期与后半个周期对称,所以本节中仅针对前半个周期中励磁电流的改进型解析式进行推导,后半个周期中的励磁电流改进解析式可以用相同的方法计算得到。
1.2.1 第1时间段
在第1时间段,t∈[t0, t1],谐振变换器的谐振电感Lr和谐振电容Cr1和Cr2发生谐振。励磁电感两端电压v1=nVout,所以励磁电流变化率为
 (9)
(9)式中,Vout为额定输出电压;Lm为励磁电感;iLm_1(t)为t∈[t0, t1]时间段的励磁电流。
可以得到iLm_1(t)的表达式为
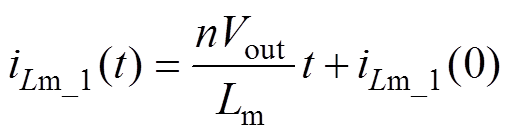 (10)
(10)式中,iLm_1(0)为t0时刻对应的励磁电流。
该时段末端t1时刻的励磁电流iLm_1(t1)为
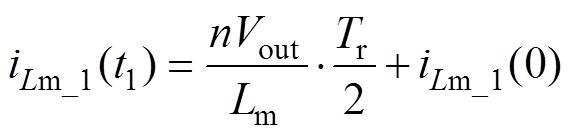 (11)
(11)初始值iLm_1(0)和iLm_1(t1)以及本节中出现的其他初始值会在第2节初始值求解部分统一求解。
1.2.2 第2时间段
谐振变换器在第2个时间段t∈(t1, t2 进入LLC三元件谐振阶段,励磁电感Lm不再被输出电压钳位。如图1所示,在前半周期中,该时间段谐振槽路输入电压vAB=vCr1。则列写电容Cr1的电压变化方程以代入励磁电流变化率的计算中,此处为了简化模型作出近似,LLC三元件谐振阶段的谐振槽路电压用谐振电容Cr1的电压平均值vCr1-av代替,vAB=vCr1-av=
进入LLC三元件谐振阶段,励磁电感Lm不再被输出电压钳位。如图1所示,在前半周期中,该时间段谐振槽路输入电压vAB=vCr1。则列写电容Cr1的电压变化方程以代入励磁电流变化率的计算中,此处为了简化模型作出近似,LLC三元件谐振阶段的谐振槽路电压用谐振电容Cr1的电压平均值vCr1-av代替,vAB=vCr1-av=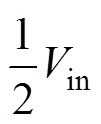 。
。
该时间段励磁电流变化率变为
 (12)
(12)此时得到励磁电流表达式iLm_2(t)为
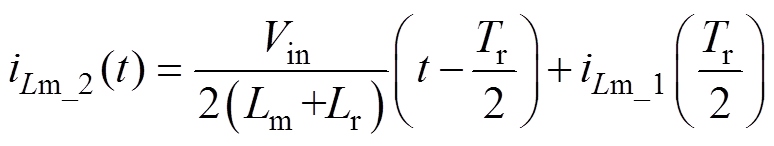 (13)
(13)
该时段t2时刻励磁电流值iLm_2(t2)为
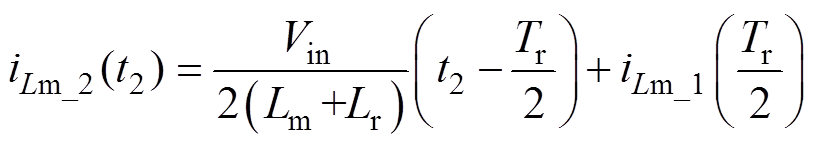 (14)
(14)1.2.3 第3时间段
图4给出了死区时间附近谐振电流iLr、励磁电流iLm和谐振槽路输入电压vAB的波形。谐振变换器在第3个时间段t∈(t2, t3],上管Q1关断,变换器进入死区,开关管结电容开始充放电。本节主要分析并求解第3时间段t∈(t2, t3]内,励磁电流的解析式。
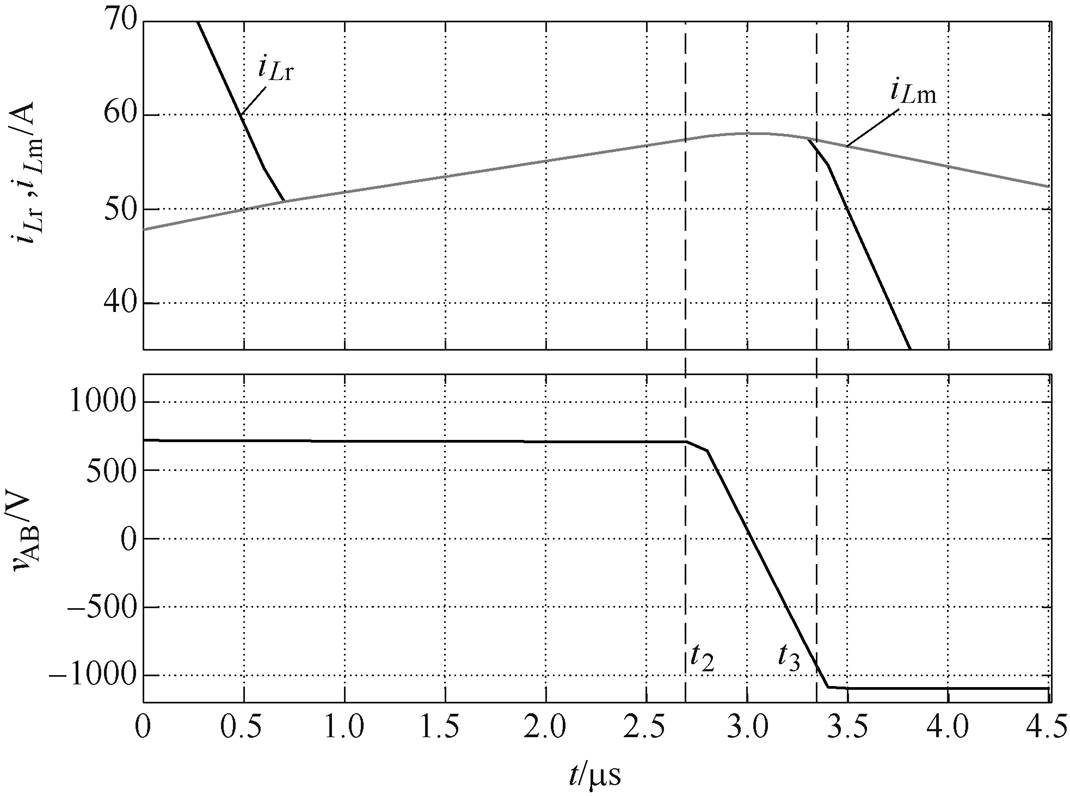
图4 死区时间附近励磁电流和谐振槽路输入电压波形
Fig.4 The waveforms of magnetizing current and input voltage of resonant tank near the dead-time
在t∈(t2, t3]的时间段内,开关管两端的电压变化率与励磁电流值有关。此处为了简化分析,考虑将励磁电流峰值iLm_peak代入到开关管两端电压变化率的分析中,得到
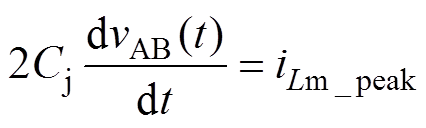 (15)
(15)式中,Cj为开关管两端输出结电容。
另外,在开关管关断进入死区之前,谐振槽路的输入电压vAB用谐振电容Cr1的电压平均值vCr1-av代替;同样地,对管开通后,vAB用谐振槽路的输入电压Cr2的电压平均值vCr2-av代替,方向取反。可得到
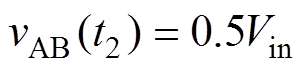 (16)
(16)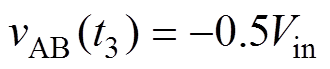 (17)
(17)
谐振槽路输入电压线性化地由0.5Vin下降至-0.5Vin。
可以推导得到谐振槽路的输入电压为
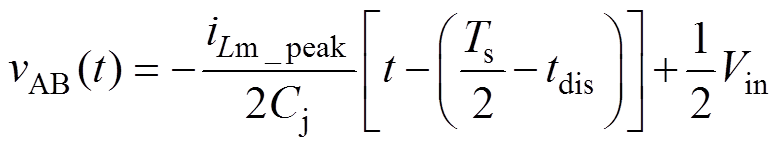 (18)
(18)其中
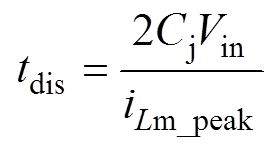 (19)
(19)
可得到该时间段励磁电流的变化率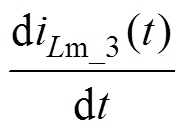 为
为
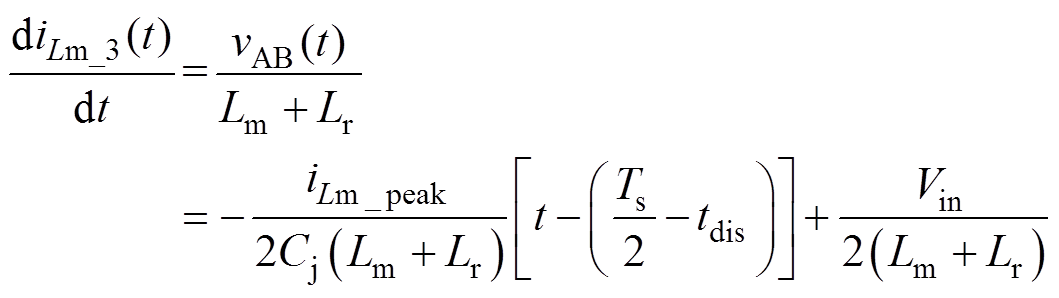 (20)
(20)励磁电流iLm_3(t)可以通过不定积分方式得到
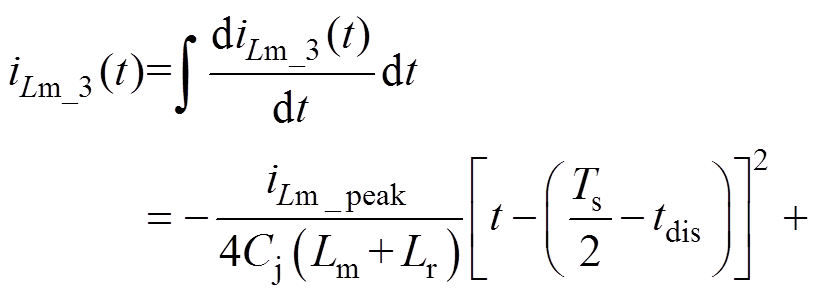
 (21)
(21)式中,iLm_C_3为一个与时间无关的常数,将会在第2节初始值求解中进行求解。另外下半周期中t∈(t3, t4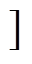 、t∈(t4, t5
、t∈(t4, t5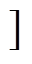 和t∈(t5, t6
和t∈(t5, t6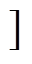 三个时间段的励磁电流表达式可以用相同的方法求解得到,此处不再赘述。通过求解改进励磁电流的表达式和变压器一次电流的表达式,可以得到谐振电流的表达式为
三个时间段的励磁电流表达式可以用相同的方法求解得到,此处不再赘述。通过求解改进励磁电流的表达式和变压器一次电流的表达式,可以得到谐振电流的表达式为
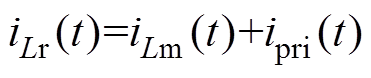 (22)
(22)
上半周期LLC谐振变换器谐振电流、励磁电流和开关管驱动脉冲如图5所示,4个关键时刻分别为t0、t1、t2和t3,其具体值在式(1)中给出。t0设为谐振电流一个周期的初始时刻,满足
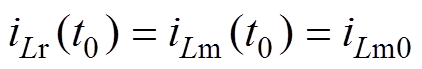 (23)
(23)
图5 上半周期LLC谐振变换器谐振电流、励磁电流和开关管驱动脉冲
Fig.5 The waveforms of resonant current, magnetizing current and driving pulses of switches in the first half switching period
t1为前半个周期中LC谐振结束时刻,满足关系式
 (24)
(24)t2为上桥臂开关管Q1关断的时刻,满足
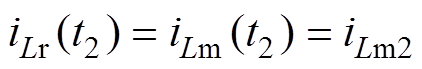 (25)
(25)
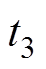 为前半周期结束时刻。此时待开通开关管Q2的结电容放电完毕,已关断开关管Q1的结电容充电完毕。根据第1节中三个不同时间段的电流解析式的推导过程可知,励磁电流的变化率
为前半周期结束时刻。此时待开通开关管Q2的结电容放电完毕,已关断开关管Q1的结电容充电完毕。根据第1节中三个不同时间段的电流解析式的推导过程可知,励磁电流的变化率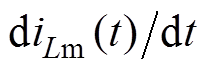 在tdis内由
在tdis内由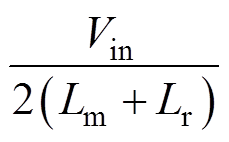 变化至0,再由0变化至
变化至0,再由0变化至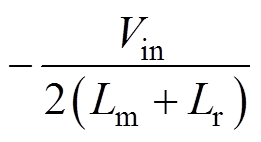 ,可以推断得励磁电流在
,可以推断得励磁电流在 处取得最大值iLm_peak。
处取得最大值iLm_peak。
图6给出了初始值之间的增量关系。根据图6所示的不同时间段内,谐振电流和励磁电流的初始值和峰值之间的关系,可以给出这些值之间的增量关系为
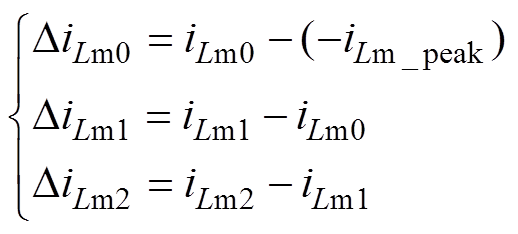 (26)
(26)
首先,励磁电流的峰值根据对称性可以计算得
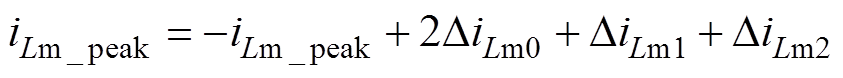 (27)
(27)化简得
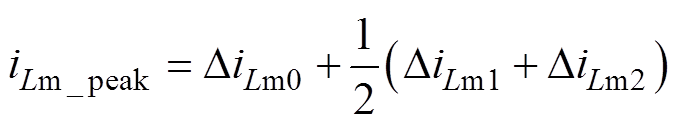 (28)
(28)
根据图6中励磁电流的变化情况和iLm_3(t)的表达式,可以计算出DiLm0、DiLm1、DiLm2的表达式分别为
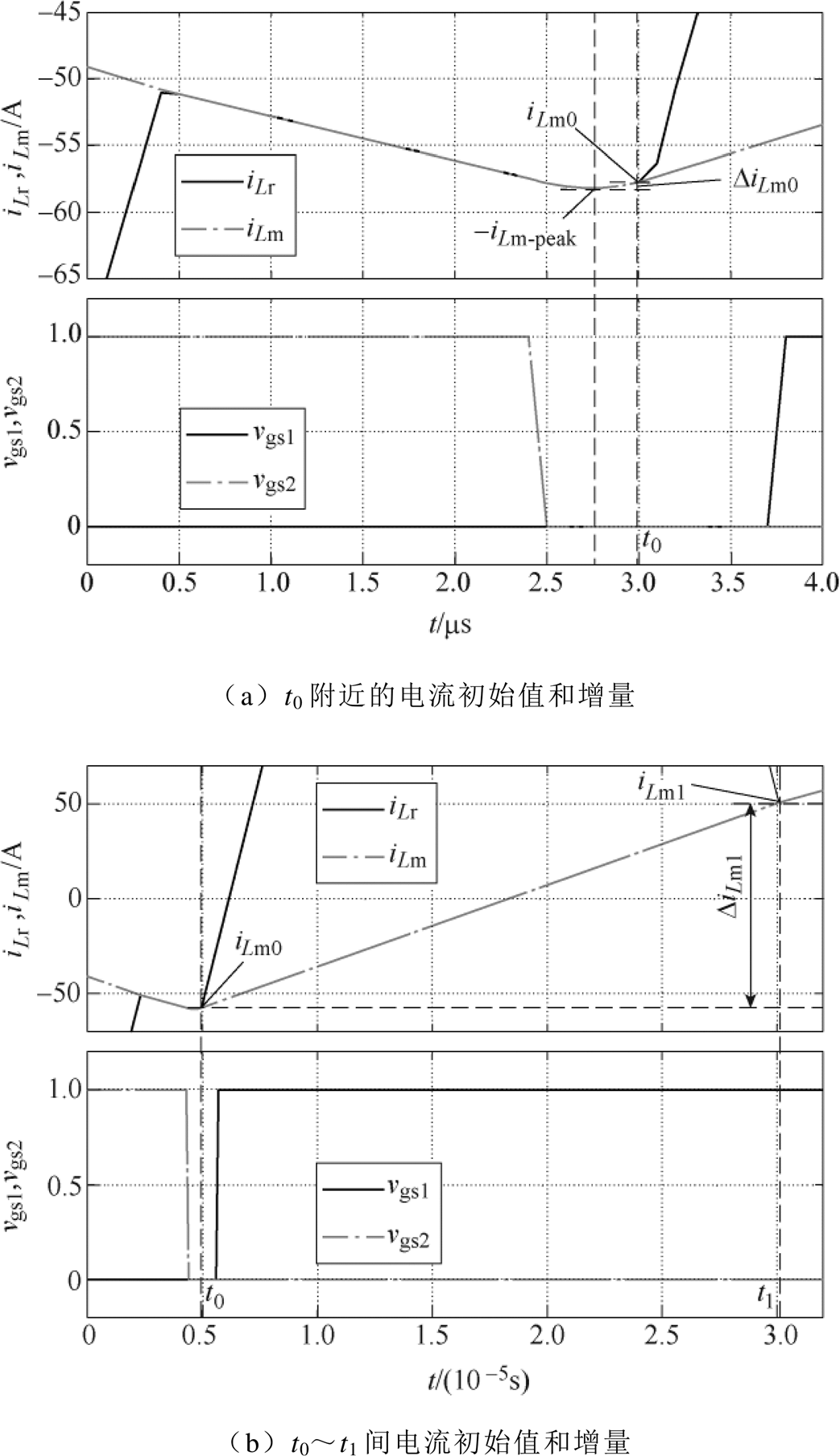
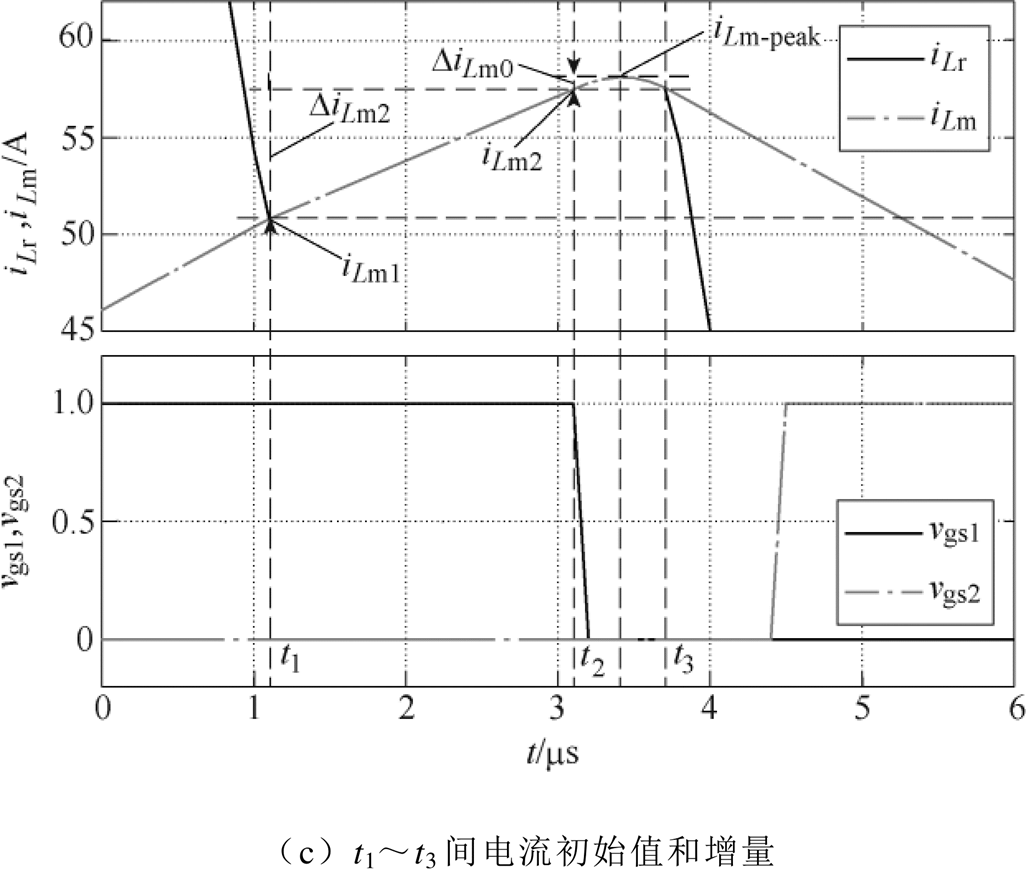
图6 三个时间段内LLC谐振变换器电流初始值与电流增量示意图
Fig.6 The initial values and incremental values of two currents of LLC resonant converter in three time periods
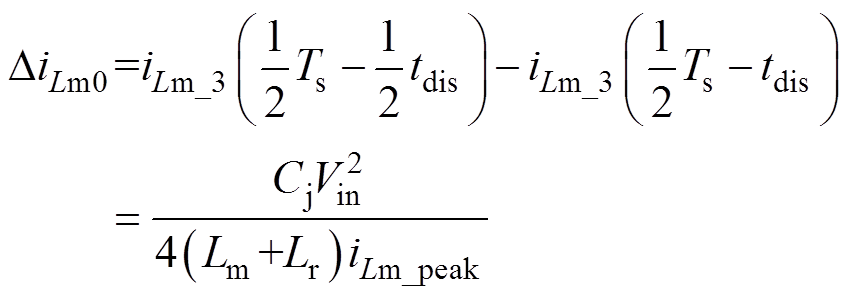 (29)
(29)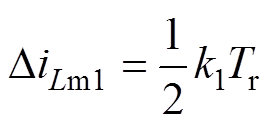 (30)
(30)
 (31)
(31)
其中
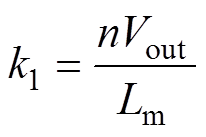 (32)
(32) (33)
(33)
根据式(28)~式(33)可以得到
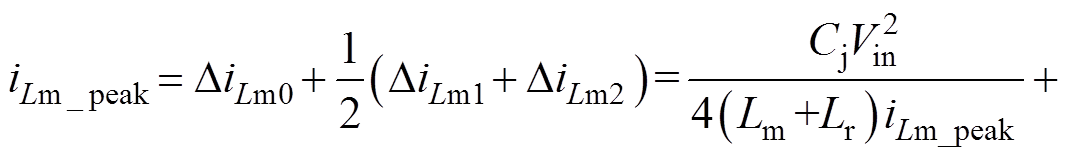
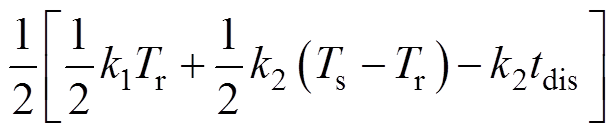 (34)
(34)
由式(34)整理可得
 (35)
(35)然后可得
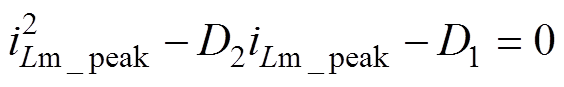 (36)
(36)
其中
 (37)
(37)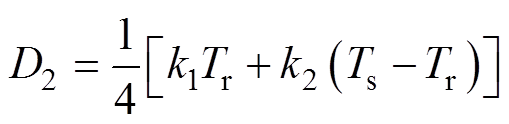 (38)
(38)
由式(36)解得
 (39)
(39)保留合适值,最终得到
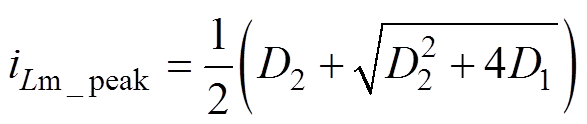 (40)
(40)
整理后可得iLm_peak为
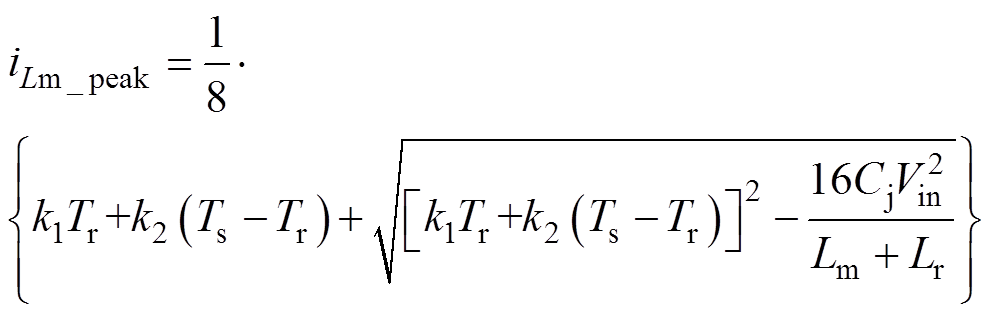 (41)
(41)首先,根据式(26)和式(41)可以得到t0时刻的初始值iLm0为
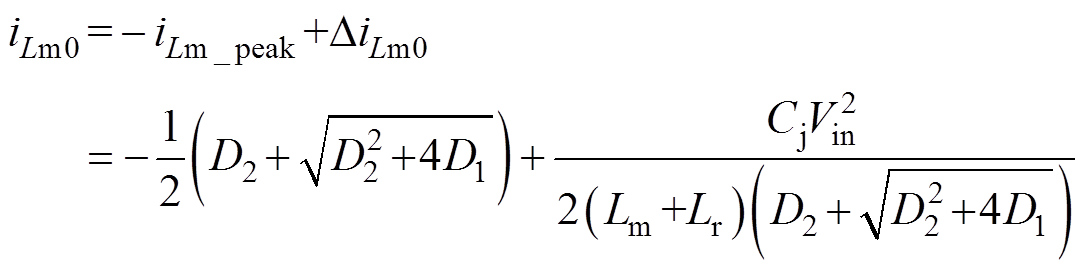 (42)
(42)
根据式(26)和式(42)可得iLm1为
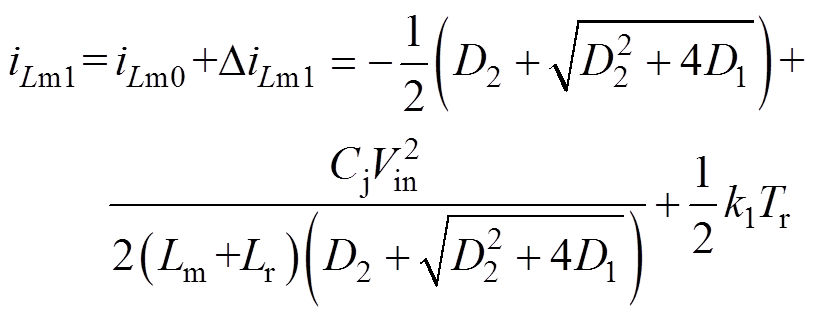 (43)
(43)然后,根据式(26)和式(43)可得iLm2为
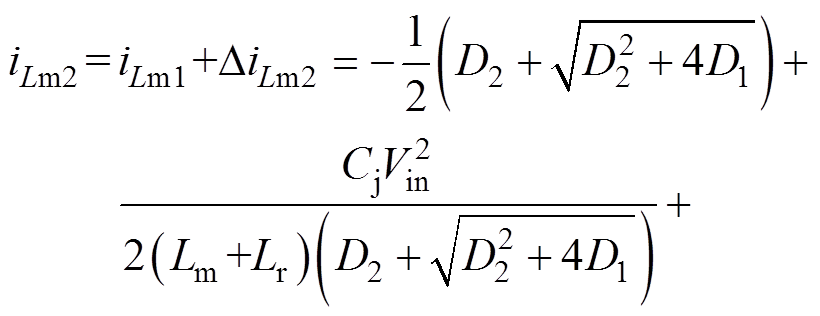
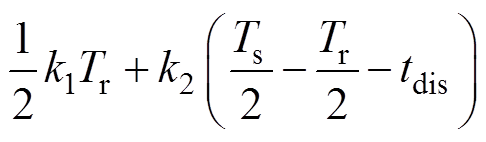 (44)
(44)最后,为了求解前半周期中第3个时间段的解析式包含的常数值,代入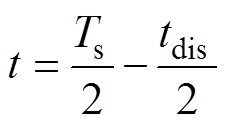 的励磁电流值iLm_peak,结合式(21),可以得到
的励磁电流值iLm_peak,结合式(21),可以得到
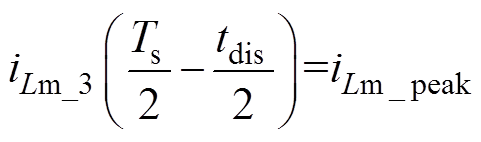 (45)
(45)
则
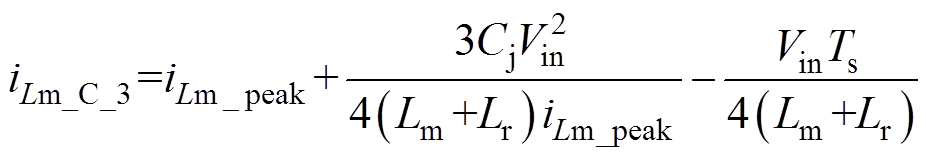 (46)
(46)后半个周期的初始值iLm3、iLm4、iLm5以及后半周期中第3个时间段解析式的常数iLm_C_6的计算过程与前半个周期相同,此处不再详述。
根据式(8)、式(22)以及计算得到的不同时间段的励磁电流表达式,最终得到整个开关周期Ts中谐振电流iLr(t)的表达式为
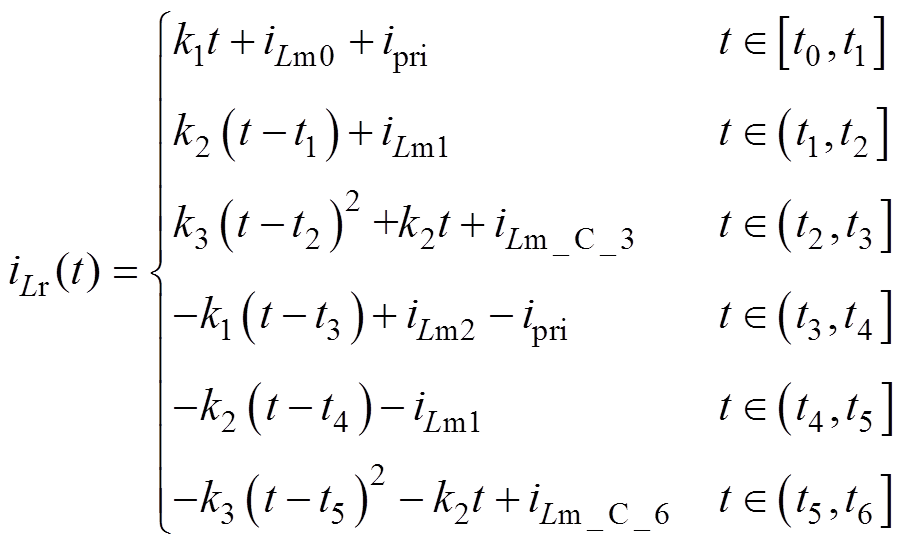 (47)
(47)其中
 (48)
(48)
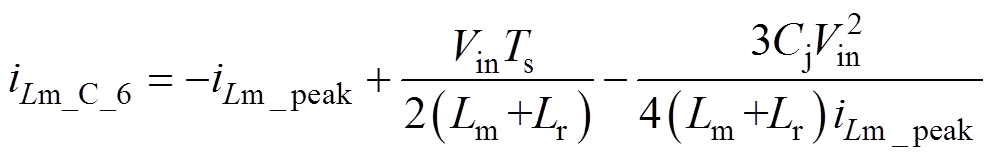 (49)
(49)为了证明本文所提改进型LLC谐振变换器谐振电流表达式的准确性,本节将改进型电流表达式得到的电流波形与仿真结果进行比较。首先利用PSIM仿真软件搭建LLC谐振变换器仿真模型,仿真步长为100ns,LLC谐振变换器的参数见表1。仿真中LLC谐振变换器采用开环控制算法,上下开关管占空比各为50%。根据所提出的改进型LLC谐振电流表达式和相应的初始值计算结果,可以得到改进表达式中一个周期的谐振电流和励磁电流波形。另外本节考虑将所提出的方法与其他两种在文献[17-18]中提出的方法以及仿真结果做比较。
表1 LLC谐振变换器参数
Tab.1 Parameters of LLC resonant converter
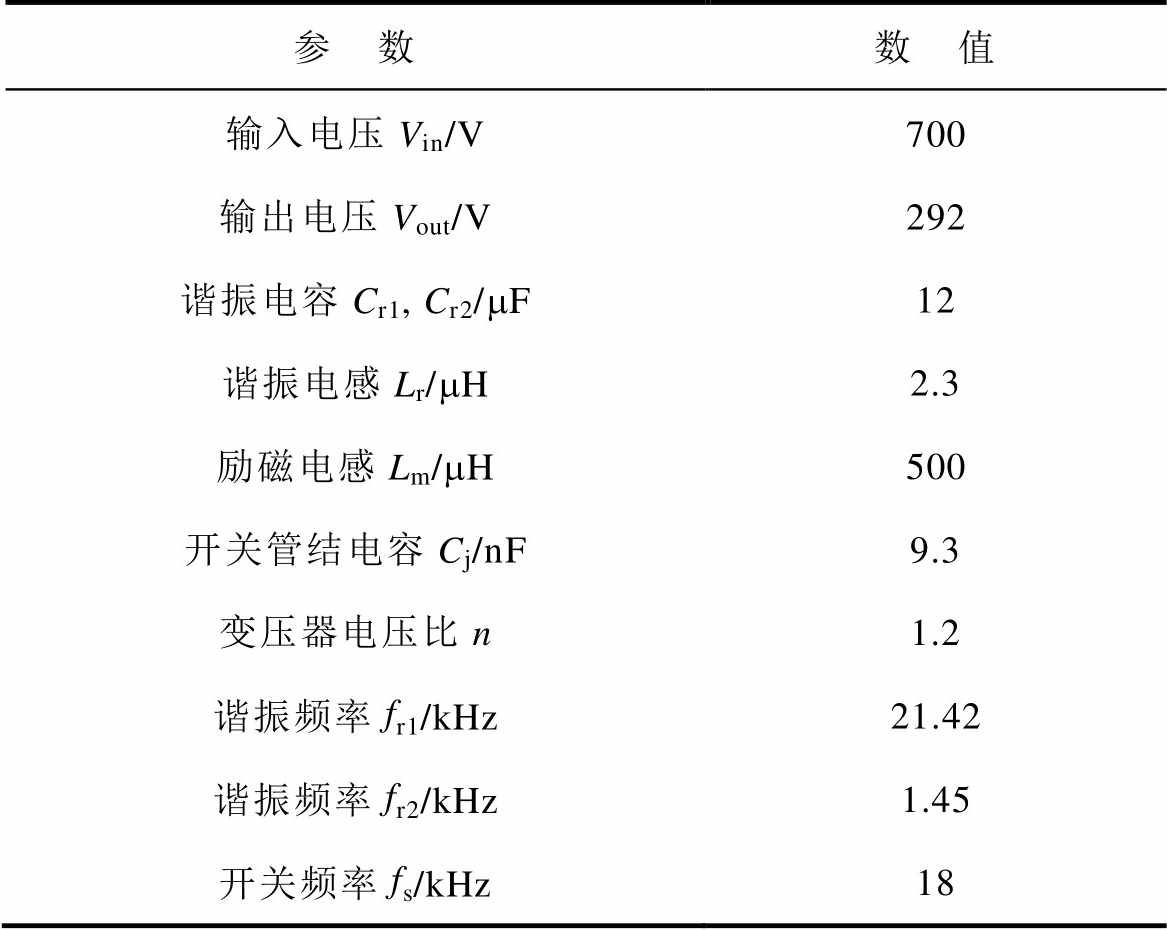
参 数数 值 输入电压Vin/V700 输出电压Vout/V292 谐振电容Cr1, Cr2/mF12 谐振电感Lr/mH2.3 励磁电感Lm/mH500 开关管结电容Cj/nF9.3 变压器电压比n1.2 谐振频率fr1/kHz21.42 谐振频率fr2/kHz1.45 开关频率fs/kHz18
3.1.1 改进型LLC解析式
仿真中负载电阻给定为8.6W,输出功率为10kW。由表1中参数和式(19)计算得出结电容放电时间tdis=1.37ms,根据软开关的需求,死区时间td给定为2ms。
图7给出了由改进型LLC电流表达式得到的谐振电流iLr和励磁电流iLm波形。所提出的电流拟合方法可以完整地拟合出连续变化的谐振电流波形和励磁电流波形。这表明,根据所提出的谐振电流和励磁电流解析式,以及对应的初值计算方法,可以较为准确地计算出谐振电流和励磁电流以及各部分 初值。
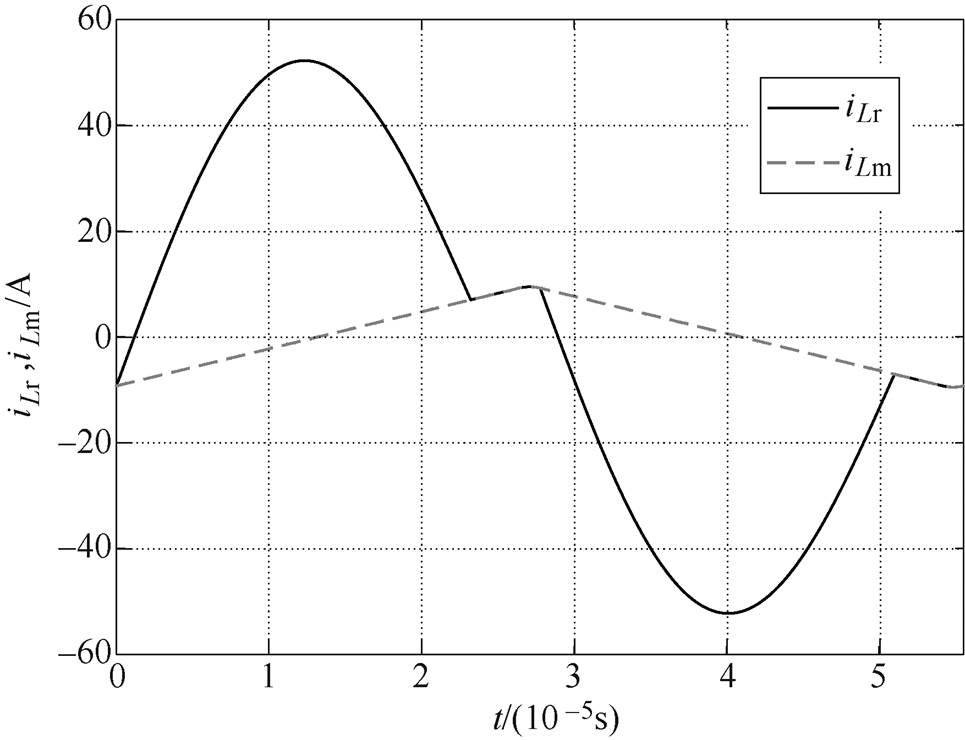
图7 改进型电流解析式得到的谐振电流和励磁电流波形
Fig.7 The resonant current and magnetizing current waveforms by the proposed improved current analytical expressions
图8给出了一个开关周期中,仿真得到的LLC谐振电流和励磁电流,和本文中所提出的LLC改进解析式得到两种电流的对比波形。图中,iLr-sim和iLm-sim分别为仿真中得到的LLC谐振电流和励磁电流。iLr-p和iLm-p分别为根据本文中所提出的改进型电流解析模型得到的波形。
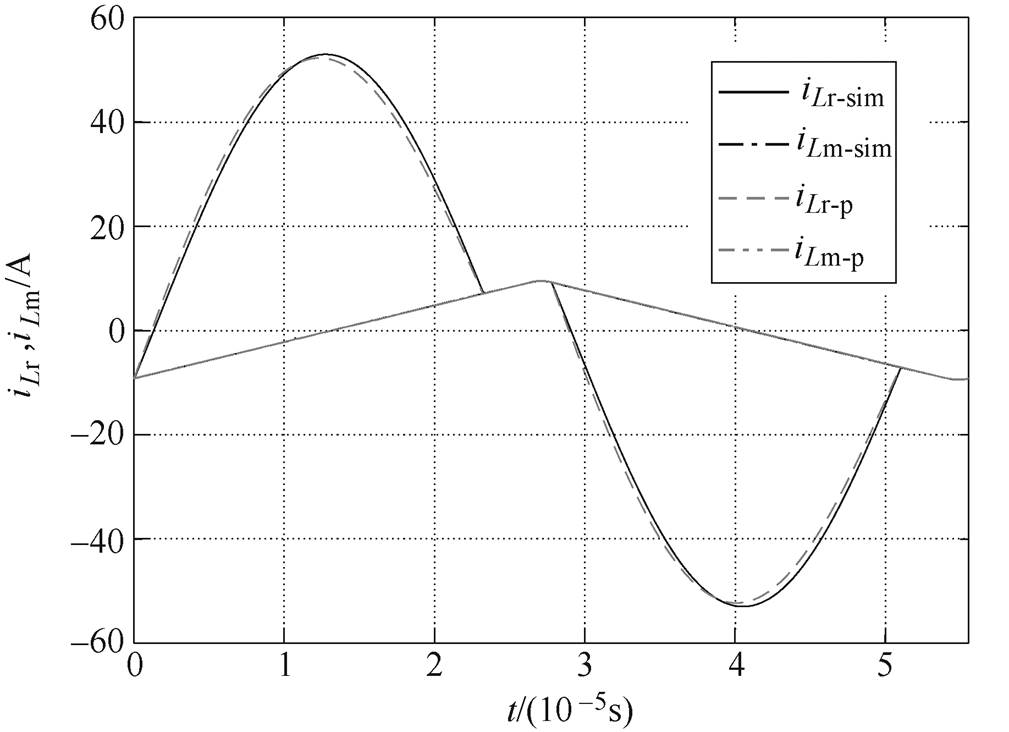
图8 改进型电流解析式得到的电流波形与仿真结果对比
Fig.8 Comparison results of current waveforms calculated by the improved current analytical expressions and simulation results
可以看出,仿真中的励磁电流和本文方法得到的励磁电流波形几乎一致。本文方法得到的谐振电流iLr-p和仿真得到的谐振电流iLr-sim存在一些误差,这是由于变压器一次电流并非纯正弦波形,将其简化为纯正弦波形会使得所提方法中计算的谐振电流值与仿真中得到的谐振电流值产生一定的偏差,但是误差值相对于谐振电流额定值较小。
3.1.2 三种解析式对比结果
图9给出了根据三种不同LLC谐振电流解析式得出的谐振电流波形和仿真中谐振电流波形的对比。图9中,实线表示仿真中的谐振电流iLr-sim波形;方法1对应的谐振电流是本文所提出的改进电流解析式得到的谐振电流iLr-1波形;方法2对应的谐振电流是文献[17]中提出的模型得到的谐振电流iLr-2波形;方法3对应的谐振电流是文献[18]中提出的模型得到的谐振电流iLr-3波形。整体上看,三种方法都能近似地描述仿真中谐振电流的变化情况。
图9b给出了死区时间附近三种不同模型中的谐振电流波形和仿真中谐振电流的对比,可以看出,在死区时间附近,本文所提出的电流解析方法得到的谐振电流波形与仿真谐振电流在变化情况和数值上都最为接近。这表明,相较于之前的模型,本文所提出的改进型LLC电流解析表达式不仅能近似拟合实际谐振电流的变化情况,而且能很好地描述LLC变换器的谐振电流在死区时间内的变化情况。

图9 三种方法获得的谐振电流波形与仿真波形对比
Fig.9 Comparison results of current waveforms calculated by three current analysis methods and simulation results
表2给出了本文中所提出的改进型电流解析方法和文献[17-18]得到的前半个周期t0、t1、t2时刻对应的谐振电流和励磁电流初始值iLm0、iLm1、iLm2,以及励磁电流峰值iLm_peak的计算结果和仿真直接测得的初始值和励磁电流峰值结果的对比。
表2 三种解析式与仿真得到的初始值结果对比
Tab.2 Comparison results of current initial values obtained by three different current analytical expressions and simulation(单位: A)
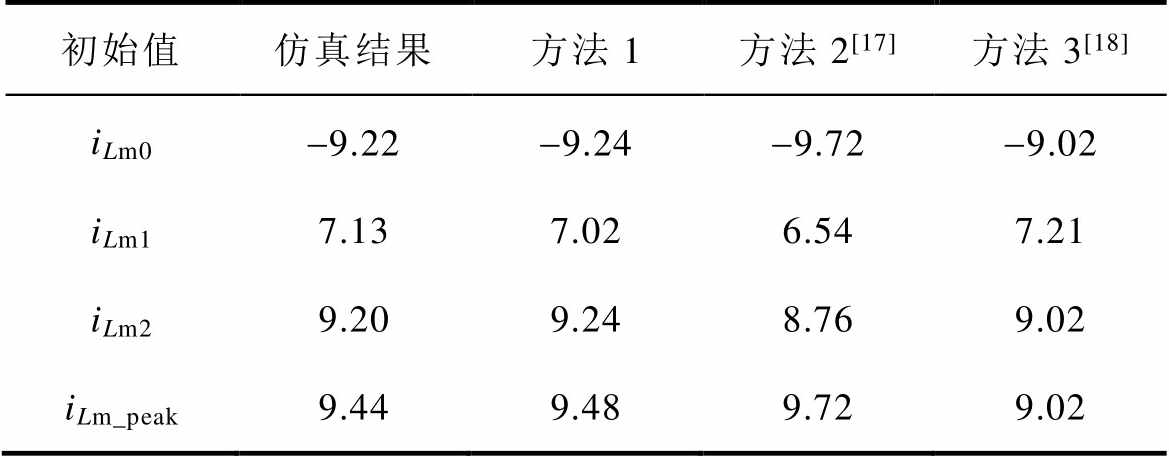
初始值仿真结果方法1方法2[17]方法3[18] iLm0-9.22-9.24-9.72-9.02 iLm17.137.026.547.21 iLm29.209.248.769.02 iLm_peak9.449.489.729.02
表3给出了三种方法得到的初值计算结果与仿真直接测得结果之间的误差,DiLm具体可表示为
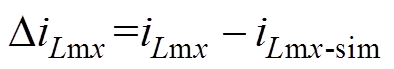 (50)
(50)式中,下标x为初值序号0、1、2,分别代表t0、t1、t2时刻的初值;下标sim为初始值或者励磁电流峰值由仿真测得。表3中,下标peak表示励磁电流峰值。
表3 三种解析式与仿真得到的初始值误差对比
Tab.3 Comparison results of the errors of current initial values between the initial values of three different current analytical expressions and simulation results(单位: A)
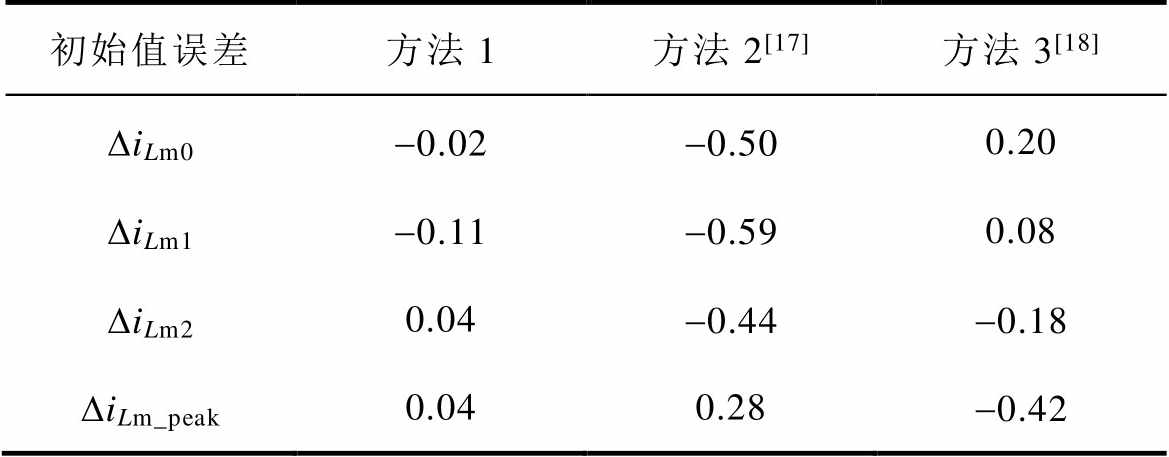
初始值误差方法1方法2[17]方法3[18] DiLm0-0.02-0.500.20 DiLm1-0.11-0.590.08 DiLm20.04-0.44-0.18 DiLm_peak0.040.28-0.42
由表2和表3可以看出,本文所提出的改进型解析式方法得到的初始值计算结果大部分情况下与仿真最接近,误差值最小。这表明,所提出的改进型谐振电流和励磁电流的解析式方法相较于之前文献[17-18]中的曲线拟合法准确性更高,尤其在死区时间内更能反映谐振电流和励磁电流的实际变化情况。
为了进一步验证所提出的改进型LLC谐振变换器电流解析式的有效性和正确性,搭建了LLC谐振变换器实验平台并进行相关实验,该实验平台如图10所示。LLC谐振变换器的各部分参数见表1,实验中,LLC谐振变换器输入电压为700V,输出电压为292V,开关频率为18kHz,负载电阻为18W,输出功率为4.7kW,死区时间设置为3.5ms。实验中LLC谐振变换器采用开环固定占空比的控制方式,上下开关管的占空比各为50%。

图10 LLC谐振变换器实验平台
Fig.10 Experimental test setup of LLC resonant converter
图11给出了LLC谐振变换器的稳态实验波形。图11中,iLr为谐振电流,iCin为输入电容电流,iCr1为谐振电容电流,vAB为谐振槽路输入电压。
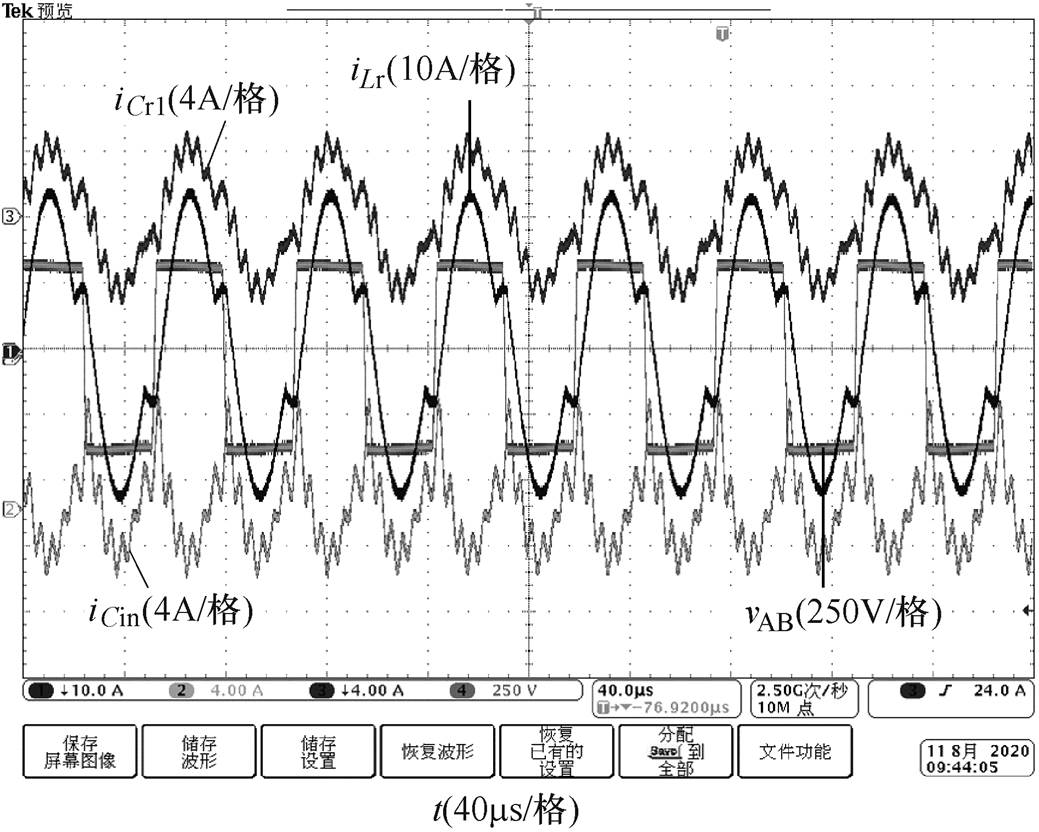
图11 LLC谐振变换器稳态实验波形
Fig.11 Steady state experimental waveforms of LLC resonant converter
在图11所示的LLC谐振变换器稳态实验波形中取一个周期的谐振电流,并且将本文所提出的改进型电流解析式计算得到的谐振电流与实验得到的谐振电流进行比较,可以得到两种谐振电流的比较结果和两种谐振电流之间的误差,比较结果如图12所示。
图12a为两种不同方法得到的谐振电流波形对比,iLr-exp为实验中得到的谐振电流,iLr-p为由本文所提出的改进型电流解析式计算得到的谐振电流。图12b为两个谐振电流之间的差值DiLr。由图12可以看出,在前半个开关周期中,所提出的改进型电流解析表达式得到的谐振电流与实验中的谐振电流几乎一致,误差值在0附近波动。由于电流探头零漂、测量误差等因素影响,实验中测得的后半周期谐振电流值小于所提出解析式计算得到的谐振电流值。
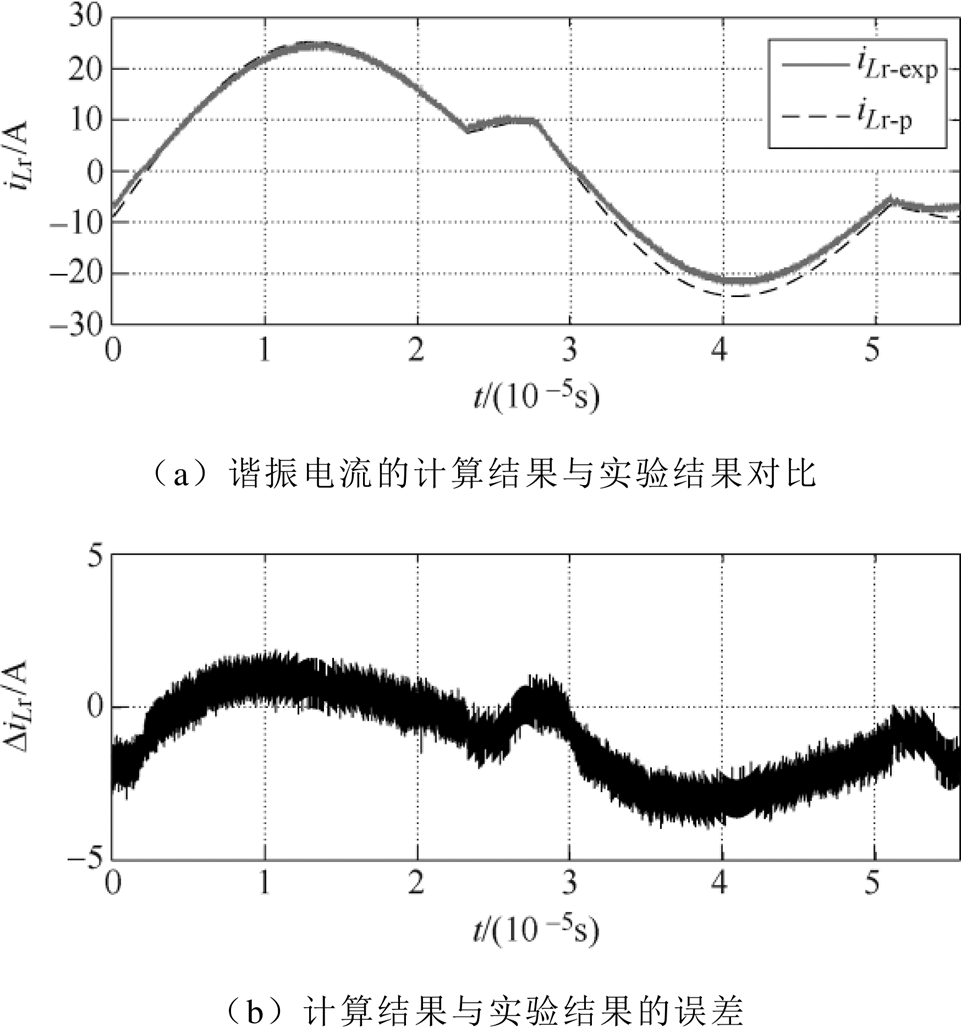
图12 改进型电流解析式计算结果与实验电流波形的比较结果
Fig.12 Comparison results of experimental resonant current and resonant current calculated by the improved current analytical expressions
本文提出一种LLC谐振变换器的改进型电流解析方法。在现有谐振电流近似拟合法的基础上,本文进一步考虑了死区时间内开关管结电容的充放电过程,结合开关管结电容的电压变化,对死区时间内谐振电流和励磁电流的变化进行精确分析,得到死区时间内的谐振电流和励磁电流的准确表达式。结合其他时间段的电流表达式,得到完整的谐振电流和励磁电流的解析式,并且基于该解析式对关键时刻初始值和其他常数进行了详细的分析计算。通过与仿真结果、其他电流拟合方法进行对比,可以得到,本文所提出的改进型电流解析式能更准确地描述死区时间内谐振电流的变化情况,其与仿真结果的误差比其他电流解析方法与仿真结果的误差更小。实验结果表明,本文所提出的电流解析方法得到的谐振电流与实验中的谐振电流比较接近,误差较小,进一步说明本文所提出的改进型电流解析式可以准确计算实际LLC谐振变换器的谐振电流值。
参考文献
[1] Zhao Chuanhong, Dujic D, Mester A, et al. Power electronic traction transformer-medium voltage pro- totype[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3257-3268.
[2] 刘建强, 赵楠, 孙帮成, 等. 基于LLC谐振变换器的电力电子牵引变压器控制策略研究[J]. 电工技术学报, 2019, 34(16): 3333-3344.
Liu Jianqiang, Zhao Nan, Sun Bangcheng, et al. Research on control strategy of power electronic traction transformer based on LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3333-3344.
[3] Fang Zhijian, Cai Tao, Duan Shanxu, et al. Optimal design methodology for LLC resonant converter in battery charging applications based on time-weighted average efficiency[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5469-5483.
[4] 徐恒山, 尹忠东, 黄永章. 考虑最大输出电压和效率的LLC 谐振变流器的设计方法[J]. 电工技术学报, 2018, 33(2): 331-341.
Xu Hengshan, Yin Zhongdong, Huang Yongzhang. Design method of LLC resonant converter con- sidering maximum output voltage and efficiency[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 331-341.
[5] Ahmed M H, Fei Chao, Lee F C, et al. Single-stage high-efficiency 48/1V sigma converter with inte- grated magnetics[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 192-202.
[6] 汤欣喜, 邢岩, 吴红飞, 等. 兼顾稳态效率和暂态升压能力的LLC变换器[J]. 电工技术学报, 2020, 35(4): 767-774.
Tang Xinxi, Xing Yan, Wu Hongfei, et al. An improved LLC converter considering steady-state efficiency and transient boost capability[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(4): 767-774.
[7] 肖龙, 伍梁, 李新, 等. 高频LLC变换器平面磁集成矩阵变压器的优化设计[J]. 电工技术学报, 2020, 35(4): 758-766.
Xiao Long, Wu Liang, Li Xin, et al. Optimal design of planar magnetic integrated matrix transformer for high frequency LLC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 758-766.
[8] 韩富强, 王议锋, 陈梦颖, 等. 多模式切换运行的拓扑变换型多谐振软开关直流变换器及参数设计方法[J]. 电工技术学报, 2019, 34(22): 4728-4738.
Han Fuqiang, Wang Yifeng, Chen Mengying, et al. A topology-morphing multi-resonant soft-switching DC- DC converter with parameter design method for multi-mode operation[J]. Transactions of China Elec- trotechnical Society, 2019, 34(22): 4728-4738.
[9] 刘晓东, 董保成, 吴慧辉, 等. 基于并联变压器切换的LLC谐振变换器宽范围效率优化控制策略[J]. 电工技术学报, 2020, 35(14): 3018-3029.
Liu Xiaodong, Dong Baocheng, Wu Huihui, et al. Wide range efficiency optimization control strategy for LLC resonant converter based on parallel trans- former switching[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3018-3029.
[10] 周国华, 范先焱, 许多, 等. 具有宽范围输入和高效率的改进型LLC谐振变换器[J]. 电机与控制学报, 2020, 24(10): 9-18.
Zhou Guohua, Fan Xianyan, Xu Duo, et al. Improved LLC resonant converter with wide range input and high efficiency[J]. Electric Machines and Control, 2020, 24(10): 9-18.
[11] Shafiei N, Saket M A, Ordonez M. Time domain analysis of LLC resonant converters in the boost mode for battery charger applications[C]//Proceedings of 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 2017: 4157-4162.
[12] Glitz E S, Ordonez M. MOSFET power loss esti- mation in LLC resonant converters: time interval analysis[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11964-11980.
[13] Feng Weiyi, Lee F C, Mattavelli P. Simplified optimal trajectory control (SOTC) for LLC resonant converters[J]. IEEE Transactions on Power Electro- nics, 2013, 28(5): 2415-2426.
[14] Xu Duo, Zhou Guohua, Huang Rui, et al. High efficiency half bridge class-D audio amplifier system with front-end symmetric bipolar outputs LLC con- verter[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 1220-1230.
[15] Kumar A, Awasthi A, Salari O, et al. A novel time domain analysis of the LLC-L resonant converter for the use of the CLL and LLC resonant converter[C]// Proceedings of 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 3453-3460.
[16] Yang Chunhsu, Liang Tsorngjuu, Chen Kaihui, et al. Loss analysis of half-bridge LLC resonant con- verter[C]//Proceedings of 2013 1st International Future Energy Electronics Conference (IFEEC), Tainan, 2013: 155-160.
[17] Jami M, Beiranvand R, Mohamadian M, et al. Opti- mization the LLC resonant converter for achieving maximum efficiency at a predetermined load value[C]// Proceedings of the 6th Power Electronics, Drive Systems Technologies Conference (PEDSTC2015), Tehran, Iran, 2015: 149-155.
[18] Yang Yugang, Zhang Lifei, Ma Tianshu. Conduction loss analysis and optimization design of full bridge LLC resonant converter[C]//Proceedings of 2018 Inter- national Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 2018: 2703-2707.
[19] Wei Yuqi, Luo Quanming, Mantooth A. Comprehen- sive comparisons between frequency-domain analysis and time-domain analysis for LLC resonant con- verter[J]. IET Power Electronics, 2020, 13(9): 1735- 1745.
An Improved Current Analytical Method for LLC Resonant Converter
Abstract In LLC resonant converter, the accurate analysis of the resonant current can realize the loss calculation of the converter. Based on the existing approximate fitting methods, an improved current analytical method for LLC resonant converter is proposed in this paper. The charging and discharging processes of the output junction capacitor of switching devices in the dead-time are detailed analyzed. Then the changes of the resonant current in the dead-time are analyzed. Moreover, the calculation method of initial values in the improved resonant current analytical expression is modified correspondingly. The resonant current calculated by the proposed method can describe the changes of the resonant current in the dead-time more accurately. The simulation results show that compared with previous methods, the resonant current calculated by the proposed method is more accurate in the dead-time. In addition, comparing the initial values and the peak values of the magnetizing current obtained by other methods, the error of the proposed method is smaller. The experimental results further prove the effectiveness and correctness of the proposed analytical method of the resonant current.
keywords:LLC resonant converter, resonant current, improved analytical method, dead-time, initial value calculation
DOI: 10.19595/j.cnki.1000-6753.tces.L90382
中图分类号:TM46
中央高校基本科研业务费专项资金资助项目(2019-JBM062)。
收稿日期 2020-07-10
改稿日期 2020-11-16
焦 健 男,1993年生,博士研究生,研究方向为LLC谐振变换器优化设计与控制。E-mail: 19117009@bjtu.edu.cn
郭希铮 男,1980年生,博士,副教授,博士生导师,研究方向为宽禁带器件(SiC MOSFET)驱动、保护以及在轨道交通的应用,大功率电力机车辅助变流器设计与控制以及实时仿真技术。E-mail: xzhguo@bjtu.edu.cn(通信作者)
(编辑 陈 诚)