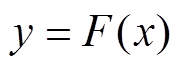 (1)
(1)摘要 电气化铁路牵引供电系统的安全可靠至关重要,然而部分地区牵引供电系统面临地震灾害威胁。为有效评估地震灾害下牵引供电系统的风险水平,该文首先采用蒙特卡洛方法模拟地震灾害并得到表征地震动强度的峰值加速度指标;然后通过分析系统主接线,建立系统的有向图逻辑模型,在此基础上,考虑系统停运概率、关键设备损失以及停运时间等因素定义风险指标,提出牵引供电系统地震灾害风险评估方法;最后选取西南地区某规划中的电气化铁路牵引供电系统作为算例,评估系统在地震灾害下的风险。结果表明,该文算法能有效量化牵引供电系统在地震灾害下的风险水平,可实现震后快速损失评估,为灾后抢险、应急物资调配提供参考,也可为牵引供电系统抗震规划提供理论依据。
关键词:牵引供电系统 地震 风险评估 蒙特卡洛模拟
我国位于欧亚大陆东南部,处于西太平洋地震带和地中海-喜马拉雅地震带之间,地震灾害较多,对部分地区电气化铁路的安全可靠运行造成极大威胁。例如,1976年唐山地震中,震区铁路正线约1 100延长千米,其中48.3%的线路遭到破坏;2008年汶川地震发生后,180趟列车在途中受阻滞留,地震造成四川境内宝成线、成昆线、成渝线、达成线等主要铁路干线及其支线不同程度受损,成都铁路系统受损线路超过2 500km。牵引供电系统沿铁路修建,更易遭受地震破坏,且一旦地震引起牵引供电系统故障,列车将失去动力无法运行,车上人员可能面临崩塌、滑坡等次生灾害风险的威胁。因此,有必要综合分析地震对牵引供电系统的影响,并定量评估地震影响下的牵引供电系统风险。
目前尚未有针对牵引供电系统的地震灾害风险评估研究,由于牵引供电系统的设备类型、设计原则以及运行环境与电力系统类似,因此电网领域的抗震评估研究可为牵引供电系统地震风险评估提供宝贵思路。其中,供电设备易损性分析是电力系统抗震分析的基础[1],其目标是评估供电设备在不同地震强度作用下发生破坏的概率,研究方法主要有理论分析与模拟计算方法[2]、振动台试验方法[3]以及震害统计分析方法[4]。震害统计分析方法利用实际的震害资料建立地震动参数与设备破坏概率的关系,具有实际指导意义,因此被广泛应用。汶川地震以来我国开展了大量电网震害调研,累积了丰富的电力设备震害资料[5-7],研究人员利用震害统计分析方法研究了变电站主要设备和输电杆塔的易损性,并得到了主要电气设备的易损性曲线[8]。
在供电设备易损性研究的基础上,国内外研究人员开始从系统层面研究地震灾害引起的损失或风险。文献[9]提出了一种结合图论、故障树与成功路径的系统分析方法,研究了典型变电站的易损性,并分析识别出系统的抗震薄弱环节。文献[10]进一步定义了变电站的功能评价指标,评估了变电站在不同强度地震下的功能损失程度。对于系统结构和能量流动更复杂的电网系统和综合能源系统,文献[11-12]从地震灾害影响下系统负荷削减的角度分析了系统损失,并定量评估了系统的抗震水平。
为进一步反映地震活动的不确定性对供电系统的影响,国内外学者引入历史地震信息或采用地震活动性模型来模拟地震灾害的随机特性。例如,文献[13-14]利用供电系统所在区域的历史地震记录,拟合获得当地的地震活动性规律,进而通过蒙特卡洛模拟地震灾害场景并评估系统的风险水平。文献[15]利用基于三级潜源区划分的地震活动性模型来描述地震事件的不确定性,并建立基于烈度分布的元件失效概率模型描述元件故障的不确定性。上述研究可辅助规划人员评估地震影响下的系统风险水平,从而制定相应方案提升系统抗灾能力。
以上电力系统相关的抗震可靠性和风险评估研究为牵引供电系统地震灾害风险评估奠定了一定基础,然而主要关注灾害事件引起的电压、潮流越限以及负荷损失,并主要采用节点电压或支路潮流越限、机组运行成本、负荷损失等指标[16-17]来量化电网风险。由于牵引供电系统特殊的运行特点,现有的指标和评估方法尚不能有效反映牵引供电系统在地震灾害影响下的损失,并准确量化其灾害风险水平。针对以上问题,本文提出一种牵引供电系统地震灾害风险评估方法,首先结合地震活动性模型和蒙特卡洛方法对地震灾害场景进行模拟;然后建立包含接触网和牵引所的牵引供电系统模型,在此基础上提出了牵引供电系统损失量化方法;最后从系统停运概率、关键设备损失以及停运时间等角度定义了风险评估指标,定量评估地震灾害下牵引供电系统的风险水平。
地震引起的地面运动常用峰值、反应谱和持续时间等地震动参数来表示,其中,地面峰值加速度(Peak Ground Acceleration, PGA)是工程抗震设计的主要依据,因此本文首先根据地震活动性模型,利用蒙特卡洛随机抽样产生地震的震级、发生时间以及震源位置,在此基础上根据PGA的衰减规律得到牵引供电设备所在场地的PGA值。
本文采用蒙特卡洛反抽样法[18-19]生成地震的震级、发生时间以及震源位置(即生成人工地震目录),对于任意随机变量X,设其分布函数为
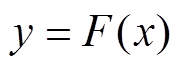 (1)
(1)由分布函数性质可知,该函数是值域为[0, 1]的单调递增函数。对式(1)进行反变换,可得
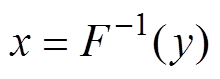 (2)
(2)
通过产生一个在[0, 1]区间均匀分布的随机数y,即可得到随机变量X的取值,通过多次独立重复抽样可以得到一系列随机变量的取值,从而基于得到的随机变量序列进行下一步分析与计算。人工地震目录的关键参数(震级、发生时间以及震源位置)均可以看作随机变量,并通过反抽样法确定。
1)地震震级的确定
通常认为地震的震级分布满足截断的G-R关系,其分布函数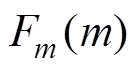 表示[20]为
表示[20]为
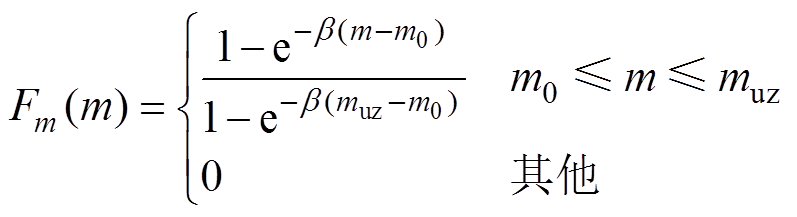 (3)
(3)式中,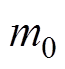 为震级下限;
为震级下限;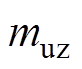 为震级上限;
为震级上限;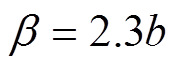 ,b为研究区域G-R关系的系数。
,b为研究区域G-R关系的系数。
利用反抽样法,产生[0, 1]区间均匀分布的随机数r,则可得到地震震级m为
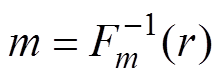 (4)
(4)式中,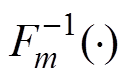 为函数
为函数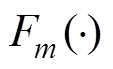 的反函数。
的反函数。
2)相邻两次地震时间间隔的确定
通常认为地震活动服从泊松分布,设相邻两次地震的时间间隔为随机变量T,则T服从指数分布,其分布函数[20]为
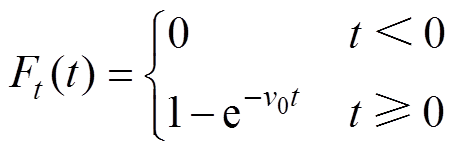 (5)
(5)式中,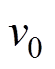 为地震的平均年发生率。
为地震的平均年发生率。
同理,利用反抽样法可以得到相邻两次地震的时间间隔为
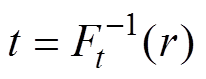 (6)
(6)式中,r为[0, 1]区间均匀分布的随机数;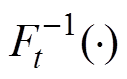 为函数
为函数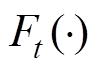 的反函数。
的反函数。
3)震源位置的确定
根据我国新版地震区划成果[21],采用地震统计区和潜在震源区组合来共同描述地震在空间分布上的不确定性:以地震统计区来描述地震在较大空间尺度上分布的不均匀性,以潜在震源区进一步描述局部地质构造条件导致的地震在较小空间尺度的不均匀性。我国一条电气化铁路可长达成百上千公里,通常穿越多个地震统计区,本文重点分析较大空间范围内(统计区尺度下)牵引供电系统的地震灾害风险,因此忽略局部地质构造条件导致的地震在较小空间尺度的不均匀性,假设震源位置在统计区内是均匀分布的,其空间位置可表示为二维随机变量(X, Y),其概率密度函数为
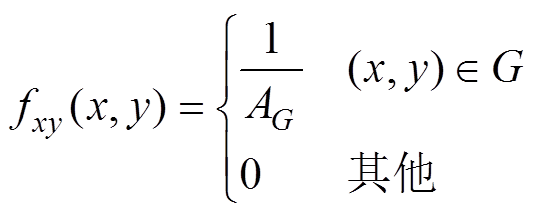 (7)
(7)式中,G为地震统计区的有界区域;AG为G的面积。
为模拟震源位置,首先获取地震统计区G的最小外接矩形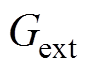 ,设
,设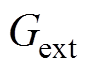 表示的区域为0≤
表示的区域为0≤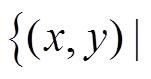
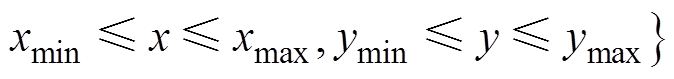 ,然后生成在区域
,然后生成在区域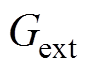 内均匀分布的点
内均匀分布的点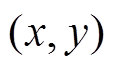 ,其中
,其中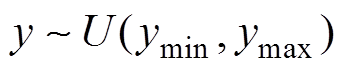 ,
,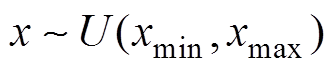 。若
。若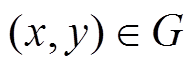 ,则接受该位置;否则,重新生成位置直到生成的位置落入统计区G。
,则接受该位置;否则,重新生成位置直到生成的位置落入统计区G。
指定年限Tstop,根据以上方法,依次产生地震震级、发生时间以及震源位置,重复多次抽样即可得到指定年限内的人工地震目录。
地震动参数衰减规律用于描述地震动参数(如PGA、地震烈度等)随震级与震源距离的变化规律,我国常用的衰减关系模型形式[22]为
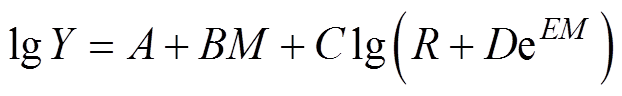 (8)
(8)式中,Y为地震动参数;M为震级;R为震中距离;A、B、C、D、E均为回归系数。为反映地震震级较大时,震源附近地震动的距离饱和特性,以6.5级作为大震和小震的分界,分段给出PGA的衰减关系[22]为
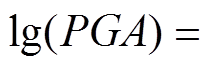
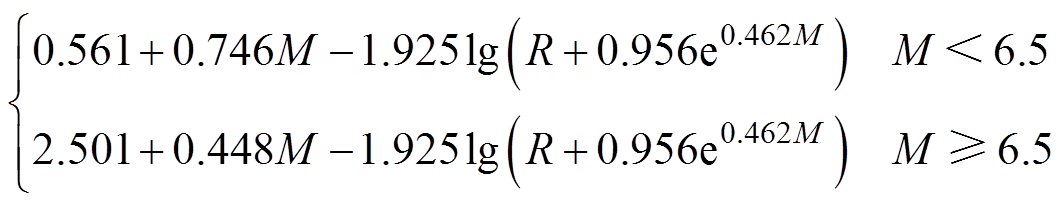 (9)
(9)利用以上衰减关系,根据地震震级以及牵引供电设备距离震源的距离,即可求得设备所处位置的PGA。
为分析牵引供电设备及系统在不同地震动强度下的功能状态,首先分析组成系统的关键设备的地震易损性,在此基础上,考虑牵引供电系统的接线形式,引入有向图逻辑模型,分析地震灾害下牵引供电系统的停运概率。
地震易损性反映供电设备或系统在不同地震动强度下损坏的概率,研究表明,高压供电设备在地震作用下的损坏概率通常服从对数正态分布[23],以PGA作为描述地震动强度的参数,供电设备的易损性函数可表示为
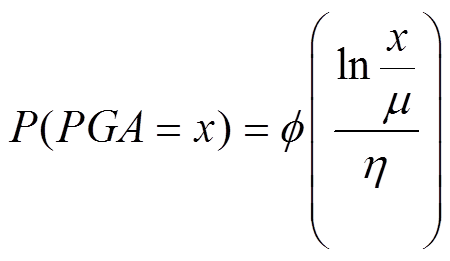 (10)
(10)式中,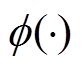 为标准正态分布的概率分布函数;
为标准正态分布的概率分布函数;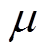 和
和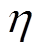 分别为中值和对数标准差。
分别为中值和对数标准差。
根据基于震害统计分析的易损性分析方法,设备易损性函数计算步骤如下:
(1)根据震级大小和设备距离震源的距离,利用式(9)的衰减关系计算得到设备所处位置的PGA。
(2)将各个设备的PGA值由小到大排序,设PAG最小值和最大值分别为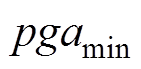 和
和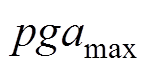 ,将区间
,将区间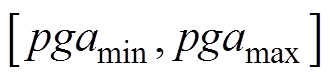 等分为Np个区间,以区间的中点作为该区间对应的PGA值,记
等分为Np个区间,以区间的中点作为该区间对应的PGA值,记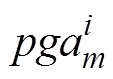 为第i个区间对应的PGA值,统计落入各个区间的设备数量。
为第i个区间对应的PGA值,统计落入各个区间的设备数量。
(3)计算每个PGA区间的存活概率分布函数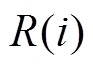 及失效概率分布函数
及失效概率分布函数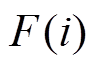 分别为
分别为
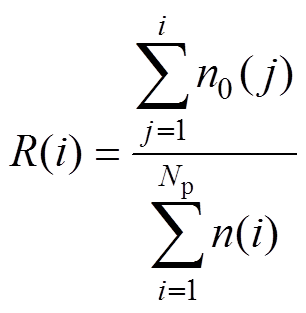 (11)
(11)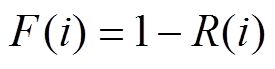 (12)
(12)
式中,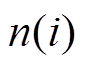 为第i个区间的设备的总数量;
为第i个区间的设备的总数量;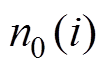 为第i个区间正常运行的设备数量,i=1, 2,…, Np。求得的
为第i个区间正常运行的设备数量,i=1, 2,…, Np。求得的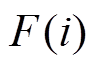 即为峰值加速度
即为峰值加速度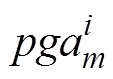 对应的失效概率,即可将式(10)改写为
对应的失效概率,即可将式(10)改写为
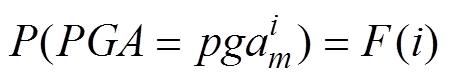 (13)
(13)从而得到关于PGA与设备失效概率的一组观测量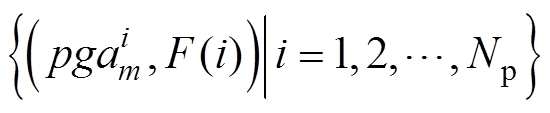 ,利用对数正态分布函数拟合以上数据即可得到设备的易损性函数。
,利用对数正态分布函数拟合以上数据即可得到设备的易损性函数。
在获取了各个关键设备易损性函数的基础上,引入有向图逻辑模型[9]反映供电设备之间的连接关系以及电能流通路径,从而分析整个牵引供电系统的功能状态,对于典型采用直接供电方式的牵引供电系统,列车正常获取电能需要牵引所将电能输送至接触网系统,同时接触网系统将电能传输至列车[24],因此本文分别建立牵引所和接触网系统的有向图逻辑模型,在此基础上将牵引所的输出作为接触网系统的输入,从而得到整个牵引供电系统的模型。
1)牵引所有向图逻辑模型
大量震害统计表明变电站震害主要集中于各类电气设备,而设备之间的连接破坏罕见[9],因此假定:①各设备之间相互独立,且设备状态分为正常和故障两种状态;②不考虑设备间连接母线的破坏。在此基础上,用节点表示关键供电设备,用连接节点的有向边表示电能的传输方向,模型的基本单元模块如图1所示,模块输出“1”表示正常,输出“0”表示故障,根据系统主接线结构将各个模块连接即构成系统的有向图逻辑模型,如图1所示。
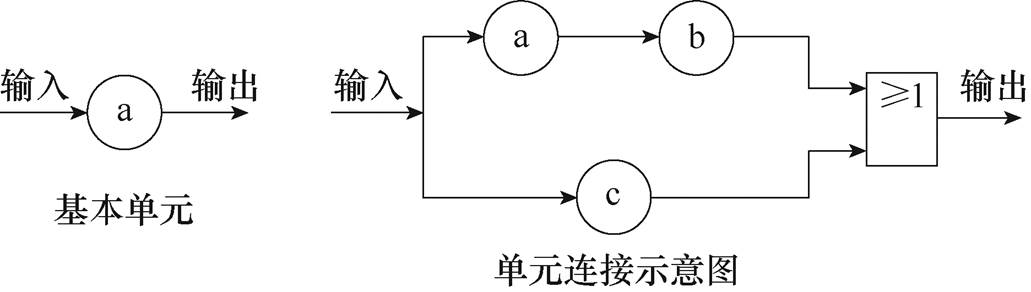
图1 有向图逻辑模型示意图
Fig.1 Demonstration of directed graph logic model
按照以上原则,根据典型牵引所的接线方式建立牵引所有向图逻辑模型,如图2所示。由于电压互感器并联在线路中,其运行状态并不直接影响系统功能,在分析系统功能状态时将其忽略。
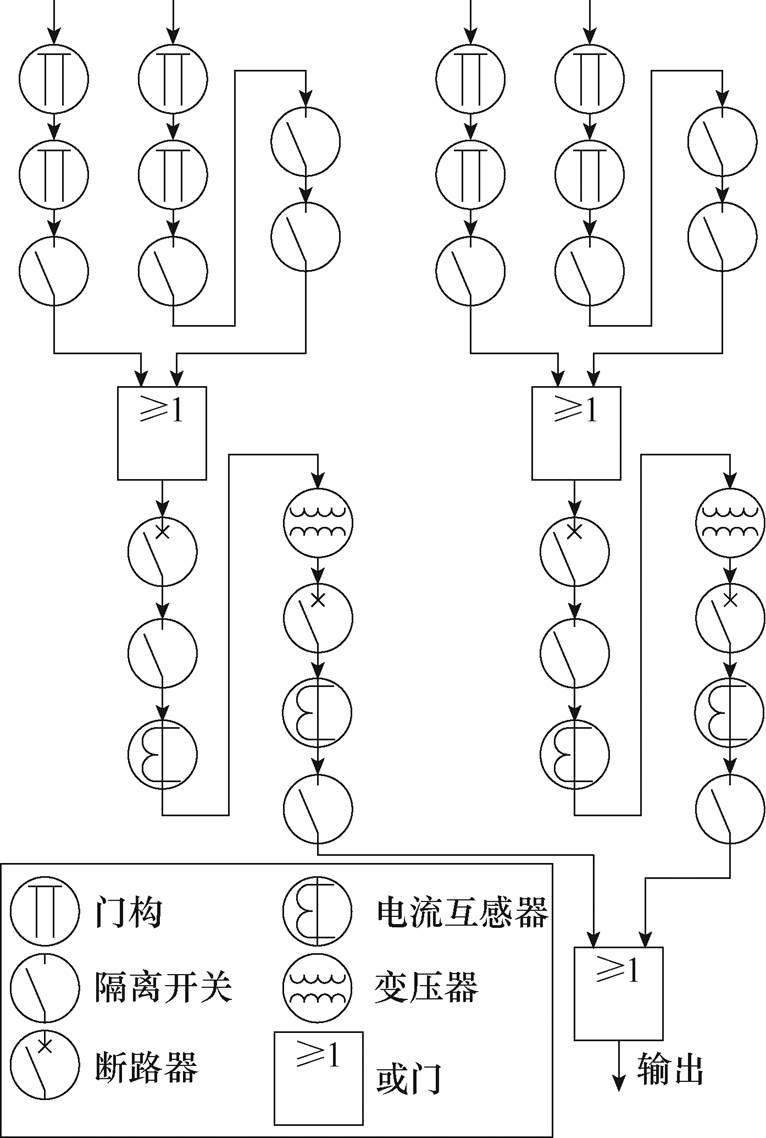
图2 典型牵引所有向图逻辑模型
Fig.2 Directed graph logic model of typical traction substation
2)接触网有向图逻辑模型
在接触网系统中,支柱是承受接触网荷载的重要部件,因此在接触网抗震研究中通常将接触网系统看作“支柱-线索”体系[25],本文将接触网支柱作为接触网系统的基本单元,则整个接触网系统可看作多个基本单元串联的系统,因此建立接触网系统的有向图逻辑模型如图3所示。
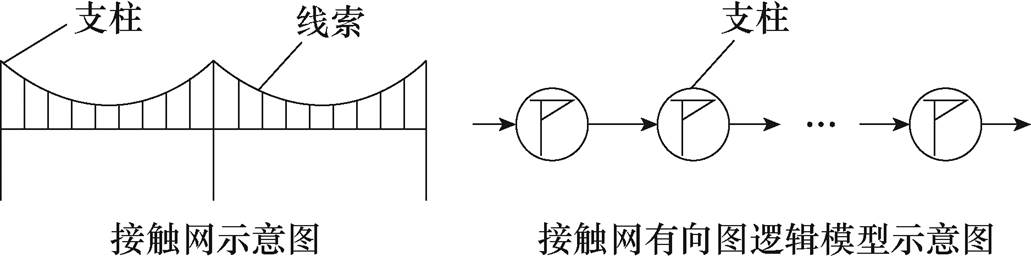
图3 接触网系统示意图及其有向图逻辑模型
Fig.3 Demonstation of the catenary system and its directed graph logic model
在分别建立了牵引所和接触网系统的有向图逻辑模型的基础上,将两部分串联即可得到整个牵引供电系统的模型。
结合地震灾害模拟方法以及牵引供电系统的有向图逻辑模型,利用蒙特卡洛随机抽样方法,首先获取各牵引供电设备所处位置的PGA,并根据供电设备的易损性函数确定各设备的功能状态,再结合有向图逻辑模型确定牵引供电系统的功能状态,重复以上过程并记录每次的系统状态,进一步统计得到相应的风险评估指标。
利用有向图逻辑模型,将牵引供电设备表示为如图1所示的基本单元,每个基本单元输出功能状态由如图4所示的两步逻辑判断确定。
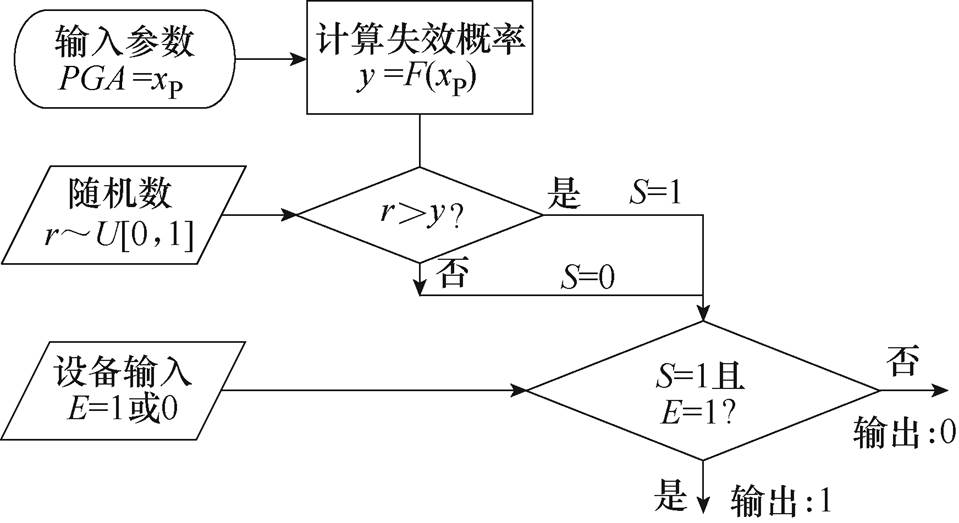
图4 牵引供电设备功能状态评估流程
Fig. 4 Flowchart of function evaluation of traction power supply equipment
(1)首先确定设备所处位置的地面运动强度指标PGA值,记为xP,结合设备的易损性函数F(x),可得到设备的失效概率为
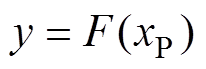 (14)
(14)产生[0, 1]区间均匀分布的随机数r与y进行比较,若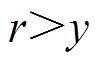 ,则设备正常工作(表示为“1”);否则,设备失效(表示为“0”)。
,则设备正常工作(表示为“1”);否则,设备失效(表示为“0”)。
(2)设备输出状态由第(1)步中判断得到的设备状态与设备输入状态共同决定,同时为“1”则设备输出状态“1”;否则,设备输出状态“0”。
根据以上方法可依次计算得到每一个设备的输出状态,针对2.2节中的牵引供电系统模型,若最后接触网输出状态为“1”,则表示列车可以正常获取电能,认为牵引供电系统正常运行;否则,认为牵引供电系统故障停运。
在地震灾害影响下,一方面会引起牵引供电设备的破坏,造成直接损失;另一方面会引起牵引供电系统停运,从而无法为列车正常供电。基于此,针对已知震源信息(震级和震源位置)的地震事件,本文定义系统停运概率、设备破坏率、系统停运时间三个指标,用以实现牵引供电系统的震后损失快速评估;针对位于某一区域的铁路沿线牵引供电系统,定义平均停运率、平均设备损失、平均停运时间以及损失超过给定值的发生率指标,以反映牵引供电系统在地震灾害下的平均风险水平。
3.2.1 已知震源信息下的风险指标
在已知震源信息下,根据3.1节中的方法进行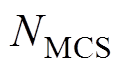 次蒙特卡洛模拟,并评估每一次模拟中的系统功能状态,定义以下风险指标:
次蒙特卡洛模拟,并评估每一次模拟中的系统功能状态,定义以下风险指标:
(1)系统停运概率:反映牵引供电系统在地震影响下无法为列车供电的概率,计算方式为
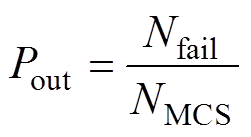 (15)
(15)式中,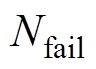 为NMCS次抽样中系统故障的次数。
为NMCS次抽样中系统故障的次数。
(2)设备破坏率:定义为关键供电设备(即图2、图3中的牵引所设备和接触网设备)损坏的数量占所有关键设备的比例,反映地震下影响供电设备的资产损失情况,计算方式为
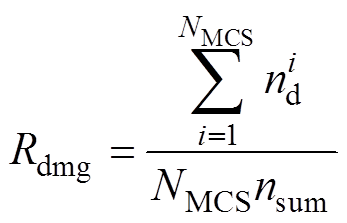 (16)
(16)式中,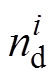 为第i次模拟中损坏的关键设备数量;
为第i次模拟中损坏的关键设备数量;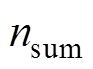 为关键设备总数量。
为关键设备总数量。
(3)系统停运时间:反映震后系统恢复供电所需要的时间。文献[26]通过调研汶川地震以来我国多个变电站的震害破坏情况以及恢复情况,统计并研究了变电站设备破坏率和系统恢复供电所需时间的关系,本文在此基础上对设备破坏率与恢复时间进行多项式拟合,从而定义系统停运时间为
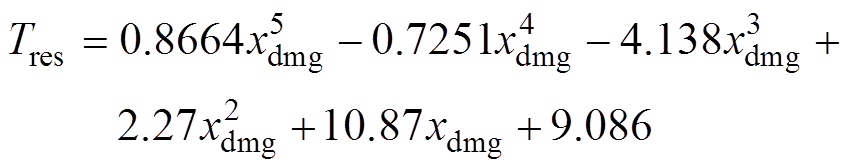 (17)
(17)式中,xdmg为标准化处理之后的设备破坏率,xdmg= 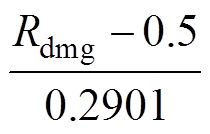 。
。
3.2.2 平均风险指标
针对位于某一区域的铁路沿线牵引供电系统,利用设备所处区域的地震活动性参数模拟产生指定时间段Tstop内的地震目录,并计算设备所在位置的PGA。然后对地震目录中的每一个地震事件评估牵引供电系统的功能状态,根据每次地震下系统功能状态的评估结果,定义以下风险指标。
(1)平均停运率:定义为在地震灾害影响下,单位时间内牵引供电系统发生功能失效的次数,单位为次/年,计算方式为
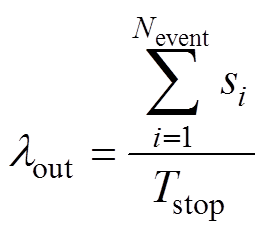 (18)
(18)式中,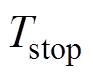 为指定的模拟时间段;
为指定的模拟时间段;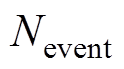 为
为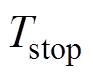 时间段内地震总数量;
时间段内地震总数量;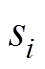 为第i次地震影响下牵引供电系统的功能状态:正常运行时
为第i次地震影响下牵引供电系统的功能状态:正常运行时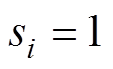 ;反之,
;反之,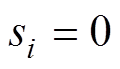 。
。
(2)平均设备损失:定义为在地震灾害影响下,单位时间内牵引供电系统关键设备的损坏数量,单位为台/年,计算方式为
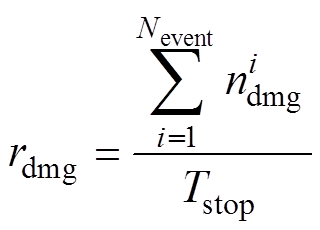 (19)
(19)式中,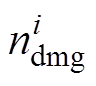 为第i次地震影响下牵引供电关键设备损坏的数量。
为第i次地震影响下牵引供电关键设备损坏的数量。
(3)平均停运时间:定义为在地震灾害影响下,单位时间内牵引供电系统故障停运的时长,单位为天/年,计算方式为
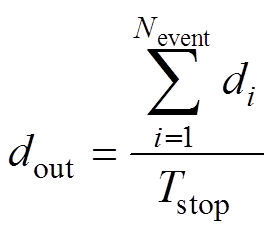 (20)
(20)式中,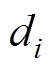 为第i次地震影响下牵引供电系统的停运时间。
为第i次地震影响下牵引供电系统的停运时间。
(4)损失事件发生率:反映地震灾害影响下,损失超过指定值的事件在单位时间内发生的次数,单位为次/年。定义关键设备损失超过指定值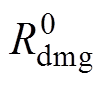 的事件发生率为
的事件发生率为
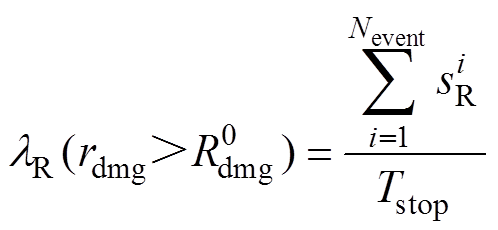 (21)
(21)式中,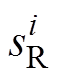 为第i次地震影响下牵引供电系统的关键设备损失状态:当设备损失大于
为第i次地震影响下牵引供电系统的关键设备损失状态:当设备损失大于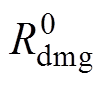 时,
时,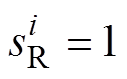 ;否则,
;否则,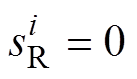 。
。
同理,定义系统停运时间超过指定值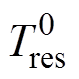 的事件发生率为
的事件发生率为
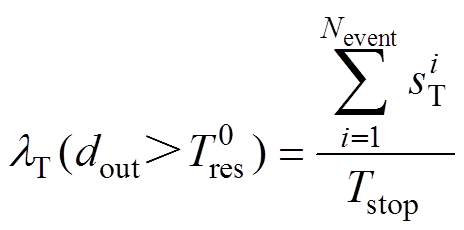 (22)
(22)式中,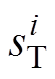 为第i次地震影响下牵引供电系统的停运时间损失状态:当系统停运时间大于
为第i次地震影响下牵引供电系统的停运时间损失状态:当系统停运时间大于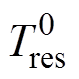 时,
时,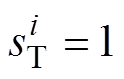 ;否则,
;否则,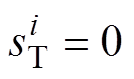 。
。
本文参考中国西南地区某规划中的电气化铁路路径及其供电系统设计原则,建立包含牵引所和接触网的牵引供电系统模型,并利用本文提出的方法评估牵引供电系统在地震灾害下的风险。
1)地震活动性参数
选取的电气化铁路区段穿越青藏高原东南部某地震统计区,根据中国地震区划图以及地震活动性模型[21],获取该统计区的地震活动性参数为:震级上限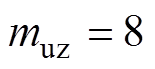 , 4级及以上地震年发生率
, 4级及以上地震年发生率 ,b= 0.85。由于4级以下的地震破坏能量较小,在工程抗震研究中通常不考虑,因此取震级下限
,b= 0.85。由于4级以下的地震破坏能量较小,在工程抗震研究中通常不考虑,因此取震级下限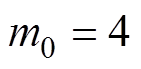 。
。
2)关键供电设备易损性函数
供电设备易损性函数的获取依赖于大量震害统计数据,而目前牵引供电系统的震害统计数据相对缺乏,但由于牵引供电系统的功能结构、设计条件以及其包含的设备类型与电力系统基本类似,关键电气设备(如变压器、断路器、隔离开关)的震害损失机理几乎一致,因此本文参考电网震害统计的相关资料[6, 8, 10],定义牵引供电系统关键设备的易损性函数参数见表1。
表1 牵引供电系统关键设备易损性函数参数
Tab.1 Parameters of the fragility functions of the key equipment in the traction power supply system
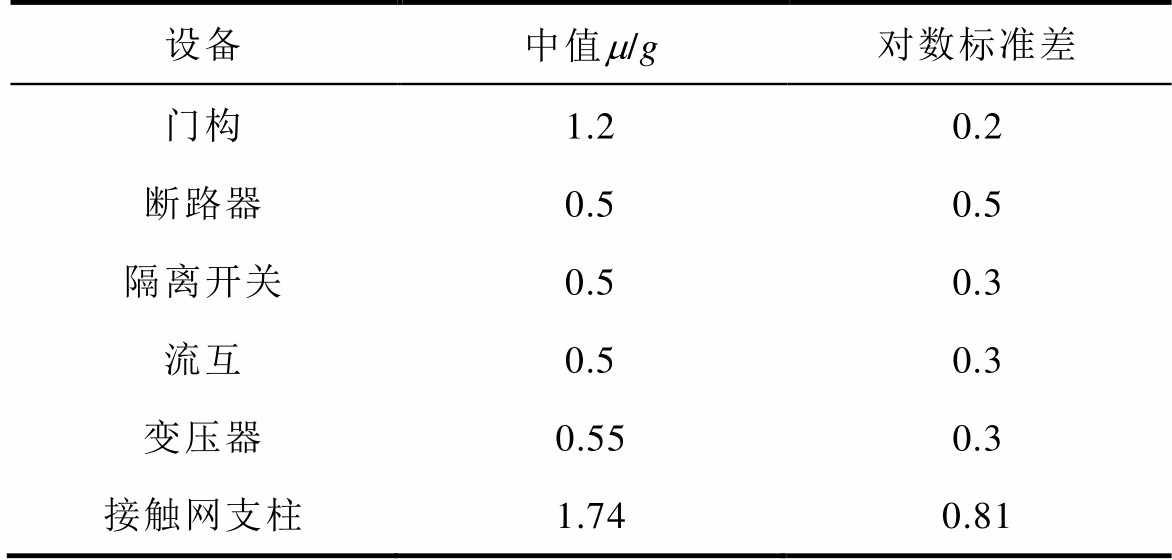
设备中值m/g对数标准差 门构1.20.2 断路器0.50.5 隔离开关0.50.3 流互0.50.3 变压器0.550.3 接触网支柱1.740.81
值得说明的是,与输电线路类似,接触网的“支柱-线索”体系对地震能量具有解耦作用,因此相比于变电站设备,接触网元件在地震作用下失效概率更小,其易损性函数抗震能力中值更高。
3)牵引供电系统地理位置分布
牵引供电系统地理位置分布示意图如图5所示,沿线牵引供电系统采用直接供电方式,每个供电区间供电范围为40km,由一个牵引所和左、右供电臂的接触网组成。据此将位于该地震统计区内的牵引供电系统划分为10个供电区间(T1~T10),如图5所示。
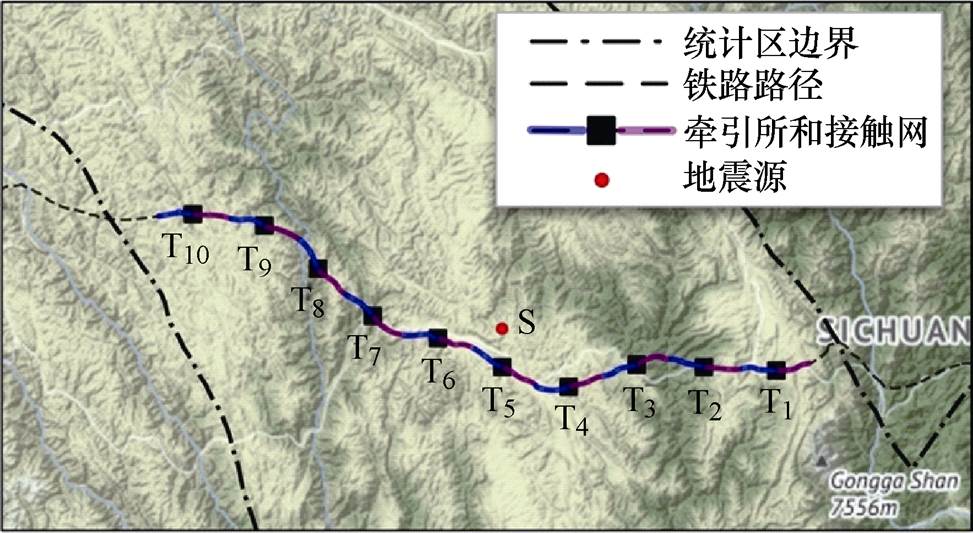
图5 牵引供电系统地理位置分布示意图
Fig.5 Locations of traction power supply systems
针对牵引供电系统T5,设置地震源位于牵引所以北10km(见图5中地震源S),利用本文方法建立牵引所和接触网的有向图逻辑模型如图2、图3所示,根据式(15)~式(17)可求得牵引供电系统在不同震级下的停运概率、设备破坏率、以及系统停运时间等风险指标,不同震级下牵引供电系统T5风险指标如图6所示。
从图6a可以看出,5级以下地震对该牵引供电系统影响较小,停运概率接近于0。当震级超过5.5级时,系统停运概率快速增大,在6.2级地震影响下系统停运概率接近1。此外,对比牵引所与接触网左、右供电臂的停运概率可以看出,相同地震强度下牵引所的停运概率低于接触网的停运概率,这是由于大多数牵引所内的供电设备有备用,而接触网为典型的串联系统,地震引起任一接触网元件破坏都会造成整个接触网系统停电。
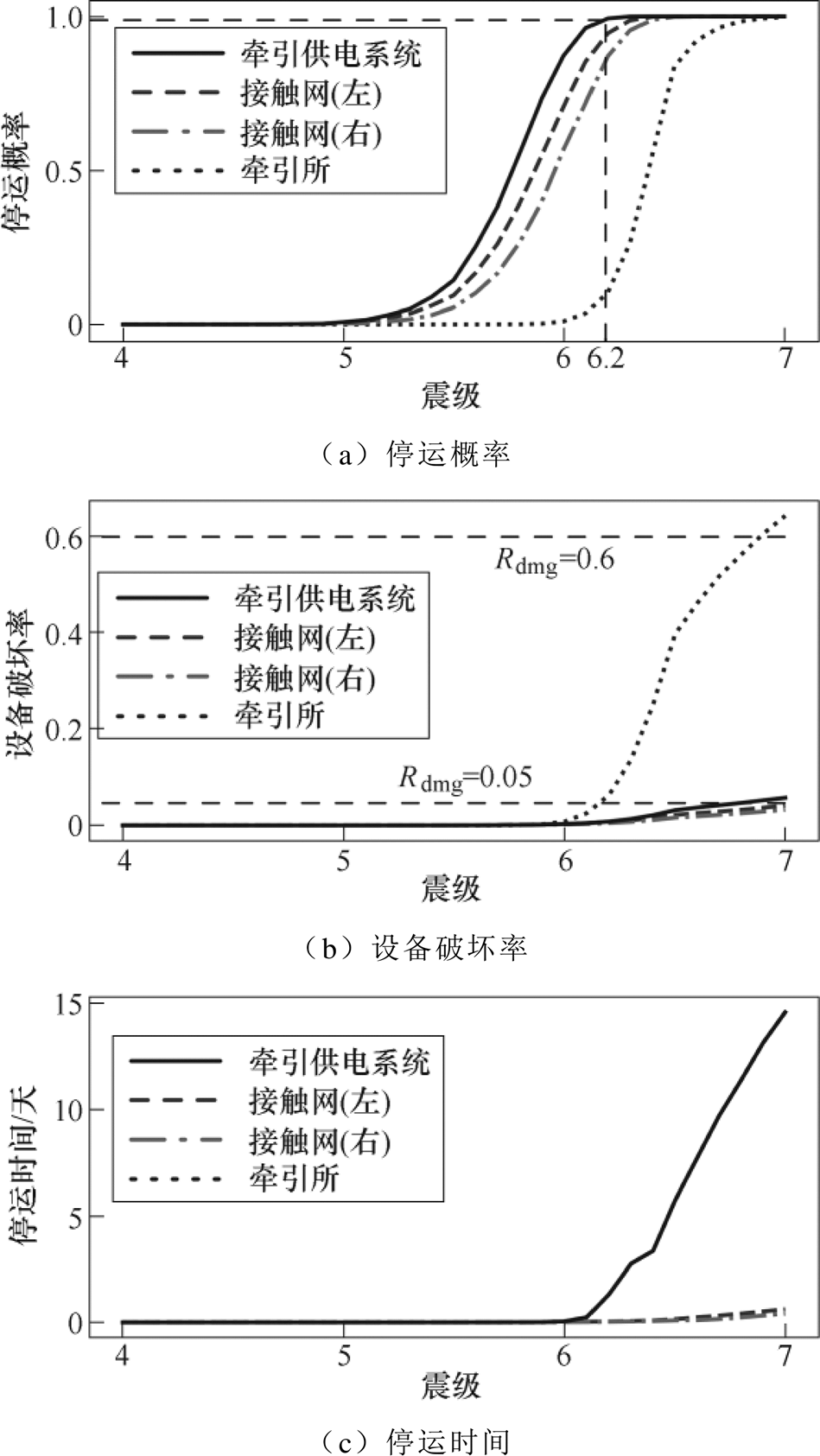
图6 不同震级下牵引供电系统T5风险指标
Fig.6 Risk indices of T5 under different magnitudes
根据图6b、图6c可以看出,6级以下地震仅造成较小比例的设备破坏,且系统可以在很短时间(约2h内)恢复供电。随着震级增加,牵引所和接触网的设备破坏率和停运时间快速增加,当震级达到7级时,牵引所设备破坏率超过0.6,停运时间接近15天。由于定义的接触网设备抗震性能优于牵引所设备,因此接触网设备破坏率远低于牵引所,在7级地震下只有不到0.05的接触网设备破坏,而超过0.6的牵引所关键设备出现损毁。
为进一步分析地震强度随距离的衰减特性及其对牵引供电系统风险指标的影响,考察当地震强度为7级时不同震源距离下牵引供电系统T5的风险指标,结果如图7所示。
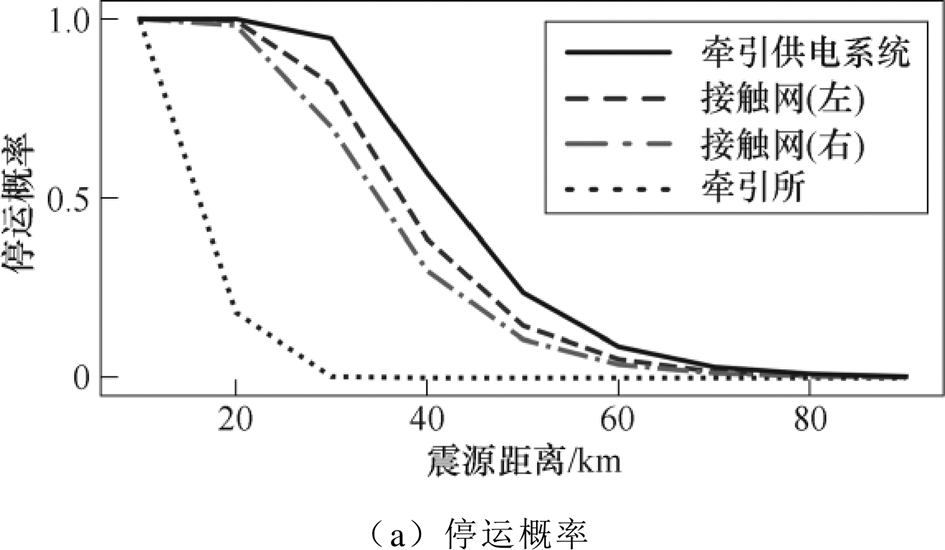
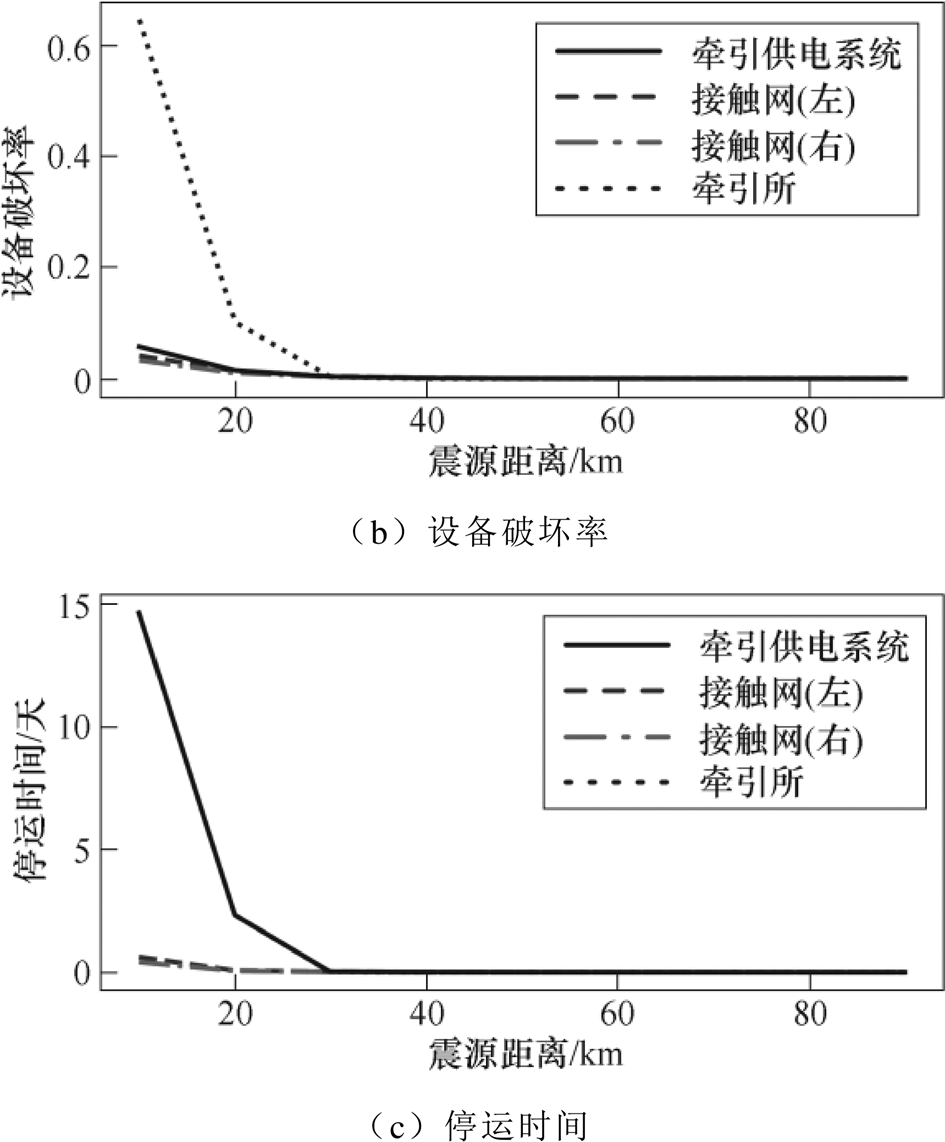
图7 不同震源距离下牵引供电系统T5风险指标
Fig.7 Risk indices of T5 under different distances
从图7a可以看出,牵引供电系统停运概率随着震源距离的增加而减小,当系统震源距离超过80km时,系统停运概率低于0.02。此外,从图7b、图7c可以看出,在设置的地震强度下,当震源距离牵引所超过30km时,虽然仍有较大概率造成系统停运,但随着地震能量和破坏力的衰减,地震对牵引供电系统的影响逐渐减小,供电设备破坏率和系统停运时间都接近0。
为研究电气化铁路沿线牵引供电系统在未来一段时间内可能遭受的地震灾害风险,以图5中穿越整个地震统计区的牵引供电系统T1~T10为例,利用本文提出的方法对其灾害风险进行评估。
首先根据获取的地震活动性参数模拟未来100年的地震目录,其地理位置分布示意图如图8所示。
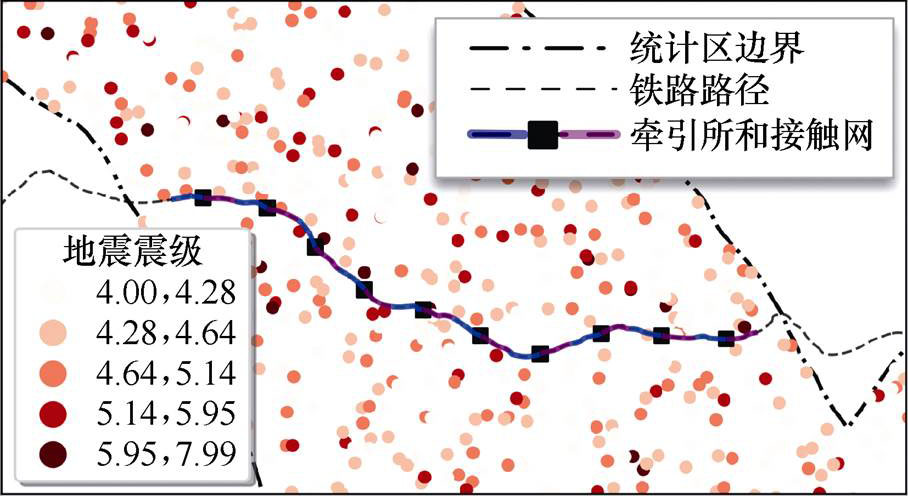
图8 模拟地震位置分布示意图
Fig.8 Spatial distribution of artificial earthquake catalog
利用本文方法评估地震目录中每一个地震事件对牵引供电系统造成的损失,从而得到系统累计故障次数、设备损失以及停电时间,模拟地震目录下牵引供电系统损失情况如图9所示。
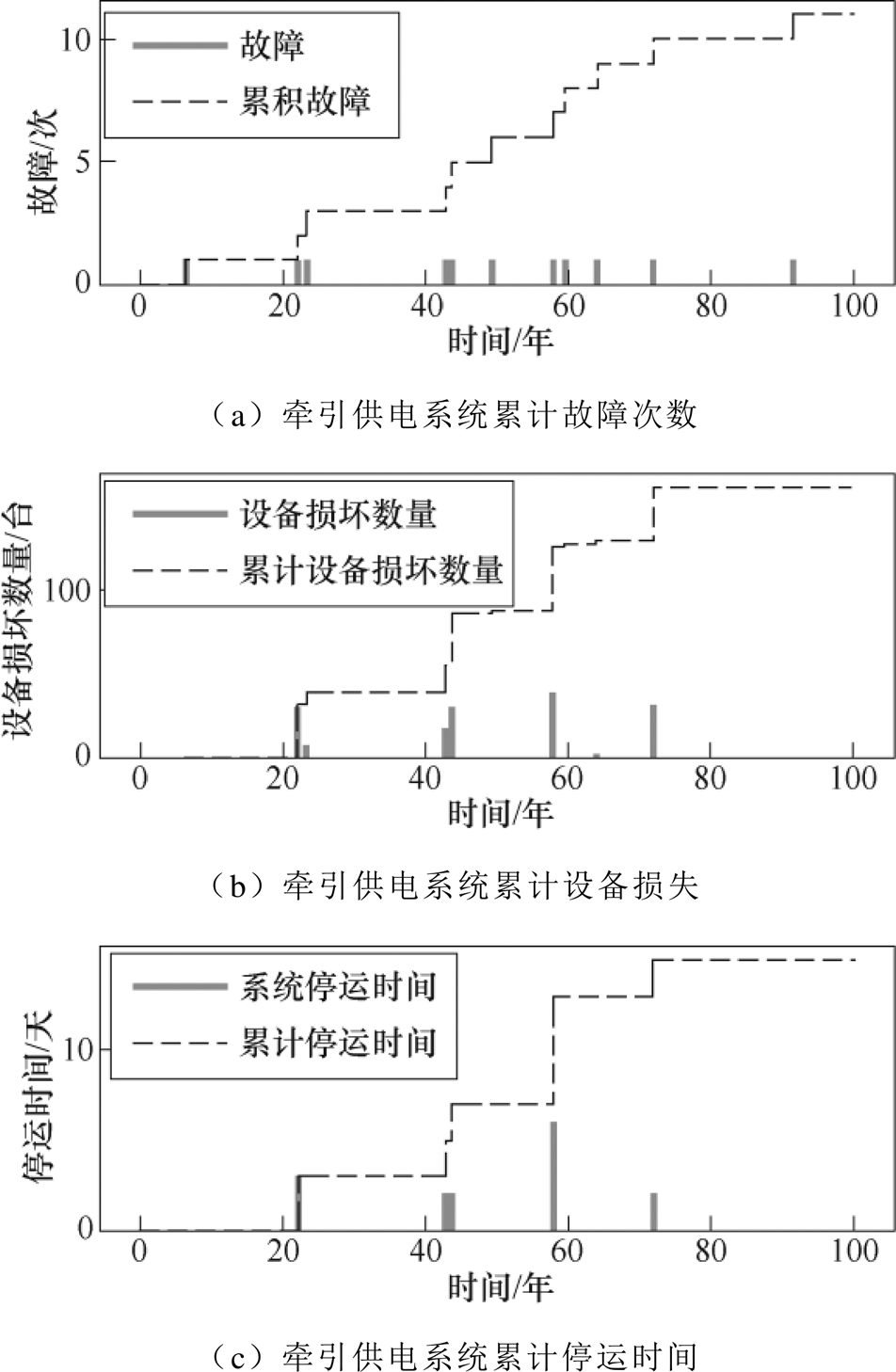
图9 模拟地震目录下牵引供电系统损失情况
Fig.9 Loss of the traction power supply system under the influence of the simulated earthquake catalog
由图9可得出,在该模拟地震目录下,牵引供电系统共发生了11次故障,累计造成牵引供电关键设备损坏161台,累计停电时间15天。
按以上流程随机生成100组地震目录,每组模拟时长均为100年,根据式(18)~式(20)可计算出牵引供电系统年平均风险指标为:平均停运率0.055 1次/年,平均设备损失0.475 9台/年,平均停运时间0.032 3天/年。根据式(21)可求得设备损失超过给定值的事件年发生率和停运时间超过给定值的事件年发生率,见表2。
表2 损失超过给定值的事件年发生率
Tab.2 Annual occurrence rate of the event that the loss exceeds a prescribed value
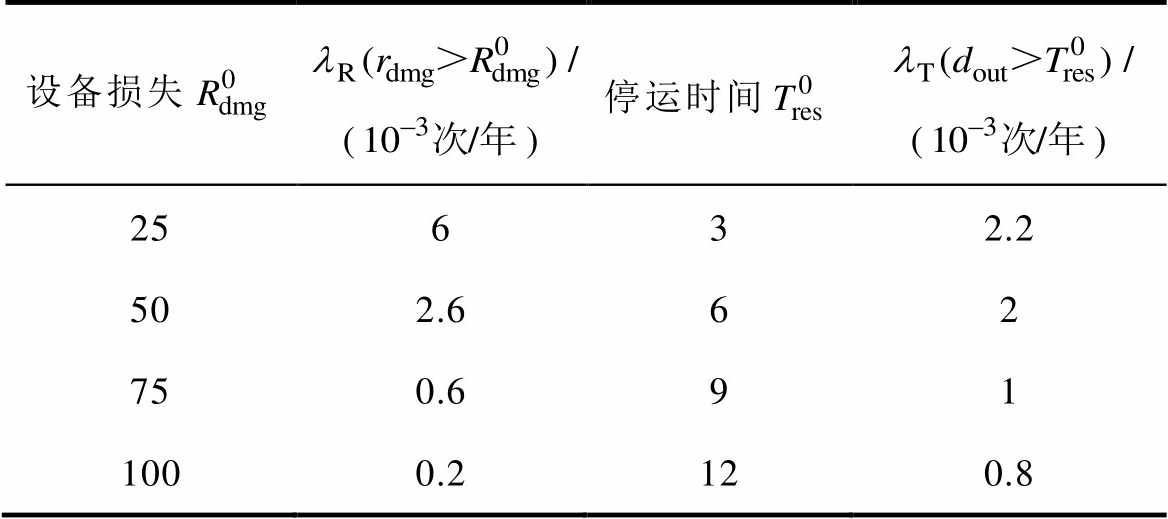
设备损失/()停运时间/() 25632.2 502.662 750.691 1000.2120.8
对比求得的平均风险指标和图9中的系统停运和损失情况可以看出,虽然发生在牵引供电系统附近的地震事件会对系统造成较大风险,但从考虑整个统计区内地震灾害计算得到的平均风险指标来看,系统的平均风险相对较小。这是由于地震事件在时间、空间分布上具有较大的随机性,大部分地震造成的损失较小,而造成极大损失的地震发生概率较小,表2列出了牵引供电系统不同损失程度的事件发生率,表明随着损失程度升高,对应事件的年发生率大幅减小,反映出地震灾害对牵引供电系统的影响具有“低概率-高损失”特点。
本文提出了一种牵引供电系统地震灾害风险评估方法,结合地震灾害模拟和牵引供电系统建模,提出了牵引供电系统损失量化方法,定义了计及系统停运概率、关键设备损失以及停运时间的风险指标,提出了牵引供电系统地震灾害风险评估方法,最后选取西南地区某规划中的电气化铁路牵引供电系统作为算例,评估了系统在地震灾害下的风险水平。本文研究表明:牵引供电系统的停运概率、设备破坏和停运时间风险随着震级降低和震源距离增加大幅降低;对比接触网和牵引所的风险指标,相同地震强度下牵引所的停运概率低于接触网的停运概率,但接触网设备破坏率低于牵引所设备破坏率;此外,地震灾害对牵引供电系统的影响具有“低概率-高损失”特点,大部分地震造成的损失较小,而造成极大损失的地震发生概率较小。利用本文方法,针对已知震源信息的地震事件,可实现牵引供电系统的快速损失评估,为灾后抢险、应急物资调配提供参考。针对位于某一区域的铁路沿线牵引供电系统,本方法可评估出系统在地震灾害下的平均风险水平以及严重损失的发生率,为牵引供电系统抗震规划提供理论依据。
参考文献
[1] 曹永兴, 邓鹤鸣, 蔡炜, 等. 电力设施应对地震及其次生灾害的研究进展[J]. 高电压技术, 2019, 45(6): 1962-1974.
Cao Yongxing, Deng Heming, Cai Wei, et al. Research progress in prevention of earthquake and secondary disasters on power facilities[J]. High Voltage Engineering, 2019, 45(6): 1962-1974.
[2] 盛晓艳, 徐德勤. 核电1E级低压开关柜抗震结构分析及改进方案[J]. 电气技术, 2019, 20(7): 67-69.
Sheng Xiaoyan, Xu Deqin. Seismic structural analysis and improvement of low voltage switchgear of grade 1E in nuclear power plant[J]. Electrical Engineering, 2019, 20(7): 67-69.
[3] 柏文, 唐柏赞, 戴君武, 等. 考虑地震和材料强度不确定性的瓷柱型电气设备易损性分析[J]. 中国电机工程学报, 2021, 41(7): 2594-2605.
Bai Wen, Tang Baizan, Dai Junwu, et al. Fragility analysis of porcelain cylindrical electrical equipment considering material strength and seismic uncertain- ties[J]. Proceedings of the CSEE, 2021, 41(7): 2594- 2605.
[4] 刘如山, 舒荣星, 熊明攀. 变电站高压电气设备易损性研究[J]. 自然灾害学报, 2018, 27(1): 9-16.
Liu Rushan, Shu Rongxing, Xiong Mingpan. Vulnera- bility study for high voltage electrical equipment in substations[J]. Journal of Natural Disasters, 2018, 27(1): 9-16.
[5] 于永清, 李光范, 李鹏, 等. 四川电网汶川地震电力设施受灾调研分析[J]. 电网技术, 2008, 32(11): 5-10.
Yu Yongqing, Li Guangfan, Li Peng, et al. Investi- gation and analysis of electric equipment damage in Sichuan power grid by Wenchuan earthquake[J]. Power System Technology, 2008, 32(11): 5-10.
[6] Eidinger J. Wenchuan earthquake impact to power systems[C]//Technical Council on Lifeline Earthquake Engineering Conference (TCLEE): Lifeline Earthquake Engineering in a Multi-Hazard Environment, Oakland, Canada, 2009: 1-12.
[7] 张中近, 刘如山, 姜立新. 基于损失统计的变电站地失评估方法[J]. 自然灾害学报, 2016, 25(4): 93-100.
Zhang Zhongjin, Liu Rushan, Jiang Lixin. Assessment method of seismic economic loss in substation based on loss statistics[J]. Journal of Natural Disasters, 2016, 25(4): 93-100.
[8] 贺海磊, 郭剑波, 谢强. 电气设备的地震灾害易损性分析[J]. 电网技术, 2011, 35(4): 25-28.
He Hailei, Guo Jianbo, Xie Qiang. Vulnerability analysis of power equipments caused by earthquake disaster[J]. Power System Technology, 2011, 35(4): 25-28.
[9] 梁黄彬, 谢强. 变电站系统的地震易损性分析方法[J]. 中国电机工程学报, 2020, 40(23): 7773-7782.
Liang Huangbin, Xie Qiang. Seismic vulnerability analysis of substation system[J]. Proceedings of the CSEE, 2020, 40(23): 7773-7782.
[10] 谢强, 梁黄彬. 变电站系统的抗震韧性评估框架[J/OL].中国电机工程学报, 2020, DOI: https://doi.org/10. 13334/j.0258-8013.pcsee.201242.
Xie Qiang, Liang Huangbin. Seismic resilience evaluation framework of substation system[J/OL]. Pro- ceedings of the CSEE, 2020, DOI: https://doi.org/10. 13334/j.0258-8013.pcsee.201242.
[11] Johnson Brandon, Vishvas Chalishazar, Eduardo Cotilla-Sanchez, et al. A Monte Carlo methodology for earthquake impact analysis on the electrical grid[J]. Electric Power Systems Research, 2020(184): 106332.
[12] 李雪, 孙霆锴, 侯恺, 等. 地震灾害下海岛综合能源系统韧性评估方法研究[J]. 中国电机工程学报, 2020, 40(17): 5476-5493.
Li Xue, Sun Tingkai, Hou Kai, et al. Evaluating resilience of island integrated energy systems with earthquake[J]. Proceedings of the CSEE, 2020, 40(17): 5476-5493.
[13] Cao Wang, Feng Kairui, Zhang Hao, et al. Seismic performance assessment of electric power systems subjected to spatially correlated earthquake excita- tions[J]. Structure and Infrastructure Engineering, 2019, 15(3): 351-361.
[14] 郑国鑫, 雷霞, 王湘, 等. 地震灾害模拟及配电网的风险评估[J]. 电工技术学报, 2020, 35(24): 5218- 5226.
Zheng Guoxin, Lei Xia, Wang Xiang, et al. Earthquake simulation and risk assessment of distri- bution network[J]. Transactions of China Electro- technical Society, 2020, 35(24): 5218-5226.
[15] 王晗, 侯恺, 余晓丹, 等. 计及地震灾害不确定性的电气互联系统韧性评估与提升方法[J/OL]. 中国电机工程学报, 2021, DOI: https://doi.org/10.13334/j.0258- 8013.pcsee.202243.
Wang Han, Hou Kai, Yu Xiaodan, et al. The assessment and improvement method of electricity- gas system resilience considering earthquake disaster uncertainty[J/OL]. Proceedings of the CSEE, 2021, DOI: https://doi.org/10.13334/j.0258-8013.pcsee.202243.
[16] 张沛, 田佳鑫, 谢桦. 计及多个风场预测误差的电力系统风险快速计算方法[J]. 电工技术学报, 2021, 36(9): 1876-1887.
Zhang Pei, Tian Jiaxin, Xie Hua. A fast risk assessment method with consideration of forecasting errors of multiple wind farms[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1876- 1887.
[17] 刘小龙, 李欣然, 刘志谱, 等. 基于风险量化与需求侧响应的综合能源系统储能事故备用优化利用[J]. 电工技术学报, 2021, 36(9): 1901-1913.
Liu Xiaolong, Li Xinran, Liu Zhipu, et al. Study on the optimal utilization of integrated energy system emergency reserve based on risk quantification and demand side response[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1901-1913.
[18] Li Wenyuan. Reliability assessment of electric power systems using Monte Carlo methods[M]. New York: Springer Science & Business Media, 2013.
[19] 谢桦, 任超宇, 郭志星, 等. 基于聚类抽样的随机潮流计算[J]. 电工技术学报, 2020, 35(23): 4940- 4948.
Xie Hua, Ren Chaoyu, Guo Zhixing, et al. Stochastic load flow calculation method based on clustering and sampling[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4940-4948.
[20] 邵霄怡, 王晓青, 窦爱霞, 等. 基于蒙特卡洛方法的地震目录模拟及相符性检验——以汾渭地震带为例[J]. 中国地震, 2018, 34(1): 35-47.
Shao Xiaoyi, Wang Xiaoqing, Dou Aixia, et al. Seismic inventory simulation and conformance test based on the Monte Carlo method—a case study of the Fenwei belt[J]. Earthquake Research in China, 2018, 34(1): 35-47.
[21] 潘华, 高孟潭, 谢富仁. 新版地震区划图地震活动性模型与参数确定[J]. 震灾防御技术, 2013, 8(1): 11-23.
Pan Hua, Gao Mengtan, Xie Furen. The earthquake activity model and seismicity parameters in the new seismic hazard map of China[J]. Technology for Earthquake Disaster Prevention, 2013, 8(1): 11-23.
[22] 俞言祥. 新一代地震区划图地震动参数衰减关系的建立与特点分析[J]. 城市与减灾, 2016(3): 34-38.
Yu Yanxiang. The establishment and characteristic analysis of the attenuation relationship of ground motion parameters for the new generation of seismic zoning maps[J]. City and Disaster Reduction, 2016(3): 34-38.
[23] Porter Keith, Robert Kennedy, Robert Bachman. Creating fragility functions for performance-based earthquake engineering[J]. Earthquake Spectra, 2007, 23(2): 471-489.
[24] 李群湛, 王辉, 黄文勋, 等. 电气化铁路牵引变电所群贯通供电系统及其关键技术[J]. 电工技术学报, 2021, 36(5): 1064-1074.
Li Qunzhan, Wang Hui, Huang Wenxun, et al. Inter- connected power supply system of traction substation group and its key technologies for the electrified railway[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1064-1074.
[25] 张俊, 谢强. 高速铁路接触网系统地震响应分析[J].铁道标准设计, 2017, 61(4): 140-146.
Zhang Jun, Xie Qiang. Analysis of seismic response of high-speed railway catenary system[J]. Railway Standard Design, 2017, 61(4): 140-146.
[26] 刘如山, 舒荣星, 胡珍秀. 变电站地震可恢复性研究[J]. 地震工程学报, 2019, 41(4): 827-833.
Liu Rushan, Shu Rongxing, Hu Zhenxiu. Study on the seismic resilience of substations[J]. China Earthguake Engineering Journal, 2019, 41(4): 827-833.
A Method of Seismic Disaster Risk Assessment for the Traction Power Supply System
Abstract The safe and reliable operation of the traction power supply system of electrified railways is of great importance. However, the system is threatened by earthquake disasters in some regions. To effectively evaluate the risk level of the traction power supply system under earthquake disasters, this paper first uses Monte Carlo method to simulate earthquake disasters to obtain the peak ground acceleration that characterizes the ground motion intensity, and then establishes a directed graph logic model of the system by analyzing the main wiring of the system. On this basis, the risk indicators are defined by considering factors such as the system outage probability, the key equipment loss, and the outage time, and a method of earthquake disaster risk assessment for the traction power supply system is proposed. Finally, the traction power supply system of an electrified railway under construction in southwest China is taken as an example to evaluate the risk level of the system under earthquake disasters. The results show that the method proposed in this paper can effectively quantify the risk level of the traction power supply system under earthquake disasters. It can achieve rapid loss assessment after the earthquake, guide post-disaster rescue and emergency resource deployment, and provide a theoretical basis for the seismic design of the traction power supply system.
keywords:Traction power supply system, earthquake, risk assessment, Monte Carlo simulation
DOI: 10.19595/j.cnki.1000-6753.tces.210878
中图分类号:U223.8
国家自然科学基金(51907166)和中国博士后科学基金(2020M680152)资助项目。
收稿日期 2021-06-17
改稿日期 2021-08-16
孙小军 男,1991年生,博士研究生,研究方向为牵引供电系统灾害风险评估。E-mail: sunxiaojun3312@163.com
林 圣 男,1983年生,教授,博士生导师,研究方向为轨道交通供电系统健康诊断。E-mail: slin@swjtu.edu.cn(通信作者)
(编辑 陈 诚)